Зависимость сопротивления от температуры | Электрикам
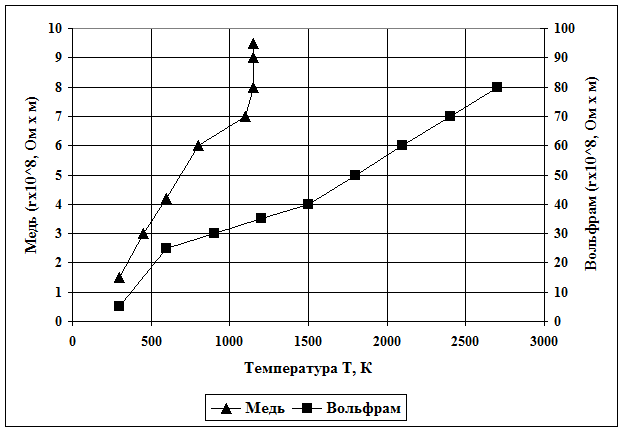
Электрическое сопротивление металлов находится в прямой зависимости от температуры. Чем выше температура металлического провода, тем выше скорость теплового движения частиц. Следовательно растёт количество столкновений свободных электронов, и снижение их свободного пробега τ. Снижение свободного пробега уменьшает удельную проводимость и, одновременно, увеличивает удельное электрическое сопротивление материала.
Удельное сопротивление электролитов и угля при нагревании наоборот уменьшается, поскольку кроме уменьшения времени τ повышается концентрация носителей зарядов.
Температурный коэффициент сопротивления
В узких границах изменения температуры 0-100°С относительное приращение сопротивления Δr большинство металлических проводов пропорционально приращению температуры Δt = t1 — t2.
Обозначения через r1 и r2 сопротивления при температурах t1 и t2 можно выразить формулой
откуда
где α — Температурный коэффициент сопротивления, численно равен относительному приращению сопротивления при нагревании проводника на 1°С.
Температурный коэффициент сопротивления для чистых металлов приблизительно равен α = 0,004°С-1, это значит, что их сопротивление увеличится на 4%, при росте температуры на 10°С.
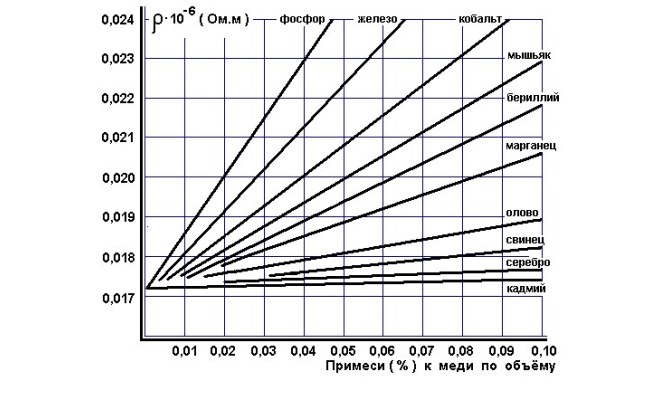
Некоторых сплавы, например, как манганин и константан обладают повышенным удельным сопротивлением и крайне низким температурным коэффициентом сопротивления. Так как обладают неправильной структурой и небольшим временем «свободного» пробега электронов. Данные сплавы нашли широкое применение при изготовлении образцовых катушек сопротивления и резисторов с постоянным (независимым от температуры) сопротивлением.
Материал такие как уголь и электролиты обладают отрицательным коэффициентом сопротивления α ≈ -0,02 на 1°С.
Явление сверхпроводимости
В ряде материалов и сплавов при снижении температуры до очень низких значений порядка единиц или десятка градусов Кельвина (0 К ≈ -273°С) возникает явление сверхпроводимости. Температура при которой наступает это явление, называется критической (Ткр) или «точкой скачка».
Проводник в котором возникает явление сверхпроводимости называют сверхпроводником. В таком проводнике может протекать электрический ток, даже если к его концам не будет приложено напряжения иначе говоря сопротивление проводника будет стремится к нулю. В таких проводниках не выделяется тепло даже при значительной плотности тока, т.е. электроны в нём не встречают препятствий и не сталкиваются при свободном движении.
Также, сверхпроводники не имеют магнитного поля. Даже если ранее оно присутствовало, то при критических температурах поле пропадет, поскольку в поверхностном слое 10-5 см образуются токи, магнитное поле которых компенсирует внешнее магнитное поле.
Состояние сверхпроводимости разрушает как сильное внешнее магнитное поле, так и поле, вызванное большим электрическим током, проходящим через сверхпроводник. Данное обстоятельство затрудняет получение в сверхпроводнике больших токов и больших плотностей тока.
#1. Как изменится удельная проводимость и сопротивление медного провода при увеличении температуры на 20 градусов.

Удельная проводимость и сопротивление увеличатся.
Удельная проводимость уменьшится, сопротивление увеличится.
Удельная проводимость вырастит, сопротивление уменьшится.
#2. Насколько изменится удельное сопротивление меди при нагревании провода до t1 = 50°C? Если начальная температура t=0°C, а сопротивление R1 = 10 Ом. Температурный коэффициент α = 0,004.
+20 Ом
+ 2 Ом
+10 Ом
t2 — t1 = 50 — 0 = 50°C
ΔR = 50°C*α*R1 = 50*0,004*10 = 2 Ом
#3. Как изменится время свободного пробега τ при нагревании угля.
Уменьшится
Увеличится
Не изменится
Завершить
Отлично!
Попытайтесь снова(
08. 09.2020
09.2020
ТОЭ
лабораторная работа 32
|
Лабораторная работа № 32
ИЗУЧЕНИЕ
ЗАВИСИМОСТИ СОПРОТИВЛЕНИЯ МЕТАЛЛОВ
Цель работы — определение температурного коэффициента сопротивления меди. Приборы и принадлежности: исследуемый медный проводник, измерительный мост или омметр, термометр.
Величина электрического
сопротивления R конкретного металлического
проводника зависит как от геометрической формы (т. R = , (1)
где r Обратная величина , т.е. , называется удельной проводимостью. Единица измерения — (См – сименс).
Величины и зависят от химических примесей, дефектов кристаллической решетки, магнитного состояния вещества, температуры, давления и других факторов. При постоянном давлении для неферромагнитных несверхпроводящих
и изотропных проводников вблизи комнатной температуры и выше (до температуры
плавления) удельное сопротивление пропорционально
Т. При низких температурах вблизи абсолютного нуля наблюдается нелинейная
зависимость (~ Т) удельного сопротивления (кривая 1 на
рис. |
||||
Рис. 1 |
||||
|
Далее рассматриваем неферромагнитные и изотропные металлические проводники. Температурную зависимость удельного сопротивления 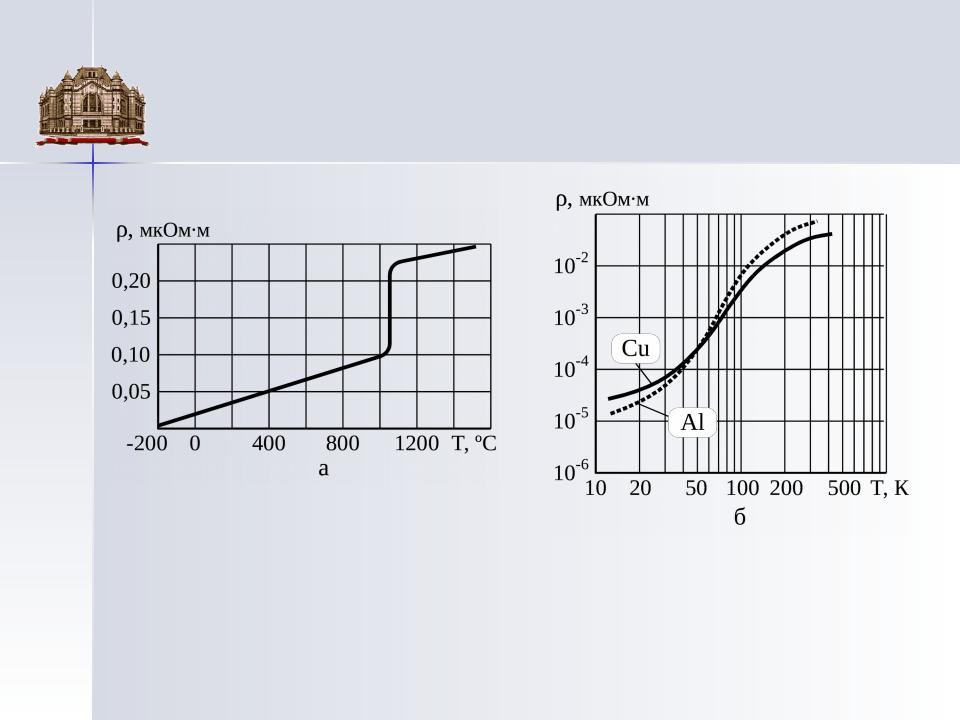 д.) кристаллической решетки, т.е.
рассеянием электронов на дефектах. В отсутствие внешнего электрического поля
(Е=0) из-за беспорядочного движения, электроны испытывают столкновение
(рассеяние) с колеблющимися в узлах
решетки, ионами, примесями и
другими. В результате чего изменяются
их направление и величина скорости движения. Поэтому, в среднем число
электронов, движущихся в одном направлении равно числу электронов, движущихся
в противоположном направлении. Соответственно,
отсутствует преимущественное направление движения электронов, скорость упорядоченного
движения равна нулю, ток – отсутствует. В грубом приближение, траекторию движения электронов проводимости
при Е=0, можно представить в следующем виде: д.) кристаллической решетки, т.е.
рассеянием электронов на дефектах. В отсутствие внешнего электрического поля
(Е=0) из-за беспорядочного движения, электроны испытывают столкновение
(рассеяние) с колеблющимися в узлах
решетки, ионами, примесями и
другими. В результате чего изменяются
их направление и величина скорости движения. Поэтому, в среднем число
электронов, движущихся в одном направлении равно числу электронов, движущихся
в противоположном направлении. Соответственно,
отсутствует преимущественное направление движения электронов, скорость упорядоченного
движения равна нулю, ток – отсутствует. В грубом приближение, траекторию движения электронов проводимости
при Е=0, можно представить в следующем виде: |
||||
|
Рис. 2 |
||||
|
где <υ> — средняя скорость
теплового движения электрона. Это мгновенная фотография беспорядочного движения электрона. Стрелками обозначены положения вектора скорости теплового движения. Под действием внешнего электрического поля электроны-проводимости будут совершать упорядоченное движение (см. рис. 3), т.к. на них будет действовать электрическая сила |
||||
|
|
||||
Рис. |
||||
|
Рассмотрим классическую теорию. Под действием внешнего электрического поля электроны будут совершать упорядоченное движение (см. рис. 3), т.к. на них действует электрическая сила Fе = еЕ , кроме того, на электрон со стороны поля кристаллической решетки действует сила сопротивления Fс = -. Поэтому общая сила, действующая на электрон, равна F = еЕ –. (2) По второму закону Ньютона mа = еЕ –. (3)
Дрейфовая скорость будет увеличиваться до тех пор, пока Fе = Fс, а = 0, т.е. еЕ = , отсюда u =. (4).
Величина, равная b = , называется подвижностью электрона.
Смысл коэффициента следующий. Пусть Е = 0, тогда (3) запишется в виде mа = –.Так как ускорение электрона определяется по формуле:
, то
, или . (5)
Из (5) следует, что u=. Если , то t = τ и это время, за ко- торое электрон уменьшает дрейфовую скорость в раз. За это время он пробегает расстояние, которое называется транспортным: L = , (6) где γ – число столкновений
(рассеяния) электронов с дефектами; – средняя длина свободного пробега электрона между
двумя последовательными столкновениями. За
время τ электрон испытывает γ число столкновений с дефектами
кристаллической решетки и пробегает транспортное расстояние L. С другой стороны, транспортное расстояние равно L=, так как электрон движется со средней скоростью. С учетом (6) получим или . (7)
Подставляя (7) в (4), найдем u = . (8)
Плотность тока равна j = nеu, (9)
где n – концентрация электронов. Подставляя (8) в (9), получим j =. (10)
Закон Ома в дифференциальной форме j =. (11)
Тогда с учетом (10) и (11) имеем и .
Полученная, с точки зрения квантовой теории, формула удельного сопротивления ρ имеет такой же вид, что и формулы (12). Но вместо m, , , рассмотренные в классической теории, в квантовой теории вводятся: эффективная масса , фермиевская скорость и длина свободного пробега . Учитывая эти изменения, формула (12) приобретет следующий вид (13): . (13)
Квантово-механические расчеты показывают, что при низких температурах число столкновений , а . Тогда удельное сопротивление ρ пропорционально и сопротивление металлов обусловлено рассеянием электронов проводимости на дефектах и ионах кристаллической решетки. При высоких температурах сопротивление в основном обусловлено рассеянием
электронов на тепловых ионах кристаллической решетки (фононах), а
сопротивление, обусловленное рассеянием электронов на дефектах, пренебрежимо
мало. Расчет показывает, что при высоких температурах удельное сопротивление зависит от температуры: , (14) где α – температурный коэффициент сопротивления; – удельное сопротивление при температуре 0 °С; t – температура по шкале Цельсия. Температурный коэффициент α равен относительному изменению удельного сопротивления при изменении температуры проводника на 1 градус: , .
Для металлических изотропных проводников коэффициент почти не зависит от температуры и примерно равен . Так как сопротивление металлических проводников зависит от [см. формулу (1)], т.е. R~, то с учетом (14) сопротивление можно представить в виде R = R0(1+).
Откуда можно найти : , (16)
где R0 – сопротивление проводника при t = 0°С.
Для металлических проводников , т.е. с увеличением температуры сопротивление увеличивается. Поэтому эти проводники называются проводниками I рода. Для электролитов, графита и других , т.е. с увеличением температуры сопротивление проводника уменьшается. Они называются проводниками II рода.
Ход работы
Схема установки приведена на
рис. 4. Исследуемый проводник помещается в колбу, заполненную непроводящей
жидкостью (масло, глицерин, дистиллированная вода). Температура измеряется
термометром. Для равномерного нагревания жидкость перемешивается мешалкой. Исследуемый проводник R подключается в качестве неизвестного сопротивления к клеммам измерительного моста. Измеряют сопротивление исследуемого проводника при комнатной температуре. Включают нагреватель и непрерывно перемешивают жидкость мешалкой. |
||||
|
Рис. 4 |
||||
|
При нагревании через каждые 5-10 °С измеряют сопротивление проводника. Измерения проводят до температуры 80-90 °С. Полученные результаты заносят в таблицу. |
||||
|
Таблица |
||||
|
||||
|
Строят зависимость R= ƒ(t),
откладывая по оси абсцисс значения температуры, а по оси ординат значения R. .
Точка а – точка, выбранная вами на полученной прямой между двумя последними экспериментальными точками. |
||||
|
Рис. 5 |
||||
|
Вопросы для допуска к работе
1. Какова цель работы? 2. Почему сопротивление металлов увеличивается с возрастанием температуры? 3. Что
называется температурным коэффициентом сопротивления? Выведите размерность
температурного коэффициента сопротивления.
Вопросы для защиты работы
1. Объясните механизм проводимости в металлах. 2. В чем существенные отличия объяснения электрического сопротивления в классической теории металлов от квантовой? 3. Вывести формулу температурной зависимости удельного сопротивления. 4. Какие проводники называются проводниками I и II рода? |
Температурный коэффициент сопротивления
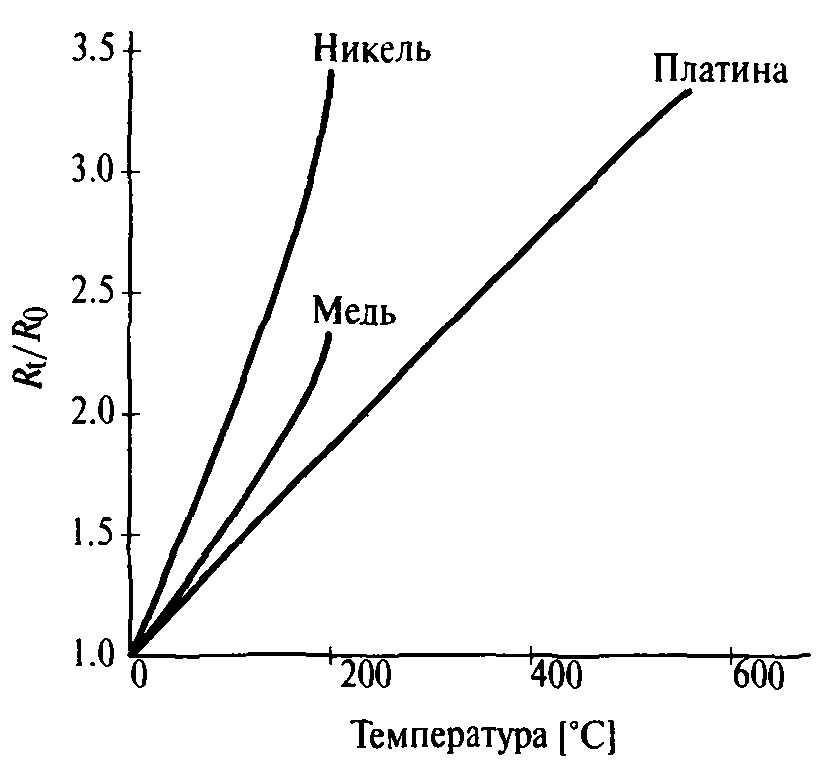
Температурный коэффициент сопротивления Поскольку электрическое сопротивление проводника, такого как медный провод, зависит от процессов столкновений внутри провода, можно было бы ожидать, что сопротивление будет увеличиваться с температурой, поскольку будет больше столкновений, и это подтверждается экспериментом. Или, выраженное через сопротивление при некоторой стандартной температуре из справочной таблицы:
| Индекс Цепи постоянного тока | |||
| Вернуться |
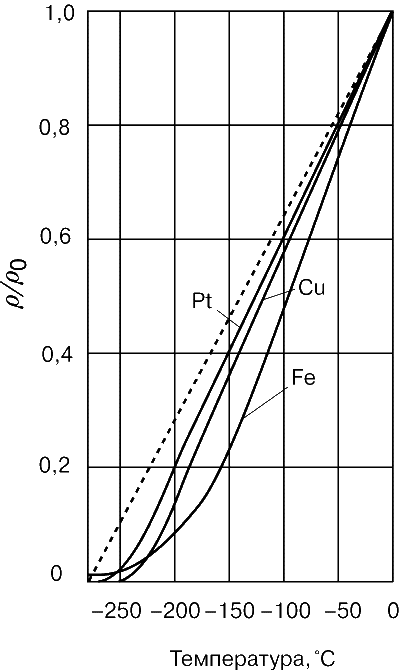
Температурная зависимость удельного сопротивления при температурах, близких к комнатной, характеризуется линейным ростом с температурой. Микроскопическое исследование проводимости показывает, что она пропорциональна длине свободного пробега между столкновениями (d), а при температурах выше примерно 15 К d ограничивается тепловыми колебаниями атомов. При экстремально низких температурах длина свободного пробега определяется преимущественно примесями или дефектами в материале и становится почти постоянной с температурой. При достаточной чистоте некоторые металлы обнаруживают переход в сверхпроводящее состояние. | Index Reference | ||
| Вернуться |
 При изменении значения будут , а не , должны быть согласованы до тех пор, пока вы не нажмете на количество, которое хотите рассчитать. При изменении значения будут , а не , должны быть согласованы до тех пор, пока вы не нажмете на количество, которое хотите рассчитать.
| Индекс Цепи постоянного тока | ||||||||||||||||
| Вернуться назад | ||||||||||||||||
Температурная зависимость удельного сопротивления полупроводников | Блог системного анализа
Ключевые выводы
При повышении температуры удельное сопротивление металла увеличивается, придавая ему положительный температурный коэффициент сопротивления.

Полупроводники имеют отрицательный температурный коэффициент сопротивления.
Удельное сопротивление внешних полупроводников больше, чем собственных полупроводников.
Температурная зависимость удельного сопротивления полупроводников играет важную роль в их применении в электронике
Электропроводность описывает легкость прохождения электрического тока через материал и является важным параметром материала . Проводники – это материалы, пропускающие через себя ток. Те, которые блокируют ток, называются изоляторами. Есть материалы, которые попадают между проводниками и изоляторами, когда ток, протекающий по ним, принимается за относительный параметр. Такие материалы известны как полупроводники.
Во всех этих материалах протекание тока может быть напрямую связано с проводимостью материала, которая является обратной величиной удельного сопротивления. Удельное сопротивление является свойством материала и зависит от температуры. Температурная зависимость удельного сопротивления полупроводников играет существенную роль в их применении в электронике. В этой статье мы рассмотрим, почему это так.
Удельное сопротивление является свойством материала и зависит от температуры. Температурная зависимость удельного сопротивления полупроводников играет существенную роль в их применении в электронике. В этой статье мы рассмотрим, почему это так.
Что такое удельное сопротивление?
Удельное сопротивление является неотъемлемым свойством материала. Это константа для материала при данной температуре. Удельное сопротивление материала можно определить как сопротивление материала единицы площади поперечного сечения и единицы длины. Удельное сопротивление материала не зависит от его длины и площади.
Соотношение между сопротивлением материала и удельным сопротивлением: материал. Единицей удельного сопротивления является ом-метр.
Электропроводность обратно пропорциональна удельному сопротивлению. Когда удельное сопротивление материала высокое, его проводимость очень низкая, и наоборот. Учитывая это соотношение, можно сказать, что удельное сопротивление металлов или проводников очень низкое.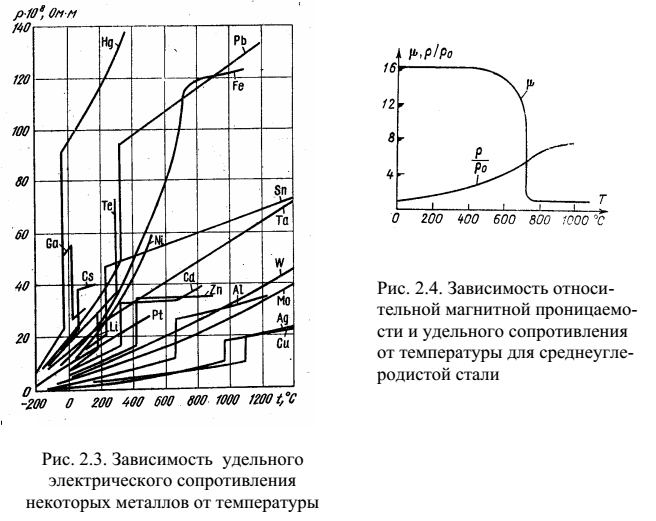 Располагая материалы в порядке возрастания удельного сопротивления, порядок: проводники, полупроводники и изоляторы.
Располагая материалы в порядке возрастания удельного сопротивления, порядок: проводники, полупроводники и изоляторы.
Далее мы рассмотрим, как температура влияет на удельное сопротивление.
Зависимость удельного сопротивления от температуры
Удельное сопротивление материала зависит от температуры. Температурная зависимость удельного сопротивления различна для проводников, полупроводников и диэлектриков. Давайте обсудим, как изменяется удельное сопротивление в проводниках и изоляторах, прежде чем обсуждать полупроводники.
Проводники
В проводниках при повышении температуры атомы начинают сильно вибрировать, что приводит к столкновению свободных электронов и других электронов. Это столкновение вызывает потерю энергии свободными электронами, которые ответственны за ток. Уменьшение движения или скорости дрейфа электронов из-за утечки энергии увеличивает удельное сопротивление проводников, особенно металлов. С повышением температуры удельное сопротивление металла также увеличивается, что придает ему положительный температурный коэффициент сопротивления. При высоких температурах удельное сопротивление проводника увеличивается, а проводимость уменьшается.
С повышением температуры удельное сопротивление металла также увеличивается, что придает ему положительный температурный коэффициент сопротивления. При высоких температурах удельное сопротивление проводника увеличивается, а проводимость уменьшается.
Изоляторы
Изоляторы смещаются в зону проводимости при повышении температуры. Удельное сопротивление изолятора уменьшается с температурой, что приводит к увеличению проводимости. Изоляторы имеют отрицательный температурный коэффициент сопротивления.
Далее мы исследуем температурную зависимость удельного сопротивления полупроводников.
Температурная зависимость удельного сопротивления полупроводников
В полупроводниках энергетическая щель между зоной проводимости и валентной зоной уменьшается с повышением температуры. Валентные электроны в полупроводниковом материале получают энергию, чтобы разорвать ковалентную связь и перейти в зону проводимости при высоких температурах. Это создает больше носителей заряда в полупроводнике при высоких температурах. Более высокая концентрация носителей заряда снижает удельное сопротивление полупроводника. Поскольку удельное сопротивление полупроводника уменьшается с повышением температуры, он становится более проводящим. Полупроводник обладает отличной проводимостью при высоких температурах.
Это создает больше носителей заряда в полупроводнике при высоких температурах. Более высокая концентрация носителей заряда снижает удельное сопротивление полупроводника. Поскольку удельное сопротивление полупроводника уменьшается с повышением температуры, он становится более проводящим. Полупроводник обладает отличной проводимостью при высоких температурах.
На приведенном ниже графике показана зависимость между удельным сопротивлением и температурой в полупроводнике. Полупроводники имеют отрицательный температурный коэффициент сопротивления. Это свойство используется для применения полупроводников в электронике. При приложении внешнего напряжения температура полупроводникового кристалла увеличивается, что, в свою очередь, увеличивает плотность в нем термически генерируемых носителей. Генерируется больше электронно-дырочных пар, что позволяет легко протекать току через полупроводник.
Удельное сопротивление в зависимости от температуры в полупроводниках
Характеристики полупроводника улучшаются путем легирования его донорными или акцепторными примесями.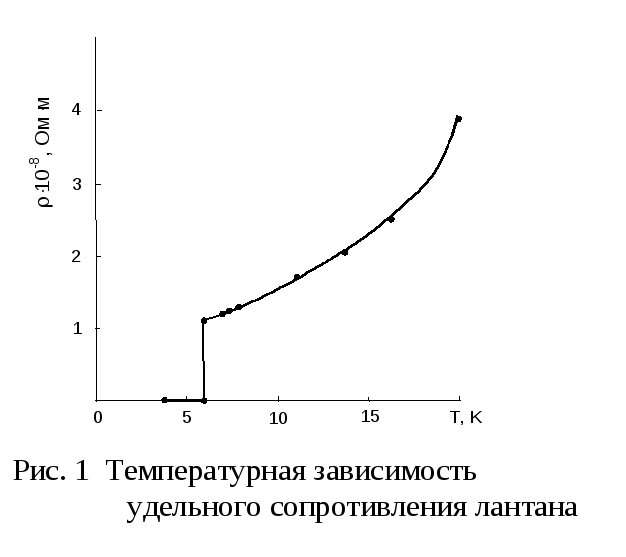


 е. размеров), так и от
физических свойств материалов. Для однородного изотропного проводника
правильной геометрической формы длиной l и площадью сечения S величина сопротивления R равна
е. размеров), так и от
физических свойств материалов. Для однородного изотропного проводника
правильной геометрической формы длиной l и площадью сечения S величина сопротивления R равна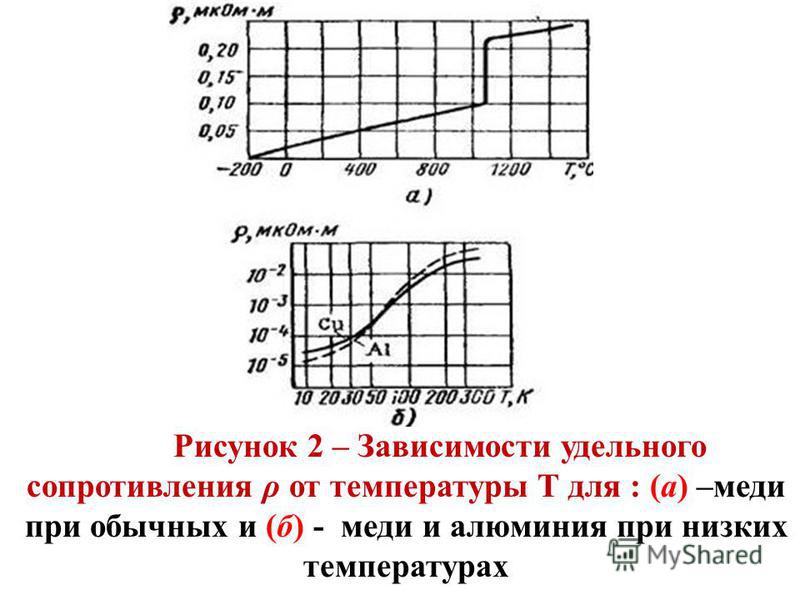
 3
3
 (12)
(12) Поэтому при высоких температурах не зависит от
Т, а . Тогда .
Поэтому при высоких температурах не зависит от
Т, а . Тогда . (15)
(15)
 Значения R0 и определяют следующим
образом: продолжают полученную прямую до пересечения с осью R (рис. 5). Точка пересечения дает значение R0. Значение вычисляют по
формуле
Значения R0 и определяют следующим
образом: продолжают полученную прямую до пересечения с осью R (рис. 5). Точка пересечения дает значение R0. Значение вычисляют по
формуле
 Интуитивный подход к температурной зависимости приводит к тому, что можно ожидать относительного изменения сопротивления, пропорционального изменению температуры:
Интуитивный подход к температурной зависимости приводит к тому, что можно ожидать относительного изменения сопротивления, пропорционального изменению температуры: Общая зависимость сводится к пропорциям:
Общая зависимость сводится к пропорциям: