Изменение ёмкости керамических конденсаторов от температуры и напряжения, или как ваш конденсатор на 4,7мкФ превращается в 0,33мкФ / Хабр
Вступление: я был озадачен.
Несколько лет назад, после более чем 25 лет работы с этими вещами, я узнал кое-что новое о керамических конденсаторах. Работая над драйвером светодиодной лампы я обнаружил, что постоянная времени RC-цепочки в моей схеме не сильно смахивает на расчётную.
Предположив, что на плату были впаяны не те компоненты, я измерил сопротивление двух резисторов составлявших делитель напряжения — они были весьма точны. Тогда был выпаян конденсатор — он так же был великолепен. Просто чтобы убедиться, я взял новые резисторы и конденсатор, измерил их, и впаял обратно. После этого я включил схему, проверил основные показатели, и ожидал увидеть что моя проблема с RC-цепочкой решена… Если бы.
Я проверял схему в её естественной среде: в корпусе, который в свою очередь сам по себе был зачехлён чтобы имитировать кожух потолочного светильника. Температура компонентов в некоторых местах достигала более чем 100ºC. Для уверенности, и чтобы освежить память я перечитал даташит на используемые конденсаторы. Так началось моё переосмысление керамических конденсаторов.
Температура компонентов в некоторых местах достигала более чем 100ºC. Для уверенности, и чтобы освежить память я перечитал даташит на используемые конденсаторы. Так началось моё переосмысление керамических конденсаторов.
Справочная информация об основных типах керамических конденсаторов.
Для тех кто этого не помнит (как практически все), в таблице 1 указана маркировка основных типов конденсаторов и её значение. Эта таблица описывает конденсаторы второго и третьего класса. Не вдаваясь глубоко в подробности, конденсаторы первого класса обычно сделаны на диэлектрике типа C0G (NP0).
Таблица 1.
| Нижняя рабочая температура | Верхняя рабочая температура | Изменение ёмкости в диапазоне (макс.) | |||
|---|---|---|---|---|---|
| Символ | Температура (ºC) | Символ | Температура (ºC) | Символ | Изменение (%) |
| Z | +10 | 2 | +45 | A | ±1.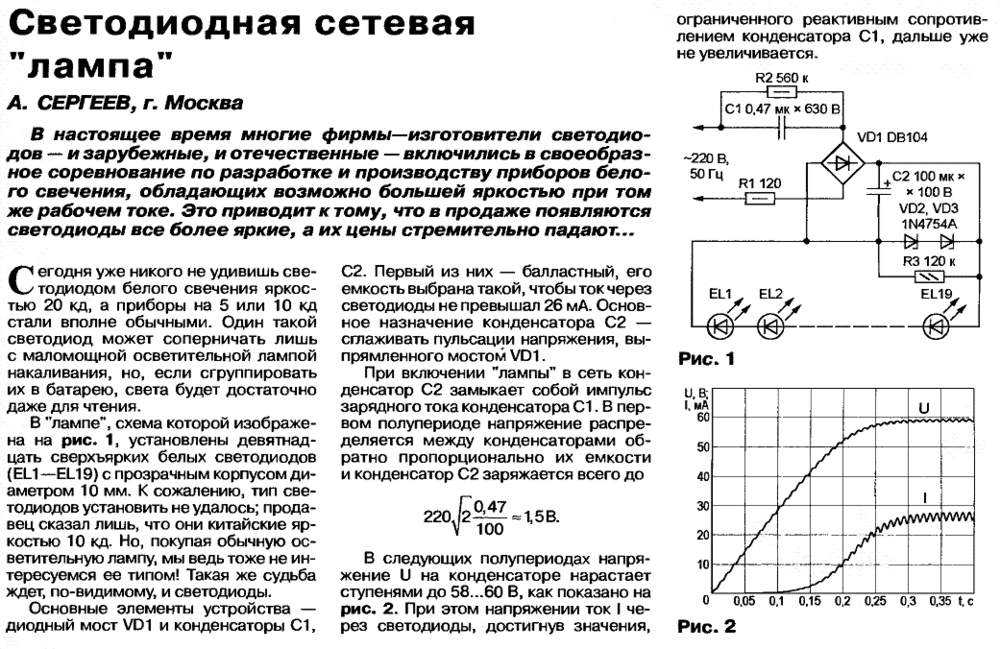 0 0 |
| Y | -30 | 4 | +65 | B | ±1.5 |
| X | -55 | 5 | +85 | C | ±2.2 |
| – | – | 6 | +105 | D | |
| – | – | 7 | +125 | E | ±4.7 |
| – | – | 8 | +150 | F | ±7.5 |
| – | – | 9 | +200 | P | ±10 |
| – | – | – | – | R | ±15 |
| – | – | – | – | S | ±22 |
| – | – | – | – | T | +22, -33 |
| – | – | – | – | U | +22, -56 |
| – | – | – | – | V | +22, -82 |
Из описанных выше на моём жизненном пути чаще всего мне попадались конденсаторы типа X5R, X7R и Y5V. Я никогда не использовал конденсаторы типа Y5V из-за их экстремально высокой чувствительности к внешним воздействиям.
Я никогда не использовал конденсаторы типа Y5V из-за их экстремально высокой чувствительности к внешним воздействиям.
Когда производитель конденсаторов разрабатывает новый продукт, он подбирает диэлектрик так, чтобы ёмкость конденсатора изменялась не более определённых пределов в определённом температурном диапазоне. Конденсаторы X7R которые я использую не должны изменять свою ёмкость более чем на ±15% (третий символ) при изменении температуры от -55ºC (первый символ) до +125ºC (второй символ). Так что, либо мне попалась плохая партия, либо что-то ещё происходит в моей схеме.
Не все X7R созданы одинаковыми.
Так как изменение постоянной времени моей RC-цепочки было куда больше, чем это могло быть объяснено температурным коэффициентом ёмкости, мне пришлось копать глубже. Глядя на то, насколько уплыла ёмкость моего конденсатора от приложенного к нему напряжения я был очень удивлён. Результат был очень далёк от того номинала, который был впаян.
Даташит также говорил, что если только увеличить типоразмер с 0805 до 1206, то результирующая ёмкость в тех же условиях будет уже 3,4мкФ! Этот момент требовал более пристального изучения.
Я нашёл, что сайты Murata® и TDK® имеют классные инструменты для построения графиков изменения ёмкости конденсаторов в зависимости от различных условий. Я прогнал через них керамические конденсаторы на 4,7мкФ для разных типоразмеров и номинальных напряжений. На рисунке 1 показаны графики построенные Murata. Были взяты конденсаторы X5R и X7R типоразмеров от 0603 до 1812 на напряжение от 6,3 до 25В.
Рисунок 1. Изменение ёмкости в зависимости от приложенного напряжения для выбранных конденсаторов.
Обратите внимание, что во-первых, при увеличении типоразмера уменьшается изменение ёмкости в зависимости от приложенного напряжения, и наоборот.
Второй интересный момент состоит в том, что в отличии от типа диэлектрика и типоразмера, номинальное напряжение похоже ни на что не влияет. Я ожидал бы, что конденсатор на 25В под напряжением 12В меньше изменит свою ёмкость, чем конденсатор на 16В под тем же напряжением. Глядя на график для X5R типоразмера 1206 мы видим, что конденсатор на 6,3В на самом деле ведёт себя лучше, чем его родня на большее номинальное напряжение.
Если взять более широкий ряд конденсаторов, то мы увидим, что это поведение характерно для всех керамических конденсаторов в целом.
Третье наблюдение состоит в том, что X7R при том же типоразмере имеет меньшую чувствительность к изменениям напряжения, чем X5R. Не знаю, насколько универсально это правило, но в моём случае это так.
Используя данные графиков, составим таблицу 2, показывающую насколько уменьшится ёмкость конденсаторов X7R при 12В.
Таблица 2. Уменьшение ёмкости конденсаторов X7R разных типоразмеров при напряжении 12В.
| Типоразмер | Ёмкость, мкФ | % от номинала |
|---|---|---|
| 0805 | 1,53 | 32,6 |
| 1206 | 3,43 | 73,0 |
| 1210 | 4,16 | 88,5 |
| 1812 | 4,18 | 88,9 |
| Номинал | 4,7 | 100 |
В моём случае я выбрал наименьший возможный типоразмер компонентов, поскольку этот параметр был критичен для моего проекта. В своём невежестве я полагал что любой конденсатор X7R будет так же хорошо работать, как другой с тем же диэлектриком — и был неправ. Чтобы RC-цепочка заработала правильно я должен был взять конденсатор того же номинала, но в большем корпусе.
Выбор правильного конденсатора
Я очень не хотел использовать конденсатор типоразмера 1210. К счастью, я имел возможность увеличить сопротивление резисторов в пять раз, уменьшив при этом ёмкость до 1мкФ. Графики на
Рисунок 2. Поведение различных конденсаторов на 1мкФ и 4,7мкФ.
Конденсатор 0603 1мкФ ведёт себя так же, как 0805 4,7мкФ. Вместе взятые 0805 и 1206 на 1мкФ чувствуют себя лучше, чем 4,7мкФ типоразмера 1210. Используя конденсатор 1мкФ в корпусе 0805 я мог сохранить требования к размерам компонентов, получив при этом в рабочем режиме 85% от исходной ёмкости, а не 30%, как было ранее.
Но это ещё не всё. Я был изрядно озадачен, ибо считал что все конденсаторы X7R
 Я связался с коллегой — специалистом по керамическим конденсаторам1. Он пояснил, что есть много материалов, которые квалифицируются как «X7R». На самом деле, любой материал который позволяет компоненту функционировать в температурном диапазоне от -55ºC до +125ºC с изменением характеристик не более чем на ±15% можно назвать «X7R». Так же он сказал, что нет каких-либо спецификаций на коэффициент изменения ёмкости от напряжения ни для X7R, ни для каких-либо других типов.
Я связался с коллегой — специалистом по керамическим конденсаторам1. Он пояснил, что есть много материалов, которые квалифицируются как «X7R». На самом деле, любой материал который позволяет компоненту функционировать в температурном диапазоне от -55ºC до +125ºC с изменением характеристик не более чем на ±15% можно назвать «X7R». Так же он сказал, что нет каких-либо спецификаций на коэффициент изменения ёмкости от напряжения ни для X7R, ни для каких-либо других типов.Это очень важный момент, и я его повторю. Производитель может называть конденсатор X7R (или X5R, или еще как-нибудь) до тех пор, пока он соответствует допускам по температурному коэффициенту ёмкости. Вне зависимости от того, насколько плох его коэффициент по напряжению.
Для инженера-разработчика этот факт только освежает старую шутку — «любой опытный инженер знает: читай даташит!»
Производители выпускают всё более миниатюрные компоненты, и вынуждены искать компромиссные материалы. Для того чтобы обеспечить необходимые ёмкостно-габаритные показатели, им приходится ухудшать коэффициенты по напряжению. Конечно, более авторитетные производители делают все возможное, чтобы свести к минимуму неблагоприятные последствия этого компромисса.
Конечно, более авторитетные производители делают все возможное, чтобы свести к минимуму неблагоприятные последствия этого компромисса.
А как насчёт типа Y5V, который я сразу отбросил? Для контрольного в голову, давайте рассмотрим обычный конденсатор Y5V. Я не буду выделять какого-то конкретного производителя этих конденсаторов — все примерно одинаковы. Выберем 4,7мкФ на 6,3В в корпусе 0603, и посмотрим его параметры при температуре +85ºC и напряжении 5В. Типовая ёмкость на 92,3% ниже номинала, или 0,33мкФ. Это так. Приложив 5В к этому конденсатору мы получаем падение ёмкости в 14 раз по сравнению с номиналом.
При температуре +85ºC и напряжении 0В ёмкость уменьшается на 68,14%, с 4,7мкФ до 1,5мкФ. Можно предположить, что приложив 5В мы получим дальнейшее уменьшение ёмкости — от 0,33мкФ до 0,11мкФ. К счастью, эти эффекты не объединяются. Уменьшение ёмкости под напряжением 5В при комнатной температуре куда хуже, чем при +85ºC.
Для ясности, в данном случае при напряжении 0В ёмкость падает от 4,7мкФ до 1,5мкФ при +85ºC, в то время как при напряжении 5В ёмкость конденсатора увеличивается от 0,33мкФ при комнатной температуре, до 0,39мкФ при +85ºC.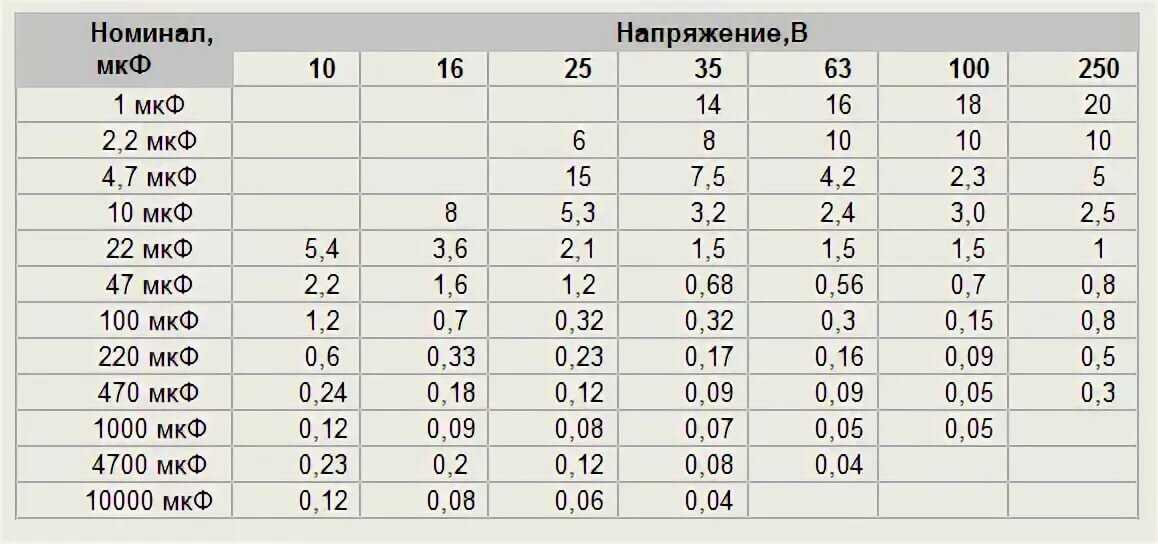 Это должно убедить вас действительно тщательно проверять все спецификации тех компонентов, которые вы используете.
Это должно убедить вас действительно тщательно проверять все спецификации тех компонентов, которые вы используете.
Вывод
В результате этого урока я уже не просто указываю типы X7R или X5R коллегам или поставщикам. Вместо этого я указываю конкретные партии конкретных поставщиков, которые я сам проверил. Я также предупреждаю клиентов о том, чтобы они перепроверяли спецификации при рассмотрении альтернативных поставщиков для производства, чтобы гарантировать что они не столкнутся с этими проблемами.
Главный вывод из всей этой истории, как вы наверное догадались, это: «читайте даташиты!». Всегда. Без исключений. Запросите дополнительные данные, если даташит не содержит достаточной информации. Помните, что обозначения керамических конденсаторов X7V, Y5V и т.д. совершенно ничего не говорят о их коэффициентах по напряжению. Инженеры должны перепроверять данные чтобы знать, реально знать о том, как используемые конденсаторы будут вести себя в реальных условиях. В общем, имейте в виду, в нашей безумной гонке за меньшими и меньшими габаритами это становится всё более важным моментом каждый день.
В общем, имейте в виду, в нашей безумной гонке за меньшими и меньшими габаритами это становится всё более важным моментом каждый день.
Об авторе
Марк Фортунато провёл большую часть жизни пытаясь сделать так, чтобы эти противные электроны оказались в нужное время в нужном месте. Он работал над различными вещами — от систем распознавания речи и микроволновой аппаратуры, до светодиодных ламп (тех, которые регулируются правильно, заметьте!). Он провёл последние 16 лет помогая клиентам приручить их аналоговые схемы. Г-н Фортунато сейчас является ведущим специалистом подразделения коммуникационных и автомобильных решений Maxim Integrated. Когда он не пасёт электроны, Марк любит тренировать молодёжь, читать публицистику, смотреть как его младший сын играет в лакросс, а старший сын играет музыку. В целом, он стремится жить в гармонии. Марк очень сожалеет, что больше не встретится с Джимом Уильямсом или Бобом Пизом.
Сноски
1 Автор хотел бы поблагодарить Криса Буркетта, инженера по применению из TDK за его объяснения «что здесь, чёрт возьми, происходит».
Murata является зарегистрированной торговой маркой компании Murata Manufacturing Co., Ltd.
TDK является зарегистрированным знаком обслуживания и зарегистрированной торговой маркой корпорации TDK.
P.S. По просьбам трудящихся — сравнительное фото конденсаторов различных типоразмеров. Шаг сетки 5мм.
Зависимость емкости конденсатора от частоты и напряжения — Студопедия
Поделись
Емкость конденсатора при повышении частоты уменьшается, так как уменьшается диэлектрическая проницаемость диэлектрика, обусловленная ослаблением релаксационных видов поляризации.
Если же в диэлектрике имеет место только электронная и ионная поляризация, то диэлектрическая проницаемость в широком диапазоне частот не должна зависеть от частоты, а следовательно не должна изменяться и емкость. Но и в этом случае емкость может изменяться за счет влияния конструктивных элементов конденсатора: его индуктивности и сопротивления обкладок и выводов.
Наличие индуктивности в конденсаторе дает увеличение его действующей емкости с ростом частоты (рис. 30), так как ток будет возрастать за счет компенсации реактивного емкостного сопротивления индуктивным сопротивлением.
Приравняем значения полных сопротивлений:
конденсатора с индуктивностью, L и емкостью
эквивалентного ему конденсатора с действующей емкостью , без индуктивности.
Пренебрегая наличием активного сопротивления можно написать:
[84]
[85]
[86]
откуда
[87]
[88]
Зависимость от частоты увеличивается как при увеличении индуктивности L так и при увеличении емкости при заданной индуктивности.
Наличие активного сопротивления r, включенного последовательно с емкостью С должно ограничивать ток, протекающий через конденсатор, причем этот эффект должен быть заметнее при увеличении частоты, так как с увеличением частоты падает емкостное реактивное сопротивление и влияние активного сопротивления на величину тока возрастает (рис. 31).
31).
Величину можно вычислить по формуле:
[89]
Увеличение емкости С при заданном r усиливает частотную зависимость.
В обычных конденсаторах сопротивление обкладок и выводов, определяющее величину r, мало, а поэтому снижение емкости C с увеличением частоты f можно заметить лишь в области радиочастот, даже при больших емкостях.
Выражения [88] и [89] являются приближенными, хотя и правильно характеризуют качественный характер частотной зависимости емкости.
Как частотная зависимость диэлектрической проницаемости, так и влияние активного сопротивления вызывают уменьшение емкости от частоты; увеличение емкости может быть обусловлено только влиянием индуктивности.
Как для полярных, так и для неполярных диэлектриков величина диэлектрической проницаемости не зависит от напряженности, а поэтому для большинства типов конденсаторов емкость не должна зависеть от величины приложенного напряжения.
Небольшое увеличение емкости при увеличении напряжения выше напряжения ионизации может наблюдаться для конденсаторов, диэлектрик которого содержит значительное число воздушных включений.
В сегнетокерамических конденсаторах диэлектрик обладает спонтанной поляризацией, для которой характерна зависимость диэлектрической проницаемости от напряжения. Для них емкость сильно зависит от напряжения, что используется для изготовления нелинейных конденсаторов – «варикондов».
напряжение — Зависимый источник тока с конденсатором
Задай вопрос
спросил
Изменено 2 года, 11 месяцев назад
Просмотрено 400 раз
\$\начало группы\$
В этой задаче по электронике я хочу определить выражение напряжения конденсатора.
Выключатель замыкается при t=0. Начальное напряжение на конденсаторе 10В.
Я попытался сделать эквивалентную схему Тевенена, и для этого я предположил, что переключатель включен. У меня не было проблем с поиском эквивалента R. Но когда я попытался определить напряжение Тевенина из-за источника тока, я не смог его получить.
Что я сделал: \$\ 7I=I_1+I_2\$ (1) и \$\ R_1I_1=R_2I_2\$ (2)
Но поскольку \$\ I=I_2 \$, уравнение дает \$\ I_1 =6I_2\$, и я ничего не получаю, когда подставляю этот результат в уравнение (2).
Если бы я мог получить значение V thévenin, думаю, я бы легко решил эту проблему.
Но если эта проблема не должна быть решена эквивалентной схемой, следует ли рассматривать закрытый ключ и ток \$\ 7I \$, протекающий через конденсатор? Я что-то упустил?
Заранее спасибо.
- напряжение
- конденсатор
- тевенин
\$\конечная группа\$
11
\$\начало группы\$
Я нашел решение в книге под названием «Электрические цепи» Нильсона и Риделя
\$\конечная группа\$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
. Конденсатор
Конденсатор— Зависит ли (паразитная) емкость от напряжения?
Задай вопрос
спросил
Изменено 3 года, 8 месяцев назад
Просмотрено 279 раз
\$\начало группы\$
Размышляя о том, как уменьшить паразитную емкость на моей плате, я задался вопросом:
Должна ли паразитная емкость зависеть от разности напряжений?
По уравнению емкости(параллельные пластины:)
$$C = \dfrac{\varepsilon \cdot A}{d}$$
Где \$\varepsilon\$ — диэлектрическая проницаемость, A — эффективная площадь, а d — расстояние.
Таким образом, согласно этому уравнению (паразитная) емкость полностью не зависит от напряжения.
Мне это кажется нелогичным.
Если у меня есть две дорожки наверху заземляющего слоя (две дорожки находятся далеко друг от друга на бесконечном расстоянии, поэтому давайте отбросим дорожку к емкости дорожки), где трасса 1 находится на 1000 В, а трасса 2 на 10 В.
Интуиция подсказывает мне, что паразитная/паразитная емкость будет выше между дорожкой 1 и землей по сравнению с дорожкой 2 и землей, в основном потому, что электрическая напряженность поля выше.
Моя интуиция верна?
- конденсатор
- паразитная емкость
\$\конечная группа\$
\$\начало группы\$
Должна ли паразитная емкость зависеть от разности напряжений?
Нет, не должен; это физическое свойство, связанное с физическими размерами и электрической проницаемостью материалов.
Более высокое электрическое поле не имеет значения.
емкость полностью не зависит от напряжения
Правильно, с одной оговоркой: некоторые паразитные емкости, связанные с PN-переходами с обратным смещением, будут изменять свою емкость в зависимости от приложенного напряжения, но это происходит из-за того, что обедненный слой растет, и, по сути, зазор между «пластинами» увеличивается, что снижает емкость.
\$\конечная группа\$
2
\$\начало группы\$
Обычно емкость не зависит от напряжения. Это функция геометрии и свойств материала — как видно из уравнения для конденсатора с плоскими пластинами, которое вы сами привели:
$$ C = \varepsilon_{r}\varepsilon_{0} \frac{A}{d} $$
Емкость может зависеть только от напряжения, если относительная диэлектрическая проницаемость зависит от напряженности электрического поля. Такие материалы не только существуют, но и достаточно распространены. В большинстве случаев эффект все же пренебрежимо мал.
Одним из примеров материала, для которого этот эффект очень важен, являются жидкие кристаллы. У них есть два важных свойства: 1.) Они жидкие. 2.) Они диэлектрически анизотропны. Это означает, что вы можете контролировать эффективную емкость, изменяя ориентацию молекул с помощью электрического поля.