Существует ли зависимость напряжения от частоты? — OneKu
Содержание статьи:Казалось бы, раскрыть зависимость напряжения от частоты просто. Стоит только обратиться с соответствующим запросом ко всезнающим поисковым системам и… убедиться, что ответа на этот вопрос попросту нет. Что же предпринять? Давайте разбираться вместе в этом непростом вопросе.
Напряжение или разность потенциалов?
Надо заметить, что напряжение и разность потенциалов — это одно и то же. По сути, это сила, которая способна заставить электрические заряды двигаться потоком. Не имеет значения, куда будет направлено это движение.
Вам будет интересно:Форма организации воспитательного процесса: основные понятия, общая характеристика, классификация
Разность потенциалов — просто другое выражение для напряжения. Оно нагляднее и, может быть, понятнее, но сути дела не меняет. Поэтому главный вопрос состоит в том, откуда берется напряжение, и от чего оно зависит.
В том, что касается домашней сети 220 Вольт, ответ простой. На гидростанции поток воды вращает ротор генератора. Энергия вращения трансформируется в силу напряжения. Атомная электростанция вначале превращает воду в пар. Он и крутит турбину. В бензоэлектростанции ротор вращает сила сгорающего бензина. Есть и другие источники, но суть всегда одна и та же: энергия превращается в напряжение.
Самое время задаться вопросом о зависимости напряжения от частоты. Но мы еще не знаем, откуда берется частота.
Что является источником частоты
Тот же самый генератор. Частота его вращения превращается в одноименное свойство напряжения. Вращайте генератор быстрее — частота будет больше. И наоборот.
Хвост не может «вилять» собакой. По той же причине частота не может изменить напряжение. Следовательно, выражение «зависимость напряжения от частоты тока» не имеет смысла?
Чтобы найти ответ, надо правильно сформулировать вопрос. Есть такая присказка про глупца и 10 ученых мужей. Он задавал неправильные вопросы, а они не могли ответить.
Если назвать напряжение другим определением, все встанет на свои места. Оно применяется для цепей, состоящих из множества разных сопротивлений. «Падение напряжения». Оба выражения часто считаются синонимами, что почти всегда неправильно. Потому что падение напряжения действительно может зависеть от частоты.
С чего бы напряжению падать?
Да просто потому, что не может не падать. Итак. Если на одном полюсе источника потенциал равен 220 Вольт, а на другом — ноль, то это падение могло произойти только в цепи. Закон Ома говорит о том, что, если в сети имеется одно сопротивление, то все напряжение на нем и упадет. Если два и больше — каждое падение будет пропорционально его величине, а их сумма равна исходной разности потенциалов.
Ну и что? Где здесь указание на зависимость напряжения от частоты тока? Пока что все зависит от величины сопротивления. Вот, если бы найти такой резистор, который меняет свои параметры при изменении частоты! Тогда и падение напряжения на нем менялось бы автоматически.
Есть такие резисторы
Их еще называют реактивными, в отличие от активных собратьев. На что же они реагируют, изменяя свою величину? На частоту! Существует 2 вида реактивных сопротивлений:
- индуктивное;
- емкостное.
Каждый вид связан со своим полем. Индуктивное — с магнитным, емкостное — с электрическим. На практике они представлены в первую очередь, соленоидами.
Они представлены на фото выше. И конденсаторами (ниже).
Их можно считать антиподами, потому что реакция на изменение частоты прямопротивоположная. Индуктивное сопротивление растет с частотой. Емкостное, наоборот, падает.
Теперь, учитывая особенности реактивных сопротивлений, в соответствии с законом Ома, можно утверждать, что зависимость напряжения от частоты переменного тока существует. Она может быть рассчитана с учетом величин реактивных сопротивлений в цепи. Только для ясности надо помнить, что речь идет именно о падении напряжения на элементе цепи.
И все-таки она существует!
Вопросительный знак в заголовке статьи превратился в восклицательный. «Яндекс» реабилитирован. Осталось только привести формулы зависимости напряжения от частоты для разных видов реактивных сопротивлений.
Емкостное: XC = 1/(w · C). Здесь w — угловая частота, C — емкость конденсатора.
Индуктивное: XL = w · L, где w — то же, что и в предыдущей формуле, L — индуктивность.
Как видно, частота влияет на величину сопротивления, изменяя его, следовательно, изменяет и падение напряжения. Если в сети имеется активное сопротивление R, емкостное XC и индуктивное XL, то сумма падений напряжений на каждом элементе будет равна разности потенциалов источника: U = Ur + Uxc+ Uxl.
Источник
Зависимость частоты и напряжений от баланса мощности
Остановимся прежде всего на основном и общем для рассматриваемых задач вопросе: выясним, от чего зависят величины частоты и напряжений, устанавливающиеся в электроэнергетической системе.
Каждый из приемников энергии, присоединенных к электрической сети, потребляет активную и реактивную мощности, величины которых, как уже отмечалось ранее, определяются величиной напряжения на его зажимах и частотой. Мощность, идущая на питание приемников энергии и покрытие потерь в сети, соединяющей приемники с некоторой узловой точкой системы, в данном режиме нагрузки зависит только от частоты и величины напряжения в данной узловой точке.
Следовательно, нагрузка любой узловой точки однозначно (в области нормальных значений частоты и напряжения) определяется частотой и напряжением в этой точке. Статические характеристики нагрузки в некоторой узловой точке представляют собой, как известно, зависимости активной и реактивной мощностей этой нагрузки от напряжения при заданной частоте. Для различных значений частоты может быть построено семейство подобных характеристик (рис. 2).
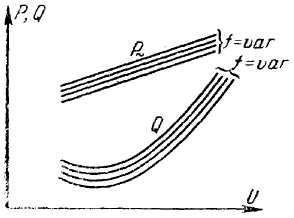
Рис. 2. Зависимости активной и реактивной мощности от напряжения
Обеспечить в данной узловой точке некоторые заданные значения частоты и напряжения можно, только передавая к ней из системы совершенно определенные величины активной и реактивной мощностей. Эти величины при заданных частоте и напряжении можно определить по соответствующим статическим характеристикам нагрузок. Если почему-либо из внешней сети в узловую точку будет поступать недостаточная активная или реактивная мощность, то заданные значения частоты и напряжения не могут установиться в этой узловой точке: параметры фактического режима будут иными. Рассмотрим несколько детальнее этот вопрос.
Пусть заданные семейства статических характеристик выражаются в неявной форме следующими зависимостями:
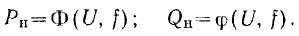
Величины активной и реактивной мощностей, притекающих к данной узловой точке системы, зависят как от величины U и фазы напряжения в этой узловой точке, так и от величин и фаз напряжений в смежных узловых точках и сопротивлений, соединяющих участки сети.
Допустим сначала для простоты, что напряжения у ближайших узловых точек неизменны по величине и фазе и имеют одинаковую частоту
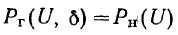
и
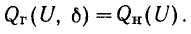
Эти два уравнения с двумя неизвестными и позволяют определить U и .
Покажем,
как графически решается эта задача.
Совместим на одной диаграмме (рис. 3)
характеристику PН = Ф1(U),
соответствующую заданному значению f,
и семейство характеристик Pг=1(U, ),
соответствующих тому же значению f,
но при разных значениях .
Так как PГ = PН,
то из этой диаграммы по точкам пересечения
может быть определена зависимость
= Ф(U),
соответствующая балансу активных
мощностей в узловой точке. Далее
аналогичным образом совмещаем на одной
диаграмме характеристику Q
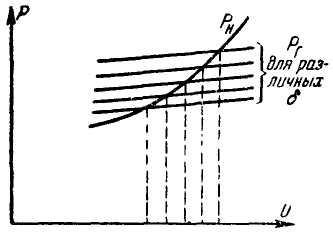
Рис. 3. Определение зависимости угла сдвига (фазы) от величины напряжения
Все наши предыдущие рассуждения относились к случаю неизменности по величине и фазе напряжений в смежных узловых точках и частоты в системе. В действительности такой неизменности нет и напряжения во всех узловых точках могут изменяться по величине и фазе; может также изменяться и частота системы.
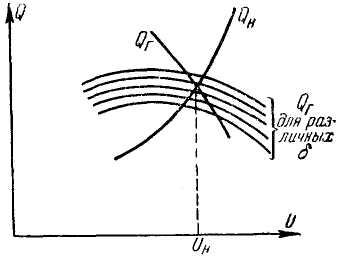
Рис. 4. Построение характеристики зависимости Q от U
Однако в системе можно найти такие узловые точки, в которых поддерживается неизменное по величине и фазе или только по величине напряжение или из которых в сеть передается определенная активная мощность.
При определенном впуске энергоносителя и нормальных значениях параметров режима первичный двигатель развивает мощность, зависящую только от частоты сети, и, следовательно, электромагнитная мощность генератора в этих условиях зависит только от частоты:
Pг=Ф(U).
При постоянстве тока возбуждения генератора неизменной является величина э.д.с. генератора Ed, а при наличии регуляторов возбуждения неизменной или почти неизменной будет величина напряжения на его выводах.
В системе должен быть баланс активных и реактивных мощностей: сумма активных и реактивных мощностей всех генераторов должна равняться сумме активных и реактивных мощностей нагрузок всех узловых точек и потерь активной и реактивной мощностей во всех элементах сетей. Следовательно, частота во всей системе, а также величина и фаза напряжения в каждой из узловых точек установятся как раз такими, которые требуются по условию баланса мощностей.
Пусть в системе установился некоторый режим. Изменим впуск энергоносителя в первичный двигатель одного из генераторов. Угол сдвига ротора этого генератора также изменится. Во всей системе произойдет изменение частоты, а также изменение величин и фаз напряжений во всех узловых точках. Эти изменения будут происходить во времени до тех пор, пока не установится новый режим баланса мощностей в системе. Процесс этот является далеко не таким простым, как можно было бы предполагать. В самом деле, например, уменьшение впуска энергоносителя вызовет уменьшение угла сдвига ротора данного генератора относительно других, активные нагрузки других генераторов возрастут. Появится небаланс на валах каждого из этих генераторов, и они начнут тормозиться. В связи с этим генератор, у первичного двигателя которого уменьшился впуск энергоносителя, также должен начать тормозиться, так как при уменьшении углов сдвига роторов остальных генераторов он должен принять добавочную нагрузку. Торможение всех генераторов будет приводить к снижению общей частоты в системе. По мере ее снижения будут уменьшаться активные мощности нагрузок узловых точек в соответствии с их частотными статическими характеристиками и увеличиваться мощности всех других генераторов в соответствии со статическими характеристиками регуляторов скорости первичных двигателей.
Оба эти фактора приведут к тому, что при достаточно большом снижении частоты вновь наступит баланс на валу каждого из генераторов; мощности, развиваемые первичными двигателями, будут балансироваться с мощностями нагрузки
генераторов. Дальнейшее снижение частоты прекратится. Необходимо учесть, что снижение частоты вызывает изменение Э.Д.С. всех генераторов, реактивных сопротивлений всех ветвей системы, а, следовательно, и всех напряжений в сети, что в свою очередь приведет к изменению активных и реактивных нагрузок всех узловых точек в соответствии с их статическими характеристиками по напряжению и частоте. Таким образом, процесс оказывается достаточно сложным.
Рассмотрим другой случай. Пусть уставка регулятора возбуждения на одном из крупных генераторов системы будет снижена. Тогда уменьшится выпуск реактивной мощности от данного генератора, что приведет к снижению напряжения по крайней мере в близлежащем районе электрической сети. Снижение напряжения в свою очередь вызовет уменьшение активных и реактивных нагрузок всех узловых точек в соответствии с их статическими характеристиками по напряжению. Появится небаланс на валу каждого из генераторов; углы сдвига их роторов, а, следовательно, и скорости их вращения будут расти. Это приведет к повышению частоты, так как генераторы, особенно близлежащие, разгрузятся. Частота в системе будет расти, пока не наступит новый баланс, обусловленный ростом активных нагрузок системы. Рост частоты в свою очередь повлияет на увеличение напряжений.
Такова сложная взаимосвязь изменений частоты, напряжения и активных и реактивных мощностей в системе. Однако для решения практических вопросов можно упростить задачу путем некоторой идеализации.
Так, отвлекаясь от изменений напряжений и реактивных мощностей, можно считать, что изменение баланса активных мощностей в системе определенным образом сказывается только на изменении частоты.
Действительно, рост активной нагрузки потребителей или снижение активной мощности генераторов в первую очередь вызывает определенное для данного режима снижение частоты в системе. Практически именно это является наиболее существенным. Менее существенным является то, что это изменение частоты будет в некоторой степени различным в зависимости от того, в какой узловой точке выросла активная нагрузка или у какого именно генератора снизилась активная мощность. Это различие обусловлено влиянием других факторов (напряжений, реактивных мощностей) и не столь велико. Снижение частоты, обусловленное возникновением дефицита активной мощности, обязательно приведет к восстановлению баланса, так как при этом в связи со снижением частоты и напряжений активная нагрузка уменьшается. В то же время регуляторы скорости первичных двигателей и частоты увеличивают впуск энергоносителя, и активная мощность генераторов растет.
Количественное соотношение, т.е. зависимость относительного изменения частоты от относительного небаланса активной мощности, не является неизменным и в зависимости от режима работы системы может колебаться в довольно широких пределах.
2. Зависимость ε от частоты приложенного напряжения.
В переменном электрическом поле Ε в полярных диэлектриках при повышении частоты f внешнего поля до некоторого значения остается неизменной. Однако при достижении некоторого критического для данного вещества значения частоты е падает и стремится к минимальному значению ε. Такая зависимость вызвана замедленным механизмом релаксационной поляризации, присущей полярным диэлектрикам.
При низкой частоте приложенного поля диполи успевают поворачиваться вслед за изменением направления поля. При частотах выше fkp диполи из-за трения уже не успевают за изменением поля и ε снижается.
Для неполярных диэлектриков, поляризация не связана с процессами трения, е не зависит от f по крайней мере в диапазоне применяемых в технике частот.
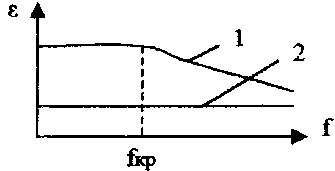
1 – полярный диэлектрик; 2 – неполярный диэлектрик
Рисунок 4. Зависимость диэлектрической проницаемости от частоты
3. Зависимость ε от температуры.
Д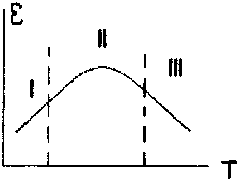 ля
полярных диэлектриков характерна
следующая зависимость ε = φ(т). Различимы
три области: I — область низких температур
— высокая вязкость материала; II — средняя
вязкость; III — низкая вязкость размягчения
материала, увеличение хаотического
теплового движения.
ля
полярных диэлектриков характерна
следующая зависимость ε = φ(т). Различимы
три области: I — область низких температур
— высокая вязкость материала; II — средняя
вязкость; III — низкая вязкость размягчения
материала, увеличение хаотического
теплового движения.
Рисунок 5. Зависимость диэлектрической проницаемости от температуры
В области I с ростом температуры увеличивается подв-ть молекул (частиц, диполей) диэлектриков, тем самым облегчает процесс поляризации и растет ε, которая достигает своего максимума в области II. Однако дальнейший рост температуры с одной стороны, снижает вязкость материала, с другой стороны, возрастает хаотическое тепловое движение частиц материала, которое мешает процессу ориентации диполей, разрушая его. Диэлектрическая проницаемость снижается.
Для неполярных диэлектриков влияние температуры на е незначительно и увеличение может, как уменьшать, так и увеличивать ε.
Зависимость ε от температуры можно учесть через температурный коэффициент диэлектрической проницаемости ТКε:
ТКε = 1/ ε • Δε / ΔТ
4. Потери в диэлектриках
За величину, характеризирующую диэлектрические потери в диэлектриках принимают отношение активной части токов к реактивной. Отношение Iа / Ip = tgσ, то есть тангенсу угла между вектором суммарного тока Iоб и его реактивной составляющей. Безразмерная величина tgσ принята за характеристику материала и называется тангенсом угла диэлектрических потерь.
Произведение ε * tgσ называется коэффициентом диэлектрических потерь. При больших значениях этого коэффициента диэлектрик склонен к перегреву и разрушению за счет выделяемой теплоты.
Д иэлектрические
потери зависят от частоты приложенного
напряжения и температуры.
иэлектрические
потери зависят от частоты приложенного
напряжения и температуры.
1 — полярные диэлектрики 2 — неполярные диэлектрики
Рисунок 6. Зависимость тангенса угла диэлектрических потерь от температуры
С ростом температуры уменьшается удельное электрическое сопротивление диэлектриков и, следовательно, растет ток сквозной проводимости. Нагрев диэлектрика влияет на процессы поляризации. В процессе нагрева сначала происходит увеличение подвижности частиц диэлектрика, что увеличивает количество теплоты, выделяемой за счет трения частиц или их ориентации. Однако дальнейшее увеличение температуры повышает хаотические колебания частиц, препятствующее поляризации. С другой стороны при нагреве снижается вязкость материала и, следовательно, уменьшается трение при ориентации дипольных частиц. Все это приводит к снижению диэлектрических потерь. Суммируя действие всех факторов, связанных с диэлектрическими потерями получаем изображение на рисунке 6 для полярных диэлектриков.
Изменение частоты приложенного напряжения влияет на диэлектрические потери. Частота влияет на потери поляризации. На ток сквозной проводимости f не влияет. Частота практически не влияет и на упругие виды поляризации. Таким образом, релаксационные виды поляризации вызывают изменение диэлектрических потерь при изменении f.
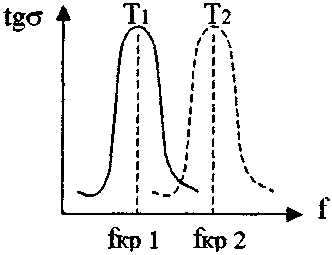
Рисунок 7. Зависимость тангенса угла диэлектрических потерь от частоты
Графическая зависимость tga = φ(f) для полярных диэлектриков повторяет tgσ = φ(Т) для тех же материалов. Это связано с тем, что при Т = const ориентация диполей сначала успевает за изменением полярности приложенного напряжения, а затем, с ростом f, пройдя максимальное значение для tgσ, начинает отставать. Вместо полного поворота вслед за полем диполи начинают колебаться все с меньшей амплитудой, что и снижает уровень диэлектрических потерь.
Значение ТК — справочный параметр, который задается для каждого диэлектрического материала.
При создании приборов и аппаратуры можно управлять характером изменения ε, используя комбинации диэлектрических материалов с различным знаком ТКε.
На е влияет влажность материала. Для всех материалов ε увеличивается с ростом влажности. Особенно чувствительны к влажности диэлектрики.
Поддержание нормальных значений частоты и напряжений в системе
Для поддержания нормальной частоты в системе в первую очередь должен быть обеспечен соответствующий этой частоте баланс активных мощностей, а следовательно, при росте активных нагрузок прежде всего должна соответственно увеличиваться активная мощность генераторов.
Возникающее при дефиците реактивных мощностей снижение напряжений также влияет на величину активных нагрузок в системе, но при обычном преобладании в составе нагрузки электродвигателей это обстоятельство является второстепенным и поддержание частоты при помощи регулирования напряжений, даже если бы оно было допустимо с точки зрения пределов изменений величины напряжений, возможно лишь в очень узком диапазоне.
Аналогично этому рост реактивной нагрузки потребителей или снижение реактивной мощности генераторов в первую очередь вызывает снижение напряжений во всех узловых точках системы. Однако здесь имеется существенное отличие от предыдущего: если частота изменяется во всей системе одинаково, то изменение напряжений существенно зависит от электрической удаленности данного места от источника изменения баланса по реактивной мощности. Снижение напряжений, вызванное изменением баланса по реактивной мощности, приведет к уменьшению реактивной нагрузки в близлежащих узловых точках системы и, кроме того, в большинстве случаев к росту реактивных мощностей генераторов. Особенно интенсивно растет генерация реактивной мощности в случае снижения напряжения в сети благодаря наличию у машин автоматических регуляторов возбуждения.
Таким образом, для поддержания нормальных напряжений в системе в первую очередь должен быть обеспечен соответствующий баланс реактивных мощностей. Возникающее при дефиците активных мощностей снижение частоты влияет на величину реактивных мощностей в системе, что в данном случае оказывается существенным, и обеспечить поддержание нормальных напряжений в системах при дефиците активной мощности и сниженной частоте не всегда удается.
Поскольку напряжения в различных точках системы различны, необходимо не только обеспечить баланс реактивных мощностей в системе, но и распределить в ней источники реактивной мощности так, чтобы напряжения во всех ее узловых точках не выходили из зоны допустимых значений. Произвольное распределение реактивных мощностей может привести к большим значениям потоков реактивной мощности на отдельных участках сети и, как следствие, к большим потерям напряжения и невозможности поддержания допустимых напряжений в отдельных пунктах системы. Следовательно, нужно стремиться устанавливать местные балансы реактивной мощности в отдельных районах сети, по возможности не допуская передачи значительной реактивной мощности, особенно через длинные линии.
Этим регулирование напряжения отличается от регулирования частоты. Произвольное распределение активных нагрузок не мешает регулированию частоты, если не учитывать изменения потерь активной мощности и если при этом не превышается пропускная способность электропередач. Однако распределение активных нагрузок в известной мере влияет на величину напряжений в отдельных узловых точках, особенно в сети с большими значениями отношений r/x.
Условия обеспечения надлежащих значений частоты и напряжений в сетях электроэнергетической системы сводятся к следующему:
1. Располагаемая активная мощность станций должна быть достаточной для того, чтобы покрыть всю активную нагрузку системы и потери активной мощности в сетях при нормальных напряжениях и частоте.
2. Располагаемая реактивная мощность генераторов и синхронных компенсаторов должна быть достаточной для того, чтобы покрыть всю реактивную нагрузку системы и потери реактивной мощности в сетях при нормальных напряжениях и частоте.
3. Распределение располагаемой реактивной мощности генераторов и синхронных компенсаторов в системе должно быть таким, чтобы в каждом районе, отделенном от других районов относительно длинными линиями, реактивная нагрузка всех потребителей вместе с потерями реактивной мощности в сетях в основном могла быть покрыта местными генераторами и компенсаторами и уравнительные потоки реактивной мощности между районами были небольшими и не приводили к значительной потере напряжений в сетях.
Невыполнение первого условия, т.е. появление дефицита (недостатка) активной мощности, приводит к невозможности поддержания нормальной частоты; невыполнение второго — к невозможности поддержания среднего уровня напряжений в сетях близ нормального значения. Наконец, невыполнение третьего условия, т.е. появление местных недостатков реактивной мощности в отдельных районах приводит к невозможности поддержания надлежащего уровня напряжений в этих районах.
Недостаток активной мощности в системе снижает не только частоту, но (при отсутствии надлежащего резерва реактивной мощности) также и напряжения, что частично уменьшает дефицит активной мощности.
Недостаток реактивной мощности не только приводит к снижению напряжений, но и увеличивает резерв активной мощности в системе за счет снижения активной мощности потребителей, что частично уменьшает недостаток реактивной мощности.
Располагая резервом активной мощности, можно несколько смягчить недостаток реактивной мощности и в очень узких пределах повысить слишком низкое напряжение, повышая для этой цели частоту в сети, что приводит к росту реактивной мощности генераторов и снижению реактивной мощности потребителей.
Имея повышенный уровень напряжений в системе, можно несколько снизить дефицит активной мощности в системе и в очень узких пределах повысить сниженную частоту, уменьшая уровень напряжений в сетях, что приводит к снижению активных нагрузок.
В заключение остановимся на характеристиках зависимости активной и реактивной мощностей потребителей от частоты и напряжения.
На рис. 5 и 6 представлены характеристики зависимости активной Р и реактивной Q мощностей потребителей от частоты f и напряжения U, построенные Теплоэлектропроектом.
Как видно из рис. 5, зависимость Р от f почти прямолинейна. Наклон этой характеристики зависит от состава нагрузок потребителей и главным образом от доли участия нагрузок в виде синхронных и асинхронных электродвигателей с постоянным моментом на валу и асинхронных электродвигателей с переменным (падающим) моментом на валу (приводы насосов и вентиляторов). Для первой группы потребителей активная мощность нагрузки почти пропорциональна первой степени частоты, т. е. при снижении частоты на 1% активная мощность снижается на 1 %. Для второй группы потребителей снижению частоты на 1 % соответствует снижение активной мощности примерно на 3%. Для других потребителей – освещения, бытовых приборов, дуговых печей – изменение частоты почти не приводит к изменению активной мощности, если при этом поддерживается неизменное напряжение.
Суммарные потери активной мощности в электрических сетях мало изменяются при изменениях частоты.
Для энергосистем в целом на 1 % снижения частоты суммарная активная нагрузка изменяется на величину 1,0 –2,0% в зависимости от состава потребителей.
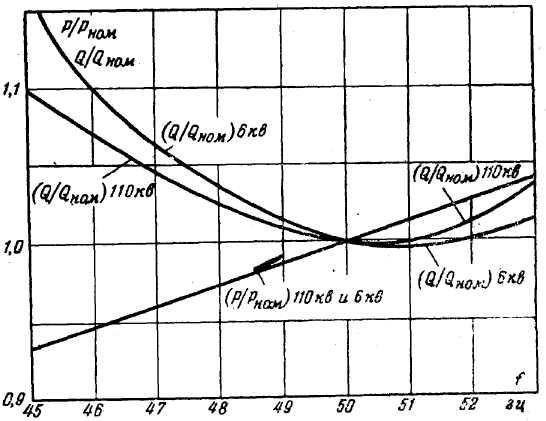
Рис. 5. Характеристика зависимости активной и реактивной мощности от частоты
Из того же рис. 5 видно, что снижение частоты приводит к росту реактивной мощности потребителей. Этот рост обусловлен главным образом увеличением магнитной индукции в асинхронных двигателях и трансформаторах при снижении частоты и соответствующим значительным (вследствие насыщения) ростом токов их намагничивания. Указанное увеличение их реактивной мощности частично компенсируется снижением потерь реактивной мощности в реактивностях рассеяния линий, трансформаторов и асинхронных электродвигателей, а также ростом зарядной мощности линий электрических сетей. Для энергосистемы в целом на 1% снижения частоты (при неизменных напряжениях) реактивная мощность возрастает примерно на 1 – 1,5%.
Из рис. 6 видно, что зависимость активной мощности потребителей от напряжения почти прямолинейна.
От величины напряжения сильно зависит активная мощность, потребляемая бытовыми приборами, дуговыми печами, а также теряемая в электрических сетях. На 1 % снижения напряжения потребляемая этими нагрузками .активная мощность снижается на 1,6 – 2%. Мощность нагрузки асинхронных двигателей очень мало зависит от изменения напряжения (только за счет небольшого изменения скольжения). Мощность нагрузки синхронных двигателей совсем не зависит от напряжения. Потери в стали трансформатора снижаются при уменьшении напряжения. Для энергосистемы в целом на 1 % снижения напряжения активная мощность снижается на величину от 0,6 % (при малой доле бытовой нагрузки) до 2 % (при большой доле бытовой нагрузки).
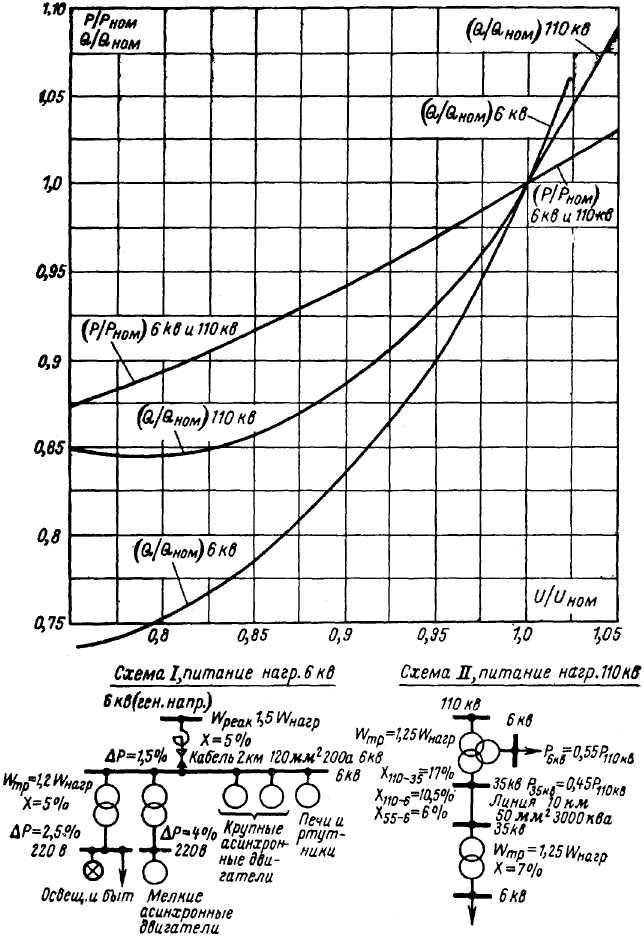
Рис. 6. Характеристика зависимости активной и реактивной мощности от напряжения
Зависимость реактивной нагрузки потребителей от напряжения имеет криволинейный характер по следующим причинам. Реактивная мощность намагничивания асинхронных двигателей и трансформаторов, составляющая значительную долю (60 – 70 %) всей реактивной нагрузки системы, резко уменьшается при снижении напряжения, что обусловливает крутой спад реактивной нагрузки при напряжениях, близких к нормальному значению (до 2 – 3 % на 1 % снижения напряжения). С другой стороны, снижение напряжения приводит к заметному росту реактивной мощности, теряемой в реактивных сопротивлениях рассеяния линий, трансформаторов и асинхронных двигателей (почти на 2 % при снижении напряжения на 1 %). Хотя при нормальном напряжении эта реактивная мощность составляет лишь 30 – 40 % всей нагрузки, но по мере снижения напряжения ее доля участия в суммарной реактивной нагрузке все время возрастает. Кроме того, зарядная мощность линий, частично покрывающая потребность энергосистемы в реактивной мощности, при снижениях напряжения падает по квадратичной зависимости, что также приводит к увеличению реактивной нагрузки энергосистемы. Поэтому при достаточно большом снижении напряжения реактивная нагрузка системы доходит до минимального значения и при дальнейшем снижении напряжения начинает возрастать. Этот минимум (Q мин) в промышленных энергетических системах имеет место при снижении напряжения до 75 – 85% нормального. Определяющим для характеристики зависимости реактивной нагрузки от напряжения является состав потребителей и в особенности коэффициент загрузки асинхронных двигателей. Чем больше коэффициент загрузки асинхронных двигателей, тем больше доля реактивной нагрузки от полей рассеяния и тем меньше доля реактивной нагрузки от токов намагничивания и, следовательно, тем меньше спад реактивной нагрузки при напряжениях, близких к нормальным, и тем выше напряжение, соответствующее минимуму реактивной нагрузки. Кривые на рис. 6 построены при средней загрузке асинхронных двигателей порядка 75% и при следующем составе потребителей: освещение и быт – 22 %, асинхронная нагрузка – 50%, синхронная нагрузка – 9%, дуговые печи и ртутные выпрямители – 11 % и потери мощности в электрических сетях –8 %
Характерные зависимости QHАГ = f(U). Для нагрузок потребителей различных отраслей промышленности приведены в литературе.
8. Зависимость сопротивления тела человека от частоты и величины напряжения
Зависимость можно представить гиперболической зависимостью, по оси х – частота, по оси y– полное сопротивление тела человекаz, чем больше частота тока, тем меньшее сопротивление току оказывает тело, т.е сопротивление с увеличением частоты – падает доrв.
Zт= 2zн+rв – сопротивление тела человека.
С ростом частоты и из-за уменьшения Xc= 1/wc, сопротивление тела падает. И на частоте свыше 1 кГц становится равнымrв
9. Время протекания тока через тело человека. Какие явления наблюдаются при длительном протекании тока.
При длительном протекании тока, наблюдается увеличение тока:
— из-за снижения сопротивления тела (нагрев, потоотделение)
— накопление физиологических воздействий последствий действий тока на организм
— повышается вероятность совпадения момента прохождения тока с фазой Т кардиоцикла (сердечный ритм, как в фильмах про скорую помощь между соседними сокращениями сердца скачек Т).
Фаза Т – заключительная часть (сокращение желудочков, выброс крови). Наиболее уязвимое воздействие электрического тока. Длительность фазы Т примерно равна 0,2 сек.
При кратковременном протекании тока вероятность совпадения его с фазой Т – мала. Если время протекания тока превышает длительность кардиоцикла (0,75- 1с ) вероятность совпадения с фазой Т и вероятность поражения – возрастает.
10. Род и частота тока. Особенности воздействия постоянного и переменного тока на человека.
При напряжении до 500В действие переменного тока – более опасно. Считается, что напряжение 120 В = тока эквивалентно ~40 В. При напряжении выше 500 В эти различия не наблюдаются.
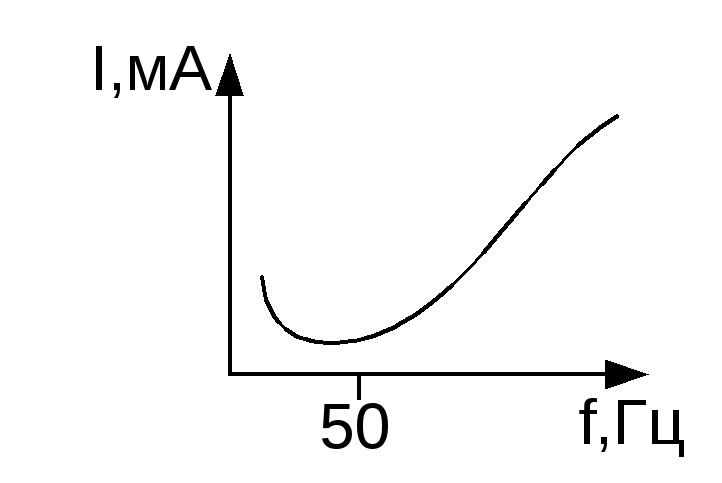
Наиболее неблагополучным является промышленный ток частотой 50 Гц. Зависимость величины неотпускающего тока от частоты, при частоте 50Гц – минимальный.
11. Двухполюсное прикосновение к твч в трехфазной и однофазной сети. Величина тока через человека в однофазной сети в зависимости от сопротивления наружного слоя кожи.
При двухполюсном подключении к трехфазной сети, токи опасны получением ожогов при протекании через тело или при воздействии дуги. При однофазном двухполюсном подключении человека к сети формула тока через человека – Iч =Uф/Rч. При двухполюсном подключении к трехфазной сети формула такая же только все надо умножить на корень из трех. Внутреннее сопротивление человека примерно постоянно равно 1 кОм, наружное сопротивление зависит от ряда факторов:
— индивидуальня особенность, чувствительность кожи, потливость
— профессия, грубость кожи
— степень увлажнения, загрязнения и пр.
12. Однополюсное подключение человека к твч. Значение тока через человека при прикосновении к трехфазной сети с изолированной и глухозаземленной нейтралью.
Электроустановки с позиции безопасности делятся на:
— ЭУ с изолированной нейтралью
— ЭУ с глухозаземленной нейтралью
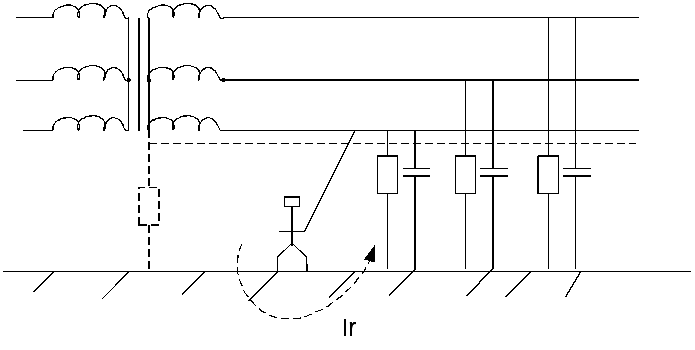
То что пунктиром, кроме тока Irобозначены элементы для установки с глухозаземленной нейтралью.
z=Rиз*Xс/корень квадратный изRиз^2+Xc^2
Iч =Uф/(Rч+z/3)
13. Замыкание на землю в электрических сетях (определение). Упрощенная схема растекания тока замыкания в грунте. Распределение потенциалов на поверхности земли одиночного полусферического заземлителя.
Замыкание на землю – случайное соединение с землей, или ее эквивалентом ТВЧ электроустановок.
Упрощенная схема замыкания ТВЧ на землю, суть такая, что в месте соприкосновения – наибольший потенциал, и по мере удаления от места соприкосновения – он падает. Ток замыкания будет стекать с поверхности заземлителя по направлению радиусов от центра сферы, т.е по кругу если сверху смотреть.Ток замыкания будет убывать по мере удаления от места замыкания в следствие увеличения площади поперечного сечения проводника, полусферы толщи земли.
S= 2пx^2, гдеS– площадь полусферы, аx- это расстояние от точки заземления до определенного места.
Плотность тока:
б=Iз/S
Потенциал ф = Iз*р(ро)/2пx, где р(ро) – удельное сопротивление почвы Ом/см.
Распределение потенциала подчиняется гиперболическому закону, на расстоянии один метр от точки замыкания потенциал уменьшается до 70%, а при х=10м потенциал составляет 8%, при х=20м, фи примерно равно 0.
14. Замыкание на корпус в электроустановке (определение). Потенциал корпуса заземленной ЭУ в случае соединения ТВЧ с корпусом. Распределение потенциалов на поверхности земли в результате стекания тока с заземлителя.
Это случайное соединение человека с корпусом ЭУ в результате механических повреждений, нарушения изоляции и т.д.
При замыкании ТВЧ на заземленный корпус оказывается под потенциалом (фи).
Напряжение прикосновения Uпр – это напряжение между двумя точками цепи тока к которому одновременно прикасается человек.
Если человек прикасается к корпусу заземленной ЭУ и находится на расстоянии х от заземления тогда Uпр = (фи(з)-фи(х))*альфа, где альфа – это коэффициент учитывающий особенности растекания тока с тела человека (сопротивление обуви, пола и пр). На рисунке изображены на каком-то расстоянии друг от друга две электроустановки, обе подключены к заземлителю в зависимости от расстояния между точкой соединия ТВЧ с землей будет увеличиваться – разность потенциалов, таким образом – большая разность будет у самой дальней ЭУ.
15. Напряжение прикосновения при замыкании ТВЧ на корпус ЭУ (определение). Зависимость напряжения прикосновения от места расположения заземлителя и человека.
Напряжение прикосновения Uпр – это напряжение между двумя точками цепи тока к которому одновременно прикасается человек.
Если человек прикасается к корпусу заземленной ЭУ и находится на расстоянии х от заземления тогда Uпр = (фи(з)-фи(х))*альфа, где альфа – это коэффициент учитывающий особенности растекания тока с тела человека (сопротивление обуви, пола и пр). На расунке изображены на каком-то расстоянии друг от друга две электроустановки, обе подключены к заземлителю в зависимости от расстояния между точкой соединия ТВЧ с землей будет увеличиваться – разность потенциалов, таким образом – большая разность будет у самой дальней ЭУ.
Регулирование скорости асинхронного двигателя изменением частоты тока статора
Изменяющийся
по частоте 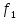 ток статора приводит к изменению угловой
скорости поля статора
ток статора приводит к изменению угловой
скорости поля статора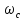
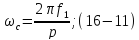
и
пропорционально изменяется скорость
ротора. Из выражения (1-1) следует, что
регулирование скорости двигателя
изменением скорости вращающегося
магнитного поля статора 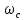 происходит без значительного изменения
скольжения и позволяет получать различные
скорости на жестких механических
характеристиках.
происходит без значительного изменения
скольжения и позволяет получать различные
скорости на жестких механических
характеристиках.
С
помощью электромашинных и полупроводниковых
устройств можно плавно изменять частоту
тока статора 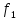 ,
а следовательно и скорость двигателя.
Скорость двигателя можно увеличить
вверх до
,
а следовательно и скорость двигателя.
Скорость двигателя можно увеличить
вверх до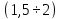
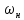 от номинальной и уменьшать в
от номинальной и уменьшать в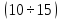 раз от номинальной.
раз от номинальной.
Верхний предел скорости ограничивается механической прочностью ротора, нижний – особенностями роботы преобразователей частоты.В настоящее время наиболее целесообразно применение тиранзисторных преобразователей частоты, в которых происходит сначала выпрямление переменного тока частоты сети, а затем инвертирование в переменный ток нужной частоты.
Для
сохранения постоянной (неизменной)
перегрузочной способности двигателя
на всех скоростях и поддержания постоянных
значений КПД и 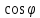 ,
одновременно с изменением частоты тока,
необходимо изменять напряжение,
подводимое к двигателю.
,
одновременно с изменением частоты тока,
необходимо изменять напряжение,
подводимое к двигателю.
Перегрузочная
способность лвигателя не будет изменяться
при изменении частоты тока статора,
если отношение критических моментов
двигателя 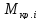 при всех частотах тока
при всех частотах тока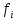 и соответствующих напряжениях
и соответствующих напряжениях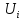 будет равно отношению соответствующих
статических моментов нагрузки
будет равно отношению соответствующих
статических моментов нагрузки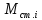 .
.
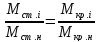 (16-12)
(16-12)
Подставим в уравнение (16-12) значения критических моментов из известного ранее соотношения:
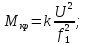
И получим:
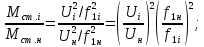
После преобразования получим (1-3):
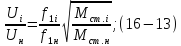
Где
: 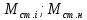 – статические моменты при скоростях,
соответствующих частотам
– статические моменты при скоростях,
соответствующих частотам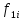 и
и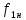 ;
;
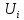 и
и 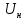 напряжения при тех же частотах тока
статора.
напряжения при тех же частотах тока
статора.
Из
уравнения (16-13) следует, что с изменением
частоты 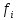 нужно так же изменить и величину
подводимого к двигателю напряжения
нужно так же изменить и величину
подводимого к двигателю напряжения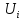 .
Т.е.для
каждой частоты
.
Т.е.для
каждой частоты 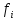 необходимо соответствующее этой частоте
напряжение
необходимо соответствующее этой частоте
напряжение 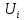 .
.
Закон изменения напряжения определяется характером зависимости статического момента от скорости.
Если пренебречь моментом холостого хода рабочего механизма, то уравнение статического момента можно записать в виде
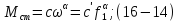
Подставив значения статических моментов (16-14) в уравнение (16-13) получим
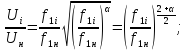 (16-15)
(16-15)
откуда 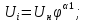
где
: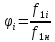 – относительная частота напряжения,
подаваемого на статор двигателя;
– относительная частота напряжения,
подаваемого на статор двигателя;
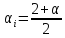 –показатель
степени, определяющий закон изменения
напряжения с изменением частоты тока
статора.
–показатель
степени, определяющий закон изменения
напряжения с изменением частоты тока
статора.
С
изменением частоты тока будут изменяться
синхронная скорость поля статора 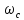 и индуктивные сопротивления обмоток
двигателя.
и индуктивные сопротивления обмоток
двигателя.
Двигатель будет развивать критический момент при критическом скольжении для данной частоты тока
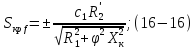
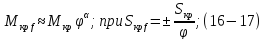
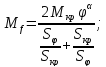
Рассмотрим регулирование напряжения для наиболее распространенных законов изменения нагрузки.
1.Статический момент не изменяется с изменением скорости
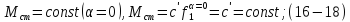
При этом уравнение (1-5)
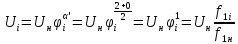
при 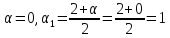
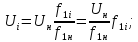
обозначим 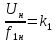 – постоянный коэффициент
– постоянный коэффициент
и
получим 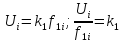
или 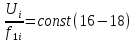
Из
(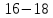 )
следует, что подводимое к двигателю
напряжение должно изменятся пропорционально
изменению частоты тока, для сохранения
постоянного отношения
)
следует, что подводимое к двигателю
напряжение должно изменятся пропорционально
изменению частоты тока, для сохранения
постоянного отношения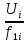 .
При этом критический момент
.
При этом критический момент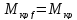 (в соответствии с (16-18)) остается без
изменений, то есть обеспечивается
постоянная перегрузочная способность
двигателя.
(в соответствии с (16-18)) остается без
изменений, то есть обеспечивается
постоянная перегрузочная способность
двигателя.
Соответствующие изменения напряжения при частотном регулировании обуславливаются необходимостью сохранения величины магнитного потока при разных частотах тока статора.
Если
пренебречь падением напряжения в обмотке
статора то можно считать, что сщгласно
уравнению 14-15 [ 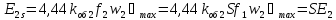 ]
]
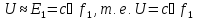
Откуда
получаем отношение
,
пропорционально потоку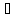 ,
который должен оставаться постоянным
,
который должен оставаться постоянным

Если
нарушить это условие, т.е. при 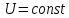 изменять только частоту тока статора
изменять только частоту тока статора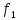 ,
то:
,
то:
а)
с уменьшением частоты тока статора 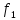 ,
поток
,
поток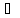 будет увеличиваться, это вызоветувеличение
потерь от намагничивающего тока;
будет увеличиваться, это вызоветувеличение
потерь от намагничивающего тока;
б)
с увеличением частоты тока статора 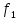 ,
поток
,
поток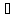 уменьшиться, что при неизменном
уменьшиться, что при неизменном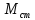 – статическом моменте сопротивления
механизма, вызовет увеличение сопротивления
току ротора, (соответственно рост
температуры).
– статическом моменте сопротивления
механизма, вызовет увеличение сопротивления
току ротора, (соответственно рост
температуры).
Таким образом, в обоих случаях двигатель будет перегреваться при моменте на валу, даже меньшем номинального значения.
Из
уравнения
(1-8) следует, что при постоянном статическом
моменте 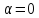 ,
,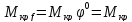 ,
критический момент остается неизменным
,
критический момент остается неизменным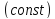 ,
а критическое скольжение
,
а критическое скольжение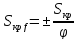 увеличивается с уменьшением частоты,
это вызвано уменьшением индуктивного
сопротивления
увеличивается с уменьшением частоты,
это вызвано уменьшением индуктивного
сопротивления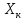 пропорционально
пропорционально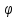 .
.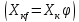 .
.
При увеличении критического скольжения критический момент наблюдается при меньшей скорости ротора.
При
низких частотах индуктивное сопротивление 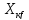 становится соизмеримым с независящим
от частоты активным сопротивлением
статора
становится соизмеримым с независящим
от частоты активным сопротивлением
статора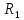 .
И при низких частотах,падение
напряжения на сопротивлении
.
И при низких частотах,падение
напряжения на сопротивлении 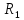 более
чувствительно снижает значение магнитного
потока и вызывает уменьшение критического
момента двигателя (кривая
более
чувствительно снижает значение магнитного
потока и вызывает уменьшение критического
момента двигателя (кривая 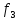 ина рис.1-1).
ина рис.1-1).
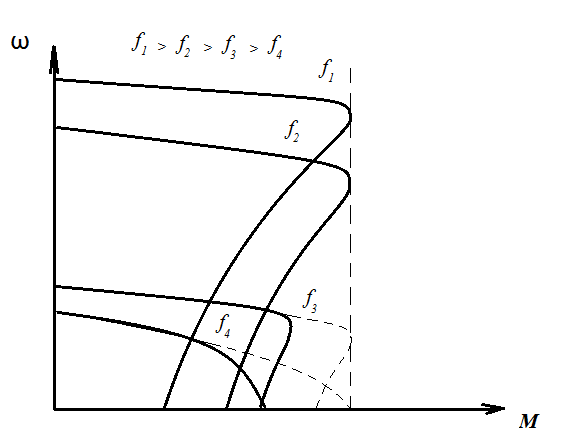
Рис.
1-1 Механическая характеристика
асинхронного двигателя при частотном
регулировании и 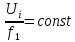 ,
,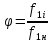 .
.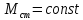
При
малых значениях индуктивности 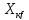 значительно увеличивается критическое
скольжение. Поэтому для поддержания
постоянного критического момента при
малых частотах напряжения снижают
медленней, чем частоту тока статора.
(Пунктирные кривые для
значительно увеличивается критическое
скольжение. Поэтому для поддержания
постоянного критического момента при
малых частотах напряжения снижают
медленней, чем частоту тока статора.
(Пунктирные кривые для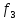 и
и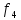 ).
).
2.3. Зависимости резонансного тока последовательного контура от частоты
Величина тока в последовательном контуре зависит от напряжения генератора и от сопротивления контура.Сопротивление контура складывается из емкостного, индуктивного и активного сопротивлений. Полное сопротивление в общем случае равно геометрической (векторной) сумме емкостного, индуктивного и активного сопротивлений.
Величина тока в последовательном контуре равна
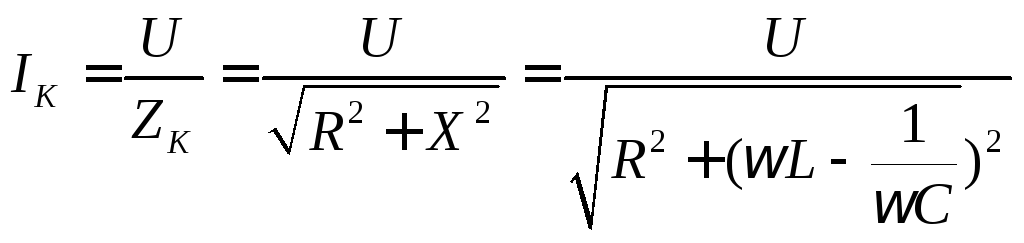 .
.
Полное сопротивление контура (импеданс) – непостоянная величина, так как емкостное сопротивление конденсатора и индуктивное сопротивление катушки зависят от частоты (рис.6).При резонансе полное сопротивление контура равно активному сопротивлению R контура. При частоте ниже резонансной преобладает емкостное сопротивление, полное сопротивление контура носит емкостный характер и контур эквивалентен конденсатору. При частоте выше резонансной преобладает индуктивное сопротивление, и полное сопротивление контура имеет индуктивный характер. При частоте выше резонансной последовательный контур эквивалентен катушке индуктивности. Контур также обладает активным сопротивлением R (сопротивлением потерь), величину которого в пределах рабочего диапазона частот контура можно считать неизменной. Реактивное сопротивление контура при разных частотах различно, поэтому угол фазового сдвига между напряжением питающего генератора и током в контуре зависит от частоты. При изменении частоты генератора от нуля до максимальной, угол фазового сдвига изменяется от – 90 градусов до + 90 градусов. При резонансной частоте фазовый сдвиг равен нулю.
Кривая, показывающая зависимость угла фазового сдвига между напряжением питающего генератора и током в контуре, называется фазочастотной характеристикой контура(рис.7).
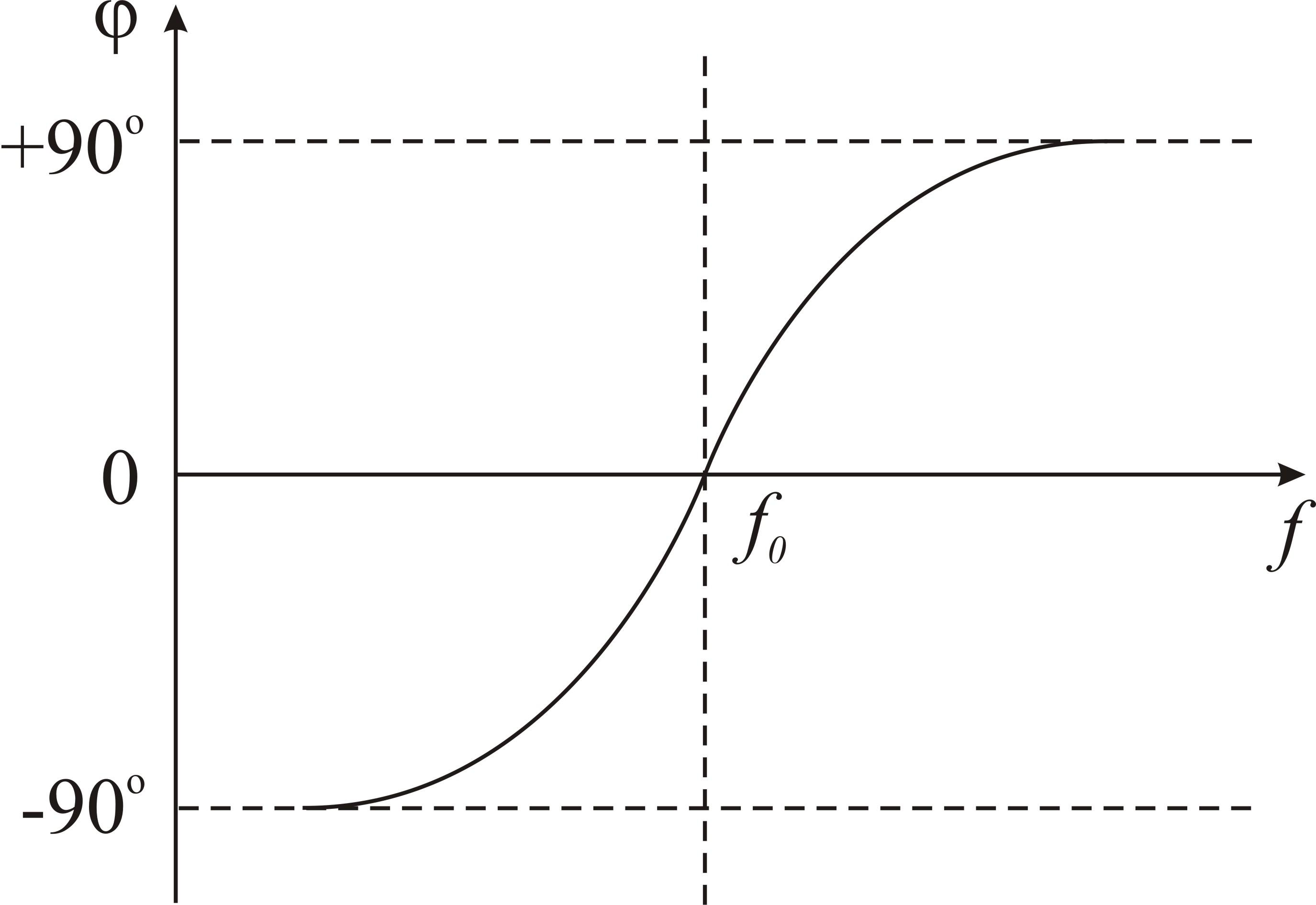
Рис.7. Фазо-частотная характеристика последовательного колебательного контура
Таким образом, при изменении частоты питающего тока изменяются величина и характер полного сопротивления последовательного контура.Поэтому амплитуда тока в контуре зависит от частоты генератора.При резонансе сопротивление контура имеет наименьшее значение и ток максимальный:
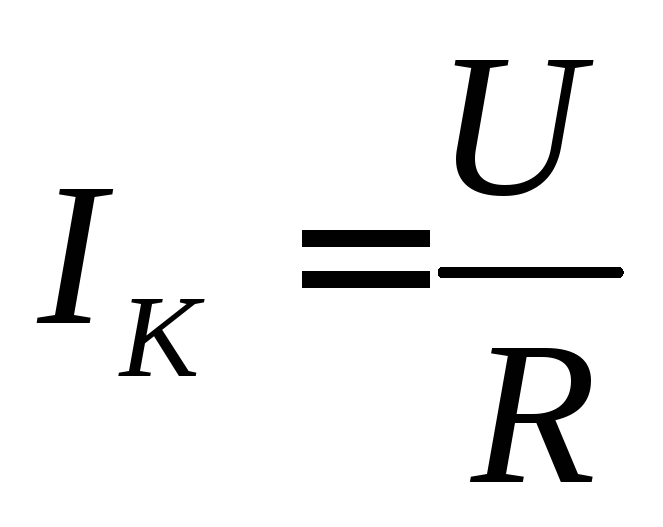 .
.
При уменьшении и увеличении частоты сопротивление контура возрастает, а ток уменьшается. Одновременно с этим увеличивается фазовый сдвиг между напряжением и током.
Кривая, показывающая зависимость тока в контуре от частоты генератора вблизи резонанса, называется резонансной кривой.
Форма резонансной кривой бывает различной и определяется добротностью контура, т. е. соотношением его активного и волнового сопротивлений. Форма резонансной кривой зависит не только от величины активного сопротивления контура, но и от соотношения между индуктивностью L и емкостью С контура, т. е. от характеристического сопротивления контура. Как было показано ранее, соотношение между характеристическим и активным сопротивлениями контура определяет добротность контура:
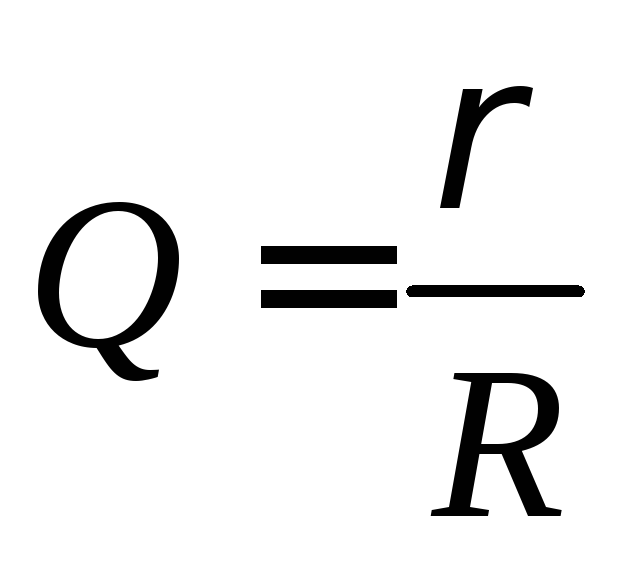 .
.
Таким образом, форма резонансной кривой последовательного контура зависит от добротности контура: чем выше добротность контура, тем острее резонансная кривая.
При изменении частоты питающего генератора изменяется напряжение на элементах контура из-за изменяющегося тока через контур.
Практический интерес представляет зависимость напряжения на конденсаторе от частоты генератора.Напряжение на конденсаторе пропорционально току в контуре и емкостному сопротивлению конденсатора:
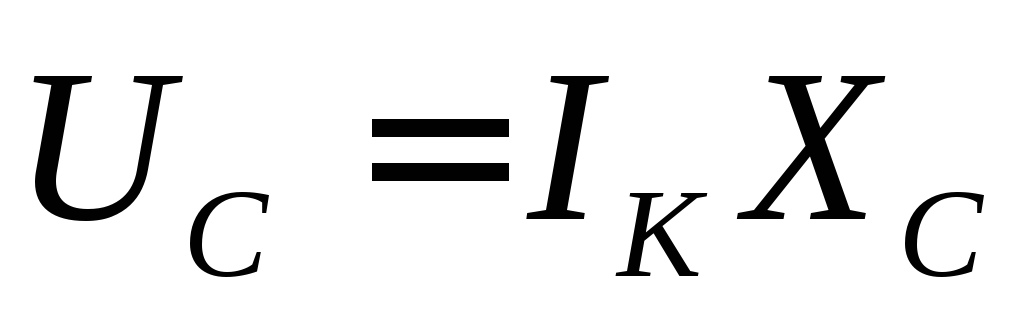 .
.
Ток в контуре вблизи резонанса резко изменяется при изменении частоты, сопротивление конденсатора при этом изменяется относительно мало. Если пренебречь этим изменением, то напряжение на конденсаторе при резонансе можно считать максимальным. Если бы емкостное сопротивление оставалось неизменным, то кривая, показывающая зависимость напряжения на конденсаторе от частоты генератора, была бы точно подобна резонансной кривой тока. Но так как емкостное сопротивление конденсатора при повышении частоты уменьшается, то резонансная кривая напряжения оказывается расположенной несимметрично относительно кривой тока (рис.8).
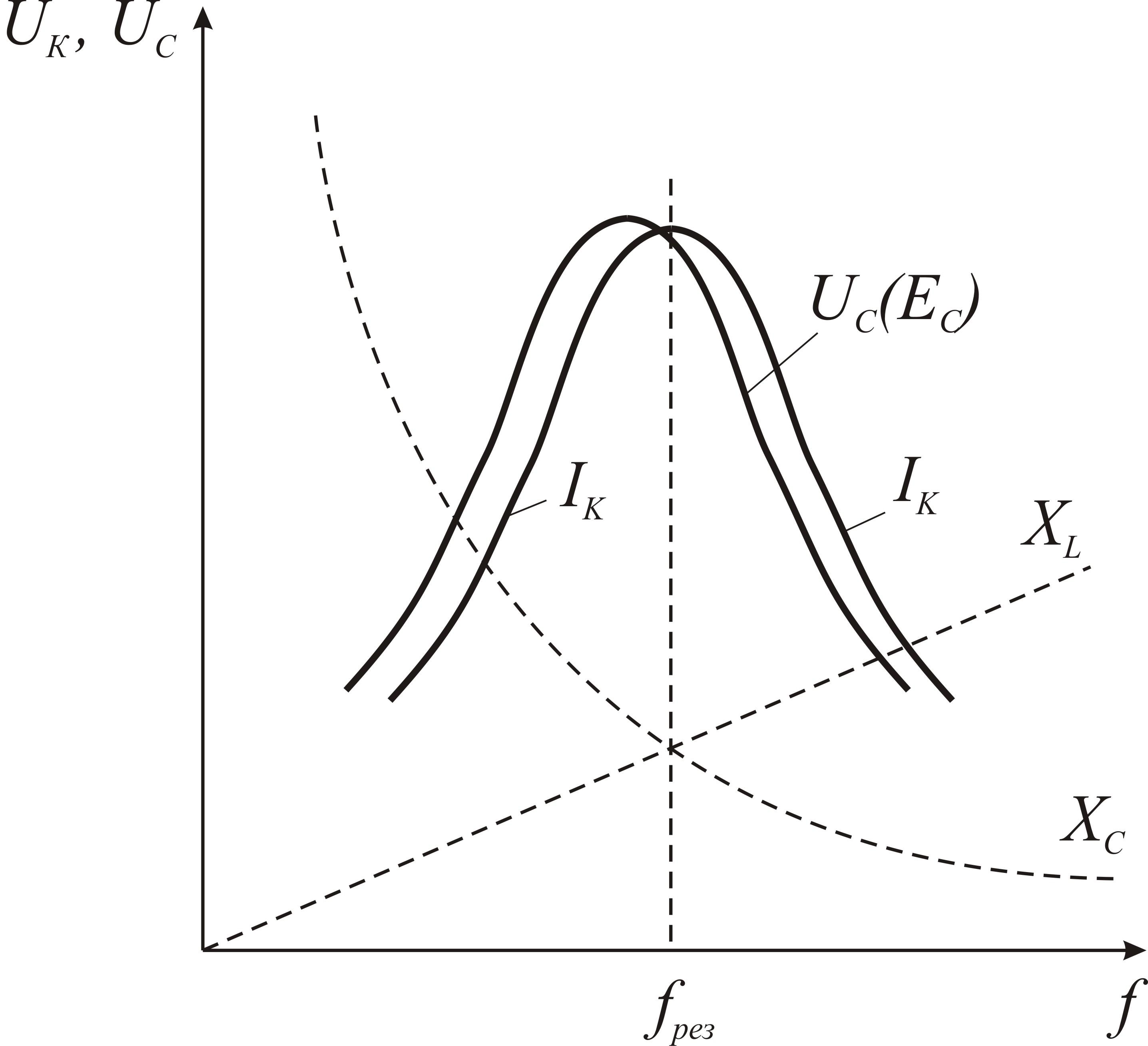
Рис.8.Зависимость напряжения на конденсаторе последовательного контура от частоты

