2.3. Эдс и напряжение в электрической цепи
Источник электрической энергии осуществляет направленное перемещение электрических зарядов по всей замкнутой цепи (рис. 1.3.).
Энергия W, которую затрачивает или может затратить источник на перемещение единицы положительного заряда по всей замкнутой цепи, характеризует электродвижущую силу источника Е (ЭДС):
Из определения следует, что ЭДС является энергетической характеристикой источника тока, а не силовой, как можно было бы решить по названию «электродвижущая сила». Единицей измерения ЭДС является вольт:
(вольт).
Энергия, затраченная на перемещение единицы положительного заряда на каком-либо участке замкнутой цепи, характеризует напряжение или падение напряжения на этом участке (внутреннем или внешнем):
Для замкнутой электрической цепи условие равновесия напряжений
(1.
3)
Таким образом, ЭДС источника (Е) можно рассматривать как сумму падений напряжения на внутреннем (U0) и на внешнем (U) участках замкнутой цепи (рис. 2.3).
Закон Ома для участка электрической цепи устанавливает зависимость между током, напряжением и сопротивлением на этом участке цепи.
Направленное перемещение электрических зарядов в проводнике (т. е. электрический ток I) происходит под действием сил однородного электрического поля (рис. 2.4). Напряженность поля определяется из выражения
где — напряжение на участке проводника длиной l. Плотность тока в проводнике пропорциональна напряженности однородного электрического поля, силы которого направленно перемещают в нем заряды:
(1.
4)
где γ — коэффициент пропорциональности, называемый удельной проводимостью, характеризующий способность проводника проводить электрический ток.
Подставив в выражение (2.4) величину напряженности однородного электрического поля, силы которого перемещают заряды в проводнике, получим
или
где — электрическое сопротивление участка проводника (RAB) длинной l,
Тогда (1.5)
Это и есть математическое выражение закона Ома для участка АВ электрической цепи.
Таким образом, ток на участке электрической цепи пропорционален напряжению на этом участке и обратно пропорционален сопротивлению этого участка
Закон Ома для участка цепи позволяет определить напряжение данном участке
(1.
6)
а также вычислить сопротивление участка электрической цепи
(1.7)
Внешняя характеристика источника ЭДС
Внешняя характеристика
отражает зависимость напряжения на зажимах источника от величины
нагрузки — тока источника, заданного нагрузкой. Напряжение на зажимах
источника меньше ЭДС
на величину падения напряжения на внутреннем сопротивлении источника. Очевидно, что напряжение на зажимах источника ЭДС тем больше, чем меньше его внутреннее сопротивление. В
идеальном источнике ЭДС R0=0, U=E (напряжение не зависит от величины
нагрузки). Однако не всегда при анализе и расчете цепи источник
электрической энергии …
Внешняя характеристика отражает зависимость напряжения на зажимах источника от величины нагрузки — тока источника, заданного нагрузкой.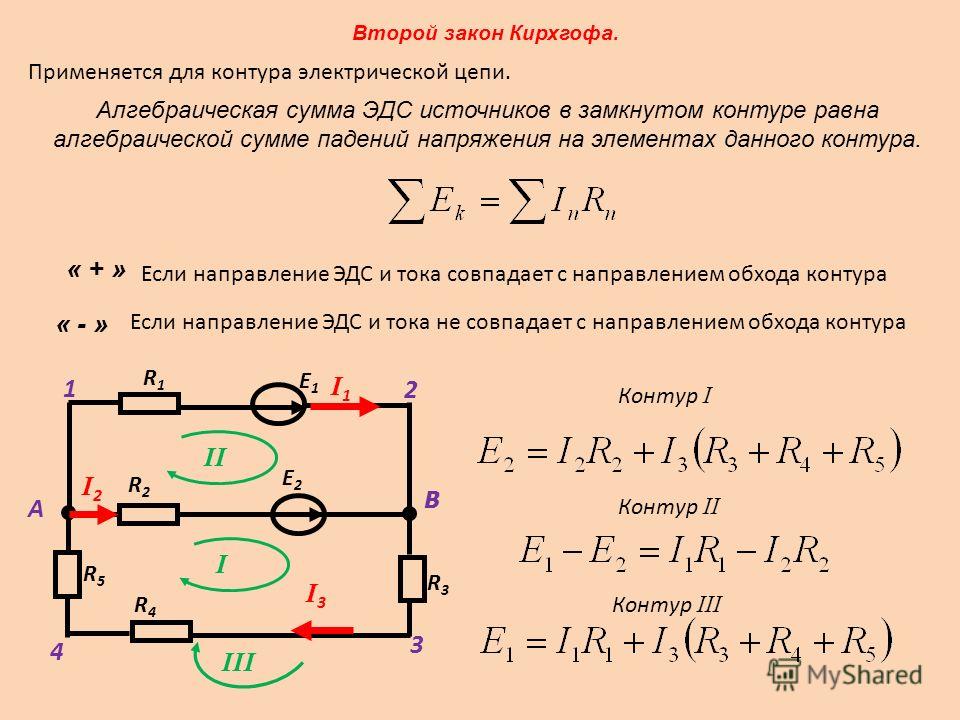
Этому уравнению соответствует внешняя характеристика источника ЭДС (рис. 1). построенная по двум точкам:
1) при I=0 E=U;
2) при U=0 E=R0I .
Очевидно, что напряжение на зажимах источника ЭДС тем больше, чем меньше его внутреннее сопротивление.
В идеальном источнике ЭДС R0=0, U=E (напряжение не зависит от величины нагрузки). Однако не всегда при анализе и расчете цепи источник электрической энергии удобно представлять в качестве источника ЭДС. Если внутреннее сопротивление источника значительно превышает внешнее сопротивление цепи, что, например, имеет место в электронике, то получим, что ток в цепи I=U/(R+R0) и при R0>>R практически не зависит от сопротивления нагрузки. В этом случае источник энергии представляют в качестве источника тока.
Рис.
1.
Разделим уравнение (1) на R0 (2):
Для идеального источника тока Rс = . Вольтамперные характеристики реального и идеального источников тока показаны на рис. 3.
Рис. 2
Рис. 3
Когда нет четкого разграничения величин R и R0 , в качестве расчетного эквивалента источника энергии можно использовать либо источник ЭДС, либо источник тока. В последнем, случае для определения падения напряжения используют выражение (3).
Режимы работы источника
1. Номинальный режим — это режим работы, на который рассчитан источник заводом-изготовителем. Для данного режима в паспорте источника указывают номинальные ток Iном и номинальное напряжение Uном или мощность Pном.
2. Режим холостого хода. В этом режиме внешняя цепь отключена от источника, ток источника I = 0 и, следовательно, напряжение на зажимах источника — напряжение холостого хода Uхх = Е — см. уравнение (1).
3. Режим короткого замыкания. Сопротивление внешней по отношению к источнику цепи равно нулю. Ток источника ограничивается только его внутренним сопротивлением. Из уравнения (1) при U=0 получаем I = Iкз = U / R0. Для уменьшения потерь энергии в источнике ЭДС R0 должно быть возможно меньшим, а в идеальном источнике R0 = 0. С учетом этого Iкз >> Iном и является недопустимым для источника.
4. Согласованный режим — это режим, при котором от источника к потребителю передается максимальная мощность. Определить эту мощность можно через параметры источника. Так, мощность, переданная в нагрузку, Р = I2R. P = Pmax при R = R0. Тогда максимальная мощность, переданная потребителю, Pmax=E2/4R0. КПД источника в согласованном режиме не превышает 50 %.
10.12.2016 Без рубрики Нет комментариев
11.4: Зависимость клеточного потенциала от концентрации
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 15199
Цели обучения
- Связь потенциалов клеток с изменениями энергии Гиббса
- Использование уравнения Нернста для определения клеточных потенциалов в нестандартных условиях
- Выполнение расчетов, включающих преобразование потенциалов клеток, изменений свободной энергии и констант равновесия
Уравнение Нернста позволяет определять клеточный потенциал в нестандартных условиях.
Он связывает измеренный клеточный потенциал с коэффициентом реакции и позволяет точно определить константы равновесия (включая константы растворимости). 9\circ_\textrm{cell}-\left(\dfrac{RT}{nF}\right)\ln Q \label{Eq3} \]
Уравнение \(\ref{Eq3}\) называется уравнением Нернста , в честь немецкого физика и химика Вальтера Нернста (1864–1941), который первым его вывел. Уравнение Нернста, пожалуй, самое важное соотношение в электрохимии. Когда окислительно-восстановительная реакция находится в равновесии (\(ΔG = 0\)), то уравнение \(\ref{Eq3}\) сводится к уравнению \(\ref{Eq31}\) и \(\ref{Eq32}\) потому что \(Q = K\), и нет чистого переноса электронов (т. е. E 9\circ_\textrm{cell}-\left(\dfrac{\textrm{0,0591 V}}{n}\right)\log Q \label{Eq4} \]
Мощность уравнения Нернста
Уравнение Нернста (\(\ref{Eq3}\)) можно использовать для определения значения E ячейки и, следовательно, направления спонтанной реакции для любой окислительно-восстановительной реакции в любых условиях.
Уравнение \(\ref{Eq4}\) позволяет нам рассчитать потенциал, связанный с любой электрохимической ячейкой при 298 K для любой комбинации концентраций реагента и продукта при любых условиях. Таким образом, мы можем определить самопроизвольное направление любой окислительно-восстановительной реакции при любых условиях, если у нас есть табличные значения соответствующих стандартных электродных потенциалов. Обратите внимание, что в уравнении \(\ref{Eq4}\) потенциал клетки изменяется на 0,059.°_{cell} = 0,25\, V \nonumber \]
Рассчитайте \(E_{cell}\) для этой реакции при следующих нестандартных условиях и определите, будет ли она протекать самопроизвольно: [Ce 4 + ] = 0,013 М, [Ce 3 + ] = 0,60 М, [Cl — ] = 0,0030 М, \(P_\mathrm{Cl_2}\) = 1,0 атм, T = 25°C.
Дано: сбалансированная окислительно-восстановительная реакция, стандартный клеточный потенциал и нестандартные условия
Запрошено: клеточный потенциал
Стратегия:
Определите количество электронов, переданных в ходе окислительно-восстановительного процесса.
Затем используйте уравнение Нернста, чтобы найти потенциал клетки в нестандартных условиях.
Решение
Мы можем использовать предоставленную информацию и уравнение Нернста для расчета ячейки E . Кроме того, поскольку температура составляет 25°C (298 K), мы можем использовать уравнение \(\ref{Eq4}\) вместо уравнения \(\ref{Eq3}\). Общая реакция включает чистый перенос двух электронов: 9{−}4(водн.) + 2h3O(ж)} \;\;\; E°_{ячейка} = −0,20\; V\nonumber \]
Рассчитайте \(E_{cell}\) для реакции при следующих нестандартных условиях и решите, будет ли реакция протекать самопроизвольно: pH 10, \(P_\mathrm{O_2}\)= 0,20 атм, [MNO 4 — ] = 1,0 × 10 -4 М, Т = 25°С.
- Ответить
E ячейка = -0,22 В; реакция не будет происходить самопроизвольно.
Таким образом, начальное напряжение больше E°, потому что \(Q<1\).
По мере протекания реакции [Zn 2 + ] в анодном отделении увеличивается по мере растворения цинкового электрода, в то время как [Cu 2 + ] в катодном отделении уменьшается по мере осаждения металлической меди на электроде. Во время этого процесса отношение Q = [Zn 2 + ]/[Cu 2 + ] неуклонно увеличивается, и поэтому напряжение на ячейке неуклонно снижается. В конце концов, [Zn 2 + ] = [Cu 2 + ], поэтому Q = 1 и E ячейка = E° ячейка . За пределами этой точки [Zn 2 + ] будет продолжать увеличиваться в анодной камере, а [Cu 2 + ] будет продолжать уменьшаться в катодной камере. Таким образом, значение Q будет увеличиваться еще больше, что приведет к дальнейшему уменьшению в ячейке E . Когда концентрации в двух отсеках противоположны исходным концентрациям (т.
е. 1,0 М Zn 2 + и 1,0 × 10 −6 M Cu 2 + ), Q = 1,0 × 10 6 , и потенциал ячейки снизится до 0,92 В.
Изменение ячейки E с \(\log{Q}\) в этом диапазоне является линейным с наклоном -0,0591/n, как показано на рисунке \(\PageIndex{1}\). По мере дальнейшего протекания реакции \(Q\) продолжает расти, и Е 9{37}\end{align} \label{Eq7} \]
Напомним, что в состоянии равновесия \(Q = K\).
Таким образом, константа равновесия реакции металлического Zn с Cu 2 + с образованием металлической Cu и Zn 2 + составляет 1,7 × 10 37 при 25°C.
Уравнение Нернста: Уравнение Нернста (opens in new window) [youtu.be]
Концентрационные ячейки
Напряжение также можно генерировать путем создания электрохимической ячейки, в которой каждое отделение содержит один и тот же окислительно-восстановительный активный раствор, но в разных концентрациях. Напряжение возникает, когда концентрации уравновешиваются. Предположим, например, что у нас есть ячейка с 0,010 М AgNO 9\circ_\textrm{ячейка}-\left(\dfrac{\textrm{0,0591 В}}{n}\right)\log Q \\[4pt] &=0-\left(\dfrac{\textrm{0,0591 В} }}{1}\right)\log\left(\dfrac{0.010}{1.0}\right) \\[4pt] &=\textrm{0.12 V} \end{align*} \nonumber \]
An Электрохимическая ячейка этого типа, в которой анодное и катодное отделения идентичны, за исключением концентрации реагента, называется концентрационной ячейкой .
По мере протекания реакции разница концентраций Ag + в двух отсеках уменьшится, как и Е ячейка . Наконец, когда концентрация Ag + одинакова в обоих отсеках, будет достигнуто равновесие, и измеренная разность потенциалов между двумя отсеками будет равна нулю (E , ячейка = 0).
Пример \(\PageIndex{2}\)
Рассчитайте напряжение в гальваническом элементе, который содержит марганцевый электрод, погруженный в 2,0 М раствор MnCl 2 в качестве катода, и марганцевый электрод, погруженный в 5,2 × 10 -2 М раствор MnSO 4 в качестве анода (Т = 25°С).
Дано: гальванический элемент, типы электродов и концентрации раствора
Запрошено: напряжение
Стратегия:
- Напишите общую реакцию, происходящую в элементе.
- Определите количество переданных электронов. Подставьте это значение в уравнение Нернста, чтобы рассчитать напряжение.
Раствор
9{-2}}{2.0}\right) \\[4pt] &=\textrm{0,047 В}\end{align*} \nonumber \]
Таким образом, марганец растворится с электрода в отсеке, в котором находится более разбавленным раствором и будет осаждаться на электроде в отсеке, где находится более концентрированный раствор.
Упражнение \(\PageIndex{2}\)
Предположим, мы построили гальванический элемент, поместив два одинаковых платиновых электрода в два стакана, соединенных соляным мостиком. Один стакан содержит 1,0 М HCl, а другой 0,010 М раствор Na 9{−} \rightarrow 2h3O(l)} \nonumber \]
Каков будет потенциал, когда цепь замкнута?
- Ответить
0,41 В
Использование клеточных потенциалов для измерения продуктов растворимости
Поскольку напряжения относительно легко точно измерить с помощью вольтметра, электрохимические методы обеспечивают удобный способ определения концентрации очень разбавленных растворов и продуктов растворимости (\(K_{sp}\) ) труднорастворимых веществ.
Как вы узнали ранее, произведения растворимости могут быть очень маленькими, со значениями меньше или равными 10 −30 . Константы равновесия такой величины практически невозможно точно измерить прямыми методами, поэтому мы должны использовать более чувствительные альтернативные методы, такие как электрохимические методы.
В одном отделении ячейки находится серебряная проволока, введенная в 1,0 М раствор Ag + ; в другом отсеке находится серебряная проволока, вставленная в 1,0 М раствор Cl —, насыщенный AgCl. В этой системе концентрация ионов Ag + в первом отсеке равна K sp . Мы можем увидеть это, разделив обе части уравнения для K sp на [Cl − ] и подставив:
\[\begin{align*}[\ce{Ag^{+}}] &= \ dfrac{K_{sp}}{[\ce{Cl^{-}}]} \\[4pt] &= \dfrac{K_{sp}}{1.
0} = K_{sp}. \end{align*} \nonumber \] 9+}]_\textrm{concentrated}}\right) \nonumber \\[4pt] &= -\textrm{0,0591 V } \log\left(\dfrac{K_{\textrm{sp}}}{1.0}\ справа) \nonumber \\[4pt] &=-\textrm{0,0591 V }\log K_{\textrm{sp}} \label{Eq122} \end{align} \]
Замкнув цепь, мы можем измерить потенциал, вызванный разницей [Ag+] в двух клетках. В этом случае экспериментально измеренное напряжение концентрационной ячейки при 25°C составляет 0,580 В. Решение уравнения \(\ref{Eq122}\) для \(K_{sp}\),
\[\begin{align* }\log K_\textrm{sp} & =\dfrac{-E_\textrm{cell}}{\textrm{0,059{-10}\end{align*} \nonumber \]
Таким образом, одно измерение потенциала может предоставить информацию, необходимую для определения значения произведения растворимости труднорастворимой соли.
Пример \(\PageIndex{3}\): растворимость сульфата свинца(II)
тот, что показан на рисунке \(\PageIndex{1}\), содержит 1,0 М раствор хорошо растворимого Pb 2 + соль [тригидрат ацетата свинца (II)] в одном отделении, соединенном солевым мостиком с 1,0 М раствором Na 2 SO 4 , насыщенным PbSO 4 , в другом.
Затем вы вставляете электрод Pb в каждое отделение и замыкаете цепь. Ваш вольтметр показывает напряжение 230 мВ. Что такое K sp для PbSO 4 ? Сообщите свой ответ до двух значащих цифр.
Дано: гальванический элемент, концентрации раствора, электроды и напряжение
Запрошено: K sp
Стратегия:
- Из предоставленной информации напишите уравнение для K sp . Выразите это уравнение через концентрацию Pb 2 + .
- Определите число электронов, переданных в электрохимической реакции. Подставьте соответствующие значения в уравнение \(\ref{Eq12}\) и найдите K sp .
Раствор
А 9{-8} & =K_\textrm{sp}\end{align*} \nonumber \]
Упражнение \(\PageIndex{3}\)
Ячейка концентрации, подобная описанной в примере \(\PageIndex {3}\) содержит 1,0 М раствор нитрата лантана [La(NO 3 ) 3 ] в одном отделении и 1,0 М раствор фторида натрия, насыщенного LaF 3 , в другом.
В каждое отделение вставляется металлическая полоска La, и цепь замыкается. Измеренный потенциал 0,32 В. Что такое К sp для LaF 3 ? Сообщите свой ответ до двух значащих цифр.
- Ответить
5,7 × 10 −17
Использование клеточных потенциалов для измерения концентраций
Еще одно применение уравнения Нернста — расчет концентрации видов с учетом измеренного потенциала и концентраций всех других видов. Мы видели пример этого в примере \(\PageIndex{3}\), в котором условия эксперимента были определены таким образом, что концентрация иона металла была равна K сп . Потенциальные измерения могут быть использованы для получения концентраций растворенных частиц и в других условиях, что объясняет широкое использование электрохимических ячеек во многих аналитических устройствах. Возможно, наиболее распространенным применением является определение [H + ] с помощью рН-метра, как показано ниже.
Пример \(\PageIndex{4}\): измерение pH
Предположим, что гальванический элемент состоит из стандартной пары Zn/Zn 2 + в одном отсеке и модифицированного водородного электрода во втором отсеке. Давление газообразного водорода составляет 1,0 атм, но [H 9{+}} (вода, ?\, М)| \ce{h3} (г, 1,0\, атм)| Pt(s) \nonumber \]
Чему равен pH раствора во втором отсеке, если измеренный потенциал в ячейке составляет 0,26 В при 25°C?
Дано: гальванический элемент, схема ячейки и потенциал ячейки
Запрошено: рН раствора
Стратегия:
- Запишите общую реакцию клетки.
- Подставьте соответствующие значения в уравнение Нернста и найдите −log[H + ] для получения рН.
Раствор
A В стандартных условиях происходит общая реакция восстановления протонов цинком с образованием H 2 (обратите внимание, что Zn находится ниже H 2 в таблице P2):
Zn(s) ) + 2H 2 + (водн.
) → Zn 2 + (водн.) + H 2 (г) E°=0,76 В
B 9 0053 Путем подстановки данных значений в упрощенный Нернст уравнения (Equation \(\ref{Eq4}\)), мы можем вычислить [H 9+}] \\
8.5 &=\mathrm{pH}\end{align*} \nonumber \]
Таким образом, потенциал гальванического элемента можно использовать для измерения pH раствора.
Упражнение \(\PageIndex{4}\)
Предположим, вы работаете в экологической лаборатории и хотите использовать электрохимический метод для измерения концентрации Pb 2 + в грунтовых водах. Вы конструируете гальванический элемент, используя стандартный кислородный электрод в одном отсеке (Е° катод = 1,23 В). В другом отсеке находится полоска свинца в образце грунтовых вод, к которому вы добавили достаточное количество уксусной кислоты, слабой органической кислоты, чтобы обеспечить электрическую проводимость. Схема ячеек выглядит следующим образом: 9{−9}\; м\)
Резюме
Уравнение Нернста можно использовать для определения направления самопроизвольной реакции любой окислительно-восстановительной реакции в водном растворе.
Уравнение Нернста позволяет определить самопроизвольное направление любой окислительно-восстановительной реакции при любых условиях реакции по значениям соответствующих стандартных электродных потенциалов. Концентрационные ячейки состоят из анодного и катодного отсеков, которые идентичны, за исключением концентрации реагента. Поскольку ΔG = 0 в равновесии, измеренный потенциал концентрационной ячейки равен нулю в равновесии (концентрации равны). Гальванический элемент также можно использовать для измерения произведения растворимости труднорастворимого вещества и расчета концентрации частиц с учетом измеренного потенциала и концентраций всех других частиц.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- № на стр.
- Теги
13.7: Электрогенераторы и противо-ЭДС
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4433
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Объяснять, как работает электрический генератор
- Определить ЭДС индукции в петле в любой момент времени, вращающейся с постоянной скоростью в магнитном поле
- Показать, что вращающиеся катушки имеют ЭДС индукции; в двигателях это называется обратной ЭДС, потому что она противодействует входу ЭДС двигателя
Множество важных явлений и устройств можно понять с помощью закона Фарадея.
В этом разделе мы рассмотрим два из них.
Электрические генераторы
Электрические генераторы индуцируют ЭДС, вращая катушку в магнитном поле, как кратко описано в ЭДС движения. Теперь рассмотрим генераторы более подробно. Рассмотрим следующий пример. 9о\)) за 15,0 мс. Круглая катушка из 200 витков имеет радиус 5,00 см и находится в однородном магнитном поле 0,80 Тл. Какая ЭДС наведена?
Рисунок \(\PageIndex{1}\): Когда эта генераторная катушка поворачивается на четверть оборота, магнитный поток \(\Phi_m\) изменяется от своего максимума до нуля, индуцируя ЭДС.Стратегия
С помощью закона индукции Фарадея находим ЭДС индукции: в примере 13.4.3. Согласно диаграмме, проекция вектора нормали к поверхности \(\hat{n}\) на магнитное поле изначально равна \(cos\, \theta\), и это вставляется определением скалярного произведения. Величина магнитного поля и площадь петли фиксируются во времени, что упрощает интегрирование. ЭДС индукции записывается по закону Фарадея: 9{-3} s} = 131 \, V.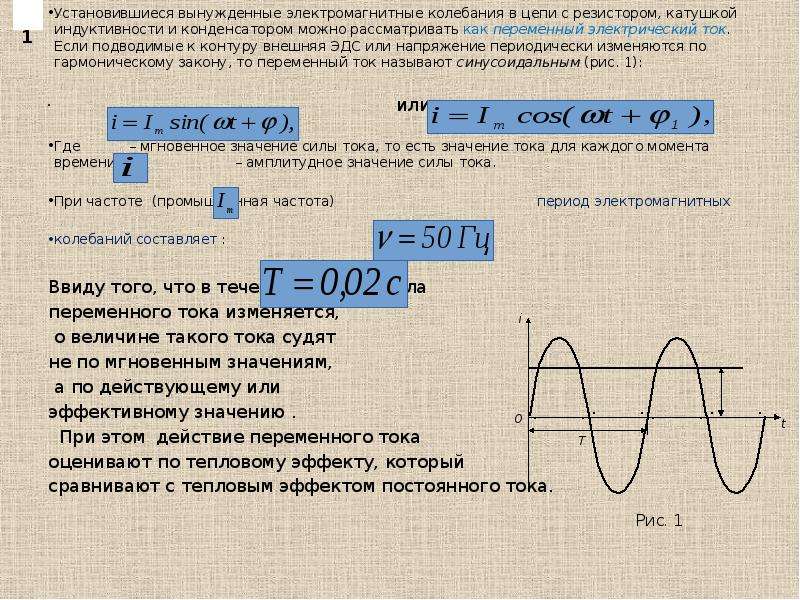
\]
Значение
Это практическое среднее значение, аналогичное 120 В, используемому в домашнем хозяйстве.
ЭДС, рассчитанная в примере \(\PageIndex{1}\), представляет собой среднее значение за одну четвертую оборота. Чему равна ЭДС в каждый момент времени? Оно изменяется в зависимости от угла между магнитным полем и перпендикуляром к катушке. Мы можем получить выражение для ЭДС как функции времени, рассматривая ЭДС движения на вращающейся прямоугольной катушке шириной w и высота l в однородном магнитном поле, как показано на рисунке \(\PageIndex{2}\).
Рисунок \(\PageIndex{2}\): Генератор с одной прямоугольной катушкой, вращающейся с постоянной угловой скоростью в однородном магнитном поле, создает ЭДС, которая изменяется синусоидально во времени. Обратите внимание, что генератор похож на двигатель, за исключением того, что вал вращается для создания тока, а не наоборот. Заряды в проводах петли испытывают магнитную силу, потому что они движутся в магнитном поле.
На заряды в вертикальных проводах действуют силы, параллельные проводу, вызывающие токи. Но находящиеся в верхнем и нижнем сегментах ощущают силу, перпендикулярную проводу, которая не вызывает тока. Таким образом, мы можем найти ЭДС индукции, рассматривая только боковые провода. ЭДС движения равна \(\epsilon = Blv\), где скорость v перпендикулярно магнитному полю B . Здесь скорость составляет угол \(\theta\) с B , так что ее составляющая, перпендикулярная B , равна v sin \(\theta\) (см. рисунок \(\PageIndex{2}\) ). Таким образом, в этом случае ЭДС, индуцированная с каждой стороны, равна \(\эпсилон = Blv \, sin \, \theta\), и они имеют одинаковое направление. Суммарная ЭДС вокруг контура тогда равна
\[\epsilon = 2 Blv \, sin \, \theta.\]
Это выражение верно, но оно не дает ЭДС как функцию времени. Чтобы найти зависимость ЭДС от времени, предположим, что катушка вращается с постоянной угловой скоростью \(\omega\).
Угол \(\theta\) связан с угловой скоростью соотношением \(\theta = \omega t\), так что \[\epsilon = 2 Blv \, sin (\omega t).\]
Теперь линейная скорость v связана с угловой скоростью \(\omega\) соотношением \(v = r\omega\). Здесь \(r = \omega/2\), так что \(v = (\omega/2)\omega\), и
\[\epsilon = 2Bl \frac{\omega}{2} \omega \, sin \, \omega t = (l\omega) Bw \, sin \, \omega t.\]
Учитывая, что площадь петли равна \(A = l\omega\), и учитывая N витков, находим, что
\[\epsilon = NBAw \, sin \, (\omega t).\]
Это ЭДС наведенная в катушке генератора N витков и площадь A вращающаяся с постоянной угловой скоростью \(ω\) в однородном магнитном поле B . Это также может быть выражено как
\[\epsilon = \epsilon_0 \, sin \, \omega t,\], где
\[\epsilon_0 = NAB\omega\]
— пиковая ЭДС, поскольку максимальное значение из \(sin (\omega t) = 1\).
Обратите внимание, что частота колебаний равна \(f = \omega/2\pi\), а период равен \(T = 1/f = 2\pi /\omega\). На рисунке \(\PageIndex{3}\) показан график ЭДС как функции времени, и теперь кажется разумным, что переменное напряжение является синусоидальным.
Тот факт, что пиковая ЭДС равна \(\epsilon_0 = NBA\omega\), имеет смысл. Чем больше количество катушек, тем больше их площадь, и чем сильнее поле, тем больше выходное напряжение. Интересно, что чем быстрее раскручивается генератор (больше ω), тем больше ЭДС. Это заметно на велосипедных генераторах, по крайней мере, на более дешевых.
На рисунке \(\PageIndex{4}\) показана схема, с помощью которой генератор может производить импульсы постоянного тока. Более сложное расположение нескольких катушек и разъемных колец может обеспечить более плавный постоянный ток, хотя для создания постоянного тока без пульсаций обычно используются электронные, а не механические средства.
В реальной жизни электрические генераторы сильно отличаются от рисунков в этом разделе, но принцип тот же. Источником механической энергии, вращающей катушку, может быть падающая вода (гидроэнергия), пар, образующийся при сжигании ископаемого топлива, или кинетическая энергия ветра. На рисунке \(\PageIndex{5}\) показан вид паровой турбины в разрезе; пар движется по лопастям, соединенным с валом, который вращает катушку внутри генератора. Генерация электрической энергии из механической энергии является основным принципом всей энергии, которая передается через наши электрические сети в наши дома.
Рисунок \(\PageIndex{5}\): Паровая турбина/генератор. Пар, образующийся при сжигании угля, воздействует на лопатки турбины, вращая вал, соединенный с генератором. Генераторы, показанные в этом разделе, очень похожи на двигатели, показанные ранее. Это не случайно.
Фактически двигатель становится генератором, когда его вал вращается. Некоторые ранние автомобили использовали свой стартер в качестве генератора. В следующем разделе мы дополнительно исследуем действие двигателя в качестве генератора.
Back Emf
Генераторы преобразуют механическую энергию в электрическую, тогда как двигатели преобразуют электрическую энергию в механическую. Таким образом, неудивительно, что двигатели и генераторы имеют одинаковую общую конструкцию. Двигатель работает, посылая ток через петлю провода, расположенную в магнитном поле. В результате магнитное поле оказывает крутящий момент на петлю. Это вращает вал, тем самым извлекая механическую работу из электрического тока, подаваемого изначально. (Обратитесь к разделу «Сила и крутящий момент в токовой петле» для обсуждения двигателей, которые помогут вам больше узнать о них, прежде чем продолжить.)
Когда катушка двигателя вращается, магнитный поток через катушку изменяется, и возникает ЭДС (в соответствии с законом Фарадея).
Таким образом, двигатель действует как генератор всякий раз, когда его катушка вращается. Это происходит независимо от того, вращается ли вал от внешнего источника, например, от ременной передачи, или от действия самого двигателя. То есть, когда двигатель совершает работу и его вал вращается, возникает ЭДС. Закон Ленца говорит нам, что ЭДС противодействует любому изменению, так что входная ЭДС, питающая двигатель, противостоит ЭДС, создаваемой самим двигателем, называемой 9.0052 противоЭДС двигателя (рисунок \(\PageIndex{6}\)).
Выходная мощность генератора двигателя представляет собой разницу между напряжением питания и противо-ЭДС. Обратная ЭДС равна нулю при первом включении двигателя, а это означает, что катушка получает полное управляющее напряжение, а двигатель потребляет максимальный ток, когда он включен, но не вращается.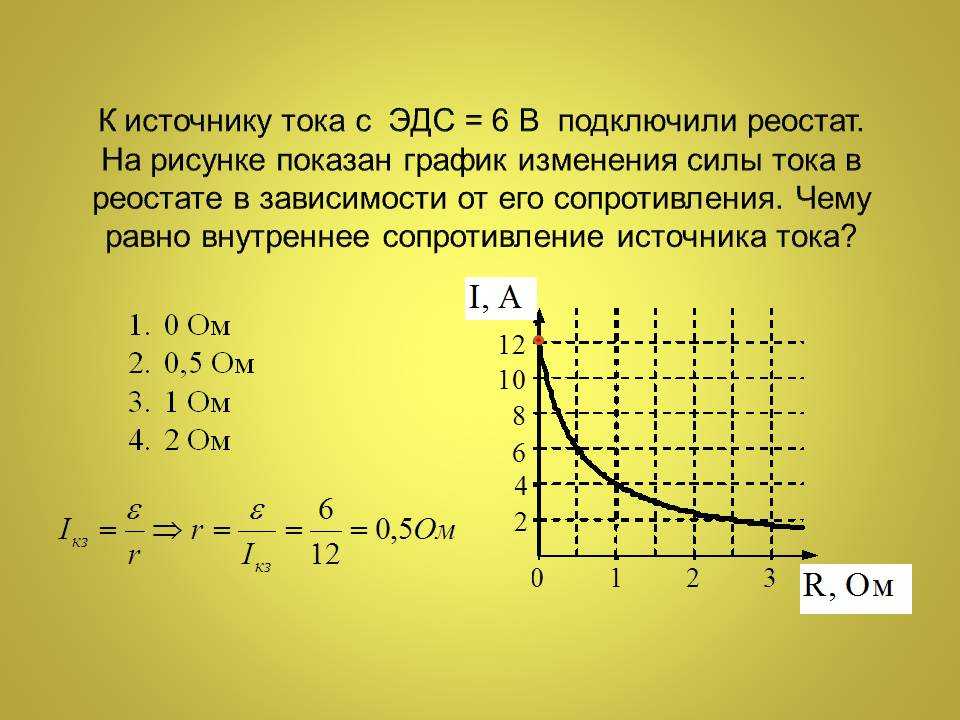
По мере того, как двигатель вращается быстрее, обратная ЭДС растет, всегда противодействуя ЭДС возбуждения, и снижает как напряжение на катушке, так и количество потребляемого ею тока. Этот эффект заметен во многих распространенных ситуациях. При первом включении пылесоса, холодильника или стиральной машины свет в той же цепи ненадолго гаснет из-за 92R)\), возможно, даже выжечь. С другой стороны, если на двигатель нет механической нагрузки, он увеличивает свою угловую скорость ω до тех пор, пока противо-ЭДС не станет почти равной движущей ЭДС. Тогда двигатель использует ровно столько энергии, сколько необходимо для преодоления трения.
Вихревые токи в железных сердечниках двигателей могут привести к значительным потерям энергии. Их обычно минимизируют за счет изготовления сердечников из тонких электроизолированных листов железа. На магнитные свойства сердечника практически не влияет ламинирование изоляционного листа, в то время как резистивный нагрев значительно снижается. Рассмотрим, например, катушки двигателя, представленные на рисунке \(\PageIndex{6}\).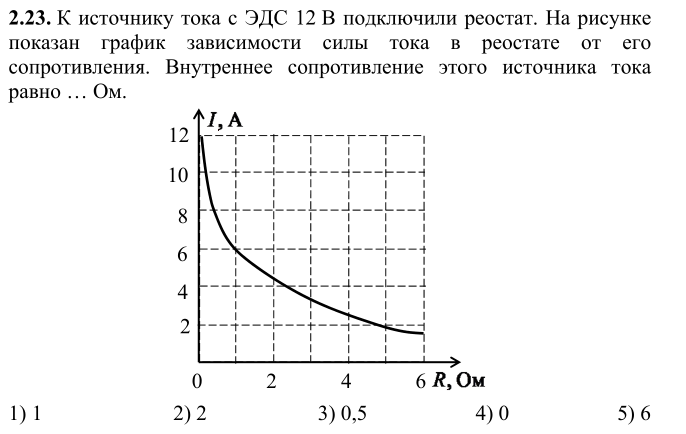
Катушки имеют эквивалентное сопротивление \(0,400 Ом, Омега\) и приводятся в действие ЭДС 48,0 В. Вскоре после включения они потребляют ток 92R = 5,76 \, кВт\) энергии в виде теплопередачи. При нормальных условиях работы этого двигателя предположим, что противо-ЭДС равна 40,0 В. Тогда при рабочей скорости общее напряжение на катушках составляет 8,0 В (48,0 В минус противо-ЭДС 40,0 В), а потребляемый ток равен
\[ I = V/R = (8,0 Ом, В)/(0,400 Ом, Омега) = 20 Ом, А.]
Тогда при нормальной нагрузке рассеиваемая мощность равна \(P = IV = (20 Ом, А)(8,0 л, В) = 160 л, Вт\). Это не создает проблем для этого двигателя, в то время как прежние 5,76 кВт сожгли бы катушки, если бы они продолжались.
Двигатель с последовательным возбуждением в работе
Общее сопротивление \((R_f + R_a)\) двигателя постоянного тока с последовательным возбуждением составляет \(2,0 \, \Omega\) (Рисунок \(\PageIndex{7}\ )). При подключении к источнику 120 В \((\epsilon_S)\) двигатель потребляет 10 А при работе с постоянной угловой скоростью.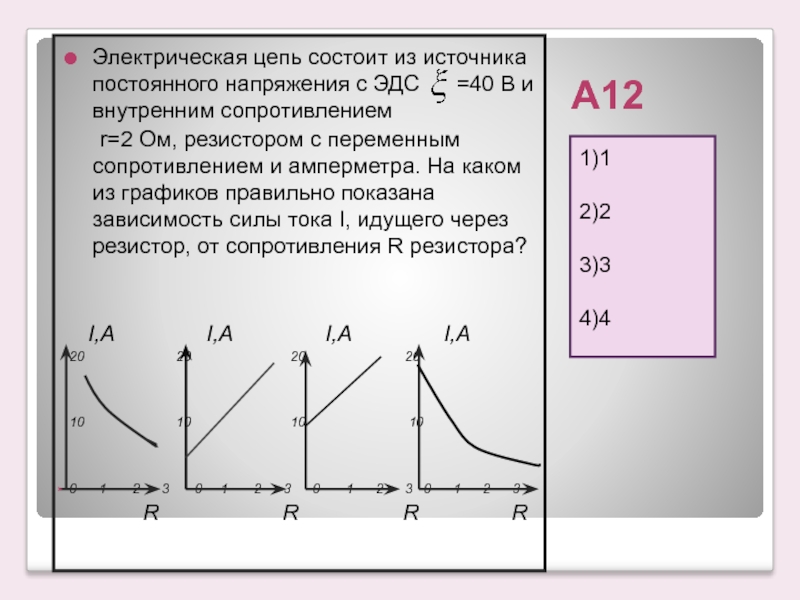
(a) Чему равна противо-ЭДС, индуцируемая во вращающейся катушке \(\epsilon_i\)? б) Какова механическая мощность двигателя? в) Какая мощность рассеивается на сопротивлении катушек? г) Какова выходная мощность источника 120 В? (e) Предположим, что нагрузка на двигатель увеличивается, что приводит к его замедлению до точки, когда он потребляет 20 А. Ответьте на пункты с (a) по (d) для этой ситуации.
Стратегия
ПротивоЭДС рассчитывается на основе разницы между подаваемым напряжением и потерями от тока через сопротивление. Мощность каждого устройства рассчитывается по одной из формул мощности на основе предоставленной информации.
Решение
- Обратная ЭДС равна \[\epsilon_i = \epsilon_S — I(R_f + RE_a) = 120 \, V — (10 \, A)(2,0 \, \Omega) = 100 \, V .\] 92 \, Вт.\]
Эта страница под названием 13.
