Сила Лоренца. Движение заряженных частиц в магнитном поле.

Опыт показывает, что магнитное поле действует не только на проводники с током, но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на заряд q ,движущийся в магнитном поле со скоростью , называется силой Лоренца.

— установлено опытным путем

Направление силы Лоренца определяется для положительных зарядов правилом левой руки (т.к. направление и для совпадают): если ладонь левой руки расположить так, чтобы вектор входил в нее, а 4 вытянутых пальца сонаправить с движением положительного заряда, то отогнутый большой палец покажет направление силы Лоренца.

Для отрицательных зарядов берется противоположное направление.

Сила Лоренца всегда направлена перпендикулярно скорости заряда и сообщает ему нормальное ускорение. Не изменяя модуля скорости, а лишь изменяя ее направление, сила Лоренца не совершает работы и кинетическая энергия заряженной частицы при движении в магнитном поле не изменяется.

Если на движущийся электрический заряд помимо магнитного поля действует и электрическое поле напряженностью , то результирующая сила

— формула Лоренца.

1. Движение заряженной частицы вдоль силовой линии, .

,

магнитное поле не действует на частицу.

Заряженная частица движется по инерции равномерно прямолинейно.

2. Движение заряженной частицы перпендикулярно силовым линиям, .

Пусть в однородное магнитное поле с индукцией влетела заряженная частица массой m с зарядом q перпендикулярно магнитным силовым линиям со скоростью .

В каждой точке поля на частицу действует . Т.к. , то . Ускорение изменяет только направление скорости, , значит, . В этих условиях тело (заряженная частица) движется равномерно по окружности.

Согласно II закону Ньютона:

(1)

Т.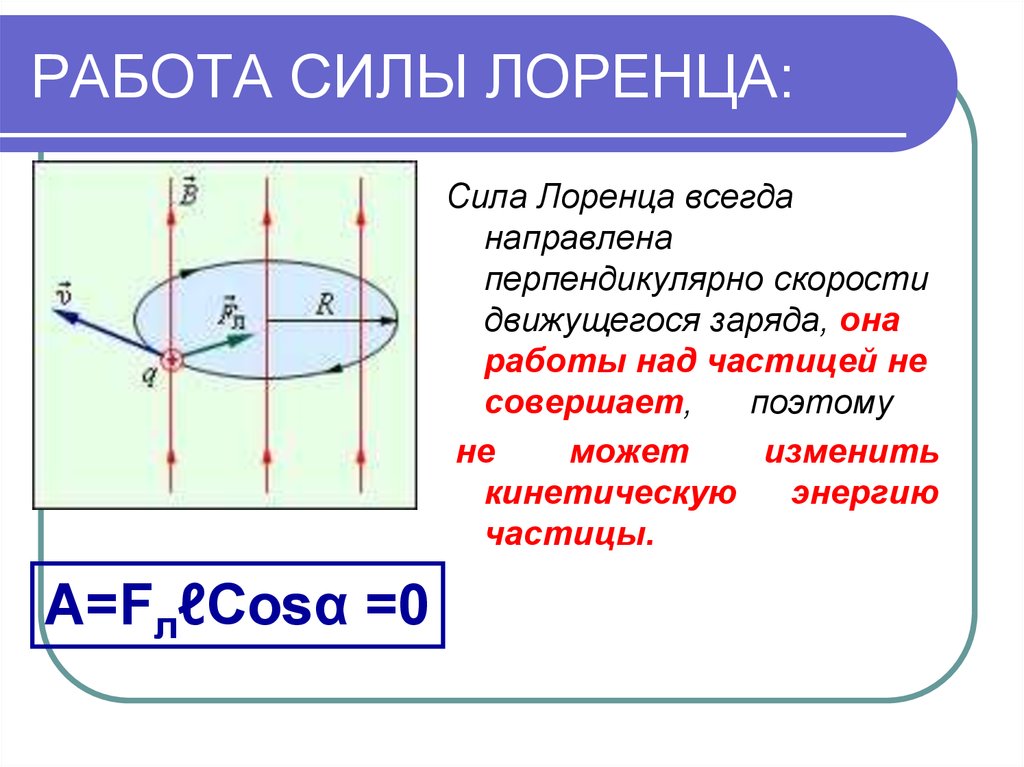 к. все величины, входящие в (1), постоянны, радиус кривизны R будет оставаться постоянным. Постоянный радиус кривизны имеет только окружность. Следовательно, движение заряда в плоскости, перпендикулярной магнитному полю, будет происходить по окружности. Чем больше , тем меньше R. При , т.е. заряд движется по прямой.

Важным результатом для приложения является тот факт, что период обращения заряда в однородном магнитном поле не зависит от его скорости.

если . (2)

Частицы, имеющие бóльшую скорость, движутся по окружности бóльшего радиуса, однако время одного полного оборота будет таким же, что и для более медленных частиц, движущихся по окружности меньшего радиуса. Данный результат положен в основу действия циклических ускорителей элементарных частиц.

3. Движение заряженной частицы произвольно по отношению к линиям магнитной индукции. Вектор скорости можно разложить на 2 составляющие:

В направлении сила Лоренца на заряд не действует, поэтому в этом направлении он движется равномерно, прямолинейно с . В направлении, перпендикулярном , он движется по окружности со скоростью Движение заряда представляет собой суперпозицию этих двух движений и происходит по винтовой линии, ось которой параллельна .

Радиус витка с учетом (1):

(3)

Шаг винтовой линии (расстояние между соседними витками)

с учетом (2):

.

Если движение происходит в неоднородном магнитном поле, индукция которого возрастает в направлении движения частицы, то R уменьшается с ростом В согласно (3). На этом основана фокусировка пучка заряженных частиц в магнитном поле. Таким образом, с помощью неоднородного магнитного поля можно управлять пучками заряженных частиц, собирать их или рассеивать подобно тому, как управляют поведением пучков световых лучей с помощью оптических линз.

Рассмотренный принцип положен в основу действия электронных микроскопов.

Ускорители заряженных частиц.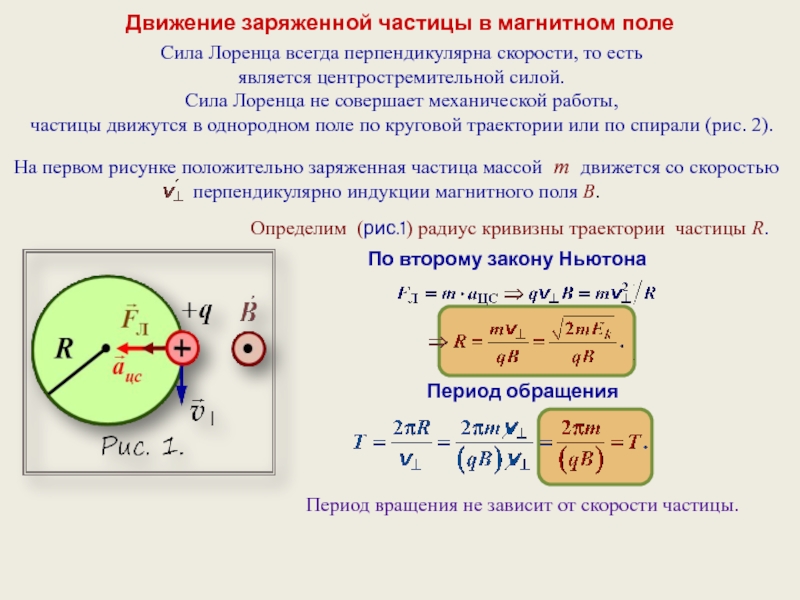

Свойство независимости периода от скорости обращения используют для того, чтобы превратить траекторию ускоряемой частицы в спираль и уменьшить размеры ускорителя. Такой принцип положен в основу работы циклотрона — родоначальника целого семейства ускорителей с магнитным полем: синхротрона, синхрофазотрона и т.д.

Ускорительная камера циклотрона представляет собой вакуумную цилиндрическую коробку, помещенную между полюсами сильного электромагнита. Камера состоит из двух металлических половинок — дуантов, между которыми создается с помощью генератора переменное электрическое напряжение с амплитудой порядка (поле только в зазоре). Частицы вводятся внутрь камера с помощью специального впускного устройства (А).

При каждом пересечении зазора частица приобретает энергию E₁ = qU. За N оборотов E = qUN, E_max~10⁷эВ.

Большая энергия в циклотроне не может быть достигнута: как следует из теории относительности: m = f(V), а при росте массы уменьшается частота обращения.

В синхроциклотронах (фазотронах) медленно уменьшается частота подаваемого напряжения.

Фазотрон — изменяется .

В синхротронах меняется индукция магнитного поля .

Синхротрон — изменяется

В синхрофазотронах — изменяется  и B.

E~10⁹ — 10¹⁰ эВ.

Ускорители заряженных частиц — устройства, в которых создаются и управляются пучки высокоэнергетических заряженных частиц под действием электрических и магнитных полей.

Принцип автофазировки предложены советским физиком Векслером (1944 г.) и американским Мак-Милланом (1945 г.).

Магнитогидродинамический (МГД) генератор — установка для непосредственного преобразования тепловой энергии в электрическую (создан в 50-х годах).

Это источник тока, принцип действия которого основан на действии магнитного поля на заряженные частицы плазмы электролитов и жидких металлов. Плазма представляет собой поток раскаленного газа, все молекулы которого ионизированы высокой температурой (~2000K).

Поток плазмы, проходя через расширяющееся сопло, ускоряется до 2000-2500 м/с и попадает в сильное магнитное поле, разделяющее положительные и отрицательные заряды, отбрасывая их на электроды. При этом во внешней цепи возникает электрический ток.

т.к. T_пл >>Т_{вн.среды},  — велико.

Применение:

1. в ускорителях;

2. в НГД — генераторах;

3. датчиках Холла;

4. для осуществления управляемых термоядерных реакций;

5. при регистрации и исследовании заряженных частиц;

6. в магнетронах.

Сила Лоренца

Сила, действующая на электрический заряд , движущийся в магнитном поле со скоростью , называется

силой Лоренца и выражается: , где — магнитная индукция. Из приведенной формулы следует, что и и поэтому сила Лоренца работы не совершает и, следовательно, не меняет кинетическую энергию свободных зарядов. Она только изменяет направление скорости движения зарядов, т.е. является центростремительной силой.

Направление силы Лоренца определяется правилом левой руки для положительного заряда. На отрицательный заряд сила действует в противоположном направлении (рисунок 10).

М

одуль силы Лоренца , где

— угол между векторами и .

Из этого выражения следует, что магнитное поле не действует на покоящийся электрический заряд.

Сила Лоренца создает центростремительное ускорение, следовательно, заряженная частица будет двигаться по окружности радиуса r, если . Отсюда:

Рисунок 10. Действие силы Лоренца на движущийся заряд

— радиус вращения заряженной частицы.

Период вращения частицы: — не зависит от скорости! Если и составляют угол   , то движение частицы будет происходить по спирали (рисунок 11).

Рисунок 11. Движение положительного заряда, попавшего в магнитное поле под углом

Шаг винтовой линии: .

Если заряженная частица влетает в сильное магнитное поле, то, пролетев в нем какую-то часть спирали, она отбрасывается полем в обратном направлении без изменения энергии частицы. Такое поле называют магнитным зеркалом и используют в ядерной физике для изоляции и удержания высокотемпературной плазмы.

Потоки выброшенных Солнцем заряженных частиц, долетая до Земли, отклоняются ее магнитным полем ( рисунок 12) и тем самым воздействуют на магнитное поле Земли. Так возникают «магнитные бури».

Рисунок 12. Отклонение заряженных частиц магнитным полем Земли

Часть заряженных частиц проникает в магнитное поле Земли и, двигаясь по спирали, оказывается как бы в ловушке (рисунок 13). Эти заряженные частицы образуют радиационные пояса вокруг Земли. В области магнитных полюсов Земли космические частицы легко проникают в атмосферу, вызывая полярные сияния.

Рисунок 13. Движение заряженных частиц, попавших в магнитное поле Земли

Если на движущийся электрический заряд помимо магнитного поля с индукцией действует еще и электрическое поле с напряженностью , то сила, действующая на заряд:

— формула Лоренца.

Циркуляция вектора по заданному замкнутому контуру – это интеграл вида:.

Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора) , где

– число проводников с током, охватываемых контуром .

Циркуляция вектора по произвольному замкнутому контуру равна произведению магнитной постоянной ₀ на алгебраическую сумму токов, охватываемых этим контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта (рисунок 14).

.

Пример:

Поле, в котором циркуляция вектора не равна 0, называется вихревым. Магнитное поле является вихревым.

П

Рисунок 14. Пример расчета токов, охватываемых произвольным контуром

оле, циркуляция вектора которого равна 0, называется потенциальным полем (например, поле вектора напряженности электростатического поля).

электромагнетизм — Почему магнитное поле не совершает никакой работы над движущимся зарядом?

Вы уже знаете, почему магнитное поле не действует на движущийся заряд: потому что так говорит закон силы Лоренца. Фактически существуют два различных закона силы для магнитного поля: один применяется к движущимся зарядам, а другой — к точечным диполям (последний может выполнять работу, когда поле неоднородно).

Похоже, ваш вопрос касается несоответствия между двумя сценариями. Мы знаем, что точечный магнитный диполь можно смоделировать как предел петли с током, когда площадь стремится к нулю, сохраняя при этом произведение площади и тока постоянным (и предполагая, что заряженные частицы, протекающие через петлю, не имеют никакого сопротивления). собственный магнитный дипольный момент). Но мы знаем, что магнитное поле не совершает никакой работы над зарядами, протекающими через токовую петлю. Как же тогда магнитное поле может совершать работу над точечным магнитным диполем? Разве предел нулевой работы не должен работать на токовых петлях, когда их площади стремятся к нулю, что это будет нулевая работа, а не ненулевая работа, которая выполняется на точечных диполях?

Чтобы разрешить этот парадокс, нам нужно проанализировать сценарий только с точки зрения наблюдаемых величин. Получается, что «какая сила на самом деле совершает работу?» не наблюдается, поэтому парадокс исчезает.

Предположим, что жесткая, изначально стационарная петля с током помещена в неоднородное внешнее магнитное поле. Петля с током будет испытывать результирующую силу, потому что сила Лоренца на одной стороне петли не будет равна и противоположна силе Лоренца на другой стороне петли (из-за неравномерности). Суммарная сила будет приблизительно равна $\nabla(m \cdot B)$, где $m$ — магнитный дипольный момент петли. 3x $, где $B$ — сумма внешнего поля и поля, создаваемого самой петлей). Таким образом, происходит передача энергии от поля $B$ к кинетической энергии петли.

В пределе, когда радиус петли стремится к нулю, то же самое. Магнитное поле теряет энергию, а точечный диполь приобретает кинетическую энергию. Прерывистости нет.

Кажущийся парадокс возникает только при более глубоком анализе того, что на самом деле происходит с жесткой токовой петлей: магнитная сила действует на носители тока и не действует на них непосредственно; работа совершается электрическими силами, которые поддерживают жесткость петли и не дают электронам покинуть провод. Для точечного диполя фактических носителей тока нет, поэтому анализировать нечего, и мы просто говорим, что магнитная сила выполняет работу напрямую.

При расчете любого наблюдаемого , имеющего отношение к точечному магнитному диполю, мы можем сделать это, приняв соответствующий предел, когда площадь токовой петли стремится к нулю. Поскольку «какая сила на самом деле совершает работу?» это не вопрос, который формулируется в терминах наблюдаемых, на самом деле в этом случае нет количества, которое можно было бы ограничить.

электромагнетизм — Работает ли магнитная часть силы Лоренца?

спросил 3 года 8 месяцев назад

Изменено 3 года, 8 месяцев назад

Просмотрено 459 раз

$\begingroup$

Магнитная часть силы Лоренца равна $$\vec F_L=q\влево(\vec v\times\vec B\вправо)$$ Поскольку эта сила всегда перпендикулярна направлению движения, мы узнали, что она не совершает никакой работы.

Однако легко заметить, что постоянные магниты притягиваются друг к другу (по крайней мере, когда юг указывает на север). Это притяжение разгоняет магниты в направлении движения, поэтому совершается работа.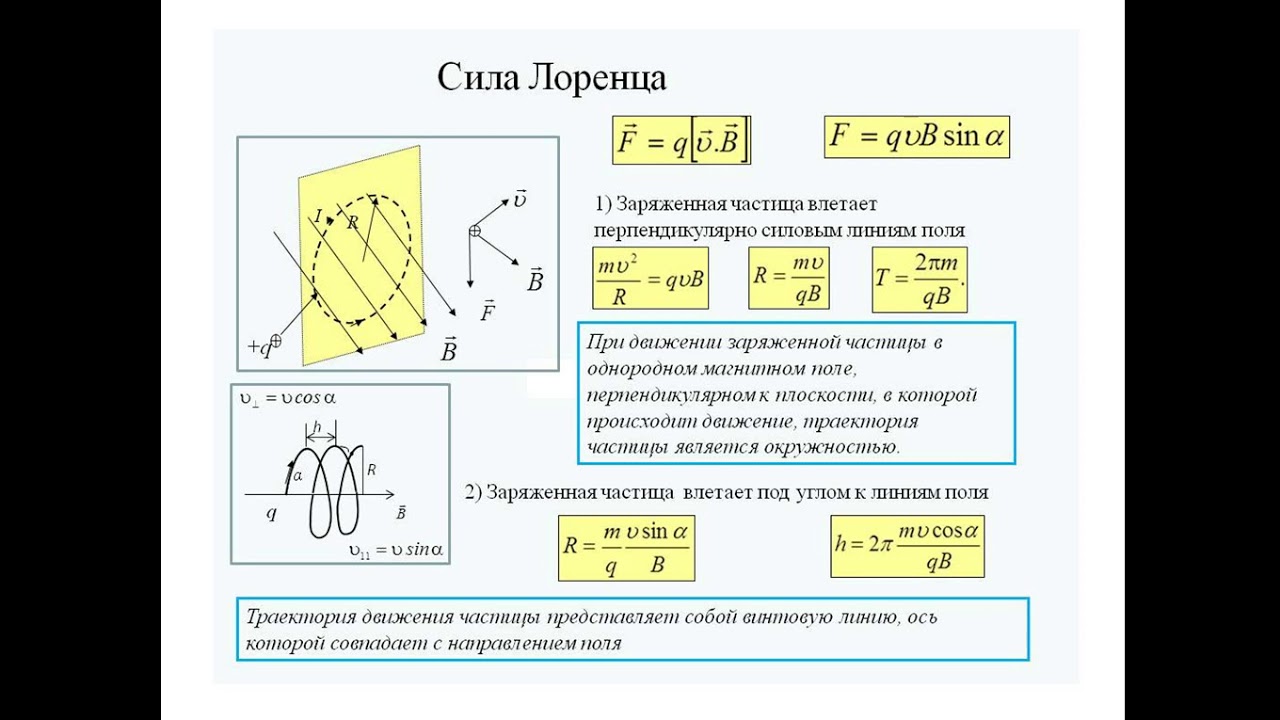 Как это возможно?

• электромагнетизм
• магнитные поля
• работа

$\endgroup$

$\begingroup$

Легче (по крайней мере для меня), чем два магнита, это два параллельных проводника с током, притягивающие друг друга. Сила притяжения равна составляющей перпендикулярной проводу магнитной силы Лоренца на носителях заряда – так называемой сила Лапласа .

Как только провода начинают двигаться вместе (и над ними совершается работа), скорость носителей заряда приобретает составляющую, перпендикулярную проводу, а магнитная сила Лоренца приобретает составляющую вдоль провода. Таким образом, если носители заряда должны продолжать двигаться с той же скоростью, над ними должна совершаться работа электрическим полем, создаваемым батареей; другими словами, необходимо преодолеть обратную ЭДС.

Таким образом, именно батарея обеспечивает работу проводов, когда они движутся вместе. Магнитная сила Лоренца действует как шкив, изменяя направление силы, которая действительно работает.

Я полагаю, что случай притяжения двух магнитов можно проанализировать аналогичным образом. Но зато у меня богатое воображение…

$\endgroup$

4

$\begingroup$

Простое, но необычное объяснение следующее. Выражение силы Лоренца можно переписать как $f_k =\frac{d(p+qA)_k} {dt} = qv_i \frac{dA_i} {dx_k} $. Когда два магнита находятся рядом и находятся в состоянии покоя, dA/dt=0. Ускорение возникает в направлении градиента A, пропорционального компоненте v, параллельной A. Эта сила совершает работу, если расстояние между магнитами изменяется.

$\endgroup$

4

$\begingroup$

Вы спрашиваете, как работают магниты? Я бы сказал, что когда вы раздвигаете магниты, вы вкладываете потенциальную энергию в систему. И когда магниты соединяются вместе, энергия высвобождается в виде звука и тепла.

$\endgroup$

$\begingroup$

Сила Лоренца определяется как полная электромагнитная сила, действующая со стороны электромагнитного поля на точечный электрический заряд. Что касается магнитной части силы Лоренца, то она никогда не может совершать работу.

Однако легко заметить, что постоянные магниты притягиваются друг к другу (по крайней мере, когда юг указывает на север). Это притяжение разгоняет магниты в направлении движения, поэтому совершается работа.

Как следует из самого определения, это магнитная сила, действующая на точечный электрический заряд, но магнит не является электрическим зарядом. Хорошо известно, что мы не можем использовать силу Лоренца для определения сил между двумя магнитами.

$\endgroup$

4

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.