Конвертер частоты и длины волны • Фотометрия — свет • Компактный калькулятор • Онлайн-конвертеры единиц измерения

Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисленияКонвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева

Период колебания волн у берегов Майами-Бич приблизительно равен 4 секундам.

Общие сведения

Частота

Частота — это величина, измеряющая как часто повторяется тот или иной периодический процесс. В физике с помощью частоты описывают свойства волновых процессов. Частота волны — количество полных циклов волнового процесса за единицу времени. Единица частоты в системе СИ — герц (Гц). Один герц равен одному колебанию в секунду.

Длина волны

Существует множество различных типов волн в природе, от вызванных ветром морских волн до электромагнитных волн. Свойства электромагнитных волн зависят от длины волны. Такие волны разделяют на несколько видов:

Резонансный магнетрон используется в микроволновых печах для подачи электромагнитной энергии в камеру печи.

• Гамма-лучи с длиной волны до 0,01 нанометра (нм).
• Рентгеновские лучи с длиной волны — от 0,01 нм до 10 нм.
• Волны ультрафиолетового диапазона, которые имеют длину от 10 до 380 нм. Человеческому глазу они не видимы.
• Свет в видимой части спектра с длиной волны 380–700 нм.
• Невидимое для людей инфракрасное излучение с длиной волны от 700 нм до 1 миллиметра.
• За инфракрасными волнами следуют микроволновые, с длиной волны от 1 миллиметра до 1 метра.
• Самые длинные — радиоволны. Их длина начинается с 1 метра.

Эта статья посвящена электромагнитному излучению, и особенно свету. В ней мы обсудим, как длина и частота волны влияют на свет, включая видимый спектр, ультрафиолетовое и инфракрасное излучение.

Электромагнитное излучение

Электромагнитное излучение — это энергия, свойства которой одновременно сходны со свойствами волн и частиц. Эта особенность называется корпускулярно-волновым дуализмом. Электромагнитные волны состоят из магнитной волны и перпендикулярной к ней электрической волны.

Энергия электромагнитного излучения — результат движения частиц, которые называются фотонами. Чем выше частота излучения, тем они более активны, и тем больше вреда они могут принести клеткам и тканям живых организмов. Это происходит потому, что чем выше частота излучения, тем больше они несут энергии. Большая энергия позволяет им изменить молекулярную структуру веществ, на которые они действуют. Именно поэтому ультрафиолетовое, рентгеновское и гамма излучение так вредно для животных и растений. Огромная часть этого излучения — в космосе. Оно присутствует и на Земле, несмотря на то, что озоновый слой атмосферы вокруг Земли блокирует большую его часть.

Атмосфера пропускает СВЧ-излучение в диапазоне частот C (с частотой от 4 до 8 Гц и с длиной волны от 7,5 до 3,75 сантиметров), которые используются для спутниковой связи

Электромагнитное излучение и атмосфера

Атмосфера земли пропускает только электромагнитное излучение с определенной частотой. Большая часть гамма-излучения, рентгеновских лучей, ультрафиолетового света, часть излучения в инфракрасном диапазоне и длинные радиоволны блокируются атмосферой Земли. Атмосфера поглощает их и не пропускает дальше. Часть электромагнитных волн, в частности, излучение в коротковолновом диапазоне, отражается от ионосферы. Все остальное излучение попадает на поверхность Земли. В верхних атмосферных слоях, то есть, дальше от поверхности Земли, больше радиации, чем в нижних слоях. Поэтому чем выше, тем опаснее для живых организмов находиться там без защитных костюмов.

Атмосфера пропускает на Землю небольшое количество ультрафиолетового света, и он приносит вред коже. Именно из-за ультрафиолетовых лучей люди обгорают на солнце и могут даже заболеть раком кожи. С другой стороны, некоторые лучи, пропускаемые атмосферой, приносят пользу. Например, инфракрасные лучи, которые попадают на поверхность Земли, используют в астрономии — инфракрасные телескопы следят за инфракрасными лучами, излучаемыми астрономическими объектами. Чем выше от поверхности Земли, тем больше инфракрасного излучения, поэтому телескопы часто устанавливают на вершинах гор и на других возвышенностях. Иногда их отправляют в космос, чтобы улучшить видимость инфракрасных лучей.

Этот осциллограф, который измеряет сетевое напряжение в розетке, показывает частоту в 59,7 герц и период колебаний 117 миллисекунд

Взаимоотношение между частотой и длиной волны

Частота и длина волны обратно пропорциональны друг другу. Это значит, что по мере увеличения длины волны частота уменьшается и наоборот. Это легко представить: если частота колебаний волнового процесса высокая, то время между колебаниями намного короче, чем у волн, частота колебаний которых меньше. Если представить волну на графике, то расстояние между ее пиками будет тем меньше, чем больше колебаний она совершает на определенном отрезке времени.

Чтобы определить скорость распространения волны в среде, необходимо умножить частоту волны на ее длину. Электромагнитные волны в вакууме всегда распространяются с одинаковой скоростью. Эта скорость известна как скорость света. Она равна 299&nbsp792&nbsp458 метрам в секунду.

Свет

Видимый свет — электромагнитные волны с частотой и длиной, которые определяют его цвет.

Длина волны и цвет

Самая короткая длина волны видимого света — 380 нанометров. Это фиолетовый цвет, за ним следуют синий и голубой, затем зеленый, желтый, оранжевый и, наконец, красный. Белый свет состоит из всех цветов сразу, то есть, белые предметы отражают все цвета. Это можно увидеть с помощью призмы. Попадающий в нее свет преломляется и выстраивается в полосу цветов в той же последовательность, что в радуге. Эта последовательность — от цветов с самой короткой длиной волны, до самой длинной. Зависимость скорости распространения света в веществе от длины волны называется дисперсией.

Радуга над рекой Ниагара

Радуга образуется похожим способом. Капли воды, рассеянные в атмосфере после дождя, ведут себя так же как призма и преломляют каждую волну. Цвета радуги настолько важны, что во многих языках существуют мнемоника, то есть прием запоминания цветов радуги, настолько простой, что запомнить их могут даже дети. Многие дети, говорящие по-русски, знают, что «Каждый охотник желает знать, где сидит фазан». Некоторые люди придумывают свою мнемонику, и это — особенно полезное упражнение для детей, так как, придумав свой собственный метод запоминания цветов радуги, они быстрее их запомнят.

Свет, к которому человеческий глаз наиболее чувствителен — зеленый, с длиной волны в 555 нм в светлой среде и 505 нм в сумерках и темноте. Различать цвета могут далеко не все животные. У кошек, например, цветное зрение не развито. С другой стороны, некоторые животные видят цвета намного лучше, чем люди. Например, некоторые виды видят ультрафиолетовый и инфракрасный свет.

Отражение света

Бриллиантовое кольцо

Цвет предмета определяется длиной волны света, отраженного с его поверхности. Белые предметы отражают все волны видимого спектра, в то время как черные — наоборот, поглощают все волны и ничего не отражают.

На первом рисунке: правильная огранка бриллиантов. Свет отражается вверх, по направлению к глазу и алмаз сверкает. На втором и третьем рисунках: неправильная огранка. Свет отражается в оправу и в стороны и алмазы выглядят тусклыми.

Один из естественных материалов с высоким коэффициентом дисперсии — алмаз. Правильно обработанные бриллианты отражают свет как от наружных, так и от внутренних граней, преломляя его, как и призма. При этом важно, чтобы большая часть этого света была отражена вверх, в сторону глаза, а не, например, вниз, внутрь оправы, где его не видно. Благодаря высокой дисперсии бриллианты очень красиво сияют на солнце и при искусственном освещении. Стекло, ограненное так же, как бриллиант, тоже сияет, но не настолько сильно. Это связано с тем, что, благодаря химическому составу, алмазы отражают свет намного лучше, чем стекло. Углы, используемые при огранке бриллиантов, имеет огромное значение, потому что слишком острые или слишком тупые углы либо не позволяют свету отражаться от внутренних стен, либо отражают свет в оправу, как показано на иллюстрации.

Спектроскопия

Для определения химического состава вещества иногда используют спектральный анализ или спектроскопию. Этот способ особенно хорош, если химический анализ вещества невозможно провести, работая с ним непосредственно, например, при определении химического состава звезд. Зная, какое электромагнитное излучение поглощает тело, можно определить, из чего оно состоит. Абсорбционная спектроскопия, являющаяся одним из разделов спектроскопии, определяет какое излучение поглощается телом. Такой анализ можно делать на расстоянии, поэтому его часто используют в астрономии, а также в работе с ядовитыми и опасными веществами.

Определение наличия электромагнитного излучения

Видимый свет, так же как и всё электромагнитное излучение — это энергия. Чем больше энергии излучается, тем легче эту радиацию измерить. Количество излученной энергии уменьшается по мере увеличения длины волны. Зрение возможно именно благодаря тому, что люди и животные распознают эту энергию и чувствуют разницу между излучением с разной длиной волны. Электромагнитное излучение разной длины ощущается глазом как разные цвета. По такому принципу работают не только глаза животных и людей, но и технологии, созданные людьми для обработки электромагнитного излучения.

Видимый свет

Люди и животные видят большой спектр электромагнитного излучения. Большинство людей и животных, например, реагируют на видимый свет, а некоторые животные — еще и на ультрафиолетовые и инфракрасные лучи. Способность различать цвета — не у всех животных — некоторые, видят только разницу между светлыми и темными поверхностями. Наш мозг определяет цвет так: фотоны электромагнитного излучения попадают в глаз на сетчатку и, проходя через нее, возбуждают колбочки, фоторецепторы глаза. В результате по нервной системе передается сигнал в мозг. Кроме колбочек, в глазах есть и другие фоторецепторы, палочки, но они не способны различать цвета. Их назначение — определять яркость и силу света.

Колбочки в сетчатке глаза чаек и многих других птиц содержит капли красного или желтого масла

В глазу обычно находится несколько видов колбочек. У людей — три типа, каждый из которых поглощает фотоны света в пределах определенных длин волны. При их поглощении происходит химическая реакция, в результате которой в мозг поступают нервные импульсы с информацией о длине волны. Эти сигналы обрабатывает зрительная зона коры головного мозга. Это — участок мозга, ответственный за восприятие звука. Каждый тип колбочек отвечает только за волны с определенной длиной, поэтому для получения полного представления о цвете, информацию, полученную от всех колбочек, складывают вместе.

У некоторых животных еще больше видов колбочек, чем у людей. Так, например, у некоторых видов рыб и птиц их от четырех до пяти типов. Интересно, что у самок некоторых животных больше типов колбочек, чем у самцов. У некоторых птиц, например у чаек, которые ловят добычу в воде или на ее поверхности, внутри колбочек есть желтые или красные капли масла, которые выступают в роли фильтра. Это помогает им видеть большее количество цветов. Подобным образом устроены глаза и у рептилий.

Этот инфракрасный термометр определяет температуру измеряемого объекта на расстоянии, по его тепловому излучению

Инфракрасный свет

У змей, в отличие от людей, не только зрительные рецепторы, но и чувствительные органы, которые реагируют на инфракрасное излучение. Они поглощают энергию инфракрасный лучей, то есть реагируют на тепло. Некоторые устройства, например приборы ночного видения, также реагируют на тепло, выделяемое инфракрасным излучателем. Такие устройства используют военные, а также для обеспечения безопасности и охраны помещений и территории. Животные, которые видят инфракрасный свет, и устройства, которые могут его распознавать, видят не только предметы, которые находятся в их поле зрения на данный момент, но и следы предметов, животных, или людей, которые находились там до этого, если не прошло слишком много времени. Например, змеям видно, если грызуны копали в земле ямку, а полицейские, которые пользуются прибором ночного видения, видят, если в земле были недавно спрятаны следы преступления, например, деньги, наркотики, или что-то другое. Устройства для регистрации инфракрасного излучения используют в телескопах, а также для проверки контейнеров и камер на герметичность. С их помощью хорошо видно место утечки тепла. В медицине изображения в инфракрасном свете используют для диагностики. В истории искусства — чтобы определить, что изображено под верхним слоем краски. Устройства ночного видения используют для охраны помещений.

Обыкновенная или зеленая игуана видит ультрафиолетовый свет. Фотография размещена с разрешения автора

Ультрафиолетовый свет

Некоторые рыбы видят ультрафиолетовый свет. Их глаза содержат пигмент, чувствительный к ультрафиолетовым лучам. Кожа рыб содержит участки, отражающие ультрафиолетовый свет, невидимый для человека и других животных — что часто используется в животном мире для маркировки пола животных, а также в социальных целях. Некоторые птицы тоже видят ультрафиолетовый свет. Это умение особенно важно во время брачного периода, когда птицы ищут потенциальных партнеров. Поверхности некоторых растений также хорошо отражают ультрафиолетовый свет, и способность его видеть помогает в поиске пищи. Кроме рыб и птиц, ультрафиолетовый свет видят некоторые рептилии, например черепахи, ящерицы и зеленые игуаны (на иллюстрации).

Человеческий глаз, как и глаза животных, поглощает ультрафиолетовый свет, но не может его обработать. У людей он разрушает клетки глаза, особенно в роговице и хрусталике. Это, в свою очередь, вызывает различные заболевания и даже слепоту. Несмотря на то, что ультрафиолетовый свет вредит зрению, небольшое его количество необходимо людям и животным, чтобы вырабатывать витамин D. Ультрафиолетовое излучение, как и инфракрасное, используют во многих отраслях, например в медицине для дезинфекции, в астрономии для наблюдения за звездами и другими объектами и в химии для отверждения жидких веществ, а также для визуализации, то есть для создания диаграмм распространения веществ в определенном пространстве. С помощью ультрафиолетового света определяют поддельные банкноты и пропуска, если на них должны быть напечатаны знаки специальными чернилами, распознаваемыми с помощью ультрафиолетового света. В случае с подделкой документов ультрафиолетовая лампа не всегда помогает, так как преступники иногда используют настоящий документ и заменяют на нем фотографию или другую информацию, так что маркировка для ультрафиолетовых ламп остается. Существует также множество других применений для ультрафиолетового излучения.

Цветовая слепота

Из-за дефектов зрения некоторые люди не в состоянии различать цвета. Эта проблема называется цветовой слепотой или дальтонизмом, по имени человека, который первый описал эту особенность зрения. Иногда люди не видят только цвета с определенной длиной волны, а иногда они не различают цвета вообще. Часто причина — недостаточно развитые или поврежденные фоторецепторы, но в некоторых случаях проблема заключается в повреждениях на проводящем пути нервной системы, например в зрительной коре головного мозга, где обрабатывается информация о цвете. Во многих случаях это состояние создает людям и животным неудобства и проблемы, но иногда неумение различать цвета, наоборот — преимущество. Это подтверждается тем, что, несмотря на долгие годы эволюции, у многих животных цветное зрение не развито. Люди и животные, которые не различают цвета, могут, например, хорошо видеть камуфляж других животных.

На этом изображении из диагностических таблиц для диагностики дальтонизма люди с нормальным зрением видят число 74

Несмотря на преимущества цветовой слепоты, в обществе ее считают проблемой, и для людей с дальтонизмом закрыта дорога в некоторые профессии. Обычно они не могут получить полные права по управлению самолетом без ограничений. Во многих странах водительские права для этих людей тоже имеют ограничения, а в некоторых случаях они не могут получить права вообще. Поэтому они не всегда могут найти работу, на которой необходимо управлять автомобилем, самолетом, и другими транспортными средствами. Также им сложно найти работу, где умение определять и использовать цвета имеет большое значение. Например, им трудно стать дизайнерами, или работать в среде, где цвет используют, как сигнал (например, об опасности).

Проводятся работы по созданию более благоприятных условий для людей с цветовой слепотой. Например, существуют таблицы, в которых цвета соответствует знакам, и в некоторых странах эти знаки используют в учреждениях и общественных местах наряду с цветом. Некоторые дизайнеры не используют или ограничивают использование цвета для передачи важной информации в своих работах. Вместо цвета, или наряду с ним, они используют яркость, текст, и другие способы выделения информации, чтобы даже люди, не различающие цвета, могли полостью получить информацию, передаваемую дизайнером. В большинстве случаев люди с цветовой слепотой не различают красный и зеленый, поэтому дизайнеры иногда заменяют комбинацию «красный = опасность, зеленый = все нормально» на красный и синий цвета. Большинство операционных систем также позволяют настроить цвета так, чтобы людям с цветовой слепотой было все видно.

Цвет в машинном зрении

Машинное зрение в цвете — быстроразвивающаяся отрасль искусственного интеллекта. До недавнего времени большая часть работы в этой области проходила с монохромными изображениями, но сейчас все больше научных лабораторий работают с цветом. Некоторые алгоритмы для работы с монохромными изображениями применяют также и для обработки цветных изображений.

Камера Canon 5D автоматически находит человеческие лица и настраивается по одному из них на резкость

Применение

Машинное зрение используется в ряде отраслей, например для управления роботами, самоуправляемыми автомобилями, и беспилотными летательными аппаратами. Оно полезно в сфере обеспечения безопасности, например для опознания людей и предметов по фотографиям, для поиска по базам данных, для отслеживания движения предметов, в зависимости от их цвета и так далее. Определение местоположения движущихся объектов позволяет компьютеру определить направление взгляда человека или следить за движением машин, людей, рук, и других предметов.

Чтобы правильно опознать незнакомые предметы, важно знать об их форме и других свойствах, но информация о цвете не настолько важна. При работе со знакомыми предметами, цвет, наоборот, помогает быстрее их распознать. Работа с цветом также удобна потому, что информация о цвете может быть получена даже с изображений с низким разрешением. Для распознавания формы предмета, в отличие от цвета, требуется высокое разрешение. Работа с цветом вместо формы предмета позволяет уменьшить время обработки изображения, и использует меньше компьютерных ресурсов. Цвет помогает распознавать предметы одинаковой формы, а также может быть использован как сигнал или знак (например, красный цвет — сигнал опасности). При этом не нужно распознавать форму этого знака, или текст, на нем написанный. На веб-сайте YouTube можно увидеть множество интересных примеров использования цветного машинного зрения.

Обработка информации о цвете

Оптическая иллюзия с цветом

Фотографии, которые обрабатывает компьютер, либо загружены пользователями, либо сняты встроенной камерой. Процесс цифровой фото- и видеосъемки освоен хорошо, но вот обработка этих изображений, особенно в цвете, связана с множеством трудностей, многие из которых еще не решены. Это связано с тем, что цветное зрение у людей и животных устроено очень сложно, и создать компьютерное зрение наподобие человеческого — непросто. Зрение, как и слух, основано на адаптации к окружающей среде. Восприятие звука зависит не только от частоты, звукового давления и продолжительности звука, но и от наличия или отсутствия в окружающей среде других звуков. Так и со зрением — восприятие цвета зависит не только от частоты и длины волны, но и от особенностей окружающей среды. Так, например, цвета окружающих предметов влияют на наше восприятие цвета.

С точки зрения эволюции такая адаптация необходима, чтобы помочь нам привыкнуть к окружающей среде и перестать обращать внимание на незначительные элементы, а направить все наше внимание на то, что меняется в окружающей обстановке. Это необходимо для того, чтобы легче замечать хищников и находить пищу. Иногда из-за этой адаптации происходят оптические иллюзии. Например, в зависимости от цвета окружающих предметов, мы воспринимаем цвет двух тел по-разному, даже когда они отражают свет с одинаковой длиной волны. На иллюстрации — пример такой оптической иллюзии. Коричневый квадрат в верхней части изображения (второй ряд, вторая колонка) выглядит светлее, чем коричневый квадрат в нижней части рисунка (пятый ряд, вторая колонка). На самом деле, их цвета одинаковы. Даже зная об этом, мы все равно воспринимаем их, как разные цвета. Поскольку наше восприятие цвета устроено так сложно, программистам трудно описать все эти нюансы в алгоритмах для машинного зрения. Несмотря на эти трудности, мы уже достигли многого в этой области.

Литература

Автор статьи: Kateryna Yuri

Unit Converter articles were edited and illustrated by Анатолий Золотков

Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.

Калькулятор звуковой частоты и длины волны • Акустика — звук • Онлайн-конвертеры единиц измерения

Этот калькулятор определяет длину волны звуковых колебаний, если известны их частота и скорость распространения звука в среде. Он также может рассчитать частоту, если известны длина волны и скорость или скорость звука, если известны частота и длина волны.

Пример: Рассчитать длину звуковой волны, распространяющейся в морской воде от гидроакустического преобразователя с частотой 50 кГц, если известно, что скорость звука в соленой воде равна 1530 м/с.

Частота

fгерц (Гц)килогерц (кГц)мегагерц (МГц)гигагерц (ГГц)

Длина волны

λнанометр (нм)микрометр (мкм)миллиметр (мм)сантиметр (см)метр (м)километр (км)дюймфутмиля

Скорость звука

vметр в секунду (м/с)километр в час (км/ч)сантиметр в секунду (см/с)фут в секунду (фут/с)миля в час (миля/ч)узел (уз)

или Среда

—ВодородГелийВоздух, 20 °CКислородДиоксид серыМорская вода, 20 °CДистиллированная вода, 20 °CЭтанолМетанолАлюминийСтальЛатуньСтеклоАлмаз

Для расчета выберите среду или введите скорость звука, затем введите частоту и нажмите кнопку Рассчитать для расчета длины волны. Можно также ввести длину волны и рассчитать частоту.

Определения и формулы

Звук — это волновой процесс. Если струна скрипки или арфы колеблется, в окружающем ее воздуха образуются зоны сжатия и разрежения, которые и представляют собой звук. Эти зоны сжатия и разрежения перемещаются поо воздуху в форме продольных волн, которые имеют ту же частоту, что и источник звука. В продольных волнах молекулы воздуха движутся параллельно движению волны. Воздух сжимается в том же направлении, в котором распространяются звуковые волны. Эти волны передают энергию голоса или колеблющейся струны. Отметим, что воздух не перемещается, когда звуковая волна проходит через него. Перемещаются только колебания, то есть зоны сжатия и разрежения. Более громкие звуки получаются при более сильных сжатиях и разрежениях.

Спектр звуковых колебаний. 1 — землетрясения, молнии и обнаружение ядерных взрывов; 2 — акустический диапазон; 3 — Слух животных; 4, Ультразвуковая очистка; 5. Терапевтическое применение ультразвука; 6 — Неразрушающий контроль и медицинская ультразвуковая диагностика; 7 — Акустическая микроскопия; 8 — Инфразвук; 9 — Слышимый диапазон; 10 — Ультразвук

Количество этих колебаний в секунду называется частотой и измеряется в герцах. Период колебаний — это длительность одного цикла колебаний, измеренная в секундах. Длина волны — это расстояние между двумя соседними повторяющимися зонами волнового процесса. Если предположить, что скорость распространения волны в среде постоянная, то длина волны обратно пропорциональна частоте.

При 20 °C звук распространяется в сухом воздухе со скоростью около 343 метра в секунду или 1 километр приблизительно за 3 секунды. Звук распространяется быстрее в жидкостях и еще быстрее в твердых телах. Например, в воде звук распространяется в 4,3 раза быстрее, чем в воздухе, в стекле — в 13 раз и в алмазе в 35 раз быстрее, чем в воздухе.

Хотя звуковые волны и морские волны движутся намного медленнее электромагнитных волн, уравнение, описывающее их движение будет одинаковым для всех трех типов волн:

или

где

f — частота волны,

v — скорость распространения волны и

λ — длина волны

Продольные и поперечные волны

В различных средах звук распространяется в виде различных видов волн. В жидкостях и газах звук распространяется в виде продольных волн. В твердых телах звук может распространяться как в виде продольных, так и в виде поперечных волн.

Для лучшего понимания обоих типов волн удобно воспользоваться механическим аналогом, которым послужит пружина Слинки. Эта пружина представляет собой модель среды (жидкости или газа). Если ее растянуть, а затем сжимать, а затем отпускать один конец, сжатие в форме волны перемещается вперед, передавая таким образом энергию с одного конца пружины в другой. Если звук распространяется в жидкости или газе, он идет от источника в форме периодических сжатий и разрежений газа или жидкости, которые перемещаются от источника звука.

Мы можем сравнить витки пружины с молекулами воздуха или воды, которые сталкиваются друг с другом. Поскольку направление движения этих сжатий и разрежений параллельно направлению движения самой волны, такие волны называются продольными.

Если начать двигать один конец пружины перпендикулярно ее оси, то создается поперечная волна. Она называется поперечной, потому что движение витков пружины перпендикулярно направлению движения волны по пружине. В такой волне энергия передается вдоль пружины, а ее витки движутся в направлении, перпендикулярном передаче энергии.

Отметим, что в нашем эксперименте пружина представляет собой среду, в которой распространяется волна, и эта среда не движется вместе с волной. Она только колеблется. Это поведение волны легко наблюдать в твердом теле, однако это справедливо также для воздуха, воды и вообще любой жидкости или газа. То есть, колебания переносятся молекулами жидкости или газа, в то время как среднее положение молекул среды не изменяется с течением времени. Это справедливо для любых типов волн.

Примеры

Возьмем на клавиатуре несколько нот и покажем их частоту и длину волны. Предположим, что звук движется в воздухе со скоростью 340 м/с. Тогда можно рассчитать длину волны нот:

Научное и традиционное название ноты	Частота, Гц	Период, мс	Длина волны, см
A3, ля малой октавы	220	4.55	156
A4, ля первой октавы	440	2.27	78
A5, ля второй октавы	880	1.14	39
A6, ля третьей октавы	1760	0.57	19.5

Волны. Физика. Курс лекций

1. Упругие волны

1.1. Упругие продольные и поперечные волны

1.2. Характеристики бегущих волн

1.2.1. Длина волны

1.2.2. Фазовая скорость волны

1.2.3. Фазовая скорость различна для разных сред

1.2.4. Фронт волны. Волновая поверхность

1.2.5. Уравнение бегущей волны

1.2.6. Волновое уравнение

1.2.7. Скорость и ускорение колеблющейся точки. Относительное смещение точек среды

1.3. Энергия упругих волн

1.4. Принцип суперпозиции волн. Групповая скорость

1.5. Интерференция волн. Стоячие волны

2. Звуковые волны

3. Электромагнитные волны

Как происходит распространение колебаний? Необходима среда для передачи колебаний или они могут передаваться без нее? Как звук от звучащего камертона доходит до слушателя? Каким образом быстропеременный ток в антенне радиопередатчика вызывает появление тока в антенне приемника? Как свет от далеких звезд достигает нашего глаза? Для рассмотрения подобного рода явлений необходимо ввести новое физическое понятие –

волна. Волновые процессы представляют общий класс явлений, несмотря на их разную природу.

Процесс распространения колебаний в пространстве называется волной.

Волны, образованные внешним воздействием, приложенным к упругой среде, называются бегущими волнами: они “бегут” от создающего их источника. Важное свойство бегущих волн заключается в том, что они переносят энергию и импульс. Если внешняя сила совершает гармонические колебания, то вызванные ею волны называются

гармоническими бегущими волнами.

Волновой процесс обусловлен наличием связей между отдельными частями системы, в зависимости от которых, мы имеем упругую волну той или иной природы.

1. Упругие волны

1. Упругими или механическими волнами называются механические возмущения (деформации), распространяющиеся в упругой среде.

Деформации в теле или среде называются упругими, если они полностью исчезают после прекращения внешних воздействий.

Тела, которые воздействуют на среду, вызывая колебания, называются

источниками волн. Распространение упругих волн не связано с переносом вещества, но волны переносят энергию, которой обеспечивает волновой процесс источник колебаний.

2. Среда называется однородной, если ее физические свойства, рассматриваемые в данной задаче, не изменяются от точки к точке.

Среда называется изотропной, если ее физические свойства, рассматриваемые в задаче, одинаковы по всем направлениям.

Среда называется линейной, если между величинами, характеризующими внешнее воздействие на среду, которое и вызывает ее изменение, существует прямо пропорциональная связь. Например, выполнение закона Гука означает, что среда линейна по своим механическим свойствам.

1.1. Упругие продольные и поперечные волны

Все волны делятся на продольные и поперечные.

Поперечные волны – упругие волны, при распространении которых частицы среды совершают колебания в направлении, перпендикулярном направлению распространения волны.

Продольные волны – упругие волны, при распространении которых частицы среды совершают колебания вдоль направления распространения волны.

Поперечные упругие волны возникают только в твердых телах, в которых возможны упругие деформации сдвига

. Продольные волны могут распространяться в жидкостях или газах, где возможны объемные деформации среды, или в твердых телах, где возникают деформации удлинения или сжатия. Исключение составляют поперечные поверхностные волны. Простые продольные колебания – это процесс распространения в пространстве областей сжатий и растяжений среды. Сжатия и растяжения среды образуются при колебаниях ее точек (частиц) около своих положений равновесия.

1.2. Характеристики бегущих волн

1.2.1. Длина волны

Минимальное расстояние, на которое распространяется волна за время, равное периоду колебания точки среды около положения равновесия, называется длиной волны.

Длиной волны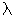

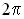называется наименьшее расстояние между двумя точками среды, совершающими колебания в фазе (т.е. разность их фаз равна ).

Если точки разделены расстоянием 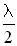, их колебания происходят в противофазе.

1.2.2. Фазовая скорость волны

Из повседневного опыта известно, что бегущие по воде волны распространяются с постоянной скоростью, пока свойства среды, например, глубина воды, не меняется, что говорит о том, что скорость распространения волнового процесса в пространстве остается постоянной. В случае гармонических бегущих волн (см. определение выше) эта скорость называется

фазовой.

Фазовая скорость 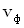— это скорость распространения данной фазы колебаний, т.е. скорость волны.

Связь длины волны 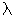, фазовой скорости 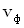и периода колебаний Т задается соотношением:

.

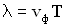Учитывая, что 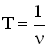, где

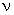
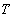— линейная частота волны, — период, а циклическая частота волны 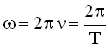, получим разные формулы для фазовой скорости:

.

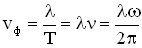Для волнового процесса характерна периодичность по времени и по пространству.

Т – период колебаний точек среды. Роль пространственного периода играет длина волны 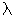. Соотношение между периодом и циклической частотой задается формулой: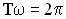

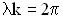. Аналогичное соотношение можно записать для длины волны и величиной k, называемой волновым числом: .

Таким образом. Можно добавить еще одно уравнение для фазовой скорости:

.

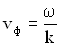1.2.3. Фазовая скорость различна для разных сред

В случае упругих поперечных волн (в твердом теле) фазовая скорость равна:

,

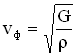где 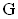— модуль сдвига среды,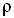

-ее плотность в невозбужденном состоянии (т.е. когда в этой среде не распространяется упругая волна).

Фазовая скорость упругих продольных волн в твердом теле равна

,

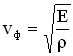где Е — модуль Юнга, 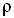— плотность невозмущенной среды (твердого тела до момента распространения по нему волны).

Фазовая скорость продольных волн в жидкости и газе определяется соотношением: ,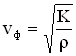

где К – модуль объемной упругости среды – величина, характеризующая способность среды сопротивляться изменению ее объема,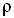

— плотность невозмущенной среды.

Фазовая скорость продольных волн в идеальном газе задается формулой: ,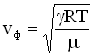

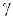— показатель адиабаты, 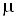— молярная масса, Т – абсолютная температура, R – универсальная газовая постоянная. Фазовая скорость в газе зависит от сорта газа (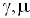) и от его термодинамического состояния (Т).

1.2.4. Фронт волны. Волновая поверхность

При прохождении волны по среде ее точки вовлекаются в колебательный процесс последовательно друг за другом.

Геометрическое место точек, до которого к некоторому моменту времени дошел колебательный процесс, называется волновым фронтом.

Геометрическое место точек, колеблющихся в фазе, называется волновой поверхностью.

Волновой фронт – частный случай волновой поверхности. Волновой фронт все время перемещается. Волновые поверхности остаются неподвижными. Они проходят через положения равновесия частиц среды, которые колеблются в одинаковой фазе.

При описании распространения волн широко используют понятие луча. Направления, в которых распространяются колебания, называются

лучами. В изотропной среде (см. определение выше) лучи перпендикулярны волновым поверхностям (фронту) и имеют вид прямых линий. В анизотропной среде, а также при дифракции волн, лучи могут искривляться.

Форма волнового фронта определяет вид волны: сферические (от точечного источника в изотропной среде), эллиптические (в анизотропной среде), цилиндрические (от протяженных источников), плоские и другие. На достаточно большом расстоянии от источника небольшой участок любого фронта можно считать плоским.

Если известно положение фронта волны в некоторый момент времени и скорость волны 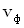, то его положение в последующий момент времени можно определить на основе принципа Гюйгенса. Согласно этому принципу все точки поверхности волнового фронта являются источниками вторичных волн. Искомое положение волнового фронта совпадает с поверхностью, огибающей фронты вторичных волн.

1.2.5. Уравнение бегущей волны

Уравнением упругой волны называется зависимость от координат и времени скалярных или векторных величин, характеризующих колебания среды при прохождении по ней волны.

Так, для волн в твердом теле такой величиной является смещение от положения равновесия любой точки тела в произвольный момент времени. Для характеристики продольных волн в жидкости или газе используют понятие избыточного давления. Избыточное давление равно разности между давлением в данный момент времени, когда по среде проходит волна, и равновесным, когда возмущений в среде нет.

Получим уравнение бегущей волны в одномерном пространстве, которое предполагаем изотропным и однородным (см. определения выше). Кроме того, силы сопротивления в среде считаем пренебрежимо малыми (т.е. нет затухания колебаний). Пусть точка О — центр (источник) колебаний, она колеблется по закону:

,

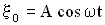где 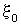— смещение точки О от положения равновесия, 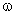— частота, А – амплитуда колебаний. Часы или секундомер №1 включаются сразу, как только начинаются колебаний точки О, и отсчитывают время t (Рисунок 2.1.1). Ось ОУ совпадает с направлением распространения волны.

Через промежуток времени 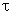процесс колебаний дойдет до точки В, и она будет колебаться по закону: .

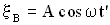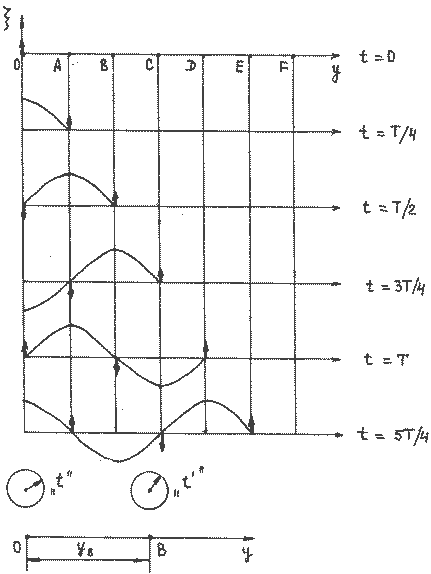
Рисунок 2.1.1.

Амплитуда колебаний в случае отсутствия затухания процесса будет такой же как и амплитуда точки О. Часы или секундомер №2 включаются тогда, когда колебательный процесс дойдет до точки В (т.е. когда начинает колебаться точка В), и отсчитывают время 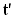. Моменты времени t и 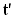связаны между собой соотношением 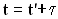или 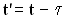. Расстояние между точками О и В обозначим 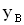. Фазовая скорость волны равна 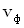, тогда 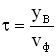. Учитывая соотношения для 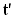и 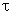и формулы 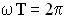и 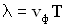, можно записать уравнение колебаний точки В в разных видах:

.

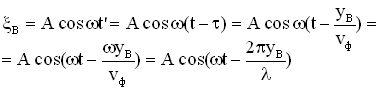Аналогично уравнению колебаний точки В запишем уравнение колебаний любой точки среды, расположенной на расстоянии y от источника колебаний:

,

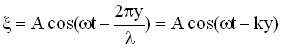где 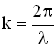— волновое число (см. определение выше).

Это уравнение и есть уравнение для смещения 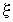любой точки пространства в любой момент времени, т.е. уравнение бегущей волны, где А – амплитуда, величина 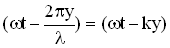— фаза волны, которая в отличии от фазы колебаний зависит и от времени “t”, и от расстояния “y” колеблющейся точки от источника колебаний.

Вернемся к разделению волн по форме фронта волны и к понятию луча, как направления распространения колебательного процесса. Учтем, что в изотропной среде лучи перпендикулярны фронту и имеют вид прямых линий. Тогда уравнение бегущей волны, полученное выше, есть уравнение плоской бегущей волны, т.е. когда фронт волны – плоскость.

Уравнение плоской отраженной волны в одномерном пространстве легко получить, если представить ее как бегущую волну в отрицательном направлении оси ОУ, что приведет к замене в уравнении бегущей волны координаты “y” на “-y”:

.

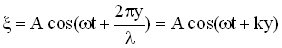Упругая волна называется синусоидальной или гармонической, если соответствующие ей колебания частиц среды являются гармоническими. Так, рассмотренные выше бегущая и отраженная волны являются гармоническими волнами.

1.2.6. Волновое уравнение

Когда мы рассматривали колебания, то для любой колебательной системы получали дифференциальное уравнение, для которого соответствующее уравнение колебаний являлось решением. Аналогично уравнение бегущей и отраженной волны являются решениями дифференциального уравнения второго порядка в частных производных, называемого волновым уравнением и имеющего вид:

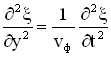, где 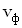— фазовая скорость волны.

Уравнения бегущей и отраженной волн и волновое уравнение представлены для случая одного измерения, т.е. распространения волны вдоль оси ОУ. В волновое уравнение входят вторые частные производные по времени и координате от смещения потому, что 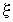есть функция двух переменных t и y.

1.2.7. Скорость и ускорение колеблющейся точки. Относительное смещение точек среды

Если смещение любой точки среды с координатой y в момент времени t задано уравнением:

,

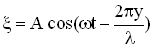то скорость этой точки есть величина 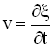, а ускорение — :

,

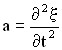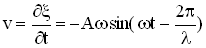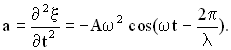
1.3. Энергия упругих волн

В среде распространяется плоская упругая волна и переносит энергию, величина которой в объеме 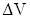равна: 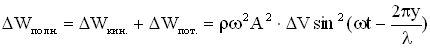, где 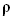— объемная плотность среды.

Если выбранный объем записать как 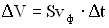, где S – площадь его поперечного сечения, а 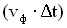— его длина, то среднее количество энергии, переносимое волной за единицу времени через поперечное сечение S, называется потоком 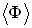через его поверхность:

.

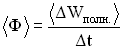Количество энергии, переносимое волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно направлению распространения волны, называется плотностью потока энергии волны.

Эта величина определяется соотношением:

,

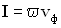где 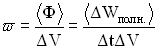-объемная плотность энергии волны, 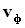— фазовая скорость волны. Так как фазовая скорость волны 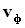— вектор, направление которого совпадает с направлением распространения волны, то можно величине плотности потока энергии I придать смысл векторной величины:

.

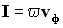Величина 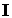, вектор плотности энергии волны, впервые была введена Н.А. Умовым в 1984 году и получила название вектора Умова. Подобная величина для электромагнитных волн называется вектором Умова — Пойнтинга.

Интенсивностью волны называется модуль среднего значения вектора Умова .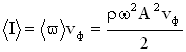

1.4. Принцип суперпозиции волн. Групповая скорость

Принцип суперпозиции (наложения) волн установлен на опыте. Он состоит в том, что в линейной среде волны от разных источников распространяются независимо, и накладываясь, не изменяют друг друга. Результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые частица получит, участвуя в каждом из слагаемых волновых процессов.

Согласно принципу суперпозиции накладываться друг на друга без взаимного искажения могут волны любой формы. В результате наложения волн результирующее колебание каждой частицы среды может происходить по любому сложному закону. Такое образование волн называется волновым пакетом. Скорость движения волнового пакета не совпадает со скоростью ни с одной из слагаемых волн. В этом случае говорят о скорости 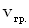волнового пакета. Скорость перемещения максимума группы волн (волнового пакета) называется групповой скоростью. Она равна скорости переноса энергии волнового пакета.

На практике мы всегда имеем дело с группой волн, так как синусоидальных волн, бесконечных в пространстве и во времени, не существует. Любая ограниченная во времени и пространстве синусоидальная волна есть волновой пакет (его называют цуг волны). Групповая скорость такого пакета совпадает с фазовой скоростью бесконечных синусоидальных волн, результатом сложения которых он является.

В общем виде связь между групповой и фазовой скоростями имеет вид:

.

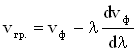1.5. Интерференция волн. Стоячие волны

1. Интерференцией волн называется явление наложение двух и более волн, при котором в зависимости от соотношения между фазами этих волн происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других.

В пространстве всегда найдутся такие точки, в которых разность фаз складываемых колебаний равна величине 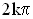, где k – целое число, т.е. волны (от разных источников) приходят в такие точки в фазе. В них будет наблюдаться устойчивое, неизменно продолжающееся все время усиление колебаний частиц. Найдутся в пространстве, где распространяется несколько волн, и такие точки, где разность фаз будет равна 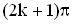, т.е. волны приходят в эти точки в противофазе. В таких точках пространства будет наблюдаться устойчивое ослабление колебаний частиц.

Устойчивая интерференционная картина возникает только при наложении таких волн, которые имеют одинаковую частоту, постоянную во времени разность фаз в каждой точке пространства. Волны, удовлетворяющие этим условиям и источники, создающие такие волны, называются когерентными. Плоские синусоидальные волны, частоты которых одинаковы, когерентны всегда.

2. Запишем условия максимумов и минимумов при интерференции. Когерентные точечные источник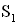и и 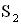испускают волны по всем направлениям. До точки наблюдения М расстояние от первого источника 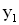, а от второго — .

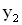Колебания точки М под действием волн от двух источников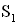 и 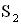описываются уравнениями:

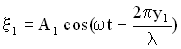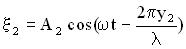, . Амплитуда результирующего колебания в точке М определится следующим образом (см. раздел “Сложение колебаний”): 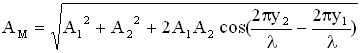. Амплитуда колебаний точки М максимальна (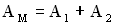), если 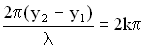, где 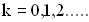Величина 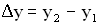называется разностью хода двух волн. Условие максимума при интерференции имеет вид: 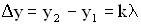. Если целое число волн укладывается на разности хода двух волн, то при их сложении наблюдается интерференционный максимум. Амплитуда колебаний точки М минимальна (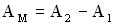), если 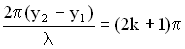, (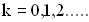). Условие минимума при интерференции имеет вид: 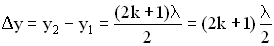.   Если нечетное число полуволн укладывается на разности хода двух волн, то при их сложении наблюдается интерференционный минимум. 3. Простейший случай интерференции наблюдается при наложении бегущей и отраженной волн, что приводит к образованию стоячей волны. Уравнения бегущей и отраженной волны имеют вид: 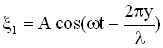, 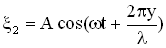Суммарное смещение 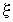частицы среды, находящейся на расстоянии y от источника колебаний, равно сумме смещени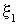й и : .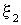

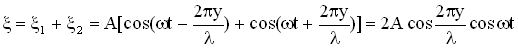Это и есть уравнение стоячей волны. Величина 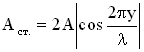— амплитуда, а (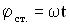) — фаза стоячей волны. Можно сказать, что частицы в стоячей волне имеют одну фазу колебаний. Амплитуда колебаний частиц в стоячей волне зависит от их координат (расстояний до источника колебаний), но не зависит от времени. Знак модуля поставлен в формуле для амплитуды стоячей волны, потому что амплитуда – величина положительная.

В стоячей волне есть точки, которые все время остаются неподвижными. Такие точки называются узлами смещения, их положение определяется из условия:

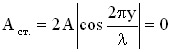, отсюда следует 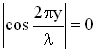. Выполнение этого соотношения будет при условии 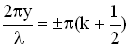для 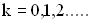Итак, координаты узлов задаются формулой:

.

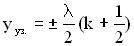Расстояние между двумя соседними узлами равно .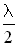

Точки среды, колеблющиеся с наибольшей амплитудой, называются пучностями стоячей волны, их положение (координаты) определяются соотношением:

.

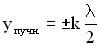Это уравнение можно получить из условия максимума амплитуды

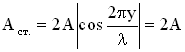, т.е. 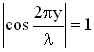. Последнее соотношение выполняется при значениях аргумента ().

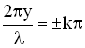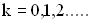Расстояние между двумя соседними пучностями равно .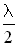

4. Изменение фазы волны при ее отражении.

Как отмечалось ранее, стоячая волна образуется при сложении бегущей и отраженной волн. Отраженную волну можно рассматривать как бегущую волну, распространяющуюся в обратном направлении и ее можно получить при отражении бегущей волны от границы двух сред. Для синусоидальных волн это означает, что при отражении от более плотной среды фаза волны скачком изменяется на радиан, а при отражении от менее плотной среды фаза волны не изменяется. Изменение фазы на радиан соответствует появлению дополнительного хода луча, равного .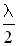

2. Звуковые волны

1. Важным видом продольных волн являются звуковые волны. Так называются волны с частотами 17 – 20000 Гц. Учение о звуке называется акустикой. В акустике изучаются волны, которые распространяются не только в воздухе, но и в любой другой среде. Упругие волны с частотой ниже 17 Гц называются инфразвуком, а с частотой выше 20000 Гц – ультразвуком.

 

Звуковые волны – упругие колебания, распространяющиеся в виде волнового процесса в газах, жидкостях, твердых телах.

2. Избыточное звуковое давление. Уравнение звуковой волны.

Уравнение упругой волны позволяет вычислить смещение любой точки пространства, по которому проходит волна, в любой момент времени. Но как говорить о смещении частиц воздуха или жидкости от положения равновесия? Звук, распространяясь в жидкости или газе, создает области сжатия и разряжение среды, в которых давление соответственно повышается или понижается по сравнению с давлением невозмущенной среды.

Если 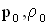— давление и плотность невозмущенной среды (среды, по которой не проходит волна), а 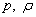— давление и плотность среды при распространении в ней волнового процесса, то величина 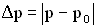называется избыточным давлением. Величина 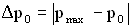есть максимальное значение избыточное давление (амплитуда избыточного давления).

Изменение избыточного давления для плоской звуковой волны (т.е. уравнение плоской звуковой волны) имеет вид:

,

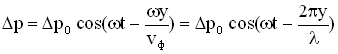где y – расстояние от источника колебаний точки, избыточное давление в которой мы определяем в момент времени t.

Если ввести величину избыточной плотности 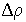и ее амплитуды 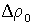так же, как мы вводили величину избыточного звукового давления, то уравнение плоской звуковой волны можно было бы записать так: 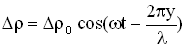. 3. Объективные и субъективные характеристики звука.

Само слово “звук” отражает два различных, но взаимосвязанных понятия: 1)звук как физическое явление; 2)звук – то восприятие, которое испытывает слуховой аппарат (человеческое ухо) и ощущения, возникающие у него при этом. Соответственно характеристики звука делятся на объективные, которые могут быть измерены физической аппаратурой, и субъективные, определяемые восприятием данного звука человеком.

К объективным (физическим) характеристикам звука относятся характеристики, которые описывают любой волновой процесс: частота, интенсивность и спектральный состав. В таблицу 3 включены сравнительные данные объективных и субъективных характеристик.

Таблица 3.

Субъективные Характеристики	Объективные характеристики
Высота звука	Высота звука определяется частотой волны
Тембр (окраска звука)	Тембр звука определяется его спектром
Громкость (сила звука)	Сила звука определяется нтенсивностью волны (или квадратом ее амплитуды)

Остановимся на некоторых определениях.

Частота звука измеряется числом колебаний частиц среды, участвующих в волновом процессе, в 1 секунду.

Интенсивность волны измеряется энергией, переносимой волной в единицу времени через единичную площадь (расположенную перпендикулярно направлению распространению волны).

Спектральный состав (спектр) звука указывает из каких колебаний состоит данный звук и как распределены амплитуды между отдельными его составляющими.

Различают сплошные и линейчатые спектры. Для субъективной оценки громкости используются величины, называемые уровнем силы звука и уровнем громкости. Все акустические величины и их размерности в СИ приведены в приложении.

3. Электромагнитные волны

1. Электромагнитными волнами называются возмущения электромагнитного поля (т.е. переменное электромагнитное поле), распространяющиеся в пространстве.

Утверждение о существовании электромагнитных волн является непосредственным следствием решения системы уравнений Максвелла. Согласно этой теории следует, что переменное электромагнитное поле распространяется в пространстве в виде волн, фазовая скорость которых равна:

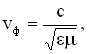
где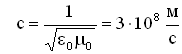 — скорость света в вакууме, 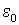, 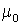— электрическая и магнитная постоянные, 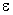, 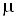— соответственно диэлектрическая и магнитная проницаемость среды.

2. Электромагнитные волны — поперечные волны. Векторы Е и Н поля электромагнитной волны взаимно перпендикулярны друг другу. Вектор скорости волны 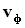и векторы Е и Н образуют правую тройку векторов (Рисунок 2.1.4).

Для сравнения ориентации тройки векторов 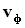, Е и Н на рисунке приведено расположение осей декартовой системы координат. Такое сопоставление уместно и в дальнейшем будет использовано для определения проекций векторов Е и Н на координатные оси.

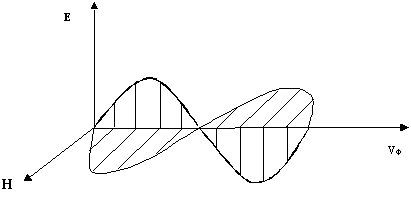
Рисунок 2.1.4

Взаимно перпендикулярные векторы Е и Н колеблются в одной фазе (их колебания синфазные). Модули этих векторов связаны соотношением:

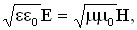
которое справедливо для любой бегущей электромагнитной волны независимо от формы ее волновых поверхностей.

3. По форме волновых поверхностей волны могут быть плоские, эллиптические, сферические и т.д..

Монохроматической волной называется электромагнитная волна одной определенной частоты. Монохроматическая волна не ограничена в пространстве и во времени. В каждой точке электромагнитного поля монохроматической волны проекции векторов Е и Н на оси координат совершают гармонические колебания одинаковой частоты 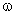. Например, для плоской монохроматической волны, распространяющейся вдоль положительного направления оси ОУ, как показано на рисунке 2.1.3.,ее уравнение имеет вид:

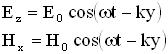
Такие волны называются плоско (или линейно) поляризованными волнами.

Плоскость, в которой происходит колебание вектора Е называют плоскостью поляризации линейно поляризованной волны, а плоскость колебаний вектора Н – плоскостью колебаний. Ранее эти названия были обратными (см. [1]).

4. Все сказанное о стоячих волнах в упругих средах относится и к электромагнитным волнам. В этом случае, однако, волна характеризуется не одним вектором, а двумя взаимно перпендикулярными векторами Е и Н.

Стоячая электромагнитная волна состоит из двух стоячих волн — магнитной и электрической, колебания которых сдвинуты по фазе на .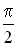

5. Энергия электромагнитных волн. Объемная плотность энергии электромагнитного поля в линейной изотропной среде задается соотношением: 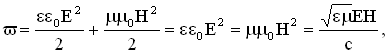с — скорость света в вакууме.

В случае плоской линейно поляризованной монохроматической волны, распространяющейся вдоль положительного направления ОY, напряженность электрического поля задается уравнением:

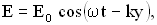
соответственно объемная плотность энергии этой волны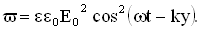

Значение объемной плотности энергии волны меняется за период от 0 до 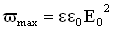.Среднее за период значение энергии равно:

.

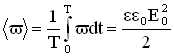6. Вектор плотности потока энергии электромагнитной волны называется вектором Умова — Пойнтинга:

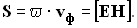
Для линейно поляризованной монохроматической волны вектор Пойнтинга направлен в сторону распространения волны и численно равен: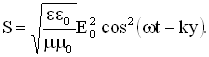

Интенсивность электромагнитной волны равна модулю среднего значения вектора Пойнтинга за период его полного колебания:

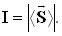
Интенсивностью электромагнитной волны называется физическая величина, численно равная энергии, переносимая волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны.

Интенсивность бегущей монохроматической волны: 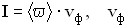— фазовая скорость волны, 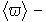среднее значение объемной плотности энергии поля волны.

Интенсивность света (электромагнитных волн, рассматриваемых в оптике) прямо пропорциональна квадрату амплитуды колебаний вектора напряженности Е поля световой волны.

Закон смещения Вина — Википедия

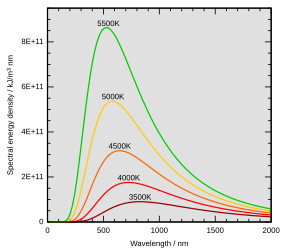
Зако́н смеще́ния Ви́на устанавливает зависимость длины волны, на которой поток излучения энергии чёрного тела достигает своего максимума, от температуры чёрного тела.

Вильгельм Вин впервые вывел этот закон в 1893 году, путём применения законов термодинамики к электромагнитному излучению.

Закон выражается формулой

λmax=b/T,{\displaystyle \lambda _{\text{max}}=b/T,}

где λmax{\displaystyle \lambda _{\text{max}}} — длина волны излучения с максимальной интенсивностью, а T{\displaystyle T} — температура. Коэффициент b=chkα{\displaystyle b={\frac {ch}{k\alpha }}} (где c — скорость света в вакууме, h — постоянная Планка, k — постоянная Больцмана, α ≈ 4,965114… — постоянная величина, корень уравнения α/5=1−e−α{\displaystyle \alpha /5=1-e^{-\alpha }}), называемый постоянной Вина, в Международной системе единиц (СИ) имеет значение 0,002898 м·К.

Для частоты света ν{\displaystyle \nu } (в герцах) закон смещения Вина имеет вид

νmax=αhkT≈5,879×1010⋅T,{\displaystyle \nu _{\text{max}}={\frac {\alpha }{h}}kT\approx 5{,}879\times 10^{10}\cdot T,}

где α ≈ 2,821439… — постоянная величина (корень уравнения α/3=1−e−α{\displaystyle \alpha /3=1-e^{-\alpha }}), k — постоянная Больцмана, h — постоянная Планка, T — температура (в кельвинах).

Различие численных постоянных здесь обусловлено различием между показателями степени в планковском распределении, записанном для длины волны и частоты излучения: в одном случае входит λ−5{\displaystyle \lambda ^{-5}}, в другом — ω3∼λ−3{\displaystyle \omega ^{3}\sim \lambda ^{-3}}. Это различие, в свою очередь, возникает из-за нелинейности связи между частотой и длиной волны:

ω=2πcλ,ddω=−λ22πcddλ.{\displaystyle \omega ={\frac {2\pi c}{\lambda }},\quad {\frac {d}{d\omega }}=-{\frac {\lambda ^{2}}{2\pi c}}{\frac {d}{d\lambda }}.}

Для вывода можно использовать выражение закона излучения Планка для абсолютно чёрного тела, записанного для длин волн:

B(λ,T)=2hcλ51ehc/λkT−1.{\displaystyle B(\lambda ,T)={\frac {2hc}{\lambda ^{5}}}{\frac {1}{e^{hc/\lambda kT}-1}}.}

Чтобы найти экстремумы этой функции в зависимости от длины волны, её следует продифференцировать по λ{\displaystyle \lambda } и приравнять производную нулю:

∂B∂λ=2hcλ61ehc/λkT−1(hckTλehc/λkT(ehc/λkT−1)−5)=0.{\displaystyle {\frac {\partial B}{\partial \lambda }}={\frac {2hc}{\lambda ^{6}}}{\frac {1}{e^{hc/\lambda kT}-1}}\left({\frac {hc}{kT\lambda }}{\frac {e^{hc/\lambda kT}}{\left(e^{hc/\lambda kT}-1\right)}}-5\right)=0.}

Из этой формулы сразу можно определить, что производная приближается к нулю, когда λ→∞{\displaystyle \lambda \to \infty } или когда ehc/λkT→∞{\displaystyle e^{hc/\lambda kT}\to \infty }, что выполняется при λ→0{\displaystyle \lambda \to 0}. Однако, оба эти случая дают минимум функции Планка B(λ){\displaystyle B(\lambda )}, которая для указанных длин волн достигает своего нуля (см. рисунок вверху). Поэтому анализ следует продолжить лишь с третьим возможным случаем, когда

hckTλehc/λkT(ehc/λkT−1)−5=0.{\displaystyle {\frac {hc}{kT\lambda }}{\frac {e^{hc/\lambda kT}}{\left(e^{hc/\lambda kT}-1\right)}}-5=0.}

Используя замену переменных x=hckTλ{\displaystyle x={\frac {hc}{kT\lambda }}}, данное уравнение можно преобразовать к виду

xexex−1−5=0.{\displaystyle {\frac {xe^{x}}{e^{x}-1}}-5=0.}

Численное решение этого уравнения даёт^[1]

x=4,965114231744276…{\displaystyle x=4{,}965114231744276\ldots }

Таким образом, используя замену переменных и значения постоянных Планка, Больцмана и скорости света, можно определить длину волны, на которой интенсивность излучения абсолютно чёрного тела достигает своего максимума:

λmax=hcx1kT=2,89776829…×10−3T,{\displaystyle \lambda _{\text{max}}={\frac {hc}{x}}{\frac {1}{kT}}={\frac {2{,}89776829\ldots \times 10^{-3}}{T}},}

где температура дана в кельвинах, а λmax{\displaystyle \lambda _{\text{max}}} — в метрах.

Согласно закону смещения Вина, чёрное тело с температурой человеческого тела (~310 K) имеет максимум теплового излучения на длине волны около 10 мкм, что соответствует инфракрасному диапазону спектра.

Реликтовое излучение имеет эффективную температуру 2,7 K и достигает своего максимума на длине волны 1 мм. Соответственно, эта длина волны принадлежит уже радиодиапазону.

1. ↑ Решение уравнения xexex−1=n{\displaystyle {\frac {xe^{x}}{e^{x}-1}}=n} невозможно выразить с помощью элементарных функций. Его точное решение можно найти с помощью W-функции Ламберта, однако в данном случае достаточно воспользоваться приближённым решением.

• B. H. Soffer and D. K. Lynch, «Some paradoxes, errors, and resolutions concerning the spectral optimization of human vision», Am. J. Phys. 67 (11), 946—953 1999.
• M. A. Heald, «Where is the ‘Wien peak’?», Am. J. Phys. 71 (12), 1322—1323 2003.