Потенциальное электрическое поле: Потенциальность электростатического поля — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Потенциал электрического поля

Потенциал. Эквипотенциальные поверхности.

В механике взаимодействие тел характеризует силой или потенциальной энергией. Электрическое поле, которое обеспечивает взаимодействие между электрически заряженными телами, также характеризуют двумя величинами. Напряженность электрического поля — это силовая характеристика. Теперь введем энергетическую характеристику — потенциал. С помощью этой величины можно будет сравнивать между собой любые точки электрического поля. Таким образом, потенциал как характеристика поля должен зависеть от значения заряда, содержащегося в этих точках. Поделим обе части формулы A = W₁ — W₂ на заряд q, получим

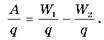
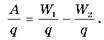
Отношение W/q не зависит от значения заряда и принимается за энергетическую характеристику, которую называют потенциалом поля в данной точке. Обозначают потенциал буквой φ.

Потенциал электрического поля φ — скалярная энергетическая характеристика поля, которая определяется отношением потенциальной энергии W положительного заряда q в данной точке поля к величине этого заряда:

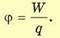
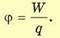
Единица потенциала — вольт:

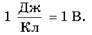
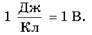
Подобно потенциальной энергии значения потенциала в данной точке зависит от выбора нулевого уровня для отсчета потенциала. Чаще всего в электродинамике за нулевой уровень берут потенциал точки, лежащей в бесконечности, а в электротехнике — на поверхности Земли.

С введением потенциала формулу для определения работы по перемещению заряда между точками 1 и 2 можно записать в виде

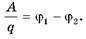
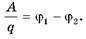
Поскольку при перемещении положительного заряда в направлении вектора напряженности электрическое поле выполняет положительную работу A = q (φ₁ — φ₂ )> 0, то потенциал φ₁ больше чем потенциал φ₂ . Таким образом, напряженность электрического поля направлена в сторону уменьшения потенциала.

Если заряд перемещать с определенной точки поля в бесконечность, то работа A = q (φ — φ_∞ ). Поскольку φ_∞ = 0, то A = qφ. Таким образом, величина потенциала φ определенной точки поля определяется работой, которую выполняет электрическое поле, перемещая единичный положительный заряд из этой точки в бесконечность,

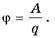
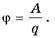
Если электрическое поле создается точечным зарядом q, то в точке, лежащей на расстоянии r от него, потенциал вычисляют по формуле

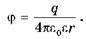
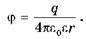
По этой формуле рассчитывают и потенциал поля заряженного шара. В таком случае r — это расстояние от центра шара до выбранной точки поля. С этой формулы видно, что на одинаковых расстояниях от точечного заряда, который создает поле, потенциал одинаков. Все эти точки лежат на поверхности сферы, описанной радиусом r вокруг точечного заряда. Такую сферу называют эквипотенциальной поверхностью.

Эквипотенциальные поверхности — геометрическое место точек в электрическом поле, которые имеют одинаковый потенциал, — один из методов наглядного изображения электрических полей.

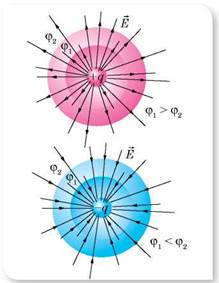
Эквипотенциальные поверхности электрических полей, созданных точечными зарядами разных знаков

Силовые линии всегда перпендикулярны эквипотенциальных поверхностей. Это означает, что работа сил поля по перемещению заряда по эквипотенциальной поверхности равна нулю.

В случае наложения электрических полей, созданных несколькими зарядами, потенциал электрического поля равен алгебраической сумме потенциалов полей, созданных отдельными зарядами, φ = φ₁ + φ₂ + φ₃ . Эквипотенциальные поверхности таких систем имеют сложную форму. Например, для системы из двух одинаковых по значению одноименных зарядов эквипотенциальные поверхности имеют вид, изображенный на рисунке. Эквипотенциальные поверхности однородного поля явлются плоскостями.

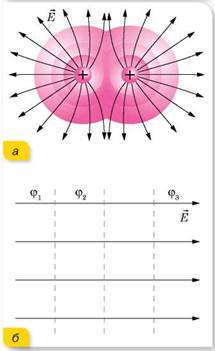
Эквипотенциальные поверхности: а — поля двух одинаковых зарядов б — однородного поля

Разность потенциалов

Практическое значение имеет не сам потенциал в точке, а изменение (разница) потенциала φ₁ — φ₂ , которое не зависит от выбора нулевого уровня отсчета потенциала. Разность потенциалов φ₁ — φ₂ еще называют напряжением и обозначают латинской буквой U. Тогда формула для работы по перемещению заряда приобретает вид

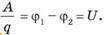
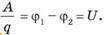
Напряжение U — это физическая величина, определяемая работой электрического поля по перемещению единичного положительного заряда между двумя точками поля,

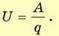
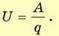
Единица разности потенциалов (напряжения), как и потенциала, — вольт,

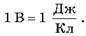
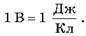
Поскольку работа сил поля по перемещению заряда зависит только от разности потенциалов, то в случае перемещения заряда с первой эквипотенциальной поверхности на другую (потенциалы которых соответственно φ₁ и φ₂ ) выполненная полем работа не зависит от траектории этого движения.

Связь напряженности электрического поля с напряжением

Из формул A = Eqd и A = qU можно установить связь между напряженностью и напряжением электрического поля: Ed = U. С этой формулы следует:

чем меньше меняется потенциал на расстоянии d, тем меньше есть напряженность электрического поля;
если потенциал не меняется, то напряженность равна нулю;
напряженность электрического поля направлена в сторону уменьшения потенциала.

Поскольку

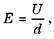
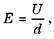
то именно из этой формулы и выводится еще одна единица напряженности — вольт на метр,

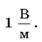
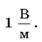
Потенциал и работа электростатического поля. Связь напряженности с потенциалом

В предыдущей теме было показано, что взаимодействие между покоящимися зарядами осуществляется через электростатическое поле. Описание электростатического поля мы рассматривали с помощью вектора напряженности , равного силе, действующей в данной точке на помещенный в неё пробный единичный положительный заряд

Существует и другой способ описания поля – с помощью потенциала. Однако для этого необходимо сначала доказать, что силы электростатического поля консервативны, а само поле потенциально.

Рассмотрим поле, создаваемое неподвижным точечным зарядом . В любой точке этого поля на пробный точечный заряд q действует сила (рис. 3.1).

Рис. 3.1

где F(r)– модуль вектора силы , – единичный вектор, определяющий положение заряда

q относительно q´, ε₀ – электрическая постоянная.

Для того, чтобы доказать, что электростатическое поле потенциально, нужно доказать, что силы электростатического поля консервативны. Из раздела «Физические основы механики» известно, что любое стационарное поле центральных сил является консервативным, т.е. работа сил этого поля не зависит от формы пути, а только от положения конечной и начальной точек.

Вычислим работу, которую совершает электростатическое поле, созданное зарядом q´ по перемещению заряда q из точки 1 в точку 2.

Работа на пути dlравна:

где dr – приращение радиус-вектора при перемещении на dl; т. е.

Тогда полная работа при перемещении q´ из точки 1 в точку 2 равна интегралу:

(3.1.1)

Получили, что работа электростатических сил не зависит от формы пути, а только лишь от координат начальной и конечной точек перемещения. Следовательно, силы поля консервативны, а само поле – потенциально.

Этот вывод можно распространить и на поле, созданное системой зарядов, так как по принципу суперпозиции полей: .

Итак, как и в механике, любое стационарное поле центральных сил является консервативными, т.е. работа сил этого поля не зависит от формы пути, а только от положения начальной и конечной точек. Именно таким свойством обладает электростатическое поле – поле, образованное системой неподвижных зарядов. Если в качестве пробного заряда, перенесенного из точки 1 (рис. 3.2) заданного поля в точку 2, взять положительный единичный заряд q, то элементарная работа сил поля будет равна:

(3.1.2)

Рис. 3.2

Тогда вся работа равна:

(3.1.3)

Такой интеграл по замкнутому контуру называется циркуляцией вектора .

Из независимости линейного интеграла от пути между двумя точками следует, что по произвольному замкнутому пути:

(3.1.5)

Это утверждение и называют теоремой о циркуляции .

Для доказательства теоремы разобьем произвольно замкнутый путь на две части: 1а2 и 2b1 (рис. 3.2). Из сказанного выше следует, что

(Интегралы по модулю равны, но знаки противоположны). Тогда работа по замкнутому пути:

Поле, обладающее такими свойствами, называется потенциальным. Любое электростатическое поле является потенциальным.

Теория по физике для ЕГЭ, пособия по подготовке и справочные материалы в Москве

Работа сил электростатического поля. Потенциал и разность потенциалов. Связь разности потенциалов с напряженностью электростатического поля. Потенциал поля точечного заряда. Эквипотенциальные поверхности.

Работа сил электростатического поля

При перемещении пробного заряда \(q\) в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении \(\Delta \vec{l}\) равна:

\[\Delta A=F\Delta l\cos\alpha=Eq\Delta l\cos\alpha=E_1 q\Delta l\]

Рассмотрим работу сил в электрическом поле, создаваемом неизменным во времени распределенным зарядом, т.е. электростатическом поле.

Электростатическое поле обладает важным свойством:

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Следствием независимости работы от формы траектории является следующее утверждение:

Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Силовые поля, обладающие этим свойством, называют или консервативными.

На замкнутой траектории работа кулоновских сил равна нулю.

Потенциальная энергия заряда \(q\), помещенного в любую точку (1) пространства, относительно фиксированной точки (0) равна работе \(A_{10}\), которую совершит электростатическое поле при перемещении заряда \(q\) из точки (1) в точку (0):

\[W_{p1} = A_{10}\]

Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора опорной точки (0). Такая неоднозначность в определении потенциальной энергии не приводит к каким-либо недоразумениям, так как физический смысл имеет не сама потенциальная энергия, а разность ее значений в двух точках пространства.

Работа, совершаемая электростатическое полем при перемещении точечного заряда \(q\) из точки (1) в точку (2), равна разности значений потенциальной энергии в этих точках и не зависит от пути перемещения заряда и от выбора точки (0).

\[A_{12} = A_{10} + A_{02} = A_{10} — A_{20} = W_{p_1} — W_{p_2}\]

Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют \(\varphi\) электрического поля:

\[\varphi=\dfrac{W_p}{q}\]

Потенциал \(\varphi\) является энергетической характеристикой электростатического поля.

Работа \(A_{12}\) по перемещению электрического заряда \(q\) из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов (\(\varphi_1-\varphi_2\)) начальной и конечной точек:

\(A_{12} = W_{p1} — W_{p2} = q\varphi_1 — q\varphi_2 = q(\varphi_1-\varphi_2)\)

Единицы измерения: \(\displaystyle [\text{В}]\) (Вольт).

Во многих задачах электростатики при вычислении потенциалов за опорную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:

Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

\[\varphi_{\infty}=\dfrac{A_{\infty}}{q}\]

Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется или поверхностью равного потенциала.

Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов:

\[\varphi =\varphi_1 + \varphi_2+ \varphi_3 + …+\varphi_n\]

потенциальное электрическое поле — это… Что такое потенциальное электрическое поле?

потенциальное электрическое поле: Электрическое поле, в котором ротор вектора напряженности электрического поля всюду равен нулю.

потенциальное силовое поле
потенциальный барьер

Смотреть что такое «потенциальное электрическое поле» в других словарях:

Потенциальное векторное поле — Потенциальное (или безвихревое) векторное поле в математике векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном… … Википедия
Потенциальное поле — Потенциальное (или безвихревое) векторное поле в математике векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном пространстве … Википедия
Градиентное поле — Потенциальное (или безвихревое) векторное поле в математике векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном пространстве … Википедия
электростатическое поле — электрическое поле неподвижных электрических зарядов. * * * ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ, электрическое поле неподвижных и не меняющихся со временем электрических зарядов, осуществляющее взаимодействие между ними.… … Энциклопедический словарь
Соленоидальное векторное поле — Содержание 1 Определение 2 Примеры 3 Этимология 4 См. также … Википедия
Силовые линии векторного поля — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей … Википедия
Ома закон — устанавливает, что сила постоянного электрического тока I в проводнике прямо пропорциональна разности потенциалов (напряжению) U между двумя фиксированными точками (сечениями) этого проводника: RI = U. (1) Коэффициент… … Большая советская энциклопедия
разность электрических потенциалов двух точек — Скалярная величина, характеризующая потенциальное электрическое поле, равная пределу отношения работы сил этого поля, при переносе положительно заряженного точечного тела из одной данной точки поля в другую, к заряду этого тела, когда заряд тела… … Политехнический терминологический толковый словарь
электродинамика — и; ж. Раздел физики, изучающий электромагнитные процессы в различных средах и вакууме. ◁ Электродинамический, ая, ое. * * * электродинамика классическая, теория электромагнитных процессов в различных средах и в вакууме. Охватывает огромную… … Энциклопедический словарь
ЭЛЕКТРОДИНАМИКА — классическая теория электромагнитных процессов в различных средах и в вакууме. Охватывает огромную совокупность явлений, в которых основную роль играют взаимодействия между заряженными частицами, осуществляемые посредством электромагнитного поля … Большой Энциклопедический словарь

Урок 27. напряжённость и потенциал электростатического поля. разность потенциалов — Физика — 10 класс

Физика, 10 класс

Урок 27. Напряжённость и потенциал электростатического поля. Разность потенциалов

Перечень вопросов, рассматриваемых на уроке:

1) Теория дальнодействия;

2) Теория близкодействия;

3) Электрическое поле;

4) Скорость электрического поля;

5) Напряжённость электрического поля;

6) Однородное и неоднородное электрическое поле;

7) Принцип суперпозиции полей;

8) Диэлектрическая проницаемость;

9) Электростатическая защита

10) Работа электрического поля;

11) Потенциал и разность потенциалов.

Глоссарий по теме:

Напряжённость — отношение силы, действующей на помещаемый в данную точку поля точечный заряд, к этому заряду.

Потенциал точки электростатического поля -отношение потенциальной энергии заряда, помещённого в данную точку, к этому заряду.

Напряжение – разность потенциалов.

Потенциальное поле – поле, работа которого по перемещению заряда по замкнутой траектории всегда равна нулю.

Напряжённость направлена в сторону убывания потенциала.

Эквипотенциальные поверхности – поверхности равного потенциала.

Свободные заряды — заряженные частицы, способные свободно перемещаться в проводнике под влиянием электрического поля.

Электростатическая индукция – явление разделения зарядов и их распределение по поверхности проводника во внешнем электрическом поле.

Основная и дополнительная литература

Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Сотский. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 290 – 320.

Рымкевич А.П. Сборник задач по физике. 9 – 11 класс. М. Дрофа, 1999 – С. 93 — 102

Теоретический материал для самостоятельного изучения

Согласно идее Фарадея электрические заряды не действуют друг на друга непосредственно. Каждый из них создаёт в окружающем пространстве электрическое поле.

Электрическое поле — это особый вид материи, посредством которой происходит взаимодействие зарядов. Скорость распространения электрического поля в вакууме равна 300000 км/с.

Напряжённость Е — силовая характеристика электрического поля.

Электрическое поле, напряженность которого одинакова во всех точках, называется однородным. Поле между параллельными пластинами однородно

Главное свойство электрического поля – это действие его на электрические заряды с некоторой силой.

Напряжённость-это отношение силы, действующей на помещаемый в данную точку поля точечный заряд, к этому заряду.

Если в данной точке пространства различные заряженные частицы создают поля, напряжённости которых Е₁, Е₂, то результирующая напряжённость поля в этой точке равна геометрической сумме напряжённостей этих полей. В этом состоит принцип суперпозиции полей.

Заряд, помещенный в электрическое поле обладает потенциальной энергией.

Потенциалом φ точки электростатического поля называют отношение потенциальной энергии Wn заряда, помещённого в данную точку, к этому заряду q.

Напряжение – это работа, совершаемая полем при перемещении заряда 1Кл.

Примеры и разбор решения заданий

1. К каждой позиции первого столбца подберите соответствующую позицию второго

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ	ФОРМУЛЫ
Напряженность
Потенциал
Потенциальная энергия заряда в однородном электростатическом поле
Разность потенциалов	_qΕd

Решение: вспомнив формулы величин, можем установить:

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ	ФОРМУЛЫ
Напряженность
Потенциал
Потенциальная энергия заряда в однородном электростатическом поле	_qΕd
Разность потенциалов

2. В однородном электрическом поле напряжённостью 1 В/м переместили заряд -25 нКл в направлении силовой линии на 2 см. Найти работу поля, изменение потенциальной энергии заряда и напряжение между начальной и конечной точками перемещения.

Решение.

Работа электрического поля при перемещении заряда вдоль силовой линии:

ΔA = — qΕΔd,

при этом изменение потенциальной энергии равно:

Напряжение между начальной и конечной точками перемещения равно:

Вычисления:

ΔA = -25 · 10^-9Kл · 10³B/м · 0,02 м = -0,5 мкДж;

Ответ:

Электричество и магнетизм

которая идет на увеличение его потенциальной энергии. Отсюда получаем потенциальную энергию диполя в электрическом поле

откуда

или

(3.8)

если положить const = 0.

Из рисунка видно, что внешнее электрическое поле стремится повернуть диполь таким образом, чтобы вектор его электрического момента р совпал по направлению с вектором Е. В этом случае , а, следовательно, и М = 0. С другой стороны, при потенциальная энергия диполя во внешнем поле принимает минимальное значение , что соответствует положению устойчивого равновесия. При отклонении диполя от этого положения снова возникает механический момент, который возвращает диполь в первоначальное положение. Другое положение равновесия, когда дипольный момент направлен против поля является неустойчивым. Потенциальная энергия в этом случае принимает максимальное значение и при небольших отклонениях от такого положения возникающие силы не возвращают диполь назад, а еще больше отклоняют его.

На рис. 3.11 показан опыт, иллюстрирующий возникновение момента электрических сил, действующих на диэлектрик в электрическом поле. На удлиненный диэлектрический образец, расположенный под некоторым углом к силовым линиям электростатического поля, действует момент сил, стремящийся развернуть этот образец вдоль поля. Диэлектрическая палочка, подвешенная за середину внутри плоского конденсатора, разворачивается перпендикулярно его пластинам после подачи на них высокого напряжения от электростатической машины. Появление вращающего момента обусловлено взаимодействием поляризовавшейся палочки с электрическим полем конденсатора.

Рис. 3.11. Момент электрических сил, действующих на диэлектрик в электрическом поле

В случае неоднородного поля на рассматриваемый диполь будет действовать еще и равнодействующая сила F_paвн, стремящаяся его сдвинуть. Мы рассмотрим здесь частный случай. Направим ось х вдоль поля Е. Пусть диполь под действием поля уже повернулся вдоль силовой линии, так что отрицательный заряд находится в точке с координатой x, а положительный заряд расположен в точке с координатой х + l. Представим себе, что величина напряженности поля зависит от координаты х. Тогда равнодействующая сила F_paвнравна

(3.9)

Такой же результат может быть получен из общего соотношения

где энергия П определена в (3.8). Если Е увеличивается с ростом x, то

и проекция равнодействующей силы положительна. Это значит, что она стремиться втянуть диполь в область, где напряженность поля больше. Этим объясняется известный эффект, когда нейтральные кусочки бумаги притягиваются к наэлектризованной расческе. В плоском конденсаторе с однородным полем они остались бы неподвижными.

Рассмотрим несколько опытов, иллюстрирующих возникновение силы, действующей на диэлектрик, помещенный в неоднородное электрическое поле.

На рис. 3.12 показано втягивание диэлектрика в пространство между обкладками плоского конденсатора. В неоднородном электростатическом поле на диэлектрик действуют силы, втягивающие его в область более сильного поля.

Рис. 3.12. Втягивание жидкого диэлектрика в плоский конденсатор

Это демонстрируется при помощи прозрачного сосуда, в который помещен плоский конденсатор, и налито некоторое количество жидкого диэлектрика — керосина (рис.3.13). Конденсатор присоединен к высоковольтному источнику питания — электростатической машине. При ее работе на нижнем краю конденсатора, в области неоднородного поля, на керосин действует сила, втягивающая его в пространство между пластинами. Поэтому уровень керосина внутри конденсатора устанавливается выше, чем снаружи. После выключения поля уровень керосина между пластинами падает до его уровня в сосуде.

Рис. 3.13. Втягивание керосина в пространство между обкладками плоского конденсатора

Видео 3.1. Эксперимент по втягиванию жидкого диэлектрика в конденсатор.

В реальных веществах нечасто встречаются диполи, образованные только двумя зарядами. Обычно мы имеем дело с более сложными системами. Но понятие электрического дипольного момента применимо и к системам со многими зарядами. В этом случае дипольный момент определяется как

(3.10)

где , — величина заряда с номером i и радиус-вектор, определяющий его местоположение, соответственно. В случае двух зарядов мы приходим к прежнему выражению

Пусть наша система зарядов электрически нейтральна. В ней есть положительные заряды, величины которых и местоположения мы обозначим индексом «+». Индексом «–» мы снабдим абсолютные величины отрицательных зарядов и их радиус-векторы. Тогда выражение (3.10) может быть записано в виде

(3.11)

В (3.11) в первом слагаемом суммирование ведется по всем положительным зарядам, а во втором — по всем отрицательным зарядам системы.

Электрическая нейтральность системы означает равенство полного положительного заряда и суммы абсолютных величин всех отрицательных зарядов

(3.12)

Введем теперь понятие «центр зарядов» — положительных R⁺ и отрицательных R^–

(3.13)

Выражения (3.13) аналогичны формулам для центра масс в механике, и потому мы назвали их центрами положительных и отрицательных зарядов, соответственно. С этими обозначениями и с учетом соотношения (3.12) мы записываем электрический дипольный момент (3.11) системы зарядов в виде

(3.14)

где l-вектор, проведенный из центра отрицательных зарядов в центр положительных зарядов. Смысл нашего упражнения заключается в демонстрации, что любую электрически нейтральную систему зарядов можно представить как некий эквивалентный диполь.

Дополнительная информация

http://webmath.exponenta.ru/dnu/lc/age/pyartli1/node9.htm — Векторное произведение.

потенциальное электрическое поле — это… Что такое потенциальное электрическое поле?

потенциальное электрическое поле: Универсальный русско-английский словарь. Академик.ру. 2011.

потенциальное циклическое течение
потенциальное энергосбережение

Смотреть что такое «потенциальное электрическое поле» в других словарях:

потенциальное электрическое поле — Электрическое поле, в котором ротор вектора напряженности электрического поля всюду равен нулю … Политехнический терминологический толковый словарь
Потенциальное векторное поле — Потенциальное (или безвихревое) векторное поле в математике векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном… … Википедия
Потенциальное поле — Потенциальное (или безвихревое) векторное поле в математике векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном пространстве … Википедия
Градиентное поле — Потенциальное (или безвихревое) векторное поле в математике векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном пространстве … Википедия
электростатическое поле — электрическое поле неподвижных электрических зарядов. * * * ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ, электрическое поле неподвижных и не меняющихся со временем электрических зарядов, осуществляющее взаимодействие между ними.… … Энциклопедический словарь
Соленоидальное векторное поле — Содержание 1 Определение 2 Примеры 3 Этимология 4 См. также … Википедия
Силовые линии векторного поля — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей … Википедия
Ома закон — устанавливает, что сила постоянного электрического тока I в проводнике прямо пропорциональна разности потенциалов (напряжению) U между двумя фиксированными точками (сечениями) этого проводника: RI = U. (1) Коэффициент… … Большая советская энциклопедия
разность электрических потенциалов двух точек — Скалярная величина, характеризующая потенциальное электрическое поле, равная пределу отношения работы сил этого поля, при переносе положительно заряженного точечного тела из одной данной точки поля в другую, к заряду этого тела, когда заряд тела… … Политехнический терминологический толковый словарь
электродинамика — и; ж. Раздел физики, изучающий электромагнитные процессы в различных средах и вакууме. ◁ Электродинамический, ая, ое. * * * электродинамика классическая, теория электромагнитных процессов в различных средах и в вакууме. Охватывает огромную… … Энциклопедический словарь
ЭЛЕКТРОДИНАМИКА — классическая теория электромагнитных процессов в различных средах и в вакууме. Охватывает огромную совокупность явлений, в которых основную роль играют взаимодействия между заряженными частицами, осуществляемые посредством электромагнитного поля … Большой Энциклопедический словарь

Связь между электрическим полем и электрическим потенциалом

- Классы
  Класс 1-3
  Класс 4-5
  Класс 6-10
  Класс 11-12
- КОНКУРСНЫЙ ЭКЗАМЕН
  BNAT 000 NC
  000 NC Книги
  Книги NCERT для класса 5
  Книги NCERT для класса 6
  Книги NCERT для класса 7
  Книги NCERT для класса 8
  Книги NCERT для класса 9
  Книги NCERT для класса 10
  Книги NCERT для класса 11
  Книги NCERT для класса 12
  NCERT Exemplar
  NCERT Exemplar Class 8
  NCERT Exemplar Class 9
  NCERT Exemplar Class 10
  NCERT Exemplar Class 11
  NCERT 9000 9000
  NCERT Exemplar Class
  Решения RS Aggarwal, класс 12
  Решения RS Aggarwal, класс 11
  Решения RS Aggarwal, класс 10
  90 003 Решения RS Aggarwal класса 9
  Решения RS Aggarwal класса 8
  Решения RS Aggarwal класса 7
  Решения RS Aggarwal класса 6
  Решения RD Sharma
  RD Sharma Class 6 Решения
  Решения RD Sharma
  Решения RD Sharma Class 8
  Решения RD Sharma Class 9
  Решения RD Sharma Class 10
  Решения RD Sharma Class 11
  Решения RD Sharma Class 12
  PHYSICS
  Механика
  Оптика
  Термодинамика Электромагнетизм
  ХИМИЯ
  Органическая химия
  Неорганическая химия
  Периодическая таблица
  MATHS
  Теорема Пифагора
  0004
  000300030004
  9000
  Простые числа
  Взаимосвязи и функции
  Последовательности и серии
  Таблицы умножения
  Детерминанты и матрицы
  Прибыль и убыток
  Полиномиальные уравнения
  Деление фракций
  000
  000
  000
  000
  000
  000 Microology
  000
  000 Microology
  000 BIOG3000
  FORMULAS
  Математические формулы
  Алгебраические формулы
  Тригонометрические формулы
  Геометрические формулы
  КАЛЬКУЛЯТОРЫ
  Математические калькуляторы
  0003000 PBS4000
  000300030002 Примеры калькуляторов химии
  Класс 6
  Образцы бумаги CBSE для класса 7
  Образцы бумаги CBSE для класса 8
  Образцы бумаги CBSE для класса 9
  Образцы бумаги CBSE для класса 10
  Образцы бумаги CBSE для класса 11
  Образцы бумаги CBSE чел для класса 12
  CBSE Контрольный документ за предыдущий год
  CBSE Контрольный документ за предыдущий год Класс 10
  Контрольный документ за предыдущий год CBSE, класс 12
  HC Verma Solutions
  HC Verma Solutions Class 11 Physics
  Решения HC Verma, класс 12, физика
  Решения Лакмира Сингха
  Решения Лакмира Сингха, класс 9
  Решения Лакмира Сингха, класс 10
  Решения Лакмира Сингха, класс 8
  Заметки CBSE
  CBSE Notes
  Примечания CBSE класса 7
  Примечания CBSE класса 8
  Примечания CBSE класса 9
  Примечания CBSE класса 10
  Примечания CBSE класса 11
  Примечания CBSE класса 12
  Примечания к редакции CBSE
  Примечания к редакции
  CBSE Class
  Примечания к редакции класса 10 CBSE
  Примечания к редакции класса 11 CBSE 9000 4
  Примечания к редакции класса 12 CBSE
  Дополнительные вопросы CBSE
  Дополнительные вопросы по математике класса 8 CBSE
  Дополнительные вопросы по науке 8 класса CBSE
  Дополнительные вопросы по математике класса 9 CBSE
  Дополнительные вопросы по науке класса 9 CBSE
  Дополнительные вопросы по математике для класса 10
  Дополнительные вопросы по науке, класс 10 по CBSE
  CBSE, класс
  , класс 3
  , класс 4
  , класс 5
  , класс 6
  , класс 7
  , класс 8
  , класс 9 Класс 10
  Класс 11
  Класс 12
  Учебные решения
  Решения NCERT
  Решения NCERT для класса 11
  Решения NCERT для класса 11 по физике
  Решения NCERT для класса 11 Химия
  Решения для биологии класса 11
  Решения NCERT для математики класса 11
  9 0003 NCERT Solutions Class 11 Accountancy
  NCERT Solutions Class 11 Business Studies
  NCERT Solutions Class 11 Economics
  NCERT Solutions Class 11 Statistics
  NCERT Solutions Class 11 Commerce
  NCERT Solutions For Class 12
  NCERT Solutions For Класс 12 по физике
  Решения NCERT для химии класса 12
  Решения NCERT для класса 12 по биологии
  Решения NCERT для класса 12 по математике
  Решения NCERT Класс 12 Бухгалтерия
  Решения NCERT, класс 12, бизнес-исследования
  Решения NCERT, класс 12 Экономика
  NCERT Solutions Class 12 Accountancy Part 1
  NCERT Solutions Class 12 Accountancy Part 2
  NCERT Solutions Class 12 Micro-Economics
  NCERT Solutions Class 12 Commerce
  NCERT Solutions Class 12 Macro-Economics
  NCERT Solutions For Класс 4
  Решения NCERT для математики класса 4
  Решения NCERT для класса 4 EVS
  Решения NCERT для класса 5
  Решения NCERT для математики класса 5
  Решения NCERT для класса 5 EVS
  Решения NCERT для класса 6
  Решения NCERT для математики класса 6
  Решения NCERT для науки класса 6
  Решения NCERT для социальных наук класса 6
  Решения NCERT для класса 6 Английский
  Решения NCERT для класса 7
  Решения NCERT для класса 7 Математика
  Решения NCERT для класса 7 Наука
  Решения NCERT для класса 7 по социальным наукам
  Решения NCERT для класса 7 Английский
  Решения NCERT для класса 8
  Решения NCERT для класса 8 Математика
  Решения NCERT для класса 8 Science
  Решения NCERT для социальных наук 8 класса
  Решение NCERT ns для класса 8 Английский
  Решения NCERT для класса 9
  Решения NCERT для социальных наук класса 9
  Решения NCERT для математики класса 9
  Решения NCERT для математики класса 9 Глава 1
  Решения NCERT для Математика класса 9 Глава 2
  Решения NCERT для математики класса 9 Глава 3
  Решения NCERT для математики класса 9 Глава 4
  Решения NCERT
  для математики класса 9 Глава 5
  Решения NCERT для математики класса 9 Глава 6
  Решения NCERT для Математика класса 9 Глава 7
  Решения NCERT для математики класса 9 Глава 8
  Решения NCERT
  для математики класса 9 Глава 9
  Решения NCERT
  для математики класса 9 Глава 10
  Решения NCERT для математики класса 9 Глава 11
  Решения NCERT для Математика класса 9 Глава 12
  Решения NCERT для математики класса 9 Глава 13
  Решения
  NCERT для математики класса 9 Глава 14
  Решения NCERT для математики класса 9 Глава 15
  Решения NCERT для науки класса 9
  Решения NCERT для науки класса 9 Глава 1
  Решения NCERT для науки класса 9 Глава 2
  Решения NCERT для класса 9 Наука Глава 3
  Решения NCERT для Науки Класса 9 Глава 4
  Решения NCERT для Науки Класса 9 Глава 5
  Решения NCERT для Науки Класса 9 Глава 6
  Решения NCERT для Науки Класса 9 Глава 7
  Решения NCERT для Класса 9 Наука Глава 8
  Решения NCERT для Науки Класса 9 Глава 9
  Решения NCERT для Науки Класса 9 Глава 10
  Решения NCERT для Науки Класса 9 Глава 12
  Решения NCERT для Науки Класса 9 Глава 11
  Решения NCERT для Класса 9 Наука Глава 13
  Решения NCERT для класса 9 Наука Глава 14
  Решения NCERT для класса 9 по науке Глава 15
  Решения NCERT для класса 10
  Решения NCERT для класса 10 по социальным наукам
  Решения NCERT для математики класса 10
  Решения NCERT для математики класса 10 Глава 1
  Решения NCERT для математики класса 10 Глава 2
  Решения NCERT для математики класса 10 Глава 3
  Решения NCERT для математики класса 10 Глава 4
  Решения NCERT для математики класса 10 Глава 5
  Решения NCERT для математики класса 10 Глава 6
  Решения NCERT для математики класса 10 Глава 7
  Решения NCERT для математики класса 10 Глава 8
  Решения NCERT для математики класса 10 Глава 9
  Решения NCERT
  для математики класса 10 Глава 10
  Решения
  NCERT для математики класса 10 Глава 11
  Решения NCERT для математики класса 10 Глава 12
  Решения NCERT для математики класса 10 Глава 13
  NCERT Sol Решения NCERT для математики класса 10 Глава 14
  Решения NCERT для математики класса 10 Глава 15
  Решения NCERT для науки класса 10
  Решения NCERT для науки класса 10 Глава 1
  Решения NCERT для науки класса 10 Глава 2
  Решения NCERT для науки класса 10, глава 3
  Решения NCERT для науки класса 10, глава 4
  Решения NCERT для науки класса 10, глава 5
  Решения NCERT для науки класса 10, глава 6
  Решения NCERT для науки класса 10, глава 7
  Решения NCERT для науки 10 класса, глава 8
  Решения NCERT для науки класса 10 Глава 9
  Решения NCERT для науки класса 10 Глава 10
  Решения NCERT для науки класса 10 Глава 11
  Решения NCERT для науки класса 10 Глава 12
  Решения NCERT для науки 10 класса Глава 13
  Решения NCERT для науки 10 класса Глава 14
  Решения NCERT для науки класса 10 Глава 15
  Решения NCERT
  для науки класса 10 Глава 16
  Учебный план NCERT
  NCERT
  Commerce
  Class 11 Commerce Syllabus
  ancy Account
  Учебный план по бизнесу, класс 11
  Учебный план по экономике, класс 11
  Учебный план по коммерции, класс 12
  Учебный план по бухгалтерии, класс 12
  Учебный план по бизнесу, класс 12
  Учебный план по экономике, класс 12 9000 9000
  Образцы документов по коммерции класса 11
  Образцы документов по коммерции класса 12
  TS Grewal Solutions
  TS Grewal Solutions Class 12 Accountancy
  TS Grewal Solutions Class 11 Accountancy
  Отчет о движении денежных средств
  Что такое Entry eurship
  Защита прав потребителей
  Что такое основной актив
  Что такое баланс
  Формат баланса
  Что такое акции
  Разница между продажей и маркетингом
  ICSE
  Документы ICSE
  Вопросы ICSE
  ML Aggarwal Solutions
  ML Aggarwal Solutions Class 10 Maths
  ML Aggarwal Solutions Class 9 Maths
  ML Aggarwal Solutions Class 8 Maths
  ML Aggarwal Solutions Class 7 Maths
  ML 6 Maths
  ML Aggarwal Solutions Class 6 Maths
  ML Aggarwal Solutions Class
  Selina Solutions
  Selina Solutions для класса 8
  Selina Solutions для Class 10
  Selina Solutions для Class 9
  Frank Solutions
  Frank Solutions для математики класса 10
  Frank Solutions для математики класса 9
  Класс ICSE 9000 2
  ICSE Class 6
  ICSE Class 7
  ICSE Class 8
  ICSE Class 9
  ICSE Class 10
  ISC Class 11
  ISC Class 12
  IAS
  Exam
  IAS
  Civil
  Сервисный экзамен
  Программа UPSC
  Бесплатная подготовка к IAS
  Текущие события
  Список статей IAS
  Пробный тест IAS 2019
  Пробный тест IAS 2019 1
  Пробный тест IAS 2019 2
  
  Экзамен KPSC KAS
  Экзамен UPPSC PCS
  Экзамен MPSC
  Экзамен RPSC RAS 
  TNPSC Group 1
  APPSC Group 1
  Экзамен BPSC
  WBPS3000 Экзамен 9000 MPC 9000 9000 MPC4000 Jam
  Вопросник UPSC 2019
  Ключ ответов UPSC 2019
  Коучинг IAS
  IA S Coaching Бангалор
  IAS Coaching Дели
  IAS Coaching Ченнаи
  IAS Coaching Хайдарабад
  IAS Coaching Mumbai
  JEE
  BYJU’SEE
  9000 JEE 9000 Основной документ JEE 9000 JEE 9000
  Вопросник JEE
  Биномиальная теорема
  Статьи JEE
  Квадратичное уравнение
  NEET
  Программа BYJU NEET
  NEET 2020
  NEET Приемлемость 9000 Критерии 9000 NEET4 9000 NEET 9000 Пример 9000 9000 NEET
  Поддержка
  Разрешение жалоб
  Служба поддержки
  Центр поддержки
  Государственные советы
  GSEB
  GSEB Syllabus
  GSEB4
  GSEB3 Образец статьи
  GSEB3 004
  MSBSHSE
  MSBSHSE Syllabus
  MSBSHSE Учебники
  Образцы статей MSBSHSE
  Вопросники MSBSHSE
  AP Board
  APSCERT
  Syll
  AP 9000SC4
  Syll
  AP
  Syll 9000SC4
  Syll
  Syll
  MP Board
  MP Board Syllabus
  MP Board Образцы документов
  Учебники MP Board
  Assam Board
  Assam Board Syllabus
  Assam Board Учебники 9000 9000 Board4 BSEB
  Bihar Board Syllabus
  Bihar Board Учебники
  Bihar Board Question Papers
  Bihar Board Model Papers
  BSE Odisha
  Odisha Board Syllabus
  Odisha Board Syllabus
  Odisha Board Syllabus
  Программа PSEB
  Учебники PSEB
  Вопросники PSEB
  RBSE
  Rajasthan Board Syllabus
  RBSE Учебники
  RBSE Question Papers
  HPBOSE
  000 HPBOSE
  HPBOSE
  JKBOSE
  Программа обучения JKBOSE
  Образцы документов JKBOSE
  Шаблон экзамена JKBOSE
  TN Board
  TN Board Syllabus
  TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 9000 Paper Papers 9000 TN Board 9000 4 JAC
  Программа JAC
  Учебники JAC
  Вопросники JAC
  Telangana Board
  Telangana Board Syllabus
  Telangana Board Учебники
  Papers Telangana Board Учебники
  Учебный план KSEEB
  Типовой вопросник KSEEB
  KBPE
  Учебный план KBPE
  Учебники KBPE
  Документы по KBPE
  9000 Доска UPMSP 9000 Доска UPMSP 9000 Доска UPMSP 9000
  Совет по Западной Бенгалии
  Учебный план Совета по Западной Бенгалии
  Учебники для Совета по Западной Бенгалии
  Вопросы для Совета по Западной Бенгалии
  UBSE
  TBSE
  Гоа Совет
  000
  NBSE0003 Board
  Manipur Board
  Haryana Board
  Государственные экзамены
  Банковские экзамены
  Экзамены SBI
  Экзамены IBPS
  Экзамены RBI
  IBPS
  03
  Экзамены SSC
  9SC2
  SSC GD
  SSC CPO 900 04
  SSC CHSL
  SSC CGL
  Экзамены RRB
  RRB JE
  RRB NTPC
  RRB ALP
  O Экзамены по страхованию
  LIC4
  LIC4
  UPSC CAPF
  Список статей государственных экзаменов
  Обучение детей
  Класс 1
  Класс 2
  Класс 3
  Академические вопросы
  Вопросы по физике
  Вопросы по химии
  .
  Электрический потенциал и разность электрических потенциалов (напряжение)
  В этой лекции мы узнаем об электрическом потенциале и разнице электрических потенциалов, которая также известна как напряжение.
  Вы можете посмотреть следующее видео или прочитать письменное руководство под видео.
  
  В предыдущей лекции мы говорили об электрической потенциальной энергии, которая зависит от заряда объекта, испытывающего электрическое поле. Теперь мы собираемся узнать об электрическом потенциале, который зависит только от положения объекта.
  
  Электрический потенциал (или просто потенциал) — это просто мера электрической потенциальной энергии на единицу заряда.
  Формула электрического потенциала
  
  Это основное уравнение для расчета электрического потенциала, которое показывает, что электрический потенциал V равен электрической потенциальной энергии U, деленной на заряд q, который будет помещен в точку на некотором расстоянии от основного заряда.
  
  Электрическая потенциальная энергия U равна постоянной Кулона k, умноженной на заряд, который создает потенциал большой Q, умноженный на заряд, который будет помещен в точку на некотором расстоянии от основного заряда small q, и деленное на это расстояние r.
  
  Чтобы вычислить электрический потенциал, нам просто нужно разделить потенциальную энергию на малую q.
  Мы можем заметить, что маленький q появляется дважды в уравнении, поэтому мы можем его сократить.
  
  Теперь у нас есть это простое уравнение.
  Уравнение показывает, что потенциал прямо пропорционален величине заряда Q — по мере увеличения заряда потенциал увеличивается, и наоборот, по мере уменьшения заряда потенциал уменьшается.
  С другой стороны, обратно пропорционально расстоянию r , потому что по мере удаления от заряда потенциал будет уменьшаться, а по мере приближения к заряду потенциал будет увеличиваться до увеличение.
  Наконец, мы получили бы количество электрической потенциальной энергии, которое в этот момент будет иметь каждая единица заряда.
  Связано: Закон Кулона
  Единица электрического потенциала
  Теперь вернемся к основному уравнению.
  
  Мы знаем, что электрическая потенциальная энергия измеряется в Джоулях, а единицей заряда является кулон. Итак, единица измерения электрического потенциала — Джоули на кулон, или одним словом Вольт.
  
  Точечный заряд равен +2 мкКл, и мы хотим найти электрический потенциал на расстоянии 15 см (0,15 м) от этого заряда.
  Теперь мы можем использовать это уравнение для вычисления электрического потенциала.
  
  Мы получили положительный электрический потенциал +1.2 × 10 ⁵ В.
  
  В случае отрицательного заряда, скажем, -2 мкКл, электрический потенциал в той же точке будет -1,2 × 10 ⁵ В. Мы получили бы то же самое. значение, но со знаком минус.
  
  Давайте взглянем на этот график электрического потенциала. Ось X показывает расстояние от заряда, а ось Y показывает электрический потенциал в определенной точке.
  
  Здесь у нас положительный заряд, а потенциал вокруг положительного заряда всегда положительный. По мере того, как вы удаляетесь от заряда, по мере того, как расстояние от заряда увеличивается, потенциал становится менее положительным и уменьшается все ближе и ближе к нулю.
  С другой стороны, у нас отрицательный заряд, а потенциал вокруг отрицательного заряда всегда отрицательный. По мере того, как вы удаляетесь от заряда, по мере того, как расстояние от заряда увеличивается, потенциал становится менее отрицательным и фактически увеличивается, также приближаясь к нулю.
  Если вы находитесь бесконечно далеко от заряда, потенциал будет равен нулю как для положительных, так и для отрицательных зарядов.
  Связано: Что такое электрический заряд и как работает электричество
  Теперь мы можем перейти к разнице электрических потенциалов или напряжению.
  По определению, разность электрических потенциалов или напряжение — это разность электрических потенциалов между конечным и начальным положением, когда над зарядом выполняется работа по изменению его потенциальной энергии.
  
  Теперь давайте рассмотрим пример, который поможет нам легко понять термин «напряжение».
  
  У нас есть положительный заряд + 1,6 × 10 ^-19 С. Это основной заряд, создающий потенциал.
  Первый круг — это первый энергетический уровень, на расстоянии 2,5 × 10 ^-11 м от заряда. Второй круг — это второй энергетический уровень, на расстоянии 4,2 × 10 ^-12 м от заряда.
  Чтобы найти разность электрических потенциалов или напряжение, нам нужно найти потенциал в точке A и потенциал в точке B.
  
  Потенциал в точке A, которая является первым уровнем энергии, будет 57,6 В.
  
  Потенциал в точке B, которая находится на большем расстоянии, будет 34,2 В. .
  Сначала мы собираемся вычислить напряжение по мере движения от A к B, а затем от B к A.
  
  В первом случае A — это наш начальный потенциал, а B — наш конечный потенциал. . Итак, разность потенциалов будет окончательной минус начальный потенциал, или 34.2–57,6 = -23,4 В. Мы получили отрицательный потенциал, что означает, что при переходе от A к B потенциал уменьшается.
  
  Во втором случае B — это наш начальный потенциал, а A — наш конечный потенциал. Итак, разность потенциалов будет 57,6-34,2 = + 23,4 В. У нас есть положительный потенциал, или когда мы идем от B к A, потенциал увеличивается.
  Что это значит?
  По мере продвижения от A к B электрический потенциал уменьшается из-за того, что у нас есть положительный основной заряд, а его линии электрического поля направлены наружу.Если мы поместим положительный тестовый заряд на первый энергетический уровень, электрическая потенциальная энергия будет больше. Точечный заряд будет отталкивать пробный заряд, потому что плотность силовых линий электрического поля намного сильнее. В B плотность силовых линий электрического поля слабее, а электрическая потенциальная энергия меньше.
  Вот и все, что касается электрического потенциала и разности электрических потенциалов. Надеюсь, это было полезно, и вы узнали что-то новое.
  .
  Физика для науки и техники II
  
  4.4 Расчет электрического поля по потенциалу от Office of Academic Technologies на Vimeo.
  Пример 1: Расчет электрического поля заряда диска по его потенциалу
  Пример 2: Расчет электрического поля кольцевого заряда по его потенциалу
  4.4 Расчет электрического поля по потенциалу
  Ранее мы изучили, как найти потенциал из электрического поля.Расчет потенциала из поля E был основан на определении потенциала, что привело нас к выражению, в котором разность потенциалов между двумя точками равна минус интегралу E dot dl, интегрированному от начальной до этой конечной точки. Итак, из этого выражения, если бы мы знали электрическое поле, мы могли бы легко вычислить разность потенциалов, которую будет испытывать заряд всякий раз, когда он перемещается по определенному пути от исходной точки к конечной.
  Теперь мы зададим противоположный вопрос и скажем: «Можем ли мы вычислить электрическое поле по потенциалу?» Ответ на это — да.Поэтому наше название — «Расчет электрического поля по потенциалу».
  В этом случае мы предполагаем, что знаем потенциал в каждой точке интересующего региона. Знание потенциала в интересующей области означает, что мы знаем все эквипотенциальные поверхности в этой области. Давайте изобразим эти эквипотенциальные поверхности с точки зрения поперечного сечения, примерно так. Следовательно, эти величины или они представляют, эти линии представляют собой поперечное сечение этих эквипотенциальных поверхностей.
  Предположим, что мы перемещаем заряд с одной эквипотенциальной поверхности на другую по определенному пути.Мы также знаем, что силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям, поэтому эти углы составляют 90 градусов, для этих эквипотенциальных поверхностей они имеют напряжение, скажем, v1, v2, v3 и так далее и так далее.
  Предположим, что по этому пути мы перемещаем наш заряд от одной эквипотенциальной поверхности к другой. Назовем этот вектор смещения l, и поэтому dl будет представлять вектор приращения смещения вдоль этого пути. Обозначим угол между E и dl как theta.
  Итак, мы видели, что напряжение было определено как или потенциал был определен как отрицательный по отношению к работе, совершаемой при перемещении заряда от бесконечности к интересующей точке на единицу испытательного заряда. Оттуда проделанная работа равна минус q раз, умножая заряд на потенциал.
  Ну, проделанная работа также равна F dl — мы можем назвать это, поскольку выполненная инкрементная работа равна F dot dl. Так как кулоновская сила, действующая на заряд, скажем, положительный заряд плюс q, который перемещается с одной эквипотенциальной поверхности на другую, равен q умноженным на E.Дополнительная работа, выполняемая путем перемещения этого заряда, когда приращение dl будет равно q E dot dl. Или, в более выразительной форме, он будет равен, поскольку это скалярное произведение, величина q E, величина dl, умноженная на косинус угла между этими двумя векторами.
  Итак, используя определение потенциала, мы можем сказать, что проделанная дополнительная работа будет равна минус q, умноженному на инкрементную разность потенциалов, через которую она проходит.
  В этом выражении левая часть этих двух выражений, левые части равны, поэтому мы можем легко приравнять правые части.Если мы это сделаем, у нас будет минус q, dV будет равно q E dl, умноженному на косинус теты. Поскольку q является общим для левой и правой частей, мы можем разделить обе части и исключить заряд, и если мы переместим dl в одну сторону выражения, чтобы собрать дифференциальные члены с одной стороны, мы получим E косинус теты равен dV над dl со знаком минус.
  Прямо здесь, я собираюсь записать это выражение в более общей форме в виде частного [неразборчиво 08:23] уравнения, а не делать это таким образом, потому что потенциальный продукт может быть функцией разных координат и это даст нам тогда E косинус теты равен минус дельта V по дельте S — я бы сказал, дель V по дельте l.
  Давайте попробуем проинтегрировать этот член тета, умноженный на косинус. Что ж, если мы продолжим направление этого вектора смещения и возьмем проекцию электрического поля вдоль этого направления, то в итоге мы получим компонент электрического поля в направлении этого вектора смещения. Мы можем назвать это компонентом вектора электрического поля в направлении l.
  Теперь представим это как E sub l. Итак, эта величина здесь дает нам компонент электрического поля в направлении вектора смещения, вектор l, поэтому мы можем утверждать, что отрицательная скорость изменения потенциала с расстоянием в любом направлении дает компонент электрического поля в этом направлении.
  Это очень важный результат и в прямоугольной системе координат, скажем, в декартовой системе координат, поэтому мы можем сказать, что x-компонента электрического поля будет равна минус частной производной потенциальной функции с этой векторной координатой x, y-составляющая электрического поля будет равна частной производной потенциала по y-составляющей, и, наконец, z-составляющая будет равна частной производной потенциала по z-составляющей.
  Теперь мы знаем, что электрическое поле — это векторная величина, а потенциал — это скалярная величина, поэтому здесь с помощью математической операции мы получаем компоненты вектора из скалярной величины. Вместо того, чтобы выражать все эти три координаты отдельными уравнениями, мы вводим систему обозначений через оператор, который называется оператором del. В прямоугольной системе координат, в декартовой системе координат это оператор в частных производных, и он равен del по единичному вектору I del x, плюс del по единичному вектору j del y, плюс del по единичному вектору del z k.
  Таким образом, в терминах этой записи мы можем выразить, что вектор электрического поля равен оператору минус дель, действующему на потенциальную функцию V. Эта операция называется Градиентом V или Градиентом потенциала. Таким образом, отрицательный градиент потенциала дает нам вектор электрического поля.
  Возможно, вы до сих пор не знакомы с частичной дифференциацией. На самом деле частичная дифференциация на самом деле не отличается от полной дифференциации. Если функция является функцией разных переменных, если мы являемся частной производной по определенной переменной, мы просто принимаем другие переменные как постоянные во время этого процесса.
  Если мы сделаем небольшой пример, связанный с этим: предположим, что у нас есть потенциал, который является функцией координат x, x и z. Итак, пусть V равно x, y, z равно 2x в квадрате y в кубе z, минус 3y в квадрате z, плюс 6xy, z в кубе.
  Теперь предположим, что потенциальная функция в данной области изменяется в соответствии с этой математической функцией. Мы хотели бы вычислить соответствующее электрическое поле в этой области. Компонент x электрического поля является отрицательной частной производной этой потенциальной функции по x, так что она будет равна минусу.Мы возьмем производную этой функции по x, и при этом мы сохраним y и z постоянными, поэтому первая из них даст нам 4x, а мы сохраним y и z постоянными, поэтому мы у нас будет y в кубе z, плюс мы возьмем производную по x.
  Второй член даст нам ноль, потому что в этом члене нет зависимости от x, и мы меняем константы y и z, поэтому мы собираемся закончить с нулем отсюда, а следующий член даст нам плюс 6yz в кубе.Таким образом, это будет x-компонента вектора электрического поля.
  Точно так же компонент y будет минус del V по сравнению с del y, который будет равен минусу — снова мы возьмем производную по y, и мы будем сохранять x и z постоянными во время процесса — и производную по y будет 3 умножить на 2, будет 6x квадрат y квадрат z, а затем минус, у нас будет 6yz для второго члена и плюс 6xz в кубе для последнего члена, как только мы возьмем производную по y.
  Наконец, компонент x будет равен минус del v над del z, который будет равен минусу — теперь мы собираемся взять производную по z, сохраняя x и y постоянными — первый из них даст нас 2x квадрат y в кубе.Второй член даст нам минус 3y в квадрате, а последний член будет плюс 18xyz в квадрате.
  Итак, теперь мы знаем компоненты вектора электрического поля. Следовательно, вектор электрического поля будет равен Exi плюс Eyj плюс Exk.
  Конечно, величина вектора электрического поля будет равна Ex в квадрате, плюс Ey в квадрате, плюс Ez в квадрате, в квадратном корне.
  Итак, как только мы знаем потенциальную функцию, мы можем легко вычислить соответствующие компоненты электрического поля, просто взяв то, что мы называем отрицательным градиентом этой потенциальной функции.
  Теперь, если вас интересует значение электрического поля в определенных точках или для конкретных x, y и z, тогда мы просто заменяем эти значения на x, y и z, чтобы получить конкретное значение электрического поля в эти конкретные моменты.
  .
  электрического потенциала | Определение, факты и Units
  Электрический потенциала, объем работ, необходимый для перемещения единицы заряда от опорной точки к определенной точке против электрического поля. Обычно точкой отсчета является Земля, хотя можно использовать любую точку, не подверженную влиянию заряда электрического поля.
  Подробнее по этой теме
  Электромагнетизм: электрические поля и силы
  Еще одно полезное поле — электрический потенциал.Он обеспечивает альтернативу электрическому полю в задачах электростатики. Потенциал …
  На диаграмме показаны силы, действующие на положительный заряд q , расположенный между двумя пластинами, A и B, электрического поля E . Электрическая сила F , прикладываемая полем к положительному заряду, равна F = qE; , чтобы переместить заряд от пластины A к пластине B, тогда должна быть приложена равная и противоположная сила ( F ′ = — qE ).Работа W, , проделанная при перемещении положительного заряда на расстояние d , составляет W = F ′ d = — qEd.
  электрический потенциал Силы, действующие на заряд q между двумя пластинами, A и B, между которыми существует электрическое поле E . Электрическая сила F , прикладываемая полем к положительному заряду, равна F = qE . Чтобы переместить заряд от пластины A к пластине B, необходимо приложить равную и противоположную силу ( F ′ = — qE ).Электрический потенциал, то есть работа W , совершенная при перемещении положительного заряда на расстояние d , составляет W = F ′ d = — qEd. Encyclopædia Britannica, Inc.
  Потенциальная энергия положительного заряда увеличивается, когда он движется против электрического поля, и уменьшается, когда он движется вместе с электрическим полем; обратное верно для отрицательного заряда. Если единичный заряд не пересекает изменяющееся магнитное поле, его потенциал в любой данной точке не зависит от пройденного пути.
  Хотя концепция электрического потенциала полезна для понимания электрических явлений, можно измерить только разницу в потенциальной энергии. Если электрическое поле определяется как сила, приходящаяся на единицу заряда, то по аналогии электрический потенциал можно рассматривать как потенциальную энергию на единицу заряда. Следовательно, работа, выполняемая при перемещении единичного заряда из одной точки в другую (например, в пределах электрической цепи), равна разнице потенциальных энергий в каждой точке. В Международной системе единиц (СИ) электрический потенциал выражается в джоулях на кулон (т.е.е., вольт), а разность потенциальной энергии измеряется вольтметром.
  Britannica Premium: удовлетворение растущих потребностей искателей знаний. Получите 30% подписки сегодня. Подпишись сейчас .