Зависимость частоты и напряжений от баланса мощности

Остановимся прежде всего на основном и общем для рассматриваемых задач вопросе: выясним, от чего зависят величины частоты и напряжений, устанавливающиеся в электроэнергетической системе.

Каждый из приемников энергии, присоединенных к электрической сети, потребляет активную и реактивную мощности, величины которых, как уже отмечалось ранее, определяются величиной напряжения на его зажимах и частотой. Мощность, идущая на питание приемников энергии и покрытие потерь в сети, соединяющей приемники с некоторой узловой точкой системы, в данном режиме нагрузки зависит только от частоты и величины напряжения в данной узловой точке.

Следовательно, нагрузка любой узловой точки однозначно (в области нормальных значений частоты и напряжения) определяется частотой и напряжением в этой точке. Статические характеристики нагрузки в некоторой узловой точке представляют собой, как известно, зависимости активной и реактивной мощностей этой нагрузки от напряжения при заданной частоте.

Для различных значений частоты может быть построено семейство подобных характеристик (рис. 2).

Рис. 2. Зависимости активной и реактивной мощности от напряжения

Обеспечить в данной узловой точке некоторые заданные значения частоты и напряжения можно, только передавая к ней из системы совершенно определенные величины активной и реактивной мощностей. Эти величины при заданных частоте и напряжении можно определить по соответствующим статическим характеристикам нагрузок. Если почему-либо из внешней сети в узловую точку будет поступать недостаточная активная или реактивная мощность, то заданные значения частоты и напряжения не могут установиться в этой узловой точке: параметры фактического режима будут иными. Рассмотрим несколько детальнее этот вопрос.

Пусть заданные семейства статических характеристик выражаются в неявной форме следующими зависимостями:

Величины активной и реактивной мощностей, притекающих к данной узловой точке системы, зависят как от величины U и фазы  напряжения в этой узловой точке, так и от величин и фаз напряжений в смежных узловых точках и сопротивлений, соединяющих участки сети.

Допустим сначала для простоты, что напряжения у ближайших узловых точек неизменны по величине и фазе и имеют одинаковую частоту f. Тогда в данной узловой точке установится совершенно определенное напряжение, величина и фаза которого определяются из условия баланса активных и реактивных мощностей: суммарные потоки активной и реактивной мощностей в данную узловую точку (Р_г и Q_г) должны быть равны соответственно активной и реактивной мощностям нагрузки в данной узловой точке (Р_н и Q_н). При заданной частоте последние будут только функциями напряжения. Тогда

и

Эти два уравнения с двумя неизвестными и позволяют определить U и .

Покажем, как графически решается эта задача. Совместим на одной диаграмме (рис. 3) характеристику P_Н = Ф₁(U), соответствующую заданному значению f, и семейство характеристик P_г=₁(U, ), соответствующих тому же значению f, но при разных значениях . Так как P_Г = P_Н, то из этой диаграммы по точкам пересечения может быть определена зависимость  = Ф(

U), соответствующая балансу активных мощностей в узловой точке. Далее аналогичным образом совмещаем на одной диаграмме характеристику Q_H = Ф₂(U) и семейство характеристик Q_Г = ₂(U, ) для различных  (рис. 4) и заданного f. При помощи найденной зависимости  = Ф(U) на каждой из характеристик Q_Г = ₂(U, ) получим точку, находящуюся на характеристике Q_Г = (U). Соединив эти точки, получим всю характеристику Q_Г = (U), соответствующую балансу активных мощностей. Тогда точка пересечения характеристик Q _H = Ф(U) и Q_Г = (U) определяет фактическое напряжение U_Н (рис. 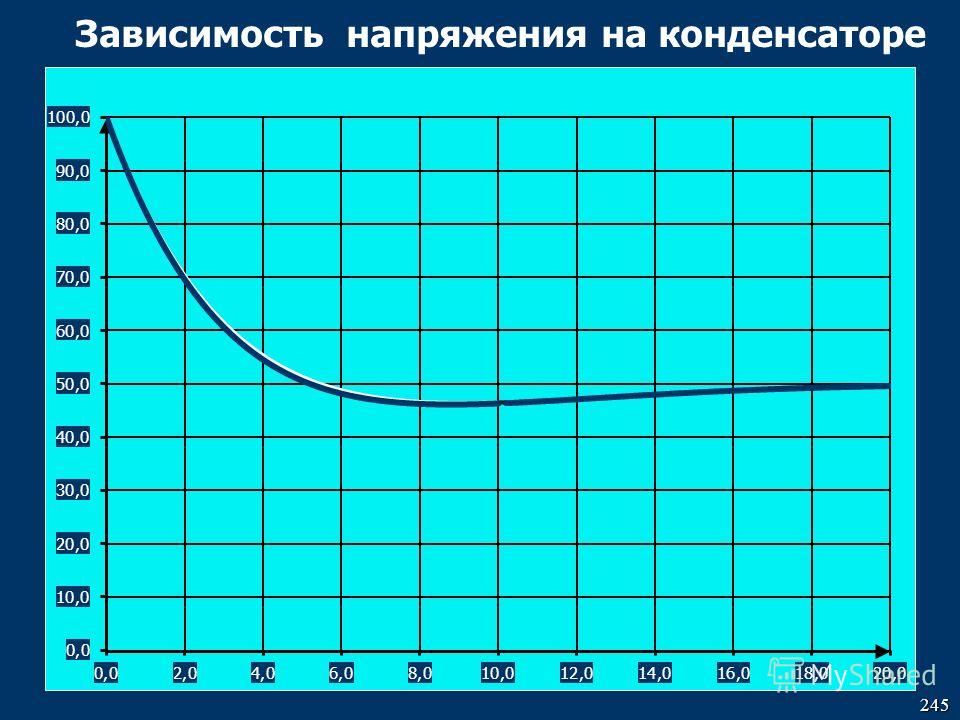4).

Рис. 3. Определение зависимости угла сдвига (фазы) от величины напряжения

Все наши предыдущие рассуждения относились к случаю неизменности по величине и фазе напряжений в смежных узловых точках и частоты в системе. В действительности такой неизменности нет и напряжения во всех узловых точках могут изменяться по величине и фазе; может также изменяться и частота системы.

Рис. 4. Построение характеристики зависимости Q от U

Однако в системе можно найти такие узловые точки, в которых поддерживается неизменное по величине и фазе или только по величине напряжение или из которых в сеть передается определенная активная мощность.

При определенном впуске энергоносителя и нормальных значениях параметров режима первичный двигатель развивает мощность, зависящую только от частоты сети, и, следовательно, электромагнитная мощность генератора в этих условиях зависит только от частоты:

P_г=Ф(U).

При постоянстве тока возбуждения генератора неизменной является величина э.д.с. генератора E_d, а при наличии регуляторов возбуждения неизменной или почти неизменной будет величина напряжения на его выводах.

В системе должен быть баланс активных и реактивных мощностей: сумма активных и реактивных мощностей всех генераторов должна равняться сумме активных и реактивных мощностей нагрузок всех узловых точек и потерь активной и реактивной мощностей во всех элементах сетей. Следовательно, частота во всей системе, а также величина и фаза напряжения в каждой из узловых точек установятся как раз такими, которые требуются по условию баланса мощностей.

Пусть в системе установился некоторый режим. Изменим впуск энергоносителя в первичный двигатель одного из генераторов. Угол сдвига ротора этого генератора также изменится. Во всей системе произойдет изменение частоты, а также изменение величин и фаз напряжений во всех узловых точках. Эти изменения будут происходить во времени до тех пор, пока не установится новый режим баланса мощностей в системе. Процесс этот является далеко не таким простым, как можно было бы предполагать. В самом деле, например, уменьшение впуска энергоносителя вызовет уменьшение угла сдвига ротора данного генератора относительно других, активные нагрузки других генераторов возрастут. Появится небаланс на валах каждого из этих генераторов, и они начнут тормозиться. В связи с этим генератор, у первичного двигателя которого уменьшился впуск энергоносителя, также должен начать тормозиться, так как при уменьшении углов сдвига роторов остальных генераторов он должен принять добавочную нагрузку. Торможение всех генераторов будет приводить к снижению общей частоты в системе. По мере ее снижения будут уменьшаться активные мощности нагрузок узловых точек в соответствии с их частотными статическими характеристиками и увеличиваться мощности всех других генераторов в соответствии со статическими характеристиками регуляторов скорости первичных двигателей

.

Оба эти фактора приведут к тому, что при достаточно большом снижении частоты вновь наступит баланс на валу каждого из генераторов; мощности, развиваемые первичными двигателями, будут балансироваться с мощностями нагрузки

генераторов. Дальнейшее снижение частоты прекратится. Необходимо учесть, что снижение частоты вызывает изменение Э.Д.С. всех генераторов, реактивных сопротивлений всех ветвей системы, а, следовательно, и всех напряжений в сети, что в свою очередь приведет к изменению активных и реактивных нагрузок всех узловых точек в соответствии с их статическими характеристиками по напряжению и частоте. Таким образом, процесс оказывается достаточно сложным.

Рассмотрим другой случай. Пусть уставка регулятора возбуждения на одном из крупных генераторов системы будет снижена. Тогда уменьшится выпуск реактивной мощности от данного генератора, что приведет к снижению напряжения по крайней мере в близлежащем районе электрической сети. Снижение напряжения в свою очередь вызовет уменьшение активных и реактивных нагрузок всех узловых точек в соответствии с их статическими характеристиками по напряжению. Появится небаланс на валу каждого из генераторов; углы сдвига их роторов, а, следовательно, и скорости их вращения будут расти. Это приведет к повышению частоты, так как генераторы, особенно близлежащие, разгрузятся. Частота в системе будет расти, пока не наступит новый баланс, обусловленный ростом активных нагрузок системы. Рост частоты в свою очередь повлияет на увеличение напряжений.

Такова сложная взаимосвязь изменений частоты, напряжения и активных и реактивных мощностей в системе. Однако для решения практических вопросов можно упростить задачу путем некоторой идеализации.

Так, отвлекаясь от изменений напряжений и реактивных мощностей, можно считать, что изменение баланса активных мощностей в системе определенным образом сказывается только на изменении частоты.

Действительно, рост активной нагрузки потребителей или снижение активной мощности генераторов в первую очередь вызывает определенное для данного режима снижение частоты в системе. Практически именно это является наиболее существенным. Менее существенным является то, что это изменение частоты будет в некоторой степени различным в зависимости от того, в какой узловой точке выросла активная нагрузка или у какого именно генератора снизилась активная мощность. Это различие обусловлено влиянием других факторов (напряжений, реактивных мощностей) и не столь велико. Снижение частоты, обусловленное возникновением дефицита активной мощности, обязательно приведет к восстановлению баланса, так как при этом в связи со снижением частоты и напряжений активная нагрузка уменьшается. В то же время регуляторы скорости первичных двигателей и частоты увеличивают впуск энергоносителя, и активная мощность генераторов растет.

Количественное соотношение, т.е. зависимость относительного изменения частоты от относительного небаланса активной мощности, не является неизменным и в зависимости от режима работы системы может колебаться в довольно широких пределах.

Существует ли зависимость напряжения от частоты?

Казалось бы, раскрыть зависимость напряжения от частоты просто. Стоит только обратиться с соответствующим запросом ко всезнающим поисковым системам и… убедиться, что ответа на этот вопрос попросту нет. Что же предпринять? Давайте разбираться вместе в этом непростом вопросе.

Напряжение или разность потенциалов?

Надо заметить, что напряжение и разность потенциалов — это одно и то же. По сути, это сила, которая способна заставить электрические заряды двигаться потоком. Не имеет значения, куда будет направлено это движение.

Разность потенциалов — просто другое выражение для напряжения. Оно нагляднее и, может быть, понятнее, но сути дела не меняет. Поэтому главный вопрос состоит в том, откуда берется напряжение, и от чего оно зависит.

В том, что касается домашней сети 220 Вольт, ответ простой. На гидростанции поток воды вращает ротор генератора. Энергия вращения трансформируется в силу напряжения. Атомная электростанция вначале превращает воду в пар. Он и крутит турбину. В бензоэлектростанции ротор вращает сила сгорающего бензина. Есть и другие источники, но суть всегда одна и та же: энергия превращается в напряжение.

Самое время задаться вопросом о зависимости напряжения от частоты. Но мы еще не знаем, откуда берется частота.

Что является источником частоты

Тот же самый генератор. Частота его вращения превращается в одноименное свойство напряжения. Вращайте генератор быстрее — частота будет больше. И наоборот.

Хвост не может «вилять» собакой. По той же причине частота не может изменить напряжение. Следовательно, выражение «зависимость напряжения от частоты тока» не имеет смысла?

Чтобы найти ответ, надо правильно сформулировать вопрос. Есть такая присказка про глупца и 10 ученых мужей. Он задавал неправильные вопросы, а они не могли ответить.

Если назвать напряжение другим определением, все встанет на свои места. Оно применяется для цепей, состоящих из множества разных сопротивлений. «Падение напряжения». Оба выражения часто считаются синонимами, что почти всегда неправильно.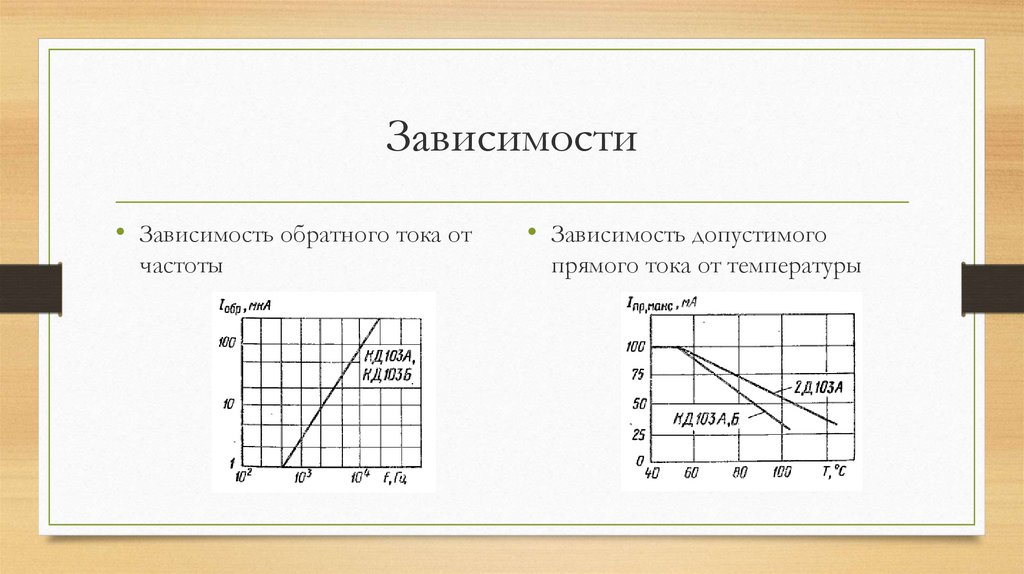 Потому что падение напряжения действительно может зависеть от частоты.

С чего бы напряжению падать?

Да просто потому, что не может не падать. Итак. Если на одном полюсе источника потенциал равен 220 Вольт, а на другом — ноль, то это падение могло произойти только в цепи. Закон Ома говорит о том, что, если в сети имеется одно сопротивление, то все напряжение на нем и упадет. Если два и больше — каждое падение будет пропорционально его величине, а их сумма равна исходной разности потенциалов.

Ну и что? Где здесь указание на зависимость напряжения от частоты тока? Пока что все зависит от величины сопротивления. Вот, если бы найти такой резистор, который меняет свои параметры при изменении частоты! Тогда и падение напряжения на нем менялось бы автоматически.

Есть такие резисторы

Их еще называют реактивными, в отличие от активных собратьев. На что же они реагируют, изменяя свою величину? На частоту! Существует 2 вида реактивных сопротивлений:

• индуктивное;
• емкостное.

Каждый вид связан со своим полем. Индуктивное — с магнитным, емкостное — с электрическим. На практике они представлены в первую очередь, соленоидами.

Они представлены на фото выше. И конденсаторами (ниже).

Их можно считать антиподами, потому что реакция на изменение частоты прямопротивоположная. Индуктивное сопротивление растет с частотой. Емкостное, наоборот, падает.

Теперь, учитывая особенности реактивных сопротивлений, в соответствии с законом Ома, можно утверждать, что зависимость напряжения от частоты переменного тока существует. Она может быть рассчитана с учетом величин реактивных сопротивлений в цепи. Только для ясности надо помнить, что речь идет именно о падении напряжения на элементе цепи.

И все-таки она существует!

Вопросительный знак в заголовке статьи превратился в восклицательный. «Яндекс» реабилитирован. Осталось только привести формулы зависимости напряжения от частоты для разных видов реактивных сопротивлений.

Емкостное: XC = 1/(w · C). Здесь w — угловая частота, C — емкость конденсатора.

Индуктивное: XL = w · L, где w — то же, что и в предыдущей формуле, L — индуктивность.

Как видно, частота влияет на величину сопротивления, изменяя его, следовательно, изменяет и падение напряжения. Если в сети имеется активное сопротивление R, емкостное XC и индуктивное XL, то сумма падений напряжений на каждом элементе будет равна разности потенциалов источника: U = U_r + U_xc+ U_xl.

Конденсатор

— Напряжение в зависимости от частоты в цепи RLC

Я собираюсь разделить этот ответ на две части: (1) как напряжение и ток зависят от частоты и (2) как напряжение на одном компоненте может быть выше, чем на источнике Напряжение.

---

ЧАСТЬ 1.

Закон Ома утверждает, что \$V = I \cdot R\$. Это уравнение было бы таким же, если бы напряжение и ток изменялись со временем: \$ v(t) = i(t) \cdot R\$. Другими словами, мгновенное напряжение равно мгновенному току , усиленный сопротивлением . Не имеет значения, являются ли напряжение или ток синусоидальными волнами, прямоугольными волнами и т. д.

Однако приведенное выше уравнение не выполняется для конденсаторов и катушек индуктивности, поскольку они являются устройствами накопления энергии. А теперь представьте на мгновение дискретный мир: общая энергия в батарее равна энергии предыдущего шага плюс все, что мы вложили в нее сейчас

$$ x(k) = x(k-1) + u(k) \Delta T $$

где \$x\$ — энергия, \$u\$ — вход, \$k\$ — дискретный момент времени, \$\Delta T\$ — шаг по времени. В непрерывном мире \$ \Delta T \rightarrow 0 \$ приведенное выше уравнение было бы

$$ \frac{d}{dt}x(t) = u(t) $$

Теперь вы готовы к уравнениям, описывающим зависимость напряжения от тока для катушек индуктивности и конденсаторов:

$$ v_L(t) = L \frac{d}{dt} i_L(t), \qquad i_C(t) = C \frac{d}{dt} v_C(t), $$

, где нижние индексы L и C обозначают катушку индуктивности и конденсатор. Обратите внимание, что хотя я использую здесь эквивалентность хранения энергии с простой математикой, два приведенных выше уравнения на самом деле взяты из физики.

Теперь попробуйте представить, что происходит с напряжением катушки индуктивности, когда ток катушки индуктивности имеет синусоидальную форму: 9\circ\$ и усиливается \$ Z_L = \omega L \$. Если сравнить это с законом Ома, то видно, что импеданс \$Z_L\$ эквивалентен сопротивлению \$R\$, с той лишь разницей, что в отличие от сопротивления импеданс зависит от частоты \$\omega\$. Кроме того, закон Ома не учитывает фазовый сдвиг. Вы можете использовать те же рассуждения для конденсаторов.

Теперь мы знаем, что вольтамперные характеристики катушек индуктивности и конденсаторов также линейны, единственная разница по сравнению с простыми резисторами в том, что усиление зависит от частоты и фазового сдвига также следует учитывать.

---

ЧАСТЬ 2.

Когда у вас есть схема RLC, у вас фактически есть два энергетических резервуара (L и C) и одна нагрузка (R). Энергетические баки не потребляют энергию , т.е. энергия все еще находится в цепи и не уходит.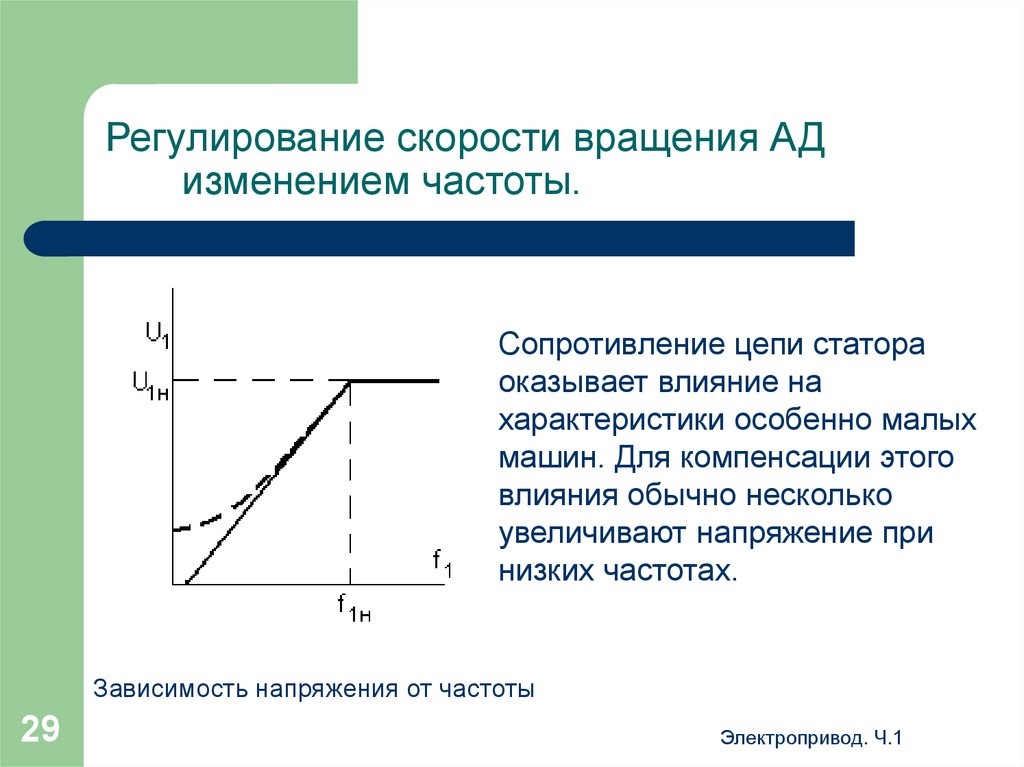 Нагрузка потребляет энергию , и когда я говорю потребляет, я имею в виду, что они преобразуют электрическую энергию в какую-то другую форму (тепло и т. д.), и энергия теряется с точки зрения схемы.

Представьте себе два энергетических резервуара как два соединенных резервуара с водой, где уровень воды (высота) равен напряжению. Когда вы перебрасываете немного воды из одного резервуара в другой, уровень воды в резервуарах меняется. Если один бак пуст, другой на максимуме. Но! Что, если уровень воды может стать отрицательным? Именно так и происходит с L и C:

• есть некий источник напряжения, генерирующий синусоидальное напряжение амплитудой \$V_S\$ на фиксированной частоте \$\omega_0\$
• есть два энергоемкостей, а именно дроссель и конденсатор, и напряжение на них тоже синусоида с амплитудой \$V_L\$ и \$V_C\$
• энергия прыгает между этими двумя энергетическими баками со скоростью, которая зависит от частоты
• , в отличие от уровня воды, напряжение может стать отрицательным!

График, который вы разместили, показывает зависимость амплитуды напряжения на катушке индуктивности и конденсаторе от частоты. На одной конкретной частоте, также известной как резонансная частота , этот график находится на минимуме или максимуме. Но чтобы иметь резонансную частоту, нужно иметь два энергетических бака.

Частоты и генераторы переменного тока. Тригонометрия и генерация однофазного переменного тока для электриков

Поколение переменного тока

В предыдущей главе мы узнали, что термин цикл означает от точки сигнала до точки, в которой сигнал начинает повторяться. Когда мы обсуждаем термин частота , мы имеем в виду, сколько циклов может произойти в одну секунду. Частота измеряется в герц (восклицаем Генриху Герцу) или герц (циклов в секунду). На частоту генератора влияют два фактора: скорость вращения и количество полюсов.

Рисунок 52. Цикл синусоиды

Когда якорь вращается в поле, он начинает создавать форму волны (как мы видели в предыдущей главе). Один полный механический оборот якоря создает одну полную синусоиду на двухполюсном генераторе переменного тока. Если двухполюсный генератор делает три полных оборота за одну секунду, он создаст за эту секунду три полных синусоидальных колебания. Мы бы сказали, что частота составляет три цикла в секунду или три герца (как говорят крутые ребята).

Скорость вращения машины измеряется в оборотах в минуту или об/мин . Однако при работе с частотой нас интересуют не минуты, а скорее секунды. Следовательно, RPM необходимо преобразовать в обороты в секунду ( RPS ). Поскольку в минуте 60 секунд, все, что нам нужно сделать, это разделить RPM на 60, чтобы преобразовать его в RPS.

Например, если якорь двухполюсного генератора переменного тока вращается со скоростью 1800 об/мин, мы можем сказать, что он вращается со скоростью 30 оборотов в секунду. Если этот генератор переменного тока имеет два полюса, то за одну секунду он будет генерировать 30 циклов напряжения. Тогда можно было бы сказать, что он имеет частоту 30 циклов в секунду или 30 герц. Частота генератора прямо пропорциональна скорости вращения генератора.

Если мы добавим полюсов к генератору, мы сможем изменить частоту. В двухполюсном генераторе переменного тока сторона А якоря (показанная на рис. 53) проходит с севера на юг, а затем с юга на север, создавая одну полную синусоиду. Если мы добавим еще два полюса, как показано на рис. 54, то сторона А якоря пройдет мимо двух северных и двух южных полюсов за один полный механический оборот.

Рис. 53. Двухполюсный генератор переменного тока

Две полные синусоидальные волны создаются за один полный механический оборот. Если двухполюсный генератор создает один цикл напряжения за одну секунду (или один герц частоты), то четырехполюсный генератор создает два цикла напряжения за одну секунду (или два герца).

Частота генератора прямо пропорциональна количеству полюсов генератора.

Рисунок 54.