Заряд и разряд конденсатора

Содержание

Значение диэлектрика

Кроме общего размера обкладок и расстояния между ними, существует ещё один параметр, влияющий на ёмкость — используемый тип изолятора. Фактор, по которому определяется способность диэлектрика повышать ёмкость конденсатора в сравнении с вакуумом, называется диэлектрической проницаемостью и описывается для разных материалов постоянной величиной от 1 и до бесконечности (теоретически):

• вакуум: 1,0000;
• воздух: 1,0006;
• бумага: 2,5—3,5;
• стекло: 3—10;
• оксиды металлов 6—20;
• электротехническая керамика: до 80.

Кроме конденсаторов с твёрдым диэлектриком (керамических, бумажных, плёночных) существуют также электролитические. В последних используют алюминиевые или танталовые пластины с оксидным изолирующим слоем в качестве одного электрода и раствор электролита в качестве другого.

Энергия, которую способны накопить большинство конденсаторов, обычно невелика — не больше сотен джоулей. К тому же она не сохраняется долго из-за неизбежной утечки заряда. Поэтому конденсаторы не могут заменить, например, аккумуляторные батареи в качестве источника питания. И хотя они способны эффективно выполнять только одну работу (сохранение заряда), их применение весьма многообразно в электрических цепях. Конденсаторы используются как фильтры, для сглаживания сетевого напряжения, в качестве устройств синхронизации и для других целей.

Синтаксис

Для пользователей XMPP клиентов, используется команда

fiz ключи

где ключи это известные параметры, параметра=значение, разделенные точкой с запятой

Обязателен ключ key=razryad при расчете разаряда конденсатора

и zaryad  при расчете заряда

Так как при других параметрах ключах будут рассчитываться совершенно другие формулы.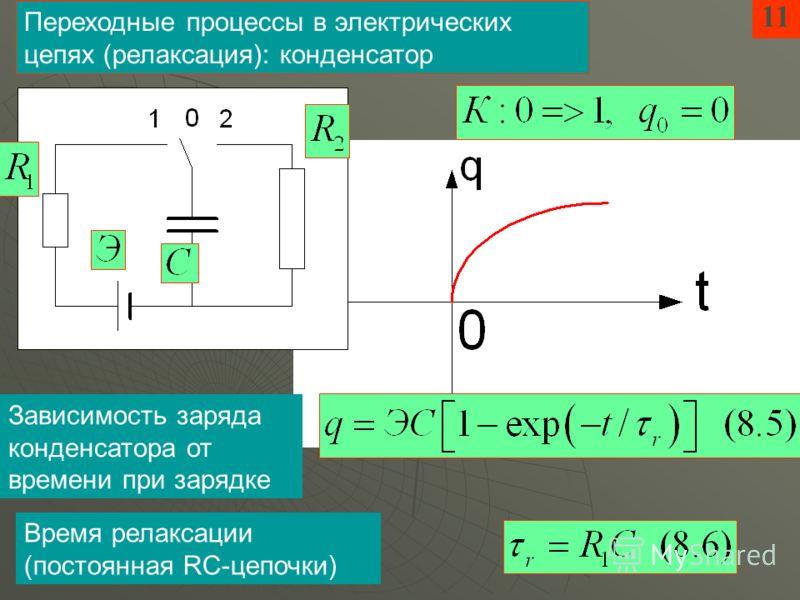 Например баллистического движения или давления над уровнем моря.

Заметьте, чем данный калькулятор  отличается от других:

Во первых: данные можно вводить не переводя из наноФарад в Фарады, а килоОмы в Омы. Если уж заданы параметры   в единицах измерения то так и пишите.  Если не напишите то считается  что данные заданы  в основным единицах СИ ( то есть метр, Фарад, Ом)

Во вторых: Расчет ведётся по тем  параметрым которые можно рассчитать зная исходные.Это очень удобно, когда нужно рассчитать любой из параметров в формуле, когда известны все остальные.  Другие известные калькуляторы могут рассчитывать только по определенному алгоритму  и только в одну сторону.

Разряд конденсатора

После того как конденсатор зарядился, отключим источник питания и подключим нагрузку R. Так как конденсатор уже заряжен, он сам превратился в источник питания. Нагрузка R образовала проход между пластинами. Отрицательно заряженные электроны, накопленные на одной пластине, согласно силе притяжения между разноименными зарядами, двинутся в сторону положительно заряженных ионов на другой пластине.

В момент подключения R, напряжение на конденсаторе то же, что и после окончания переходного периода зарядки. Начальный ток по закону Ома будет равняться напряжению на обкладках, разделенном на сопротивление нагрузки.

Как только в цепи пойдет ток, конденсатор начнет разряжаться. По мере потери заряда, напряжение начнет падать. Следовательно, ток тоже упадет. По мере понижения значений напряжения и тока, будет снижаться их скорость падения.

Время зарядки и разрядки конденсатора зависит от двух параметров – емкости конденсатора C и общего сопротивления в цепи R. Чем больше емкость конденсатора, тем большее количество заряда должно пройти по цепи, и тем больше времени потребует процесс зарядки/разрядки ( ток определяется как количество заряда, прошедшего по проводнику за единицу времени). Чем больше сопротивление R, тем меньше ток. Соответственно, больше времени потребуется на зарядку.

Продукт RC (сопротивление, умноженное на емкость) формирует временную константу ? (тау). За один ? конденсатор заряжается или разряжается на 63%. За пять ? конденсатор заряжается или разряжается полностью.

Для наглядности подставим значения: конденсатор емкостью в 20 микрофарад, сопротивление в 1 килоом и источник питания в 10В. Процесс заряда будет выглядеть следующим образом:

Заряд конденсатора. Ток

По своему предназначению конденсатор напоминает батарейку, однако все же он сильно отличается по принципу работы, максимальной емкости, а также скорости зарядки/разрядки.

Рассмотрим принцип работы плоского конденсатора. Если подключить к нему источник питания, на одной пластине проводника начнут собираться отрицательно заряженные частицы в виде электронов, на другой – положительно заряженные частицы в виде ионов. Поскольку между обкладками находиться диэлектрик, заряженные частицы не могут «перескочить» на противоположную сторону конденсатора. Тем не менее, электроны передвигаются от источника питания — до пластины конденсатора. Поэтому в цепи идет электрический ток.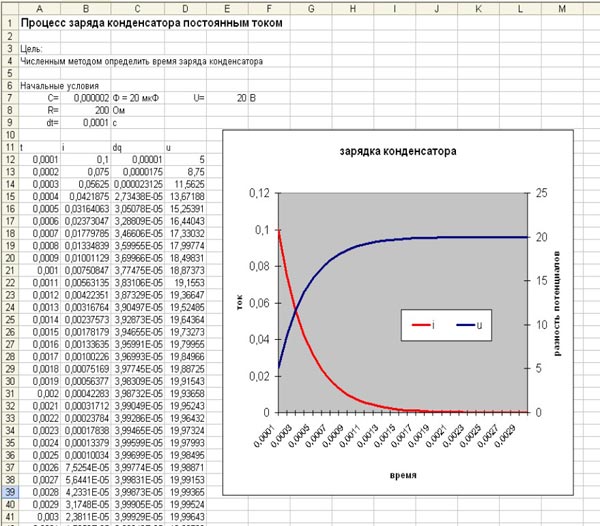

В самом начале включения конденсатора в цепь, на его обкладках больше всего свободного места. Следовательно, начальный ток в этот момент встречает меньше всего сопротивления и является максимальным. По мере заполнения конденсатора заряженными частицами ток постепенно падает, пока не закончится свободное место на обкладках и ток совсем не прекратится.

Время между состояниями «пустого» конденсатора с максимальным значением тока, и «полного» конденсатора с минимальным значением тока (т.е. его отсутствием), называют переходным периодом заряда конденсатора.

Формула

Нахождение тока конденсаторного заряда происходит по формуле, представленной ниже. Измеряется он в фарадах, что равно кулону или вольту.

Формула нахождения заряда конденсатора

В целомэто элемент электросети, накапливающий и сохраняющий напряжение в ней. Бывает разного типа и размера, к примеру, электролитическим, керамическим и танталовым. Состоит, в основном, из нескольких токопроводящих обкладок с диэлектриком. Его емкость зависит от размеров диэлектрика и заполнителя между обкладками. Заряжается благодаря электричеству. Определить ток конденсаторного заряда можно измерительными приборами и формулой.

Устройство и принцип работы

В простейшем варианте конструкция состоит из двух электродов в форме проводящих пластин (называемых обкладками), разделённых диэлектриком, толщина которого ничтожно мала по сравнению с размерами обкладок. Практически применяемые радиоэлектронные компоненты содержат много слоёв диэлектрика и электродов. В качестве обозначения конденсатора на схеме используются два параллельных отрезка с пространством между ними. Они символизируют металлические пластины обкладок физического прибора, электрически разделённые между собой.

Многие считают Майкла Фарадея автором изобретения, но на самом деле это не так. Но он сделал главное — продемонстрировал первые практические примеры и способы использования этого прибора для хранения электрического заряда в своих экспериментах. Благодаря Фарадею человечество получило способ измерять возможность накапливать заряд. Эта величина называется ёмкостью и измеряется в Фарадах.

https://youtube.com/watch?v=tuVEW69oXuw

Работу конденсатора можно проиллюстрировать на примере событий, проходящих во вспышке цифровой фотокамеры за отрезок времени между нажатием кнопки и тем моментом, когда вспышка погаснет. Основой электронной схемы этого осветительного устройства является конденсатор, в котором происходит следующее:

• Зарядка. После нажатия кнопки поток электронов приходит в конденсатор и останавливается на одной из его пластин благодаря диэлектрику. Этот поток называется зарядным током.
• Накопление. Поскольку под действием электродвижущей силы всё больше и больше электронов будут поступать на обкладку и распределяться по ней, отрицательный заряд обкладки может расти до момента, пока накопленный потенциал не будет отталкивать поступающий избыточный поток электронов. Вторая пластина из-за дефицита электронов приобретает положительный заряд, по модулю равный отрицательному на первой. Зарядный ток будет протекать до тех пор, пока напряжение на обеих пластинах не сравняется с приложенным. Сила или скорость тока зарядки будет находиться на максимальном уровне в момент, когда пластины полностью разряжены, и приблизится к нулю в момент, когда напряжение на обкладках и источнике будут равны.
• Сохранение. Поскольку обкладки заряжены противоположно, ионы и электроны будут притягиваться друг к другу, но не смогут соединиться из-за диэлектрической прослойки, создавая электростатическое поле. Благодаря этому полю конденсатор удерживает и сохраняет заряд.
• Разряд. Если в цепи появляется возможность для электронов протечь другим путём, то напряжение, накопленное между положительными и отрицательными зарядами обкладок, мгновенно реализуется в электрический ток, импульс которого в лампе вспышки преобразуется в световую энергию.

Определение заряда

Определить, заряжен ли проводник, можно специальным измерительным прибором. К примеру, сделать это можно при помощи индикаторной отвертки. При разряде избыточные виды электронов, имеющих левую пластину, будут перемещены через некоторое время по проводам к правой части пластины, то есть они будут смещены к местам, где их недостаточно.

Обратите внимание! Когда число электронов будет одинаковым, то разряд прекратится и проводная энергия вместе с сопротивлением исчезнет. Использование измерительного оборудования для определения конденсаторного заряда

Использование измерительного оборудования для определения конденсаторного заряда

Процессы зарядки и разрядки конденсаторов.

С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:

Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?

Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.

При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:

В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.

Как видите, здесь нет ничего сложного

Относительная диэлектрическая проницаемость

Не менее значимым фактором, влияющим на емкость конденсатора, является такое свойство материала между обкладками как относительная диэлектрическая проницаемость. Это безразмерная физическая величина, которая показывает во сколько раз сила взаимодействия двух свободных зарядов в диэлектрике меньше, чем в вакууме.

Материалы с более высокой диэлектрической проницаемостью позволяют обеспечить большую емкость. Объясняется это эффектом поляризации – смещением электронов атомов диэлектрика в сторону положительно заряженной пластины конденсатора.

Поляризация создает внутренне электрическое поле диэлектрика, которое ослабляет общую разность потенциала (напряжения) конденсатора. Напряжение U препятствует притоку заряда Q на конденсатор. Следовательно, понижение напряжения способствует размещению на конденсаторе большего количества электрического заряда.

Ниже приведены примеры значений диэлектрической проницаемости для некоторых изоляционных материалов, используемых в конденсаторах.

Воздух – 1.0005

Бумага – от 2.5 до 3.5

Стекло – от 3 до 10

Слюда – от 5 до 7

Порошки оксидов металлов – от 6 до 20

Плоский конденсатор.

Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:

Такое устройство называется плоским конденсатором, а пластины – обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).

А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.

Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:

Каждая из обкладок конденсатора в отдельности создает электрическое поле:

• положительно заряженная пластина (+q) создает поле, напряженность которого равна E_{+}
• отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_{-}

Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:

E = \frac{\sigma}{2\varepsilon_0\thinspace\varepsilon}

Здесь \sigma– это поверхностная плотность заряда: \sigma = \frac{q}{S}, а \varepsilon – диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:

E_+ = E_- = \frac{q}{2\varepsilon_0\thinspace\varepsilon S}

Но направления векторов разные – внутри конденсатора вектора направлены в одну сторону, а вне – в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:

E = E_+ + E_- = \frac{q}{2\varepsilon_0\thinspace\varepsilon S} + \frac{q}{2\varepsilon_0\thinspace\varepsilon S} = \frac{q}{\varepsilon_0\thinspace\varepsilon S}

А какая же будет величина напряженности вне конденсатора? А все просто – слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0

От чего зависит емкость

Емкость это свойство накопления и удержания электрозаряда. Чем она больше, тем больше заряд, увеличивающий вместимость сосуда с газовым баллоном. Она зависит от того, какова форма и размер электродов. Также зависит от того, какое расположение и свойство имеет диэлектрик, разделяющий электрод. Есть плоский конденсаторный источник с параллельной и цилиндрической пластиной.

Имеет не только специально предусмотренное устройство, но и несколько проводников, которые разделены при помощи диэлектрика. Емкость существенно влияет на электротехнические установки переменного тока.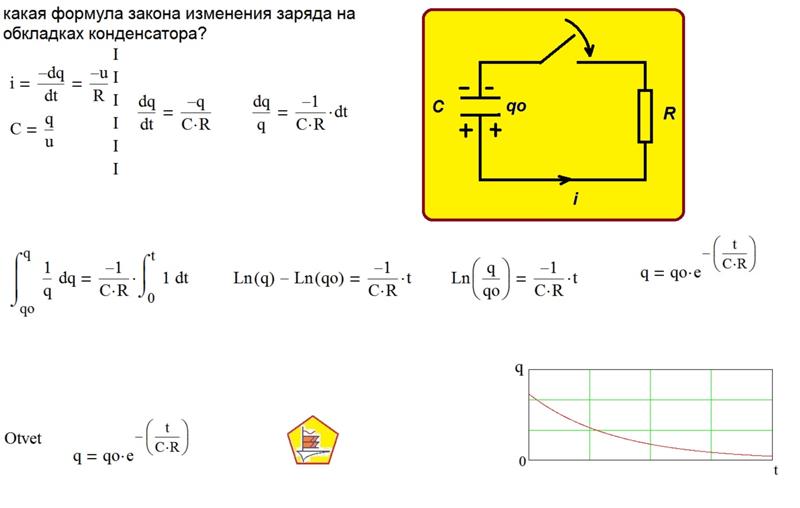 К примеру, источник с определенной емкостью имеется электрический провод с живым электрическим кабелем, жилой и металлической кабельной оболочкой.

От чего зависит емкость

Емкость и энергия конденсатора.

Важнейшей характеристикой является электрическая емкость конденсатора. Это физическая величина, которая определяется как отношение заряда конденсатора q одного из проводников к разности потенциалов между проводниками:

C = \frac{q}{\Delta\varphi} = \frac{q}{U}

Емкость конденсатора изменяется в Фарадах, но величина 1 Ф является довольно большой, поэтому чаще всего емкость измерятся в микрофарадах (мкФ), нанофарадах (нФ) и пикофарадах (пФ). А поскольку мы уже вывели формулу для расчета напряженности, то давайте выразим напряжение на конденсаторе следующим образом:

U = Ed = \frac{qd}{\varepsilon_0\thinspace\varepsilon S}

Здесь у нас d – это расстояние между пластинами конденсатора, а q – заряд конденсатора. Подставим эту формулу в выражение для емкости:

C = \frac{q\varepsilon_0\thinspace\varepsilon S}{qd} = \frac{\varepsilon_0\thinspace\varepsilon S}{d}

Если в качестве диэлектрика у нас выступает воздух, то во всех формулах можно подставить \varepsilon = 1. 2}{2C}

Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение. Это такая величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.

Итак, мы сегодня рассмотрели основные свойства конденсаторов, их устройство и характеристики! Так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений и маркировку. Не пропустите!

 

 

Помогла ли вам статья?

Задать вопрос

Пишите ваши рекомендации и задавайте вопросы в комментариях

Устройство для резонансного заряда конденсатора в новом варианте

ОИЯИ получил патент на устройство для резонансного заряда конденсатора за авторством Сергея Доли и Виктора Смирнова. Права на подобное устройство этих же авторов были защищены ярким патентом 2020 года, теперь же внесенные в конструкцию устройства изменения позволяют авторам полностью защитить изобретение от копирования. Модифицированная конструкция устройства позволяет получать только отрицательное напряжение, но более высокого значения.

Авторы изобретения В. И. Смирнов и С. Н. Доля

Резонансный заряд состоит из нескольких циклов заряда-перезаряда конденсатора, напряжение на котором растет от цикла к циклу и в несколько раз превысит двойное напряжение источника питания. Идея запатентованного устройства практически идентична идее одного из их предыдущих патентов № 2734903 «Устройство для резонансного заряда конденсатора», полученному два года назад и ставшему одним из ста лучших изобретений России второй половины 2020 года. Различие между устройствами заключается в том, что в перезарядной цепи вместо транзистора используется диод, что в равной степени позволяет получить желаемый изобретателями результат – решить техническую задачу заряда конденсатора до напряжения, в несколько раз превышающего напряжение источника питания, а также сократить время заряда.

Схема изобретения № 2770864

«Суперконденсаторы с использованием новой технологии в скором времени планируется применять в составе схем, где необходим мгновенный максимум мощности. Например, в автомобильных или локомотивных стартерах. Экономический эффект достигается за счет использования менее мощных и более доступных источников питания», — считают в Федеральной службе по интеллектуальной собственности РФ.

Сейчас суперконденсаторы высоко востребованы, поэтому растет вероятность, что патент будет использоваться сторонними организациями. Иногда это может происходить в обход приобретения лицензии. Поэтому с целью полной защиты патентных прав сотрудники ОИЯИ зарегистрировали дополнительный патент.

«Прежний патент можно было легко обойти, заменив всего один элемент. Мы составили новую заявку на патент, внеся в конструкцию некоторые изменения, которые уже не позволяют обойти авторские права», — прокомментировал один из авторов патента Виктор Иванович Смирнов. Также он рассказал, что различия в используемых элементах электрической цепи приводят к тому, что в первом варианте с транзистором можно получать как положительное, так и отрицательное напряжение, а в варианте с диодом – только отрицательное, но приблизительно на пять процентов выше.

Подробнее об изобретении. Патент № 2770864

Устройство для резонансного заряда конденсатора относится к области электротехники и преобразовательной техники и может применяться для питания импульсных нагрузок. Устройство включает источник питания, последовательно подключенный к нему транзистор, индуктивность и конденсатор. Параллельно конденсатору подключены перезарядная индуктивность и диод. Благодаря многократным зарядам и перезарядам конденсатора до напряжения противоположного знака, амплитуды тока заряда от цикла к циклу возрастают по величине, тем самым от цикла к циклу увеличивается энергия, передаваемая конденсатору от источника питания, растет напряжение и сокращается время заряда конденсатора.

зарядка — Время заряда конденсатора — два метода два разных ответа

\$\начало группы\$

Я немного озадачен и прошу помощи в следующем:

Теоретический конденсатор 100 Ф заряжается от постоянного источника питания значениями V = 50В, I = 50А, ESR конденсатора = 5 МОм

Чтобы рассчитать время зарядки крышки:

Подход 1: [Рассчитать время, используя скорость потока энергии]

Емкость конденсатора = 0,5xCxV^2 = 0,5x100x50^2 = 125 кДж 9(-2,5/(0,005×100)) = 49,88 В

Как видно, после 5 постоянных времени (2,5 с) напряжение на конденсаторе составляет 99 % при использовании подхода 2.

Очевидно, что это правильный подход с использованием установленного формула.

Почему подход 1 так сильно отличается? Что я упускаю в обоих случаях?

• конденсатор
• зарядка
• энергия

\$\конечная группа\$

2

\$\начало группы\$

Ваша постоянная времени 0,5 секунды явно получена из вашего ESR конденсатора 5 МОм. Итак, то, что вы фактически предлагаете в качестве цепи заряда, выглядит так:

^{смоделируйте эту цепь — схема создана с помощью CircuitLab}

Итак, начните с разомкнутого переключателя и разряженного конденсатора. Теперь замкните переключатель. Какой ток заряда?

То есть 50/0,005 или 10 000 ампер.

Сравните это с 50-амперным пределом зарядного устройства постоянной мощности. Вы думаете, что это может иметь какое-то отношение к этому?

\$\конечная группа\$

4

\$\начало группы\$

• вы пренебрегаете потерями ESR в своих уравнениях сохранения энергии.

• Зарядка шапки или аккумулятора никогда не является «постоянной мощностью», если только V*I не будет постоянным, что не относится к CC для цоколя с низким начальным состоянием.

Аккумуляторы

• имеют минимальный диапазон зарядного напряжения 10%, поэтому CC близок к Постоянная мощность, но нет.

Для постоянной мощности ток должен уменьшаться по мере уменьшения погрешности целевого напряжения = P=V*I out, что соответствует увеличению выходного импеданса. Тем не менее, для быстрой зарядки CC обычно лучше всего подходит для CV в течение <= 10% времени, чтобы зарядить вторичный заряд до 5% CC для отсечки. Все батареи и электролитические крышки имеют эту функцию памяти, более или менее в зависимости от химического состава.

• Использование фотоэлектрических модулей с постоянной солнечной энергией и эффективностью является особым случаем.
• управление MPPT ДОЛЖНО согласовать импеданс нагрузки с импедансом источника PV
• , то крышка или зарядное устройство должны использовать максимальную эффективность при постоянной мощности, чтобы соответствовать выходной мощности PV, которая исходит из низкого начального состояния Vcap, что означает, что I снижается с ростом V, так что V(t)*I(t)out = effic. * Пин

\$\конечная группа\$

\$\начало группы\$

Проблема уже в следующем предположении:

Теоретический конденсатор емкостью 100 Ф заряжается от источника постоянного питания со значениями V = 50В, I = 50А, ESR конденсатора = 5 мОм

Напряжение на разъемах конденсатора:

$$U_{\text{разъемы}} = U_{\text{конденсатор}} + I * ESR$$

Или:

$$U_{\ text{connectors}}(t) = \frac{Q(t)}{C} + I(t) * ESR$$

«Зарядка конденсатора» означает, что \$Q(t)\$ со временем увеличивается .

Однако это означает, что \$U(t)=50V\$ и \$I(t)=50A\$ не могут оба быть постоянными.

Вы можете использовать постоянный источник питания; однако в этом случае произведение \$P(t)=U(t)*I(t)\$ является постоянным, но ни \$U(t)\$, ни \$I(t)=\frac{P_ {\text{const.}}}{U(t)}\$ является константой.

\$\конечная группа\$

\$\начало группы\$

Ваша проблема, как сказано, избыточна. Если вы знаете, что V = 50 В и I = 50 А, ESR должно быть 1 Ом при t = 0 и постепенно падать с течением времени по мере увеличения напряжения, хранящегося на конденсаторе.

Если мы предположим, что V и I могут составлять 50 единиц или меньше, вы можете легко рассчитать линейное изменение… начиная с 1/4 В (из-за ESR) и увеличивая (помните, амперы — это кулоны в секунду, а фарады — это кулоны на вольт) при 0,5 В/с вплоть до 50 В. Однако в этот момент 0,25 В связано с ESR * током, поэтому ток будет падать экспоненциально, когда крышка завершит зарядку.

\$\конечная группа\$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

. Расчет времени заряда конденсатора

— инженерное мышление

Узнайте, как рассчитать время зарядки конденсатора с резистором, в этом учебном пособии по зарядке RC-цепи с примерами работ

Допустим, у нас есть батарея на девять вольт, конденсатор на 100 микрофарад, резистор на десять килоом и переключатель, который все в серии. Конденсатор полностью разряжен, и мы считываем 0 вольт на двух выводах. Когда мы замыкаем переключатель, конденсатор заряжается. Напряжение будет увеличиваться до тех пор, пока не сравняется с напряжением батареи. Повышение напряжения не мгновенное.

Будет экспоненциальная кривая. Сначала; напряжение быстро увеличивается, а затем замедляется, пока не достигнет того же уровня напряжения, что и батарея. Мы разделили эту кривую на шесть сегментов, но нас интересуют только первые пять, потому что на пятом маркере мы в основном на полном напряжении, поэтому мы можем игнорировать все, что находится дальше этого. Каждый сегмент представляет нечто, называемое постоянной времени. Следовательно, поскольку у нас есть пять сегментов, у нас есть пять постоянных времени, поэтому потребуется пять постоянных времени, чтобы зарядить конденсатор от нуля до чуть менее 100%.

Все, что нам нужно сделать, это вычислить длину одной постоянной времени. А потом умножаем это на пять. Для расчета постоянной времени мы используем следующую формулу: постоянная времени (в секундах) равна сопротивлению в омах, умноженному на емкость в фарадах. Итак, мы конвертируем резистор в омы, а емкость конденсатора в фарады и видим, что 10 000 ом, умноженные на 0,0001 фарад, равняются единице.

Итак, в этом примере постоянная времени равна 1 секунде. Следовательно, пять из них составляют 5 секунд, то есть конденсатору требуется 5 секунд, чтобы полностью зарядиться до 9.вольт. Если бы резистор был всего 1000 Ом, постоянная времени была бы 0,1 секунды, поэтому для достижения 9 вольт потребовалось бы 0,5 секунды. Если бы конденсатор был на 1000 микрофарад, то в сумме это заняло бы 50 секунд.

Таким образом, по мере увеличения размера конденсатора время, затрачиваемое на это, также будет увеличиваться.

Если значение резистора увеличивается, то время, необходимое для этого, также увеличивается. Возвращаясь к нашей исходной схеме, мы можем вычислить уровень напряжения для каждой постоянной времени. В точке 1 напряжение всегда 63,2%. Вторая точка — 86,5%. Третий пункт равен 95%, четвертая точка — 98,2%, пятая точка — 99,3%. Таким образом, напряжение никогда не достигнет 100%. Именно поэтому мы останавливаемся всего на пяти пунктах. Итак, в этом примере через 1 секунду напряжение на конденсаторе составляет 5,68 вольт. Через 2 секунды это 7,78 вольт.

Через 3 секунды 8,55 вольт. Через 4 секунды это 8,83 вольта, а через 5 секунд — 8,94 вольта. Если вам нужен более точный ответ, мы также можем рассчитать каждую точку таким образом. Помните, что, поскольку это последовательно, ток цепи уменьшается, а напряжение конденсатора увеличивается. При полном напряжении ток в цепи не течет.

Если бы резистор был лампой, то он мгновенно достигал бы полной яркости при замыкании ключа, но затем тускнел бы, когда конденсатор достигал полного напряжения.

Когда мы обеспечиваем путь для разрядки конденсатора, электроны покидают конденсатор, и напряжение на конденсаторе уменьшается. Он не разряжается мгновенно, а следует экспоненциальной кривой. Мы разделили эту кривую на шесть сегментов, но опять же, нас интересуют только первые пять. В первом случае напряжение всегда 36,8%.

Вторая точка будет равна 13,5%. Третий пункт будет 5%. Четвертая точка будет равна 1,8%, а пятая — 0,7%. Например, если бы у нас была батарея на девять вольт, лампа с сопротивлением 500 Ом и конденсатор на 2000 мкФ, наша постоянная времени была бы 500 Ом, умноженная на 0,002 фарад, что составляет 1 секунду.

Так что в момент отключения аккумулятора конденсатор будет на 9 вольт. И поскольку он питает цепь, лампа также будет испытывать 9 вольт. Через одну постоянную времени – в данном случае 1 секунду, напряжение будет 36,8%, что равно 3,312 вольта.