Умножение вектора на число презентация, доклад
УМНОЖЕНИЕ
ВЕКТОРА НА ЧИСЛО
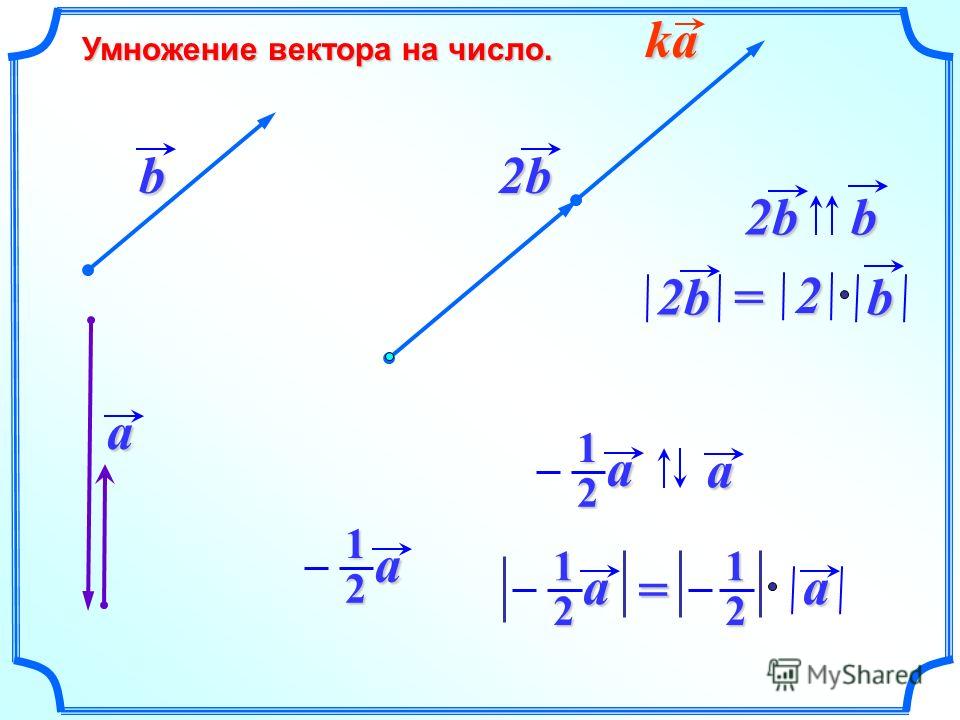
Умножение вектора на число.
Умножение вектора на число.
Умножение вектора на число.
Произведение любого вектора на число нуль есть нулевой вектор.
Произведение нулевого вектора на любое число считается нулевой вектор.
A
B
C
D
N
M
R
E
S
F
H
J
K
L
Z
Q
V
T
Y
U
Назовите вектор, который получится в результате умножения.
I
O
P
X
G
х
-4
0
х
A
B
C
D
N
M
R
E
S
F
H
J
K
L
Z
Q
V
T
Y
U
I
O
P
X
G
х
х
х
х
х не существует
1
х
-1
2
х
3
A
C
O
K
T
B
О – точка пересечения медиан треугольника.
х
х
х
–4
A
C
7
T
B
х
3
х
х
BC = DA
8
В
С
ABCD – трапеция.
А
D
10
х
–0,8
DA = BC
х
В
С
ABCD – параллелограмм. CS : SB = 5 : 3
А
D
BS = DA
х
S
х
Умножение вектора на число обладает следующими основными свойствами.
Сочетательный закон
Первый распределительный закон
Второй распределительный закон
1
2
3
Рисунок иллюстрирует сочетательный закон. Представлен случай, когда k = 2, l = 3.
Представлен случай, когда k = 2, l = 3.
Сочетательный закон
1
B
O
B
Рисунок иллюстрирует первый распределительный закон. Представлен случай, когда k = 3, l = 2.
O
Первый распределительный закон
2
OB =
O
Второй распределительный закон
3
A
Рисунок иллюстрирует второй распределительный закон.
На рисунке , коэффициент подобия
k
A1
B1
B
С другой стороны,
Таким образом,
=
№ 781 Пусть
Выразите через и
векторы
ЗАДАЧА №4
Построить вектор
С
А
В
ЗАДАЧА №5
Построить вектор
С
А
В
ЗАДАЧА№6
Построить вектор.
С
А
В
=
АВСD – параллелограмм.
D
ЗАДАЧА№7
Построить вектор.
С
А
В
D
АВСD – параллелограмм.
АВСD – ромб. Е ВС, ВЕ : ЕС = 3 : 1,
К – середина DC, АВ = , AD = . Выразите через
векторы и векторы:
С
А
В
D
Прежде, чем ввести еще одно действие – умножение вектора на число, обратимся к примеру. Представим себе, что один автомобиль движется прямолинейно с постоянной скоростью, второй движется в том же направлении со скоростью, вдвое большей, а третий автомобиль движется им навстречу, т.е. в противоположном направлении, и величина его скорости такая же, как у второго автомобиля.
Скачать презентацию
Опорный конспект по геометрии дистанционное обучение
ОПОРНЫЙ КОНСПЕКТ 8 класс
(дистанционное обучение)
Умножение вектора на число. Применение векторов к решению задач
На данном уроке мы рассмотрим новую операцию над векторами – умножение вектора на число. Кроме того, мы сформулируем законы умножения и научимся применять знания о векторах к решению различных задач.
На предыдущих уроках мы рассмотрели понятие вектора, ввели определения коллинеарных, сонаправленных, противонаправленных и равных векторов. Научились складывать и вычитать векторы, ввели законы сложения. Теперь нам нужно научиться умножать вектор на число. Особенность данной операции состоит в том, что число – это просто численная величина, не имеющая направления, а вектор – это направленный отрезок, имеющий численное измерение и направление.
Рассмотрим такую ситуацию: по дороге едут два автомобиля, скорость одного – 30 км/ч, а второго – 60 км/ч. Очевидно, что скорость второго автомобиля в два раза больше скорости первого, и скорость второго можно выразить через скорость первого, умножив скорость первого на два.
Очевидно, что скорость второго автомобиля в два раза больше скорости первого, и скорость второго можно выразить через скорость первого, умножив скорость первого на два.
Определение
Произведение ненулевого вектора на число k – такой вектор , длина которого равна , причем векторы и сонаправлены при и противонаправлены при . Произведение нулевого вектора на любое число – это нулевой вектор.
Пусть задан вектор (см. Рис. 1). Вектор – это вектор, направленный в ту же сторону, но длина его в два раза больше.
Вектор имеет длину, в два раза большую, чем вектор и ему противонаправлен.
Рис. 1
Законы умножения
Законы, которым подчиняется операция умножения вектора на число:
– сочетательный закон;
– первый распределительный закон;
– второй распределительный закон.
Решение задач
Анализ данных законов показывает, что действия с векторами аналогичны действиям с алгебраическими выражениями.
Пример 1 – упростить выражение:
Раскроем скобки:
Приведем подобные:
Пример 2: Дан отрезок АВ (см. Рис. 2). Точка С – середина отрезка, точка О – произвольная точка плоскости. , . Доказать, что вектор .
Рис. 2). Точка С – середина отрезка, точка О – произвольная точка плоскости. , . Доказать, что вектор .
Решение:
1 способ: применим правило треугольника и выразим вектор как сумму двух векторов:
С другой стороны:
Получили систему двух уравнений:
Рис. 2
Сложим уравнения системы:
, так как С – середина АВ, значит, модули данных векторов равны, но они противонаправлены, значит, их сумма – это нулевой вектор.
Получаем:
Поделим обе части на два:
Что и требовалось доказать.
2 способ:
Раскроем скобки и приведем подобные:
Пример 3: Доказать, что средняя линия трапеции параллельна основаниям и равна их полусумме.
Мы знаем, что средняя линия трапеции соединяет середины ее боковых сторон, кроме того, мы знаем, что основания трапеции параллельны.
Воспользуемся правилом многоугольника и выразим вектор как сумму векторов:
Рис. 3
С другой стороны,
Получаем систему уравнений:
Выполним сложение уравнений системы, получаем:
Векторы противоположны и дают в сумме нулевой вектор, так как М – середина АВ, то есть модули данных векторов равны, кроме того, очевидно, что они противонаправлены. Аналогично векторы дают в сумме нулевой вектор. Таким образом, получаем:
Аналогично векторы дают в сумме нулевой вектор. Таким образом, получаем:
Поделим обе части на два:
Таким образом, мы доказали, что средняя линия равна полусумме оснований. Кроме того, равенство вектора сумме говорит о том, что прямая MN параллельна основаниям трапеции.
Итак, в данном уроке мы изучили операцию умножения вектора на число и сформулировали законы умножения. Кроме того, мы научились применять факты о векторах к решению различных задач.
Домашнее задание
Задание 1: для произвольного четырехугольника MNPQ докажите, что: ; .
Задание 2: сторона равностороннего треугольника равна а. Найдите: ; ; ; ; .
Задание 3: точки M и N – середины сторон АВ и ВС треугольника . Выразите векторы , , , через векторы , .
ТЕСТ ПО ТЕМЕ
8 КЛАСС
УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
ПРИМЕНЕНИЕ ВЕКТОРОВ К РЕШЕНИЮ ЗАДАЧ
ВАРИАНТ 1
А1. Заданы векторы
Найдите вектор
А2. Известно, что выполнено равенство
Известно, что выполнено равенство
Выразите вектор
через векторы
А3. Найдите величину
В1. В параллелограмме ABCD дано:
Выразите вектор
через векторы
В2. Векторы a и b связаны с векторами m и n равенствами
Выразите векторы m и n через векторы a и b.
С1. Пусть
Выразите вектор
через векторы
Вариант 2
А1. Заданы векторы
Найдите вектор
А2. Известно, что выполнено равенство
Выразите вектор
через векторы
А3. Найдите величину
В1. В параллелограмме ABCD дано:
Выразите вектор
через векторы
В2. Векторы a и b связаны с векторами m и n равенствами
Выразите векторы m и n через векторы a и b.
С1. Пусть
Выразите вектор
Адрес публикации: https://www. prodlenka.org/metodicheskie-razrabotki/427178-opornyj-konspekt-po-geometrii-distancionnoe-o
prodlenka.org/metodicheskie-razrabotki/427178-opornyj-konspekt-po-geometrii-distancionnoe-o
Умножение вектора на число Л.С. Атанасян «Геометрия 7-9» Савченко Е.М., учитель презентация, доклад, проект
Умножение
вектора на число
Л.С. Атанасян «Геометрия 7-9»
Прежде, чем ввести еще одно действие – умножение вектора на число, обратимся к примеру. Представим себе, что один автомобиль движется прямолинейно с постоянной скоростью, второй движется в том же направлении со скоростью, вдвое большей, а третий автомобиль движется им навстречу, т.е. в противоположном направлении, и величина его скорости такая же, как у второго автомобиля.
Умножение вектора на число.
Умножение вектора на число.
Умножение вектора на число.
Произведение любого вектора на число нуль есть нулевой вектор.
Произведение нулевого вектора на любое число считается нулевой вектор.
A
B
C
D
N
M
R
E
S
F
H
J
K
L
Z
Q
V
T
Y
U
Назовите вектор, который получится в результате умножения.
I
O
P
X
G
х
-4
0
х
A
B
C
D
N
M
R
E
S
F
H
J
K
L
Z
Q
V
T
Y
U
I
O
P
X
G
х
х
х
х
х не существует
1
х
-1
2
х
3
A
C
O
K
T
B
О – точка пересечения медиан треугольника.
х
х
х
–4
A
C
7
T
B
х
3
х
х
х
1,25
A
C
T
B
ТВ = АС
х
Длина вектора TB на 25% больше длины вектора АС
-0,75
BC = DA
8
В
С
ABCD – трапеция.
А
D
10
х
–0,8
DA = BC
х
В
С
ABCD – параллелограмм. CS : SB = 5 : 3
А
D
BS = DA
х
S
х
Умножение вектора на число обладает следующими основными свойствами.
Сочетательный закон
Первый распределительный закон
Второй распределительный закон
1
2
3
Рисунок иллюстрирует сочетательный закон. Представлен случай, когда k = 2, l = 3.
Сочетательный закон
1
B
O
B
Рисунок иллюстрирует первый распределительный закон. Представлен случай, когда k = 3, l = 2.
O
Первый распределительный закон
2
OB =
O
Второй распределительный закон
3
A
Рисунок иллюстрирует второй распределительный закон.
На рисунке , коэффициент подобия
k
A1
B1
B
Таким образом,
=
№ 781 Пусть
Выразите через и
векторы
Задача
Построить вектор
С
А
В
Задача
Построить вектор
С
А
В
Задача
Построить вектор.
С
А
В
=
АВСD – параллелограмм.
D
Построить вектор.
С
А
В
D
Задача
АВСD – параллелограмм.
B
Точка С – середина отрезка АВ,
а О – произвольная точка плоскости. Доказать, что
Задача
A
A
Задача
Докажите теорему о средней линии
треугольника.
В
С
N
M
Теорема
Средняя линия трапеции параллельна
основаниям и равна их полусумме.
Дано:
трапеция АВСD, MN- средняя линия
Доказать:
Правило
многоугольника
A
В
С
D
Доказать:
Задача
АВСD – ромб. Е ВС, ВЕ : ЕС = 3 : 1,
Е ВС, ВЕ : ЕС = 3 : 1,
К – середина DC, АВ = , AD = . Выразите через
векторы и векторы:
С
А
В
D
Скачать презентацию
Операции с матрицами
Что касается линейной алгебры, то двумя наиболее важными операциями с векторами являются сложение векторов [сложение двух (или более) векторов] и скалярное умножение (умножение вектора на скаляр). Аналогичные операции определены для матриц.
Добавление матрицы . Если A и B являются матрицами одинакового размера , то их можно складывать. (Это похоже на ограничение на сложение векторов, а именно, только векторы из одного и того же пространства R n можно добавить; например, вы не можете добавить 2-вектор к 3-вектору.) Если A = [ a ij ] и B = [ b ij ] оба равны m n матриц, то их сумма, C = A + B , также является матрицей m x n , и ее элементы задаются формулой
Таким образом, чтобы найти записи A + B , просто добавьте соответствующие записи A и B .
Пример 1 : Рассмотрим следующие матрицы:
Какие два можно добавить? Какова их сумма?
Поскольку можно добавлять только матрицы одинакового размера, определяется только сумма F + H ( G нельзя добавлять ни к F , ни к H ). Сумма F и H это
Поскольку сложение действительных чисел коммутативно, отсюда следует, что сложение матриц (когда оно определено) также коммутативно; то есть для любых матриц A и B одинакового размера A + B всегда будет равно B + A .
Пример 2 : Если любую матрицу A добавить к нулевой матрице того же размера, то результат явно будет равен A :
Это матричный аналог утверждения a + 0 = 0 + a = a , которое выражает тот факт, что число 0 является аддитивной единицей в множестве действительных чисел.
Пример 3 : Найдите матрицу B такую, что A + B = C , где
Если
, то матричное уравнение A + B = C становится
Поскольку две матрицы равны тогда и только тогда, когда они имеют одинаковый размер и их соответствующие элементы равны, это последнее уравнение подразумевает
Следовательно,
Этот пример мотивирует определение матрицы вычитанием : если A и B являются матрицами одинакового размера, то элементы A − B находятся простым вычитанием элементов B из соответствующие записи А . Поскольку уравнение A + B = C эквивалентно B = C − A , использование матричного вычитания выше даст тот же результат:
Скалярное умножение . Матрицу можно умножить на скаляр следующим образом. Если A = [ a ij ] — матрица, а k — скаляр, то
Матрицу можно умножить на скаляр следующим образом. Если A = [ a ij ] — матрица, а k — скаляр, то
То есть матрица кА получается путем умножения каждой записи A на k .
Пример 4 : Если
, то скаляр, кратный 2 A , получается путем умножения каждой записи A на 2:
Пример 5 : Если A и B являются матрицами одинакового размера, то A − B = A + (− B ), где − B является кратным −1) Б . Если
, затем
Это определение вычитания матриц согласуется с определением, показанным в примере 8.
Пример 6 : Если
, затем
Умножение матриц . Безусловно, наиболее важной операцией с матрицами является умножение матриц , процесс умножения одной матрицы на другую. Первый шаг в определении умножения матриц — вспомнить определение скалярного произведения двух векторов. Пусть r и c — два n ‐вектора. Записав r в виде матрицы строк 1 x n и c в виде матрицы столбцов n x 1, скалярное произведение r и c равно
Первый шаг в определении умножения матриц — вспомнить определение скалярного произведения двух векторов. Пусть r и c — два n ‐вектора. Записав r в виде матрицы строк 1 x n и c в виде матрицы столбцов n x 1, скалярное произведение r и c равно
Обратите внимание, что для определения скалярного произведения r и c оба должны содержать одинаковое количество записей. Кроме того, здесь важен порядок, в котором эти матрицы записаны в этом произведении: сначала идет вектор-строка, затем — вектор-столбец.
Теперь последний шаг: как перемножаются две общие матрицы? Во-первых, чтобы сформировать продукт AB, количество столбцов A должно совпадать с количеством строк B ; если это условие не выполняется, то продукт AB не определен. Этот критерий вытекает из установленного выше ограничения на умножение матрицы строк r на матрицу столбцов c , а именно, что количество элементов в r должно совпадать с количеством элементов в с .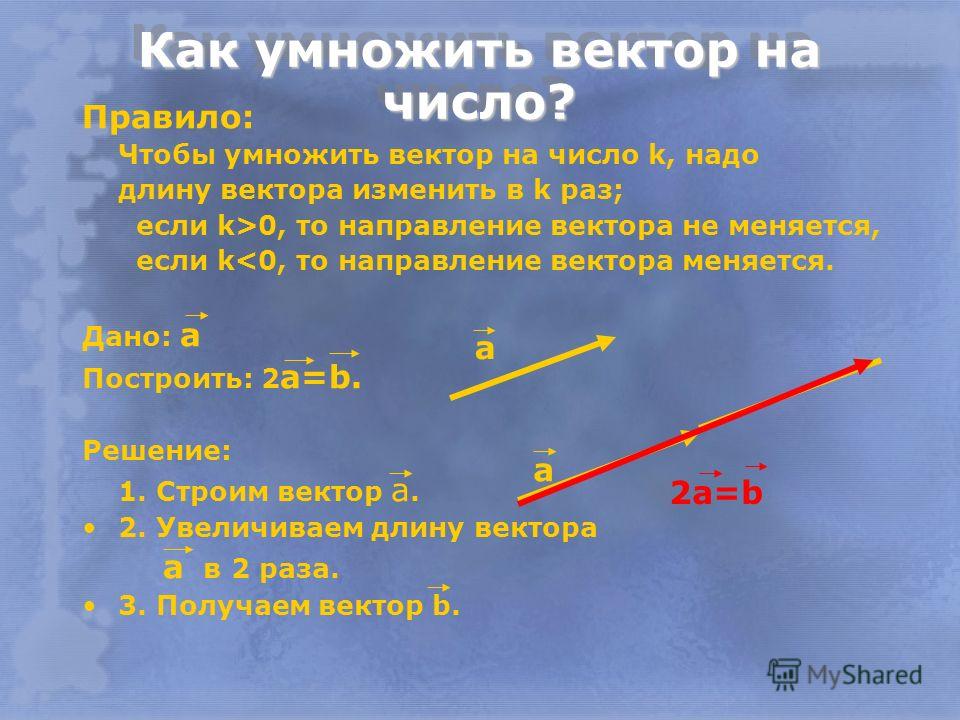 Если A равно m x n и B равно n x p , то произведение AB определено, а размер матрицы произведения 0 0 0 9 0 9 0 8 AB 900 р . Следующая диаграмма помогает определить, определен ли матричный продукт, и если да, то определить размер продукта:
Если A равно m x n и B равно n x p , то произведение AB определено, а размер матрицы произведения 0 0 0 9 0 9 0 8 AB 900 р . Следующая диаграмма помогает определить, определен ли матричный продукт, и если да, то определить размер продукта:
Думая о матрице m x n A , состоящей из векторов-строк R 1 , R 2 ,…, R M из R N и N x P MATRIX B B B B B B B B и N. P MATRIX AS x P . векторы столбцов C 1 , C 2 ,…, C P Из R N ,
и
правило вычисления элементов матричного произведения AB is r i · c j = ( AB ) 90, 8ij 90 Пример 7 : Даны две матрицы определить, какой матричный продукт, AB или BA , определен и оценить его. Поскольку A равно 2 x 3, а B равно 3 x 4, произведение AB в указанном порядке определено, а размер матрицы произведения равен AB будет 2 x 4. Произведение BA определяется как , а не как , поскольку первый фактор ( B ) имеет 4 столбца, а второй фактор ( A ) имеет только 2 строки. Количество столбцов первой матрицы должно совпадать с количеством строк второй матрицы, чтобы можно было определить их произведение. Скалярное произведение строки 1 в A и столбца 1 в B дает запись (1, 1) в AB . С 90 003 запись (1, 1) в AB равна 1: Скалярное произведение строки 1 в A и столбца 2 в B дает запись (1, 2) в AB , и скалярное произведение строки 1 в A и столбца 3 в B дает запись (1, 3) в AB : Первая строка произведения завершается путем скалярного произведения строки 1 в A и столбца 4 в B , что дает запись (1, 4) в AB : Теперь для второй строки AB : Скалярное произведение строки 2 в A и столбца 1 в B дает (2, 1) запись в AB , и скалярное произведение строки 2 в A и столбца 2 в B дает запись (2, 2) в AB : Наконец, взяв скалярное произведение строки 2 в A со столбцами 3 и 4 в B дает (соответственно) (2, 3) и (2, 4) записи в AB : Следовательно, Пример 8 : Если и вычислить запись (3, 5) произведения CD . Во-первых, обратите внимание, что поскольку C равно 4 x 5, а D равно 5 x 6, произведение CD действительно определено, и его размер равен 4 x 6. Однако нет необходимости вычислять все двадцать четыре записи из CD , если требуется только одна конкретная запись. Запись (3, 5) числа CD представляет собой скалярное произведение строки 3 числа C и столбца 5 числа D : Пример 9 : Если убедиться, что , но В частности, обратите внимание, что хотя оба продукта AB и BA определены, AB не равно BA ; на самом деле, они даже не одного размера! Предыдущий пример иллюстрирует, пожалуй, самое важное различие между умножением скаляров и умножением матриц. Для действительных чисел a и b всегда выполняется уравнение ab = ba , т. е. умножение действительных чисел коммутативно; порядок, в котором записаны факторы, не имеет значения. Поскольку C равен 3 x 2, а D равен 2 x 2, продукт CD определен, его размер равен 3 x 2, а Произведение DC , однако, не определено, поскольку количество столбцов D (которое равно 2) не равно количеству строк C (которое равно 3). Следовательно, CD ≠ DC , поскольку DC даже не существует. Из-за чувствительности к порядку, в котором записаны коэффициенты, обычно не говорят просто: «Умножьте матрицы на и B на ». Обычно важно указать, какая матрица стоит первой, а какая второй в продукте. Пример 10 : Если и x — это вектор (−2, 3), покажите, как A можно умножить справа на x , и вычислите произведение. Поскольку A равно 2 x 2, чтобы умножить A справа на матрицу, эта матрица должна иметь 2 строки. Следовательно, если x записывается как 2 x 1 столбец матрица , то произведение A x может быть вычислено, и результатом будет другая матрица столбца 2 x 1: Пример 11 : Рассмотрим матрицы Если A справа умножить на B , получится , но если A слева умножить на B , то получится Обратите внимание, что оба продукта определены и имеют одинаковый размер, но они не равны. Пример 12 : Если A и B являются квадратными матрицами такими, что AB = BA , то говорят, что A и B коммутируют с . Покажите, что любые две квадратные диагональные матрицы порядка 2 коммутируют. Пусть — две произвольные диагональные матрицы 2 x 2. Затем и Since a 11 b 11 = b 11 a 11 and a 22 b 22 = b 22 a 22 , AB действительно равно BA , что и требовалось. Хотя умножение матриц обычно не коммутативно, оно иногда коммутативно; например, если , затем Несмотря на подобные примеры, следует отметить, что в общем случае умножение матриц не является коммутативным . Есть еще одно различие между умножением скаляров и умножением матриц. Если a и b — действительные числа, то уравнение ab = 0 подразумевает, что a = 0 или b = 0. То есть единственный способ, которым произведение действительных чисел может равняться 0, — это если по крайней мере один из множителей сам равен 0. Однако аналогичное утверждение для матриц неверно. Например, если , затем Обратите внимание, что хотя ни G , ни H не являются нулевой матрицей, продукт GH является таковым. Еще одно различие между умножением скаляров и умножением матриц заключается в отсутствии общего закона сокращения для умножения матриц. Если а, b и с являются действительными числами, причем а ≠ 0, то при сокращении множителя а уравнение ab = ac подразумевает b = c . Для матричного умножения такого закона не существует; то есть утверждение AB = AC означает, что , а не подразумевает B = C , даже если A не равно нулю. потом оба и Таким образом, хотя AB = AC и A не является нулевой матрицей, B не равно C . Пример 13 : Хотя умножение матриц не всегда коммутативно, оно равно , всегда ассоциативно . То есть, если A, B и C являются любыми тремя матрицами, для которых определено произведение (AB)C , то произведение A(BC) также определено, и То есть, пока порядок факторов неизменен, то, как они сгруппированы , не имеет значения. Проверить закон ассоциативности для матриц Первый с продукт (AB)C — это Сейчас, с продукт A(BC) Следовательно, (AB)C = A(BC) , как и ожидалось. Обратите внимание, что ассоциативный закон подразумевает, что произведение A, B и C (в таком порядке) может быть записано просто как ABC ; круглые скобки не нужны для устранения какой-либо неоднозначности, потому что двусмысленности нет. Пример 14 : Для матриц проверьте уравнение ( AB ) T = B T A T . Первый, подразумевает Сейчас, с B T A T действительно равно ( AB ) T . На самом деле уравнение справедливо для любых двух матриц, для которых определено произведение AB . Это говорит о том, что если произведение AB определено, то транспонирование произведения равно произведению транспонирования в обратном порядке . Матрицы идентичности . Нулевая матрица 0 m x n играет роль аддитивного тождества в наборе m x n матриц точно так же, как число 0 играет роль в множестве действительных чисел (вспомните пример 7). То есть если A — это матрица m x n и 0 = 0 m x n , затем Это матричный аналог утверждения, что для любого действительного числа a , Имея на руках аддитивную идентичность, вы можете спросить: «А как насчет мультипликативной идентичности ?» В наборе действительных чисел мультипликативным тождеством является число 1, так как Есть ли матрица, которая играет эту роль ? Рассмотрим матрицы и убедитесь, что и Таким образом, AI = IA = A . — это мультипликативная идентичность в наборе матриц 2 x 2. Аналогично, матрица — это мультипликативная идентичность в наборе матриц 3 x 3 и так далее. (Обратите внимание, что I 3 — это матрица [δ ij ] 3 x 3 .) В общем случае матрица I n — матрица n x 8 диагональных элементов, равная 1—8 диагональным элементам 90 называется единичной матрицей порядка n и служит мультипликативной идентичностью в наборе всех n x n матриц. Существует ли мультипликативная идентичность в наборе всех m x n матриц, если m ≠ n ? Для любой матрицы A в M M x N ( R ), Matrix I M — Left Identity ( I M A = ) и I 33 N A = ), и I 33 N A = ) и I 33. Пример 15 : Если A является квадратной матрицей, то A 2 обозначает произведение AA, A 3 обозначает произведение AAA и так далее. Если А это матрица показывают, что A 3 = − A . Расчет показывает, что А 2 = − I . Умножение обеих частей этого уравнения на A дает A 3 = − A , что и требовалось. [Техническое примечание: можно показать, что в определенном смысле набор матриц вида , где a и b — действительные числа, структурно идентично набору комплексных чисел , a + bi . Пример 16 : Найти недиагональную матрицу, коммутирующую с Проблема просит недиагональную матрицу B такой, что AB = BA . Как и A , матрица B должна быть 2 x 2. Один из способов получить такую матрицу B состоит в том, чтобы сформировать A 2 , поскольку если B = A 2 , (Это уравнение доказывает, что A 2 будет коммутировать с A для любой квадратной матрицы A ; кроме того, оно подсказывает, как можно доказать, что каждые интегральная степень квадратной матрицы А будет коммутировать с А . В данном случае , который не является диагональным. Эта матрица B действительно коммутирует с A , что подтверждается вычислениями и Пример 17 : Если докажи что для каждого положительного целого числа n . Несколько предварительных расчетов показывают, что данная формула верна: Однако, чтобы установить, что формула верна для всех положительных целых чисел n , необходимо привести общее доказательство. Это будет сделано здесь с использованием принципа математической индукции , который звучит следующим образом. Пусть P(n) обозначает предложение относительно натурального числа n . Если можно показать, что и , то оператор P(n) действителен для всех положительных целых чисел n . Поскольку A 1 = A , утверждение P (1) безусловно верно, поскольку Теперь, если предположить, что P(n) верно, то есть предположить, что теперь необходимо установить справедливость утверждения P ( n + 1), что равно Но это утверждение действительно верно, потому что По принципу математической индукции доказательство завершено. Обратная матрица . Пусть a — заданное действительное число. Поскольку 1 является мультипликативным тождеством в множестве действительных чисел, если существует число b такое, что затем b называется обратной или мультипликативное обратное от к и обозначается через -1 (или 1/ через ). затем B называется (мультипликативным) обратным числа A и обозначается как A −1 (читается « A обратное»). Пример 18 : Если , затем с и Еще одно различие между умножением скаляров и умножением матриц обеспечивается существованием инверсий. Хотя каждое ненулевое действительное число имеет обратное, существуют ненулевые матрицы, не имеющие обратной . Пример 19 : Показать, что ненулевая матрица не имеет обратного. Если бы у этой матрицы была обратная, то для некоторых значений a, b, c и d . Однако, поскольку вторая строка A является нулевой строкой, вы можете видеть, что вторая строка произведения также должна быть нулевой строкой: (Когда звездочка * появляется в качестве записи в матрице, это означает, что фактическое значение этой записи не имеет отношения к настоящему обсуждению.) Поскольку запись (2, 2) произведения не может равняться 1, произведение не может равняться единичной матрице. Поэтому построить матрицу, обратную для 9, невозможно.0007 А 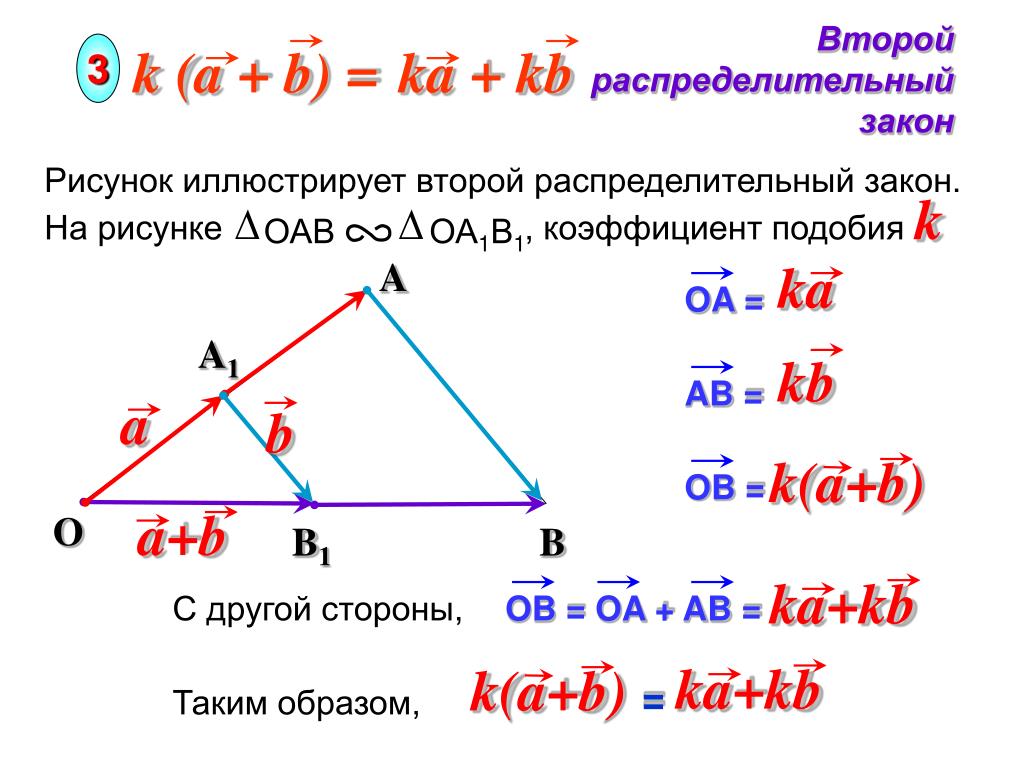
 Однако утверждение о том, что умножение матриц коммутативно, совершенно неверно. Для матриц А и B , приведенный в Примере 9, оба продукта AB и BA были определены, но они определенно не были идентичными. На самом деле матрица АВ была 2 х 2, а матрица ВА была 3 х 3. Вот еще одна иллюстрация некоммутативности матричного умножения: Рассмотрим матрицы
Однако утверждение о том, что умножение матриц коммутативно, совершенно неверно. Для матриц А и B , приведенный в Примере 9, оба продукта AB и BA были определены, но они определенно не были идентичными. На самом деле матрица АВ была 2 х 2, а матрица ВА была 3 х 3. Вот еще одна иллюстрация некоммутативности матричного умножения: Рассмотрим матрицы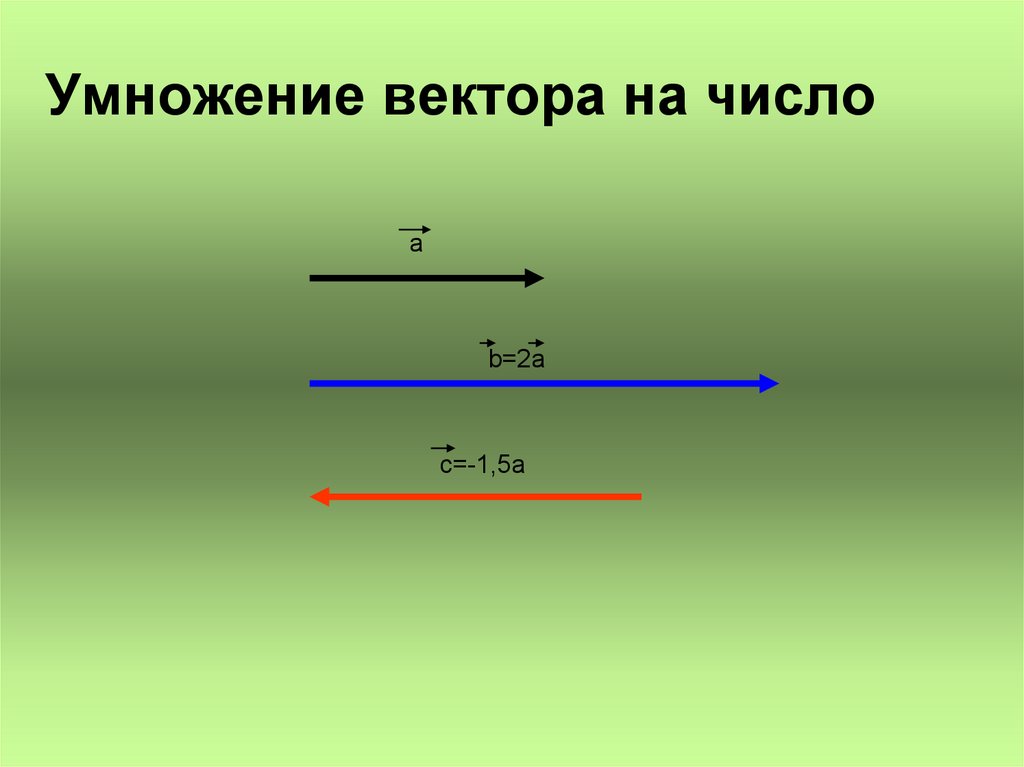 По этой причине утверждение «Умножить A справа на B » означает получение продукта AB , а «Умножить A слева на B » означает формирование продукта BA .
По этой причине утверждение «Умножить A справа на B » означает получение продукта AB , а «Умножить A слева на B » означает формирование продукта BA .

 Например, если
Например, если 
 В самом деле, можно легко показать, что для этой матрицы I оба произведения AI и IA будут равны A для любой матрицы 2 x 2 A . Следовательно,
В самом деле, можно легко показать, что для этой матрицы I оба произведения AI и IA будут равны A для любой матрицы 2 x 2 A . Следовательно, — это правильный идентификатор ( AI n = A ). Таким образом, в отличие от набора n x n матриц, набор неквадратных m x n матриц не обладает кв. двусторонним тождеством, потому что I м ≠ I n если м ≠ n .
— это правильный идентификатор ( AI n = A ). Таким образом, в отличие от набора n x n матриц, набор неквадратных m x n матриц не обладает кв. двусторонним тождеством, потому что I м ≠ I n если м ≠ n . Поскольку матрица A в этом примере имеет такой вид (с a = 0 и b = 1), A соответствует комплексному числу 0 + 1 i = i и аналогу матричного уравнения A 2 = − I , полученному выше i 2 = −1, уравнение, определяющее мнимую единицу, i .]
Поскольку матрица A в этом примере имеет такой вид (с a = 0 и b = 1), A соответствует комплексному числу 0 + 1 i = i и аналогу матричного уравнения A 2 = − I , полученному выше i 2 = −1, уравнение, определяющее мнимую единицу, i .] )
) В данном случае оператор P(n) является утверждением
В данном случае оператор P(n) является утверждением Аналог этого утверждения для квадратных матриц выглядит следующим образом. Пусть A будет данной матрицей n x n . Поскольку I = I n является мультипликативным тождеством в наборе n x n матриц, если существует матрица B такая, что
Аналог этого утверждения для квадратных матриц выглядит следующим образом. Пусть A будет данной матрицей n x n . Поскольку I = I n является мультипликативным тождеством в наборе n x n матриц, если существует матрица B такая, что
Если матрица имеет обратную, говорят, что она обратима . Матрица в примере 23 обратима, а матрица в примере 24 — нет. Позже вы изучите различные критерии для определения того, является ли данная квадратная матрица обратимой.
Пример 20 : Пример 18 показал, что
Учитывая, что
проверить уравнение ( AB ) −1 = B −1 А -1 .
Сначала вычислите AB :
Затем вычислить B −1 A −1 :
Теперь, поскольку произведение AB и B −1 A −1 равно I ,
B −1 A −1 действительно является обратным AB . На самом деле уравнение
верно для любых обратимых квадратных матриц того же размера. Это говорит о том, что если A и B — обратимые матрицы одного размера, то их произведение AB также обратимо, а обратное произведение равно произведению обратных в обратном порядке . (Сравните это уравнение с уравнением, включающим транспонирование в примере 14 выше.) Этот результат можно доказать в общем случае, применив ассоциативный закон для матричного умножения. С
и
следует, что ( AB ) −1 = B −1 A −1 , что и требовалось.
Пример 21 : Матрица, обратная
это
Покажите, что обратное число B T равно ( B −1 ) T .
Форма Б Т и ( B −1 ) T и умножить:
Этот расчет показывает, что ( B −1 ) T является обратным к B T . [Строго говоря, он показывает только то, что ( B −1 ) T является правым обратным к B T , то есть когда оно умножает B T справа, продукт является личностью. Также верно, что ( B −1 ) T B T = I , что означает ( B —1 ) T — Left из B T . Однако нет необходимости явно проверять оба уравнения: если квадратная матрица имеет обратную, нет различия между левой и правой обратной матрицей. ] Таким образом,
] Таким образом,
уравнение, которое на самом деле верно для любой обратимой квадратной матрицы Б . Это уравнение говорит о том, что если матрица обратима, то обратима и ее транспонирование, а инверсия транспонирования — это транспонирование инверсии.
Пример 22 : Используйте распределительное свойство для умножения матриц, A ( B ± C ) = AB ± AC , чтобы ответить на этот вопрос: если матрица 2 x 2 удовлетворяет D 900 уравнение D 2 − D − 6 I = 0 , какое выражение для D −1 ?
По приведенному выше распределительному свойству D 2 − D = D 2 − DI = D(D − I) . Поэтому из уравнения D 2 − D − 6 I = 0 следует D(D − I) = 6 I . Умножение обеих частей этого уравнения на 1/6 дает
Умножение обеих частей этого уравнения на 1/6 дает
, что подразумевает
В качестве иллюстрации этого результата матрица
удовлетворяет уравнению D 2 − D − 6 I = 0 , как вы можете убедиться. С 90 003
и
матрица 1/6 ( D-I ) действительно равна D -1 , как заявлено.
Пример 23 : Уравнение ( a + b ) 2 = a 2 + 2 ab + b 2 является тождеством, если a и b — действительные числа. Покажите, однако, что ( A + B ) 2 = A 2 + 2 AB + B 2 — НЕ АДИДИНТ, ЕСЛИ A и B являются матрицами 2 x 2. [Примечание: распределительные законы для умножения матриц таковы: A ( B ± C ) = AB ± AC , приведенный в примере 22, и Закон о сообщении, ( A ± B ) C = AC ± B. .]
.]
Дистрибутивные законы для матричного умножения подразумевают
Поскольку умножение матриц не является коммутативным, BA обычно не будет равно AB , поэтому сумма BA + AB не может быть записана как 2 АБ . В общем случае ( А + В ) 2 ≠ А 2 + 2 АВ + В 2 . [Любые матрицы A и B , которые не коммутируют друг с другом (например, матрицы в примере 16 выше), дадут конкретный контрпример к утверждению ( A + B ) 2 = A 8 2 + 2 AB + B 2 , что также установило бы, что это не личность.]
Пример 24 : Предположим, что B является обратимым. Если A коммутирует с B , покажите, что A также будет коммутировать с B −1 .
Доказательство . Сказать « A коммутирует с B » означает AB = BA . Умножьте это уравнение на B −1 слева и справа и используйте ассоциативность:
Сказать « A коммутирует с B » означает AB = BA . Умножьте это уравнение на B −1 слева и справа и используйте ассоциативность:
Пример 25 : Число 0 имеет только один квадратный корень: 0. Покажите, однако, что нулевая матрица (2 на 2) имеет бесконечно много квадратных корней, найдя все матрицы 2 x 2 A такие, что A 2 = 0 .
Точно так же, как число a называется квадратным корнем из b , если a 2 = b , матрица A называется квадратным корнем из B , если А 2 = Б . Пусть
— произвольная матрица 2 x 2. Возведение его в квадрат и установка результата равным 0 дает
Элементы (1, 2) в последнем уравнении подразумевают b ( a + d ) = 0, что выполняется, если (Случай 1) b = 0 или (Случай 2) d = − и .
Случай 1. Если b = 0, диагональные записи подразумевают a = 0 и d = 0, а (2, 1) записи подразумевают, что c является произвольным. Таким образом, для любого значения c каждая матрица вида
— это квадратный корень из 0 2×2 .
Случай 2. Если d = − a , то обе недиагональные записи будут равны 0, а диагональные записи будут равны a 2 + bc . Таким образом, если b и c выбраны так, что bc = − a 2 , A 2 будет равно 0 .
Аналогичная цепочка рассуждений, начинающаяся с (2, 1) записей, приводит либо к a = c = d = 0 (и b произвольно), либо к тому же выводу, что и раньше: пока b и c выбраны так, что bc = − a 2 , матрица A 2 будет равна 0 .
Все эти случаи можно резюмировать следующим образом. Любая матрица следующей формы будет обладать тем свойством, что ее квадрат представляет собой нулевую матрицу 2 на 2:
Поскольку существует бесконечно много значений a, b и c , таких что bc = − a 2 , нулевая матрица 0 2×2 имеет бесконечно много квадратных корней. Например, выбор a = 4, b = 2 и c = −8 дает ненулевую матрицу
.
, квадрат которого равен
Умножение матриц: определение и правила
Клэр хочет знать, что произойдет, если она возьмет вектор, который начинается в начале координат и заканчивается в (1, 1), и повернет его против часовой стрелки на 90 o вокруг начала координат. А также, что происходит с вектором, когда она увеличивает его в 3 раза.
Это можно сделать физически, нарисовав вектор на графическом листе, обведя вектор на кальке и повернув кальку 90 o против часовой стрелки. Для масштабирования мы могли бы использовать линейку, чтобы увеличить вектор в три раза.
Для масштабирования мы могли бы использовать линейку, чтобы увеличить вектор в три раза.
Но есть более простой способ сделать это с помощью умножения матриц!
Мы представляем вектор, который начинается в начале координат (0, 0) и заканчивается в (1, 1), матрицей порядка 2 × 1, где первая строка задает x-компоненту, а вторая строка задает y-компоненту как 11.
Для поворота этого вектора на 90 o против часовой стрелки мы просто умножаем матрицу вращения, которая равна 0-110, на матрицу 11, и это дает нам результирующий вектор. Для масштабирования вектора мы просто умножаем матрицу 11 на скаляр 3.
В этой статье мы узнаем, как выполнить умножение двух матриц и как умножить матрицу на скаляр.
Как умножить матрицу на скаляр?
Чтобы умножить скаляр на матрицу, мы просто умножаем каждый элемент матрицы на скаляр.
В приведенном выше примере, когда нам нужно масштабировать вектор с коэффициентом 3, нам нужно было умножить скаляр 3 на матрицу 11. Для этого нам просто нужно умножить каждый элемент матрицы на скаляр. В этом случае результатом снова будет матрица 33,9.0003
Для этого нам просто нужно умножить каждый элемент матрицы на скаляр. В этом случае результатом снова будет матрица 33,9.0003
В общем, если нам нужно умножить скаляр, скажем, u, на матрицу A=abcd, мы получим
uA=u×abcd=u×au×bu×cu×d.
1. Умножив скаляр 4 на матрицу 363340, мы получим 4×34×63×64×34×44×0=12241812160.
2. Если матрица A=123494567, то 2A=2×12×22×32×42×92×42×52×62×7=2468188101214.
Как перемножить две матрицы?
В отличие от сложения и вычитания матриц, мы не требуем, чтобы матрица имела один и тот же порядок для выполнения умножения матриц. Однако количество столбцов первой матрицы должно быть равно количеству строк второй матрицы. Это условие совместимости, которое необходимо проверить для выполнения матричного умножения.
Для выполнения умножения двух матриц проверка совместимости заключается в том, что количество столбцов первой матрицы должно быть равно количеству строк второй матрицы.
Матрицы A=124864304,B=356 имеют порядок 3×3 и 1×3 соответственно.
Мы можем умножить матрицу B на A, записанную как BA, так как количество столбцов B и количество строк A одинаковы.
Однако мы не можем умножить A на B, записанное как AB, так как количество столбцов в A равно 3, а количество строк в B равно 1, что не одно и то же.
Также важно отметить, что AB≠BA. Это отличается от умножения целых чисел, где 2×3=3×2=6. При умножении матриц важен порядок, в котором перемножаются матрицы. Как видно из этого примера, мы можем сделать BA, но не AB.
Рассмотрим две матрицы A и B с порядками m×n и p×q. Предположим, мы хотим умножить их на A, являющуюся первой матрицей, и B, являющуюся второй матрицей, тогда
- по тесту совместимости, количество столбцов в A = количеству столбцов в B, то есть n = p;
- порядок матрицы AB будет равен количеству строк в A × количеству столбцов в B, то есть m × q;
- элемент в строке i и столбце j матрицы AB находится путем суммирования произведения всех элементов строки i матрицы A на соответствующие элементы столбца j матрицы B.

Рассмотрим две матрицы A=24 ,В=57.
Порядок этих матриц 1×2 и 2×1 соответственно.
Шаг 1: Выполните тест на совместимость.
Мы можем найти AB, поскольку количество столбцов в A = количеству строк в B = 2.
Шаг 2: Найдите порядок матрицы произведения.
Матрица AB будет иметь то же количество строк, что и A, и такое же количество столбцов, как B. В этом случае порядок AB будет 1×1.
Шаг 3: Найдите элементы матрицы произведений .
AB=2457=_
Единственный элемент матрицы AB можно получить, умножив элементы первой строки A24 на соответствующие элементы первого столбца B57 и сложив результаты.
То есть (2×5)+(4×7)=10+28=38.
Это причина проверки совместимости. Количество элементов в каждой строке A будет таким же, как количество элементов в каждом столбце B. Таким образом, произведение AB = 38.
Теперь найдем BA для того же примера.
Шаг 1: Выполните тест на совместимость.
Совместимость для этого умножения состоит в том, что количество столбцов B = количеству строк A = 1.
Шаг 2: Найдите порядок матрицы произведения.
Порядок матрицы BA = количество строк B × количество столбцов A = 2×2.
Шаг 3: Найдите элементы матрицы произведений .
BA=5724=____
Элемент в строке 1 и столбце 1 BA находится путем умножения соответствующих элементов первой строки B5 на первый столбец A2. В этом случае, поскольку у нас есть только один элемент, мы имеем 5×2=10.
Элемент в строке 1 и столбце 2 БА находится путем умножения соответствующих элементов первой строки B5 на второй столбец A4. То есть 5×4=20.
Элемент в строке 2 и столбце 1 BA находится путем умножения соответствующих элементов второй строки B7 на первый столбец A2. То есть 7×2=14.
То есть 7×2=14.
Аналогично t элемент в строке 2 и столбце 2 из ВА =7×4=28. Следовательно, матрица BA равна 10201428.
В общем, рассмотрим две матрицы A=abcd,B=efgh.
Шаг 1: Выполните тест на совместимость.
Количество столбцов в A = количеству строк в B = 2, поэтому мы можем найти AB.
Шаг 2: Найдите порядок матрицы произведения.
Результирующая матрица имеет то же количество строк, что и A, и такое же количество столбцов, что и B. В этом случае порядок AB будет 2×2.
Шаг 3: Найдите элементы матрицы произведений .
Элемент в строке 1 и столбце 1 таблицы AB находится из первой строки строки Aab и первого столбца таблицы Beg. Умножаем соответствующие элементы и складываем результаты. То есть (а×е)+(б×г).
Элемент в строке 1 и столбце 2 таблицы AB определяется из первой строки таблицы Aab и второго столбца таблицы Bfh. То есть (a×f)+(b×h).
То есть (a×f)+(b×h).
Аналогично находим остальные элементы матрицы и получаем
AB=abcdefgh=(a×e)+(b×g)(a×f)+(b×h)(c×e)+(d×g)(c×f)+(d×h) .
Мы хотим найти произведение матриц AB
A=123246,B=124635.
Решение
Шаг 1 — Проверка совместимости: количество столбцов A = количество строк B = 3.
Шаг 2 — Порядок матрицы произведения: количество строк A ×количество столбцов B = 2×2.
Шаг 3 — Нахождение элементов матрицы произведения:
Элемент в строке 1 и столбце 1 AB получается из
123 и 143 как (1×1)+(2×4)+(3×3)=18.
Элемент в строке 1 и столбце 2 AB получается из
123 и 265 как (1×2)+(2×6)+(3×5)=29.
Аналогично получаем остальные элементы AB. Следовательно,
АВ=18293658.
Учитывая A=20131440-2,B=1230-214-10, найдите матрицу AB.
Решение
Шаг 1 — Проверка совместимости: количество столбцов A = количество строк B = 3.
Шаг 2 — Порядок матрицы произведения: количество строк A × количество столбцов B = 3×3.
Шаг 3 — Нахождение элементов AB:
AB=(2×1)+(0×0)+(1×4)(2×2)+(0×-2)+(1× -1)(2×3)+(0×1)+(1×0)(3×1)+(1×0)+(4×4)(3×2)+(1×-2)+ (4×-1)(3×3)+(1×1)+(4×0)(4×1)+(0×0)+(-2×4)(4×2)+(0× -2)+(-2×-1)(4×3)+(0×1)+(-2×0)=2+0+44+0-16+0+03+0+166-2- 49+1+04+0-88+0+212+0+0=63619010-41012
Умножение матриц — ключевые выводы
- Умножение матрицы на скаляр: Чтобы умножить скаляр на матрицу, мы просто умножаем каждый элемент матрицы на скаляр.
- Умножение двух матриц: Порядок умножения матриц имеет значение.
Шаг 1: Выполните тест на совместимость.
Количество столбцов первой матрицы = количеству строк второй матрицы
Шаг 2: Найдите порядок матрицы произведения.
Количество строк первой матрицы × количество столбцов второй матрицы
Шаг 3: Найдите элементы матрицы произведения.
Умножить соответствующие элементы строк первой матрицы на элементы столбцов второй матрицы и сложить их.
Комплексные числа: умножение на
Комплексные числа: умножениеАлгебраическое умножение.
Комплексное умножение — более сложная операция для понимания как с алгебраической, так и с геометрической точки зрения. Давайте сначала сделаем это алгебраически и возьмем определенные комплексные числа для умножения, скажем, 3 + 2 i и 1 + 4 i. В каждом из них по два слагаемых, поэтому, умножив их, мы получим четыре слагаемых: Теперь 12 i + 2 i упрощается до 14 i, , конечно. А как насчет 8 i 2 ? Помните, мы ввели i как сокращение от √1, квадратного корня из 1. Другими словами, i — это число, квадрат которого равен 1. Таким образом, 8 i 2 равняется 8. Следовательно, произведение (3 + 2 i )(1 + 4 i ) равно 5 + 14 я.
Следовательно, произведение (3 + 2 i )(1 + 4 i ) равно 5 + 14 я.
Если обобщить этот пример, то получится общее правило умножения
Помните, что ( xu yv ), действительная часть произведения, есть произведение действительных частей минус произведение мнимых частей, но ( xv + yu ), мнимая часть произведения произведение, представляет собой сумму двух произведений одной действительной части и другой мнимой части.
Давайте рассмотрим некоторые частные случаи умножения.
Умножение комплексного числа на действительное число
В приведенной выше формуле для умножения, если v равно нулю, вы получаете формулу для умножения комплексного числа x + yi и действительного числа u вместе: Другими словами, вы просто умножаете обе части комплексного числа на действительное число. Например, 2 умножить на 3 + i — это всего лишь 6 + 2 i. Геометрически, когда вы удваиваете комплексное число, просто удваивайте расстояние от начала координат, 0. Точно так же, когда вы умножаете комплексное число z на 1/2, результат будет на полпути между 0 и z. Умножение на 2 можно рассматривать как преобразование, которое растягивает комплексную плоскость C в 2 раза от 0; и умножение на 1/2 как преобразование, которое сжимает C до 0.
Например, 2 умножить на 3 + i — это всего лишь 6 + 2 i. Геометрически, когда вы удваиваете комплексное число, просто удваивайте расстояние от начала координат, 0. Точно так же, когда вы умножаете комплексное число z на 1/2, результат будет на полпути между 0 и z. Умножение на 2 можно рассматривать как преобразование, которое растягивает комплексную плоскость C в 2 раза от 0; и умножение на 1/2 как преобразование, которое сжимает C до 0.
Умножение и абсолютное значение.
Несмотря на то, что мы рассмотрели только один случай умножения, этого достаточно, чтобы предположить, что абсолютное значение zw (т. е. расстояние от 0 до zw ) может быть абсолютным значением z , умноженным на абсолютное значение . ж. Это было, когда w было реальным числом u чуть выше. На самом деле, это верно в целом: Проверка этого тождества является упражнением в алгебре. Чтобы доказать это, мы докажем, что это верно для квадратов, поэтому нам не нужно иметь дело с квадратными корнями. Мы покажем | ЗВ | 2 = | с | 2 | с | 2 . Пусть z будет x + yi, и пусть w будет u + vi. Тогда по формуле умножения zw равно ( xu yv ) + ( xv + yu ) i. Напомним из раздела об абсолютных значениях, что
Чтобы доказать это, мы докажем, что это верно для квадратов, поэтому нам не нужно иметь дело с квадратными корнями. Мы покажем | ЗВ | 2 = | с | 2 | с | 2 . Пусть z будет x + yi, и пусть w будет u + vi. Тогда по формуле умножения zw равно ( xu yv ) + ( xv + yu ) i. Напомним из раздела об абсолютных значениях, что
Точно так же у нас есть
и, поскольку zw = ( xu yv ) + ( xv + yu ) i,
Итак, чтобы показать | ZW | 2 = | с | 2 | с | 2 , все, что вам нужно сделать, это показать, что
и это простое упражнение по алгебре.
Полномочия
i. Для нашего следующего частного случая умножения рассмотрим различные степени мнимой единицы i. Мы начали с предположения, что i 2 = 1. Как насчет и 3 ? Это всего лишь i 2 умножить на и , и это 1 умножить на i. Следовательно, i 3 = i. Это интересно: куб и является собственным отрицанием. Далее рассмотрим i 4 . Это квадрат i 2 , то есть квадрат 1. Таким образом, i 4 = 1. Другими словами, i является корнем четвертой степени из 1. Вы можете показать, что i является еще одним корнем четвертой степени из 1. А так как 1 и 1 являются квадратными корнями из 1, теперь мы знаем все четыре корня четвертой степени из 1, а именно, 1, i, 1 и i. Это наблюдение связано с основной теоремой алгебры, поскольку уравнение z 4 = 1 является уравнением четвертой степени, поэтому должно иметь ровно четыре корня.
Higher powers of i are easy to find now that we know i 4 = 1. For example, i 5 is i times i 4 , and that’s just i . Вы можете уменьшить степень и на 4 и не изменить результат. Другой пример: i 11 = i 7 = i 3 = i.
Как насчет отрицательных сил и ? Чему равно число i, ?
то есть i 1 ? По той же причине, по которой вы можете вычесть 4 из степени i и не изменить результат, вы также можете прибавить 4 к степени i. Это означает i 1 = i 3 = i. Таким образом, обратное число i равно i. Представьте себе число, обратное значение которого является его собственным отрицанием! Конечно, легко проверить, что i умножить на i равно 1, так что, конечно, i и i обратны.
Корни единства.
Различные корни из 1 называются корнями из единицы. В общем, по основной теореме алгебры число n корней из единицы равно n, , так как имеется n корней уравнения n -й степени z u 1 = 0. Квадратные корни из единицы равны 1 и 1. Четвертые корни составляют ± 1, ± 92 317 i, 92 318, как отмечалось ранее в разделе об абсолютном значении. Кроме того, в этом разделе упоминалось, что ±√2/2 ± i √2/2 были квадратными корнями из i и i, , а теперь с помощью формулы умножения это легко проверить. Следовательно, восемь восьмикореней из единицы равны ±1, ± i, и ±√2/2 ± i √2/2. Обратите внимание, как эти восемь корней единства равномерно распределены по единичному кругу. Мы можем использовать геометрию, чтобы найти некоторые другие корни из единицы, в частности кубические корни и корни шестой степени из единицы. Но давайте немного подождем их.
Умножение комплексного числа на
i. В нашей цели найти геометрическую интерпретацию комплексного умножения, давайте рассмотрим следующее умножение произвольного комплексного числа z = x + yi на i.Давайте интерпретируем это утверждение геометрически. Точка z в C расположена на х единиц правее мнимой оси и на y единиц выше действительной оси. Точка z и расположены на и единиц левее и на х единиц выше. Произошло то, что умножение на i привело к повороту к точке z 90° против часовой стрелки вокруг начала координат к точке z i. Говоря короче, умножение на дает поворот на 90° против часовой стрелки около 0.
Таким же образом можно проанализировать, что делает умножение на i .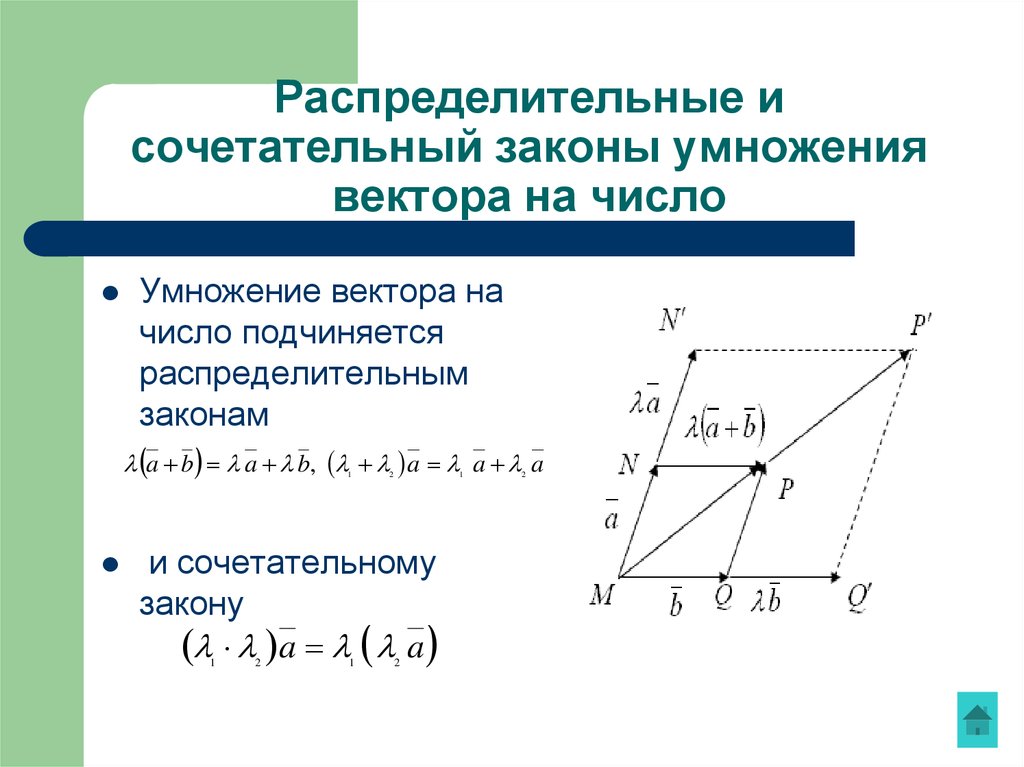 Вы найдете это умножение на i дает поворот на 90° по часовой стрелке относительно 0. Когда мы не указываем против часовой стрелки или по часовой стрелке при обращении к поворотам или углам, мы будем следовать стандартному соглашению, что подразумевается вращение против часовой стрелки. Тогда мы можем сказать, что умножение на i дает поворот на 90° относительно 0 или, если хотите, поворот на 270° относительно 0.
Вы найдете это умножение на i дает поворот на 90° по часовой стрелке относительно 0. Когда мы не указываем против часовой стрелки или по часовой стрелке при обращении к поворотам или углам, мы будем следовать стандартному соглашению, что подразумевается вращение против часовой стрелки. Тогда мы можем сказать, что умножение на i дает поворот на 90° относительно 0 или, если хотите, поворот на 270° относительно 0.
Геометрическая интерпретация умножения.
Чтобы полностью оправдать то, что мы собираемся увидеть, необходима тригонометрия, и это делается в необязательном разделе. А пока мы увидим результаты без обоснования. Мы видели два особых случая умножения, один на вещественные числа, что приводит к масштабированию, другой на 9.2317 и , что приводит к вращению. Общий случай представляет собой комбинацию масштабирования и поворота. Пусть z и w — точки комплексной плоскости C . Нарисуйте линии от 0 до z и от 0 до w . Длины этих линий являются абсолютными значениями | с | и | w | соответственно. Мы уже знаем, что длина строки от 0 до zw будет абсолютной величиной | ZW | что равно | г | | с |. (На диаграмме | z | составляет около 1,6, а | w | составляет около 2,1, поэтому | zw | должно быть около 3,4. Обратите внимание, что единичный круг заштрихован.) Что мы не делаем знать направление линии от 0 до zw.
Длины этих линий являются абсолютными значениями | с | и | w | соответственно. Мы уже знаем, что длина строки от 0 до zw будет абсолютной величиной | ZW | что равно | г | | с |. (На диаграмме | z | составляет около 1,6, а | w | составляет около 2,1, поэтому | zw | должно быть около 3,4. Обратите внимание, что единичный круг заштрихован.) Что мы не делаем знать направление линии от 0 до zw.
Ответ: «углы складываются». Мы определим направление линии от 0 до z по определенному углу, называемому аргументом of z , иногда обозначаемым arg( з ). Это угол, вершина которого равна 0, первая сторона — положительная действительная ось, а вторая сторона — линия от 0 до z. Другая точка w имеет угол arg( w ). Тогда произведение zw будет иметь угол, являющийся суммой углов arg( z ) + arg( w ). (На диаграмме arg( z ) составляет около 20°, а arg( w ) составляет около 45°, поэтому arg( zw ) должно быть около 65°.


