Физический класс | Законы постоянного тока. Электрический ток в металлах «

Понять природу электрического тока не так-то просто. Изучение этой темы позволит вам получить общие представления о постоянном электрическом токе, его законах. Вы научитесь собирать электрические цепи, выполнять измерения и простейшие расчеты.

 

Электрическим током считается любое упорядоченное движение заряженных частиц. В металлах такими частицами являются свободные электроны. Но, чтобы электроны заставить двигаться в определенном направлении, нужно в проводнике создать электрическое поле.

 

До открытия электрона в 1890 г. направление тока условно  рассматривалось как направление перемещения положительного заряда. Под действием электрического поля заряды начинают двигаться в область меньшего потенциала.  Движение зарядов длится до тех пор, пока потенциалы на концах проводника не станут равными. Хотя известно, что электрический ток в металлах создают свободные электроны, но до сих пор существует соглашение, в соответствии с которым

за направление тока принято движение положительных зарядов.

 

Чтобы электрический ток не прекращался длительное время, цепь должна содержать источник тока и быть замкнутой. Благодаря источнику тока, электродвижущая сила (ЭДС) обеспечивает постоянную разность потенциалов в цепи. Таким образом, в замкнутой цепи именно ЭДС поддерживает направленное движение зарядов.

 

Электрический ток характеризуется физической величиной – силой тока, а работа электрического поля на участке цепи – напряжением. Зависимость между силой тока и напряжением для металлов экспериментально установил в 1826 году Г. Ом.

 

При наличии источника тока закон Ома для замкнутой цепи записывается с учетом ЭДС, внешнего сопротивления цепи и внутреннего сопротивления источника тока.

 

 

Содержание

 

Условия существования электрического тока —>

Электронная теория проводимости металлов —>

Схема электрической цепи —>

Закон Ома для участка цепи —>

Закон Ома для замкнутой цепи —>

Закон Джоуля-Ленца —>

Закономерности последовательного и параллельного соединения проводников —>

Зависимость сопротивления металлов от температуры —>

Определение ЭДС и внутреннего сопротивления источника тока —>

Изучение последовательного и параллельного соединения проводников —>

 

Постоянный электрический ток. Законы постоянного тока

6

МУ составлены доц.Петренко Л.Г. 21.11.2000

Постоянный электрический ток, его характеристики и условия существования. Сила электрического тока. Вектор плотности тока. Электрическое сопротивление проводников. Сторонние силы. Электродвижущая сила. Разность электрических потенциалов, электрическое напряжение. Законы Ома и Джоуля-Ленца в интегральной и дифференциальной формах. Электрический ток в сплошной среде. Правила Кирхгофа.

В проводниках (твёрдых, жидких и газообразных), помещённых в электрическое поле, возникает электрический ток.

Электрический ток — это направленное, упорядоченное движение электрически заряженных частиц

. Такими частицами могут быть электроны или ионы (электронная или ионная проводимость). За направление электрического тока принято направление движения положительных электрических зарядов. Постоянный электрический ток — это ток, при котором за единицу времени через любое поперечное сечение проводника протекает одинаковый электрический заряд.

О наличии в цепи электрического тока судят по косвенным признакам — по магнитному, тепловому или химическому действию этого тока. Химическое действие не проявляется только

в металлах, тепловое действие — только в сверхпроводниках. Магнитное действие тока проявляется всегда. Фарадей говорил: «Нет действия более характерного для тока, чем его магнитное действие». Это явление лежит в основе работы электроизмерительных приборов.

Условия существования электрического тока — наличие электрического поля и свободных носителей заряда.

Для поддержания непрерывного тока должна существовать замкнутая цепь и устройство, разделяющее заряды и поддерживающее напряжение в цепи. Эти устройства называются источниками или генераторами тока.

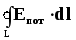Электрическое поле перемещает заряды от большего потенциала ₁ к меньшему ₂ (₁>₂). В замкнутой цепи потенциальные силы, осуществляющие это перемещение, не могут поддерживать постоянный электрический ток, так как = 0 (здесь — напряжённость электростатического поля,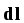— элемент длины контура). Для поддержания в цепи постоянного тока на каком-то её участке заряды должны перемещаться от меньшего потенциала ₂ к большему ₁. Это может происходить внутри источника тока и только под воздействием сил, имеющих не потенциальную природу, так называемых сторонних сил. Действие сторонних сил характеризуется электродвижущей (электроразделительной) силой — ЭДС. Мерой ЭДС является разность потенциалов на разомкнутых клеммах источника тока. ЭДС обозначается  и измеряется в вольтах [] = 1 В. В замкнутом проводящем контуре ЭДС равна работе сторонних сил по перемещению единичного положительного заряда вдоль всего контура :

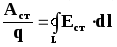 = , (1)

где 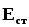— напряжённость поля сторонних сил,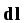— элемент длины контура.

Сторонние силы могут иметь химическую природу — гальванические элементы, аккумуляторы, электромагнитную

природу — электрогенераторы, фотоэлектрическую — фотоэлементы и т.д.

Физическая величина, характеризующая работу и электрических, и сторонних сил по перемещению единичного положительного заряда по замкнутому контуру, называется напряжением:

U = (₁ — ₂)  . (2)

Количественными характеристиками электрического тока являются сила тока и плотность тока.

Сила тока — скалярная величина, равная заряду, переносимому через поперечное сечение проводника за единицу времени

:

I = 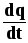. (3)

В СИ сила тока измеряется в амперах: [ I ] = 1A.

Плотность тока — векторная величина, определяемая силой тока, проходящего через единицу площади поперечного сечения s_ проводника:

J = 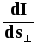. (4)

Вектор плотности тока ориентирован по направлению упорядоченного движения положительных зарядов и равен

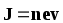, (5)

где n — концентрация носителей заряда, e — их заряд (элементарный заряд), 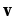— вектор скорости упорядоченного движения зарядов в проводнике. В СИ плотность тока измеряется в амперах, делённых на квадратный метр: [J ] = 1A/м

2.

Постоянный электрический ток возникает под действием постоянного напряжения и может существовать только в замкнутой цепи. При этом I и 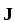не изменяются с течением времени.

В однородной среде — I = J s_, (6)

в неоднородной — I = 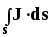. (7)

Условия существования постоянного электрического тока.

 

Для существования постоянного электрического тока необходимо наличие свободных заряженных частиц и наличие источника тока. в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля.

Источник тока — устройство, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля. В источнике тока на заряженные частицы в замкнутой цепи действуют сторонние силы. Причины возникновения сторонних сил в различных источниках тока различны. Например в аккумуляторах и гальванических элементах сторонние силы возникают благодаря протеканию химических реакций, в генераторах электростанций они возникают  при движении проводника в магнитном поле, в фотоэлементах — при действия света на электроны в металлах и полупроводниках.

Электродвижущей силой источника тока называют отношение работы сторонних сил к величине положительного заряда, переносимого от отрицательного полюса источника тока к положительному.

 

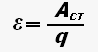
Основные понятия.

 

Сила тока — скалярная физическая величина, равная отношению заряда, прошедшего через проводник, ко времени, за которое этот заряд прошел.

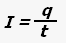
где I — сила тока, q — величина заряда (количество электричества), t — время прохождения заряда.

Плотность тока — векторная физическая величина, равная отношению силы тока к площади поперечного сечения проводника.

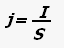
где j —плотность тока,  S — площадь сечения проводника.

Направление вектора плотности тока совпадает с направлением движения положительно заряженных частиц.

Напряжение — скалярная физическая величина, равная отношению полной работе кулоновских и сторонних сил при перемещении положительного заряда на участке к значению этого заряда.

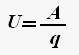
где A — полная работа сторонних и кулоновских сил,  q — электрический заряд.

Электрическое сопротивление — физическая величина, характеризующая  электрические свойства участка цепи.

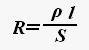
где ρ — удельное сопротивление проводника, l — длина участка проводника,  S — площадь поперечного сечения проводника.

 

Проводимостью называется величина, обратная сопротивлению

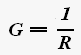
где  G — проводимость.

 

 

Законы Ома.

 

Закон Ома для однородного участка цепи.

Сила тока в однородном участке цепи прямо пропорциональна напряжению при постоянном сопротивлении участка  и обратно пропорциональна сопротивлению участка при постоянном напряжении.

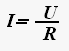
где U — напряжение на участке,  R — сопротивление участка.

 

 

Закон Ома для произвольного участка цепи, содержащего источник постоянного тока.

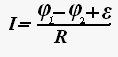
где   φ₁ — φ₂ + ε = U напряжение на заданном участке цепи, R — электрическое сопротивление  заданного участка цепи.

 

 

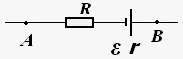
Закон Ома для полной цепи.

Сила тока в полной цепи равна отношению электродвижущей силы источника к сумме сопротивлений внешнего и внутреннего участка цепи.

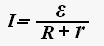
где R — электрическое сопротивление внешнего участка цепи,  r — электрическое сопротивление внутреннего участка цепи.

 

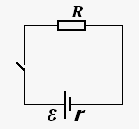
Короткое замыкание.

Из закона Ома для полной цепи следует, что сила тока в цепи  с заданным источником тока зависит только от сопротивления внешней цепи R.

Если к полюсам источника тока подсоединить проводник с сопротивлением  R<< r, то тогда только  ЭДС источника тока и его сопротивление будут определять  значение силы тока в цепи. Такое значение силы тока будет являться предельным для данного источника тока и называется током короткого замыкания. 

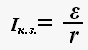
Электродвижущая сила. Любой источник тока характеризуется электродвижущей силой, или, сокращенно, ЭДС. Так, на круглой батарейке для карманного фонарика написано: 1,5 В. Что это значит?    Соедините проводником два металлических шарика, несущих заряды противоположных знаков. Под влиянием электрического поля этих зарядов в проводнике возникает электрический ток (рис.15.7). Но этот ток будет очень кратковременным. Заряды быстро нейтрализуют друг друга, потенциалы шариков станут одинаковыми, и электрическое поле исчезнет.

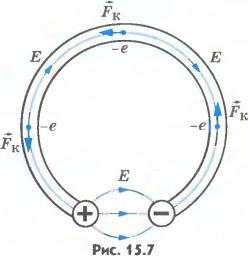
   Сторонние силы. Для того чтобы ток был постоянным, надо поддерживать постоянное напряжение между шариками. Для этого необходимо устройство (источник тока), которое перемещало бы заряды от одного шарика к другому в направлении, противоположном направлению сил, действующих на эти заряды со стороны электрического поля шариков. В таком устройстве на заряды, кроме электрических сил, должны действовать силы неэлектростатического происхождения (рис.15.8). Одно лишь электрическое поле заряженных частиц (кулоновское поле) не способно поддерживать постоянный ток в цепи.

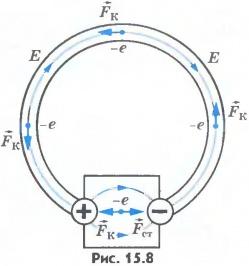
   Любые силы, действующие на электрически заряженные частицы, за исключением сил электростатического происхождения (т. е. кулоновских), называют сторонними силами.    Вывод о необходимости сторонних сил для поддержания постоянного тока в цепи станет еще очевиднее, если обратиться к закону сохранения энергии. Электростатическое поле потенциально. Работа этого поля при перемещении в нем заряженных частиц вдоль замкнутой электрической цепи равна нулю. Прохождение же тока по проводникам сопровождается выделением энергии — проводник нагревается. Следовательно, в цепи должен быть какой-то источник энергии, поставляющий ее в цепь. В нем, помимо кулоновских сил, обязательно должны действовать сторонние, непотенциальные силы. Работа этих сил вдоль замкнутого контура должна быть отлична от нуля. Именно в процессе совершения работы этими силами заряженные частицы приобретают внутри источника тока энергию и отдают ее затем проводникам электрической цепи.    Сторонние силы приводят в движение заряженные частицы внутри всех источников тока: в генераторах на электростанциях, в гальванических элементах, аккумуляторах и т. д.    При замыкании цепи создается электрическое поле во всех проводниках цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны от положительно заряженного электрода к отрицательному), а во внешней цепи их приводит в движение электрическое поле (см. рис.15.8).    Природа сторонних сил. Природа сторонних сил может быть разнообразной. В генераторах электростанций сторонние силы — это силы, действующие со стороны магнитного поля на электроны в движущемся проводнике.    В гальваническом элементе, например элементе Вольта, действуют химические силы. Элемент Вольта состоит из цинкового и медного электродов, помещенных в раствор серной кислоты. Химические силы вызывают растворение цинка в кислоте. В раствор переходят положительно заряженные ионы цинка, а сам цинковый электрод при этом заряжается отрицательно. (Медь очень мало растворяется в серной кислоте.) Между цинковым и медным электродами появляется разность потенциалов, которая и обусловливает ток в замкнутой электрической цепи.    Электродвижущая сила. Действие сторонних сил характеризуется важной физической величиной, называемой электродвижущей силой (сокращенно ЭДС).   Электродвижущая сила источника тока равна отношению работы сторонних сил при перемещении заряда по замкнутому контуру к величине этого заряда:

   Электродвижущую силу, как и напряжение, выражают в вольтах.    Можно говорить также об электродвижущей силе и на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единичного заряда) не во всем контуре, а только на данном участке. Электродвижущая сила гальванического элементаесть величина, численно равная работе сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории перемещения зарядов. Так, например, работа сторонних сил при перемещении заряда между клеммами источника тока вне самого источника равна нулю.    Теперь вы знаете, что такое ЭДС. Если на батарейке написано 1,5 В, то это означает, что сторонние силы (химические в данном случае) совершают работу 1,5 Дж при перемещении заряда в 1 Кл от одного полюса батарейки к другому. Постоянный ток не может существовать в замкнутой цепи, если в ней не действуют сторонние силы, т. е. нет ЭДС.

ПАРАЛЛЕЛЬНОЕ И ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ПРОВОДНИКОВ

Включим в электрическую цепь в качестве нагузки ( потребителей тока) две лампы накаливания, каждая из которых обладает каким-то определенным сопротивлением, и каждую из которых  можно заменить проводником с таким же сопротивлением.

ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ

Расчет параметров электрической цепи  при последовательном соединении сопротивлений:

1. сила тока во всех последовательно соединенных участках цепи одинакова 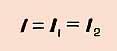2. напряжение в цепи, состоящей из нескольких последовательно соединенных участков,  равно сумме напряжений на каждом участке 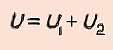3.сопротивление цепи, состоящей из нескольких последовательно соединенных участков,  равно сумме сопротивлений каждого участка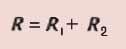

4. работа электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме работ на отдельных участках

А = А1 + А2 5. мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участка

Р = Р1 + Р2

ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ

 

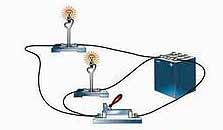
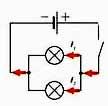Расчет параметров электрической цепи при параллельном соединении сопротивлений:

1. сила тока в неразветвленном участке цепи равна сумме сил токов во всех параллельно соединенных участках

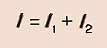
2. напряжение на всех параллельно соединенных участках цепи одинаково

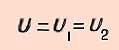  3. при параллельном соединении сопротивлений складываются величины, обратные сопротивлению :

( R — сопротивление проводника, 1/R — электрическая проводимость проводника)

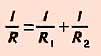Если в цепь включены параллельно только два сопротивления, то:

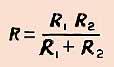
( при параллельном соединении общее сопротивление цепи меньше меньшего из включенных сопротивлений )

4. работа электрического тока в цепи, состоящей из параллельно соединенных участков,  равна сумме работ на отдельных участках: A=A1+A2 5. мощность электрического тока в цепи, состоящей из параллельно соединенных участков,  равна сумме мощностей на отдельных участках: P=P1+P2

Для двух сопротивлений: 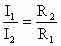 т.е. чем больше сопротивление, тем меньше в нём сила тока.

Закон Джоуля-Ленца — физический закон, который позволяет определить тепловое дествие тока в цепи, по этому закону: 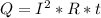, где I — сила тока в цепи, R — сопротивление, t — время. Данная формула была вычесленена путём создания цепи: гальванический эллемент (батарейка), резистор и амперметр. Резистор окунали в жидкость, в которую вставляли термометр и мерили темпиратуру. Вот так они и вывели свой закон и навсегда себя впечатали в историю, но даже без их опытов можно было вывести этот же закон:

U=A/q   A=U*q=U*I*t=I^2*R*t   но даже не смотря на это честь и хвала этим людям.

Закон Джоуля Ленца определяет выделенное количество тепла на участке электрической цепи обладающей конечным сопротивлением при прохождении тока через нее. Обязательным условием является тот факт, что на этом участке цепи должны отсутствовать химические превращения.

РАБОТА ЭЛЕКТРИЧЕСКОГО ТОКА

Работа электрического тока показывает, какая работа была совершена электрическим полем при перемещении зарядов по проводнику.

Зная две формулы: I = q/t ….. и ….. U = A/q  можно вывести формулу для расчета работы электрического тока: 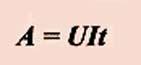Работа электрического тока равна произведению силы тока на напряжение и на время протекания тока в цепи.

Единица измерения работы электрического тока в системе СИ: [ A ] = 1 Дж = 1A. B . c

НАУЧИСЬ, ПРИГОДИТСЯ !  При расчетах работы электрического тока часто применяется  внесистемная кратная единица работы электрического тока: 1 кВт.ч (киловатт-час).

1 кВт.ч = ………..Вт.с = 3 600 000 Дж

В каждой квартире для учета израсходованной электроэнергии устанавливаются специальные приборы-счетчики электроэнергии, которые показывают работу электрического тока,  совершенную за какой-то отрезок времени при включении различных бытовых электроприборов.  Эти счетчики показывают работу электрического тока ( расход электроэнергии) в «кВт.ч».

Необходимо научиться рассчитывать стоимость израсходованной электроэнергии! Внимательно разбираемся в решении задачи на странице 122 учебника (параграф 52) ! 

МОЩНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА

Мощность электрического тока показывает работу тока, совершенную в единицу времени и равна отношению совершенной работы ко времени, в течение которого эта работа была совершена.

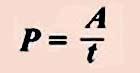
(мощность в механике принято обозначать буквой N, в электротехнике — буквой Р) так как А = IUt, то мощность электрического тока равна:

или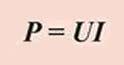 

Единица мощности электрического тока в системе СИ:

[ P ] = 1 Вт (ватт) = 1 А . B

 Законы Кирхгофа – правила, которые показывают, как соотносятся токи и напряжения в электрических цепях.Эти правила были сформулированы Густавом Кирхгофом в 1845 году. В литературе часто называют законами Кирхгофа, но это не верно, так как они не являются законами природы, а были выведены из третьего уравнения Максвелла при неизменном магнитном поле. Но все же, первое более привычное для них название, поэтому и мы будет их называть, как это принято в литературе – законы Кирхгофа.

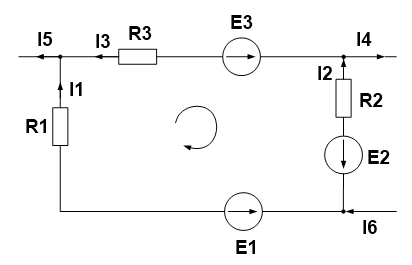
   Первый закон Кирхгофа – сумма токов сходящихся в узле равна нулю. 

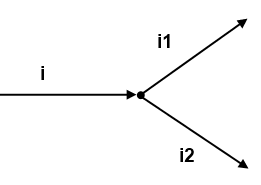
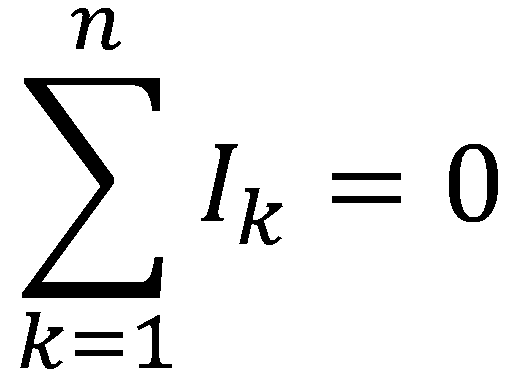
       Давайте разбираться. Узел это точка, соединяющая ветви. Ветвью называется участок цепи между узлами. На рисунке видно, что ток i входит в узел, а из узла выходят токи i₁ и i₂. Составляем выражение по первому закона Кирхгофа, учитывая, что токи, входящие в узел имеют знак плюс, а токи, исходящие из узла имеют знак минус i-i₁-i₂=0. Ток i как бы растекается на два тока поменьше и равен сумме токов i₁ и i₂ i=i₁+i₂. Но если бы, например, ток i₂входил в узел, тогда бы ток I определялся как i=i₁-i₂. Важно учитывать знаки при составлении уравнения.

   Первый закон Кирхгофа это следствие закона сохранения электричества: заряд, приходящий к узлу за некоторый промежуток времени, равен заряду, уходящему за этот же интервал времени от узла, т.е. электрический заряд в узле не накапливается и не исчезает.

    Второй закон Кирхгофа – алгебраическая сумма ЭДС, действующая в замкнутом контуре, равна алгебраической сумме падений напряжения в этом контуре. 

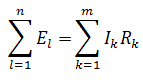
 Напряжение выражено как произведение тока на сопротивление (по закону Ома). 

 

  В этом законе тоже существуют свои правила по применению. Для начала нужно задать стрелкой направление обхода контура. Затем просуммировать ЭДСи напряжения соответственно, беря со знаком плюс, если величина совпадает с направлением обхода и минус, если не совпадает. Составим уравнение по второму закону Кирхгофа, для нашей схемы. Смотрим на нашу стрелку, E₂ и Е₃совпадают с ней по направлению, значит знак плюс, а Е₁ направлено в противоположную сторону, значит знак минус. Теперь смотрим на напряжения, ток I₁ совпадает по направлению со стрелкой, а токи I₂ и I₃ направлены противоположно. Следовательно:

              -E₁+E₂+E₃=I₁R₁-I₂R₂-I₃R₃

   На основании законов Кирхгофа составлены методы анализа цепейпеременного синусоидального тока. Метод контурных токов – метод основанный на применении второго закона Кирхгофа и метод узловых потенциаловоснованный на применении первого закона Кирхгофа.

определения и формулы :: SYL.ru

Закон Ома был впервые сформулирован немецким физиком и математиком Георгом Симоном Омом. Закон Ома является основным законом для электрических цепей с постоянным током. Он устанавливает связь между напряжением или падением потенциала, силой тока и сопротивлением в цепи. Рассмотрим подробнее закон Ома и другие основные законы постоянного тока.

Историческая справка

Георг Симон Ом родился в городе Эрлангене (Германия) 16 марта 1789 года в протестантской семье. С раннего детства он начал работать в слесарной мастерской своего отца. Карьера физика началась у Ома в Политехническом университете Нюрнберга. До конца своих дней он преподавал физику в университете Мюнхена.

Главной заслугой Ома в физике является то, что он ввел и описал такую физическую величину, как электрическое сопротивление. Он впервые сформулировал в математическом виде взаимосвязь между разницей потенциалов, силой тока и электрическим сопротивлением в цепи, за что единица сопротивления была названа по его фамилии.

Новые идеи Ома не сразу приняло мировое научное сообщество, лишь в 1841 году Королевское Общество в Лондоне наградило Ома медалью Копли, а Мюнхенский университет в 1849 году выделил ему кафедру физики.

Ом на протяжении своей научной деятельности занимался не только электрическими цепями. В 1840 году он изучал звуковые волны, а с 1852 года занимался оптикой, в частности, феноменом интерференции. Умер ученый в Мюнхене 6 июля 1854 года.

Эксперименты Ома

Перед тем как Ом изложил свой знаменитый закон для постоянного тока, другие ученые провели множество экспериментов с электрическими цепями. Следует отметить эксперименты британца Генри Кавендиша, который исследовал поведение банок Лейдена в 1781 году, но так и не смог опубликовать свои выводы.

В настоящее время физики располагают инструментами, которые позволяют с необходимой точностью измерить любые параметры электрической цепи, в конце XVIII-начале XIX века таких приборов не было, что создавало сложности для открытия Омом закона для постоянного тока.

Именно поэтому Ом решил самостоятельно изготовить такой прибор. В частности, он использовал крутильные весы Кулона, но усовершенствовал их, добавив к ним магнитный элемент. При этом ученый использовал открытие Гансом Христианом Эрстедом в 1819 году того факта, что проводник с током оказывает силовое воздействие на намагниченную иглу, находящуюся поблизости от него. Используя свои новые крутильные весы, проводящие кабели различной длины, источник электрического тока и сосуды с ртутью, Ом смог измерить уменьшение силы, с которой проводник с током действует на иглу при увеличении длины этого проводника.

В результате этих экспериментов ученый получил следующую математическую зависимость: V = 0,41lg (1+x), где V — напряжение в цепи, x — длина проводника с током. Это выражение впоследствии привело ученого к формулировке закона постоянного тока.

Понятие о силе электрического тока

Прежде чем рассматривать закон Ома для постоянного тока, введем понятие силы тока. Некоторые частицы в природе обладают так называемым электрическим зарядом. Понятие силы тока непосредственно связано с перемещением этих заряженных частиц, которые в большинстве случаев являются либо ионами, либо электронами. Под силой тока в физике понимают количество заряда, который проходит через сечение проводника за единицу времени, что математически выражается в виде следующего выражения: I = dq/dt.

Единицей силы тока в СИ является ампер (А), 1 А — это такая сила тока, при которой через проводник за 1 с переносится заряд в 1 Кл. Поскольку положительные и отрицательные заряды движутся в противоположных направлениях в одном и том же электрическом поле, то силу тока принято определять по направлению движения положительных зарядов.

Скорость движения заряженных частиц в электрическом поле

В физике закон постоянного тока формулируется для I=const, а это означает, что каждая частица-носитель электрического заряда должна двигаться с постоянной скоростью. Однако чтобы существовал электрический ток, необходимо наличие заряженных частиц, способных двигаться, а также существование электрического поля. Последнее действует на электрический заряд q с определенной силой. Эта сила определяется по формуле: F = q*E, здесь E — напряженность электрического поля.

Согласно второму закону Ньютона, заряженная частица приобретает ускорение a = q*E/m, где m — масса частицы. Поскольку все величины в этом выражении являются постоянными, то и ускорение также будет неизменным и отличным от нуля. Все эти рассуждения справедливы для случая движения заряда в пустом пространстве, если же он движется в какой-либо среде, то со стороны среды возникает некоторое сопротивление.

Например, движущийся под действием электрической силы в металлическом проводнике электрон испытывает постоянные столкновения с ионами, образующими металлическую кристаллическую решетку. Эти столкновения приводят к тому, что электрон начинает двигаться с постоянной скоростью, которая называется скоростью дрейфа. Именно во взаимодействии электрона с ионами решетки заключается природа электрического сопротивления.

Движение электрона в металлическом проводнике можно сравнить с движением капли дождя в воздухе, поскольку эта капля не падает с ускорением свободного падения, а совершает равномерное движение из-за воздействия силы сопротивления со стороны воздуха.

Локальный закон Ома

В каждой школе начинают изучать в 8 классе законы постоянного тока. При этом формулируют закон Ома сначала в локальной форме. Чтобы это сделать, возьмем для примера металлический проводник.

В металле валентные электроны, то есть электроны, находящиеся на внешних энергетических оболочках атомов, слабо связаны с атомными ядрами, поэтому в объемном материале они не принадлежат конкретному атомному ядру, а являются свободными или обобществленными. Каждый такой электрон при комнатной температуре хаотично движется в металлическом кристалле. Это движение подобно движению молекулы в газе. Скорость теплового движения электрона велика, она составляет порядка 10⁶ м/с. Поскольку движение является равновероятным во всех направлениях, то оно не приводит к возникновению электрического тока.

Ток появляется, если этот проводник поместить в электрическое поле. В результате этого электрон приобретает дрейфовую скорость, порядок величины которой составляет 10^-6 м/с. В результате сила электрического тока через площадь сечения A запишется в виде следующей формулы: I = n*q²*E*t*A/m_e, здесь n — количество электронов, которые проходят через площадку A за время t, которое является временем между двумя столкновениями электрона с ионами решетки, m_e — масса электрона.

Полученное выражение можно переписать в виде J = I/A = σ*E, где J — плотность электрического тока, σ — свойство материала, которое называется электрической проводимостью. Это выражение для плотности тока носит название закона Ома для постоянного тока в локальной форме.

Закон Ома в макроскопической форме

В школе в 8 классе закон постоянного тока также рассматривается в макроскопической форме. Его легко можно получить из соответствующего закона в локальной форме. Для этого необходимо определить напряжение или падение потенциала в электрической цепи в виде следующего выражения: ΔV = E*l, где l — длина проводника с током, а ΔV — напряжение на его концах.

В результате закон Ома примет вид: ΔV = I*l/(σ*A) = R*I, где R — электрическое сопротивление. Как видно из закона постоянного электрического тока в макроскопической форме, величина R является обратной величине электрической проводимости σ, то есть чем лучше материал проводит ток, тем меньше его электрическое сопротивление. Также важно заметить, что в то время как σ является свойством материала, из которого сделан проводник, R является свойством конкретного проводника, и зависит не только от материала, но и от геометрических его параметров (длины и площади сечения).

Применимость и важность классического закона Ома

Закон Ома в классической или макроскопической форме записывается в виде: V = I*R. Для металлов R является постоянной величиной, независимо от силы тока, проходящего через проводник. Однако, в некоторых материалах, например, в полупроводниках, это не так. Материалы, в которых электрическое сопротивление является постоянной величиной, называются линейными или омическими. Для них вольт-амперная характеристика, то есть функция зависимости напряжения от силы тока U(I) является линейной.

Закон Ома не может считаться фундаментальным законом природы, поскольку он справедлив только для определенного класса материалов, главным образом, это металлы. Однако, он играет важную роль в физике и в повседневной жизни, поскольку позволяет простым образом определить важные физические величины в электрической цепи. В частности, благодаря закону Ома для цепи постоянного тока вычисляют потери электроэнергии при ее передаче и потреблении. Закон Ома также используют для вычисления необходимого значения сопротивления, которое следует включить в электрическую цепь, чтобы она выполняла свои функции с максимальным КПД.

Зависимость удельного сопротивления от температуры для омических материалов

Рассматривая законы цепей постоянного тока, следует упомянуть о том, как изменяется сопротивление с увеличением температуры. По аналогии с электрической проводимостью материала в физике вводят понятие удельного электрического сопротивления ρ, оно с сопротивлением связано следующей формулой: R = l*ρ/A.

Эмпирическим путем установлено, что для омических материалов ρ подчиняется следующей зависимости от температуры: ρ = ρ₀*[1+α(T-T₀)+β(T-T₀)²+…], здесь ρ₀ — удельное сопротивление данного материала при температуре T₀, которую часто полагают равной 20°C.

Для металлических материалов в интервале от 0 до 200 °C удельное сопротивление линейно зависит от температуры, то есть ρ = ρ₀*[1+α(T-T₀)], где α — коэффициент температурного сопротивления, который для металлов является положительной величиной, это говорит о том, что электрическое сопротивление линейно увеличивается с ростом температуры для металлов. Такое поведение связано с уменьшением расстояния, которое проходит электрон между двумя столкновениями с ионами решетки, при увеличении температуры.

Интересно отметить, что у полупроводников удельное сопротивление уменьшается с ростом температуры. Этот факт связан с увеличением количества носителей электрического тока при нагреве полупроводникового материала, например, кремния или германия.

Законы Кирхгофа

В школах в 10 классе законы постоянного тока не ограничиваются только законом Ома. По школьной программе также изучают законы Кирхгофа. Существуют два закона Кирхгофа для постоянного тока. Основаны они на законе сохранения энергии и заряда в электрической цепи. Ниже приведены формулировки для обоих законов Кирхгофа:

1. Для любого узла электрической цепи сумма всех токов, входящих в этот узел, равна сумме токов, выходящих из него. Эта формулировка отражает закон сохранения заряда.
2. В любом замкнутом контуре цепи сумма всех падений напряжения на элементах этого контура равна напряжению, которое подводится к нему. Второй закон Кирхгофа отражает сохранение потенциальной энергии в электрической цепи.

Записаны впервые эти законы были в 1846 году. В настоящее время они широко используются в электрической инженерии и электронике для определения неизвестных токов, напряжений и сопротивлений в цепях. Отметим, что в случае наличия ненулевого электрического сопротивления в цепи R, часть электрической энергии будет превращаться в тепло Q, которое называется джоулевским и вычисляется по формуле Q = I²Rt, где t — время протекания тока по элементу цепи с сопротивлением R.

Практическое применение законов Ома и Кирхгофа

Приведем пример задачи на законы постоянного тока. На рисунке ниже приведен пример электрической цепи, которая состоит из двух контуров, двух источников напряжения и 5 резисторов с различным сопротивлением. Задача заключается в нахождении неизвестных токов I_x и I_y. Сразу следует сказать, что направление в обоих контурах выбрано произвольно, в данном случае по часовой стрелке.

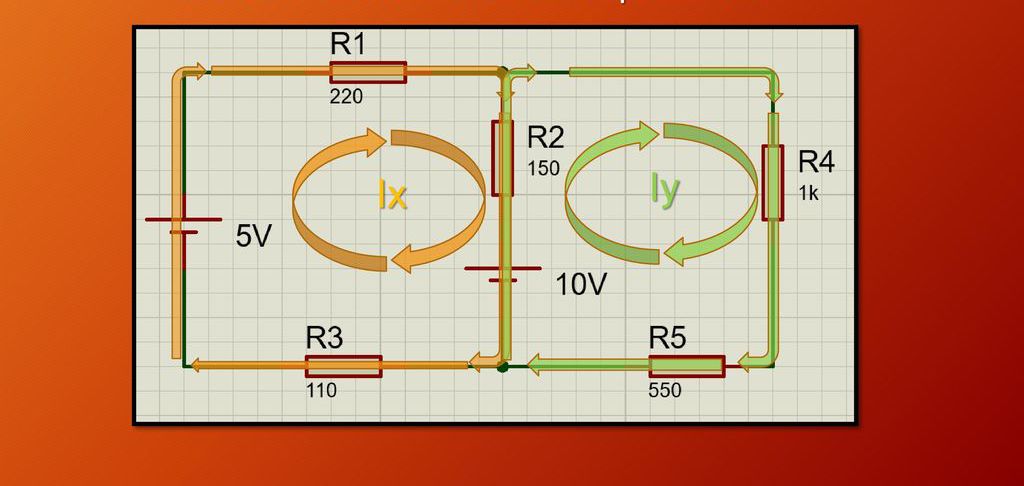
Далее необходимо рассмотреть каждый контур по отдельности. Для начала обратим внимание на контур с неизвестным током I_x. Для выбранного контура необходимо применить второй закон Кирхгофа, то есть закон, который говорит о равенстве падений напряжения на всех резисторах и напряжения питания от всех источников тока. Применяя этот закон, получаем: 5-10 = I_x*R₁+(I_x-I_y)*R₂+I_x*R₃. При составлении этого выражения учитывался знак выбранного направления силы тока I_x, как положительного направления, поэтому разность потенциалов на источнике в 5 В является положительной, а на источнике в 10 В — отрицательной. Также отметим, что рассматривая данный контур, также необходимо учитывать ток I_y, который течет согласно введенным обозначениям через резистор R₂.

Теперь получим аналогичное уравнение для второго контура с неизвестным током I_y. Это выражение будет иметь вид: 10 = (I_y-I_x)*R₂+I_y*R₄+I_y*R₅. Во втором контуре существует только один источник питания (10 В), поэтому только он входит в полученное из 2-го закона Кирхгофа выражение.

Таким образом, получено два уравнения, в которых имеется две неизвестных: I_x и I_y. Осталось объединить эти выражения в систему линейных уравнений, и решить ее. Приведенный ниже рисунок показывает рассматриваемую электрическую цепь и полученную систему уравнений для определения неизвестных токов.

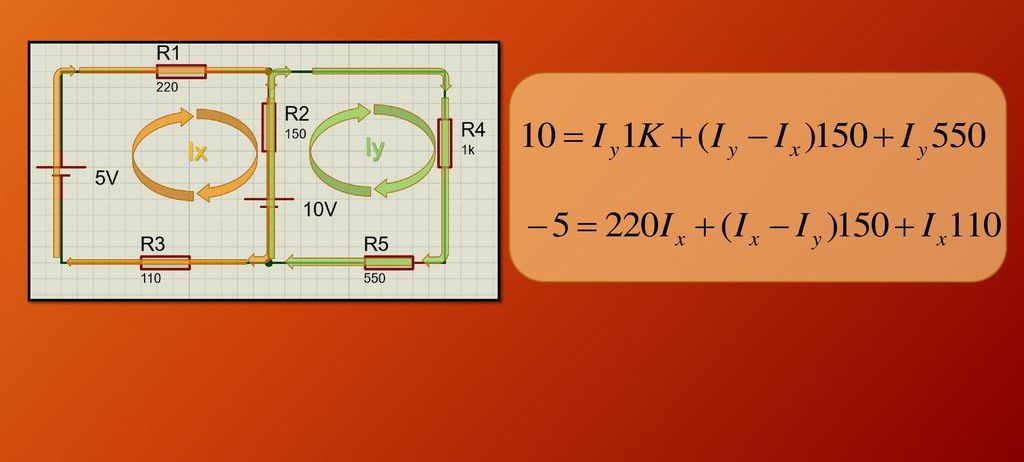
Решая систему уравнений, получаем, что I_x = -0,00882 А = -8,82 мА, а I_y = 0,0051 А = 5,1 мА. Знак «минус» говорит о том, что в действительности ток течет в направлении, которое противоположно выбранному. В итоге через резисторы R₁, R₃ течет ток 8,82 мА, через резисторы R₄, R₅ — 5,1 мА, а через резистор R₂ — I_y-I_x = 13,92 мА.

Законы постоянного тока в физике

Основные законы постоянного тока

Для того чтобы существовал электрический ток необходимо наличие его свободных носителей, которые могут перемещаться упорядоченно и электрического поля, которое имеет восполняемую энергию, заставляющую двигаться свободные заряды. Количественно электрический ток измеряют при помощи силы тока.

Сила тока- это физическая величина, равная заряду (q), который проходит через поперечное сечение в единицу времени:

   

Если сила тока постоянна во времени (по величине и направлению), то ток называют постоянным. Для постоянного тока его сила вычисляется как:

   

Закон Ома для однородного участка цепи

Эмпирически было установлено, что сила тока (), текущая по однородному проводнику прямо пропорциональна напряжению () на концах проводника:

   

где — сопротивление проводника, зависящее от материала ( — удельное сопротивление проводника), размеров и геометрии проводника ( — длина проводника, S — площадь поперечного сечения проводника). Однородным участком цепи называют участок цепи, который не имеет источника тока (), — потенциалы на концах участка цепи; — ЭДС источника.

При последовательном соединении сопротивлений выполняются следующие соотношения:

В случае параллельного соединения проводников имеем:

Закон Ома можно записать в дифференциальной форме:

   

где — плотность тока в точке проводника; — напряженность электрического поля в той же точке, что и плотность тока (данный закон выполняется и для переменных полей).

Закон Ома для неоднородного участка цепи

Если на участке цепи имеется ЭДС (), разность потенциалов на концах участка , то сила тока на таком участке равна:

   

где — полное сопротивление цепи; — внутреннее сопротивление источника; — внешнее сопротивление цепи.

Закон Джоуля — Ленца

Если ток идет по неподвижному проводнику, то количество тепла, выделяемое данным элементом проводника () равно:

   

Выражение (12) закон Джоуля — Ленца в интегральном виде.

В дифференциальной форме этот закон запишется как:

   

Примеры решения задач

Постоянный электрический ток. Закон Ома для участка цепи. Работа и мощность постоянного тока. Закон Джоуля-Ленца. Закон Ома для полной цепи. Закон электролиза Фарадея. Электрические цепи — последовательное и параллельное соединение. Правила Кирхгофа.

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа.  / / Постоянный электрический ток. Закон Ома для участка цепи. Работа и мощность постоянного тока. Закон Джоуля-Ленца. Закон Ома для полной цепи. Закон электролиза Фарадея. Электрические цепи — последовательное и параллельное соединение. Правила Кирхгофа. Поделиться:    Постоянный электрический ток. Закон Ома для участка цепи. Работа и мощность постоянного тока. Закон Джоуля-Ленца. Закон Ома для полной цепи. Закон электролиза Фарадея. Электрические цепи — последовательное и параллельное соединение. Правила Кирхгофа. Электрический ток: Закон Ома для участка цепи: Сила тока I на участке цепи прямо пропорциональна приложенному напряжению U  и обратно пропорциональна сопротивлению проводника R: Работа и мощность постоянного тока, ЭДС: Закон Джоуля-Ленца: Количество теплоты Q, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику : Закон Ома для полной цепи: Закон электролиза Фарадея: Электрические цепи — последовательное и параллельное соединение: