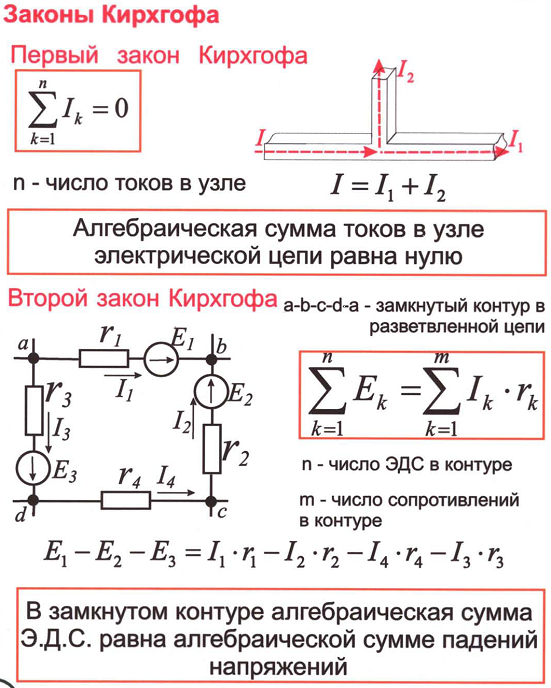
Первый закон Кирхгофа
- Details
- 26 November 2016
Господа, всем здравствуйте!
Сегодняшний разговор пойдет про законы Кирхгофа первый закон Кирхгофа. Зачеркивание здесь стоит неспроста. Дело в том, что первоначально я планировал рассказать сразу про оба закона (или правила, кому как больше нравится) Кирхгофа в одной статье. Однако когда статья была практически написана за исключением некоторых рисуночков и еще пары моментов по мелочи, я обнаружил, что она получилась какой-то слишком большой. Поэтому я решил разделить эту статью на две. С одной стороны, это позволит вам легче усвоить материал, потому что небольшие порции легче осмысляются. С другой стороны, это позволит мне спокойно дорисовать картинки, пока вы читаете эту статью. Одни плюсы, в общем .
Итак, первый закон Кирхгофа… Звучит не очень, не правда ли? Чисто психологически какая-то сложность проскальзывает в этих звуках.
Однако спешу вас успокоить. На самом деле законы Кирхгофа весьма просты и не имеют ничего общего с великими и ужасными гипотезами математиков. Всего этих законов два. Первый совсем простой, второй чуть потруднее. Поскольку обычно дела лучше начинать с простого и к тому же здесь он по счастливому стечению обстоятельств идет под номером один, с первого закона мы и начнем.
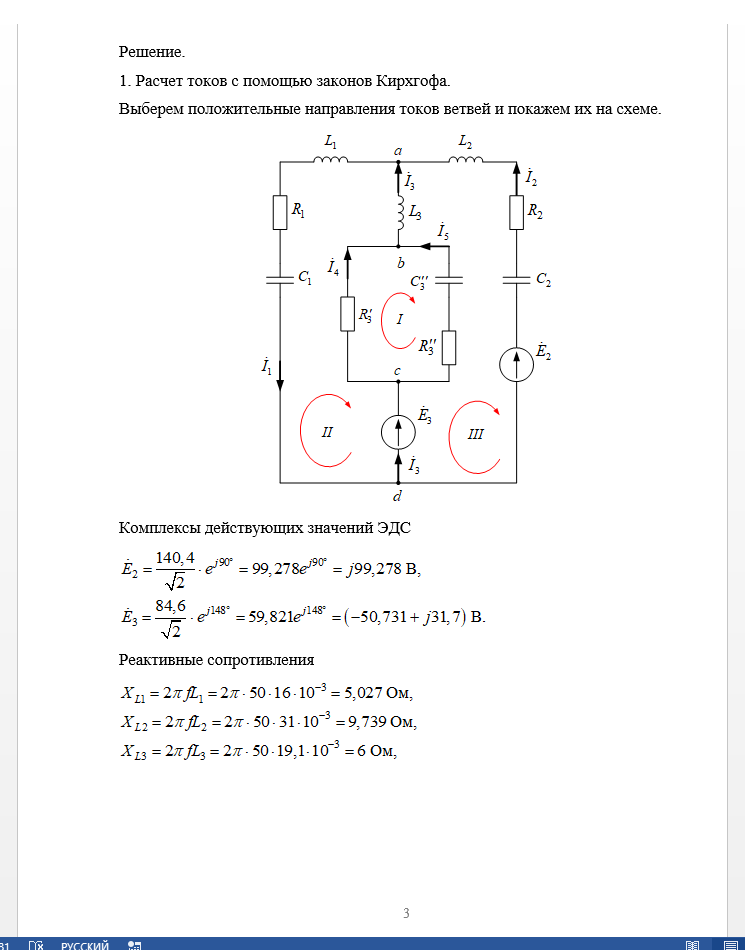
Но прежде чем говорить про первый закон Кирхгофа введем понятие узла цепи. Узел цепи – это точка, в которой сходится несколько проводников (больше двух). Допустим, это может быть клемма батарейки, если от нее запитано несколько потребителей. Или точка соединения нескольких нагрузок в электрической схеме. Дальше по рисункам это будет более понятно. Итак, 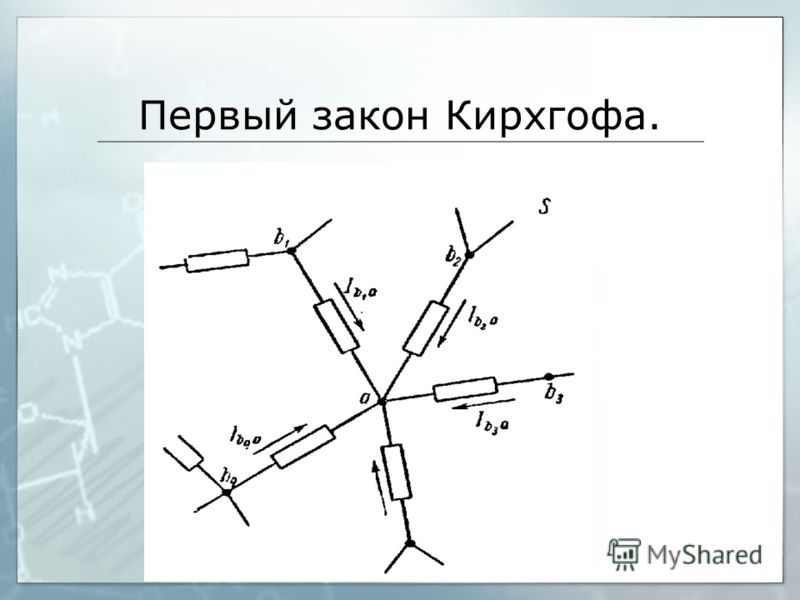
Давайте разберем подробнее, что же здесь подразумевается под понятием алгебраическая сумма и почему она равна нулю в данном случае. Для этого давайте посмотрим на рисунок 1, где изображен как раз-таки тот самый узел, про который речь шла абзацем выше. Сам узел здесь изображен большой жирной точкой оранжевого цвета.
Рисунок 1 – Узел цепи
Как мы видим, в этом узле сходится аж 5 проводников: два красных и три синих. В красных проводниках токи I1 и I2 текут в направлении к узлу, они втекают в узел. В синих проводниках токи I3, I4, I5 текут в направлении от узла, они вытекают из узла. Как мы помним из статьи про силу тока, если течет ток I, то через сечение проводника за время Δt проносится некоторый заряд Δq.
Будем считать, что втекающие токи приносят в узел заряд
А теперь внимание, господа, важный момент. Заряды в узлах не накапливаются. Если бы это было иначе, то потенциал бы узла не оставался бы постоянным, он бы все время рос с течением времени в ту или иную сторону (в плюс или в минус) причем чуть ли не до бесконечности. Однако на практике этого нет. То есть, если перевести эту фразу на язык математики, получается, что изменение заряда
Заряды в узлах не накапливаются. Если бы это было иначе, то потенциал бы узла не оставался бы постоянным, он бы все время рос с течением времени в ту или иную сторону (в плюс или в минус) причем чуть ли не до бесконечности. Однако на практике этого нет. То есть, если перевести эту фразу на язык математики, получается, что изменение заряда
Сократив равенство на Δt, получим
Господа, вот это вот самое равенство и есть первый закон Кирхгофа! То, что мы называли алгебраической суммой токов как раз написано выше, и она равна нулю. То есть алгебраическая сумма здесь – это сумма с учетом знака тока, причем втекающим токам присваивается знак плюс, а вытекающим – минус. Можно и наоборот, не суть. Правило на самом деле довольно полезное в жизни. Для любителей труЪ-математических записей первый закон Кирхгофа можно представить вот в таком виде
где Ik – ток (с учетом знака) в ветви с номеров k, причем всего этих ветвей 
В сущности, все то же самое, только под общим значком суммы, который, вне всякого сомнения, например, при ответе на экзамене, добавит солидности к вашему ответу и даст вам плюс десять к карме .
Если мы перенесем все слагаемые со знаком минус в правую часть, то получится
То есть, выражаясь простым языком, сколько тока втекло в узел, столько из него и вытечет.
Например, если в узел втекает 10 ампер и 15 ампер по двум проводам (в сумме 25 ампер), то из него может вытекать, скажем, 5 ампер, 7 ампер и 13 ампер по трем проводам (в сумме тоже 25 ампер). Но никак не 15 ампер, 12 ампер и 18 ампер. Как именно распределятся токи по этим трем проводам – это зависит от нагрузок на этих линиях и это уже совсем другой вопрос. Его мы рассмотрим чуть позже и обязательно научимся считать эти токи.
Для запоминания первого закона Кирхгофа и еще лучшего его осмысления нам на помощь придет все та же аналогия с водопроводом, которой мы уже пользовались в предыдущих статьях. Представим себе, что узел электрической цепи – это типа водопроводной крестовины. Такой, как изображена на рисунке 2.
Представим себе, что узел электрической цепи – это типа водопроводной крестовины. Такой, как изображена на рисунке 2.
Рисунок 2 – Крестовина
Обычно подвод воды к крестовине осуществляется по одной трубе, и вода распределяется на трех потребителей. Ровно такая крестовина стоит у меня на даче. К ней подходит труба от магистрального водопровода и эта крестовина раздает водичку на уличную раковину и на два шланга, которые предназначены для орошения ближней и дальней зоны владений. Так вот, что бы там ни было, при любом раскладе я смогу выжать с выходов крестовины ровно столько воды, сколько в нее втечет. Если на вход крестовины поступает 20 литров воды в минуту, то это значит, что я могу получить, например, по 8 литров воды в минуту с двух шлангов для полива и еще 4 литра в минуту лить на себя в раковине (в сумме все те же 20 литров в минуту). Либо, например, я могу закрыть раковину и один из шлангов и получать все эти 20 литров воды в минуту из второго шланга.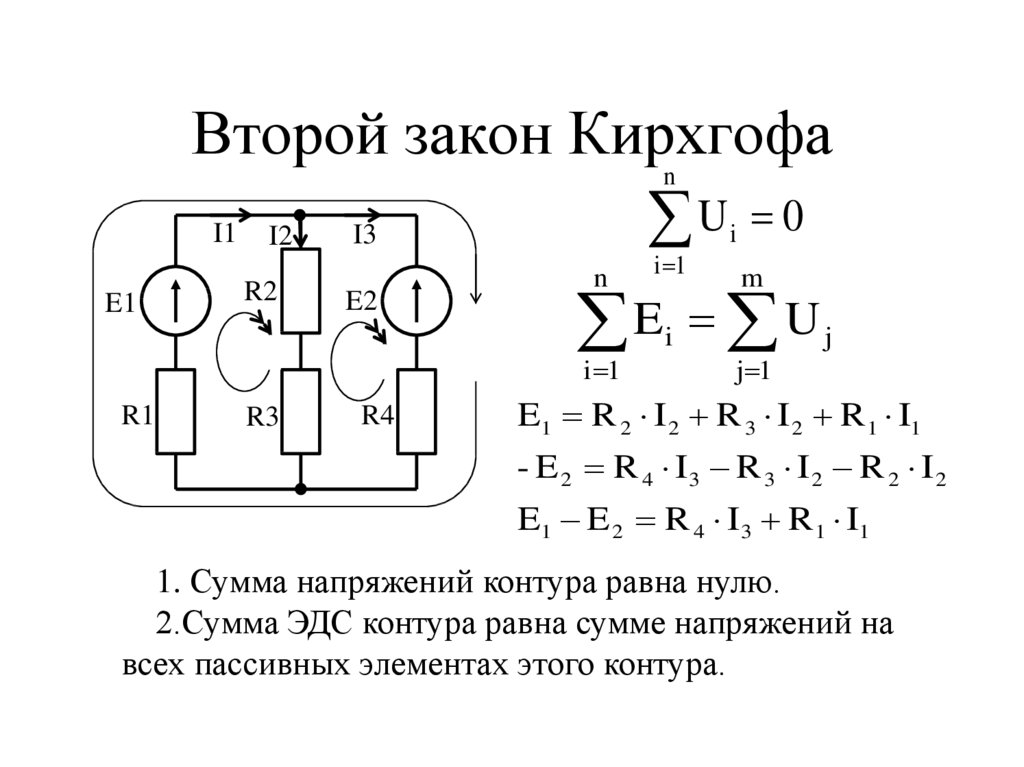
Итак, господа, на этом интересном симбиозе электрики и сантехники закончим нашу статью. Надеюсь, она была вам полезна. Огромной вам всем удачи и пока!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Social button for Joomla
Формулы для расчета электрических цепей постоянного тока
3.2 Второй закон Кирхгофа
Второй закон Кирхгофа применяется к контурам и
формулируется следующим образом: алгебраическая сумма падений напряжений по
любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих
вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений
равно нулю.
Для постоянных напряжений:
Для переменных напряжений:
Иными словами, при обходе цепи по контуру, потенциал,
изменяясь, возвращается к исходному значению.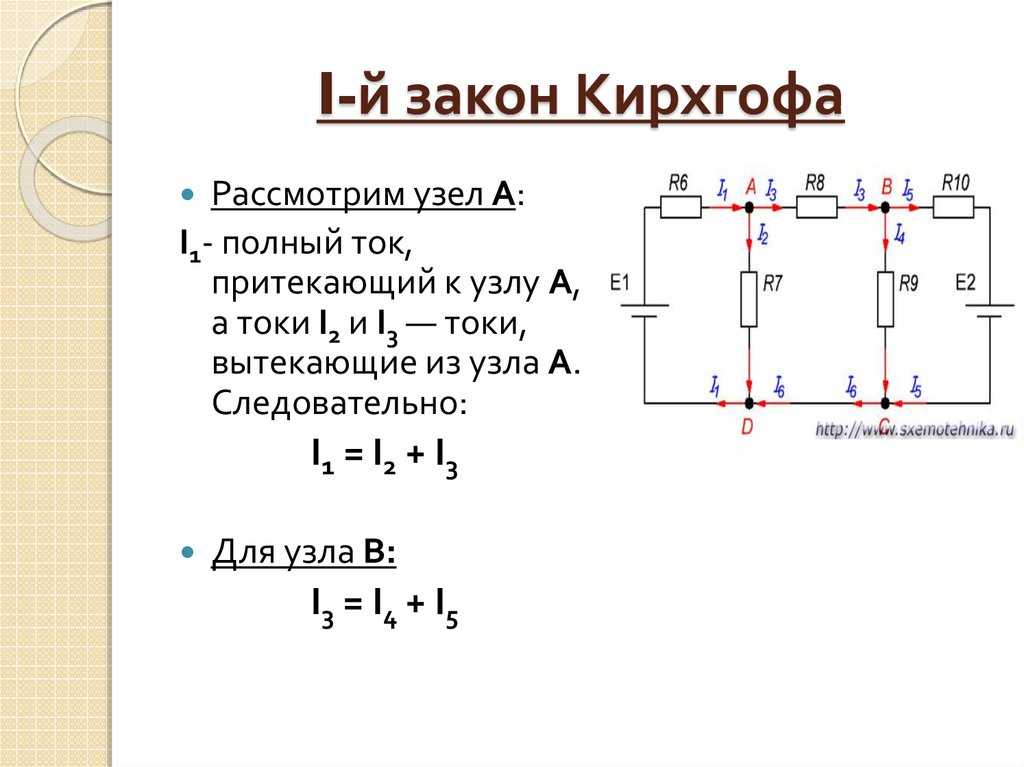 Если цепь содержит m ветвей, из
Если цепь содержит m ветвей, из
которых содержат источники тока ветви в количестве mi, то она
описывается m-mi— (у — 1) уравнениями напряжений.
Частным случаем второго правила для цепи, состоящей из одного контура, является
закон Ома для этой цепи.
Рисунок 2 — Схема электрическая принципиальная расчетной цепи
В итоге на схеме, рисунок 2, остаётся четыре узла, так как узел есть
точка цепи, в которой сходятся не менее трех ветвей. Если в месте пересечения
двух линий на электрической схеме поставлена точка, то в этом месте есть
электрическое соединение двух линий, в противном случае его нет. Узел, в
котором сходятся две ветви, одна из которых является продолжением другой,
называют устранимым или вырожденным узлом.
Рассчитываю количество уравнений по первому и второму закону Кирхгофа.
у = 5 — число узлов;
в = 6 — число ветвей;
вит = 0 — число ветвей с источником тока.
Количество уравнений по первому закону Кирхгофа n1 = у −1 = 4 Количество уравнений по второму
закону Кирхгофа n2 = в − вит −(у − 1) = 4
Согласно первому заданию составляю системы уравнений по первому и второму
законам Кирхгофа. По 1-му закону Кирхгофа для (у-1) узлов схемы, с учетом токов
По 1-му закону Кирхгофа для (у-1) узлов схемы, с учетом токов
от источников тока, где y —
число узлов схемы. Уравнение для последнего узла не составляют, т.к. оно
совпало бы с уравнением, полученным при суммировании уже составленных уравнений
для предыдущих узлов (т.е. линейно-независимых уравнений — (y-1)). При составлении уравнений
следуют правилу: если ток выходит из узла, то его записывают со знаком
«-«, если входит — то со знаком «+».
Уравнения по первому закону Кирхгофа:
1) I1 + I2— I3 = 0 (по 1 точке)
) -I1 — I4 + I5 = 0
(по 2 точке)
) I3 — I4 — I6 = 0 (по 3 точке)
) -I2 — I5 — I6 = 0 (по 4 точке)
Для составления уравнений по второму закону Кирхгофа, используется
нарисованная схема, показанная на рисунке 3.
Рисунок 3 — Схема электрическая принципиальная расчетной цепи
Уравнения по второму закону Кирхгофа:
I. I1R1 + I2R2
I1R1 + I2R2
+ I3R3 = E3 + E2+ E1
II. -I1R1 — I4R4
+ I5R5 = E1. I3R3 + I4R4
+ I6R6 = E3
IV. -I2R2 — I5R5
— I6R6 = E2
4. Метод контурных токов
Метод основан на введении промежуточной неизвестной величины — контурного
тока и использовании 2 закона Кирхгофа.
Контурный ток — собственный ток каждого независимого контура.
Реальный ток в ветвях определяется как алгебраическая сумма
соответствующих контурных токов. Число неизвестных в этом методе равно числу
уравнений, которые необходимо было бы составить для схемы по второму закону
Кирхгофа, то есть числу независимых контуров [(m — mi) — (у — 1)].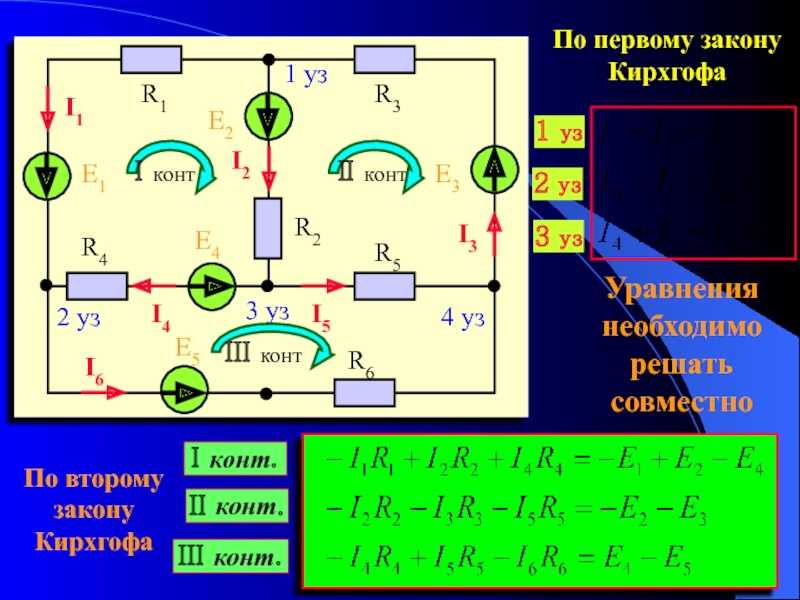
Для каждого независимого контура (ячейки) составляют расчетное контурное
уравнение согласно правилу: левая часть равна сумме произведений контурного
тока на собственное сопротивление этого контура, взятое со знаком плюс, и
контурных токов прилегающих контуров на сопротивления смежных ветвей, взятых со
знаком минус: правая часть равна алгебраической сумме ЭДС этого контура —
контурной ЭДС.
Пусть электрическая цепь содержит n контуров (независимых). Согласно II
закону Кирхгофа получаем следующую систему из n линейных уравнений:
При этом следует считать , если условные положительные направления контурных токов в
одной ветви контуров K и m совпадают, и , если они противоположны.
где D1 D2 Dn — дополнение
D — определитель системы.
Расчёт установившегося режима в цепи переменного тока комплексным методом
выполняется в следующей последовательности:
Составляется электрическая схема, на которой все источники и пассивные
элементы представляются комплексными величинами соответственно напряжений,
токов, сопротивлений (проводимостей). Выбирается условно положительное
Выбирается условно положительное
направление для комплексных значений напряжений, ЭДС и токов. Согласно
уравнениям электрических цепей (Ома, Кирхгофа) в комплексной форме составляются
алгебраические уравнения для рассчитываемой цепи. Уравнения цепи разрешаются
относительно искомых переменных (токов, напряжений) в их комплексной форме.
Основные методы расчета цепей переменного тока и их задачи
Расчет цепей переменного тока решает те же задачи, что и расчет цепей постоянного тока: определение характеристик цепи и (или) законов их изменения.
Переменный ток описывают с помощью периодических функций — косинуса или синуса. Чаще всего используют синусоидальную форму представления сигнала.
В электротехнике используют комплексные числа и комплексную форму записи переменного тока. Все рассмотренные методы расчета цепей постоянного тока применимы и для цепей переменного тока с той лишь разницей, что все выражения и законы будут записываться в комплексной форме.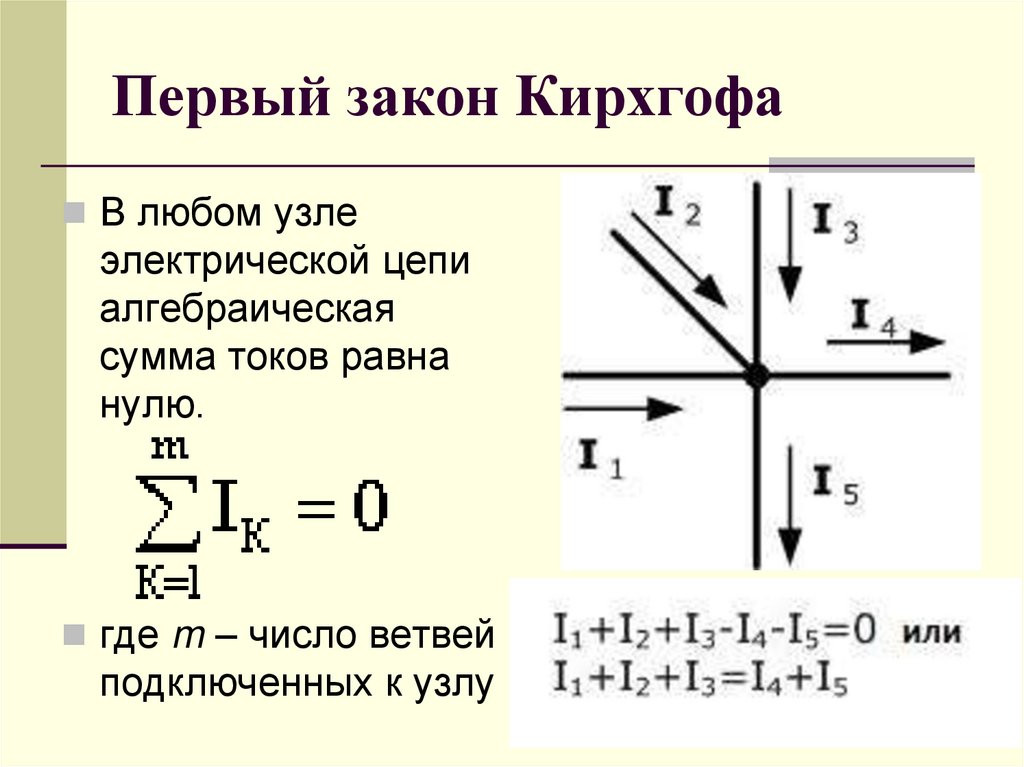
Запишем первый закон Кирхгофа в комплексном виде: алгебраическая сумма комплексов токов в узле равна нулю.
Второй закон Кирхгофа: в контуре алгебраическая сумма комплексов падений напряжений на пассивных элементах равна алгебраической сумме комплексов ЭДС и напряжений источников энергии.
Также при расчете цепей учитывают, что в цепях переменного тока полное сопротивление Z состоит из действительной части R и мнимой — jx.
Мнимую часть сопротивления называют реактивным сопротивление и рассчитывают как разницу между реактивными сопротивлениями индуктивного xL и емкостного элементов xC.
Метки
- алгоритм расчет цепей при несинусоидальных периодических воздействиях
- алгоритм расчета цепей периодического несинусоидального тока
- баланс мощностей
- ВАХ нелинейного элемента
- Векторная диаграмма
- ветви связи
- взаимная индуктивность
- взаимная проводимость
- вольт-амперная характеристика нелинейного элемента
- второй закон Кирхгофа
- второй закон Кирхгофа для магнитных цепей
- входная проводимость
- гармоники напряжения
- гармоники тока
- Генератор напряжения
- генератор тока
- главные контуры
- графический метод расчета нелинейных электрических цепей
- динамическое сопротивление
- дифференциальное сопротивление
- емкость двухпроводной линии
- емкость коаксиального кабеля
- емкость конденсатора
- емкость однопроводной линии
- емкость плоского конденсатора
- емкость цилиндрического конденсатора
- закон Ампера
- закон Био Савара Лапласа
- закон Ома
- закон полного тока
- закон электромагнитной индукции
- Законы Кирхгофа
- индуктивность
- индуктивность двухпроводной линии
- индуктивность однопроводной линии
- индуктивность соленоида
- катушка со сталью
- Конденсатор в цепи постоянного тока
- контурные токи
- коэффициент амплитуды
- коэффициент гармоник
- коэффициент искажения
- коэффициент магнитной связи
- коэффициент мощности трансформатора
- коэффициент трансформации
- коэффициент формы
- кусочно-линейная аппроксимация
- магнитная постоянная
- магнитная цепь
- магнитный поток рассеяния
- метод активного двухполюсника
- метод двух узлов
- метод контурных токов
- метод наложения
- метод узловых напряжений
- метод узловых потенциалов
- метод эквивалентного генератора
- метод эквивалентного источника ЭДС
- Метод эквивалентных преобразований
- методы расчета магнитных цепей
- независимые контуры
- нелинейный элемент
- несинусоидальный периодический ток
- обобщенный закон Ома
- опорный узел
- основной магнитный поток
- параллельное соединение конденсаторов
- первый закон Кирхгофа
- первый закон Кирхгофа для магнитных цепей
- последовательное соединение конденсаторов
- последовательный колебательный контур
- постоянная составляющая тока
- потери в меди
- потери в стали
- приведенный трансформатор
- Примеры расчета схем при несинусоидальных периодических воздействиях
- принцип взаимности
- принцип компенсации
- расчет гармоник тока
- расчет магнитной цепи
- расчет нелинейных цепей постоянного тока
- расчет цепей несинусоидального тока
- Расчет цепи конденсаторов
- расчет цепи с несинусоидальными периодическими источниками
- Резонанс в электрической цепи
- решение задач магнитные цепи
- сила Ампера
- сила Лоренца
- Символический метод
- собственная проводимость
- статическое сопротивление
- сферический конденсатор
- теорема об эквивалентном источнике
- теорема Тевенена
- топографическая диаграмма
- Трансформаторы
- трехфазная система
- удельная энергия магнитного поля
- уравнения трансформатора
- Цепи с конденсаторами
- частичные токи
- чередование фаз
- ЭДС самоиндукции
- эквивалентная схема трансформатора
- электрическая постоянная
- электроемкость
- энергия магнитного поля
Формула напряжения тока.
 Как найти, вычислить электрическое напряжение.
Как найти, вычислить электрическое напряжение.Тема: как рассчитать величину напряжения зная ток, сопротивление, мощность.
Как известно у электрического напряжения должна быть своя мера, которая изначально соответствует той величине, что рассчитана для питания того или иного электротехнического устройства. Превышение или снижение величины этого напряжения питания негативно влияет на электрическую технику, вплоть до полного выхода ее из строя. А что такое напряжение? Это разность электрических потенциалов. То есть, если для простоты понимания его сравнить с водой, то это примерно будет соответствовать давлению. По научному электрическое напряжение — это физическая величина, показывающая, какую работу совершает на данном участке ток при перемещении по этому участку единичного заряда.
Наиболее распространенной формулой напряжения тока является та, в которой имеются три основные электрические величины, а именно это само напряжение, ток и сопротивление. Ну, а формула эта известна под названием закона Ома (нахождение электрического напряжения, разности потенциалов).
Звучит эта формула следующим образом — электрическое напряжение равно произведению силы тока на сопротивление. Напомню, в электротехнике для различных физических величин существуют свои единицы измерения. Единицей измерения напряжения является «Вольт» (в честь ученого Алессандро Вольта, который открыл это явление). Единица измерения силы тока — «Ампер», и сопротивления — «Ом». В итоге мы имеем — электрическое напряжение в 1 вольт будет равно 1 ампер умноженный на 1 ом.
Помимо этого второй наиболее используемой формулой напряжения тока является та, в которой это самое напряжение можно найти зная электрическую мощность и силу тока.
Звучит эта формула следующим образом — электрическое напряжение равно отношению мощности к силе тока (чтобы найти напряжение нужно мощность разделить на ток). Сама же мощность находится путем перемножения тока на напряжение. Ну, и чтобы найти силу тока нужно мощность разделить на напряжение. Все предельно просто. Единицей измерения электрической мощности является «Ватт». Следовательно 1 вольт будет равен 1 ватт деленный на 1 ампер.
Следовательно 1 вольт будет равен 1 ватт деленный на 1 ампер.
Ну, а теперь приведу более научную формулу электрического напряжения, которая содержит в себе «работу» и «заряды».
В этой формуле показывается отношение совершаемой работы по перемещению электрического заряда. На практике же данная формула вам вряд ли понадобится. Наиболее встречаемой будет та, которая содержит в себе ток, сопротивление и мощность (то есть первые две формулы). Но, хочу предупредить, что она будет верна лишь для случая применения активных сопротивлений. То есть, когда расчеты производятся для электрической цепи, у которой имеется сопротивления в виде обычных резисторов, нагревателей (со спиралью нихрома), лампочек накаливания и так далее, то приведенная формула будет работать. В случае использования реактивного сопротивления (наличии в цепи индуктивности или емкости) нужна будет другая формула напряжения тока, которая учитывает также частоту напряжения, индуктивность, емкость.
P.S. Формула закона Ома является фундаментальной, и именно по ней всегда можно найти одну неизвестную величину из двух известных (ток, напряжение, сопротивление).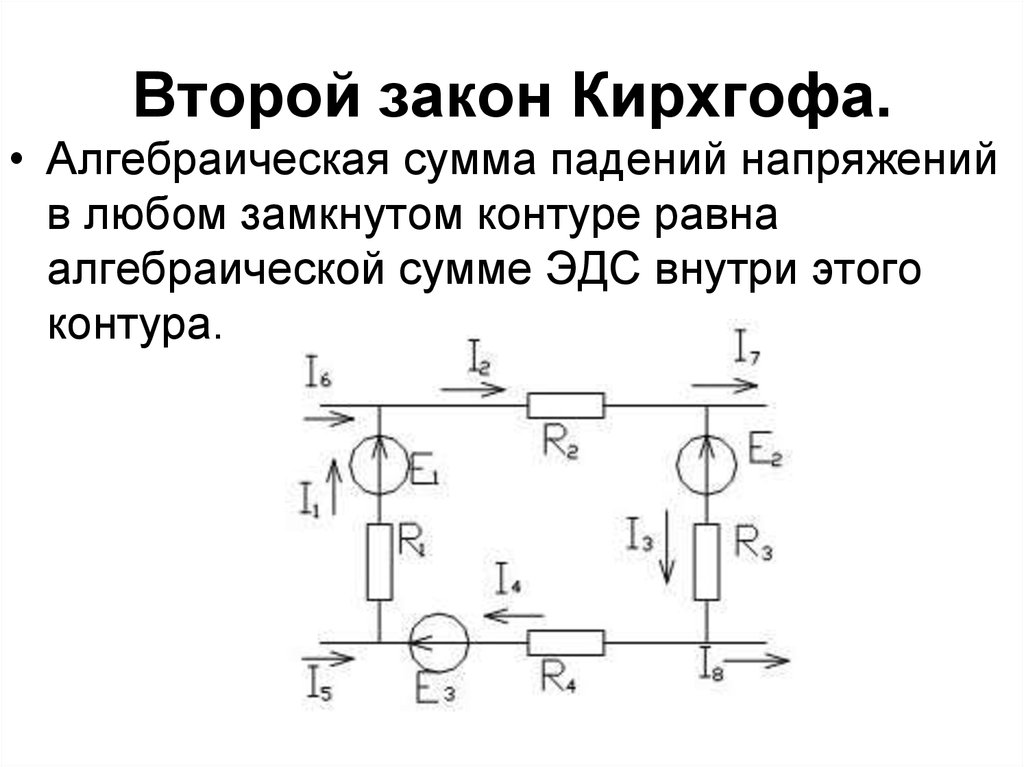 На практике закон ома будет применяться очень часто, так что его просто необходимо знать наизусть каждому электрику и электронику.
На практике закон ома будет применяться очень часто, так что его просто необходимо знать наизусть каждому электрику и электронику.
Пускорегулирующие реостаты
Реостаты, имеющие ступенчатое сделаны из резисторов и переключающего устройства, состоящего, в свою очередь, из неподвижных контактов, одного скользящего контакта. Здесь же имеется привод.
Пускорегулирующие реостаты имеют полюсы якоря, который присоединяется к неподвижным контактам. Подвижный контакт замыкает и размыкает ступени сопротивления, а также и другие цепи, которые управляются данным реостатом. Привод в реостате может быть двигательным или ручным. Это что такое? Реостат такого типа широко распространен. Но недостатки у такой конструкции все же имеются. Это большое количество проводов для монтажа и деталей для крепежа. Особенно много их в реостатах возбуждения с большим числом ступеней.
Реостаты, наполненные маслом, состоят из переключающего устройства и пакетов резисторов, которые встроены в бак и погружены в масло. Пакеты состоят из элементов, выполненных из Они прикрепляются к крышке бака.
Пакеты состоят из элементов, выполненных из Они прикрепляются к крышке бака.
Устройство переключения имеет вид барабана и является осью с прикрепленными к ней частями цилиндрической поверхности, которые соединены, согласно схеме. Неподвижные контакты, которые соединены с элементами резистора, крепятся на неподвижную рейку. Когда ось барабана поворачивается приводом либо маховиком, эти части перемыкают неподвижные контакты, являясь контактами подвижными. Этим изменяется сопротивление в цепи.
Вышесказанное полностью проясняет вопрос, что такое реостат. Как видно, это очень важный элемент, который широко применяется в различных
§ 1 Реостат: принцип работы и устройство
Важным элементом управления сопротивлением электрической цепи является реостат. В нем используется проводник из известного материала с определенной длинной, позволяющей рассчитать его сопротивление. Принцип работы заключается в изменении сопротивления, а значит, появляется возможность регулировать силу тока и напряжение в электрических цепях. Рассмотрим устройство реостата.
Рассмотрим устройство реостата.
На рисунке 1 представлен реостат, состоящий из керамической трубы (1), на которую намотан провод (2) и имеются два контакта (3а), также штанга, в конце которой расположен контакт (3б). По ней движется скользящий контакт (4), который называют «ползун».
При расположении «ползуна» посередине (рис. 2а) только половина проводника принимает участие в электрической цепи. При передвижении его дальше (рис. 2б) длина проводника возрастает, и сопротивление увеличивается, но сила тока уменьшается. Передвигаем «ползун» в противоположную сторону (рис. 2в), и сопротивление уменьшится, а сила тока в цепи возрастет.
Внутри реостат полый, так как при протекании тока происходит нагревание реостата, а полость способствует быстрому охлаждению.
§ 2 Обозначения реостата на схемах и его использование
Как известно, каждый элемент цепи обозначается символом. Обозначение реостата (рис. 3):
Красный прямоугольник — сопротивление, синий — контакт, подводящий провод, зеленый — скользящий контакт. Если ползунок передвинуть влево, сопротивление реостата уменьшается, а при движении вправо — увеличивается.
Если ползунок передвинуть влево, сопротивление реостата уменьшается, а при движении вправо — увеличивается.
Используют еще одно обозначение реостата (рис. 4):
На схеме прямоугольник обозначает сопротивление, а стрелка — то, что его можно изменять.
В электрическую цепь реостат включают последовательно. Рассмотрим схему включения реостата (рис. 5):
Зажимы (1) и (2) подключаются к источнику тока. Второй контакт подсоединен к ползунку. Увеличивая сопротивление реостата, накал лампочки (3) начинает уменьшаться, а значит, ток в цепи тоже уменьшается. Если уменьшить сопротивление реостата лампочка будет гореть ярче.
Реостат — универсальный прибор. Его используют в бытовых приборах. Например, в телевизорах для регулирования громкости и при переключении каналов. Для безопасности используют реостаты с защитным кожухом (рис. 6).
Список использованной литературы:
- Физика. 8 класс: Учебник для общеобразовательных учреждений /А.В. Перышкин. – М.: Дрофа, 2010.

- Физика 7-9. Учебник. И.В. Кривченко.
- Физика. Справочник. О.Ф. Кабардин. – М.: АСТ-ПРЕСС, 2010.
Электрические сети зациклены на передаче электроэнергии от источника к потребителю, которые являются основными элементами цепочки. Но кроме них в электрическую цепь вставляются и другие составляющие, к примеру, управляющие элементы, к которым относится реостат или любой другой прибор с таким же принципом действия. Устройство реостата – это проводник определенного сечения и длины, через которые можно узнать сопротивление проводника. Конечно, обговаривается и его материал. Изменяя сопротивление прибора, а, точнее, проводника, можно регулировать величину силы тока и напряжения в сети. Итак, реостат – это прибор, регулирующий напряжение и ток.
Виды мощностей
Мощностью называется измеряемая физическая величина, которая равна скорости изменения с преобразованием, передачей или потреблением системной энергии. Согласно более узкому понятию, это показатель, который равен отношению затраченного времени на работы к самому периоду, который тратится на работу. Обозначается в механике символом N. В электротехнической науке используется буква P. Нередко можно увидеть также символ W, от слова ватт.
Обозначается в механике символом N. В электротехнической науке используется буква P. Нередко можно увидеть также символ W, от слова ватт.
Мощность переменного тока -это произведение силы тока с напряжением и косинусом сдвига фаз. При этом беспрепятственно можно посчитать только активную и реактивную разновидность. Узнать полное мощностное значение можно через векторную зависимость этих показателей и площади.
Основные мощностные разновидности
Активная мощность
Активной называется полезная сила, определяющая процесс прямого преобразования электроэнергии в необходимый вид силы. В каждом электроприборе преобразовывается она по-своему. К примеру, в лампочке получается свет с теплом, в утюге — тепло, а в электрическом двигателе — механическая энергия. Соответственно, показывает КПД устройства.
Активная разновидность
Реактивная мощность
Реактивной называется та, которая определяется при помощи электромагнитного поля. Образуется при работе электроприборов
Обратите внимание! Это вредная и паразитная мощностная характеристика, которая определяется тем, каков характер нагрузки. Для лампочки она равняется нулю, а для электродвигателя она может быть равна большим значением
Для лампочки она равняется нулю, а для электродвигателя она может быть равна большим значением
Разница между величинами в том, что активно действующая мощностная характеристика показывает КПД устройств, а реактивная является передачей этого КПД. Разница также наблюдается в определении, символе, формуле и значимости.
Обратите внимание! Что касается значения, то вторая нужна лишь для того, чтобы управлять создавшимся напряжением от первой величины и преодолевать мощностные колебания. Обе измеряются в ваттах и имеют большое значение в электромагнитном излучении, механической форме генератора или акустической волне
Активно применяются в промышленности.
Реактивная разновидность
Полная мощность
Полная — это сумма активной с реактивной мощностью. Равна сетевому мощностному показателю. Это произведение напряжения с током в момент игнорирования фазы угла между ними. Вся рассеиваемая с поглощаемой и возвращаемой энергией — это полная энергия.
Это произведение напряжения и тока, единица измерения которого это ватт, перемноженный на ампер. При активности цепи, полная равняется активной. Если речь идет об индуктивной или емкостной схеме, то полная больше, чем активная.
При активности цепи, полная равняется активной. Если речь идет об индуктивной или емкостной схеме, то полная больше, чем активная.
Вам это будет интересно Особенности конденсаторов
Полная разновидность
Комплексная мощность
Это сумма всех мощностных показателей фаз источника электроэнергии. Это комплексный показатель, модуль которого равняется полному мощностному показателю электроцепи. Аргументом является фазовый сдвиг между электротоком с сетевым напряжением. Может быть выражена уравнением, где суммарный мощностный показатель, который генерируют источники электроэнергии, равен суммарному мощностному показателю, который потребляется в электроцепи.
Обратите внимание! Вычисляется посредством использования соответствующей формулы. Так, необходимо комплексное напряжение перемножить на комплексны ток или же удвоенное значение комплексного тока перемножить на импеданс
Также можно удвоенное значение комплексного напряжения поделить на удвоенное значение импеданса.
Комплексная разновидность
Двухканальный регулятор для мотора
Используется для независимого управления парой моторов одновременно. Питание осуществляется от напряжения в диапазоне от 2 до 12 вольт. Ток нагрузки рассчитан до 1,5А на каждый канал.
Конструкция устройства
Основные компоненты конструкции представлены на фото.10 и включают: два подстроечных резистора для регулировки 2-го канала (№1) и 1-го канала (№2), три двухсекционных винтовых клеммника для выхода на 2-ой мотор (№3), для выхода на 1-ый мотор (№4) и для входа (№5).
Примечание.1 Установка винтовых клеммников не обязательна. С помощью тонкого монтажного многожильного провода можно подключить мотор и источник питания напрямую.
Принцип работы
Схема двухканального регулятора идентична электрической схеме одноканального регулятора. Состоит из двух частей (рис.2). Основное отличие: резистор переменного сопротивления замен на подстроечный резистор. Скорость вращения валов устанавливается заранее.
Примечание.2. Для оперативной регулировки скорости кручения моторов подстроечные резисторы заменяют с помощью монтажного провода с резисторами переменного сопротивления с показателями сопротивлений, указанными на схеме.
Материалы и детали
Понадобится печатная плата размером 30×30 мм, изготовленная из фольгированного с одной стороны листа стеклотекстолита толщиной 1-1,5 мм. В таблице 2 приведен список радиокомпонентов.
Процесс сборки
После скачивания архивного файла, размещенного в конце статьи, нужно разархивировать его и распечатать. На глянцевой бумаге печатают чертеж регулятора для термоперевода (файл termo2), а монтажный чертеж (файл montag2) – на белом листе офисной (формат А4).
Чертеж монтажной платы наклеивают к токоведущим дорожкам на противоположной стороне печатной платы . Формируют отверстия на монтажом чертеже в посадочных местах. Монтажный чертеж крепится к печатной плате сухим клеем, при этом отверстия должны совпасть. Производится цоколёвка транзистора КТ815. Для проверки нужно временно соединить монтажным проводом входы 1 и 2 .
Для проверки нужно временно соединить монтажным проводом входы 1 и 2 .
Любой из входов подключают к полюсу источника питания (в примере показана батарейка 9 вольт). Минус источника питания при этом крепят к центру клеммника
Важно помнить: черный провод «-», а красный «+»
Моторы должны быть подключены к двум клеммникам, также необходимо установить нужную скорость. После успешных испытаний нужно удалить временное соединение входов и установить устройство на модель робота. Двухканальный регулятор мотора готов!
В АРХИВЕ представленные необходимые схемы и чертежи для работы. Эмиттеры транзисторов помечены красными стрелками.
радиолюбительский портал
Физические формулы и примеры вычислений
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв.
 = R1+R2.
= R1+R2.
У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.
Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:
- R1 = 1 Ом;
- R2 = 2 Ом;
- R3 = 3 Ом;
- R4 = 6 Ом;
- R5 = 9 Ом;
- R6 = 18 Ом;
- R7 = 2Ом;
- R8 = 2Ом;
- R9 = 8 Ом;
- R10 = 4 Ом.
Напряжение, поданное на схему:
U = 24 В.
Требуется рассчитать токи на всех резистивных элементах.
Исходная цепь
Для расчётов применяется закон Ома:
I = U/R, подставляя вместо R эквивалентное сопротивление.
Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте. Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения
Делают расчёты для каждого такого звена, после – всей цепи целиком
Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.
На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:
- АВ – участок, имеющий две параллельных ветви;
- ВС – отрезок, вмещающий в себя последовательное сопряжение;
- CD – отрезок схемы с расположением трёх параллельных цепочек.
Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.
Последовательно соединённые резисторы R2 и R3
Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.
Смешанное включение на участке CD
Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:
- Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
- Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
- Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.
Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.
Результат первого свёртывания
Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:
- Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
- Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
- 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.
В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.
Результат последующего свёртывания
Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:
Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.
= Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.
Далее, используя закон Ома, находят ток в последнем последовательном участке:
I = U/ Rэкв. = 24/56,83 = 0,42 А.
Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:
- UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
- UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
- UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.
Следующим шагом станет определение токов на параллельных отрезках AB и CD
- I1 = UAB/R1 = 0,35/1 = 0,35 А;
- I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
- I3 = UCD/R6 = 0,17/18 = 0,009 А;
- I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
- I7 = UCD/R10 = 0,17/4 = 0,04 А.
Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.
U9 = R9*I6 = 8*0,02 = 0,16 В.
Теперь напряжение, падающее на Rэкв.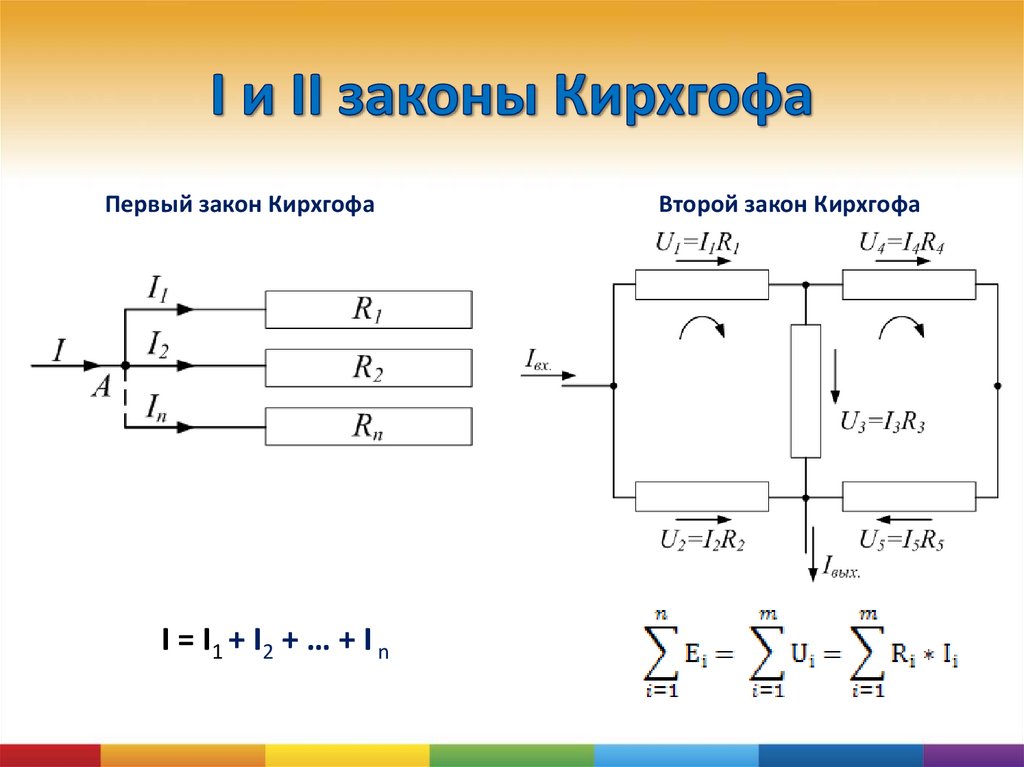 7,8, будет разностью между U CD и U9.
7,8, будет разностью между U CD и U9.
U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.
После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:
- I4 = U7,8/R7 = 1/2 = 0,5 A;
- I5 = U7,8/R8 = 1/2 = 0,5 A.
Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.
Лекция на тему «Законы Ома, законы Кирхгофа»
Электротехника и электроника – 10
Дата 11.12
Группа А-19
Учебная дисциплина ОП.03 Электротехника и электроника
Тема занятия Законы Ома, законы Кирхгофа
Форма лекция
1 Законы Ома
2 Электрическая
энергия и мощность. КПД
КПД
3 Способы соединения резисторов
4 Законы Кирхгофа
— Прочитать лекцию
— Записать основные определения и законы
1 Законы Ома
Зависимость электрического тока от параметров цепи выражается с помощью закона Ома.
Рисунок 1 – Полная (замкнутая) электрическая цепь
Закон Ома для полной цепи: сила тока в цепи прямо пропорциональна ЭДС источника и обратно пропорциональна полному сопротивлению цепи.
где R—сопротивление потребителя, Ом; rо—внутреннее сопротивление источника, Ом.
Внутренним
сопротивлением обладают все источники электрической энергии. Если источник
механический генератор, то сопротивление его обмотки является внутренним.
Закон Ома для участка цепи: сила тока на участке цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
2 Электрическая энергия и мощность. КПД
Работа, совершаемая током по переносу заряженных частиц, является
𝑊 = 𝑃 ∙ 𝑡
где t—время выработки или потребления электрической энергии.
Единицей измерения электрической энергии является Дж (джоуль). Более крупной единицей учета энергии служит КВт·ч (киловатт час), ее используют для учета энергии на транспорте, в промышленности, в быту. Прибором для учета электроэнергии служит счетчик. При расчете энергии источника и потребителя необходимо учитывать различные напряжения на этих устройствах из-за потери энергии, напряжения при передаче.
Рисунок 2 — Электронные и индукционный счетчики электрической энергии
Расчетные формулы электрической энергии источника и потребителя отличаются на величину потерь:
энергия источника
𝑊и = 𝑈и ∙ 𝐼 ∙ 𝑡
энергия потребителя
𝑊п = 𝑈п ∙ 𝐼 ∙ 𝑡
Потеря энергии в соединительных проводах
∆𝑊 = 𝐼2 ∙ 𝑅пр ∙ 𝑡
где RПР – сопротивление соединительных
проводов.
В источниках электрической энергии различные виды энергии преобразуются в электрическую. В потребителях происходит обратный процесс — электрическая энергия преобразуется в любой вид энергии. Скорость преобразования одного вида энергии в другой называется мощностью.
𝑃 = 𝑈 ∙ 𝐼 = 𝐼2 ∙ 𝑅
Единицей мощности является Вт (ватт) и более крупная единица кВт (киловатт), прибором для измерения мощности — ваттметр.
Рисунок 3 – Включение в цепь и условное обозначение ваттметра на схеме
В любой электрической цепи существует баланс мощностей. Вся мощность, поставляемая источником в электрическую цепь, расходуется между потребителями, и некоторая часть тратится на преодоление сопротивления соединительных проводов. Равенство между мощностью источника и мощностью потребителя с учетом потерь называется балансом мощностей.
𝑃ист = 𝑃потр + ∆𝑃
где ΔΡ — потери мощности, Вт.
Если источников и потребителей несколько, тогда формула баланса мощностей будет иметь вид
∑𝑃ист = ∑𝑃потр + ∆𝑃
Качество работы электрической цепи, аппаратов и устройств оценивается коэффициентом полезного действия — КПД. Определяется КПД отношением полезной мощности к затраченной, выраженным в процентах.
Полезной мощностью является мощность потребителя, а затраченной мощность источника, поэтому КПД можно записать
3 Способы соединения резисторов
Последовательным называют соединение, при котором условный конец первого потребителя соединяется с условным началом второго, конец второго – с началом третьего и т.д. (рисунок 4).
Рисунок 4 – Последовательное соединение резисторов
К источнику цепь подключена крайними
зажимами, к которым приложено напряжение UОБЩ.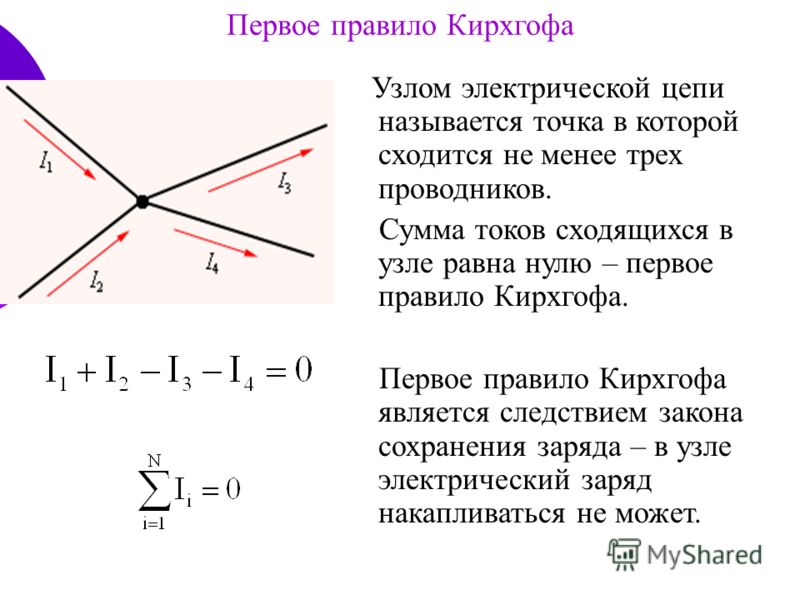 На каждом резисторе
(потребителе) величина напряжения или падения напряжения будет определяться
величиной сопротивления. Согласно закону Ома, чем больше сопротивление, тем больше
на нём падение напряжения.
На каждом резисторе
(потребителе) величина напряжения или падения напряжения будет определяться
величиной сопротивления. Согласно закону Ома, чем больше сопротивление, тем больше
на нём падение напряжения.
При последовательном соединении сумма напряжений на потребителях равна напряжению на зажимах цепи
Поскольку в цепи нет узлов, то по всем участкам проходит один и тот же ток, т.е.
Увеличение числа последовательно соединенных потребителей приводит к увеличению сопротивления всей цепи. Эквивалентное сопротивление цепи равно сумме сопротивлений всех потребителей
Законы последовательного соединения приемников:
𝐼 = 𝐼1 = 𝐼2 = 𝐼3 — сила тока на всех участках цепи одинаковая
— напряжение на зажимах источника равно сумме напряжений 𝑈 = 𝑈1 + 𝑈2 + 𝑈3 на ее отдельных резисторах
— эквивалентное (общее) сопротивление цепи равно сумме
𝑅экв = 𝑅1 + 𝑅2 + 𝑅3 сопротивлений ее резисторов
Если в цепи последовательного соединения произойдет короткое
замыкание одного потребителя, то сопротивление цепи уменьшится
на величину короткозамкнутого сопротивления.
𝑅экв = 𝑅1 + 𝑅3
Рисунок 5 – Короткое замыкание в цепи последовательного соединения
Если в цепи перегорит один потребитель, то вся цепь работать не будет. Это является недостатком последовательного соединения, из-за чего соединение применяется редко.
Используют последовательное соединение для увеличения сопротивления цепи и ограничения тока.
Параллельным называют соединение, при котором все потребители имеют два общие точки соединения (узлы). Схему электрической цепи такого соединения можно изобразить графически (рисунок 6).
или
Параллельным соединением приемников (рисунок 6) электрической энергии называется соединение, при котором начала всех ветвей электрической цепи присоединяются к первому узлу, концы этих же ветвей присоединяются ко второму узлу.
Узел — точка, в котором сходится более двух проводников.
Ветвь — каждый из проводников, расположенный между двумя узлами.
Разветвление — все вместе параллельно соединенные проводники
Поскольку все потребители имеют две общие точки, включенные между зажимами источника, то они попадают под одну и ту же разность потенциалов, т.е. под одно напряжение.
Рисунок 6 – Схема параллельного соединения резисторов
Следовательно, на всех потребителях величина напряжения одинакова и равна напряжению на зажимах цепи.
Величина тока, проходящего через резисторы, зависит от величины сопротивления (согласно закону Ома). Токи на резисторах (рисунок 6) обозначим I1, I2,
I3, ток всей цепи Iобщ. В узел «А» входит общий ток цепи, выходят – токи резисторов.
Законы параллельного соединения приемников
— напряжение на зажимах источника и напряжения на ее
𝑈общ = 𝑈1 = 𝑈2 = 𝑈3 отдельных резисторах одинаково
сила тока в неразветвленной части цепи равна сумме токов в 𝐼общ = 𝐼1 + 𝐼2 + 𝐼3 разветвлении
— эквивалентная (общая) проводимость цепи равна сумме 𝐺экв = 𝐺1 + 𝐺2 + 𝐺3 проводимостей отдельных ветвей, составляющих цепь
С увеличением числа параллельно соединенных потребителей, увеличивается число путей для прохождения токов, следовательно, увеличивается проводимость цепи
Поскольку проводимость величина обратная
сопротивлению, то увеличение числа потребителей в параллельной цепи приведет к
снижению её сопротивления.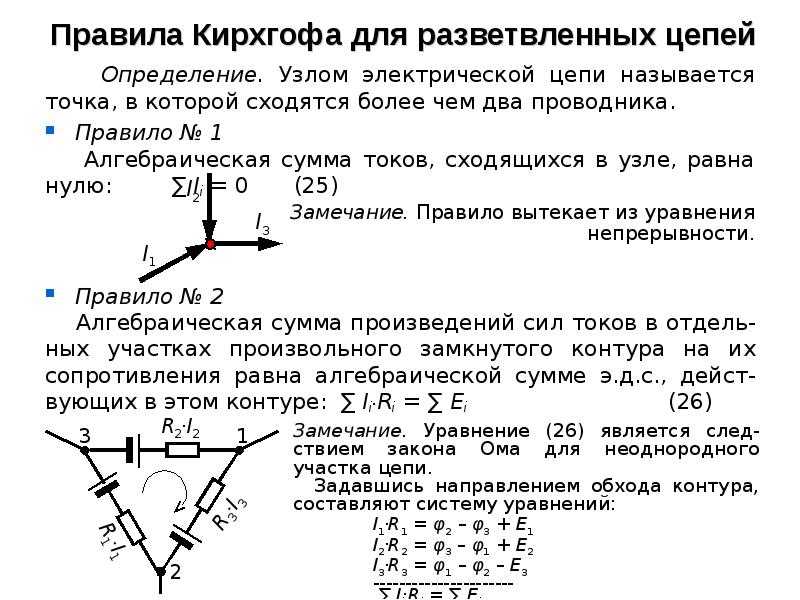 Эквивалентное сопротивление цепи можно записать
формулой
Эквивалентное сопротивление цепи можно записать
формулой
Для двух параллельно соединенных потребителей (рисунок 7) формулу
эквивалентного сопротивления цепи можно представить в виде
Рисунок 7
Для трех параллельно соединенных потребителей формулу эквивалентного сопротивления цепи можно представить в виде
Нередко в цепи встречается большое количество потребителей, имеющих одинаковое сопротивление и соединенных параллельно (рисунок 8). В этом случае их эквивалентное сопротивление удобнее определить по формуле
Рисунок 8
Если в цепи параллельного соединения вышел из строя
один потребитель, то остальные остаются в работе. Этот факт является
достоинством параллельного соединения. Например, если в цепи их трех лампочек
одна перегорела, то сохраняются пути прохождения тока, и две лампочки будут
работать. Сопротивление цепи при этом увеличится (рисунок 9, а).
Этот факт является
достоинством параллельного соединения. Например, если в цепи их трех лампочек
одна перегорела, то сохраняются пути прохождения тока, и две лампочки будут
работать. Сопротивление цепи при этом увеличится (рисунок 9, а).
Рисунок 9
Но если произошло короткое замыкание одного потребителя, то произойдет короткое замыкание источника питания электрической цепи (рисунок 9, б). Чтобы источник не вышел из строя, на входе цепи параллельного соединения устанавливают аппараты защиты или ограничивающие ток устройства. Сопротивление цепи при коротком замыкании равняется нулю.
Вывод: Так как напряжение между узлами постоянно, то токи в ветвях не зависят друг от друга. Поэтому при отключении одной из ветвей все остальные ветви будут продолжать работать.
Чем больше ветвей в параллельном соединении, тем меньше общее сопротивление всей цепи.
При
параллельном соединении резисторов их общее сопротивление будет меньше
наименьшего из сопротивлений.
Цепи параллельного соединения используют для снижения величины сопротивления цепи, при необходимости получения одинакового напряжения на потребителях.
4 Законы Кирхгофа
Законы Кирхгофа лежат в основе анализа электрических цепей.
4.1 Первый закон Кирхгофа
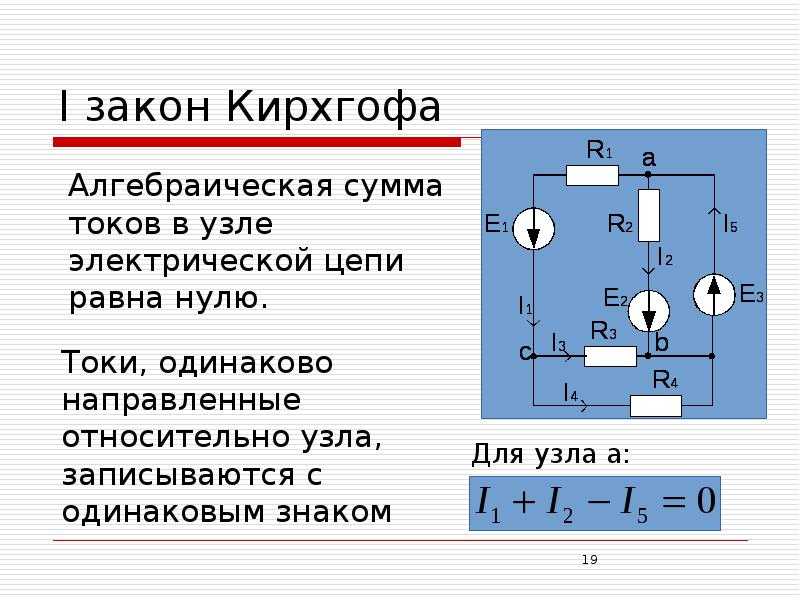
Алгебраическая сумма токов в узле электрической цепи равна нулю. Узел – место соединения трех и более ветвей. Математически это записывается так:
∑𝐼 = 0
Эта формула является математическим выражением первого закона Кирхгофа: сумма токов, входящих в узел равна сумме токов, выходящих из узла.
Всем токам,
направленным от узла, в уравнении приписывается одинаковый знак, например,
положительный, тогда все токи, направленные к узлу, войдут в уравнение с
отрицательным знаком и наоборот. На рис. 10 показан узел, в котором сходятся
три ветви. Ветвь – участок цепи, заключенный между двумя узлами, по которому
протекает один и тот же ток.
Ветвь – участок цепи, заключенный между двумя узлами, по которому
протекает один и тот же ток.
Рисунок 10 — Узел, в котором сходятся четыре ветви
(первый закон Киргофа)
Первый закон Кирхгофа можно сформулировать иначе. Например, в узел
(рисунок 10) входят токи I1 и I, выходит ток I2, значит I1+I=I2, а если ток I2 перенести в левую часть уравнения, то получим I1-I2+I=0. Тогда первый закон Кирхгофа будет сформулирован иначе алгебраическая сумма всех токов в узле равна нулю. В этом случае токи, входящие в узел в формуле со знаком «плюс», выходящие — с «минусом».
Первый закон Кирхгофа отражает тот факт, что в узле электрический заряд не накапливается и не расходуется. Сумма электрических зарядов, приходящих к узлу, равна сумме зарядов, уходящих от узла за один и тот же промежуток времени.
4.2 Второй закон Кирхгофа
Алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме напряжений на элементах этого контура:
∑𝐸 = ∑𝑈
Контур –
замкнутый путь по нескольким ветвям. Если в рассматриваемом контуре отсутствуют
ЭДС, то уравнение принимает вид
Если в рассматриваемом контуре отсутствуют
ЭДС, то уравнение принимает вид
∑𝑈 = 0
При составлении уравнений по второму закону Кирхгофа выбирают произвольное направление обхода контура (рисунок 11). При этом ЭДС и напряжения, совпадающие с направлением обхода, берутся с одинаковыми знаками, например, со знаками «+». Например, для схемы (рисунок 11) имеем
𝐸1 − 𝐸2 = 𝑈1 + 𝑈2 + 𝑈3 − 𝑈4
Рисунок 11 — Произвольное направление обхода контура (второй закон Киргофа) Второй закон Кирхгофа можно применять и для контуров, которые состоят не только из участков схемы, но и из напряжений между какими-либо точками схемы. Так, для контура 4 – 5 – 3 – 6 – 4, состоящего из участка цепи 4 – 5 – 3 и напряжения 4 – 6 –
3, можно составить уравнение
𝐸2 = −𝐼3𝑅3 − 𝑈43
где 𝑈43 – напряжение между точками
4 и 3 схемы, В.
Решенная задача по законам Кирхгофа
В приведенной ниже схеме найдите токи и их направления.
Данные о проблеме
Резисторы:
- R 1 = 0,5 Ом;
- R 2 = 0,5 Ом;
- R 3 = 1 Ом;
- R 4 = 0,5 Ом;
- R 5 = 0,5 Ом;
- R 6 = 3 Ом;
- R 7 = 1 Ом.
Батареи:
- E 1 = 20 В;
- E 2 = 20 В;
- E 3 = 6 В;
Решение
Во-первых, для каждой ветви цепи мы произвольно выбираем направление тока. В EFAB филиал, у нас есть текущий я 1 по часовой стрелке, в ответвлении БЭ ток i 2 с B по E и в филиале EDCB текущий i 3 против часовой стрелки. Во-вторых, для каждого контура схемы мы назначаем
направление, также произвольное, для обхода сетки. α-сетка ( ABEFA ) по часовой стрелке и β-сетка
( BCDEB ) также по часовой стрелке. Все эти элементы мы видим на рисунке 1.
В EFAB филиал, у нас есть текущий я 1 по часовой стрелке, в ответвлении БЭ ток i 2 с B по E и в филиале EDCB текущий i 3 против часовой стрелки. Во-вторых, для каждого контура схемы мы назначаем
направление, также произвольное, для обхода сетки. α-сетка ( ABEFA ) по часовой стрелке и β-сетка
( BCDEB ) также по часовой стрелке. Все эти элементы мы видим на рисунке 1.
фигура 1
- Использование Первый закон Кирхгофа
\[ \bbox[#99CCFF,10px] {\ сумма_ {п} я_ {п} = 0} \]
Токи i 1 и i 3 текут в узел B и ток i 2 поток из узла.
\[ \начать{собирать} i_{2}=i_{1}+i_{3} \тег{I} \конец{собрать} \]
- Использование Второй закон Кирхгофа
\[ \bbox[#99CCFF,10px] {\ сумма_ {п} V_ {п} = 0} \]
Для α-сетки от точки A в выбранном направлении, забывая β-сетку, (рис. 2)
фигура 2
\[ R_{2}i_{1}+R_{4}i_{2}+E_{2}+R_{5}i_{2}+R_{3}i_{1}+R_{1}i_{1}- Е_{1}=0 \]
подставляя данные задачи
\[ \начать{собирать} 0,5i_{1}+0,5i_{2}+20+0,5i_{2}+1i_{1}+0,5i_{1}-20=0\\ 2i_{1}+i_{2}=0 \tag{II} \конец{собрать} \]
Для α-сетки от точки до в выбранном направлении, забывая β-сетку, (рис.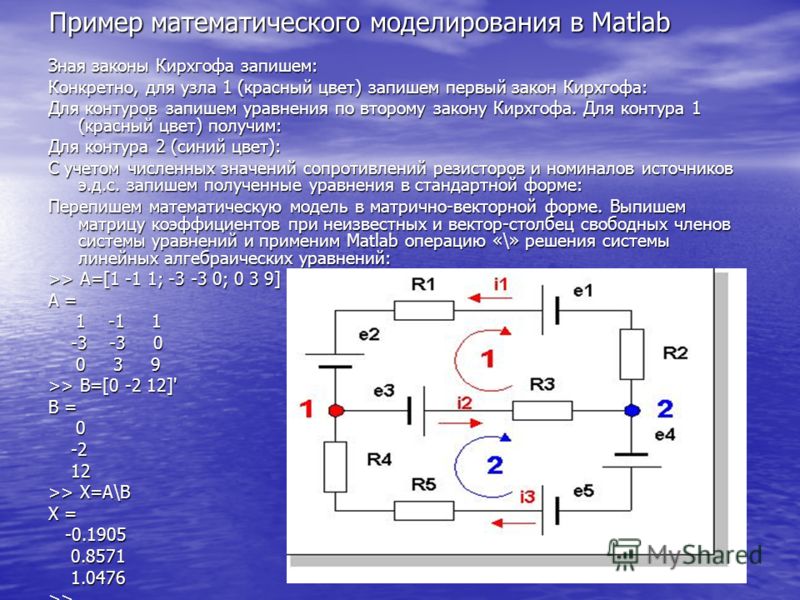 3)
3)
Рисунок 3
\[ -R_{6}i_{3}+E_{3}-R_{7}i_{3}-R_{5}i_{2}-E_{2}-R_{4}i_{2}=0 \]
подставляя данные
\[ \начать{собирать} -3i_{3}+6-1i_{3}-0,5i_{2}-20-0,5i_{2}=0\\ -i_{2}-4i_{3}-14=0\\ -i_{2}-4i_{3}=14 \tag{III} \конец{собрать} \]
Уравнения (I), (II) и (III) можно записать в виде системы линейных уравнений с тремя переменными ( и 1 , и 2 и и 3 )
\[ \оставил\{ \начать{массив} \;i_{2}=i_{1}+i_{3}\\ \;2i_{1}+i_{2}=0\\ \;-i_{2}-4i_{3}=14 \конец{массив}\право. \]
решение второго уравнения для i 1
\[ \начать{собирать} i_{1}=\frac{-{i_{2}}}{2} \tag{IV} \конец{собрать} \]
решение третьего уравнения для i 2
\[ \начать{собирать} i_{3}=\frac{-14-i_{2}}{4} \tag{V} \конец{собрать} \]
подставляя выражения (IV) и (V) в первое уравнение
\[ \начать{собирать} i_{2}=\frac{-{i_{2}}}{2}+\frac{\left(\;-14-i_{2}\;\right)}{4}\\ -i_{2}-\frac{i_{2}}{2}+\frac{\left(\;-14-i_{2}\;\right)}{4}=0 \конец{собрать} \]
Наименьшее общее кратное ( LCM ) 1, 2 и 4 равно 4
\[ \начать{собирать} \frac{-4i_{2}-2i_{2}-14-i_{2}}{4}=0\\ -4i_{2}-2i_{2}-14-i_{2}=0,4\\ -7i_{2}-14=0\\ -7i_{2}=14\\ i_{2}=\frac{14}{-7}\\ i_{2}=-2\;\text{A} \tag{VI} \конец{собрать} \]
подставляя значение (VI) в выражения (IV) и (V), находим значения i 1 и и 3 соответственно
\[ \начать{собирать} i_{1}=\frac{-{(-2)}}{2}\\ я_{1}=1\;\текст{А} \конец{собрать} \]
\[ \начать{собирать} i_{3}=\frac{-14-(-2)}{4}\\ i_{3}=\frac{-14+2}{4}\\ i_{3}=\frac{-12}{4}\\ я_{3}=-3\;\текст{А} \конец{собрать} \]
Поскольку значения токов i 2 и i 3 отрицательны, это указывает на
что их реальные направления противоположны принятым на рис. 1. Значения токов равны и 1 =1 А, и 2 =2 А,
а также и 3 =3 А,
и их направления показаны на рисунке 4.
1. Значения токов равны и 1 =1 А, и 2 =2 А,
а также и 3 =3 А,
и их направления показаны на рисунке 4.
Рисунок 4
Электричество — Законы Кирхгофа — Физика 299
Электричество — Законы Кирхгофа — Физика 299 «Эксперт — это человек, который сделал все
ошибки, которые можно совершить в узкой области. »
Теорема соединения
В любой соединение в цепи ток, поступающий в соединение должен равняться току, выходящему из соединения.
(Это не более чем констатация сохранение заряда)
Теорема о петлеСумма изменение потенциала при обходе любого полного петля нулевая.

(эквивалент сохранения энергии)
- Конвенции
Как обычно, чтобы обеспечить стабильные результаты применения этих законов, мы должны придерживаться нескольких конвенций относительно токов и потенциалов в цепях.
Потенциалы :
- При перемещении резистивного устройства в направлении ток, изменение потенциала равно -iR. Наоборот, если сопротивление проходится в противоположном направлении текущее изменение потенциала равно +iR.
- При перемещении ЭДС в направлении ЭДС изменение потенциала равно +ε. Наоборот, если ЭДС при прохождении против направления ЭДС изменение потенциал равен -ε.
Токи:При постановке задачи текущее направление в любом конкретный элемент схемы назначается произвольно.
Затем к цепи применяются законы Китчоффа. актуальные направления. После решения полученного уравнения, если ток отрицательный, что означает «фактический» текущее направление противоположно произвольно выбранному направление.
законы Кирхгофа применимы к любой цепи к получить набор уравнений, связывающих токи, сопротивления и ЭДС в цепи. Затем эти уравнения могут быть решены для неизвестных величин в цепи. Для любой цепи выполните следующие действия.
- Обозначьте ток, протекающий в каждой части цепи, имея в виду, что ток будет «расщепляться» при достижении узел. Направление определенного направления ток не имеет значения — см. текущее соглашение выше.
- В каждом соединении цепи используйте теорему о соединении, чтобы запишите уравнения, связывающие токи, входящие и уход.
- Определите все возможные петли в схеме и пометьте.
- Для каждого цикла выберите начальное местоположение, затем используйте цикл теорему, чтобы записать уравнение, связывающее изменения в потенциал, который должен быть равен нулю после прохождения полного петля.
- Решите систему уравнений из 2. и 4., чтобы получить неизвестные параметры цепи.
В качестве примера рассмотрим схему ниже. С 3 ЭДС мы не можем использовать последовательный/параллельный анализ.
Соединения:a: I 1 = I 2 + I 3
b: I 3 + I 2 1 0 = Петли:1 (включая ε 1 начиная с пересечения по часовой стрелке): — I 3 R 4 — ε 3 — I 1 R 2 + ε 1 — I 1 R 1 = 0Глядя на эти уравнения, становится ясно, что два соединения уравнения эквивалентны, и это петлевое уравнение 3 просто сумма уравнений контура 1 и 2.
2 (включая ε 2 начиная с перемещения по часовой стрелке): — I 2 R 3 — ε 2 + ε 3 + I 3 R 4 = 0
3 (включая ε1 и ε 2 начиная с по часовой стрелке): — I 2 R 3 — ε 2 — я 1 R 2 + ε 1 — I 1 R 1 = 0Следовательно, существует только 3 независимых уравнений (а, 1 и 2), которые мы можем решить, скажем, для токи I 1 , I 2 и I 3 .
Обратите внимание, что в более сложных схемах будет гораздо больше соединений и большое количество возможных петель. Вам нужно всего лишь применить теорему о петле к такому количеству петель, чтобы получить число независимых уравнений, необходимых для определения неизвестные параметры. Это если у вас есть 3 неизвестных величин, вам понадобится всего 3 независимых уравнения.
Что вы получите, если у вас есть Авогадро количество ослов?
Ответ: патока (моль ослов)
Dr. C.L. Davis
Факультет физики
Университет Луисвилля
электронная почта : [email protected]
4.
3 Правила Кирхгофа | Техасский шлюз
Цели обученияПервое правило КирхгофаВторое правило КирхгофаПрименение правил Кирхгофа
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Анализ сложной схемы с использованием правил Кирхгофа, применяя соглашения для определения правильных знаков различных термов
Информация, представленная в этом разделе, поддерживает следующие цели обучения и научные практики AP®:
- 5.B.9.1 Учащийся может построить или интерпретировать график изменения энергии в электрической цепи только с одной батареей и резисторами, включенными последовательно и/или, максимум, в одной параллельной ветви в качестве приложения. Закон сохранения энергии (правило петли Кирхгофа). (СП 1.1, 1.4)
- 5.B.9.2 Учащийся может применить концепцию сохранения энергии к планированию эксперимента, который продемонстрирует справедливость правила Кирхгофа для контура в цепи только с батареей и резисторами либо последовательно, либо, не более , одна пара параллельных ветвей.
(СП 4.2, 6.4, 7.2)
- 5.B.9.3 Учащийся может применять закон сохранения энергии (правило петли Кирхгофа) в расчетах, включающих полную разность электрических потенциалов для полных цепей только с одной батареей и резисторами, соединенными последовательно и/или, не более , одна параллельная ветвь. (Ст.2.2, 6.4, 7.2)
- 5.B.9.4 Учащийся способен анализировать экспериментальные данные, включая анализ экспериментальной неопределенности, который продемонстрирует справедливость правила цикла Кирхгофа. (П.5.1)
- 5.B.9.5 Учащийся может использовать принципы сохранения энергии (правило петли Кирхгофа) для описания и прогнозирования разности электрических потенциалов, заряда и тока в установившихся цепях, состоящих из различных комбинаций резисторов и конденсаторов.
. (Ст. 6.4)
- 5.C.3.1 Учащийся может применить закон сохранения электрического заряда (правило соединения Кирхгофа) для сравнения электрического тока в различных сегментах электрической цепи с одной батареей и последовательно соединенными резисторами и, самое большее, одну параллельную ветвь и предсказать, как эти значения изменятся при изменении конфигурации схемы. (СП 6.4, 7.2)
- 5.C.3.2 Учащийся может разработать исследование электрической цепи с одним или несколькими резисторами, в котором можно собрать и проанализировать доказательства сохранения электрического заряда. (Ст. 4.1, 4.2, 5.1)
- 5.C.3.3 Учащийся может использовать описание или принципиальную схему электрической цепи для расчета неизвестных значений тока в различных сегментах или ответвлениях цепи.
(СП 1.4, 2.2)
- 5.C.3.4 Учащийся может предсказать или объяснить значения тока при последовательном и параллельном расположении резисторов и других разветвленных цепей, используя правило соединения Кирхгофа, и связать это правило с законом сохранения заряда. (Ст. 6.4, 7.2)
- 5.C.3.5 Учащийся может определять недостающие значения и направление электрического тока в ветвях цепи с резисторами и НО конденсаторами по значениям и направлениям тока в других ветвях цепи путем соответствующего выбора узлов и применения правила соединения. (СП 1.4, 2.2)
Многие сложные схемы, такие как схема на рис. 4.23, не могут быть проанализированы с помощью последовательно-параллельных методов, разработанных в разделе Резисторы, включенные последовательно и параллельно, и Электродвижущая сила: напряжение на клеммах.
Однако есть два правила анализа цепей, которые можно использовать для анализа любой схемы, простой или сложной. Эти правила являются частными случаями законов сохранения заряда и сохранения энергии. Эти правила известны как правила Кирхгофа в честь их изобретателя Густава Кирхгофа (1824–1887).
Рисунок 4.23 Эту схему нельзя свести к комбинации последовательного и параллельного соединений. Для его анализа можно использовать правила Кирхгофа, специальные приложения законов сохранения заряда и энергии. (Примечание. Буква E на рисунке обозначает электродвижущую силу, эдс.)
Правила Кирхгофа
- Первое правило Кирхгофа — правило пересечения. Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения.
- Второе правило Кирхгофа — правило петли. Алгебраическая сумма изменений потенциала вокруг любой замкнутой цепи (петли) должна быть равна нулю.
Теперь будут даны объяснения двух правил, за которыми следуют советы по решению проблем для применения правил Кирхгофа и рабочий пример, который их использует.
Первое правило Кирхгофа
Первое правило Кирхгофа (правило соединения) представляет собой применение закона сохранения заряда к соединению; это показано на рис. 4.24. Ток — это поток заряда, а заряд сохраняется; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу. Первое правило Кирхгофа требует, чтобы I1=I2+I3I1=I2+I3 size 12{I rSub { size 8{1} } =I rSub { size 8{2} } +I rSub { size 8{3} } } {} ( см рисунок). Подобные уравнения могут и будут использоваться для анализа схем и решения схемных задач.
Создание соединений: законы сохранения
Правила Кирхгофа для анализа цепей представляют собой применение законов сохранения к цепям. Первое правило — применение закона сохранения заряда, а второе правило — применение закона сохранения энергии. Законы сохранения, даже используемые в конкретных приложениях, таких как анализ цепей, настолько просты, что составляют основу этого приложения.
Рисунок 4.24 Правило соединения.
На диаграмме показан пример первого правила Кирхгофа, где сумма токов, поступающих в соединение, равна сумме токов, выходящих из соединения. В этом случае ток, поступающий в переход, разделяется и выходит в виде двух токов, так что I1=I2+I3.I1=I2+I3. размер 12{I rSub { размер 8{1} } =I rSub { размер 8{2} } +I rSub { размер 8{3} } } {} Здесь I1I1 размер 12{I rSub {размер 8{1}} } {} должен быть 11 А, так как I2I2 размер 12{I rSub { размер 8{2} } } {} равен 7 А, а I3I3 размер 12{I rSub { размер 8{3} } } {} равен 4 А.
Второе правило Кирхгофа
Второе правило Кирхгофа (правило цикла) является применением закона сохранения энергии. Правило цикла сформулировано с точки зрения потенциала, размера VV 12 {V} {}, а не потенциальной энергии, но они связаны, поскольку PEelec = qV. PEelec = qV. size 12{ ital «PE» rSub { size 8{«elec»} } = ital «qV»} {} Напомним, что ЭДС — это разность потенциалов источника, когда ток не течет. В замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в цепь или из нее.
На рис. 4.25 показаны изменения потенциала в простой последовательной цепи.
Второе правило Кирхгофа требует, чтобы ЭДС-Ir-IR1-IR2=0.ЭДС-Ir-IR1-IR2=0. size 12{«emf» — ital «Ir» — ital «IR» rSub { size 8{1} } — ital «IR» rSub { size 8{2} } =0} {} Переставлено, это emf=Ir+ IR1+IR2,ЭДС=Ir+IR1+IR2, размер 12{«ЭДС»= ital «Ir»+ ital «IR» rSub { размер 8{1} } + ital «IR» rSub {размер 8{2} } } {} что означает, что ЭДС равна сумме 12{ ital «IR»} {} (напряжение) падений в контуре.
Рисунок 4.25 Правило цикла. Пример второго правила Кирхгофа, согласно которому сумма изменений потенциала вокруг замкнутого контура должна быть равна нулю. (a) В этой стандартной схеме простой последовательной цепи ЭДС подает 18 В, которое сводится к нулю сопротивлениями, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки, в сумме 18 В. (b) Этот вид в перспективе представляет потенциал как что-то вроде американских горок, где заряд увеличивается в потенциале за счет ЭДС и уменьшается за счет сопротивления.
(Обратите внимание, что буква E означает ЭДС.)
Применение правил Кирхгофа
Применяя правила Кирхгофа, мы получаем уравнения, позволяющие находить неизвестные в цепях. Неизвестными могут быть токи, ЭДС или сопротивления. Каждый раз, когда применяется правило, создается уравнение. Если независимых уравнений столько же, сколько неизвестных, то задача решаема. При применении правил Кирхгофа вы должны принять два решения. Эти решения определяют знаки различных величин в уравнениях, которые вы получаете, применяя правила.
- Применяя первое правило Кирхгофа, правило соединения, вы должны пометить ток в каждой ветви и решить, в каком направлении он течет. Например, на рис. 4.23, рис. 4.24 и рис. 4.25 токи обозначены I1, I1, размер 12{I rSub { размер 8{1} } } {}I2, I2, размер 12{I rSub { размер 8{2 } } } {}I3,I3, размер 12{I rSub {размер 8{3} } } {} и размер II 12{I} {}, и стрелки указывают их направления. Здесь нет никакого риска, потому что, если вы выберете неправильное направление, ток будет правильной величины, но отрицательным.
- Применяя второе правило Кирхгофа, правило петли, вы должны определить замкнутую петлю и решить, в каком направлении ее обойти, по часовой или против часовой стрелки. Например, на рис. 4.25 петля была пройдена в том же направлении, что и ток (по часовой стрелке). Опять же, нет никакого риска; обход цепи в противоположном направлении меняет знак каждого члена уравнения на противоположное, что похоже на умножение обеих частей уравнения на –1,–1.
Рисунок 4.26 и следующие пункты помогут вам правильно расставить знаки плюс или минус при применении правила цикла. Обратите внимание, что резисторы и ЭДС пересекаются при переходе от a к b. Во многих схемах будет необходимо построить более одного контура. При обходе каждой петли нужно следить за знаком изменения потенциала (см. пример 4.5).
Рисунок 4.26 Каждый из этих резисторов и источников напряжения проходит от a до b. Возможные изменения показаны под каждым элементом и пояснены в тексте. (Обратите внимание, что буква E означает ЭДС.
)
- Когда резистор перемещается в том же направлении, что и ток, изменение потенциала равно −IR−IR size 12{- ital «IR»} {} (см. рис. 4.26).
- При перемещении резистора в направлении, противоположном току, изменение потенциала составляет +IR+IR размер 12{+ ital «IR»} {} (см. рис. 4.26).
- Когда ЭДС перемещается от –– к + (в том же направлении, в котором движется положительный заряд), изменение потенциала составляет +ЭДС (см. рис. 4.26).
- Когда ЭДС перемещается от + к –– (противоположно направлению движения положительного заряда), изменение потенциала равно −− величине 12{ — {}} {}ЭДС (см. рис. 4.26).
Пример 4.5 Расчет тока: использование правил Кирхгофа
Найдите токи, протекающие в цепи на рис. 4.27.
Рисунок 4.27 Эта схема аналогична схеме на рисунке 4.23, но указаны сопротивления и ЭДС. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви помечены и предполагается, что они движутся в показанных направлениях.
В этом примере для нахождения токов используются правила Кирхгофа.
Стратегия
Эта схема настолько сложна, что токи нельзя найти с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. Токи обозначены I1, I1, размер 12{I rSub { размер 8{1} } } {}I2, I2, размер 12{I rSub { размер 8{2} } } {} и I3I3 размер 12{I rSub { размер 8{3} } } {} на рисунке, и были сделаны предположения об их направлениях. Места на схеме обозначены буквами от a до h. В решении мы будем применять правила соединения и петли, ища три независимых уравнения, которые позволят нам найти три неизвестных тока.
Решение
Начнем с применения первого правила Кирхгофа или правила соединения в точке а. Это дает
4,54 I1=I2+I3I1=I2+I3 размер 12{I rSub { размер 8{1} } =I rSub { размер 8{2} } +I rSub {размер 8{3} } } {}
, так как I1I1 размер 12{I rSub { размер 8{1} } } {} впадает в соединение, а I2I2 размер 12{I rSub { размер 8{2} } } {} и I3I3 размер 12{I rSub { размер 8{ 3} } } {} вытекают.
Применение правила соединения в точке e приводит к точно такому же уравнению, так что никакой новой информации не получается. Это одно уравнение с тремя неизвестными — нужны три независимых уравнения, поэтому необходимо применить правило цикла.
Теперь рассмотрим цикл abcdea. Переходя от a к b, мы пересекаем R2R2 размер 12{R rSub { размер 8{2} } } {} в том же (предполагаемом) направлении текущего I2,I2, размер 12{I rSub { размер 8{2} } } {} поэтому изменение потенциала равно −I2R2.−I2R2. size 12{ — I rSub { size 8{2} } R rSub { size 8{2} } } {} Затем, переходя от b к c, мы переходим от –– к +, так что изменение потенциала равно +ЭДС1.+ ЭДС1. size 12{+»emf» rSub { size 8{1} } } {} Переход внутреннего сопротивления r1r1 size 12{r rSub { size 8{1} } } {} от c к d дает -I2r1.-I2r1. size 12{ — I rSub { size 8{2} } r rSub { size 8{1} } } {} Завершение цикла переходом от d к a снова пересекает резистор в том же направлении, что и его ток, давая изменение в потенциал -I1R1.-I1R1. размер 12{ — I rSub { размер 8{1} } R rSub { размер 8{1} } } {}
Правило цикла гласит, что сумма изменений потенциала равна нулю.
Таким образом,
4,55 −I2R2+emf1−I2r1−I1R1=−I2(R2+r1)+emf1−I1R1=0,−I2R2+emf1−I2r1−I1R1=−I2(R2+r1)+emf1−I1R1=0 . размер 12{ — I rSub { размер 8{2} } R rSub { размер 8{2} } +»emf» rSub { размер 8{1} } — I rSub { размер 8{2} } r rSub { размер 8{ 1} } — I rSub { размер 8 {1} } R rSub { размер 8 {1} } = — I rSub { размер 8 {2} } \( R rSub { размер 8 {2} } +r rSub { размер 8 {1} } \) +»emf» rSub { размер 8{1} } — I rSub { размер 8{1} } R rSub { размер 8{1} } =0} {}
Подстановка значений сопротивления и ЭДС из принципиальной схемы и отмена единицы измерения ампер дает
4,56 −3I2+18−6I1=0,−3I2+18−6I1=0. size 12{ — 3I rSub { size 8{2} } +»18″ — 6I rSub { size 8{1} } =0} {}
Теперь применим правило цикла к aefgha (мы могли бы выбрать и abcdefgha) аналогично дает
4,57 +I1R1+I3R3+I3r2-emf2= +I1R1+I3R3+r2-emf2=0.+I1R1+I3R3+I3r2-emf2= +I1R1+I3R3+r2-emf2=0. размер 12{+I rSub { размер 8{1} } R rSub { размер 8{1} } +I rSub { размер 8{3} } R rSub { размер 8{3} } +I rSub { размер 8{3} } r rSub { размер 8{2} } — «emf» rSub { размер 8{2} } «=+»I rSub { размер 8{1} } R rSub { размер 8{1} } +I rSub { размер 8 {3} } левый (R rSub { размер 8 {3} } +r rSub { размер 8 {2} } правый ) — «emf» rSub { размер 8 {2} } = 0} {}
Обратите внимание, что знаки меняются местами по сравнению с другим циклом, потому что элементы перемещаются в противоположном направлении.
С введенными значениями это становится
4,58 +6I1+2I3-45=0.+6I1+2I3-45=0. size 12{+6I rSub { size 8{1} } +2I rSub { size 8{3} } — «45»=0} {}
Этих трех уравнений достаточно для решения трех неизвестных токов. Сначала решите второе уравнение для I2.I2. размер 12{I rSub { размер 8{2} } } {}
4,59 I2=6−2I1I2=6−2I1 размер 12{I rSub { размер 8{2} } =6 — 2I rSub { размер 8{1} } } {}
Теперь решите третье уравнение для I3.I3. размер 12{I rSub { размер 8{3} } } {}
4,60 I3=22,5−3I1I3=22,5−3I1 размер 12{I rSub { размер 8{3} } =»22″ «.» 5 — 3I rSub { size 8{1} } } {}
Подстановка этих двух новых уравнений в первое позволяет найти значение для I1.I1. размер 12{I rSub { размер 8{1} } } {}
4,61 I1=I2+I3=(6−2I1)+(22,5−3I1)=28,5−5I1I1=I2+I3=(6−2I1)+ (22,5−3I1)=28,5−5I1 размер 12{I rSub { размер 8{1} } =I rSub { размер 8{2} } +I rSub { размер 8{3} } = \( 6 — 2I rSub { размер 8{1} } \) + \(«22» «.» 5 — 3I rSub { размер 8{1} } \) =»28″ «.» 5 — 5I rSub {размер 8{1} } } {}
Объединение терминов дает
4,62 6I1=28,5 и 6I1=28,5 и размер 12{6I rSub { размер 8{1} } =»28″ «.
» 5} {}
4,63 I1=4,75 A.I1=4,75 A. размер 12{I rSub { размер 8{1} } =4 «.» «75»» A»} {}
Подстановка этого значения для I1I1 size 12{I rSub { size 8{1} } } {} обратно в четвертое уравнение дает
4,64 I2=6−2I1=6−9,50I2 =6−2I1=6−9,50 размер 12{I rSub { размер 8{2} } =6 — 2I rSub { размер 8{1} } =6 — 9 «.» «50»} {}
4,65 I2=-3,50 A.I2=-3,50 A. размер 12{I rSub { размер 8{2} } = — 3 «.» «50» «А»} {}
Знак минус означает, что I2I2 размер 12{I rSub { размер 8{2} } } {} течет в направлении, противоположном предполагаемому на рис. 4.27.
Наконец, подстановка значения I1I1 size 12{I rSub { size 8{1} } } {} в пятое уравнение дает
4,66 I3=22,5−3I1=22,5−14,25I3=22,5−3I1=22,5−14,25 размер 12{I rSub {размер 8{3}} =»22″ «.» 5 — 3I rSub {размер 8{1}} =»22″ «.» 5 — «14» «. «25»} {}
4,67 I3=8,25 A.I3=8,25 A. размер 12{I rSub { размер 8{3} } =8 «.» «25» «А»} {}
Обсуждение
Просто для проверки отметим, что действительно I1=I2+I3.
I1=I2+I3. size 12{I rSub { size 8{1} } =I rSub { size 8{2} } +I rSub { size 8{3} } } {} Результаты также можно проверить, введя все значения в поле уравнение для петли abcdefgha.
Стратегии решения задач по правилам Кирхгофа
- Убедитесь, что имеется четкая принципиальная схема, на которой вы можете отметить все известные и неизвестные сопротивления, ЭДС и токи. Если ток неизвестен, вы должны присвоить ему направление. Это необходимо для определения признаков потенциальных изменений. Если вы зададите направление неправильно, то обнаружится, что ток имеет отрицательное значение — никакого вреда не будет.
- Примените правило соединения к любому соединению в цепи. Каждый раз, когда применяется правило соединения, вы должны получать уравнение с током, которого не было в предыдущем приложении — если нет, то уравнение является избыточным.
- Примените правило цикла к такому количеству циклов, которое необходимо для поиска неизвестных в задаче.
(Независимых уравнений должно быть столько же, сколько и неизвестных.) Чтобы применить правило цикла, вы должны выбрать направление обхода цикла. Затем тщательно и последовательно определите знаки потенциальных изменений для каждого элемента, используя четыре маркированных пункта, рассмотренных выше в сочетании с рис. 4.26.
- Решите уравнения для неизвестных. Это может включать в себя множество алгебраических шагов, требующих тщательной проверки и перепроверки.
- Проверьте, разумны ли и последовательны ли ответы. Числа должны быть правильного порядка, ни чрезмерно большими, ни исчезающе малыми. Признаки должны быть разумными — например, отсутствие сопротивления не должно быть отрицательным. Убедитесь, что полученные значения удовлетворяют различным уравнениям, полученным в результате применения правил. Например, токи должны удовлетворять правилу соединения.
Материал в этом разделе теоретически верен. Мы должны быть в состоянии проверить это, произведя измерения тока и напряжения.
На самом деле, некоторые из устройств, используемых для проведения таких измерений, являются прямым применением принципов, рассмотренных до сих пор, и рассматриваются в следующих модулях. Как мы увидим, отсюда вытекает очень простой, даже глубокий факт: проведение измерения изменяет измеряемую величину.
Проверьте свое понимание
Можно ли применять правила Кирхгофа к простым последовательным и параллельным цепям, или они ограничены для использования в более сложных цепях, которые не являются комбинацией последовательной и параллельной?
Решение
Правила Кирхгофа можно применить к любой схеме, поскольку они являются приложениями к схемам двух законов сохранения. Законы сохранения являются наиболее широко применимыми принципами в физике. Обычно математически проще использовать правила для последовательной и параллельной схемы в более простых схемах, поэтому мы подчеркиваем правила Кирхгофа для использования в более сложных ситуациях.
Но правила последовательностей и параллелей можно вывести из правил Кирхгофа. Кроме того, правила Кирхгофа могут быть распространены на устройства, отличные от резисторов и ЭДС, такие как конденсаторы, и являются одним из основных устройств анализа в анализе цепей.
Выполнение соединений: параллельные резисторы
Показанная ниже простая схема с двумя параллельными резисторами и источником напряжения реализована в лабораторном эксперименте с ɛ = 6,00 ± 0,02 В и R 1 = 4,8 ± 0,1 Ом и R 2 = 9,6 ± 0,1 Ом. Значения включают допуск на экспериментальные погрешности, поскольку их нельзя измерить с полной уверенностью. Например, если вы измерите сопротивление резистора несколько раз, вы можете получить немного разные результаты. Следовательно, значения выражаются с некоторым уровнем неопределенности.
Рисунок 4.28
В лабораторном эксперименте токи, измеренные в двух резисторах, равны I 1 = 1,27 А и I 2 = 0,62 А соответственно.
Проверим эти значения с помощью законов Кирхгофа.
For the two loops,
E − I I R I = 0 or I I = E/R I
E − I II R II = 0 или I II = Э/Р II .
Преобразование заданных неопределенности для напряжения и сопротивления в проценты, мы получаем
E = 6,00 В ± 0,33%
R I = 4,8 Ом ± 2,08%
1111111111111111119 = 2,08%
111111111111111111111196969%
11111111111111111111119 = 2,08%. Ом ± 1,04%.
Теперь найдем токи двух контуров. В то время как напряжение делится на сопротивление, чтобы найти ток, неопределенности в напряжении и сопротивлении напрямую добавляются, чтобы найти неопределенность в значении тока.


 = R1+R2.
= R1+R2.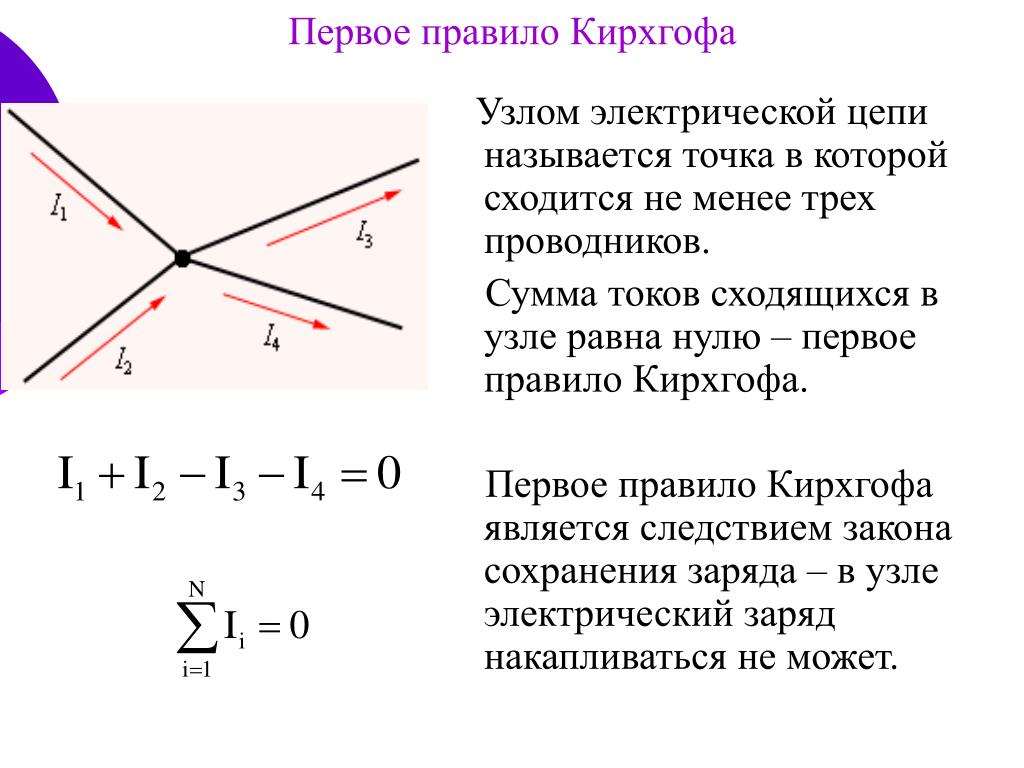
 Затем к цепи применяются законы Китчоффа.
актуальные направления. После решения полученного
уравнения, если ток отрицательный, что означает «фактический»
текущее направление противоположно произвольно выбранному
направление.
Затем к цепи применяются законы Китчоффа.
актуальные направления. После решения полученного
уравнения, если ток отрицательный, что означает «фактический»
текущее направление противоположно произвольно выбранному
направление. 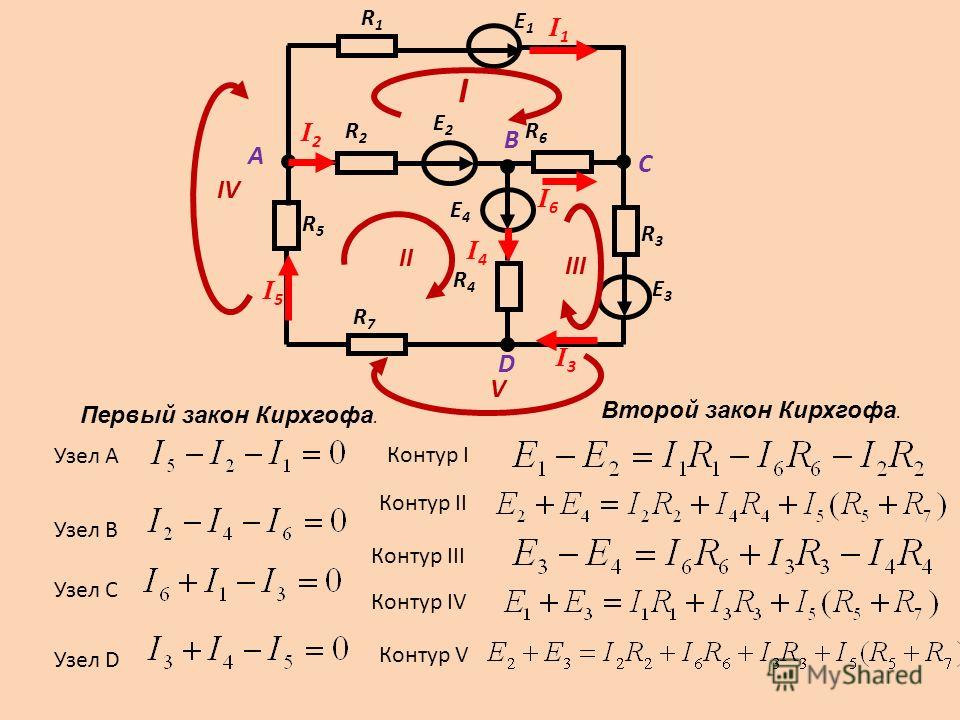
 Следовательно, существует только 3
независимых уравнений (а, 1 и 2), которые мы можем решить, скажем, для
токи I 1 , I 2 и I 3 .
Следовательно, существует только 3
независимых уравнений (а, 1 и 2), которые мы можем решить, скажем, для
токи I 1 , I 2 и I 3 .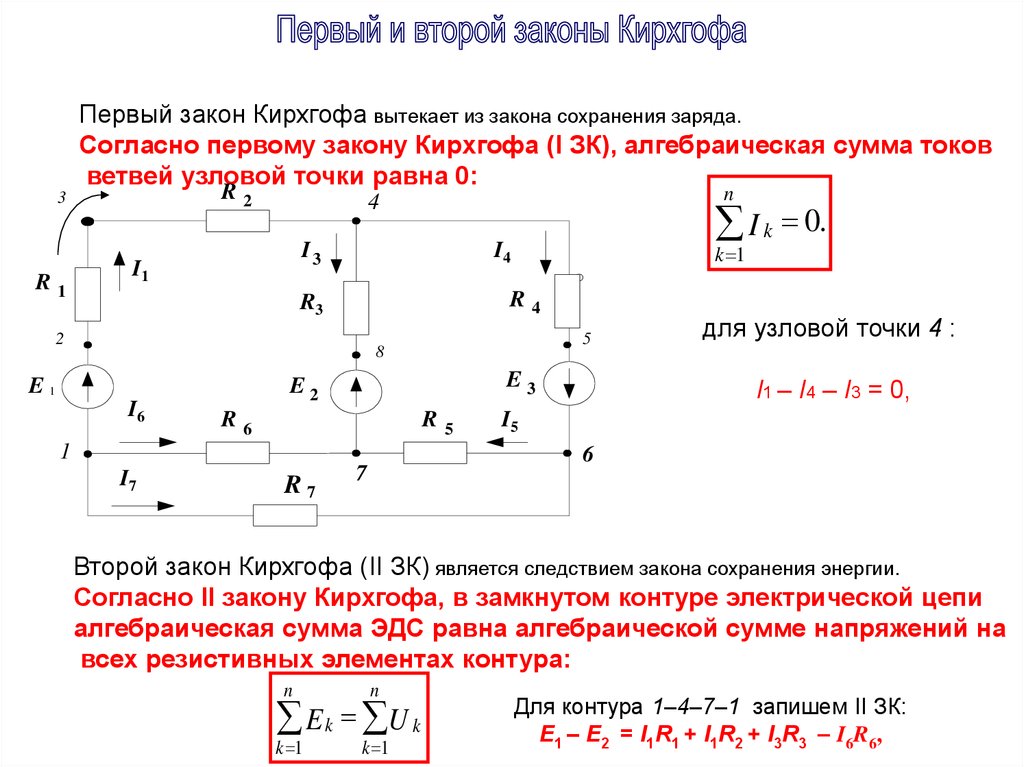 3 Правила Кирхгофа | Техасский шлюз
3 Правила Кирхгофа | Техасский шлюз (СП 4.2, 6.4, 7.2)
(СП 4.2, 6.4, 7.2)  . (Ст. 6.4)
. (Ст. 6.4)  (СП 1.4, 2.2)
(СП 1.4, 2.2) 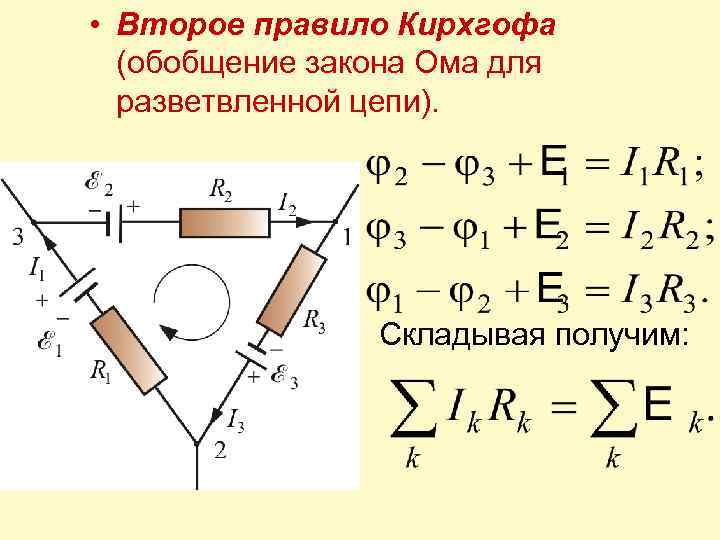 Однако есть два правила анализа цепей, которые можно использовать для анализа любой схемы, простой или сложной. Эти правила являются частными случаями законов сохранения заряда и сохранения энергии. Эти правила известны как правила Кирхгофа в честь их изобретателя Густава Кирхгофа (1824–1887).
Однако есть два правила анализа цепей, которые можно использовать для анализа любой схемы, простой или сложной. Эти правила являются частными случаями законов сохранения заряда и сохранения энергии. Эти правила известны как правила Кирхгофа в честь их изобретателя Густава Кирхгофа (1824–1887).
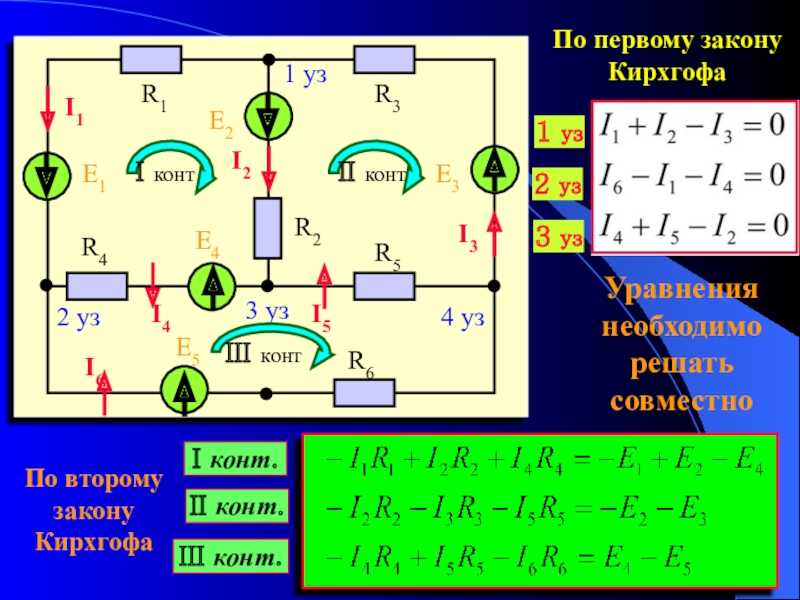 На диаграмме показан пример первого правила Кирхгофа, где сумма токов, поступающих в соединение, равна сумме токов, выходящих из соединения. В этом случае ток, поступающий в переход, разделяется и выходит в виде двух токов, так что I1=I2+I3.I1=I2+I3. размер 12{I rSub { размер 8{1} } =I rSub { размер 8{2} } +I rSub { размер 8{3} } } {} Здесь I1I1 размер 12{I rSub {размер 8{1}} } {} должен быть 11 А, так как I2I2 размер 12{I rSub { размер 8{2} } } {} равен 7 А, а I3I3 размер 12{I rSub { размер 8{3} } } {} равен 4 А.
На диаграмме показан пример первого правила Кирхгофа, где сумма токов, поступающих в соединение, равна сумме токов, выходящих из соединения. В этом случае ток, поступающий в переход, разделяется и выходит в виде двух токов, так что I1=I2+I3.I1=I2+I3. размер 12{I rSub { размер 8{1} } =I rSub { размер 8{2} } +I rSub { размер 8{3} } } {} Здесь I1I1 размер 12{I rSub {размер 8{1}} } {} должен быть 11 А, так как I2I2 размер 12{I rSub { размер 8{2} } } {} равен 7 А, а I3I3 размер 12{I rSub { размер 8{3} } } {} равен 4 А. На рис. 4.25 показаны изменения потенциала в простой последовательной цепи.
На рис. 4.25 показаны изменения потенциала в простой последовательной цепи.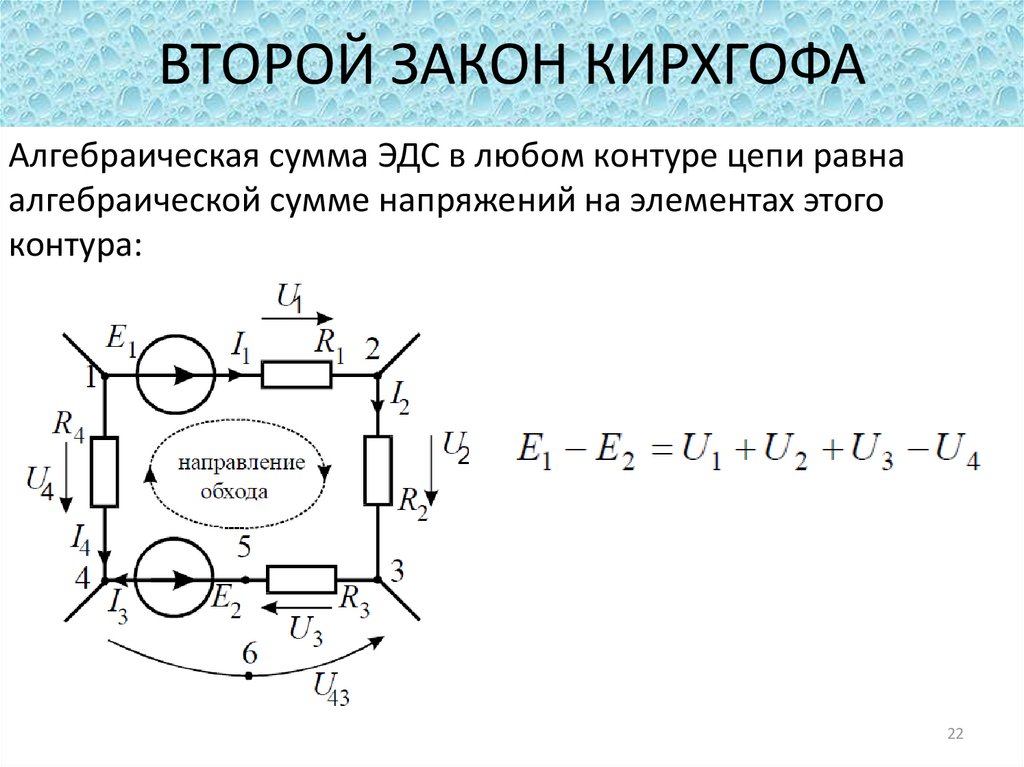 (Обратите внимание, что буква E означает ЭДС.)
(Обратите внимание, что буква E означает ЭДС.)
 )
) В этом примере для нахождения токов используются правила Кирхгофа.
В этом примере для нахождения токов используются правила Кирхгофа. Применение правила соединения в точке e приводит к точно такому же уравнению, так что никакой новой информации не получается. Это одно уравнение с тремя неизвестными — нужны три независимых уравнения, поэтому необходимо применить правило цикла.
Применение правила соединения в точке e приводит к точно такому же уравнению, так что никакой новой информации не получается. Это одно уравнение с тремя неизвестными — нужны три независимых уравнения, поэтому необходимо применить правило цикла. Таким образом,
Таким образом, С введенными значениями это становится
С введенными значениями это становится » 5} {}
» 5} {} I1=I2+I3. size 12{I rSub { size 8{1} } =I rSub { size 8{2} } +I rSub { size 8{3} } } {} Результаты также можно проверить, введя все значения в поле уравнение для петли abcdefgha.
I1=I2+I3. size 12{I rSub { size 8{1} } =I rSub { size 8{2} } +I rSub { size 8{3} } } {} Результаты также можно проверить, введя все значения в поле уравнение для петли abcdefgha.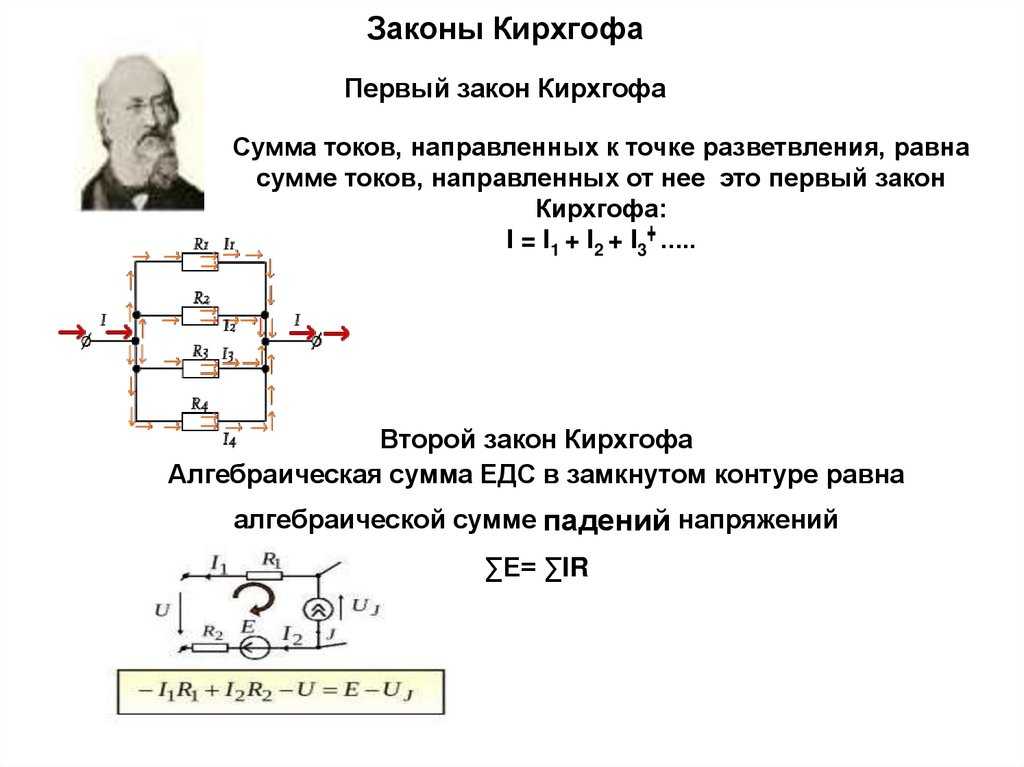 (Независимых уравнений должно быть столько же, сколько и неизвестных.) Чтобы применить правило цикла, вы должны выбрать направление обхода цикла. Затем тщательно и последовательно определите знаки потенциальных изменений для каждого элемента, используя четыре маркированных пункта, рассмотренных выше в сочетании с рис. 4.26.
(Независимых уравнений должно быть столько же, сколько и неизвестных.) Чтобы применить правило цикла, вы должны выбрать направление обхода цикла. Затем тщательно и последовательно определите знаки потенциальных изменений для каждого элемента, используя четыре маркированных пункта, рассмотренных выше в сочетании с рис. 4.26. На самом деле, некоторые из устройств, используемых для проведения таких измерений, являются прямым применением принципов, рассмотренных до сих пор, и рассматриваются в следующих модулях. Как мы увидим, отсюда вытекает очень простой, даже глубокий факт: проведение измерения изменяет измеряемую величину.
На самом деле, некоторые из устройств, используемых для проведения таких измерений, являются прямым применением принципов, рассмотренных до сих пор, и рассматриваются в следующих модулях. Как мы увидим, отсюда вытекает очень простой, даже глубокий факт: проведение измерения изменяет измеряемую величину. Но правила последовательностей и параллелей можно вывести из правил Кирхгофа. Кроме того, правила Кирхгофа могут быть распространены на устройства, отличные от резисторов и ЭДС, такие как конденсаторы, и являются одним из основных устройств анализа в анализе цепей.
Но правила последовательностей и параллелей можно вывести из правил Кирхгофа. Кроме того, правила Кирхгофа могут быть распространены на устройства, отличные от резисторов и ЭДС, такие как конденсаторы, и являются одним из основных устройств анализа в анализе цепей. Проверим эти значения с помощью законов Кирхгофа.
Проверим эти значения с помощью законов Кирхгофа.