Закон всемирного тяготения, теория и онлайн калькуляторы

Закон всемирного тяготения, теория и онлайн калькуляторы

К началу XVII века гелиоцентрическая система мира была признана большинством ученых. Однако в то время не были понятны причины и законы, по которым планеты движутся.

И. Кеплер обработал результаты множества своих наблюдений и своего коллеги Т. Браге, сформулировал законы перемещения планет вокруг Солнца. Стало понятно, что для объяснения законов Кеплера, следует определить, какие силы действуют на планеты. Но Кеплеру и его современникам не удалось это выполнить. Задачу решил И. Ньютон.

Приблизительно, можно считать, что планеты перемещаются равномерно по орбитам, близким к окружностям. При таком виде движения материальной точки у нее имеется центростремительное ускорение, которое направлено к центру орбиты (для планеты, центростремительной ускорение направлено к Солнцу). Из второго закона Ньютона следует, что на планету, действует некоторая сила, которая порождает нормальное ускорение. 2\cdot кг}.\ $ Гравитационная постоянная численно равна силе взаимодействия материальных точек, имеющих массы по одному килограмму, расположенный на расстоянии в один метр. Гравитационная постоянная находится экспериментально.

Одним из первых эксперимент по измерению силы тяготения в лабораторных условиях поставил Кавендиш. Так была определена гравитационная постоянная.

Примеры задач с решением

Пример

Задание. В чем состоит суть опыта Кавендиша по измерению силы гравитации?

Решение. Сделаем рисунок.

Для проведения эксперимента Кавендиш использовал крутильные весы (рис.1). На тонкой кварцевой нити подвешивался легкий стержень. На нити жестко закреплялось маленькое зеркало. Луч света попадал на зеркало, отражался от него и падал на шкалу. Если стержень поворачивался, то луч перемещался по шкале. Так отмечался угол закручивания нити. На концах стержня были закреплены два шарика из свинца, каждый массой $m$. {-6}$Н

Читать дальше: закон Гука.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Раздел динамики. Три закона Ньютона. Закон всемирного тяготения – StudyWay

В настоящее время ЕГЭ по физике проходит в виде решения задач. Задание, содержащиеся в КИМах определяются согласно кодификатору элементов содержания и требований к подготовке выпускников к проведению ЕГЭ.
Для успешной подготовки к ЕГЭ, в этой статье рассмотрена физика, а именно раздел динамики, включая формулы для подготовки к ЕГЭ, статья охватывает следующие темы:
– Первый закон И. Ньютона;
– Второй закон И. Ньютона;
– Третий закон И. Ньютона;
– Закон всемирного тяготения;
– Сила упругости. Закон Гука.
Приступим к изучению тем и примеров решения задач.
В динамике выделяют три закона открытых И. Ньютоном, они позволяют определить движение для любой системы.
Первый закон Ньютона

Первый закон открыт в конце 17 века. Закон звучит следующим образом: существуют инерциальные системы отсчёта, в которых тела движутся равномерно и прямо по линии, если на них не оказывают влияние другие силы.
Закон инерции: в случае, когда на тело не оказывают влияния внешние воздействий, то у данного тела сохраняется состояние покоя. Это значит, что все тела могут оставаться в первоначальном состоянии, то есть если тело находится в движении, то оно будет в таком же состоянии. Если оно неподвижно, то продолжает стоять без изменений, пока не появится сила, заставляющая его двигаться.
Инерциальной системой отсчёта называют систему, находящуюся в состоянии движении или покое.
Неинерциальной системой называют движущуюся с ускорением систему.
Инерциальными считаются системы, находящиеся в состоянии покоя или движения, при этом, движение должно быть равномерным и прямолинейным.
Неинерциальными считаются системы, имеющие ускорение.
Существует также гелиоцентрическая модель отсчёта, в ней начало координат совмещено с солнцем.
Первый закон Ньютона не содержит формул, поэтому рассмотрим примеры:
– Наиболее популярным объяснением является резкое торможение. Тело движется в направлении автомобиля, поэтому при резком торможении автомобиль сильно дёргается. Если же автомобиль плавно затормозит, соответственно, его движение будет нерезким;
– Движение наверх и вниз. Американские горки поднимаются наверх за счёт накопленной потенциальной энергии при крутом спуске.
Второй закон Ньютона

Второй закон открыт около 1666 года, он гласит: В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, является пропорциональным вызывающим его силам. Силы для ускорения предмета зависят от его массы.
Ньютон нашёл общее между ускорением и силой, F– сила, действующая на тело, масса – m, ускорение –a.
Важно помнить о том, что:
– Этот закон называют основополагающим в разделе динамики;
– Тело подразумевает точку, её движение находят в инерциальной системе отсчёта.
Формула второго закона: ma = F, F = ma. 2
m = 50 кг.
Помним формулу второго закона: F = mа. Далее подставляет известные значения.
F = 50 кг * 0,6 = 30 H.
Ответ: F = 30 H.
Третий закон Ньютона

Третий закон открыли в 1725 году: действию F всегда есть противодействие, то есть взаимодействия двух дел равны и направлены по прямой в противоположные стороны. Формула: F12 = -F21.
Пример. Для строительства моста нужно высчитать нагрузку. Данную нагрузку можно узнать с помощью третьего закона. При этом, на мост давят держащие опоры, поэтому строительство ведётся по определённой схеме, которая рассчитывает большую выносливость.
Рассмотрим пример решения задачи: на стуле стоит портфель. На него действуют силы равные 500 H. Согласно третьему закону сверху на него действует та же сила, равная 500 H.
Следует, что F1 = F2. То есть, чем больше масса тела, тем меньше его ускорение.
Следует помнить о том, что третий закон применяется исключительно в инерциальных системах отсчёта.
Закон всемирного тяготения
В школьной программе изучение закона всемирного тяготения при подготовке к ЕГЭ является важной темой. Издавна люди смотрели на звёзды и понимали, что ими что-то движет. Но люди не догадывались, что притяжением управляет один закон. В 1687 году И. Ньютон открыл закон всемирного тяготения.
Согласно известной всем версии, Ньютон увидел падающее с дерева яблоко. Он стал размышлять о том, что на все тела действует некая определённая сила, которая позволяет им притягиваться к Земле.
Формула данного закона выглядит таким образом: F=G*(m1*m2)/r2. При этом, G – постоянная гравитации, равная 6,67408(31)•10−11. Это величина, которая воздействует на любой объект нашей планеты.
Позднее закон всемирного тяготения стали применять в астрономии и механике, так как с его помощью объясняется процесс движения различных тел. Любой объект будет находиться в невесомости, объясняется это тем, что объект находится в космосе и сила притяжения на него не действует.
Примером закона всемирного тяготения является запуск в космос спутника (это произошло в 1957 году). При этом, спутник постоянно находился в равном расстоянии над Землёй, это обусловлено тем, что наша планета притягивает одинаково в различных направлениях. 2 = 2,4 H
Ответ: 2,4 H.
Сила упругости. Закон Гука

Закон Гука является основным в теории упругости. Немаловажное значение в процессе подготовки к сдаче ЕГЭ по физике имеет тема о силе упругости, открытая Робертом Гуком – английский учёный, данный закон открыл в 1660 году в возрасте двадцати пяти лет.
Закон гласит: сила упругости, которая возникает при растяжении или сжатии тела является пропорциональной значению по изменению длины тела.
Сила упругости – это сила, которая возникает при деформации тела, данная сила возвращает тело в его первоначальное состояние.
При деформации тело пытается вернуться в первоначальное состояние, это объясняется электромагнитным воздействием на молекулярном уровне.
Формула закона: пусть х – упругость тела, тогда Fx = -kx, k – жёсткость тела.
Жёсткость зависит от материала и размера тела, она составляет ньютон на метр (1Н / м). Чем больше жёсткость, тем меньше оно подвержено деформации под воздействием сил. Стоит помнить о том, что закон Гука достоверно применяют при упругой деформации, т.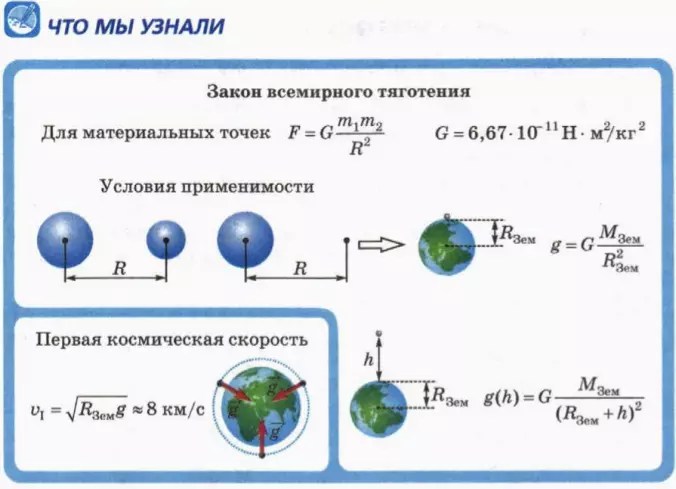 е. деформация должна быть малой. При большой деформации тела длина перестаёт быть прямо пропорциональной силе, а при сильной деформации тело разрушается.
Рассмотрим пример задачи: проволоку разрезали ровно пополам, её жёсткость составляет 90 H/m. Нужно найти жёсткость обеих проволок.
Решение: k = F/x.
Согласно условию задачи, жёсткость пропорциональна длине проволоки.
k1 = 2k = 180 H/m.
Ответ: 180 H/m.
Таким образом, мы рассмотрели одни из важных тем раздела динамики: три закона Исаака Ньютона, закон всемирного тяготения и силу упругости, закон Роберта Гука. Изучив данные материалы по теме и просмотрев примеры решения задач, вы сможете решить схожие задание на ЕГЭ по физике. 

6.5 Универсальный закон всемирного тяготения Ньютона – College Physics 2e

Цели обучения

К концу этого раздела вы сможете:

• Объясните гравитационную силу Земли.
• Опишите гравитационное воздействие Луны на Землю.
• Обсудить невесомость в космосе.
• Изучить эксперимент Кавендиша

Что общего у ноющих ног, падающего яблока и орбиты Луны? Каждая из них вызвана силой гравитации. Наши ноги напряжены, поддерживая наш вес — силу земного притяжения, действующую на нас. Яблоко падает с дерева из-за той же силы, действующей на высоте нескольких метров над поверхностью Земли. А Луна вращается вокруг Земли потому, что гравитация способна обеспечить необходимую центростремительную силу на расстоянии сотен миллионов метров. На самом деле одна и та же сила заставляет планеты вращаться вокруг Солнца, звезды — вокруг центра галактики, а галактики — группироваться вместе. Гравитация — еще один пример лежащей в основе простоты природы. Это самая слабая из четырех основных сил, встречающихся в природе, и в некотором смысле наименее изученная. Это сила, действующая на расстоянии, без физического контакта, и выражается формулой, действующей повсюду во Вселенной, для масс и расстояний, которые варьируются от крошечных до огромных.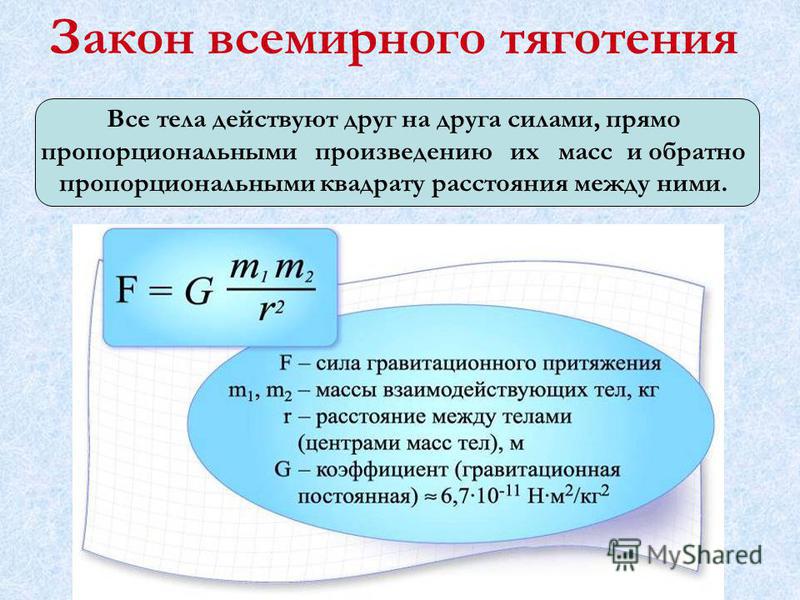

Сэр Исаак Ньютон был первым ученым, который точно определил гравитационную силу и показал, что она может объяснить как падающие тела, так и астрономические движения. См. Рисунок 6.17. Но Ньютон был не первым, кто заподозрил, что одна и та же сила вызывает и наш вес, и движение планет. Его предшественник Галилео Галилей утверждал, что падающие тела и движение планет имеют одну и ту же причину. Некоторые из современников Ньютона, такие как Роберт Гук, Кристофер Рен и Эдмунд Галлей, также добились определенного прогресса в понимании гравитации. Но Ньютон первым предложил точную математическую форму и с помощью этой формы показал, что движение небесных тел должно представлять собой конические сечения — окружности, эллипсы, параболы и гиперболы. Это теоретическое предсказание было большим триумфом — уже некоторое время было известно, что луны, планеты и кометы следуют по таким путям, но никто не мог предложить механизм, который заставлял бы их следовать именно по этим путям, а не по другим.

Другие выдающиеся ученые и математики того времени, особенно за пределами Англии, не хотели принимать принципы Ньютона. Потребовалась работа другого выдающегося философа, писателя и ученого, Эмили дю Шатле, чтобы установить ньютоновское тяготение как точный и всеобъемлющий закон. Дю Шатле, который ранее заложил основу для понимания сохранения энергии, а также принципа отсутствия массы у света, перевел и дополнил ключевую работу Ньютона. Она также использовала исчисление для объяснения гравитации, что помогло ее принять.

Рисунок 6.17 Согласно ранним сообщениям, Ньютон был вдохновлен установить связь между падающими телами и астрономическими движениями, когда увидел, как яблоко падает с дерева, и понял, что если сила гравитации может распространиться над землей на дерево, она также может достичь Солнца. Вдохновение яблоком Ньютона является частью мирового фольклора и даже может быть основано на фактах. Универсальный закон тяготения Ньютона и его законы движения ответили на очень старые вопросы о природе и оказали огромную поддержку представлению о лежащей в основе простоте и единстве природы.

Как и многие революционные открытия, оно не было сразу принято. Выдающийся французский ученый и философ Эмили дю Шатле помогла утвердить теорию Ньютона во Франции и континентальной Европе.

Гравитационная сила относительно проста. Она всегда притягательна и зависит только от вовлеченных масс и расстояния между ними. Говоря современным языком, универсальный закон всемирного тяготения Ньютона гласит, что каждая частица во Вселенной притягивает любую другую частицу с силой вдоль соединяющей их линии. Сила прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.

Рисунок 6.18 Гравитационное притяжение происходит вдоль линии, соединяющей центры масс этих двух тел. Величина силы одинакова на каждом из них, что соответствует третьему закону Ньютона.

Предупреждение о заблуждении

Величина силы, действующей на каждый объект (один имеет большую массу, чем другой), одинакова, что соответствует третьему закону Ньютона.

Тела, с которыми мы имеем дело, имеют тенденцию быть большими. Чтобы упростить ситуацию, мы предполагаем, что тело действует так, как если бы вся его масса была сосредоточена в одной конкретной точке, называемой центром масс (ЦМ), которая будет дополнительно изучена в разделе «Импульс движения и столкновения». Для двух тел, имеющих массы mm и MM с расстоянием rr между их центрами масс, уравнение универсального закона всемирного тяготения Ньютона имеет вид

F=GmMr2,F=GmMr2,

6.40

где FF — величина гравитационной силы, а GG — коэффициент пропорциональности, называемый гравитационной постоянной. GG — это универсальная гравитационная постоянная, то есть считается, что она одинакова во всей Вселенной. Экспериментально было измерено:

G=6,674×10−11 Н⋅м2кг2G=6,674×10−11Н⋅м2кг2

6,41

в единицах СИ. Обратите внимание, что единицы GG таковы, что сила в ньютонах получается из F=GmMr2F=GmMr2 при рассмотрении массы в килограммах и расстояния в метрах. Например, две массы массой 1000 кг, разделенные расстоянием 1000 м, будут испытывать гравитационное притяжение 6,674×10-11Н6,674×10-11Н. Это чрезвычайно малая сила. Небольшая величина гравитационной силы согласуется с повседневным опытом. Мы не осознаем, что даже большие объекты, такие как горы, воздействуют на нас гравитационными силами. На самом деле вес нашего тела — это сила притяжения

всей Земли на нас с массой 6×1024кг6×1024кг.

Напомним, что ускорение свободного падения gg составляет около 9,80 м/с29,80 м/с2 на Земле. Теперь мы можем определить, почему это так. Вес объекта мг — это гравитационная сила между ним и Землей. Подстановка мг вместо FF в законе всемирного тяготения Ньютона дает

мг=GmMr2, мг=GmMr2,

6,42

, где mm — масса объекта, MM — масса Земли, а rr — расстояние до центр Земли (расстояние между центрами масс объекта и Земли). См. Рисунок 6. 19.. Масса mm объекта сокращается, остается уравнение для gg:

g=GMr2.g=GMr2.

6,43

Подстановка известных значений массы и радиуса Земли (до трех значащих цифр),

m2kg2×5,98×1024kg(6,38×106m)2,

6,44

и получаем значение ускорения падающего тела:

g=9,80м/с2.g=9,80м/с2.

6,45

Рисунок 6.19 Расстояние между центрами масс Земли и объектом на ее поверхности почти равно радиусу Земли, потому что Земля намного больше объекта.

Это ожидаемое значение и не зависит от массы тела . Закон всемирного тяготения Ньютона продвигает наблюдение Галилея о том, что все массы падают с одинаковым ускорением, на шаг дальше, объясняя наблюдение с точки зрения силы, которая заставляет объекты падать, — фактически с точки зрения универсально существующей силы притяжения между массами.

Домашний эксперимент

Возьмите шарик, шарик и ложку и бросьте их с одной высоты. Они падают на пол одновременно? Если вы также уроните лист бумаги, будет ли он вести себя как другие предметы? Объясните свои наблюдения.

Установление связей

Попытки понять силу гравитации все еще предпринимаются. Как мы увидим в физике элементарных частиц, современная физика исследует связи гравитации с другими силами, пространством и временем. Общая теория относительности меняет наш взгляд на гравитацию, заставляя нас думать о гравитации как о искривлении пространства и времени.

В следующем примере мы проводим сравнение, подобное тому, которое сделал сам Ньютон. Он отметил, что если сила гравитации заставляет Луну вращаться вокруг Земли, то ускорение свободного падения должно равняться центростремительному ускорению Луны на ее орбите. Ньютон обнаружил, что два ускорения совпадают «почти почти».

Пример 6,6

Гравитационная сила Земли — это центростремительная сила, заставляющая Луну двигаться по криволинейной траектории

(a) Найдите ускорение силы тяжести Земли на расстоянии от Луны.

(b) Вычислите центростремительное ускорение, необходимое для удержания Луны на своей орбите (предполагается, что она движется по круговой орбите вокруг неподвижной Земли), и сравните его с только что найденным значением ускорения под действием силы тяжести Земли.

Стратегия для (а)

Этот расчет такой же, как и расчет ускорения силы тяжести на поверхности Земли, за исключением того, что это расстояние от центра Земли до центра Луны. Радиус почти круговой орбиты Луны составляет 3,84×108 м3,84×108 м.

Решение для (a)

Подставляя известные значения в выражение для gg, найденное выше, помня, что MM — это масса Земли, а не Луны, получаем (3,84×108м)2=2,70×10-3м/с.2g=GMr2=6,67×10-11Н⋅м2кг2×5,98×1024 кг(3,84×108 м)2=2,70×10–3 м/с.2

6,46

Стратегия для (b)

Центростремительное ускорение можно рассчитать, используя любую форму

ac=v2rac=rω2}.ac =v2rac=rω2}.

6,47

Мы решили использовать вторую форму:

ac=rω2,ac=rω2,

6,48

, где ωω — угловая скорость Луны относительно Земли.

Решение для (b)

Учитывая, что период (время, необходимое для совершения одного полного оборота) обращения Луны по орбите составляет 27,3 дня, (d) и используя

1 d×24ч×60мин×60смин=86400 с1 d×24ч×60минч×60смин=86400 с

6,49

мы видим, что

2π рад (27,3 д) (86 400 с / д) = 2,66 × 10–6 рад.

6,50

Центростремительное ускорение равно

ac=rω2=(3,84×108м)(2,66×10-6рад/с)2=2,72×10-3м/с. ×10−6рад/с)2=2,72×10−3м/с.2

6,51

Ускорение направлено к центру Земли.

Обсуждение

Центростремительное ускорение Луны, найденное в (b), отличается менее чем на 1% от ускорения земного притяжения, найденного в (a). Это согласие является приблизительным, потому что орбита Луны слегка эллиптическая, а Земля не является стационарной (скорее, система Земля-Луна вращается вокруг своего центра масс, который расположен примерно на 1700 км ниже поверхности Земли). Явный вывод состоит в том, что гравитационная сила Земли заставляет Луну вращаться вокруг Земли.

Почему Земля не остается неподвижной, когда Луна вращается вокруг нее? Это связано с тем, что, как и ожидалось из третьего закона Ньютона, если Земля воздействует на Луну, то Луна должна оказывать на Землю равную и противоположную силу (см. рис. 6.20). Мы не ощущаем влияние Луны на движение Земли, потому что гравитация Луны перемещает наши тела вместе с Землей, но на Земле есть и другие признаки, которые ясно показывают влияние гравитационной силы Луны, как обсуждалось в книге «Спутники и законы Кеплера: аргумент в пользу Простота.

Рисунок 6.20 а) Земля и Луна вращаются примерно раз в месяц вокруг своего общего центра масс. (b) Их центр масс вращается вокруг Солнца по эллиптической орбите, но путь Земли вокруг Солнца имеет «изгибы». Подобные колебания на траекториях звезд наблюдались и считаются прямым свидетельством того, что планеты вращаются вокруг этих звезд. Это важно, потому что отраженный свет планет часто слишком тусклый, чтобы его можно было наблюдать.

Приливы

Океанские приливы — один из хорошо наблюдаемых результатов гравитации Луны, действующей на Землю. Рисунок 6.21 представляет собой упрощенный рисунок положения Луны относительно приливов. Поскольку вода легко течет по поверхности Земли, прилив создается на стороне Земли, ближайшей к Луне, где гравитационное притяжение Луны сильнее всего. Почему на противоположной стороне Земли также бывает прилив? Ответ заключается в том, что Земля притягивается к Луне больше, чем вода на дальней стороне, потому что Земля ближе к Луне. Таким образом, вода на стороне Земли, ближайшей к Луне, отрывается от Земли, а Земля отрывается от воды на дальней стороне. Когда Земля вращается, приливная выпуклость (воздействие приливных сил между вращающимся вокруг естественным спутником и основной планетой, вокруг которой он вращается) сохраняет свою ориентацию относительно Луны. Таким образом, в день бывает два прилива (фактический период прилива составляет около 12 часов 25,2 минуты, потому что Луна также движется по своей орбите каждый день).

Рисунок 6.21 Луна вызывает океанские приливы, притягивая воду на ближней стороне больше, чем Землю, и притягивая Землю больше, чем воду на дальней стороне. Расстояния и размеры не в масштабе. Для этого упрощенного представления системы Земля-Луна в любом месте в день бывает два прилива и два отлива, потому что Земля вращается под приливной выпуклостью.

Солнце также влияет на приливы, хотя его влияние примерно вдвое меньше, чем у Луны. Однако самые большие приливы, называемые весенними приливами, происходят, когда Земля, Луна и Солнце выстраиваются на одной линии. Наименьшие приливы, называемые квадратными приливами, возникают, когда Солнце находится на 9°.Угол 0º90º относительно выравнивания Земля-Луна.

Рисунок 6.22 (а, б) весенние приливы: самые высокие приливы возникают, когда Земля, Луна и Солнце выровнены. (c) Квадратный прилив: Самые низкие приливы возникают, когда Солнце находится под углом 90º90º к выравниванию Земли и Луны. Обратите внимание, что этот рисунок выполнен не в масштабе.

Приливы характерны не только для Земли, но и для многих астрономических систем. Самые экстремальные приливы возникают там, где гравитационная сила наиболее сильна и изменяется наиболее быстро, например вблизи черных дыр (см. рис. 6.23). В нашей галактике наблюдалось несколько вероятных кандидатов в черные дыры. Они имеют массу больше, чем у Солнца, но имеют диаметр всего несколько километров в поперечнике. Приливные силы вблизи них настолько велики, что могут фактически оторвать материю от звезды-компаньона.

Рисунок 6.23 Черная дыра — это объект с такой сильной гравитацией, что даже свет не может вырваться из нее. Эта черная дыра была создана сверхновой одной звезды в двухзвездной системе. Приливные силы, создаваемые черной дырой, настолько велики, что отрывают материю от звезды-компаньона. Это вещество сжимается и нагревается по мере того, как оно всасывается в черную дыру, создавая свет и рентгеновские лучи, наблюдаемые с Земли.

«Невесомость» и микрогравитация

В отличие от огромной гравитационной силы вблизи черных дыр существует видимое гравитационное поле, с которым сталкиваются астронавты на орбите Земли. Как действует «невесомость» на космонавта, который месяцами находится на орбите? А как насчет влияния невесомости на рост растений? Невесомость не означает, что на космонавта не действует гравитационная сила. На орбите космонавта нет «невесомости». Этот термин просто означает, что космонавт находится в свободном падении, ускоряясь с ускорением за счет силы тяжести. Если трос лифта порвется, пассажиры внутри окажутся в свободном падении и ощутят невесомость. Вы можете испытывать короткие периоды невесомости на некоторых аттракционах в парках развлечений.

Рисунок 6.24 Астронавты испытывают невесомость на борту Международной космической станции. (кредит: НАСА)

Микрогравитация относится к среде, в которой кажущееся суммарное ускорение тела мало по сравнению с ускорением, создаваемым Землей на ее поверхности. Многие интересные темы биологии и физики были изучены за последние три десятилетия в условиях микрогравитации. Непосредственное беспокойство вызывает влияние на астронавтов длительного пребывания в открытом космосе, например, на Международной космической станции. Исследователи заметили, что в такой среде мышцы атрофируются (истощаются). Существует также соответствующая потеря костной массы. Продолжаются исследования адаптации сердечно-сосудистой системы к космическому полету. На Земле кровяное давление обычно выше в ногах, чем в голове, потому что более высокий столб крови оказывает на него нисходящую силу из-за гравитации. Когда вы стоите, 70% вашей крови находится ниже уровня сердца, а в горизонтальном положении происходит прямо противоположное. Какое значение имеет отсутствие этого перепада давления для сердца?

Некоторые открытия в области физиологии человека в космосе могут иметь клиническое значение для лечения заболеваний на Земле. С другой стороны, известно, что космический полет влияет на иммунную систему человека, что, возможно, делает членов экипажа более уязвимыми к инфекционным заболеваниям. Эксперименты в космосе также показали, что некоторые бактерии растут быстрее в условиях микрогравитации, чем на Земле. Тем не менее, исследования показывают, что производство микробных антибиотиков может увеличиться в два раза в культурах, выращенных в космосе. Можно надеяться, что удастся понять эти механизмы, чтобы можно было добиться аналогичных успехов на местах. В другой области физических космических исследований в космическом пространстве были выращены неорганические кристаллы и кристаллы белков, которые имеют гораздо более высокое качество, чем любые, выращенные на Земле, поэтому кристаллографические исследования их структуры могут дать гораздо лучшие результаты.

Растения эволюционировали под воздействием силы тяжести и с помощью датчиков силы тяжести. Корни растут вниз, а побеги растут вверх. Растения могли бы обеспечить систему жизнеобеспечения для длительных космических миссий, восстанавливая атмосферу, очищая воду и производя пищу. Некоторые исследования показали, что гравитация не влияет на рост и развитие растений, но все еще существует неопределенность в отношении структурных изменений растений, выращенных в условиях микрогравитации.

Эксперимент Кавендиша: тогда и сейчас

Как отмечалось ранее, универсальная гравитационная постоянная GG определяется экспериментально. Это определение впервые было точно сделано Генри Кавендишем (1731–1810), английским ученым, в 1798 году, более чем через 100 лет после того, как Ньютон опубликовал свой универсальный закон всемирного тяготения. Измерение GG является очень простым и важным, поскольку оно определяет силу одной из четырех сил в природе. Эксперимент Кавендиша был очень трудным, потому что он измерил крошечное гравитационное притяжение между двумя массами обычного размера (не более десятков килограммов) с помощью прибора, подобного изображенному на рис. 6.25. Примечательно, что его значение для GG отличается менее чем на 1% от лучшего современного значения.

Одним из важных следствий знания GG было то, что, наконец, можно было получить точное значение массы Земли. Это было сделано путем максимально точного измерения ускорения свободного падения, а затем вычисления массы Земли ММ из соотношения, которое дает универсальный закон всемирного тяготения Ньютона:

mg=GmMr2,mg=GmMr2,

6,52

где mm — масса объекта, MM — масса Земли, rr — расстояние до центра Земли (расстояние между центрами масс объект и Земля). См. Рисунок 6.18. Масса mm объекта сокращается, остается уравнение для gg:

г=GMr2.g=GMr2.

6,53

Перестановка для решения ММ дает

М=гр2Г.М=гр2Г.

6,54

Таким образом, ММ можно рассчитать, поскольку все величины справа, включая радиус Земли rr, известны из прямых измерений. В книге «Спутники и законы Кеплера: аргумент в пользу простоты» мы увидим, что знание GG также позволяет определять астрономические массы. Интересно, что из всех фундаментальных констант в физике GG наименее точно определена.

Эксперимент Кавендиша также используется для изучения других аспектов гравитации. Один из самых интересных вопросов заключается в том, зависит ли сила гравитации от вещества, а также от массы — например, оказывает ли один килограмм свинца такое же гравитационное притяжение, как один килограмм воды. Венгерский ученый по имени Роланд фон Этвёш начал это исследование в начале 20-го века. Он обнаружил с точностью до пяти частей на миллиард, что гравитационная сила не зависит от вещества. Такие эксперименты продолжаются и сегодня, и они улучшили измерения Этвеша. Эксперименты типа Кавендиша, такие как эксперименты Эрика Адельбергера и других в Вашингтонском университете, также наложили серьезные ограничения на возможность существования пятого взаимодействия и подтвердили главное предсказание общей теории относительности — гравитационная энергия вносит свой вклад в массу покоя. В текущих измерениях используются крутильные весы и параллельная пластина (а не сферы, как использовал Кавендиш), чтобы изучить, как закон тяготения Ньютона работает на субмиллиметровых расстояниях. Отклоняются ли гравитационные эффекты от закона обратных квадратов на таком мелком масштабе? Пока никаких отклонений не наблюдается.

Рисунок 6,25 Кавендиш использовал подобный прибор для измерения гравитационного притяжения между двумя подвешенными сферами (мм) и двумя на подставке (ММ), наблюдая за величиной кручения (скручивания), создаваемого волокном. Расстояние между массами можно варьировать, чтобы проверить зависимость силы от расстояния. Современные эксперименты этого типа продолжают исследовать гравитацию.

Закон всемирного тяготения Ньютона — определение, характеристики, примеры и ответы на часто задаваемые вопросы Вдохновением сэра Исаака Ньютона для вывода революционного закона всемирного тяготения было яблоко, упавшее с дерева. Мы все хорошо знакомы с историей Ньютона и тем, как он открыл гравитацию. Падение яблока заставило его открыть гравитацию Ньютона и закон всемирного тяготения. Закон всемирного тяготения Ньютона играет важную роль в механике.

Ньютон из любопытства задал простой вопрос: почему яблоко падает, а не вбок или вверх!!! Позже Ньютон понял, что земля должна быть ответственна за падение яблока вниз перпендикулярно земле. Это был главный поворотный момент, и тогда он разработал закон всемирного тяготения.

Сила притяжения между любыми двумя телами. По сути, все объекты во Вселенной притягиваются друг к другу с определенной силой, но в большинстве случаев сила либо слишком слаба, либо слишком мала, чтобы ее можно было наблюдать из-за очень большого расстояния между ними. 9{2}}\].

(Изображение скоро будет загружено)

Что такое закон всемирного тяготения Ньютона?

Закон всемирного тяготения является важным открытием в области физики. Это дает представление о взаимосвязи между массой и силой. Закон тяготения гласит, что каждый объект во Вселенной притягивает любой другой объект так, что прилагаемая сила будет пропорциональна произведению масс и обратно пропорциональна квадрату расстояния между ними.

9{2}\], значение изменится, если используются другие единицы измерения.

(\[m_{1}~и~m_{2}\]) — это массы двух частиц, которые обычно измеряются в килограммах.

r — это расстояние по прямой между двумя частицами, которое обычно измеряется в метрах.

В соответствии с законом всемирного тяготения Ньютона

Математически мы пишем:

Рассмотрим два объекта с массами \[m_{1}~и~m_{2}\], разделенные расстоянием r, как показано на рисунке.

(Изображение скоро будет загружено) 9{2}\]

Уравнение (4) известно как математическая форма закона тяготения Ньютона или закона гравитационной силы. Из уравнения (4) находим, что силы, действующие друг на друга, будут прямо пропорциональны произведению масс точек и обратно пропорциональны квадрату расстояния между ними. Он также известен как закон обратных квадратов. В некоторых статьях его также называют первым законом всемирного тяготения.

Гравитационная сила, действующая между двумя объектами, обусловлена ​​только их массой. Гравитационная сила является одной из четырех основных сил физики. Иногда ее также называют гравитацией Ньютона или гравитацией Ньютона. Сила гравитации действует во всей Вселенной. Для значительной гравитационной силы один из двух объектов должен быть больше другого.

Характеристики Силы Гравитации

Ниже приведены характеристики Силы Гравитации:

• Сила Гравитации является центральной силой.

• Гравитационная сила – это взаимная сила.

• Гравитационная сила зависит от массы.

• Гравитационная сила является силой притяжения.

• Гравитационная сила не зависит от присутствия других массовых тел.

• Сила гравитации — это сила дальнего действия.

• Сила гравитации универсальна.

• Гравитационная сила является самой слабой среди основных сил природы.

• Сила гравитации всегда притягивает и направлена ​​вдоль линии соединения двух взаимодействующих тел. {th}\].

Вес

• Из закона всемирного тяготения или закона тяготения Ньютона мы поняли, что масса является важнейшей сущностью. Между массой и весом всегда происходит путаница, мы считаем массу и вес одним и тем же, но на самом деле они взаимосвязаны, но отличны друг от друга.

• Вес — это гравитационная сила, действующая на любой объект определенной массы. Вес объекта можно оценить, умножив массу m объекта на ускорение силы тяжести g на поверхности Земли. Измеренное ускорение силы тяжести у поверхности Земли составляет около \[9{2}\].

• Мера того, сколько материи содержится в объекте, называется массой, а вес является мерой гравитационной силы, действующей на материал в данном гравитационном поле; таким образом, масса и вес пропорциональны друг другу.

• Вт ∝ м

• Где,

• м — Масса объекта

• W = мг

  9 0008

• Где,

• г — ускорение свободного падения. 9{4}\] 

  F = 19,59 Н

  Следовательно, сила притяжения между Землей и человеком равна 882,3 Н.

  2. Почему Луна не врезается в Землю? Какова величина гравитации на Луне в ньютонах?

  Ответ: Луна — естественный спутник Земли. Силы скорости и гравитации удерживают Луну на постоянной орбите вокруг Земли. Кажется, что Луна вращается вокруг Земли, не подвергаясь влиянию гравитации. Однако причина, по которой Луна остается на орбите, точна из-за гравитации.