Гравитационные силы, закон всемирного тяготения

 

Известно, что все тела в природе взаимно притягиваются друг к другу. И. Ньютон показал, что причина, вызывающая падение камня на Землю, движение Луны вокруг Земли и планет вокруг Солнца, одна и та же — это сила всемирного тяготения (гравитационная сила), действующая меж­ду любыми телами.

Гравитационные силы являются центральными, т. е. они направлены вдоль прямой, соединяющей взаимодействующие материальные точки.

Гравитационное взаимодействие между телами осущест­вляется с помощью гравитационного поля, порождаемого телами и являющегося одной из форм существования ма­терии. С каждым телом неразрывно связано гравитационное поле, проявляю­щееся в том, что на помещенную в поле материальную точку действует гравитационная сила, пропорциональная массе этой точки.

Закон всемирного тяготения был установлен Ньютоном в 1687 г. и формулируется так: две мате­риальные точки притягиваются друг к другу с сила­ми, прямо пропорциональными их массам и обратно пропорциональными квадрату расстояния между ними:

, (2. 23)

где – гравитационная постоянная, имеющая одно и то же значение для всех тел и равное – .

Физический смысл гравитационной постоянной заклю­чается в том, что она численно равна силе взаимодействия двух тел массой 1 кг каждое, расположенных на расстоя­нии 1 м друг от друга.

Легко видеть, что гравитационные силы весьма малы. Так, сила притяжения между двумя вагонами массы 30 т каждый, расположенными на расстоянии 5 м один от другого, равна 2,4

^. 10^-3 Н.

В формулу (2.23) для силы гравитационного взаимодейст­вия тел входят величины и — массы тел. Эти массы характеризуют гравитационное взаимодействие тел. С дру­гой стороны, как говорилось ранее, масса проявляет себя в качестве меры инертности в явлениях, описываемых вто­рым законом Ньютона. Поэтому, иногда первую называют гравитационной массой, а вторую — инертной массой.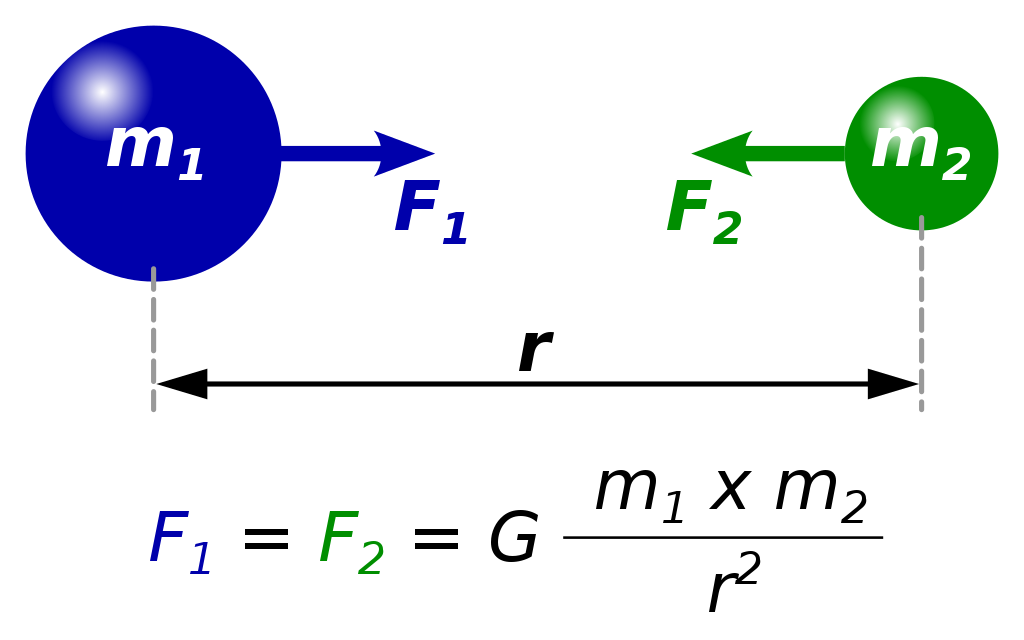 По­скольку в настоящее время эквивалентность обеих масс можно считать доказанной, в дальнейшем мы не будем их различать, но будем помнить, что

одной и той же величи­ной — массой — характеризуются два различных свойства тела.

Одним из проявлений силы взаимного тяготения яв­ляется сила тяжести — сила притяжения тел к Земле. Если на тело действует только сила тяжести, то оно совер­шает свободное падение. Следовательно, свободное падение — это движение тела в безвоздушном прост­ранстве (вакууме) под действием силы тяжести. Кинематические закономерности данного движения были рассмотрены нами выше.

Весом тела называется сила, с которой тело действует на горизонтальную подставку или на вертикаль­ный подвес вследствие гравитационного притяжения к Земле

. Это определение относится к системе отсчета, связан­ной с подставкой или подвесом. Оно соответствует прак­тике определения веса в земных условиях с помощью динамометра.

Рассмотрим, как изменяется вес тела, движущегося в вертикальном на­правлении с ускорением вместе с опорой (рисунок 2.1 а, б, в). На тело действуют сила тяжести и сила реакции опоры .

 

 

Рисунок 2.1 – Движение тела и опоры в вертикальном направлении

с различным ускорением.

 

Запишем основное уравнение динамики в векторной форме для трех случаев:

. (2.25)

В проекции на ось OY для каждого случая в отдельности:

1) если тело покоится, или движется равномерно и прямолинейно (рисунок 2.1 а), то

.

По третьему закону Ньютона модули сил .

Следовательно, вес тела

.

2) если тело движется вверх с ускорением (рисунок 2.1 б), то

.

Значит, (тело испытывает перегрузки).

3) если тело движется вертикально вниз с ускорением (рисунок 2.

1 в), то

.

Следовательно, вес тела

 

. (2.26)

Если , то .

Состояние тела, когда его вес равен нулю, называют невесомостью. Из сказанного выше видно, что всякое свободно падающее тело (т. е. тело, движущееся только под действием силы тяжести) находится в состоя­нии невесомости.

Таким образом, в общем случае вес тела при вертикальном движении может быть в об­щем случае выражен формулой:

 

. (2.27)

 

Закон всемирного тяготения лежит в основе расчетов скоростей движения спутников Земли и других космических тел. Для того чтобы тело стало искусственным спутником, его надо под­нять на некоторую высоту (вывести на орбиту) и сообщить ему горизон­тальную относительно поверхности Земли скорость. Для запуска спутников используются ракеты. После вывода на орбиту ракета раз­гоняет спутник до требуемой скорости, после этого спутник отделяет­ся от ракеты-носителя и продолжает свое движение по орбите только под действием силы тяготения.

Лекция 3 Закон со­хранения импульса

3.1 Законы сохранения и свойства пространства и времени

3.2 Импульс тела, закон со­хранения импульса

3.3 Уравнение движения тела переменной массы

3.4 Формула Циолковского

 

 

---

Дата добавления: 2017-01-08; просмотров: 4104; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

---

План конспект урока по физике в 10 классе «Закон всемирного тяготения. Движение в гравитационном поле.»

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №70 г. Липецка

План-конспект урока по физике

в 10 классе

«Закон всемирного тяготения.

Движение в гравитационном поле»

подготовила

учитель физики и математики

Мартынова Ольга Анатольевна

г.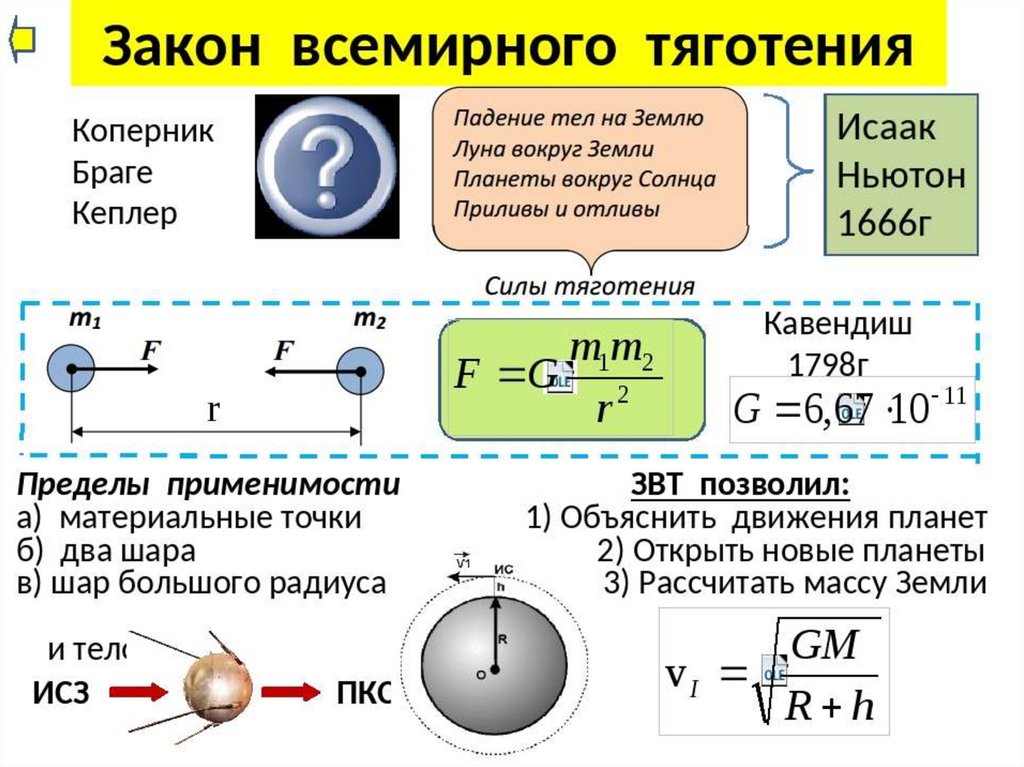 Липецк

2015

Цель урока – изучить закон всемирного тяготения, показать его практическую значимость. Шире раскрыть понятие взаимодействия тел на примере этого закона и ознакомить учащихся с областью действия гравитационных сил.

Тип урока: урок изучения нового материала.

Задачи урока:

Образовательные:

• изучить движение тел в гравитационном поле; выработать умения воспринимать и излагать новый материал;

• показать практическую значимость изученного материала;

• сформировать понятие гравитационных сил;

• добиться усвоения закона всемирного тяготения;

• познакомить с опытным определением гравитационной постоянной.

Воспитательные:

Развивающие:

• развивать речь, мышление;

• совершенствовать умственную деятельность: анализ, синтез, классификация, способность наблюдать, делать выводы, выделять существенные признаки объектов, выдвигать гипотезы, проверять результаты.

Оборудование к уроку: видеопроектор, экран, презентация

Домашнее задание: §15, упр15.

План урока:

1. Организация начала урока, формулировка темы и цели урока – 1 мин.

2. Повторение пройденного материала по теме « Основные понятия динамики» – 6 мин.

3. Новый материал – 12 мин.

4. Решение практической задачи – 6 мин.

5. Значение закона – 10 мин.

6. Применение закона – 8 мин.

7. Подведение итогов урока – 2 мин.

Организационный момент.

1. Создание проблемной ситуации.

(на слайде картинки падение тел на Землю, движение планет вокруг Солнца, приливы и отливы, планеты, Вселенная).

Вопрос учителя: Что общего между этими природными явлениями?

Что такое гравитация?

(отв. Гравитация – это взаимодействие между всеми телами на Земле и за ее пределами)

Сформулируем тему урока и запишем.

ТЕМА УРОКА: «ДВИЖЕНИЕ ТЕЛА В ГРАВИТАЦИОННОМ ПОЛЕ»

2. Для того, чтобы изучить данное явление вспомним необходимые понятия, которые понадобятся нам при изучении данной темы.

Вопросы:

1. Что такое сила? Единицы ее измерения?

2. Какие силы существуют в природе?

3. Чем характеризуется сила?

4. Сформулируйте второй закон Ньютона?

5. Какую роль в движении играет масса? Что такое масса?

6. Почему в борьбе и в боксе используют разделение спортсменов по весовым категориям?

7. Как движется тело если на него не действует сила?

8. Что такое свободное падение тел?

3. Изучение нового материала.

Лирическое отступление.

Видеоролик.

Гипотеза Ньютона: «Причина, вызывающая падение камня на Землю, движение Луны вокруг Земли и планет вокруг Солнца, одна и та же»

Ньютон предположил, что существует единый закон всемирного тяготения, которому подвластны все тела во Вселенной – от яблока до планеты.

Если бы я был Ньютоном

Давайте попробуем смоделировать ситуацию как будто время повернулось вспять и мы попали на триста лет назад. Каждый из вас стал бы Исааком Ньютоном.

Предложите: От каких величин зависит сила притяжения между телами?

(от массы, от расстояния между телами)

Сформулируйте задачу:

Определите силу с которой два тела массами M и m действуют друг на друга находящихся на расстоянии R друг от друга.

G = 6,67·10^-11 н·м²/кг² – гравитационная постоянная.

Формулировка (вывод): Два любых тела притягиваются друг к другу с силой, прямо пропорциональной произведению масс этих тел и обратно пропорционально квадрату расстояния между ними.

А теперь Вы побудьте Ньютонами и перенеситесь на триста лет назад. Решите задачу.

Рассчитайте силу притяжения между друг другом.

4. Ярчайшим примером применения закона Всемирного тяготения является запуск искусственного спутника Земли советскими учеными в 1957 году.

Вопрос: А что нужно сделать, чтобы тело стало искусственным спутником Земли?

Задача: Рассчитаем, с какой скоростью должно вылететь тело, чтобы стать искусственным спутником Земли, то есть обращаться вблизи Земли по круговой орбите.

— Земля является однородным шаром с радиусом 6400 км.

— На тело не действуют никакие силы, кроме силы тяготения, направленной к центру Земли.

— Спутник будем считать материальной точкой.

Р
ешение:

Ответ :

Вопрос: Что нужно, чтоб тело может стало искусственным спутником Земли?

(Нужно тело вывести за пределы земной атмосферы и придать ему определенную скорость, направленную по касательной к окружности, по которой он будет двигаться.)

Задача: Ваш космический корабль произвел вынужденную посадку на одну из планет Солнечной системы. Определить скорость космического корабля для запуска его на круговую орбиту планеты. Атмосферы планет разреженные (можно пренебречь силами сопротивления).

5. Решение задач.

1. Космический корабль массой 8 т приблизился к орбитальной космической станции массой 20 т на расстояние 500 м. Найдите силу их взаимного притяжения.

2. На каком расстоянии сила притяжения между двумя телами массой по

1 000 кг каждое, будет равна 6,67∙10⁹ Н?

3. Два одинаковых шарика находятся на расстоянии 1 м друг от друга и притягиваются с силой 6,67 ∙10^-15 Н. Какова масса каждого шарика?

VI. Закрепление нового материала.

Вопросы:

1.Какое явление называется всемирным тяготением?

2. Кто и когда открыл закон всемирного тяготения?

3. Как читается закон всемирного тяготения?

4. В каких случаях можно применять закон всемирного тяготения?

5. Притягивается ли к Земле яблоко, висящее на ветке дерева?

6. Домашнее задание.

Перспективное домашнее задание: Вам сообщили, что через год тяготение «отключится». Подготовить проект спасения человечества (срок 2 недели).

Список использованной литературы:

1. Я.И. Перельман. Занимательная физика. Книга 2. Москва. Наука, 2004г., с. 163-165.

2. Л.А.Горев. Занимательные опыты по физике. Москва. Просвещение, 2003г., с. 38-40.

3. В А.Золотов. Вопросы и задачи по физике. Москва. Просвещение, 2012 г

13. Закон всемирного тяготения. Поле тяготения, его напряженность и потенциальная энергия гравитационного взаимодействия.

Между всякими двумя материальными точками действуют силы взаимного притяжения, которые прямо пропорциональны массам точек и обратно пропорционально квадрату расстояния между ними (закон всемирного тяготения).

где F – сила взаимного притяжения материальных точек, m₁ и m₂ их массы, r – расстояние между точками, G – гравитационная постоянная (G =6.67*10^-11 м³/(кг*с

2))

ГРАВИТАЦИОННОЕ ПОЛЕ (поле тяготения), один из видов поля физического, посредством которого осуществляется гравитационное взаимодействие (притяжение) тел, например Солнца и планет Солнечной системы, планет и их спутников, Земли и находящихся на ней или вблизи нее тел.

Силовой характеристикой полей служит напряженность – векторная величина

где F – сила тяготения, действующая на материальную точку массой m, помещенную в некоторую точку поля.

Напряженность гравитационного поля, создаваемого планетой, массу M которой можно считать распределенной сферически-симметрично.

где r –расстояние от центра планеты до интересующей нас точки поля, находящейся вне планеты.

Потенциалом гравитационного поля называется скалярная величина

где П – потенциальная энергия материальной точки массой m, помещенной в данную точку поля.

Потенциал гравитационного поля, создаваемого планетой, массу M которой можно считать распределенной сферически-симметрично.

где r – расстояние от центра планеты до интересующей нас точки поля, находящейся вне планеты.

Потенциальная энергия гравитационного взаимодействия двух материальных точек массами m₁ и m₂ (шаров с массой, распределенной сферически-симмитрично), находящихся на расстоянии r друг от друга.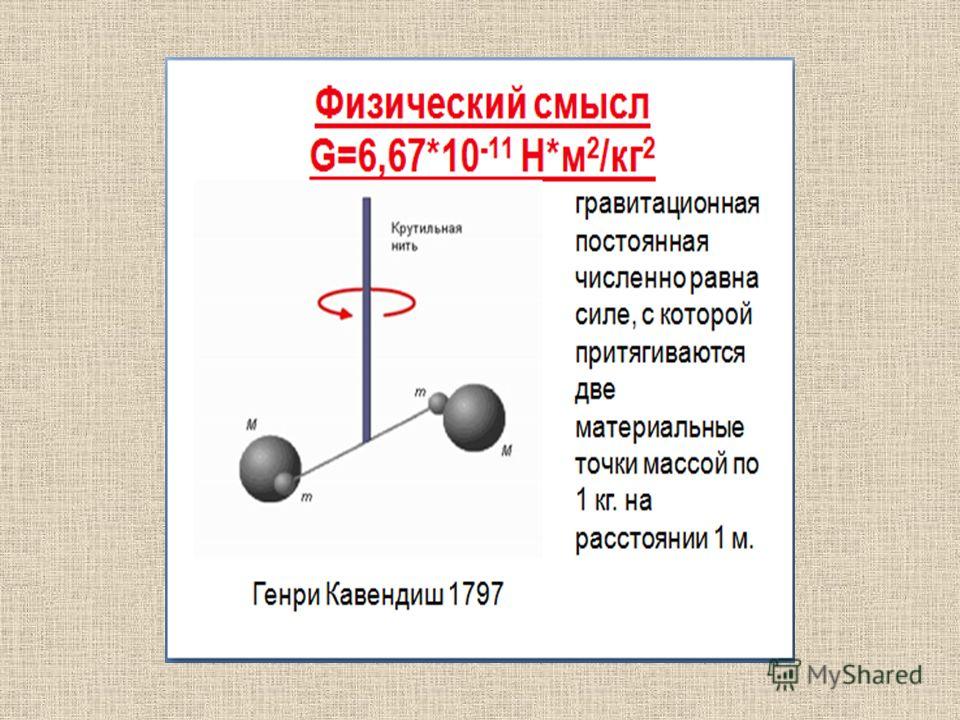

Потенциальную энергию бесконечно удаленных друг от друга материальных точек принято считать равной нулю.

Гравитационные поля (поля тяготения) являются потенциальными, то есть работа поля по перемещению тела из точки 1 в точку 2 не зависит от формы траектории, а определяется лишь разностью потенциальных энергий тела в точках 1 и 2 соответственно:

A₁₂ = П₁ – П₂.

Из этого равенства ясно, что определенный физический смысл имеет лишь разность потенциальных энергий в различных точках поля. Численное же значение потенциальной энергии в отдельной точке особого смысла не имеет, оно всегда определяется с точностью до некоторой постоянной величины. Вот почему при решении конкретных задач нулевой уровень потенциальной энергии можно выбирать произвольно, в наиболее удобной точке.

Космические скорости.

Первая космическая скорость — скорость, которую необходимо придать баллистическому снаряду, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы поместить его на круговую орбиту с радиусом равном радиусу планеты.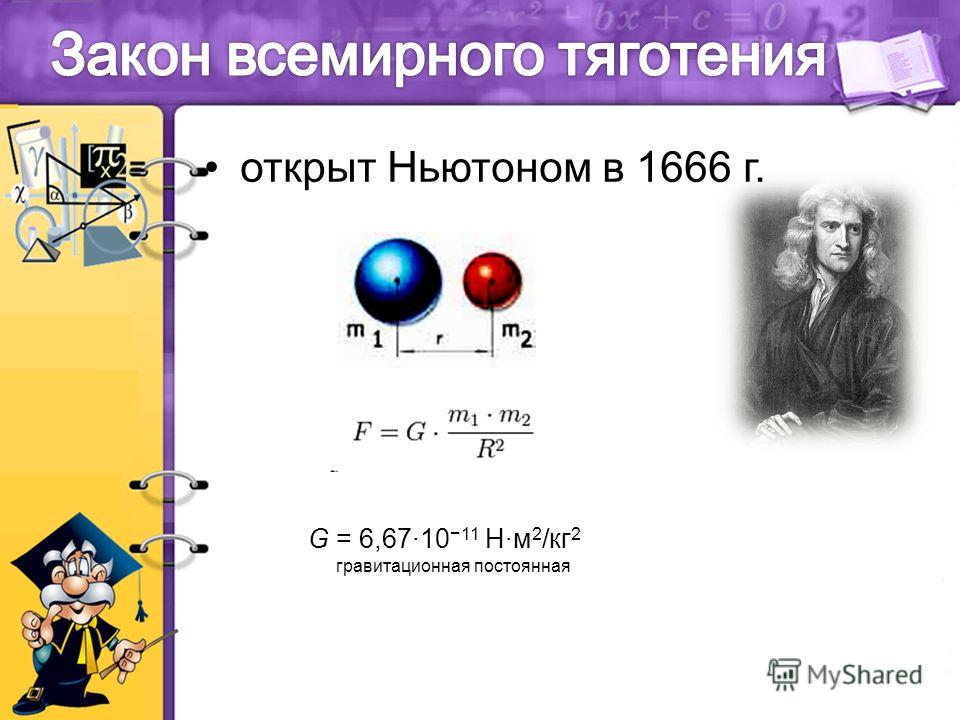 Иными словами, первая космическая скорость — это скорость, с которой надо бросить камень в горизонтальном направлении, чтобы он больше не упал на Землю. Для вычисления первой космической скорости необходимо рассмотреть равенство центробежной силы и силы тяготения действующих на снаряд на круговой орбите.

где m — масса снаряда, M — масса планеты, G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2), — первая космическая скорость, R — радиус планеты. Подставляя численные значения (для Земли, M = 5,97·1024 кг, R = 6 378 000 м), найдем

7,9 км/с

Первую космическую скорость можно определить через ускорение свободного падения — так как g = GM/R², то

.

Первой космической скорости недоста точно для того, чтобы тело могло выйти из сферы земного притяжения. Необходимая для этого скорость называется второй кос мической. Второй космической (или пара болической) скоростью v₂ называют ту наименьшую скорость, которую надо со общить телу, чтобы оно могло преодолеть притяжение Земли и превратиться в спут ник Солнца, т.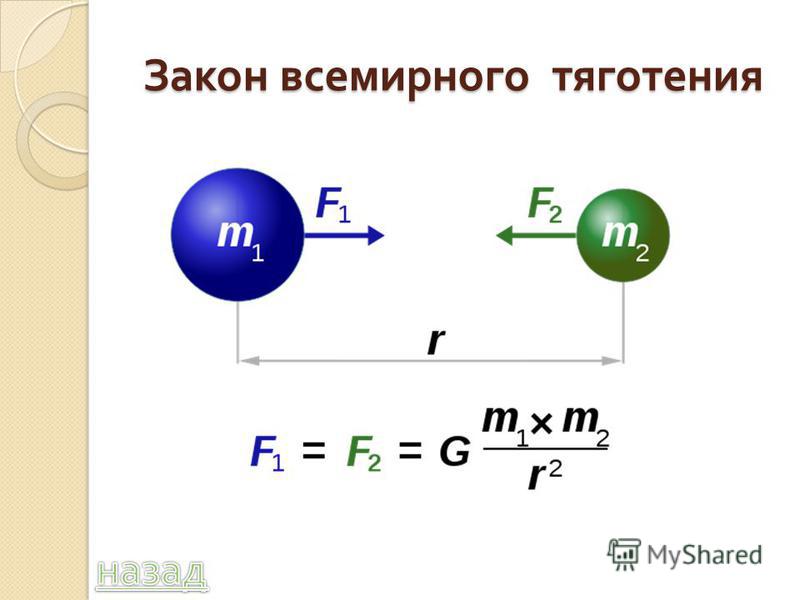 е. чтобы его орбита в поле тяготения Земли стала параболической. Для того чтобы тело (при отсутствии со противления среды) могло преодолеть земное притяжение и уйти в космическое пространство, необходимо, чтобы его кине тическая энергия была равна работе, совершаемой против сил тяготения:

Между первой и второй космическими скоростями существует простое соотношение:

Для того чтобы покинуть пределы солнечной системы, тело должно преодолеть, кроме сил притяжения к земле, также и силы притяжения к Солнцу. Необходимая для этого скорость запуска тела с поверхности Земли называется третьей космической скоростью V3. Скорость V3 зависит от направления запуска. При запуске в направлении орбитального движения Земли эта скорость минимальна и составляет около 17 км/с. При запуске в направлении, противоположном направлению движения Земли, V3 равняется примерно 73 км/с.

Закон всемирного тяготения Ньютона

Гравитационное поле

Рис. 1. Однородное поле

Рис. 2. Гравитационное поле
в большем масштабе.

Рис. 3. Гравитационное
поле Земли в целом.

Мы можем представить силу гравитационного притяжения в виде поля. Поле — это графическое представление силы силы и направления, в котором ощущается сила.

В локальной области на поверхности Земли гравитационное поле практически однородно. Мы можем видеть это, потому что количество линий поля на единицу не меняется. Если бы сила была сильнее в определенной области, количество силовых линий в этой области увеличилось бы. Силовые линии действуют вниз к центру Земли, но в этом масштабе гравитационное поле однородно, как показано на рисунке 1.

В более широком масштабе гравитационное поле меняется по направлению и величине. Направление силовых линий перпендикулярно поверхности Земли. По мере увеличения высоты над поверхностью Земли величина силы уменьшается, о чем свидетельствует увеличение расстояния между силовыми линиями.

Если рассматривать Землю в целом, (рис. 3), гравитационное поле направлено к центру Земли. На противоположных сторонах Земли гравитационное поле имеет противоположную величину.

Универсальный закон всемирного тяготения

Земля оказывает гравитационное воздействие на человека, а человек оказывает такое же, но противоположное воздействие на Землю. Исаак Ньютон был первым, кто понял, что причиной падения яблок на землю является гравитация, но эта же сила удерживает Луну на орбите вокруг Земли.

Рис. 4. Сила пропорциональна
массе и обратно пропорциональна
квадрату расстояния

Сила тяжести всегда действует между парами тел и пропорциональна их массам. Однако сила тяжести также зависит от расстояния между двумя телами. По мере того, как два тела удаляются друг от друга, гравитационная сила между ними уменьшается пропорционально квадрату их расстояния друг от друга.

(1)

, где m и M — массы двух тел соответственно, а r — расстояние между центрами масс двух тел. Константа пропорциональности называется универсальной постоянной гравитации или также «большой G» и имеет значение 6,67 x 10 9 .0039 -11 Н.м ² .кг ^-2 или м ^3. кг ^-1 .с ^-2

Flash анимация. Сила тяжести на массу 1 кг.

Ускорение свободного падения

Мы знакомы с измерением веса объекта как силы, притягивающей его к центру Земли, используя F = мг . Объединяя это уравнение с уравнением всемирного закона тяготения, мы получаем г = гм/г ² . Таким образом, сила тяжести зависит от массы тела и обратно пропорциональна квадрату расстояния r .

Невесомость

Когда космонавт парит в космосе, он чувствует, что не имеет веса, но, как мы видели, сила гравитации распространяется далеко за пределы атмосферы. Она уменьшается пропорционально квадрату расстояния, но на каждый объект действует гравитационная сила. Невесомость возникает из-за того, что космический корабль и все, что внутри, движется по орбите, и поэтому все падает с одинаковой скоростью.

Изменение g с расстоянием

Гравитационное ускорение Земли уменьшается с высотой над поверхностью с обратной квадратичной зависимостью. На поверхности Земли г = GM _E /R _E . На расстоянии, равном удвоенному радиусу Земли от центра Земли, 2 r _E ускорение свободного падения равно GM _E /4. В 3 р _Е , г = ГМ _Е /9и так далее.

9 ²
3 9.0110 4 r _E

р	г
1 r E	GM / r E 2
2 r E	GM /4 r E 2
3 R E	GM / R E 2
GM /16 r E 2
5 r E	GM /25 r E 2

График показывает это изменение как функцию расстояния от центра Земли

Рисунок 5. Изменение g в зависимости от расстояния, измеренного в единицах радиуса Земли. Зеленая линия показывает более точные теоретические значения.

Рисунок 6. Расчет г внутри Земли

Какова ценность г внутри Земли? Если мы предположим, что Земля имеет постоянную плотность, мы можем вычислить массу из уравнения

масса = плотность x объем

Предположим также, что Земля имеет сферическую форму (на самом деле это сплюснутый сфероид, то есть шире на экваторе, чем на полюсах). Объем шара V = 4/3 π r _E ³ . Где r _E — радиус Земли (6400 км).

Если бы мы углубились в землю на расстояние ч , новый радиус был бы r _E — ч . Масса, создающая гравитационную силу, равна (4/3) π ( r _E — h ) ³ ρ

Тогда значение ускорения свободного падения внутри Земли равно

g = (4/3) G π ( r _E — h ) ³ ρ/( r _E — h ) ² = (4/3) G ρ π ( r _E — h )

Имеет линейную или прямолинейную зависимость от радиуса. Плотность можно найти, рассчитав массу и объем Земли. ρ=M _E /V _E .

Более продвинутое теоретическое предсказание величины силы тяжести показано зеленой линией на рисунке 6. Реальное изменение силы тяжести зависит от изменения плотности материала с глубиной.

Картографирование изменения g

Изменение гравитационного поля Земли постоянно и точно измеряется спутниками Gravitational Recovery And Climate Experiment (GRACE). Эти спутники следуют друг за другом на одинаковых орбитах, но разделены небольшим расстоянием друг от друга. Спутники

(GRACE) измеряют изменение гравитационного поля Земли.

Если бы плотность Земли была постоянной, то расстояние между спутниками не менялось бы по мере их обращения вокруг Земли. Однако небольшие изменения в гравитационном поле заставляют спутники сближаться или отдаляться друг от друга.

Аномалии гравитационного поля Земли (миллигалы).

Изменение гравитационного ускорения Земли показано на рисунке. Изменение гравитации составляет 9,80665 мс ² ± 50 миллигал (галилео — это единица ускорения в сгс, 1 галлон = 0,01 м/с ² ).

Гравитационная сила и Луна

Ньютон был первым, кто предположил, что сила, ответственная за притяжение объектов к земле (например, яблок), также может отвечать за удержание Луны на ее круговой орбите. Он знал, что гравитационная сила уменьшается с высотой над поверхностью Земли, но не знал, как она меняется. Расстояние от Земли до Луны было точно установлено, как и время, необходимое Луне для обращения вокруг Земли. Из этой информации Ньютон смог вычислить ускорение свободного падения, ответственное за центростремительную силу. С T как 27,3 дня, r как 384 000 км или около 60 земных радиусов. Ускорение a = v ² / r = (2π r/T ) ² /r это 0,00272 мс ² . Ускорение свободного падения на Земле g _E составляет 9,81 мс ^-2 . Отношение g _E / g _m ≈3600, означающее, что гравитационная сила притяжения, удерживающая Луну на орбите, в 3600 раз меньше, чем на Земле. На расстоянии 60 r , в 3600 раз меньшая гравитация была бы такой же, как если бы гравитационная сила имела обратную квадратичную зависимость. (т. е. 60 r ² . Ньютон открыл, как закон всемирного тяготения уменьшается с расстоянием, просто зная время, необходимое Луне для обращения вокруг Земли, ее расстояние от Земли и значение силы тяжести на Земле. Что составляет еще одна причина, почему он считается одним из выдающихся ученых в истории

Гравитационная сила и движение планет

В то время было убедительно, что Луна вращалась вокруг Земли под действием гравитации. Это не обязательно означало, что планеты также удерживались на своих орбитах гравитационной силой. Кеплер открыл три закона движения планет. Его третий закон гласит, что квадрат периода движения по отношению к кубу расстояния является константой. Если предположить, что планеты вращаются вокруг Солнца по круговой орбите, то центростремительное ускорение равно a = 9.0033 v ² / r _m , где v — скорость движения Луны вокруг Земли. Скорость определяется расстоянием/временем, где расстояние — это длина окружности, 2π r орбиты, а T — период обращения Луны. Следовательно, скорость равна (4π ² / r ² )

Центростремительное ускорение обеспечивается ускорением свободного падения. Его величина г = ГМ ₀ / р ² .

a = v ² / r =(4π r _m ² / T ² )/ r

Therefore, GM ₀ / r ² =4πr _m / T _m ²

T ² / r _m ³ =4π ² GM ₀

Поскольку масса и универсальная гравитационная постоянная не меняются, Ньютон показал, что сила гравитации отвечает за удержание планет на их орбитах.

Гравитационный потенциал

Определение поля гравитационного потенциала:

Потенциал определяется как работа, совершаемая при перемещении тела единичной массы из бесконечности в точку. Так как работа над телом совершается под действием силы тяжести, то совершенная работа отрицательна.

С точки зрения математики,

Нуль для гравитационного потенциала берется на бесконечности, потому что это удобная точка отсчета для любого объекта во Вселенной. Помните, что для нуля гравитационной потенциальной энергии мы выбираем Землю в качестве удобной точки отсчета. В этом нет несоответствия, так как существенны только различия в потенциале.

Гравитационный потенциал всегда отрицательный, что указывает на то, что поле работает, приближая объект. На рисунке ниже показан гравитационный потенциал Земли и Луны. Потенциальные поля складываются алгебраически. Мы видим, что для отправки ракеты на Луну нам нужно только создать силу, чтобы ракета вышла из поля гравитационного потенциала Земли и вошла в поле гравитационного потенциала Луны.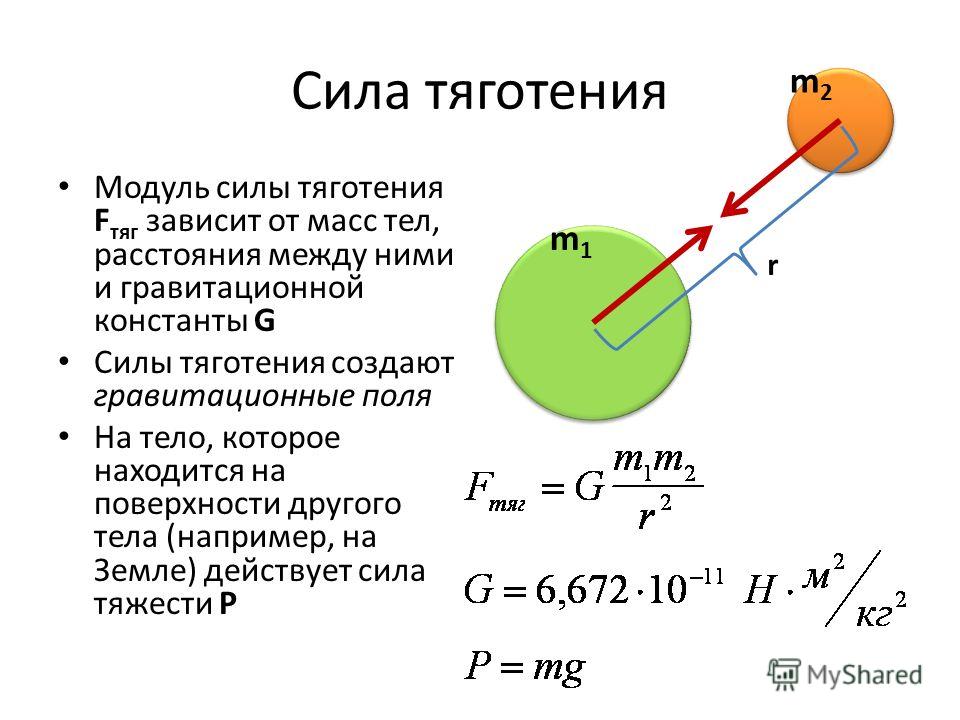 После этого ракета будет ускоряться к Луне за счет потенциала Луны.

Гравитационный потенциал Земли, Луны и их сумма.

Сила, действующая на объект при заданном потенциале, определяется наклоном потенциала в этой точке.

Скорость убегания

Если кинетическая энергия, сообщаемая объекту, равна гравитационному потенциалу, то без учета сопротивления воздуха объект может покинуть гравитационное поле Земли.

Обратите внимание, что скорость убегания не зависит от массы объекта, но зависит от массы тела, M от которого пытаются сбежать.

Итак, если мы хотим, чтобы ракета вырвалась из гравитационного поля Земли, с какой скоростью она должна двигаться, прежде чем двигатели перестанут ее разгонять?

Наши состояния формулы, V = √ (2 GM / R )

V = √ (2 x 6,67 x 10 ^-11 [N.M ² .KG ^-2 ] x 5.9766. x 10 ²⁴ [кг]/6,378 x 10 ⁶ [м]

v = 11,17 x 10 ⁶ [мс ^-1 ] ≈ 11.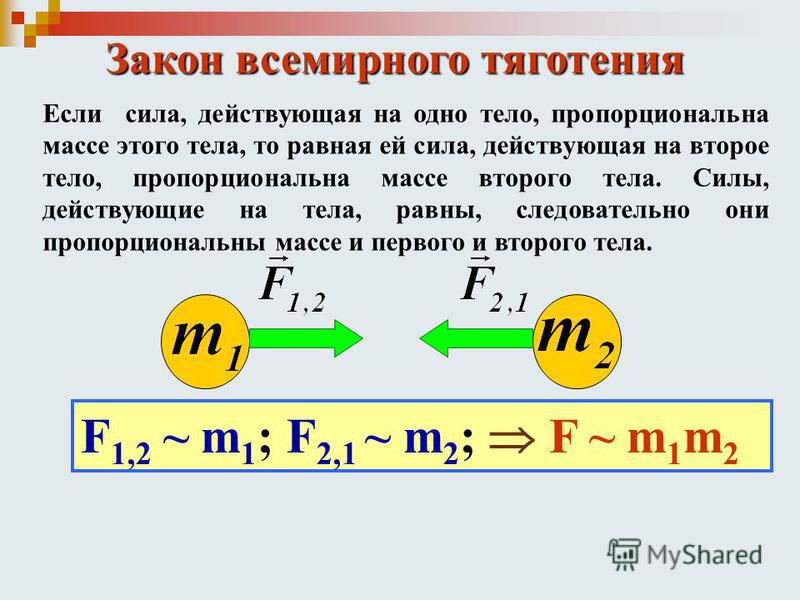 2 km.s ^-1

Body	Mass x M E	Radius x r E
Mercury	0.0558	0.398
Venus	0.815	0.95
Earth	1	1
The Moon	0.0123	0.273
Mars	0.107	0.532
Jupiter	318	11.2
Saturn	95.1	9.41
Uranus	14.5	4.06
Neptune	17.2	3.88

Table 2 , Массы и радиусы планет в нашей Солнечной системе. Международный астрономический союз (МАС) постановил, что Плутон больше нельзя классифицировать как планету, а как карликовую планету, поэтому он был исключен из списка. Однако его масса и радиус равны (0,01 м _E и 0,2 r _E ) соответственно. Также показаны данные для Луны.

Потенциальная гравитационная энергия

Помните определение потенциальной гравитационной энергии, P.E. = м г · ч , и теперь мы говорим, что гравитационный потенциал равен В = — Гм · / r . Нет ли какой-то нестыковки? Можно показать, что различия в потенциальной энергии важны.

Пусть r = r _E + h , где h << r _E . Затем V ( R ) — V ( R _E ) = GMM (1/ R _E -1/ R ) является разницей в потенциале гравита.

GMm ( r _E + h — r _E )/( r _E ( r _E + h )

≈ GMm ( h / r _E ² )

= mgh since g = GM / r ²

Summary

Fields are a графическое изображение сил, действующих на единицу массы в пространстве. Сила поля определяется количеством линий поля на единицу площади. Гравитационные поля всегда притягательны.

Сила между двумя телами массами M и m равна F=GMm/r ² где M и m — массы двух тел, r — расстояние между ними. Где G — универсальная постоянная гравитации G = 6,67 x 10 ^-11 [Н·м ² кг ^-2 ] или [кг]

Гравитационное поле — Scienceaid

Под редакцией Tosin Emmanuel, Sharingnowledge, Jen Moreau, Sarmal

7 Части:

Гравитационное поле

Универсальный закон гравита0005

Гравитационный потенциал

Скорость убегания

Ссылка на эту статью

Комментарии

Содержание

• 1 Гравитационное поле
• 2 Универсальный закон всемирного тяготения
• 3 Связь между ускорением свободного падения и гравитационной постоянной
• 4 Гравитационный потенциал
• 5 Скорость убегания
• 6 Ссылка на эту статью
• 7 комментариев

Гравитационное поле

Оксфордский словарь английского языка определяет гравитационное поле как «область пространства, окружающую тело, в которой другое тело испытывает силу гравитационного притяжения», ^[1] . Когда сэра Исаака Ньютона ударили яблоком по голове, когда он сидел под деревом, он обнаружил притяжение к земной поверхности, которое назвал гравитационной силой. Это открытие привело Ньютона к фундаментальным исследованиям силы притяжения между двумя поверхностями или массами в гравитационном поле. 92

Где M1= Первое тело (масса)

 М2= Второе тело (масса)
            r = расстояние между двумя телами
           G = гравитационная постоянная, равная 6,67x10-11 Нм-2/кг2.
 

Связь между ускорением свободного падения и гравитационной постоянной

Гравитационная постоянная (G) используется для расчета силы притяжения между любыми двумя массами. Ускорение свободного падения (g) — это ускорение у поверхности земли из-за притяжения между массой земли и объектами, притягиваемыми к земле, которые находятся близко к поверхности земли.

Было ли это полезно? Да | Нет| Мне нужна помощь

На самом деле значение G не постоянно на поверхности земли. Например, гравитационная постоянная, зарегистрированная в полярных областях, бесспорно отличается от гравитационной постоянной вблизи экватора. Его значение варьируется в зависимости от земной поверхности. Важно обсудить взаимосвязь между гравитационной постоянной (G) и ускорением свободного падения (g), потому что она дает нам точное значение одного, если другое известно в любой точке земного шара. 92- _Е

Где ME= масса земли

 G= Гравитационная постоянная
            rE= радиус земли
 

Потенциал гравитации

Потенциальная гравитационная энергия между двумя объектами определенной массы представляет собой потенциал движения объектов, вызванный их гравитационным притяжением. Это притяжение превращает потенциальную энергию в кинетическую энергию, и объекты будут двигаться навстречу друг другу.

Было ли это полезно? Да | Нет| мне нужна помощь

Гравитационный потенциал можно описать как работу, совершаемую при переносе единицы массы из бесконечности на поверхность,

Математически,

  В=ГМ/р 
 

Где V=гравитационный потенциал М = Масса r = расстояние друг от друга

Скорость убегания

Скорость убегания — это скорость, с которой объект должен двигаться, чтобы освободиться от гравитации планеты и покинуть ее без дальнейшего движения. Кроме того, это скорость или скорость, необходимая объекту для удаления под действием силы тяжести. 92=2g_E

  v=√(2gr_E ) 
 

Где v=скорость требуется, чтобы покинуть планету (скорость убегания)

 rE=радиус Земли
            g = ускорение свободного падения
 

Из приведенного выше выражения для скорости убегания мы можем вычислить скорость убегания любой планеты. Скорость убегания Земли составляет 11313 мс-1, а скорость убегания Луны — 2456 мс-1. Чем больше планета, тем выше скорость убегания.

Было ли это полезно? Да | Нет| Мне нужна помощь

Ссылка на эту статью

Если вам нужно сослаться на эту статью в своей работе, вы можете скопировать и вставить следующее в зависимости от требуемого формата:

АПА (Американская психологическая ассоциация)
Гравитационное поле. (2017). В ScienceAid . Получено 20 октября 2022 г. с https://scienceaid.net/Gravitational_Field

MLA (Modern Language Association) «Гравитационное поле». ScienceAid , scienceaid.net/Gravitational_Field, дата обращения 20 октября 2022 г.

Чикаго/Турабиан ScienceAid.net. «Гравитационное поле». По состоянию на 20 октября 2022 г. https://scienceaid.net/Gravitaional_Field.

Комментарии

1. ↑ https://en.oxforddictionaries.com/definition/gravitational_field

Категории : Физика

Недавние правки: Джен Моро, Sharingknowledge, Тосин Эммануэль 9-2 \end{align}

Закон всемирного тяготения Ньютона по форме очень похож на закон Кулона (который имеет дело с электрическими зарядами), однако гравитация всегда притягивает. Существуют положительные и отрицательные электрические заряды, но никто никогда не наблюдал «отрицательную массу».

8.2.2 Определение напряженности гравитационного поля

8.2.3 Выведите выражение для гравитационного поля как функцию расстояния от точки массы.

В физике часто говорят о полях (электрических, магнитных, гравитационных…). Поля — это абстрактное понятие. Цокос описывает поле так: «…поле [A] в этом контексте означает, что в каждой точке пространства определена определенная величина». Для гравитации это означает, что если мы поместим массу в гравитационное поле, масса почувствует приложенную к ней силу. 92} \end{align}

Мы видим, что сила гравитационного поля — это просто ускорение силы тяжести в данном месте. Сила гравитационного поля является векторной величиной (как и большинство полей), она указывает направление, в котором масса будет ускоряться, если ее поместить в поле.

Примечание. Нижние индексы 1 и 2 или буква «m» в нижнем регистре являются просто метками и сами по себе не важны.

8.2.4 Выведите выражение для гравитационного поля на поверхности планеты. 92} \end{align}

«Гравитационное поле» — это способ визуализировать ускорение или силу массивного тела. Гравитация всегда притягивает, и поэтому «гравитационное поле» для одиночного массивного тела выглядит так, как показано на рисунке ниже:

Украдено у Цокоса, 2-е издание, стр. 288

8.2.5 Решить задачи, связанные с гравитационными силами и полями.

Пример 1: Найдите среднюю силу между Солнцем и Землей.

+Решение

Пример 2: Если расстояние между двумя телами увеличить вдвое, что произойдет с гравитационной силой между ними?

+Решение

Пример 3: Найдите ускорение свободного падения на планете, масса которой в 10 раз больше массы Земли, а радиус в 20 раз больше.

+Решение

8.2.6 Определение гравитационной потенциальной энергии и гравитационного потенциала

В прошлом мы определяли гравитационную потенциальную энергию как , где m — масса объекта, g — ускорение свободного падения, а h — высота над определенная (выбранная) точка нулевой потенциальной энергии. Это справедливо только тогда, когда ускорение силы тяжести или сила гравитационного поля постоянны.

Возьмем в качестве примера массу m на расстоянии R от массы M, как показано ниже.

Цокос 2-е изд. Pg 289

Если масса перемещается, работа, совершаемая над массой, равна изменению потенциальной энергии (при условии, что движение медленное, чтобы не добавлять кинетическую энергию). Работа определяется как , однако сила не постоянна и зависит от расстояния. Чтобы найти экспресс для работы нужен исчисление, вывод ИБ не обязательная информация, привожу просто для интересующихся. 9\inf{} \end{align}

Примечание: проделанная работа отрицательна. Это потому, что сила и перемещение направлены в противоположные стороны. Это также делает гравитационную потенциальную энергию отрицательной.

Отсюда мы можем сказать, что два тела с массой, разделенной расстоянием R, обладают потенциальной энергией:

(16)

\begin{align} PE_g = -G {m_1 m_2 \over R} \end{align}

Если масса переместится очень далеко, в бесконечность, масса будет иметь нулевую гравитационную потенциальную энергию!

Потенциальная энергия отрицательна, потому что мы определили потенциальную энергию равной нулю, когда объекты бесконечно далеко друг от друга (что имеет смысл). Совершенная работа или изменение потенциальной энергии совершенно не зависит от пройденного пути, т. е. зависит только от начального и конечного положения. Это верно при работе с консервативными силами (гравитация, электричество, магнетизм…).

На диаграмме справа масса m перемещалась по показанному пути (большая зеленая точка — планета с массой M) выполненная работа:

(17)

\begin{align} W = -G {Mm \over R} \end{align}

8.2.7 Укажите выражение для гравитационного потенциала, обусловленного точечной массой.

В физике мы говорим о потенциалах, их не следует путать с потенциальной энергией, они связаны, но это разные вещи.

Гравитационный потенциал — это поле, но это скаляр, а не вектор. Один из способов представить гравитационный потенциал состоит в том, что это гравитационная потенциальная энергия на единицу массы. Гравитационный потенциал, обусловленный точечной массой (или однородной сферой), можно математически описать как:

(18)

\begin{align} V = — {E_p \over m} = — G{M \over r} \end{align}

Где V — гравитационный потенциал. Гравитационный потенциал дает нам способ описать «гравитацию» из-за одной массы. Мы можем получить некоторую информацию о гравитации без необходимости использовать или знать о второй массе.

В физике более высокого уровня понятие потенциала может быть очень полезным, градиент (математическая операция) гравитационного потенциала равен отрицательному значению напряженности гравитационного поля.

8.2.8 Объясните понятие скорости убегания.

Когда масса подбрасывается вверх с низкой начальной скоростью, она падает обратно. Из энергетического аргумента можно сказать, что это результат того, что объект имеет ненулевую (или отрицательную) потенциальную энергию, есть потенциальная энергия, которая пытается заставить массу упасть обратно. Но если бы объект мог иметь нулевую гравитационную потенциальную энергию, он бы никогда не упал обратно. Полная энергия массы m, где единственной действующей силой является сила тяжести из-за второй массы M, может быть описана как: 92 -G{Mm \over r} \end{align}

В этом уравнении мы предполагаем, что масса M постоянна.

Если мы хотим отправить спутник за пределы Земли или за пределы Солнечной системы для разведки или исследования, нам в основном нужно иметь возможность подбросить его вверх, чтобы он не упал обратно. Чтобы что-то не упало обратно, оно должно быть «свободным от гравитации». Как упоминалось ранее, если объект перемещается в «бесконечность», у него не будет гравитационной потенциальной энергии, то есть он свободен от эффектов гравитации. Сила гравитации не имеет ограничений на то, как далеко она простирается, отсутствие гравитации означает, что кинетическая энергия объекта (при условии отсутствия других сил) больше, чем его гравитационная потенциальная энергия. 92 — G{Mm \over r} = 0 \end{align}

(22)

\begin{align} v_{escape} = \sqrt{G{2M \over r}} \end{align}

Эта скорость известна как скорость убегания. гравитационное притяжение другой массы M. Обратите внимание, что скорость убегания не зависит от массы объектов. Скорость убегания Земли составляет примерно 11 км/с ^-1 .