Закон Био–Савара • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Магнитное поле в точке пространства, создаваемое малым отрезком проводника, по которому течет электрический ток, пропорционально силе тока, обратно пропорционально квадрату расстояния от этой точки до проводника и направлено перпендикулярно по отношению и к току, и к направлению на проводник.

Одним из величайших прорывов в естествознании XIX века стала серия открытий, позволивших установить неразрывную связь между двумя, казалось бы, не связанными между собой природными феноменами — электричеством и магнетизмом, — которые на поверку оказались просто двумя сторонами одной медали. Одним из первых фрагментов пазла, который предстояло собрать ученым, стало осознание того, что движущиеся электрические заряды (то есть электрический ток) могут порождать магнитное поле. Это открытие сделал датский ученый Ханс Кристиан Эрстед (см. открытие Эрстеда), а представил его в количественной форме французский ученый Андре-Мари Ампер (см.

Закон Ампера). Обобщением этой работы стал закон Био—Савара (его еще называют «закон Био—Савара—Лапласа». — Прим. переводчика), содержащий окончательную формулировку соотношения между электрическими токами и магнитными полями, которые они производят.

Жан Батист Био, яркий и смелый ученый, был профессором физики в Сорбонне и действительным членом французской Академии наук. Сразу после открытия Эрстеда вместе со своим коллегой Феликсом Саваром он принялся за изучение взаимосвязи между электрическим током и магнитными полями.

В отличие от Ампера, изучавшего магнитные поля опосредованно, путем измерения силы взаимодействия между парами проводников с током, Био и Савар предприняли прямые измерения магнитных полей, используя для этого множество легких магнитных стрелок компасов. Смысл их закона проще всего понять, если представить себе, что проводник с током разбит на крошечные отрезки — т. н.

элементы тока (такой подход предложил ученым их старший коллега Пьер Симон Лаплас (Pierre-Simon Laplace, 1749–1827), стоявший у истоков дифференциального и интегрального исчисления, который затем и обобщил полученные результаты.  — Прим. переводчика). На каждом из этих крошечных отрезков кривизной проводника можно пренебречь — их можно рассматривать как отрезки прямой. Так вот, согласно закону Био—Савара, магнитное поле В на расстоянии r от такого элемента тока пропорционально

IL/r²

где I — сила тока, а L — длина элемента тока.

Я уже упоминал, что закон Био—Савара является наиболее полным формальным обобщением взаимосвязи между электрическим током и магнитным полем. Это значит, что можно взять проводник с током сколь угодно сложной и асимметричной конфигурации и разбить его на элементы тока. Каждый элемент вносит свой вклад в магнитное поле в рассчитываемой точке. Сделав эти расчеты, мы можем затем просуммировать вклад от каждого элемента проводника и найти общее магнитное поле (этот процесс суммирования относится к области высшей математики и выглядит он достаточно сложно). Таким образом, закон Ампера является частным случаем закона Био—Савара для случая линейного проводника.

Я еще не сказал, что закон Био—Савара предсказывает также направление получающегося магнитного поля. Это направление можно определить с помощью так называемого правила правой руки, ставшего настоящим бичом целых поколений студентов физических и технических вузов. Правило гласит: если вытянутый указательный палец правой руки показывает направление электрического тока в элементе тока, а средний палец направлен на точку, в которой вы вычисляете магнитное поле, то выставленный под прямым углом к двум другим пальцам большой палец укажет направление магнитного поля.

Как я уже говорил, полное математическое выражение закона Био—Савара требует довольно сложных вычислений, поскольку оно представляет собой интегральное уравнение. Оно является, по сути, общим решением четвертого уравнения Максвелла.

См. также:

Векторный анализ закона Био – Савара – Лапласа

Векторный анализ закона

                Био – Савара — Лапласа

 

       Магнитное поле проводника с током в электродинамике определяется законом Био – Савара – Лапласа.

      Этот закон оперирует векторами, направление которых не совпадает с векторами, наблюдаемыми в эксперименте. Тройка векторов, получаемая из этой формулы, и тройка векторов, наблюдаемая в эксперименте, различны.

       Это произошло потому, что существующая физическая модель электрического тока не позволяет правильно направить вектора напряженностей физических полей.

Векторный анализ закона Био – Савара – Лапласа показал, что в   эксперименте направление электрического и магнитного вектора лежат в разных плоскостях (перекрещиваются).

Вектора, полученные из закона Био – Савара – Лапласа, пересекаются. Они образуют тройку векторов, не совпадающую с тройкой векторов, наблюдаемой в эксперименте.

Эмпирическое правило правого винта (буравчика) в электродинамике определяет направление магнитного поля проводника с током, которое не совпадает с направлением магнитного поля, полученного из закона Био – Савара — Лапласа. 

«Головка винта, ввинчиваемого по направлению электрического тока, вращается в направлении линий магнитной индукции». [1]

Правило правого винта (буравчика) предполагает, что вектора  перекрещиваются (рис.2), т.е. они не имеют общего начала.

Закон Био – Савара – Лапласа описывает пересекающиеся вектора (рис.8.1), которые имеют общее начало.

 «Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж. Био (1774 — 1862) и Ф. Саваром (1791 — 1841). Результаты этих опытов были обобщены выдающимся французским математиком и физиком П. Лапласом.

Закон Био — Савара — Лапласа для проводника с током , элемент  которого создает в некоторой точке А (рис. 1) индукцию поля , записывается в виде

,                   (1)

где  — вектор, по модулю равный длине  элемента проводника и совпадающий по направлению с током,

 — радиус — вектор, проведенный из элемента  проводника в точку А поля,

 — модуль радиуса — вектора .

Направление  перпендикулярно  и , т.е. перпендикулярно плоскости, в которой они лежат, и

совпадает с касательной». [1]

Из эксперимента следует вывод, что тройка векторов перекрещивается. Из  формулы (7) следует другой вывод: тройка векторов имеет общее начало, т.е. они пересекается.

 

Рис. 1. Тройка векторов, соответствующая закону          Био – Савара — Лапласа.

 

       Перекрещивающиеся вектора (рис.2) не могут быть приведены к общему началу (рис.1), поэтому основная формула закона Био – Савара – Лапласа, вектора которой имеют общее начало, физически не корректна.

Покажем это. На (рис. 1.) показана правая тройка векторов ,  и , построенная в соответствии с аксиомами векторной алгебры по формуле (1).      

        В векторной алгебре есть несколько условий векторного произведения векторов  и , результатом которого является     вектор .

1. Вектор  ортогонален векторам  и .

2. Если   и  не коллинеарные, то  векторы ,  и  образуют правую тройку векторов.

Сравним теоретическую тройку векторов, получаемых из закона Био – Савара – Лапласа (рис. 1), с тройкой векторов, наблюдаемой в реальном физическом эксперименте (рис. 6.2).

Рис. 2. Тройка векторов, наблюдаемая в физическом эксперименте.

 

Тройки векторов на рис. 1 и рис. 2 не совпадают.

        На (рис. 1) вектор имеет точку приложения .

        На (рис. 2) — точку  приложения .

         На (рис.1) вектор  перпендикулярен касательной, а на    (рис.2) совпадает с ней.

Очевидно, что вектора, выведенные из закона Био — Савара — Лапласа (рис.1), не соответствуют векторам, наблюдаемым в реальном физическом эксперименте (рис. 2).

Рассмотрим возможность согласования теоретической тройки векторов и экспериментальной тройки векторов.

Для этого рассмотрим возможность перенесения начала  вектора из точки О в точку А.

В соответствии с аксиомами векторной алгебры точку приложения вектора  без изменения можно переносить только вдоль линии ее действия.

Есть  теорема из статики в отношении вектора силы:

«действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела». [2]

Вектор  можно перенести и параллельно его точке приложения, как это требуется для соответствия теоретического закона Био — Савара — Лапласа физическому эксперименту, но при этом появляется момент этого вектора относительно новой точки приложения. Это также удобно показать на примере теоремы из статики:

«Силу, приложенную к абсолютно твердому телу, можно, не изменяя оказываемого ею действия, переносить из данной точки в любую другую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда сила переносится». [2]

 

Рис. 3. Перенос точки приложения вектора  из точки  в точку  в соответствии с аксиомами векторной алгебры.

 

Корректный перенос вектора  из точки  в точку  возможен только в соответствии с аксиомами векторной алгебры. В этом случае необходимо добавить момент вектора  относительно точки А. 

Для переноса начала вектора нужно добавить пару векторов  и , равных по модулю  в точку А (рис. 3).

 Добавление пары векторов  и  происходит в соответствии с аксиомами векторной алгебры и не изменяет действия вектора . Поскольку , мы можем в точке  вместо вектора  поместить вектор , а пару векторов  и  заменить моментом этих векторов относительно точки  — вектором магнитного момента  (рис.4).

На рис. 4. показаны вектора, выведенные из формулы (1), выражающей закон Био — Савара — Лапласа, в соответствии с аксиомами векторной алгебры.

Как видно на (рис.4), в законе Био — Савара — Лапласа, для его соответствия физическому эксперименту, должен быть добавлен вектор магнитного момента .

Рис. 4. Перенос вектора  из точки  в точку  в соответствии с аксиомами векторной алгебры.

 

В результате векторного анализа закона Био — Савара — Лапласа были выявлены некоторые проблемы электродинамики.

       1. Для соответствия экспериментально наблюдаемым векторам, в формулу Био — Савара – Лапласа нужно добавить момент .

      Этого нельзя сделать, поскольку в эксперименте этого момента не наблюдается.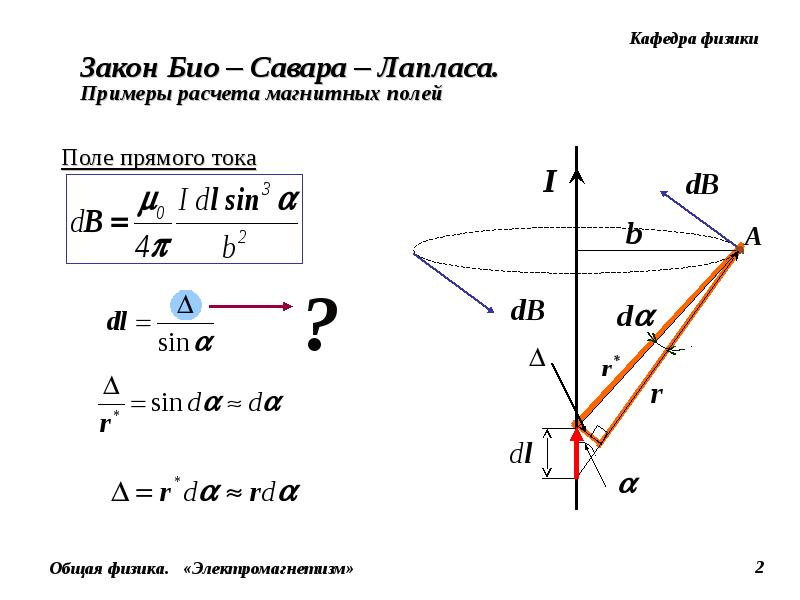

Из векторного анализа следует, что вектора, построенные по закону Био — Савара – Лапласа, не совпадают с векторами, наблюдаемыми в эксперименте.

Вывод: Теория электрического тока не соответствует экспериментально наблюдаемому физическому явлению.

 

   Литература

 

1.  Трофимова Т. И. Курс Физики. «Высшая школа». М.,1997.

2.  Тарг С.М. Краткий курс теоретической механики. М., «Высшая школа». 1995.

3. Дрюков В.М. О чём молчат физики. Тула, 2004.

4. http://www.sciteclibrary.ru/rus/avtors/d.html

5. http://drjukow.narod.ru/

6. Дрюков В.М. Физика. Дополнительные материалы. Тула изд. ООО Аквариус. 2021

 

Задачи на закон Био Савара Лапласа с решением

Закон Био-Савара-Лапласа в магнитостатике – примерно то же самое, что и закон Кулона в электростатике. С помощью этого закона определяется индукция магнитного поля, созданного постоянным электрическим током. В сегодняшней статье разберем несколько примеров решения задач по магнитостатике на применение закона Био-Савара-Лапласа.

Присоединяйтесь к нам в телеграме, чтобы вовремя получать полезную рассылку и актуальные новости. А еще, не пропустите приятные скидки и акции на нашем втором канале.

Закон Био-Савара-Лапласа: решение задач

В нашем блоге есть материалы, которые помогут справиться с задачами по разным темам:

1. Общая памятка по решению физических задач.
2. Более 40 формул по физике. 

Задача на закон Био-Савара-Лапласа №1

Условие 

Прямой провод согнут в виде квадрата со стороной а=8 см. Какой силы ток надо пропустить по проводнику, чтобы напряженность магнитного поля в точке пересечения диагоналей была 20 А/м?

Решение

Согласно принципу суперпозиции напряженность магнитного поля в точке пересечения диагоналей квадрата будет равна сумме напряженностей, которые создают стороны.  Поскольку стороны одинаковые, то:

H=4h2=4B1μ0

Будем использовать формулу для магнитной индукции поля, создаваемого отрезком прямого провода с током (выводится из закона Био-Савара-Лапласа):

B=μ02πIr0cosαB1=μ02πIa2cosα=μ02πIacosα, α=45°

Тогда для напряженности в точке пересечения диагоналей получим:

Н=4πIacosα

Отсюда можем выразить ток:

I=πah5cosα=3,14×0,08×204cos45=1,78 А  

Ответ: 1,78 А.

Задача на закон Био-Савара-Лапласа №2

Условие

Используя закон Био-Савара-Лапласа, определите магнитную индукцию в вакууме B поля в центре кругового проводника радиусом 10 см, если сила тока в проводнике равна 5 A.

Решение

Модуль магнитной индукции в центре кругового тока вычисляется по формуле:

B=μ0μI2rμ=1 — магнитная проницаемость для вакуумаμ0=1,25×10-6 Гнм — магнитная постоянная

Вычислим индукцию:

В=1,25×10-6×1×52×0,1=3,1×10-5 Тл

Ответ: 0,31 мкТл.

Задача на закон Био-Савара-Лапласа №3

Условие

Используя закон Био-Савара-Лапласа выведите формулу для индукуии из предыдущей задачи.

Решение

Пусть ток идет по тонкому проводу в форме окружности, имеющей радиус R.

Разобъем провод на бесконечно малые элементы dl. Каждый такой элемент создает в центре окружности индукцию dB, направленную вдоль положительной нормали к контуру. По закону Био-Савара-Лапласа:

B=μ04πIdlsinαr2

Угол альфа между векторами r и Idl равен 90 градусам, а r=R. Тогда, можно записать:

Интегрируя это выражение по контуру, получим:

Ответ: см. выше.

Задача на закон Био-Савара-Лапласа №4

Условие

По квадратной рамке со стороной a=0,2 м течет ток 4 А. Определить напряженность и индукцию магнитного поля в центре рамки.

Решение

Будем рассматривать каждую из четырех сторон рамки, как отдельный проводник, создающий в ее центре магнитную индукцию. Направление векторно-магнитной индукции определяется по правилу правого винта: все векторы направлены в одну сторону, перпендикулярно рамке.

Найдем индукцию, создаваемую одной стороной рамки:

B1=μμ0I4πr(cosα1-cosα2)

r=a2α1=45°α2=135°В1=μμ0I2πa(cos45-cos135)

По принципу суперпозиции, запишем формулу для общей индукции в центре рамки и вычислим:

B=4B1=2μμ0Iπa(cos45-cos135)B=1×1,25×10-6×42×3,14×0,2(0,707+0,707)=22,6×10-6 Тл

Ответ: 22,6 мкТл.

Задача на закон Био-Савара-Лапласа №5

Условие

Проводник согнут в виде правильного треугольника со стороной а=20 см. Какой ток протекает по периметру треугольника, если в его центре напряженность поля равна Н = 71,64 А/м?

Решение

Условно разбиваем проводник на три проводника, каждый из которых создает магнитное поле. По закону Био – Савара – Лапласа элемент контура dl, по которому течет ток I, создает в некоторой точке А пространства магнитное поле напряженностью:

dH0=Isinα4πr2dl

r – расстояние от точки А до элемента тока dl, α – угол между радиус-вектором и элементом тока dl. Напряженность магнитного поля в точке О будет равна:

Н0=∫-∞+∞Isinα4πr2dl

Учтем, что:

l=b×ctgαdl=-bdαsin2αr=bsinα

Теперь выражение для напряженности можно переписать в следующем виде:

H0=-I4πb∫α1α2sinαdα=I4πbcosα1-cosα2b=a2tgαH0=I2π×a×tgαcosα1-cosα2

Из рисунка видно, что угол α1 равен 30 градусам, а угол α2 = 150. Очевидно, что результирующая напряженность:

Н=3Н0

Н=3I2π×a×tg30cos30-cos150

Отсюда найдем ток:

I=2πH×a×tg303(cos30-cos150)=2×3,14×71,64×0,2×0,5773(0,866+0,866)=10А

Ответ: 10 А.

Вопросы на закон Био-Савара-Лапласа

Вопрос 1. Сформулируйте закон Био-Савара-Лапласа

Ответ. Закон Био-Савара-Лапласа гласит:

Магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока.

B⇀=∑B⇀ii

Элементарный участок dl с током I создает магнитную индукцию:

B=μ04πIdlsinαr2

Здесь альфа — угол между радиусом-вектором и направлением тока в проводнике.

Вопрос 2. Что такое магнитная индукция?

Ответ. Магнитная индукция — векторная физическая величина, силовая характеристика магнитного поля. Определяет, с какой силой поле действует на заряд, движущийся в нем.

Вопрос 3. Сформулируйте теорему о циркуляции магнитной индукции.

Ответ. Циркуляция вектора магнитной индукции по произвольному замкнутому контуру, охватывающему токи, прямо пропорциональна алгебраической сумме токов, пронизывающих этот контур:

∮Вdl=μ0∑iIi

Вопрос 4. Как определяется направление вектора магнитной индукции?

Ответ. Направление вектора магнитной индукции определяется по правилу буравчика (правого винта):

Направление вращения головки винта дает направление вектора магнитной индукции, поступательное движение винта соответствует направлению тока в элементе.

Вопрос 5. Что такое напряженность магнитного поля?

Ответ. Напряженность — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M. Связана с индукцией формулой:

H⇀=B⇀μ0

Нужна помощь в решении задач и выполнении других заданий? Профессиональный сервис для учащихся всегда к вашим услугам.

Закон Био — Савара — Лапласа и его применение к расчету магнитного поля

| на главную | доп. материалы | физика как наука и предмет | электричество и электромагнетизм |

Организационные, контрольно-распорядительные и инженерно-технические услуги
в сфере жилой, коммерческой и иной недвижимости. Московский регион. Официально.

Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж. Био (1774—1862) и Ф. Саваром (1791—1841). Результаты этих опытов были обобщены выдающимся французским математиком и физиком П. Лапласом.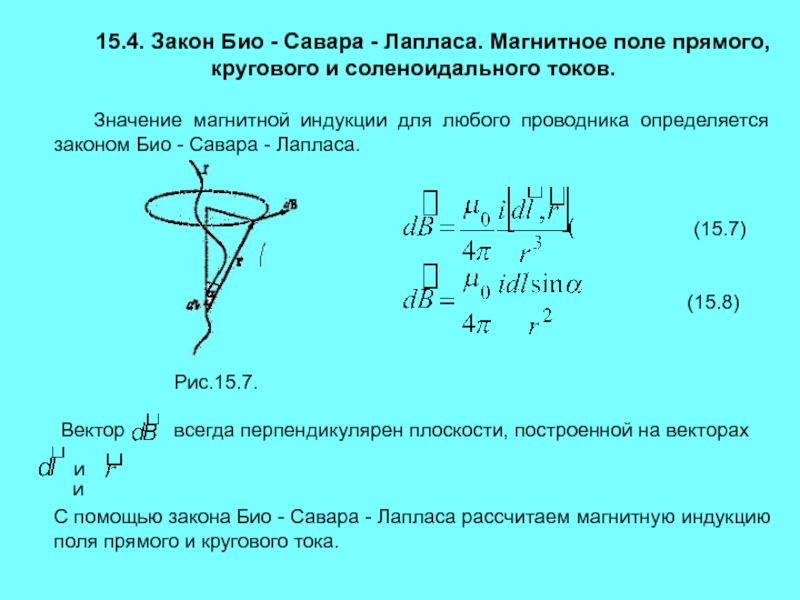

Закон Био — Савара — Лапласа для проводника с током I, элемент dl  которого создает в некоторой точке А (рис. 164) индукцию поля dB, записывается в виде

                                                      (110.1)

где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r—радиус-вектор, проведанный из элемента dl проводника в точку А поля, r — модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение винта соответствует направлению тока в элементе.

Модуль вектора dB определяется выражением

                                                    (110. 2)

где a — угол между векторами dl и r.

Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:

                                                      (110.3)

Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную сим­метрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера.

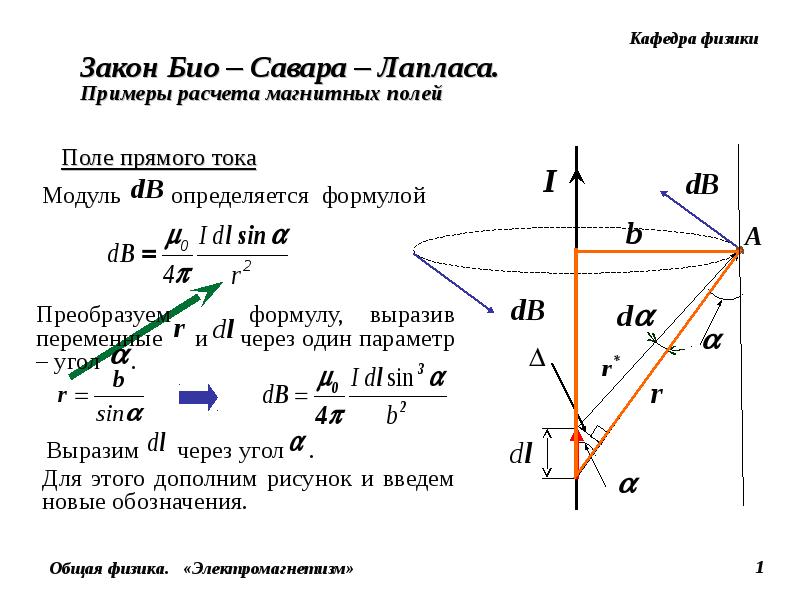
1. Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к вам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол a (угол между векторами dl и r), выразив через него все остальные величины. Из рис. 165 следует, что

(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна

                                                       (110.4)

Так как угол a  для всех элементов прямого тока изменяется в пределах от 0 до p, то, согласно (110.3) и (110.4),

Следовательно, магнитная индукция поля прямого тока

                                                                       (110.5)

2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка.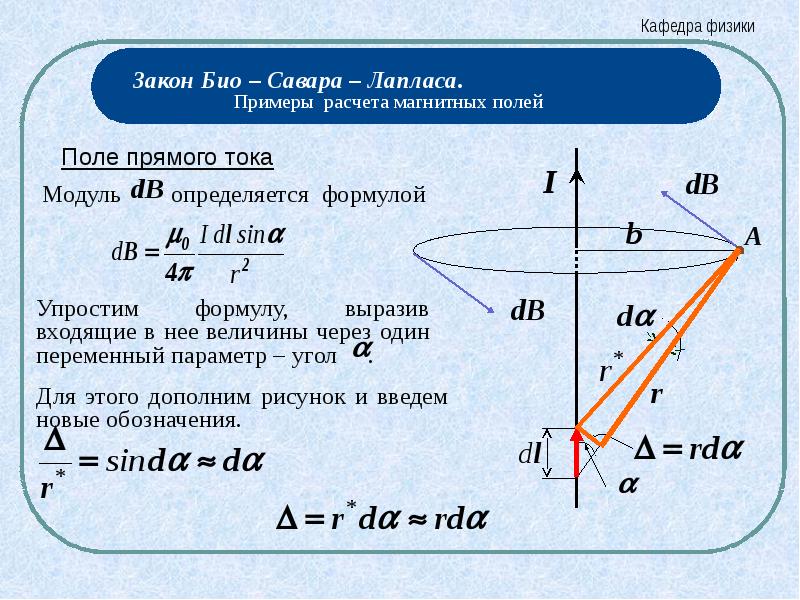 Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sina =1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),

Тогда

Следовательно, магнитная индукция поля в центре кругового проводника с током

---

Закон Био — Савара — Лапласа и его применение к расчету магнитного поля

Магнитное поле постоянных токов различ­ной формы изучалось французскими уче­ными Ж. Био (1774—1862) и Ф. Саваром (1791 —1841). Результаты этих опытов бы­ли обобщены выдающимся французским математиком и физиком П. Лапласом.

Закон Био — Савара — Лапласа для проводника с током I, элемент которого dlсоздает в некоторой точке А (рис. 164) индукцию поля dB, записывается в виде

где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r — радиус-вектор,

проведенный из элемента dl проводника в точку А поля, r — модуль радиуса-векто­ра г. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в ко­торой они лежат, и совпадает с каса­тельной к линии магнитной индукции. Это направление может быть найдено по пра­вилу нахождения линий магнитной индук­ции (правилу правого винта): направле­ние вращения головки винта дает направ­ление dB, если поступательное движение винта соответствует направлению тока в элементе.

Модуль вектора dB определяется вы­ражением:

где а — угол между векторами dl и г.

Для магнитного поля, как и для элек­трического, справедлив принцип суперпо­зиции: магнитная индукция результирую­щего поля, создаваемого несколькими то­ками или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каж­дым током или движущимся зарядом в от­дельности:

Расчет характеристик магнитного поля (В и Н) по приведенным формулам в об­щем случае довольно сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био — Савара — Лапласа совместно с принци­пом суперпозиции позволяет довольно просто рассчитать конкретные поля. Рас­смотрим два примера.

1. Магнитное поле прямого тока — тока, текущего по тонкому прямому про-

воду бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одина­ковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве по­стоянной интегрирования выберем угол а (угол между векторами dl и r), выразив через него все остальные величины. Из рис. 165 следует, что

(радиус дуги CD вследствие малости dlравен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.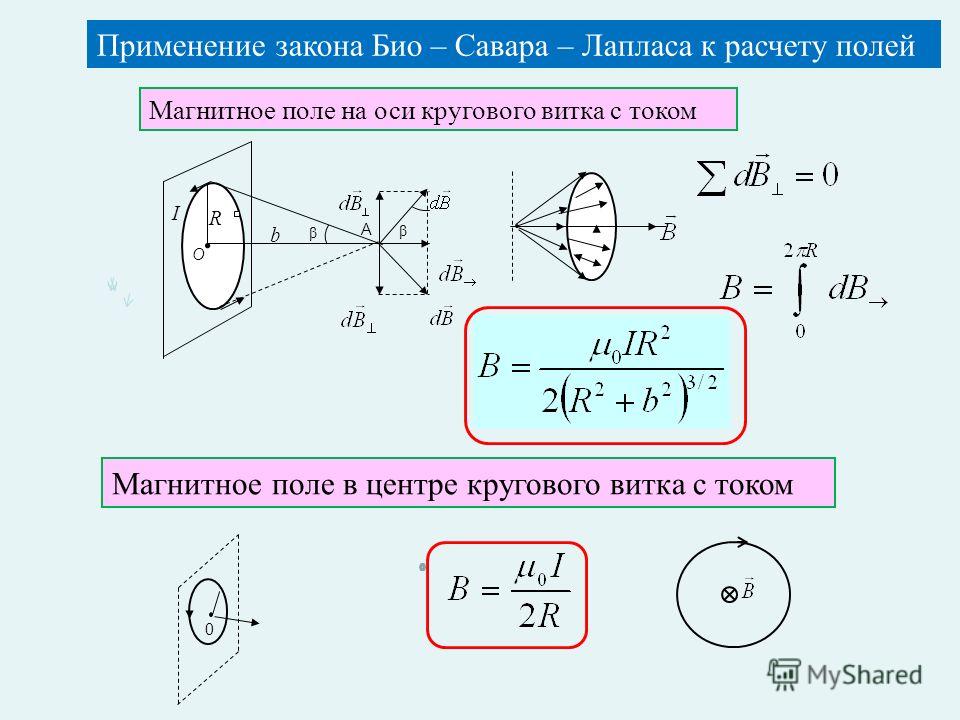 2), получим, что маг­нитная индукция, создаваемая одним эле­ментом проводника, равна

Так как угол а для всех элементов прямо­го тока изменяется в пределах от 0 до я, то, согласно (110.3) и (110.4),

Следовательно, магнитная индукция поля прямого тока

2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следу­ет из рисунка, все элементы кругового проводника с током создают в центре магнитное поле одинакового направления — вдоль нормали от витка.

Поэтому сложе­ние векторов dB можно заменить сложени­ем их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sina=1) и расстояние всех эле­ментов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),

Тогда

Следовательно, магнитная индукция поля в центре кругового проводника с током

Закон Био-Савара-Лапласа — презентация онлайн

1.

ФИЗИКА Закон Био-Савара-Лапласа Центр дистанционного обучения
ФИЗИКА
Закон Био-Савара-Лапласа
ФИО преподавателя: Сафронов Александр Аркадьевич
e-mail: [email protected]
Online-edu.mirea.ru
online.mirea.ru
Центр дистанционного обучения
МАГНЕТИЗМ
В Тл
Взаимодействие проводников с током
а)
б)
I1
I1
I2
I2
Рис. 1
online.mirea.ru
Центр дистанционного обучения
Правило правого
буравчика
Магнитное поле бесконечного
проводника с током.
Опыт Эрстеда (1820 г.)
I
B
Рис. 3
Рис. 2
online.mirea.ru
Центр дистанционного обучения
Магнитное поле в центре кругового витка с током
B
I
Рис. 4
online.mirea.ru
Центр дистанционного обучения
Демонстрация магнитного поля полосовых магнитов
при помощи железных опилок
а)
б)
Рис. 5
в)
online.mirea.ru
Центр дистанционного обучения
Магнитное поле полосового магнита и
катушки с током
Рис. 6
online.mirea.ru
Центр дистанционного обучения
Векторное произведение
При печати
При письме
c a b
c a b
c a ,b b ,a
c ab sin
Правило правого буравчика: для определения направления
вектора c необходимо по кратчайшему повороту крутить
ручку штопора от первого вектора ко второму (от a к b ),
тогда то, куда будет вкручиваться сам штопор и есть
направление вектора c .
online.mirea.ru
Центр дистанционного обучения
c
b
a
а)
b
c
б)
a
Рис. 7
Правило левой руки: четыре пальца
левой руки по
направлению первого вектора a , второй вектор b входит
в ладонь, оттопыренный
большой
палец
покажет
направление вектора c .
online.mirea.ru
Центр дистанционного обучения
Закон Био-Савара-Лапласа
r
0 dl ,r
dB
A
3
4
r
dB
(1)
магнитная
проницаемость
вещества
1
dl
Рис. 8
I
вакуум
0 магнитная постоянная
6 Гн
0 1,257 10
м
online.mirea.ru
Центр дистанционного обучения
Пример 1. Расчет магнитного поля в центре кругового
витка.
И
2.226
а)
B Bi
li
r
B
I
Рис. 9
(1.6)
B
0 I
2r
B Bi
0 I li r
B
3
4
r
0 I
B
li
4 r 2
0 I
B
2 r
4 r 2
(1.1)
(1.2)
(1.3)
(1.4)
(1.5)
online.mirea.ru
Центр дистанционного обучения
Пример 2. Магнитное поле проводника конечной длины.
a
O
2
0 I
cos 1 cos 2 (2.1)
B12
4 a
2
1
I
Рис. 10
1
online.mirea.ru
Центр дистанционного обучения
Пример 3. Магнитное поле бесконечно длинного
проводника на расстоянии
.
a
0 I
cos 1 cos 2
B12
4 a
1 0
I
a
Рис. 11
O
(2.1)
2
0 I
B
2 a
(3. 1)
online.mirea.ru
Центр дистанционного обучения
И 2.235 Определить магнитную индукцию в
точке О, если проводник с током I имеет вид,
показанный на рис.:
R
О
Рис. 12
online.mirea.ru
Центр дистанционного обучения
И 2.235 Определить магнитную индукцию в
точке О, если проводник с током I имеет вид,
показанный на рис.:
2
1
R
О
Рис. 12
3
B B1 B2 B3
(4.1)
B1 B3 0
(4.2)
1
B2 Bокружности
2
(4.3)
В B2
(4.4)
0 I
4R
online.mirea.ru
Центр дистанционного обучения
R
О
Рис. 13
online.mirea.ru
Центр дистанционного обучения
B B1 B2 B3
2
R
3
О
Рис. 13
(4.8)
(4.9)
B3 0
B B1 B2
1
3
B2 Bокружности
4
(4.5)
(4.6)
Для полупрямой 1 используем
выражение (2.1).
0 I 3 0 I
B
4 R 8 R
1 0, 2
2
0 I
B1
4 R
(4. 7)
online.mirea.ru
Центр дистанционного обучения
R
О
Рис. 14
online.mirea.ru
Центр дистанционного обучения
3
R
2
О
Рис. 14
1
B B1 B2 B3
(4.10)
B B1 B2 B3
(4.11)
0 I 0 I
B 2
4 R 4 R
(4.12)
0 I 0 I
B
2 R 4 R
(4.13)
online.mirea.ru
Центр дистанционного обучения
И 2.239 а) Найти магнитную индукцию в точке О, если
проводник с током I = 8,0 A имеет вид:
R
Рис. 15
online.mirea.ru
Центр дистанционного обучения
И 2.239 а) Найти магнитную индукцию в точке О, если
проводник с током I = 8,0 A имеет
вид:
B2
B B1 B2 B3 (5.1)
2
0 I
В
13
(5.2)
R
1
B13
3 Рис. 15
2 R
0 I
B2
(5.3)
4R
B
2
2
B13 B2
2
(5.4)
2
0 I 0 I
B
(5.5)
2 R 4 R
online.mirea.ru
Центр дистанционного обучения
И 2. 226 б) По круговому витку радиуса R = 100 мм из
тонкого провода циркулирует ток I = 1,00 А. Найти
магнитную индукцию на оси витка на расстоянии
x = 100 мм от его центра.
x
R
Рис. 16
I
online.mirea.ru
Центр дистанционного обучения
И 2.226 б) По круговому витку радиуса R = 100 мм из
тонкого провода циркулирует ток I = 1,00 А. Найти
магнитную индукцию на оси витка на расстоянии
x = 100 мм от его центра.
(6.1)
B B
y
B
x
i
Bi
r
R
Рис. 16
I
0 I li r
(6.2)
Bi
4 r 3
B y B Bi sin (6.3)
li
0 I
B
sin li (6.4)
4 r 2
online.mirea.ru
Центр дистанционного обучения
R
sin
r
(6.5)
li 2 R
(6.6)
2
2
r x R
B
2
0 IR 2
(6.7)
3
2
2 2
2x R
(6.8)
online.mirea.ru
Центр дистанционного обучения
И 2.229 Ток I течет по тонкому проводнику, который
имеет вид правильного n-угольника, вписанного в
окружность радиуса R. Найти магнитную индукцию
в центре данного контура. Исследовать случай n .
online.mirea.ru
Центр дистанционного обучения
И 2.229 Ток I течет по тонкому проводнику, который
имеет вид правильного n-угольника, вписанного в
окружность радиуса R. Найти магнитную индукцию
в центре данного контура. Исследовать случай n .
1
R
2
a
R
n
B Bi
(7.1)
i 1
B0 вклад от одной стороны
0 I
B
cos
cos
12
1
2
Рис. 17
4 a
2
2 1
1
n
2
2
(2.1)
(7.2)
online.mirea.ru
Центр дистанционного обучения
cos 1 sin
(7.3)
n
cos 2 cos 1 sin
a R cos
B0
0 I 2 sin
4 R cos
(7.4)
n
(7.5)
n
n
0 Itg
2 R
n
(7.6)
n
online.mirea.ru
Центр дистанционного обучения
В nB0
B
При
B
n ,
0 I
2R
n
n 0 Itg
2 R
(7. {-6}\) \(\frac{Гн}{м}\)

\(\pi\) — число Пи \(\approx 3.14\)

\(I\) — сила тока текущего по проводнику \((А)\)

\(\vec{r}\) — расстояние \((м)\)

\(\vec{\Delta L}\) — длина малого элемента проводника \((м)\)

\(\mu\) — относительная магнитная проницаемость среды

Исследование магнитного поля катушки

Цель работы : изучить распределение индукции магнитного поля на оси катушки, познакомиться с применением датчика Холла.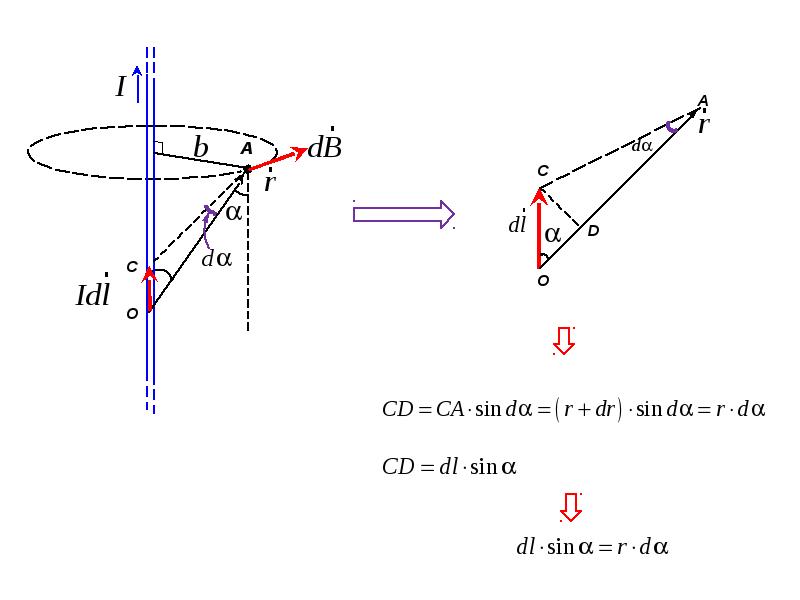

Оборудование : испытательная катушка, блок питания, миллиамперметр, мультиметр, датчик Холла.

ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Магнитное поле — это форма материи, которая действует на магниты, на проводники с током и движущиеся заряды.Источником магнитного поля могут быть постоянные магниты, проводники с электрическим током и движущиеся электрические заряды, элементарные частицы с магнитным моментом.

Силовой характеристикой магнитного поля является вектор магнитной индукции IN . По определению индукция равна отношению максимального момента силы к магнитному моменту стрелки или рамки с током: либо, согласно закону Ампера, как отношение максимальной силы, действующей на проводник, к силе тока и длина проводника:.

Теоретический расчет индукции магнитного поля проводников любой формы основан на применении принципа суперпозиции и закона Био — Савара — Лапласа для проводящего элемента длиной дл , через который протекает ток Дж :

, (1)

где m — относительная магнитная проницаемость среды; GN / м — магнитная постоянная; r — радиус-вектор, проведенный от элемента dl проводника к точке наблюдения; a — угол между элементом dl и радиус-вектором r (рис. 1) .

Направление вектора дБ можно определить по правилу буравчика. Если пропустить буравчик через ток в проводнике, то направление движения конца ручки буравчика в точке наблюдения будет указывать направление вектора индукции магнитного поля (рис. 1).

Вывод формулы индукции магнитного поля катушки будет производиться в два этапа. Сначала определяем по закону Био — Савара — Лапласа индукцию магнитного поля одного витка радиуса R с током Дж на его оси на расстоянии x от центра (рис.2). Выбираем небольшой элемент катушки длиной дл . Вектор dl направлен по касательной к катушке, перпендикулярно радиус-вектору r so sin α = 1. Вектор индукции d  элемента катушки по правилу буравчика будет направлен перпендикулярно радиус-вектору r . Векторы индукции других элементов катушки также направлены, совпадая с образующими конуса. Полученные векторы индукции будут совпадать с осью катушки и определяется интегралом. Интегрируя и подставляя, получаем формулу индукции магнитного поля катушки

. (2)

На втором этапе определяем распределение индукции магнитного поля по оси катушки с однородной обмоткой, по виткам которой протекает ток Дж . Выделите на расстоянии x от середины поперечного сечения катушки элементарный слой длиной dx с числом витков dN = ndx , где n — концентрация витков, то есть количество витков на единичная длина катушки (рис.3). В некоторой фиксированной точке A оси на расстоянии l от середины индукция выбранных витков определяется по формуле (2) при токе JdN = Jn dx. Результирующая индукция в точке A может быть определена путем суммирования по всем виткам катушки, то есть интеграла .

Интегрируем по переменному — угол β. С рисунка. Дифференцируя, получаем формулу связи.Подставляя его под знак интеграла и интегрируя, получаем

. (3)

Здесь β 1 и β 2 — углы между радиус-векторами, проведенными из точки наблюдения A в крайних витках, и осью катушки.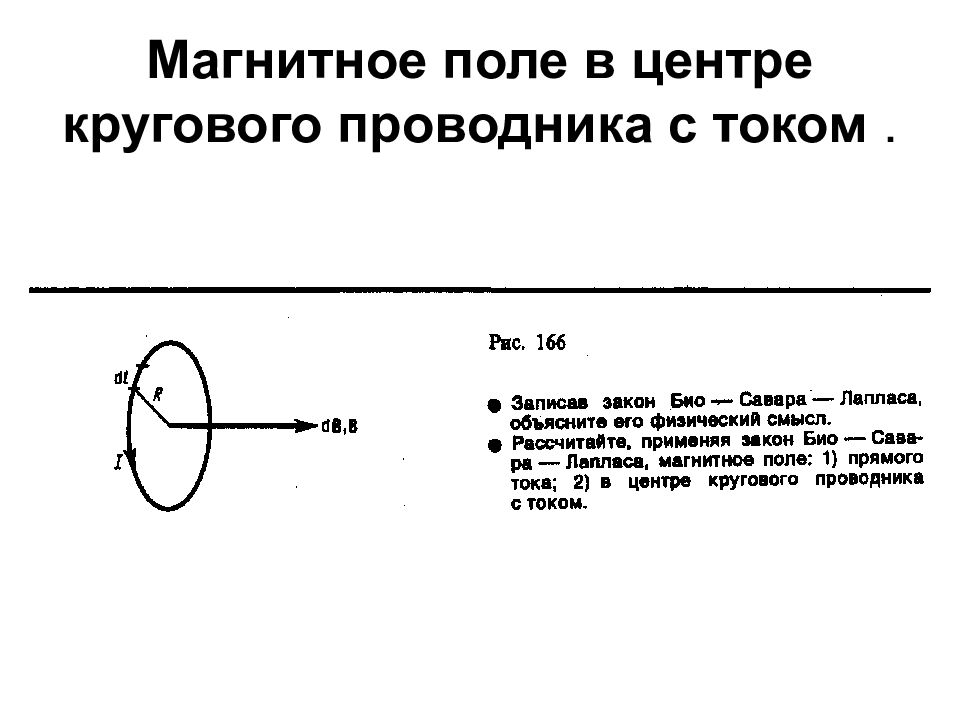 Через координату точки наблюдения их можно вычислить по формулам где L– половина длины катушки.

Экспериментальное исследование зависимости индукции магнитного поля от оси катушки в лабораторных условиях проводится с помощью датчика Холла.Эффект Холла заключается в появлении поперечной разности потенциалов в проводнике с током, помещенном в магнитное поле. Пусть по образцу в виде пластины с размерами d, b, c протекает ток (рис. 4). При движении со скоростью дрейфа В зарядов действует сила Лоренца. Если носители заряда положительные, то по правилу левой руки под действием силы Лоренца они будут отклоняться в левую сторону пластины, если отрицательные, то отрицательные заряды будут отклоняться влево (рис. .4). В обоих случаях возникает поперечное электрическое поле, препятствующее последующему отклонению зарядов.

Накопление зарядов на гранях прекратится и наступит равновесие, когда сила Лоренца уравновесится силой возникающего электрического поля. EMF Hall будут равны. Скорость дрейфа заряда В можно определить по силе тока. Сила тока по определению равна заряду носителей тока в проводнике, проходящему через поперечное сечение проводника в единицу времени.Длина такого проводника численно равна скорости, а объем равен В постоянного тока. Т.е. Здесь n q, e — концентрация и заряд носителей. Подставляя скорость в формулу ЭДС Холла, получаем. Следовательно, индукцию измеряемого магнитного поля можно определить по формуле

, (4)

где C — постоянная датчика.

Лабораторная установка состоит из источника постоянного тока, к которому подключен модуль, в котором находится испытательная катушка.Датчик Холла перемещается по оси катушки, его координата определяется шкалой линейки. ЭДС Холла измеряется мультиметром. Модуль и блок питания соединены кабелем.

ЗАВЕРШЕНИЕ РАБОТЫ

1. Проверить подключение мультиметра к гнездам «RA» модуля. Установите зонд датчика Холла в середину катушки. Включите предел измерения мультиметра 200 мВ. Убедитесь, что ЭДС Холла близка к нулю.

2. Подключить блок питания к сети 220 В.Установите регулятор (5-24 В) на ток Дж в катушке в диапазоне 1,0–3,0 А. Занести в табл. 1. Запишите в таблицу. 1 параметры катушки и константа ИЗ .

Таблица 1

3. Измерьте ЭДС Холла, перемещая датчик с возможным интервалом хода каждые 2 см. Запишите расстояния и ЭДС в таблице 2.

Выключите бытовые приборы

стол 2

4. Произведите расчеты. Определите индукцию магнитного поля в точках наблюдения по формуле (4).Запишите в таблицу. 2.

5. Построить график зависимости индукции от расстояния x Размер графика не менее половины страницы. Рядом с точками проведите плавную линию, чтобы отклонение точек было минимальным.

6. Определите теоретическое значение индукции в центре катушки по формуле:. Сравните с экспериментальным значением IN 0 в середине катушки. Делать выводы.

ТЕСТОВЫЕ ВОПРОСЫ

1.Дайте определение магнитному полю и вектору индукции.

2. Запишите и сформулируйте закон Био — Савара — Лапласа, сформулируйте правило буравчика и приведите пример.

3. Выведите формулу индукции магнитного поля на оси поворота.

4. Запишите формулу индукции магнитного поля для токовой катушки. Нарисуйте график зависимости индукции от расстояния.

5. Объясните причину эффекта Холла.

6. Выведите формулу для ЭДС Холла.

Цель работы : изучить распределение индукции магнитного поля на оси катушки, познакомиться с применением датчика Холла.

Оборудование : Модуль FPA 04 с исследуемой катушкой, ИП со встроенным амперметром, мультиметр М89, датчик Холла.

ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Магнитное поле — это форма материи, которая действует на магниты, на проводники с током и на движущиеся электрические заряды.И наоборот, источником магнитного поля могут быть постоянные магниты, проводники с электрическим током и движущиеся электрические заряды.

Силовой характеристикой магнитного поля является вектор магнитной индукции IN . По определению индукция равна отношению максимального момента сил к магнитному моменту магнитной стрелки или рамки с током: или, согласно закону Ампера, равна отношению максимальной силы, действующей на проводник, к сила тока и длина жилы:.

Теоретический расчет индукции магнитного поля проводников любой формы основан на применении принципа суперпозиции и закона Био — Савара — Лапласа для проводящего элемента длиной дл , через который протекает ток Дж :

, (1)

где m — относительная магнитная проницаемость среды; GN / м — магнитная постоянная; r — радиус-вектор, проведенный от элемента dl проводника к точке наблюдения; a — угол между элементом dl и радиус-вектором r (рис.1) .

→

Направление вектора дБ можно определить по правилу буравчика. Если пропустить стабилизатор через ток в проводнике, то направление движения конца рукоятки карданного подвеса в точке наблюдения будет указывать направление вектора индукции магнитного поля (рис. 1).

В работе исследуется магнитное поле катушки с током. Теоретический вывод формулы индукции магнитного поля катушки проведем в два этапа.Сначала по закону Био — Савара — Лапласа определяем индукцию магнитного поля одного витка радиуса R с током Дж на его оси на расстоянии x от центра (рис.2). Выбираем небольшой элемент катушки длиной дл . Вектор dl направлен по касательной к катушке, перпендикулярно радиус-вектору r so sin α = 1. Вектор индукции d  элемента катушки по правилу буравчика будет направлен перпендикулярно радиус-вектору r .Векторы индукции других элементов катушки также направлены, совпадая с образующими конуса. Полученные векторы индукции будут совпадать с осью катушки и определяется интегралом

. Интегрируя и подставляя, получаем формулу индукции катушки

. (2)

На втором этапе определяем распределение индукции магнитного поля вдоль оси катушки с однородной обмоткой. Выделите на расстоянии x от середины поперечного сечения катушки элементарный слой длиной dx с числом витков dN = ndx , где n — концентрация витков, то есть количество витков на единичная длина катушки (рис.3). В некоторой фиксированной точке A оси на расстоянии l от середины катушки индукция выбранных витков определяется по формуле (2) при токе Jn dx. Результирующая индукция в точке A может быть определена путем суммирования по всем виткам катушки, то есть интеграла .

Интегрируем в переменную — угол β. С рисунка. Дифференцируя, получаем формулу связи. Подставляя его под знак интеграла и интегрируя, получаем

.(3)

Здесь β 1 и β 2 — углы между радиус-векторами, проведенными из точки наблюдения A в крайних витках, и осью катушки. Через координату точки наблюдения их можно рассчитать по формулам

и

, где L– половина длины катушки.

Экспериментальное исследование зависимости индукции магнитного поля от оси катушки в лабораторных условиях проводится с помощью датчика Холла.Эффект Холла заключается в появлении поперечной разности потенциалов в проводнике с током, помещенном в магнитное поле. Пусть по образцу в виде пластины с размерами d, b, c протекает ток (рис. 4). При движении со скоростью дрейфа В заряжается , действуя силой Лоренца. Если носители заряда положительные, то по правилу левой руки под действием силы Лоренца они будут отклоняться в левую сторону пластины, если отрицательные, то отрицательные заряды будут отклоняться влево (рис. .4). В обоих случаях возникает поперечное электрическое поле. По знаку напряжения можно определить знак носителей заряда в пластине.

Накопление зарядов на гранях прекратится и наступит равновесие, когда сила Лоренца уравновесится силой возникающего электрического поля. EMF Hall будут равны. Скорость дрейфа заряда В можно определить по силе тока. Сила тока по определению равна заряду носителей тока в проводнике, проходящему через поперечное сечение проводника в единицу времени.Длина такого проводника численно равна скорости, а объем равен В постоянного тока. Т.е. Здесь n q, e — концентрация и заряд носителей. Подставляя скорость в формулу ЭДС Холла, получаем. Следовательно, индукцию можно определить по формуле

, (4)

где C — постоянная датчика.

Лабораторная установка состоит из модуля FPE 04, в котором расположена катушка, и источника питания. Датчик Холла перемещается по оси катушки, его координата определяется шкалой линейки.ЭДС Холла измеряется мультиметром.

ЗАВЕРШЕНИЕ РАБОТЫ

1. Проверить подключение мультиметра к гнездам RA модуля , выставить предел измерения 200 мВ. Установите зонд в катушку.

2. Подключите источник питания к сети 220 В. Установите регулятор (5–24 В) на ток катушки в диапазоне 1,0–3,0 А. Запишите в таблицу. 1 сила тока, параметры катушки и постоянная датчика ИЗ .

Таблица 1

3.Измерьте ЭДС Холла, перемещая датчик по всему интервалу хода каждые 2 см. Запишите расстояния и ЭДС в таблице 2.

Выключите бытовые приборы

4. Произведите расчеты. Определите индукцию в точках наблюдения по формуле (4). Запишите в таблицу. 2.

5. Построить зависимость индукции магнитного поля от расстояния x Размер графика не менее половины страницы. Рядом с точками проведите плавную линию, чтобы отклонение точек было минимальным.

стол 2

6. Определите теоретическое значение индукции в центре катушки по формуле:

. Сравните с экспериментальным значением IN 0 в центре катушки. Делать выводы.

ТЕСТОВЫЕ ВОПРОСЫ

1. Дайте определение магнитного поля и вектора индукции.

2. Запишите и сформулируйте закон Био — Савара — Лапласа, сформулируйте правило буравчика и приведите пример.

3. Выведите формулу индукции магнитного поля на оси поворота.

4. Запишите формулу индукции магнитного поля для токовой катушки. Нарисуйте график зависимости индукции от расстояния.

5. Объясните причину эффекта Холла.

6. Выведите формулу для ЭДС Холла.

Механика. Ключевые определения — онлайн-презентация

1. Механика

Физика. Основное блюдо
МЕХАНИКА

2. Ключевые определения

КЛЮЧЕВЫЕ ОПРЕДЕЛЕНИЯ
Механика — раздел физики, изучающий
законы механического движения и причины, которые
изменить движение.
Механизм — изменение относительного
положения тел или их частей в
пространство с течением времени.

3. Виды механики

ВИДЫ МЕХАНИКИ
Классический
Механика (GalileyNewton)
Изучение законов
движение
макроскопические тела,
какие скорости равны
маленький
по сравнению с
оценка
свет в вакууме.
в / с
Релятивистское изучение законов
г. движение
макроскопические тела с
скорости сопоставимы с c.
На основе СТО.
Квантовое изучение законов
движение
макроскопические тела
(Отдельные атомы и
элементарные частицы)

4. Кинематика, динамика, статика

КИНЕМАТИКА, ДИНАМИКА, СТАТИКА
Кинематика (от греческого слова kinema motion) — раздел механики, изучающий
геометрические свойства движения
кузова без учета веса
и действующие на них силы.
Динамика (от греч. Dynamis — сила)
изучение движения тел в связи
с причинами, вызывающими это движение.

5. Кинематика, динамика, статика

КИНЕМАТИКА, ДИНАМИКА, СТАТИКА
Статика (от греч. Statike — баланс) —
изучение условий равновесия
тела.
Поскольку весы — это частный случай движения,
законы статики являются естественным следствием
законов динамики и в этом курсе
не учили.

6. Модели в механике

МОДЕЛИ в механике
Материал — размер корпуса, форма
точка внутренней структуры, которую в этой задаче можно игнорировать
Абсолютно прочный — корпус, который ни в каком
состояние кузов нельзя деформировать и под все
обстоятельства расстояние между двумя точками тела
Остается постоянным
Абсолютно упругий — корпус, деформация которого
тело подчиняется закону Гука, и после
прекращение действия внешней силы принимает исходный размер и форму

7.Система и тело обратного отсчета

СИСТЕМА И ТЕЛО ОТСЧЕТА
Каждое движение относительное, поэтому необходимо
описать условия движения на любом другом
тело будет отсчитываться от движения
тело. Выбранный для этой цели кузов под названием
тело обратного отсчета.
На практике для описания движения необходимо
общаться с телом обратного отсчета
система координат (декартова, сферическая,
цилиндрические и др.).

8.эталонная система

эталонная система
Система отсчета — набор координат
и часы, относящиеся к корпусу, относительно которых
движение изучается.
Движения тела, как и материя, не могут
вообще быть вне времени и пространства. Материя,
пространство и время неразрывно связаны с каждым
другое (нет места без материи и времени, и
наоборот).

9. Кинематика материальной точки

КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Положение точки A в пространстве может быть
определяется радиус-вектором, взятым из
контрольная точка O или начало координат

10.смещение, путь

СМЕЩЕНИЕ, ПУТЬ
При перемещении точки А из точки 1 в точку
2 его радиус-вектора изменится по величине и
направление, т. е. зависит от времени t.
Географическое место всех точек называется траекторией
точка.
Длина пути — это путь Δs. Если
точка движется по прямой, затем
инкремент — это путь Δs.

11. скорость

СКОРОСТЬ
Вектор средней скорости определяется как отношение смещения
вектора к моменту времени Δt, за это движение произошло
Вектор
совпадает с
направление
вектор

12.Мгновенная скорость

МГНОВЕННАЯ СКОРОСТЬ
При Δt = 0 Δ — бесконечно малая часть
траектория
Движение ΔS = Δr совпадает с движением
траектория) В этом случае мгновенная
скорость может быть выражена скалярным значением пути:

13. Мгновенная скорость

МГНОВЕННАЯ СКОРОСТЬ

14. Ускорение. Нормальное и тангенциальное ускорение

УСКОРЕНИЕ. НОРМАЛЬНОЕ И КАСАТЕЛЬНОЕ
УСКОРЕНИЕ
В случае произвольной скорости не
оставаться в постоянном движении.Скоростной показатель
изменение величины и направления
Ускорение характеризуется

15. Ускорение

УСКОРЕНИЕ
Введем единичный вектор, связанный с точкой 1 и направленный по касательной к оси
. траектория точки 1 (векторы и 1 совпадение). Тогда мы можем написать:
Где — величина скорости.

16. Ускорение

УСКОРЕНИЕ
Находим общее ускорение (производная)

17. Касательное и нормальное ускорение

ТАНГЕНЦИАЛЬНОЕ И НОРМАЛЬНОЕ УСКОРЕНИЕ

18.Кинематика вращательного движения

КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Движение твердого тела, в котором два
точки O и O ‘фиксированы, называются вращательными
движение вокруг фиксированной оси, и фиксированная линия
OO ‘называется осью вращения.

19. Угловая скорость

УГЛОВАЯ СКОРОСТЬ
Это вектор угловой скорости численно равен первому
. производная угла по времени и направленная по вращению
направление оси (и всегда в одном направлении).

20. Контакт линейной и угловой скорости

КОНТАКТЫ ЛИНЕЙНОЙ И УГЛОВОЙ СКОРОСТИ
Пусть — линейная скорость точки М.
За промежуток времени dt точка M проходит
кстати одновременно
(Центральный угол). Тогда

21. Концепции вращательного движения

КОНЦЕПЦИИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Период Т — период времени, в течение которого организм совершает
полный оборот (поворот на угол)
Частота ν — число оборотов
тело за 1 секунду

22.Угловое ускорение

УГЛОВОЕ УСКОРЕНИЕ
Выразим нормальное и тангенциальное ускорение M
через угловую скорость и угловое ускорение

23. Связь между линейными и угловыми величинами вращательного движения:

СВЯЗЬ МЕЖДУ ЛИНЕЙНЫМ И
УГЛОВЫЕ ЗНАЧЕНИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ:

24. Связь между линейными и угловыми величинами вращательного движения:

СВЯЗЬ МЕЖДУ ЛИНЕЙНЫМ И
УГЛОВЫЕ ЗНАЧЕНИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ:

25.динамика

ДИНАМИКА
Динамика (от греч. Dynamis — сила)
изучение движения тел в связи
с причинами, вызывающими это движение.

26. Первый закон Ньютона. Инерционные системы

ПЕРВЫЙ ЗАКОН НЬЮТОНА. ИНЕРЦИАЛЬНЫЕ СИСТЕМЫ
Так называемая классическая или ньютоновская механика
три закона динамики, сформулированные в
Ньютона в 1687 году. Эти законы играют решающую роль
в механике и стоят (как и все законы
физика) обобщение результатов обширных
человеческий опыт.

27. Первый закон Ньютона

ПЕРВЫЙ ЗАКОН НЬЮТОНА
Каждая материальная точка хранит состояние покоя или
равномерное прямолинейное движение до момента
воздействие других тел не заставит ее
изменить это состояние.

28. Первый закон Ньютона

ПЕРВЫЙ ЗАКОН НЬЮТОНА
Оба эти состояния похожи тем, что
ускорение кузова равно нулю. Таким образом, первые
закон формулировки можно представить следующим образом:
скорость любого тела остается постоянной (в
в частности, ноль), при ударе по корпусу
другими органами это не вызовет изменений.

29. Первый закон Ньютона

ПЕРВЫЙ ЗАКОН НЬЮТОНА
Стремление сохранить тело в состоянии покоя или
равномерное прямолинейное движение называется инерцией.
Поэтому первый закон Ньютона называется законом
. инерция.

30. инерция

ИНЕРЦИЯ
Инерциальной системой отсчета является такая система координат
ссылка на который материал
точка, свободная от внешних воздействий, либо на
покоятся или движутся равномерно (т. е. при постоянном
скорость).
Таким образом, первый закон Ньютона утверждает существование
инерциальных систем отсчета.

31. Масса и импульс тела

МАССА И МОЩНОСТЬ ТЕЛА
Воздействие этого тела другими телами вызывает изменение
по его скорости, т.е. по ускорению этого тела.
Опыт показывает, что такой же эффект по
разные тела разного размера ускорение. Каждые
тело сопротивляется попыткам изменить свое состояние движения. Это
свойство тел, как мы уже сказали, называется инерцией
(это следует из первого закона Ньютона).
Мера инерции тела — это величина, называемая
. масса.
Чтобы определить массу тела, нужно сравнить
это с весом, принятым за стандартную массу тела (или
сравните с уже известной массой тела).

32. Масса и импульс тела

МАССА И МОЩНОСТЬ ТЕЛА
Масса — величина добавки (масса тела
г. равна сумме масс деталей,
составляют это тело).
Системы, взаимодействующие только друг с другом, заявили
быть закрытым.
Рассмотрим замкнутую систему из двух тел
. массы и столкнуться с этими двумя телами

33. Масса и импульс тела

МАССА И МОМЕНТ ТЕЛА
Опыт показывает, что скорости у них противоположные
направления, разные по знаку, но равные по абсолютной величине
значение

34. Масса и импульс тела

МАССА И МОМЕНТ ТЕЛА
С учетом направления
скорости можно написать:

35.импульс тела

МОМЕНТ ТЕЛА

36. Второй закон Ньютона

ВТОРОЙ ЗАКОН НЬЮТОНА
скорость изменения количества движения тела
равной действующей на него силе.
Из этого можно сделать вывод, что смена
импульс тела равен
импульс силы.

37. Третий закон Ньютона

Третий закон Ньютона
Взаимодействующие тела действуют друг на друга с одинаковой силой, но противоположно
в направлении сил:

38.Каждое действие вызывает одинаково сильное противодействие. ОППОЗИЦИЯ

39. Закон сохранения количества движения

Закон сохранения количества движения
Механическая система называется закрытой (или изолированной), если на нее не действует
. внешними силами, т. е. не взаимодействует с внешними телами.
Строго говоря, каждая реальная система тел никогда не бывает замкнутой, потому что
при условии минимального воздействия гравитационных сил.Однако если
внутренние силы намного больше внешних, что можно считать такую ​​систему
закрытые (например — солнечная система).
Для замкнутой системы равнодействующий вектор внешних сил равен
равен нулю:

40. Закон сохранения количества движения

ЗАКОН СОХРАНЕНИЯ МОМЕНТА
Во всех процессах, происходящих в закрытых
системы, скорость центра масс
остается неизменной.
Закон сохранения количества движения — единица
основных законов природы.Ему было
полученный как следствие законов Ньютона,
но это также верно для микрочастиц и
к релятивистским скоростям

41. Гравитация и вес

ГРАВИТАЦИЯ И ВЕС
Одна из фундаментальных сил — сила тяжести проявляется на Земле в виде
гравитационная сила — сила, с которой все тела притягиваются к Земле.
У поверхности Земли все тела падают с одинаковым ускорением — ускорением
. гравитации g, (вспомним школьный опыт — «трубка Ньютона»).Отсюда следует, что в
система отсчета, связанная с землей, для каждого тела сила тяжести
ускорение свободного падения
гравитация

42. Гравитация и вес

ГРАВИТАЦИЯ И ВЕС
Если корпус подвешен или поставлен на опору, сила
гравитация уравновешивается силой, которая называется
опора реакции или подвеска

43. силы трения

СИЛЫ ТРЕНИЯ
Трение делится на внешнее и внутреннее.
Внешнее трение возникает при относительном
движение двух контактирующих тел (скольжение
трение или трение покоя).
Внутреннее трение возникает при относительном перемещении
частей одного и того же твердого тела (например,
жидкость или газ).

44. силы трения

СИЛЫ ТРЕНИЯ
Силы трения — тангенциальные силы, возникающие в
контактные поверхности корпусов и препятствий
их относительное движение
коэффициент трения

45.силы трения

СИЛА ТРЕНИЯ

46. Наклонная плоскость

НАКЛОННАЯ ПЛОСКОСТЬ

47. ЭНЕРГИЯ. Работа. ЗАКОНЫ О СОХРАНЕНИИ

ЭНЕРГЕТИКА. РАБОТА. ЗАКОНЫ СОХРАНЕНИЯ

48. Потенциальная энергия

ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
Если система материальных тел
консервативные силы, можно ввести
понятие потенциальной энергии.
Работа, проделанная консервативными силами, когда
изменение конфигурации системы, то есть
при положении корпусов относительно
кадр, независимо от того, было ли это изменение
реализовано

49.Формула для потенциальной энергии

ФОРМУЛА ДЛЯ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ

50. Кинетическая энергия

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
Функция статуса системы, которая составляет
определяется только скоростью его движения называется
кинетическая энергия.
Кинетическая энергия системы является функцией
состояния движения системы.

51. ЕДИНИЦЫ ИЗМЕРЕНИЯ ЭНЕРГИИ

ЕДИНИЦЫ ИЗМЕРЕНИЯ ЭНЕРГИИ
Энергия измеряется в единицах СИ в силе
работает на расстоянии в ньютонах на метр
(джоули)

52.Контакт кинетической энергии с импульсом стр.

КОНТАКТ КИНЕТИЧЕСКОЙ ЭНЕРГИИ С
MOMENTUM P.

53. Контакт кинетической энергии с произведением.

КОНТАКТ КИНЕТИЧЕСКОЙ ЭНЕРГИИ С
РАБОТА.
Если на тело действует постоянная сила, оно переместится на
в направлении силы. Затем блок
операция движения тела v. 1 to Vol.
2, это произведение силы F на перемещение dr

54. Контакт кинетической энергии с работой.

КОНТАКТ КИНЕТИЧЕСКОЙ ЭНЕРГИИ С
РАБОТА.
Следовательно, работа силы, приложенная к
тело на пути r численно равно
изменение кинетической энергии тела:
кинетическая энергия равна вариации dK
внешние силы:
Работа, как и кинетическая энергия
измеряется в джоулях.
МОЩНОСТЬ
Скорость выполнения работы (передача энергии) называется
. мощность.
Власть — это работа, выполненная за единицу времени.
мгновенная мощность
средняя мощность
Блок питания -Ватт

56.Консервативные и неконсервативные силы

КОНСЕРВАТИВНЫЕ И НЕКОНСЕРВАТИВНЫЕ
СИЛЫ
Также контактные взаимодействия наблюдались взаимодействия
между телами, удаленными друг от друга. Это
взаимодействие происходит через физические поля
(особая форма материи).
Каждое тело создает вокруг себя поле, которое
проявляется в воздействии на другие органы.

57. Консервативные и неконсервативные силы

КОНСЕРВАТИВНЫЕ И НЕКОНСЕРВАТИВНЫЕ
СИЛЫ
Силы, работа которых не зависит от пути
которое движущееся тело, и зависит от начального и
Конечное положение тела называют консервативным.

58. Консервативные и неконсервативные силы

КОНСЕРВАТИВНЫЕ И НЕКОНСЕРВАТИВНЫЕ
СИЛЫ
Консервативные силы: гравитация, электростатика
силы, силы центрального стационарного поля.
Неконсервативные силы: сила трения,
силы вихревого электрического поля.
Консервативная система — такая внутренняя сила, что
только консервативный внешний — консервативный и
стационарный.

59. Связь между потенциальной энергией и силой

СВЯЗЬ МЕЖДУ ПОТЕНЦИАЛОМ
ЭНЕРГИЯ И СИЛА
Пространство, в котором есть консервативные
силы, называемые потенциальным полем.
Каждая точка соответствует потенциальному полю
значение прочности
действующий на тело, а значение потенциала
energy U.

60. Закон сохранения механической энергии

ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ
ЭНЕРГИЯ
Закон сохранения объединяет
результаты, полученные нами ранее.
В сороковых годах девятнадцатого века произведений
г. Р. Майер, Гельмгольц и Джон. Джоуль (всего на
в разное время и независимо от каждого
прочее) доказано законом
г. сохранение и преобразование энергии.

61. Закон сохранения механической энергии

ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ энергии
ЭНЕРГИЯ
Для консервативной системы частиц всего
энергия системы:
Для закона сохранения механических
энергия: полная механическая энергия Консерваторно-консервативная система материала
баллов остается неизменным.

62. Для закрытой системы

ДЛЯ ЗАКРЫТОЙ СИСТЕМЫ
полная механическая энергия замкнутого
система материальных точек, между которыми
есть только консервативные силы, осталось
постоянный.

63. Столкновения

СОТРУДНИКИ

64. Абсолютно упругое центральное столкновение

АБСОЛЮТНО УПРУГИЕ ЦЕНТРАЛЬНОЕ СОЕДИНЕНИЕ
При абсолютно упругом ударе — это удар,
в котором нет преобразования механической
энергия в другие формы энергии.

65. Неупругое столкновение

НЕУПРУГОЕ СОЕДИНЕНИЕ
Неупругое столкновение — столкновение двух тел в
г. которые тело вместе и двигаться вперед как
один.

66. Динамика вращательного движения ТВЕРДОГО тела

ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
ТВЕРДОЕ ТЕЛО

67.Динамика вращательного движения твердого тела относительно оси

ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
ТЕЛО, СВЯЗАННОЕ С ОСЬЮ

68. МОМЕНТ ИНЕРЦИИ

МОМЕНТ ИНЕРЦИИ

69. Уравнение динамики основного тела вращения вокруг фиксированной оси

УРАВНЕНИЕ ДИНАМИКИ ГЛАВНОГО ТЕЛА
ВРАЩЕНИЕ ВОКРУГ ФИКСИРОВАННОЙ ОСИ

70. ДОПОЛНИТЕЛЬНОЕ УРАВНЕНИЕS

ВСПОМОГАТЕЛЬНЫЕ УРАВНЕНИЯ

71. Теорема Штейнера

ТЕОРЕМА ШТЕЙНЕРА
Момент инерции
относительно любой оси вращения равна
время его инерции
относительно параллельной оси, проходящей через
центр масс C массы тела плюс
произведение квадрата расстояния между
оси.

72. Кинетическая энергия вращающегося тела

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТЕЛА
Кинетическая энергия — величина добавки, поэтому
что кинетическая энергия тела, движущегося по
произвольным образом, это сумма кинетических
энергии всех n материальных точек, по которым это
тело может мысленно сломаться:

73. поступательное и вращательное движение

ПЕРЕВОД И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
Полная кинетическая энергия тела:

74.релятивистская механика

РЕЛЯТИВИСТСКАЯ МЕХАНИКА

75. Принцип относительности Галилея.

ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ.
При описании механики предполагалось, что все скорости
тела намного меньше скорости света. Причина
это то, что механика Ньютона (классическая) неверна, на
скорости тел близки к скорости света
Правильная теория для этого случая называется
релятивистская механика или специальная теория
Теория относительности

76.Преобразование Галилея

Преобразование Галилея
По классической механике: механический
явления происходят одинаково в двух ссылочных
рамы, движущиеся равномерно по прямой линии
относительно друг друга.

77. Преобразование Галилея

Преобразование Галилея

78. Интервал пространства

ИНТЕРВАЛ ПРОСТРАНСТВА

79. Преобразование Галилея

Преобразование Галилея
Моменты времени в разных системах отсчета
совпадают с точностью до постоянного значения, определяемого по
процедура синхронизации часов

80.Принцип относительности Галилея.

ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ.
Законы природы, определяющие перемены
в состоянии движения механических систем
не зависят от того, какой из двух инерционных
системы отсчета они принадлежат

81. Принцип относительности Эйнштейна

ПРИНЦИП ОТНОСИТЕЛЬНОСТИ Эйнштейна
В 1905 г. в журнале «Анналы физики» было 90 263 человека. опубликовала известную статью А. Эйнштейна «О
году. Электродинамика движущихся тел »,
г. которой специальная теория относительности (СТО) была
представлен.
Потом было много статей и книг
объясняя, разъясняя, интерпретируя эту теорию.

82. два постулата Эйнштейна

ДВА ПОСТУЛАТА ЭЙНШТЕЙНА

83. два постулата Эйнштейна

ДВА ПОСТУЛАТА ЭЙНШТЕЙНА
1. Все законы природы одинаковы во всех инерционных
справочные системы.
2. Скорость света в вакууме такая же
во всех инерциальных системах отсчета, а не
зависят от скорости источника и
светоприемник.

84. Преобразования Лоренца

Преобразования Лоренца
Формула преобразования при переходе с одной
инерциальную систему в другую с учетом
Постулаты Эйнштейна предложили Лоренца в 1904 г.

85. Преобразования Лоренца

Преобразования Лоренца
Лоренц установил связь между
координаты и время события в кадре
k и k ‘на основе постулатов СТО
Таким образом, на высоких оборотах, сопоставимых со скоростью
света получил Лоренц

86.Преобразования Лоренца

Преобразования Лоренца

87. Четвертое измерение

ЧЕТВЕРТОЕ ИЗМЕРЕНИЕ
Истинный физический смысл Lorentz
преобразований была впервые создана в 1905 году
Эйнштейном в СТО. В теории относительности,
время иногда называют четвертым измерением.
Точнее, значение ct того же
измерение как x, y, z ведет себя как четвертое пространство
координировать. В теории относительности ct и x
проявляют себя из математического
точка зрения аналогичным образом.

88. Четвертое измерение

ЧЕТВЕРТОЕ ИЗМЕРЕНИЕ

89. Четвертое измерение

ЧЕТВЕРТОЕ ИЗМЕРЕНИЕ
На малых скоростях или на бесконечной скорости — случайное повреждение
теория дальних взаимодействий), Lorentz
превращения превращаются в
Галилея трансформация (принцип соответствия).

90. Выводы преобразований Лоренца

ВЫВОДЫ ЛОРЕНЦА
ПРЕОБРАЗОВАНИЯ
1) Преобразования Лоренца демонстрируют
неразрывная связь пространственно-временная
свойства нашего мира (мира четырехмерного).
2) На основе преобразования Лоренца
можно описать относительностью
одновременность.
3) Необходимо ввести релятивистский
Закон сложения скоростей.

91. Длина сокращения Лоренца (длина тел в различных системах отсчета)

ДЛИНА СОКРАЩЕНИЯ ЛОРЕНЦА
(ДЛИНА КОРПУСОВ В РАЗНЫХ РАМАХ
СПРАВКА)
длина движущегося тела меньше длины покоя

92. Время замедления (Продолжительность события в разных системах отсчета)

ВРЕМЯ ЗАМЕДЛЕНИЯ
(ПРОДОЛЖИТЕЛЬНОСТЬ СОБЫТИЯ ОТЛИЧАЕТСЯ
РАМКИ ИСПОЛЬЗОВАНИЯ)
Правильное время — наименьшее (движущиеся часы идут
медленнее отдыхает)

93.Масса, импульс и энергия в релятивистской механике

МАССА, МОМЕНТ И ЭНЕРГИЯ В
РЕЛЯТИВИСТСКАЯ МЕХАНИКА

94. Релятивистское увеличение массы частиц материи

ОТНОСИТЕЛЬНОЕ УВЕЛИЧЕНИЕ МАССЫ
ЧАСТИЦЫ ВЕЩЕСТВА

95. Релятивистское выражение для импульса

Релятивистское выражение для
MOMENTUM

96. Релятивистское выражение для энергии

Релятивистское выражение для
ЭНЕРГИЯ

97.Молекулярно-кинетическая теория

МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ

98. Влияние пара

ВЛИЯНИЕ ПАРА
Шаровой водометный движитель, установленный на трубчатых стойках, по реакции
обеспечивается выходящим паром, было продемонстрировано
2000 лет назад Герой Александрии.

99. Основные понятия и определения молекулярной физики и термодинамики

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Набор тел, составляющих макроскопический
Система называется термодинамической системой.
Система может находиться в разных состояниях. Модель
величины, характеризующие состояние системы,
Состояние называемые параметры: давление P, T
температура, объем V и т. д.
Связь между P, T, V специфическая
для каждого тела называется уравнением состояния.

100. Основные понятия и определения молекулярной физики и термодинамики

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Любой параметр, имеющий определенное значение для каждого
состояния равновесия является функцией
состояние системы.Система равновесия — такая
система, параметры состояния которой
одинаково во всех точках системы и не
изменение во времени (при постоянном внешнем
условия). Таким образом в равновесие выбрано
макроскопическая часть системы.

101. Основные понятия и определения молекулярной физики и термодинамики

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Процесс — переход с одного
состояние равновесия в другое.Расслабление —
возврат системы в состояние равновесия.
Время прохождения — время релаксации

102. Атомный вес химических элементов (атомный вес) A

АТОМНЫЙ ВЕС ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
(АТОМНЫЙ ВЕС) A

103. Молекулярный вес (MW)

МОЛЕКУЛЯРНЫЙ ВЕС (MW)
Отсюда можно найти много атомов и
молекул в килограммах:

104. Определения

ОПРЕДЕЛЕНИЯ
В термодинамике широко используется понятие к-моль, моль,
Число Авогадро и число Лошмидта.Даем
определение этих величин.
Мол — нормированное количество любого вещества в газообразном состоянии,
жидкое или твердое состояние. 1 моль — количество граммов материала
равной его молекулярной массе.

105. Номер Авогадро

Номер Авогадро
В 1811 году Авогадро предположил, что количество частиц на
кмоль любого вещества постоянна и равна названному, в
Следствие, номер Авогадро
Молярная масса — масса одного моля (μ)

106.номер Loschmidt

НОМЕР LOSCHMIDT
При одинаковых температурах и давлениях всех газов
содержится в единице объема такое же количество молекул.
Количество молекул идеального газа, содержащихся в 1 м3 ниже
нормальных условиях, называется номер Лошмидта:
k = 1,38 · 10 (-23) Дж / К — постоянная Больцмана

107. Давление. Основное уравнение молекулярно-кинетической теории

ДАВЛЕНИЕ. ОСНОВНОЕ УРАВНЕНИЕ
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ
давление газа — там
Последствие столкновения газа
молекулы со стенками сосуда.

108. Давление

ДАВЛЕНИЕ

109. Основное уравнение молекулярно-кинетической теории газов.

ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИКИ
ТЕОРИЯ ГАЗОВ.
Давление газа определяется по среднему
кинетическая энергия поступательного движения
молекулы.

110. Температура

ТЕМПЕРАТУРА
R — универсальная газовая постоянная

111. Основное уравнение молекулярно-кинетической теории-2

ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИКИ
ТЕОРИЯ-2

112.Вероятность события. Концепция распределения скорости молекул газа

ВЕРОЯТНОСТЬ СОБЫТИЯ. КОНЦЕПЦИЯ
РАСПРЕДЕЛЕНИЯ СКОРОСТИ
МОЛЕКУЛЫ ГАЗА
С точки зрения атомно-молекулярной
структура ценностей вещества найдена в
макроскопическая физика, смысл среднего
значения, которые берут некоторые из функций из
микроскопические переменные системы. Значения
этот вид называется статистикой.Примеры таких
переменные: давление, температура, плотность
и другие.

113. Вероятность наступления события. Концепция распределения скорости молекул газа

ВЕРОЯТНОСТЬ СОБЫТИЯ. КОНЦЕПЦИЯ
РАСПРЕДЕЛЕНИЯ СКОРОСТИ
МОЛЕКУЛЫ ГАЗА
Большое количество сталкивающихся атомов и
молекулы вызывают важные закономерности в
поведение статистических переменных, не свойственное
отдельные атомы и молекулы.? Эти
паттерны называются вероятностными или статистическими

114. Функция распределения Максвелла

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА
Предположим, что есть n одинаковых молекул в
состояние случайного теплового движения при определенном
температура. После каждого акта столкновения
между молекулами, их скорость изменяется
случайным образом.
стационарное состояние равновесия —
установили в результате невероятно большой
количество столкновений, количество молекул
в данном диапазоне скоростей сохраняется постоянной.

115. Функция распределения Максвелла

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА

116. Функция распределения скорости

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СКОРОСТИ
функция указывает долю одиночных
молекул газа объем, абсолютный
скорости заключены в одну скорость
диапазон, включающий заданную скорость.

117. Барометрическая формула

БАРОМЕТРИЧЕСКАЯ ФОРМУЛА
Атмосферное давление на высоте h за счет
вес вышележащих слоев газа.

118. Первый закон термодинамики

ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ

119. Первый закон термодинамики

ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
Q ΔU A
Количество тепла, передаваемого телу,
идет на увеличение внутренней энергии и тела
для выполнения работы:

120. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ

ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
ΔU Q A
изменение внутренней энергии тела
равно разнице между заявленными
и тепло тела произведенной работы
Тело

121.Применение первого закона термодинамики к изопроцессам идеальных газов

ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА
ТЕРМОДИНАМИКА К ИЗОПРОЦЕССАМ
ИДЕАЛЬНЫЕ ГАЗЫ
Изо — процессы, в которых один из
термодинамические параметры остаются постоянными

122. Изотермический процесс

ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС
изотермическое расширение
Условия потока
Т конст.
Q A
Q 0
р
U =
V
0
A 0

123. Изотермический процесс

ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС
Изотермическое сжатие
Т конст.
Условия потока
p
V
U = 0
Q A
Q 0
А 0

124.изохорный нагрев

ИЗОХОРНЫЙ НАГРЕВ
V const
Q U
Q 0
p
2
1
V
U Q
U 0
A 0

125. изохорическое охлаждение

изохорическое охлаждение
V const
Q U
Q 0
p
1
U Q
U 0
2
V
A 0

126. Удлинение и сжатие изобары

РАСШИРЕНИЕ И СЖАТИЕ ISOBAR
Домашнее задание
p const

127. Адиабатический процесс

АДИАБАТИЧЕСКИЙ ПРОЦЕСС
Адиабатический процесс — процесс, при котором нагревается
обмен с окружающей средой.
Q 0
В случае адиабатического процесса система
не работает из-за уменьшения внутреннего
энергия
A U

128. Домашнее задание

ДОМАШНЕЕ ЗАДАНИЕ
Законы процессов
Энтропия S — это отношение полученного срока или
передал тепло температуре-D, в которой этот
процесс состоялся.
dQ
DS
T

130. Для обратимых процессов, изменение энтропии:

ДЛЯ ОБРАТНЫХ ПРОЦЕССОВ, ЭНТРОПИЯ
ИЗМЕНЕНИЕ:
ΔS обр 0, т.к.
dQобр
Т
0
Это выражение называется Clausius
. равенство.

131. Второй закон термодинамики

ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
Он не может обработать, единственный результат —
преобразование всего тепла, производимого
обогреватель в эквивалентной работе (формулировка Кельвина)
2. Не может быть вечного двигателя
автомат второго рода (редакция
Томпсон-Планк).
3. Он не может обработать, единственный результат —
передача энергии от холодного тела к горячему
(Формулировка Клаузиуса).

132. ТЕРМИЧЕСКИЕ МАШИНЫ

Круговой процесс или цикл, называемый таким
процесс, в котором термодинамическое тело
возвращается в исходное состояние.

133. Круговой процесс

Круговой процесс
Цикл совершаемого идеального газа можно разделить
в процессы:
расширения (1-2)
Сжатие (2 — 1) газа

134. Круговой процесс

ЦИРКУЛЯРНЫЙ ПРОЦЕСС
Круговые процессы лежат в основе всех тепловых машин: внутренний
двигатели внутреннего сгорания, паровые и газовые турбины, паровые и
холодильные машины и др.В результате круговой процесс
система возвращается в исходное состояние и, следовательно, полный
изменение внутренней энергии газа равно нулю: dU = 0
Тогда первый закон термодинамики для кругового процесса
Q ΔU A A

135. Круговой процесс

ЦИРКУЛЯРНЫЙ ПРОЦЕСС
Процесс называется обратимым, если он продолжается в
таким образом, что после процесса это может быть
проводится в обратном направлении через
такое же промежуточное состояние, что и прямой
процесс.После кругового обратимого процесса no
изменения в окружающей среде вокруг
системы, не произойдет. В то же время
под средой понимается совокупность всех несистемных
тела, с которыми система взаимодействует напрямую.

136. Круговой процесс

Круговой процесс
Процесс называется необратимым, если он занимает
место так, чтобы после окончания системы можно было
не вернуться в исходное состояние после предыдущего
промежуточные состояния.Невозможно провести
необратимый циклический процесс, в любую точку
окружающая среда осталась неизменной.

137. Тепловые двигатели

ТЕПЛОВЫЕ ДВИГАТЕЛИ
Тепловая машина вызвала пакетный двигатель для работы
из-за возникающего тепла снаружи.

138. Идеальный тепловой двигатель

ИДЕАЛЬНЫЙ ТЕПЛОВОЙ ДВИГАТЕЛЬ
Наибольший КПД ТЭНа при заданном
температуры Т1 и Т2 холодильника имеет тепловая машина
рабочая жидкость, которая расширяется и сжимается по циклу Карно
график, состоящий из двух изотерм и двух адиабатических

139.Цикл Карно

ЦИКЛ КАРНО

140. Цикл Карно

ЦИКЛ КАРНО
Цикл, как выяснил Карно, является наиболее экономичным и представляет собой циклический тип
. процесс, состоящий из двух изотерм и двух адиабатических

141. КПД Машина Карно

КПД МАШИНА КАРНО
A Q1 Q2
2 квартал
Т2
η
1
1.
1 квартал
1 квартал
1 квартал
T1

142. Реальные газы

РЕАЛЬНЫЕ ГАЗЫ

143. Реальные газы

РЕАЛЬНЫЕ ГАЗЫ
Уравнение Менделеева — Клапейрона — самое простое и надежное
и известное уравнение состояния идеального газа.
м
PV RT
μ
Реальные газы описываются уравнением
состояние идеального газа является приблизительным, и
отклонения от идеального поведения стали
заметно при высоких давлениях и низких
температуры, особенно при газе
близок к конденсации.

144. Реальные газы

РЕАЛЬНЫЕ ГАЗЫ
Первая поправка к уравнению состояния идеального газа —
учитывая его собственный объем, занимаемый молекулами реального
газ. В уравнении Дюпре (1864)
P (V νb) νRT
константа b учитывает собственное
молярный объем молекул.

145. Реальные газы

РЕАЛЬНЫЕ ГАЗЫ
При понижении температуры межмолекулярный
взаимодействие в реальных газах приводит к конденсации (жидкость
поколение). Межмолекулярное притяжение эквивалентно
наличие некоторого внутреннего давления газа P *
(иногда называемое статическим давлением). Первоначально P * значение
учтено в общих чертах в модели
уравнение Гирне (1865)
(P P *) (V νb) νRT

146. Уравнение Ван-дер-Ваальса

Уравнение Ван-дер-Ваальса
Ван дер Ваальс дал функциональную интерпретацию
внутреннего давления.По модели
сил притяжения Ван-дер-Ваальса между
г. молекул (сила Ван-дер-Ваальса) обратно пропорциональна
пропорционально шестой степени расстояния
между ними, или вторая степень
объем, занимаемый газом. Также считается
что сила притяжения добавила к
внешнее давление.

147. Уравнение Ван-дер-Ваальса

УРАВНЕНИЕ ВАН-ДЕР ВААЛЬСА
С учетом этих соображений уравнение идеального газа
состояние преобразуется в уравнение сил Ван-дер-Ваальса:
2
ν а
(V νb) П 2
V
νRT
или за одну родинку

(Вм б) П 2 νRT
Вм

148.Реальные газы

РЕАЛЬНЫЕ ГАЗЫ
Реальные газы — газы, свойства которых зависят от
по молекулярному взаимодействию. Под нормальным
условия, когда средняя потенциальная энергия
межмолекулярного взаимодействия намного меньше
чем средняя кинетическая энергия
молекулы, свойства реального и идеального
газы различаются незначительно. Поведение этих
газов резко меняется при высоких давлениях и низких
температуры, при которых начинаются квантовые эффекты, до
появляться.

149. Сила Ван-дер-Ваальса

Сила Ван-дер-Ваальса
Ван дер Ваальс объяснил свойства настоящего
газы и жидкости, предположил, что на малых
расстояния между молекулами отталкивающие
сил, которые заменяются увеличивающимися
силы притяжения на расстоянии.

150. Сила Ван-дер-Ваальса

Сила Ван-дер-Ваальса
Межмолекулярные взаимодействия электрические в
природы и состоят из сил притяжения
(ориентация, индукция, дисперсия) и
силы отталкивания.

151. Внутренняя энергия газа Ван-дер-Ваальса

ВНУТРЕННЯЯ ЭНЕРГИЯ ГАЗОВОГО ФУРГОНА
WAALS
Энергия одного моля газовой силы Ван-дер-Ваальса равна
состоит из:
внутренняя энергия молекул газа;
кинетическая энергия теплового движения центра масс
молекул
потенциальная энергия взаимного притяжения молекул

152. Сила Ван-дер-Ваальса

СИЛА ВАН-ДЕР-ВААЛЬСА
Главная ценность Ван-дер-Ваальса
уравнение определяется следующими факторами
1) Уравнение получено из модели
. свойства реальных газов и жидкостей, и
не результат эмпирической функции выбора f
(P, V, T), который описывает свойства реального
газы;

153.Van der Waals Force

VAN DER WAALS FORCE
2) Уравнение долгое время рассматривалось как
Общий вид уравнения состояния вещественного
газов, на базе которых было построено много
другие уравнения состояния; 3) Используя уравнение
войск Ван-дер-Ваальса первыми совершили
описать явление переноса газа
в жидкость и проанализировать критические явления.
В связи с этим у Van der Waals есть
преимущество даже перед более точным
уравнения в вириальной форме.

154. Эффект Джоуля-Томсона

Эффект Джоуля-Томсона
Если идеальный газ адиабатически расширяется и
одновременно выполняет работу, значит
охлаждается, так как в данном случае работа ведется на
за счет своей внутренней энергии.
Аналогичный процесс, но на реальном газе — адиабатический
расширение реального газа до комиссии
положительная работа внешних сил

155. Эффект Джоуля-Томсона

Эффект Джоуля-Томсона
Эффект Джоуля-Томсона заключается в изменении температуры на 90 ° 263 ° С. газ в результате медленного потока газа под
постоянный перепад давления через реактор — местный
препятствие для потока газа, такое как пористая мембрана
расположен на пути потока.

156. Эффект Джоуля-Томсона

Эффект Джоуля-Томсона
Эффект Джоуля-Томсона указывает на присутствие
газ в межмолекулярных силах. Газ выполняет
внешние работы — последующие слои газа
проталкивается и выполняет рабочую силу
внешнее давление, обеспечивающее стационарный поток
сам газ. Работа проталкивания
дроссельная часть газового объема V1 под давлением
P1 — это P1V1, дроссель этой порции газа занимает
том V2 и работает P2V2.

157. Сжижение газов

СЖИЖЕНИЕ ГАЗОВ
Конверсия любого газа в жидкость — газ
ожижение — возможно только при температуре
ниже критического значения.

158. Сжижение газов

СЖИЖЕНИЕ ГАЗОВ
1 — цилиндр компрессора; 2 — ребра охлаждения; 3 регенератора; 4 — насморк; 5 — изоляция; Расширитель на 6 цилиндров.

159. Сжижение газов

СЖИЖЕНИЕ ГАЗОВ

160. электричество

ЭЛЕКТРИЧЕСТВО
ПРИРОДА
Первые известные проявления «зверя
». электричество »были разрядами электрических рыб.
Электрический сом был изображен даже на
. древнеегипетские гробницы и Гален (130-200
лет нашей эры) рекомендуется
«электротерапия» этими рыбками,
проходивший врачебную практику на гладиаторском турнире
сражения в Древнем Риме.
ИСТОРИЯ
В 1746-54 гг. Франклин объяснил действие
из лейденской банки, построен первый плоский конденсатор
состоящий из двух параллельных металлических пластин, разделенных друг от друга
слоем стекла, изобрел громоотвод в 1750 г.,
г. в 1753 году доказал электрическую природу молнии
(опыт работы с воздушным змеем) и тож
земное и атмосферное электричество.В 1750 году он
разработал теорию электрических явлений —
так называемая «унитарная теория», согласно которой
электричество представляет собой особую тонкую жидкость, пронизывающую
все кузов
ИСТОРИЯ
Лейденский банк был изобретен в 1745 году независимым голландским профессором Питером Ван
Мушенброк (1692-1761) и немецкий прелат Эвальд Георг фон Клейст. Модель
диэлектриком в этом конденсаторе было стекло сосуда, а пластинами вода в
сосуд и ладонь экспериментатора, удерживающая сосуд.Выход
внутренняя облицовка представляла собой металлический проводник, пропущенный в сосуд и погруженный в
вода. В 1746 году появились различные модификации лейденской банки. Лейденский банк
позволял хранить и хранить относительно большие заряды, порядка микрокуба.

164. электрический заряд

ЭЛЕКТРИЧЕСКИЙ ЗАРЯД
Электрические заряды не существуют сами по себе, но являются внутренними свойствами
. элементарные частицы — электроны, протоны и др.
Опытный в 1914 году американский физик Р.Милликен показал, что
Электрический заряд дискретный.
Заряд q любого тела является целым кратным элементарного электрического
заряд: q = n × e.
е 1,6 10
19
Кл

165. Закон сохранения заряда

ЗАКОН СОХРАНЕНИЯ ЗАРЯДА
Закон сохранения заряда является одним из
основные законы природы, сформулированные в 1747 г. Б.
Франклина и подтверждено в 1843 г. М. Фарадеем:
алгебраическая сумма зарядов, возникающих в любом электрическом
процесса по всем органам, участвующим в процессе —
нуль.
Суммарный электрический заряд замкнутой системы не
заменить

166. Электрический заряд

ЭЛЕКТРИЧЕСКИЙ ЗАРЯД
Электростатика — это раздел, изучающий статику
(неподвижные) заряды и связанные с ними электрические
поля.
ЗАКОНЫ

168. Закон Кулона

ЗАКОН КУЛОНА
Большой вклад в изучение явлений
электростатики был сделан знаменитым
Французский ученый
С. Кулон.
В 1785 году экспериментально установил закон
. взаимодействия неподвижных точечных электрических зарядов.

169. Взаимодействие электрических зарядов в вакууме.

ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ В А
ВАКУУМ.
Точечный заряд (q) — это заряженное тело,
размеры ничтожно малы по сравнению с
с расстоянием до других заряженных тел с
с которым он взаимодействует.

170. Закон Кулона

ЗАКОН КУЛОНА
Сила взаимодействия точечных зарядов в
вакуум пропорционален значению
заряда и обратно пропорциональна
квадрат расстояния между ними.
q1q2
Ф к0 2
r

171. коэффициент

КОЭФФИЦИЕНТ
Где ε0 — электрическая постоянная;
4p здесь выражают сферическую симметрию
Закон Кулона.
Н м
k0
9 10
2
4 0
Кл
1
9
2

172. Напряженность электростатического поля

ПРОЧНОСТЬ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Вокруг заряда всегда есть электрическое поле,
главное свойство которого — то, что любой другой
на заряд, помещенный в это поле, действует сила.
Электрические и магнитные поля — это особый случай
. более общий — электромагнитное поле (ЭМП).
Они могут разводить друг друга, превращаться друг в друга.
Если заряды не двигаются, то магнит
поле не возникает.

173. Напряженность электростатического поля

ПРОЧНОСТЬ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Силовая характеристика поля, создаваемого зарядом q, равна
коэффициент силы, действующей на испытательный заряд q ‘, расположенный на
заданной точки поля к значению этого заряда, называемого
напряженность электростатического поля, т.е.е.
F
q
E
2
q ‘4 0 r

174. Силовые линии электростатического поля

ПОЛЕВЫЕ ЛИНИИ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Теорема Остроградского-Гаусса, которую мы
докажу и обсудим позже, устанавливает
связь между электрическими зарядами и
электрическое поле. Это более общий и более
изящная формулировка закона Кулона.

175. Силовые линии

СИЛОВЫЕ ЛИНИИ
Силовые линии — это линии, касательные к которым при любой точке
точка поля совпадает с направлением
вектор напряжения

176.Теорема Остроградского-Гаусса

ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА
Итак, по определению, поток электрического поля
вектор силы равен числу
линии натяжения, пересекающие поверхность S.

177. Теорема Остроградского-Гаусса

ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА
ФЕ
q
Е dS
n
S
ε0
Поток вектора напряженности электрического поля через замкнутую поверхность в
вакуум равен алгебраической сумме всех зарядов, находящихся внутри поверхности
делится на ε0.
1
ФE dV
ε0 В

178. потенциал

ПОТЕНЦИАЛ
Работа электростатических сил не
зависят от формы пути, но только от
координаты начальной и конечной точек
смещение. Следовательно, напряженность поля
консервативны, а само поле
потенциально.

179. разность потенциалов

ПОТЕНЦИАЛЬНАЯ РАЗНИЦА
W
φ.
q ‘
Из этого выражения следует, что
потенциал численно равен потенциалу
энергия, которой обладает единичный положительный заряд на уровне
заданная точка поля.

180. ДИЭЛЕКТРИКА В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ

В идеальном диэлектрике свободные заряды, то есть
способен перемещаться на значительные расстояния
(превышающие расстояния между атомами), нет.
Но это не значит, что диэлектрик поставлен
в электростатическом поле не реагирует на это, что
в нем ничего не происходит.

181. ДИЭЛЕКТРИКА В ЭЛЕКТРОСТАТИЧЕСКОЙ ПОЛЕ

Смещение электрических зарядов вещества под
действие электрического поля называется поляризацией.
Способность к поляризации — главное свойство диэлектриков.

182. ДИЭЛЕКТРИКА В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ

Внутри диэлектрика электрические заряды диполей компенсируются
друг друга. А вот на внешних поверхностях диэлектрика,
рядом с электродами появляются заряды противоположного знака
(поверхностно-связанные заряды).

183. Различные виды диэлектриков

РАЗНЫЕ ДИЭЛЕКТРИКИ
В 1920 г. спонтанная (спонтанная) поляризация
был открыт.
Вся группа веществ получила название
. сегнетоэлектрики (или сегнетоэлектрики).
Все сегнетоэлектрики обладают резкой анизотропией
свойства (сегнетоэлектрические свойства могут быть
наблюдается только вдоль одной из осей кристалла). В
г. изотропные диэлектрики, поляризация всего
молекулы одинаковы, для анизотропных поляризация, а следовательно, и поляризация
вектор в разные стороны разный.

184. Различные виды диэлектриков

РАЗНЫЕ ДИЭЛЕКТРИКИ
Среди диэлектриков есть вещества под названием
. электрет-диэлектрики, сохраняющие
поляризованное состояние в течение длительного времени после удаления
внешнее электростатическое поле (аналоги
постоянные магниты).

185. Различные виды диэлектриков

РАЗНЫЕ ДИЭЛЕКТРИКИ
Некоторые диэлектрики поляризованы не только под
действие электрического поля, но и под действием
действие механической деформации. Это
явление называется пьезоэлектрическим эффектом.
Явление было обнаружено
г. братья Пьер и Жак Кюри в 1880 году.

186. Различные виды диэлектриков

РАЗЛИЧНЫЕ ВИДЫ ДИЭЛЕКТРИКОВ
Пироэлектричество — появление электрика
зарядов на поверхности некоторых кристаллов, когда
они нагреваются или охлаждаются.
При нагревании один конец диэлектрика составляет
заряжается положительно, а при охлаждении тоже
отрицательный.
Появление обвинений связано с
изменение существующей поляризации как
температура кристаллов меняется.

187. Электрический ток в газах. Газовые разряды и их применение

ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ. ГАЗ
РАЗРЯДЫ И ИХ ПРИМЕНЕНИЕ

188. Явление ионизации и рекомбинации в газах

ЯВЛЕНИЕ ИОНИЗАЦИИ И
РЕКОМБИНАЦИЯ В ГАЗАХ
Процесс ионизации заключается в том, что под
воздействие высокой температуры или некоторых лучей на молекулы
газ теряет электроны и тем самым превращается в положительные ионы.
Ток в газах — противоток ионов и свободный
электроны.
Одновременно с процессом ионизации происходит
обратный процесс рекомбинации (иначе — молизация).
Рекомбинация — это нейтрализация, когда разные ионы
встретились, или воссоединение иона и электрона в
нейтральная молекула (атом).
Факторы, под действием которых происходит ионизация в
газа называются внешними ионизаторами, а проводимость
Возникновение здесь называется несамостоятельной проводимостью.

189. Автономный газовый разряд

САМОХОДНЫЙ ГАЗОВЫЙ ВЫПУСК
Самостоятельный разряд — газовый разряд
которые носители тока возникают в результате
те процессы в газе, которые происходят из-за
напряжение, приложенное к газу.
То есть этот разряд продолжается после
ионизатор останавливается.

190. Автономный газовый разряд

АВТОНОМНЫЙ ГАЗОВЫЙ ВЫПУСК
При перекрытии межэлектродного промежутка
полностью проводящая газоразрядная плазма,
происходит его поломка.
Напряжение, при котором пробой
возникает межэлектродный зазор называется
напряжение пробоя.

191. Условия для образования и поддержания автономного газового разряда

УСЛОВИЯ ОБРАЗОВАНИЯ И
ТЕХНИЧЕСКОЕ ОБСЛУЖИВАНИЕ НЕЗАВИСИМОГО ГАЗА
РАЗРЯД

192. Виды заряда

ВИДЫ ЗАРЯДА
В зависимости от давления газа электрод
конфигурация и параметры внешней цепи,
есть четыре типа автономных разрядов:
Светящийся заряд;
Искровой заряд;
Дуговый заряд;
Заряд короны.

193. Светящийся заряд

Светящийся заряд
Тлеющий заряд происходит при низких давлениях (в
г. вакуумные трубки).
Его можно наблюдать в стеклянной трубке с плоским
металлические электроды, припаянные на концах.
Возле катода тонкий светящийся слой,
катодная светящаяся пленка

194. Искровой заряд

ИСКРОВЫЙ ЗАРЯД
Искровой заряд возникает в газе, обычно на 90 ° 263 °. давления порядка атмосферного Rm.
Для него характерна прерывистая форма.
По внешнему виду искровой разряд
пучок светлый, зигзагообразный разветвленный тонкий
полосы, мгновенно протыкающие разрядный промежуток,
быстро отмирают и постоянно заменяют каждый
Другие.
Эти полоски называются искровыми каналами.

195. Дуговый заряд

ДУГОВЫЙ ЗАРЯД
Если после получения искрового заряда от
мощный источник, постепенно уменьшайте расстояние
между электродами разряд от
прерывистый становится непрерывным новая форма
Возникает газовый заряд, называемый дуговым зарядом.

196. Коронный разряд

КОРОННЫЙ РАЗРЯД
Коронный разряд возникает в сильном неоднородном электрическом поле при относительно высокой концентрации газа
давления (порядка атмосферного
давление).
Такое поле можно получить между двумя
электроды, на поверхности одного из которых имеется
большая кривизна (тонкая проволока, наконечник).

197. Применение газовой заправки

ПРИМЕНЕНИЕ ГАЗОВОЙ ЗАРЯДКИ
Газоразрядные устройства очень разнообразны, и отличаются по типу
. тип используемого разряда.
Используются для стабилизации напряжения, защиты от
перенапряжение, выполнять функции переключения, указать
электрическое состояние
В последнее время для усиления защиты уязвимых и
ответственные объекты, например, ракетные установки,
различные формы управления молнией
реализовано, в частности, лазерное зажигание молнии.
Лазерное инициирование основано на создании ионизированного
канал в воздухе с помощью лазерного излучения.

198. Эмиссия электронов из проводников

ИЗЛУЧЕНИЕ ЭЛЕКТРОНОВ ИЗ ПРОВОДНИКОВ
Электрон свободен только в пределах металла. As
как только он пытается пересечь границу «металл-вакуум»,
Между электроном и
возникает кулоновская сила притяжения. избыточный положительный заряд, образованный на поверхности

199. Эмиссия электронов из проводников

ИЗЛУЧЕНИЕ ЭЛЕКТРОНОВ ИЗ ПРОВОДНИКОВ
Облако электронов образуется у поверхности,
и двойной электрический слой сформирован на
интерфейс
Разница потенциалов

200.Термоэлектронная эмиссия

ТЕРМИОННАЯ ИЗЛУЧЕНИЕ
Величина работы выхода зависит от
о химической природе вещества, о его
термодинамическое состояние, а также состояние
интерфейс.
Если энергии достаточно для выполнения
работа выхода сообщается электронам с помощью
нагрев, затем процесс выхода электронов из
металл называется термоэлектронной эмиссией.

201. Холодное и взрывоопасное излучение

ХОЛОДНОЕ И ВЗРЫВООБРАЗОВАНИЕ
Электронное излучение, вызванное действием
силы электрического поля на свободные электроны в металле
называется холодной или автоэлектронной.
Для этого напряженность поля должна быть достаточной
и условие
Авых e φ вн φ пов eEd,
Здесь d — толщина двойного электрика
слой на медиаинтерфейсе.

202. Автоэлектронное излучение

АВТОЭЛЕКТРОННОЕ ИЗЛУЧЕНИЕ
Автоэмиссию можно наблюдать в хорошо откачанном вакууме
трубка с катодом в качестве наконечника и анодом в качестве наконечника
обычный электрод с плоской или слегка изогнутой поверхностью.

203. Автоэлектронное излучение

АВТОЭЛЕКТРОННОЕ ИЗЛУЧЕНИЕ
Напряженность электрического поля на поверхности острия с радиусом кривизны r и
потенциал U относительно анода равен
U
E.
r

204. Магнетизм

МАГНИТИЗМ

205. Магнитные взаимодействия

МАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ
В космосе возникает магнитное поле
окружающие намагниченные тела.
В это поле помещена небольшая магнитная стрелка
установлен в каждой из своих точек в очень
определенным путем, тем самым указав направление
поле.
Конец стрелки, который в магнитном
поле Земли указывает на север, называется
север, а наоборот — юг.

206. Когда магнитная стрелка отклоняется от направления магнитного поля, стрелка воздействует на механический крутящий момент Mcr,

КОГДА МАГНИТНАЯ ИГЛА УКАЗЫВАЕТСЯ ОТ НАПРАВЛЕНИЯ МАГНИТНОГО ПОЛЯ,
ARROW ACTS
МЕХАНИЧЕСКИЙ МОМЕНТ MCR, ПРОПОРЦИОНАЛЬНЫЙ СИНУСУ УГЛА ОТКЛОНЕНИЯ Α И
ТЕНДЕНЦИЯ ПОВОРОТА ПО УКАЗАННОМУ НАПРАВЛЕНИЮ.

207. Разница между постоянными магнитами и электрическими диполями заключается в следующем:

РАЗНИЦА МЕЖДУ ПОСТОЯННЫМИ МАГНИТАМИ И ЭЛЕКТРИЧЕСКИМИ ДИПОЛЯМИ
КАК СЛЕДУЕТ:
Электрический диполь всегда состоит из зарядов одинаковой величины и противоположных знаков.
Постоянный магнит, разрезанный пополам, превращается в два меньших магнита, каждый из которых имеет
как северный, так и южный полюса.

208. Открытие Эрстеда

Открытие Эрстеда
При установке магнитной иглы в непосредственный
вблизи проводника с током он обнаружил, что
когда ток течет по проводнику,
стрелка отклоняется; после отключения тока
стрелка возвращается в исходное положение.
Из описанного опыта
Эрстед заключает:
вокруг прямолинейный
проводник с током
есть магнитное поле.

209. Магнитная индукция

МАГНИТНАЯ ИНДУКЦИЯ
силовая характеристика магнитного поля, может
быть представлены с помощью силовых линий магнитного поля.
Так как M — момент силы и
магнитный момент характеристики
вращательного движения, можно предположить, что
магнитное поле вихревое.

210. Bio — Savard — Закон Лапласа-Ампера

BIO — SAVARD — ЗАКОН ЛАПЛАСА-АМПЕРА
В 1820 году французские физики Жан Батист Био
и Феликс Савар провели исследования
магнитные поля токов различной формы.A
Французский математик Пьер Лаплас
резюмировал эти исследования.

211. Bio — Savard — закон Лапласа-Ампера

BIO — SAVARD — ЗАКОН ЛАПЛАСА-АМПЕРА

212. Bio — Savard — закон Лапласа-Ампера

BIO — SAVARD — ЗАКОН ЛАПЛАСА-АМПЕРА
Здесь: I — ток;
— вектор, совпадающий с элементарным
часть тока и направлена ​​в направлении
к которому течет ток;
— радиус-вектор, взятый из текущего
элемент до точки, в которой мы определяем;
r — модуль радиус-вектора;
k — коэффициент пропорциональности, зависящий от
система единиц.

213. Элемент полевого проводника с током

ПОЛЕВОЙ ПРОВОДНИК С ТОКОМ

214. Закон Био — Савара — Лапласа для вакуума можно записать следующим образом.

THE BIO — SAVARD — ЗАКОН ЛАПЛАСА ДЛЯ
ВАКУУМ МОЖНО НАПИСАТЬ СЛЕДУЮЩИМ.
магнитный
постоянный.

215. Напряженность магнитного поля

ПРОЧНОСТЬ МАГНИТНОГО ПОЛЯ
Магнитное поле — одна из форм
проявление электромагнитного поля,
особенность которого в том, что это поле действует только на
движущиеся частицы и тела с помощью электрического
заряда, а также на намагниченных телах.

216. Магнитное поле

МАГНИТНОЕ ПОЛЕ
Магнитное поле создают проводники с током, движущиеся электрические
заряженные частицы и тела, а также переменные электрические поля.
Силовой характеристикой магнитного поля является вектор магнитного поля
. индукция поля, создаваемого одиночным зарядом в вакууме.

217. Теорема Гаусса для вектора магнитной индукции

ТЕОРЕМА ГАУССА ДЛЯ МАГНИТНОЙ ИНДУКЦИИ
ВЕКТОР

218.Классификация ускорителя

КЛАССИФИКАЦИЯ УСКОРИТЕЛЯ
Ускорителями заряженных частиц являются устройства
которые пучки заряженных частиц высоких энергий
(электроны, протоны, мезоны и др.) созданы
и управляется под действием электрического и
магнитные поля.

219. Любой ускоритель характеризуется:

ЛЮБОЙ УСКОРИТЕЛЬ ХАРАКТЕРИСТИКИ:
тип ускоренных частиц
дисперсия частиц по энергиям,
интенсивность луча.
Ускорители делятся на
непрерывный (равномерный по времени луч)
импульс (частицы в них ускоряются в
порции — импульсы). Последние
характеризуется длительностью импульса.

220. Любой ускоритель характеризуется

ЛЮБОЙ УСКОРИТЕЛЬ ХАРАКТЕРИСТИК
По форме траектории и
механизм ускорения частиц,
ускорителей делятся на
линейная,
циклический
индукция.
В линейных ускорителях траектории частиц равны
близко к прямым,
в циклических и индуктивных траекториях
частицы представляют собой круги или спирали.

221. Циклические ускорители

ЦИКЛИЧЕСКИЕ БУСТЕРЫ
Циклотрон — это циклический резонансный ускоритель марки
. тяжелые частицы (протоны, ионы).

222. Микротрон

МИКРОТРОН
электронный циклотрон) — циклический резонанс
ускоритель в котором, как и в циклотроне, оба
магнитное поле и частота
ускоряющее поле постоянное во времени, но
состояние резонанса при разгоне
процесс сохранен за счет изменения в
коэффициент ускорения.

223. Фазотрон

PHASOTRON
(синхроциклотрон) — циклический резонансный ускоритель
тяжелых заряженных частиц (например,
протоны, ионы, α-частицы),
управляющее магнитное поле постоянное,
частота ускоряющего электрического поля
медленно изменяется с периодом

226. СИЛЫ, ДЕЙСТВУЮЩИЕ НА ДВИЖУЩИЕСЯ ЗАРЯДЫ В МАГНИТНОМ ПОЛЕ

227. Закон Ампера

ЗАКОН АМПЕРА
два проводника с током взаимодействуют с каждым
другой с силой:

228.Модуль силы, действующей на проводник

МОДУЛЬ СИЛЫ, ДЕЙСТВУЮЩЕЙ НА провод
ПРОВОДНИК

229. Работа амперной силы

РАБОТА АМПЕРНОЙ СИЛЫ

230. ПРАВИЛО ЛЕВОЙ РУКИ

231. Взаимодействие бесконечно малых элементов dl1, dl2 параллельными токами I1 и I2:

ВЗАИМОДЕЙСТВИЕ БЕСКОНЕЧНО МАЛЫХ ЭЛЕМЕНТОВ
DL1, DL2 ПАРАЛЛЕЛЬНЫЕ ТОКИ I1 И I2:
токи, текущие в одном направлении
притягивают друг друга;
— токи разнонаправленные —
Отбито

232.Воздействие магнитного поля на рамку с током

ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ НА
РАМА С ТОКОМ
Рамка с током I в униформе
магнитное поле α — угол между и (
направление нормали связано с
направление тока по правилу
кутикула).

233. Воздействие магнитного поля на рамку с током

ВОЗДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА
РАМА С ТОКОМ

234.Momentum

MOMENTUM

235. Магнитная индукция

МАГНИТНАЯ ИНДУКЦИЯ

236. Магнитные блоки

МАГНИТНЫЕ УСТАНОВКИ
Закон Ампера используется для определения единицы
сила тока — амперы.

237. Единицы магнитной индукции

ЕДИНИЦЫ МАГНИТНОЙ ИНДУКЦИИ

238. Я мог бы обрушить Бруклинский мост за час

Я МОГ СНИЗИТЬ
БРУКЛИНСКИЙ МОСТ В ЧАСЕ

239. Таблица основных характеристик магнитного поля

ТАБЛИЦА ОСНОВНЫХ ХАРАКТЕРИСТИК
МАГНИТНОЕ ПОЛЕ

240.Сила Лоренца

СИЛА ЛОРЕНЦА

241. Сила Лоренца

СИЛА ЛОРЕНЦА

242. Сила Лоренца

СИЛА ЛОРЕНЦА

243. Часто сила Лоренца представляет собой сумму электрических и магнитных сил:

OFTEN THE LORENTZ FORCE THE
ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ СИЛЫ:

244. Сила Лоренца

СИЛА ЛОРЕНЦА

245. Ссылка

Ссылка
Сила Лоренца:
Полная сила, действующая на заряд в электромагнитном поле, составляет
F = FE + Fm = qE + q [u, B].
Магнитная составляющая силы Лоренца перпендикулярна вектору скорости,
элементарная работа этой силы равна нулю.
Force Fm изменяет направление движения, но не величину скорости.
Индукция магнитного поля B измеряется в СИ в теслах (Тл).
Элемент dl проводника с током I в магнитном поле наводится индукцией B,
определяется законом Ампера:
dF = I [dl, B].

246. Явление самоиндукции

ЯВЛЕНИЕ САМОИНДУКЦИИ
До сих пор мы рассматривали возможность изменения магнитных полей без оплаты
внимание к их источнику.На практике магнитные поля чаще всего составляют
создается с использованием различных типов соленоидов, то есть многооборотных цепей с током.

247. Явление самоиндукции

ЯВЛЕНИЕ САМОИНДУКЦИИ
Индуцированная ЭДС, возникающая в самой цепи, называется самоиндуцированной ЭДС, а само явление называется самоиндукцией.
Если индукция ЭДС возникает в соседней цепи, то
мы говорим о явлении взаимной индукции.
Понятно, что природа явления
одинаковые, и разные названия — чтобы подчеркнуть место происхождения
индукции ЭДС.
Явление самоиндукции было обнаружено прибором
Американский ученый Дж. Генри в 1831 году.

248. Явление самоиндукции

ЯВЛЕНИЕ САМОИНДУКЦИИ
Ток I, протекающий в любой цепи, создает
магнитный поток Ψ, проникающий через ту же
схема.
Если я изменю, изменится, поэтому индуцированный
ЭДС будет индуцирована в цепи.
Индуктивность такой цепи принята равной
единица индуктивности в СИ, в которой полный поток
Ψ = 1 В возникает при токе I = 1А.
Эта единица называется Генри (Hn).

250. индуктивность соленоида

индуктивность соленоида
Lсол μμ 0 н В
2

251. При изменении тока в цепи в ней возникает ЭДС самоиндукции, равная

ПРИ ИЗМЕНЕНИИ ТОКА В ЦЕПИ,
В НЕЙ ВОЗНИКАЕТ ЭДС САМОИНДУКЦИИ,
РАВНО
д д
dI
Ei IL L
dt dt
dt

252. Знак минус в этой формуле обусловлен правилом Ленца.

ЗНАК «МИНУС» В ДАННОЙ ФОРМУЛЕ ОБЯЗАТЕЛЬНО
ПРАВИЛО ЛЕНЦА.
dI
Ei L
dt

253. Индуктивность трансформатора

ИНДУКТИВНОСТЬ ТРАНСФОРМАТОРА
Используется явление взаимной индукции
в распространенных устройствах — трансформаторах.
Трансформатор изобрел Яблочков,
Русский ученый, 1876г. За отдельную мощность
поставка отдельных источников электрического света
(Свеча Яблочкова).

254. Индуктивность трансформатора

ИНДУКТИВНОСТЬ ТРАНСФОРМАТОРА

255. При переменной ЭДС в первичной обмотке

ПРИ ПЕРЕМЕННОЙ ЭДС В ПЕРВИЧНОЙ ОБМОТКЕ
ОБМОТКА
д (Н1Ф)
dФ
E1
N1
dt
dt
E1
N1
E2
Н2

256.Коэффициент трансформации

Коэффициент трансформации
E2 N 2
η.
E1 N1

257. Энергия и работа

ЭНЕРГЕТИКА И РАБОТА
LI
A
2
2

258. Диамагнетики и парамагнетики в магнитном поле.

ДИАМАГНИТЫ И ПАРАМАГНИТЫ В А
МАГНИТНОЕ ПОЛЕ.
Микроскопическая плотность токов в
намагниченное вещество чрезвычайно сложно и
сильно различается даже в пределах одного атома. Но мы
интересуются средними магнитными полями
создается большим количеством атомов.
Как было сказано, характеристика намагниченного
состояние материи — это векторная величина —
намагниченность, равная отношению
магнитный момент небольшого объема материи до
значение этого объема:

259. Диамагнетики и парамагнетики в магнитном поле.

ДИАМАГНИТЫ И ПАРАМАГНИТЫ В А
МАГНИТНОЕ ПОЛЕ.
1
J
V
PM I,
n
i 1

260. Диамагнетизм

ДИАМАГНЕТИЗМ
свойство веществ намагничиваться по отношению к
приложенное магнитное поле.
Диамагнитные материалы — это вещества, магнитные
моменты атомов в отсутствие внешнего поля
равны нулю, поскольку магнитные моменты всех
электроны атома взаимно компенсируются (для
например, инертные газы, водород, азот, NaCl, Bi, Cu,
Ag, Au и др.).
Когда диамагнитное вещество вводится в
магнитное поле, его атомы приобретают наведенное магнитное поле
моменты ΔPm, направленные против вектора.

261.Парамагнетизм

ПАРАМАГНЕТИЗМ
свойство веществ во внешнем магнитном
поле намагничено в направлении этого поля,
поэтому внутри парамагнетика действие
индуцированное внутреннее поле добавляется к действию
внешнее поле.
Парамагнитные вещества — вещества
атомы которого имеют в отсутствие внешнего
магнитное поле, ненулевой магнитный момент.

262. Paramagnetics

PARAMAGNETICS
B
μ
1
В0

263.Диамагнетизм

ДИАМАГНЕТИКА
B
μ
1
B0

Закон Био-Савара: определение и примеры — видео и стенограмма урока

Упрощенное уравнение

Использование закона Био-Савара требует исчисления. Вот почему есть дБ и дл . Это бесконечно малые элементы магнитного поля и проволочные элементы. Таким образом, нам придется интегрироваться в отношении этих элементов. Но мы можем использовать более простую версию закона для идеально прямого провода.-6, умноженный на ток, проходящий через провод, I , измеренный в амперах, деленный на 2pi, умноженный на радиус от провода, r , измеренный в метрах. Таким образом, это уравнение помогает нам вычислить магнитное поле с радиусом r от прямого провода, по которому проходит ток I .

Уравнение дает нам величину магнитного поля, но магнитное поле является вектором, так что насчет направления? Магнитное поле, создаваемое токоведущим проводом, имеет форму концентрических кругов.Но мы должны выяснить, направлены ли эти круги по часовой стрелке или против часовой стрелки (скажем, сверху). Для этого мы используем правило правой руки.

Я хочу, чтобы вы прямо сейчас дали экрану большой палец вверх. Я серьезно — покажите экран правой рукой. Это должно быть твоей правой рукой. Если вы укажете большим пальцем в направлении тока этого провода, ваши пальцы будут сгибаться в направлении магнитного поля. Они будут следовать за стрелками концентрических кругов.Вот как вы определяете направление.

Пример расчета

Хорошо, давайте рассмотрим пример. Допустим, у вас есть провод, по которому течет ток 0,1 А, и вас просят рассчитать магнитное поле на расстоянии 0,5 метра от этого провода. Прежде всего, как обычно, запишите то, что мы знаем. I равен 0,1 ампера, а r равен 0,5 метра. Нас просят рассчитать магнитное поле, поэтому B =?.-8 тесла.

Наконец, нам нужно найти направление. Основываясь на этой диаграмме, показывающей интересующее нас положение, в каком направлении указывает это магнитное поле? Что ж, возьмите правую руку и сложите большой палец вверх. Затем направьте большой палец в направлении тока — вверх к верхней части экрана. -8 тесла и направлено на экран.(Или, если бы это был лист бумаги, он был бы на странице.)

И все — готово.

Краткое содержание урока

Закон Био-Савара — это уравнение, которое описывает магнитное поле, создаваемое токоведущим проводом, и позволяет рассчитать его напряженность в различных точках. Это выглядит так. Использование закона Био-Савара требует исчисления, но мы можем использовать более простую версию закона для идеально прямого провода.-6, умноженный на ток, проходящий через провод, I , измеренный в амперах, деленный на 2pi, умноженный на радиус от провода, r , измеренный в метрах. Таким образом, это уравнение помогает нам вычислить магнитное поле с радиусом r от прямого провода, по которому проходит ток I .

Чтобы определить направление этого магнитного поля, мы используем правило правой руки. Если вы укажете большим пальцем в направлении тока в проводе, ваши пальцы будут сгибаться вокруг этого провода в направлении магнитного поля.Это покажет вам, в какую сторону идут стрелки на концентрических кругах.

Итак, используя закон Био-Савара и правило правой руки, мы можем выяснить все, что нам нужно знать о магнитном поле, создаваемом токоведущим проводом.

Вектор напряженности электрического поля в заданной точке. Как определить направление вектора натяжения

1 .Два вида электрических зарядов и их свойства. Наименьший неделимый электрический заряд.Закон сохранения электрических зарядов. Закон Кулона. Единица оплаты. Электростатическое поле. Метод обнаружения поля. Напряжение как характеристическое электростатическое поле. Вектор напряжения, его направление. Точечный заряд напряженного электрического поля. Единицы напряжения. Принцип суперпозиции полей.

Электрический заряд — значение инвариантно, то есть не зависит от системы отсчета, и, следовательно, не зависит от того, движется ли заряд или он находится в состоянии покоя.

два вида (типов) электрических зарядов : положительные и отрицательные заряды.

Экспериментально установлено, что одноименные заряды отталкиваются, а противоположные — притягиваются.

Электрически нейтральное тело должно иметь равное количество положительных и отрицательных зарядов, но их распределение по объему тела должно быть равномерным.

Закон сохранения электронной почты. заряд : алгебраическая сумма элек.Заряды любой замкнутой системы (системы, не обменивающейся зарядами с внешним теплом) остаются неизменными, какие бы процессы ни происходили внутри этой системы.

Заряды элеков спонтанно не возникают и не возникают, их можно только разделить и передать от одного тела к другому.

Существует наименьший заряд, он назывался элементарным зарядом — это заряд, которым обладает электрон, а заряд на теле кратен этому элементарному заряду: e = 1.6 * 10 -19 Класс . Отрицательный элементарный заряд связан с электроном, а положительный — с позитроном, у которого заряд и масса количественно совпадают с зарядом и массой электрона. Однако из-за того, что позитрон имеет короткое время жизни, они отсутствуют на телах, и поэтому они объясняют положительный или отрицательный заряд тел либо недостатком, либо избытком электронов в телах.

Закон Кулона: силы взаимодействия двух точечных зарядов в однородной и изотропной среде прямо пропорциональны произведению этих зарядов и обратно пропорциональны квадрату расстояния между ними, равны друг другу и направлены по прямой, проходящей через эти заряды. обвинения. г — расстояние между зарядами q 1 и q 2, k — коэффициент пропорциональности, зависящий от выбора системы физических единиц.

м / ф, а = 8,85 * 10 -12 ф / м — диэлектрическая проницаемость

Точечный заряд следует понимать как заряды, сосредоточенные на телах, линейные размеры которых малы по сравнению с расстояниями между ними.

В данном случае заряд измеряется в кулонах — количество электричества, протекающего через поперечное сечение проводника за одну секунду при токе 1 ампер.

Сила F направлена ​​вдоль линии, соединяющей заряды, т.е. является центральной силой и соответствующим притяжением (F0) в случае одинаковых зарядов. Эта сила называется мощностью кулонов.

Более поздние исследования Фарадея показали, что электрическое взаимодействие между заряженными телами зависит от свойств среды, в которой эти взаимодействия происходят.

Заряженные тела могут воздействовать друг на друга, не касаясь электрического поля.Поле, создаваемое неподвижными электрическими частицами, называется электростатическим.

Спонсор размещения P&G Статьи по теме «Как определить направление вектора напряженности» Как найти силу магнитного поля Как определить направление момента силы Как определить направление вектора магнитной индукции

Инструкция руководство

Если еще один заряд Q0 поместить в электрическое поле, создаваемое зарядом Q, то он подействует на него с определенной силой.Эта характеристика называется электрическим полем E. Это отношение силы F, с которой поле действует на положительный электрический заряд Q0 в определенной точке пространства, к величине этого заряда: E = F / Q0. В зависимости от конкретной точки пространства значение напряженности поля E может варьироваться, что выражается формулой E = E (x, y, z, t). Следовательно, напряженность электрического поля относится к векторным физическим величинам. Поскольку напряженность поля зависит от силы, действующей на точечный заряд, то вектор электрического поля E совпадает с вектором силы F.Согласно закону Кулона, сила, с которой две заряженные частицы взаимодействуют в вакууме, направлена ​​по прямой линии, соединяющей эти заряды. Майкл Фарадей предложил визуально изобразить поле электрического заряда с помощью линий напряжения. Эти прямые совпадают с вектором натяжения во всех точках касательной. На рисунках они обычно обозначены стрелками. Если электрическое поле однородно, а вектор его напряженности постоянен по модулю и направлению, то линии напряжения параллельны ему.Если электрическое поле создается положительно заряженным телом, линии напряжения направлены от него, а в случае отрицательно заряженной частицы — к нему. Как просто

Другие новости по теме:

Силовое поле, часть пространства, в каждой точке которого действует определенная сила, зависящая только от положения выбранной точки. Если, например, у нас есть заряженное тело, то на заряд, помещенный в любую точку рядом с ним, будет действовать сила электрического притяжения (или

Потенциал — это энергетическая характеристика электрического поля.Чтобы найти его значение, вам нужно, чтобы потенциальная энергия разделила заряд в данной точке электрического поля на сам заряд. Для разных типов полей используются разные формулы расчета потенциала. Вам понадобится —

Есть два способа определить величину электрического заряда. Первый — измерить силу взаимодействия неизвестного заряда с известным и, используя закон Кулона, вычислить ее значение. Второй — ввести заряд в известное электрическое поле и измерить силу, с которой он действует на него.Для измерения

Чтобы найти напряженность электрического поля, введите в него известный пробный заряд. Измерьте силу, действующую на него со стороны поля, и рассчитайте величину натяжения. Если электрическое поле создается точечным зарядом или конденсатором, рассчитайте его с помощью специального

.

В задачах по физике иногда требуется найти заряд тела на основе его взаимодействия с электрическим полем или другими телами. В большинстве случаев размерами самого тела пренебрегают, чтобы не рассчитывать распределение элементарных зарядов по его массе или поверхности.Спонсор размещения

Чтобы определить модуль точечных зарядов одинаковой величины, измерьте силу их взаимодействия и расстояние между ними и произведите расчет. Если вам нужно найти модуль заряда отдельных точечных тел, введите их в электрическое поле с известной напряженностью и измерьте силу, с которой поле

Напряженность магнитного поля H — это векторная физическая величина, результат разности между вектором магнитной индукции и вектором намагниченности.В системе SI он измеряется в амперах на метр, в GHS — в эрстедах. Спонсор размещения P&G Статьи по теме «Как определить напряженность магнитного поля» Как определить

Сила Лоренца определяет интенсивность воздействия электрического поля на точечный заряд. В некоторых случаях это означает силу, с которой магнитное поле действует на заряд q, который движется со скоростью V, в других — совокупное влияние электрического и магнитного полей.

Электромагнитные волны (ЭМВ).

Электрическое поле, создаваемое неподвижными электрическими зарядами, остается неизменным с течением времени. Такое поле называется потенциальным электрическим полем (электростатическим полем). Магнитное поле, создаваемое постоянным электрическим током, остается неизменным с течением времени. Эти поля существуют независимо друг от друга. Картина существенно меняется, если электрическое поле создается движущимися электрическими зарядами. Согласно теории Максвелла, электрическое поле, которое изменяется во времени, создает магнитное поле, которое изменяется во времени

и наоборот, изменяющееся со временем магнитное поле , которое по своей природе является вихрем , создает вихревое электрическое поле (линии электропередач, т.е.е., линии напряженности такого электрического поля замкнуты) (рис. 1).

Рис. 1. Графическое изображение взаимосвязи вихревого электрического и магнитного полей.

вектор электрического поля

— вектор индукции магнитного поля, связан с вектором магнитного поля соотношением (- магнитная проницаемость среды).
Согласно maxwell , переменное магнитное поле всегда связано с генерируемым им электрическим полем, а переменное электрическое поле всегда связано с генерируемым им магнитным полем, т.е.е. электрическое и магнитное поля «связаны» и неразрывно связаны друг с другом и образуют единое электромагнитное поле .
Чтобы установить количественные отношения между изменяющимся электрическим полем и вызываемым им магнитным полем, Максвелл ввел так называемый ток смещения . Ток смещения объяснял прохождение переменного электрического тока через конденсатор между его пластинами, то есть через те части цепи, где нет проводников.Максвелл предположил, что ток смещения, как и ток проводимости, создает магнитное поле. Ток смещения по своей сути представляет собой электрическое поле, которое изменяется со временем, поэтому ток смещения также существует в вакууме. Введя понятие тока смещения, Максвелл по-новому подошел к рассмотрению замкнутых цепей переменного тока. Когда ток проводимости прерывается на концах проводника, ток смещения продолжается и т. Д. Следовательно, полный ток в цепи переменного тока можно представить суммой токов проводимости и токов смещения.

При неравномерном движении электрических зарядов, в частности при их колебательном движении, а значит, и при любом переменном токе, электрическое и магнитное поля со временем изменятся; эти изменения будут передаваться из одной точки пространства в другую, образуя, предсказанное Максвеллом, электромагнитную ( EM ) волну . Далее было показано, что скорость распространения электромагнитных волн ( Emv ) в вакууме имеет значение, совпадающее с экспериментально полученным значением скорости света.Обобщение экспериментальных данных (эксперименты Эрстеда, сила Ампера, закон Био-Савара-Лапласа, основной закон электромагнитной индукции) привело к выводу, что при распространении электромагнитных волн электрическое и магнитное поля имеют взаимно перпендикулярную ориентацию. В направлении распространения электромагнитная волна может быть представлена ​​двумя синусоидами, лежащими во взаимно перпендикулярных плоскостях. Один из них изображает колебания вектора электрического поля, а другой — вектора магнитного поля.Оба вектора колеблются в одной фазе, т.е. одновременно достигают максимального и нулевого значений. Направление распространения электромагнитной волны (направление вектора
скорости) определяется правилом правого винта (буравчика) (рис. 2). Рисунок хорошо иллюстрирует тот факт, что ЭМ волны поперечные , так как колебания векторов и происходят в плоскостях, перпендикулярных направлению распространения волны (ось Oy ).

Рис.2. Графическое изображение электромагнитной волны. Электромагнитная теория Максвелла была блестяще подтверждена экспериментами Герца по распространению электромагнитных волн.

Общие свойства ЭМВ.
1. Поперечное ЭМВ. Векторы электрического и магнитного полей взаимно перпендикулярны и образуют правую систему с направлением распространения волны.
2. Скорость (фаза) распространения в непроводящей среде, где

Измерение неупругого протон-протонного сечения при √ s = 7 ТэВ с помощью детектора ATLAS

University at Albany, Albany, NY, USA

M.С. Алам, Дж. Эрнст и В. Рохо

Физический факультет Университета Альберты, Эдмонтон, Альберта, Канада

С. Бахинипати, Н.Дж. Бьюкенен, К. Чан, Л. Чен, Д.М. Гингрич, М. Ким, С. Лю, Р. В. Мур, Дж. Л. Пинфолд, Н. Сони и HS. Субрамания

Физический факультет Университета Анкары, Анкара

О. Чакир, А.К. Ciftci, R. Ciftci & S. Persembe

LAPP, CNRS / IN2P3 and Université de Savoie, Анси-ле-Вье, Франция

L.Аперио Белла, Б. Обер, Н. Бергер, Дж. Колас, Л. Ди Чаччо, T.K.O. Доан, С. Элльес, П. Гез, М. Гуанер, К. Гой, Т. Гийемен, Л. Хелари, Т. Гринова, Г. Ионеску, А. Джереми, С. Джезекель, М. Катаока, Дж. Лаббе, Р. Лафай, Ж. Левек, вице-президент Lombardo, N. Massol, P. Perrodo, H. Przysiezniak, G. Sauvage, T. Todorov, D. Tsionou, I. Wingerter-Seez, R. Zitoun & Y. Zolnierowski

Отдел физики высоких энергий, Argonne National Лаборатория, Аргонн, Иллинойс, США

Л. Асквит, Р.Э. Блэр, С. Чеканов, Дж. У. Доусон, Д. Феллманн, Г.Ф. Геральтовский, В. Гуарино, Д. Хилл, Н. Хилл, К. Карр, Т. ЛеКомпте, Д. Малон, Э. Мэй, Л. Нодульман, А. Парамонов, Л.Е. Прайс, Дж. Праудфут, Б. Сальвачуа Феррандо, Дж.Л. Шлерет, Р.В. Станек, Д.Г. Андервуд, П. ван Геммерен, А. Ваньячин, Р. Йошида и Дж. Чжан

Физический факультет Университета Аризоны, Тусон, Аризона, США

Э. Чеу, К.А. Джонс, В. Кошик, К. Lampen, W. Lampl, X. Lei, P. Loch, P. Mal, F.Рюр, JP Rutherfoord, L. Shaver, MA Shupe & EW Varnes

Физический факультет Техасского университета в Арлингтоне, Арлингтон, Техас, США

А. Брандт, Х. Браун, К. Де, А. Фарбин, Л. Хилан, CM Эрнандес, Х. Ким, П. Нильссон, Н. Озтюрк, Р. Правахан, Э. Саркисян-Гринбаум, М. Сосеби, Б. Сперлок, А. Stradling, G. Usai, A. Vartapetian, A. White & J. Yu

Физический факультет Афинского университета, Афины, Греция

A.Антонаки, Д. Фассулиотис, В. Джакумопулу, Н. Джокарис, П. Иоанну, К. Куркумелис, А. Манусакис-Кацикакис, Г. Цанакос и К. Веллидис

Физический факультет, Национальный технический университет Афин, Зографу, Греция

Т. Алексопулос, Р. Аврамиду, М. Дрис, А. Филиппас, М. Фокитис, EN Газис, Г. Яковидис, Э. Кацуфис, С. Леонцинис, С. Мальтезос, Э. Маунтрича, Э. Панагиотопулу, Т. Пападопулу, П. Савва, Г. Циполитис, С. Влахос и Л. Ксаплантерис

Институт физики Академии наук Азербайджана, Баку, Азербайджан

О.Абдинов, М. Алиев, Ф. Халил-зада и С. Рзаева

Institut de Física d’Altes Energies и Автономный университет Барселоны и ICREA, Барселона, Испания

J. Abdallah, M. Bosman, M.P. Касадо, М. Кавалли-Сфорца, М. Кониди, Б. Демиркоз, М. Досил, X. Эспинал Курулл, Л. Фиорини, С. Гринштейн, К. Хелсенс, И. Корольков, М. Мартинес, Э. Меони, Л. М. Мир, Л. Мираллес Верж, Дж. Надаль , К. Осуна, А. Пачеко Пейдж, К. Падилья Аранда, Э. Перес Кодина, И. Риу, В. Россетти, Э.Сегура, А. Суккурро, С. Сушков, Ф. Вивес Ваке, М. Вольпи и В. Форверк

Институт физики Белградского университета, Белград

И. Борянович, Й. Крстич, Д.С. Попович, Д. Reljic, Dj. Sijacki, Lj. Симич, Н. Враньес и М. Враньес Милосавлевич

Физико-технический факультет Бергенского университета, Берген, Норвегия

Т. Буанес, Т. Берджесс, Г. Эйген, Л.Г. Йохансен, А. Кастанас, В. Либих, А. Липняцка, Б. Мон, О.К. Ой, П.Л. Rosendahl, H. Sandaker, T.B. Сьюрсен, Б. Стугу, А. Тоноян и М. Угланд

Физический отдел, Национальная лаборатория Лоуренса Беркли и Калифорнийский университет, Беркли, Калифорния, США

J-F. Аргуин, А. Бах, А. Барбаро Галтьери, Р. Барнетт, Дж. Берингер, Дж. Биесиада, П. Калафиура, А. Чочо, М. Кук, С. Дубе, К. Эйнсвайлер, Р. Эли, А. Гапоненко, М. Гарсиа-Сиверес, М. Гилкризе, К. Haber, B. Heinemann, I. Hinchliffe, S.-C. Сюй, М. Гурвиц, Дж. Джозеф, А.Korn, W. Lavrijsen, C. Leggett, P. Loscutoff, J. Lys, R.J. Мадарас, Д. Куорри, К. Рувидель, М.И. Scherzer, M. Shapiro, J. Siegrist, L.A. Skinnari, G. Stavropoulos, M. Tatarkhanov, L. Tompkins, S. Vahsen, D. Varouchas, J. Virzi, W-M. Яо, Ю. Яо и С. Зенц

Физический факультет, Университет Гумбольдта, Берлин, Германия

М. Алиев, Г. Брандт, Ф. Джорджи, С. Гранканьоло, Р. Херрберг, О. Кинд, Х. Коланоски, Р. Кви, Х. Лакер, М. Лейтон, Т. Лозе, Р. Мандриш, А.Никифоров, Ю. Родригес Гарсия, Х. Шульц и М. Цур Недден

Центр фундаментальной физики и лаборатория физики высоких энергий им. Альберта Эйнштейна, Бернский университет, Берн, Швейцария

А. Батталья, H.P. Бек, К. Борер, А. Эредитато, Т. Фонсека Мартин, В. Галло, С. Хауг, С. Кабана, К. Претцл, К. Топфель, Н. Вентури и М.С. Вебер

Школа физики и астрономии, Бирмингемский университет, Бирмингем, Великобритания

H.S. Бансил, Дж.Брациник, Д. Чарльтон, Нью-Джерси Коллинз, К.Дж. Кертис, Дж.Д. Доуэлл, Дж. Гарви, Д.Р. Хэдли, К. Харрисон, К. Хоукс, С.Дж. Head, S.J. Хиллер, Дж. Лилли, Дж. Махоут, Т.А. Мартин, Т. Маклафлан, П.Р. Ньюман, С.В. О’Нил, Дж. Д. Палмер, М. Слейтер, Дж. П. Томас, П. Д. Томпсон, П. Уоткинс, А. Уотсон, М.Ф. Уотсон и Дж. А. Wilson

Физический факультет Университета Богазичи, Стамбул

Т. Акдоган, Э. Арик, М. Арик, О. Доган, С. Истин, В. Озкан и Т. Радор

INFN Sezione di Bologna

S.Антонелли, Л. Беллагамба, А. Бертин, М. Бинди, Д. Боскерини, А. Бруни, Г. Бруни, М. Бруски, Д. Кафорио, К. Чокка, М. Корради, С. Де Кастро, Р. Ди Сипио, Л. Фаббри, Б. Джакоббе, П. Джусти, М.К. Джа, И. Масса, А. Менгарелли, С. Монзани, М. Пиччинини, А. Полини, Л. Ринальди, К. Сбарра, А. Сбрицци, Н. Семприни-Чезари, Р. Спиги, С. Валентинетти, М. Villa, A. Vitale и A. Zoccoli

Physikalisches Institut, Боннский университет, Бонн, Германия

M. Alhroob, CF Андерс, Д.Арутинов, М. Бакхаус, М. Барберо, Д. Барч, И. Брок, Дж. Каммин, М. Кристинциани, К. Деш, Дж. Дингфельдер, П. Фишер, Г. Гайкен, Ч. Гейх-Гимбель, Л. Гонелла, М. Гавранек, С. Хиллер, Ф. Хюггинг, Т. Инс, М. Янус, Г. Хориаули, П. Кувесарки, Т. Кокотт, В.В. Костюхин, Я. Косеберг, Х. Крюгер, А. Крут, К. Лапуар, М. Лемахер, А. Leyko, C. Limbach, T. Loddenkoetter, M. Mathes, M. Mazur, S. Meuser, N. Möser, K. Mueller, G. Nanava, T. Nattermann, A.-E. Нунцио-Кирос, Г. Нуньес Ханнингер, И.Перич, Т. Погосян, С. Псорулас, Б. Радикс, О. Рунольфссон, С. Шепе, К. Шмиден, М. Шмитц, Дж. Шумахер, Я. Стиллингс, Т. Стокманнс, Дж. Терхааг, Дж. Трейс, Ж.-В. Цунг, К. Учида, М. Уленброк, Н. Власов, А. Фогель, Э. фон Тёрне, Н. Вермес, П. Винеманн, К. Цендлер, Р. Циммерманн и С. Циммерманн

Департамент физики, Бостонский университет, Бостон, Массачусетс, США

SP Ahlen, KM Блэк, Дж.М. Батлер, Р.Д. Харрингтон, Э. Хейзен, М. Левандовска, Дж. Лав, А.Марин, Н. Nation, C. Posch, J.T. Шэнк, С.П. Уитакер, З. Ян и С. Юсеф

Физический факультет Университета Брандейса, Уолтем, Массачусетс, США

С. Аефски, К. Амелунг, Дж. Р. Бенсингер, К. Блокер, Л. Кирш, Д. Помрой, Н. Сквороднев и Х. Велленштейн

Федеральный университет Рио-де-Жанейро COPPE / EE / IF, Рио-де-Жанейро

L.P. Caloba, A.S. Cerqueira, R. Coura Torres, A. Da Rocha Gesualdi Mello, P.V.M. Да Силва, M.A.B. сделать Вале, К.Майданчик, Ф. Марроким, А.А. Непомучено, М. Перантони и Дж. М. Сейшас

Физический отдел, Брукхейвенская национальная лаборатория, Аптон, Нью-Йорк, США

D.L. Адамс, К. Ассамаган, доктор медицины Бейкер, М. Бегель, К. Берниус, Х. Чен, В. Чернятин, П.Е. Де Кастро Фариа Сальгадо, Р. Дуллипуди, М. Эрнст, Т. Гадфорт, Б. Гиббард, Х.А. Гордон, З. Гринвуд, Р. Хакенбург, А. Климентов, Ф. Ланни, Д. Лиссауэр, Д. Линн, Х. Ма, Т. Маэно, С. Маевски, П. Невски, К. Николопулос, Д. Оливейра Дамазио, Ф.Пейдж, С. Паниткин, В. Парк, М.-А. Плейер, А. Поблагев, В. Полихронакос, С. Протопопеску, М. Пурохит, Д. Рам, С. Раджагопалан, Г. Редлингер, Л. Сойер, С. Снайдер, Дж. Зондерикер, П. Стейнберг, И. Штумер, Х. Такай, MC Тамсетт, Ф. Таррад, А. Триведи, А. Ундрус, Т. Венаус, С. Уайт, С. Йе и Д. Ю

Национальный институт физики и ядерной инженерии, Бухарест

К. Алекса, Э. Бадеску, В. Болдеа, С.И. Буда, И. Каприни, М. Каприни, К. Карамарку, М. Чубанкан, С.Константинеску, Ч.-М. Кучук, П. Дита, С. Дита, Л. Мику, Д. Пантеа, Г.А. Popeneciu, M. Rotaru & G. Stoicea

Departamento de Física, Universidad de Buenos Aires, Буэнос-Айрес, Аргентина

M.L. Гонсалес Сильва, Г. Отеро-и-Гарсон, Р. Пьегайя и Дж. Ромео

Лаборатория Кавендиша, Кембриджский университет, Кембридж, Великобритания

С. Аск, Т. Барбер, Н. Барлоу, Дж. Р. Бэтли, Ф. Brochu, W. Buttinger, J.R. Carter, J.D. Chapman, C. Cowden, S.Т. Френч, Ж.А. Frost, J.C. Hill, T.J. Khoo, C.G. Лестер, В. Мёллер, М.А. Паркер, А.В. Филлипс, Д. Робинсон, Т. Сандовал, М. Томсон и К.П. Ward

Физический факультет Карлтонского университета, Оттава, Онтарио, Канада

J.P. Archambault, C.D. Кожокару, Д. Гиллберг, М. Хакзад, К. Лю, Т.Г. Маккарти, Ф. Окхэм, К. Рандрианаривони, Р. Уэно, М.Г. Vincter & K. Whalen

CERN, Женева, Швейцария

M. Aleksa, P. Amaral, F.Ангинолфи, С. Арфауи, М.А. Баак, К. Бачас, Дж. Бачи, Ф. Бальтасар дос Сантос Педроса, Д. Банфи, М. Баттистин, Ф. Беллина, О. Бельтрамелло, Д. Берге, Ф. Бертинелли, Р. Бьянки, Дж. Бланшо, Дж. А. Богертс, Дж. Бойд, А. Брем, Дж. Бремер, Х. Буркхарт, Ф. Бутин, С. Кампана, M.D.M. Кейпанс Гарридо, Т. Карли, Ф. Катанео, А. Катиначчо, А. Каттай, А. Черри, Д. Хромек-Буркхарт, Дж. Кук, Д. Коте, Х.О. Даниэльссон, Дж.П. Даувернь, М. Де Оливейра Бранко, А. Делл’Акуа, М. Дельмастро, Н. Делруэль, А. Ди Джироламо, Б.Ди Джироламо, Б. Ди Микко, Ф. Диттус, Р. Добинсон, Э. Добсон, Дж. Допке, Х. Древерманн, А. Дударев, М. Дюрссен, М. Данфорд, Ф. Дидак, Т. Эйферт, Н. Эллис, М. Элсинг, К. Фабр, П. Фарту, П. Фасснахт, И. Федорко, Дж. Фламмер, А. Фусса, Д. Фрэнсис, С. Франц, Р. Фроешль, Д. Фройдево, Э. Фуллана Торрегроса , К. Гэблдон, М.В. Галлас, Н. Гарелли, В. Гаронн, J-C. Гайде, Ф. Джанотти, С. Гибсон, Дж. Годлевски, А. Гонидек, Л. Гуссенс, Б. Горини, П. Графстрем, Х.М. Грей, Дж. Грогнуц, М. Груве, С. Хаас, Ф.Хан, С. Хайдер, М. Хэтч, М. Хаушильд, Р.Дж. Хокингс, А. Энрикес Коррейя, Л. Эрвас, А. Хокер, М. Хухтинен, Дж. Иниго-Гольфин, М. Р. Якель, П. Дженни, О. Йонссон, К. Джорам, Дж. Каплон, Н. Кершен, Т. Ключникова, Дж. Кноблох, Б. Коблиц, К. Конеке, Т. Коффас, Д. Коллар, М. Дж. Котамаки, Й. Квита, А. Ла Роса, М. Ламанна, К. Ланцш, К. Лассер, М. Лассниг, Г. Леманн Миотто , П. Личард, Л. Маньони, С. Малюков, А. Мапелли, Л. Мапелли, Дж. Ф. Маршан, Б. Мартин, Дж. М. Моугэн, Р.А. Макларен, К.Menot, A. Messina, T.C. Meyer, S. Michal, P. Miele, J. Molina-Perez, A.K. Морли, Г. Морначки, Д. Мюнстерманн, А. Наирц, Г. Негри, М. Несси, Б. Никкевер, Т. Нииникоски, М. Нордберг, Т. Найман, С. Палестини, о. Пасторе, Т. Поли, Р. Пенго, Х. Пернеггер, Б.А. Петерсен, Дж. Петерсен, Дж. Пиаквадио, О. Пиротт, К. Поммес, А. Поплтон, Дж. Пулар, Л. Прибыл, М. Дж. Прайс, М. Раймонд, К. Рембсер, Д. Рода душ Сантуш, С. Роу , А. Зальцбургер, DO Саву, С. Шленкер, М. Шотт, С. Шу, Г. Шулер, А.Сфирла, С. Шимицу, Дж. Слопер, Г. Спиго, Р. Спивокс, Э. Станецка, М.С. Стоктон, Т. Сумида, Б. Сзелесс, Г.П. Тапперн, Х. Тен Кейт, Ф. Дж. Тике Айрес Вьегас, И. Торчиани, Л. Трембле, А. Триколи, К. Царучас, Х. Тирвайнен, Г. Унал, Д. ван дер Стер, В. Ванделли, Г. Вандони, Ф. Варела Родригес, Р. Венесс, Э. Винек, Р. Восс, Р. Вюллермет, П.С. Wells, T. Wengler, S. Wenig, P. Werner, H.G. Wilkens, F. Winklmeier, J. Wotschack, Z. Zajacova, P.F. Zema, A. Zsenei & L. Zwalinski

Институт Энрико Ферми, Чикагский университет, Чикаго, Иллинойс, США

K.Дж. Андерсон, А. Бовейя, Э. Брубакер, Ф. Канелли, Г. Чоудалакис, Т. Костин, Э. Дж. Feng, M. Fiascaris, R.W. Gardner, A. Gupta, I. Jen-La Plante, A. Kapliy, C. Melachrinos, F.S. Мерритт, P.U.E. Onyisi, MJ Oreglia, JE Pilcher, MJ Shochet & JM Tuggle

Departamento de Fisica, Pontificia Universidad Catòlica de Chile, Santiago

MA Diaz, B. Panes, F. Quinonez, D. Romero Maltrana

& P.

Институт физики высоких энергий Китайской академии наук, Пекин

Y.Бай, С. Ченг, Х. Хан, С. Цзинь, Ф. Лу, К. Оуян, Л.Ю. Шан, Г. Тонг, Ю. Се, Г. Сю, Ю. Ян, Л. Юань и С. Чжэн

Лаборатория корпускулярной физики, Клермонский университет и университет Блеза Паскаля и CNRS / IN2P3, Обьер-Седекс, Франция.

E. Busato, D. Calvet, S. Calvet, R. Camacho Toro, D. Cinca, R. Febbraro, N. Ghodbane, P.L.Y. Грис, К. Гишени, Д. Паллин, Ф. Подлиски, К. Сантони, Л. П. Сейс, Ф. Вазей и С. Вирет

Лаборатория Невиса, Колумбийский университет, Ирвингтон, штат Нью-Йорк, США

T.Андин, А. Ангерами, Дж. Бройманс, К. Копич, Дж. Додд, Н. Грау, Дж. Го, Э. У. Хьюз, М. Лельчук, Д. Лопес Матеос, З. Маршалл, Дж. Парсонс, А. Пенсон, К. Перес, В. Перес Реале, Ф. Спано, П.М. Тутс, Д. Урбаниец, Э. Уильямс, В. Уиллис, Э. Вульф и Л. Живкович

Институт Нильса Бора, Копенгагенский университет, Кобенхавн, Дания

Н. Боэларт, М. Дам, К. Дриуичи, JR Hansen, JB Hansen, JD Hansen, PH Hansen, S. Heisterkamp, ​​S. Jakobsen, P. Jež, M.D. Joergensen, P.Кадлечик, Э. Klinkby, J. Lundquist, R. Mackeprang, S. Mehlhase, T.C. Петерсен, Б. Ренш, М. Симонян и С. Кселла

INFN Gruppo Collegato di Cosenza

М. Капуа, Г. Крозетти, С. Фацио, Л. Ла Ротонда, А. Мастроберардино, Г. Морелло, Д. Сальваторе, М. Скьоппа, Г. Сусинно и Э. Тасси

Факультет физики и прикладной информатики, AGH-Университет науки и технологий, Краков, Польша

К. Циба, В. Домбровски, М. Двузник , М.Идзик, К. Елен, Д. Киселевская, С. Коперный, Т.З. Ковальский, Б. Миндур, Э. Руликовска-Заребска и Б. Точек

Институт ядерной физики им. Генрика Неводничански Польской академии наук, Краков, Польша

Э. Банас, Й. Блоки, П.А. Брукман де Ренстром, Д. Дерендарз, Э. Горницки, З. Хайдук, В. Ивански, А. Качмарска, К. Корцил, П. Малецки, П. Малецки, А. Ольшевский, Я. Ольшовска, Э. Рихтер-Вас, А. Трзупек, М. Турала, М.В. Вольтер, Б.К. Wosiek & A. Zemla

Физический факультет Южного методистского университета, Даллас, Техас, США

R.К. Дайя, К. Диндар Ягчи, А. Фиран, Д. Голдин, Х.К. Хадаванд, Дж. Хоффман, Ю. Ильченко, Р. Ишмухаметов, Д. Иоффе, С. Кама, А. Касми, Р. Кехо, З. Лян, Л. Лу, П. Ренкель, Р. Р. Риос, Р. Стройновски, Дж. Йе и П. Заржицкий

Физический факультет Техасского университета в Далласе, Ричардсон, Техас, США

М. Ахсан, Э. Галяев, Дж. М. Изен, X. Лу и К. Ривз

DESY, Гамбург и Цойтен, Германия

П. Бехтле, Э. Бергеаас Куутманн, М.Бёлер, В. Эренфельд, В. Феррара, Г. Фишер, А. Глазов, М. Гебель, Л.С. Гомес Фахардо, Х. Гонсалвес Пинто Фирмино да Коста, Б. Госджик, И.М. Грегор, К.Х. Хиллер, И. Христова, У. Хусеманн, М. Хименес Беленгер, С. Йонерт, М. Карневский, Й. Каци, Т. Коно, К. Ланге, Э. Лободзинска, Д. Людвиг, С. Мэттиг, М. Мединнис , Л. Мийович, К. Мениг, Т. Науманн, М. Ножичка, Т. Перес Кавальканти, Д. Петчулл, С.М. Пец, Р. Плакаките, З. Цинь, И. Рубинский, Х.Дж. Штельцер, К. Такманн, М. Терворт, П. Ванков, М. Вити, М.A. Wildt & H. Zhu

Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany

M. Bunse, D. Dobos, C. Gössling, F. Hirsch, J. Klaiber-Lodewigs, R. Клингенберг, О. Кразель, М. Мас, И. Райзингер, Й. Вальберсло, Й. Вебер и Р. Вунсторф

Institut für Kern- und Teilchenphysik, Технический университет Дрездена, Дрезден, Германия

T. Göpfert, D Кар, М. Кобель, К. Леонхардт, А. Людвиг, WF Мадер, X.Prudent, R. Schwierz, F. Seifert, P. Steinbach, A. Straessner & A. Vest

Физический факультет Университета Дьюка, Дарем, Северная Каролина, США

A.T.H. Арсе, Д. Бенджамин, А. Боччи, В.Л. Эбенштейн, А.Дж. Фаулер, Б. Ко, А. Котвал, С.Х. О, К. Ван и Дж. Ямаока

SUPA — Школа физики и астрономии, Эдинбургский университет, Эдинбург, Великобритания

W. Bhimji, A.G. Buckley, P.J. Clark, B.J. O’Brien & B.M. Wynne

Fachhochschule Wiener Neustadt, Винер-Нойштадт, Австрия

E.Griesmayer

INFN Laboratori Nazionali di Frascati, Фраскати, Италия

A. Annovi, M. Antonelli, H. Bilokon, F. Cerutti, M. Curatolo, B. Esposito, M.L. Феррер, К. Гатти, П. Лаурелли, Г. Маккарроне, А. Сансони, М. Теста, Э. Вилукки, Г. Вольпи и М. Вен

Fakultät für Mathematik und Physik, Университет Альберта Людвига, Фрайбург i.Br., Германия

G. Aad, F. Ahles, M. Beckingham, R. Bernhard, U. Bitenc, R. Bruneliere, S. Caron, C.Карпентьери, А. Христов, А. Дальхофф, Дж. Дитрих, С. Эккерт, М. Фелинг-Кашек, М. Флехль, Дж. Глатцер, Дж. Хартерт, М. Хельдманн, Г. Хертен, С. Хорнер, К. Якобс, К. Кеттерер, М. Коллефрат, AI Кононов, С. Куен, С. Лай, У. Ландграф, К. Лохвассер, И. Людвиг, Дж. Людвиг, Д. Ламб, К. Махбуби, Дж. Мейнхардт, В. Мор, Х. Нильсен, У. Парзефаль, X. Portell Bueso, M. Rammensee, K. Runge, Z. Rurikova, E. Schmidt, M. Schumacher, F. Siegert, K. Stoerig, JE Sundermann, KK Темминг, С. Тома, Дж. Тобиас, В.Цискаридзе, М. Вентури, И. Виварелли, Х. фон Радзевски, М. Варсинский, К. Вайзер, М. Вернер, Л.А.М. Wiik, S. Winkelmann, S. Xie & S. Zimmermann

Section de Physique, Université de Genève, Женева, Швейцария

A.A. Абделалим, Г. Александр, М. Бакес, П.Дж. Белл, W.H. Белл, Э. Берглунд, А. Блондель, Ф. Буччи, А. Кларк, В. Дао, Д. Феррере, С. Гадомски, Дж. Э. Гарсия Наварро, О. Гаумер, С. Гонсалес-Севилья, М. Гулетт, А. Гамильтон, А. Леже, А. Листер, Д. Мачина, Б.Мартин Дит Латур, Б. Микулец, Л. Монета, К. Мора Эррера, M-C. Morone, S. Nektarijevic, F. Orellana, G. Pásztor, M. Pohl, A. Robichaud-Veronneau, K. Rosbach, L. Rosselet & X. Wu

INFN Sezione di Genova

D. Barberis, R Беккерле, К. Казо, А. Коккаро, Т. Корнелиссен, С. Кунео, М. Дамери, Г. Дарбо, А. Ферретто Пароди, Г. Гальярди, К. Джемме, П. Мореттини, М. Ольчезе, Б. Оскулати, Ф. Пароди, Л.П. Росси и К. Скьяви

Институт физики и HEP, Академия наук Грузии и Тбилисский государственный университет, Тбилиси, Грузия

L.Чиковани, Т. Джобава, Дж. Хубуа, Г. Мчедлидзе, М. Мосидзе, Э. Цхададзе

II Physikalisches Institut, Justus-Liebig-Universität Giessen, Giessen, Германия

А. Аствацатуров, М. Дюрен и Х. Стензель

SUPA — Школа физики и астрономии, Гласговский университет Великобритания

SE Оллвуд-Спайерс, Р.Л. Бейтс, Д. Бриттон, П. Бусси, К.М. Buttar, C. Collins-Tooth, S. D’Auria, T. Doherty, A.T. Дойл, С. Ферраг, Дж. Феррандо, А.Геммелл, М. Кеньон, Х. Макглоун, А. Мораес, В. О’Ши, К. Оропеза Баррера, А. Пикфорд, А. Робсон, Д. Х. Саксон, К. Шоу, К. Смит, Р.Д.Сент-Дени, Г. Стил, Г.А. Стюарт, А. Thompson, K. Wraight & C. Wright

II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany

C. Ay, U. Blumenschein, O. Brandt, J. Erdmann, D. Evangelakou, M. Джордж, Дж. Гросс-Кнеттер, С. Гиндон, Дж. Халлер, А. Хенрикс, К. Хенсель, М. Кейл, А. Кну, Ф. Кон, Н. Кригер, К.Kroeninger, E. Magradze, A. Mann, J. Meyer, A. Quadt, A. Roe, E. Shabalina, M. Uhrmacher, P. Weber & J. Weingarten

Laboratoire de Physique Subatomique et de Cosmologie, Université Жозеф Фурье и CNRS / IN2P3 и Национальный политехнический институт Гренобля, Гренобль, Франция

S. Albrand, ML. Андрие, Б. Клеман, Ж. Колло, С. Крепе-Реноден, П. де Сентиньон, П.А. Дельсарт, Дж. Донини, Д. Дзахини, Дж. Хостачи, Э. Лайн, Ф. Ледруа-Гийон, А. Льерес, А.Люкотт, Ф. Малек, Ф. Мартин, Ф. Полчи, Дж. Старк, X. Сан, Б. Трокме и К. Вейдерт

Физический факультет Хэмптонского университета, Хэмптон, Вирджиния, США

T.N. Адди, А. Харви, К. Макфарлейн, Т. Шин и В.И. Василакопулос

Лаборатория физики элементарных частиц и космологии, Гарвардский университет, Кембридж, Массачусетс, США

Дж. Баррейро Гимарайнш да Коста, А. Беллони, Г.В. Бранденбург, М. Франклин, П. Херст, Дж. Хут, Л. Джинти, М. Каган, В.Мартинес Оутсхорн, К. Меркурио, К. Миллс, С. Моэд, М. Мори, С. Прасад, Б.С. Smith & G. Zevi della Porta

Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg

V. Andrei, J.T. Чайлдерс, Т. Dietzsch, F. Föhlisch, C. Geweniger, P. Hanke, M. Henke, A. Khomich, E.-E. Клюге, В. Лендерманн, К. Мейер, Ф. Мюллер, С. Поддар, В. Шарф, Х.-К. Шульц-Кулон, Р. Стамен и М. Весселс

Факультет естественных наук, Хиросимский университет, Хиросима, Япония

T.Ohsugi

Факультет прикладных информационных наук, Технологический институт Хиросимы, Хиросима, Япония

Y. Nagasaka

Физический факультет Университета Индианы, Блумингтон, Индиана, США

С. Брюнет, П. Ветански, Х. Эванс, П. Ганьон, В. Джайн, Ф. Люринг, CP Марино, Х. Огрен, Дж. Пенвелл, Д. Прайс, Д. Руст, Д. Уиттингтон, Янг и Д. Зиеминска

Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Инсбрук, Австрия

B.Эпп, П. Джуссел, Э. Кнерингер, Д. Кун и Г. Рудольф

Университет Айовы, Айова-Сити, Айова, США

П.К. Бехера, М. Лимпер, У. Маллик и Р. Зайдан

Кафедра физики и астрономии, Университет штата Айова, Эймс, штат Айова, США

К. Чен, Дж. Кокран, Ф. Дудзяк, А. Лебедев, В ВИДЕ Mete, W.T. Meyer, A. Nelson, S. Prell, E.I. Розенберг, А. Руис-Мартинес, Н. Триплетт, К. Ямамото

Объединенный институт ядерных исследований ОИЯИ Дубна, Дубна, Россия

I.Н. Александров, А. Барашков, Д.Ю. Бардин, В.А. Бедняков, И. Бойко, И. Будагов, Г.А. Челков, А. Чеплаков, В.Ф. Чепурнов, М. Чижов, Д. Дедович, М. Демичев, Г.Л. Глонти, М.И. Госткин, Н. Григалашвили, Ю. Гусаков, Н. Гусейнов, Л.В. Калиновская, М. Казаринов, Г.Д. Кекелидзе, Д. Харченко, Н. Хованский, Э. Храмов, В. Колесников, В. Котов, У. Кручонак, З.В. Крумштейн, В. Кухтин, Э. Ладыгин, А.Б. Лазарев, И. Манджавидзе, И. Минашвили, М. Минеев, К. Николаев, А.Г. Ольчевский, В.Д. Пешехонов, В. Романов, Л.Румянцев, Н.А.Русакович, Р.Садыков, А.Н. Сисакян, Н.Д. Топилин, В. Виноградов и А. Жемчугов

KEK, Организация по исследованию ускорителей высоких энергий, Цукуба, Япония

К. Амако, Ю. Араи, Ю. Дои, Т. Харуяма, Ю. Икегами, М. Икено, К. Исии, М. Ишино, Х. Ивасаки, Дж. Канзаки, Т. Кохрики, Т. Кондо, Ю. Макида, А. Манабе, С. Мицуи, Ю. Морита, К. Мураками, К. Нагано, М. Нодзаки, С. Odaka, TK Оска, О. Сасаки, Т. Сасаки, Ю. Судзуки, С.Танака, С. Терада, Дж. Тодзё, К. Токусуку, С. Цуно, Ю. Унно, М. Ямада, А. Ямамото и Ю. Ясу

Высшая школа естественных наук, Университет Кобе, Кобе, Япония

А. Акияма, Т. Хаякава, Ю. Хомма, Р. Ичимия, А. Исикава, К. Кавагоэ, М. Кинг, Х. Киямура, Х. Курашиге, Т. Мацусита, К. Миядзаки, Т. Нишияма, А. Очи, С. Окада, К. Омачи, К. Суита, Х. Такеда, К. Тани, К. Токунага и Ю. Ямадзаки

Факультет естественных наук, Университет Киото, Киото, Япония

N.Сасао

Педагогический университет Киото, Киото, Япония

Р. Такашима

Instituto de Física La Plata, Universidad Nacional de La Plata и CONICET, Ла-Плата, Аргентина

X.S. Андуага, М. Дова, Ф. Монтичелли и М.Ф. Tripiana

Физический факультет, Ланкастерский университет, Ланкастер, Великобритания

А.Е. Бартон, Г. Борисов, Е.В. Бухова-Такер, Т. Бродбек, Дж.Р. Кэтмор, С. Читэм, А. Чилингаров, Р.Дэвидсон, Л. Де Мора, Х. Фокс, R.C.W. Хендерсон, Дж. Хьюз, Р.В.Л. Джонс, В. Картвелишвили, Р. Лонг, П.А. С любовью, П. Ратов, Т.Дж. Sloan, M. Smizanska & J. Walder

INFN Sezione di Lecce

M. Bianco, G. Cataldi, A. Cazzato, G. Chiodini, R. Crupi, E. Gorini, F. Grancagnolo, A. Guida , Р. Перрино, М. Примавера, С. Спаньоло и А. Вентура

Лаборатория Оливера Лоджа, Ливерпульский университет, Ливерпуль, Великобритания

PP Олпорт, Н.Остин, С. Бурдин, М. Д’Онофрио, П. Дерван, Т. Гриншоу, К. Б. Гвильям, Х.С. Хейворд, М.А.Хоулден, Дж. Джексон, T.J. Джонс, Б. King, M. Klein, U. Klein, T. Kluge, J. Kretzschmar, P. Laycock, S.J. Максфилд, А. Мехта, С. Мигас, П.М. Причард, Г. Селлерс, Дж. Х. Фоссебельд, П. Валлер, К. Виглесворт и Б. Врона

Физический факультет, Институт Йожефа Стефана и Университет Любляны, Любляна, Словения

В. Циндро, И. Доленц, А. Филипчич, А. Горишек, BPКершеван, Г. Крамбергер, Б. Мачек, И. Мандич, М. Микуж и А. Тихонов

Физический факультет Лондонского университета королевы Марии, Лондон, Великобритания

П. Адрагна, М. Бона, А.А. Картер, Л. Черрито, Э. Эйзенхандлер, К. Эллис, М.П.Дж. Лэндон, С. Ллойд, Дж. Морин, Дж. Д. Моррис, Э. Пиккаро, Дж. Полл, Э. Ризви, К. Стивенсон, М. Тейшейра Диас Кастанхейра и Д. Трейнор

Физический факультет Лондонского королевского университета Холлоуэй, Суррей, Великобритания

М.А. Алам, Т. Берри, В. Бойсверт, Г. Бурман, Н. Дж. Купер-Смит, Г. Коуэн, К.А. Эдвардс, С. Джордж, Р. Гонсало, Д. Хайден, Дж. Килвингтон, А. Миседжук, М. Роуз, Дж. А. Стронг и П. Тейшейра-Диас

Департамент физики и астрономии, Университетский колледж Лондона, Лондон, Великобритания

С. Бейкер, П. Бернат, С. П. Биеник, С. Бёзер, Дж. М. Баттерворт, Т. Байатт, М. Кампанелли, ИА Christidi, B.D. Купер, А. Дэвисон, С. Дин, Дж. Дрохан, Э. Янсен, Т. Джонс, Н. Константинидис, Дж.Monk, M. Nash, E. Nurse, R. Prabhu, A. Richards, J.E.M. Робинсон, П. Шервуд, Б. Симмонс, К. Тейлор, Б.М. Во и П.А. Wijeratne

Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC и Университет Париж-Дидро и CNRS / IN2P3, Париж, Франция

Т. Бо, С. Бордони, Г. Кальдерини, А. Камар, П. Каваллери, Э. Шарере, С. Де Чекко, Ф. Деру, Д. Имбо, М. В. Красный, М. Куна, Д. Лакур, Б. Лафорж, С. Лаплас, О. Ле Дорц, Дж. Леллуш, Г. Маркиори, I .Николич-Аудит, Дж. Окарис, М. Ридель, Л. Роос, Ф. Швемлинг, Т. Тевено-Пельцер, С. Тринказ-Дювоид, Т. Trinh & F. Vannucci

Fysiska Instituten, Lunds Universitet, Лунд, Швеция

T.P.A. Окессон, А. Алонсо, С.С. Боккетта, Дж. Грот-Йенсен, В. Хедберг, Г. Ярлског, Б. Лундберг, Э. Литкен, Б. Мейроз, Дж. У. Mjörnmark & ​​O. Smirnova

Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Мадрид, Испания

F.Баррейро, Дж. Кантеро, Х. Де ла Торре, Дж. Дель Песо, К. Гласман, Л. Лабарга, Т. Лагури, Дж. Льоренте Мерино, Л. Марч, Э. Небот, С. Родье и Дж. Террон

Institut für Physik, Universität Mainz, Майнц, Германия

M. Aharrouche, O. Arnaez, M. Bendel, W. Blum, V. Büscher, S. Eckweiler, K. Edmonds, F. Ellinghaus, E. Ertel , Ф. Фидлер, Дж. Флекнер, К. Герингер, К. Гендель, М. Хольфельд, В. Джи, Г. Кавамура, К. Кляйнкнехт, С. Кениг, Л. Кёпке, М. Лунгвиц, Л. Мазетти, К. .Мейер, Д. Морено, А. Нойзидл, С. Рике, Х. Г. Сандер, У. Шефер, К. Шмитт, К. Шредер, Г. Сирагуса, С. Таппрогге и Т. Ву Ань

Школа физики и астрономии , Манчестерский университет, Манчестер, Великобритания

J. Almond, G. Brown, V. Chavda, BE Кокс, К. Да Виа, И.П. Duerdoth, A. Forti, J.M. Foster, J. Howarth, R.E. Hughes-Jones, M. Ibbotson, G. Jones, J.R. Keates, M. Kelly, S.D. Коля, J.L. Lane, F.K. Лёбингер, Р. Маршалл, А.С.Мартынюк, М. Маркс, Я. Масик, П.С. Миягава, А. О, М. Оуэн, Дж. Р. Патер, А. Д. Пилкингтон, В. Г. Плано, К. Шваненбергер, С. Сноу, К. Tevlin, S. Watts & U.K. Yang

CPPM, Aix-Marseille Université и CNRS / IN2P3, Марсель, Франция

S. Aoun, C.P. Би, К. Бенчук, К. Бернарде, Н. Буссон, Дж. К. Клеменс, Ю. Коаду, П. Дельпьер, Ф. Джама, Ф. Этьен, Л. Фелиджони, Ф. Анри-Куанье, Д. Хоффманн, Ф. Губо , EBFG Knoops, E. Le Guirriec, B. Li, E. Monnier, J. Odier, E. Petit, P. Pralavorio, Z.Цянь, А. Розанов, М. Талби, Н. Таннури, С. Тиссеран, Дж. Тот, Ф. Тушард и Л. Вакавант

Физический факультет Массачусетского университета, Амхерст, Массачусетс, США

B. Брау, Дж. Колон, К. Даллапиккола, А. Мид, EJW Мойс, Э. Томпсон, Н. ван Элдик, С. Виллок и М.Дж. Вудстра

Физический факультет Университета Макгилла, Монреаль, Квебек, Канада

Б. Чапло, Ф. Корриво, М. Доббс, М.-А. Дюфур, Х. Гюлер, М. Клеметти, С.Х. Робертсон, К. Сантамарина Риос, М. Шрам, Б. Вашон и А. Уорбертон

Школа физики, Мельбурнский университет, Виктория, Австралия

E.L. Барберио, В. Дэви, Н. Дэвидсон, К.Ю. Фельцманн, С.И. Кази, А. Лимозани, Г.Ф. Moorhead, A. Phan, M.E. Sevior, Q.T. Шао, Г. Тейлор и М.Дж. Уайт

Физический факультет Мичиганского университета, Анн-Арбор, штат Мичиган, США

А.Дж. Армбрустер, Дж. Чапман, М. Сирилли, Т. Дай, Э. Диль, А.Эппиг, К. Ферретти, С. Гольдфарб, Д. Харпер, Д. Левин, Х. Ли, Х. Лю, Дж. Б. Лю, С. П. Мак Ки, Х.А. Нил, Н. Паникашвили, Дж. Пурдхэм, Дж. Киан, Д. Шейрих, Дж. Страндберг, Р. П. Тун, С. Валч, А. Уилсон, Х. Янг и Б. Чжоу

Департамент физики и астрономии, Университет штата Мичиган, Ист-Лансинг, штат Мичиган, США

М. Аболинс, Г. Арабидзе, Р. Брок, К. Бромберг, С. Когрон, Г. Комун, А. Ди Маттиа, В. Федорко, Р. Хаузер, С. Хайм, Дж. Л. Хольцбауэр, Дж. Хьюстон, Дж. Колл, Дж.Краус, Дж. Линнеманн, П. Мангерд, Б. Мартин, Р.Дж. Миллер, Б. Поуп, П. Райан, Р. Швинхорст, К. Толлефсон и Х. Чжан

INFN Sezione di Milano

Э. Ачерби, Ф. Алессандрия, Г. Алимонти, А. Андреацца, Г. Баккаглиони, Г. Баттистони , Мичиган Бесана, Ф. Броджи, Л. Карминати, Д. Кавалли, Г. Коста, Л. Делл’Аста, М. Фанти, А. Фаварето, Д. Джунни, И. Колецу, Т. Лари, А. Лаззаро, Л. Манделли, М. Маццанти, К. Мерони, С. Монтесано, Л. Перини, К. Пицио, Ф. Рагуза, С.Рескони, Г. Ривольтелла, Л. Росси, М. Сорби, Г.Ф. Тартарелли, К. Тронкон, Р. Турра, Г. Веньи и Г. Вольпини

B.I. Институт физики им. Степанова НАН Беларуси, Минск, Республика Беларусь

А. Богоуч, С. Харкуша, Ю. Кульчицкий, Ю.А. Курочкин, И. Сацункевич, П.В. Цярешка

Национальный научно-образовательный центр физики элементарных частиц и высоких энергий, Минск, Республика Беларусь

В. Гилевский, П.Кужир, В. Румянцев, П. Старовойтов и С. Януш

Физический факультет Массачусетского технологического института, Кембридж, Массачусетс, США

FE Taylor

Группа физики частиц, Монреальский университет, Монреаль, Квебек, Канада

G. Azuelos, P. Banerjee, J. Bouchami, M. Davies, J. Ferland, A. Gutierrez, C. Lebel, C. Leroy, JA Макана Гоя, Дж. П. Мартин, Р. Мехтиев и О. Скаллон

P.N. Физический институт им. П.Н. Лебедева РАН, Москва, Россия

А.В. Акимов, С.П. Баранов, И.Л. Гавриленко, А.А. Комар, Р. Машинистов, С.В. Муравьев, П.Ю. Нечаева, А.Шмелева, А.А. Снесарев, В. Сулин и В. Тихомирова

Институт теоретической и экспериментальной физики (ИТЭФ), Москва, Россия

А. Артамонов, П.А. Горбунов, В. Хованский, П. Шаталов, И.И. Цукерман

Московский инженерно-физический институт (МИФИ), Москва, Россия

А. Антонов, К. Белоцкий, В.Г. Бондаренко, О.Булеков, Б. Долгошеин, В. Канцеров, С. Морозов, А. Романюк, С.Ю. Смирнов и Е. Солдатов

Институт ядерной физики им. Скобельцына МГУ им. М.В. Ломоносова, Москва, Россия

Л.К. Гладилин, Ю.В. Гришкевич, В. Крамаренко, В. Рудь, С.Ю. Сивоклоков, Л. Смирнова

Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Германия

S. Adomeit, O. Biebel, P. Calfayan, J. de Graat, M. Deile, G.Duckeck, J. Ebke, J. Elmsheuser, A. Engl, C. Galea, M.H. Genest, R. Hertenberger, J. Kennedy, C. Kummer, F. Legger, M. Lichtnecker, R. Mameghani, T.A. Мюллер, Т. Нуннеманн, Ф. Раушер, П. Резничек, Б. Рукерт, М.П. Sanders, D. Schaile, J. Schieck, C. Serfon, A. Staude, R. Walker, J.Z. Will & X. Zhuang

Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Мюнхен, Германия

М. Адерхольц, Т. Бариллари, М. Беймфорде, С. Бетке, Д. Каприотти, Г. Кортиана, Д.Даннхейм, Х. Дитль, Дж. Дубберт, Т. Эрих, М. Дж. Флауэрдью, П. Джованнини, Т. Гёттферт, М. Гро, П. Хефнер, Д. Хауфф, А. Янч, С. Кайзер, А. Э. Кирюнин, С. Клут, О. Кортнер, С. Кортнер, С. Котов, Х. Кроха, Г. Лутц, А. Маккиоло, А. Манц, С. Менке, С. Мордик-Мёк, Х. Г. Мозер, Р. Нисиус, Х. Оберлак , GE Поспелов, И. Потрап, Э. Раутер, Р. Рихтер, Д. Салихагич, П. Шахт, Р. Зейстер, С. Стонек, К. Вальдеранис, Х. фон дер Шмитт, Й. фон Лёбен, П. Вайгель и В. Журавлов

Институт прикладных наук Нагасаки, Нагасаки, Япония

М.Симодзима и Я. Танака

Высшая школа естественных наук, Нагойский университет, Нагоя, Япония

С. Хасэгава, Ю. Ито, Т. Охима, Ю. Окумура, Т. Сугимото, Ю. Такахаши, М. Томото и J. Wakabayashi

INFN Sezione di Napoli

A. Aloisio, MG Альвигги, В. Канале, Л. Капассо, Дж. Карлино, Ф. Севенини, Дж. Чифтари, Ф. Конвенти, Р. де Асмундис, М. Делла Пьетра, Д. делла Вольпе, А. Дориа, Р. Джордано, Г. Якобуччи, П. Иенго, В. Изцо, Л.Мерола, Э. Мусто, С. Патричелли, Э. Росси и Г. Сехниаидзе

Кафедра физики и астрономии, Университет Нью-Мексико, Альбукерке, Нью-Мексико, США

И. Горелов, М. Р. Хёферкамп, Дж. Меткалф, SC Seidel, K. Toms & R. Wang

Институт математики, астрофизики и физики элементарных частиц, Radboud University Nijmegen / Nikhef, Nijmegen, Netherlands

MA Chelstowska, M. Consonni, N. De Groot, F. Filthaut, ПФ Клок, А.С.Кениг, Ф.Кецвельд, М. Раас и С.Дж.В.П. Timmermans

Национальный институт субатомной физики Nikhef и Амстердамский университет, Амстердам, Нидерланды

S. Bentvelsen, G.J. Боббинк, К. Бос, Х. Ботеренбруд, Э.Дж. Буис, А.П. Колин, Р. Данкерс, К. Даум, П. де Йонг, Л. Де Нойдж, А.Д. Доксиадис, П. Феррари, Х. Гаритаонандия, Д.А.А. Geerts, M. Gosselink, F. Hartjes, N.P. Хесси, О. Игонкина, М.С. Кайл, С. Клоус, П. Клуит, Э. Коффеман, А. Кутсман, Х. Ли, Ф. Линде, Г. Луийкс, Г.Massaro, J. Mechnich, A. Muijs, I. Mussche, JP Ottersbach, O. Peters, A. Reichold, M. Rijpstra, N. Ruckstuhl, G. Salamanna, R. Sandstroem, J. Snuverink, D. Ta, M Циакирис, Э. Турлей, Х. ван дер Грааф, Э. ван дер Краай, Р. Ван дер Леу, Э. ван дер Поэль, Б. Ван Эйк, З. ван Кестерен, И. ван Вулпен, В. Веркерке, JC Vermeulen & M. Vreeswijk

Физический факультет Университета Северного Иллинойса, ДеКалб, Иллинойс, США

Р. Калкинс, Д. Чакраборти, JG Роча де Лима, К.Suhr & V. Zutshi

Институт ядерной физики им. Будкера (ИЯФ), Новосибирск, Россия

О. Белобородова, В.Б. Бобровников, А.А. Богданчиков, В.А. Казанин, Г. Колачев, А.Король, В.Малышев, А.Л. Масленников, Д.А. Максимов, И. Орлов, С.В. Пелеганчук, А.Г. Шамов, К. Сковпен, А. Сухарев, А. Талышев, Ю.А. Тихонов и А. Зайцев

Физический факультет Нью-Йоркского университета, Нью-Йорк, Нью-Йорк, США

Б. Будик, Д. Касадей, К.Кранмер, Р. Джилкибаев, Л. Хофт ван Хуйсдуйнен, Р. Коноплич, А. Краснахоркай, Г.Х. Льюис, А. Минсер, П. Немети, Р.М. Невес, К. Прокофьев, А. Шибата и Л. Чжао

Университет штата Огайо, Колумбус, Огайо, США

У. Фернандо, М.Дж. Фишер, К.К. Ган, Х. Каган, Р.Д. Касс, Дж. Мосс, А.М. Рахими и М. Стрэнг

Факультет естественных наук, Университет Окаяма, Окаяма, Япония

И. Накано

Гомер Л. Додж Кафедра физики и астрономии, Университет Оклахомы, Норман, Оклахома, США

B .Эбботт, П. Гутьеррес, Г.С. Хуанг, Д.К. Яна, А. Марзин, Р. Мира-Леббай, М. Салим, Х. Северини, П. Скубич, Дж. Сноу и М. Штраус

Физический факультет Государственного университета Оклахомы, Стиллуотер, штат Оклахома, США

Б. Аби, А. Ханов и Ф. Ризатдинова

Университет Палацкого, RCPTM, Оломоуц, Чешская Республика

П. Хамал, А. Кочнар и Л. Нозка

Центр физики высоких энергий, Университет Орегона , Юджин, штат Орегон, США

J.Э. Брау, К. Potter, E. Ptacek, A. Reinsch, M. Robinson, J. Searcy, M. Shamim, N.B. Синев, Д. Стром и Э. Торренс

LAL, Univ. Paris-Sud и CNRS / IN2P3, Орсе, Франция

H. Abreu, C. Arnault, E. Auge, P. Barrillon, M. Benoit, S. Binet, J.-B. Бланшар, К. Бурдариос, Д. Бретон, К. Коллар, К. Де Ла Тай, Ж. Б. Де Виви де Реги, С. Диглио, Л. Дюфло, М. Эскалье, А. К. Фалу, Л. Файяр, Д. Фурнье, Дж. .-F. Гриваз, М. Хеллер, С. Анро-Версиль, Ж. Гривнак, Л.Иэкономиду-Файярд, Дж. Идаррага, М. Кадо, А. Лунис, Н. Маковец, П. Матрикон, Ю. Накахама, Ф. Нидеркорн, Л. Поджиоли, П. Пьюзо, А. Рено, Д. Руссо, X. Руан, Г. Рыбкин, Дж. Б. Сован, Дж. Шааршмидт, А. С. Шаффер, Л. Серин, С. Симион, Р. Танака, Дж. Дж. Veillet, I. Vukotic, F. Wicek, D. Zerwas & Z. Zhang

Высшая школа естественных наук, Осакский университет, Осака, Япония

K. Hanagaki, M. Hirose, T. Meguro, M. Nomachi & Ю. Сугая

Физический факультет Университета Осло, Осло, Норвегия

Л.Бугге, Т. Буран, Д. Камерон, З. Чычула, Б.К. Gjelsten, E. Lund, F. Ould-Saada, K. Pajchel, Y. Pylypchenko, A.L. Read, O. Rohne, B.H. Самсет, С. Стапнес, А. Стрэндли и А. Тага

Физический факультет Оксфордского университета, Оксфорд, Великобритания

А. Абдесселам, Р. Аполл, А.Дж. Барр, П. Бошемин, К.Р. Бодди, Н.Д. Бретт, Дж. Бьюкенен, Р.М. Бэкингем, Д. Буйра-Кларк, П. Коу, Э. Кониавитис, А.М. Купер-Саркар, М. Дехар, К. Доглиони, С.М. Фаррингтон, Э.Дж. Галлас, Л.Гилберт, К. Гвенлан, Б.М. Хоуз, А. Холмс, К. Хортон, Д.Ф. Хауэлл, Т. Хаффман, К. Иссевер, М. Карагоз, Р.С. Б. Кинг, Г. Кирш, Н. Кунду, А. Ларнер, В. Лау, А. Лаворато, З. Лян, С.С.А. Ливермор, Дж. Локен, К. Маттраверс, П. Мермод, Р. Б. Никерсон, А. Пиндер, Н. К. Райдер, Д. Шорт, J.C-L. Ценг, Г.Х.А. Фиххаузер, А. Вайдберг, С. Уайтхед и Дж. Вуден

INFN Sezione di Pavia

М. Белломо, М. Камбиаги, К. Конта, Р. Феррари, С. Франчино, М. Браттернали, Г.Гаудио, М. Ливан, А. Негри, Г. Полеселло, Д.М. Ребуцци, А. Римольди, М. Усленги и В. Верчези

Физический факультет Пенсильванского университета, Филадельфия, Пенсильвания, США

Дж. Элисон, Дж. Дегенхардт, М. Донега, Н. Дресснандт, С. Фратина, М. Ханс, Э. Хайнс, Б. Джексон, Дж. Кролл, Дж. Канкл, Британская Колумбия ЛеГейт, Э. Липелес, Ф.Ф. Мартин, Д. Оливито, Р. Оспанов, Р. Рис, Дж. Штальман, Э. Томсон, П. Вагнер и Х. Х. Уильямс

Петербургский институт ядерной физики, Гатчина, Россия

О.Л. Федин, В. Грачев, О.Г. Гребенюк, В. Малеев, С. Нестеров, Ю.Ф. Рябов, В. Щегельский, Э. Седых, Д. Селиверстов, Й.К. Zalite

INFN Sezione di Pisa

F. Bertolucci, M. Cascella, V. Cavasinni, F. Crescioli, T. Del Prete, A. Dotti, P. Francavilla, V. Giangiobbe, A. Lupi, E. Маццони, К. Рода, Ф. Сарри и З. Зенонос

Кафедра физики и астрономии, Питтсбургский университет, Питтсбург, Пенсильвания, США

Дж. Будро, К.Булахуаш, В. Клиланд, Т. Киттельманн, Дж. Мюллер, В. Паолоне, Д. Приер, В. Савинов, В. Цулайя, С. Вендлер и Р. Юсуфмия

Laboratorio de Instrumentacao e Fisica Experimental de Particulas — LIP, Лиссабон, Португалия

A. Amorim, N. Anjos, J. Carvalho, NF Castro, P. Conde Muiño, A. Do Valle Wemans, M.C.N. Fiolhais, A. Gomes, P.M. Хорхе, Л. Лопес, Х. Мачадо Мигуэнс, П.Дж. Магалхаес Мартинс, А. Майо, Х. Манейра, А. Мораиш, М. Оливейра, А. Онофре, А. Пальма, Дж.Пина, Б. Пинто, Х. Сантос, J.G. Сараива, Дж. Силва, М. Соареш, Ф. Велозо и Х. Вольтерс

Институт физики Академии наук Чешской Республики, Прага, Чешская Республика

Дж. Чудоба, П. Галлус, Й. Гюнтер , I. Hruska, V. Juranek, O. Kepka, A. Kupco, V. Kus, O. Kvasnicka, L. Lipinsky, M. Lokajicek, M. Marcisovsky, M. Mikestikova, M. Myska, S. Nemecek, M Панускова, П. Ружичка, Я. Шованцова, П. Сичо, П. Староба, М. Сватос, М. Тасевский, Т. Тич, Дж. Валента и В.Врба

Физико-математический факультет Карлова университета в Праге, Прага, Чешская Республика

Т. Давидек, Й. Долейси, З. Долезал, З. Драсал, П. Кодис, Р. Лейтнер, Я. Новакова, М. Рыбар, М. Спуста, П. Страхота, М. Сук, Т. Сикора, П. Тас, С. Валкар, В. Воробель и И. Вильгельм

Чешский технический университет в Праге, Прага, Чехия

К. Аугстен, Т. Холи, Т. Хораздовский, З. Губачек, Я. Якубек, З. Когоут, В. Краль, Ф.Крейчи, С. Поспишил, В. Симак, Т. Славичек, К. Смолек, Й. Содомка, М. Солар, Я. Солц, В. Сопко, Б. Сопко, И. Стекл, Д. Туречек, В. Вацек, М. Власак, П. Вокац

Государственный научно-исследовательский центр Институт физики высоких энергий, Протвино, Россия

В.В. Аммосов, А.Борисов, Н.И. Божко, С.П. Денисов, Р. Фахрутдинов, А. Фенюк, В.А. Гапиенко, С. Головня, С.А.Горохов, В. Горячев, В. Гущин, А. Ивашин, В. Кабаченко, А. Карюхин, А.Г. Холоденко, А.М. Кивер, С.В. Копиков, В. Корешев, В.А. Коротков, А. Кожин, В. Лапин, А. Ларионов, М. Левицкий, А.А. Минаенко, Г. Митрофанов, А. Моисеев, А.Г.Мягков, В.Николаенко, А.В. Плескач, В. Рядовиков, А.А. Солодков, О. Соловьянов, Е.А. Старченко, Ю.М. Свиридов, А.П. Воробьев, А.С. Вовенко, В. Заец, А. Зайцев, А. Зенин, О.Зенин, В.В. Змушко

Отдел физики элементарных частиц, Лаборатория Резерфорда Эпплтона, Дидкот, Великобритания

T. Adye, J.T. Бейнс, Б.M. Barnett, D. Botterill, S. Burke, R.W. Clifft, A. Dewhurst, D. Emeliyanov, S.M. Фишер, Б.Дж. Галлоп, К.Н.П. Ну и дела, А. Гиллман, Д. Гринфилд, С.Дж. Хейвуд, Дж. Кирк, Н.А.Маккуббин, С.Дж. МакМэхон, Р.П. Миддлтон, У.Дж. Мюррей, П.Р. Нортон, П.В. Филлипс, D.P.C. Sankey, WG Scott, J. Strube, M. Tyndel, M. Weber, FJ Wickens & M. Wielers

Физический факультет, Университет Реджайны, Реджайна, Саскачеван, Канада

К. Бенслама, X. Джу, Ю. Мин, Е.О. Ортега и Г.V. Ybeles Smit

Ritsumeikan University, Kusatsu, Shiga, Japan

S. Tanaka

INFN Sezione di Roma I

F. Anulli, G. Artoni, P. Bagnaia, C. Bini, S. Боррони, Р. Калои, А. Каваллари, Дж. Чапетти, А. Д’Орацио, Д. Де Педис, А. Де Сальво, К. Диониси, С. Фальчиано, С. Джентиле, С. Джагу, М. Джунта, Ф. Лакава, Ф. Ло Стерцо, К. Люси, Л. Луминари, К. Майани, Ф. Марцано, Г. Мирабелли, А. Нисати, Э. Паскуалуччи, Э. Петроло, Л. Понтекорво, М.Rescigno, S. Rosati, F. Safai Tehrani, A. Sidoti, E. Solfaroli Camillocci, F. Spila, P. Valente, R. Vari, S. Veneziano & L. Zanello

INFN Sezione di Roma Tor Vergata

Г. Айелли, П. Камарри, Р. Кардарелли, Г. Каттани, А. Ди Чаччо, Р. Ди Нардо, А. Ди Симоне, Б. Либерти, Ф. Марчезе, А. Паолони, А. Саламон и Р. Santonico

INFN Sezione di Roma Tre

C. Bacci, A. Baroncelli, M. Biglietti, P. Branchini, F. Ceradini, S.Ди Луиза, А. Фарилла, Э. Грациани, М. Йодиче, Д. Орестано, А. Пассери, Ф. Пасторе, Ф. Петруччи, Ф. Руджери, Э. Спирити и К. Станеску

Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies — Université Hassan II, Casablanca

D. Benchekroun, A. Chafaq, M. Gouighri, A. Hoummada & S. Lablak

DSM / IRFU (Institut de Recherches Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, Франция

H.Бачаку, Ф. Бауэр, Н. Бессон, Н.М. Болнет, М. Бунекамп, Л. Шевалье, Дж. Эрнвейн, А.И. Этьенвр, А. Формика, Л. Готье, П.Ф. Giraud, C. Guyot, S. Hassani, W. Kozanecki, E. Lancon, J.F. Laporte, E. Le Menedeu, M. Legendre, B. Lenzi, B. Mansoulie, J-P. Meyer, N. Morange, R. Nicolaidou, A. Ouraou, D.M. Помареде, Б. Резенде, С. Р. Ройон, Ф. Шуне, Дж. Швиндлинг, О. Симард и М. Виршо

Санта-Крус Институт физики элементарных частиц, Калифорнийский университет Санта-Крус, Санта-Крус, Калифорния, США

A .Бангерт, С. Чуриду, Д.С. Дамиани, Т. Дуббс, К. Фаулер, А.А. Грилло, Г.А. Заяц, А. Литке, В. Локман, П. Manning, J. Mitrevski, J. Nielsen, H.F-W. Садрозинский, Б.А. Schumm & A. Seiden

Физический факультет Вашингтонского университета, Сиэтл, Вашингтон, США

D.A. Форбуш, А.Г. Гуссиу, Дж. Гриффитс, О.М. Харрис, В. Куйкендалл, Х. Дж. Любатти, П. Мокетт, А. Поличчио, Дж. Ротберг, Д. Вентура, М. Вердуччи, Дж. К. Ван, Г. Уоттс и Т. Чжао

Кафедра физики и астрономии Университета Шеффилда, Шеффилд, Великобритания

C.Анастопулос, К. Бут, П. Бут, Д. Костанцо, Т. Кухадар Донсельманн, И. Доусон, Р. Даксфилд, М. Ходжкинсон, П. Ходжсон, П. Йоханссон, Э.В. Королькова, А. Мейн, Я. Макфайден, Л. Николас, С. Оуэн, Э. Паганис, М.Р. Саттон, Д. Тови, А. Туа и Д. Сюй

Физический факультет Университета Синсю, Нагано, Япония

Я. Хасегава, Х. Охшита и Т. Такешита

Физическая физика, Университет Зигена, Зиген, Германия

П. Бухгольц, Х.Цирр, И. Флек, Б. Гаур, К. Грибель, М. Холдер, И. Ибрагимов, М. Раммес, В. Сипица, Т. Шталь, В. Валковяк и М. Циолковски

Физический факультет, Саймон Университет Фрейзера, Бернаби, Британская Колумбия, Канада

Э. Доу, Дж. Годфри, Дж. Р. Комарагири, округ Колумбия О’Нил, М. Петтени, Д. Схаутен, Б. Стелцер, М. Троттье-Макдональд и М.С. Веттерли

SLAC Национальная ускорительная лаборатория, Стэнфорд, Калифорния, США

И. Арасена, Т. Барклоу, Р.Бартольдус, H.S. Бава, Б. Батлер, Дж. Коган, Ю. Гао, П. Гренье, А. Хаас, П. Ханссон, К. Хорн, П. Джексон, К.Дж. Кенни, П.С. Ким, М. Кочян, Т. Кой, А.Дж. Лоу, Д.В. Миллер, Р. Маунт, С. Нельсон, Т.К. Нельсон, А. Сальников, А. Шварцман, Д. Сильверштейн, Д. Смит, Э. Штраус, Д. Су, М.Г. Уилсон, М. Витген и К. Янг

Факультет математики, физики и информатики, Университет Коменского, Братислава

Л. Баткова, Т. Блазек, П. Федерич, М. Печи, П. Ставина, И.Сикора, С. Токар и Т. Жениш

Физический факультет Йоханнесбургского университета, Йоханнесбург

М. Оруссо

Физический факультет Стокгольмского университета

Б. Осман, К. Бом, К. Бом , Д. Эрикссон, К. Геллерстедт, С. Хеллман, А. Хидвеги, SO Холмгрен, М. Йохансен, К.Э. Йоханссон, К. Джон-Анд, Дж. Лессер, Дж. Лундберг, Д.А. Милстед, Т. Моа, Б. Нордквист, К.С. Ohm, A. Papadelis, M. Ramstedt, B. Sellden, S.B. Сильверштейн, Дж.Sjolin, S. Strandberg, M. Tylmad & Z. Yang

Физический факультет Королевского технологического института, Стокгольм, Швеция

KJ. Grahn & B. Lund-Jensen

Департамент физики и астрономии, Университет Стоуни-Брук, Стоуни-Брук, Нью-Йорк, США

А. Ахмад, Р. Капуто, К. Делука, Э. Деветак, Б. ДеВильд, Р. . Энгельманн, Дж. Фарли, Дж. Дж. Гудсон, В. Грасси, Дж. Gray, J. Hobbs, J. Jia, A. Khodinov, R.L. McCarthy, S. Mohapatra, M. Rijssenbeek, R.Д. Шамбергер, Дж. Ступак, Д. Цыбычев и А. Юркевич

Кафедра физики и астрономии, Сассекский университет, Брайтон, Великобритания

В. Бартч, А. Де Санто, К. Дж. Поттер и Ф. Сальваторе

Школа физики, Сиднейский университет, Сидней, Австралия

JSH Ли, Н. Патель, А.Ф. Сааведра, К.Е. Варвелл, А. Waugh & B. Yabsley

Институт физики, Academia Sinica, Тайбэй, Тайвань

M.L. Chu, S. Hou, S.C. Lee, S.C. Lin, D. Liu, R. Mazini, Z. Meng, Z.L. Рен, Д.А. Сох, П.К. Teng, J. Wang, S.M. Wang, Z. Weng, J. Zhong & Y. Zhou

Физический факультет Техниона: Израильский институт. of Technology, Хайфа, Израиль

С. Бехар Харпаз, С. Бен Ами, С. Бресслер, А. Д. Хершенхорн, Э. Кайомовиц, Х. Ландсман, Р. Лифшиц, Ю. Розен, С. Тарем и С. Валлекорса

Школа физики и астрономии Раймонда и Беверли Саклер, Тель-Авивский университет, Тель-Авив, Израиль

H.Абрамович, Г. Александер, Н. Амрам, Г. Белла, О. Бенари, Ю. Бенхамму, Э. Бродет, Э. Эцион, А. Гершон, Дж. Гинзбург, Н. Гуттман, Н. Ход, А. Крейзель, Ю. Махалалель, Ю. Манвес, Ю. Орен, Э. Рейнхерц-Аронис, И. Саде, Ю. Сильвер, А. Соффер, Н. Тайблум и Э. Урковски

Физический факультет Университета Аристотеля в Салониках, Салоники, Греция

Д. Илиадис, К. Кордас, В. Кускура, И. Номидис, А. Петридис, К. Петриду и Д. Сампсонидис

Международный центр физики элементарных частиц и факультет физики Университета Токио, Токио, Япония

г.Акимото, С. Асаи, Ю. Адзума, Т. Дохма, М. Имори, Н. Каная, М. Канеда, Ю. Катаока, Т. Кавамото, К. Кессоку, Т. Кобаяси, Т. Кубота, Т. Машимо, Т. Масубучи, Х. Мацумото, Х. Мацунага, К. Накамура, Ю. Ниномия, Х. Номото, С. Ода, Т. Окуяма, Х. Сакамото, Дж. Танака, К. Тераши, И. Уэда, С. Ямамото, Т. Ямамура и Т. Ямадзаки

Высшая школа науки и технологий, Токийский столичный университет, Токио, Япония

У. Братцлер и К. Фукунага

Физический факультет Токийского технологического института, Токио , Япония

O.Джинноути, Т. Канно и М. Кузе

Физический факультет, Университет Торонто, Торонто, Онтарио, Канада

D.C. Bailey, T. Bain, B. Beare, B. Brelier, S.L. Cheung, P.O. Девивейрос, С. Даливал, Т. Фарук, Б. Фатхолахзаде, А. Гибсон, Б. Го, Э. Янковски, П. Кригер, К. Ле Манер, Ф.К. Мартенс, Р. Орр, Р. Резвани, Г.А. Розенбаум, П. Сандху, П. Савард, П. Синерво, Т. Спрейцер, Д. Тардиф, Р.Дж. Teuscher, P.D. Томпсон и В. Трищук

TRIUMF, Ванкувер, Британская Колумбия

A.Канепа, Б. Карон, С.В. Чекулаев, Д. Фортин, MJ Losty, IM Nugent, CJ Oram, O. Stelzer-Chilton, R. Tafirout & IM Trigger

Институт чистых и прикладных наук Университета Цукуба, Ибараки, Япония

К. Хара , SH Ким, М. Курата, К. Нагаи и Ф. Укегава

Научно-технический центр, Университет Тафтса, Медфорд, Массачусетс, США

С. Гамильтон, А. Напьер, С. Ролли, К. Слива и С. Тодорова-Нова

Centro de Investigaciones, Universidad Antonio Narino, Богота, Колумбия

M.Лосада, К.Ф. Лоурейро, Л. Мендоса Навас, Дж. Наварро и Д. Родригес

Кафедра физики и астрономии Калифорнийского университета в Ирвине, Ирвин, Калифорния, США

B.H. Бенедикт, Т. Болд, доктор медицины Чоботару, Дж. Денг, М. Добсон, И. Гоф Эшрич, И. Грабовска-Болд, Д. Хокинс, А.Дж. Ланкфорд, Х. Окава, Р. Портер, Д.А. Сканниккио, А. Таффард, Б. Тоггерсон, Г. Унель, М. Верт, С.Дж. Уиллер-Эллис, Д. Уайтсон и Н. Чжоу

INFN Gruppo Collegato di Udine

B.С. Ачарья, Д. Кауз, М. Кобаль, Б. Де Лотто, У. Де Санктис, К. Дель Папа, М. Пинамонти, К. Шоу и К. Сурулиз

Физический факультет Иллинойского университета, Урбана, Иллинойс, США

Н. Бенекос, Дж. Коггесхолл, А. Кортес-Гонсалес, Д. Эрреде, С. Эрреде, Х. Ханданян, К. Ли, TM Лисс, А. Маккарн, М.С. Нойбауэр и И. Вишу

Кафедра физики и астрономии, Уппсальский университет, Упсала, Швеция

К. Беланже-Шампань, Р. Бреннер, К.П. Буселло, Т. Экелоф, М. Эллерт, А. Феррари и С. Дж. Хансен

Instituto de Física Corpuscular (IFIC) и Departamento de Física Atómica, Molecular y Nuclear и Departamento de Ingenierá Electrónica and Institónica de Microelect IMB-CNM), Университет Валенсии и CSIC, Валенсия, Испания

Г. Аморос, С. Кабрера Урбан, В. Кастильо Хименес, М. Дж. Коста, К. Эскобар, А. Феррер, Х. Фустер, К. Гарсия, С. Гонсалес де ла Ос, Й. Эрнандес Хименес, Э.Хигон-Родригес, А. Ирлес Квилес, М. Качи, К. Лакаста, В. Лакуэста, С. Марти-Гарсия, М. Миньяно, В.А. Мицу, Р. Молес-Валлс, М. Морено Лласер, Э. Оливер Гарсиа, M.T. Перес Гарсия-Эстань, Э. Рос, Дж. Солт, К.А. Соланс, У. Сольдевила, Х. Санчес, Э. Торро Пастор, Э. Вальядолид Гальего, Я. Валлс Феррер, М. Виллаплана Перес, М. Вос и А. Вильдауэр

Физический факультет Университета Британской Колумбии, Ванкувер, Британская Колумбия, Канада

Д. Аксен, К. Гей, C.W.Loh, W.J. Mills, A. Muir, S. Swedish & S. Viel

Департамент физики и астрономии, Университет Виктории, Виктория, Британская Колумбия, Канада

A. Astbury, Sw. Банерджи, В. Бансал, Ф. Бергхаус, Л. Курни, М. Финке-Килер, Р. Килер, Р. Ковалевски, М. Лефевр, Дж-Р. Лессард, Р. Макферсон, М. Пламондон и Р. Соби

Университет Васэда, Токио, Япония

Н. Кимура и К. Йорита

Отдел физики частиц, Научный институт Вейцмана, Реховот, Израиль

R.Алон, Л. Барак, Э. Духовни, Т. Франк, О. Габизон, Э. Гросс, А. Клиер, Д. Леллуш, Л. Дж. Левинсон, Г. Микенберг, А. Милов, Д. Мильштейн, И. Рот, О. Силберт, В. Смахтин и О. Вителлс

Физический факультет Висконсинского университета, Мэдисон, Висконсин, США

Р. Асфандияров, Г.Д. Каррильо Монтойя, AM Кастанеда Эрнандес, Э. Кастанеда-Миранда, Х. Чен, А. Дос Аньос, Я. Фанг, Д. Фашинг, Л. Флорес Кастильо, С. Гонсалес, О. Гуцвиллер, Х. Джи, Л. Кашиф, А. Леунг Фук Чеонг, Х.Ли, Л.Л. Ма, Б.Р. Мелладо Гарсия, Ю. Пан, С. Патарайя, М. Педраса Моралес, Х. Пэн, Дж. Поведа, У. Куэйл, Т. Саранги, Х. Ван, В. Виденманн, С.Л. Wu, Y. Zhu & G. Zobernig

Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Вюрцбург, Германия

P. Fleischmann, J. Meyer, A. Redelbach, R. Ströhmer & T.5 Trefzger 9000

Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany

M. Barisonzi, K.Х. Бекс, Дж. Бук, Х.М. Браун, Дж. Дрис, С. Флейшманн, Т. Флик, П. Герлах, К. Глица, Г. Горфин, К. Гра, К. Хамахер, Т. Харенберг, Т. Хенсс, Д. Хиршбюль, М. Имхаузер, С. Калинин, С. Керстен, А. Хорошилов, А. Кутц, Т. Куль, Т. Ленц, Г. Ленцен, П. Мэттиг, М. Мехтель, М. Сандхофф, С. Сандвосс, Г. Сартисон, Я. Шультес, А. Зибель, П. Штурм, Дж. Тадом, Т. Т. Восс, В. Вагнер , H. Wahlen, D. Wicke & C. Zeitnitz

Физический факультет Йельского университета, Нью-Хейвен, Коннектикут, США

J.Адельман, Г. Атоян, Б. Ауэрбах, О.К. Бейкер, С. Бедикян, К. Куэнка Альменар, С. Демерс, Ф. Гарберсон, Т. Голлинг, Д. Гест, П.Дж. Хсу, Б. Каплан, Л. Ли, С. Локвиц, А. Логинов, А.Дж. Мартин, М. Шмидт, Д. Шерман, М. Тиойе, П. Типтон, Р. Уолл и М. Целлер

Ереванский физический институт, Ереван, Армения

В. Грабски и Х. Акопян

Domaine scientifique de la Doua , Centre de Calcul CNRS / IN2P3, Villeurbanne, Cedex, France

C.Бискарат, Э. Коньерас и Г. Рахал

Физический факультет Университета Думлупинар, Кутахья

Х. Дуран Йылдиз

Физический факультет Университета Гази, Анкара

М. Йилмаз

Физика, Университет экономики и технологий TOBB, Анкара

S. Sultansoy

Турецкое управление по атомной энергии, Анкара, Турция

I. Turk Cakir

Институт ядерных наук Винча, Белград, Сербия

I.Божович-Елисавчич, Дж. Мамужич и М. Мудринич

Отделение физики, Университет Догус, Стамбул

С.А.Цетин

Отделение инженерной физики, Университет Газиантепа, Газиантеп

Beddall, A. Beddall, A. Bingul & F. Diblen

Dipartimento di Fisica, Università di Bologna, Болонья, Италия

С. Антонелли, А. Бертин, М. Бинди, Д. Кафорио, К. Чокка, С. Де Кастро, Р. Ди Сипио, Л. Фаббри, И.Масса, А. Менгарелли, С. Монзани, М. Пиччинини, К. Сбарра, А. Сбрицци, Н. Семприни-Чезари, С. Валентинетти, М. Вилла, А. Витале и А. Зокколи

Instituto de Fisica , Universidade de Sao Paulo, Сан-Паулу, Бразилия

M. Donadelli & MAL Leite

University Politehnica Bucharest, Bucharest

G.L. Darlea

Departamento de Física, Universidad Técnica Federico Santa María, Вальпараисо, Чили

W.К. Брукс, С. Кулешов, Р. Пезоа и Ф. Прокошин

Кафедра современной физики Китайского технологического университета, Аньхой

Л. Хан, Ю. Цзян, Г. Цзинь, С. Ли , М. Лю, Ю. Лю, Х. Ван, Ю. Ву, К. Сю, Д. Чжан, Х. Чжан и З. Чжао

Физический факультет Нанкинского университета, Цзянсу

С. Чен, Т. Чен, Дж. Пинг и Дж. Ю

Группа физики высоких энергий, Шаньдунский университет, Шаньдун, Китай

C.Фэн, П. Ге, М. Хе, Дж. Мяо, Дж. Ван, З. Чжан и К.Г. Zhu

Dipartimento di Fisica, Università della Calabria, Arcavata di Rende, Италия

М. Капуа, Г. Крозетти, С. Фацио, Л. Ла Ротонда, А. Мастроберардино, Г. Морелло, Д. Сальваторе, М. . Schioppa, G. Susinno & E. Tassi

Dipartimento di Fisica, Università di Genova, Genova, Italy

D. Barberis, C. Caso, A. Coccaro, T. Cornelissen, S. Cuneo, M. Dameri , А. Ферретто Пароди, Г.Gagliardi, B. Osculati, F. Parodi и C. Schiavi

Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg

V. Radescu, S. Schaetzel & A. Schöning

, Ruprecht-Karls-Universität Heidelberg, Мангейм, Германия

A. Kugel, R. Maenner & N. Schroer

Dipartimento di Fisica, Università del Salento, Lecce, Italy

M. Bianco, A. Cazzato, A. Cazzato, A. Cazzato, A. Cazzato, A. Cazzato, A. Cazzato, A. Cazzato, A. Cazzato, A. Cazzato, A. Cazzato, A. Cazzato, A. Cazzato .Crupi, E. Gorini, A. Guida, S. Spagnolo & A. Ventura

Dipartimento di Fisica, Università di Milano, Milano, Italy

E. Acerbi, A. Andreazza, M.I. Бесана, Л. Карминати, Л. Делль’Аста, М. Фанти, А. Фаварето, А. Лаззаро, С. Монтесано, Л. Перини, К. Пицио, Ф. Рагуза, Г. Риволтелла, Л. Росси, М. Sorbi, R. Turra & G. Vegni

Dipartimento di Scienze Fisiche, Università di Napoli, Неаполь, Италия

A. Aloisio, MG Альвигги, В.Канале, Л. Капассо, Ф. Севенини, Дж. Чифнари, Д. делла Вольпе, Р. Джордано, П. Йенго, Л. Мерола, Э. Мусто, С. Патричелли и Э. Росси

Dipartimento di Fisica Nucleare e Teorica, Università di Pavia, Павия, Италия

M. Cambiaghi, C. Conta, S. Franchino, M. Fraternali, M. Livan, A. Negri, DM Ребуцци, А. Римольди и М. Усленги

Dipartimento di Fisica E. Fermi, Università di Pisa, Пиза, Италия

F. Bertolucci, M. Cascella, V.Кавасинни, Ф. Крешиоли, Т. Дель Прете, А. Дотти, П. Франкавилла, В. Джангиоббе, А. Лупи, Э. Маццони, К. Рода, Ф. Сарри и З. Зенонос

Departamento de Fisica Teorica y del Cosmos and CAFPE, Университет Гранады, Гранада, Испания

JA Агилар-Сааведра

Dipartimento di Fisica, Università La Sapienza, Roma, Italy

G. Artoni, P. Bagnaia, C. Bini, S. Borroni, R. Caloi, A. Cavallari, G. Ciapetti, A. Д’Орацио, К. Диониси, С.Джентиле, С. Джагу, М. Джунта, Ф. Лакава, Ф. Ло Стерцо, К. Лючи, К. Майани, С. Розати, Ф. Сафай Тегерани, А. Сидоти, Э. Сольфароли Камиллокчи, Ф. Спила и Л. Занелло

Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy

G. Aielli, P. Camarri, G. Cattani, A. Di Ciaccio, R. Di Nardo, A. Di Simone, F. Марчезе, А. Паолони и Р. Сантонико

Dipartimento di Fisica, Università Roma Tre, Рим, Италия

К. Баччи, М.Biglietti, F. Ceradini, S. Di Luise, D. Orestano, F. Pastore, F. Petrucci & F. Ruggieri

Centre National de l’Energie des Sciences Techniques Nucleaires, Рабат

H. Ghazlane

Факультет наук Semlalia Département de Physique, Université Cadi Ayyad, BP 2390 Marrakech 40000.

M. El Kacimi & D. Goujdami

Faculté des Sciences, Université Mohamed Premier и LPTPM, Oujda

J.E.Derkaoui & M. Ouchrif

Faculté des Sciences, Université Mohammed V, Rabat, Marocco

R. Cherkaoui El Moursli

Отделение субъядерной физики, Институт экспериментальной физики Словацкой академии наук, Кошице, Кошице Республика

J. Antos, D. Bruncko, J. Ferencei, E. Kladiva, M. Seman & P. ​​Strizenec

Школа физики, Университет Витватерсранда, Йоханнесбург, Южная Африка

K.JC Leney & T. Vickey

Центр Оскара Кляйна, Стокгольм, Швеция

Б. Осман, К. Клемент, К. Геллерстедт, С. Хеллман, М. Йохансен, К. Йон-Анд, Дж. Лундберг, DA Милстед, Т. Моа, Б. Нордквист, К.С. Ohm, M. Ramstedt, J. Sjolin, S. Strandberg, M. Tylmad & Z. Yang

Департамент физики и астрономии Йоркского университета, Торонто, Канада

W. Taylor

ICTP, Триест

БС Ачарья и К.Suruliz

Dipartimento di Fisica, Università di Udine, Udine, Italy

D. Cauz, M. Cobal, B. De Lotto, U. De Sanctis, C. Del Papa, M. Pinamonti & K. Shaw

Laboratorio de Instrumentacao e Fisica Experimental de Particulas — LIP, Лиссабон, Португалия

JA Агилар-Сааведра

Faculdade de Ciencias and CFNUL, Universidade de Lisboa, Lisboa, Portugal

A. Amorim, A. Gomes, P.M. Хорхе, Л. Лопес, А.Майо, А. Мораис, А. Пальма, Дж. Пина, Б. Пинто, Дж. Дж. Сараива и Дж. Сильва

CPPM, Университет Экс-Марсель и CNRS / IN2P3, Марсель, Франция

С. Арфауи

TRIUMF, Ванкувер, Британская Колумбия, Канада

Г. Азуелос, D.M. Гингрич, Ф. Окхэм, П. Савард и М.С. Веттерли

Физический факультет Калифорнийского государственного университета, Фресно, Калифорния, Соединенные Штаты Америки

H.S. Бава, Ю. Гао и А.Дж. Lowe

Факультет физики и прикладной информатики, AGH-University of Science and Technology, Краков, Польша

T.Болд и И. Грабовска-Болд

Физический факультет Коимбрского университета, Коимбра, Португалия

Дж. Карвалью, M.C.N. Fiolhais, PJ Magalhaes Martins, M. Oliveira & H. Wolters

di Napoli Parthenope, Napoli, Italy

F. Conventi & M. Della Pietra

Институт физики частиц (IPP), Канада

F Корриво, РА Макферсон, С. Робертсон, Р. Соби и Р. Дж. Teuscher

Физический факультет Ближневосточного технического университета, Анкара, Турция

B.Demirkoz

Louisiana Tech University, Растон, штат Луизиана, Соединенные Штаты Америки

R. Dhullipudi, Z.D. Гринвуд и Л. Сойер

Группа физики элементарных частиц, Монреальский университет, Монреаль, Канада

Х. Гюлер

Институт физики Академии наук Азербайджана, Баку, Азербайджан

Н. Гусейнов

Institut für Experimentalphysik, Universität Hamburg, Hamburg, Germany

T.Kono, M. Terwort & MA Wildt

Manhattan College, New York NY, Соединенные Штаты Америки

R. Konoplich

Школа физики и инженерии, Университет Сунь Ятсена, Гуаньчжоу, Китай

Z Лян Д.А. Soh & Z. Weng

Academia Sinica Grid Computing, Институт физики, Academia Sinica, Тайбэй, Тайвань

S.C. Lin

Группа физики высоких энергий, Университет Шаньдун, Шаньдун, Китай

D.Лю и З. Мэн

Калифорнийский технологический институт, Пасадена, Калифорния, Соединенные Штаты Америки

Д. Лопес Матеос, З. Маршалл и К. Перес

Отдел физики частиц, Лаборатория Резерфорда Эпплтона, Дидкот, Соединенное Королевство

C. Mattravers & M. Nash

Section de Physique, Université de Genève, Женева, Швейцария

M. Nessi

Departamento de Fisica, Universidade de Minho, Брага, Португалия

A.Онофре

Кафедра физики и астрономии, Университет Южной Каролины, Колумбия, Южная Каролина, Соединенные Штаты Америки

У. Парк, М. Пурохит и А. Триведи

Исследовательский институт ядерной физики и частиц KFKI, Будапешт, Венгрия

Г. Пастор и Й. Тот

Институт физики Ягеллонского университета, Краков, Польша

Э. Рихтер-Вас

Физический факультет Оксфордского университета, Оксфорд, Великобритания

Т.Vickey

DSM / IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, Франция

J. Yu

de Physique Nucléaire et de Hautes Energies, UPMC и Université Paris-Diderot и CNRS / IN2P3, Париж, Франция

L. Yuan

Физический факультет Нанкинского университета, Цзянсу, Китай

Дж. Чжун

Все Авторы внесли свой вклад в публикацию, по-разному участвуя в проектировании и создании детектора, написании автономного программного обеспечения, эксплуатации и калибровке детектора и анализе анализа обработанных данных.

Какова циркуляция вектора натяжения в замкнутом контуре? Теорема о циркуляции вектора напряжений. Примеры задач с решением

Циркуляция вектора напряжения — это работа, которую совершают электрические силы, когда одиночный положительный заряд движется по замкнутому пути. L

Практическое значение

Теорема циркуляции играет в магнитостатике примерно ту же роль, что и теорема Гаусса для электростатики. В частности, при наличии определенной симметрии задачи позволяет просто найти величину магнитного поля во всем пространстве для заданных токов.Например, чтобы рассчитать магнитное поле от бесконечного прямолинейного проводника с током по закону Био — Савара — Лапласа, вам потребуется вычислить неочевидный интеграл, а теорема циркуляции (с учетом осевой симметрии задачи ) позволяет дать мгновенный ответ:

26. Диполь. Дипольное поле.

Электрический дипольный момент — это векторная физическая величина, которая наряду с общим зарядом (и редко используемыми высшими мультипольными моментами) характеризует электрические свойства системы заряженных частиц (распределение зарядов) в смысле создаваемого им поля и действия внешних полей на нем.Основной характеристикой после полного заряда и положения системы в целом (ее радиус-вектора) является характеристика конфигурации зарядов системы при наблюдении на расстоянии.

Его поле. При фиксированных угловых координатах (то есть на луче, идущем от центра электрического диполя к бесконечности) напряженность статического электрического поля диполя или, в общем случае, нейтральной системы зарядов с ненулевым дипольным моментом, при на больших расстояниях r асимптотически приближается к r — 3, электрический потенциал приближается к r — 2.Таким образом, статическое поле диполя затухает на больших расстояниях быстрее, чем поле простого заряда (но медленнее, чем поле любого более высокого мультиполя).

Напряженное электрическое поле и электрический потенциал неподвижного или медленно движущегося диполя (или, в общем, нейтральной системы зарядов с ненулевым дипольным моментом) с электрическим дипольным моментом на больших расстояниях в главном приближении выражается как:

, где — единичный вектор от центра диполя в направлении точки измерения, а точка обозначает скалярное произведение.

Выражения (в том же приближении, идентично совпадающие с приведенными выше формулами) для продольной (вдоль вектора радиуса, проведенного от диполя к этой точке) и поперечной составляющей напряженности электрического поля:

где — угол между направлением вектора дипольного момента и радиус-вектором к точке. Третья компонента напряженности электрического поля — ортогональная плоскости, в которой лежат вектор дипольного момента и радиус-вектор — всегда равна нулю.

27. Структура диэлектрика. Диэлектрик во внешнем поле электронной почты. Механизмы диэлектрической поляризации

Структура диэлектрика.

Вещество, введенное в электрическое поле, может его существенно изменить. Это связано с тем, что материя состоит из заряженных частиц. В отсутствие внешнего поля частицы распределены внутри вещества таким образом, что создаваемое ими электрическое поле в среднем по объемам, включающим большое количество атомов или молекул, равно нулю.При наличии внешнего поля происходит перераспределение заряженных частиц и в веществе возникает собственное электрическое поле. Суммарное электрическое поле складывается в соответствии с принципом суперпозиции внешнего поля и внутреннего поля, созданного заряженными частицами материи.

В отличие от проводников, диэлектрики (изоляторы) не имеют свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля во всем объеме диэлектрика.

Диэлектрик во внешнем поле электронной почты.

Когда диэлектрик вводится во внешнее электрическое поле, в нем происходит определенное перераспределение зарядов, составляющих атомы или молекулы. В результате такого перераспределения на поверхности диэлектрического образца излишки нескомпенсированы , относящиеся к заряда. Все заряженные частицы, образующие макроскопические связанные заряды, по-прежнему являются частью своих атомов.

Связанные заряды создают электрическое поле, которое направлено внутрь диэлектрика противоположно вектору напряженности внешнего поля.Этот процесс называется диэлектрическая поляризация … В результате полное электрическое поле внутри диэлектрика оказывается меньше по абсолютной величине, чем внешнее поле

Физическая величина, равный модулю отношения напряженности внешнего электрического поля в вакууме к модулю Напряженность полного поля в однородном диэлектрике называется диэлектрической проницаемостью веществ .

Механизмы диэлектрической поляризации

Существует несколько механизмов поляризации диэлектриков.Основными из них являются ориентация и электронная поляризация. Эти механизмы проявляются в основном в поляризации газовых и жидких диэлектриков.

Ориентация или дипольная поляризация возникает в случае полярных диэлектриков , состоящий из молекул, центры распределения положительных и отрицательных зарядов которых не совпадают. Такими молекулами являются микроскопические электрических диполей — нейтральный набор из двух зарядов, равных по величине и противоположных по знаку, расположенных на некотором расстоянии друг от друга.Дипольным моментом обладает, например, молекула воды, а также молекулы ряда других диэлектриков (H 2 S, NO 2 и т. Д.).

В отсутствие внешнего электрического поля оси молекулярных диполей ориентированы случайным образом из-за теплового движения, так что на поверхности диэлектрика и в любом элементе объема электрический заряд в среднем равен нулю.

Когда диэлектрик вводится во внешнее поле, происходит частичная ориентация молекулярных диполей.В результате на поверхности диэлектрика появляются нескомпенсированные макроскопические связанные заряды, создающие поле, направленное против внешнего поля (рис. 1.5.3).

Поляризация полярных диэлектриков сильно зависит от температуры, поскольку тепловое движение молекул играет роль дезориентирующего фактора.

Электронный или эластичный механизм проявляется в поляризации неполярных диэлектриков, молекулы которых не обладают дипольным моментом в отсутствие внешнего поля.Под действием электрического поля молекулы неполярных диэлектриков деформируются — положительные заряды смещаются в направлении вектора, а отрицательные — в противоположном. В результате каждая молекула превращается в электрический диполь, ось которого направлена ​​вдоль внешнего поля. На поверхности диэлектрика появляются нескомпенсированные связанные заряды, создающие свою собственную направленность навстречу внешнему полю. Так происходит поляризация неполярного диэлектрика (рис.1.5.4).

Деформация неполярных молекул под действием внешнего электрического поля не зависит от их теплового движения; следовательно, поляризация неполярного диэлектрика не зависит от температуры. Примером неполярной молекулы является молекула метана CH 4. В этой молекуле четырехкратно ионизованный ион углерода C 4– расположен в центре правильной пирамиды, в вершинах которой находятся ионы водорода H +. При приложении внешнего электрического поля ион углерода смещается из центра пирамиды, и молекула имеет дипольный момент, пропорциональный внешнему полю.

Электрическое поле связанных зарядов, возникающее при поляризации полярных и неполярных диэлектриков, изменяется по модулю прямо пропорционально модулю внешнего поля. В очень сильных электрических полях эта закономерность может нарушаться, а затем возникают различные нелинейные эффекты. … В случае полярных диэлектриков в сильных полях наблюдается эффект насыщения , когда все молекулярные диполи выстраиваются вдоль силовых линий. В случае неполярных диэлектриков сильное внешнее поле, сравнимое по величине с внутриатомным полем, может значительно деформировать атомы или молекулы вещества и изменить их электрические свойства.Однако эти явления практически не наблюдаются, так как для этого необходимы поля с напряженностью порядка 10 10 –10 12 В / м. Между тем электрический пробой диэлектрика происходит гораздо раньше.

Во многих неполярных молекулах электронные оболочки деформируются при поляризации, поэтому этот механизм называется электронной поляризацией … Этот механизм универсален, так как деформация электронных оболочек под действием внешнего поля происходит в атомах, молекулах и ионах любого диэлектрика.

В случае твердых кристаллических диэлектриков так называемая ионная поляризация , при котором ионы разного знака, составляющие кристаллическую решетку, при приложении внешнего поля смещаются в противоположные стороны, в результате чего на гранях кристалла появляются связанные (нескомпенсированные) заряды. Примером такого механизма является поляризация кристалла NaCl, в котором ионы Na + и Cl — образуют две вложенные друг в друга подрешетки. В отсутствие внешнего поля каждая элементарная ячейка кристалл NaCl (см. Часть I § 3.6) электрически нейтрален и не имеет дипольного момента. Во внешнем электрическом поле обе подрешетки смещены в противоположные стороны, т.е. кристалл поляризован.

С поляризацией неоднородный диэлектрик связанных зарядов могут возникать не только на поверхности, но и в объеме диэлектрика. В этом случае электрическое поле связанных зарядов и полное поле могут иметь сложную структуру в зависимости от геометрии диэлектрика. Утверждение, что электрическое поле диэлектрика по абсолютной величине в ε раз меньше внешнего поля, строго справедливо только в случае однородного диэлектрика , заполняя все пространство, в котором создается внешнее поле.В частности:

Если в однородном диэлектрике с диэлектрической проницаемостью ε присутствует точечный заряд Q , то напряженность поля, создаваемого этим зарядом в какой-то момент, и потенциал φ в ε раз меньше, чем в вакууме:

28 . Проводников. Поле электронной почты в проводниках. Электроемкость.

Конденсатор.

Взаимодействие неподвижных зарядов осуществляется посредством электростатического поля. Электростатическое поле описывается с помощью вектора напряженности ($ \\ overline (E) $), который определяется как сила ($ \\ overline (F) $), действующая на единичный положительный заряд, помещенный в точку поля под рассмотрение:

\ [\ overline (E) = \ frac (\ overline (F)) (q) \ left (1 \ right). \\]

Электростатические силы консервативны, это означает, что их работа на замкнутом пути ($ L $) равна нулю:

, где $ \\ overline (r) $ — это движение.

Интеграл в формуле (2) называется циркуляцией вектора напряженности электростатического поля. Циркуляция вектора $ \\ overline (E) $ — это работа, которую кулоновские силы могут совершать, перемещая по контуру положительный заряд, равный единице.

Учитывая, что $ q \ ne 0 $, получаем:

\ [\ oint \ nolimits_L (\ overline (E) d \ overline (r) =) 0 \ left (3 \\ верно). \\]

Теорема о циркуляции вектора напряженности электростатического поля утверждает, что циркуляция $ \\ overline (E) $ в замкнутом контуре равна нулю.

В дифференциальной форме теорема циркуляции записывается как:

Этот тип записи (4) удобно использовать для проверки потенциальности векторного поля. Потенциальное поле является безвихревым.

Как следствие циркуляционной теоремы $ \ overline (E) $: работа при перемещении заряда из одной точки поля в другую не зависит от формы траектории движения.

Из теоремы о циркуляции следует, что линии электростатического поля не замкнуты, они начинаются с положительного заряда и заканчиваются отрицательным зарядом.

Теорема о циркуляции для вектора напряженности магнитного поля

Физическая величина ($ \ overline (H) $), которая является характеристикой магнитного поля, равной:

\ [\ overline (H) = \ frac (\ overline (B)) ((\\ mu) _0) — (\\ overline (P)) _ m (5) \\]

называется напряжённостью магнитного поля. $ \\ overline (B) $ — вектор магнитной индукции поля; $ (\\ mu) _0 $ — магнитная постоянная; $ (\ overline (P)) _ m $ — вектор намагниченности.

Циркуляция вектора напряженности магнитного поля равна алгебраической сумме токов проводимости, которые покрываются замкнутым контуром, по которому считается циркуляция:

\\ [\\ oint \\ limits_L (\\ overline (H) d \ overline (r) = \ sum (I_m) \ left (6 \ right).) \]

Если направление обхода контура связано с направлением тока посредством правило правого винта, то ток в сумме (5) стоит со знаком плюс.

В общем случае циркуляция вектора напряженности отлична от нуля, что означает, что магнитное поле является вихревым полем, а не потенциалом.

Теорема о циркуляции вектора напряженности магнитного поля доказана на основе закона Био-Савара-Лапласа и принципа суперпозиции.

Теорема о циркуляции для вектора $ \ overline (H) $ играет роль, аналогичную роли теоремы Гаусса для вектора напряженности электрического поля. Если в распределении токов есть симметрия, то с помощью циркуляционной теоремы $ \\ overline (H), $ находится сама напряженность магнитного поля.2 \ вправо) \ наверху (j) \ вправо). $

Решение. Из теоремы о циркуляции, записанной в дифференциальной форме:

следует, что если вихрь поля равен нулю, то поле является потенциальным. Используя определение ротора:

\ = \ frac (\ partial E_y) (\ partial x) \ overline (k) — \ frac (\ partial E_x) (\ partial y) \ черта (к) \ влево (1,3 \ вправо). \\]

Частные производные от $ \ overline (E) $ равны:

\ [\ frac (\\ partial E_y) (\ partial x) = A \ cdot 2x ;; \ \ frac (\ partial E_x) (\ partial y) = A \ cdot 2x \ \ left (1.4 \ правая). \\]

Подставляя (1.4) в (1.3), получаем

\ = 0. \]

Ответ. Поле потенциальное.

Пример 2

Задача. Какова циркуляция вектора напряженности магнитного поля для замкнутого контура $ L $ (рис. 1), если $ I_1 = 5 \ A ;; \ I_2 = 2 \ A ;; \ I_3 = 10 \ A ;; \ I_4 = 1 \ A? $

Решение. В основе решения задачи лежит теорема о циркуляции вектора напряженности магнитного поля:

\ [\ oint \ limits_L (\ overline (H) d \ overline (r) = \ sum (I_m) \ left (2.1 \\ right).) \\]

Цепь $ L $ покрывает три тока, поэтому:

\\ [\\ oint \\ limits_L (\\ overline (H) d \ overline (r) = I_1-I_2 + I_3.) \\]

Рассчитаем тираж:

\ [\ oint \\ limits_L (\ overline (H) d \ overline (r) = 5-2 + 10 \ u003d 13 \ (A).) \]

Ответ. $ \ oint \ limits_L (\ overline (H) d \ overline (r) = 13A \.)

$

Теорема о циркуляции

Ранее мы выяснили, что на заряд (q), находящийся в электростатическом поле, действуют консервативные силы, работа ($ A $) которых на любом замкнутом пути (L) равна ноль:

, где $ \\ overrightarrow (s) $ — вектор смещения (не путать с площадью), $ \\ overrightarrow (E) $ — вектор напряженности поля.

Для единичного положительного заряда можно записать:

Интеграл в левой части уравнения (2) — это циркуляция вектора напряжения вдоль контура L. Характерным свойством электростатического поля является циркуляция его напряженности. вектор вдоль любого замкнутого контура равен нулю. Это утверждение называется теоремой о циркуляции вектора напряженности электростатического поля.

Докажем теорему о циркуляции, исходя из того, что работа поля по перемещению заряда не зависит от траектории движения заряда в электростатическом поле, что выражается равенством:

где $ L_1 \\ и \\ L_2 $ — разные пути между точками A и B.Учтем, что при замене пределов интегрирования получаем:

Выражение (4) представляется как:

где $ L = L_1 + L_2 $. Это доказывает теорему.

Следствием теоремы о циркуляции является то, что линии напряженности электростатического поля не замкнуты. Они начинаются с положительных зарядов и заканчиваются отрицательными или уходят в бесконечность. Теорема верна именно для статических зарядов. Еще одно следствие теоремы: непрерывность касательных составляющих растяжения (в отличие от нормальных составляющих).Это означает, что составляющие натяжения, которые касаются любой выбранной поверхности в любой точке, имеют равные значения с обеих сторон поверхности.

Выберите произвольную поверхность S, которая опирается на контур L (рис. 1).

В соответствии с формулой Стокса (теорема Стокса) интеграл от ротора вектора напряжений ($ rot \\ overrightarrow (E) $), взятый по поверхности S, равен циркуляции вектора напряжений вдоль контур, на котором эта поверхность опирается:

где $ d \ overrightarrow (S) = dS \ cdot \ overrightarrow (n) $, $ \ overrightarrow (n) $ — единичный вектор, перпендикулярный отрезку dS.Ротор ($ rot \\ overrightarrow (E) $) характеризует интенсивность «вихря» вектора. Наглядное представление векторного ротора можно получить, поместив небольшую легкую крыльчатку (рис. 2) в поток жидкости. В тех местах, где ротор не равен нулю, будет вращаться крыльчатка, причем скорость ее вращения будет тем больше, чем больше проекция модуля проекции ротора на ось крыльчатки.

При практическом расчете ротора чаще всего используются следующие формулы:

Поскольку в соответствии с уравнением (6) циркуляция вектора натяжения равна нулю, получаем:

Условие (8) должно выполняться для любой поверхности S, лежащей на контуре L.Это возможно, только если подынтегральное выражение равно:

и для каждой точки поля.

По аналогии с крыльчаткой на рис. 2 представьте себе электрическую «крыльчатку». На концах такой «крыльчатки» находятся заряды q такой же величины. Система помещается в однородное поле с напряженностью E. В тех местах, где $ rot \\ overrightarrow (E) \\ ne 0 $, такое «устройство» будет вращаться с ускорением, которое зависит от проекции ротора на крыльчатку. ось. В случае электростатического поля такое «устройство» не будет вращаться ни при какой ориентации оси.Поскольку отличительной особенностью электростатического поля является то, что оно является безвихревым. Уравнение (9) представляет теорему о циркуляции в дифференциальной форме.

Пример 1

Задача: На рис. 3 показано электростатическое поле. Что вы можете сказать о характеристиках этого поля по рисунку?

Об этом поле можно сказать, что существование такого электростатического поля невозможно. Если выбрать контур (он показан пунктирной линией). Для такой схемы циркуляция вектора напряжений:

\ [\ oint \ limits_L (\ overrightarrow (E) d \ overrightarrow (s) \ ne 0) \ left (1.1 \\ right), \\]

, что противоречит теореме о циркуляции для электростатического поля. Напряженность поля определяется плотностью силовых линий, она не одинакова в разных частях поля, в результате работа в замкнутом контуре будет отличаться от нуля, следовательно, циркуляция вектора напряженности равна не ноль.

Пример 2

Задание: На основе теоремы о циркуляции показать, что тангенциальные компоненты вектора напряженности электростатического поля не изменяются при пересечении границы раздела диэлектриков.

Рассмотрим границу между двумя диэлектриками с диэлектрической проницаемостью $ (\ varepsilon) _2 \ и \ (\ varepsilon) _1 $ (рис. 4). Выберем на этой границе небольшой прямоугольный контур с параметрами a — длина, b — ширина. Ось X проходит через середины сторон b.

Для электростатического поля выполняется теорема циркуляции, которая выражается уравнением:

\\ [\ oint \\ limits_L (\\ overrightarrow (E) d \ overrightarrow (s) = 0 \\ \ \ left (2.1 \ справа).) \]

Для малых размеров контура, циркуляции вектора напряжений и в соответствии с указанным направлением обхода контура интеграл в формуле (2.1) можно представить в виде:

\ \ [\\ oint \\ limits_L (\\ overrightarrow (E) d \\ overrightarrow (s) = E_ (1x) a-E_ (2x) a + \ left \ langle E_b \ right \ rangle 2b) = 0 \\ \\ left (2,2 \ right),) \\]

где $ \ left \ langle E_b \ right \ rangle $ — среднее значение $ \ overrightarrow (E) $ в областях, перпендикулярных интерфейсу.

Из (2.2) следует, что:

\ [((E) _ (2x) -E_ (1x)) a = \ left \ langle E_b \ right \ rangle 2b \ (2.3) . \\]

Если $ b \ to 0 $, то получаем, что:

Выражение (2.4) выполняется при произвольном выборе оси X, которая лежит на границе раздела диэлектриков. Если представить вектор натяжения в виде двух составляющих (тангенциальной $ E _ (\ tau) \ $ и нормальной $ E_n $):

\ [\ overrightarrow (E_1) = \ overrightarrow (E_ (1n)) + \ overrightarrow (E_ (1 \ tau)), \ overrightarrow (E_2) = \ overrightarrow (E_ (2n)) + \ overrightarrow (E_ (2 \\ В данном случае от (2.4) запишем:

где $ E _ (\ tau i) $ — проекция вектора интенсивности на единичный вектор $ \ tau $, направленный вдоль границы раздела диэлектриков.

радиус

r с полным зарядом Q заряжается равномерно с насыпной плотностью dQ / dV  ( = заряда за единицу объема). Принимая во внимание соображения симметрии (см. Раздел 3), можно показать, что для напряженности поля вне шара будет получен тот же результат, что и в предыдущем случае (см. (82.3)). Внутри мяча напряженность поля будет другой. Сфера радиуса — r « покрывает заряд с общим зарядом Q заряжается равномерно с = 4/3 r» 3  Q » Следовательно, согласно теореме Гаусса (81.2), 4r «2 . E /  0 = 4/3 r 3  /  0. С учетом того, что  = Q / (4/3 R 3), получаем = Q » Таким образом, напряженность поля вне однородно заряженного шара описывается формулой (82.3), а внутри линейно изменяется с расстоянием

согласно выражению (82.4). График зависимости r » из /  0 = 4/3 r 3  /  0. С учетом того, что  = Q / (4/3 R 3), получаем , изображенное на рис. 130. r 5. Поле равномерно заряженного бесконечного цилиндра (резьбы).

Бесконечный цилиндр (рис.131) равномерно заряжен

r с общим зарядом Q заряжен равномерно с линейной плотностью  ( = dQ / dt — заряд на единицу длины).Из соображений симметрии следует, что линии растяжения будут направлены по радиусам круглых сечений цилиндра с одинаковой плотностью во всех направлениях относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим соосный заряженный цилиндр радиусом и высотой r . l векторный поток . E через торцы соосного цилиндра равен нулю (концы параллельны линиям натяжения), а через боковую поверхность -2 rl  эл. По теореме Гаусса (81.2) при r> R 2 rlE =  откуда  векторный поток /  0 , если

r , то замкнутая поверхность не содержит зарядов внутри, следовательно, в этой области = 0. Таким образом, напряженность поля вне равномерно заряженного бесконечного цилиндра определяется выражением (82.5), а внутри поля нет Это. /  0 = 4/3 r 3  /  0. Учитывая, что  = Q / (4/3 R 3), получаем § 83.Циркуляция вектора напряженности электростатического поля

Если в электростатическом поле точечный заряд

из точки Q ровно 1 по произвольной траектории (рис. 132) движется другой точечный заряд Q 0, затем сила, приложенная к заряду, совершает работу. Рабочая сила 2 f {! LANG-d2a33790e5bf28b33cdbf61722a06989!} по элементарному смещению dl равно

Работа при перемещении заряда Q 0 из точки 1 ровно 2

не зависит от траектории движения, а определяется только положениями исходной 1 и окончательный 2 балла.Следовательно, электростатическое поле точечного заряда равно потенциал, и электростатические силы — консервативное (см. §12).

Из формулы (83.1) следует, что работа, совершаемая при движении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, то есть

Если мы возьмем единственную положительную точку заряд как заряд, переносимый в электростатическом поле, то элементарная работа сил поля на пути d векторный поток равен через концы соосного цилиндра равен нулю (концы параллельны линиям напряжения) , а через боковую поверхность -2 d векторный поток = E векторный поток dl, где /  0 = 4/3 r 3  /  0.Учитывая, что  = Q / (4/3 R 3), получаем векторный поток = E cos — проекция вектора через торцы соосного цилиндра равна нулю (концы параллельны линиям натяжения), и через боковую поверхность -2 по направлению элементарного движения. Тогда формулу (83.2) можно записать в виде

Интеграл

, называемый циркуляцией вектора напряжения. Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю.Силовое поле со свойством (83.3) называется потенциалом . Из исчезающего вектора циркуляции через концы соосного цилиндра равен нулю (концы параллельны линиям напряжения), а через боковую поверхность -2 следует, что линии напряженности электростатического поля не могут быть замкнутые, они начинаются и заканчиваются на зарядах (соответственно положительных или отрицательных) или уходят в бесконечность.

Формула (83.3) верна только для электростатического поля.Ниже будет показано, что условие (83.3) не выполняется для поля движущихся зарядов (для него циркуляция вектора напряженности отлична от нуля).

кружок у знака интеграла в (3.14) означает, что интеграл берется по замкнутому контуру. Интеграл вида (3.14) по замкнутому контуру называется вектором обращения . Следовательно, вектор циркуляции электростатическое поле , вычислено по любому замкнутому контуру, равно нулю. Это общее свойство всех полей консервативных сил (потенциальных полей).

(3,17)

Если ввести следующее обозначение:

(3,18)

, то формула (3.17) запишется в компактном виде:

Введенный нами математический объект называется градиентным оператором , а формула (3.19) читается так: «вектор равен минус градиенту j».

Эквипотенциальные поверхности, их связь с силовыми линиями.

Из самого названия следует, что эквипотенциальных поверхностей — это поверхности с равным потенциалом … Следовательно, уравнение эквипотенциальной поверхности выглядит так:

Форма эквипотенциальных поверхностей связана с формой силовых линий: эквипотенциальных поверхностей расположены так, что в каждой точке пространства силовая линия и эквипотенциальная поверхность взаимно перпендикулярны.

Если мы договоримся нарисовать эквипотенциальные поверхности так, чтобы разность потенциалов между двумя соседними поверхностями была , то же самое , то по плотности эквипотенциальных поверхностей можно судить о величине напряженности поля.

Если разрезать эквипотенциальную поверхность плоскостью, то в разрезе мы получим линии равнопотенциальных, эквипотенциальных линий.

Проводники и диэлектрики. Заряженный проводник. Проводник во внешнем электрическом поле.

Проводники — это вещества, в которых есть свободные электрические заряды. Концентрация свободных зарядов в металлических проводниках того же порядка, что и концентрация атомов. Эти заряды могут перемещаться внутри проводника, если в нем создается электрическое поле.

Диэлектрики — это вещества, в которых почти нет свободных электрических зарядов.

В идеальной диэлектрической модели нет свободных зарядов.

Полупроводники по концентрации свободных зарядов они занимают промежуточное положение между проводниками и диэлектриками … Их концентрация свободных зарядов сильно зависит от температуры.

Если проводник заряжен, то свободные заряды в нем начнут двигаться, и они будут двигаться до тех пор, пока электрическое поле в проводнике не станет равным нулю, поскольку сила, действующая на заряд, равна:

Если, то согласно (3.16):

,

тех. все производные потенциала равны нулю, следовательно, внутри заряженного проводника потенциал постоянен, т.е. объем проводника и поверхность — эквипотенциальные.

Если E = 0 всюду внутри проводника, то поток вектора напряженности электрического поля через любую замкнутую поверхность внутри проводника равен нулю. Согласно теореме Гаусса это означает, что объемная плотность заряда внутри проводника равна нулю. Весь заряд проводника распределяется по его поверхности. Напряженность электрического поля вне проводника перпендикулярна его поверхности, поскольку она эквипотенциальна.

Возьмем небольшой участок на поверхности проводника и построим на нем «гауссовский ящик», как это делается при вычислении поля около равномерно заряженной плоскости. Внутри проводника E = 0, значит.

% PDF-1.2 % 974 0 объект > эндобдж xref 974 80 0000000016 00000 н. 0000001952 00000 н. 0000002052 00000 н. 0000002816 00000 н. 0000003159 00000 п. 0000003575 00000 н. 0000003698 00000 н. 0000003974 00000 н. 0000005081 00000 н. 0000005367 00000 н. 0000006482 00000 н. 0000006505 00000 н. 0000008480 00000 н. 0000008503 00000 н. 0000010265 00000 п. 0000010288 00000 п. 0000012085 00000 п. 0000012108 00000 п. 0000012393 00000 п. 0000013508 00000 п. 0000015341 00000 п. 0000015364 00000 п. 0000015479 00000 п. 0000017322 00000 п. 0000017345 00000 п. 0000019170 00000 п. 0000019193 00000 п. 0000019460 00000 п. 0000019750 00000 п. 0000021566 00000 п. 0000021590 00000 п. 0000021612 00000 п. 0000021634 00000 п. 0000023488 00000 п. 0000023511 00000 п. 0000024019 00000 п. 0000024043 00000 п. 0000026394 00000 п. 0000026418 00000 п. 0000028203 00000 п. 0000028227 00000 п.