Курс физики. Том II. Учение об электричестве
Курс физики. Том II. Учение об электричестве
ОглавлениеЧАСТЬ ТРЕТЬЯ. § 2. Количество электричества. Закон Кулона § 3. Атомное строение электричества § 4. Напряженность электрического поля § 5. Теорема Острогдадского — Гаусса § 6. Вектор электрической индукции § 7. Примеры применения теоремы Остроградского — Гаусса § 8. Потенциал электрического поля § 9. Формулы электростатики в практической системе единиц ГЛАВА II. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ § 10. Распределение электричества по поверхностй заряженных проводников § 11. Электризация проводников в поле и деформация поля проводниками § 12. Контактная разность потенциалов § 13. Электроемкость § 14. Расчет электроемкости конденсаторов § 16. Энергия поля § 17. Электрометры § 18. О природе электрических явлений ГЛАВА III. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ § 19. Дипольная и электронная поляризация диэлектриков. Сегнетоэлектрики § 20. Деформация поля диэлектриками § 21. Электрическая восприимчивость § 22.  Электронная теория диэлектриков Электронная теория диэлектриков§ 23. Пьезоэлектрические и пироэлектрические явления § 24. Электроконвекционные явления (электрофорез, электроэндосмос и др.) ГЛАВА IV. ПОСТОЯННЫЙ ТОК § 25. Величина тока. Электродвижущая сила и напряжение § 27. Закон Джоуля — Ленца § 28. Дифференциальная форма законов Ома и Джоуля — Ленца. Соотношение аналогии между проводимостью и емкостью ГЛАВА V. ТОК В МЕТАЛЛАХ § 29. Сведения об электропроводности. Термометры сопротивления, болометры, тензометры § 30. Закон Видемана — Франца. Теория электропроводности металлов § 31. Сверхпроводимость § 32. Термоэлектрические явления и их применение § 33. Зависимость термоэлектродвижущей силы от температуры спаев. Явление Пельтье ГЛАВА VI. ТОК В ПОЛУПРОВОДНИКАХ § 34. Полупроводники § 35. Понятие о зонной теории электропроводности § 36. Применения полупроводников § 37. Электролиз. Законы Фарадея.  Электрохимические эквиваленты. Потенциалы разложения Электрохимические эквиваленты. Потенциалы разложения§ 38. Вторичные реакции на электрэдах. Применения электролиза § 39. Подвижность ионов и электропроводность растворов § 40. Гальванические элементы. Электрохимическая природа коррозии § 41. Электродные потенциалы § 42. Аккумуляторы § 43. Свободная энергия гальванической цепи. Концентрационные элементы ГЛАВА VIII. ТОК В ГАЗАХ § 44. Ионизация и электропроводность газов § 45. Типы и механизм разряда в газах § 46. Катодные и анодные лучи § 47. Тлеющий разряд § 49. Искровой разряд. Молния ГЛАВА IX. ТОК ЭЛЕКТРОННОЙ ЭМИССИИ. ЭЛЕКТРОННЫЕ ЛАМПЫ § 50. Термоэлектронная эмиссия. Формула Ричардсона — Дёшмена § 51. Торможение электронного потока. Рентгеновы трубки § 52. Пустотные выпрямители тока (диоды, кенотроны) § 53. Усилительные электронные лампы (триоды) § 54. Фотоэлектрический эффект. Фотоэлементы. Фотореле § 55. Вторичная электронная эмиссия.  Электронные умножители Электронные умножители§ 56. Динатронный эффект. Экранированные радиолампы ГЛАВА X. МАГНИТНОЕ ПОЛЕ § 57. Исторические сведения. Закон Кулона для магнитных полюсов § 58. Магнитные величины и соотношения, аналогичные электрическим § 60. Магнитное поле тока § 61. Закон Био и Савара § 62. Магнитодвижущая сила. Поток индукции электромагнита § 63. Магнитные свойства веществ и их использование § 64. Электронная теория магнетизма ГЛАВА XI. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ТОК § 65. Формула Ампера и ее трактовка по Фарадею § 66. Работа, производимая током при перемещении проводника в магнитном поле. Электромоторы § 67. Отклоняющее действие магнитного поля на электронный поток (в вакууме и в металле) § 68. Электродинамические измерительные приборы. Гальванометры, Осциллографы § 69. Формулы электродинамики в практической системе единиц ГЛАВА XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ  Электромагнитная индукция Электромагнитная индукция§ 71. Закон Ленца. Картина электромагнитного поля по Фарадею § 72. Закон Фарадея. Индукционное измерение магнитного потока и магнитодвижущей силы. Вихревые токи § 73. Явление самоиндукции. Индуктивность. Законы нарастания и спада тока при включении и выключении цепи § 74. Энергия магнитного поля тока. Индуктивность и энергия электромагнита. Индуктивность кабеля § 75. Взаимная индуктивность. Энергия взаимодействия токов. Коэффициент взаимной индукции катушек с общим сердечником § 77. Электромагнитное происхождение массы электрона ГЛАВА XIII. ПЕРЕМЕННЫЙ ТОК § 78. Генерирование переменного тока § 79. Работа генератора электрической энергии на нагрузку Эффективные значения напряжения и величины тока § 80. Емкостное сопротивление и индуктивное сопротивление § 81. Активные и реактивные токи. Коэффициент мощности (cos f). Потери (tg b) § 82. Обобщенный закон Ома § 83.  Электрический резонанс Электрический резонанс§ 84. Трансформация тока § 85. Трехфазный ток. Синхронные и асинхронные моторы § 86. Индуктор § 87. Колебательный контур § 88. Вибратор Герца (возбуждение колебательного контура индуктором). Токи Тесла § 89. Электромагнитные волны. Вектор Умова — Пойнтинга § 90. Излучение электрического диполя. Волны в двухпроводной линии. Антенны § 91. Распространение электромагнитных волн. Роль ионосферы. «Радиоокно» в космос § 92. Ламповые генераторы электрических колебаний § 93. Модуляция электрических колебаний § 94. Прием, детектирование и усиление радиосигналов. Супергетеродины § 95. Преобразование звуковых колебаний в электрические и электрических в звуковые. Электрозапись и воспроизведение звука § 97. Сантиметровые волны и их распространение в волноводах § 98. Радиолокация. Генерирование ультракоротких волн (клистроны и магнетроны) |
Решение задач на закон Ома и законы Кирхгофа
Методы анализа, основанные на законах Ома и законах Кирхгофа
Закон Ома устанавливает зависимость между напряжением и током на пассивной ветви, а также позволяет определить ток по известным потенциалам на концах ветви с источником напряжения.
Законы Кирхгофа применяют для нахождения токов в ветвях линейных и нелинейных схем при любом законе изменения во времени токов и напряжений.
Метод эквивалентных преобразований. При эквивалентных преобразований отдельные участки электрической цепи заменяются более простыми. Эквивалентность преобразования состоит в том, что токи и напряжения в непреобразованной части схемы не изменяются.
Последовательное упрощение схемы продолжается до ее преобразования в одноконтурную схему, после чего для расчета используется закон Ома.
Метод эквивалентных преобразований используется для нахождения внутреннего сопротивления эквивалентного генератора.
При помощи метода эквивалентных преобразований облегчают расчет расчет нелинейной цепи, упростив линейную часть цепи эквивалентными преобразованиями.
Принято пользоваться приведенным ниже алгоритмом метода законов Кирхгофа.
1. Произвольно выбирают положительные направления токов в ветвях и обозначают их на схеме.
2. Составляют уравнения по первому закону Кирхгофа: на одно уравнение меньше числа узлов (для последнего узла уравнение будет зависимым от предыдущих уравнений).
3. Выбирают независимые (главные) контуры и направление их обхода. Удобно для всех контуров выбрать одинаковое направление обхода.
4. Записывают уравнения по второму закону Кирхгофа для выбранных контуров.
5. Решая полученную систему уравнений, определяют искомые токи.
Задача 1.1. Определить эквивалентное сопротивление цепи между зажимами a и b при разомкнутом и замкнутом ключе К методом эквивалентных преобразований (рис. 1.1, a).
Рис. 1.1
Решение. Сохраняя топологию схемы, трансформируем ее к виду, удобному для анализа (отправная точка – потенциалы узлов c и d равны между собой).
Из рис. 1.1, б следует:
1. При разомкнутом ключе К
Rab=R1⋅R3R1+R3+(R47+R5+R6)⋅R2(R47+R5+R6)+R2.» role=»presentation»>Rab=R1⋅R3R1+R3+(R47+R5+R6)⋅R2(R47+R5+R6)+R2.Rab=R1⋅R3R1+R3+(R47+R5+R6)⋅R2(R47+R5+R6)+R2.
2. При замкнутом ключе К
R47=R1⋅R3R1+R3+R47⋅R2R47+R2,» role=»presentation»>R47=R1⋅R3R1+R3+R47⋅R2R47+R2,R47=R1⋅R3R1+R3+R47⋅R2R47+R2,
где
R47=R4⋅R7R4+R7.» role=»presentation»>R47=R4⋅R7R4+R7.R47=R4⋅R7R4+R7.
Задача 1.2. Определить методом эквивалентных преобразований сопротивление цепи между зажимами a и b при разомкнутом и замкнутом ключе К для схемы, изображенной на рис. 1.2.
Рис. 1.2
Решение. Совершим поворот части схемы относительно зажимов c и d. В результате получим (рис. 1.3):
Рис. 1.3
1. При разомкнутом ключе К
Rab=(R1+R3)⋅(R2+R4)(R1+R3)+(R2+R4). » role=»presentation»>Rab=(R1+R3)⋅(R2+R4)(R1+R3)+(R2+R4).Rab=(R1+R3)⋅(R2+R4)(R1+R3)+(R2+R4).
» role=»presentation»>Rab=(R1+R3)⋅(R2+R4)(R1+R3)+(R2+R4).Rab=(R1+R3)⋅(R2+R4)(R1+R3)+(R2+R4).
2. При замкнутом ключе К
Rab=R1⋅R4R1+R4+R2⋅R3R2+R3.» role=»presentation»>Rab=R1⋅R4R1+R4+R2⋅R3R2+R3.Rab=R1⋅R4R1+R4+R2⋅R3R2+R3.
Задача 1.3. Найти сопротивление между зажимами a и b для схемы, изображенной на рис. 1.4.
Рис. 1.4
Решение. К точке 2 подходят условные «начало» сопротивления R2 и «концы» сопротивлений Rlи R3.
К точке 3 подходят «начала» сопротивлений R1 и R3 и «конец» сопротивления R2.
Но тогда, все «начала» сопротивлений и все их «концы» соединяются соответственно в одни точки. А значит, по определению, имеем параллельное соединение приемников (рис. 1.5).
Рис. 1.5
Таким образом, сопротивление между зажимами a и b:
Rab=1Yab=11R1+1R2+1R3. » role=»presentation»>Rab=1Yab=11R1+1R2+1R3.Rab=1Yab=11R1+1R2+1R3.
» role=»presentation»>Rab=1Yab=11R1+1R2+1R3.Rab=1Yab=11R1+1R2+1R3.
Задача 1.4. Найти сопротивление R13, R14, R17 между различными парами вершин куба, ребра которого имеют заданное сопротивление R (рис. 1.6).
Рис. 1.6
Решение. Задачу проще всего решить методом амперметра и вольтметра. Суть метода заключается в следующем. Если к фиксированным точкам схемы a и b подвести условно известное напряжение Uab и определить ток I во внешней цепи, то искомое сопротивление Rab = Uab/I. При этом напряжение Uab (показание вольтметра) в соответствии с законами Кирхгофаопределяется как функция тока I (показание амперметра).
1. Расчетная схема для определения сопротивления R13 имеет вид, представленный на рис. 1.7.
1.7.
Рис. 1.7
В силу симметрии потенциалы точек 2 и 6 (4 и 8) равны между собой. Поэтому токи в ребрах. 2 – 6 и 4 – 8 отсутствуют.
Перераспределение токов I1 и I2 легко находится из первого закона Кирхгофа и соответствует рисунку 1.7.
Соотношение между токами найдем из второго закона Кирхгофа:
U14=U15+U58+U84;I1⋅R=I2⋅R+12I2⋅R+0=32I2⋅R.» role=»presentation»>U14=U15+U58+U84;I1⋅R=I2⋅R+12I2⋅R+0=32I2⋅R.U14=U15+U58+U84;I1⋅R=I2⋅R+12I2⋅R+0=32I2⋅R.
Откуда:
I1=32I2;  I2=23I1.» role=»presentation»>I1=32I2; I2=23I1.I1=32I2; I2=23I1.
А значит, общий ток
I=2I1+I2=2I1+23I1=83I1.» role=»presentation»>I=2I1+I2=2I1+23I1=83I1.I=2I1+I2=2I1+23I1=83I1.
Но
U13=I⋅R13=83I1⋅R13=U12+U23=2I1⋅R.» role=»presentation»>U13=I⋅R13=83I1⋅R13=U12+U23=2I1⋅R.U13=I⋅R13=83I1⋅R13=U12+U23=2I1⋅R.
Откуда, сокращая на I1, имеем 8/3·R13 = 2R. Или, что-то же, искомое R13 = 3/4·R.
2. Расчетная схема для определения сопротивления R14 имеет вид, представленный на рис. 1.8.
Рис. 1.8
В силу симметрии токи в ребрах 1 – 2, 1 – 4, 2 – 3 и 4 – 3 равны между собой. А значит, в соответствии с первым законом Кирхгофа, токи в ребрах 2 – 6 и 4 – 8 отсутствуют.
Перераспределение неизвестных токов I1, I2, I3, I4 находится из первого закона Кирхгофа (и симметрии цепи) и соответствует рис. 1.8.
Поскольку падение напряжения
U23=U26+U67+U73;I4⋅R=I3⋅R+2I3⋅R+I3⋅R=4I3⋅R,» role=»presentation»>U23=U26+U67+U73;I4⋅R=I3⋅R+2I3⋅R+I3⋅R=4I3⋅R,U23=U26+U67+U73;I4⋅R=I3⋅R+2I3⋅R+I3⋅R=4I3⋅R,
то, сокращая на R, имеем:
I4=4I3″ role=»presentation»>I4=4I3I4=4I3
или
I3=14I4. » role=»presentation»>I3=14I4.I3=14I4.
» role=»presentation»>I3=14I4.I3=14I4.
Ток
I2=I3+I4=14I4+I4=54I4″ role=»presentation»>I2=I3+I4=14I4+I4=54I4I2=I3+I4=14I4+I4=54I4
или
I4=45I2.» role=»presentation»>I4=45I2.I4=45I2.
Но
U14=U15+U58+U84;I1⋅R=I2⋅R+I4⋅R+I2⋅R=I2⋅R+54I2⋅R+I2⋅R=145I2⋅R.» role=»presentation»>U14=U15+U58+U84;I1⋅R=I2⋅R+I4⋅R+I2⋅R=I2⋅R+54I2⋅R+I2⋅R=145I2⋅R.U14=U15+U58+U84;I1⋅R=I2⋅R+I4⋅R+I2⋅R=I2⋅R+54I2⋅R+I2⋅R=145I2⋅R.
Откуда, сокращая на R, имеем:
I1=145I2″ role=»presentation»>I1=145I2I1=145I2
или
I2=514I1.» role=»presentation»>I2=514I1.I2=514I1.
Но
U14=I⋅R14=(I1+2I2)⋅R14=(I1+1014I1)⋅R14=2414I1⋅R14=I1⋅R.» role=»presentation»>U14=I⋅R14=(I1+2I2)⋅R14=(I1+1014I1)⋅R14=2414I1⋅R14=I1⋅R.U14=I⋅R14=(I1+2I2)⋅R14=(I1+1014I1)⋅R14=2414I1⋅R14=I1⋅R.
Или, что то же, искомое R14 = 14/24·R = 7/12·R.
3. Расчетная схема для определения сопротивления R17 имеет вид, представленный на рис. 1.9.
Рис. 1.9
В силу диагональной симметрии схемы полный ток I = 3I1.
Падение напряжения
U17=U14+U43+U37;I⋅R17=I1⋅R+12I1⋅R+I1⋅R=52I1⋅R.» role=»presentation»>U17=U14+U43+U37;I⋅R17=I1⋅R+12I1⋅R+I1⋅R=52I1⋅R.U17=U14+U43+U37;I⋅R17=I1⋅R+12I1⋅R+I1⋅R=52I1⋅R.
Откуда искомое сопротивление R17 = 5/6·R.
Задача 1.5. Определить методом эквивалентных преобразований токи в ветвях цепи (рис. 1 10,а) и показание вольтметра, включенного между точками c и d, считая, что его сопротивление во много раз превышает сопротивление каждого из элементов цепи.
Чему равно показание амперметра, включенного между точками c и d, сопротивление которого считать равным нулю?
Рис. 1.10
1.10
Сопротивления элементов цепи: R1 =10 Ом, R2 = R3 = R5 = 25 Ом и R4 = 50 Ом, а приложенное к ней напряжение U = 120 В.
Решение. Расчет показания вольтметра. Из условия вытекает, что его включение не оказывает влияния на распределение токов в цепи. Для расчета токов сначала определяем эквивалентное сопротивление всей цепи (рис. 1.10, а):
R=R1+(R2+R4)⋅(R3+R5)(R2+R4)+(R3+R5)=10+75⋅50125=40   Ом.» role=»presentation»>R=R1+(R2+R4)⋅(R3+R5)(R2+R4)+(R3+R5)=10+75⋅50125=40 Ом.R=R1+(R2+R4)⋅(R3+R5)(R2+R4)+(R3+R5)=10+75⋅50125=40 Ом.
В неразветвленной части цепи протекает ток
I1=UR=12040=3  A.» role=»presentation»>I1=UR=12040=3 A.I1=UR=12040=3 A.
Токи, протекающие через сопротивления (R2 + R4) и (R3 + R5) можно найти различными способами.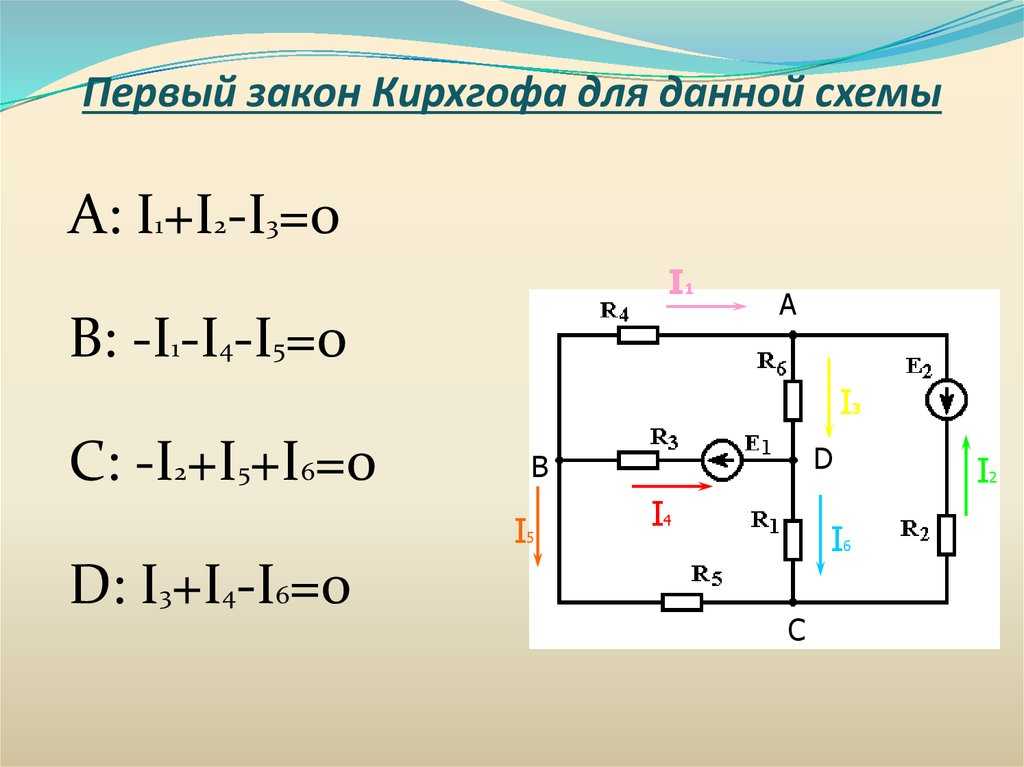
1. В параллельных ветвях токи распределяются обратно пропорционально их сопротивлениям (формула разброса токов):
I2=I1⋅R3+R5(R2+R4)+(R3+R5)=3⋅50125=1,2  A;I3=I1⋅R2+R4(R2+R4)+(R3+R5)=3⋅75125=1,8  A.» role=»presentation»>I2=I1⋅R3+R5(R2+R4)+(R3+R5)=3⋅50125=1,2 A;I3=I1⋅R2+R4(R2+R4)+(R3+R5)=3⋅75125=1,8 A.I2=I1⋅R3+R5(R2+R4)+(R3+R5)=3⋅50125=1,2 A;I3=I1⋅R2+R4(R2+R4)+(R3+R5)=3⋅75125=1,8 A.
2. Найдем напряжение на зажимах параллельных ветвей:
Uab=I1⋅(R2+R4)⋅(R3+R5)(R2+R4)+(R3+R5)=3⋅75⋅50125=90   B.» role=»presentation»>Uab=I1⋅(R2+R4)⋅(R3+R5)(R2+R4)+(R3+R5)=3⋅75⋅50125=90 B.Uab=I1⋅(R2+R4)⋅(R3+R5)(R2+R4)+(R3+R5)=3⋅75⋅50125=90 B.
Токи в ветвях с сопротивлениями R2 + R4 и R3 + R5 равны:
I2=UabR2+R4=9075=1,2  A;  I3=UabR3+R5=9050=1,8  A.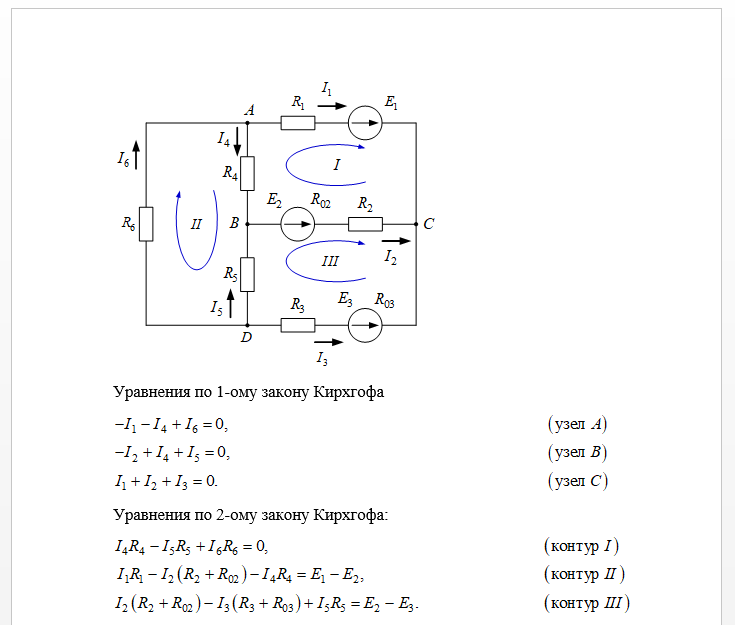 » role=»presentation»>I2=UabR2+R4=9075=1,2 A; I3=UabR3+R5=9050=1,8 A.I2=UabR2+R4=9075=1,2 A; I3=UabR3+R5=9050=1,8 A.
» role=»presentation»>I2=UabR2+R4=9075=1,2 A; I3=UabR3+R5=9050=1,8 A.I2=UabR2+R4=9075=1,2 A; I3=UabR3+R5=9050=1,8 A.
Напряжение на зажимах параллельных ветвей может быть найдено как разность между приложенным напряжением и падением напряжения на сопротивлении R1: Uab = U – R1·I1.
Найдем показание вольтметра, равное напряжению между точками с и d:
UV=Ucd=−I2⋅R2+I3⋅R3=−1,2⋅25+1,8⋅25=15  B.» role=»presentation»>UV=Ucd=−I2⋅R2+I3⋅R3=−1,2⋅25+1,8⋅25=15 B.UV=Ucd=−I2⋅R2+I3⋅R3=−1,2⋅25+1,8⋅25=15 B.
Наконец, вычислим ток, проходящий через амперметр; он равен току короткого замыкания I’cd (рис. 1.10, б). Для его нахождения вычислим токи:
I′1=UR1+R2⋅R3R2+R3+R4⋅R5R4+R5=14447  A;I′2=I′1⋅R3R2+R3=7247  A;  I′4=I′1⋅R5R4+R5=4847  A.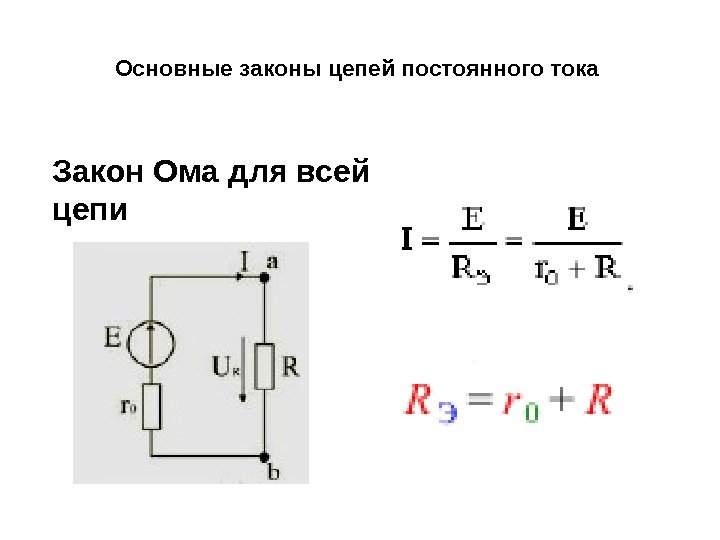 » role=»presentation»>I′1=UR1+R2⋅R3R2+R3+R4⋅R5R4+R5=14447 A;I′2=I′1⋅R3R2+R3=7247 A; I′4=I′1⋅R5R4+R5=4847 A.I′1=UR1+R2⋅R3R2+R3+R4⋅R5R4+R5=14447 A;I′2=I′1⋅R3R2+R3=7247 A; I′4=I′1⋅R5R4+R5=4847 A.
» role=»presentation»>I′1=UR1+R2⋅R3R2+R3+R4⋅R5R4+R5=14447 A;I′2=I′1⋅R3R2+R3=7247 A; I′4=I′1⋅R5R4+R5=4847 A.I′1=UR1+R2⋅R3R2+R3+R4⋅R5R4+R5=14447 A;I′2=I′1⋅R3R2+R3=7247 A; I′4=I′1⋅R5R4+R5=4847 A.
Искомый ток, проходящий через амперметр,
IA=I′cd=I′2−I′4=2447=0,51  A.» role=»presentation»>IA=I′cd=I′2−I′4=2447=0,51 A.IA=I′cd=I′2−I′4=2447=0,51 A.
Задача 1.6. В схеме рис. 1.11 заданы сопротивления приемников, величины ЭДС и источника тока отдельных ветвей. Рассчитать неизвестные токи, ЭДС E2 и сопротивление R5, пользуясь законами Кирхгофа.
Рис. 1.11
Правильность решения проверить по балансу мощностей. Для наружного контура построить потенциальную диаграмму и определить показание вольтметра.
Решение
1. Всего в схеме пять ветвей, неизвестных токов I1, I2, I5 – три, неизвестных величин E2 и R5 – две, для нахождения которых составам три уравнения по первому закону Кирхгофа и два – по второму закону Кирхгофа:
для узла  b:   J=I4+I5;для узла  d:   −I5−I3+I1=0;для контура  I:   I5R5−I4R4=E3+E4;для контура  II:   I1R1+I2R2=E1+E2−E3. » role=»presentation»>для узла b: J=I4+I5;для узла d: −I5−I3+I1=0;для контура I: I5R5−I4R4=E3+E4;для контура II: I1R1+I2R2=E1+E2−E3.для узла b: J=I4+I5;для узла d: −I5−I3+I1=0;для контура I: I5R5−I4R4=E3+E4;для контура II: I1R1+I2R2=E1+E2−E3.
» role=»presentation»>для узла b: J=I4+I5;для узла d: −I5−I3+I1=0;для контура I: I5R5−I4R4=E3+E4;для контура II: I1R1+I2R2=E1+E2−E3.для узла b: J=I4+I5;для узла d: −I5−I3+I1=0;для контура I: I5R5−I4R4=E3+E4;для контура II: I1R1+I2R2=E1+E2−E3.
Из первых трех уравнений находим токи:
I5=J−I4=4−2=2  A;I1=I5+I3=2+3=5  A;I2=−J+I1=−4+5=1  A.» role=»presentation»>I5=J−I4=4−2=2 A;I1=I5+I3=2+3=5 A;I2=−J+I1=−4+5=1 A.I5=J−I4=4−2=2 A;I1=I5+I3=2+3=5 A;I2=−J+I1=−4+5=1 A.
из четвертого уравнения
R5=E3+E4+I4⋅R4I5=10+6+142=15  Ом.» role=»presentation»>R5=E3+E4+I4⋅R4I5=10+6+142=15 Ом.R5=E3+E4+I4⋅R4I5=10+6+142=15 Ом.
Величину E2 определяем из последнего уравнения:
E2=I1⋅R1+I2⋅R2−E1+E3=5⋅10+10⋅1−100+10=−30  B. » role=»presentation»>E2=I1⋅R1+I2⋅R2−E1+E3=5⋅10+10⋅1−100+10=−30 B.E2=I1⋅R1+I2⋅R2−E1+E3=5⋅10+10⋅1−100+10=−30 B.
» role=»presentation»>E2=I1⋅R1+I2⋅R2−E1+E3=5⋅10+10⋅1−100+10=−30 B.E2=I1⋅R1+I2⋅R2−E1+E3=5⋅10+10⋅1−100+10=−30 B.
2. Для построения потенциальной диаграммы найдем потенциалы всех точек контура abcdea, приняв исходный потенциал точки a равным нулю:
φe=φa−I1⋅R1=0+5⋅10=50  B;φd=φe−E1=50−100=−50  B;φb=φd+I5⋅R5=−50+2⋅15=−20  B.» role=»presentation»>φe=φa−I1⋅R1=0+5⋅10=50 B;φd=φe−E1=50−100=−50 B;φb=φd+I5⋅R5=−50+2⋅15=−20 B.φe=φa−I1⋅R1=0+5⋅10=50 B;φd=φe−E1=50−100=−50 B;φb=φd+I5⋅R5=−50+2⋅15=−20 B.
3. По найденным потенциалам строим потенциальную диаграмму, откладывая по оси ординат потенциалы точек, а по оси абсцисс – сопротивления участков (рис. 1.12).
Рис. 1.12
3. Из потенциальной диаграммы легко определить разность потенциалов между точками b и c Ubc = 70 В, что и будет показывать вольтметр.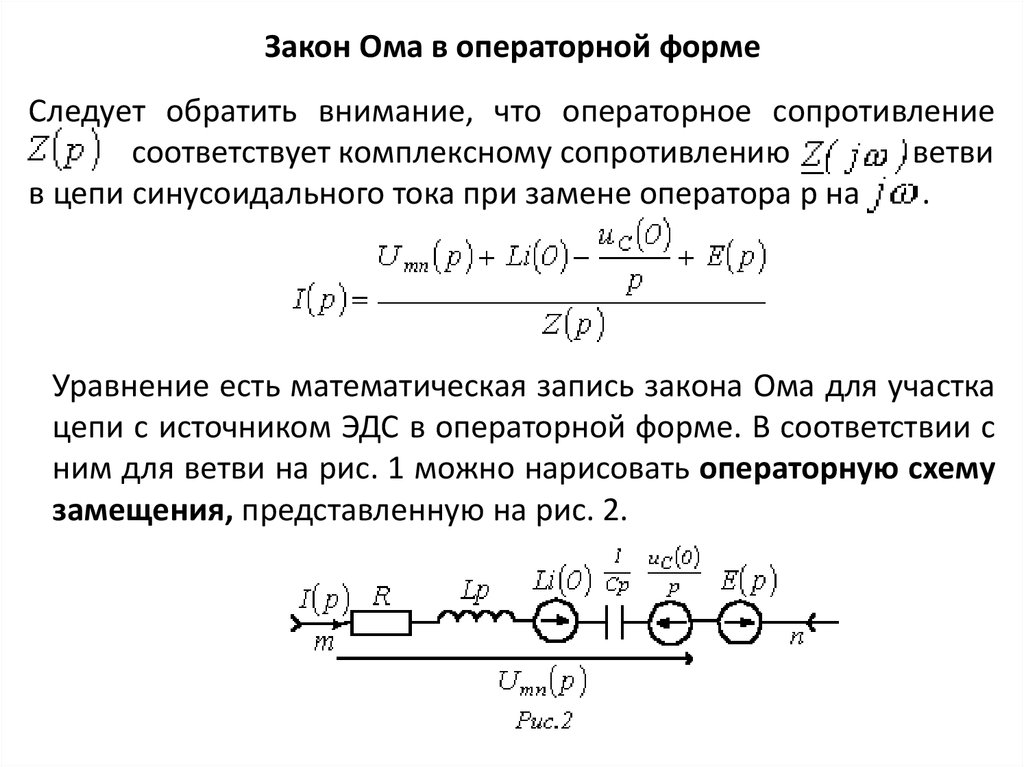
4. Произведем проверку баланса мощностей:
Pисточников=E1⋅I1+E2⋅I2+E3⋅(−I3)+E4⋅(−I4)+Uba⋅J;Pпотребителей=I12⋅R1+I22⋅R2+I42⋅R4+I52⋅R5.» role=»presentation»>Pисточников=E1⋅I1+E2⋅I2+E3⋅(−I3)+E4⋅(−I4)+Uba⋅J;Pпотребителей=I21⋅R1+I22⋅R2+I24⋅R4+I25⋅R5.Pисточников=E1⋅I1+E2⋅I2+E3⋅(−I3)+E4⋅(−I4)+Uba⋅J;Pпотребителей=I12⋅R1+I22⋅R2+I42⋅R4+I52⋅R5.
В этом уравнении нам неизвестно напряжение на зажимах источника тока Uba, которое легко найти из потенциальной диаграммы: Uba = –20 В. С учетом этого
Pисточников=100⋅5+(−30)⋅1+10⋅(−3)+6⋅(−2)+(−20)⋅4=348  Вт;Pпотребителей=52⋅10+12⋅10+32⋅0+22⋅7+22⋅15=348  Вт;Pисточников=Pпотребителей=348  Вт. » role=»presentation»>Pисточников=100⋅5+(−30)⋅1+10⋅(−3)+6⋅(−2)+(−20)⋅4=348 Вт;Pпотребителей=52⋅10+12⋅10+32⋅0+22⋅7+22⋅15=348 Вт;Pисточников=Pпотребителей=348 Вт.Pисточников=100⋅5+(−30)⋅1+10⋅(−3)+6⋅(−2)+(−20)⋅4=348 Вт;Pпотребителей=52⋅10+12⋅10+32⋅0+22⋅7+22⋅15=348 Вт;Pисточников=Pпотребителей=348 Вт.
» role=»presentation»>Pисточников=100⋅5+(−30)⋅1+10⋅(−3)+6⋅(−2)+(−20)⋅4=348 Вт;Pпотребителей=52⋅10+12⋅10+32⋅0+22⋅7+22⋅15=348 Вт;Pисточников=Pпотребителей=348 Вт.Pисточников=100⋅5+(−30)⋅1+10⋅(−3)+6⋅(−2)+(−20)⋅4=348 Вт;Pпотребителей=52⋅10+12⋅10+32⋅0+22⋅7+22⋅15=348 Вт;Pисточников=Pпотребителей=348 Вт.
Назначение Целью этого лабораторного эксперимента является исследование закона Ома и закона Кирхгофа. Фон
При постоянной разности потенциалов , применяется к проводящему материалу, плотность тока, , установлено, что прямо пропорциональна напряженности электрического поля, , создается внутри материала. Константа пропорциональности известна как электропроводность, и отношение известно как
Электрическое поле, созданное разностью потенциалов, устанавливает ток, , в проводнике прямо пропорциональна разности потенциалов. Учитывая сопротивление материала заданной длины, более полезная и знакомая форма закона Ома может быть получена из уравнения 1, а именно
где константа пропорциональности,
,
это сопротивление проводника.
В этой лабораторной работе мы будем использовать уравнение 2 и различные резисторы, чтобы получить четкое понимание цепей постоянного тока. Вы должны знать, что резисторы подключены в серии , как показано на рисунке 1, имеют эквивалентное сопротивление , , следующее
И наоборот, резисторы на рисунке 2 соединены через параллельно и эквивалентное сопротивление для этой конфигурации определяется выражением
Снова приложенная ЭДС создает ток, протекающий в цепи, но на этот раз
одинаковым является падение напряжения на каждом резисторе, а не ток.
При анализе более сложных цепей постоянного тока полезно использовать два легко формулируемых принципы, известные как Правила Кирхгофа . Их можно сформулировать следующим образом:
Цели
Оборудование и установка
Советы и предостережения
Помощь онлайн
Шаблон лабораторного отчета Каждая лабораторная группа должна
скачать шаблон лабораторного отчета
и заполните соответствующую информацию при выполнении эксперимента . Например, группа в лаборатории таблица № 5, работающая над экспериментом по закону идеального газа, переименует свой файл шаблона как «5 Gas Law.doc» . Вопросы о подталкивании Эти подталкивающих вопросов предназначены для получить ответ от вашей группы и проверить ваш TA , как вы делаете лабораторию . Они следует ответить в лабораторной тетради. Общие подталкивания
Вопросы Эти вопросы также можно найти в шаблоне описания лабораторной работы.
Примечания ТА
Данные, результаты и графики Введите пароль ТА, чтобы просмотреть образцы данных и результаты этого
эксперимент (формат MS Excel): Ответы на вопросы Введите пароль ТА для просмотра ответов на вопросы из этого
эксперимент (формат MS Word): Эксперименты с КУПОЛОМ На данный момент нет
КУПОЛ эксперименты
связанных с этим экспериментом. Если у вас есть вопрос или комментарий, отправьте электронное письмо координатору лаборатории: Джерри Хестер | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | Copyright © 2006. Университет Клемсона. Все права защищены. Фото предоставлено Corel Draw. Последнее изменение 27.01.2006 14:25:18 |
Закон Кирхгофа о напряжении действительно не работает?
Густав Кирхгоф (1824-1887) был опытным прусским физиком и приборостроителем, наиболее известным своими законами о цепях тока и напряжения. Первый закон Кирхгофа, известный как закон токов, утверждает, что алгебраическая сумма токов в сети проводников, сходящихся в одной точке, равна нулю. Второй закон Кирхгофа, известный как его закон напряжения, гласит, что сумма напряжений с учетом их полярности в замкнутой цепи равна нулю.
Первый закон Кирхгофа, известный как закон токов, утверждает, что алгебраическая сумма токов в сети проводников, сходящихся в одной точке, равна нулю. Второй закон Кирхгофа, известный как его закон напряжения, гласит, что сумма напряжений с учетом их полярности в замкнутой цепи равна нулю.
Текущий закон Кирхгофа основан на сохранении заряда, измеряемого в кулонах, то есть тока, проинтегрированного по времени (умноженного на). SPICE и подобное программное обеспечение для моделирования цепей используют матричную версию токового закона Кирхгофа вместе с законом Ома для выполнения узлового анализа более сложных цепей. Таким образом, вы могли бы подумать, что на данный момент в законах Кирхгофа мало спорного. Это подводит нас к серии видеороликов на YouTube, которые, как ни странно, исследуют идею о том, что законы Кирхгофа могут не выполняться при определенных обстоятельствах.
Видео, с которого началась эта тема, не было снято кем-то из научных кругов. Это был бывший M.I. T. Профессор Уолтер Левин, который утверждал, что учить тому, что закон напряжения Кирхгофа является абсолютным, является преступлением, потому что на самом деле он не всегда верен. Далее он говорит, что подавляющее большинство учебников по физике ошибочны в этом вопросе, и что многие профессора физики и электротехники, которые не согласны с ним, неправы, и, наконец, если вы не согласны с ним, вы просто не понимаете закон Фарадея. .
T. Профессор Уолтер Левин, который утверждал, что учить тому, что закон напряжения Кирхгофа является абсолютным, является преступлением, потому что на самом деле он не всегда верен. Далее он говорит, что подавляющее большинство учебников по физике ошибочны в этом вопросе, и что многие профессора физики и электротехники, которые не согласны с ним, неправы, и, наконец, если вы не согласны с ним, вы просто не понимаете закон Фарадея. .
Левин поясняет свою точку зрения, описывая 1-вольтовую батарею, соединенную последовательно с двумя резисторами номиналами 100 и 900 Ом с общим сопротивлением 1000 Ом. Таким образом будет условный ток через цепь 1 мА. Ключевым моментом, который следует отметить, является то, где в этой цепи находится вольтметр для измерения конкретных параметров. Подключив вольтметр к резистору 900 Ом, вы получите показание 900 мВ; через резистор 100 Ом даст показание 100 мВ. Конечно, закон напряжения Кирхгофа говорит, что источник напряжения должен суммироваться с падением напряжения на сопротивлениях. Все идет нормально.
Все идет нормально.
Затем Левин удаляет батарею из цепи, так что она просто состоит из петли, содержащей два резистора. Рядом с этой схемой он вводит катушку последовательно с выключателем и батареей. Когда переключатель замыкается, это вызывает всплеск тока через катушку, которая создает магнитное поле. Со временем это магнитное поле увеличивается. Возрастающее магнитное поле индуцирует ток в замкнутом контуре, содержащем два первоначальных резистора. По мере увеличения магнитного поля увеличивается и ток в контуре с двумя резисторами. Теперь предположим, что в определенный момент времени возрастающее магнитное поле индуцирует ток силой 1 мА в контуре с двумя резисторами. Таким образом, будет 1 мА через 900 Ом дает 900 мВ и 1 мА через 100 Ом дает 100 мВ, всего 1 В.
Таким образом, мы имеем два падения напряжения в замкнутой цепи. Но в этой цепи нет источника напряжения, по крайней мере, такого, который подключен напрямую. Таким образом, сумма падений напряжения плюс (в данном случае несуществующих) источников напряжения не равна нулю, как указывает закон Кирхгофа. Отсюда и полемика.
Отсюда и полемика.
Конечно, в действительности провода двухрезисторной замкнутой цепи представляют собой вторичную обмотку трансформатора. Первичная обмотка трансформатора представляет собой цепь батареи/переключателя/катушки. В момент времени, когда в петле индуцируется 1 мА, мы все еще видим 100 и 900 мВ, индуцированный между двумя резисторами. Следует отметить, что вторичный контур резистора/трансформатора можно рассматривать как параллельную цепь, в которой вторичная обмотка трансформатора параллельна двум резисторам. Правило параллельных цепей заключается в том, что напряжение везде одинаково. Таким образом, на двух резисторах есть один вольт, один вольт на вторичной обмотке трансформатора.
Теперь предположим, что мы останавливаем время, мысленный эксперимент, который позволяет нам анализировать изменение напряжения в цепи, как в цепи постоянного тока. В этом случае вторичная обмотка трансформатора может быть смоделирована как 1-вольтовая батарея. Тогда мы все равно увидим 900 и 100 мВ падают на два резистора. Сложение двух падений напряжения с суммой источника 1 В до нуля, как указывает закон Кирхгофа.
Сложение двух падений напряжения с суммой источника 1 В до нуля, как указывает закон Кирхгофа.
Опять же, пока все хорошо. Но в мысленном эксперименте профессора Левина он указывает, что провода между двумя резисторами являются сверхпроводниками и, следовательно, не имеют сопротивления. Таким образом, провода, составляющие вторичную обмотку трансформатора, имеют сопротивление, равное нулю. Другими словами, у нас есть напряжение на чем-то, что имеет нулевое сопротивление. Но по закону Ома не может быть напряжения на чем-то, что имеет нулевое сопротивление. Отсюда проблема с законом Кирхгофа.
Видеоблогеры, такие как Боб Дюамель из RSD Academy и Мехди Садагдар из ElectroBoom, говорят, что это неправильное понимание закона Ома. Здесь мы подытожим объяснение, представленное в видео Боба Дюамеля. Дюамель начинает с указания на то, что в первоначальном эксперименте Георга Ома в качестве источника напряжения использовалась термопара. Ом обнаружил, что его знаменитое уравнение не будет работать, если он не допустит, что сам источник напряжения имеет сопротивление. И с этим сопротивлением нужно было обращаться так, как если бы оно было последовательно с источником. Сегодня, когда мы пишем закон Ома для цепи, мы обычно смешиваем сопротивление источника с остальным сопротивлением цепи.
И с этим сопротивлением нужно было обращаться так, как если бы оно было последовательно с источником. Сегодня, когда мы пишем закон Ома для цепи, мы обычно смешиваем сопротивление источника с остальным сопротивлением цепи.
Что касается схемы в мысленном эксперименте, подразумевается, что два отрезка провода, служащие вторичной обмоткой трансформатора, должны быть смоделированы как источник плюс сопротивление источника. Если считать провода сверхпроводниками, то сопротивление их источника равно нулю. Но сопротивление источника последовательно с источником, а не через него. Следовательно, если мы предположим, что сопротивление источника равно нулю, мы просто имеем идеальный источник напряжения с нулевым внутренним сопротивлением. Следовательно, закон Ома остается в силе.
Левин сделал тот же аргумент для другой простой цепи, состоящей из источника напряжения, переключателя и последовательной цепи, состоящей из катушки индуктивности, конденсатора и резистора. В этом случае он предполагает, что катушка индуктивности состоит из сверхпроводящего провода и, таким образом, падает ноль вольт, когда переключатель замыкается, замыкая цепь. Таким образом, он говорит, что закон Ома предсказывает ноль вольт на сверхпроводящем индукторе.
Таким образом, он говорит, что закон Ома предсказывает ноль вольт на сверхпроводящем индукторе.
Однако, как объясняет Дюамель, индуктор ведет себя как источник напряжения, когда он накапливает энергию и пытается передать ее в направлении, противоположном направлению исходного тока. Таким образом, катушка индуктивности, хранящая энергию, имеет сопротивление источника, последовательное с напряжением источника, и, следовательно, напряжение действительно появляется на сверхпроводящей катушке индуктивности.
Профессор Левин в своем видео предполагает, что те, кто с ним не согласен, не понимают консервативных и неконсервативных направлений. Консервативный характер электрического поля означает, что линейный интеграл электрического поля вдоль замкнутого пути равен нулю. В качестве простого примера рассмотрим схему, состоящую из двух последовательно соединенных 1-вольтовых батарей с двумя резисторами по 1 Ом. Начиная с отрицательной клеммы первой батареи, энергия возрастает от нуля до 1 В через первую батарею, снова возрастает с 1 В до 2 В через положительную клемму второй батареи, затем падает на один вольт при прохождении через первую батарею. резисторе, затем, наконец, падает с 1 В до нуля вольт, проходя через второй резистор. Таким образом, в консервативном поле (или петле) мы получаем потенциал и используем его для работы.
резисторе, затем, наконец, падает с 1 В до нуля вольт, проходя через второй резистор. Таким образом, в консервативном поле (или петле) мы получаем потенциал и используем его для работы.
Неконсервативное поле — это поле, в котором интеграл по некоторому пути не равен нулю. Здесь рассмотрим катушку в схеме первого примера. Когда на него подается напряжение, он создает изменяющееся магнитное поле, которое, в свою очередь, вызывает электрическое поле. И электрическое поле имеет вращательную составляющую. Электрическое поле можно представить серией 1-вольтовых батарей, расположенных по кругу вокруг провода катушки. Ключевым моментом является то, что нельзя определить, где находится точка с нулевым напряжением в кругу батарей. Таким образом, во время движения по кругу не происходит увеличения или уменьшения потенциала.
Интерпретация этой модели заключается в том, что электрон в поле воспринимает вращательную силу в 1 вольт. Теперь предположим, что в поле есть проволочная петля, несущая электроны. Теперь предположим, что в проводе произошел обрыв. Вольтметр, помещенный через разрыв в проводе, измеряет напряжение, которое можно использовать для совершения работы. Поскольку петля теперь является источником напряжения, она должна иметь последовательное сопротивление. Таким образом, поле E, которое перемещает ток, все еще неконсервативно, но потенциал, развивающийся через зазор, консервативен. Если через зазор поместить резистор, работа будет совершаться при протекании через него тока. Таким образом, мы имеем консервативную схему, встроенную в неконсервативное поле.
Теперь предположим, что в проводе произошел обрыв. Вольтметр, помещенный через разрыв в проводе, измеряет напряжение, которое можно использовать для совершения работы. Поскольку петля теперь является источником напряжения, она должна иметь последовательное сопротивление. Таким образом, поле E, которое перемещает ток, все еще неконсервативно, но потенциал, развивающийся через зазор, консервативен. Если через зазор поместить резистор, работа будет совершаться при протекании через него тока. Таким образом, мы имеем консервативную схему, встроенную в неконсервативное поле.
Наконец, профессор Левин присоединил два разных щупа осциллографа к оригинальной петле с двумя резисторами. Оба зонда были прикреплены в одной и той же точке; то есть оба положительных щупа на одной стороне соединения с двумя резисторами, оба соединения заземления осциллографа на другой стороне соединения с двумя резисторами. Но когда переключатель замыкал ближайшую катушку, две результирующие трассы всплесков напряжения отличались друг от друга, хотя оба соединения находились в одной и той же точке цепи.


 правила использования резисторов в цепях постоянного тока, соединенных последовательно и параллельно.
правила использования резисторов в цепях постоянного тока, соединенных последовательно и параллельно. Не все материалы подчиняются этому соотношению, но те
которые, например, большинство металлов, известны как омические материалы . Мы
видно из этого соотношения, что единица сопротивления, Ом , определяется как
Не все материалы подчиняются этому соотношению, но те
которые, например, большинство металлов, известны как омические материалы . Мы
видно из этого соотношения, что единица сопротивления, Ом , определяется как Для резисторов, соединенных последовательно, ток через каждый
резистор идентичен. Если известны сопротивления и сила тока,
падение напряжения на каждом резисторе можно определить из уравнения 2.
Для резисторов, соединенных последовательно, ток через каждый
резистор идентичен. Если известны сопротивления и сила тока,
падение напряжения на каждом резисторе можно определить из уравнения 2. Затем можно определить ток через каждую ветвь цепи, используя
Уравнение 2.
Затем можно определить ток через каждую ветвь цепи, используя
Уравнение 2. Когда ток встречается с переходом, сумма
токи, входящие в соединение, должны быть равны сумме токов
выезд с развязки.
Когда ток встречается с переходом, сумма
токи, входящие в соединение, должны быть равны сумме токов
выезд с развязки.
 Измерьте токи в цепи и
падение напряжения на каждом элементе цепи и показать, что кривая Кирхгофа
К этой схеме применяется правило напряжения (т. е. уравнение 7).
Измерьте токи в цепи и
падение напряжения на каждом элементе цепи и показать, что кривая Кирхгофа
К этой схеме применяется правило напряжения (т. е. уравнение 7). Обратите внимание, нет необходимости регулировать
цепь, как только она будет правильно подключена.
Обратите внимание, нет необходимости регулировать
цепь, как только она будет правильно подключена. Снова см.
Раздел «Советы и предостережения».
Снова см.
Раздел «Советы и предостережения».
 Все электрические
с цепями следует обращаться осторожно!
Все электрические
с цепями следует обращаться осторожно!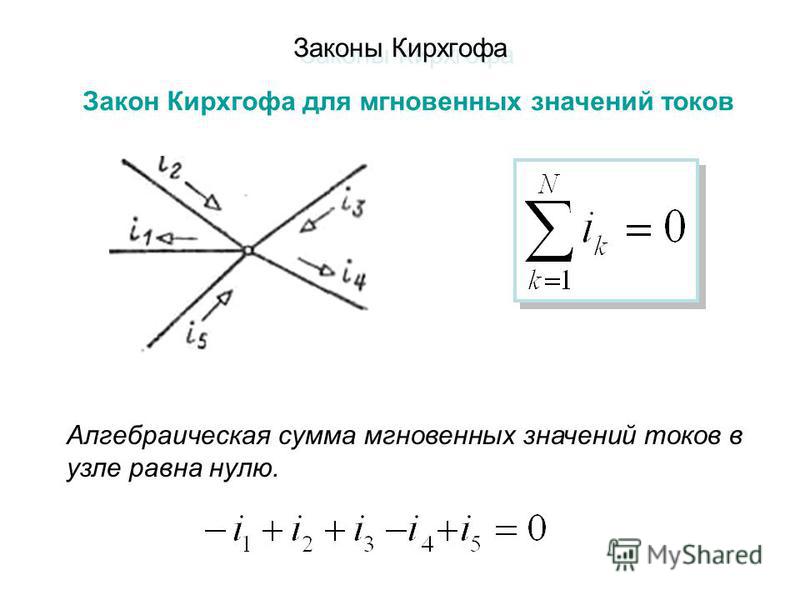
 Каждый человек в группе
следует распечатать раздел «Вопросы» и ответить на них индивидуально.
Поскольку каждая лабораторная группа сдает электронную копию лабораторного отчета, обязательно переименуйте файл шаблона лабораторного отчета. Соглашение об именах такое же, как
следует:
Каждый человек в группе
следует распечатать раздел «Вопросы» и ответить на них индивидуально.
Поскольку каждая лабораторная группа сдает электронную копию лабораторного отчета, обязательно переименуйте файл шаблона лабораторного отчета. Соглашение об именах такое же, как
следует: Здесь мы предполагаем, что источник питания не имеет внутреннего сопротивления.
Здесь мы предполагаем, что источник питания не имеет внутреннего сопротивления. Может
вы думаете об умном способе настройки вашей схемы, чтобы упростить ее
измерить ток, втекающий в каждую ветвь?
Может
вы думаете об умном способе настройки вашей схемы, чтобы упростить ее
измерить ток, втекающий в каждую ветвь?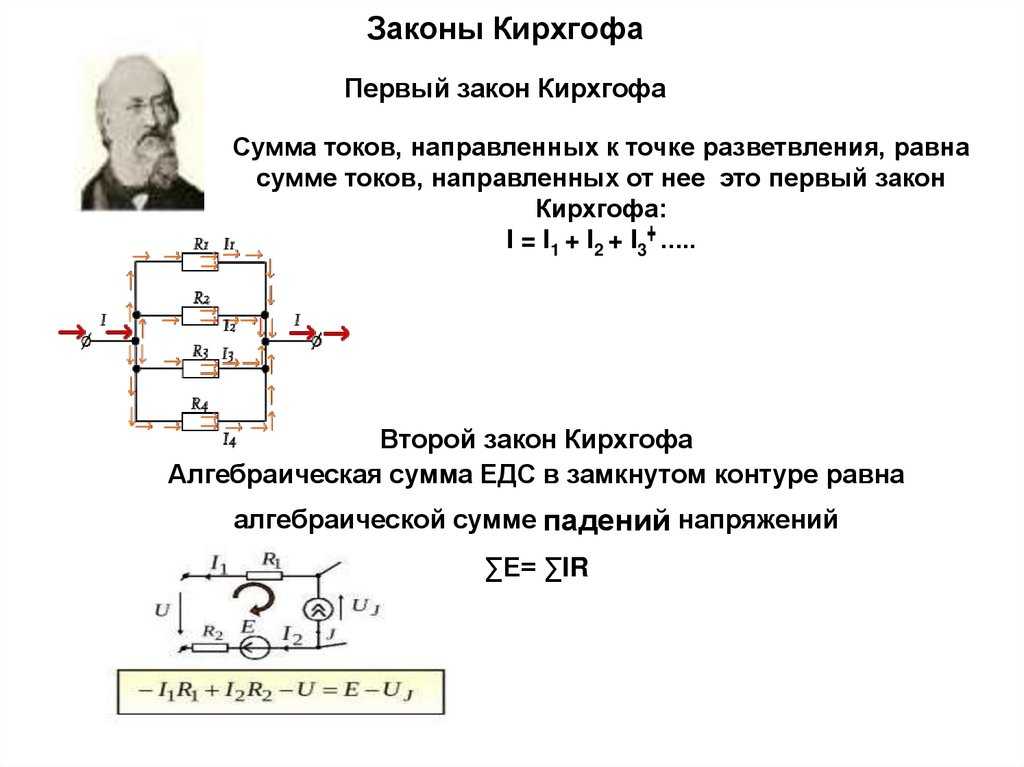 На них должны ответить
каждой особи группы. Это не командная деятельность. Каждый человек должен
приложить свою копию к лабораторному отчету непосредственно перед передачей лабораторной работы вашему
ТА.
На них должны ответить
каждой особи группы. Это не командная деятельность. Каждый человек должен
приложить свою копию к лабораторному отчету непосредственно перед передачей лабораторной работы вашему
ТА.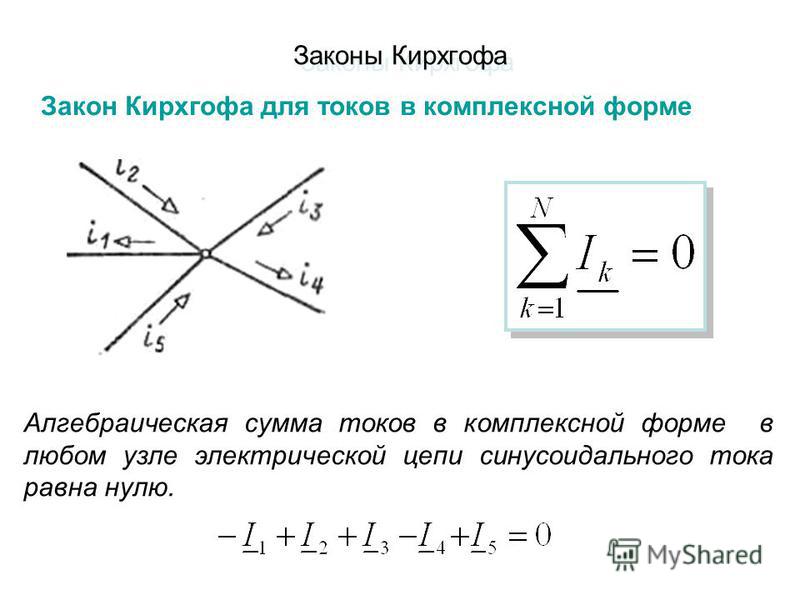 Каковы значения токов через каждую лампочку, если
?
Предположим, что лампочки идентичны.
Каковы значения токов через каждую лампочку, если
?
Предположим, что лампочки идентичны.