Закон Ома в интегральной и дифференциальной форме
Нужна помощь в написании работы?
Узнать стоимость
Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС)
|
(7.6.1) |
Для однородного линейного проводника выразим R через ρ:
|
, |
(7.6.2) |
ρ – удельное объемное сопротивление; = .
Найдем связь между и в бесконечно малом объеме проводника – закон Ома в дифференциальной форме.
В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов движутся в направлении действия силы, т.е. вектор плотности тока и вектор напряженности поля сонаправлены(рис. 7.6).
7.6).
: Исходя из закона Ома (7.6.1), имеем
А мы знаем, что или . Отсюда можно записать
|
, |
(7.6.3) |
это запись закона Ома в дифференциальной форме.
Здесь – удельная электропроводность., Размерность σ – .
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.
Расчет стоимостиГарантииОтзывы
Плотность тока можно выразить через заряд электрона е, количество зарядов n и дрейфовую скорость :
.
Обозначим , тогда ;
|
(7. |
Теперь, если удельную электропроводность σ выразить через е, n и b: то вновь получим выражение закона Ома в дифференциальной форме:
-вектор плотности тока
Закон Джоуля Ленца
Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину напряженности электрического поля
Математически может быть выражен в следующей форме:
где — мощность выделения тепла в единице объёма, — плотность электрического тока, — напряжённость электрического поля, σ — проводимость среды, а точкой обозначено скалярное произведение.
Поможем написать любую работу на аналогичную тему
Реферат
Закон Ома в интегральной и дифференциальной форме
От 250 руб
Контрольная работа
Закон Ома в интегральной и дифференциальной форме
От 250 руб
Курсовая работа
Закон Ома в интегральной и дифференциальной форме
От 700 руб
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Поделись с друзьями
|
Заглавная страница
КАТЕГОРИИ: Археология Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 7 из 18Следующая ⇒ Подставив выражение для сопротивления R=pl/S в закон Ома I=U/R, получим I/S=U/pl, где величина, обратная удельному сопротивлению, называется удельной электрической проводимостью вещества проводника. Ее единица — сименс на метр (См/м). Учитывая, что U/l=E – напряженность электрического поля в проводнике, I/S=j – плотность тока, формулу I/S=U/pl можно записать в виде j= E j= E – это выражение – закон Ома в дифференциальной форме. Плотность тока в любой точке пространства пропорциональна напряженности поля в этой точке. (если поля не слишком большие). J= Закон Ома в интегральной форме Умножим скалярно на dl : ; -закон Ома для неоднородного участка Для однородного =0 => Для замкнутой( =0):
Закон Джоуля-Ленца в дифференциальной форме Рассмотрим однородный проводник, к концам которого приложено напряжение U . собой перемещение заряда dq под действием электрического поля, то работа тока dA=Udq=IUdt Если сопротивление проводника R, то, используя закон Ома, получим dA= Если ток проходит по неподвижному металлическому проводнику, то вся работа тока идет на его нагревание и, по закону сохранения энергии dq=dA. Таким образом dq=IUdt= Это выражение представляет собой закон Джоуля-Ленца. Выделим в проводнике элементарный цилиндрический объем dV=dSdl(ось цилиндра совпадает с направлением тока), сопротивление которого . По закону Джоуля-Ленца, за время dt в этом объеме выделится теплота Количество теплоты, выделяющееся за единицу времени в единице объема, называется удельной тепловой мощностью тока. Она равна: Используя дифференциальную форму закона Ома и соотношение p=1/y, получим Формулы и называют законом Джоуля-Ленца в дифференциальной форме. Билет №17 Классическая электронная теория электропроводности металлов и ее опытные обоснования. Вывод законов Ома и Джоуля-Ленца из электронных представлений. Закон Видемана-Франца. Затруднения классической теории электропроводности металлов. 1) Носителями тока в металлах являются свободные электроны (Первый из таких опытов, подтверждающих то, что электрон – носитель заряда—опыт Рикке, в котором в течение года электрический ток пропускался через три последовательно соединенных с тщательно отшлифованными торцами металлических цилиндра (Сu, Аl, Сu) одинакового радиуса. Несмотря на то что общий заряд, прошедший через эти цилиндры, достигал огромного значения (3,5-10+6 Кл), никаких, даже микроскопических, следов переноса не обнаружилось. Это явилось экспериментальным доказательством того, что ионы в металлах не участвуют в переносе электричества, а перенос заряда в металле осуществляется частицами, которые являются общими для всех металлов.) 2) Свободные электроны ведут себя как идеальный электронный газ. теплового движения электронов , которая для T=300K равна 1.1*10+5 м/с. Это скорость теплового движения электронов, которое является хаотическим, не может привести к возникновению тока.
3) При наложении внешнего электрического поля на металлический проводник кроме теплового движения электронов возникает их упорядоченное движение, т. е. возникает электрический ток. Среднюю скорость <V> упорядоченного движения электронов можно оценить согласно формуле для плотности тока: j= ne<V>. <V><<<U>, т.е. даже при очень больших плотностях тока средняя скорость упорядоченного движения электронов, обусловливающего электрический ток, значительно меньше их скорости теплового движения. Поэтому при вычислениях результирующую скорость (<V>+<U>) можно заменять скоростью теплового движения <U>. Закон Ома. Пусть в металлическом проводнике существует электрическое поле. Напряженностью E= const. Co стороны поля заряд е испытывает действие силы F = eE и приобретает ускорение a=F/m=eE/m. Таким образом, во время свободного пробега электроны движутся равноускоренно, приобретая к концу свободного пробега скорость где <t> — среднее время между двумя последовательными соударениями с ионами решетки. Согласно теории Друде, в конце свободного пробега электрон, сталкиваясь с ионами решетки, отдает им накопленную в поле энергию, поэтому скорость его упорядоченного движения становится равной нулю. Следовательно, средняя скорость направленного движения электрона Классическая теория металлов не учитывает распределения электронов по скоростям, поэтому среднее время <t> свободного пробега определяется средней длиной свободного пробега <l> и средней скоростью движения электронов относительно кристаллической решетки проводника, равной <U>+<V> (<U>— средняя скорость теплового движения электронов). <V>=eE<l>/(2m<U>) Плотность тока в металлическом проводнике, откуда видно, что плотность тока пропорциональна напряженности поля, т. е. получи ли закон Ома в дифференциальной форме.
Закон Джоуля-Ленца К концу свободного пробега электрон под действием поля приобретает дополнительную кинетическую энергию . При соударении электрона с ионом эта энергия полностью передается решетке и идет на увеличение внутренней энергии металла, т. е. на его нагревание. За единицу времени электрон испытывает с узлами решетки в среднем <z> столкновений: <z>=<U>/<l> Если п — концентрация электронов, то в единицу времени происходит n < z > столкновений и решетке передается энергия w=n<z><E>, которая идет на нагревание проводника. Таким образом энергию, передаваемую решетке в единице объема проводника за единицу времени Величина w является удельной тепловой мощностью тока. пропорциональности между w в по есть удельная проводимость у; следовательно, выражение — закон Джоуля — Ленца в дифференциальной форме. Закон Видемана-Франца Видеманом и Францем экспериментально установлен закон, согласно , где -постоянная, зависящая от рода металла. Элементарная классическая теория электропроводности металлов позволила найти значение , где k — постоянная Больцмана. Это значение хорошо согласуется с опытными данными. Однако, как оказалось впоследствии, это согласие теоретического значения с опытным случайно; Лоренц, применив к электронному газу статистику Максвелла — Больцмана, учтя тем самым распределение электронов скоростям, получил, что привело к резкому расхождению теории c опытом. Таким образом, классическая теория электропроводности металлов объяснила законы Ома и Джоуля — Ленца, а также дала качественное объяснение закона Видемана — Франца. Рассмотрим некоторые из них. Температурим зависимость сопротивления. Из формулы удельной проводимости следует, что сопротивление металлов, т. е. величина, обратно пропорциональная у, должна возрастать пропорционально Этот вывод электронной теории противоречит опытным данным, Оценка средней длины свободного пробега электронов в металле. Чтобы получить у, совпадающие с опытными значениями, надо принимать </> значительно больше истинных, другими словами, предполагать, что электрон проходит без соударений с ионами решетки сотни междоузельных расстояний, что не согласуется с теорией Друде — Лоренца. Теплоемкость металлов. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемкости электронного газа. Указанные расхождения теории с опытом можно объяснить тем, что движение в металлах подчиняется не законам классической механики, а законам квантовой механики и, следовательно, поведение электронов проводимости надо описывать не статистикой Максвелла-Больцмана, а квантовой статистикой. Недостатки классической электронной теории 1) Учет распределения скоростей электронов (по Максвелу) приводит к худшему согласованию с экспериментальными результатами. 2) Температурная зависимость электропроводности металлов не совпадает с экспериментальной Теория: Эксперимент: 3) Чтобы получить численное совпадение для в теории с экспериментом, надо считать, что составляет примерно 100 межатомных расстояний. 4) Вопрос о теплоемкости Согласно МКТ: C=6/2R+3/2R у металлов больше C=6/2R у неметаллов (т. Малярная теплоемкость всех твердых тел одинакова n=6/2R Вывод: Классическая теория электропроводности многого не учитывает
Тема №18 ⇐ Предыдущая234567891011Следующая ⇒ Читайте также: Алгоритмические операторы Matlab Конструирование и порядок расчёта дорожной одежды Исследования учёных: почему помогают молитвы? Почему терпят неудачу многие предприниматели? |
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 192; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
электромагнетизм — Закон Фарадея: интегральные и дифференциальные формы
Задавать вопрос
спросил
Изменено 2 года, 11 месяцев назад
Просмотрено 13 тысяч раз
$\begingroup$
Рассмотрим как интегральное, так и дифференциальное уравнения, выражающие закон Фарадея (3-е уравнение Максвелла):
$$\oint_{\partial \Sigma} \mathbf E \cdot d\mathbf l = -\frac{d}{ dt}\iint_{\Sigma} \mathbf B \cdot d\mathbf S $$
А
$$\nabla \times \mathbf E = -\frac{\partial \mathbf B}{\partial t}$ $
Мне они кажутся немного контрастными. Если мы посмотрим на первый, то увидим, что изменение во времени потока магнитного поля порождает индуцированное напряжение: предположим, что это изменение осуществляется путем изменения поверхности S во времени.
Если мы посмотрим на первый, то увидим, что изменение во времени потока магнитного поля порождает индуцированное напряжение: предположим, что это изменение осуществляется путем изменения поверхности S во времени.
Соответственно ротора Е не будет, так как нет изменения во времени магнитного поля (а только его потока).
Другая ситуация такова: мы меняем во времени S и B, но так, чтобы поток оставался постоянным (например, мы соответственно уменьшаем S и увеличиваем B). В этом случае будет ротор Е, а не индуцированное напряжение.
Где решение?
- электромагнетизм
- электромагнитное излучение
- магнитные поля
- электрические поля
- уравнения Максвелла
$\endgroup$
2
$\begingroup$
Я думаю, важно знать, что две формы закона Фарадея математически эквивалентны только тогда, когда поверхность остается постоянной (если поверхность зависит от времени, см. https://en.m.wikipedia.org/wiki/Faraday% 27s_закон_индукции#Доказательство).
https://en.m.wikipedia.org/wiki/Faraday% 27s_закон_индукции#Доказательство).
Начиная с дифференциальной формы закона Фарадея $$\nabla\times E=-\frac{\partial B}{\partial t}$$ Это местное заявление. Сначала проинтегрируем в обе стороны по произвольной поверхности $\Sigma$, $$\int_{\Sigma}\nabla\times E \cdot da=-\int_{\Sigma}\frac{\partial B}{\partial t} \cdot da$$ В левой части приведенного выше уравнения мы используем теорему Стокса, $\int_{\Sigma}\nabla\times E \cdot da=\oint_{\partial \Sigma} E \cdot dl$, где $\partial \ Sigma$ — граница поверхности. В правой части мы утверждаем, что поверхность не меняется со временем, поэтому знак производной может быть перемещен за пределы знака интеграла; кроме того, интеграл теперь является только функцией времени, поэтому оправдано использование символа полной производной. Итак, мы получаем $$\oint_{\partial \Sigma} E \cdot dl=-\frac{d}{dt}\int_{\Sigma}B \cdot da$$ что является интегральной формой закона Фарадея.
$\endgroup$
4
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Вывод в интегральной и дифференциальной формах
Электричество и магнетизм
Уравнения Максвелла Уравнения Максвелла — это основные уравнения электромагнетизма, которые представляют собой совокупность закона Гаусса для электричества, закона Гаусса для магнетизма, закона Фарадея для электромагнитной индукции и закона Ампера для токов в проводниках. Уравнения Максвелла дают математическую модель электрических, оптических и радиотехнологий, таких как производство электроэнергии, электродвигатели, беспроводная связь, радары, линзы и т. д.
Эти уравнения объясняют, как магнитные и электрические поля создаются зарядами.
Эти уравнения являются частью всеобъемлющей и симметричной теории электромагнетизма, которая необходима для понимания электромагнитных волн, оптики, радио- и телепередачи, микроволновых печей и поездов на магнитной подушке.
Четыре уравнения Максвелла для свободного пространства:
Первое уравнение Максвелла (закон Гаусса для электричества)
Закон Гаусса утверждает, что поток, проходящий через любую замкнутую поверхность, равен 1/ε0, умноженному на общий заряд, заключенный в этой поверхности .
Интегральная форма 1-го уравнения Максвелла
Интегральная форма 1-го уравнения Максвелла.
Первое уравнение Максвелла в дифференциальной форме
Оно называется дифференциальной формой первого уравнения Максвелла.
Второе уравнение Максвелла (закон Гаусса для магнетизма)
Закон Гаусса для магнетизма утверждает, что суммарный поток магнитного поля через замкнутую поверхность равен нулю, поскольку монополи магнита не существуют.
второе уравнение МаксвеллаТретье уравнение Максвелла (закон электромагнитной индукции Фарадея)
Согласно закону электромагнитной индукции Фарадея
третье уравнение МаксвеллаЧетвертое уравнение Максвелла (закон Ампера)
Величина магнитного поля в любой точке прямо пропорциональна к силе тока и обратно пропорционально расстоянию точки от прямых проводников называется законом Ампера.


 6.4)
6.4)

 За время dt через сечение проводника переносится заряд dq = Idt . Так как ток представляет
За время dt через сечение проводника переносится заряд dq = Idt . Так как ток представляет


 <V><<<U>, поэтому <t>=<l>/<U>
<V><<<U>, поэтому <t>=<l>/<U> Коэффициент
Коэффициент Однако она помимо рассмотренных противоречий в законе Видемана- Франца столкнулась еще с рядом трудностей при объяснении различных опытных данных.
Однако она помимо рассмотренных противоречий в законе Видемана- Франца столкнулась еще с рядом трудностей при объяснении различных опытных данных. Поэтому атомная (т. е. на 1 моль) теплоемкость металла должна быть значительно большей. Наличие электронов проводимости не сказывается на значении теплоемкости, что не объясняется классической электронной теорией.
Поэтому атомная (т. е. на 1 моль) теплоемкость металла должна быть значительно большей. Наличие электронов проводимости не сказывается на значении теплоемкости, что не объясняется классической электронной теорией. к. нет электрического газа)
к. нет электрического газа) 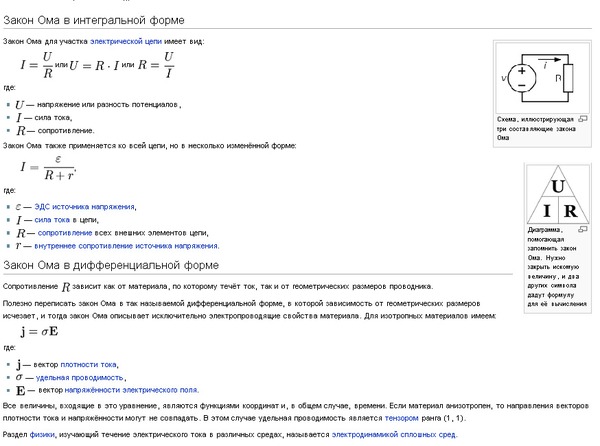 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.)