Закон ома в дифференциальной форме — КиберПедия

Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из по­вторяющихся рабочих циклов, каждый из которых соответствует… Основы обеспечения единства измерений: Обеспечение единства измерений — деятельность метрологических служб, направленная на достижение… Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда… Интересное: Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов… Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории. .. Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция

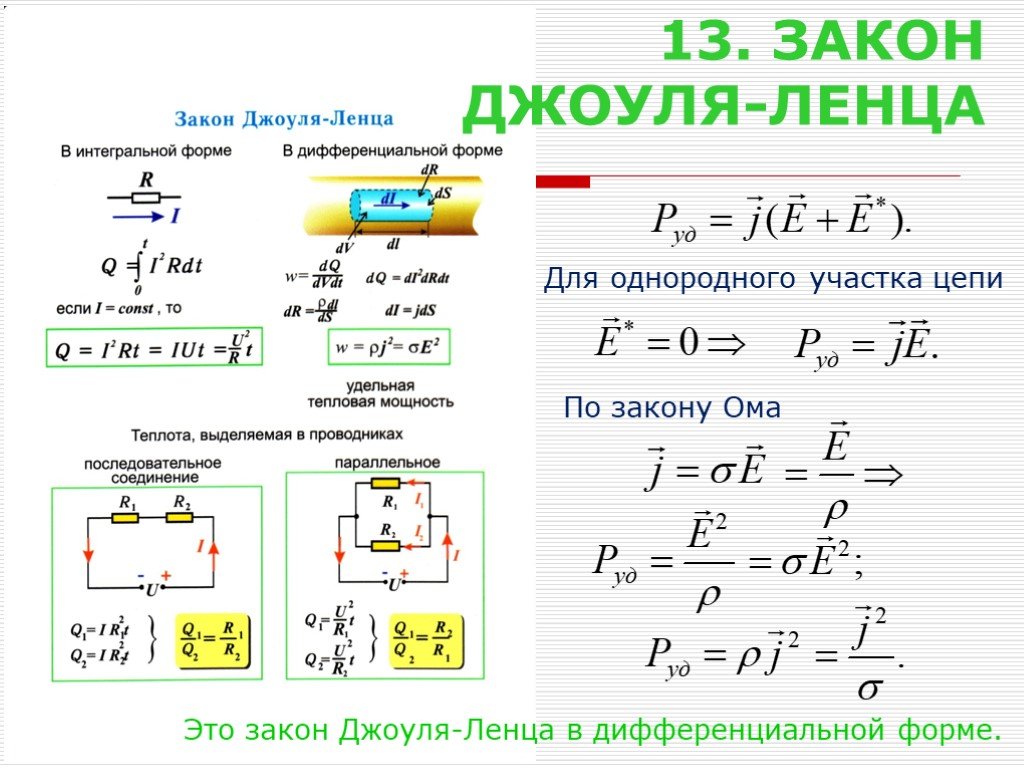
⇐ ПредыдущаяСтр 12 из 19Следующая ⇒ Немецкий физик Г. Ом (1787 – 1854) экспериментально установил, что сила тока на участке, не содержащем ЭДС прямо пропорциональна напряжению: , (11) где коэффициент пропорциональности G = 1 / R и называется электрической проводимостью проводника. Для линейных проводников с постоянным поперечным сечением , (12) где γ = 1 / ρ – удельная электропроводность материала, ρ – удельное сопротивление,S – площадь поперечного сечения проводника, – его длина. Тогда для изотропного проводника выражение (11) с учётом (12) примет вид: . (13) Теперь для плотности тока (2) с учётом, что – напряжённость поля в проводнике, получим: . (14) Выражение (14) в векторной форме это закон Ома в дифференциальной форме: . (15) Получим в дифференциальной форме закон Джоуля-Ленца. Количество теплоты, выделяющееся в элементе проводника, объёмом за времяdt: . (16) Теперь, количество теплоты, которое выделяется в единице объема проводника за единицу времени, будет: . (17) Эта величина называется удельной тепловой мощностью тока. II. Электрическое сопротивление проводника Электрическое сопротивление проводника: 1) величина, характеризующая противодействие проводника или электрической цепи электрическому току; 2) структурный элемент электрической цепи, включаемый в цепь для ограничения или регулирования силы тока. Электрическое сопротивление металлов зависит от материала проводника, его длины и поперечного сечения, температуры и состояния проводника (давления, механических сил растяжения и сжатия, т.е. внешних факторов, влияющих на кристаллическое строение металлических проводников). Зависимость сопротивления от материала, длины и площади поперечного сечения проводника: , где r — удельное сопротивление проводника; l – длина проводника; S – площадь поперечного сечения проводника.   Обобщенный закон Ома в интегральной форме для участка цепи и полной цепи. Обобщенный закон Ома в интегральной форме для участка цепи: где – электрическое сопротивление участка цепи 1-2, сопротивление внешней цепи, внутреннее сопротивление источника ЭДС; –разность потенциалов на участке цепи 1-2. Закон Ома для неоднородного участка цепи: Произведение электрического сопротивления участка цепи на силу тока в нем равно сумме падения электрического потенциала на этом участке и ЭДС всех источников электрической энергии, включенных на данном участке. Правило знаков для ЭДС: если напряженность поля сторонних сил в источнике совпадает с направлением выбранного обхода, то при подсчете ЭДС этого источника нужно считать положительным, в противном случае — отрицательным. Закон Ома для полной цепи:Если электрическая цепь замкнута, то , тогда где ε – алгебраическая сумма отдельных ЭДС в данной цепи, сопротивление внешней цепи, внутреннее сопротивление источника тока.   Напряжение на участке цепи. Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка. На рис. 13 изображен участок цепи, на котором есть резистор сопротивлением и нет ЭДС. Крайние точки этого участка обозначены буквами a и b. Пусть ток течет от точки a к точке b. Рис. 13. Участок электрической цепи На участке без ЭДС ток течет от более высокого потенциала к более низкому. Следовательно, потенциал точки a выше потенциала точки bна величину, равную произведению тока на сопротивление : . В соответствии с определением, напряжение между точками a и b .(8) Другими словами, напряжение на резисторе равно произведению тока, протекающего по резистору, на величину сопротивления этого резистора. В электротехнике разность потенциалов на концах резистора принято называть либо «напряжением на резисторе», либо «падением напряжения». В литературе встречаются оба этих определения. Рассмотрим теперь вопрос о напряжении на участке цепи, содержащем не только резистор, но и источник ЭДС. На рис. 14 а и б показаны участки некоторых цепей, по которым протекает ток .. Найдем напряжение между точками a и c для этих участков. а) б) Рис. 14. Участки электрической цепи По определению .(9) Выразим потенциал точки a через потенциал точки c. При перемещении от точки c к точке b (рис. 14,а) идем встречно ЭДС , поэтому потенциал точки b оказывается меньше, чем потенциал точки c на величину ЭДС , т. е. .(10) На рис. 14,б при перемещении от точки c к точке b идем согласно ЭДС и потому потенциал точки b оказывается больше, чем потенциал точки cна величину ЭДС , т.е. .(11) Ранее говорилось, что на участке цепи без ЭДС ток течет от более высокого потенциала к более низкому. Поэтому в обеих схемах рис. 14 потенциал точки a выше, чем потенциал точки b на величину падения напряжения на резисторе сопротивлением : . (12) Таким образом, для рис. 14,а имеем , или .(13) И для рис. 14, б имеем , или .(14) Положительное направление напряжения указывают на схемах стрелкой. Стрелка должна быть направлена от первой буквы индекса ко второй. Так, положительное направление напряжения изобразится стрелкой, направленной от a к c. Из самого определения напряжения следует также, что . Поэтому . Другими словами, изменение чередования индексов равносильно изменению знака этого напряжения. Из изложенного ясно, что напряжение может быть и положительной, и отрицательной величиной.   ⇐ Предыдущая78910111213141516Следующая ⇒ Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой. .. 

Ома закон | это… Что такое Ома закон?

Зако́н Ома — это физический закон, определяющий связь между напряжением, силой тока и сопротивлением проводника в электрической цепи. Назван в честь его первооткрывателя Георга Ома. Суть закона проста: сила тока в проводнике прямо пропорциональна напряжению между концами проводника, если при прохождении тока свойства проводника не изменяются. Следует также иметь в виду, что закон Ома является фундаментальным и может быть применён к любой физической системе, в которой действуют потоки частиц или полей, преодолевающие сопротивление. Его можно применять для расчёта гидравлических, пневматических, магнитных, электрических, световых, тепловых потоков и т. д., также, как и Правила Кирхгофа, однако, такое приложение этого закона используется крайне редко в рамках узко специализированных расчётов.

Закон Ома формулируется так: Сила тока в однородном участке цепи прямо пропорциональна напряжению, приложенному к участку, и обратно пропорциональна характеристике участка, которую называют электрическим сопротивлением этого участка.

Ток, А	Напряжение, В	Сопротивление, Ом	Мощность, Вт
I	U	R	P

Содержание 1 История закона Ома 2 Закон Ома в интегральной форме 3 Закон Ома в дифференциальной форме 4 Закон Ома для переменного тока 5 Объяснение закона Ома 6 См. также

История закона Ома

Георг Ом, проводя эксперименты с проводником, установил, что сила тока I в проводнике пропорциональна напряжению U, приложенному к его концам:

,

или

.

Коэффициент пропорциональности назвали электропроводностью, а величину принято именовать электрическим сопротивлением проводника.

Закон Ома был открыт в 1827 году.

Закон Ома в интегральной форме

Схема, иллюстрирующая три составляющие закона Ома

Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления

Закон Ома для участка электрической цепи имеет вид:

U = RI

где:

• U — напряжение или разность потенциалов,
• I — сила тока,
• R — сопротивление.

Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:

,

где:

• — ЭДС цепи,
• I — сила тока в цепи,
• R — сопротивление всех элементов цепи,
• r — внутреннее сопротивление источника питания.

Закон Ома в дифференциальной форме

Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

где:

• — вектор плотности тока,
• σ — удельная проводимость,
• — вектор напряжённости электрического поля.

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока

Если цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), а ток является синусоидальным с циклической частотой ω, то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где:

• U = U₀e^iωt — напряжение или разность потенциалов,
• I — сила тока,
• Z = Re^—iδ — комплексное сопротивление (импеданс),
• R = (R_a²+R_r²)^1/2 — полное сопротивление,
• R_r = ωL — 1/ωC — реактивное сопротивление (разность индуктивного и емкостного),
• R_а — активное (омическое) сопротивление, не зависящее от частоты,
• δ = —arctg R_r/R_a — сдвиг фаз между напряжением и силой тока.

При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведен взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, U = U₀sin(ωt + φ) подбором такой , что . Тогда все значения токов и напряжений в схеме надо считать как

Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.

Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.

Объяснение закона Ома

Закон Ома можно просто объяснить при помощи теории Друде

См. также

• Правила Кирхгофа

Закон

Ом | PureHistory

Закон Ома

Объяснение закона Ома

V, I и R, параметры закона Ома

Закон Ома утверждает, что ток, протекающий через проводник между двумя точками, прямо пропорционален разности потенциалов в этих двух точках. Вводя константу пропорциональности, сопротивление, приходим к обычному математическому уравнению, описывающему эту зависимость:

, где I  – сила тока в проводнике в амперах,  В  – разность потенциалов, измеренная на  проводнике в единицах вольт, и  R  – сопротивление проводника в единицах Ом. В частности, закон Ома гласит, что R в этом отношении постоянна и не зависит от тока.

Закон назван в честь немецкого физика Георга Ома, который в трактате, опубликованном в 1827 году, описал измерения приложенного напряжения и тока в простых электрических цепях, содержащих провода различной длины. Он представил немного более сложное уравнение, чем приведенное выше (см. Раздел «История» ниже), чтобы объяснить свои экспериментальные результаты. Приведенное выше уравнение является современной формой закона Ома.

В физике термин закон Ома также используется для обозначения различных обобщений закона, первоначально сформулированного Омом. Самый простой пример:

.

, где J — плотность тока в данном месте резистивного материала, E — электрическое поле в этом месте, а σ — зависящий от материала параметр, называемый проводимостью. Эта переформулировка закона Ома принадлежит Густаву Кирхгофу.

История

В январе 1781 года, до работы Георга Ома, Генри Кавендиш экспериментировал с лейденскими банками и стеклянными трубками разного диаметра и длины, наполненными раствором соли. Он измерил силу тока, отметив, насколько сильным был удар, когда он замыкал цепь своим телом. Кавендиш писал, что «скорость» (ток) изменяется прямо как «степень электризации» (напряжение). В то время он не сообщал о своих результатах другим ученым, и его результаты были неизвестны до тех пор, пока Максвелл не опубликовал их в 1879 году..

Ом выполнил свою работу по сопротивлению в 1825 и 1826 годах и опубликовал свои результаты в 1827 году в виде книги Die galvanische Kette, mathematisch Bearbeitet (Гальваническая цепь исследована математически). Он черпал значительное вдохновение из работы Фурье по теплопроводности при теоретическом объяснении своей работы. Для экспериментов он сначала использовал вольтовые столбы, но позже применил к ним гермопару, так как это обеспечивало более стабильный источник напряжения с точки зрения внутреннего сопротивления и постоянной разности потенциалов. Он использовал гальванометр для измерения тока и знал, что напряжение между клеммами термопары пропорционально температуре перехода. Затем он добавил тестовые провода разной длины, диаметра и материала, чтобы завершить схему. Он обнаружил, что его данные можно смоделировать с помощью уравнения

, где x — показание гальванометра, l — длина испытательного проводника, a — зависит только от температуры спая термопары, а b — постоянная всей установки. Исходя из этого, Ом определил свой закон пропорциональности и опубликовал свои результаты.

Закон Ома был, вероятно, самым важным из первых количественных описаний физики электричества. Сегодня мы считаем это почти очевидным. Когда Ом впервые опубликовал свою работу, это было не так; критики отнеслись к его трактовке предмета в штыки. Они назвали его работу «паутиной голых фантазий», а министр образования Германии заявил, что «профессор, проповедующий такие ереси, недостоин преподавать науку». Преобладавшая в то время в Германии научная философия утверждала, что нет необходимости проводить эксперименты для развития понимания природы, потому что природа так хорошо упорядочена, и что научные истины могут быть выведены только с помощью рассуждений. Кроме того, брат Ома Мартин, математик, боролся с немецкой системой образования. Эти факторы препятствовали принятию работы Ома, и его работа не получила широкого признания до 1840-х гг. К счастью, Ом получил признание за свой вклад в науку задолго до своей смерти.

В 1850-х годах закон Ома был известен как таковой и широко считался доказанным, а альтернативы, такие как «закон Барлоу», были дискредитированы с точки зрения реальных приложений к проектированию телеграфных систем, как это обсуждалось Сэмюэлем Ф. Б. Морзе в 1855 году.

В то время как старый термин для электрической проводимости, мОм (обратная единица измерения сопротивления ом), все еще используется, новое название, сименс, было принято в 1971 году в честь Эрнста Вернера фон Сименса. Сименс предпочтительнее в официальных документах.

В 1920-х годах было обнаружено, что ток через идеальный резистор на самом деле имеет статистические флуктуации, которые зависят от температуры, даже когда напряжение и сопротивление точно постоянны; это колебание, теперь известное как шум Джонсона-Найквиста, связано с дискретным характером заряда. Этот тепловой эффект подразумевает, что измерения тока и напряжения, которые проводятся в течение достаточно коротких периодов времени, будут давать отношения V/I, которые колеблются от значения R, подразумеваемого средним по времени или средним по ансамблю измеренным током; Закон Ома остается верным для среднего тока в случае обычных резистивных материалов.

Работа Ома задолго до появления уравнений Максвелла и любого понимания частотно-зависимых эффектов в цепях переменного тока. Современные разработки в электромагнитной теории и теории цепей не противоречат закону Ома, когда они оцениваются в соответствующих пределах.

Объем

Закон Ома — это эмпирический закон, обобщение многих экспериментов, показавших, что для большинства материалов сила тока приблизительно пропорциональна электрическому полю. Оно менее фундаментально, чем уравнения Максвелла, и не всегда соблюдается. Любой данный материал разрушается под действием достаточно сильного электрического поля, а некоторые материалы, представляющие интерес для электротехники, являются «неомическими» в слабых полях.

Закон Ома наблюдался в широком диапазоне масштабов длины. В начале 20 века считалось, что закон Ома не работает в атомном масштабе, но эксперименты не подтвердили это ожидание. По состоянию на 2012 год исследователи продемонстрировали, что закон Ома работает для кремниевых проводов размером от четырех атомов в ширину и одного атома в высоту.

Микроскопическое происхождение

Электроны модели Друде (показаны здесь синим цветом) постоянно отскакивают от более тяжелых стационарных кристаллических ионов (показаны красным).

Модель Друде и классическая и квантовая проводимость

Зависимость плотности тока от приложенного электрического поля по существу носит квантово-механический характер; (см. Классическая и квантовая проводимость). Качественное описание, ведущее к закону Ома, может быть основано на классической механике с использованием модели Друде, разработанной Полом Друде в 1900 году.

В модели Друде электроны (или другие носители заряда) рассматриваются как пинболы, прыгающие среди ионов, составляющих структуру материала. Электроны будут ускоряться в направлении, противоположном электрическому полю, за счет среднего электрического поля в месте их нахождения. Однако при каждом столкновении электрон отклоняется в случайном направлении со скоростью, намного превышающей скорость, приобретаемую электрическим полем. Конечным результатом является то, что электроны выбирают зигзагообразный путь из-за столкновений, но обычно дрейфуют в направлении, противоположном электрическому полю.

Затем скорость дрейфа определяет плотность электрического тока и ее связь с E и не зависит от столкновений. Друде рассчитал среднюю скорость дрейфа из столкновения. Поскольку и импульс, и плотность тока пропорциональны скорости дрейфа, плотность тока становится пропорциональной приложенному электрическому полю; это приводит к закону Ома.

Гидравлический аналог

 Гидравлическая аналогия иногда используется для описания закона Ома. Давление воды, измеряемое в паскалях (или PSI), является аналогом напряжения, поскольку установление разницы давлений воды между двумя точками вдоль (горизонтальной) трубы заставляет воду течь. Скорость потока воды, например, в литрах в секунду, является аналогом тока, например, в кулонах в секунду. Наконец, ограничители потока, такие как отверстия в трубах между точками, где измеряется давление воды, являются аналогом резисторов. Мы говорим, что скорость потока воды через ограничитель отверстия пропорциональна разности давления воды на ограничителе. Точно так же скорость протекания электрического заряда, то есть электрического тока, через электрический резистор пропорциональна разности напряжений, измеренных на резисторе.

Переменные расхода и давления могут быть рассчитаны в сети потока жидкости с использованием аналогии гидравлического сопротивления. Метод может применяться как к стационарным, так и к переходным режимам течения. В области линейного ламинарного течения закон Пуазейля описывает гидравлическое сопротивление трубы, но в области турбулентного течения отношения давление-расход становятся нелинейными.

Гидравлическая аналогия закона Ома использовалась, например, для аппроксимации кровотока в системе кровообращения.

Анализ цепи

Треугольник закона Ома

В анализе цепей три эквивалентных выражения закона Ома используются взаимозаменяемо:

Каждое уравнение цитируется в некоторых источниках как определяющее соотношение закона Ома, или все три цитируются, или выводятся из пропорциональной формы, или даже иногда могут быть приведены только два уравнения, которые не соответствуют исходному утверждению Ома.

Взаимозаменяемость уравнения может быть представлена ​​треугольником, где V (напряжение) расположено в верхней части, I (ток) помещено в левую часть, а R (сопротивление) помещено в правую часть. Линия, разделяющая левую и правую части, указывает на умножение, а разделитель между верхней и нижней частями указывает на деление (отсюда и черта деления).

Резистивные цепи

Резисторы – это элементы цепи, препятствующие прохождению электрического заряда в соответствии с законом Ома, и рассчитанные на определенное значение сопротивления  Р . На принципиальной схеме резистор показан зигзагообразным символом. Элемент (резистор или проводник), который ведет себя в соответствии с законом Ома в некотором рабочем диапазоне, называется омическим устройством (или омическим резистором ), поскольку закона Ома и одного значения сопротивления достаточно, чтобы описать поведение устройство в этом диапазоне.

Закон Ома выполняется для цепей, содержащих только резистивные элементы (без емкостей или индуктивностей) для всех форм управляющего напряжения или тока, независимо от того, является ли управляющее напряжение или ток постоянным (постоянным) или изменяющимся во времени, например переменным. В любой момент времени для таких цепей справедлив закон Ома.

Резисторы, входящие в состав серии или параллельно , могут быть сгруппированы вместе в одно «эквивалентное сопротивление», чтобы применить закон Ома при анализе цепи. Применение закона Ома проиллюстрировано примерами в статье «Как анализировать резистивные цепи с помощью закона Ома» на wikiHow.

Реактивные цепи с изменяющимися во времени сигналами

Когда реактивные элементы, такие как конденсаторы, катушки индуктивности или линии передачи, включены в цепь, к которой применяется переменное или изменяющееся во времени напряжение или ток, соотношение между напряжением и током становится решением дифференциального уравнения, поэтому закон Ома (как выше) не применяется напрямую, поскольку эта форма содержит только сопротивления, имеющие значение R, а не комплексные импедансы, которые могут включать емкость («C») или индуктивность («L»).

Уравнения для неизменных во времени цепей переменного тока имеют ту же форму, что и закон Ома, однако переменные обобщаются до комплексных чисел, а формы сигналов тока и напряжения представляют собой комплексные экспоненты.

В этом подходе кривая напряжения или тока принимает форму, где t  – это время,  с  – комплексный параметр, а  A  – комплексный скаляр. В любой линейной стационарной системе все токи и напряжения могут быть выражены одними и теми же s  параметр в качестве входных данных для системы, позволяющий компенсировать изменяющийся во времени комплексный экспоненциальный член и описать систему алгебраически в терминах комплексных скаляров в формах сигналов тока и напряжения.

Комплексным обобщением сопротивления является импеданс, обычно обозначаемый Z ; можно показать, что для катушки индуктивности

и для конденсатора

Теперь мы можем написать,

, где В и I — комплексные скаляры напряжения и тока соответственно, а Z — комплексное сопротивление.

Эта форма закона Ома, где Z занимает место R , обобщает более простую форму. Когда Z сложный, только действительная часть отвечает за рассеивание тепла.

В общей цепи переменного тока Z сильно зависит от параметра частоты s , а также соотношение между напряжением и током.

Для общего случая устойчивой синусоиды параметр s принимается равным комплексной синусоиде. Действительные части таких сложных сигналов тока и напряжения описывают фактические синусоидальные токи и напряжения в цепи, которые могут находиться в разных фазах из-за разных комплексных скаляров.

https://en.wikipedia.org/wiki/Ohm’s_law

электромагнетизм — Что такое закон Ома для индуцированного тока?

$\begingroup$

В этой книге на стр. $313$ в последнем абзаце написано, что закон Ома, т. е. $R (константа)=\frac{\epsilon_{ind}}{I}$, справедлив для наведенного тока в цепи. Они определяют $R$ как сумму сопротивлений всех резистивных элементов цепи, $I$ как ток и $\epsilon_{ind}$ как ЭДС индукции. У меня есть два сомнения относительно значения терминов $I$ и $\epsilon_{ind}$.

1. Какой ток представляет $I$? Представляет ли он индуцированный или чистый ток в цепи? Предположим, что в цепь также подключена батарея, цепь удерживается в области, где изменяется ее магнитный поток. Батарея и изменяющийся магнитный поток будут производить ток. Представляет ли $I$ чистый ток в цепи, т. е. чистую сумму тока, производимого батареей и потоком, или просто индуцированный ток?
2. Вокруг какого цикла вычисляется $\epsilon_{ind}$? Может быть бесконечно много замкнутых линий, вдоль которых мы можем вычислить $\epsilon_{ind}$, тогда какой петле соответствует $\epsilon_{ind}$? См. схему. Две черные линии представляют собой кривые, проходящие по поверхности провода, зеленые и синие линии представляют собой петлю внутри провода, а красные линии представляют собой возрастающее однородное магнитное поле. Я могу вычислить $\epsilon_{ind}$ по синей, зеленой и двум черным петлям. Но чей $\epsilon_{ind}$ использовать в формуле?

• электромагнетизм
• электростатика
• электричество
• электрический ток
• электромагнитная индукция

$\endgroup$

$\begingroup$

Учитывая петлю $\partial S$, которая является граничной кривой простой в остальном произвольной поверхности $\mathcal S$, вычислить магнитный поток $\Phi$ через эту поверхность, заданный $\Phi = \int_{\ mathcal {S}} \mathbf B \cdot d\mathbf{S}$. По индукции Фарадея число ЭДС $\mathcal V$, индуцированная по периметру$\partial \mathcal {S}$ : $\mathcal V = \oint_{\partial S} \mathbf E \cdot d\mathbf{\ell} = -\frac {\ парциальное \Phi} {dt} $. Эта $\mathcal V$ существует как контурный интеграл независимо от того, есть ли где-нибудь ток, но если $\partial \mathcal S$ находится вдоль добросовестного проводника, металлической проволоки, то эта ЭДС сделает заряды двигаться внутри провода, так что если сопротивление провода равно $R$, то по нему будет течь ток $I$ такой, что $I=\frac{\mathcal V}{R}$. Таким образом, ток будет зависеть не только от его сопротивления и от изменяющегося во времени магнитного поля, но и от формы провода и его расположения относительно поля. Важно отметить, что поскольку поле $\mathbf {B}$ соленоидальное, $\nabla \cdot\mathbf{B}=0$, сам поток $\Phi$ равен не зависит от деталей остовной поверхности, вместо этого геометрически поток $\Phi$ зависит только от граничной кривой $\partial \mathcal {S}$. С разными петлями вы получаете разный поток и ЭДС .

$\endgroup$

$\begingroup$

Согласно книге, в цепи присутствует переменный ток, индуцируемый в катушке II катушкой I. Дифференциальное уравнение для цепи: $$L\frac{\partial I}{\partial t} + RI = ЭДС$$

Если L (индуктивность катушки) слишком мала по сравнению с R, цепь можно считать в основном резистивной, и $ЭДС = RI$. Ток всегда весь ток цепи.

$\endgroup$

1

$\begingroup$

Наведенный ток обусловлен проницаемостью провода, а не сопротивлением.