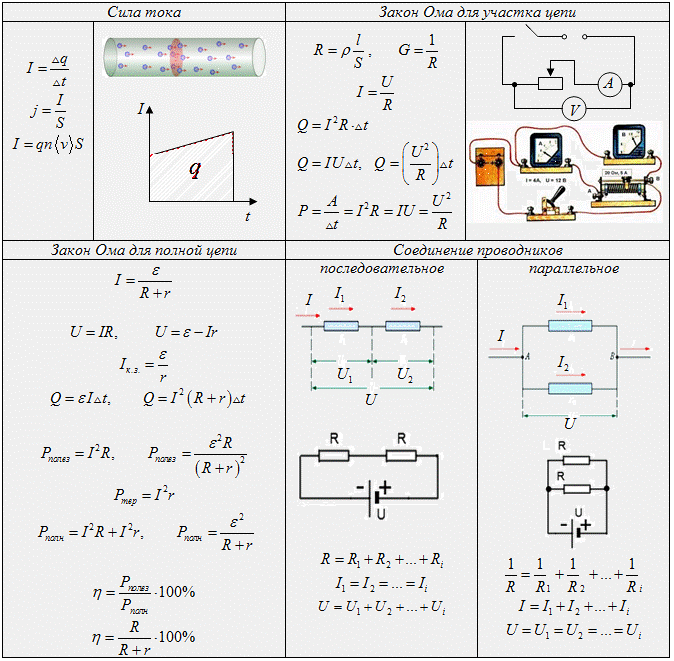
Закон Ома
Закон Ома для участка цепи
Соберем электрическую цепь (рисунок 1, а), состоящую из аккумулятора 1 напряжением в 2 В, рычажного реостата 2, двух измерительных приборов – вольтметра 3 и амперметра 4 и соединительных проводов 5. Установим в цепи при помощи реостата сопротивление, равное 2 Ом. Тогда вольтметр, включенный на зажимы аккумулятора, покажет напряжение в 2 В, а амперметр, включенный последовательно в цепь, покажет ток, равный 1 А. Увеличим напряжение до 4 В путем включения другого аккумулятора (рисунок 1, б). При том же сопротивлении в цепи – 2 Ом – амперметр покажет уже ток 2 А. Аккумулятор напряжением 6 В изменит показание амперметра до 3 А (рисунок 1, в). Сведем наши наблюдения в таблицу 1.
Рисунок 1. Изменение тока в электрической цепи путем изменения напряжения при неизменном сопротивлении
Таблица 1
Зависимость тока в цепи от напряжения при неизменном сопротивлении
| Напряжение цепи в В | Сопротивление цепи в Ом | Ток цепи в А |
| 2 4 6 | 2 2 2 | 1 2 3 |
Отсюда можно сделать вывод, что ток в цепи при постоянном сопротивлении тем больше, чем больше напряжение этой цепи, причем ток будет увеличиваться во столько раз, во сколько раз увеличивается напряжение.
Теперь в такой же цепи поставим аккумулятор с напряжением 2 В и установим при помощи реостата сопротивление в цепи, равное 1 Ом (рисунок 2, а). Тогда амперметр покажет 2 А. Увеличим реостатом сопротивление до 2 Ом (рисунок 2, б). Показание амперметра (при том же напряжении цепи) будет уже 1 А.
Рисунок 2. Изменение тока в электрической цепи путем изменения сопротивления при неизменном напряжении
При сопротивлении в цепи 3 Ом (рисунок 2, в) показание амперметра будет 2/3 А.
Результат опыта сведем в таблицу 2.
Таблица 2
Зависимость тока в цепи от сопротивления при неизменном напряжении
| Напряжение цепи в В | Сопротивление цепи в Ом | Ток цепи в А |
| 2 2 2 | 1 2 3 | 2 1 2/3 |
Отсюда следует вывод, что при постоянном напряжении ток в цепи будет тем больше, чем меньше сопротивление этой цепи, причем ток в цепи увеличивается во столько раз, во сколько раз уменьшается сопротивление цепи.
Как показывают опыты, ток на участке цепи прямо пропорционален напряжению на этом участке и обратно пропорционален сопротивлению того же участка. Эта зависимость известна под названием закон Ома.
Если обозначим: I – ток в амперах; U – напряжение в вольтах; r – сопротивление в омах, то закон Ома можно представить формулой:
то есть ток на данном участке цепи равен напряжению на этом участке, деленному на сопротивление того же участка.
Пример 1. Определить ток, который будет проходить по нити лампы накаливания, если нить имеет неизменное сопротивление 240 Ом, а лампа включена в сеть с напряжением 120 В.
Пользуясь формулой закона Ома, можно определить также напряжение и сопротивление цепи.
U = I × r ,
то есть напряжение цепи равно произведению тока на сопротивление этой цепи и
то есть сопротивление цепи равно напряжению, деленному на ток цепи.
Пример 2. Какое нужно напряжение, чтобы в цепи с сопротивлением 6 Ом протекал ток 20 А?
U = I × r = 20 × 6 = 120 В .
Пример 3. По спирали электрической плитки протекает ток в 5 А. Плитка включена в сеть с напряжением 220 В. Определить сопротивление спирали электрической плитки.
Если в формуле U = I × r ток равен 1 А, а сопротивление 1 Ом, то напряжение будет равно 1 В:
1 В = 1 А × 1 Ом .
Отсюда заключаем: напряжение в 1 В действует в цепи с сопротивлением 1 Ом при токе в 1 А.
Потеря напряжения
Рисунок 3. Потеря напряжения вдоль электрической цепи
На рисунке 3 приведена электрическая цепь, состоящая из аккумулятора, сопротивления r и длинных соединительных проводов, имеющих свое определенное сопротивление.
Как видно из рисунка 3, вольтметр, присоединенный к зажимам аккумулятора, показывает 2 В. Уже в середине линии вольтметр показывает только 1,9 В, а около сопротивления r напряжение равно всего 1,8 В. Такое уменьшение напряжения вдоль цепи между отдельными точками этой цепи называется потерей (падением) напряжения.
Уже в середине линии вольтметр показывает только 1,9 В, а около сопротивления r напряжение равно всего 1,8 В. Такое уменьшение напряжения вдоль цепи между отдельными точками этой цепи называется потерей (падением) напряжения.
Потеря напряжения вдоль электрической цепи происходит потому, что часть приложенного напряжения расходуется на преодоление сопротивления цепи. При этом потеря напряжения на участке цепи будет тем больше, чем больше ток и чем больше сопротивление этого участка цепи. Из закона Ома для участка цепи следует, что потеря напряжения в вольтах на участке цепи равно току в амперах, протекающему по этому участку, умноженному на сопротивление в омах того же участка:
U = I × r .
Пример 4. От генератора, напряжение на зажимах которого 115 В, электроэнергия передается электродвигателю по проводам, сопротивление которых 0,1 Ом. Определить напряжение на зажимах двигателя, если он потребляет ток в 50 А.
Очевидно, что на зажимах двигателя напряжение будет меньше, чем на зажимах генератора, так как в линии будет потеря напряжения. По формуле определяем, что потеря напряжения равна:
U = I × r = 50 × 0,1 = 5 В.
Если в линии потеря напряжения равна 5 В, то напряжение у электродвигателя будет 115 – 5 = 110 В.
Пример 5. Генератор дает напряжение 240 В. Электроэнергия по линии из двух медных проводов длиной по 350 м, сечением 10 мм² передается к электродвигателю, потребляющему ток в 15 А. Требуется узнать напряжение на зажимах двигателя.
Напряжение на зажимах двигателя будет меньше напряжения генератора на величину потери напряжения в линии. Потеря напряжения в линии U = I × r.
Так как сопротивление r проводов неизвестно, определяем его по формуле:
где ρ – удельное сопротивление меди; длина l равна 700 м, так как току приходится идти от генератора к двигателю и оттуда обратно к генератору.
Подставляя r в формулу, получим:
U = I × r = 15 × 1,22 = 18,3 В
Следовательно, напряжение на зажимах двигателя будет 240 – 18,3 = 221,7 В
Пример 6. Определить поперечное сечение алюминиевых проводов, которое необходимо применить, чтобы подвести электрическую энергию к двигателю, работающему при напряжении в 120 В и токе в 20 А. Энергия к двигателю будет подаваться от генератора напряжением 127 В по линии длиной 150 м.
Находим допустимую потерю напряжения:
127 – 120 = 7 В .
Сопротивление проводов линии должно быть равно:
Из формулы
определим сечение провода:
где ρ – удельное сопротивление алюминия.
По справочнику выбираем имеющееся сечение 25 мм².
Если ту же линию выполнить медным проводом, то сечение его будет равно:
где ρ – удельное сопротивление меди.
Выбираем сечение 16 мм².
Отметим еще, что иногда приходится умышленно добиваться потери напряжения, чтобы уменьшить величину приложенного напряжения.
Пример 7. Для устойчивого горения электрической дуги требуется ток 10 А при напряжении 40 В. Определить величину добавочного сопротивления, которое нужно включить последовательно с дуговой установкой, чтобы питать ее от сети с напряжением 120 В.
Потеря напряжения в добавочном сопротивлении составит:
120 – 40 = 80 В .
Зная потерю напряжения в добавочном сопротивлении и ток, протекающий через него, можно по закону Ома для участка цепи определить величину этого сопротивления:
Закон Ома для полной цепи
При рассмотрении электрической цепи мы до сих пор не принимали в расчет того, что путь тока проходит не только по внешней части цепи, но также и по внутренней части цепи, внутри самого элемента, аккумулятора или другого источника напряжения.
Электрический ток, проходя по внутренней части цепи, преодолевает ее внутреннее сопротивление и потому внутри источника напряжения также происходит падение напряжения.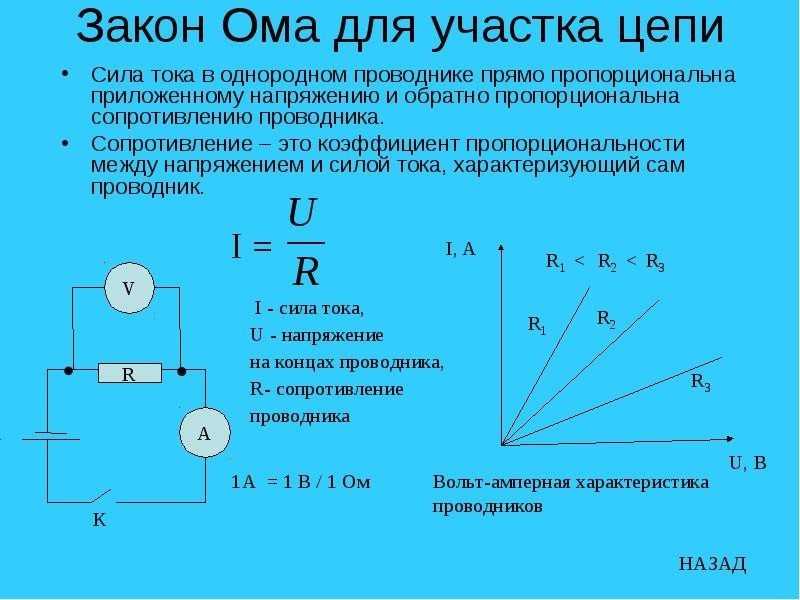
Следовательно, электродвижущая сила (э. д. с.) источника электрической энергии идет на покрытие внутренних и внешних потерь напряжения в цепи.
Если обозначить E – электродвижущую силу в вольтах, I – ток в амперах, r – сопротивление внешней цепи в омах, r0 – сопротивление внутренней цепи в омах, U0 – внутреннее падение напряжения и U – внешнее падение напряжения цепи, то получим, что
E = U0 + U = I × r0 + I × r = I × (r0 + r),
Это и есть формула закона Ома для всей (полной) цепи. Словами она читается так: ток в электрической цепи равен электродвижущей силе, деленной на сопротивление всей цепи (сумму внутреннего и внешнего сопротивлений).
Пример 8. Электродвижущая сила E элемента равна 1,5 В, его внутреннее сопротивление r0 = 0,3 Ом.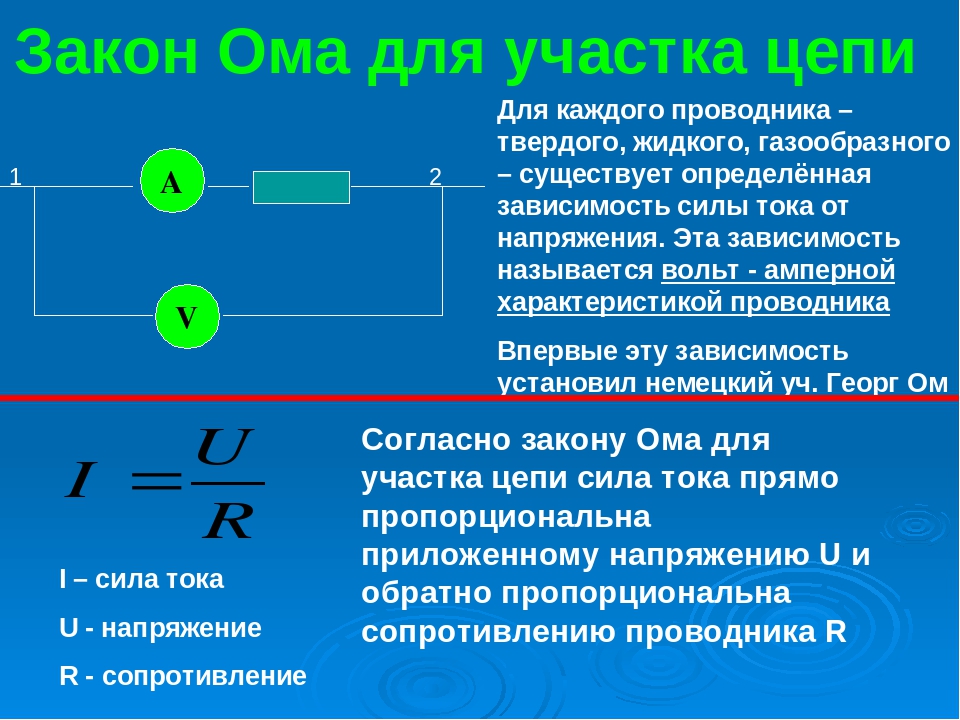 Элемент замкнут на сопротивление r = 2,7 Ом. Определить ток в цепи.
Элемент замкнут на сопротивление r = 2,7 Ом. Определить ток в цепи.
Пример 9. Определить э. д. с. элемента E, замкнутого на сопротивление r = 2 Ом, если ток в цепи I = 0,6 А. Внутреннее сопротивление элемента r0 = 0,5 Ом.
Вольтметр, включенный на зажимы элемента, покажет напряжение на них, равное напряжению сети или падению напряжения во внешней цепи.
U = I × r = 0,6 × 2 = 1,2 В.
Следовательно, часть э. д. с. элемента идет на покрытие внутренних потерь, а остальная часть – 1,2 В отдается в сеть.
Внутреннее падение напряжения
U0 = I × r0 = 0,6 × 0,5 = 0,3 В.
Так как E = U0 + U, то
E = 0,3 + 1,2 =1,5 В
Тот же ответ можно получить, если воспользоваться формулой закона Ома для полной цепи:
откуда
E = I × (r0 + r) = 0,6 × (0,5 +2) = 1,5 В.
Вольтметр, включенный на зажимы любого источника э. д. с. во время его работы, показывает напряжение на них или напряжение сети. При размыкании электрической цепи ток по ней проходить не будет. Ток не будет проходить также и внутри источника э. д. с., а следовательно, не будет и внутреннего падения напряжения. Поэтому вольтметр при разомкнутой цепи покажет э. д. с. источника электрической энергии.
Таким образом, вольтметр, включенный на зажимы источника э. д. с. показывает:
а) при замкнутой электрической цепи – напряжение сети;
б) при разомкнутой электрической цепи – э. д. с. источника электрической энергии.
Пример 10. Электродвижущая сила элемента 1,8 В. Он замкнут на сопротивление r =2,7 Ом. Ток в цепи равен 0,5 А. Определить внутреннее сопротивление r0 элемента и внутреннее падение напряжения U0.
Так как r = 2,7 Ом, то
r0 = 3,6 – 2,7 = 0,9 Ом ;
U0 = I × r0 = 0,5 × 0,9 = 0,45 В .
Из решенных примеров видно, что показание вольтметра, включенного на зажимы источника э. д. с., не остается постоянным при различных условиях работы электрической цепи. При увеличении тока в цепи увеличивается также внутреннее падение напряжения. Поэтому при неизменной э. д. с. на долю внешней сети будет приходиться все меньшее и меньшее напряжение.
В таблице 3 показано, как меняется напряжение электрической цепи (U) в зависимости от изменения внешнего сопротивления (r) при неизменных э. д. с. (E) и внутреннем сопротивлении (r0) источника энергии.
Таблица 3
Зависимость напряжения цепи от сопротивления r при неизменных э. д. с. и внутреннем сопротивлении r0
| E | r0 | r | U0 = I × r0 | U = I × r | |
| 2 2 2 | 0,5 0,5 0,5 | 2 1 0,5 | 0,8 1,33 2 | 0,4 0,67 1 | 1,6 1,33 1 |
Источник: Кузнецов М. И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560с.
И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560с.
Для того чтобы производить подобные вычисления в электротехнике, необходимо владеть познаниями в области высшей математики. Но всё начинается с малого, с её основ, со средней школы. Если вы заканчиваете школу, готовитесь к экзамену и последующему поступлению в ВУЗ, вам полезно бы знать каков проходной бал. В этом вам поможет шкала перевода профильных баллов ЕГЭ по математике в 2021 году. Учитесь лучше, и тогда вам откроются все дороги к профессии электротехники.
Закон Ома для участка цепи | 8 класс
Содержание
Для описания процесса протекания электрического тока в цепи у нас есть уже три характеристики: сила тока, напряжение и сопротивление.
Мы выяснили, что некоторые из них связаны между собой. Сила тока зависит от напряжения. Эти величины прямо пропорциональны друг другу. Во сколько раз увеличивается напряжение на концах проводника, во столько же раз увеличивается сила тока в нем. Проводник мы меняли в этих опытах, сопротивление оставалось постоянным.
Проводник мы меняли в этих опытах, сопротивление оставалось постоянным.
Далее мы узнали, что сила тока зависит и от электрического сопротивления проводника. Показания амперметра при подключении в цепь разных проводников менялись. Напряжение при этом оставалось в этих проводниках постоянным.
Но мы пока не установили, каким образом между собой связаны сразу эти три величины. На данном уроке мы опытным путем докажем эту связь и познакомимся с законом Ома для участка цепи.
Опытное определение зависимости силы тока от сопротивления при постоянном напряжении
Для того, чтобы определить зависимость силы тока от сопротивления проводника, мы проведем еще один опыт. Теперь мы будем знать электрическое сопротивление тех проводников, которые будем использовать.
Обратите внимание, что в ходе опыта напряжение на концах используемых проводников должно быть постоянным. Эта величина не должна изменяться, чтобы мы могли корректно оценить зависимость силы тока от сопротивления.
Соберем электрическую цепь из источника тока, ключа, амперметра, проводника. К проводнику параллельно подсоединим вольтметр (рисунок 1).
Проводников у нас будет три разных. Они обладают разными сопротивлениями. Мы будем поочередно подключать их в цепь. Каждый раз мы будем фиксировать показания амперметра.
По показаниям вольтметра необходимо следить, чтобы напряжение на концах каждого проводника было одинаковым.
Рисунок 1. Установление зависимости силы тока от сопротивления проводника{"questions":[{"content":"При экспериментальном исследовании зависимости силы тока в проводнике от его сопротивления необходимо следить, чтобы[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["напряжение на концах проводника оставалось постоянным","вольтметр был подсоединен в цепь последовательно","сила тока в цепи не изменялась"],"explanations":["","Вольтметр НИКОГДА не подсоединяется в цепь последовательно. Только параллельно.","Сила тока в цепи будет равна силе тока в проводнике. Если мы говорим об определении зависимости, это подразумевает, что исследуемые величины будут изменяться."],"answer":[0]}}}]}
Если мы говорим об определении зависимости, это подразумевает, что исследуемые величины будут изменяться."],"answer":[0]}}}]}Связь силы тока и сопротивления
Проведя все измерения, мы занесли их результаты в таблицу 1.
| № опыта | Напряжение на концах проводника, $В$ | Сопротивление проводника, $Ом$ | Сила тока в цепи, $А$ |
| 1 | 2 | 1 | 2 |
| 2 | 2 | 2 | 1 |
| 3 | 2 | 4 | 0,5 |
Давайте проанализируем наши результаты.
В первом опыте сила тока составила $2 \space А$ при сопротивлении проводника в $1 \space Ом$.
Для следующего опыта мы взяли проводник с сопротивлением в $2 \space Ом$. Это в два раза больше, чем в первом опыте. А вот сила тока составила $1 \space А$. Она стала в два раза меньше.
В третьем опыте сопротивление проводника было равно $4 \space Ом$. То есть, в четыре раза больше, чем в первом опыте. Сила тока стала равна $0.5 \space А$. Она уменьшилась в четыре раза.
Напряжение на концах проводников во всех трех опытах оставалось постоянным. Оно было равно $2 \space В$.
Так какова зависимость силы тока в проводнике от сопротивления этого проводника?
Из наших опытов мы можем сделать определенный вывод.
Сила тока в проводнике обратно пропорциональна сопротивлению проводника.
{"questions":[{"content":"Сопротивление проводника и сила тока в нем[[choice-6]]","widgets":{"choice-6":{"type":"choice","options":["обратно пропорциональны друг другу","прямо пропорциональны друг другу","не зависят друг от друга"],"explanations":["","Так связаны между собой сила тока и напряжение.",""],"answer":[0]}}}]}Закон Ома для участка цепи
В 1827 году немецкий физик Георг Ом (рисунок 2) открыл закон, описывающий зависимость силы тока от напряжения на концах проводника и сопротивления этого проводника. Проводник является частью электрической цепи. Этот закон был назван в честь этого ученого и называется законом Ома для участка цепи.
Проводник является частью электрической цепи. Этот закон был назван в честь этого ученого и называется законом Ома для участка цепи.
Как формулируется закон Ома?
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
$I = \frac{U}{R}$,
где $I$ — сила тока в участке цепи, $U$ — напряжение на концах этого участка, $R$ — электрическое сопротивление участка.
{"questions":[{"content":"Формула, описывающая закон Ома для участка цепи, имеет следующий вид:[[choice-10]]","widgets":{"choice-10":{"type":"choice","options":["$I = \\frac{U}{R}$","$U = \\frac{I}{R}$","$I = \\frac{q}{t}$","$U = \\frac{A}{q}$"],"explanations":["","","Это определение силы тока. ","Это определение напряжения."],"answer":[0]}}}]}
","Это определение напряжения."],"answer":[0]}}}]}График зависимости силы тока от сопротивления проводника
На рисунке 3 изображен график зависимости силы тока от сопротивления. Напряжение при этом на концах проводника остается постоянным.
Рисунок 3. График зависимости силы тока в цепи от сопротивленияЗдесь по горизонтальной оси отложены сопротивления проводников в омах, а по вертикальной — сила тока в амперах.
Формулы для вычисления напряжения и сопротивления
Из формулы $I = \frac{U}{R}$ мы можем выразить напряжение и сопротивление:
$U = IR$,
$R = \frac{U}{I}$.
При расчете сопротивления проводника помните, что $R$ — постоянная величина для каждого проводника. Она не будет изменяться при изменениях силы тока или напряжения.
{"questions":[{"content":"При увеличении напряжения на участке цепи[[choice-17]]","widgets":{"choice-17":{"type":"choice","options":["сопротивление этого участка не изменится","сопротивление этого участка увеличится","сопротивление этого участка уменьшится"],"explanations":["Прямо пропорционально напряжению увеличится сила тока в цепи. Сопротивление является свойством самого проводника и не зависит от изменений напряжения или силы тока.","",""],"answer":[0]}}}]}
Сопротивление является свойством самого проводника и не зависит от изменений напряжения или силы тока.","",""],"answer":[0]}}}]}Упражнения
Упражнение №1
Напряжение на зажимах электрического утюга $220 \space В$, сопротивление нагревательного элемента утюга $50 \space Ом$. Чему равна сила тока в нагревательном элементе?
Дано:
$U = 220 \space В$
$R = 50 \space Ом$
$I — ?$
Показать решение и ответ
Скрыть
Решение:
Закон Ома для участка цепи: $I = \frac{U}{R}$.
Рассчитаем силу тока:
$I = \frac{220 \space В}{50 \space Ом} = 4.4 \space А$.
Ответ: $I = 4.4 \space А$.
Упражнение №2
Сила тока в спирали электрической лампы $0.7 \space А$, сопротивление лампы $310 \space Ом$. Определите напряжение, под которым находится лампа.
Дано:
$I = 0.7 \space А$
$R = 310 \space Ом$
$u — ?$
Показать решение и ответ
Скрыть
Решение:
Закон Ома для участка цепи: $I = \frac{U}{R}$.
Выразим отсюда напряжение и рассчитаем его:
$U = IR$,
$U = 0.7 \space А \cdot 310 \space Ом = 217 \space В$.
Ответ: $U = 217 \space В$.
Упражнение №3
Каким сопротивлением обладает вольтметр, рассчитанный на $150 \space В$, если сила тока в нем не должна превышать $0.01 \space А$?
Дано:
$U_{max} = 150 \space В$
$I_{max} = 0.01 \space А$
$R — ?$
Показать решение и ответ
Скрыть
Решение:
Запишем закон Ома для участка цепи: $I = \frac{U}{R}$.
Выразим отсюда сопротивление и рассчитаем его значение, используя максимальные значения напряжения и силы тока, соответствующие прибору:
$R = \frac{U_{max}}{I_{max}}$,
$R = \frac{150 \space В}{0.01 \space А} = 15 \space 000 \space Ом = 15 \space кОм$.
Ответ: $R = 15 \space кОм$.
Упражнение №4
Определите по графику (рисунок 4) сопротивление проводника.
Рисунок 4. График зависимости силы тока в проводнике от напряженияВозьмем из графика данные. При напряжении, равном $10 \space В$, сила тока в проводнике равна $2.5 \space А$. Запишем условие задачи и решим ее.
При напряжении, равном $10 \space В$, сила тока в проводнике равна $2.5 \space А$. Запишем условие задачи и решим ее.
Обратите внимание, что сопротивление $R$ не зависит ни от силы тока, ни от напряжения. Поэтому вы можете выбирать другие значения силы тока и напряжения из графика. Ваш ответ к этой задаче от этого не изменится.
Дано:
$U = 10 \space В$
$I = 2.5 \space А$
$R — ?$
Показать решение и ответ
Скрыть
Решение:
Запишем закон Ома для участка цепи: $I = \frac{U}{R}$.
Выразим отсюда сопротивление и рассчитаем его значение, используя данные графика:
$R = \frac{U}{I}$,
$R = \frac{10 \space В}{2.5 \space А} = 4 \space Ом$.
Ответ: $R = 4 \space Ом$.
Упражнение №5
Рассмотрите рисунок 1 и таблицу результатов опыта, выполняемого в соответствии с этим рисунком. Что изменится на рисунке и в схеме электрической цепи, когда будут проводиться опыты №2 и №3, указанные в таблице 1?
Для опыта №2:
на рисунке будет подключен другой проводник, имеющий сопротивление $2 \space Ом$. Амперметр будет показывать силу тока, равную $1 \space A$.
Амперметр будет показывать силу тока, равную $1 \space A$.
Для опыта №3:
на рисунке ничего не изменится. Это иллюстрация именно этого опыта (в цепь подключен проводник с сопротивлением $4 \space Ом$).
Схема электрической цепи будет одинаковой для всех трех опытов, если не отмечать сопротивление проводника (рисунок 5).
Рисунок 5. Схема электрической цепи для опытов по определения зависимости силы тока от сопротивленияУпражнение №6
По показаниям приборов (рисунок 6) определите сопротивление проводника АВ.
Рисунок 6. Зависимость силы тока от свойств проводниковДано:
$U = 4 \space В$
$I = 1 \space А$
$R — ?$
Показать решение и ответ
Скрыть
Решение:
Выразим сопротивление из закона Ома для участка цепи:
$I = \frac{U}{R}$,
$R = \frac{U}{I}$.
Из прошлого урока: этот проводник AB — железная проволока. Рассчитаем ее сопротивление:
$R = \frac{4 \space В}{1 \space А} = 4 \space Ом$.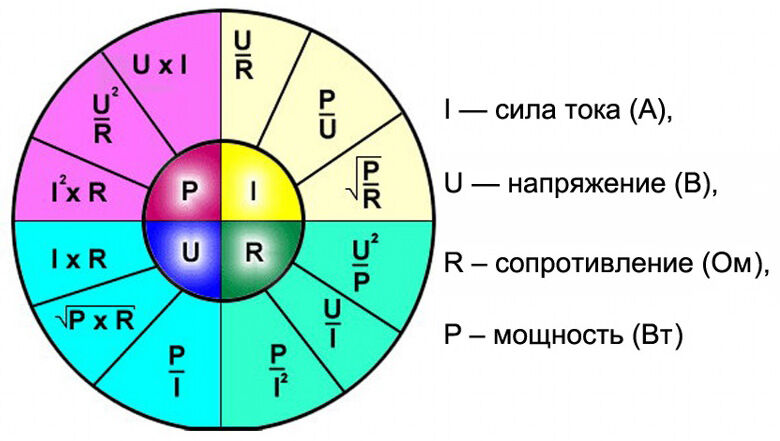
Ответ: $R = 4 \space Ом$.
Упражнение №7
На рисунке 7 изображены графики зависимости силы тока от напряжения для двух проводников А и В. Какой из этих проводников обладает большим сопротивлением? Определите сопротивление каждого из проводников.
Рисунок 7. Графики зависимости силы тока от напряжения для двух проводниковВозьмем данные из графиков. Для проводника A выберем напряжение, равное $6 \space В$. При таком напряжении сила тока в этом проводнике будет равна $3 \space А$. Для проводника B возьмем значение напряжения, равное $4 \space В$. Ему соответствует сила тока, равная $1 \space А$. Теперь мы можем записать условия задачи и решить ее.
Дано:
$U_A = 6 \space В$
$I_A = 3 \space А$
$U_B = 4 \space В$
$I_B = 1 \space А$
$R_A — ?$
$R_B — ?$
Показать решение и ответ
Скрыть
Решение:
Закон Ома для участка цепи: $I = \frac{U}{R}$.
Выразим сопротивление: $R = \frac{U}{I}$.
Рассчитаем сопротивление для проводника A:
$R_A = \frac{U_A}{I_A}$,
$R_A = \frac{6 \space В}{3 \space А} = 2 \space Ом$.
Рассчитаем сопротивление для проводника B:
$R_B = \frac{U_B}{I_B}$,
$R_B = \frac{4 \space В}{1 \space А} = 4 \space Ом$.
Проводник B обладает большим сопротивлением, чем проводник A. Его сопротивление больше в 2 раза $(\frac{R_B}{R_A} = \frac{4 \space Ом}{2 \space Ом} = 2$).
Ответ: сопротивление проводника B в 2 раза больше сопротивления проводника A; $R_A = 2 \space Ом$, $R_B = 4 \space Ом$.
ЗАКОН ОМА (сопротивление и падение напряжения)
ЗАКОН ОМА Существует простая зависимость между током, протекающим по проводящему пути, и разностью потенциалов между концами пути. По мере увеличения разности потенциалов ток увеличивается , см. схему ниже. Два значения пропорциональны. То есть удвоение разности потенциалов удваивает ток. Утроенная разность потенциалов утроит ток и так далее.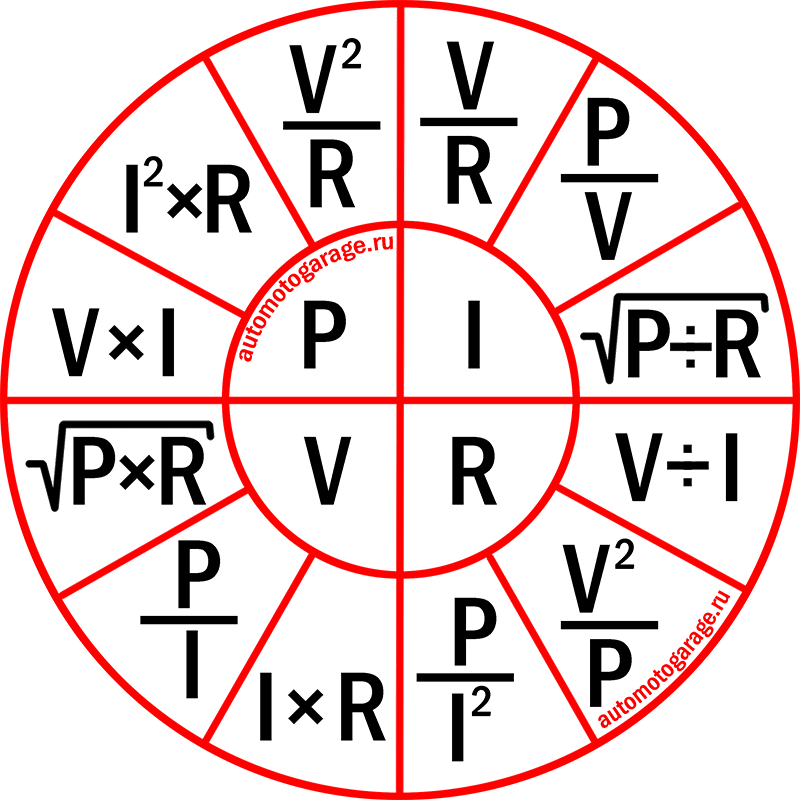 Это пропорциональное соотношение между разностью потенциалов и током называется законом Ома в честь Георга Ома. Он был немецким ученым, открывшим эту взаимосвязь в начале 1800-х годов.
Это пропорциональное соотношение между разностью потенциалов и током называется законом Ома в честь Георга Ома. Он был немецким ученым, открывшим эту взаимосвязь в начале 1800-х годов.
Закон Ома обычно выражается в математической форме. Уравнение записывается следующим образом:
E = I x R
где E = разность потенциалов между концами проводника
I = ток через проводник
R = коэффициент пропорциональности между E и I значение R называется сопротивлением проводника. он измеряется в единицах, называемых олмами. Один Ом определяется как сопротивление проводника, по которому течет ток силой 1 А, когда разность потенциалов между его концами составляет 1 В.
Греческая буква Ω (омега) используется в качестве символа для обозначения единицы измерения Ом. Например, 40 Ом означает сопротивление 40 Ом. Когда вы пишете большие или маленькие значения сопротивления, вы можете использовать префиксы для упрощения записи. В таблице показано несколько примеров использования общих префиксов.
Вы можете использовать закон Ома для вычисления третьего значения в уравнении, если вам известны любые два значения. Например, предположим, что вы знаете, что по проводнику течет ток силой 0,50 А, когда разность потенциалов между его концами равна 25 В. Какой будет сила тока, если вы увеличите разность потенциалов до 35 В?
Чтобы ответить на этот вопрос, вы можете использовать закон Ома в два этапа. Сначала вы вычисляете сопротивление проводника, используя данные тока и разности потенциалов. Затем вы используете это значение сопротивления для расчета тока при увеличении разности потенциалов до 35 В. Эти расчеты показаны на схеме.
Обратите внимание на приведенную выше схему, что единицы измерения включены в расчеты. Вы должны делать то же самое, когда решаете проблемы. Уравнение является физическим уравнением. Буквы обозначают физические величины, а не только числа.
Сопротивление и падение напряжения
Разность потенциалов от одного конца проводящего пути до другого зависит от того, к чему подключены эти концы. Но разность потенциалов между другими парами точек лишь частично зависит от того, с чем соединены концы пути. Это также зависит от сопротивления между точками по сравнению с общим сопротивлением.
Но разность потенциалов между другими парами точек лишь частично зависит от того, с чем соединены концы пути. Это также зависит от сопротивления между точками по сравнению с общим сопротивлением.
Пример поможет вам понять этот момент. Предположим, токопроводящий путь состоит из трех участков, каждый из которых имеет разное сопротивление. Эти секции соединены последовательно, то есть встык, см. схему ниже. Весь ток в пути проходит через каждый резистор.
Предположим, что три секции имеют общее сопротивление 100 Ом. Предположим далее, что разность потенциалов между концами пути равна 100 В. Используя закон Ома, можно рассчитать, что сила тока в цепи равна 1А.
Если вы измерите разность потенциалов от одного конца пути до различных точек между участками, вы обнаружите, что разность потенциалов меньше 100 В. Если ваш измерительный прибор охватывает только один участок, разность потенциалов будет еще меньше. И если он не охватывает ни одного участка, разность потенциалов равна нулю.
Вы можете думать об этом сокращении как об уменьшении разности потенциалов по мере того, как вы проходите все меньше и меньше всего пути. Общее название этого уменьшения разности потенциалов на пути — падение напряжения .
Вы можете использовать закон Ома, чтобы понять, почему разность потенциалов уменьшается, когда вы измеряете ее только на части пути. Через каждый резистор проходит такой же ток, как и по всему пути. Следовательно, по закону Ома разность потенциалов на каждом участке равна произведению этого тока на сопротивление участка.
Например, разность потенциалов на участке А в приведенной выше цепи составляет 50 В, поскольку ток равен 1 А (1 А x 50 Ом = 50 В). Если вычислить разность потенциалов на всех трех участках и сложить вместе три результата, общая сумма будет равна разности потенциалов на всем пути.
Падение напряжения пропорционально величине сопротивления в измеряемом диапазоне. Если половина полного сопротивления включена в пролет, падение напряжения равно разности потенциалов на всем пути.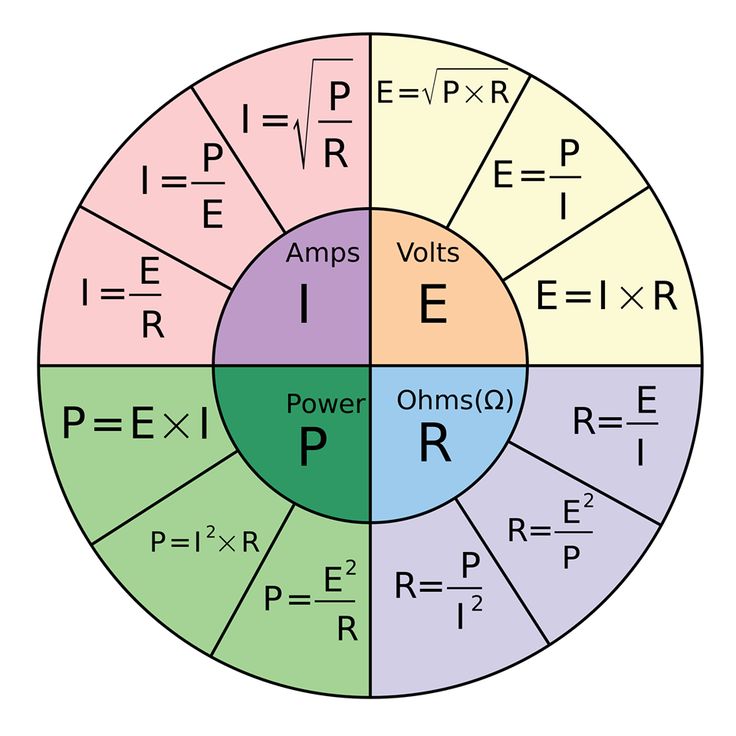 Если включить 80% полного сопротивления, падение напряжения составит 80% разности потенциалов на всем пути.
Если включить 80% полного сопротивления, падение напряжения составит 80% разности потенциалов на всем пути.
Калькулятор закона Ома
Закон Ома — это фундаментальный принцип в области электричества и электроники, который формирует основу для понимания того, как ведут себя электрические цепи. Калькулятор закона Ома — это инструмент, который поможет вам понять этот принцип, позволяя рассчитать взаимосвязь между электрическим током, напряжением и сопротивлением в цепи. С помощью калькулятора вы можете ввести любые два из трех значений (напряжение, сопротивление или ток) и быстро определить третье неизвестное значение. Это делает его ценным инструментом для инженеров-электриков, техников и энтузиастов-любителей, которым необходимо понимать поведение электрической цепи.
Независимо от того, работаете ли вы со сложной электрической системой или просто пытаетесь устранить неполадки в цепи, калькулятор закона Ома — это важный инструмент, который поможет вам понять, как работают электрические цепи.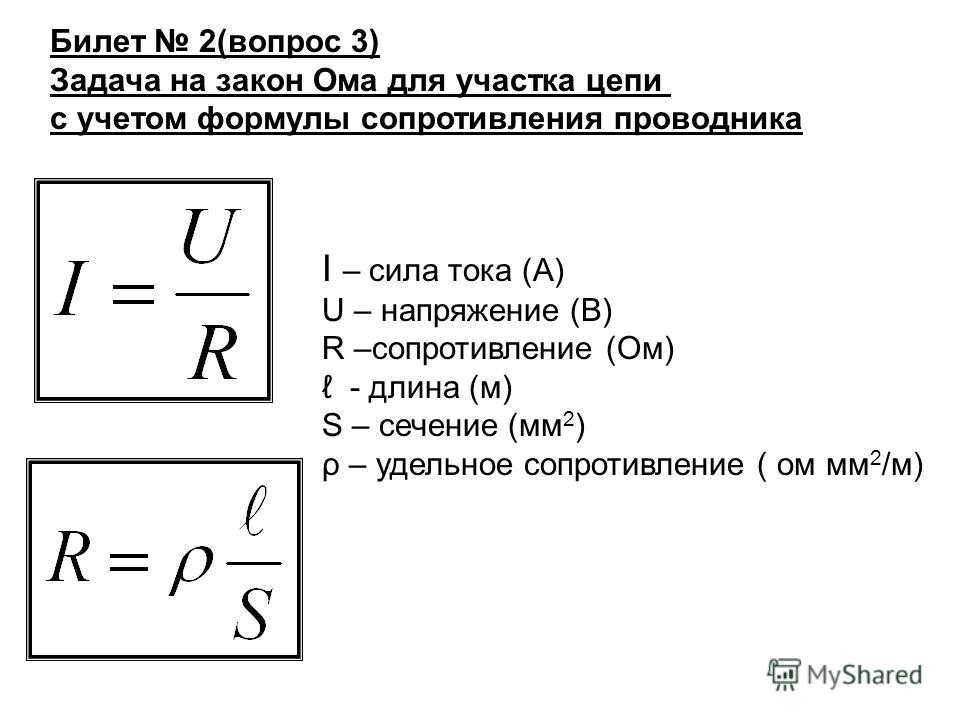 Благодаря удобному интерфейсу и простым вычислениям он предоставляет доступный способ визуализации взаимосвязей между напряжением, током и сопротивлением в цепи. Являетесь ли вы опытным профессионалом или только начинаете, калькулятор закона Ома станет незаменимым инструментом для всех, кто работает с электрическими цепями.
Благодаря удобному интерфейсу и простым вычислениям он предоставляет доступный способ визуализации взаимосвязей между напряжением, током и сопротивлением в цепи. Являетесь ли вы опытным профессионалом или только начинаете, калькулятор закона Ома станет незаменимым инструментом для всех, кто работает с электрическими цепями.
Сопротивление (Ом):
Ток (А):
© 2018-2023 electricmag.com
Понимание колеса закона Ома в 2023 году: бесплатный калькулятор закона Ома!
Если вы электрик или специалист по системам вентиляции и кондиционирования , вам необходимо четко понимать закон Ома.
Помогает описать электрические цепи и взаимосвязь между напряжением и током.
Понимание закона Ома позволит вам контролировать ток в цепи и знать, когда добавлять резисторы.
Все равно? Просто нажмите здесь для нашего бесплатного калькулятора колеса закона Ома. Вот оно!
✅ Как использовать закон Ома
Закон Ома гласит, что ток между двумя точками прямо пропорционален напряжению в двух точках электрического проводника.
Лучший способ узнать этот закон — использовать круговую диаграмму Закона Ома.
Включает простую формулу с тремя электрическими переменными: напряжением, током и сопротивлением.
R — сопротивление, измеряемое в омах, Ω I — сила тока, измеряемая в амперах или амперах , V) в углу треугольника с V наверху.Эта визуализация демонстрирует взаимосвязь между переменными .
Он также может помочь вам определить, сколько ампер будет потреблять цепь, если вы не можете использовать амперметр.
Поместите палец на единицу , которую вы хотите рассчитать, будь то сопротивление, напряжение или ток.
Об остальном позаботится формула закона Ома.
Это потому, что ток через две точки проводника прямо пропорционален его напряжению.
При этом электрический ток обратно пропорционален сопротивлению.
Вы можете представить колесо закона Ома, используя следующие математические уравнения:
- I (ток) x R (сопротивление) = V (напряжение)
- В (напряжение) / I (ток) = R (сопротивление)
- В (напряжение) / R (сопротивление) = I (ток)
Если у вас есть два известных значения, вы можете рассчитать оставшуюся единицу, используя эти формулы.
Сначала подставьте известные значения в формулу.
Во-вторых, умножьте или разделите их (или используйте калькулятор) в зависимости от других значений. Это так просто. 😉
✅
Примеры закона ОмаМы хотим найти сопротивление электрической цепи, измеренное в омах.
Мы знаем, что напряжение 24 вольта, а сопротивление цепи равно шести омам.
Как рассчитать электрический ток? Подставив известные значения в формулу закона Ома:
- 24 вольта / 6 Ом = 4 ампера
Теперь вы знаете значение отсутствующей переменной .
Вы можете использовать закон Ома, если в формуле известны две единичные переменные.
Вот еще один пример, в котором у вас есть 200 вольт и 20 ампер:
- 200 вольт / 20 ампер = 10 Ом
✅
Колесо формулы закона Ома Колесо формулы закона Ома Колесо формулы закона Ома добавляет еще одну переменную: мощность (P) измеряется в Вт .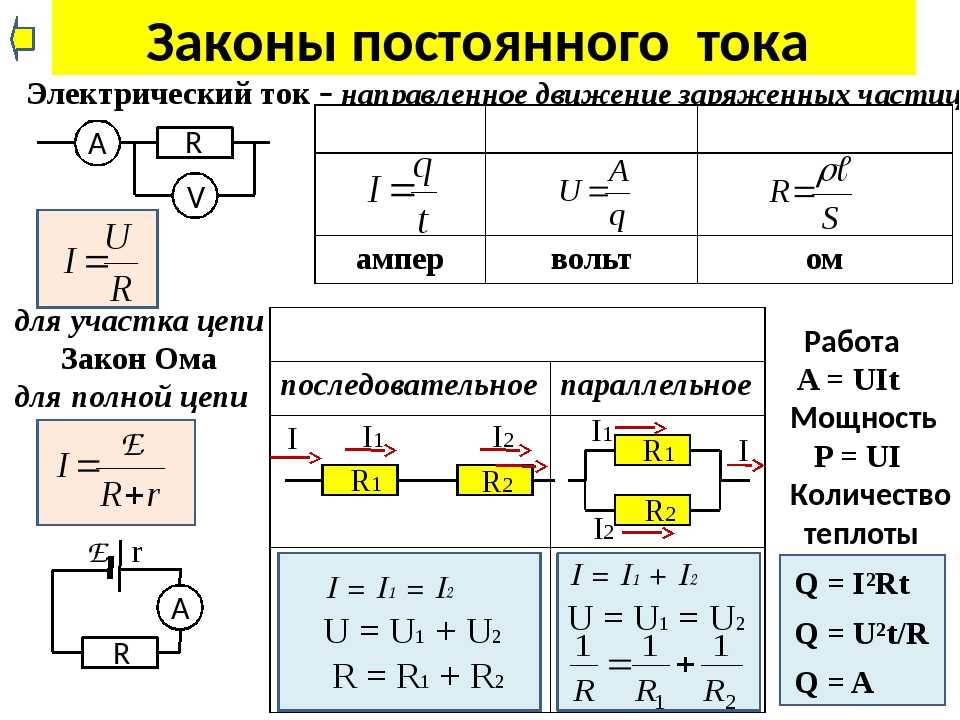
В этом случае мощность определяется как скорость передачи энергии по цепи в единицу времени, выраженная в ваттах.
Колесо формул объединяет круговую диаграмму с законом Ома. Он содержит четыре единицы.
Хотя колесо формул может показаться сложным, им так же легко пользоваться, как круговой диаграммой.
Каждый квадрант диаграммы содержит формулы, выражающие взаимосвязь между двумя переменными, независимо от того, прямо пропорциональны они или нет.
В каждом квадранте вы найдете по три формулы.
📋
Вот четыре шага, которые необходимо выполнить при использовании колеса закона Ома.1) Определите, для какой переменной вам нужно найти: мощность (P), сопротивление (R), ампер (I) и вольт (E или V).
2) Определите, какие переменные вам уже известны: мощность (P), сопротивление (R), амперы (I) и вольты (E или V).
3) Найдите формулу, в которую можно подставить два ваших значения.
4) Решить уравнение.
При решении формулы используйте совместимые единицы измерения. Если вы используете омы и амперы, это нормально, потому что они работают вместе.
Однако, если у вас есть килоомы, вы должны преобразовать число в омы, прежде чем вычислять ответ.
В противном случае вы получите гораздо меньший результат, чем ожидалось.
То же самое применимо, если вы используете киловатты вместо ватт или миллиамперы вместо ампер.
✅
Принципы закона ОмаЗакон Ома предлагает полезный способ изучения взаимосвязи между переменными.
Все, что вам нужно сделать, это изменить значение одной переменной в формуле.
В результате вы увидите пропорциональное увеличение или уменьшение ответа.
Допустим, вы хотите увеличить сопротивление. Это повлияет на другие компоненты в уравнениях.
Вот три примера, иллюстрирующие эту динамику:
- 240 вольт / 5 Ом = 48 ампер
- 240 вольт / 10 Ом = 24 ампера
- 240 вольт / 20 Ом = 12 ампер
Эти формулы показывают постепенное увеличение сопротивления.
Что происходит в результате?
Напряжение тоже растет, при условии, что сопротивление цепей не меняется.
Давайте повторим этот пример, изменив напряжение:
- 240 вольт / 10 Ом = 24 ампера
- 480 вольт / 10 Ом = 48 ампер
- 960 вольт / 10 Ом = 96 ампер
Напряжение в этих уравнениях неуклонно растет.
При этом сопротивление остается прежним.
Следовательно, электрическая энергия тока увеличивается пропорционально напряжению.
✅
Когда использовать колесо закона ОмаУ закона Ома нет недостатка в реальных приложениях .
Вы можете использовать формулы для решения широкого круга проблем в мире HVAC.
Например, это удобный вариант при работе с рабочей схемой.
Допустим, вы не можете измерить сопротивление рабочей цепи .
Одним из вариантов было бы отключить цепь и таким образом измерить сопротивление.
Однако этот вариант требует ненужного количества времени и усилий.
Колесо закона Ома позволяет рассчитать значение сопротивления в секундах.
Закон Ома также часто сочетается с законом Джоуля (в котором используется формула P (мощность) = IV для расчета мощности резистивных элементов, когда переменная неизвестна.
Например, если вы знаете ток (I) и сопротивление (R), но не напряжение, вы можете заменить V в законе Джоуля на закон Ома, чтобы найти мощность в ваттах.Вы получите P = I (IR).
Как правило, закон Ома лучше всего работает при постоянном напряжении или токе возбуждения .
Цепи постоянного тока (DC) имеют постоянный поток электричества, который легко измерить.
Если у вас нет этой стабильности, определение напряжения и тока становится сложнее.
Например, вы не можете применять формулы при работе с цепями переменного тока, также известными как изменяющиеся во времени цепи .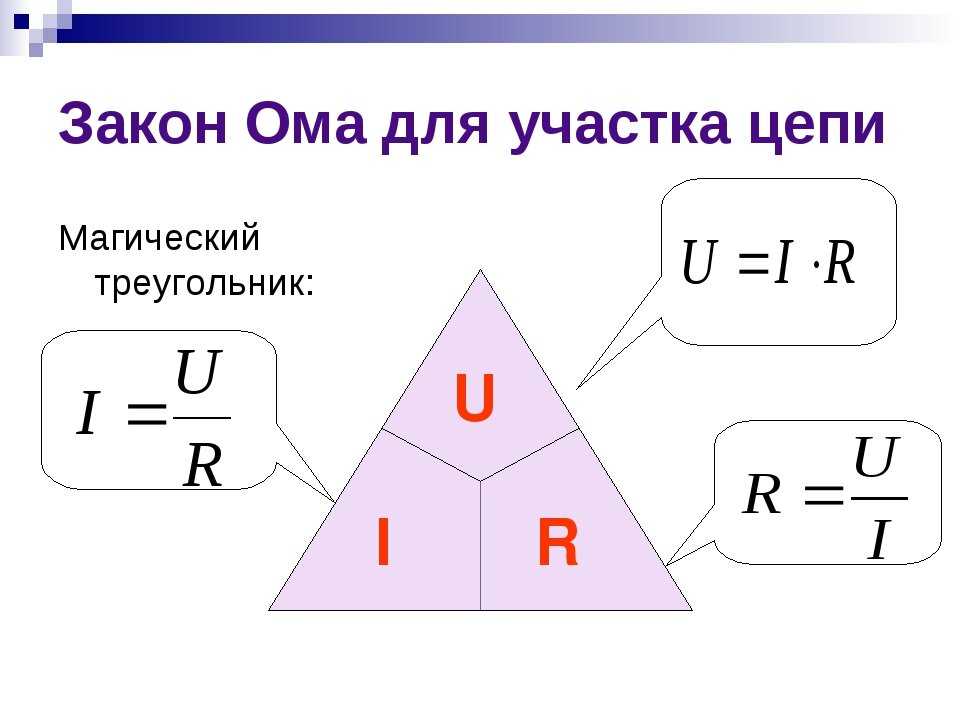
Это потому, что они не учитывают реактивное сопротивление , который вы найдете в этом типе схемы.
Обратите внимание, что вы можете настроить формулы для учета импеданса (Z) , но это урок для другой статьи.
✅
Калькулятор закона ОмаВам нужно рассчитать электрический ток в крайнем случае?
Мы подготовили для вас калькулятор закона Ома.
Калькулятор может работать с уравнениями, в которых используются мощность, напряжение, ток и сопротивление.
Введите два значения и нажмите «Ввод», чтобы решить формулу.
Хотя этот калькулятор облегчит вашу работу,
Независимо от того, являетесь ли вы учеником HVAC или опытным техником, вам необходимо четко понимать эти концепции.
Вы можете использовать формулы для решения различных задач при работе с электроэнергией, резистивными элементами, напряжением, током и т.


 Если мы говорим об определении зависимости, это подразумевает, что исследуемые величины будут изменяться."],"answer":[0]}}}]}
Если мы говорим об определении зависимости, это подразумевает, что исследуемые величины будут изменяться."],"answer":[0]}}}]}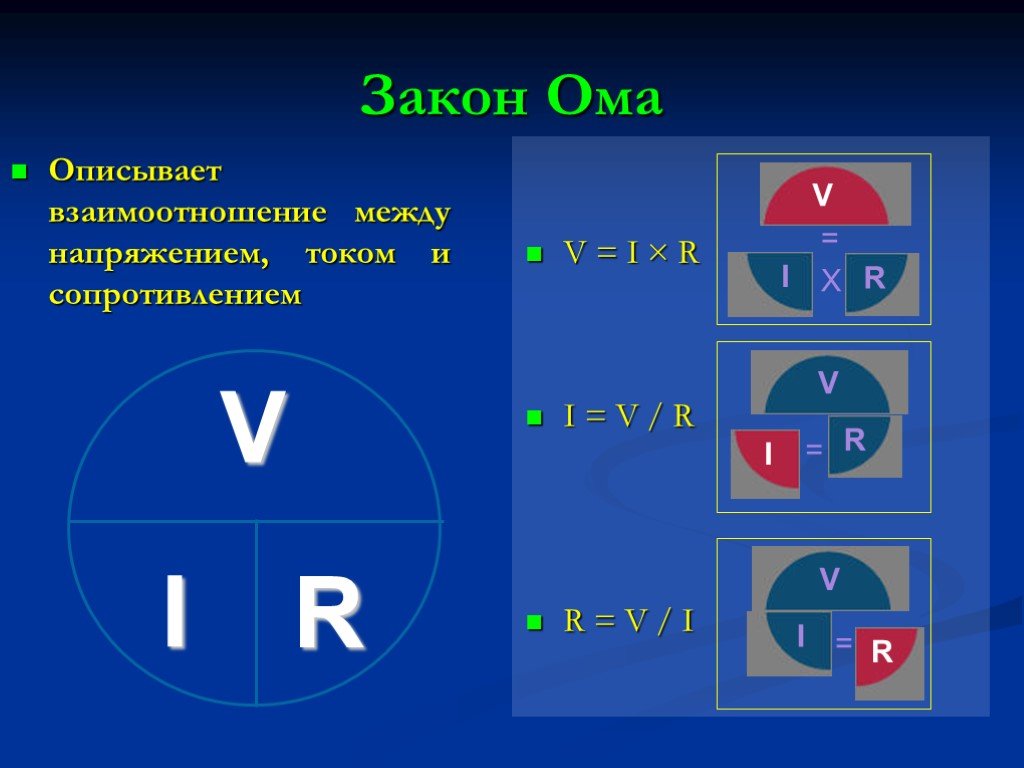 ","Это определение напряжения."],"answer":[0]}}}]}
","Это определение напряжения."],"answer":[0]}}}]} Сопротивление является свойством самого проводника и не зависит от изменений напряжения или силы тока.","",""],"answer":[0]}}}]}
Сопротивление является свойством самого проводника и не зависит от изменений напряжения или силы тока.","",""],"answer":[0]}}}]}