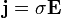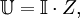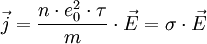простое объяснение для чайников с формулой и понятиями

Говорят: «не знаешь закон Ома – сиди дома». Так давайте же узнаем (вспомним), что это за закон, и смело пойдем гулять.

Основные понятия закона Ома

Как понять закон Ома? Нужно просто разобраться в том, что есть что в его определении. И начать следует с определения силы тока, напряжения и сопротивления.

Сила тока I

Пусть в каком-то проводнике течет ток. То есть, происходит направленное движение заряженных частиц – допустим, это электроны. Каждый электрон обладает элементарным электрическим зарядом (e= -1,60217662 × 10^-19 Кулона). В таком случае через некоторую поверхность за определенный промежуток времени пройдет конкретный электрический заряд, равный сумме всех зарядов протекших электронов.

Отношение заряда к времени и называется силой тока. Чем больший заряд проходит через проводник за определенное время, тем больше сила тока. Сила тока измеряется в

Амперах.

Напряжение U, или разность потенциалов

Это как раз та штука, которая заставляет электроны двигаться. Электрический потенциал характеризует способность поля совершать работу по переносу заряда из одной точки в другую. Так, между двумя точками проводника существует разность потенциалов, и электрическое поле совершает работу по переносу заряда.

Физическая величина, равная работе эффективного электрического поля при переносе электрического заряда, и называется напряжением. Измеряется в Вольтах. Один

Вольт – это напряжение, которое при перемещении заряда в 1 Кл совершает работу, равную 1 Джоуль.

Сопротивление R

Ток, как известно, течет в проводнике. Пусть это будет какой-нибудь провод. Двигаясь по проводу под действием поля, электроны сталкиваются с атомами провода, проводник греется, атомы в кристаллической решетке начинают колебаться, создавая электронам еще больше проблем для передвижения. Име

Ома закон — это… Что такое Ома закон?

Зако́н Ома — это физический закон, определяющий связь между напряжением, силой тока и сопротивлением проводника в электрической цепи. Назван в честь его первооткрывателя Георга Ома. Суть закона проста: сила тока в проводнике прямо пропорциональна напряжению между концами проводника, если при прохождении тока свойства проводника не изменяются. Следует также иметь в виду, что закон Ома является фундаментальным и может быть применён к любой физической системе, в которой действуют потоки частиц или полей, преодолевающие сопротивление. Его можно применять для расчёта гидравлических, пневматических, магнитных, электрических, световых, тепловых потоков и т. д., также, как и Правила Кирхгофа, однако, такое приложение этого закона используется крайне редко в рамках узко специализированных расчётов.

Закон Ома формулируется так: Сила тока в однородном участке цепи прямо пропорциональна напряжению, приложенному к участку, и обратно пропорциональна характеристике участка, которую называют электрическим сопротивлением этого участка.

Ток, А	Напряжение, В	Сопротивление, Ом	Мощность, Вт
I	U	R	P

История закона Ома

Георг Ом, проводя эксперименты с проводником, установил, что сила тока I в проводнике пропорциональна напряжению U, приложенному к его концам:

,

или

.

Коэффициент пропорциональности 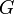назвали электропроводностью, а величину 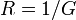принято именовать электрическим сопротивлением проводника.

Закон Ома был открыт в 1827 году.

Закон Ома в интегральной форме

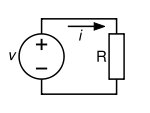
Схема, иллюстрирующая три составляющие закона Ома

Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления

Закон Ома для участка электрической цепи имеет вид:

U = RI

где:

• U — напряжение или разность потенциалов,
• I — сила тока,
• R — сопротивление.

Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:

,

где:

Закон Ома в дифференциальной форме

Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

где:

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока

Если цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), а ток является синусоидальным с циклической частотой ω, то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где:

• U = U₀e^iωt — напряжение или разность потенциалов,
• I — сила тока,
• Z = Re^—iδ — комплексное сопротивление (импеданс),
• R = (R_a²+R_r²)^1/2 — полное сопротивление,
• R_r = ωL — 1/ωC — реактивное сопротивление (разность индуктивного и емкостного),
• R_а — активное (омическое) сопротивление, не зависящее от частоты,
• δ = —arctg R_r/R_a — сдвиг фаз между напряжением и силой тока.

При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведен взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру,

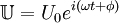U = U₀sin(ωt + φ) подбором такой , что 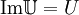. Тогда все значения токов и напряжений в схеме надо считать как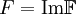

Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.

Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.

Объяснение закона Ома

Закон Ома можно просто объяснить при помощи теории Друде

См. также

Wikimedia Foundation. 2010.

ЗАКОН ОМА это что такое ЗАКОН ОМА: определение — История.НЭС

ЗАКОН ОМА

Проводник — это просто пассивная составная часть электрической цепи. Такое мнение превалировало вплоть до сороковых годов девятнадцатого столетия. Так зачем зря тратить время на его исследование? Одним из первых ученых, занявшихся вопросом проводимости проводников, был Стефано Марианини (1790–1866). К своему открытию он пришел случайно, изучая напряжение батарей. Стефано заметил, что с увеличением числа элементов Вольтова столба электромагнитное воздействие на стрелку не увеличивается заметным образом. Это заставило Марианини сразу же подумать, что каждый вольтов элемент представляет собой препятствие для прохождения тока. Он провел опыты с парами «активными» и «неактивными» (т. е. состоящими из двух медных пластинок, разделенных влажной прокладкой) и опытным путем нашел отношение, в котором современный читатель узнает частный случай закона Ома, когда сопротивление внешней цепи не принимается во внимание, как это и было в опыте Марианини. Ом признавал заслуги Марианини, хотя его труды и не стали непосредственной помощью в работе. Георг Симон Ом (1789–1854) родился в Эрлангене, в семье потомственного слесаря. Роль отца в воспитании мальчика была огромной, и, пожалуй, он всем тем, чего добился в жизни, обязан отцу. После окончания школы Георг поступил в городскую гимназию. Гимназия Эрлангена курировалась университетом и представляла собой учебное заведение, соответствующее тому времени. Успешно окончив гимназию, Георг весной 1805 года приступил к изучению математики, физики и философии на философском факультете Эрлангенского университета. Проучившись три семестра, Ом принял приглашение занять место учителя математики в частной школе швейцарского городка Готтштадта. В 1809 году Георгу было предложено освободить место и принять приглашение на должность преподавателя математики в город Нейштадт. Другого выхода не было, и к Рождеству он перебрался на новое место. Но мечта окончить университет не покидает Ома. В 1811 году он возвращается в Эрланген. Самостоятельные занятия Ома были настолько плодотворными, что он в том же году смог окончить университет, успешно защитить диссертацию и получить степень доктора философии. Сразу же по окончании университета ему была предложена должность приват-доцента кафедры математики этого же университета. Преподавательская работа вполне соответствовала желаниям и способностям Ома. Но, проработав всего три семестра, он по материальным соображениям, которые почти всю жизнь преследовали его, вынужден был подыскивать более оплачиваемую должность. Королевским решением от 16 декабря 1812 года Ом был назначен учителем математики и физики школы в Бамберге. В феврале 1816 года реальная школа в Бамберге была закрыта. Учителю математики предложили за ту же плату проводить занятия в переполненных классах местной подготовительной школы. Потеряв всякую надежду найти подходящую преподавательскую работу, отчаявшийся доктор философии неожиданно получает предложение занять место учителя математики и физики в иезуитской коллегии Кельна. Он немедленно выезжает к месту будущей работы. Здесь, в Кельне, он проработал девять лет. Именно здесь он «превратился» из математика в физика. Наличие свободного времени способствовало формированию Ома как физика-исследователя. Он с увлечением отдается новой работе, просиживая долгие часы в мастерской коллегии и в хранилище приборов. Ом занялся исследованиями электричества. Он начал свои экспериментальные исследования с определения относительных величин проводимости различных проводников. Применив метод, который стал теперь классическим, он подключал последовательно между двумя точками цепи тонкие проводники из различных материалов одинакового диаметра и изменял их длину так, чтобы получалась определенная величина тока. Как пишет В.В. Кошманов, «Ом знал о появлении работ Барлоу и Беккереля, в которых были описаны экспериментальные поиски закона электрических цепей. Знал он и о результатах, к которым пришли эти исследователи. Хотя и Ом, и Барлоу, и Беккерель в качестве регистрирующего прибора использовали магнитную стрелку, соблюдали особую тщательность в соединении цепи и источник электрического тока в принципе был одной и той же конструкции, однако полученные ими результаты были различными. Истина упорно ускользала от исследователей. Необходимо было, прежде всего, устранить самый значительный источник погрешностей, каким, по мнению Ома, была гальваническая батарея. Уже в своих первых опытах Ом заметил, что магнитное действие тока при замыкании цепи произвольной проволокой уменьшается со временем… Это снижение практически не прекращалось с течением времени, и ясно было, что заниматься поиском закона электрических цепей при таком положении дел бессмысленно. Нужно было или использовать другой тип генератора электрической энергии из уже имеющихся, или создавать новый, или разрабатывать схему, в которой изменение ЭДС не сказывалось бы на результатах опыта. Ом пошел по первому пути». После опубликования первой статьи Ома Поггендорф посоветовал ему отказаться от химических элементов и воспользоваться лучше термопарой медь — висмут, незадолго до этого введенной Зеебеком. Ом прислушался к этому совету и повторил свои опыты, собрав установку с термоэлектрической батареей, во внешнюю цепь которой включались последовательно восемь медных проволок одинакового диаметра, но разной длины. Силу тока он измерял с помощью своего рода крутильных весов, образуемых магнитной стрелкой, подвешенной на металлической нити. Когда ток, параллельный стрелке, отклонял ее, Ом закручивал нить, на которо

сколько есть законов Ома, и о чём они?

Существует всего один закон Ома, он гласит, что ток в цепи пропорционален ЭДС источника и обратнопропорционален сумме сопротивлений внешней цепи и источника тока. Выглядит он так: <img src=»//content.foto.my.mail.ru/mail/majorreserve/_answers/i-42.jpg» > На практике чаще используют закон Ома для участка цепи, он вытекает из общего закона, если считать, что сопротивление источника тока (внутреннее сопротивление) много меньше сопротивления внешнего контура, то есть r = 0,его можно записать в 3-х вариантах: <img src=»//content.foto.my.mail.ru/mail/majorreserve/_answers/i-43.jpg» >

а не 2 ли их. о чём не вспомню.

По-моему есть Закон Ома при полной и неполной цепи .. а о чем???. мда.. сложный вопрос)))

Два и один общий, и частный и всё о сопротивлении прохождению электротока. Ещё и Киргофа еасть.

Я знаю один ток в цепи прямопропорционален напряжению и обратно пропорционален сопротивлению.

Я, например, знаю только один его закон из электрофизики (в общем виде) : сила тока в проводнике прямо пропорциональна напряжению на его концах и обратнопропорциональна его сопротивлению. I = U / R.

про электрическое сопротивление, вобще то только один

Зако&#769;н О&#769;ма — это физический закон, определяющий связь между напряжением, силой тока и сопротивлением проводника в электрической цепи. Назван в честь его первооткрывателя Георга Ома. Суть закона проста: сила тока в проводнике прямо пропорциональна напряжению между концами проводника, если при прохождении тока свойства проводника не изменяются. Следует также иметь в виду, что закон Ома является фундаментальным и может быть применён к любой физической системе, в которой действуют потоки частиц или полей, преодолевающие сопротивление. Осталбные-типа для участка, цепи, для трёхфазной цепи и т. д. — частные виды закона.

Некоторые путают разные записи закона Ома с разными законами Ома. Закон Ома можно записать в интергральной и дифференциальной форме; для мгновенных, средних, действующих или комплексных величин (для переменного тока).

2 закона, для участка цепи (I=U/R) и для полной цепи (I=E/(R+r))

3 закона. 1. Закон Ома для однородного участка цепи, 2. Закон Ома для замкнутой цепи, 3. Закон Ома для неоднородного участка цепи.

4й закон ома: тело посланное нах$й назад не возвращается!

ОМА ЗАКОН — это… Что такое ОМА ЗАКОН?

— линейнаясвязь между силой тока I на участке электрич. цепи и приложеннымк этому участку напряжением U (интегральная форма О. з.) или междуплотностью тока j и напряжённостью электрич. поля в проводнике (дифференц. О. з. в интегральной форме установленв 1826 Г. Омом (G. Ohm):

U= RI,(1)

где R — коэф., зависящий от материалапроводника, его геометрии, темп-ры и называемый омическим сопротивлениемили просто сопротивлением. Соотношение (1) описывает участок электрич. электродвижущей силы. Чтобы в замкнутойсистеме проводников (электрич. цепи) мог течь стационарный ток, в этойсистеме должны быть участки, где действуют электрич. поля неэлектростатич. — эдс, действующая в неразветвлённой цепи, то вместо (1) имеем

где R — полное сопротивление замкнутойцепи, включающее внутр. сопротивление источника эдс. Это соотношение паз. Кирхгофа правила. О. з. обобщается на случай переменных (меняющихсяпо гармонич. закону) квазистационарных токов и электрич. цепей, содержащихнаряду с омическим (или, как говорят в таких случаях, активным) сопротивлениемещё и электрич. ёмкости С и индуктивности L. В этом случаеудобно записывать связи между силой тока I и напряжением U вкомплексной форме, понимая под истинными значениями этих величин ReI и ReU соответственно. Введение комплексного сопротивления, или импеданса,

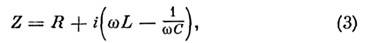
приводит к О. з. для цепи переменного тока:

U= ZI

[напряжение и ток зависят от времени позакону ехр 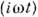].Мнимая часть в ф-ле (3) наз. реактивным сопротивлением. Правила Кирхгофаостаются в силе и для цепи, включающей наряду с активным (омическим) иреактивные сопротивления; при этом вместо омических сопротивлений участкацепи следует подставить соответствующий импеданс.
О. з. в дифференциальной форме записываетсяв виде

где коэф. пропорциональности 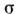наз. электропроводностью. О. з. в интегральной форме может бытьполучен из соотношения (4), если проинтегрировать последнее по объёму рассматриваемогопроводника и учесть, что 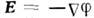и напряжение на участке АВ есть 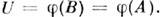Коэф. R и 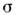связанысоотношением (для цилипдрич. проводников)

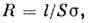
где l — длина проводника,S — площадь его поперечного сечения.
Линейная связь между j и E в проводнике обусловлена линейной зависимостью эфф. силы трения, действующейна носители заряда, от их скорости. Микроскопия, определение плотноститока 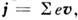где е — заряд носителя, v —

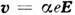его скорость (суммирование производитсяпо всем носителям заряда, находящимся в единице объёма проводника). Еслипри движении носителя на него действует сила трения, линейно зависящаяот скорости (как это имеет место при жидком трении), то и, следовательно,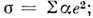коэф.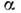наз. подвижностью носителей заряда. Отклонения от О. з. практическивсегда обусловлены изменением плотности и ср. времени свободного пробеганосителей при изменении электрич. поля (полупроводники, газовый разряд).В полуметалле висмуте отклонения от О. з. имеют место при плотностях токавыше, чем (0,5 — 1) х 10

10 А/м ² (Е. С. Боровик, 1953).В металлах отклонений от О. з. не наблюдалось, хотя для ряда металлов (медь, 10 А/м ².
При наличии в проводнике сил неэлектрпч. Е следуетпонимать сумму напряжённостей электрич. поля и поля сторонних сил, Е- > Е+ Е ^стор (напр., в случае неоднородного поля темп-рЕ ^стор ~ 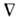Т).
В анизотропных проводниках (монокристаллы, j и Е в общем случаене совпадают, однако сохраняется линейная связь между компонентами . и Е:

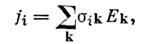
где 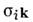— тензор проводимости; i, k= 1, 2, 3.
О. з. (4) записан для неподвижных (относительнонаблюдателя) проводников. Для движущихся со скоростью и (|и|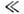с )проводниковвместо (4) следует писать

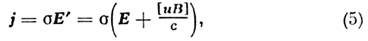
где Е’ = Е+ [ иВ]/с — электрич. поло в собств. системе проводника, Е и В -электрич. и магн. поля в системе наблюдателя. Релятивистское обобщение(5) в векторном виде можно записать так:

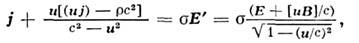
где 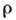— плотность заряда в системе наблюдателя,

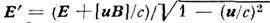— электрич. поле в собств. системе проводника.
О. з. для плазмы может иметь вид, отличныйот (4) (см. Ома обобщённый закон).

Лит.: Савельев И. В., Курс общейфизики, 2 изд., т. 2, М., 1982; Парселл Э., Электричество и магнетизм, электромагнитные волны, М., 1985.

А. И. Ахиезер, И. А. Ахиезер,

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
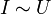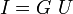
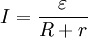