Что показывает вольтметр? | Техника и Программы

Для того чтобы понять смысл этого вопроса, давайте внимательно рассмот­рим график синусоидального напряжения на рис. 4.2. В каждый момент вре­мени величина напряжения в нем разная — соответственно, будет разной и величина тока через резистор нагрузки, на который мы подадим такое напряжение. В моменты времени, обозначенные 772 и Т (то есть кратные поло­вине периода нашего колебания) напряжение на нагрузке вообще будет рав­но нулю (ток через резистор не течет), а в промежутках между ними — меня­ется вплоть до некоей максимальной величины, равной амплитудному значению А. Точно так же будет меняться ток через нагрузку, а следователь­но, и выделяемая мощность (которая от направления тока не зависит — фи­зики скажут, что мощность есть величина скалярная, а не векторная). Но процесс выделения тепла крайне инерционен — даже такой маленький пред­мет, как волосок лампочки накаливания, за 1/100 секунды, которые проходят между пиками напряжения в промышленной сети частотой 50 Гц, не успевает заметно остыть. Поэтому нас чаще всего интересует именно средняя мощ­ность за большой промежуток времени. Чему она будет равна?

Чтобы точно ответить на этот вопрос, нужно брать интегралы: средняя мощ­ность за период есть интеграл по времени от квадрата функции напряжения. Здесь мы приведем только результат: величина средней мощности в цепи пе­ременного тока определяется т. н. действующим значением напряжения (Щ, которое для синусоидального колебания связано с амплитудным его значением (f/a) следующей формулой:. Точно такая же формула справедлива для тока. Когда говорят «пе­ременное напряжение 220 В», то всегда имеется в виду именно действующее значение. При этом амплитудное значение равно примерно 311В, что легко подсчитать, если умножить 220 на корень из двух. Это значение нужно всегда иметь в виду при выборе компонентов для работы в сетях переменного тока — если взять диод, рассчитанный на 250 В, то он легко может выйти из строя при работе в обычной сети, в которой мгновенное значение превышает 300 В, хотя действующее значение и равно 220 В. А вот для компонентов, использующих эффект нагревания (лампочек, резисторов и т. п.) при расчете допустимой мощности нужно иметь в виду именно действующее значение.

Называть действующее значение «средним» неверно, правильно называть его среднеквадратическим (по способу вычисления — через квадрат функции от времени). Но существует и понятия среднего значения, причем не одно, а даже два. Просто «среднее» (строго по смыслу названия) — сумма всех мгновенных значений за период. Так как нижняя часть синусоиды (под осью абсцисс) стро­го симметрична относительно верхней, то можно даже не брать интегралов, чтобы сообразить, что среднее значение синусоидального напряжения, пока­занного на рис. 4.2, в точности равно нулю — положительная часть компенси­рует отрицательную. Но такая величина малоинформативна, поэтому чаще ис­пользуют средневыпрямленное (среднеамплитудное) значение, при котором знаки не учитываются (то есть в интеграл подставляется абсолютная величина напряжения). Эта величина (U связана с амплитудным значением (U по формулето есть равно примерно 1,57-f/c-

Рис. 4.5. Графики некоторых колебаний несинусоидальной формы

Для постоянного напряжения и тока действующее, среднее и среднеампли-тудное значения совпадают и равны просто величине напряжения (тока). Од­нако на практике часто встречаются переменные колебания, форма которых отличается и от постоянной величины, и от строго синусоидальной. Осцил­лограммы некоторых из них показаны на рис. 4.5. Для таких сигналов приве­денные выше соотношения для действующего и среднего значений недейст­вительны! Самый простой случай изображен на рис. 4.5, в— колебание представляет собой синусоиду, но сдвинутую вверх на величину амплитуды. Такой сигнал можно представить, как сумму постоянного напряжения вели­чиной А (постоянная составляющая) и переменного синусоидального (пере­менная составляющая). Соответственно, среднее значение его будет равно А, а действующее A-^aHi. Для прямоугольного колебания (рис. 4.5, б) с равны­ми по длительности положительными и отрицательными полуволнами (сим-

метричного меандра ) соотношения очень просты: действующее значение = среднеамплитудному = амплитудному, как и для постоянного тока, а вот среднее значение равно, как и для синуса, нулю. В часто встречающемся на практике случае, когда минимум прямоугольного напряжения совпадает с нулем, то есть напряжение колеблется от нуля до напряжения питания (на рис. 4.5 не показано), такой меандр можно рассматривать аналогично случаю рис. 4.5, в, как сумму постоянного напряжения и прямоугольного. Для самого верхнего случая (рис. 4.5, а), который представляет собой синусоидальное напряжение, пропущенное через двухполупериодный выпрямитель (см. главу Р), действующее и среднеамплитудное значения будут равны соответствующим значениям для синусоиды, а вот среднее будет равно не нулю, а совпадать со среднеамплитудным. Для самого нижнего случая (рис. 4.5, г) указать все эти величины вообще непросто, так как они зависят от формы сигнала.

Но, даже выучив все это, вы все равно не сможете измерять величины напря­жений и токов несинусоидальной формы с помощью мультиметра! Не забы­вайте об этом, как и о том, что для каждого мультиметра есть предельные значения частоты колебаний — если вы включите мультиметр в цепь с ины­ми параметрами, он может показать все, что угодно — «погоду на Марсе», по распространенному выражению. Измерительные приборы для переменного напряжения проградуированы в значениях действующего напряжения, но измеряют они, как правило, среднеамплитудное (по крайней мере, большин­ство — на подробностях мы не будем сейчас задерживаться), и сообразить, как именно пересчитать показания, далеко не всегда просто. А для сложных сигналов, как на рис. 4.5, г, это выливается в сущую головоломку на уровне задач для студентов мехмата. Выручить может осциллограф и знание соот­ношений, приведенных ранее для сигналов самой распространенной формы, ну а для более сложных вычислять действующие и средние значения нам и не потребуется.

Заметки на полях

Единственный прибор, который правильно покажет значение действующего напряжения любой формы —- это аналоговый вольтметр электромагнитной системы (их легко узнать по неравномерной шкале, деления на которой к кон­цу отстоят все дальше и дальше друг от друга). Для того чтобы несинусои­дальное напряжение измерить цифровым прибором, между измеряемой вели­чиной и вольтметром можно вставить интегрирующий фильтр (фильтр нижних частот), описанный в главе 5.

Для прямоугольных напряжений, представляющих собой меандр, подобный рис. 4.5, б, существует еще одна важная характеристика. Никто ведь не за­прещает представить себе прямоугольное напряжение, в котором впадины короче или длиннее всплесков. В электронике меандр без дополнительных пояснений означает симметричную форму прямоугольного напряжения, при которой впадины строго равны всплескам по длительности, но, вообще гово­ря, это необязательно. На рис. 4.6 приведены два примера таких напряжений в сравнении с симметричным меандром. Характеристика соотношений меж­ду длительностями частей периода называется скважностью и определяется, как отношение длительности всего периода к длительности положительной части (именно так, а не наоборот, то есть величина скважности всегда боль­ше I). Для меандра скважность равна 2, для узких коротких импульсбв она будет больше 2, для широких — меньше.

Какое напряжение должен показывать вольтметр — MOREREMONTA

Для того чтобы понять смысл этого вопроса, давайте внимательно рассмот­рим график синусоидального напряжения на рис. 4.2. В каждый момент вре­мени величина напряжения в нем разная — соответственно, будет разной и величина тока через резистор нагрузки, на который мы подадим такое напряжение. В моменты времени, обозначенные 772 и Т (то есть кратные поло­вине периода нашего колебания) напряжение на нагрузке вообще будет рав­но нулю (ток через резистор не течет), а в промежутках между ними — меня­ется вплоть до некоей максимальной величины, равной амплитудному значению А. Точно так же будет меняться ток через нагрузку, а следователь­но, и выделяемая мощность (которая от направления тока не зависит — фи­зики скажут, что мощность есть величина скалярная, а не векторная). Но процесс выделения тепла крайне инерционен — даже такой маленький пред­мет, как волосок лампочки накаливания, за 1/100 секунды, которые проходят между пиками напряжения в промышленной сети частотой 50 Гц, не успевает заметно остыть. Поэтому нас чаще всего интересует именно средняя мощ­ность за большой промежуток времени. Чему она будет равна?

Чтобы точно ответить на этот вопрос, нужно брать интегралы: средняя мощ­ность за период есть интеграл по времени от квадрата функции напряжения. Здесь мы приведем только результат: величина средней мощности в цепи пе­ременного тока определяется т. н. действующим значением напряжения (Щ, которое для синусоидального колебания связано с амплитудным его значением (f/a) следующей формулой:. Точно такая же формула справедлива для тока. Когда говорят «пе­ременное напряжение 220 В», то всегда имеется в виду именно действующее значение. При этом амплитудное значение равно примерно 311В, что легко подсчитать, если умножить 220 на корень из двух. Это значение нужно всегда иметь в виду при выборе компонентов для работы в сетях переменного тока — если взять диод, рассчитанный на 250 В, то он легко может выйти из строя при работе в обычной сети, в которой мгновенное значение превышает 300 В, хотя действующее значение и равно 220 В. А вот для компонентов, использующих эффект нагревания (лампочек, резисторов и т. п.) при расчете допустимой мощности нужно иметь в виду именно действующее значение.

Называть действующее значение «средним» неверно, правильно называть его среднеквадратическим (по способу вычисления — через квадрат функции от времени). Но существует и понятия среднего значения, причем не одно, а даже два. Просто «среднее» (строго по смыслу названия) — сумма всех мгновенных значений за период. Так как нижняя часть синусоиды (под осью абсцисс) стро­го симметрична относительно верхней, то можно даже не брать интегралов, чтобы сообразить, что среднее значение синусоидального напряжения, пока­занного на рис. 4.2, в точности равно нулю — положительная часть компенси­рует отрицательную. Но такая величина малоинформативна, поэтому чаще ис­пользуют средневыпрямленное (среднеамплитудное) значение, при котором знаки не учитываются (то есть в интеграл подставляется абсолютная величина напряжения). Эта величина (U связана с амплитудным значением (U по формуле

то есть равно примерно 1,57-f/c-

Рис. 4.5. Графики некоторых колебаний несинусоидальной формы

Для постоянного напряжения и тока действующее, среднее и среднеампли-тудное значения совпадают и равны просто величине напряжения (тока). Од­нако на практике часто встречаются переменные колебания, форма которых отличается и от постоянной величины, и от строго синусоидальной. Осцил­лограммы некоторых из них показаны на рис. 4.5. Для таких сигналов приве­денные выше соотношения для действующего и среднего значений недейст­вительны! Самый простой случай изображен на рис. 4.5, в— колебание представляет собой синусоиду, но сдвинутую вверх на величину амплитуды. Такой сигнал можно представить, как сумму постоянного напряжения вели­чиной А (постоянная составляющая) и переменного синусоидального (пере­менная составляющая). Соответственно, среднее значение его будет равно А, а действующее A-^aHi. Для прямоугольного колебания (рис. 4.5, б) с равны­ми по длительности положительными и отрицательными полуволнами (сим-

метричного меандра ) соотношения очень просты: действующее значение = среднеамплитудному = амплитудному, как и для постоянного тока, а вот среднее значение равно, как и для синуса, нулю. В часто встречающемся на практике случае, когда минимум прямоугольного напряжения совпадает с нулем, то есть напряжение колеблется от нуля до напряжения питания (на рис. 4.5 не показано), такой меандр можно рассматривать аналогично случаю рис. 4.5, в, как сумму постоянного напряжения и прямоугольного. Для самого верхнего случая (рис. 4.5, а), который представляет собой синусоидальное напряжение, пропущенное через двухполупериодный выпрямитель (см. главу Р), действующее и среднеамплитудное значения будут равны соответствующим значениям для синусоиды, а вот среднее будет равно не нулю, а совпадать со среднеамплитудным. Для самого нижнего случая (рис. 4.5, г) указать все эти величины вообще непросто, так как они зависят от формы сигнала.

Но, даже выучив все это, вы все равно не сможете измерять величины напря­жений и токов несинусоидальной формы с помощью мультиметра! Не забы­вайте об этом, как и о том, что для каждого мультиметра есть предельные значения частоты колебаний — если вы включите мультиметр в цепь с ины­ми параметрами, он может показать все, что угодно — «погоду на Марсе», по распространенному выражению. Измерительные приборы для переменного напряжения проградуированы в значениях действующего напряжения, но измеряют они, как правило, среднеамплитудное (по крайней мере, большин­ство — на подробностях мы не будем сейчас задерживаться), и сообразить, как именно пересчитать показания, далеко не всегда просто. А для сложных сигналов, как на рис. 4.5, г, это выливается в сущую головоломку на уровне задач для студентов мехмата. Выручить может осциллограф и знание соот­ношений, приведенных ранее для сигналов самой распространенной формы, ну а для более сложных вычислять действующие и средние значения нам и не потребуется.

Заметки на полях

Единственный прибор, который правильно покажет значение действующего напряжения любой формы —- это аналоговый вольтметр электромагнитной системы (их легко узнать по неравномерной шкале, деления на которой к кон­цу отстоят все дальше и дальше друг от друга). Для того чтобы несинусои­дальное напряжение измерить цифровым прибором, между измеряемой вели­чиной и вольтметром можно вставить интегрирующий фильтр (фильтр нижних частот), описанный в главе 5.

Для прямоугольных напряжений, представляющих собой меандр, подобный рис. 4.5, б, существует еще одна важная характеристика. Никто ведь не за­прещает представить себе прямоугольное напряжение, в котором впадины короче или длиннее всплесков. В электронике меандр без дополнительных пояснений означает симметричную форму прямоугольного напряжения, при которой впадины строго равны всплескам по длительности, но, вообще гово­ря, это необязательно. На рис. 4.6 приведены два примера таких напряжений в сравнении с симметричным меандром. Характеристика соотношений меж­ду длительностями частей периода называется скважностью и определяется, как отношение длительности всего периода к длительности положительной части (именно так, а не наоборот, то есть величина скважности всегда боль­ше I). Для меандра скважность равна 2, для узких коротких импульсбв она будет больше 2, для широких — меньше.

Для того чтобы понять смысл этого вопроса, давайте внимательно рассмот­рим график синусоидального напряжения на рис. 4.2. В каждый момент вре­мени величина напряжения в нем разная — соответственно, будет разной и величина тока через резистор нагрузки, на который мы подадим такое напряжение. В моменты времени, обозначенные 772 и Т (то есть кратные поло­вине периода нашего колебания) напряжение на нагрузке вообще будет рав­но нулю (ток через резистор не течет), а в промежутках между ними — меня­ется вплоть до некоей максимальной величины, равной амплитудному значению А. Точно так же будет меняться ток через нагрузку, а следователь­но, и выделяемая мощность (которая от направления тока не зависит — фи­зики скажут, что мощность есть величина скалярная, а не векторная). Но процесс выделения тепла крайне инерционен — даже такой маленький пред­мет, как волосок лампочки накаливания, за 1/100 секунды, которые проходят между пиками напряжения в промышленной сети частотой 50 Гц, не успевает заметно остыть. Поэтому нас чаще всего интересует именно средняя мощ­ность за большой промежуток времени. Чему она будет равна?

Чтобы точно ответить на этот вопрос, нужно брать интегралы: средняя мощ­ность за период есть интеграл по времени от квадрата функции напряжения. Здесь мы приведем только результат: величина средней мощности в цепи пе­ременного тока определяется т. н. действующим значением напряжения (Щ, которое для синусоидального колебания связано с амплитудным его значением (f/a) следующей формулой:. Точно такая же формула справедлива для тока. Когда говорят «пе­ременное напряжение 220 В», то всегда имеется в виду именно действующее значение. При этом амплитудное значение равно примерно 311В, что легко подсчитать, если умножить 220 на корень из двух. Это значение нужно всегда иметь в виду при выборе компонентов для работы в сетях переменного тока — если взять диод, рассчитанный на 250 В, то он легко может выйти из строя при работе в обычной сети, в которой мгновенное значение превышает 300 В, хотя действующее значение и равно 220 В. А вот для компонентов, использующих эффект нагревания (лампочек, резисторов и т. п.) при расчете допустимой мощности нужно иметь в виду именно действующее значение.

Называть действующее значение «средним» неверно, правильно называть его среднеквадратическим (по способу вычисления — через квадрат функции от времени). Но существует и понятия среднего значения, причем не одно, а даже два. Просто «среднее» (строго по смыслу названия) — сумма всех мгновенных значений за период. Так как нижняя часть синусоиды (под осью абсцисс) стро­го симметрична относительно верхней, то можно даже не брать интегралов, чтобы сообразить, что среднее значение синусоидального напряжения, пока­занного на рис. 4.2, в точности равно нулю — положительная часть компенси­рует отрицательную. Но такая величина малоинформативна, поэтому чаще ис­пользуют средневыпрямленное (среднеамплитудное) значение, при котором знаки не учитываются (то есть в интеграл подставляется абсолютная величина напряжения). Эта величина (U связана с амплитудным значением (U по формулето есть равно примерно 1,57-f/c-

Рис. 4.5. Графики некоторых колебаний несинусоидальной формы

Для постоянного напряжения и тока действующее, среднее и среднеампли-тудное значения совпадают и равны просто величине напряжения (тока). Од­нако на практике часто встречаются переменные колебания, форма которых отличается и от постоянной величины, и от строго синусоидальной. Осцил­лограммы некоторых из них показаны на рис. 4.5. Для таких сигналов приве­денные выше соотношения для действующего и среднего значений недейст­вительны! Самый простой случай изображен на рис. 4.5, в— колебание представляет собой синусоиду, но сдвинутую вверх на величину амплитуды. Такой сигнал можно представить, как сумму постоянного напряжения вели­чиной А (постоянная составляющая) и переменного синусоидального (пере­менная составляющая). Соответственно, среднее значение его будет равно А, а действующее A-^aHi. Для прямоугольного колебания (рис. 4.5, б) с равны­ми по длительности положительными и отрицательными полуволнами (сим-

метричного меандра ) соотношения очень просты: действующее значение = среднеамплитудному = амплитудному, как и для постоянного тока, а вот среднее значение равно, как и для синуса, нулю. В часто встречающемся на практике случае, когда минимум прямоугольного напряжения совпадает с нулем, то есть напряжение колеблется от нуля до напряжения питания (на рис. 4.5 не показано), такой меандр можно рассматривать аналогично случаю рис. 4.5, в, как сумму постоянного напряжения и прямоугольного. Для самого верхнего случая (рис. 4.5, а), который представляет собой синусоидальное напряжение, пропущенное через двухполупериодный выпрямитель (см. главу Р), действующее и среднеамплитудное значения будут равны соответствующим значениям для синусоиды, а вот среднее будет равно не нулю, а совпадать со среднеамплитудным. Для самого нижнего случая (рис. 4.5, г) указать все эти величины вообще непросто, так как они зависят от формы сигнала.

Но, даже выучив все это, вы все равно не сможете измерять величины напря­жений и токов несинусоидальной формы с помощью мультиметра! Не забы­вайте об этом, как и о том, что для каждого мультиметра есть предельные значения частоты колебаний — если вы включите мультиметр в цепь с ины­ми параметрами, он может показать все, что угодно — «погоду на Марсе», по распространенному выражению. Измерительные приборы для переменного напряжения проградуированы в значениях действующего напряжения, но измеряют они, как правило, среднеамплитудное (по крайней мере, большин­ство — на подробностях мы не будем сейчас задерживаться), и сообразить, как именно пересчитать показания, далеко не всегда просто. А для сложных сигналов, как на рис. 4.5, г, это выливается в сущую головоломку на уровне задач для студентов мехмата. Выручить может осциллограф и знание соот­ношений, приведенных ранее для сигналов самой распространенной формы, ну а для более сложных вычислять действующие и средние значения нам и не потребуется.

Заметки на полях

Единственный прибор, который правильно покажет значение действующего напряжения любой формы —- это аналоговый вольтметр электромагнитной системы (их легко узнать по неравномерной шкале, деления на которой к кон­цу отстоят все дальше и дальше друг от друга). Для того чтобы несинусои­дальное напряжение измерить цифровым прибором, между измеряемой вели­чиной и вольтметром можно вставить интегрирующий фильтр (фильтр нижних частот), описанный в главе 5.

Для прямоугольных напряжений, представляющих собой меандр, подобный рис. 4.5, б, существует еще одна важная характеристика. Никто ведь не за­прещает представить себе прямоугольное напряжение, в котором впадины короче или длиннее всплесков. В электронике меандр без дополнительных пояснений означает симметричную форму прямоугольного напряжения, при которой впадины строго равны всплескам по длительности, но, вообще гово­ря, это необязательно. На рис. 4.6 приведены два примера таких напряжений в сравнении с симметричным меандром. Характеристика соотношений меж­ду длительностями частей периода называется скважностью и определяется, как отношение длительности всего периода к длительности положительной части (именно так, а не наоборот, то есть величина скважности всегда боль­ше I). Для меандра скважность равна 2, для узких коротких импульсбв она будет больше 2, для широких — меньше.

Выясняем, что должен показывать вольтметр при проверке состояния аккумулятора.

В былые времена аккумуляторы были настолько дефицитным товаром, что автовладельцы буквально тряслись над ними, всеми силами стараясь прислушаться к их самочувствию. У самых опытных была припасена не только дистиллированная вода, но и кислота. Ареометр считался обязательным прибором, а зарядные устройства внушали уважение одними только массогабаритными показателями. Честно говоря, принципиальных изменений с тех пор батареи не претерпели. Но вот владельцы пообленились: самым сложным прибором для проверки состояния батареи для них теперь является разве что вольтметр.

Не секрет, что за вольтметром мы лезем обычно тогда, когда батарея уже приказала долго жить или находится на грани.

проверка аккумулятора вольтметром

проверка аккумулятора вольтметром

Каким же должно быть напряжение на клеммах аккумулятора и как его правильно мерить?

Вообще говоря, надо контролировать так называемое напряжение разомкнутой цепи (НРЦ). Его проверяют на холодном двигателе при снятой клемме — иначе откуда взяться разомкнутой цепи? Но на практике часто халтурят: проводят замеры не снимая клемму. Грешат этим даже бывалые электрики. Если же проводить измерения правильно, то НРЦ должно составлять не менее 12,5 В для батареи любого типа. При этом напряжение чаще всего окажется чуть выше.

проверка аккумулятора вольтметром

А если напряжение ниже? Извольте подзарядить! После зарядки и выдержки отключенной от зарядного устройства батареи в течение 10–15 ч НРЦ должно составлять 12,6–12,8 В. Иногда бывает и чуть больше.

Что еще можно померить? Конечно, напряжение при работающем двигателе: сразу будет ясно, идет зарядка от генератора или нет.

проверка аккумулятора вольтметром

Кстати о подзарядке. Напряжение на клеммах после ее окончания будет меняться. Например, в конце заряда (вскоре после отключения зарядного устройства) оно может составлять 13,5 В, а через сутки — допустим, 12,6 В. Это нормальное явление.

Аккумулятор

При взгляде на форму батареи, с которой мы начали разговор про напряжение, сразу становится ясно: тут вольтметр уже не нужен. Раздуло корпус вследствие замерзания электролита. И хотя корпус выдержал, но структура пластин аккумулятора безвозвратно повреждена ледяными кристаллами. Придется покупать новый аккумулятор. А всего-то нужно было либо периодически подзаряжать батарею от сетевого зарядного устройства, либо периодически пускать двигатель. Во втором случае пускать двигатель приходится на довольно продолжительное время, примерно 20–30 минут после прогрева, чтобы мотор поработал на повышенных оборотах. В противном случае энергия, потраченная на работу стартера, не будет восполнена.

Ну, а идеальный вариант длительного хранения аккумулятора зимой выработали еще наши деды. Снять с машины, подзарядить, хранить в прохладном помещении и иногда проверять плотность, в крайнем случае напряжение. И как все живое — ждем весны!

Электрическое напряжение. Единицы напряжения. Вольтметр

1008. Выразите в вольтах напряжение: 400 мВ; 80 кВ; 200 мВ; 300 мВ.

1009. Можно ли от одного и того же источника тока получить различную силу тока? Как это сделать?
Можно, включив в сеть переменное сопротивление.

1010. Сопротивление осветительного прибора 1,2 Ом, напряжение 48 В. Какой силы ток проходит через прибор?

1011. Определите силу тока, проходящего через лампочку накаливания, если напряжение на ней 110 В, а сопротивление ее во время горения 80 Ом.

1012. Напряжение на электрическом утюге равно 220 В, а сопротивление его нагревательного элемента 50 Ом. Какой силы ток течет через утюг?

1013. В электрическую сеть напряжением 220 В включен электрический звонок сопротивлением 480 Ом. Какова сила тока, текущего через звонок?

1014. Сила тока в волоске электролампочки равна 0,8 А. Сопротивление волоска в нагретом состоянии 275 Ом. Найдите напряжение, при котором горит лампочка.

1015. По металлическому проводу сопротивлением 20 Ом идет ток силой 0,2 А. Определите напряжение на концах провода.

1016. Амперметр, включенный в цепь с никелиновой проволокой сопротивлением 2,5 Ом, показывает силу тока 1,2 А. Какое напряжение покажет вольтметр, подключенный к концам никелиновой проволоки?

1017. Через электрическую лампочку сопротивлением 440 Ом течет ток силой 0,5 А. При каком напряжении в сети горит лампочка?

1018. Сопротивление человеческого тела в среднем составляет 50 кОм. Какое напряжение опасно для человека, если известно, что ток силой более 0,01 А может оказаться смертельным?

1019. В трамвайной сети напряжение 575 В. Средняя сила тока, проходящего по обмотке трамвайного мотора, 71 А. Каково сопротивление обмотки?

1020. Сила тока в электрическом кипятильнике 5 А при напряжении в сети 110 В. Определите сопротивление кипятильника.

1021. Какое сопротивление имеет вольтметр, рассчитанный на 127 В, если по нему течет ток, равный 0,02 А?

1022. Определите сопротивление спирали лампы накаливания, если через нее течет ток силой 0,12 А при напряжении на концах сети, равном 120 В.

1023. Сила тока в лампе 0,25 А при напряжении 120 В. Каково сопротивление горящей лампы?

1024. Каким должно быть напряжение на концах участка цепи, чтобы сила тока в проводнике равнялась 1,0 А, если при напряжении 3 В сила тока в этом же проводнике равна 0,5 А.

1025. Вольтметр показывает напряжение 2,5 В на концах участка цепи сопротивлением 1,4 Ом. Включенный в эту же цепь амперметр показывает силу тока 1,8 А. Верно ли показание амперметра?

1026. Изобразите графически зависимость тока от напряжения на участке цепи.

1027. Можно ли амперметр сопротивлением 0,02 Ом, рассчитанный на максимальный ток 10 А, подключить непосредственно к аккумулятору, напряжение на полюсах которого 2 В?

1028. Используя график зависимости тока от напряжения (рис. 100), найдите сопротивление.

1029. Амперметр, включенный в цепь, показывает силу тока 1,8 А. Правильны ли показания амперметра, если выверенный вольтметр показывает на концах сопротивления
1,4 Ом напряжение 2,5 В?

1030. Определите сопротивление обмотки мотора трамвайного вагона, если при испытании напряжением 57,5 В оказалось, что сила тока в ней равна 71 А.

 

1031. Каково сопротивление нити накала электролампочки, если через нее проходит ток силой 0,12 А при напряжении на концах нити, равном 120 В?

1032. Определите напряжение на концах проводника, сопротивление которого равно 20 Ом, если по проводнику идет ток силой 0,2 А.

1033. Какое напряжение покажет вольтметр, подключенный к концам никелиновой проволоки с сопротивлением 2,5 0м, если амперметр, включенный в цепь, показал силу тока 1,2 А?

1034. К ртутному столбику длиной 100 см и сечением 1 мм² приложено напряжение 1 В. Определите силу тока. Попытайтесь ответить, почему за единицу сопротивления выбрано сопротивление ртутного столбика длиной не 100 см, а 106,3 см.

 

Какое напряжение должен показывать вольтметр

В радиолюбительской практике это наиболее распространенный вид измерений. Например, при ремонте телевизора измеряются напряжения в характерных точках устройства, а именно на выводах транзисторов и микросхем. Если есть под рукой принципиальная схема, и на ней указаны режимы транзисторов и микросхем, то найти неисправность опытному мастеру не составит труда.

При налаживании конструкций, собранных своими руками, без измерения напряжений обойтись нельзя. Исключения составляют лишь классические схемы, про которые пишут примерно так: «Если конструкция собрана из исправных деталей, то наладки не требуется, заработает сразу».

Как правило, это классические схемы электроники, например, мультивибратор. Такой же подход может получиться даже к усилителю звуковой частоты, если он собран на специализированной микросхеме. Как наглядный пример TDA 7294 и еще много микросхем этой серии. Но качество «интегральных» усилителей невелико, и истинные ценители строят свои усилители на дискретных транзисторах, а порою на электронных лампах. И вот тут-то без налаживания и связанных с этим измерений напряжений просто не обойтись.

Как и что предстоит измерять

Показано на рисунке 1.

Возможно, кто-то скажет, мол, что тут можно измерять? И какой смысл собирать подобную цепь? Да, практического применения для такой схемы найти, наверно, трудно. А для познавательных целей она вполне подойдет.

Прежде всего, следует обратить внимание на то, как подключается вольтметр. Поскольку на рисунке показана цепь постоянного тока, то и вольтметр подключается с соблюдением полярности, указанной на приборе в виде знаков «плюс» и «минус». В основном это замечание справедливо для стрелочного прибора: при несоблюдении полярности стрелка отклонится в обратную сторону, по направлению к нулевому делению шкалы. Так что получится какой-то отрицательный ноль.

Цифровые приборы, мультиметры, в этом плане более демократичны. Даже если измерительные щупы подключены в обратной полярности, напряжение все равно будет измерено, только на шкале перед результатом появится знак «минус».

Еще на что следует обратить внимание при измерении напряжений это диапазон измерений прибора. Если предполагаемое напряжение находится в пределах, например, 10…200 милливольт, то такому диапазону соответствует шкала прибора 200 милливольт, а измерение упомянутого напряжения по шкале 1000 вольт вряд ли даст вразумительный результат.

Так же следует выбирать диапазон измерений и в других случаях. Для измеряемого напряжения 100 вольт вполне подойдет диапазон 200В и даже 1000В. Результат будет один и тот же. Это что касается современного мультиметра.

Если же измерения производятся старым добрым стрелочным прибором, то для измерения напряжения 100В следует выбрать диапазон измерений, когда показания находятся в середине шкалы, что позволяет осуществить более точный отсчет.

И еще одна классическая рекомендация по использованию вольтметра, а именно: если величина измеряемого напряжения неизвестна, то измерения следует начинать, установив вольтметр на самый большой диапазон. Ведь если измеряемое напряжение будет 1В, а диапазон будет 1000В, самая большая опасность в неверных показаниях прибора. Если же получится наоборот, — диапазон измерений 1В, а измеряемое напряжение 1000, покупки нового прибора просто не избежать.

Что покажет вольтметр

Но, пожалуй, вернемся к рисунку 1, и попробуем определить, что, же покажут оба вольтметра. Для того, чтобы это определить, придется воспользоваться законом Ома. Задачу можно решить за несколько шагов.

Во-первых, рассчитать ток в цепи. Для этого надо напряжение источника (на рисунке это гальваническая батарея с напряжением 1,5 В) разделить на сопротивление цепи. При последовательном соединении резисторов это будет просто сумма их сопротивлений. В виде формулы это выглядит примерно так: I = U / (R1 + R2) = 4,5 / (100 + 150) = 0,018 (А) = 180 (мА).

Маленькое замечание: если выражение 4,5 / (100 + 150) скопировать в буфер обмена, затем вставить в окно виндоус-калькулятора, то после нажатия клавиши «равно» будет получен результат вычислений. На практике вычисляются еще более сложные выражения, содержащие квадратные и фигурные скобки, степени и функции.

Во-вторых, получить результаты измерений, как падение напряжения на каждом резисторе:

U1 = I * R1 = 0,018 * 100 = 1,8 (В),

U2 = I * R2 = 0,018 * 150 = 2,7 (В),

Для проверки правильности вычислений достаточно сложить оба получившиеся значения падения напряжений. Сумма должна быть равна напряжению батареи.

Возможно, у кого-то может возникнуть вопрос: «А если делитель будет не из двух резисторов, а из трех или даже из десяти? Как определить падение напряжения на каждом из них?». Точно так же, как и в описанном случае. Сначала надо определить общее сопротивление цепи и рассчитать общий ток.

После чего этот уже известный ток просто умножить на сопротивление соответствующего резистора. Иногда такие вычисления делать приходится, но тут тоже есть одно но. Чтобы не сомневаться в полученных результатах ток в формулы следует подставлять в Амперах, а сопротивление в Омах. Тогда, вне всяких сомнений, результат получится в Вольтах.

Входное сопротивление вольтметра

Сейчас все привыкли пользоваться приборами китайского производства. Но это не говорит о том, что качество у них никудышное. Просто в отечестве никто не додумался до производства собственных мультиметров, а стрелочные тестеры делать, видимо, разучились. Просто обидно за державу.

Рис. 2. Мультиметр DT838

Когда-то в инструкциях к приборам указывались их технические характеристики. В частности для вольтметров и стрелочных тестеров это было входное сопротивление, и указывалось оно в Килоомах/Вольт. Были приборы с сопротивлением 10 К/В и 20 К/В. Последние считались более точными, поскольку меньше подсаживали измеряемое напряжение и показывали более точный результат. Сказанное можно подтвердить рисунком 3.

На рисунке показан делитель напряжения из двух резисторов. Сопротивление каждого резистора 1КОм, напряжение питания 3В. Нетрудно догадаться, даже считать ничего не надо, что на каждом резисторе будет ровно половина напряжения.

Теперь представим, что измерения проводятся прибором ТЛ4, который в режиме измерения напряжений имеет входное сопротивление 10КОм/В. При указанном на схеме напряжении вполне подходит предел измерений 3В, на котором полное сопротивление вольтметра составит 10*3 = 30(КОм).

Таким образом, получается, что параллельно резистору сопротивлением в 1КОм подключено еще 30КОм. Тогда общее сопротивление при параллельном включении составит 999,999Ом. Хотя и несколько меньше меньшего, но не намного. Поэтому погрешность результата измерения напряжения будет незначительна.

В случае, если оба резистора делителя имеют номинал 1 мегаом, то результаты расчета будут выглядеть примерно так:

Суммарное сопротивление параллельно соединенного вольтметра и резистора R1 будет меньше меньшего, а по расчету составит 29,126КОм. Кто не верит, может для практики пересчитать по формулам для параллельного соединения сопротивлений.

Общий ток в цепи делителя: I = U / (R1 + R2) = 3 / (1000 + 29,126) = 0,0029150949446423470012418304464176 (мА).

Значения сопротивлений подставлены в килоомах, поэтому ток получился в миллиамперах. Тогда получается, что вольтметр покажет

0,0029150949446423470012418304464176 * 29,126 ≈ 0,085 В.

А ожидалась половина, т.е. полтора вольта! Если ток в миллиамперах, сопротивление в килоомах, то результат получается в вольтах. Хотя и не по системе СИ, но иногда поступают и так.

Конечно, такой делитель несколько не реален: зачем на напряжение всего 3В ставить резисторы сопротивлением 1 мегаом? А может где-нибудь такой делитель и применяется, вот только напряжение на нем надо мерить совсем другим прибором.

Например, один из самых дешевых китайских мультиметров DT838, на всех диапазонах измерения напряжений обладает входным сопротивлением 1 мегаом, намного выше, чем прибор в предыдущем примере. Но это вовсе не говорит о том, что стрелочные авометры отжили свой век. В некоторых случаях они просто незаменимы.

Измерение переменных напряжений

Все методы и рекомендации, касающиеся измерения постоянных напряжений, справедливы и для переменных: вольтметр включается параллельно участку цепи, входное сопротивление вольтметра должно быть по возможности большим, диапазон измерений должен соответствовать измеряемому напряжению. Но при измерении переменных напряжений следует учитывать еще два фактора, которых постоянное напряжение не имеет. Это частота напряжения и его форма.

Измерения могут проводиться двумя типами приборов: либо современным цифровым мультиметром, либо «допотопным» стрелочным тестером. Естественно, что оба прибора при таком измерении включаются в режим измерения переменных напряжений. Оба прибора рассчитаны на измерение напряжений синусоидальной формы, и при этом будут показывать действующее значение напряжения.

Действующее напряжение U составляет 0,707 амплитудного напряжения Uм.

U = Uм/√2 = 0,707 * Uм, откуда можно сделать вывод, что Uм = U * √2 = 1,41 * U

Здесь уместно привести широко распространенный пример. При измерении переменного напряжения прибор показал 220В, значит, амплитудное значение по формуле получится

Uм = U * √2 = 1,41 * U = 220 * 1,41 = 310В.

Этот расчет подтверждается каждый раз, когда сетевое напряжение выпрямляется диодным мостом после которого стоит хотя бы один электролитический конденсатор: если померить постоянное напряжение на выходе моста, то прибор покажет как раз 310В. Эту цифру следует запомнить, она может пригодиться при разработке и ремонте импульсных блоков питания.

Указанная формула справедлива для всех напряжений, если они будут иметь синусоидальную форму. Например, после понижающего трансформатора имеется 12В переменки. Тогда после выпрямления и сглаживания на конденсаторе получится

12 * 1,41 = 16,92 почти 17В. Но это если не подключена нагрузка. При подключенной нагрузке постоянное напряжение подсядет почти до 12В. В случае, когда форма напряжения иная, чем синусоида эти формулы не работают, приборы показывают не то, что от них ожидалось. На этих напряжениях измерения производятся другими приборами, например, осциллографом.

Еще один фактор, влияющий на показания вольтметра это частота. Например, цифровой мультиметр DT838 согласно своих характеристик меряет переменные напряжения в диапазоне частот 45…450Гц. Несколько лучше в этом плане выглядит старенький стрелочный тестер ТЛ4.

В диапазоне напряжений до 30В его частотный диапазон составляет 40…15000Гц (почти весь звуковой диапазон, можно пользоваться при настройке усилителей), но с увеличением напряжения допустимая частота падает. В диапазоне 100В это 40…4000Гц, 300В 40…2000Гц, а в диапазоне 1000В всего 40…700Гц. Вот тут уже бесспорная победа над цифровым прибором. Эти цифры также справедливы лишь для напряжений синусоидальной формы.

Хотя иногда и не требуется никаких данных о форме, частоте и амплитуде переменных напряжений. Например, как определить работает гетеродин коротковолнового приемника или нет? Почему приемник ничего не «ловит»?

Оказывается, все очень просто, если воспользоваться стрелочным прибором. Надо включить его на любой предел измерения переменных напряжений и одним щупом (!) коснуться выводов транзистора гетеродина. Если есть высокочастотные колебания, то они продетектируются диодами внутри прибора, и стрелка отклонится на некоторую часть шкалы.

Вольтметр – это прибор, назначение которого измерять электродвижущую силу (ЕДС) на определенном участке электрической цепи, или проще – прибор для измерениянапряжения (разность электрических потенциалов). Этот прибор всегда подключается параллельно элементу питания или нагрузке. Измеренное значение вольтметр показывает в Вольтах.

Если говорить об идеальном вольтметре, то он должен обладать бесконечным внутренним сопротивлением, чтобы точно измерять напряжение и не оказывать побочного воздействия на цепь. Именно поэтому в приборах высокого класса стараются сделать максимально возможным внутреннее сопротивление, от которого зависит точность измерения и помехи, создаваемые вольтметром в электрической цепи.

Рисунок — Формулы измерения напряжения

Если говорить о способе монтажа, то вольтметры подразделяют на три основные группы:

Как становится ясно из названия, стационарные приборы используются там, где необходим постоянный контроль, щитовые – в распределительных щитках и на приборных панелях, а переносные – в компактных приборах, которые можно использовать в любом месте.

Рисунок — Схема подключения вольтметра

Посмотрите видео о подключении вольтметра:

По назначению все вольтметры делятся

Вольтметры переменного тока, как и постоянного используются для измерений в сетях с соответствующим типом тока, а вот селективные – могут отделять гармоническую составляющую сложного сигнала, и определять среднеквадратическое значение напряжения.

Импульсный вольтметр обычно используют для измерений амплитуды постоянных импульсных сигналов, а также они способны точно определить амплитуду одиночного импульса.

Фазочувствительные приборы могут измерять изменения составляющих комплексных напряжений, благодаря чему становится возможным точное исследование амплитудно-фазовой характеристики усилителей, и прочих подобных схем.

По принципу действия различают электронные (цифровые или аналоговые), и электромеханические вольтметры (электромагнитные, термоэлектрические, а также магнитоэлектрические, электродинамические и электростатические).

Все электромеханические приборы, за исключением термоэлектрических, по сути, являются обычным измерительным механизмом с показывающим устройством. Во всех них для расширения пределов измерений применяются дополнительные сопротивления.

Приборы данной категории, не смотря на довольно высокое внутреннее сопротивление, имеют относительно большую погрешность, что делает невозможным их использование в ходе экспериментов и исследований, где требуется повышенная точность данных.

Термоэлектрический вольтметр использует для замеров электродвижущую силу одной или нескольких термопар, которые греются из-за тока входящего сигнала. Они более точны и компактны, в сравнении с электромеханическими измерителями напряжения.

Электронные вольтметры в свою очередь подразделяются на цифровые и аналоговые.

Цифровой вольтметр преобразует постоянное значение напряжения в цифровой сигнал, который и выводится на табло прибора. Делается это при помощи аналого-цифрового преобразователя.

В аналоговых вольтметрах помимо магнитоэлектрического измерителя и дополнительных резисторов в обязательном порядке присутствует измерительный усилитель, позволяющий в несколько раз повысить внутреннее сопротивление прибора, и соответственно – улучшить точность показаний.

Рассмотрим несколько вольтметров разных производителей

1. В3-57 — микровольтметр

Измерительное устройство модели В3-57 — вольтметр-преобразователь среднеквадратич. показаний. Разработан для замеров среднеквадратич. значения напряжений произвольной формы и их линейного преобразован. в напряжение постоян. тока. Шкала прибора промаркирована в среднеквадратич. значениях напряжения и децибелах (от 0 дБ и до 0,775 В). Используется при контроле и наладке разнообразных радиотелетехнических устройств и средств связи, вычислении частотных характеристик широкополосных аппаратов, обследованиях шумовых устойчивых сигналов и т. д.

— Пределы замеров напряжений 10 мкВ — 300 В с граничными зонами: 0,03-0,1-0,3-1-3-10-30-100-300мВ 1-3-10-30-100-300В

— Границы частот 5 Гц — 5 МГц

— Допустимая погрешность, %: ±1 (30-300 мВ), ±1,5 (1-10 мВ), ±2,5 (0,1-0,3 мВ и 1-300 В), ±4 (0,03 мВ)

— Входное сопротивл.5 МОм ±20%

— Входная емкость: 27пФ (0,03-300 мВ) и 12 пФ (1-300 В)

— Напряжение на выходе линейного преобразоват. 1 В

— Сопротивление на выходе линейного преобразоват. 1 кОм ±10%

— Предельный коэфф. амплитуды сигнала 6*(Uk/Ux)

2.Вольтметры переменного напряжения АКИП-2401

— Измерение ср.квадратического значения переменного напряжения

— Диапазон частот: 5 Гц…5 МГц

— Диапазон измерения напряжения: 50 мкВ…300 В (6 пределов)

— Два измерительных ВЧ входа: Кан1 / Кан2

— Максимальное разрешение: 0,0001 мВ

— Отображение уровня входного сигнала в дБн, дБм, Uпик

— Автоматический или ручной выбор пределов измерений, удержание результата (Hold)

3. Вольтметр В7-40/1

Высококачественный цифровой универсальный прибор, предназначенный для измерения постоянного и переменного напряжений, силы токов и сопротивления постоянному току. вольтметр В7-40/1 применяется при производстве радиоаппаратуры и электрорадиоэлементов, при научных и экспериментальных исследованиях, в лабораторных и цеховых условиях. Встроенный в вольтметр В7-40/1 интерфейс IEEE 488 позволяет успешно использовать его в составе автоматизированных информационно — измерительных систем.

Вольтметр В7-40/1 соответствует жестким условия эксплуатации.

— Точность измерения по постоянному току вольтметра В7-40/1 — 0,05 %

— Максимальная разрешающая способность В7-40/1 — 1 мкВ; 10 мкА; 1 мОм

— Диапазоны 0,2; 20; 200; 1000 (2000) В

— Разрешение 1, 10, 100 мкВ; 1; 10 мВ

— Основная погрешность измерения ±(0,04 %+ 5 ед. мл. р)

— на диапазоне 0,2 В не менее 1 ГОм

— на диапазоне 2 В не менее 2 ГОм

— на диапазонах 200….1000 В, не менее 10 МОм

Ещё одно видео о способе подключения вольтметра:

Для того чтобы понять смысл этого вопроса, давайте внимательно рассмот­рим график синусоидального напряжения на рис. 4.2. В каждый момент вре­мени величина напряжения в нем разная — соответственно, будет разной и величина тока через резистор нагрузки, на который мы подадим такое напряжение. В моменты времени, обозначенные 772 и Т (то есть кратные поло­вине периода нашего колебания) напряжение на нагрузке вообще будет рав­но нулю (ток через резистор не течет), а в промежутках между ними — меня­ется вплоть до некоей максимальной величины, равной амплитудному значению А. Точно так же будет меняться ток через нагрузку, а следователь­но, и выделяемая мощность (которая от направления тока не зависит — фи­зики скажут, что мощность есть величина скалярная, а не векторная). Но процесс выделения тепла крайне инерционен — даже такой маленький пред­мет, как волосок лампочки накаливания, за 1/100 секунды, которые проходят между пиками напряжения в промышленной сети частотой 50 Гц, не успевает заметно остыть. Поэтому нас чаще всего интересует именно средняя мощ­ность за большой промежуток времени. Чему она будет равна?

Чтобы точно ответить на этот вопрос, нужно брать интегралы: средняя мощ­ность за период есть интеграл по времени от квадрата функции напряжения. Здесь мы приведем только результат: величина средней мощности в цепи пе­ременного тока определяется т. н. действующим значением напряжения (Щ, которое для синусоидального колебания связано с амплитудным его значением (f/a) следующей формулой:. Точно такая же формула справедлива для тока. Когда говорят «пе­ременное напряжение 220 В», то всегда имеется в виду именно действующее значение. При этом амплитудное значение равно примерно 311В, что легко подсчитать, если умножить 220 на корень из двух. Это значение нужно всегда иметь в виду при выборе компонентов для работы в сетях переменного тока — если взять диод, рассчитанный на 250 В, то он легко может выйти из строя при работе в обычной сети, в которой мгновенное значение превышает 300 В, хотя действующее значение и равно 220 В. А вот для компонентов, использующих эффект нагревания (лампочек, резисторов и т. п.) при расчете допустимой мощности нужно иметь в виду именно действующее значение.

Называть действующее значение «средним» неверно, правильно называть его среднеквадратическим (по способу вычисления — через квадрат функции от времени). Но существует и понятия среднего значения, причем не одно, а даже два. Просто «среднее» (строго по смыслу названия) — сумма всех мгновенных значений за период. Так как нижняя часть синусоиды (под осью абсцисс) стро­го симметрична относительно верхней, то можно даже не брать интегралов, чтобы сообразить, что среднее значение синусоидального напряжения, пока­занного на рис. 4.2, в точности равно нулю — положительная часть компенси­рует отрицательную. Но такая величина малоинформативна, поэтому чаще ис­пользуют средневыпрямленное (среднеамплитудное) значение, при котором знаки не учитываются (то есть в интеграл подставляется абсолютная величина напряжения). Эта величина (U связана с амплитудным значением (U по формулето есть равно примерно 1,57-f/c-

Рис. 4.5. Графики некоторых колебаний несинусоидальной формы

Для постоянного напряжения и тока действующее, среднее и среднеампли-тудное значения совпадают и равны просто величине напряжения (тока). Од­нако на практике часто встречаются переменные колебания, форма которых отличается и от постоянной величины, и от строго синусоидальной. Осцил­лограммы некоторых из них показаны на рис. 4.5. Для таких сигналов приве­денные выше соотношения для действующего и среднего значений недейст­вительны! Самый простой случай изображен на рис. 4.5, в— колебание представляет собой синусоиду, но сдвинутую вверх на величину амплитуды. Такой сигнал можно представить, как сумму постоянного напряжения вели­чиной А (постоянная составляющая) и переменного синусоидального (пере­менная составляющая). Соответственно, среднее значение его будет равно А, а действующее A-^aHi. Для прямоугольного колебания (рис. 4.5, б) с равны­ми по длительности положительными и отрицательными полуволнами (сим-

метричного меандра ) соотношения очень просты: действующее значение = среднеамплитудному = амплитудному, как и для постоянного тока, а вот среднее значение равно, как и для синуса, нулю. В часто встречающемся на практике случае, когда минимум прямоугольного напряжения совпадает с нулем, то есть напряжение колеблется от нуля до напряжения питания (на рис. 4.5 не показано), такой меандр можно рассматривать аналогично случаю рис. 4.5, в, как сумму постоянного напряжения и прямоугольного. Для самого верхнего случая (рис. 4.5, а), который представляет собой синусоидальное напряжение, пропущенное через двухполупериодный выпрямитель (см. главу Р), действующее и среднеамплитудное значения будут равны соответствующим значениям для синусоиды, а вот среднее будет равно не нулю, а совпадать со среднеамплитудным. Для самого нижнего случая (рис. 4.5, г) указать все эти величины вообще непросто, так как они зависят от формы сигнала.

Но, даже выучив все это, вы все равно не сможете измерять величины напря­жений и токов несинусоидальной формы с помощью мультиметра! Не забы­вайте об этом, как и о том, что для каждого мультиметра есть предельные значения частоты колебаний — если вы включите мультиметр в цепь с ины­ми параметрами, он может показать все, что угодно — «погоду на Марсе», по распространенному выражению. Измерительные приборы для переменного напряжения проградуированы в значениях действующего напряжения, но измеряют они, как правило, среднеамплитудное (по крайней мере, большин­ство — на подробностях мы не будем сейчас задерживаться), и сообразить, как именно пересчитать показания, далеко не всегда просто. А для сложных сигналов, как на рис. 4.5, г, это выливается в сущую головоломку на уровне задач для студентов мехмата. Выручить может осциллограф и знание соот­ношений, приведенных ранее для сигналов самой распространенной формы, ну а для более сложных вычислять действующие и средние значения нам и не потребуется.

Заметки на полях

Единственный прибор, который правильно покажет значение действующего напряжения любой формы —- это аналоговый вольтметр электромагнитной системы (их легко узнать по неравномерной шкале, деления на которой к кон­цу отстоят все дальше и дальше друг от друга). Для того чтобы несинусои­дальное напряжение измерить цифровым прибором, между измеряемой вели­чиной и вольтметром можно вставить интегрирующий фильтр (фильтр нижних частот), описанный в главе 5.

Для прямоугольных напряжений, представляющих собой меандр, подобный рис. 4.5, б, существует еще одна важная характеристика. Никто ведь не за­прещает представить себе прямоугольное напряжение, в котором впадины короче или длиннее всплесков. В электронике меандр без дополнительных пояснений означает симметричную форму прямоугольного напряжения, при которой впадины строго равны всплескам по длительности, но, вообще гово­ря, это необязательно. На рис. 4.6 приведены два примера таких напряжений в сравнении с симметричным меандром. Характеристика соотношений меж­ду длительностями частей периода называется скважностью и определяется, как отношение длительности всего периода к длительности положительной части (именно так, а не наоборот, то есть величина скважности всегда боль­ше I). Для меандра скважность равна 2, для узких коротких импульсбв она будет больше 2, для широких — меньше.

Понравилась статья? добавь ее в закладки, чтобы не потерять — ЖМИ «Ctrl + D»

на Ваш сайт.

Что показывает вольтметр? Вольтметр. Измерение напряжения

Для измерения напряжения используют вольтметр. Вольтметр внешне похож на амперметр, но, в цепь он включается иначе.

Поскольку напряжение может существовать только между какими-то точками, для включения вольтметра в цепь используют параллельное подключение. Как и у амперметра, у вольтметра есть две клеммы, одна из которых помечена знаком «+». Эту клемму следует соединять с положительным полюсом, чтобы прибор работал правильно.

Напряжение, как таковое не может существовать в одной точке, поскольку теряется смысл самого понятия «напряжение». Поэтому когда мы говорим о напряжении на участке цепи, мы имеем ввиду, напряжение между двумя конкретными точками. Чтобы измерить напряжение между полюсами источника, клеммы подключают непосредственно к источнику. Так, если подключить вольтметр к полюсам стандартной пальчиковой батарейки, мы увидим, что напряжение составляет от одного до полутора вольт.

Упражнения.

Задача 1. На рисунке показана цепь, в которой ток в лампочке измеряется с помощью амперметра. В цепь включается вольтметр так, как показано на рисунке. Амперметр показывает 500 мА, а вольтметр — 5 В. Что покажут приборы при нажатии на включатель?

При нажатии на выключатель, лампочка будет выключена из цепи, т.е. по ней перестанет проходить ток. Поэтому амперметр покажет 0 А. Вольтметр же измеряет напряжение между полюсами источника, а выключение лампочки на это напряжение никак не влияет. Поэтому вольтметр по-прежнему будет показывать 5 В.

Задача 2. Одна клемма вольтметра подключена к выключателю. Вольтметр показывает 12 В. Что будет показывать вольтметр при нажатии на выключатель?

Конечно, он будет показывать 0 В, потому что при нажатии на выключатель, подключенная к нему клемма тоже выключится из цепи, и фактически, вольтметр не будет подключен.

Задача 3. У вас есть рубильник, с помощью которого вы можете контролировать силу тока в цепи. У рубильника есть 5 положений: 0, 1, 2, 3 и 4 А. К цепи подключена лампочка и вольтметр. На данный момент напряжение составляет 4 В, а ток — 2 А. Сможете ли вы поддерживать постоянную яркость лампочки, если напряжение может увеличиться вдвое, уменьшиться в полтора раза или уменьшиться на 2 В?

Нужно подумать, от чего зависит яркость лампочки. Мы уже говорили, что яркость лампочки менялась при скачках напряжения из-за того, что ток совершал различную работу. Но, в данной ситуации у нас есть возможность изменять силу тока. Значит, надо попытаться изменениями силы тока компенсировать изменения напряжения, чтобы работа тока была постоянной. Именно в этом и состоит вопрос в нашей задаче: сможем ли мы удерживать работу постоянной.

2.1.1. Мгновенное

2.1.2. Действующее

2.1.3. Амплитудное

2.1.4. Прибавленное

2.1.5. Максимальное

Что такое источник тока

2.2.1. Любой источник электрической энергии

2.2.2. Источник ЭДС

2.2.3. Источник напряжения

2.2.4. Источник питания, имеющий большое внутреннее сопротивление

2.2.5. Источник пульсирующего напряжения

2.3. Напряжение, приложенное к цепи, равно 100 В, ток в ней 10 А и отстает по фазе на 60º. Чему равно наибольшее и наименьшее значения мгновенной мощности p ?

2.3.1. 1000 Вт и -300Вт

2.3.2. 1500 Вт и -500 Вт

2.3.3. 850 Вт и -450 Вт

2.3.4. 500 Вт и -500 Вт

2.4. Внутренняя проводимость идеального генератора тока

2.5. Амплитуда тока равна 5 А, фаза равна 45 ° . Укажите комплексную амплитуду тока.

2.51.1. I=5e j 45 A

2.5.2. I=5e –j45 A

2.5.3. I=-5-e j45 A

2.5.4. I=5e j-45 A

2.5.5. I=5-e j -45 A

В сеть включено параллельно 88 одинаковых лампочек с общим сопротивлением 5 Ом. Определить величину тока в каждой лампочке, если напряжение в сети равно 220 В.

2.6.4. Для решения задачи недостаточно данных.

По какой формуле определяется резонансная частота колебательного контура?

2.7.1.

2.7.2.

2.7.3.

2.7.4.

Емкость контура увеличили. Как надо изменить остальные параметры, чтобы не изменилась собственная частота и добротность контура?

2.8.1. Увеличить L и ум

Какое значение напряжения показывает вольтметр переменного тока?

⇐ ПредыдущаяСтр 3 из 3

2.1.1. Мгновенное

2.1.2. Действующее

2.1.3. Амплитудное

2.1.4. Прибавленное

2.1.5. Максимальное

 

Что такое источник тока

2.2.1. Любой источник электрической энергии

2.2.2. Источник ЭДС

2.2.3. Источник напряжения

2.2.4. Источник питания, имеющий большое внутреннее сопротивление

2.2.5. Источник пульсирующего напряжения

2.3. Напряжение, приложенное к цепи, равно 100 В, ток в ней 10 А и отстает по фазе на 60º. Чему равно наибольшее и наименьшее значения мгновенной мощности p?

2.3.1. 1000 Вт и -300Вт

2.3.2. 1500 Вт и -500 Вт

2.3.3. 850 Вт и -450 Вт

2.3.4. 500 Вт и -500 Вт

 

2.4.Внутренняя проводимость идеального генератора тока

1. 0

^2. 1

3.

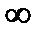
4. —

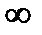
5. 100

2.5.Амплитуда тока равна 5 А, фаза равна 45^° . Укажите комплексную амплитуду тока.

2.51.1. I=5e^j45 A

2.5.2. I=5e ^–j45 A

2.5.3. I=-5-e^j45 A

2.5.4. I=5e^j-45 A

2.5.5. I=5-e^j-45 A

 

В сеть включено параллельно 88 одинаковых лампочек с общим сопротивлением 5 Ом. Определить величину тока в каждой лампочке, если напряжение в сети равно 220 В.

2.6.1. I=0,5 А

2.6.2. I=44 А

2.6.3. I=5 А

2.6.4. Для решения задачи недостаточно данных.

 

По какой формуле определяется резонансная частота колебательного контура?

2.7.1.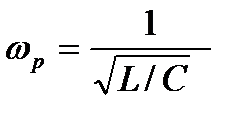

2.7.2.

 

 

2.7.3.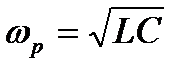

2.7.4.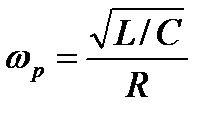

Емкость контура увеличили. Как надо изменить остальные параметры, чтобы не изменилась собственная частота и добротность контура?

2.8.1. Увеличить L и уменьшить R

2.8.2. Увеличить L

2.8.3. Уменьшить L и R

 

2.9. Имеется две лампы накаливания с одинаковым номинальным напряжением Uн=110 В и номинальной мощностью Pн1=10 Вт, Pн2=150 Вт. Можно ли использовать эти лампы для освещения помещения, где напряжения сети 220 В?

2.9.1. Для решения задачи не хватает данных

2.9.2. Можно

2.9.3. Можно, если их соединить параллельно

2.9.4. Нельзя

2.10. Какое соотношение между активной и реактивной мощностями при cosj = 0,707?

2.10.1. Активная мощность больше реактивной в 0,707 раза

2.10.2. Активная мощность равна реактивной

2.10.3. Активная мощность меньше реактивной в 0,707 раза

2.10.4. Для решения задачи недостаточно данных

 

Как изменится величина тока, если в участок, состоящий из 4 одинаковых, последовательно соединенных резисторов добавить еще один?

2.11.1. Не изменится

2.11.2. Увеличится

2.11.3. Увеличится в 2 раза.

2.11.4. Уменьшится

 

2.12. Чему равна частота постоянного тока?

2.12.1. f=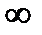

2.12.2. f=50 Гц

2.12.3. f =100 Гц

2.12.4. f=0

2.12.5. f=25 Гц

 

 

2.13. Последовательная резистивно-индуктивно-емкостная схема имеет следующие компоненты: X_L = 30 Ом, Хc = 42 Ом, R = 15 Ом. На каком из элементов наименьшее падение напряжения?

2.13.1. Резисторе

2.13.2. Катушке индуктивности

2.13.3. Конденсаторе

2.14. Внутреннее сопротивление идеального генератора напряжения равно:

2.14.1. 1

2.14.2.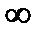

2.14.3. —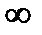

2.14.4. 100

2.14.5. 0

2.15. Показание вольтметра при коротком замыкании в цепи:

2.15.1. Изменяется больше предела

2.15.2. Не меняется

2.15.3. Mах напряжение

2.15.4. Ноль

2.15.5. Min напряжение

 

 

Как необходимо соединить первичные элементы в батарею, чтобы увеличить напряжение и ток батареи?

2.16.1. Параллельно

2.16.2. Последовательно

2.16.3. Смешанно

2.16.4. Это невозможно

 

Какая из указанных величин позволяет рассчитать величину внутреннего сопротивления активного двухполюсника?

2.17.1. Ток короткого замыкания

2.17.2. ЭДС короткого замыкания

2.17.3. ЭДС холостого хода

2.17.4. ЭДС холостого хода и ток короткого замыкания

 

Каким способом можно лампы, рассчитанные на напряжения 127 В, включить в сеть с напряжением 220 В.

2.18.1. Параллельно

2.18.2. Последовательно

2.18.3. Смешанно

2.18.4. Это невозможно

 

2.19. Уравнение мгновенного значения переменного тока в общем виде:

2.19.1.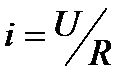

 

2.19.2.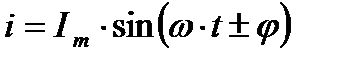

 

2.19.3.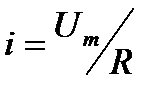

 

2.19.4.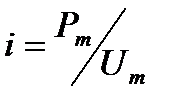

 

2.19.5.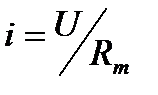

2.20. Угол сдвига фаз между U и I в цепи с активным сопротивлением R:

2.21.1. 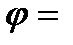0°

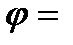2.21.2. 30°

2.21.3. 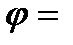45°

2.21.4. 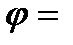90°

2.21.5. 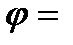120°

 

Какой метод расчета цепей постоянного тока наиболее удобно применить для исследования режима работы одной определенной ветви сложной цепи?

2.21.1. Наложения

2.21.2. Узлового напряжения

2.21.3. Узловых и контурных уравнений

2.21.4. Эквивалентного генератора

 

2.22. Полная проводимость y цепи с параллельно включенными элементами R, L, C:

2.22.1.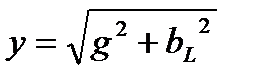

2.22.2.

2.22.3.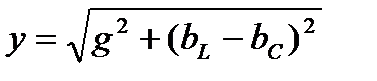

2.22.4.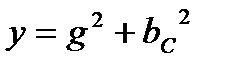

2.22.5.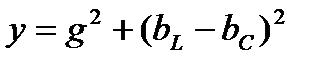

 

Общее сопротивление двух потребителей при последовательном соединении 100 Ом, при параллельном соединении 24 Ом. Найти сопротивление каждого потребителя.

2.23.1. 100 Ом, 24 Ом

2.23.2. 40 Ом , 60 Ом

2.23.3. 50 Ом, 50 Ом

2.23.4. Для решения задачи недостаточно данных.

 

Индуктивное сопротивление катушки в 3 раза больше активного сопротивления. При напряжении на зажимах 120 В активная мощность в этой катушке составляет 1200 Вт. Чему равны активное сопротивление R и коэффициент мощности cosj?

2.24.1. R =12 Ом; cosj = 0,32

2.24.2. R=24 Ом; cosj=0,45

2.24.3. R=10,6 Ом; cosj=0,4

2.24.4. R=3,9 Ом; cosj=0,35

 

Рекомендуемые страницы: