Закон Ома для участка и полной замкнутой цепи
В
1826 г. немецкий ученый Георг Ом
экспериментально установил прямую
пропорциональную зависимость между
силой тока I
в проводнике и напряжением U
на его концах: 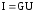 ,
гдеG
— электрическая
проводимость проводника.
Величина, обратная проводимости
называется электрическим
сопротивлением проводника R.
Таким образом, закон
Ома для участка цепи, не содержащего
источника э.д.с.,
имеет вид
,
гдеG
— электрическая
проводимость проводника.
Величина, обратная проводимости
называется электрическим
сопротивлением проводника R.
Таким образом, закон
Ома для участка цепи, не содержащего
источника э.д.с.,
имеет вид 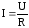 . Учитывая,
что в общем случае участок цепи может
содержать и э.д.с.,закон
Ома следует
представить в виде
. Учитывая,
что в общем случае участок цепи может
содержать и э.д.с.,закон
Ома следует
представить в виде 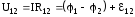 .
.
Сопротивление
проводника зависит от его размеров,
формы и материала, из которого он
изготовлен. Для однородного линейного
проводника 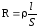
Если
цепь замкнута, то 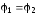 ,
,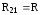 ,
гдеR
— общее сопротивление всей цепи, включая
сопротивление источника э.д.с. Тогда
,
гдеR
— общее сопротивление всей цепи, включая
сопротивление источника э.д.с. Тогда
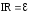 ,
где
— алгебраическая сумма всех э.д.с.,
имеющихся в этой цепи.
,
где
— алгебраическая сумма всех э.д.с.,
имеющихся в этой цепи. Принято
называть сопротивление источника тока
r
— внутренним,
а сопротивление всей остальной цепи
R
— внешним.
Окончательный вид формулы закона Ома
для замкнутой цепи 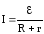 .
В системе единиц СИ напряжение и э.д.с.
измеряются в Вольтах (В), сопротивление
— в Омах (Ом), удельное электрическое
сопротивление — в Ом-метрах (Омм),
электрическая проводимость в Сименсах (См).
.
В системе единиц СИ напряжение и э.д.с.
измеряются в Вольтах (В), сопротивление
— в Омах (Ом), удельное электрическое
сопротивление — в Ом-метрах (Омм),
электрическая проводимость в Сименсах (См).
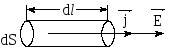
Рис.2.1. Отрезок проводника.
Закон Ома можно записать и для плотности тока. Рассмотрим участок электрической длиной dl и поперечным сечением dS (рис.2.1). Сила тока на этом участке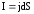 ,
сопротивление
,
сопротивление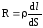 ,
падение напряжения
,
падение напряжения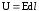
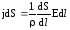 .
Отсюда
.
Отсюда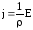 или
или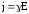 ,
где
,
где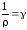 —удельная электрическая
проводимость проводника или удельная электропроводность.
В векторном виде имеем
—удельная электрическая
проводимость проводника или удельная электропроводность.
В векторном виде имеем 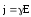
1.14 Сопротивление проводника. Явление сверхпроводимости.
Способность
вещества проводить ток характеризуется
его удельной
проводимостью ,
либо удельным
сопротивлением .
Их величина определяется химической
природой проводника и условиями, в
частности температурой, при которой он
находится. Для большинства металлов
растет с температурой приблизительно
по линейному закону: 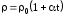
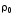 — удельное сопротивление при 0С,
t
— температура по шкале Цельсия,
— температурный коэффициент
сопротивления близкий к 1/273 К-1 при не очень низких температурах.
Так как R,
то
— удельное сопротивление при 0С,
t
— температура по шкале Цельсия,
— температурный коэффициент
сопротивления близкий к 1/273 К-1 при не очень низких температурах.
Так как R,
то 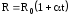 ,
где
,
где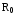 — сопротивление при 0С.
Преобразовав две последние формулы,
можно записать
— сопротивление при 0С.
Преобразовав две последние формулы,
можно записать 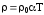 и
и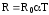
При низких температурах нарушается линейность зависимости сопротивления металлов от температуры и при температуре 0 К наблюдается остаточное сопротивление Rост. Величина Rост зависит от чистоты материала и наличия в нем механических напряжений. Лишь у идеально чистого металла с идеально правильной кристаллической решеткой Rост 0 при Т0 (пунктирная часть кривой).
1.15 Работа и мощность тока, закон Джоуля-Ленца.
Определим
работу, совершаемую постоянным током
в проводнике, имеющем сопротивление R
и находящемся под напряжением 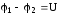 .
Так как ток представляет собой
перемещение зарядаq
под действием поля, то работу тока можно
определить по формуле
.
Так как ток представляет собой
перемещение зарядаq
под действием поля, то работу тока можно
определить по формуле 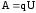 .
Учитывая формулу
.
Учитывая формулу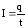 и закон Ома, получим
и закон Ома, получим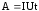
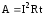 ,
или
,
или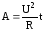 ,
гдеt
— время протекания тока. Поделив обе
части равенства на t,
получим выражения для мощности постоянного тока N
,
гдеt
— время протекания тока. Поделив обе
части равенства на t,
получим выражения для мощности постоянного тока N 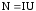 ,
, 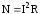 ,
,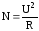 .
Работа тока в системе единиц СИ измеряется
в доулях (Дж), а мощность — в ваттах (Вт).
На практике применяются также внесистемные
единицы работы тока: ватт-час (Втч)
и киловатт-час (кВтч).
1Втч
— работа тока мощностью 1Вт в течение
одного часа. 1Втч=3.610
.
Работа тока в системе единиц СИ измеряется
в доулях (Дж), а мощность — в ваттах (Вт).
На практике применяются также внесистемные
единицы работы тока: ватт-час (Втч)
и киловатт-час (кВтч).
1Втч
— работа тока мощностью 1Вт в течение
одного часа. 1Втч=3.610
Опыт
показывает, что ток всегда вызывает
некоторое нагревание проводника.
Нагревание обусловлено тем, что
кинетическая энергия движущихся по
проводнику электронов (т.е. энергия
тока) при каждом их столкновении с ионами
металлической решетки переходит в
теплоту Q.
Если ток идет по неподвижному
металлическому проводнику, то вся
работа тока расходуется на его нагревание
и, следуя закону сохранения энергии,
можно записать 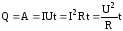
На тепловом действии тока основан целый ряд электрических приборов и установок: тепловые электроизмерительные приборы, электропечи, электросварочная аппаратура, бытовые электронагревательные приборы — чайники, кипятильники, утюги. В пищевой промышленности широко применяется метод электроконтактного нагрева, заключающийся в том, что электрический ток, проходя через продукт, обладающий определенным сопротивлением, вызывает его равномерное нагревание. Например, для производства колбасных изделий через дозатор фарш поступает в формы, торцевые стенки которых служат электродами. При такой обработке обеспечивается равномерность нагрева по всему объему продукта, возможность поддержания определенного температурного режима, наивысшая биологическая ценность изделия, наименьшие длительность процесса и расход энергии.
Определим удельную
тепловую мощность тока ,
т.е. количество теплоты, выделяющееся
в единице объема за единицу времени.
Выделим в проводнике элементарный
цилиндрический объем dV
с поперечным сечением dS
и длиной dl параллельной направлению тока, и
сопротивлением 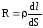 ,
,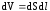 .
По закону Джоуля-Ленца, за времяdt
в этом объеме выделится теплота
.
По закону Джоуля-Ленца, за времяdt
в этом объеме выделится теплота 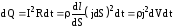 .
Тогда
.
Тогда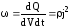 и,
используя закон Ома для плотности тока
и,
используя закон Ома для плотности тока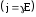 и соотношение
и соотношение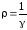 ,
получим
,
получим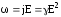 .
Эти соотношения выражаютзакон
Джоуля-Ленца в дифференциальной форме.
.
Эти соотношения выражаютзакон
Джоуля-Ленца в дифференциальной форме.
1.16. Правило Кирхгофа для разветвленных электрических цепей.
До сих пор нами рассматривались простейшие электрические цепи, состоящие из одного замкнутого неразветвленного контура. На всех его участках силы тока одинаковы. Расчет I, R, в такой цепи выполняется с помощью законов Ома.
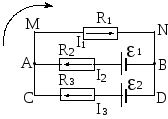
Рис.2.2.Разветвленная электрическая цепь.
Более сложной является разветвленная электрическая цепь, состоящая из нескольких замкнутых контуров, имеющих общие участки. В каждом контуре может быть несколько источников тока. Силы тока на отдельных участках замкнутого контура могут быть различными по величине и направлению (рис.2.2). В 1847 г. Г.Кирхгоф сформулировал два правила, значительно упрощающих расчет разветвленных цепей. Первое
правило Кирхгофа: алгебраическая
сумма сил токов в узле равна нулю: 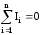 .Узел — точка цепи, в которой сходятся не менее
трех проводников. В электрической
цепи на рис.2.2 имеются два узла А и В.
Ток, входящий в узел, считается
положительным, выходящий — отрицательным.
Например, для узла А первое правило
Кирхгофа следует записать
.Узел — точка цепи, в которой сходятся не менее
трех проводников. В электрической
цепи на рис.2.2 имеются два узла А и В.
Ток, входящий в узел, считается
положительным, выходящий — отрицательным.
Например, для узла А первое правило
Кирхгофа следует записать 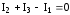 .
.
Первое правило выражает закон сохранения электрического заряда, так как ни в одной точке цепи они не могут возникать или исчезать.
Второе
правило Кирхгофа относится к любому замкнутому контуру,
выделенному в разветвленной цепи: алгебраическая
сумма произведений токов на сопротивления,
включая и внутренние, на всех участках
замкнутого контура равна алгебраической
сумме электродвижущих сил, встречающихся
в этом контуре 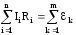 .
Контур ‑ это замкнутый участок
схемы, по которому можно пройти и
вернуться в исходную точку. Второе
правило Кирхгофа получается из закона
Ома, записанного для всех участков от
узла до узла (ветвей) разветвленной
схемы. В электрической цепи на рис.2.2
имеются три контура:AMNBA,
CABDC,
CMNDC.
При этом, токи Ii в ветвях контура, совпадающие с произвольно
выбранным направлением обхода
контура, считаются положительными, а
направленные навстречу обхода —
отрицательными. Э.д.с., проходимые от
«+» к «-» считаются положительными и
наоборот. В рассматриваемой электрической
цепи (рис.2.2) выберем обход контуров по
часовой стрелке и запишем для них
уравнения по II
правилу Кирхгофа: для AMNBА
.
Контур ‑ это замкнутый участок
схемы, по которому можно пройти и
вернуться в исходную точку. Второе
правило Кирхгофа получается из закона
Ома, записанного для всех участков от
узла до узла (ветвей) разветвленной
схемы. В электрической цепи на рис.2.2
имеются три контура:AMNBA,
CABDC,
CMNDC.
При этом, токи Ii в ветвях контура, совпадающие с произвольно
выбранным направлением обхода
контура, считаются положительными, а
направленные навстречу обхода —
отрицательными. Э.д.с., проходимые от
«+» к «-» считаются положительными и
наоборот. В рассматриваемой электрической
цепи (рис.2.2) выберем обход контуров по
часовой стрелке и запишем для них
уравнения по II
правилу Кирхгофа: для AMNBА 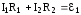 ;
дляCABDС
;
дляCABDС 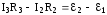 ;
дляCMNDС
;
дляCMNDС 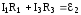 .
В данном примере внутренними сопротивлениями
источников тока пренебрегаем. Первое
и второе правила Кирхгофа позволяют
составить систему линейных алгебраических
уравнений, которые связывают параметры
(I,
R,
.
В данном примере внутренними сопротивлениями
источников тока пренебрегаем. Первое
и второе правила Кирхгофа позволяют
составить систему линейных алгебраических
уравнений, которые связывают параметры
(I,
R, 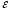 )
и позволяют, зная одни, найти другие.
)
и позволяют, зная одни, найти другие.
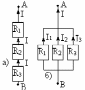
Рис.2.3. а) Последовательное соединение сопротивлений; б) Параллельное соединение сопротивлений.
Простые электрические цепи имеют очень большое практическое применение. В повседневной жизни полезно знать, как подключить динамики или проигрыватель к стереосистеме, как подсоединить сигнализацию для охраны или автомобильный кассетный проигрыватель, как зарядить аккумуляторы или осветить новогоднюю елку. Большинство
электрических цепей содержит комбинацию
последовательно или параллельно
подключенных резисторов (резистор — это
элемент цепи, обладающий только
сопротивлением). Полное сопротивление
участка цепи определяется отношением
падения напряжения на нем к величине
силы тока 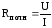 .
При последовательном соединении
(рис.2.3 а) через все резисторы течет
один и тот же ток. При параллельном
соединении (рис.2.3 б) полный ток равен
сумме токов, текущих в отдельных
резисторах.
.
При последовательном соединении
(рис.2.3 а) через все резисторы течет
один и тот же ток. При параллельном
соединении (рис.2.3 б) полный ток равен
сумме токов, текущих в отдельных
резисторах.
При
последовательном соединении падение
напряжения на участке АВ равно 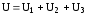 ,
т.е. сумме падений напряжения на трех
резисторах. Разделим обе части равенства
наI
и получим
,
т.е. сумме падений напряжения на трех
резисторах. Разделим обе части равенства
наI
и получим 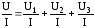 ,
т.е.
,
т.е.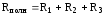 .
Таким образом, полное сопротивление
участка цепи, состоящего из последовательно
соединенных резисторов, равно их
алгебраической сумме
.
Таким образом, полное сопротивление
участка цепи, состоящего из последовательно
соединенных резисторов, равно их
алгебраической сумме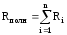 .
.
При
параллельном соединении (рис..2.3 б)
мы имеем 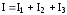 .
Разделим обе части равенства наU,
где U
— падение напряжения на участке цепи
АВ, причем
.
Разделим обе части равенства наU,
где U
— падение напряжения на участке цепи
АВ, причем 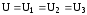 ,
и получим
,
и получим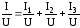 .
Из этого равенства следует
.
Из этого равенства следует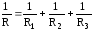 .
Величина обратная полному сопротивлению
параллельно соединенных резисторов
равна алгебраической сумме величин их
обратных сопротивлений
.
Величина обратная полному сопротивлению
параллельно соединенных резисторов
равна алгебраической сумме величин их
обратных сопротивлений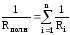 .
.
В электрическую цепь может быть включено регулируемое (изменяющееся с помощью специального движка), сопротивление, которое называется реостатом. По назначению реостаты делятся на пусковые, служащие для ограничения силы тока во время пуска двигателей, и регулирующие — для регулировки силы тока в цепи (постепенное снижение освещенности в театральных залах), регулировки скорости вращения электродвигателей и т.д. Реостат может быть использован в качестве так называемого датчика перемещения. В автоматических регуляторах уровня жидкости в резервуарах применяется поплавково-реостатный датчик. Специальный поплавок крепится к движку реостата. Изменение уровня жидкости сдвигает поплавок, изменяет сопротивление реостата, и следовательно, силы тока в цепи, величина которого дает информацию об уровне.
Закон Ома для замкнутой цепи
Н а
рисунке 2 показана простейшая замкнутая
цепь, состоящая из реального источника
э.д.с. Е, имеющего внутреннее сопротивлениеRвти нагрузочного
резистора с сопротивлениемR(сопротивление соединительных проводов
включено в сопротивлениеRрезистора).
а
рисунке 2 показана простейшая замкнутая
цепь, состоящая из реального источника
э.д.с. Е, имеющего внутреннее сопротивлениеRвти нагрузочного
резистора с сопротивлениемR(сопротивление соединительных проводов
включено в сопротивлениеRрезистора).
Закон Ома для замкнутой цепиформулируется следующим образом:сила тока (ток, величина тока) прямо пропорциональна электродвижущей силе (э.д.с.) источника и записывается в виде:
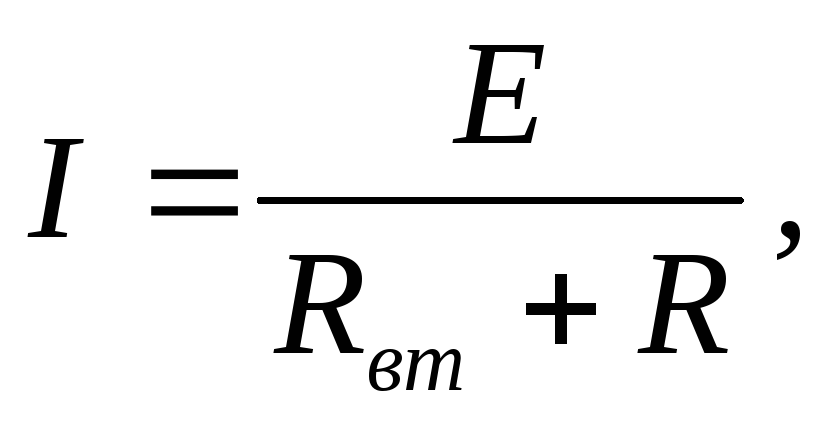
(4)
где 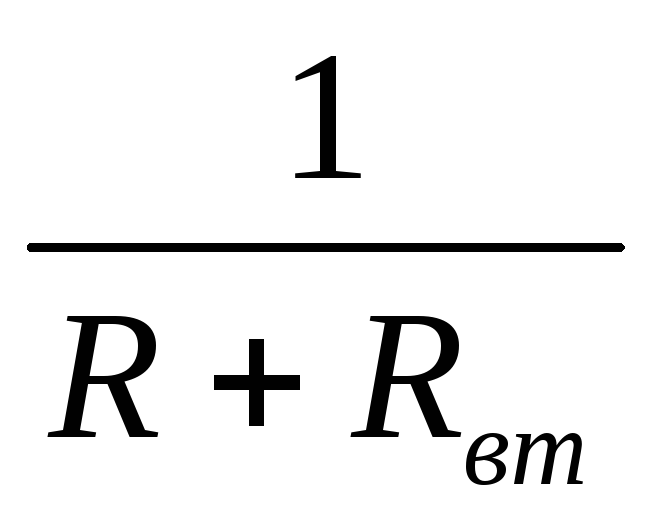 – коэффициент пропорциональности.
– коэффициент пропорциональности.
П
(4а)
ерепишем равенство (4) в виде 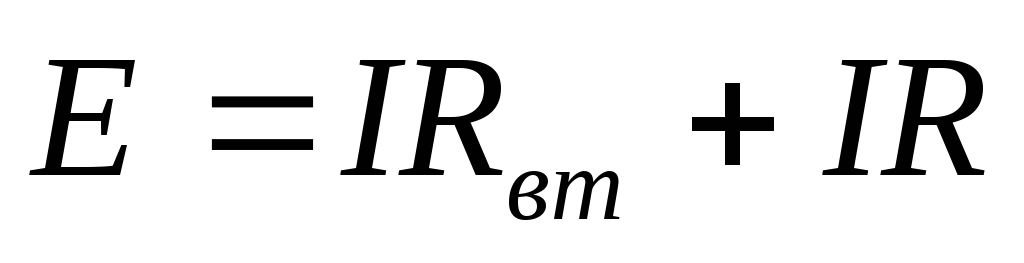
и введем обозначение U=IR– напряжение на выходных зажимах источника э.д.с. (генератора), которое одновременно является падением напряжения, создаваемым токомIна внешнем сопротивленииRнагрузочного резистора.
П
(5)
одставив это обозначение в правую часть равенства (4а), можно получить следующую зависимость: 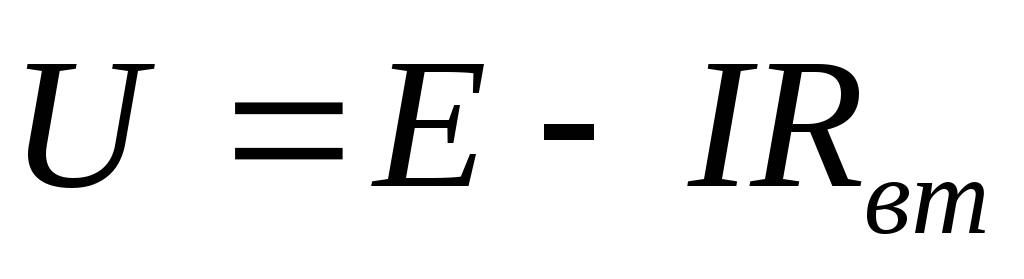 ,
,
к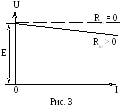 оторая
представляет собой аналитическое
выражение внешней характеристики
источника э.д.с. Эту зависимость можно
сокращенно записать в видеU = F(I) при E = const, Rвт = const. Внешней
характеристикой принято называть графическую
зависимость U = F(I),
показанную на рисунке 3.
оторая
представляет собой аналитическое
выражение внешней характеристики
источника э.д.с. Эту зависимость можно
сокращенно записать в видеU = F(I) при E = const, Rвт = const. Внешней
характеристикой принято называть графическую
зависимость U = F(I),
показанную на рисунке 3.
Сплошной линией показана внешняя характеристика реального источника э.д.с., в котором с ростом тока I увеличивается падение напряжения на внутреннем сопротивлении IRвт, в результате чего с ростом тока выходное напряжение источника U уменьшается. Пунктирной линией на рисунке 3 показана внешняя характеристика идеального источника э.д.с., у которого отсутствует внутреннее сопротивление (Rвт = 0), а, следовательно, и внутреннее падение напряжения (IRвт = 0). В результате равенство (5) принимает вид
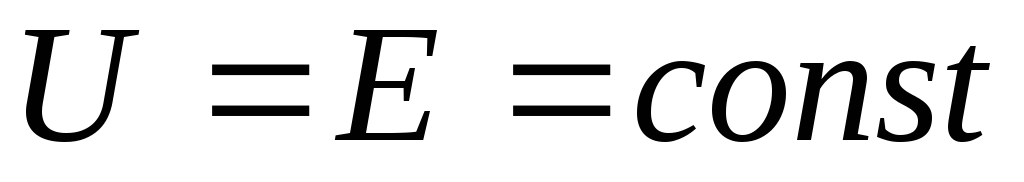
(5а)
,и характеристика представляет собой горизонтальную линию. Такой идеальный источник называют источником (генератором) бесконечной мощности, поскольку он гарантирует постоянство напряжения при сколь угодно больших токах нагрузки.
Закон Ома для участка цепи, содержащего источник э.Д.С. (обобщенный закон Ома)
На рисунках 4а и 4б показаны одинаковые участки, содержащие последовательно включенные резистор R и источник э.д.с. Е, по которым протекает ток I одного и того же направления. Что касается источников, то э.д.с. в схеме на рисунке 4а совпадает с направлением тока, а на рисунке 4б – действует встречно с током.
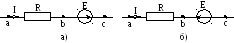
Рис. 4
К
(6)
ак известно,под напряжением Uна участке цепипонимают разность электрических потенциаловφмежду крайними точками этого участка (аисна рисунке 4). Ток всегда течет от более высокого потенциала к более низкому потенциалу. Поскольку ток в обоих случаях (рис. 4а и 4б) направлен от точкиак точкес, то напряжение 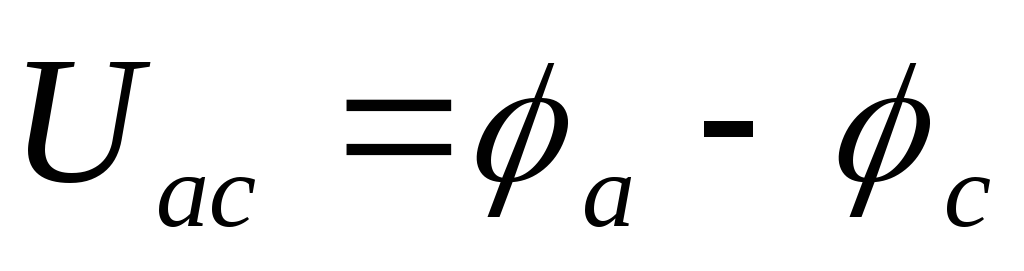
Выразим более высокий потенциал точки ачерез потенциал точкис. При
перемещении (рис. 4а) от точкиск
точкеb(встречно к
направлению э.д.с. Е) потенциал точкиbоказывается ниже потенциала точкисна величину э.д.с. Е, то есть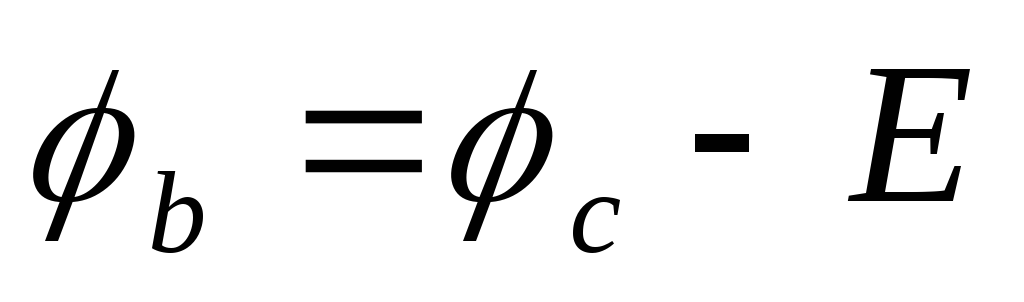 .
Применительно к схеме на рисунке 4б
потенциал точкиbбудет выше на величину э.д.с. Е, то есть
.
Применительно к схеме на рисунке 4б
потенциал точкиbбудет выше на величину э.д.с. Е, то есть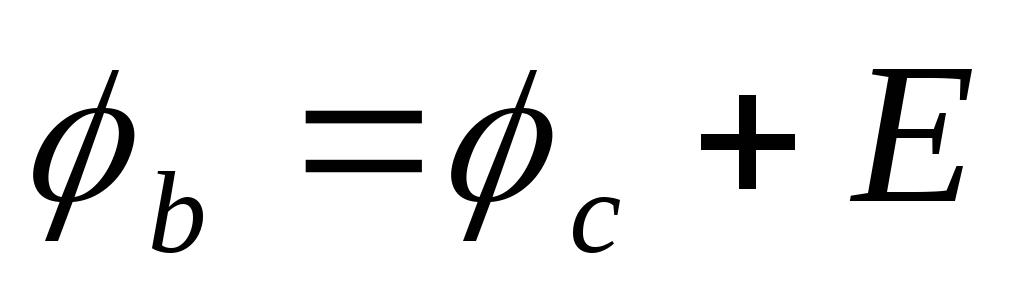 .
Поскольку потенциал точкиавыше
потенциала точкиbна
величину падения напряженияIRна резисторе с сопротивлениемR,
то
.
Поскольку потенциал точкиавыше
потенциала точкиbна
величину падения напряженияIRна резисторе с сопротивлениемR,
то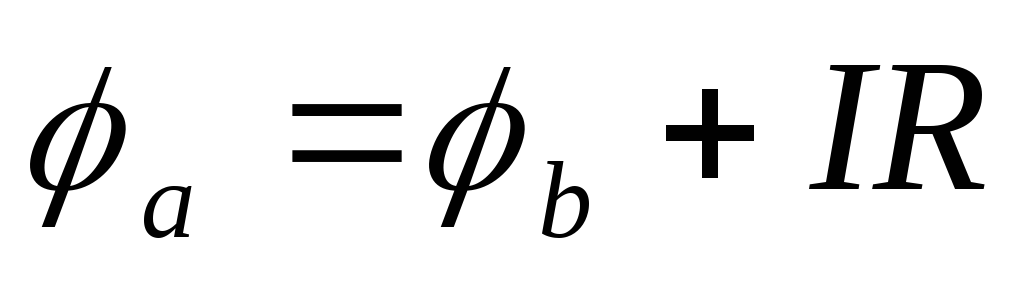 .
.
Таким образом, для рисунка 4а: 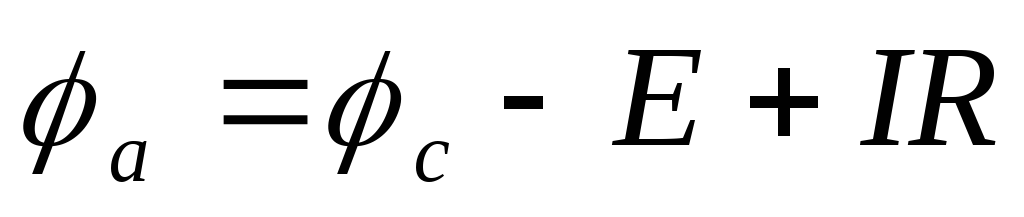 ,
а для рисунка 4б:
,
а для рисунка 4б: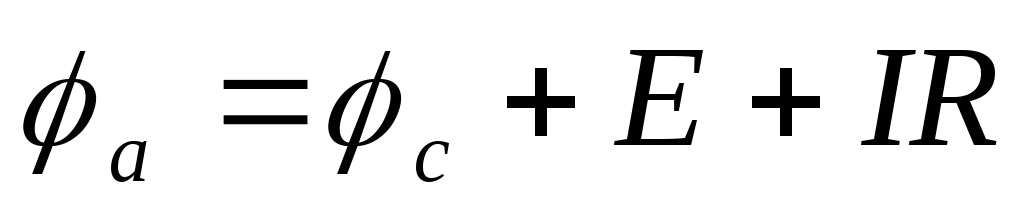 .
.
Соответственно напряжение между границами аисучастка:
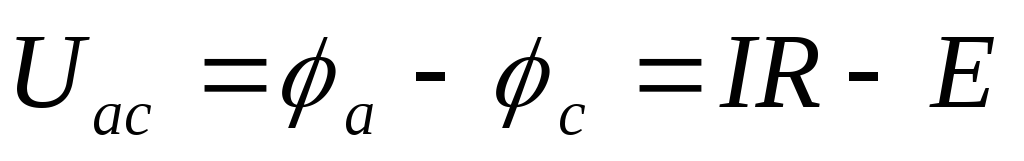 ;
;
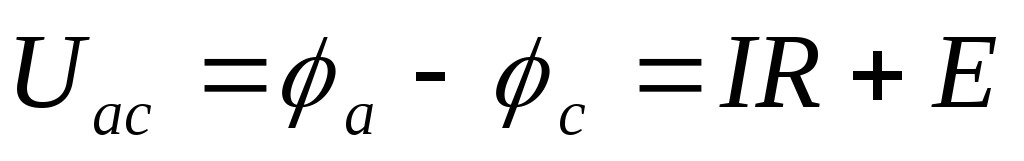 .
.
Решив равенства (6а) и (6б) относительно тока, получим обобщенный закон Ома (закон Ома для участка цепи, содержащего источник э.д.с.):
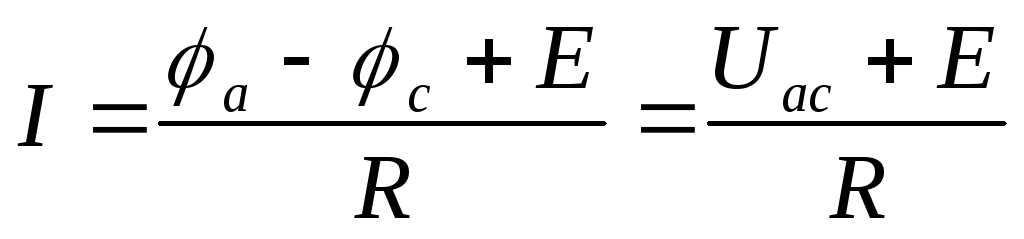 ;
;
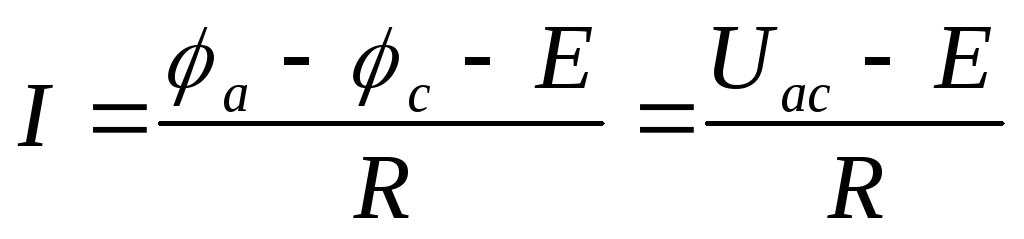 .
.
В общем случае
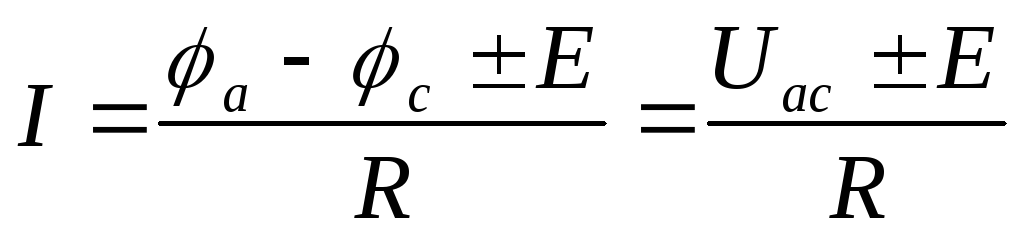
(7)
В частном случае, когда э.д.с. отсутствует (Е = 0) уравнение (7) превращается в закон Ома для участка цепи, не содержащего э.д.с. (1).
Т. Закон Ома — PhysBook
Закон Ома для замкнутой цепи
Замкнутая цепь (рис. 2) состоит из двух частей — внутренней и внешней. Внутренняя часть цепи представляет собой источник тока, обладающий внутренним сопротивлением r; внешняя — различные потребители, соединительные провода, приборы и т.д. Общее сопротивление внешней части обозначается R. Тогда полное сопротивление цепи равно r + R.
Рис. 2
По закону Ома для внешнего участка цепи 1 → 2 имеем:
\(~\varphi_1 — \varphi_2 = IR .\)Внутренний участок цепи 2 → 1 является неоднородным. Согласно закону Ома, \(~\varphi_2 — \varphi_1 + \varepsilon = Ir\). Сложив эти равенства, получим
\(~\varepsilon = IR + Ir . \qquad (1)\)Отсюда
\(~I = \frac{\varepsilon}{R + r} . \qquad (2)\)Последняя формула представляет собой закон Ома для замкнутой цепи постоянного тока. Сила тока в цепи прямо пропорциональна ЭДС источника и обратно пропорциональна полному сопротивлению цепи.
Так как для однородного участка цепи разность потенциалов есть напряжение, то \(~\varphi_1 — \varphi_2 = IR = U\) и формулу (1) можно записать:
\(~\varepsilon = U + Ir \Rightarrow U = \varepsilon — Ir .\)Из этой формулы видно, что напряжение на внешнем участке уменьшается с увеличением силы тока в цепи при ε = const.
Подставим в последнюю формулу силу тока (2), получим
\(~U = \varepsilon \left( 1 — \frac{r}{R + r} \right) .\)Проанализируем это выражение для некоторых предельных режимов работы цепи.
а) При разомкнутой цепи (R → ∞) U = ε, т.е. напряжение на полюсах источника тока при разомкнутой цепи равно ЭДС источника тока.
На этом основана возможность приблизительного измерения ЭДС источника тока с помощью вольтметра, сопротивление которого много больше внутреннего сопротивления источника тока (\(~R_v \gg r\)). Для этого вольтметр подключают к клеммам источника тока.
б) Если к клеммам источника тока подключить проводник, сопротивление которого \(~R \ll r\), то R + r ≈ r, тогда \(~U = \varepsilon \left( 1 — \frac{r}{r} \right) = 0\) , а сила тока \(~I = \frac{\varepsilon}{r}\) — достигает максимального значения.
Подключение к полюсам источника тока проводника с ничтожно малым сопротивлением называется коротким замыканием, а максимальную для данного источника силу тока называют током короткого замыкания:
\(~I_{kz} = \frac{\varepsilon}{r} .\)У источников с малым значением r (например, у свинцовых аккумуляторов r = 0,1 — 0,01 Ом) сила тока короткого замыкания очень велика. Особенно опасно короткое замыкание в осветительных сетях, питаемых от подстанций (ε > 100 В), Ikz может достигнуть тысячи ампер. Чтобы избежать пожаров, в такие цепи включают предохранители.
Запишем закон Ома для полной цепи в случае последовательного и параллельного соединения источников тока в батарею. При последовательном соединении источников «-» одного источника соединяется с «+» второго, «-» второго с «+» третьего и т.д. (рис. 3, а). Если ε1 = ε2 = ε3 а r1 = r2 = r3 то εb = 3ε1, rb = 3r1. В этом случае закон Ома для полной цепи имеет вид\[~I = \frac{\varepsilon_b}{R + r_b} = \frac{3 \varepsilon_1}{R + 3r_1}\], или для n одинаковых источников \(~I = \frac{n \varepsilon_1}{R + nr_1}\).
Рис. 3
Последовательное соединение применяют в том случае, когда внешнее сопротивление \(~R \gg nr_1\), тогда \(~I = \frac{n \varepsilon_1}{R}\) и батарея может дать силу тока, в n раз большую, чем сила тока от одного источника.
При параллельном соединении источников тока все «+» источников соединены вместе и «-» источников — также вместе (рис. 3, б). В этом случае
\(~\varepsilon_b = \varepsilon_1 ; \ r_b = \frac{r_1}{3}.\)Откуда \(~I = \frac{\varepsilon_1}{R + \frac{r_1}{3}}\) .
Для n одинаковых источников \(~I = \frac{\varepsilon_1}{R + \frac{r_1}{n}}\) .
Параллельное соединение источников тока применяют тогда, когда нужно получить источник тока с малым внутренним сопротивлением или когда для нормальной работы потребителя электроэнергии в цепи должен протекать ток. больший, чем допустимый ток одного источника.
Параллельное соединение выгодно, когда R невелико по сравнению с r.
Иногда применяют смешанное соединение источников.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 262-264.
Закон Ома для замкнутой цепи
Определение полной замкнутой цепи
Полную замкнутую цепь (рис.1) можно рассматривать как последовательное соединение сопротивления внешней цепи (R) и внутреннего сопротивления источника тока (r). То есть:

Рис. 1
Если заменить источник тока таким, что его внутренне сопротивление равно такому же сопротивлению как и у предыдущего, то ток в цепи изменится. То есть ток в цепи зависит и от внутреннего сопротивления источника и от его ЭДС. Количественно все эти величины: ЭДС ($\mathcal E$) источника, его внутренне сопротивление, силу тока в цепи (I), электросопротивление цепи (R) связывает закон Ома.
Связь локального закона Ома с интегральным законом для замкнутой цепи
Допустим, что электрические токи текут в тонких проводах. В этом случае направления токов совпадают с направлением оси провода. Для тонких проводов можно считать, что плотность тока $\overrightarrow{j}=const$ в любой точке поперечного сечения провода. В нашем случае можно записать, что сила тока равна:
где $S$ — площадь поперечного сечения проводника. Пусть мы имеем дело с постоянным током (I=const) вдоль всего проводника. Допустим, что в цепи присутствует источник ЭДС ($\mathcal E$). В данном случае локальная формулировка закона Ома будет иметь вид:
где $\overrightarrow{E}$ напряженность поля кулоновских сил, $\overrightarrow{E_{stor}}$ — напряженность поля сторонних сил, $\sigma $ — удельная проводимость, $\overrightarrow{e}$- единичный вектор, направленный по току. Для тонкого провода можно записать выражение (3), как:
Умножим выражение (4) на элемент длины проводника (dl) и найдем интеграл по участку проводника от точки 1 до точки 2. Так как силу тока мы признали постоянной, то имеем:
Электростатическое поле потенциально, следовательно:
Второй интеграл в выражении (5) не равен нулю только в пределах источника ЭДС. Он не зависит от положения точек 1 и 2. Они должны находиться только вне источника.
Считают, что ЭДС источника больше нуля, если путь 1-2 пересекает источник от отрицательного полюса к положительному.
где $R’$ — электросопротивление, $\rho $ — удельное сопротивление. Таким образом, из выражения (5) получаем:
Мы получили закон Ома в интегральной форме. В том случае, если цепь замкнута, то ${\varphi }_1={\varphi }_2$, следовательно:
где $R’$ — электросопротивление всей цепи, электросопротивление нагрузки и внутреннее сопротивление источника тока. То есть закон Ома для замкнутой цепи запишем как:
где $r$ — электросопротивление источника тока.
Довольно часто приходится решать задачи, в которых напряжение на концах участка цепи не известно, но заданы сопротивления составных частей цепи и ЭДС источника, который питает цепь. Тогда используют закон Ома в виде (11) для расчета силы тока, которая течет в цепи.
Пример 1
Задание: Источник тока имеет внутреннее электросопротивление равное r . Найдите падение потенциала внутри источника ($U_r$) внутри элемента, если ток в цепи равен I. Как вычислить внешнее электросопротивление цепи при заданных условиях?
Решение:
В качестве основы для решения задачи используем закон Ома для замкнутой цепи:
\[I=\frac{\mathcal E}{R+r}\left(1.1\right).\]Из формулы (1.1) легко получить формулу для расчета внешнего сопротивления:
\[I\left(R+r\right)=\mathcal E\to \mathcal E-Ir=IR\to R=\frac{\mathcal E}{I}-r.\]Для того чтобы вычислить падение напряжения внутри источника тока, используем закон Ома для участка цепи:
\[{I=\frac{U_r}{r}\to U}_r=Ir\ \left(1.2\right).\]Ответ: $U_r=Ir,$ $R=\frac{\mathcal E}{I}-r.$
Пример 2
Задание: Источник тока имеет внутреннее сопротивление равное r=1 Ом и ЭДС равную $\mathcal E$=10В. Найдите КПД источника ($\eta $), если ток в цепи равен I=5 А.
Решение:
Коэффициент полезного действия источника тока равен отношению:
\[\eta =\frac{P’}{P}\left(2.1\right),\]где $P’$ — мощность (полезная мощность), которая выделяется внешним участком цепи, $P$- полная мощность, которая развивается источником. При этом:
\[P’=I^2R\ \left(2.2\right),\ \] \[P=\mathcal E I\ \left(2.3\right).\]Следовательно, КПД источника можно выразить как:
\[\eta =\frac{I^2R\ }{\mathcal E I}=\frac{IR}{\mathcal E}\left(2.4\right).\]Следуя закону Ома для замкнутой цепи запишем:
\[I=\frac{\mathcal E}{R+r}\left(2.5\right).\]Выразим из (2.5) электросопротивление внешней цепи, получим:
\[R=\frac{\mathcal E}{I}-r(2.6).\]Подставим (2.6) в выражение для КПД (2.4), получим:
\[\eta =\frac{I\left(\frac{\mathcal E}{I}-r\right)}{\mathcal E}=\frac{\mathcal E-Ir}{\mathcal E}.\]Подставим численные данные, проведем вычисления, получим:
\[\eta =\frac{10-5\cdot 1}{10}\cdot 100\%=50\%\]Ответ: 50%

