Физика, 9 кл. (Буховерцев Б.Б.)

Физика, 9 кл. (Буховерцев Б.Б.)

Буховцев Б.Б., Климонтович Ю.Л., Мякишев Г.Я. Физика. 9 класс. Учебник. — 6-е изд. — М.: Просвещение, 1982. — 272 с. В учебнике на современном уровне изложены фундаментальные вопросы школьной программы, представлены основные технические применения законов физики, рассмотрены методы решения задач. Книга адресована учащимся средних школ, слушателям и преподавателям подготовительных отделений вузов, а также читателям, занимающимся самообразованием и готовящимся к поступлению в вуз. Оглавление ТЕПЛОВЫЕ ЯВЛЕНИЯ. МОЛЕКУЛЯРНАЯ ФИЗИКА Глава I. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ. РАЗМЕРЫ МОЛЕКУЛ 2. МАССА МОЛЕКУЛ. ПОСТОЯННАЯ АВОГАДРО 3. БРОУНОВСКОЕ ДВИЖЕНИЕ. 4. СИЛЫ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ 5. СТРОЕНИЕ ГАЗООБРАЗНЫХ, ЖИДКИХ И ТВЕРДЫХ ТЕЛ 6. ИДЕАЛЬНЫЙ ГАЗ В МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ 7. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ I Глава II. ТЕМПЕРАТУРА. ЭНЕРГИЯ ТЕПЛОВОГО ДВИЖЕНИЯ МОЛЕКУЛ 8. ТЕПЛОВОЕ РАВНОВЕСИЕ. ТЕМПЕРАТУРА 9. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ 10. АБСОЛЮТНАЯ ТЕМПЕРАТУРА. ТЕМПЕРАТУРА — МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ 11. ИЗМЕРЕНИЕ СКОРОСТЕЙ МОЛЕКУЛ ГАЗА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ II Глава III. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ГАЗОВЫЕ ЗАКОНЫ 12. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА 13. ПРИМЕНЕНИЕ УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА К РАЗЛИЧНЫМ ПРОЦЕССАМ 14. ПРИМЕНЕНИЕ ГАЗОВ В ТЕХНИКЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ III Глава IV. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 16. РАБОТА В ТЕРМОДИНАМИКЕ 17. КОЛИЧЕСТВО ТЕПЛОТЫ 18. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 19. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ К РАЗЛИЧНЫМ ПРОЦЕССАМ 20. НЕОБРАТИМОСТЬ ПРОЦЕССОВ В ПРИРОДЕ 21. ПРИНЦИПЫ ДЕЙСТВИЯ ТЕПЛОВЫХ ДВИГАТЕЛЕЙ 22. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ (КПД) ТЕПЛОВОГО ДВИГАТЕЛЯ. ТЕПЛОВЫЕ ДВИГАТЕЛИ И ОХРАНА ПРИРОДЫ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ IV Глава V. ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ЖИДКОСТЕЙ И ГАЗОВ 23. НАСЫЩЕННЫЙ ПАР 24. ЗАВИСИМОСТЬ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА ОТ ТЕМПЕРАТУРЫ. КИПЕНИЕ. КРИТИЧЕСКАЯ ТЕМПЕРАТУРА 25. ВЛАЖНОСТЬ ВОЗДУХА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ V Глава VI. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТЕЙ 27. СИЛА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ 28. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ VI Глава VII. ТВЕРДЫЕ ТЕЛА 29. КРИСТАЛЛИЧЕСКИЕ ТЕЛА 30. АМОРФНЫЕ ТЕЛА 31. ДЕФОРМАЦИЯ. ВИДЫ ДЕФОРМАЦИИ ТВЕРДЫХ ТЕЛ 32. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДИАГРАММА РАСТЯЖЕНИЯ 33. ПЛАСТИЧНОСТЬ И ХРУПКОСТЬ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ VII ОСНОВЫ ЭЛЕКТРОДИНАМИКИ 34. ЧТО ТАКОЕ ЭЛЕКТРОДИНАМИКА? Глава VIII. ЭЛЕКТРОСТАТИКА 35. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ 36. ЗАРЯЖЕННЫЕ ТЕЛА. ЭЛЕКТРИЗАЦИЯ ТЕЛ 37. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА 38. ОСНОВНОЙ ЗАКОН ЭЛЕКТРОСТАТИКИ — ЗАКОН КУЛОНА 39. ЕДИНИЦА ЭЛЕКТРИЧЕСКОГО ЗАРЯДА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 40. БЛИЗКОДЕЙСТВИЕ И ДЕЙСТВИЕ НА РАССТОЯНИИ 41. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 42. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ 43. СИЛОВЫЕ ЛИНИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ 44. ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ 45. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ РАВНОМЕРНО ЗАРЯЖЕННОГО ПРОВОДЯЩЕГО ШАРА И БЕСКОНЕЧНОЙ ПЛОСКОСТИ 46. ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ДВА ВИДА ДИЭЛЕКТРИКОВ 47. ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ. ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ 48. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ 49. ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ И РАЗНОСТЬ ПОТЕНЦИАЛОВ 50. ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ТОЧЕЧНОГО ЗАРЯДА 51. СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ЭЛЕКТРИЧЕСКОГО ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ. ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ 52. ИЗМЕРЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 53. ЭЛЕКТРОЕМКОСТЬ. ЕДИНИЦЫ ЭЛЕКТРОЕМКОСТИ 54. КОНДЕНСАТОРЫ. ЭЛЕКТРОЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА 55. ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА. ПРИМЕНЕНИЯ КОНДЕНСАТОРОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ X Глава IX. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК 56. ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА ТОКА 57. УСЛОВИЯ, НЕОБХОДИМЫЕ ДЛЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА 58. ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. СОПРОТИВЛЕНИЕ 59. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ПРОВОДНИКА ОТ ТЕМПЕРАТУРЫ 60. СВЕРХПРОВОДИМОСТЬ 61. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ 62. ИЗМЕРЕНИЕ СИЛЫ ТОКА И НАПРЯЖЕНИЯ 63. РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 64. ЭЛЕКТРОДВИЖУЩАЯ СИЛА 65. ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ IX Глава X. ЭЛЕКТРИЧЕСКИЙ ТОК В РАЗЛИЧНЫХ СРЕДАХ 66. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ РАЗЛИЧНЫХ ВЕЩЕСТВ 67. ЭЛЕКТРОННАЯ ПРОВОДИМОСТЬ МЕТАЛЛОВ 68. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ 69. ЗАКОН ЭЛЕКТРОЛИЗА 70. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ 71. НЕСАМОСТОЯТЕЛЬНЫЙ И САМОСТОЯТЕЛЬНЫЙ РАЗРЯДЫ 72. РАЗЛИЧНЫЕ ТИПЫ САМОСТОЯТЕЛЬНОГО РАЗРЯДА И ИХ ТЕХНИЧЕСКИЕ ПРИМЕНЕНИЯ 73. ПЛАЗМА 74. ЭЛЕКТРИЧЕСКИЙ ТОК В ВАКУУМЕ 75. ДВУХЭЛЕКТРОДНАЯ ЭЛЕКТРОННАЯ ЛАМПА-ДИОД 76. ЭЛЕКТРОННЫЕ ПУЧКИ. ЭЛЕКТРОННОЛУЧЕВАЯ ТРУБКА 77. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ 78. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ ПРИ НАЛИЧИИ ПРИМЕСЕЙ 79. ЭЛЕКТРИЧЕСКИЙ ТОК ЧЕРЕЗ КОНТАКТ ПОЛУПРОВОДНИКОВ p- И n- ТИПОВ 80. ПОЛУПРОВОДНИКОВЫЙ ДИОД 81. ТРАНЗИСТОР 82. ТЕРМИСТОРЫ И ФОТОРЕЗИСТОРЫ ПРИМЕР РЕШЕНИЯ ЗАДАЧИ КРАТКИЕ ИТОГИ ГЛАВЫ X Глава XI. МАГНИТНОЕ ПОЛЕ 83. ВЗАИМОДЕЙСТВИЕ ТОКОВ. МАГНИТНОЕ ПОЛЕ 84. ВЕКТОР МАГНИТНОЙ ИНДУКЦИИ 85. ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ 86. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ 87. МОДУЛЬ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ. МАГНИТНЫЙ ПОТОК 88. ЗАКОН АМПЕРА 89. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД. СИЛА ЛОРЕНЦА 90. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ XI Глава XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ 91. ОТКРЫТИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 92. НАПРАВЛЕНИЕ ИНДУКЦИОННОГО ТОКА. ПРАВИЛО ЛЕНЦА 93. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 94. ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 95. ЭДС ИНДУКЦИИ В ДВИЖУЩИХСЯ ПРОВОДНИКАХ 96. САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ 97. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА 98. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРОДИНАМИКИ И ИХ ТЕХНИЧЕСКОЕ ПРИМЕНЕНИЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ XII ЗАКЛЮЧЕНИЕ ЛАБОРАТОРНЫЕ РАБОТЫ ОТВЕТЫ К УПРАЖНЕНИЯМ

1. Фотометрия.

%PDF-1.6 % 1 0 obj > /Metadata 4 0 R /OCProperties > > > ] /ON [ 5 0 R ] /Order [ ] /RBGroups [ ] >> /OCGs [ 5 0 R ] >> /Pages 7 0 R /StructTreeRoot 30 0 R /Type /Catalog >> endobj 2 0 obj /CreationDate (D:20130711143933+03’00’) /Creator (Microsoft Word 2013) /ModDate (D:20130711144145+03’00’) /Producer (Microsoft Word 2013) /Title >> endobj 3 0 obj > /Font > >> /Fields 278 0 R >> endobj 4 0 obj > stream application/pdf

Юра

1. Фотометрия.

2013-07-11T14:39:33+03:00Microsoft® Word 20132013-07-11T14:41:45+03:002013-07-11T14:41:45+03:00Microsoft® Word 2013uuid:1de896c6-a96d-42d9-8387-15f71bdb6931uuid:3aabc18f-2ed0-4035-a986-9c36ba79138b endstream endobj 5 0 obj > /PageElement > /Print > /View > >> >> endobj 6 0 obj > stream x͙oFW_Pݑ_@KaAC10d@V/gYĒO r%S#Re$eBT&C!yN!j^B;Rd;I*0d *)y|),U0O߫K_՟Vwq.

&/%;1d/@d/@d/TԪ~wW777]|rJs>?c|l}\wTrVvֻܨ>J&sĒw鋝Q5~[s(ZtwnյBs°:]C_|f!2XNm׋`|}Rv=~Mׁ;knr{>,Wzo87HgωVJ6{nXWSAuuz=Pk4355⠮ᔮlQ*ހ(Ocvn;z+N׹ H.P3″PoE]`?*,PbCXZP QfxhHG7 uD)Q6J0x̬/B}پqC

Circuits Review: AP® Physics 1 & 2 Crash Course Review

Проще говоря, цепь представляет собой замкнутую проводящую проволочную петлю с некоторыми элементами, такими как батареи, резисторы и конденсаторы. В AP® Physics 1 рассматриваются только батареи и резисторы; Физика 2 также охватывает конденсаторы. В этой статье мы рассмотрим характеристики цепей, резисторов и конденсаторов, а также решим несколько примеров задач, аналогичных тем, которые используются на экзаменах AP® Physics 1 и 2.

Текущий

Электрический ток определяется как заряд, проходящий через площадь поперечного сечения за время:

Электрический ток = заряд за время.

Заряд измеряется в кулонах (C), поэтому ток измеряется в кулонах в секунду или в амперах: 1A=1C/s. Например, если через резистор за 10 с прошло заряд 5,0 Кл, ток будет (5,0 Кл)/(10 с) = 0,5 А. Физики обычно обозначают ток буквой I. Обычно используются как строчные, так и заглавные буквы.

Вот краткое объяснение микроскопического происхождения электрического тока:

Электрический ток: краткий микроскопический взгляд

Электрические цепи полезны, потому что они управляют потоком электрического заряда. Представьте металлическую проволоку. Вы могли знать из курса химии, что металлические связи образуются, когда каждый атом делит свой валентный электрон (электроны) со всеми другими атомами — электроны не «прикреплены» к какому-либо отдельному атому и, следовательно, образуют «электронное море».

Когда электронное «море» демонстрирует чистое движение в определенном направлении вдоль провода, мы говорим, что провод несет электрический ток . Электрический ток движется в направлении, противоположном направлению электронов, потому что электроны заряжены отрицательно; физики используют направление, в котором положительные заряды двигались бы (если бы они могли двигаться, поскольку атомные ядра тяжелые) в качестве условного знака.

Электронное «море» движется очень, очень медленно (порядка микрометров в секунду), но электронов так много, что даже очень медленное движение создает измеримый ток.

Хотя настоящие электроны могут не перемещаться по всей цепи, ток должен это делать. Вот почему цепи должны быть закрыты , или не иметь разрывов. Если в цепи есть разрыв, то ток не может пройти туда и обратно, и мы говорим, что цепь разомкнута.

В стационарной цепи ни в одном узле не накапливается заряд (узел — это место соединения двух или более проводов). Следовательно, ток, входящий в узел, должен быть равен току, выходящему из узла:

Ток на входе = ток на выходе.

Это называется правилом узлов Кирхгофа, правилом узлов Кирхгофа, или первым законом Кирхгофа . Это формулировка принципа сохранения заряда в узле цепи.

Напряжение

Разность потенциалов определяется как изменение потенциальной энергии на единицу заряда:

Разность потенциалов = (изменение потенциальной энергии) / (заряд).

Поскольку потенциальная энергия измеряется в джоулях (Дж), а заряд — в кулонах (Кл), напряжение измеряется в джоулях на кулон или вольтах: 1 В = 1 Дж/Кл. Физики обозначают напряжение заглавной буквой V. Мы говорим «разность напряжений», потому что ни одна точка в цепи не имеет определенного истинного напряжения — только разница в напряжении между двумя точками в цепи имеет физический смысл.

Когда ток проходит через элемент цепи, заряженные частицы могут приобретать потенциальную энергию (положительная разность потенциалов) или терять потенциальную энергию (отрицательная разность потенциалов). На каждом элементе цепи существует определенная разность напряжений, но когда ток совершает круговое движение, его энергия должна быть такой же, как в начале:

Сумма разностей напряжений в замкнутом контуре должна быть равна нулю.

Это называется Правило цикла Кирхгофа  или Второй закон Кирхгофа .

Имейте в виду, что термины «разность напряжений», «разность потенциалов», «падение напряжения», «изменение потенциала» и другие подобные термины означают одно и то же.

Обычно батареи необходимы для поддержания отличного от нуля электрического тока в цепи. В частности, сопротивление цепи вызывает потерю энергии, которая восполняется за счет химической энергии батареи. Напряжение на батарее называется электродвижущей силой , или ЭДС:

ЭДС = электродвижущая сила = увеличение напряжения на батарее.

Электродвижущая «сила» не является истинной силой; название — историческая реликвия, заменить которую пока никто не удосужился. Вы можете прочитать ЭДС батареи на ее этикетке; например, небольшие прямоугольные батареи обычно имеют ЭДС 9В.

Символ цепи батареи на экзаменах AP®:

Источник изображения: Wikimedia Commons

Более длинная линия на символе батареи всегда соответствует более высокому напряжению. (Вы можете увидеть батареи с большим количеством линий; по-прежнему должны быть одна короткая и одна длинная линия на концах символа.) Если ЭДС батареи равна 9V, то мы говорим, что разность потенциалов на аккумуляторе слева направо составляет 9 В. Разность потенциалов справа налево равна -9В.

Сопротивление

Сопротивление – это свойство элемента цепи, вызывающее потерю энергии. Например, если материал провода не является идеально проводящим (нет ничего, кроме сверхпроводников), то энергия будет теряться при протекании тока по проводу. Часто элементы схемы разрабатываются так, чтобы преднамеренно вызывать потерю энергии; эти элементы схемы называются резисторы . Символ цепи для резистора на экзамене AP®:

Источник изображения: Wikimedia Commons

Все резисторы и сопротивления, которые вы встречаете в AP® Physics, подчиняются соотношению, известному как Закон Ома:

V=IR.

В этом уравнении V — разность потенциалов на элементе цепи, I — ток через элемент, а R — его сопротивление. Элементы цепи, подчиняющиеся этому закону, называются Омическими.

Помните, мы говорили, что V — это изменение потенциальной энергии на один заряд. Когда мы умножаем на ток, мы получаем изменение потенциальной энергии за время: 92/R,

Последние два выражения получаются путем замены V=IR в различных формах в самом левом равенстве. Функция батареи состоит в том, чтобы компенсировать эту потерю энергии путем преобразования ее химической энергии в электрическую энергию, которая в конечном итоге рассеивается в виде тепла резистором (ами) в соответствии с приведенной выше формулой. Вот почему батарейки разряжаются!

Комбинация сопротивлений

На экзамене AP® вы увидите резисторы, соединенные друг с другом в различных комбинациях. Все традиционные комбинации можно разбить на более простые комбинации двух типов: последовательные и параллельные.

Почти наверняка вас попросят найти «эквивалентное сопротивление» комбинации резисторов. «Эквивалентное сопротивление» означает сопротивление одного резистора, который дает такой же ток при той же разности напряжений, что и исходная комбинация, или, что то же самое, сопротивление одного резистора, который дает такую ​​же разность напряжений при том же токе. Все, что нам нужно, чтобы вывести формулу для комбинаций резисторов, — это закон Ома, V = IR и законы Кирхгофа.

Резисторы, включенные последовательно

Резисторы, соединенные последовательно, соединяются по одному пути тока; вы можете думать о них как о двух водяных колесах на одной и той же реке. Ниже приведены два последовательных резистора и желаемое эквивалентное сопротивление.

Один и тот же ток I проходит через { R }_{ 1 } и { R }_{ 2 }, поэтому напряжения на этих резисторах равны

{ V }_{ 1 }={ IR }_{ 1 }, {V}_{2}={IR}_{2}.

Суммарное напряжение на комбинации 9 В.0003

{ V }_{ 1 }+{ V }_{ 2 }=I ({ R }_{ 1 }+{ R }_{ 2 }).

Мы хотим, чтобы эквивалентное сопротивление давало то же напряжение, что и общее напряжение комбинации:

{ V }_{ eq }={ V }_{ 1 }+{ V }_{ 2 }= I ({ R }_{ 1 }+{ R }_{ 2 }).

Так как { V }_{ eq }={ IR }_{ eq }, мы имеем { R }_{ eq }={ R }_{ 1 }+{ R }_{ 2 }. Распространяя это на произвольное количество последовательно соединенных резисторов, эквивалентное сопротивление последовательных резисторов составляет

{R}_{eq}={ R }_{ 1 }+{ R }_{ 2 }+{ R }_{ 3 }

Параллельные резисторы

Параллельные резисторы соединены отдельными ветвями, которые соединяются вместе до и после прохождения тока через параллельные резисторы:

На приведенном выше рисунке общий ток I разделяется на меньшие токи I ₁ и I ₂ , которые проходят через резисторы R ₁ и R ₂ соответственно. По правилу пересечения Кирхгофа

I ={ I }_{ 1 }+{ I }_{ 2 }.

По правилу Кирхгофа для контура, состоящего из резисторов 1 и 2,

{ V }_{ 1 }={ V }_{ 2 }, или

{ R }_{ 1 }{ I }_{ 1 }={ Р }_{ 12}{ Я }_{ 2 }

{ I }_{ 2 }={ R }_{ 1 }{ I }_{ 1 }/{ R }_{ 2 }.

Подставив это в правило пересечения Кирхгофа, мы получим

I = { I }_{ 1 }(1+{ R }_{ 1 }/{ R }_{ 2 }).

Напряжение на эквивалентном сопротивлении по определению равно либо напряжению на резисторе 1, либо на резисторе 2 (они равны):

{ R }_{ eq }I={ R }_{ 1 }{I }_{ 1 }.

Объединив это с предыдущим уравнением, мы получим \dfrac{1}{R_{eq}} = \dfrac{1}{R_1} + \dfrac{1}{R_2}. Распространяя на произвольное количество резисторов, эквивалентное сопротивление параллельных резисторов определяется по формуле:

{\dfrac{1}{R_{eq}} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3} }.

Чтобы найти эквивалентное сопротивление алгебраически, это уравнение предлагает вам сложить обратные величины параллельных сопротивлений и получить обратную сумму. Это желаемое эквивалентное сопротивление.

Вот пример проблемы, в которой участвуют как параллельные, так и последовательные резисторы.

Эквивалентное сопротивление

Ток силой 2 А проходит через комбинацию резисторов, приведенную ниже:

(a) Найдите ток через каждый резистор.

(b) Найдите мощность, рассеиваемую каждым резистором.

(c) Найдите эквивалентное сопротивление комбинации.

(d) Найдите полную мощность, рассеиваемую этой комбинацией.

Решение:

(a) Весь ток должен проходить через резистор 15 Ом, поэтому ток через него равен 2,0 А. Параллельная комбинация состоит из двух одинаковых сопротивлений, поэтому ток через любое из них равен 1,0 А. Если бы эти сопротивления не были одинаковыми, вам пришлось бы использовать законы Кирхгофа для составления уравнений { 1 }={ R }_{ 2 }{ I }_{ 2 },

, а затем найдите { I }_{ 1 }   и {I }_{ 2 }.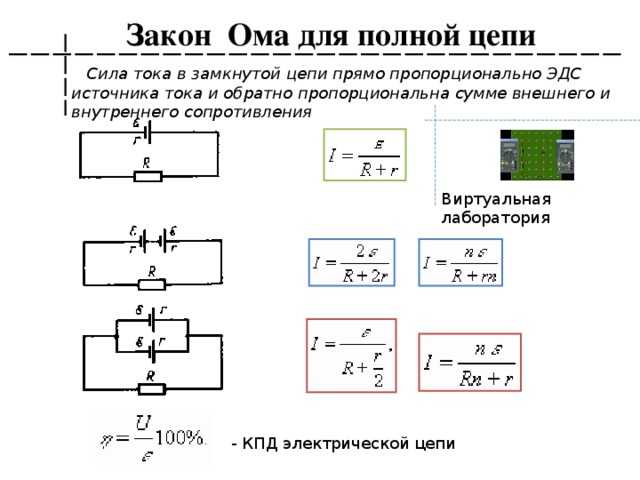 9{ 2 }(15\Омега)=60 Вт.

(c) Эквивалентное сопротивление параллельной комбинации определяется как

\dfrac{1}{R_{parallel}} = \dfrac{1}{10 \Omega} + \dfrac{1}{10 \Omega} , или R_{parallel} = 5 \Omega.

Эквивалентное сопротивление всей комбинации получается путем суммирования сопротивления первой комбинации с остальным сопротивлением последовательно:

R_{eq} = 5 \Omega + 15 \Omega = {20 \Omega}.

(d) Поскольку напряжение и ток идентичны в эквивалентных сопротивлениях и комбинациях сопротивлений, мощность также одинакова. Мы можем просто использовать формулу мощности 92(20 \Омега) = {80 Вт}.

Конечно, это равно сумме мощностей, рассеиваемых тремя резисторами в части (b).

Емкость (только для физики 2)

Конденсатор представляет собой устройство, состоящее из двух металлических пластин , разделенных небольшим расстоянием, которые могут содержать изолятор, например бумагу или керамику.

Ниже приведен символ емкости на экзамене AP® Physics 2; вы можете увидеть символическое изображение двух пластин:

Символ цепи для неполяризованного конденсатора. Источник изображения: Wikimedia Commons

Конденсатор имеет емкость для накопления заряда: одна пластина заряжена положительно и имеет более высокий потенциал; другая пластина заряжена отрицательно и имеет более низкий потенциал. Чем выше емкость, тем больше заряда он может хранить при данной разности напряжений. Мы называем это отношение емкостью, которую обозначают заглавной буквой C.

Q=CV.

Q представляет величину заряда на любой пластине, а V представляет собой разность потенциалов между двумя пластинами. Емкость измеряется в кулонах на вольт; физики называют эту единицу Фарада :

1F=1C/V.

Подумайте об уравнении Q=CV. Если V постоянно, то и Q остается постоянным. Поскольку отсутствие изменения заряда означает отсутствие протекания тока,

В полностью заряженный конденсатор не втекает и не выходит ток.

Ток течет, только если конденсатор заряжается или разряжается. Вам не придется беспокоиться об этом на экзамене AP® Physics 2: вопросы касаются только стационарного поведения конденсаторов — когда они полностью заряжены или не заряжены вообще.

92}{2C} = \dfrac{QV}{2}.

Если вы запомните одну формулу, то сможете получить две другие, подставив различные формы определения емкости, Q=CV.

Объединение емкостей (только для физики 2)

Законы нахождения эквивалентных емкостей обратны законам для сопротивлений. Выводы очень похожи, поэтому я не буду выводить формулы для эквивалентных емкостей, но вот они:

Конденсаторы серии

{\ dfrac {1} {C_ {eq, ряд}} = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3}}.

Параллельные конденсаторы

{C_{экв, параллельно} = C_1 + C_2 + C_3}

Давайте решим пример задачи, похожей на ту, с которой вы можете столкнуться на экзамене AP® Physics 2.

Эквивалентная емкость

На приведенной ниже диаграмме емкость каждого конденсатора составляет 10 мФ, а напряжение на комбинации составляет 5,0 В.

(a) Найдите напряжение на каждом конденсаторе.

(b) Найдите заряд каждого конденсатора.

(c) Найдите эквивалентную емкость.

(d) Найдите полную энергию, запасенную в цепи.

Решение:

(a) Напряжение на обеих ветвях должно быть одинаковым по правилу Кирхгофа. Поскольку емкости двух конденсаторов в верхней ветви равны, оба имеют разность потенциалов 2,5 В. Разность потенциалов на нижнем конденсаторе составляет 5,0 В.

(b) Используя уравнение Q=CV, находим

{ Q }_{ верх }=(10 мФ)(2,5 В)=25 мКл,

{ Q }_{ низ }= (10 мФ)(5 В) =50мКл.

(c) Используя правило сложения рядов, эквивалентная емкость верхней ветви определяется как

\dfrac{1}{C_{top}} = \dfrac{1}{10 мФ} + \dfrac{1} {10 мФ} или C_{top} = 5 мФ.

Используя правило параллельного сложения на обеих ветвях,

C_{eq} = 5 мФ + 10 мФ = {15 мФ}.

(d) Мы знаем эквивалентную емкость комбинации и полное напряжение на ней, поэтому по формуле энергии 92}{2} = {0,19 Дж}.

Завершающие схемы для экзаменов AP® по физике 1 и 2

Вот важные уравнения, которые вы должны знать для экзаменов AP® по физике 1 и 2.

Правило Kirchhoff’s Junction

Curance In = Curance Out

Правило петли Kirchhoff’s

.2}{2C} = \dfrac{QV}{2}

Эквивалентная емкость серии

  {\dfrac{1}{C_{eq, series}} = \dfrac{1}{C_1} + \dfrac{1}{C_2} + \dfrac{1}{ С_3}}

Параллельная эквивалентная емкость

{C_{экв, параллель} = C_1 + C_2 + C_3}

Ищете практику AP® Physics 1 & 2?

Ознакомьтесь с другими нашими статьями по AP® Physics 1 & 2.

Вы также можете найти тысячи практических вопросов на Albert.io. Albert.io позволяет вам настроить учебный процесс так, чтобы он ориентировался на практику, в которой вам больше всего нужна помощь. Мы дадим вам сложные практические вопросы, которые помогут вам освоить AP® Physics 1 и 2.

Начните практиковать здесь .

Вы учитель или администратор, заинтересованный в повышении успеваемости учащихся по AP® Physics 1 и 2?

Узнайте больше о наших школьных лицензиях здесь .

Закон Ома – определение, формула, применение, примеры

Закон Ома определяется как зависимость между электрическим током и разностью потенциалов. Ток, протекающий по большинству проводников, прямо пропорционален его напряжению. Георг Симон Ом, немецкий физик, первым экспериментально проверил закон Ома.

Содержание

Определение закона Ома Единица сопротивления Проводимость Единица удельного сопротивления Электропроводность Зависимость между напряжением, током и сопротивлением Экспериментальная проверка закона Ома Расчет электрической мощности по закону Ома Исключения из закона Ома Микроскопическая форма закона Ома Применение закона Ома Ограничения закона Ома Решенные примеры Часто задаваемые вопросы (FAQ)

В нем говорится, что ток, протекающий между двумя точками в проводнике, прямо пропорционален разности потенциалов между двумя точками.

Формула закона Ома

I ∝ V при постоянной температуре

В/И = Р

или В = ИК

где R — константа.

Постоянная R называется сопротивлением проводника. Его значение зависит от природы проводника, его размеров и окружающей среды (например, температуры). Закон Ома не универсален (т.е. не все проводники подчиняются закону Ома). Проводники, подчиняющиеся закону Ома, называются омическими проводниками. Однако сопротивление всегда определяется как отношение V/I.

Для проводника с площадью поперечного сечения A сопротивление между участками A и B, разделенными длиной l, определяется выражением R _AB = ρ l/A

где l = длина провода

• A = площадь поперечного сечения и 90 512
• ρ = удельное сопротивление или удельное сопротивление проводника. (Ее значение зависит от природы материала проводника и его температуры.)

Единица сопротивления

Единицей сопротивления в системе СИ является ом.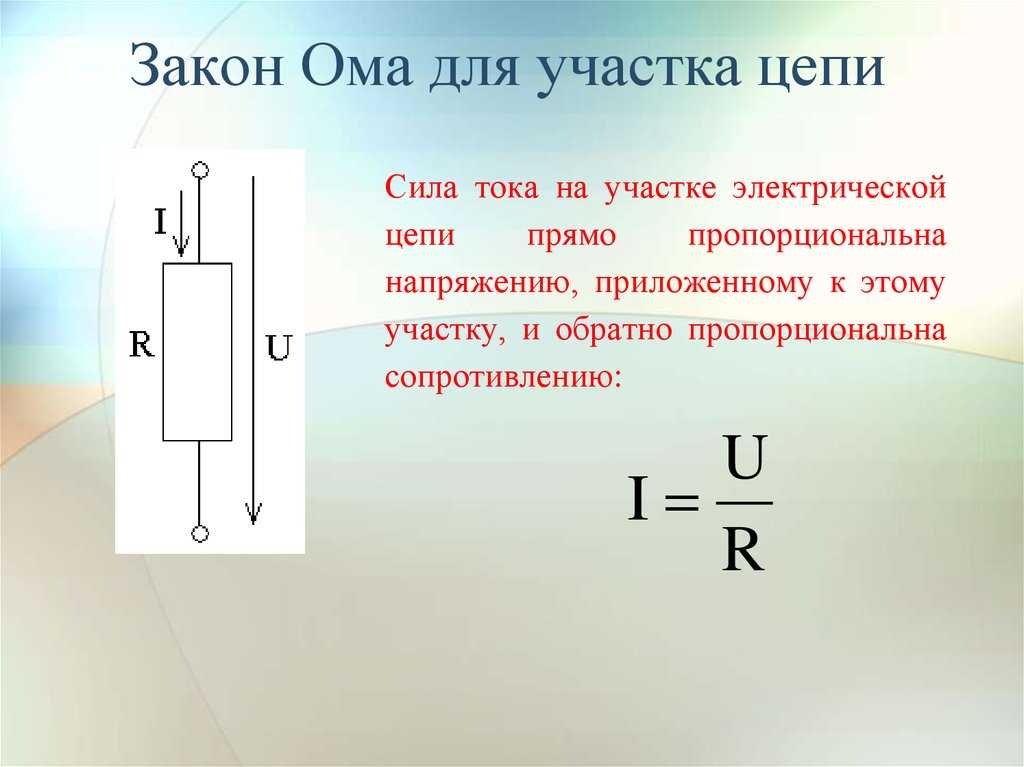 Обозначается Ω. 1 Ом (Ом) = 1 вольт ампер-1

Проводимость

Обратная величина сопротивления называется проводимостью. Обозначается G.

Г = 1/Р; Его единицей СИ является ом — 1 или мхо или симен.

Единица удельного сопротивления

Мы знаем, что R = ρl/A

ρ = РА/л

В системе СИ единица удельного сопротивления = ом × метр ² / метр = ом-метр. или Ом ^-м

Электропроводность

Он определяется как величина, обратная удельному сопротивлению, и обозначается σ.

или,σ = 1/ρ

Единицей проводимости в СИ является ом ^-1 метр ^-1 или симен м ^-1

Связь между напряжением, током и сопротивлением

Анализируя серии 1, 2 и 3, мы понимаем, что удвоение и утроение напряжения приводит к удвоению и утроению тока в цепи. Точно так же, сравнивая серии 1 и 4 и серии 2 и 5, мы понимаем, что удвоение общего сопротивления вдвое уменьшает ток цепи.

Экспериментальная проверка закона Ома

Следующий эксперимент может проверить закон Ома:

Требуемый аппарат:

• Резистор
• Амперметр
• Вольтметр
• Аккумулятор
• Вставной ключ
• Реостат

Схема цепи:

Процедура:

• Как правило, ключ К закрыт, а реостат настроен на получение минимального показания амперметра А и вольтметра V.
• Ток в цепи постепенно увеличивают, перемещая скользящий вывод реостата. При этом регистрируют ток, протекающий по цепи, и соответствующее значение разности потенциалов на проводе сопротивления (R).
• Таким образом получают разные наборы значений напряжения и тока.
• Для каждого набора значений V и I рассчитывается отношение V/I.
• Когда вы рассчитаете соотношение ввода/вывода для каждого случая, вы обнаружите, что оно одинаково. Следовательно, V/I = R, что является константой.
• Нарисуйте график зависимости тока от разности потенциалов. Это будет прямая линия. Это показывает, что ток пропорционален разности потенциалов.

Расчет электрической мощности по закону Ома

Энергия преобразуется из электрической энергии движущихся зарядов в какую-либо другую форму энергии, такую ​​как механическая энергия, тепловая энергия или энергия, хранящаяся в магнитных полях или электрических полях, известная как электрическая энергия. Единицей мощности является ватт. Электрическая мощность может быть рассчитана с использованием закона Ома и подстановки значений напряжения, тока и сопротивления.

Формула мощности

• когда заданы значения напряжения и тока: Р = ВИ

• Если даны значения напряжения и сопротивления: P = V ² / R

• Если заданы значения тока и сопротивления: P = I ² R

Исключения из закона Ома

• Проводники, подчиняющиеся закону Ома, называются омическими проводниками. Сопротивление омического проводника не зависит от разности потенциалов или силы тока.
• Ток пропорционален приложенной разности потенциалов при сохранении постоянных физических условий. Таким образом, график V – I для омического проводника представляет собой прямую линию, проходящую через начало координат.
• Проводники, не подчиняющиеся закону Ома, называются неомическими проводниками. Для таких проводников график между разностью потенциалов и током не является прямой линией, проходящей через начало координат, т.е. электронные лампы, полупроводники и т. д.

Микроскопическая форма закона Ома

Мы знаем, что i = neAvd и vd = eE/mτ

i = neA τ

или,J = i/A = ne ² E/mτ

или, J = E/ρ, где ρ = m/ne ² τ

или Дж = σE [σ = 1/ρ ]

что является микроскопической формой закона Ома.

Применение закона Ома

Основные применения закона Ома:

• Для определения напряжения, тока или сопротивления электрической цепи.
• Закон Ома поддерживает желаемое падение напряжения на электронных компонентах.
• Закон Ома также используется в амперметре постоянного тока и других шунтах постоянного тока для шунтирования тока.

Ограничения закона Ома

Ниже приведены ограничения закона Ома:

• Закон Ома не применяется к однотактным электрическим элементам, таким как диоды и транзисторы, потому что они позволяют электрическому току течь только в одном направлении.
• Для нелинейных электрических элементов с такими параметрами, как емкость, сопротивление и т. д., отношение напряжения к току не будет постоянным во времени, что затрудняет использование закона Ома.

Решенные примеры

Q1. Если сопротивление железа равно 40 Ом и через сопротивление протекает ток силой 3,2 А. Найдите напряжение между двумя точками.

Ответ. Учитывая, что R= 40 Ом

я = 3,2 А

Сейчас,

V = I × R

Подставляя данные значения получаем,

В = 3,2 А × 40 Ом = 128 В

В = 128 В

Q2.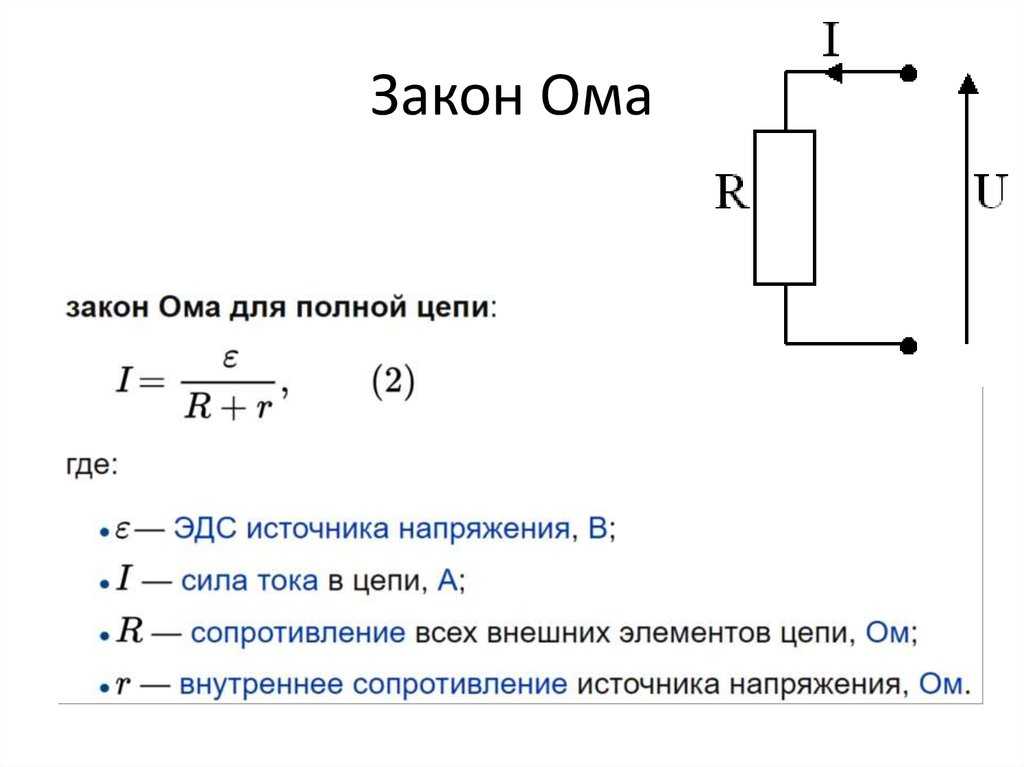 К лампочке подключен источник ЭДС напряжением 10 В. Через него протекает электрический ток силой 5 А. Считайте, что проводящие провода не имеют сопротивления. Найдите сопротивление электроприбора.

Ответ. Дано, В = 10 В

я = 5 А

R = V ÷ I

R = 10 В ÷ 5 А = 2 Ом

R = 2 Ом

Часто задаваемые вопросы (FAQ)

Q1. Государственный закон Ома?

Ответ. Ток в проводнике между двумя точками прямо пропорционален приложенному к этим двум точкам напряжению.

Q2. Что такое единица СИ закона Ома?

Ответ. Единицей электрического сопротивления в системе СИ является Ом (Ом).

Q3. Кто изобрел закон Ома?

Ответ. Георг Ом, полное имя Георг Симон Ом (род. 16 марта 1789 г., Эрланген, Бавария [Германия] — умер 6 июля 1854 г., Мюнхен), немецкий физик, открывший закон.