Про закон Ома в популярном изложении

Электрический ток и опасное напряжение невозможно услышать (за исключением гудящих высоковольтных линий и электроустановок). Токоведущие части, находящиеся под напряжением, ничем не отличаются по внешнему виду.

Невозможно узнать их и по запаху, и повышенной температурой в штатных режимах работы они не отличаются. Но включаем в безмолвную и тихую розетку пылесос, щелкаем выключателем – и энергия словно берется из ниоткуда, сама по себе, материализуясь в виде шума и компрессии внутри бытового прибора.

Опять же, если мы воткнем в разъемы розетки два гвоздя и возьмемся за них, то буквально всем своим телом ощутим реальность и объективность существования электрического тока. Делать это, конечно, настоятельно не рекомендуется.

Но примеры с пылесосом и гвоздями наглядно демонстрируют нам, что изучение и понимание основных законов электротехники способствует безопасности при обращении с бытовым электричеством, а также устранению суеверных предубеждений, связанных с электрическим током и напряжением.

Итак, рассмотрим один, самый ценный закон электротехники, который полезно знать. И попытаемся сделать это в как можно более популярной форме.

Содержание статьи

Открытие закона Ома

Дифференциальная форма записи закона Ома

Интегральная форма записи закона Ома для участка цепи

Закон Ома для переменного тока

Интегральная форма записи для полной цепи

Интегральная форма записи закона Ома для участка цепи, содержащего источник ЭДС

В каких случаях не выполняется закон Ома

Открытие закона Ома

В 1827 г. немецкий физик Георг Симон Ом сформулировал закон, связывающий величины электрического тока, электродвижущей силы батареи и сопротивления простой электрической цепи, составленной из батареи и соединяющих ее полюса последовательно включенных разнородных проводников. Кроме того, он обнаружил, что различные вещества оказывают электрическому току различное сопротивление.

Ом экспериментально установил, что в последовательной цепи, составленной из нескольких участков с проводниками разного сопротивления, ток во всех участках одинаков, различна только разность потенциалов на проводниках, которую Ом назвал «падением напряжения».

В нормальном, несверхпроводящем металлическом проводнике имеет место закон Ома. Для участка проводника, не содержащего источника электродвижущей силы (гальванического элемента, аккумулятора, генератора, термопары, источника фотоэдс и т. д.), закон Ома заключается в том, что сила тока пропорциональна разности потенциалов на концах участка. Коэффициент пропорциональности называют сопротивлением.

Первая запись о законе Ома в лабораторной книге Георга Симона Ома сегодня хранится в архивах Немецкого музея в Мюнхене:

Открытие закона Ома было очень важным этапом исследований электрических и магнитных явлений, имевших большое практическое значение. Закон Ома и открытые в дальнейшем законы  Кирхгофа впервые дали возможность производить расчеты электрических цепей и легли в основу зародившейся электротехники.

Виды законов Ома

1. Дифференциальная форма записи закона Ома

Самый главный закон электротехники – это, конечно, закон Ома. О его существовании знают даже люди, не имеющие отношения к электротехнике. Но между тем вопрос «А знаешь ли ты закон Ома?» в технических ВУЗах является ловушкой для зарвавшихся и самонадеянных школяров. Товарищ, разумеется, отвечает, что закон Ома знает отлично, и тогда к нему обращаются с просьбой привести этот закон в дифференциальной форме. Тут-то и выясняется, что школяру или первокурснику еще учиться и учиться.

Однако дифференциальная форма записи закона Ома на практике почти неприменима. Она отражает зависимость между плотностью тока и напряженностью поля:

j=G*E,

где G – это проводимость цепи; Е – напряженность электрического тока.

Все это – попытки выразить электрический ток, принимая во внимание только физические свойства материала проводника, без учета его геометрических параметров (длина, диаметр и тому подобное). Дифференциальная форма записи закона Ома – это чистая теория, знание ее в быту совершенно не требуется.

2. Интегральная форма записи закона Ома для участка цепи

Иное дело – интегральная форма записи. Она тоже имеет несколько разновидностей.

Самой популярной из них является закон Ома для участка цепи: I=U/R

Говоря по-другому, ток в участке цепи всегда тем выше, чем больше приложенное к этому участку напряжение и чем меньше сопротивление этого участка.

Вот этот «вид» закона Ома просто обязателен к запоминанию для всех, кому хоть иногда приходится иметь дело с электричеством. Благо, и зависимость-то совсем простая. Ведь напряжение в сети можно считать неизменным.

Для розетки оно равно 220 вольт. Поэтому получается, что ток в цепи зависит только от сопротивления цепи, подключаемой к розетке. Отсюда простая мораль: за этим сопротивлением надо следить.

Короткие замыкания, которые у всех на слуху, случаются именно по причине низкого сопротивления внешней цепи. Предположим, что из-за неправильного соединения проводов в ответвительной коробке фазный и нулевой провода оказались напрямую соединены между собой. Тогда сопротивление участка цепи резко снизится практически до нуля, а ток так же резко возрастет до очень большой величины.

Если электропроводка выполнена правильно, то сработает автоматический выключатель, а если его нет, или он неисправен или подобран неправильно, то провод не справится с возросшим током, нагреется, расплавится и, возможно, вызовет пожар.

Но бывает, что приборы, включенные в розетку и отработавшие уже далеко не один час, становятся причиной короткого замыкания. Типичный случай – вентилятор, обмотки двигателя которого подверглись перегреву из-за заклинивания лопастей.

Изоляция обмоток двигателя не рассчитана на серьезный нагрев, она быстро приходит в негодность. В результате появляются межвитковые короткие замыкания, которые снижают сопротивление и, в соответствии с законом Ома, также ведут к увеличению тока.

Повышенный ток, в свою очередь, приводит изоляцию обмоток в полную негодность, и наступает уже не межвитковое, а самое настоящее, полноценное короткое замыкание. Ток идет помимо обмоток, сразу из фазного в нулевой провод. Правда, все сказанное может случиться только с совсем простым и дешевым вентилятором, не оборудованным тепловой защитой.

Шпаргалка по закону Ома для участка цепи:

Закон Ома для переменного тока

Надо отметить, что приведенная запись закона Ома описывает участок цепи с постоянным напряжением. В сетях переменного напряжения существует дополнительное реактивное сопротивление, а полное сопротивление приобретает значение квадратного корня из суммы квадратов активного и реактивного сопротивления.

Закон Ома для участка цепи переменного тока принимает вид: I=U/Z,

где Z – полное сопротивление цепи.

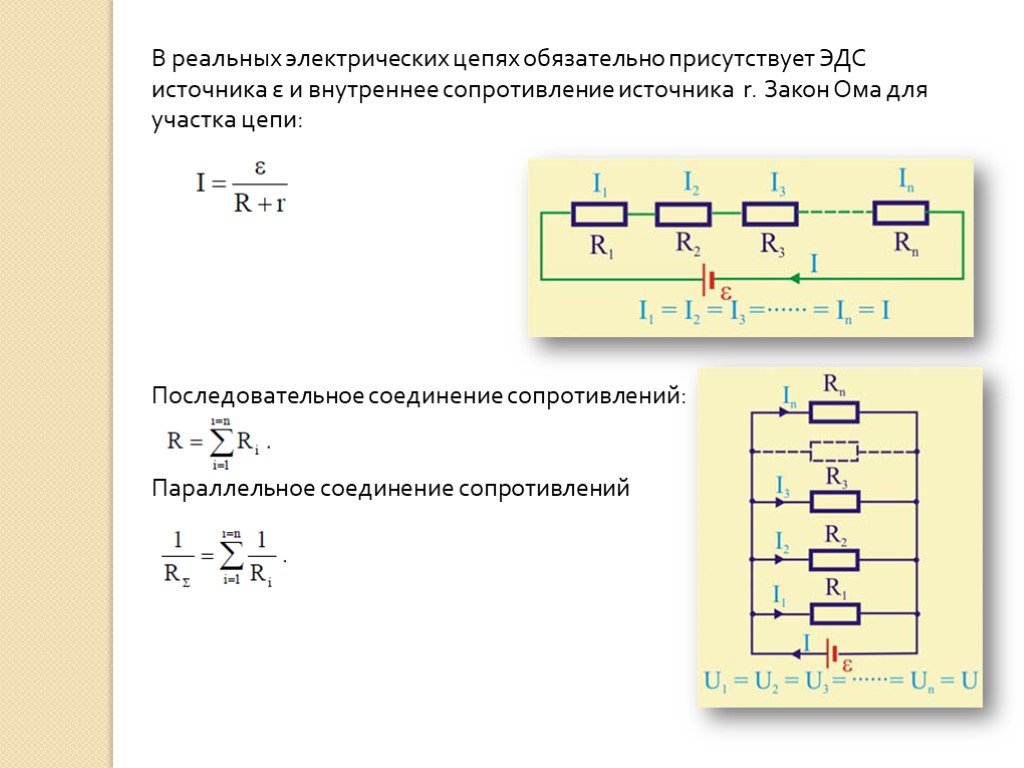
Но большое реактивное сопротивление свойственно, прежде всего, мощным электрическим машинам и силовой преобразовательной технике. Внутреннее электрическое сопротивление бытовых приборов и светильников практически полностью является активным. Поэтому в быту для расчетов можно пользоваться самой простой формой записи закона Ома: I=U/R.

3. Интегральная форма записи для полной цепи

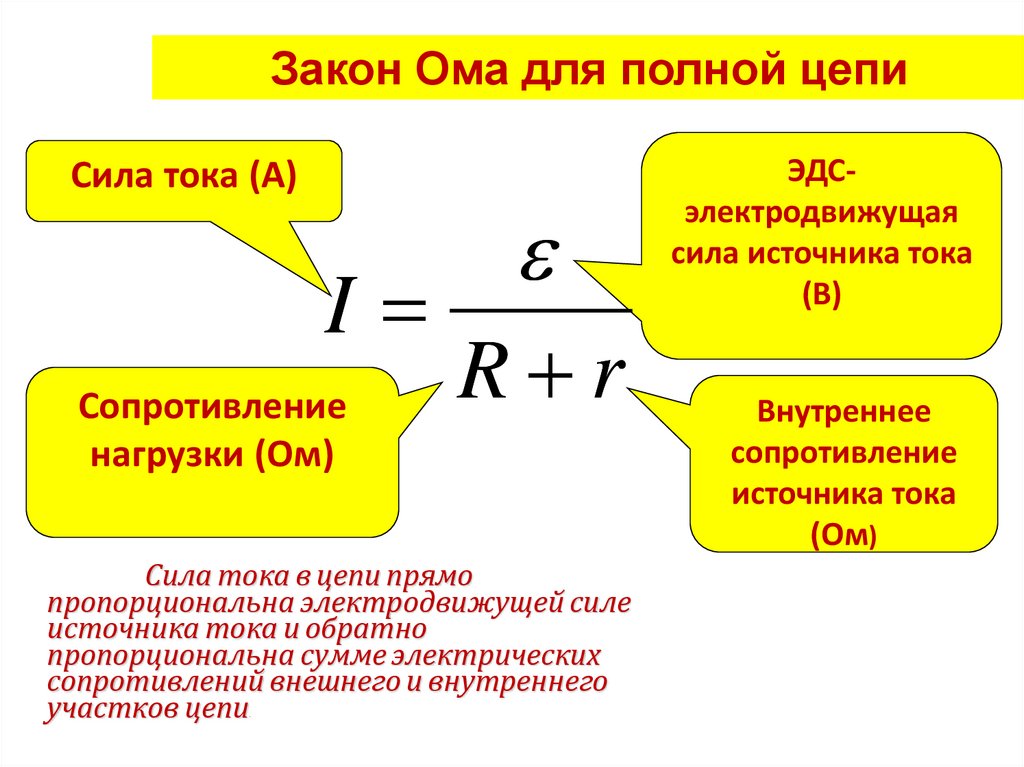
Раз есть форма записи закона для участка цепи, то существует и закон Ома для полной цепи: I=E/(r+R).

Здесь r – внутреннее сопротивление источника ЭДС сети, а R – полное сопротивление самой цепи.

За физической моделью для иллюстрации этого подвида закона Ома далеко ходить не надо – это бортовая электрическая сеть автомобиля, аккумулятор в которой является источником ЭДС.

Нельзя считать, что сопротивление аккумулятора равно абсолютному нулю, поэтому даже при прямом замыкании между его клеммами (отсутствии сопротивления R) ток вырастет не до бесконечности, а просто до высокого значения.

Однако этого высокого значения, конечно, хватит для того, чтобы вызвать расплавление проводов и возгорание обшивки авто. Поэтому электрические цепи автомобилей защищают от короткого замыкания при помощи предохранителей.

Такой защиты может оказаться недостаточно, если замыкание произойдет до блока предохранителей относительно аккумулятора, или если вовсе один из предохранителей заменен на кусок медной проволоки. Тогда спасение только в одном – необходимо как можно быстрее разорвать цепь полностью, откинув «массу», то есть минусовую клемму.

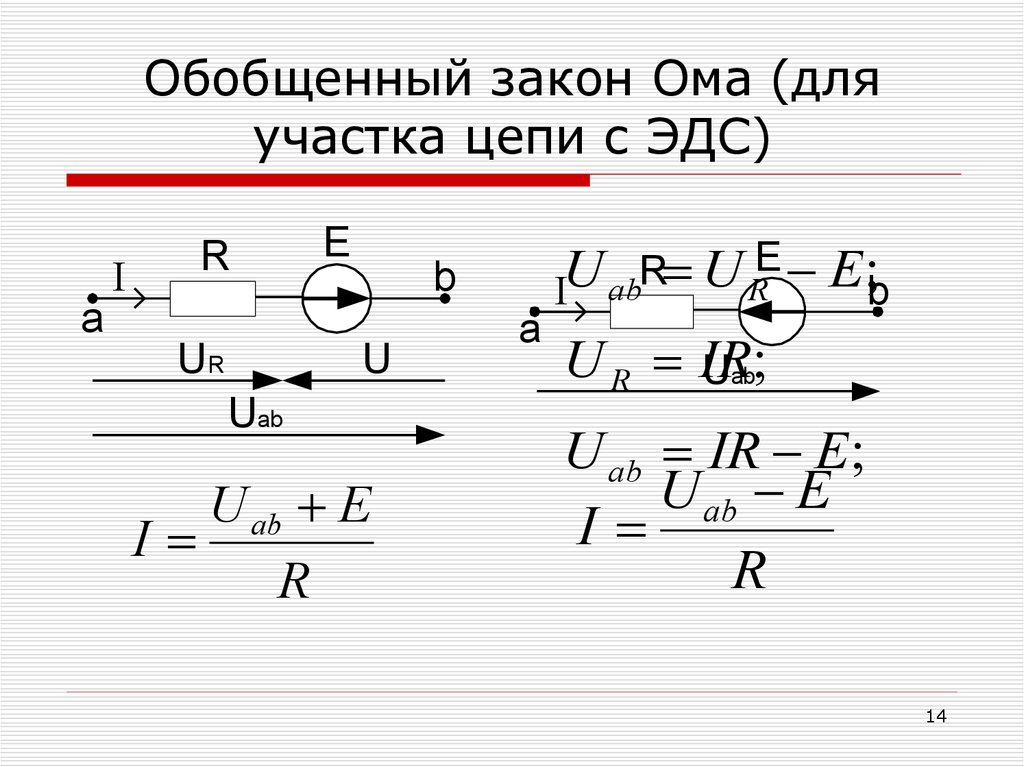
4. Интегральная форма записи закона Ома для участка цепи, содержащего источник ЭДС

Следует упомянуть и о том, что есть и еще одна разновидность закона Ома – для участка цепи, содержащего источник ЭДС:

I=(U+E)/(r+R)

или

I=(U-E)/(r+R)

Здесь U – это разность потенциалов в начале и в окончании рассматриваемого участка цепи. Знак перед величиной ЭДС зависит от направленности ее относительно напряжения.

Воспользоваться законом Ома для участка цепи нередко приходится при определении параметров цепи, когда часть схемы недоступна для детального изучения и не интересует нас.

Допустим, она скрыта неразъемными деталями корпуса. В оставшейся схеме имеется источник ЭДС и элементы с известным сопротивлением. Тогда, замерив напряжение на входе неизвестной части схемы, можно вычислить ток, а после этого – и сопротивление неизвестного элемента.

В каких случаях не выполняется закон Ома

Закон Ома не является универсальной связью между током и напряжением. Для металлов (в несверхпроводящем состоянии) закон Ома имеет место вплоть до весьма больших плотностей тока. Для полупроводников и газов пропорциональность между током и напряжением наблюдается лишь при малых напряжениях.

Термоэлектронный ток в вакууме не подчиняется закону Ома даже при малых напряжениях — в этом случае сила тока пропорциональна U3/2. В вольтовой дуге с увеличением тока напряжение падает (падающая вольтамперная характеристика), так что не может быть и речи о выполнении закона Ома.

Выражение I=U/R, однако, записывают даже в случае, когда закон Ома не выполняется. Тогда оно служит определением сопротивления R = U/I. Если сопротивление не зависит от величины тока, закон Ома имеет место. Если сопротивление само меняется с изменением тока (как, например, сопротивление газа при газовом разряде), то никакой пропорциональности между напряжением и током нет, а значит, нет и закона Ома.

Выводы

Таким образом, мы можем увидеть, что «простой» закон Ома далеко не так прост, как кому-то, возможно, казалось. Зная все формы интегральной записи законов Ома, можно понять и легко запомнить многие требования электробезопасности, а также приобрести уверенность в обращении с электричеством.

Андрей Повный

Источник: http://electrik.info

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3. 1 МКТ
  • 3.2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5. 2 Волновая оптика
  • 5.3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.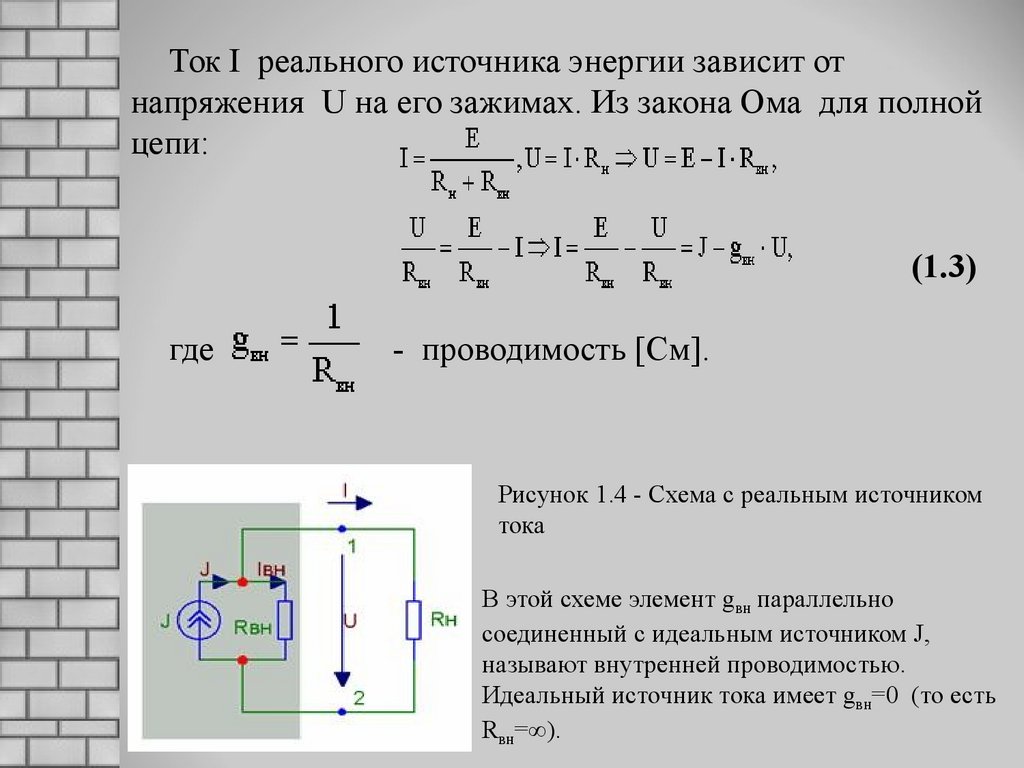

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

Сопротивление и простые схемы – Колледж физики

Глава 20 Электрический ток, сопротивление и закон Ома

Резюме

• Объясните происхождение закона Ома.
• Расчет напряжения, тока или сопротивления по закону Ома.
• Объясните, что такое омический материал.
• Опишите простую схему.

Что управляет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, настенные розетки и т. д., которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и в широком смысле называются источниками напряжения. Когда источник напряжения подключен к проводнику, он применяет разность потенциалов [латекс]{В}[/латекс], которая создает электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.

Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению [латекс]{В}[/латекс]. Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что сила тока в металлической проволоке прямо пропорциональна приложенному напряжению :

.

[латекс] {I \propto V}. [/латекс]

Это важное соотношение известно как закон Ома. Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием. Это эмпирический закон, аналогичный закону трения — экспериментально наблюдаемому явлению. Такая линейная зависимость не всегда имеет место.

Если напряжение управляет током, что этому препятствует? Электрическое свойство, препятствующее току (грубо похожее на трение и сопротивление воздуха), называется сопротивлением RR размером 12{R} {}. Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление определяется как обратно пропорциональное току, или

[латекс] {I \ propto} [/латекс] [латекс] {\ гидроразрыва {1} {R}}. [/латекс]

Так, например, ток уменьшается вдвое, если сопротивление удваивается. Сочетание отношений тока к напряжению и тока к сопротивлению дает

[латекс] {I =} [/латекс] [латекс] {\ гидроразрыва {V} {R}}. [/латекс]

Это соотношение также называют законом Ома. Закон Ома в этой форме действительно определяет сопротивление для определенных материалов. Закон Ома (как и закон Гука) не является универсальным. Многие вещества, для которых выполняется закон Ома, называются омическими. К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы обладают сопротивлением [латекс]{R}[/латекс], которое не зависит от напряжения [латекс]{В}[/латекс] и тока [латекс]{I}[/латекс]. Объект, который имеет простое сопротивление, называется резистор , даже если его сопротивление мало. Единицей сопротивления является ом, который обозначается символом [латекс]\Омега[/латекс] (греческая омега в верхнем регистре). Перестановка [латекс]{I = V/R}[/латекс] дает [латекс]{R = V/I}[/латекс], поэтому единицами сопротивления являются 1 Ом = 1 вольт на ампер:

[латекс] {1 \; \ Omega = 1} [/ латекс] [латекс] {\ гидроразрыва {V} {A}} [/ латекс]

На рис. 1 показана схема простой цепи. Простая схема имеет один источник напряжения и один резистор. Можно предположить, что провода, соединяющие источник напряжения с резистором, имеют незначительное сопротивление, или их сопротивление может быть включено в [латекс]{R}[/латекс].

Рисунок 1. Простая электрическая цепь, в которой замкнутый путь для протекания тока обеспечивается проводниками (обычно металлическими проводами), соединяющими нагрузку с клеммами батареи, представленными красными параллельными линиями. Зигзагообразный символ представляет одиночный резистор и включает любое сопротивление в соединениях с источником напряжения.

Пример 1: расчет сопротивления: автомобильная фара

Чему равно сопротивление автомобильной фары, через которую протекает ток 2,50 А при подаче на нее напряжения 12,0 В?

Стратегия

Мы можем изменить закон Ома, как указано в [latex]{I=V/R}[/latex], и использовать его для нахождения сопротивления.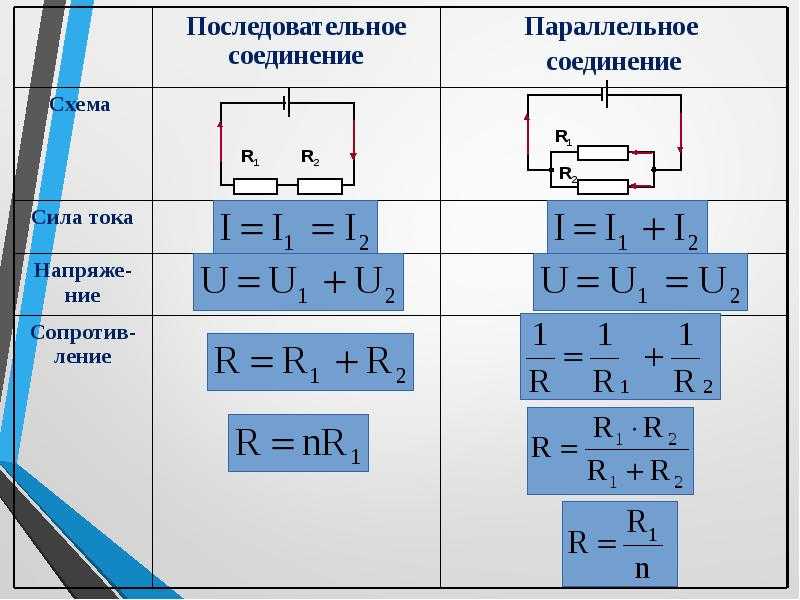

Решение

Перестановка [латекс]{I = V/R}[/латекс] и подстановка известных значений дает

[латекс]{R =}[/латекс] [латекс]{\ гидроразрыва {V}{ I}}[/латекс] [латекс]{=}[/латекс] [латекс]{\ гидроразрыва {12,0 \;\текст{V}}{2,50 \;\textbf{A}}}[/латекс] [латекс ]{= 4.80 \;\Omega }[/latex]

Обсуждение

Это относительно небольшое сопротивление, но оно больше морозостойкости фары. Как мы увидим в главе 20.3. Сопротивление и удельное сопротивление, сопротивление обычно увеличивается с температурой, поэтому лампочка имеет более низкое сопротивление при первом включении и будет потреблять значительно больший ток в течение короткого периода прогрева. 9{-5} \;\Omega}[/latex], а сверхпроводники вообще не имеют сопротивления (они неомические). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в главе 20.3 Сопротивление и удельное сопротивление.

Дополнительные сведения можно получить, решив [латекс]{I = V/R}[/латекс], что даст

[латекс]{V = ИК}. [/латекс]

Это выражение для [латекс]{V}[/латекс] можно интерпретировать как падение напряжения на резисторе, вызванное протеканием тока [латекс]{I}[/латекс]. Для обозначения этого напряжения часто используется фраза [латекс]{IR}[/латекс]  drop . Например, фара в примере 1 имеет падение [латекс]{ИК}[/латекс] 12,0 В. Если измерить напряжение в различных точках цепи, будет видно, что оно увеличивается в источнике напряжения и уменьшается в конце. резистор. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор подобен трубе, которая снижает давление и ограничивает поток из-за своего сопротивления. Сохранение энергии имеет здесь важные последствия. Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой схеме (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку [латекс]{PE = q \Delta V}[/латекс] и тот же [латекс] Через каждый проходит {q}[/latex].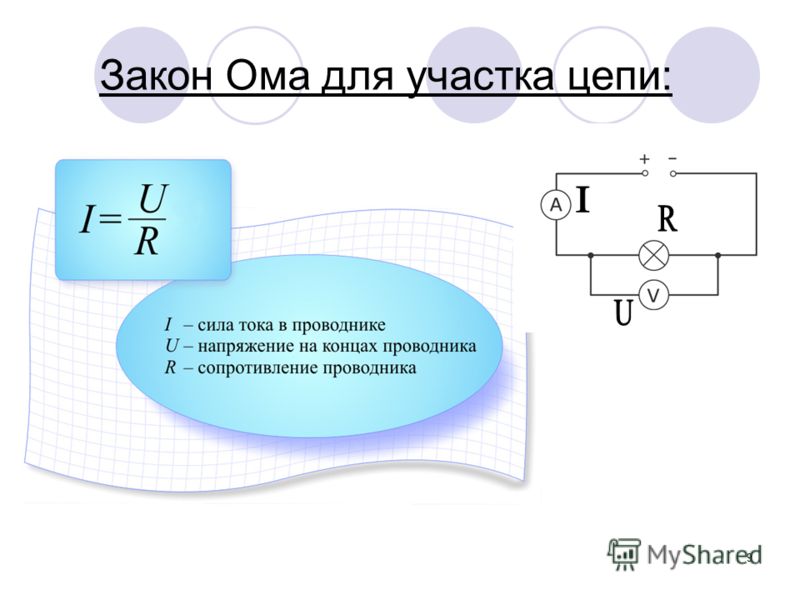 Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. (См. рис. 2.)

Рисунок 2. Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.

Соединения: сохранение энергии

В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. О сохранении энергии здесь свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним только резистором. Мы обнаружим, что закон сохранения энергии имеет и другие важные применения в цепях и является мощным инструментом анализа цепей.

PhET Исследования: Закон Ома

Посмотрите, как формула закона Ома соотносится с простой цепью. Отрегулируйте напряжение и сопротивление и посмотрите, как изменится ток в соответствии с законом Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.

Рис. 3. Закон Ома

• Простая цепь — это цепь, в которой есть один источник напряжения и одно сопротивление.
• Одна формулировка закона Ома дает взаимосвязь между током [латекс]{I}[/латекс], напряжением [латекс]{В}[/латекс] и сопротивлением [латекс]{R}[/латекс] в простой цепи быть [латекс]{I = \frac{V}{R}}[/латекс].
• Сопротивление выражается в омах ([латекс]{\Омега}[/латекс]), связанных с вольтами и амперами по формуле [латекс]{1 \;\Омега = 1 \;\текст{V} / \textbf{A} }[/латекс].
• Падение напряжения или [латекс]{IR}[/латекс] на резисторе, вызванное протеканием через него тока, определяемое как [латекс]{V = IR}[/латекс].

Закон Ома

эмпирическое соотношение, утверждающее, что ток I пропорционален разности потенциалов В , ∝ В ; его часто записывают как I = V/R , где R — сопротивление

.

сопротивление

электрическое свойство, препятствующее току; для омических материалов это отношение напряжения к току, R = V/I

Ом

единица сопротивления, определяемая как 1 Ом = 1 В/А

омический

тип материала, для которого действует закон Ома

простая схема

схема с одним источником напряжения и одним резистором

 

Сопротивление и закон Ома – Физические науки

Закон Ома

Закон Ома гласит, что ток пропорционален напряжению; цепи являются омическими, если они подчиняются соотношению V=IR.

Цели обучения

Контрастная форма графиков ток-напряжение для омических и неомических цепей

Основные выводы

Ключевые моменты

• Напряжение управляет током, а сопротивление препятствует ему.
• Закон Ома относится к пропорциональному отношению между напряжением и током. Это также относится к конкретному уравнению V = IR, которое справедливо при рассмотрении цепей, содержащих простые резисторы (сопротивление которых не зависит от напряжения и тока).
• Цепи или компоненты, которые подчиняются соотношению V=IR, известны как омические и имеют графики зависимости тока от напряжения, которые являются линейными и проходят через начало координат.
• Имеются неомические компоненты и цепи; их графики ВАХ нелинейны и/или не проходят через начало координат.

Ключевые термины

• простая схема : Цепь с одним источником напряжения и одним резистором.
• омический : То, что подчиняется закону Ома.

Закон Ома

Что вызывает ток? Мы можем думать о различных устройствах, таких как батареи, генераторы, настенные розетки и т. д., которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и в широком смысле называются источниками напряжения. Когда источник напряжения подключен к проводнику, он применяет разность потенциалов V, которая создает электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток. Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению V. Немецкий физик Георг Симон Ом (1787-1854) первым экспериментально продемонстрировал, что сила тока в металлической проволоке прямо пропорциональна приложенному напряжению: [latex]\text{I} \propto \text{V}[/latex ].

Это важное соотношение известно как закон Ома. Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием. Это эмпирический закон, аналогичный закону трения — экспериментально наблюдаемому явлению.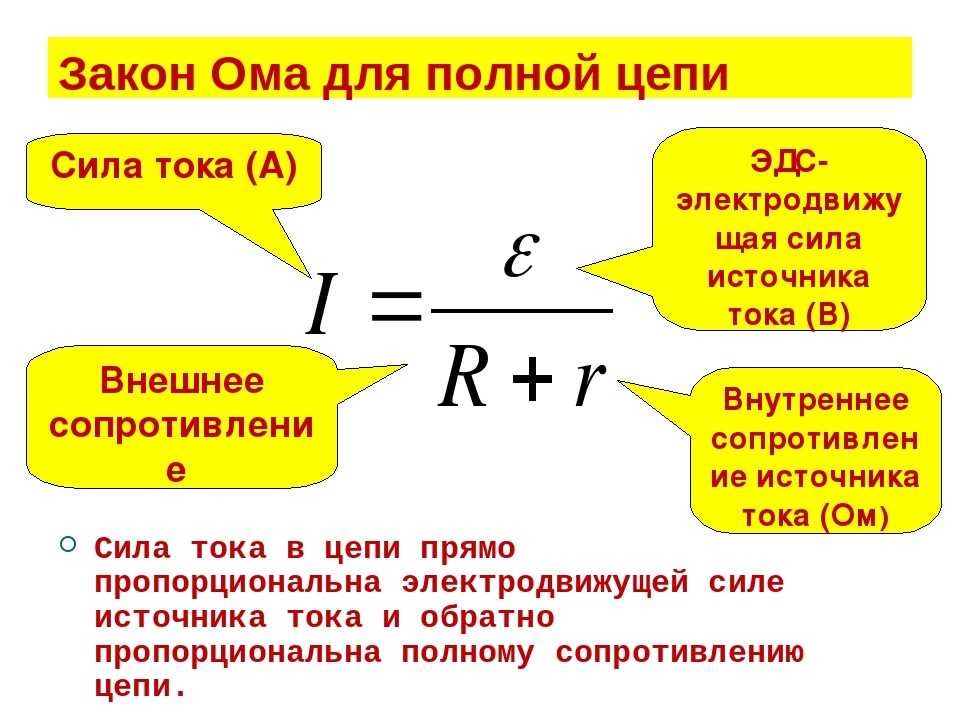 Такая линейная зависимость не всегда имеет место. Напомним, что в то время как напряжение управляет током, сопротивление препятствует ему. Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Таким образом, ток обратно пропорционален сопротивлению: [latex]\text{I} \propto \frac{1}{\text{R}}[/latex].

Простая цепь : Простая электрическая цепь, в которой замкнутый путь для протекания тока обеспечивается проводниками (обычно металлическими проводами), соединяющими нагрузку с клеммами батареи, представленными красными параллельными линиями. Зигзагообразный символ представляет одиночный резистор и включает любое сопротивление в соединениях с источником напряжения.

Единицей измерения сопротивления является ом, где 1 Ом = 1 В/А. Мы можем объединить два приведенных выше соотношения, чтобы получить I = V/R. Эту зависимость также называют законом Ома. В этой форме закон Ома действительно определяет сопротивление для определенных материалов. Закон Ома (как и закон Гука) не является универсальным. Многие вещества, для которых выполняется закон Ома, называются омическими. К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление R, не зависящее от напряжения V и тока I. Предмет, имеющий простое сопротивление, называется резистором, даже если его сопротивление мало.

Падение напряжения : Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.

Дополнительную информацию можно получить, решив I=V/R относительно V, что даст V=IR. Это выражение для V можно интерпретировать как падение напряжения на резисторе, вызванное протеканием тока I. Для этого напряжения часто используется фраза IR drop. Если измерять напряжение в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости.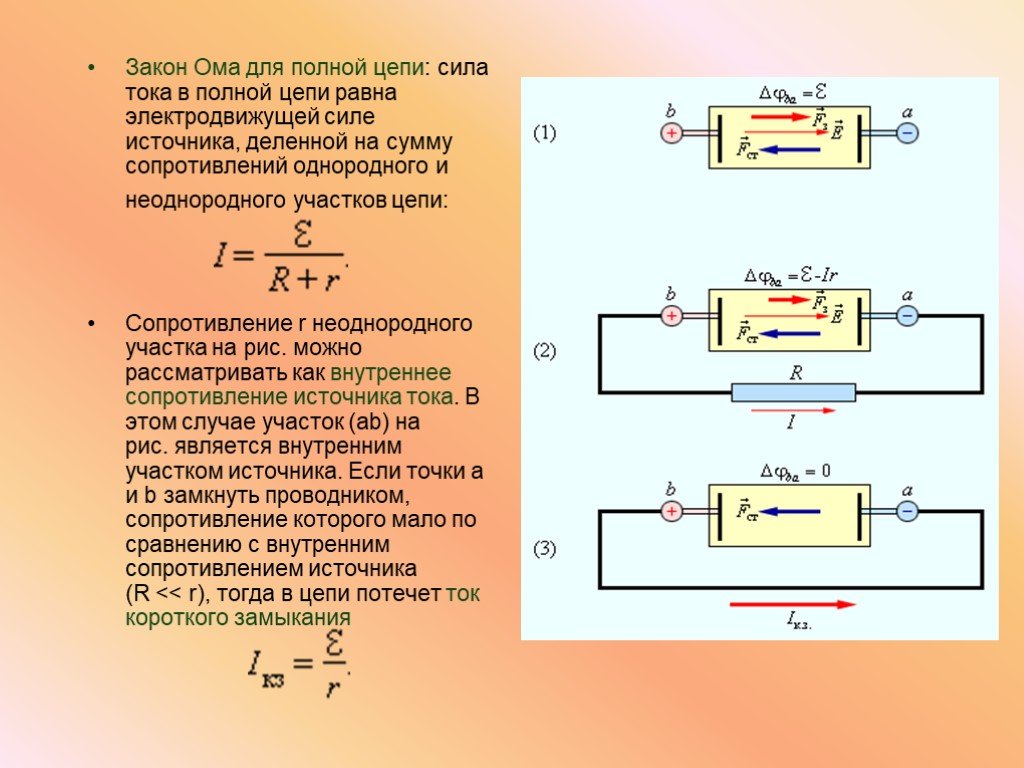 Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор подобен трубе, которая снижает давление и ограничивает поток из-за своего сопротивления. Сохранение энергии имеет здесь важные последствия. Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой схеме (одна с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку E = qΔV, и через каждый протекает одно и то же q. Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны.

В истинно омическом устройстве одно и то же значение сопротивления будет рассчитываться из R = V/I независимо от значения приложенного напряжения V. То есть отношение V/I является постоянным, и когда ток изображается как функция напряжения кривая линейна (прямая линия). Если напряжение форсируется до некоторого значения V, то это напряжение V, деленное на измеренный ток I, будет равно R. Или, если ток форсируется до некоторого значения I, то измеренное напряжение V, деленное на этот ток I, также равно R. Мы визуализируем график зависимости I от V в виде прямой линии. Однако есть компоненты электрических цепей, которые не подчиняются закону Ома; то есть их связь между током и напряжением (их ВАХ) является нелинейной (или неомической). Примером может служить диод с p-n переходом.

Кривые вольтамперной характеристики : Кривые ВАХ четырех устройств: двух резисторов, диода и батареи. Два резистора подчиняются закону Ома: график представляет собой прямую линию, проходящую через начало координат. Два других устройства не подчиняются закону Ома.

Закон Ома : Краткий обзор закона Ома.

Температура и сверхпроводимость

Сверхпроводимость — это явление нулевого электрического сопротивления и выброса магнитных полей в некоторых материалах ниже критической температуры.

Цели обучения

Описать поведение сверхпроводника при температуре ниже критической и в слабом внешнем магнитном поле

Основные выводы

Ключевые моменты

• Сверхпроводимость является термодинамической фазой и обладает определенными отличительными свойствами, которые в значительной степени независимы микроскопических деталей.
• В сверхпроводящих материалах характеристики сверхпроводимости проявляются при понижении температуры ниже критической. Возникновение сверхпроводимости сопровождается резкими изменениями различных физических свойств.
• Когда сверхпроводник помещается в слабое внешнее магнитное поле H и охлаждается ниже его температуры перехода, магнитное поле выбрасывается.
• Сверхпроводники способны поддерживать ток без приложенного напряжения.

Ключевые термины

• высокотемпературные сверхпроводники : Материалы, которые ведут себя как сверхпроводники при необычно высоких температурах (выше примерно 30 К).
• критическая температура : В сверхпроводящих материалах характеристики сверхпроводимости проявляются при этой температуре (и продолжаются ниже).
• сверхпроводимость : Свойство материала, при котором он не оказывает сопротивления потоку электрического тока.

Сверхпроводимость — это явление абсолютно нулевого электрического сопротивления и выброса магнитных полей, происходящее в некоторых материалах при охлаждении ниже характерной критической температуры. Он был обнаружен Хайке Камерлинг-Оннесом (показан на фото) 8 апреля 1911 года в Лейдене.

Хайке Камерлинг-Оннес : Хайке Камерлинг-Оннес (1853-1919)26).

Большинство физических свойств сверхпроводников различаются от материала к материалу, например, теплоемкость и критическая температура, критическое поле и критическая плотность тока, при которых сверхпроводимость разрушается. С другой стороны, существует класс свойств, не зависящих от основного материала.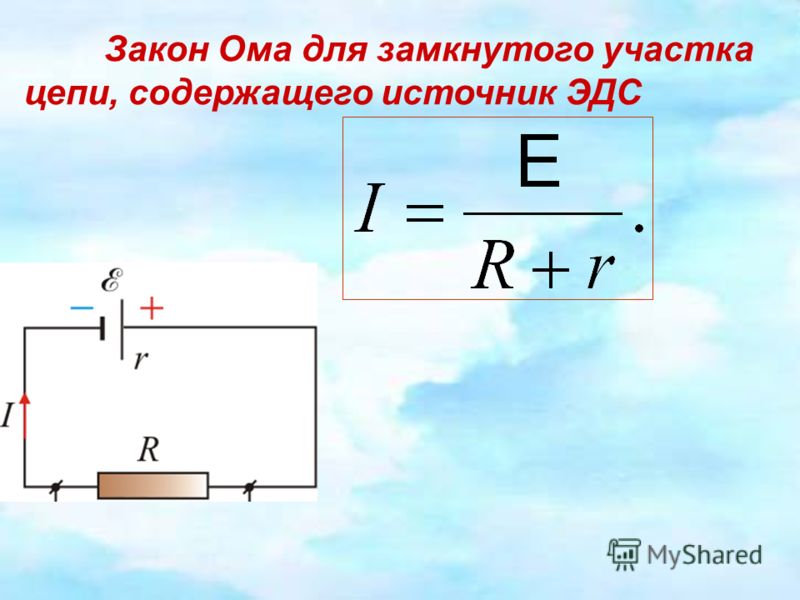 Например, все сверхпроводники имеют точно нулевое удельное сопротивление для низких приложенных токов, когда нет магнитного поля или если приложенное поле не превышает критического значения. Существование этих «универсальных» свойств подразумевает, что сверхпроводимость является термодинамической фазой и, таким образом, обладает определенными отличительными свойствами, которые в значительной степени не зависят от микроскопических деталей.

В сверхпроводящих материалах характеристики сверхпроводимости проявляются, когда температура T опускается ниже критической температуры T _c . Возникновение сверхпроводимости сопровождается резкими изменениями различных физических свойств — отличительной чертой фазового перехода. Например, электронная теплоемкость пропорциональна температуре в обычном (несверхпроводящем) режиме. При сверхпроводящем переходе она претерпевает прерывистый скачок и после этого перестает быть линейной, как показано на рис. 9.0005

Когда сверхпроводник помещается в слабое внешнее магнитное поле H и охлаждается ниже его температуры перехода, магнитное поле выбрасывается. Эффект Мейснера не приводит к полному выбросу поля. Скорее поле проникает в сверхпроводник на очень небольшое расстояние (характеризуемое параметром λ), называемое лондоновской глубиной проникновения. Он экспоненциально затухает до нуля внутри объема материала. Эффект Мейснера является определяющей характеристикой сверхпроводимости. Для большинства сверхпроводников лондоновская глубина проникновения составляет порядка 100 нм.

Сверхпроводящий фазовый переход : Поведение теплоемкости (cv, синий) и удельного сопротивления (ρ, зеленый) при сверхпроводящем фазовом переходе.

Сверхпроводники также способны поддерживать ток без какого-либо приложенного напряжения — свойство, используемое в сверхпроводящих электромагнитах, например, в аппаратах МРТ. Эксперименты показали, что токи в сверхпроводящих катушках могут сохраняться годами без какого-либо заметного ухудшения. Экспериментальные данные указывают на текущую продолжительность жизни не менее 100 000 лет. Теоретические оценки времени жизни постоянного тока могут превышать расчетное время жизни Вселенной, в зависимости от геометрии проволоки и температуры.

Значение этой критической температуры зависит от материала. Обычно обычные сверхпроводники имеют критические температуры в диапазоне от примерно 20 К до менее 1 К. Например, твердая ртуть имеет критическую температуру 4,2 К. По состоянию на 2009 г. самая высокая критическая температура, обнаруженная для обычного сверхпроводника, составляет 39 К для магния. диборид (MgB ₂ ), хотя экзотические свойства этого материала вызывают некоторые сомнения в правильности отнесения его к «обычным» сверхпроводникам. Высокотемпературные сверхпроводники могут иметь гораздо более высокие критические температуры. Например, YBa ₂ Cu ₃ O ₇ , один из первых открытых купратных сверхпроводников, имеет критическую температуру 92 К; были обнаружены купраты на основе ртути с критическими температурами выше 130 К. Следует отметить, что химический состав и кристаллическая структура сверхпроводящих материалов могут быть довольно сложными, как показано на рис. Ячейка сверхпроводника YBaCuO. Атомы обозначены разными цветами.

Сопротивление и удельное сопротивление

Сопротивление и удельное сопротивление описывают степень, в которой объект или материал препятствует прохождению электрического тока.

Цели обучения

Определить свойства материала, описываемые сопротивлением и удельным сопротивлением

Ключевые выводы

Ключевые моменты

• Сопротивление объекта (например, резистора) зависит от его формы и материала, из которого он изготовлен. он составлен.
• Удельное сопротивление ρ является внутренним свойством материала и прямо пропорционально общему сопротивлению R, внешней величине, которая зависит от длины и площади поперечного сечения резистора.
• Удельное сопротивление различных материалов сильно различается. Точно так же резисторы варьируются на много порядков.
• Резисторы расположены последовательно или параллельно. Эквивалентное сопротивление сети резисторов, соединенных последовательно, равно сумме всех сопротивлений. Инверсия эквивалентного сопротивления сети резисторов, соединенных параллельно, представляет собой сумму инверсий сопротивления каждого резистора.

Ключевые термины

• Эквивалентное сопротивление серии : Сопротивление сети резисторов, расположенных таким образом, что напряжение в сети является суммой напряжений на каждом резисторе. В этом случае эквивалентное сопротивление представляет собой сумму сопротивлений всех резисторов в сети.
• параллельное эквивалентное сопротивление : сопротивление сети, при которой на каждый резистор действует одна и та же разность потенциалов (напряжение), так что токи через них складываются. В этом случае обратное эквивалентное сопротивление равно сумме обратного сопротивления всех резисторов в сети.
• удельное сопротивление : Обычно сопротивление материала электрическому току; в частности, степень сопротивления материала потоку электричества.

Сопротивление и удельное сопротивление

Сопротивление — это электрическое свойство, препятствующее прохождению тока. Ток, протекающий по проводу (или резистору), подобен воде, протекающей по трубе, а падение напряжения на проводе подобно падению давления, проталкивающему воду по трубе. Сопротивление пропорционально тому, какое давление требуется для достижения данного потока, а проводимость пропорциональна тому, какой поток возникает при данном давлении. Проводимость и сопротивление обратны. Сопротивление объекта зависит от его формы и материала, из которого он состоит. Цилиндрический резистор легко анализировать, и таким образом мы можем получить представление о сопротивлении более сложных форм. Как и следовало ожидать, электрическое сопротивление цилиндра R прямо пропорционально его длине L, аналогично сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше столкновений зарядов с его атомами произойдет. Чем больше диаметр цилиндра, тем больший ток он может пропускать (опять же, аналогично потоку жидкости по трубе). На самом деле, R обратно пропорционально площади поперечного сечения цилиндра A.

Цилиндрический резистор : однородный цилиндр длиной L и площадью поперечного сечения A. Его сопротивление потоку тока аналогично сопротивлению, оказываемому трубой потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление. Чем больше его площадь поперечного сечения А, тем меньше его сопротивление.

Как уже упоминалось, для данной формы сопротивление зависит от материала, из которого состоит объект. Различные материалы оказывают различное сопротивление потоку заряда. Определим удельное сопротивление ρ вещества так, чтобы сопротивление R объекта было прямо пропорционально ρ. Удельное сопротивление ρ составляет внутреннее свойство материала, не зависящее от его формы или размера. Напротив, сопротивление R является внешним свойством, которое зависит от размера и формы резистора. (Аналогичная внутренняя/внешняя связь существует между теплоемкостью C и удельной теплоемкостью c). Напомним, что объект, сопротивление которого пропорционально напряжению и току, называется резистором.

Типовой резистор : Типовой резистор с осевым выводом.

Что определяет удельное сопротивление? Удельное сопротивление различных материалов сильно различается. Например, проводимость тефлона примерно в 1030 раз ниже проводимости меди. Почему такая разница? Грубо говоря, металл имеет большое количество «делокализованных» электронов, которые не застревают в одном месте, а свободно перемещаются на большие расстояния, тогда как в изоляторе (например, в тефлоне) каждый электрон прочно связан с одним атомом, и требуется большая сила, чтобы вытащить его. Точно так же резисторы варьируются на много порядков. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 10 ¹² Ом или больше. Сопротивление рук и ног сухого человека может составлять 10 ⁵ Ом, тогда как сопротивление человеческого сердца составляет около 10 ³ Ом. Метровый отрезок медной проволоки большого диаметра может иметь сопротивление 10 ⁻⁵ Ом, а сверхпроводники вообще не имеют сопротивления (они неомические). Разность потенциалов (напряжение) в сети представляет собой сумму этих напряжений, поэтому общее сопротивление (эквивалентное последовательное сопротивление) можно найти как сумму этих сопротивлений:

[латекс] \ text {R} _ {\ text {eq}} = \ text {R} _ {1} + \ text {R} _ {2} + \ cdots + \ text {R} _ {\ текст{N}}[/латекс].

Как частный случай, сопротивление N резисторов, соединенных последовательно, каждый из которых имеет одинаковое сопротивление R, определяется как NR. Каждый резистор в параллельной конфигурации подвержен одинаковой разности потенциалов (напряжению), однако токи через них добавлять. Таким образом, можно рассчитать эквивалентное сопротивление (Req) сети:

[латекс]\frac{1}{\text{R}_{\text{eq}}}=\frac{1}{\text{R }_{1}}+\frac{1}{\text{R}_{2}}+\cdots +\frac{1}{\text{R}_{\text{N}}}[/latex ].

Параллельное эквивалентное сопротивление может быть представлено в уравнениях двумя вертикальными линиями «||» (как в геометрии) в упрощенном виде. Иногда вместо «||» используются две косые черты «//», если в клавиатуре или шрифте отсутствует символ вертикальной линии. Для случая двух параллельных резисторов это можно рассчитать, используя:

[латекс]\text{R}_{\text{eq}}=\text{R}_{1}\parallel\text{R} _{2}=\frac{\text{R}_{1}\text{R}_{2}}{\text{R}_{1}+\text{R}_{2}}[/ латекс].

Как частный случай, сопротивление N резисторов, соединенных параллельно, каждый из которых имеет одинаковое сопротивление R, выражается как R/N. Сеть резисторов, представляющая собой комбинацию параллельных и последовательных соединений, может быть разбита на более мелкие части, которые являются либо одним, либо другим, как показано на рис. 9.0005

Сеть резисторов : В этой комбинированной схеме цепь может быть разбита на последовательный и параллельный компоненты.

Однако некоторые сложные цепи резисторов не могут быть разрешены таким образом. Они требуют более сложного анализа схемы. Одним из практических применений этих взаимосвязей является то, что нестандартное значение сопротивления обычно может быть синтезировано путем последовательного или параллельного соединения ряда стандартных значений. Это также можно использовать для получения сопротивления с более высокой номинальной мощностью, чем у отдельных используемых резисторов. В частном случае N одинаковых резисторов, соединенных последовательно или параллельно, номинальная мощность отдельных резисторов умножается на N.

Сопротивление, резисторы и удельное сопротивление : Краткий обзор сопротивления, резисторов и удельного сопротивления.

Зависимость сопротивления от температуры

Удельное сопротивление и сопротивление зависят от температуры с линейной зависимостью при малых изменениях температуры и нелинейной при больших.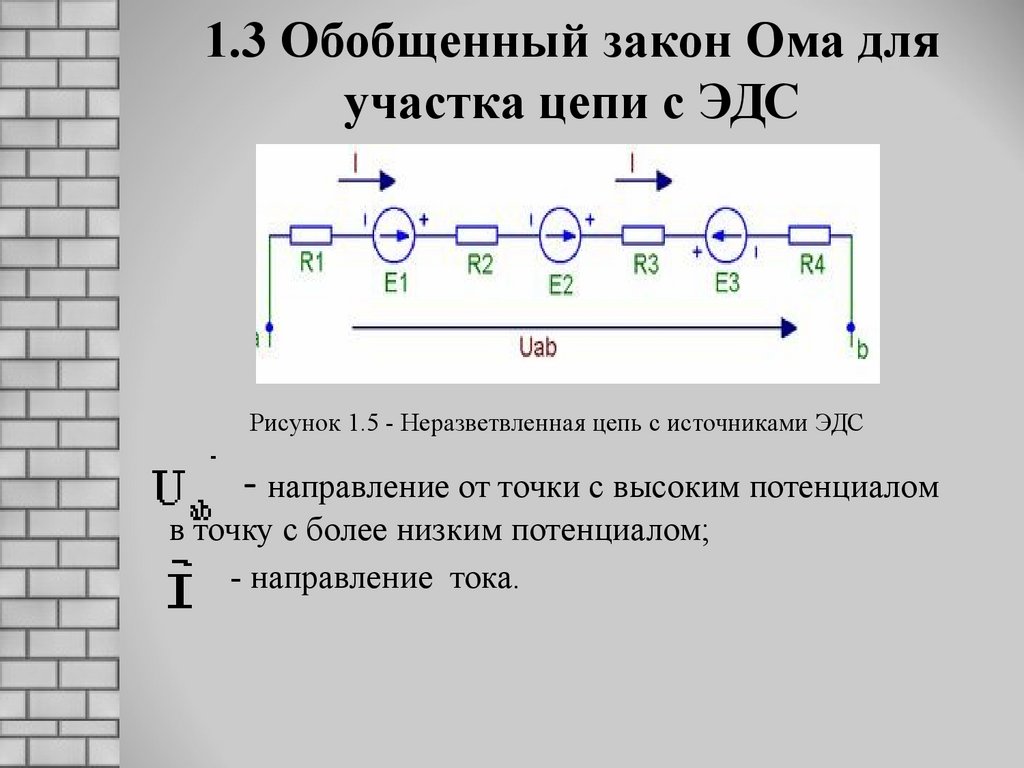

Цели обучения

Сравнение температурной зависимости удельного сопротивления и сопротивления при больших и малых изменениях температуры

Основные выводы

Ключевые моменты

• При изменении температуры на 100ºC или менее удельное сопротивление (ρ) зависит от изменения температуры ΔT следующим образом: [латекс]\text{p} = \text{p}_{0}(1 + \alpha \ Delta \text{T})[/latex] где ρ ₀ — исходное удельное сопротивление, а α — температурный коэффициент удельного сопротивления.
• При больших изменениях температуры наблюдается нелинейное изменение удельного сопротивления в зависимости от температуры.
• Сопротивление объекта демонстрирует такую ​​же температурную зависимость, как и удельное сопротивление, поскольку сопротивление прямо пропорционально удельному сопротивлению.

Ключевые термины

• удельное сопротивление : Обычно сопротивление материала электрическому току; в частности, степень сопротивления материала потоку электричества.
• температурный коэффициент удельного сопротивления : Эмпирическая величина, обозначаемая α, которая описывает изменение сопротивления или удельного сопротивления материала в зависимости от температуры.
• полупроводник : Вещество с электрическими свойствами, промежуточными между хорошим проводником и хорошим изолятором.

Удельное сопротивление всех материалов зависит от температуры. Некоторые материалы могут стать сверхпроводниками (нулевое удельное сопротивление) при очень низких температурах (см. ). И наоборот, удельное сопротивление проводников увеличивается с повышением температуры. Поскольку атомы вибрируют быстрее и преодолевают большие расстояния при более высоких температурах, электроны, движущиеся через металл, например, создают больше столкновений, что фактически увеличивает удельное сопротивление. При относительно небольших изменениях температуры (около 100ºC или менее) удельное сопротивление ρ зависит от изменения температуры ΔT, как это выражается в следующем уравнении:

Сопротивление образца ртути : Сопротивление образца ртути равно нулю при очень низких температурах — это сверхпроводник примерно до 4,2 К. Выше этой критической температуры его сопротивление делает резкий скачок, а затем увеличивается почти до линейно с температурой.

[латекс]\текст{р} = \текст{р}_{0}(1 + \альфа \Дельта \текст{Т})[/латекс]

, где ρ ₀ — исходное удельное сопротивление и α – температурный коэффициент удельного сопротивления. Для больших изменений температуры α может варьироваться, или может потребоваться нелинейное уравнение для нахождения ρ. По этой причине обычно указывается суффикс для температуры, при которой измерялось вещество (например, α ₁₅ ), и соотношение сохраняется только в диапазоне температур, близких к контрольному. Обратите внимание, что α положителен для металлов, что означает, что их удельное сопротивление увеличивается с температурой. Температурный коэффициент обычно составляет от +3×10 ^-3 К ^-1 до +6×10 ^-3 К ^-1 для металлов с температурой, близкой к комнатной. Некоторые сплавы были разработаны специально, чтобы иметь небольшую температурную зависимость. Манганин (состоящий из меди, марганца и никеля), например, имеет α, близкую к нулю, поэтому его удельное сопротивление мало зависит от температуры. Это полезно, например, для создания эталона сопротивления, не зависящего от температуры.

Обратите внимание, что для полупроводников α отрицательно, а это означает, что их удельное сопротивление уменьшается с повышением температуры. Они становятся лучшими проводниками при более высокой температуре, потому что повышенное тепловое возбуждение увеличивает количество свободных зарядов, доступных для переноса тока. Это свойство уменьшения ρ с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках.

Сопротивление объекта также зависит от температуры, так как R ₀ прямо пропорционально ρ. Для цилиндра мы знаем, что R=ρL/A, поэтому, если L и A не сильно изменяются с температурой, R будет иметь ту же температурную зависимость, что и ρ. (Исследование коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, и поэтому влияние температуры на L и A примерно на два порядка меньше, чем на ρ.