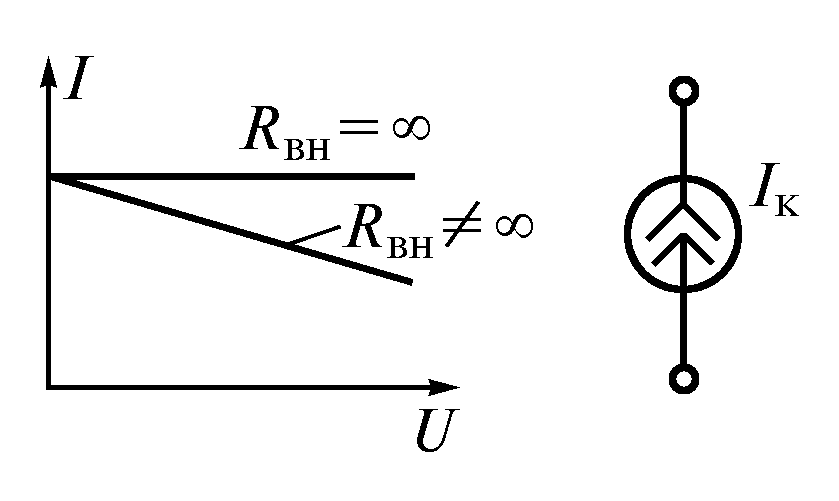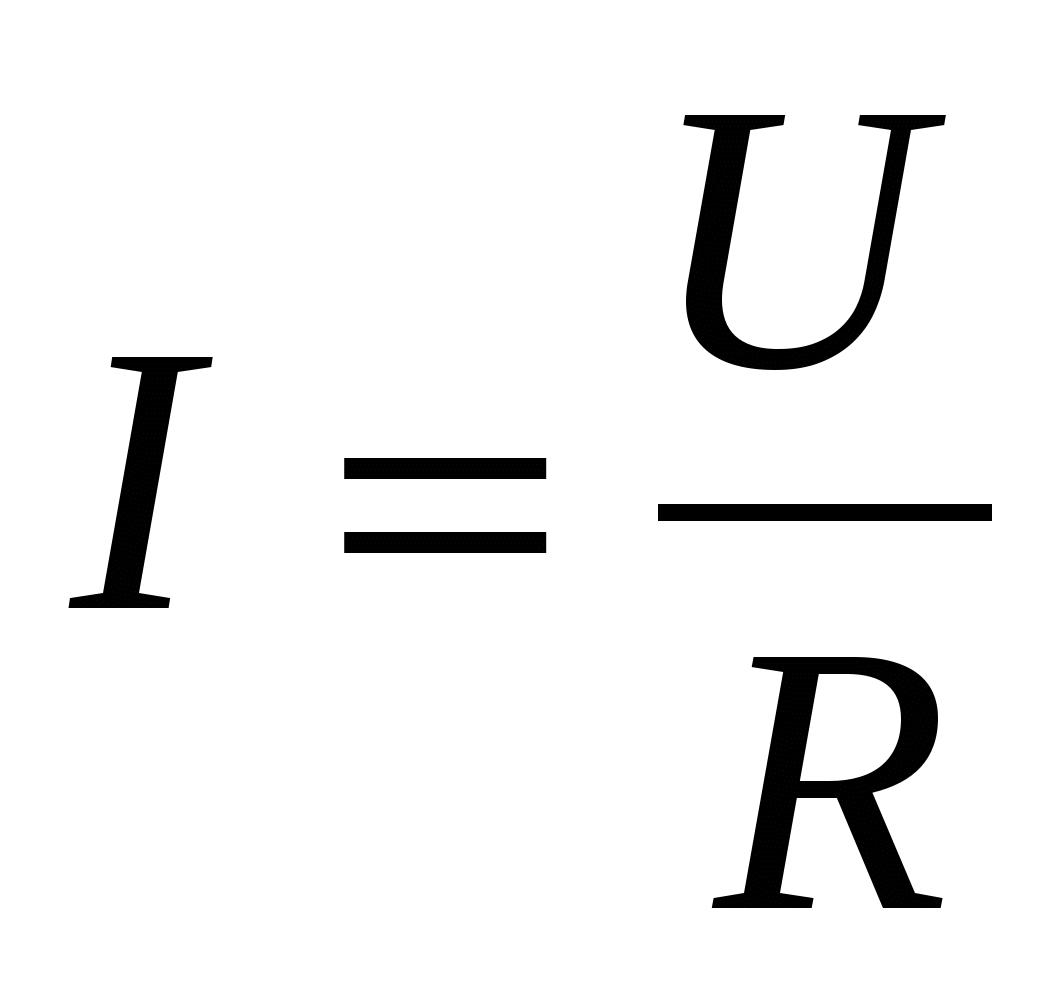Закон Ома для участка цепи с источником ЭДС. (Лекция N 5)
Возьмем два участка цепи a—bи c—d (см. рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на рис. 1 положительных направлений напряжений и токов.
Объединяя оба случая, получим
| (1) |
или для постоянного тока
| . | (2) |
Формулы (1) и (2) являются аналитическим выражением закона Ома для участка цепи с источником ЭДС, согласно которому ток на участке цепи с источником ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной на сопротивление участка. В случае переменного тока все указанные величины суть комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление совпадает с выбранным направлением тока, и со знаком “-”, если их направление противоположно направлению тока.
Основы символического метода расчета цепей
синусоидального тока
Расчет цепей переменного синусоидального тока может производиться не только путем построения векторных диаграмм, но и аналитически – путем операций с комплексами, символически изображающими синусоидальные ЭДС, напряжения и токи. Достоинством векторных диаграмм является их наглядность, недостатком – малая точность графических построений. Применение символического метода позволяет производить расчеты цепей с большой степенью точности.
Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа и законе Ома в комплексной форме.
Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных величин.
1. Первый закон Кирхгофа в комплексной форме:
| . | (3) |
2. Второй закон Кирхгофа в комплексной форме:
| (4) |
или применительно к схемам замещения с источниками ЭДС
| . | (5) |
3. Соответственно матричная запись законов Кирхгофа в комплексной форме имеет вид:
§ первый закон Кирхгофа:
| . ; | (6) |
§ второй закон Кирхгофа
| . | (7) |
Пример.
Дано:
Рис. 2
Решение:
1. .
2. .
3.
.
4. Принимая начальную фазу напряжения за нуль, запишем:
.
Тогда
.
5. Поскольку ток распределяется обратно пропорционально сопротивлению ветвей (это вытекает из закона Ома), то
6. .
7. Аналогичный результат можно получить, составив для данной схемы уравнения по законам Кирхгофа в комплексной форме
или после подстановки численных значений параметров схемы
Специальные методы расчета
Режим работы любой цепи полностью характеризуется уравнениями, составленными на основании законов Кирхгофа. При этом необходимо составить и решить систему с n неизвестными, что может оказаться весьма трудоемкой задачей при большом числе
Метод контурных токов
Идея метода контурных токов: уравнения составляются только по второму закону
Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих
по замкнутым контурам, т.е. в случае выбора главных контуров равных токам ветвей
связи. Число уравнений равно числу независимых контуров, т.е. числу ветвей связи
графа . Первый закон Кирхгофа выполняется автоматически.
Контуры можно выбирать произвольно, лишь бы их число было равно
Направления истинных и контурных токов выбираются произвольно. Выбор положительных направлений перед началом расчета может не определять действительные направления токов в цепи. Если в результате расчета какой-либо из токов, как и при использовании уравнений по законам Кирхгофа, получится со знаком “-”, это означает, что его истинное направление противоположно.
Пусть имеем схему по рис. 3.
Выразим токи ветвей через контурные токи:
;
; ;
; .
Обойдя контур aeda, по второму закону Кирхгофа имеем
.
Поскольку ,
то
.
Таким образом, получили уравнение для первого контура относительно контурных токов. Аналогично можно составить уравнения для второго, третьего и четвертого контуров:
совместно с первым решить их относительно контурных токов и затем по уравнениям, связывающим контурные токи и токи ветвей, найти последние.
Однако данная система уравнений может быть составлена формальным путем:
При составлении уравнений необходимо помнить следующее:
— сумма сопротивлений, входящих в i-й контур;
— сумма сопротивлений, общих для i-го и k-го контуров, причем ;
члены на главной диагонали всегда пишутся со знаком “+”;
знак “+” перед остальными членами ставится в случае, если через общее сопротивление i-й и k- й контурные токи проходят в одном направлении, в противном случае ставится знак “-”;
если i-й и k- й контуры не имеют общих сопротивлений, то
в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в контур: со знаком “+”, если направление ЭДС совпадает с выбранным направлением контурного тока, и “-”, если не совпадает.
В нашем случае, для первого уравнения системы, имеем:
Следует обратить внимание на то, что, поскольку , коэффициенты контурных уравнений всегда симметричны относительно главной диагонали.
Если в цепи содержатся помимо источников ЭДС источники тока, то они учитываются
в левых частях уравнений как известные контурные токи: k- й контурный ток, проходящий через ветвь с k-
м источником тока равен этому току
Метод узловых потенциалов
Данный метод вытекает из первого закона Кирхгофа. В качестве неизвестных принимаются потенциалы узлов, по найденным значениям которых с помощью закона Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного из узлов (любого) принимается равным нулю. Таким образом, число неизвестных потенциалов, а следовательно, и число уравнений равно , т.е. числу ветвей дерева .
Пусть имеем схему по рис. 4, в которой примем .
Допустим, что и известны. Тогда значения токов на основании закона Ома для участка цепи с источником ЭДС
Запишем уравнение по первому закону Кирхгофа для узла а:
и подставим значения входящих в него токов, определенных выше:
.
Сгруппировав соответствующие члены, получим:
.
Аналогично можно записать для узла b:
.
Как и по методу контурных токов, система уравнений по методу узловых потенциалов может быть составлена формальным путем. При этом необходимо руководствоваться следующими правилами:
1. В левой части i-го уравнения записывается со знаком “+”потенциал i-го узла, для которого составляется данное i-е уравнение, умноженный на сумму проводимостей ветвей, присоединенных к данному i-му узлу, и со знаком “-”потенциал соседних узлов, каждый из которых умножен на сумму проводимостей ветвей, присоединенных к i-му и k-му узлам.
Из сказанного следует, что все члены , стоящие на главной диагонали в левой части системы уравнений, записываются со знаком “+”, а все остальные – со знаком “-”, причем . Последнее равенство по аналогии с методом контурных токов обеспечивает симметрию коэффициентов уравнений относительно главной диагонали.
2. В правой части i-го уравнения записывается так называемый узловой ток , равный сумме произведений ЭДС ветвей, подходящих к i-му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком “+”, если соответствующая ЭДС направлена к i-му узлу, в противном случае ставится знак “-”. Если в подходящих к i-му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.
В заключение отметим, что выбор того или иного из рассмотренных методов определяется тем, что следует найти, а также тем, какой из них обеспечивает меньший порядок системы уравнений. При расчете токов при одинаковом числе уравнений предпочтительнее использовать метод контурных токов, так как он не требует дополнительных вычислений с использованием закона Ома. Метод узловых потенциалов очень удобен при расчетах многофазных цепей, но не удобен при расчете цепей со взаимной индуктивностью.
Литература
1. Основы теории цепей: Учеб.для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с
.
Контрольные вопросы и задачи
1. В ветви на рис. 1 . Определить ток .
Ответ: .
2. В чем заключается сущность символического метода расчета цепей синусоидального тока?
3. В чем состоит сущность метода контурных токов?
4. В чем состоит сущность метода узловых потенциалов?
5. В цепи на рис. 5 ; ;
; . Методом контурных токов определить комплексы действующих значений токов ветвей.Ответ: ; ; .
6. В цепи на рис. 6 . Рассчитать токи в ветвях, используя метод узловых потенциалов.
Ответ: ; ; ; ; ; ; .
Закон ома для участка цепи, содержащего эдс
Закон
Ома для участка цепи, содержащего ЭДС,
позволяет найти ток этого участка по
известной разности потенциалов на
концах этого участка и имеющейся на
этом участке ЭДС 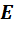 .
Так из уравнения (1-13) имеем для схемы
рис. 1-14, а
.
Так из уравнения (1-13) имеем для схемы
рис. 1-14, а
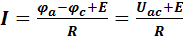 . (1-16)
. (1-16)
Аналогично из уравнения (1-14) для схемы рис. 1-14, б следует
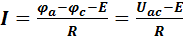 . (1-17)
. (1-17)
Уравнения
(1-16) и (1-17) выражают собой закон Ома для
участка цепи, содержащего ЭДС, для разных
случаев включения ЭДС  .
.
Выражение потенциала люлой точки схемы через потенциалы соседних точек
Рассмотрим на примере схемы рис. 1-15.
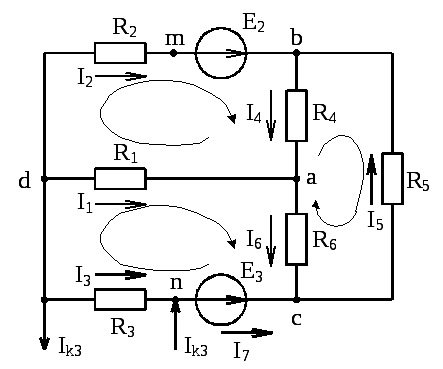
Рис. 1-15. Схема электрической цепи
Перед расчетом произвольно выбираются направления токов во всех ветвях и больше не меняются в процессе расчета.
Найдем разность потенциалов между точками d и n на пути ncabmd.
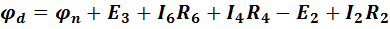 ;
;
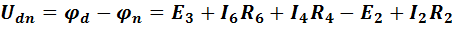 .
(1-18)
.
(1-18)
При
движении от точки n к точке c потенциал скачком возрастает на величину
ЭДС 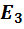 .
На участках ca и ab движемся против тока, т.е. в сторону
возрастания потенциала, поэтому падения
напряжения
.
На участках ca и ab движемся против тока, т.е. в сторону
возрастания потенциала, поэтому падения
напряжения 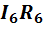 и
и 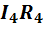 входят в выражение (1-18) со знаком «плюс».
Далее на участке bm скачок потенциала, поэтому падение
напряжения
входят в выражение (1-18) со знаком «плюс».
Далее на участке bm скачок потенциала, поэтому падение
напряжения 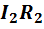 входит в выражение (1-18) со знаком «плюс».
входит в выражение (1-18) со знаком «плюс».
Разность потенциалов между точками d и n по кратчайшему пути будет:
Udn = I3R3. (1-19)
Знак «плюс» соответствует возрастанию потенциала при движении от точки n к точке d по току.
Если при расчете по двум разным путям между одними и теми же точками получается одинаковая разность потенциалов, то можно считать, что токи рассчитаны верно. Это дополнительное средство проверки правильности расчета.
Найдем теперь разность потенциалов между точками b и m на пути mdncab:
Ubm = I2R2 – I3R3 + E3 + I6R6 + I4R4; (1-20)
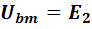 .
(1-21)
.
(1-21)
Первый и второй законы кирхгофа. Составление уравнений для расчета токов в схемах при наличии в них источников эдс и тока
Первый закон Кирхгофа формируется следующим образом: алгебраическая сумма токов, сходящихся в узле равна нулю. Математически это записывается так:
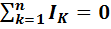 . (1-22)
. (1-22)
Здесь n – число узлов, для которых составляются уравнения по первому закону Кирхгофа.
Положительными считаются токи, подходящие к узлу, отрицательными – отходящие от узла.
В схеме рис. 1-15 пять узлов: a, b, c, d, n. Количество уравнений, которые нужно составить по первому закону Кирхгофа, равно числу узлов без единицы:
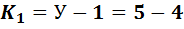 . (1-23)
. (1-23)
Здесь У=5 число узлов.
Узлы, для которых составляются уравнения, выбираются произвольно.
Составим четыре уравнения по первому закону Кирхгофа для узлов a, b, c, d:
 ;
(1-24)
;
(1-24)
b) 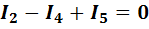 ;
(1-25)
;
(1-25)
c) 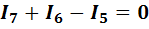 ;
(1-26)
;
(1-26)
d) — 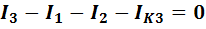 .
(1-27)
.
(1-27)
Уравнение для последнего узла не составляется, так как оно может быть выведено из ранее составленных уравнений (1-24), (1-25), (1-26) и (1-27).
В схеме рис. 1-15 число ветвей В равно семи, оно всегда равно числу неизвестных токов.
Второй закон Кирхгофа формулируется следующим образом: алгебраическая сумма падений напряжений вдоль любого замкнутого контура равно алгебраической сумме ЭДС того же контура.
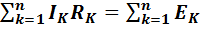 . (1-28)
. (1-28)
Здесь n – число контуров, для которых составляются уравнения по второму закону Кирхгофа.
Любой замкнутый путь в схеме называется электрическим контуром. Ветвь с источником тока не учитывается при подсчете числа контуров.
Так в схеме рис. 1-15 шесть контуров: admba, acnda, abca, cndabc, cadmbc и cndmbc.
Независимым контуром называется такой контур, в который входит хотя бы одна новая ветвь, не вошедшая в предыдущие контуры.
Независимых контуров на схеме рис. 1-15 всего три: admba, adnca, abca.
Контуры 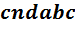 ,
, 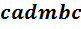 и
и 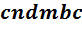 не
являются независимыми контурами, так
как входящие в них ветви уже использованы
при составлении первых трех контуров.
не
являются независимыми контурами, так
как входящие в них ветви уже использованы
при составлении первых трех контуров.
Выберем также произвольно направления обхода независимых контуров, например, все по часовой стрелке.
Число
уравнений 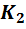 , которые
нужно составить по второму закону
Кирхгофа равно числу ветвей
, которые
нужно составить по второму закону
Кирхгофа равно числу ветвей 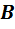 минус
минус 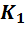 ,
т.е. число уравнений, составленных по
первому закону Кирхгофа
,
т.е. число уравнений, составленных по
первому закону Кирхгофа
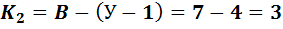 . (1-29)
. (1-29)
Это
всегда равно числу независимых контуров 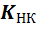
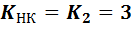 .
(1-30)
.
(1-30)
При составлении уравнений по второму закону Кирхгофа падение напряжения следует считать положительным, если направление тока в данной ветви совпадает с направлением обхода контура, и отрицательным – если ток не совпадает с направлением обхода.
Составим уравнения по второму закону Кирхгофа для выбранных независимых контуров:
admba 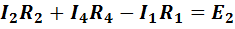 ;
(1-31)
;
(1-31)
abca 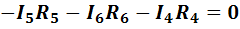 ;
(1-32)
;
(1-32)
acnda I1R1 + I6R6 – I3R3 = -E3. (1-33)
ЭДС контура берутся со знаком «плюс», если их направления совпадают с направлением обхода контура, и «минус» — если не совпадают.
16
1.3. Закон Ома
В 1827 г. немецкий физик Г. Ом, проведя серию точных экспериментов, установил один из основных законов электрического тока. Он гласит: постоянный электрический ток в участке электрической цепи прямо пропорционален напряжению на этом участке.
Закон Ома имеет различные формы записи.
В дифференциальной форме для участка цепи без ЭДС он имеет вид
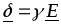 ,
(1.2)
,
(1.2)
где 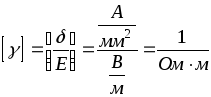 – удельная проводимость.
– удельная проводимость.
Рассмотрим
прямолинейный проводник постоянного
сечения s (рис. 1.6): 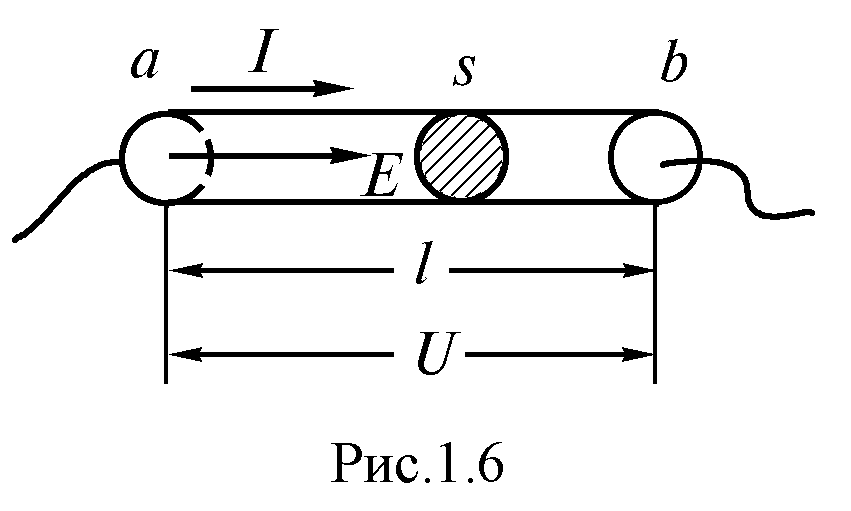
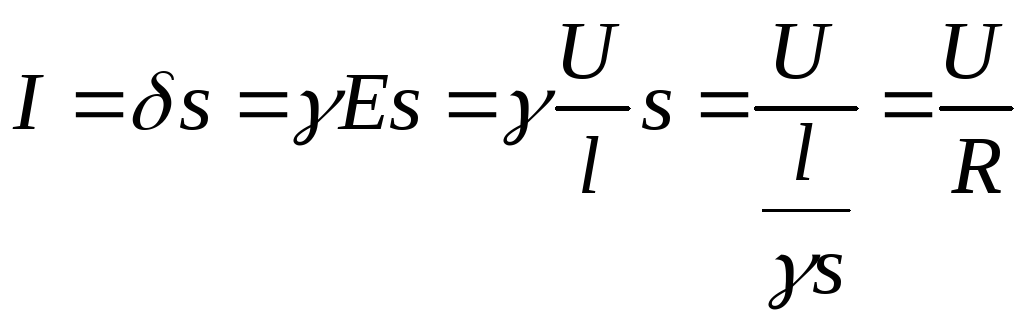 .
(1.3)
.
(1.3)
Рис. 1.6
Это вторая форма записи закона Ома для участка цепи без ЭДС, которая называется интегральной. Он формулируется следующим образом: ток в проводнике равен отношению падения напряжения на участке проводника к электрическому сопротивлению участка.
Электрическое сопротивление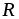 прямо
пропорционально длине
прямо
пропорционально длине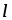 и обратно пропорционально площади
поперечного сечения проводника:
и обратно пропорционально площади
поперечного сечения проводника:
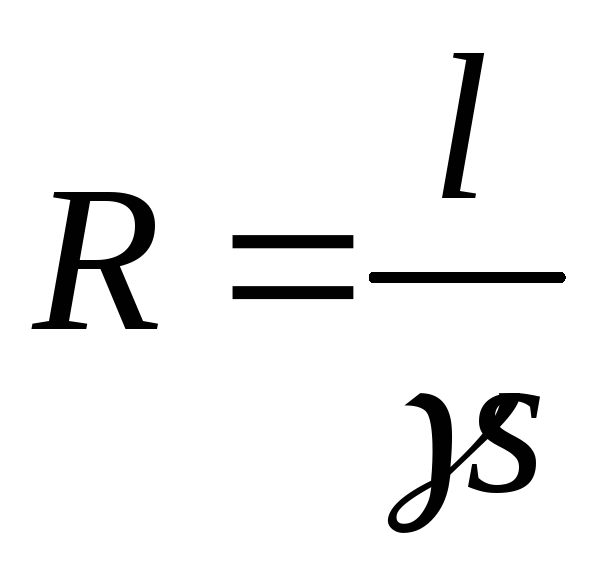 .
(1.4)
.
(1.4)
Размерность сопротивления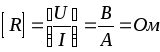 .
.
Таким образом, сопротивление– это скалярная величина, характеризующая проводящие свойства цепи. Оно равно отношению постоянного напряжения на участке цепи к току в нем при отсутствии на участке ЭДС:
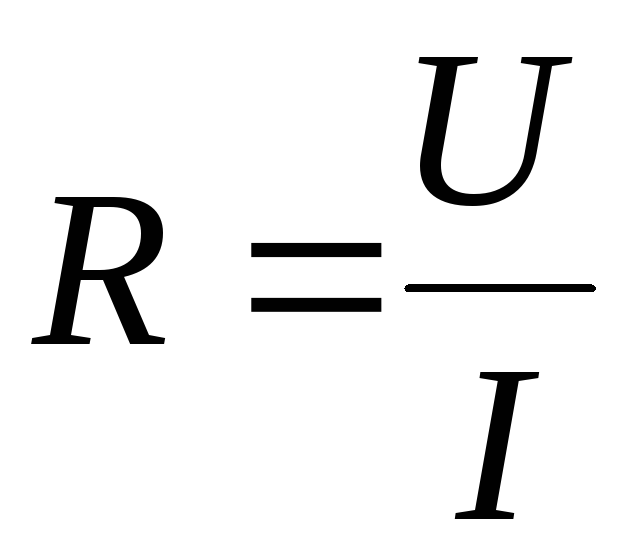 .
(1.5)
.
(1.5)
Сопротивление – это величина, показывающая, что в данном участке цепи происходит преобразование энергии.
Величина, обратная сопротивлению, называется проводимостью:
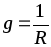 .
(1.6)
.
(1.6)
Размерность проводимости – сименс (См). 1 См = 1/Ом.
Удельное сопротивление:
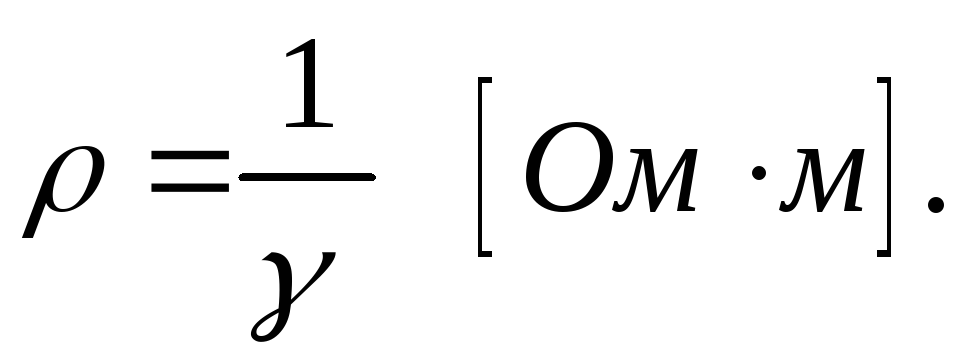 (1.7)
(1.7)
Тогда
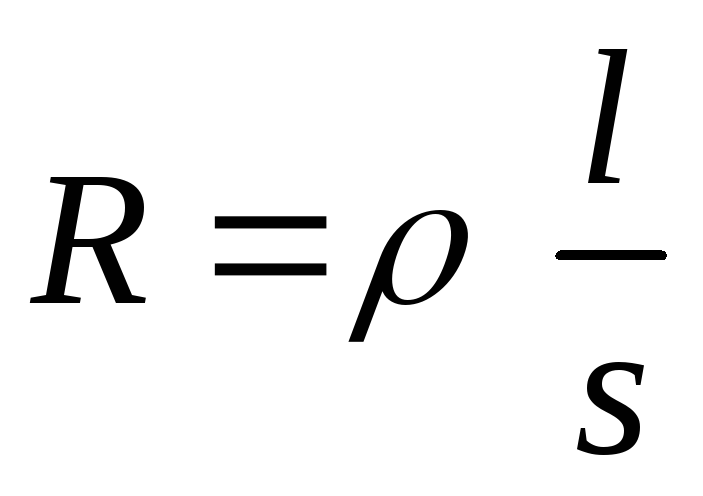 .
(1.8)
.
(1.8)
Удельное сопротивление получено экспериментально для всех материалов и приведено в справочниках.
Обмотки реостатов и нагревательных приборов изготавливают из сплавов с большим удельным сопротивлением (нихром, фехраль и т.п.).
Устройства, которые включают в электрическую цепь для ограничения или регулирования тока, называются резисторами или реостатами.
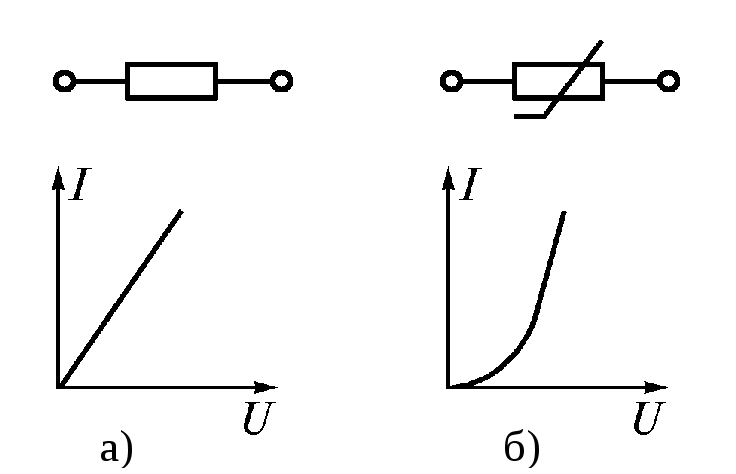
Рис. 1.7
Зависимость тока резистораIот подводимого напряженияUназывается еговольтамперной характеристикой(ВАХ). Если сопротивление резистора не зависит от тока, то его ВАХ представляет собой прямую линию (рис. 1.7 а), проходящую через начало координат. Такой резистор называетсялинейным. Резистор, ВАХ которого не является прямой линией (рис. 1.7 б), называетсянелинейным. Электрические цепи, содержащие только линейные элементы, называют линейными. Если в цепи имеется хотя бы один нелинейный элемент, вся цепь называетсянелинейной.1.4. Источник эдс и источник тока
При преобразовании
любого вида энергии в электрическую
энергию в источниках происходит за
счет электродвижущей силы (ЭДС). Электродвижущая
сила 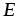 характеризует действие сторонних
(неэлектрических) сил в источниках
постоянного или переменного тока. В
замкнутом проводящем контуре она
равна работе этих сил по перемещению
единичного положительного заряда
вдоль этого контура. Сторонние силы
приводят в движение заряженные частицы
внутри источника электрической
энергии: генераторов, гальванических
элементов и т.д. ЭДС определяется как
отношение работы
характеризует действие сторонних
(неэлектрических) сил в источниках
постоянного или переменного тока. В
замкнутом проводящем контуре она
равна работе этих сил по перемещению
единичного положительного заряда
вдоль этого контура. Сторонние силы
приводят в движение заряженные частицы
внутри источника электрической
энергии: генераторов, гальванических
элементов и т.д. ЭДС определяется как
отношение работы 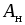 ,
совершаемой сторонними силами при
переносе заряженной частицы внутри
источника, к ее заряду:
,
совершаемой сторонними силами при
переносе заряженной частицы внутри
источника, к ее заряду:
 .
.
Если 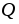 =
1Кл, то
=
1Кл, то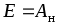 .
.
Следовательно, ЭДС равна работе, совершаемой сторонними силами при переносе единицы заряда внутри источника от зажима с меньшим потенциалом к зажиму с большим потенциалом. Ее можно представить разностью потенциалов или напряжением между положительным и отрицательным зажимами источника энергии при отсутствии в нем тока.
В замкнутой электрической цепи под действием ЭДС источника возникает ток. Цепь, в которой ток не изменяется во времени, называют цепью постоянного тока. При расчете и анализе электрических цепей источник электрической энергии представляют либо источником ЭДС, либо источником тока.
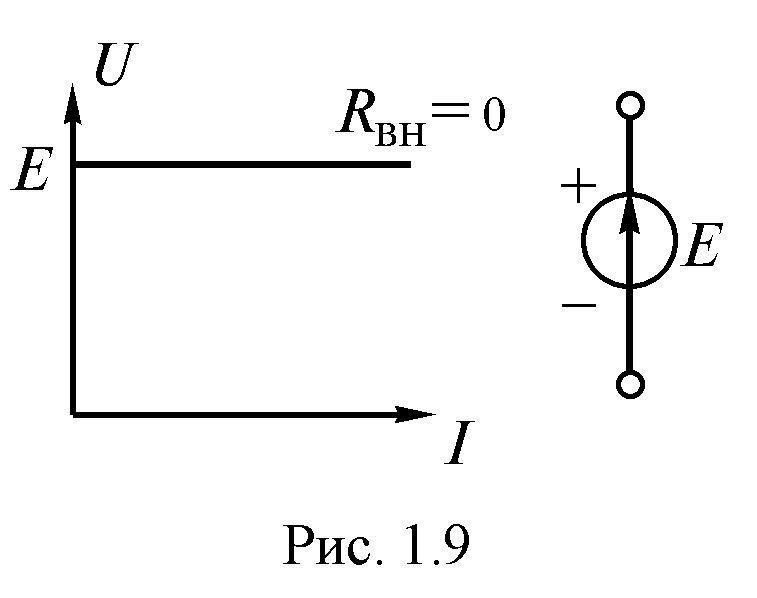
Идеальным источником ЭДС (рис. 1.8) называют такой источник энергии, ЭДС которого не зависит от протекающего через него тока и равна ЭДС реального источника, а его внутреннее сопротивление равно нулю. На рис. 1.8 показаны условные обозначения и вольтамперная характеристика идеального источника ЭДС.
За положительное направление ЭДС
источника принимается направление
возрастания потенциала внутри этого
источника. Внутреннее сопротивление 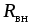 показывает, что часть энергии,
вырабатываемой источником, используется
внутри источника. Схема замещения
реального источника (
показывает, что часть энергии,
вырабатываемой источником, используется
внутри источника. Схема замещения
реального источника (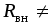 0)
может быть представлена в виде
последовательного соединения идеального
источника ЭДС и внутреннего сопротивления
(рис. 1.9). Реальный источник называют
источником напряжения.
0)
может быть представлена в виде
последовательного соединения идеального
источника ЭДС и внутреннего сопротивления
(рис. 1.9). Реальный источник называют
источником напряжения.
|
|
Рис. 1.8 | Рис. 1.9 |
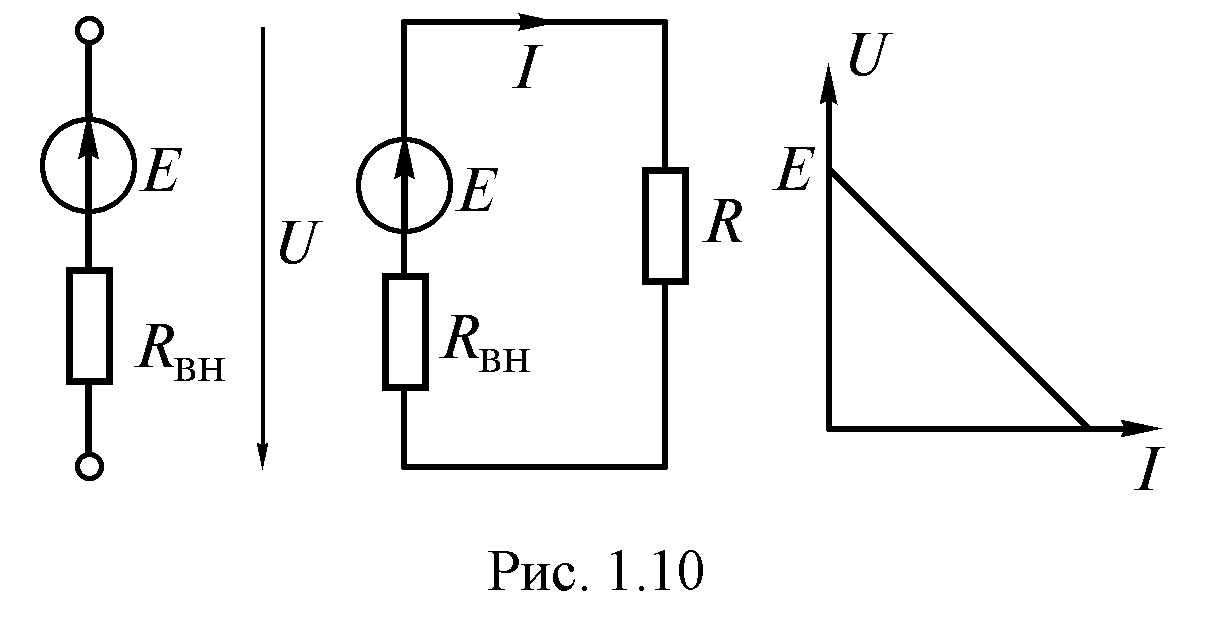
Ток в цепи (рис. 1.9) определяется по закону Ома:
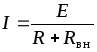 .
(1.9)
.
(1.9)
Из последней формулы видно, что внутреннее сопротивление оказывает влияние на ток в электрической цепи.
Напряжение на зажимах источника или на нагрузке (рис. 1.9) определяется по формуле
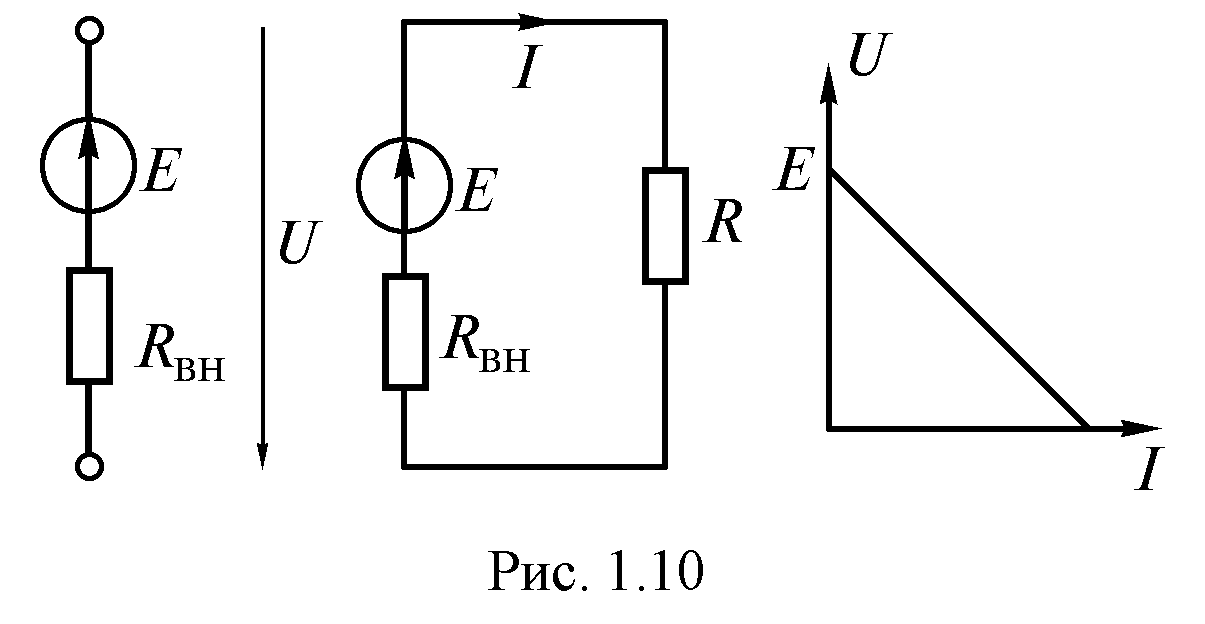
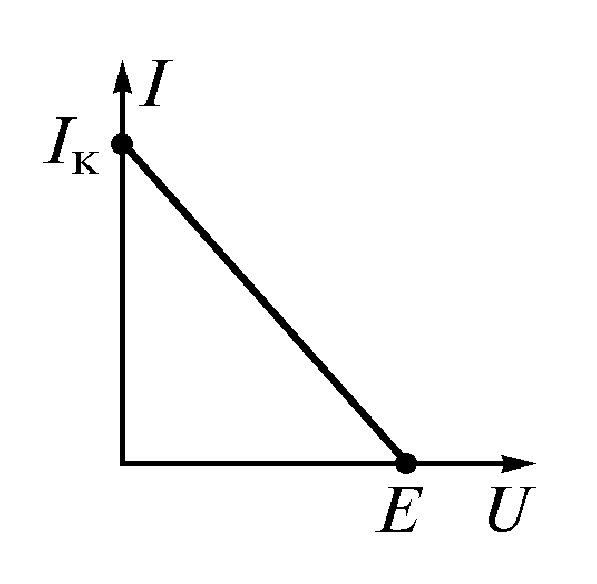
Рис. 1.10
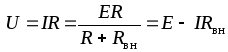 .
(1.10)
.
(1.10)ВАХ источников электрической энергии часто называют внешними характеристиками. Внешняя характеристика реального источника описывается уравнением (1.10). Ее можно построить по данным двух опытов (рис. 1.10):
холостого хода 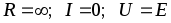 ;
;
короткого замыкания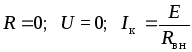 .
.
Источником токаназывают такой
идеализированный источник электрической
энергии, который вырабатывает ток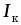 ,
не зависящий от нагрузки
,
не зависящий от нагрузки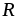 цепи и равный частному от деления ЭДС
реального источника на его внутреннее
сопротивление:
цепи и равный частному от деления ЭДС
реального источника на его внутреннее
сопротивление:
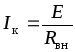 .
(1.11)
.
(1.11)
Чтобы обеспечить постоянство тока 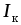 независимо от нагрузки
независимо от нагрузки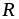 ,
необходимо выполнить условия: а)
,
необходимо выполнить условия: а)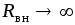 ;
б)
;
б)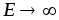 .
.
Идеальный источник тока можно считать
реальным, если внутреннее сопротивление 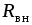 подключить параллельно сопротивлению
нагрузки. ВАХ и условное обозначение
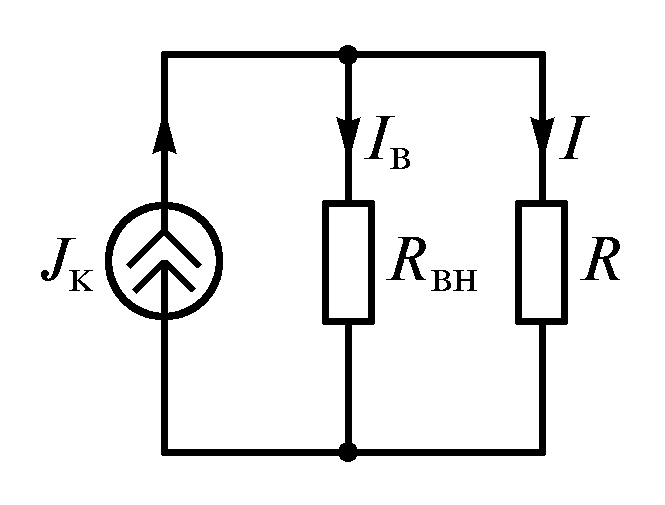
источника тока показаны на рис. 1.11. Схема
замещения реального источника представлена
на рис. 1.12.
подключить параллельно сопротивлению
нагрузки. ВАХ и условное обозначение
источника тока показаны на рис. 1.11. Схема
замещения реального источника представлена
на рис. 1.12.
Ток в нагрузке
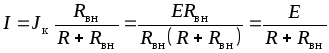 .
(1.12)
.
(1.12)
| |
Рис. 1.11 | Рис. 1.12 |
Следовательно, при расчете цепей источники тока могут быть заменены источниками ЭДС и наоборот.
Каждый из двух расчетных эквивалентов является равноценным. В дальнейшем будем использовать в основном источник ЭДС.
Эквивалентность источников обеспечивается при равенстве напряжений при холостом ходе и равенстве токов при коротком замыкании.
Закон Ома для участка цепи, содержащего ЭДС | Учеба-Легко.РФ
Закон Ома для участка цепи, содержащего источник ЭДС. Обобщенный закон Ома. Закон (правило) Ома для участка цепи, содержащего источник ЭДС, позволяет найти ток этого участка по известной разности потенциалов (φа — φс)на концах участка цепи и имеющейся на этом участке ЭДС E.
Так, по уравнению (1.2) для схемы рис. 2.6, а
I = (φa — φc + E) / R = (Uac + E) / R;
по уравнению (2.2а) для схемы рис. 2.6, б
I = (φa — φc — E) / R = (Uac — E) / R.
В общем случае
(2.3а)
Уравнение (2.3а) математически выражает закон Ома для участка цепи, содержащего источник ЭДС; знак плюс перед Е соответствует рис. 2.6, а, знак минус — рис. 2.6, б. В частном случае при Е = 0 уравнение (2.3а) переходит в уравнение (2.3).
Закон Ома для полной цепи:
, (2)
где:
- — ЭДС источника напряжения(В),
- — сила тока в цепи (А),
- — сопротивление всех внешних элементов цепи (Ом),
- — внутреннее сопротивление источника напряжения (Ом).
Из закона Ома для полной цепи вытекают следствия:
- При r< сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
- При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.
Часто выражение:
(3)
(где есть напряжение или падение напряжения, или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».
Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:
(4)
То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.
К другой записи формулы (3), а именно:
(5)
Применима другая формулировка:
| Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи. |
Выражение (5) можно переписать в виде:
(6)
где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо, впоследствии переименованный в Си́менс
В заключение предлагаем Вашему вниманию шпаргалку по этой теме:
Закон Ома для участка цепи
Мы уже познакомились с тремя важными характеристиками электрической цепи. Напряжение, сила тока и сопротивление связаны между собой. Как мы уже выяснили, сила тока в цепи прямо пропорциональна напряжению на концах проводника. Также, мы узнали, что чем больше сопротивление, тем меньше сила тока в проводнике при одинаковом напряжении. Конкретную зависимость силы тока от сопротивления установил Георг Ом, проводя свои опыты. Он подключал к одному и тому же источнику проводники с разным сопротивлением и измерял силу тока.

С помощью вольтметра можно убедиться, что напряжение на концах проводника постоянно, а с помощью амперметра — измерить силу тока. Так же, как и в опытах с напряжением, мы записываем результаты измерений в таблицу и строим график.

Из таблицы видно, что сила тока уменьшается ровно во столько раз, во сколько увеличивается сопротивление, поэтому график представляет собой ветвь гиперболы. Из этого можно сделать вывод, что сила тока в цепи обратно пропорциональна сопротивлению.
Обобщив результаты опытов, Ом сформулировал закон для участка цепи: сила тока на участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна сопротивлению:

Таким образом, мы узнали, как связаны между собой сила тока, напряжение и сопротивление.
Из формулы, описывающей закон Ома, видно, что зная две из трёх этих величин, можно легко вычислить третью. Например, из формулы мы можем выразить сопротивление, которое будет равно отношению напряжения к силе тока:

Несмотря на это, следует помнить о том, что сопротивление — это характеристика проводника, которая никак не зависит от напряжения и силы тока.
Закон Ома для участка цепи очень часто используется в различных расчетах, связанных с электрическими цепями, поэтому, важно, чтобы было четкое понимание этого закона.
Примеры решения задач.
Задача 1. Сопротивление нагревательного элемента чайника 22 Ом. Зная, что напряжение в розетке составляет 220 В, найдите силу тока в нагревательном элементе (сопротивлением проводов можно пренебречь).

Задача 2. За какое время чайник из предыдущей задачи нагреет 2 л воды до кипения, если предположить, что его КПД составляет 40%, а температура воды 20 оС?

Задача 3. На графике показаны две прямые, описывающие зависимость силы тока от напряжения в проводниках 1 и 2. Определите сопротивление каждого из проводников.

Каждая точка прямой 1 соответствует значениям силы тока и напряжения в данном проводнике. Поэтому можно взять любую пару таких значений, и поделить значение напряжения на значение силы тока. Логичнее использовать точку, которая наиболее близка к точным значениям, указанным на графике. Получим, что сопротивление в проводнике 1 равно 25 Ом. Аналогичным способом, вычислим сопротивление в проводнике 2. Получим 100 Ом.
Задача 4. К пятивольтной батарейке подсоединили лампочку, через которую проходит ток вдвое меньше, чем в лампочке, подсоединенной к двухвольтной батарейке. Найдите отношение сопротивлений проводников.

Задача 5. Каким сопротивлением должны обладать вольтметр и амперметр?
Включение амперметра в цепь добавляет некоторое сопротивление, как и включение любого другого элемента. Из формулы видно, что если сопротивление амперметра будет сравнимо с сопротивлением цепи, то амперметр существенно изменит силу тока, которую он измеряет. Поэтому, сопротивление амперметра должно быть очень маленьким, чтобы наиболее точно измерять силу тока в цепи. Например, если сопротивление амперметра составляет четверть от сопротивления цепи, то это уменьшит силу тока на 20%. Однако, если сопротивление амперметра составляет меньше одной сотой от сопротивления цепи, то им можно пренебречь.
Чтобы измерять напряжение с минимальными погрешностями необходимо сделать так, чтобы через вольтметр практически не проходил ток, иначе, это повлияет на напряжение. Поэтому, вольтметр, наоборот, должен иметь очень большое сопротивление. Действительно, если вольтметр будет обладать большим сопротивлением, то ток, проходящий через вольтметр, будет ничтожно мал, и это никак не повлияет на работу цепи.

Закон Ома для участка цепи
Закон для участка электрической цепи без источника тока
Если в проводнике течет ток, то потенциал в разных его точках различается. Падение напряжения означает, что отлична от нуля составляющая напряженности поля, которая направлена вдоль проводника ($E_{\tau }$).
Напряжённостью поля называется векторная физическая величина, являющаяся отношением силы, действующей на заряд, к величине этого заряда.
Следовательно, напряженность поля у поверхности проводника с током не перпендикулярна к проводящей поверхности.
Для того чтобы в проводнике существовал постоянный ток, необходимо чтобы действовала внешняя сила, которая равна $E_{\tau }\cdot q_e$, где $q_e$ — заряд электрона, то значит, на движущиеся электроны действует сила трения. Или иначе говорят, что проводники имеют сопротивление ($R$). Сопротивление — это тот коэффициент, который связывает силу тока и напряжение.
Свой закон Ом получил эмпирически. Если построить вольтамперную характеристику электрического проводника, то легко заметить, что $I\sim U$. В соответствии с законом сила тока, которая течет по металлическому проводнику, может быть найдена:
где $R$ — сопротивление проводника или просто сопротивление.
Данная формула — это общая формулировка закона Ома.
В том случае, если источников ЭДС в электрической цепи нет (иногда в таком случае говорят, что проводник однороден в смысле сторонних сил), то напряжение $U$ — совпадает с разностью потенциалов.
Для неоднородного участка цепи
Для участков электрических цепей с источником ЭДС закон Ома запишем в виде:
$I=\frac{\left({\varphi }_1-{\varphi }_2\right)+\mathcal{E}}{R}\ \left(2\right)$, где:
- $\mathcal{E}$ — ЭДС источника тока,
- $R$ —сопротивление рассматриваемого участка цепи.
$\mathcal{E}$, как и сила тока является алгебраической величиной. В том случае, если выбор положительного $\mathcal{E}$ совпадает с направлением положительных зарядов, то $\mathcal{E}$ считается положительной. Если $\mathcal{E}$ препятствует перемещению зарядов, то $\mathcal{E}$ получают, используя то, что в такой цепи ${\varphi }_1={\varphi }_2$, следовательно:
$I=\frac{\mathcal E}{R}\left(3\right)$
где $R$ — сумма вех сопротивлений.
Применение закона Ома
Закон Ома используется, например, при измерении напряжения с помощью вольтметра. Вольтметр — это гальванометр, последовательно с которым соединено небольшое сопротивление. При подключении вольтметра к точкам участка цепи, напряжение между которыми мы планируем измерить, в вольтметр ответвляется часть тока. Сила данного тока $(I)$ по закону Ома в виде (1) пропорциональна напряжению между заданными точками. Следовательно, зная чувствительность вольтметра по току и его сопротивление, можно найти напряжение, используя подходящую формулировку закона Ома. Это напряжение наносят на шкалу прибора.
Ток через вольтметр должен быть очень небольшим, для того чтобы подключение вольтметра сильно не изменяло силу тока и распределение напряжения в цепи. С этой целью сопротивление самого вольтметра делают очень большим в сравнении с сопротивлением внешнего (по отношению к вольтметру) участка цепи.
Закон Ома — один из самых важных законов электричества. Но он имеет смысл только в случае, когда сопротивление проводника не зависит от приложенного к нему напряжению и силы тока. К такому типу проводников относят: металлы, уголь, электролиты. Для ионизированных газов закон Ома не всегда справедлив.
Задание № 1: Используя закон Ома, получите формулу для расчёта суммарного сопротивления трех последовательно соединенных проводников имеющих сопротивления $R_1,R_2,R_3$. Обобщите полученную формулу для $n$ проводников.
Рисунок 1. Схема соединения. Автор24 — интернет-биржа студенческих работ
Решение:
При последовательном соединении проводников (рис.1), $I=const$, а суммарное напряжение в цепи находится как сумма напряжений на концах каждого проводника:
$I=const,\ U=U_1+U_2+U_3\left(1.1\right)$
В качестве основы для решения задачи можно использовать закон Ома для однородного участка цепи. Для всей цепи запишем:
$U=IR\ (1.2)$
в формуле (1.2) $R$ — искомое напряжение, обратно пропорциональное сопротивлению.
Для одного сопротивления:
где $R_1$ — сопротивление первого проводника, $U_1$ — напряжение на нем.
Подставим в закон Ома (1.2) выражение для напряженности (1.1) и выражения для токов, которые текут через отдельные проводники (1.3) получим:
Сократим в (1.4) токи, получим формулу для расчета суммарного сопротивления для цепи из трех последовательных сопротивлений:
Ответ: Для трех сопротивлений $R=R_1+R_2+R_3.$ Для n — сопротивлений: $R=R_1+R_2+\dots +R_n.$
Задание № 2: Чему равно ЭДС ($\mathcal E$) и сопротивление источника $\mathcal E$, если он эквивалентен двум источникам тока, которые характеризуются ЭДС: $ \mathcal E_1 и\ \mathcal E_2$ и внутренними сопротивлениями: $r_1и\ r_2$, соединенными параллельно (рис.2).
Рисунок 2. Схема соединения. Автор24 — интернет-биржа студенческих работ
Решение:
За основу решения задачи примем закон Ома. Запишем его дважды для неоднородного участка цепи 1-2, учитываем, что соединение источников тока параллельное:
Выразим токи из (2.1), получим:
Суммарный ток, который дают источники можно найти как сумму токов:
По условиям задачи эквивалентный источник должен давать ток равный $I$ (2.3), и разность потенциалов в точках 1 и 2 равна $U_{21}\ $(2.4), для него запишем:
Сравним формулу (2.5) и (2.4).
Ответ: $\mathcal E=\frac{r_2\mathcal E_1+r_1\mathcal E_2}{r_1+r_2}$,
$r=\frac{r_1r_2}{r_1+r_2}$.
Закон Ома для участка цепи.
Закон Ома для участка цепи.
Цель: формирование знаний о взаимосвязи силы тока, напряжения и сопротивления на участке цепи.
Задачи:
Образовательная:
1) силы тока от напряжения на концах проводника, если при этом сопротивление проводника не меняется;
2) силы тока от сопротивления участка цепи, если при этом напряжение остается постоянным;
сделать вывод о взаимосвязи силы тока, напряжения и сопротивления;
Показать практическое применение закона Ома.
Развивающая:
развивать умения наблюдать, сопоставлять, сравнивать и обобщать результаты экспериментов;
продолжить формирование умений пользоваться теоретическими и экспериментальными методами физической науки для обоснования выводов по изучаемой теме и для решения задач.
Воспитательная:
развивать познавательный интерес к предмету;
воспитывать культуру речи и культуру работы в коллективе, тренировка рационального метода запоминания формул.
Тип урока: Комбинированный.
Оборудование: источник тока; амперметр; вольтметр; магазин сопротивлений; реостат; соединительные провода; датчик электрического напряжения ,датчик электрического тока амперметр .
Ход урока
I. Организация начала урока.
II. Актуализация знаний.
Любую электрическую цепь можно охарактеризовать силой тока, напряжением и сопротивлением. Каждая из этих величин имеет свою характеристику. Давайте вспомним, что мы изучили о каждой из этих величин.
(слайд 1)
Величины на слайде (1) закрыты номерами 1,2,3. Учащиеся I,II,III рядов поочередно выбирают номер, под которым находится величина, и дают ей полную характеристику по плану:
Структура знаний о физической величине. (слайд 2)
Какое явление или свойство тел определяет (характеризует) данная величина.
Определение величины .
Формула (для производной величины – формула, выражающая связь данной величины с другими).
Какая это величина – скалярная или векторная.
Единицы измерения данной величины.
Способы измерения величины.
Характеристики электрической цепи
Сила тока
Напряжение
Сопротивление
Электродвижущая сила
I
U
R
ε
какой электрический заряд проходит через поперечное сечение проводника за единицу времени.
какую работу совершает электрическое поле по перемещению единичного заряда.
величину, характеризующую способность проводника ограничивать силу тока.
какую работу совершают сторонние силы по перемещению единичного заряда в источнике.

отношением заряда, проходящего через поперечное сечение проводника ко времени, в течение которого этот заряд движется.
отношением работы поля по перемещению заряда из начальной точки в конечную к этому заряду.
отношением напряжения на участке цепи к силе тока.
отношением работы сторонних сил к переносимому электрическому заряду.
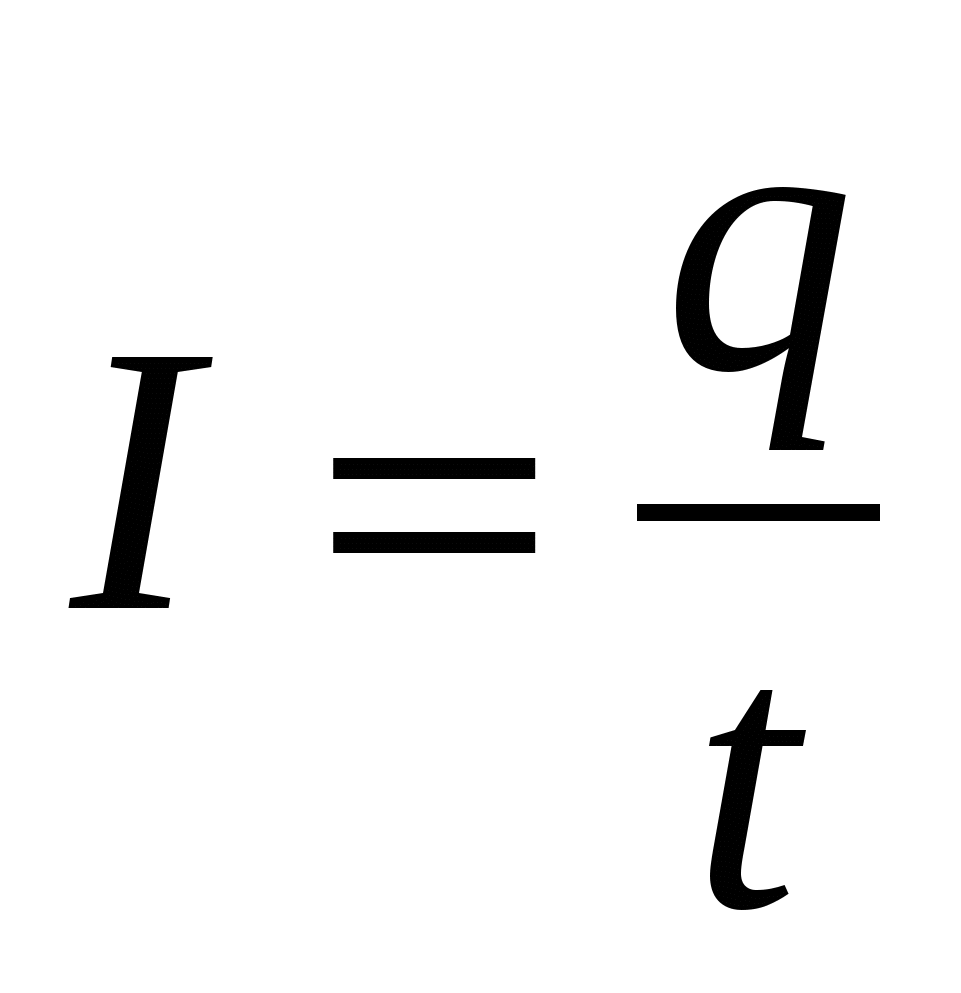
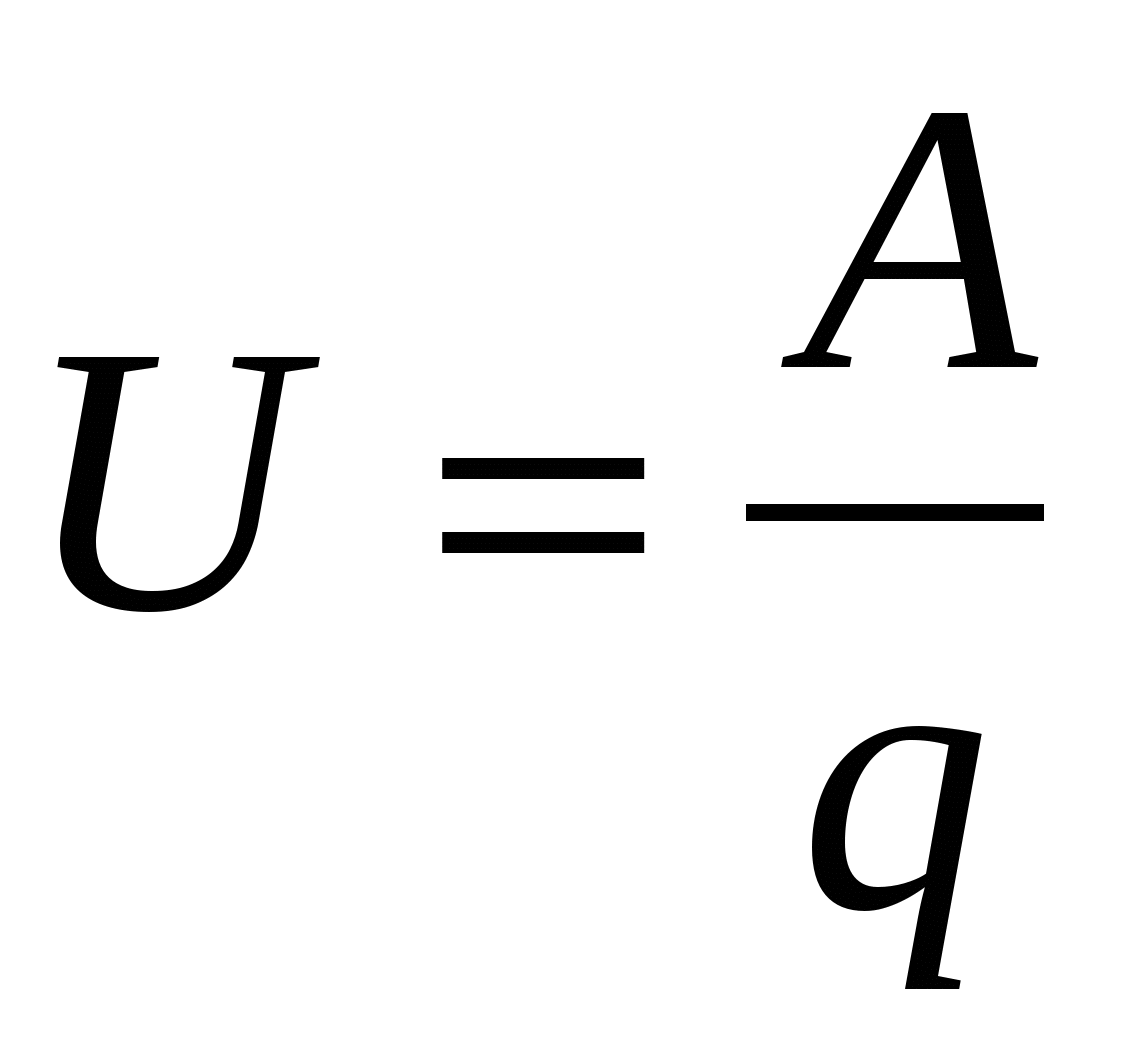
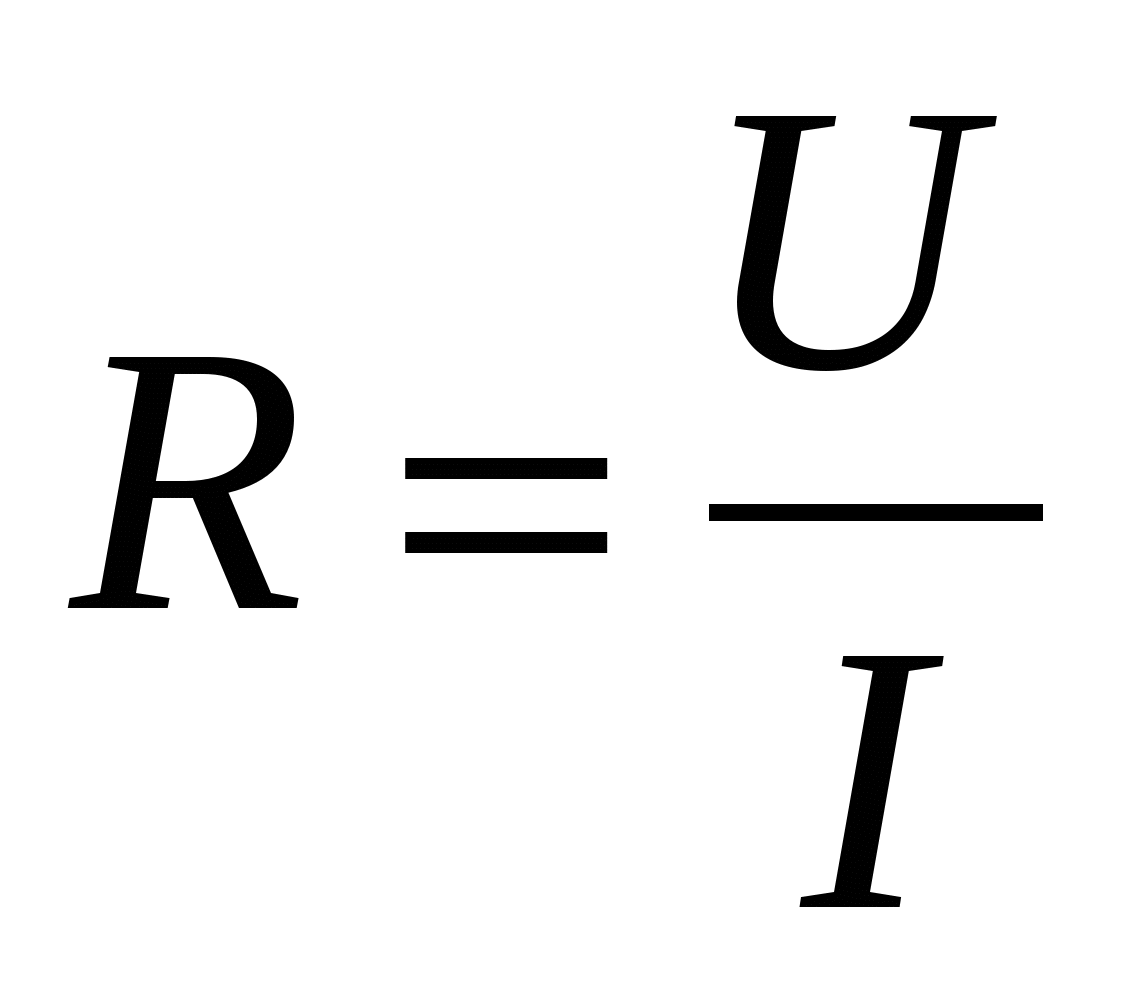
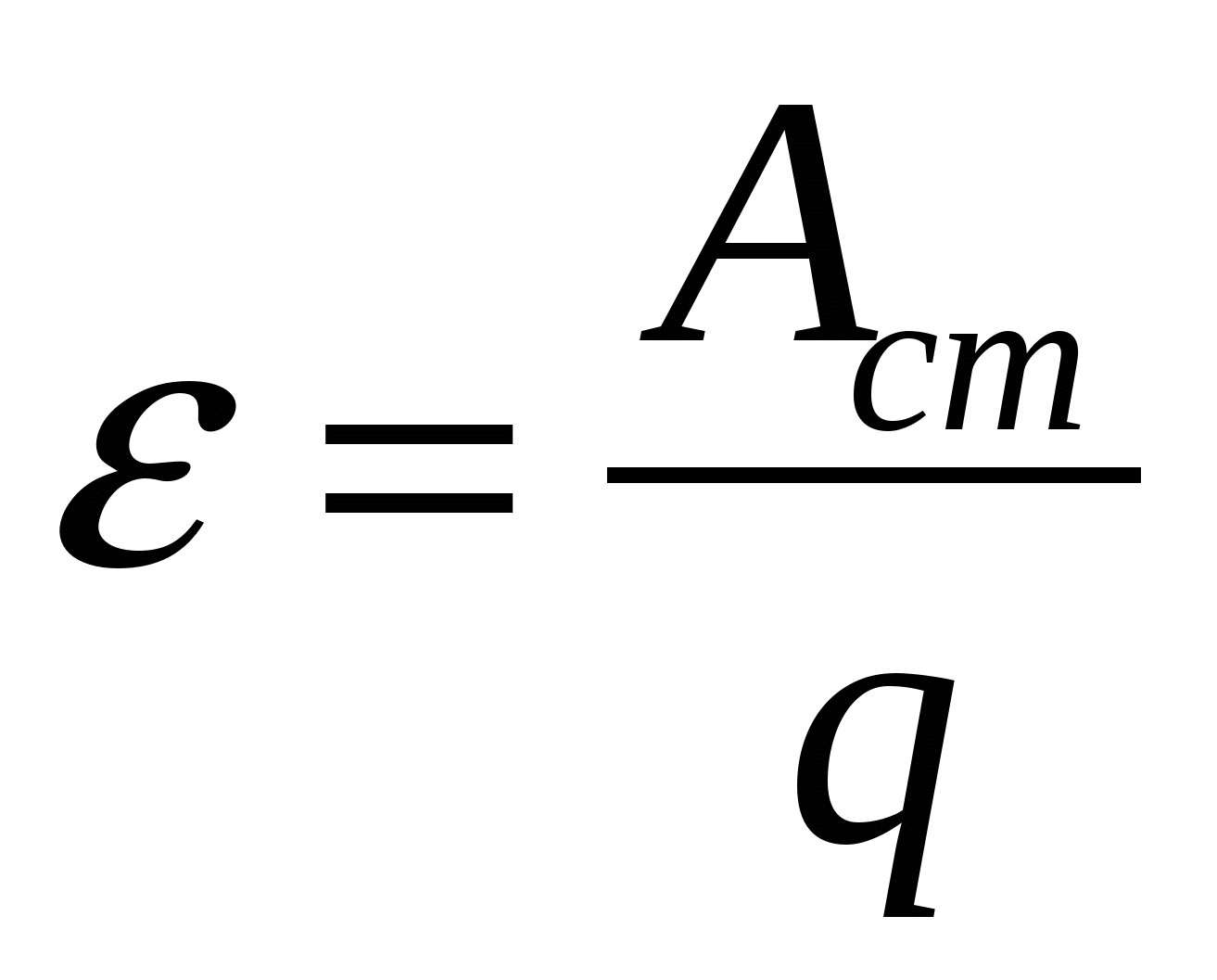

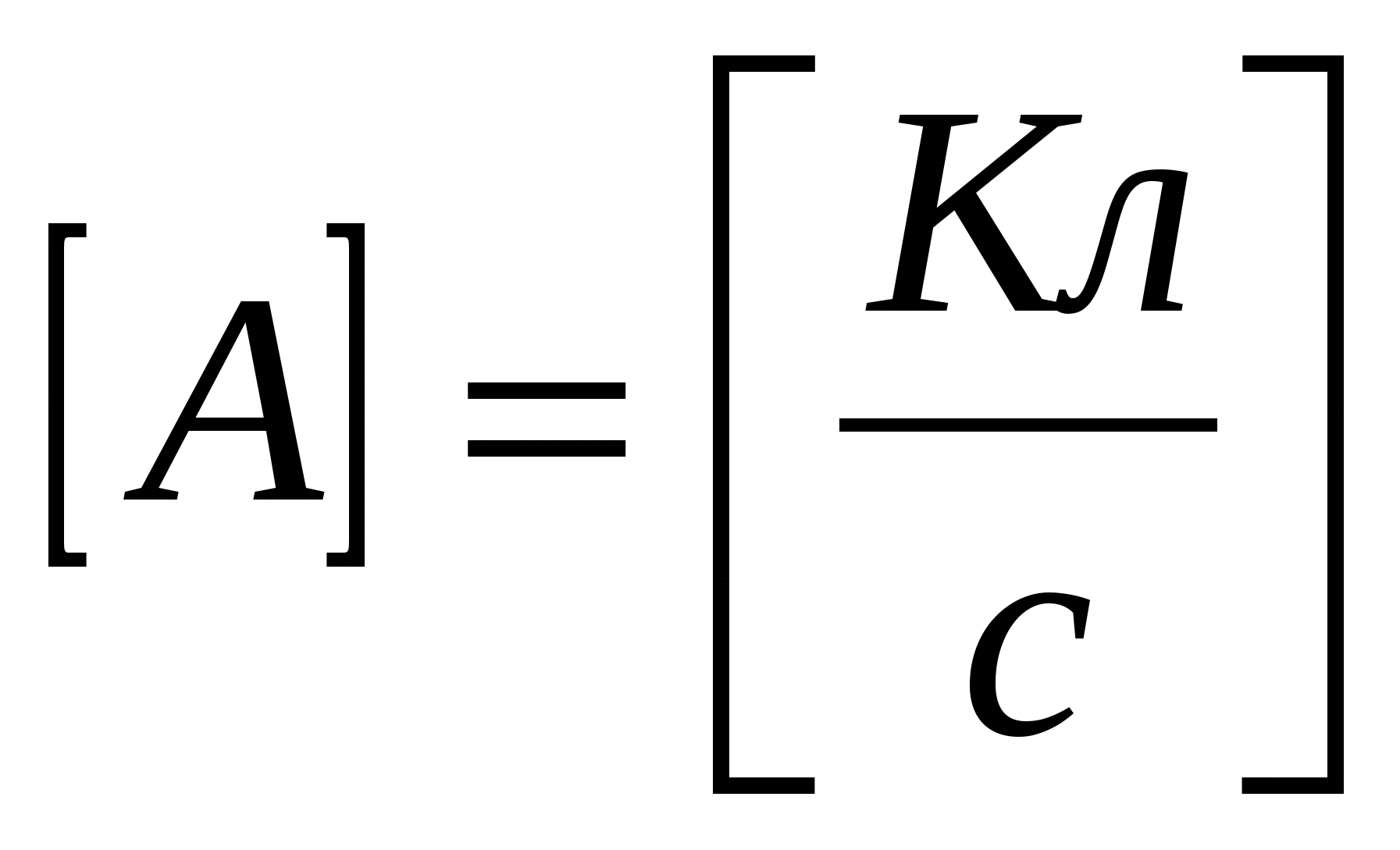
(ампер)
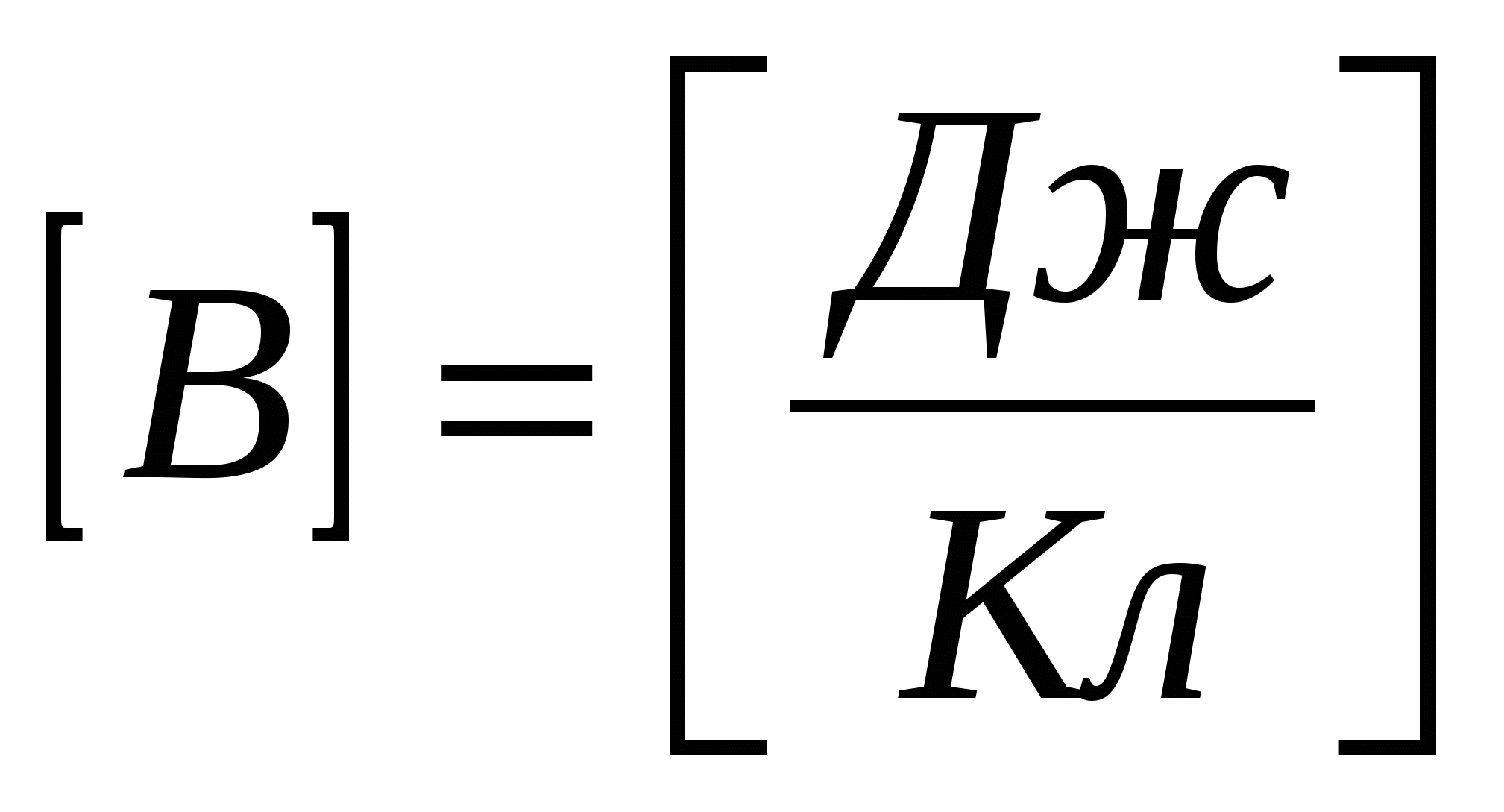
(вольт)
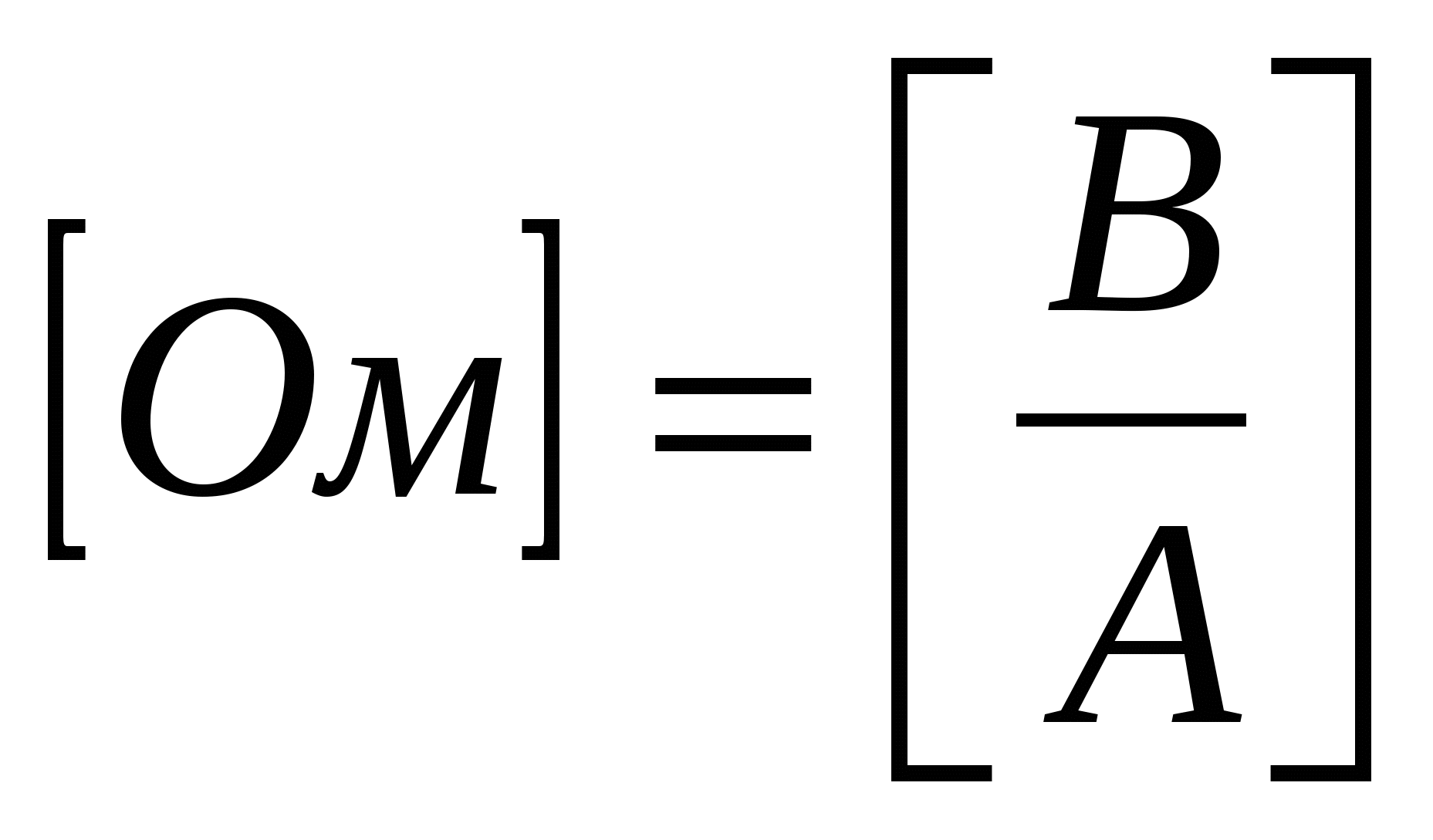
(ом)
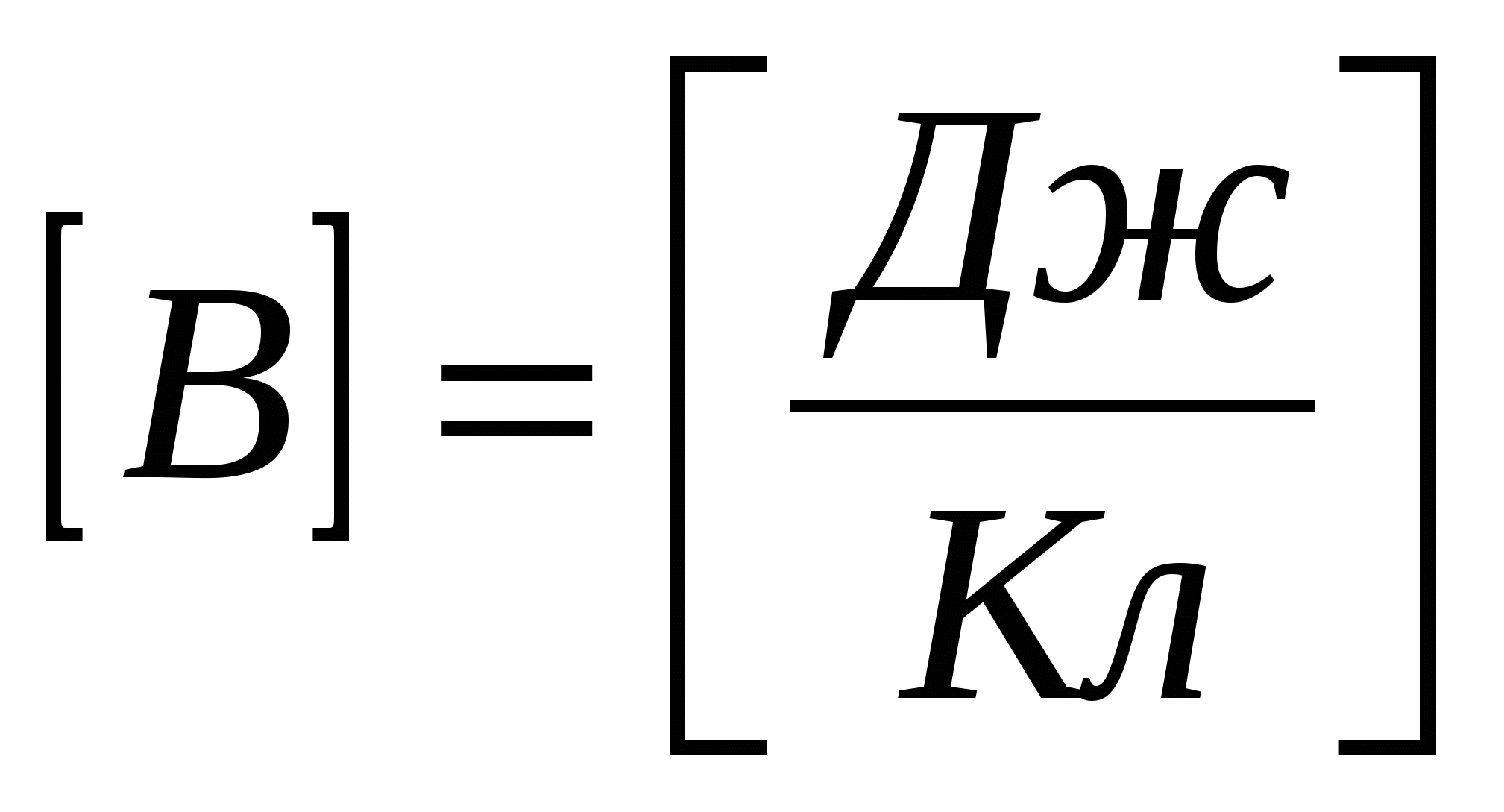
(вольт)











T —  — время
— время
q — 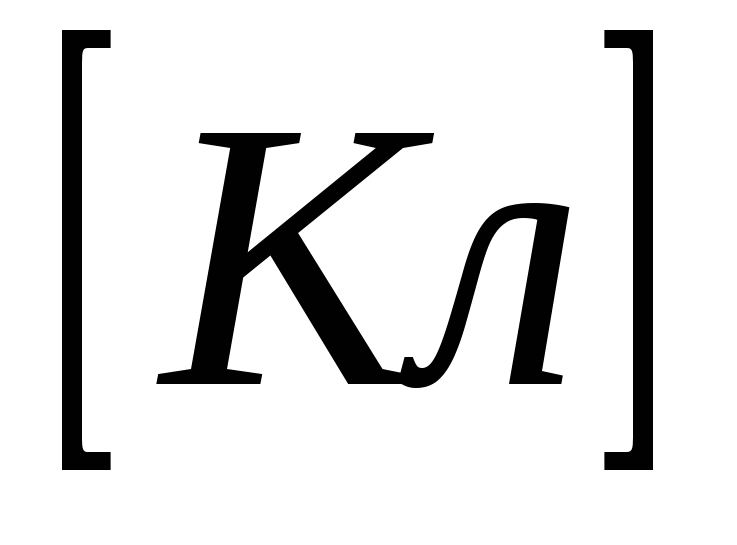 -заряд
-заряд
A – работа электрического поля по перемещению заряда.
Сопротивление зависит от материала, из которого изготовлен проводник и его геометрических размеров.
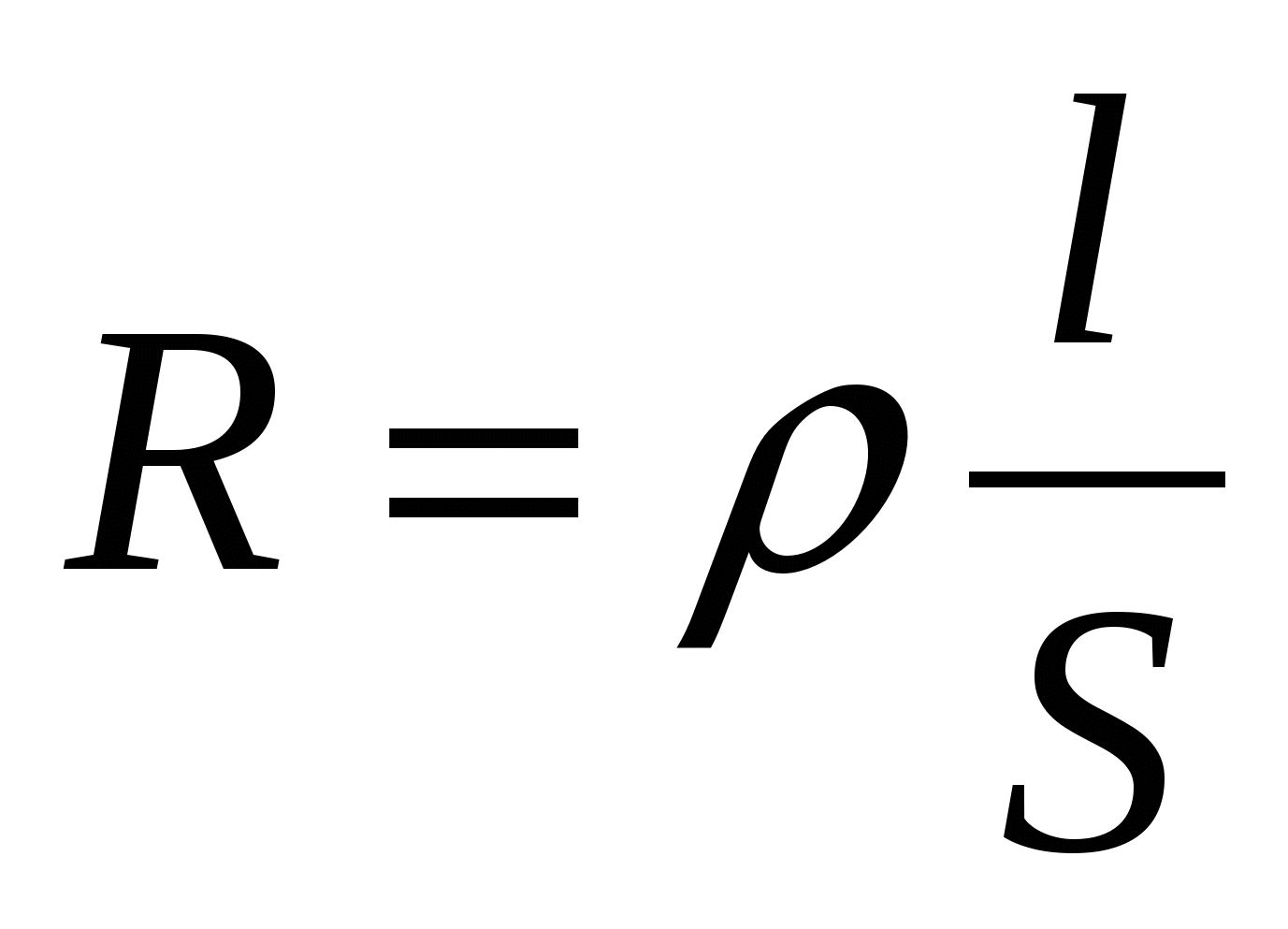
l – длина проводника
S – площадь поперечного сечения проводника
ρ – удельное сопротивление проводника
Характеризует зависимость электрической энергии в источнике от его внутреннего устройства.
(слайд 3)
III. Постановка цели.
Между величинами силой тока, напряжением и сопротивлением существует связь, которую впервые теоретически и экспериментально установил немецкий ученый Георг Ом.
Сегодня на уроке попытаемся повторить эксперименты Ома и установить закон, который носит его имя.
Тема урока: Закон Ома для участка цепи (слайд 3).
IV. Решение поставленной цели. Изучение нового материала.
(Виртуальная школа Кирилла и Мефодия, снятие вольт-амперной характеристики (интерактив))
Учебная проблема 1. ( ОК)
ОК)
(слайд 4) (слайд 5)
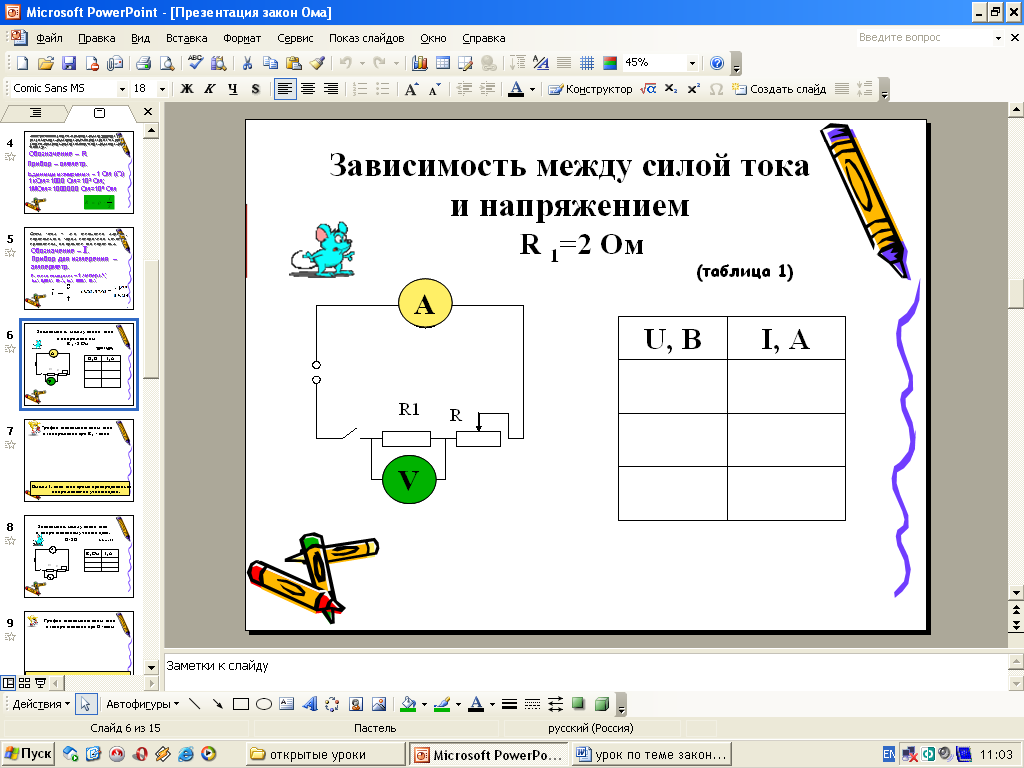
а) Соберем электрическую цепь, схема которой изображена  на слайде 3.
на слайде 3.
б) Назовите основные элементы цепи. Какие измерительные приборы включены
в цепь на участке 1и 2? Почему?
 в) Установим зависимость между силой тока и напряжением, оставляя сопротивление R1
в) Установим зависимость между силой тока и напряжением, оставляя сопротивление R1
постоянным.
Для этого с помощью реостата изменяем силу тока и фиксируем значения, которые
показывают амперметр и вольтметр соответственно. Полученные данные занесем
в таблицу 1.
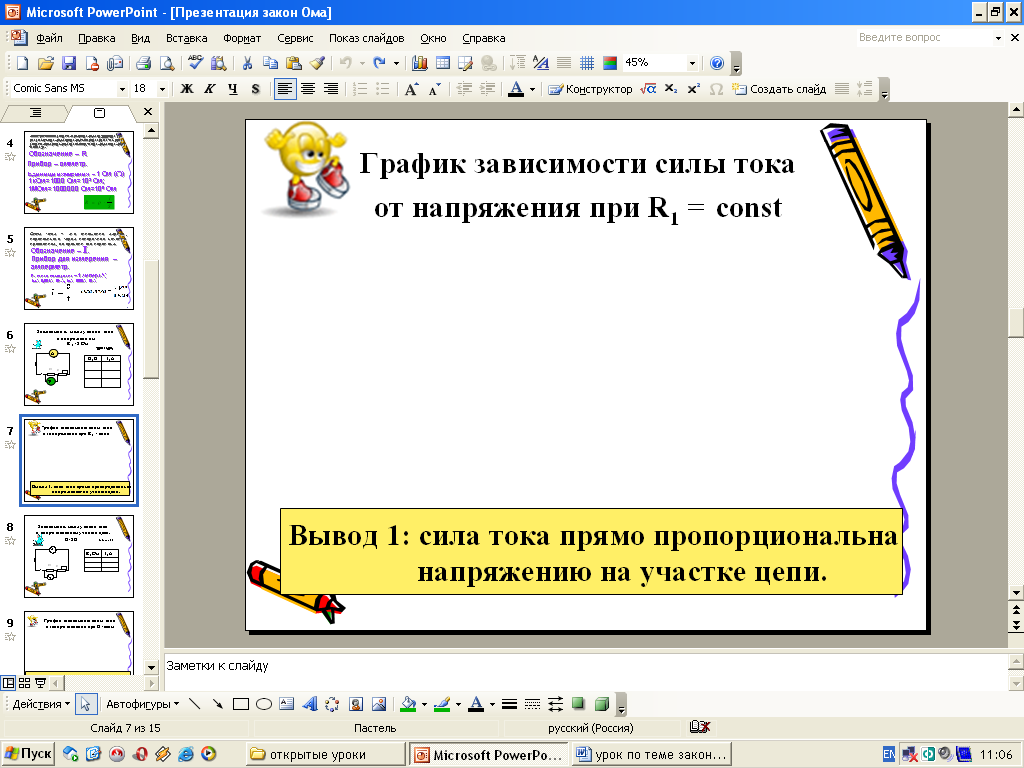
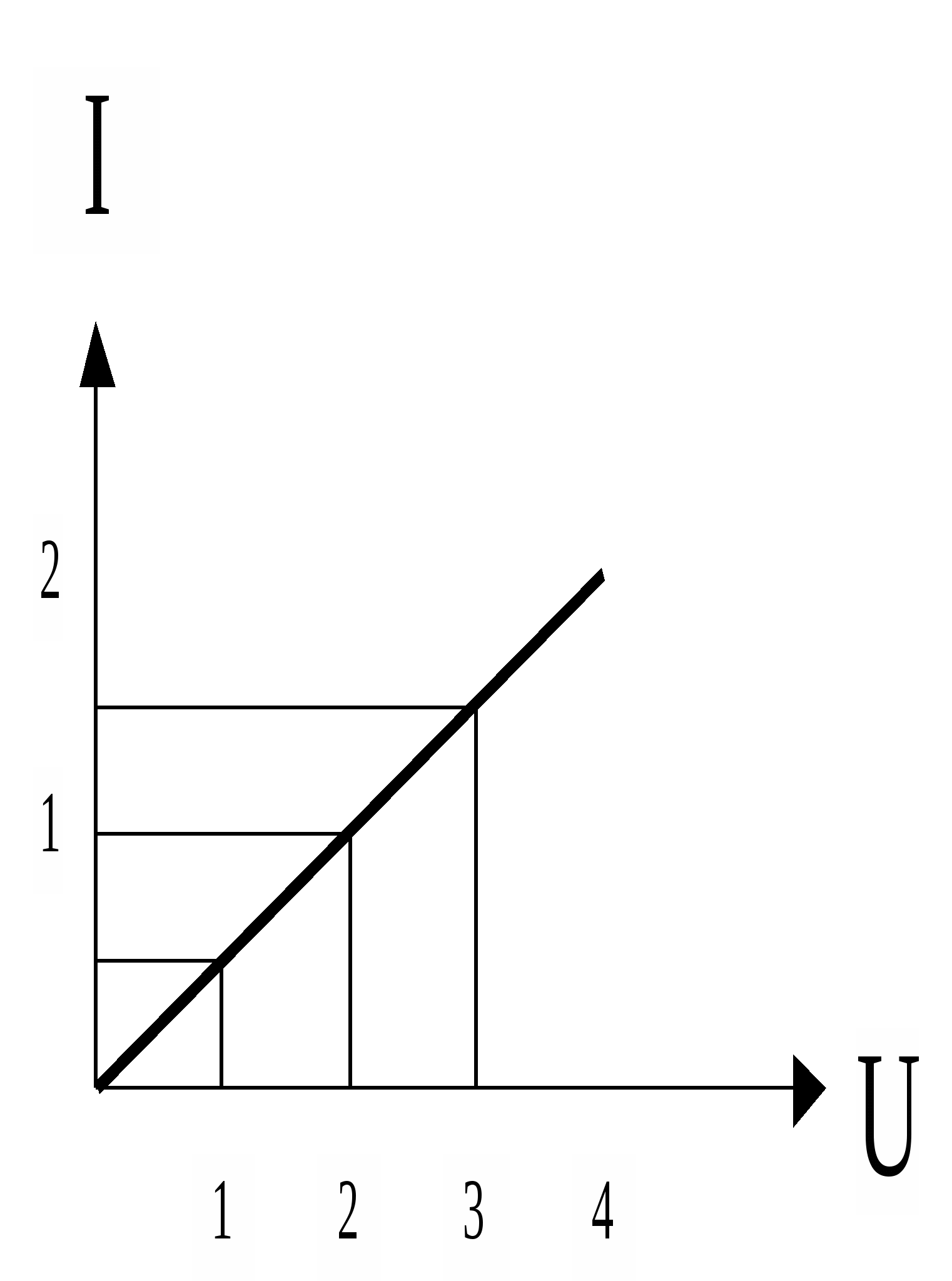
г) Изобразите полученную зависимость графически. Сделайте вывод о зависимости силы
тока от напряжения на участке цепи?
Вывод 1: сила тока прямо пропорциональна напряжению на участке цепи.
У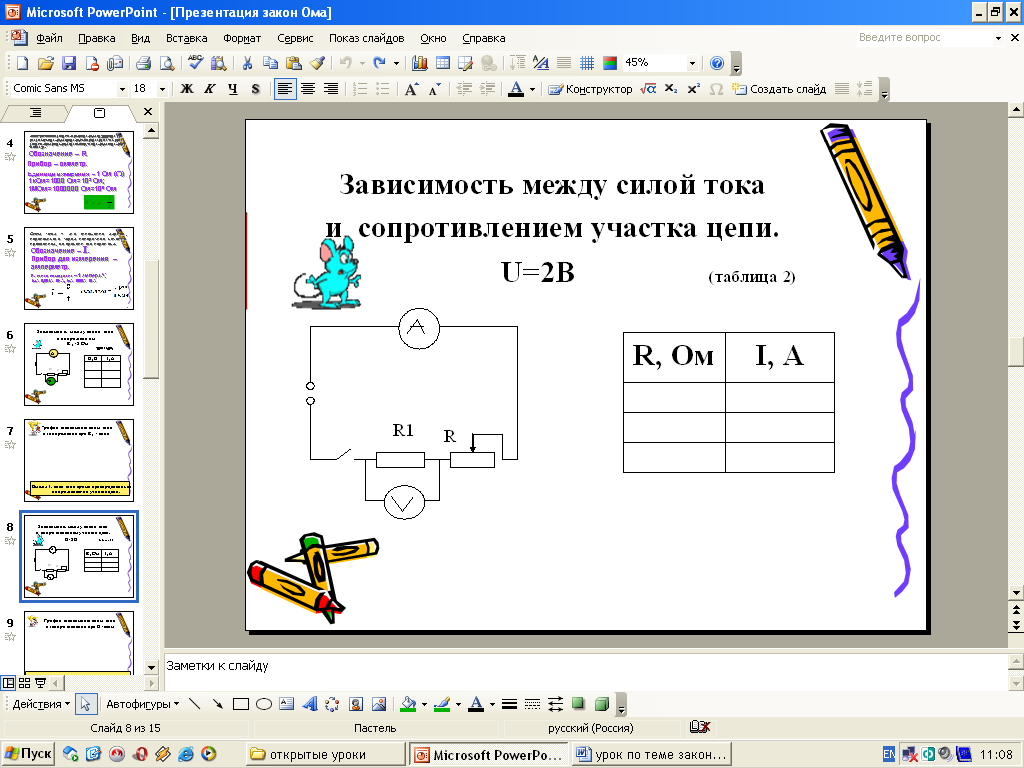
 чебная проблема 2.
чебная проблема 2. 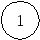 (ОК)
(ОК)
(слайд 6) (слайд 7)
а) Установим зависимость между силой тока и сопротивлением участка цепи R1.
Для этого будем изменять сопротивление R1, поддерживая при помощи реостата R
напряжение на концах проводника постоянным.
Полученные данные занесем в таблицу 2.
б) Изобразите полученную зависимость графически. Сделайте вывод о зависимости силы
тока от сопротивления участка цепи?
Вывод 2: сила тока обратно пропорциональна сопротивлению участка цепи.
Учитель: Объедините полученные выводы и сделайте общий вывод о зависимости между силой тока, напряжением и сопротивлением.
Ученик: сила тока в цепи прямо пропорциональна напряжению и обратно
пропорциональна сопротивлению.
Учитель: Зависимость силы тока от напряжения на концах участка цепи и сопротивления этого участка называется законом Ома, который установил его в 1827 году.
(слайд 8)
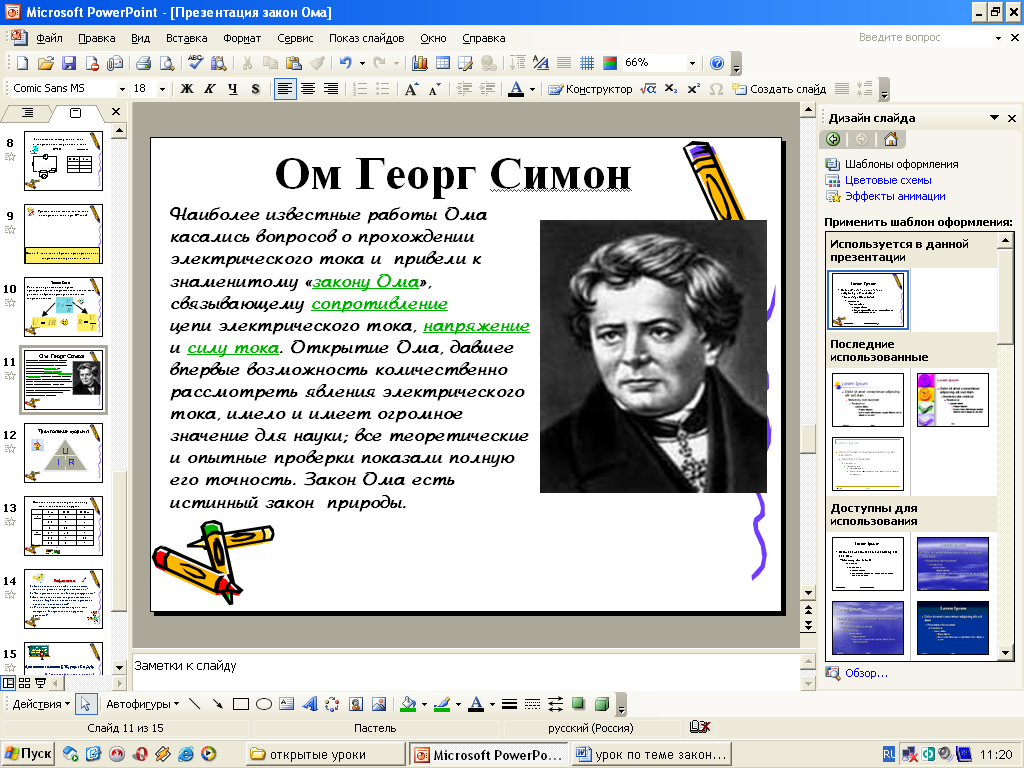
Ом Георг Симон
16 марта 1787 года — 6 июля 1854 года
Начало формы
Конец формы
История жизни
Замечательный немецкий физик Георг Симон Ом (1787-1854), чье имя носит знаменитый закон электротехники и единица электрического сопротивления, родился 16марта 1789 г. в Эрлангене (федеральная земля Бавария). Его отец был известным в городе мастером-механиком. Мальчик Ом помогал отцу в мастерской и многому у него научился. Быть бы ему механиком и продолжать дело отца, но Ом был честолюбив, хотел стать ученым и работать в лучших германских университетах. Он поступил учиться в университет в Эрлангене и закончил его в 1813 г. Его первая работа — учитель физики и математики реальной школы в Бамберге.
После нескольких лет работы в школе мечта Ома осуществилась. В 1817 г. он стал профессором математики Иезуитского колледжа в Кельне. Здесь Ом занялся исследованиями в области электричества, используя батарею Вольта. Ом составлял электрические цепи из проводников различной толщины, из различных материалов, различной длины (причем проволоку он протягивал сам, используя собственную технологию), пытаясь понять законы этих цепей.Сложность его работы можно понять, вспомнив, что никаких измерительных приборов еще не было и о силе тока в цепи можно было судить по различным косвенным эффектам. Ому очень пригодились те навыки работы, которые он приобрел, работая в мастерской с отцом. А еще ему очень пригодилось упорство, ибо эксперименты шли в течение 9 лет.
Для характеристики проводников Ом в1820 г. ввел понятие «сопротивление», ему казалось, что проводник сопротивляется току. По-английски и по-французски сопротивление называется resistance, поэтому современный схемный элемент называется резистором, а первая буква R с легкой руки Ома до сих пор используется как обозначение резистора в схемах. В 1827 г. вышел основополагающий труд Ома «Математическое исследование гальванических цепей», в котором и был сформулирован знаменитый закон Ома.
Казалось бы, столь простая математическая формула, которую сейчас изучают в школах, должна заслужить всеобщее признание, но получилось наоборот. Коллеги приняли в штыки выводы Ома, начались насмешки над ним. Обиженный Ом уволился из колледжа в Кельне. В последующие годы Ом жил в бедности, работая частным учителем в Берлине. Только в 1833 г. ему удалось устроиться на работу в Политехническую школу в Нюрнберге.
Тем временем за границей признали важность работ Ома. В 1841 г. Британское Королевское общество наградило его золотой медалью, а в 1842 г. избрало Ома своим действительным членом. Наконец, в1849 г. Ом стал профессором Мюнхенского университета. Всего 5 лет он имел возможность полноценно работать и преподавать. 7 июля 1854 г. Георг Симон Ом скончался.
В 1893 г. Международный электротехнический конгресс принял решение ввести единицу электрического сопротивления и назвал ее именем Георга Симона Ома, подчеркнув тем самым важность его открытия для электротехники.
Опорный конспект
З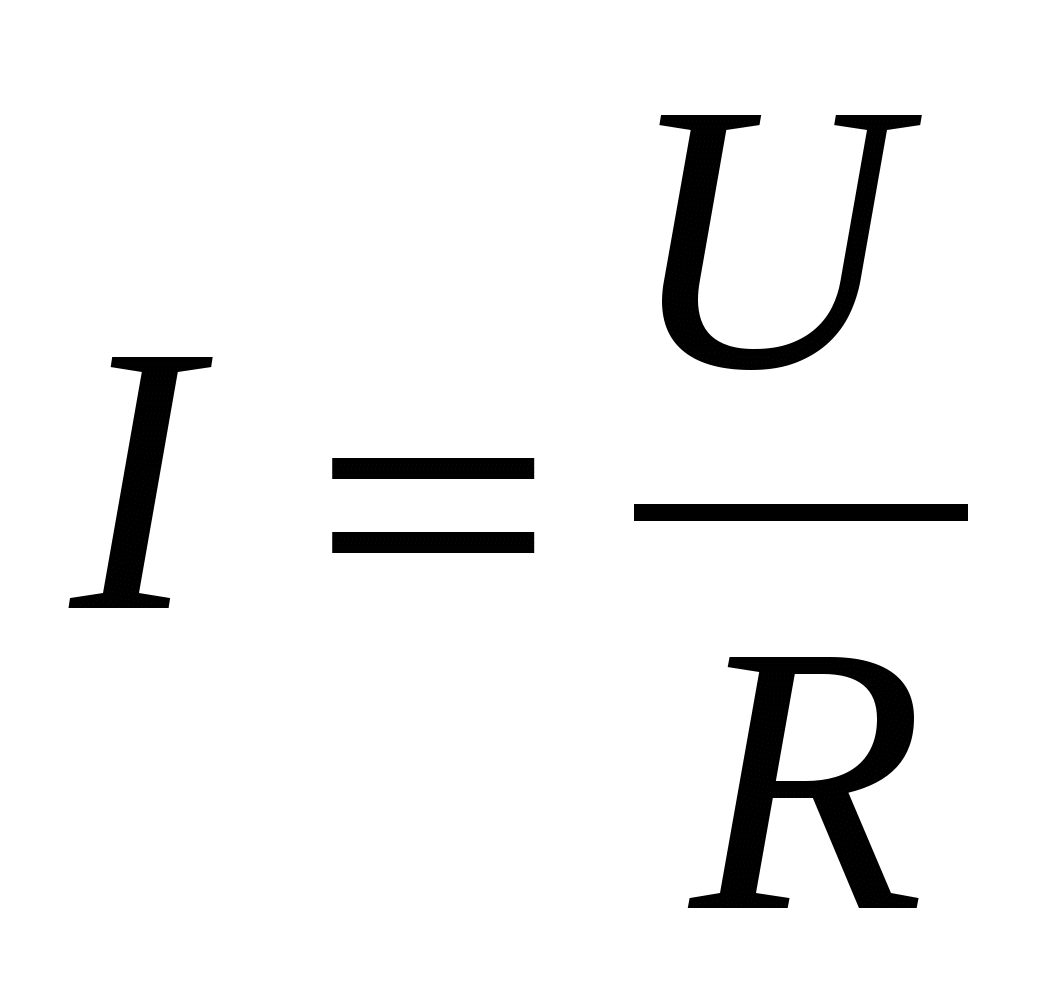 акон Ома читается так: сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
акон Ома читается так: сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
где I – сила тока в цепи;
U – напряжение на этом участке;
R – сопротивление участка.
Этот закон выражает зависимость между тремя величинами, зная две из них всегда можно найти третью неизвестную величину.
Выразите из формулы закона Ома напряжение и сопротивление.
(слайд 9)
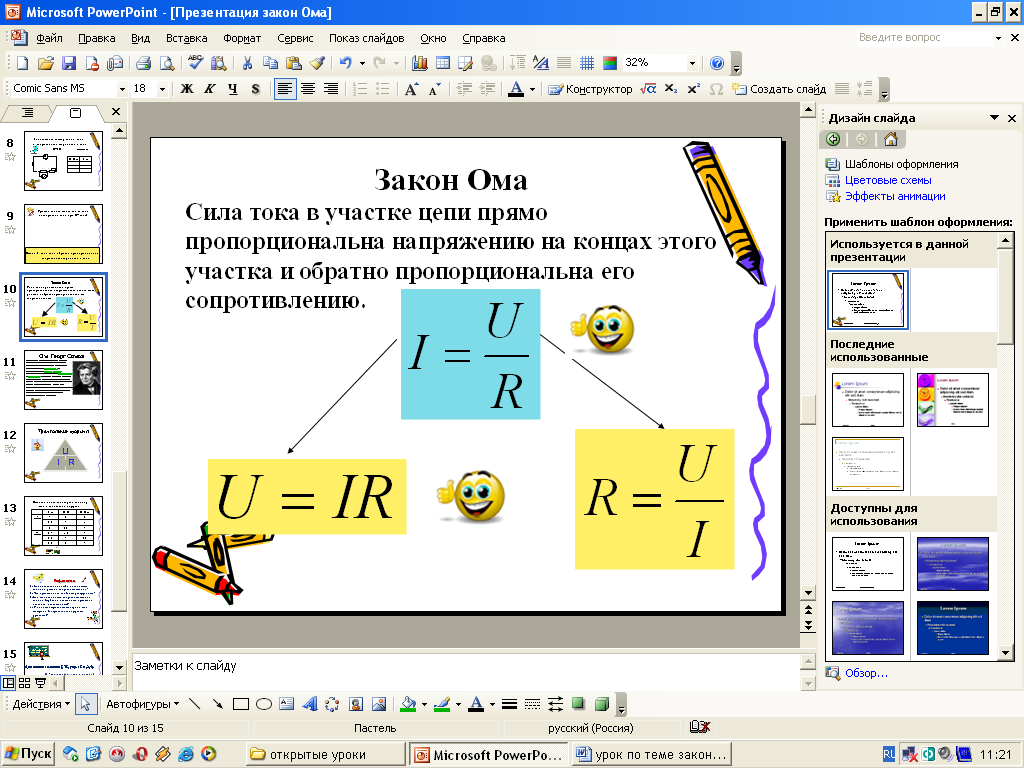
Учитель: запишите эти формулы и запомните их. Мы будем ими пользоваться при решении задач.
А теперь скажите, верно ли утверждение, что сопротивление проводника прямо пропорционально напряжению на этом проводнике и обратно пропорционально силе тока в нем?
Ученик: сопротивление проводника можно вычислить по формуле 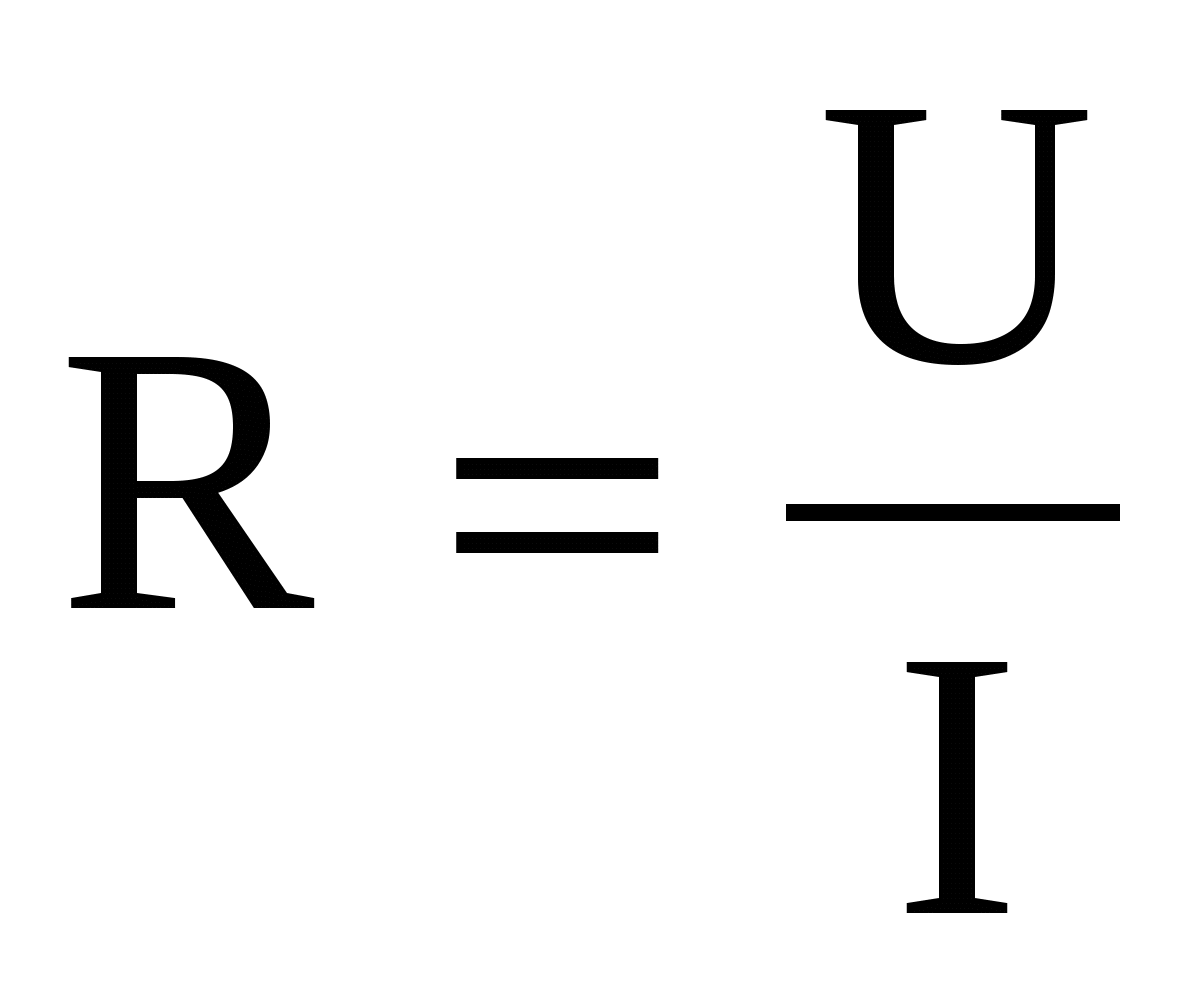 , однако, оно постоянно для данного проводника и не зависит ни от напряжения, ни от силы тока в нем.
, однако, оно постоянно для данного проводника и не зависит ни от напряжения, ни от силы тока в нем.
Учитель: верно, сопротивление – это физическая величина, характеризующая свойства данного проводника, оно не зависит ни от напряжения, ни от силы тока в проводнике. Изменение напряжения на участке цепи влечет за собой изменение силы тока, но отношение U/I остается для данного проводника постоянным.
V. Выводы:
Cила тока прямо пропорциональна напряжению на участке цепи.
Сила тока обратно пропорциональна сопротивлению участка цепи.
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.

Сопротивление – это физическая величина, характеризующая способность проводника ограничивать силу тока, оно не зависит ни от напряжения, ни от силы тока в проводнике.
VI. Закрепление материала.
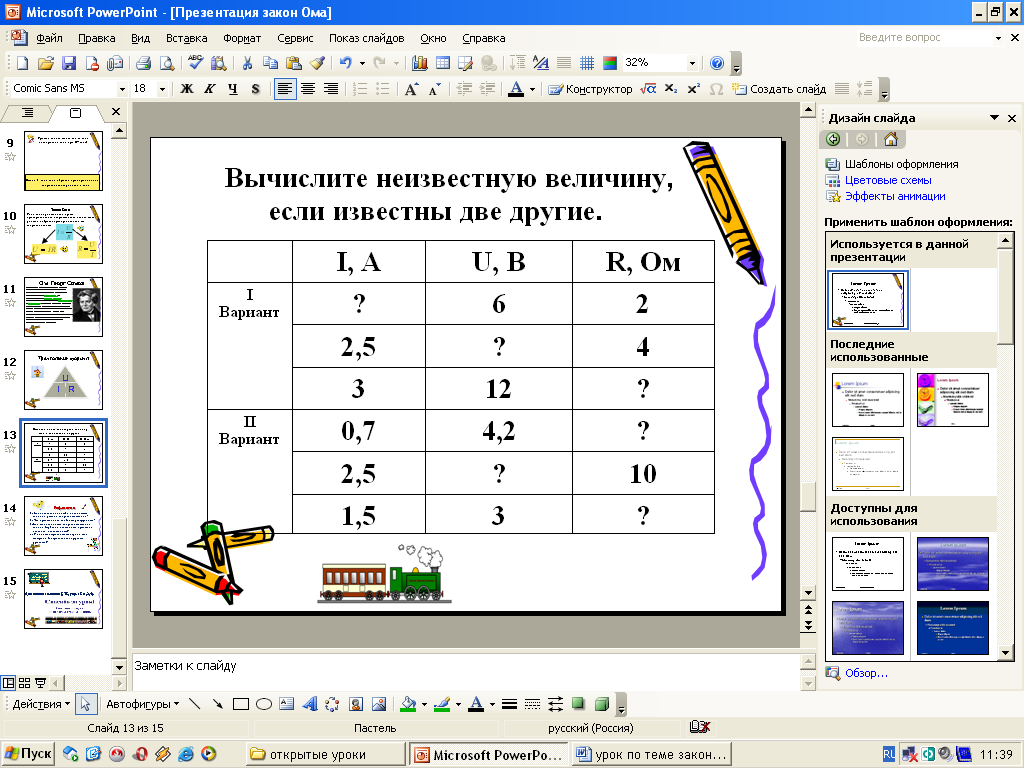
Вычислите неизвестную величину, если известны две другие.
(слайд 10)


 ;
(1-24)
;
(1-24)