| Величина | Формула | Обозначение и единица измерения | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Закон Ома для цепи переменного тока с реактивным сопротивлением | U = I·Z I = U / Z |
I— ток в цепи, А; U — напряжение в цепи, В; Z — полное сопротивление цепи, Ом |
|||||||
| Соотношение токов и напряжений в трехфазной системе: соединение в звезду | Iл = Iф Uл = √3·Uф |
Iл, Iф
— линейный и фазный ток, А; Uл, Uф — линейное и фазное напряжение, В |
|||||||
| Соотношение токов и напряжений в трехфазной системе: соединение в треугольник | Iл = √3·Iф Uл = Uф |
||||||||
| Распределение тока в двух параллельных ветвях цепи переменного тока | I1, I2 — ток
первой и второй ветвей, А; z1, z2 — сопротивления первой и второй ветвей, Ом |
||||||||
| Коэффициент мощности |
|
r — активное сопротивление, Ом; Z — полное сопротивление, Ом; P — активная мощность, Вт; S — кажущаяся (полная) мощность, В·А |
|||||||
| Мощность в цепи постоянного тока | P = UI P = I2R P = U2 / R |
U — напряжение, В; I — ток, А; R — сопротивление, Ом; |
|||||||
| Мощность в цепи переменного тока: однофазного | P = UIcosφ Q = UIsinφ
|
P — активная мощность, Вт; Q — реактивная мощность, вар; S — кажущаяся (полная) мощность, В·А; Iл, Iф — линейный и фазный ток, А; Uл, Uф — линейное и фазное напряжение, В |
|||||||
| Мощность в цепи переменного тока:
трехфазного [независимо от схемы соединения (звезда или треугольник) для симметричной трехфазной цепи] |
P = 3UфIфcosφ
= √3UлIл Q = 3UфIфsinφ = √3UлIлsinφ S = 3UфIф = √3UлIл |
||||||||
| Мощность в цепи переменного тока: трехфазного [независимо от схемы соединения для трехфазной цепи при неравномерной нагрузке] |
|
||||||||
| Энергия в цепи постоянного тока | W — энергия, Вт·ч; t — время, ч |
||||||||
| Энергия в цепи переменного тока: однофазного | Wa = UIcosφ t = Pt Wp = UIsinφ t = Qt |
Wa — активная энергия,
Втч; Wp — реактивная энергия, варч; t — время, ч |
|||||||
| Энергия в цепи переменного тока: трехфазного | Wa = √3UIcosφ t = Pt Wp = √3UIsinφ t = Qt |
||||||||
| Формула | Обозначение и единица измерения |
Расчет трехфазных цепей (Лекция №17)
Трехфазные цепи являются разновидностью цепей синусоидального тока, и, следовательно, все рассмотренные ранее методы расчета и анализа в символической форме в полной мере распространяются на них. Анализ трехфазных систем удобно осуществлять с использованием векторных диаграмм, позволяющих достаточно просто определять фазовые сдвиги между переменными. Однако определенная специфика многофазных цепей вносит характерные особенности в их расчет, что, в первую очередь, касается анализа их работы в симметричных режимах.
Многофазный приемник и вообще многофазная цепь называются симметричными, если в них комплексные сопротивления соответствующих фаз одинаковы, т.е. если . В противном случае они являются несимметричными. Равенство модулей указанных сопротивлений не является достаточным условием симметрии цепи. Так, например трехфазный приемник на рис. 1,а является симметричным, а на рис. 1,б – нет даже при условии: .
Если к симметричной трехфазной цепи приложена симметричная трехфазная система напряжений генератора, то в ней будет иметь место симметричная система токов. Такой режим работы трехфазной цепи называется
Так для симметричного режима работы цепи на рис. 2,а при известных линейном напряжении и сопротивлениях фаз можно записать
,
где определяется характером нагрузки .
Тогда на основании вышесказанного
;
.
Комплексы линейных токов можно найти с использованием векторной диаграммы на рис. 2,б, из которой вытекает:
При анализе сложных схем, работающих в симметричном режиме, расчет осуществляется с помощью двух основных приемов:
Все треугольники заменяются эквивалентными звездами. Поскольку треугольники симметричны, то в соответствии с формулами преобразования «треугольник-звезда» .
Так как все исходные и вновь полученные звезды нагрузки симметричны, то потенциалы их нейтральных точек одинаковы. Следовательно, без изменения режима работы цепи их можно (мысленно) соединить нейтральным проводом. После этого из схемы выделяется базовая фаза (обычно фаза А), для которой и осуществляется расчет, по результатам которого определяются соответствующие величины в других фазах.
Пусть, например, при заданном фазном напряжении необходимо определить линейные токи и в схеме на рис. 3, все сопротивления в которой известны.
В соответствии с указанной методикой выделим расчетную фазу А, которая представлена на рис. 4. Здесь , .
Тогда для тока можно записать
,
и соответственно .
Расчет несимметричных режимов работы трехфазных систем
Если хотя бы одно из условий симметрии не выполняется, в трехфазной цепи имеет место несимметричный режим работы. Такие режимы при наличии в цепи только статической нагрузки и пренебрежении падением напряжения в генераторе рассчитываются для всей цепи в целом любым из рассмотренных ранее методов расчета. При этом фазные напряжения генератора заменяются соответствующими источниками ЭДС. Можно отметить, что, поскольку в многофазных цепях, помимо токов, обычно представляют интерес также потенциалы узлов, чаще других для расчета сложных схем применяется метод узловых потенциалов. Для анализа несимметричных режимов работы трехфазных цепей с электрическими машинами в основном применяется метод симметричных составляющих, который будет рассмотрен далее.
При заданных линейных напряжениях наиболее просто рассчитываются трехфазные цепи при соединении в треугольник. Пусть в схеме на рис. 2,а . Тогда при известных комплексах линейных напряжений в соответствии с законом Ома
; ; .
По найденным фазным токам приемника на основании первого закона Кирхгофа определяются линейные токи:
.
Обычно на практике известны не комплексы линейных напряжений, а их модули. В этом случае необходимо предварительное определение начальных фаз этих напряжений, что можно осуществить, например, графически. Для этого, приняв , по заданным модулям напряжений, строим треугольник (см. рис.5), из которого (путем замера) определяем значения углов a и b.
Тогда
Искомые углы a и b могут быть также найдены аналитически на основании теоремы косинусов:
При соединении фаз генератора и нагрузки в звезду и наличии нейтрального провода с нулевым сопротивлением фазные напряжения нагрузки равны соответствующим напряжениям на фазах источника. В этом случае фазные токи легко определяются по закону Ома, т.е. путем деления известных напряжений на фазах потребителя на соответствующие сопротивления. Однако, если сопротивление нейтрального провода велико или он отсутствует, требуется более сложный расчет.
Рассмотрим трехфазную цепь на рис. 6,а. При симметричном питании и несимметричной нагрузке ей в общем случае будет соответствовать векторная диаграмма напряжений (см. рис. 6,б), на которой нейтральные точки источника и приемника занимают разные положения, т.е. .
Разность потенциалов нейтральных точек генератора и нагрузки называется напряжением смещения нейтральной точки (обычно принимается, что ) или просто напряжением смещения нейтрали. Чем оно больше, тем сильнее несимметрия фазных напряжений на нагрузке, что наглядно иллюстрирует векторная диаграмма на рис. 6,б.
Для расчета токов в цепи на рис. 6,а необходимо знать напряжение смещения нейтрали. Если оно известно, то напряжения на фазах нагрузки равны:
.
Тогда для искомых токов можно записать:
.
Соотношение для напряжения смещения нейтрали, записанное на основании метода узловых потенциалов, имеет вид
| . | (1) |
При наличии нейтрального провода с нулевым сопротивлением , и из (1) . В случае отсутствия нейтрального провода . При симметричной нагрузке с учетом того, что , из (1) вытекает .
В качестве примера анализа несимметричного режима работы цепи с использованием соотношения (1) определим, какая из ламп в схеме на рис. 7 с прямым чередованием фаз источника будет гореть ярче, если .
Запишем выражения комплексных сопротивлений фаз нагрузки:
Тогда для напряжения смещения нейтрали будем иметь
Напряжения на фазах нагрузки (здесь и далее индекс N у фазных напряжений источника опускается)
Таким образом, наиболее ярко будет гореть лампочка в фазе С.
В заключение отметим, что если при соединении в звезду задаются линейные напряжения (что обычно имеет место на практике), то с учетом того, что сумма последних равна нулю, их можно однозначно задать с помощью двух источников ЭДС, например, и . Тогда, поскольку при этом , соотношение (1) трансформируется в формулу
| . | (2) |
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- Какой многофазный приемник является симметричным?
- Какой режим работы трехфазной цепи называется симметричным?
- В чем заключается специфика расчета симметричных режимов работы трехфазных цепей?
- С помощью каких приемов трехфазная симметричная схема сводится к расчетной однофазной?
- Что такое напряжение смещения нейтрали, как оно определяется?
- Как можно определить комплексы линейных напряжений, если заданы их модули?
- Что обеспечивает нейтральный провод с нулевым сопротивлением?
- В цепи на рис. 6,а ; ; ; . Линейное напряжение равно 380 В.
- В схеме предыдущей задачи ; . Остальные параметры те же.
- В задаче 8 нейтральный провод оборван.
- В задаче 9 нейтральный провод оборван.
Определить ток в нейтральном проводе.
Ответ: .
Определить ток в нейтральном проводе.
Ответ: .
Определить фазные напряжения на нагрузке.
Ответ: ; ; .
Определить фазные напряжения на нагрузке.
Ответ: ; ; .
4.5. Расчет трехфазных цепей соединением треугольник
П
Рис. 3. 11. 3.12.
ри соединении треугольником (рис. 4.11.) каждая фаза приемника подключена к двум линейным проводам, поэтому каждое фазное напряжение равно соответствующему линейному напряжению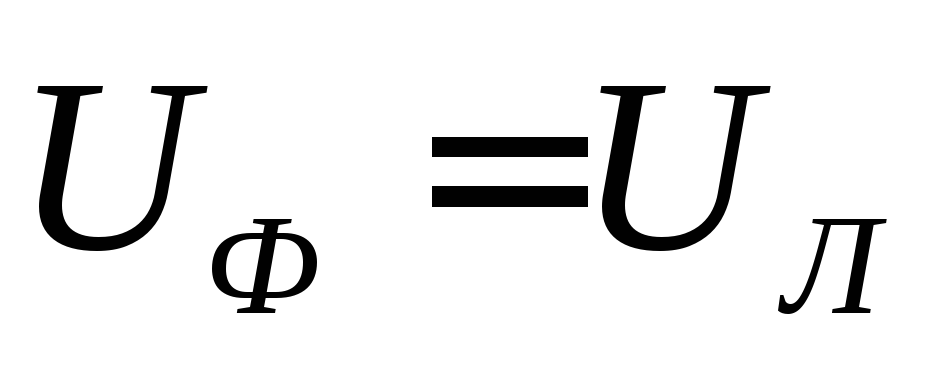 .
.Таким образом, соединение треугольником следует применять тогда, когда каждая фаза трехфазного приемника рассчитана на напряжение, равное номинальному линейному напряжению сети.
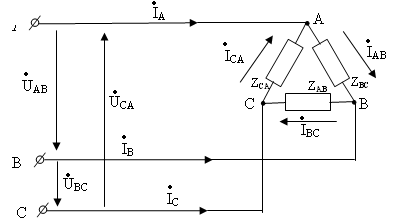
Рис. 4.11.
Фазные токи 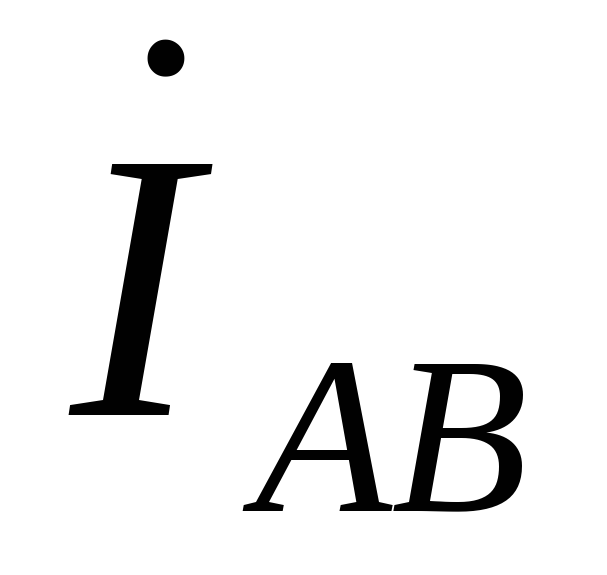 ,
,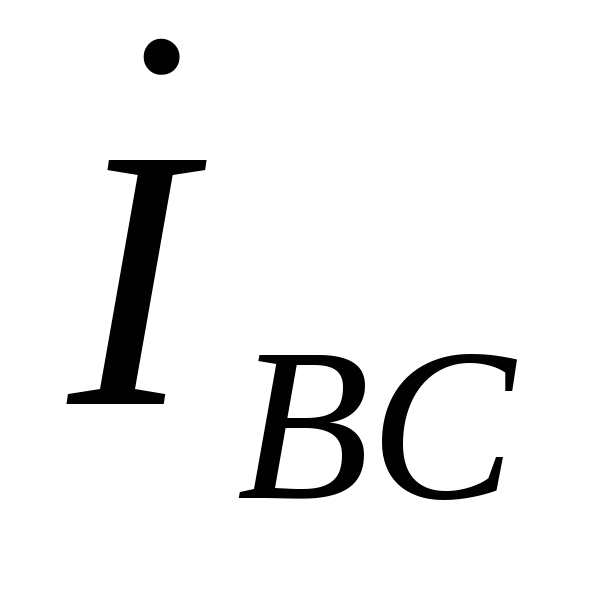 ,
, в общем случае не равны линейным токам
в общем случае не равны линейным токам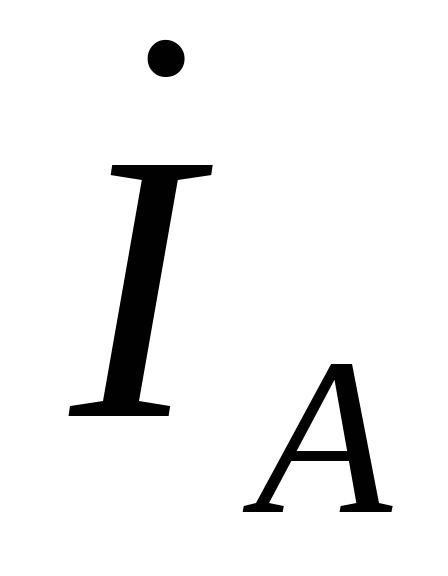 ,
,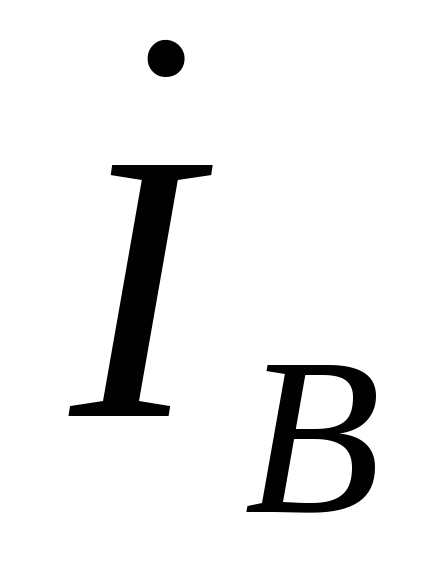 ,
,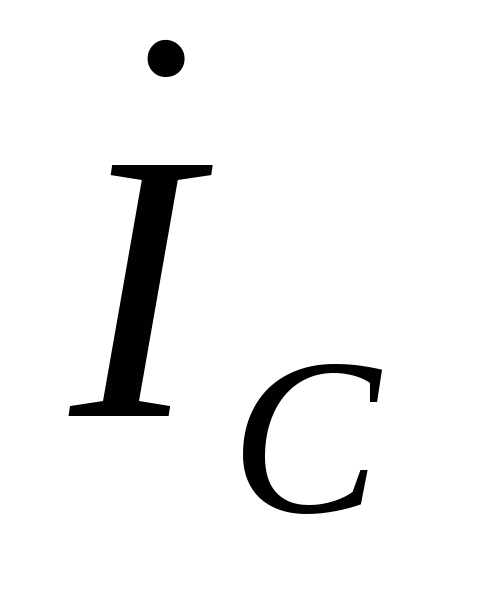 и могут быть найдены по следующим
соотношениям:
и могут быть найдены по следующим
соотношениям:
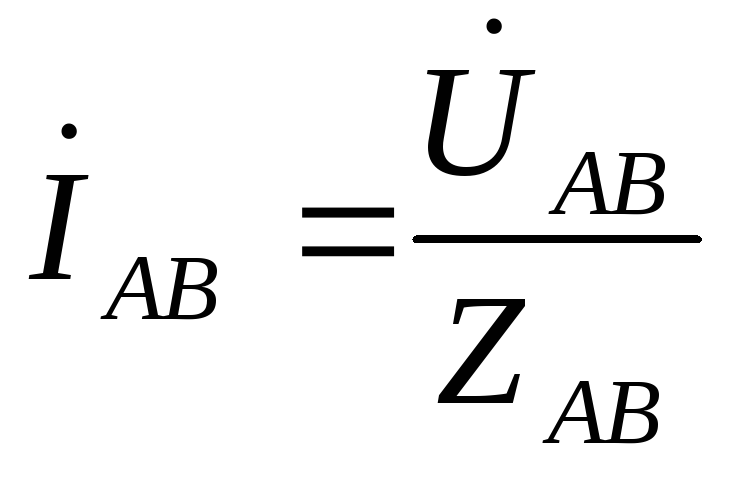 ,
, 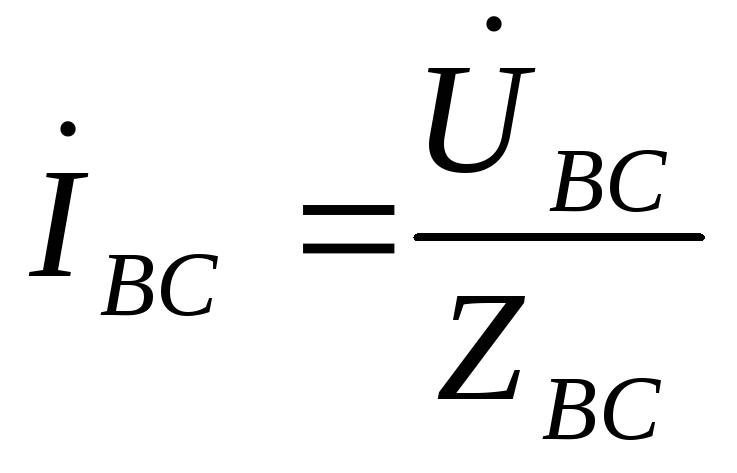 ,
,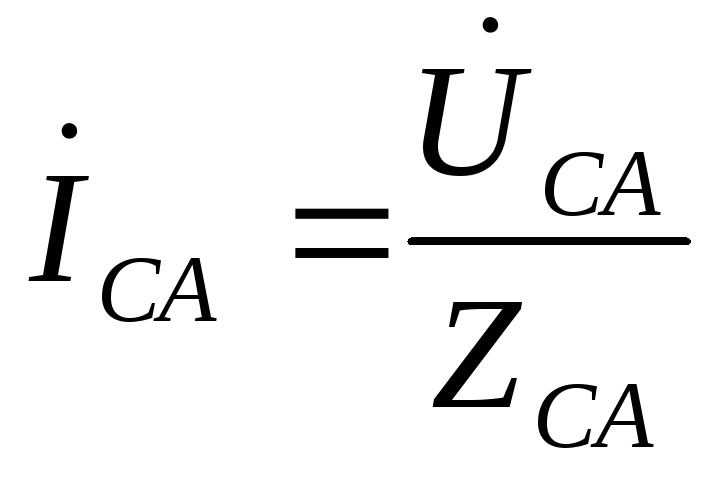 .
.
Линейные токи 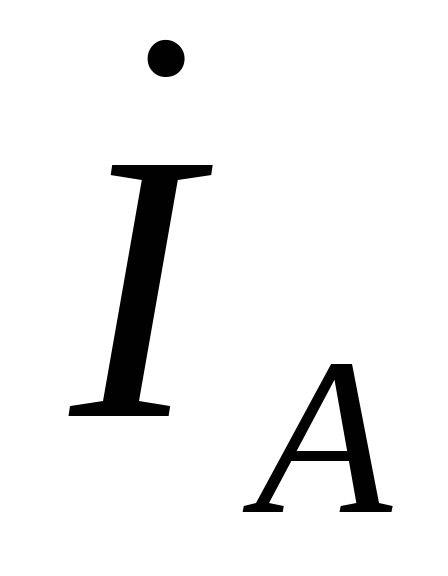 ,
,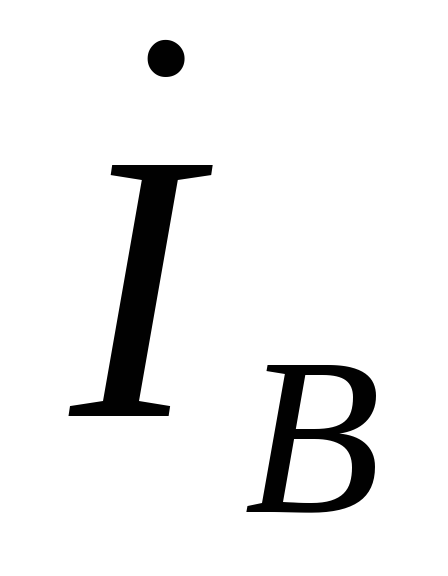 ,
,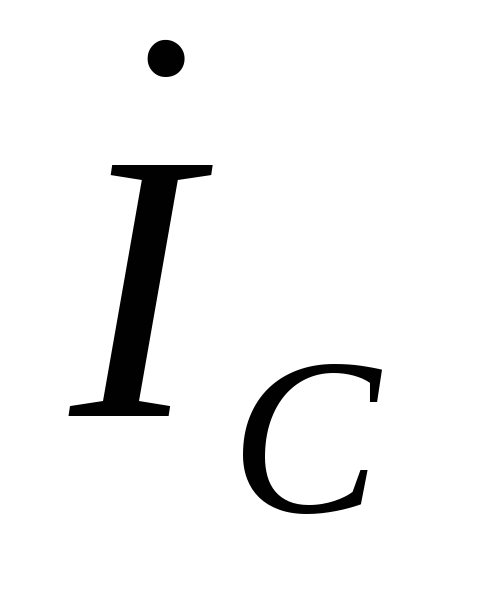 могут быть определены через значения
фазных токов. Из первого закона Кирхгофа
запишем:
могут быть определены через значения
фазных токов. Из первого закона Кирхгофа
запишем:
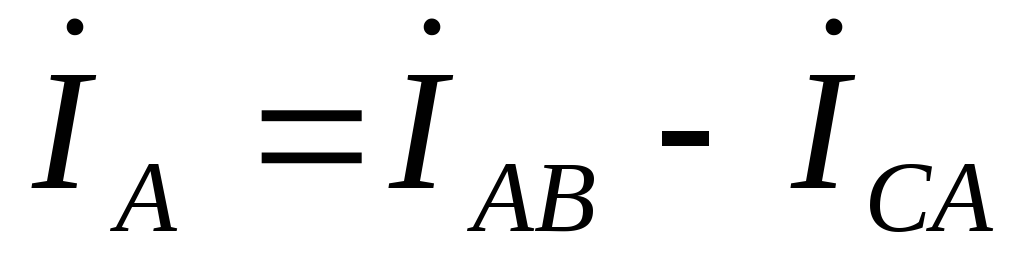 ,
, 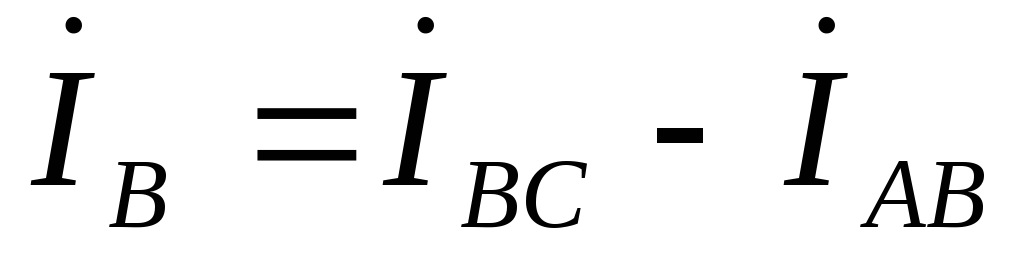 ,
, .
.
Использую указанные соотношения и имея векторы фазных токов, можно построить векторную диаграмму линейных токов (рис. 4.12.).
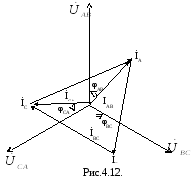
При симметричной
нагрузке соединением «треугольник»
равны в отдельности активные и полные
реактивные сопротивления всех фаз 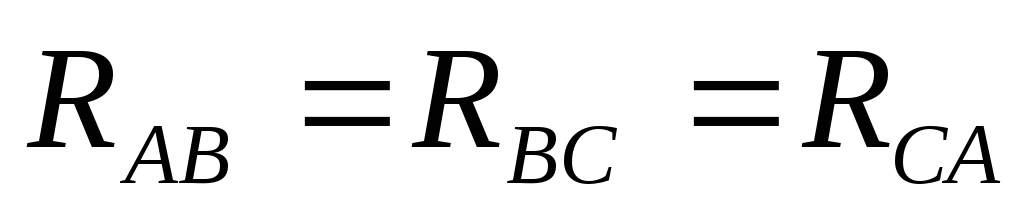 ,
,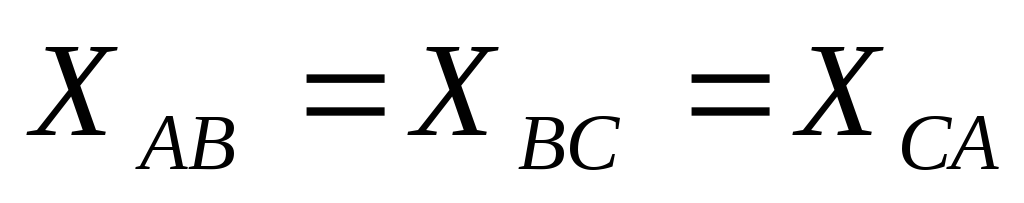
Однако, как правило,
однофазные приемники подключаются не
одновременно. Нагрузку можно считать
симметричной лишь тогда, когда включены
все приемники. Для каждой фазы могут
быть использованы все методы расчета,
рассмотренные ранее применительно к
однофазной цепи с одним источником.
Зная, например, фазные напряжения и
сопротивления, можно по закону Ома найти
фазные токи по формулам 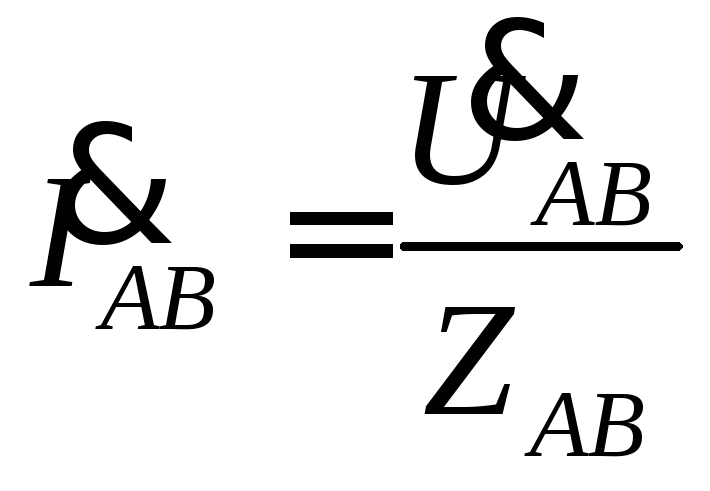 ,
,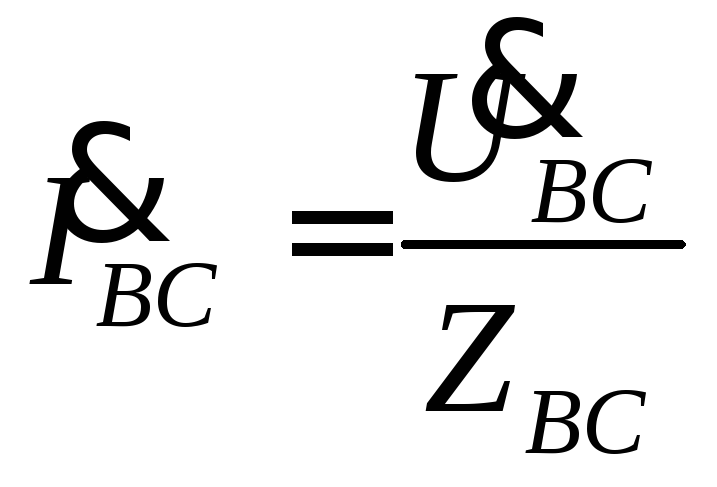 ,
,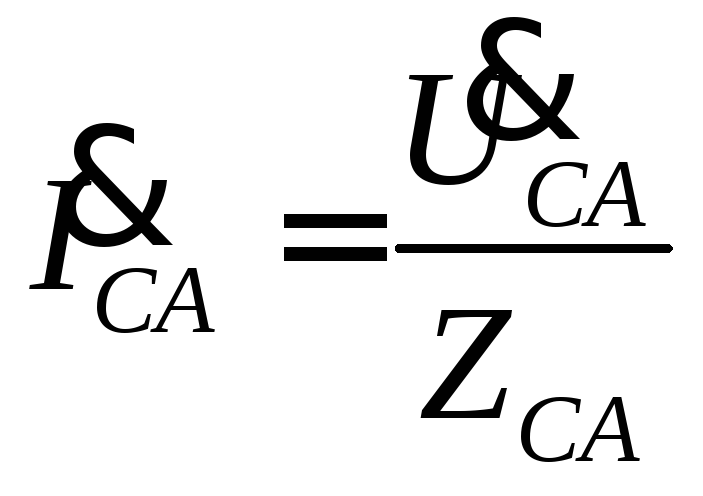
При симметричной
нагрузке, 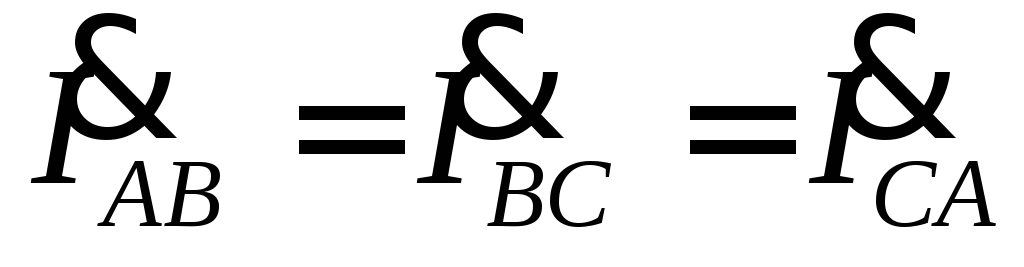 ,
,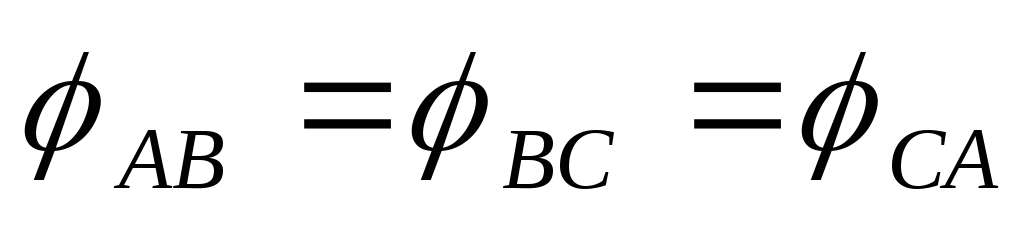 -фазные токи равны друг другу и сдвинуты
по фазе относительно соответствующих
фазных напряжений на одинаковые углы.
-фазные токи равны друг другу и сдвинуты
по фазе относительно соответствующих
фазных напряжений на одинаковые углы.
В
Рис. 3. 13.
екторная диаграмма фазных напряжений и токов на рис. 4.13. показывает, что при симметричной нагрузке векторы фазных токов равны по величине и сдвинуты по фазе относительно друг друга на угол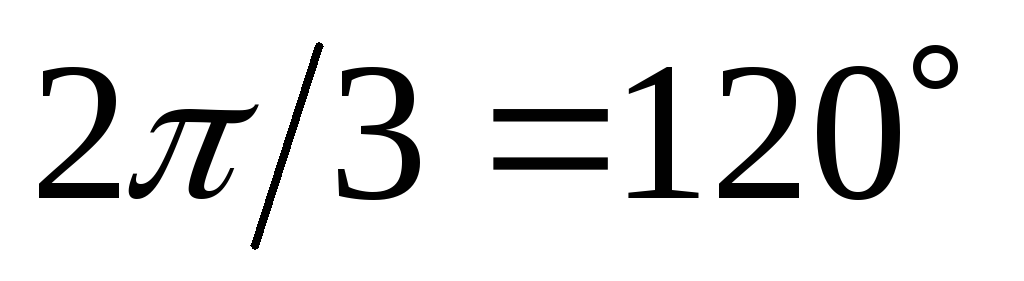 .
. Векторы линейных
токов 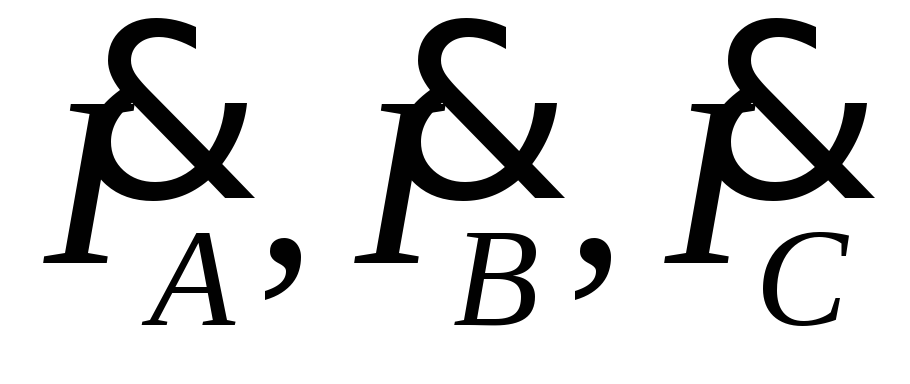 изображают результирующими векторов
фазных токов, как показано на рис. 4.13.
Из векторной диаграммы следует, что
изображают результирующими векторов
фазных токов, как показано на рис. 4.13.
Из векторной диаграммы следует, что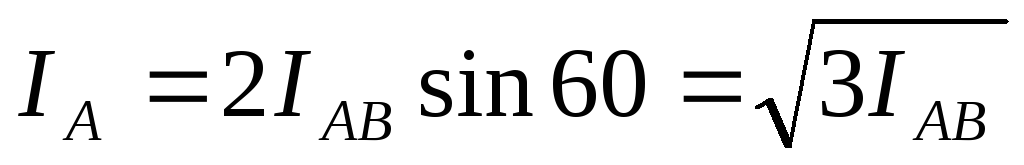 .
.
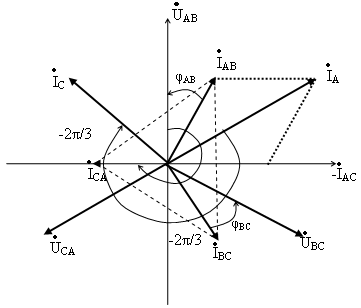
Рис. 4.13.
Такое же соотношение существует между любыми другими фазными и линейными токами. Поэтому можно написать, что при симметричной нагрузке
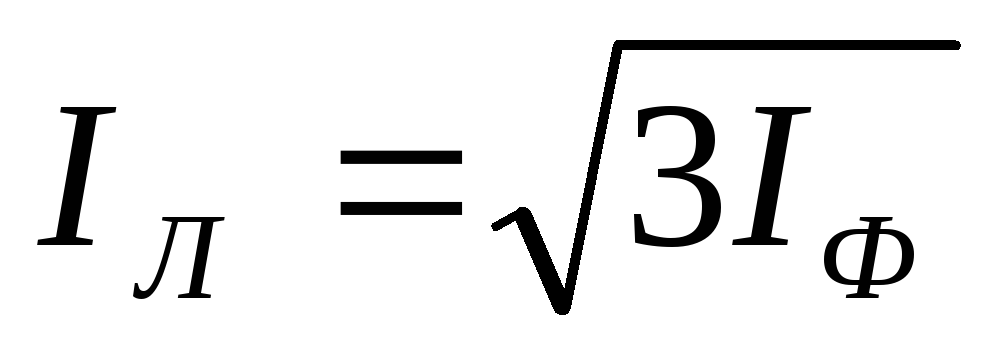 .
.
Зная фазные напряжения, токи и углы сдвига фаз между ними, либо токи и сопротивления, можно найти фазные мощности. Например, мощности фазы АВ будут равны
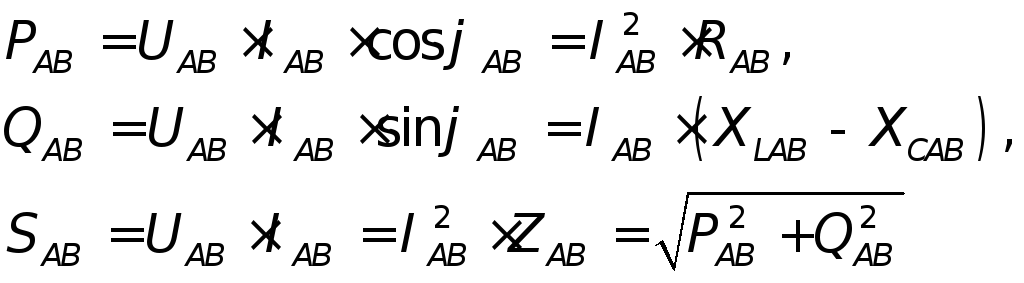
Таким же путем
находим мощности фаз ВС и СА. В силу
равенства напряжений, токов, углов
сдвига фаз и сопротивлений при симметричной
нагрузке 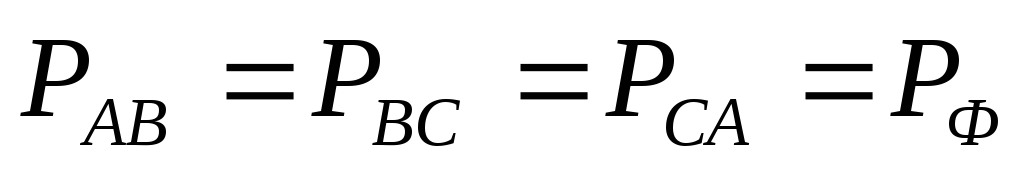 ,
,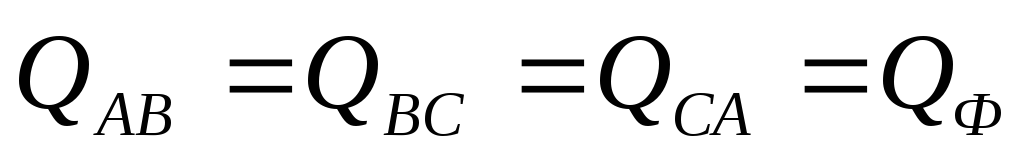 ,
,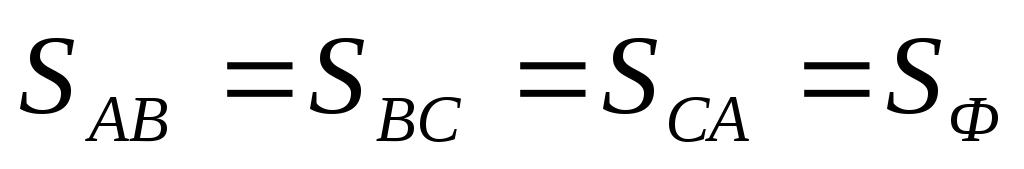 .
.
При симметричной
нагрузке активная Р,
реактивная Q и полная S мощности трехфазного приемника 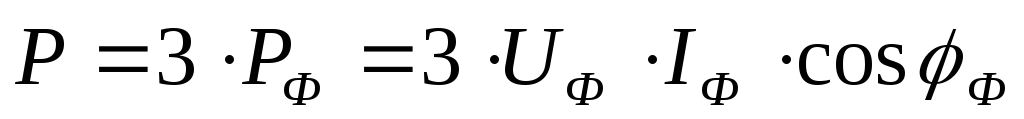 ,
,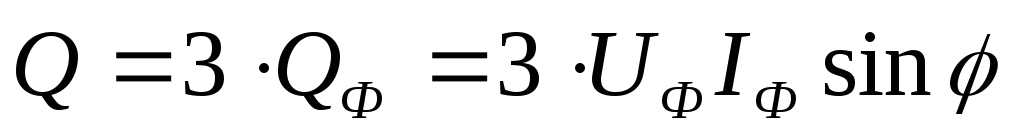 ,
,
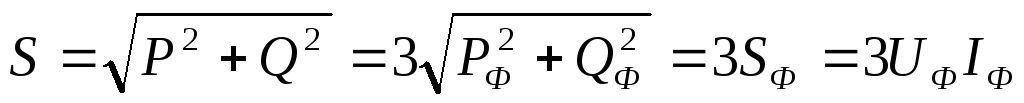 .
.
В качестве
номинальных напряжений и токов трехфазных
приемников указываются обычно линейные
напряжения и токи. Учитывая это, мощности
трехфазных приемников желательно также
выражать через линейные напряжения и
токи 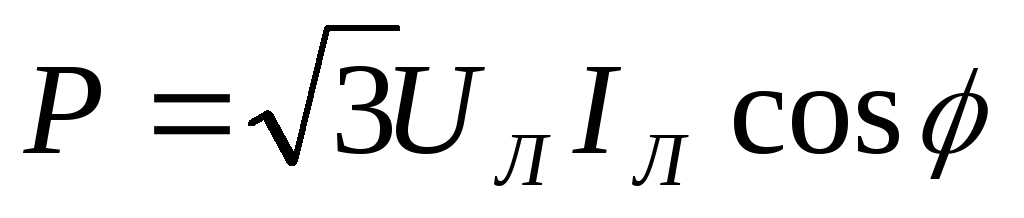 ,
,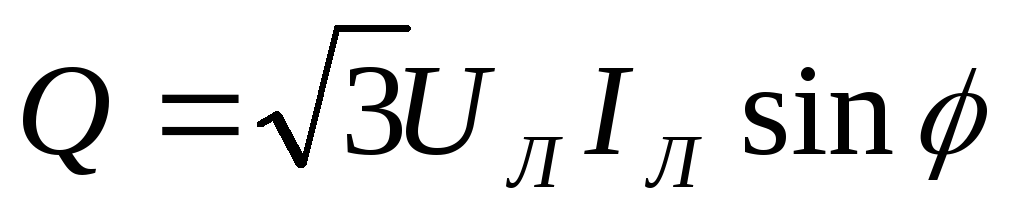 ,
,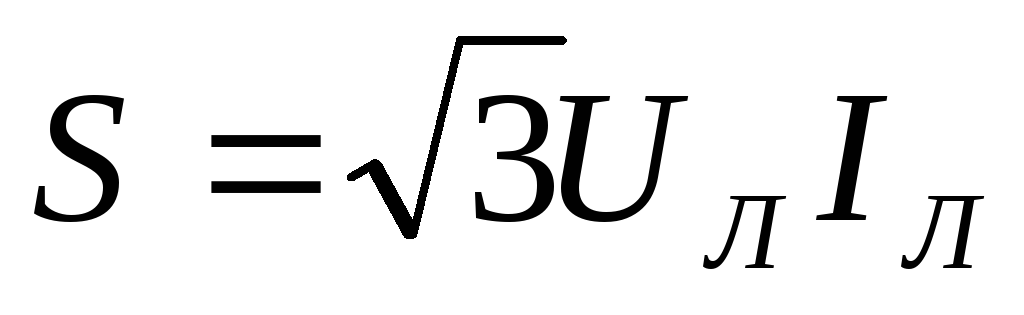 .
.
4.6. Несимметричные нагрузки при соединении треугольником
Несимметричной нагрузкой считают такую, при которой активное или реактивное сопротивление хотя бы одной из фаз не равно сопротивлениям других фаз (рис. 4.14.) rAB = rBC = rC; XAB=XBC≠X CA. В таком случае при несимметричной нагрузке ZAB ≠ ZBC ≠ ZCA.
Фазные токи, углы сдвига фаз между фазными напряжениями и токами, а также мощности могут быть определены по формулам
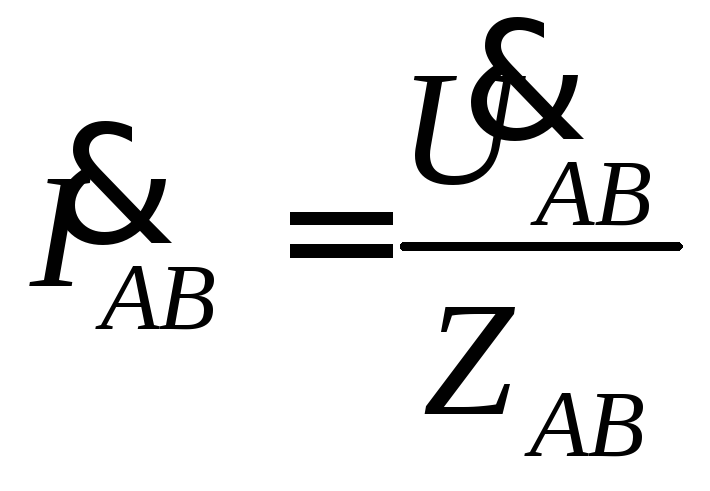 ,
, 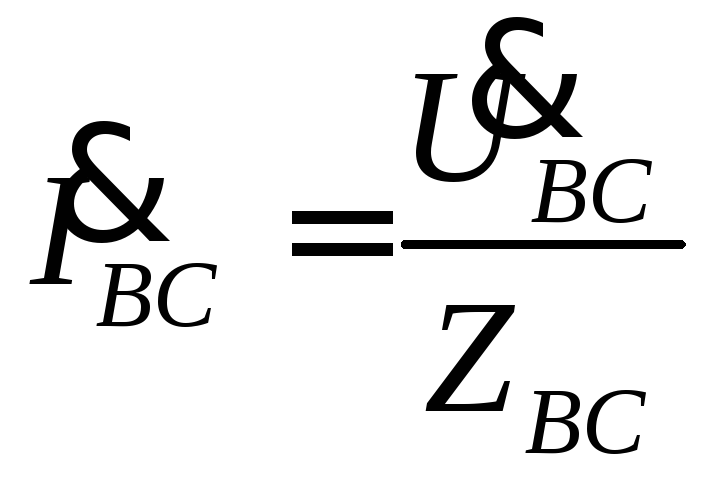 ,
,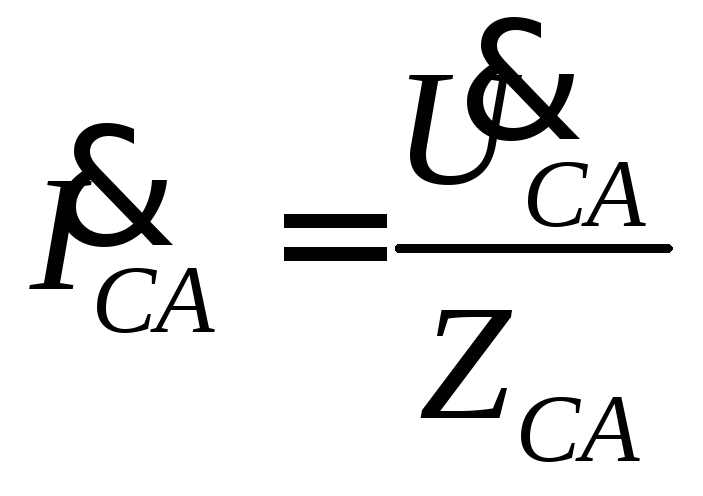
Так как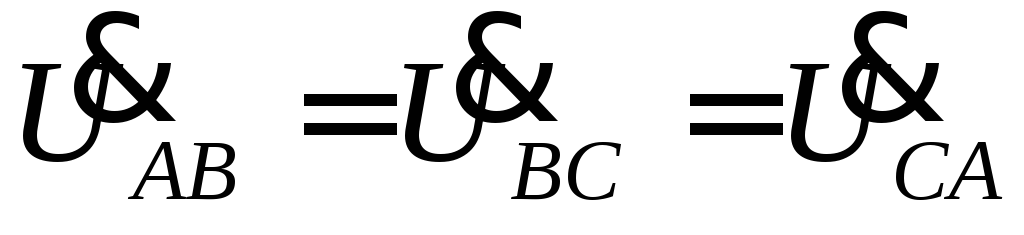 ,
а при несимметричной нагрузкеZAB ≠ ZBC ≠ ZCA, то
,
а при несимметричной нагрузкеZAB ≠ ZBC ≠ ZCA, то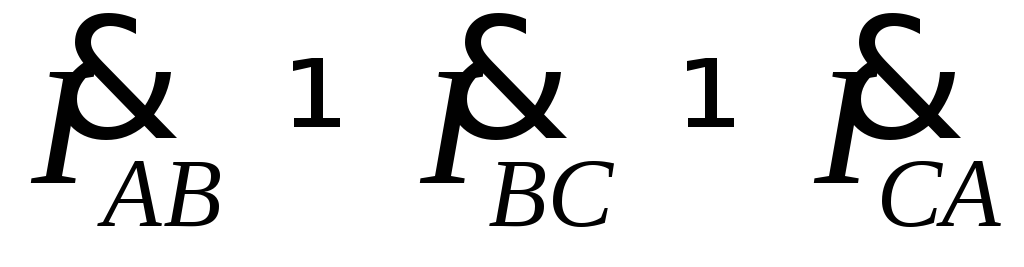 .
.
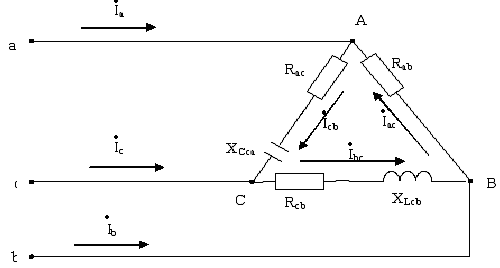
Рис. 4.14.
Углы сдвига фаз
между фазными токами и напряжениями
зависят от величины и характера
сопротивлений фаз и могут быть определены
следующим образом 
 ;
;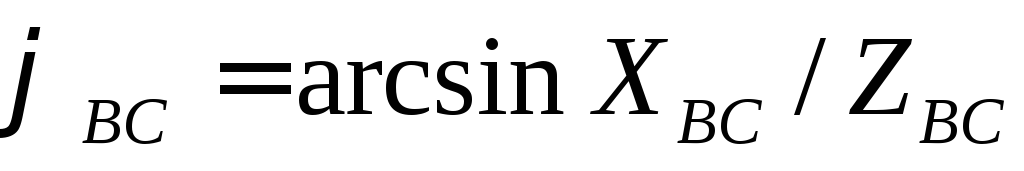 ;
;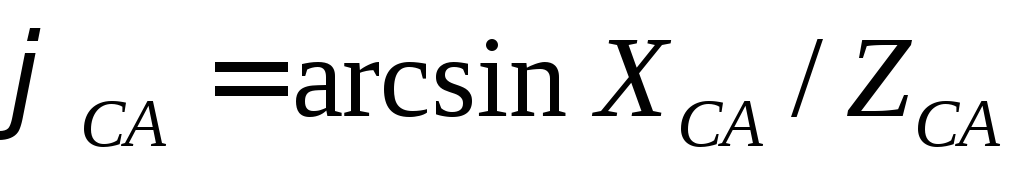 .
.
Т.о., при несимметричной нагрузке фазные токи, углы сдвига фаз и фазные мощности в общем случае различные.
Зная фазные напряжения, токи и углы сдвига фаз между ними, либо токи и сопротивления, можно найти фазные мощности. Например, мощности фазы AB

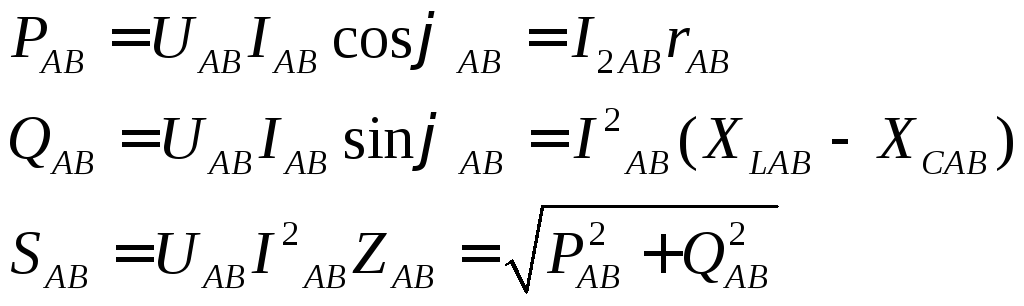
Активные и реактивные
мощности приемника 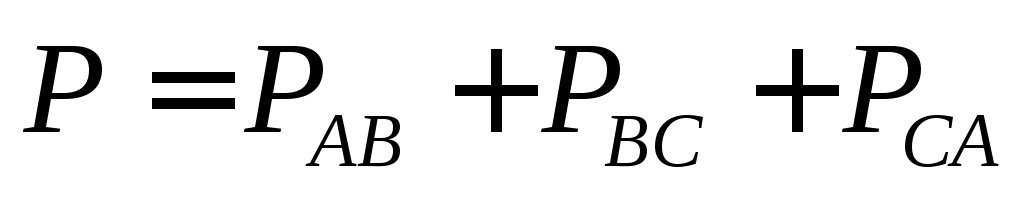 ;
;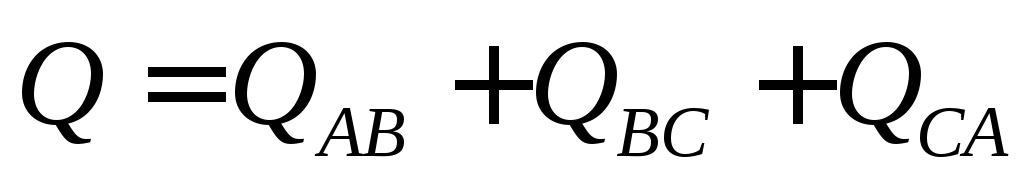 .
.
Векторная диаграмма
при несимметричной нагрузке для случая,
когда в фазе AB
имеется активное сопротивление, в фазе
BC
– активное и индуктивное сопротивления,
фазе CA
– активное и емкостное сопротивления,
приведена на рис. 4.15. Построение векторов
линейных токов произведено в соответствии
с выражениями 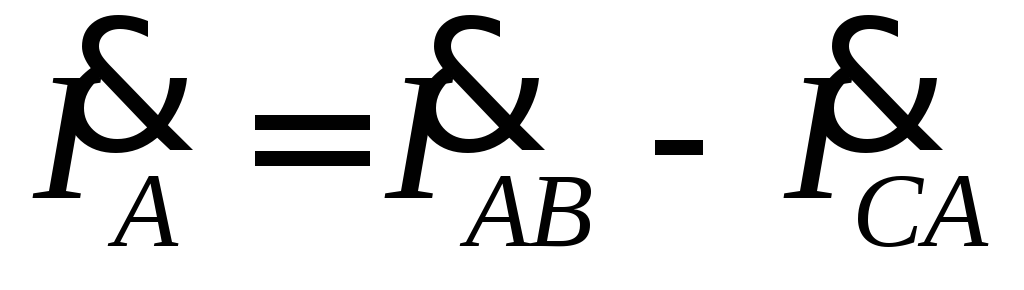 ,
, 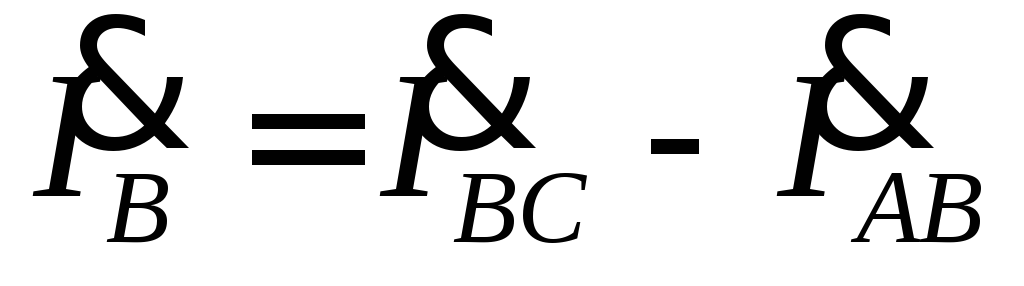 ,
,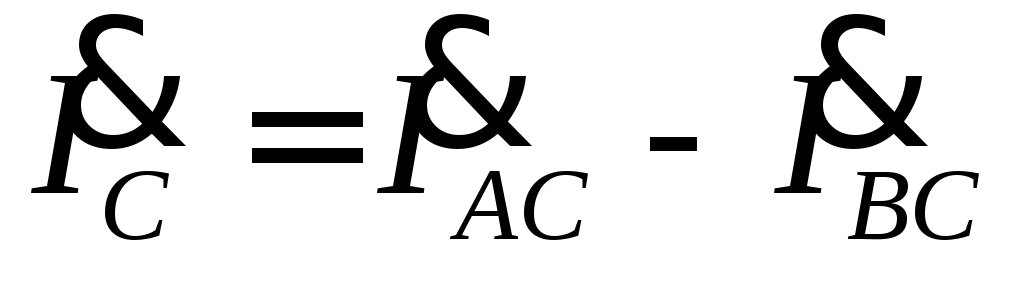 .
.
Е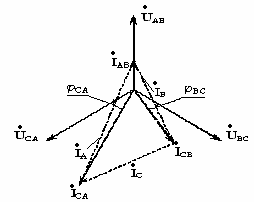 сли
кроме фазных токов, требуется определить
линейные токи, то их можно так же
определить по векторной диаграмме, не
прибегая к решению задачи в комплексной
форме.
сли
кроме фазных токов, требуется определить
линейные токи, то их можно так же
определить по векторной диаграмме, не
прибегая к решению задачи в комплексной
форме.
Рис. 4.15.
О
Рис. 3. 15.
тключение нагрузки одной из фаз можно считать частным случаем несимметричной нагрузки, при которой сопротивление отключенной фазы равно бесконечности. Так при отключении фазыCA сопротивление Z CA = ∞. При этом, ток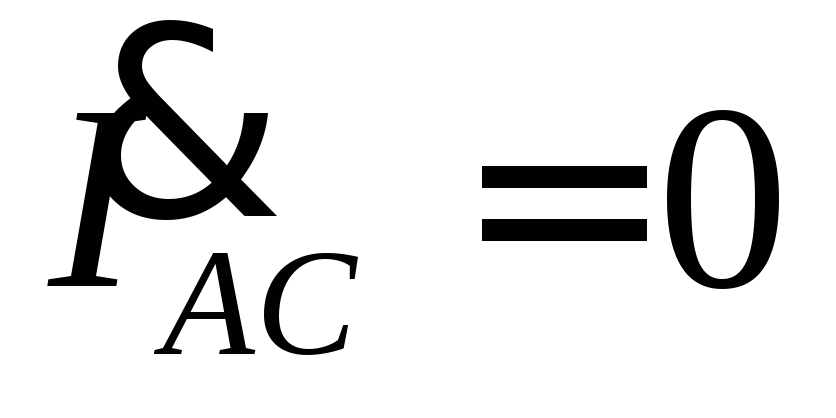 ;
фазные токи
;
фазные токи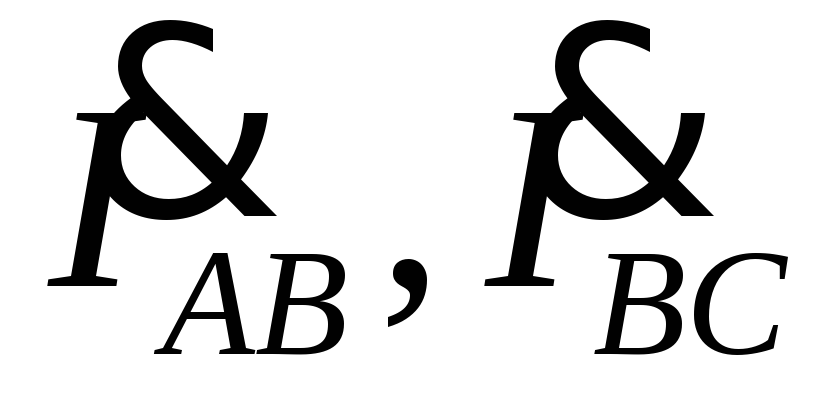 ,
а также углыφAB, φ BC не изменятся, а линейные токи
,
а также углыφAB, φ BC не изменятся, а линейные токи 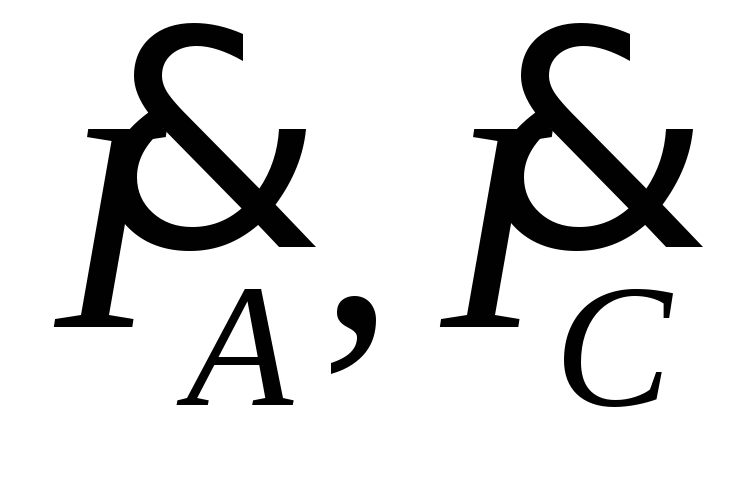 уменьшатся и будут равны
уменьшатся и будут равны 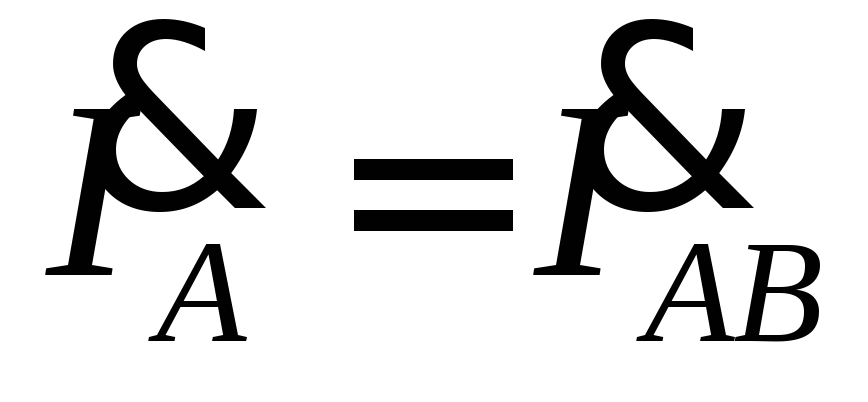 ,
, 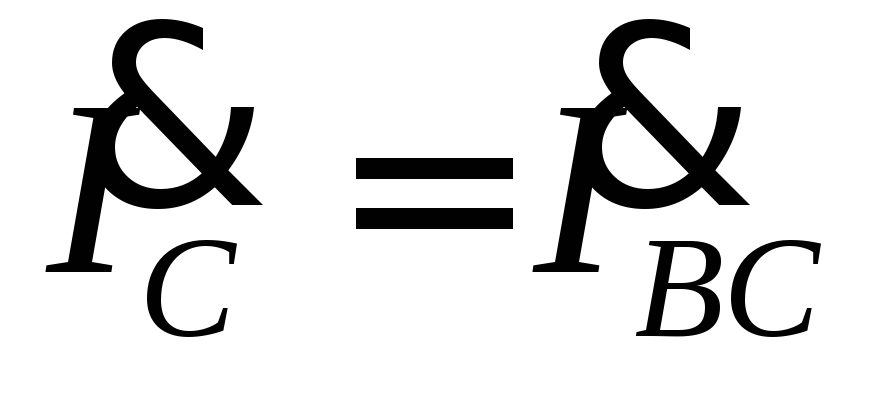 .
.2.4 Закон Ома в комплексной форме для цепей синусоидального тока
Составными элементами цепей синусоидального тока являются активное сопротивление, индуктивность и емкость. Термин сопротивление для цепей синусоидального тока не полный, т. к. сопротивление переменному току оказывают не только элементы цепи, в которых выделяется энергия в виде тепла (активные сопротивления), но и элементы, в которых энергия запасается в электрическом и магнитном полях. Такие элементы называются реактивными сопротивлениями и ими обладают индуктивность и емкость.
Синусоидальный ток в активном сопротивлении
Рассмотрим случай, когда начальные фазы отличаются от нуля. Ток и напряжение определены формулами
| (2.20) |
а
начальные фазы тока и напряжения равны 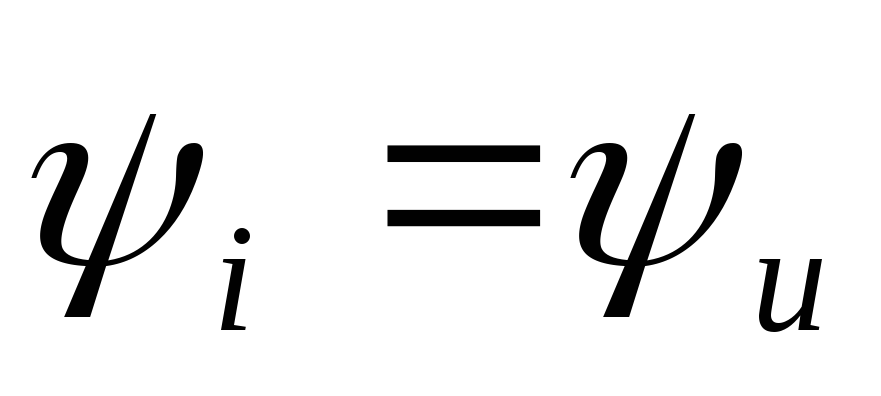 ,
т. е. ток и напряжение совпадают по фазе.
,
т. е. ток и напряжение совпадают по фазе.
В комплексном виде ток и напряжение на резистивном элементе:
| (2.21) |
т.
к. начальные фазы 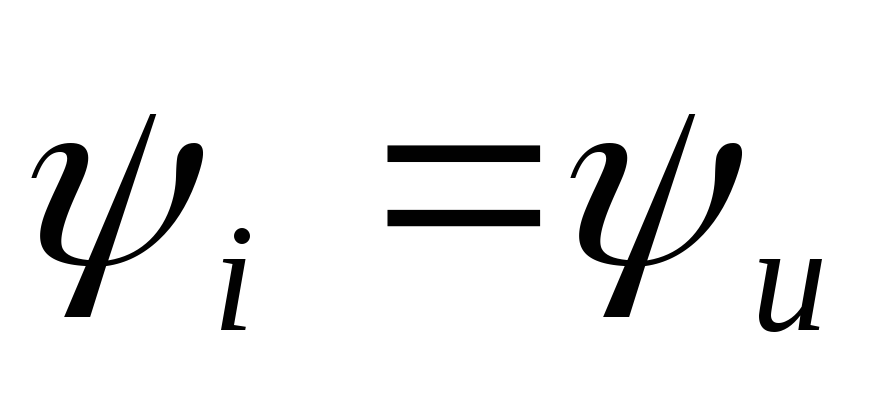 равны, то закон Ома для действующих
величин в комплексной форме для
резистивного элемента будет:
равны, то закон Ома для действующих
величин в комплексной форме для
резистивного элемента будет:
| (2.22) |
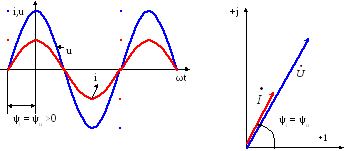
Рисунок 2.6 – Изменение мгновенных значений тока и напряжения на активном сопротивлении и векторная диаграмма при наличии начальной фазы
Индуктивность в цепи синусоидального тока
Любая обмотка (катушка) обладает индуктивностью L и активным сопротивлением R.. На схеме замещения катушку представляют в виде последовательно соединенных индуктивности и сопротивления.
Выделим из схемы одну индуктивность, удалив активное сопротивление. Если в индуктивном элементе течет ток:
| (2.23) |
то в катушке наводится ЭДС самоиндукции и появляется напряжение:
| (2.24) |
При этом амплитуды тока и напряжения соотносятся как:
| (2.25) |
где
величина 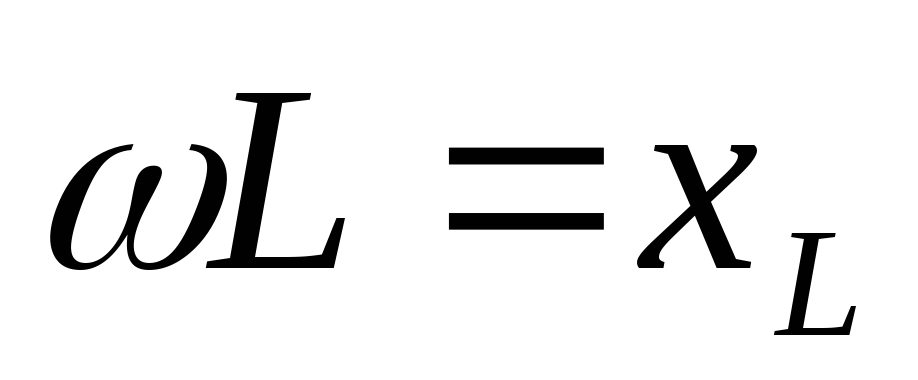 – индуктивное сопротивление [Ом].
– индуктивное сопротивление [Ом].
Разность
фаз показывает, что ток отстает по фазе
от напряжения на угол 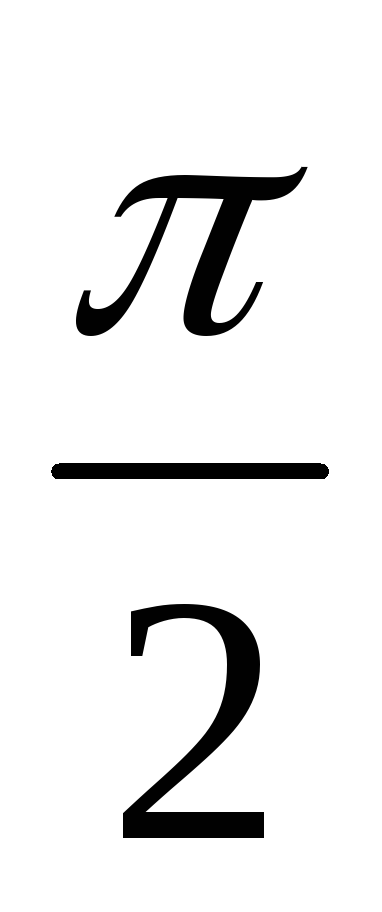 .
.
| (2.26) |
Комплексные величины тока и напряжения равны:
| (2.27) |
Закон Ома в комплексной форме для индуктивного элемента
| (2.28) |
где 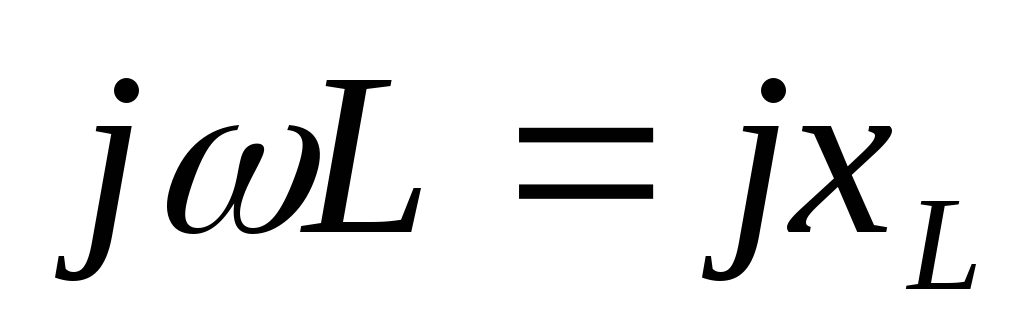 – комплексное сопротивление индуктивного
элемента.
– комплексное сопротивление индуктивного
элемента.
Если
начальный угол тока равен нулю, то
графики мгновенных значений и векторная
диаграмма выглядят следующим образом
(рисунок 2.7). Но для реальной катушки
индуктивности падение напряжение равно
сумме напряжений на индуктивности (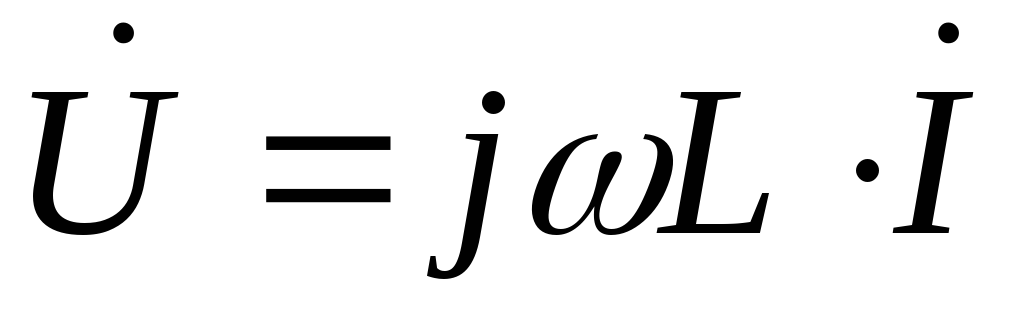 )
и на активном сопротивлении (
)
и на активном сопротивлении (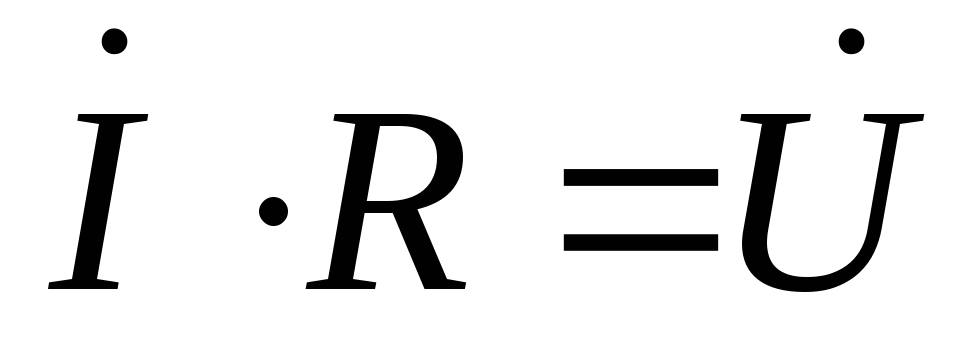 ).
Тогда суммарный вектор напряжения
).
Тогда суммарный вектор напряжения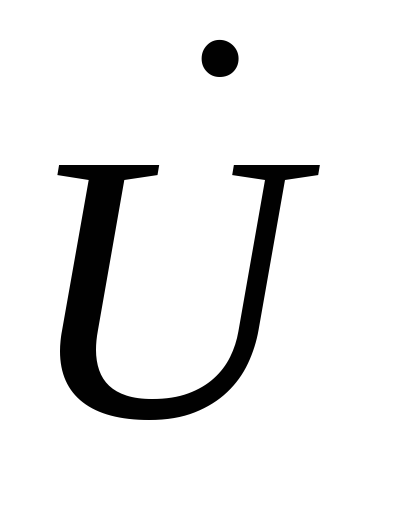 будет опережать ток на угол
будет опережать ток на угол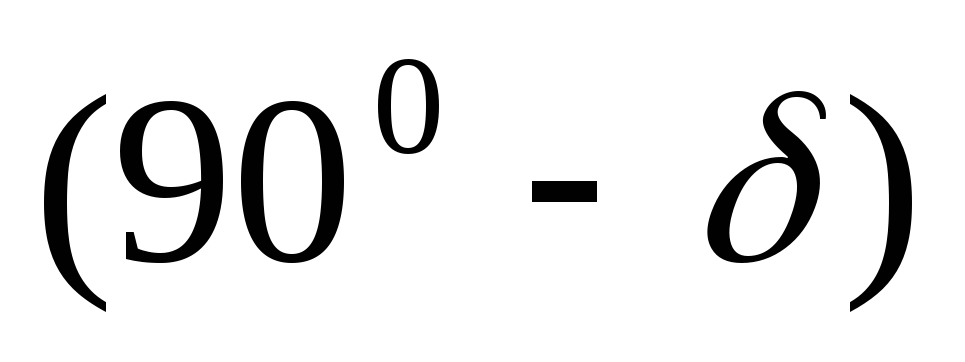 .
Причем
.
Причем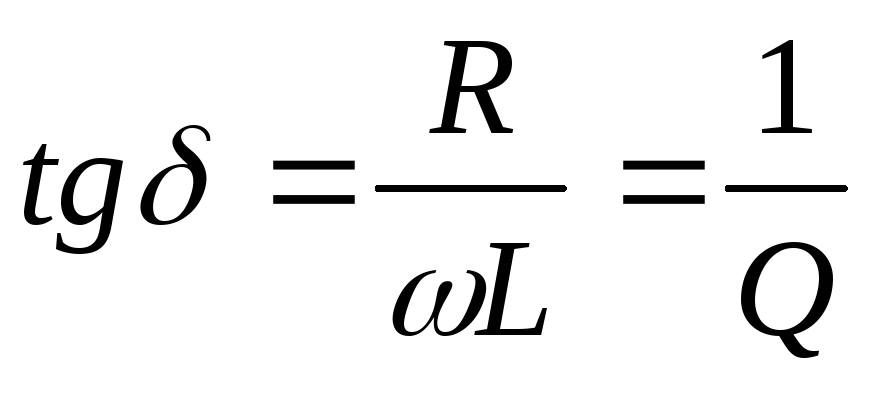 ,
гдеQ
– добротность катушки.
,
гдеQ
– добротность катушки.
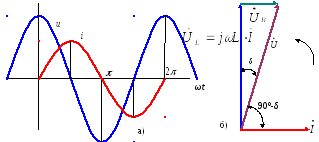
Рисунок
2.7 – Изменение мгновенных значений
тока и напряжения на индуктивном
элементе и векторная диаграмма при
начальном угле тока 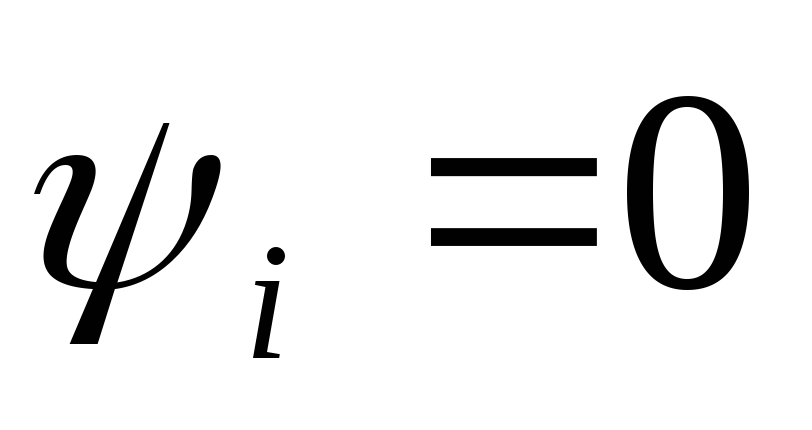
Конденсатор в цепи синусоидального тока
Если
приложенное к конденсатору напряжение
не меняется во времени, то заряды на
его обкладках неизменны и ток через
конденсатор не проходит (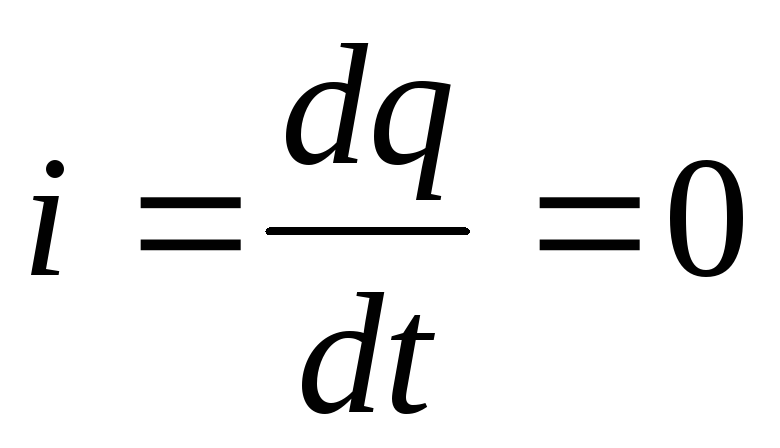 ).
При изменении напряжения по синусоидальному
закону
).
При изменении напряжения по синусоидальному
закону
| (2.29) |
по этому же закону будет изменяться и заряд q конденсатора, который будет периодически перезаряжаться. Периодическая перезарядка конденсатора сопровождается протеканием через него зарядного тока:
| (2.30) |
Отсюда видно, что ток на конденсаторе опережает по фазе напряжение на 900, т. е. разность фаз между током и напряжением
| (2.31) |
Амплитуды тока и напряжения связаны соотношением:
| (2.32) |
разделив
которые на 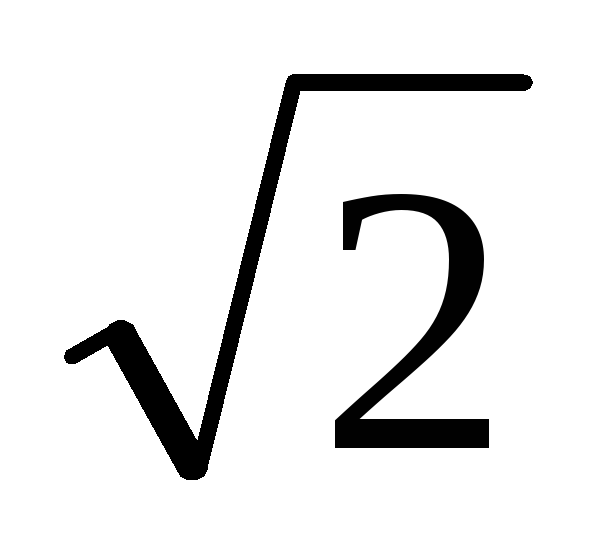 ,
получим соотношение для действующих
значений:
,
получим соотношение для действующих
значений:
| (2.33) |
где 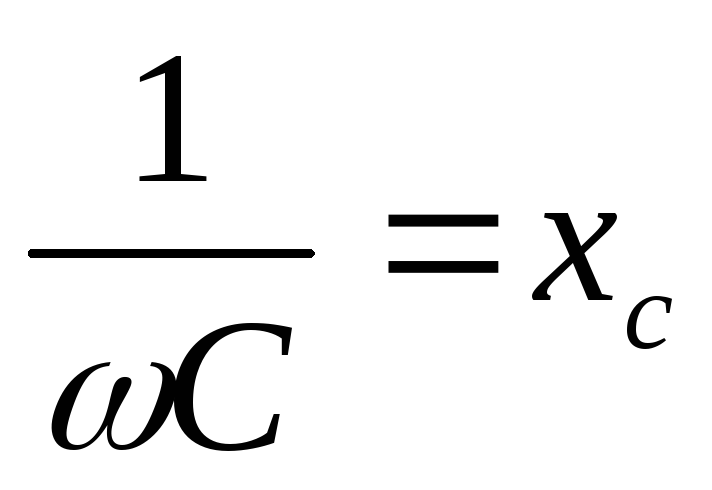 – емкостное сопротивление [Ом].
– емкостное сопротивление [Ом].
Закон Ома в комплексной форме записи:
| (2.34) |
где 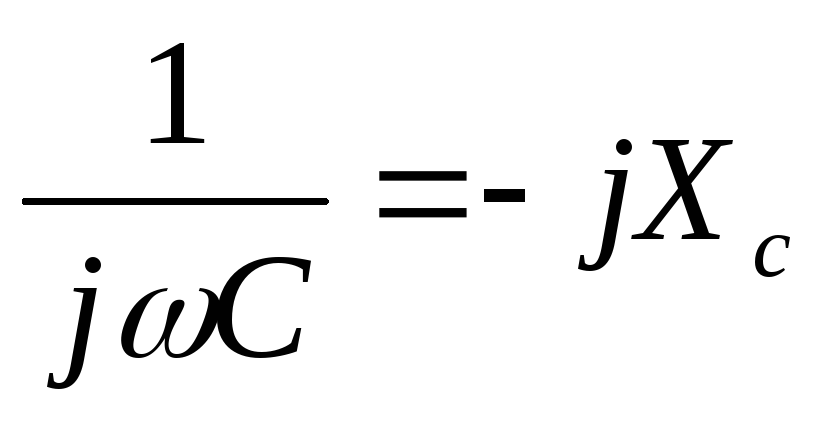 – комплексное емкостное сопротивление.
– комплексное емкостное сопротивление.
При прохождении синусоидального тока через конденсатор предполагается, что диэлектрик, разделяющий его пластины, является идеальным. Однако в реальном диэлектрике всегда имеются потери энергии, связанные c вязким трением при повороте дипольных молекул, а также наличием небольшой проводимости. Эти потери относительно малы, но если их требуется учесть, то составляют схему замещения, где параллельно емкости включают активное сопротивление, потери в котором имитируют потери энергии в реальном диэлектрике.
Тогда
суммарный ток через конденсатор равен
геометрической сумме двух токов: 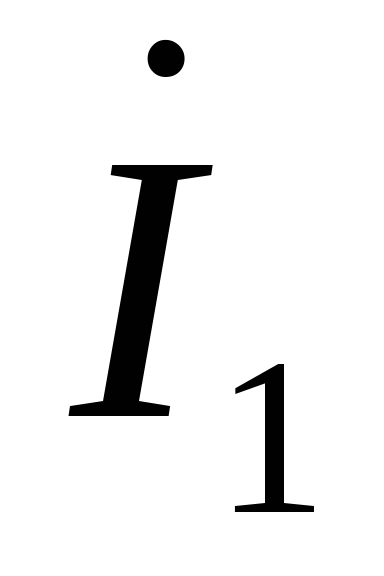 – через емкость и
– через емкость и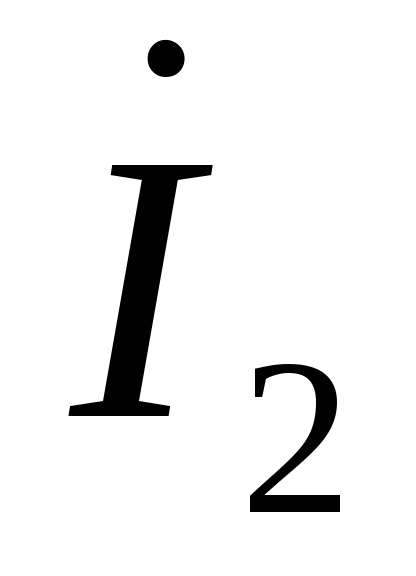 – через активное сопротивление.
– через активное сопротивление.
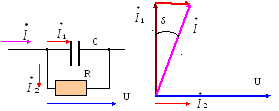
Рисунок 2.8 – Схема замещения (а) и векторная диаграмма (б)
конденсатора, заполненного диэлектриком
В конденсаторе с диэлектриком ток опережает напряжение на угол (900— δ), где δ называется углом диэлектрических потерь. Для реальных конденсаторов он выражается через tgδ и указывается в таблицах.
1. Основные понятия и определения.
Трехфазные цепи синусоидального тока
План
2.
1. Основные понятия и определения
Трехфазная цепь является частным случаем многофазных электрических систем, представляющих собой совокупность электрических цепей, в которых действуют ЭДС одинаковой частоты, сдвинутые по фазе относительно друг друга на определенный угол. Отметим, что обычно эти ЭДС, в первую очередь в силовой энергетике, синусоидальны. Однако, в современных электромеханических системах, где для управления исполнительными двигателями используются преобразователи частоты, система напряжений в общем случае является несинусоидальной.
Трехфазная цепь является совокупностью трех электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, сдвинутые относительно друг друга по фазе на 120o, создаваемые общим источником.
Каждую из частей многофазной системы, характеризующуюся одинаковым током, называют фазой, т.е. фаза – это участок цепи, относящийся к соответствующей обмотке генератора или трансформатора, линии и нагрузке.
Обратить внимание! Понятие «фаза» имеет в электротехнике два различных значения:
фаза как аргумент синусоидально изменяющейся величины;
фаза как составная часть многофазной электрической системы.
Трехфазная цепь состоит из трехфазного генератора, соединительных проводов и приемников или нагрузки, которые могут быть однофазными или трехфазными.
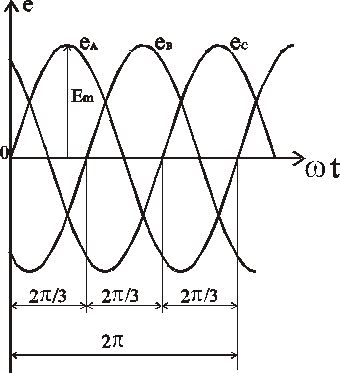
Трехфазный генератор представляет собой синхронную машину. На статоре генератора размещена обмотка, состоящая из трех частей или фаз, пространственно смещенных относительно друг друга на 120o. В фазах генератора индуктируется симметричная трехфазная система ЭДС, в которой электродвижущие силы одинаковы по амплитуде и различаются по фазе на 120o. Запишем мгновенные значения и комплексы действующих значений ЭДС.
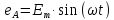
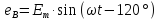
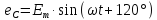
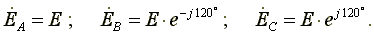
Сумма электродвижущих сил симметричной трехфазной системы в любой момент времени равна нулю.
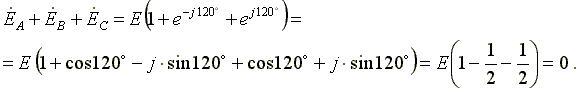
Соответственно 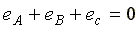
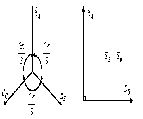
На схемах трехфазных цепей начала фаз обозначают первыми буквами латинского алфавита ( А, В, С ), а концы — последними буквами ( X, Y, Z ). Направления ЭДС указывают от конца фазы обмотки генератора к ее началу.
Каждая фаза нагрузки соединяется с фазой генератора двумя проводами: прямым и обратным. Получается несвязанная трехфазная система, в которой имеется шесть соединительных проводов. Чтобы уменьшить количество соединительных проводов, используют трехфазные цепи, соединенные звездой или треугольником.
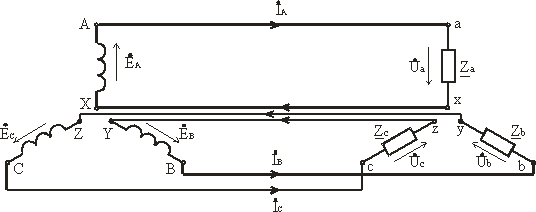
2. Соединение в звезду. Схема, определения
Если концы всех фаз генератора соединить в общий узел, а начала фаз соединить с нагрузкой, образующей трехлучевую звезду сопротивлений, получится трехфазная цепь, соединенная звездой. При этом три обратных провода сливаются в один, называемый нулевым или нейтральным. Трехфазная цепь, соединенная звездой, изображена на рис.
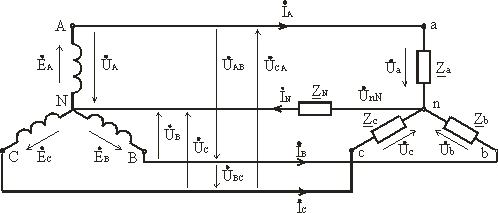
Провода, идущие от источника к нагрузке называют линейными проводами, провод, соединяющий нейтральные точки источника N и приемника N’ называют нейтральным (нулевым) проводом.
Напряжения между началами фаз или между линейными проводами называют линейными напряжениями (UAB, UBC, UCA)
Напряжения между началом и концом фазы или между линейным и нейтральным проводами называются фазными напряжениями (UA, UB, UC у источника; Ua, Ub, Uc у приемника).
Токи в фазах приемника или источника называют фазными токами, токи в линейных проводах — линейными токами. Так как линейные провода соединены последовательно с фазами источника и приемника, линейные токи при соединении звездой являются одновременно фазными токами.
Iл = Iф.
ZN — сопротивление нейтрального провода.
Ток, протекающий в нейтральном проводе, обозначают IN.
Линейные напряжения равны геометрическим разностям соответствующих фазных напряжений
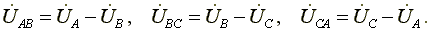 (7.1)
(7.1)
На рис. 7.2 изображена векторная диаграмма фазных и линейных напряжений симметричного источника.
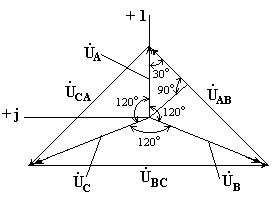
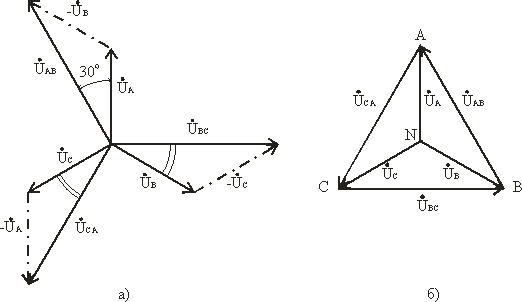
Из векторной диаграммы видно, что
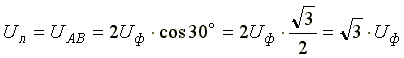
При симметричной системе ЭДС источника линейное напряжение больше фазного в √3 раз.
Uл = √3 Uф
Классификация приемников в трехфазной цепи
Приемники, включаемые в трехфазную цепь, могут быть либо однофазными, либо трехфазными. К однофазным приемникам относятся электрические лампы накаливания и другие осветительные приборы, различные бытовые приборы, однофазные двигатели и т.д. К трехфазным приемникам относятся трехфазные асинхронные двигатели и индукционные печи. Обычно комплексные сопротивления фаз трехфазных приемников равны между собой:
(3.9)
Za = Zb = Zc = Zejφ.
Такие приемники называют симметричными. Если это условие не выполняется, то приемники называют несимметричными. При этом, если Za = Zb = Zc, то трехфазный приемник называют равномерным, если φa = φb = φc, то однородным.
Четырехпроводная цепь
Для расчета трехфазной цепи применимы все методы, используемые для расчета линейных цепей. Обычно сопротивления проводов и внутреннее сопротивление генератора меньше сопротивлений приемников, поэтому для упрощения расчетов таких цепей (если не требуется большая точность) сопротивления проводов можно не учитывать (ZЛ = 0, ZN = 0). Тогда фазные напряжения приемника Ua, Ub и Uc будут равны соответственно фазным напряжениям источника электрической энергии(генератора или вторичной обмотки трансформатора), т.е. Ua = UA; Ub = UB; Uc = UC. Если полные комплексные сопротивления фаз приемника равны Za = Zb = Zc, то токи в каждой фазе можно определить по формулам
(3.10)
İa = Úa / Za; İb = Úb / Zb; İc = Úc / Zc.
В соответствии с первым законом Кирхгофа ток в нейтральном проводе
(3.11)
İN = İa + İb + İc = İA + İB + İC.
Симметричная нагрузка приемника
При симметричной системе напряжений и симметричной нагрузке, когда Za = Zb = Zc, т.е. когда Ra = Rb = Rc = Rф и Xa = Xb = Xc = Xф, фазные токи равны по значению и углы сдвига фаз одинаковы
(3.12)
Ia = Ib = Ic = Iф = Uф / Zф,
(3.13)
φa = φb = φc = φ = arctg (Xф/Rф).
Построив векторную диаграмму токов для симметричного приемника (рис. 3.8), легко установить, что геометрическая сумма трех векторов тока равна нулю: İa + İb + İc = 0. Следовательно, в случае симметричной нагрузки ток в нейтральном проводе IN = 0, поэтому необходимость в нейтральном проводе отпадает.
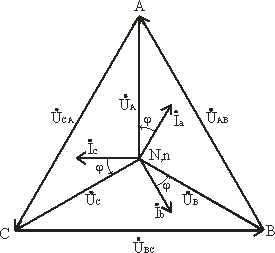
Рис. 3.8
Несимметричная нагрузка приемника
При симметричной системе напряжений и несимметричной нагрузке, когда Za ≠ Zb ≠ Zc и φa ≠ φb ≠ φc токи в фазах потребителя различны и определяются по закону Ома
İa = Úa / Za; İb = Úb / Zb; İc = Úc / Zc.
Ток в нейтральном проводе İN равен геометрической сумме фазных токов
İN = İa + İb + İc.
Напряжения
будут Ua = UA;
Ub = UB;
Uc = UC,
UФ = UЛ / 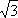 ,
благодаря нейтральному проводу при
ZN = 0.
,
благодаря нейтральному проводу при
ZN = 0.
Следовательно, нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке.
Поэтому в четырехпроводную сеть включают однофазные несимметричные нагрузки, например, электрические лампы накаливания. Режим работы каждой фазы нагрузки, находящейся под неизменным фазным напряжением генератора, не будет зависеть от режима работы других фаз.
Векторная диаграмма при несимметричной нагрузке приведена на рис. 3.9
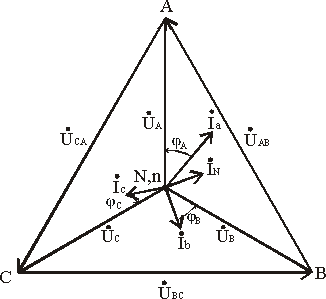
Рис. 3.9
Трехпроводная электрическая цепь
Схема соединения источника и приемника звездой без нейтрального провода приведена на рис. 3.10.
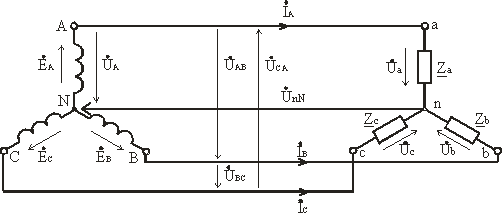
Рис. 3.10
При симметричной нагрузке, когда Za = Zb = Zc = Zφ, напряжение между нейтральной точкой источника N и нейтральной точкой приемника n равно нулю, UnN = 0.
Соотношение
между фазными и линейными напряжениями
приемника также равно 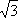 ,
т.е. UФ = UЛ /
,
т.е. UФ = UЛ / 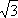 ,
а токи в фазах определяются по тем же
формулам (3.12, 3.13), что и для четырехпроводной
цепи. В случае симметричного приемника
достаточно определить ток только в
одной из фаз. Сдвиг фаз между током и
соответствующим напряжением
φ = arctg (X / R).
,
а токи в фазах определяются по тем же
формулам (3.12, 3.13), что и для четырехпроводной
цепи. В случае симметричного приемника
достаточно определить ток только в
одной из фаз. Сдвиг фаз между током и
соответствующим напряжением
φ = arctg (X / R).
При несимметричной нагрузке Za ≠ Zb ≠ Zc между нейтральными точками приемника и источника электроэнергии возникает напряжение смещения нейтрали UnN.
Для определения напряжения смещения нейтрали можно воспользоваться формулой межузлового напряжения, так как схема рис 3.10 представляет собой схему с двумя узлами,
(3.14)
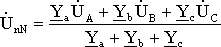 ,
,
где: Ya = 1 / Za; Yb = 1 / Zb; Yc = 1 / Zc – комплексы проводимостей фаз нагрузки.
Очевидно, что теперь напряжения на фазах приемника будут отличаться друг от друга. Из второго закона Кирхгофа следует, что
(3.15)
Úa = ÚA — ÚnN; Úb = ÚB — ÚnN; Úc = ÚC — ÚnN.
Зная фазные напряжения приемника, можно определить фазные токи:
(3.16)
İa = Úa / Za = Ya Úa; İb = Úb / Zb = Yb Úb; İc = Úc / Zc = Yc Úc.
Векторы фазных напряжений можно определить графически, построив векторную (топографическую) диаграмму фазных напряжений источника питания и UnN (рис. 3.11).
При изменении величины (или характера) фазных сопротивлений напряжение смещений нейтрали UnN может изменяться в широких пределах. При этом нейтральная точка приемника n на диаграмме может занимать разные положения, а фазные напряжения приемника Úa, Úb и Úc могут отличаться друг от друга весьма существенно.
Таким образом, при симметричной нагрузке нейтральный провод можно удалить и это не повлияет на фазные напряжения приемника. При несимметричной нагрузке и отсутствии нейтрального провода фазные напряжения нагрузки уже не связаны жестко с фазными напряжениями генератора, так как на нагрузку воздействуют только линейные напряжения генератора. Несимметричная нагрузка в таких условиях вызывает несимметрию ее фазных напряжений Úa, Úb, Úc и смещение ее нейтральной точки n из центра треугольника напряжений (смещение нейтрали).
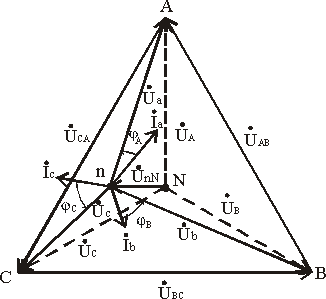
Рис. 3.11
Направление смещения нейтрали зависит от последовательности фаз системы и характера нагрузки.
Поэтому нейтральный провод необходим для того, чтобы:
выравнивать фазные напряжения приемника при несимметричной нагрузке;
подключать к трехфазной цепи однофазные приемники с номинальным напряжением в
 раз
меньше номинального линейного напряжения
сети.
раз
меньше номинального линейного напряжения
сети.
Следует иметь в виду, что в цепь нейтрального провода нельзя ставить предохранитель, так как перегорание предохранителя приведет к разрыву нейтрального провода и появлению значительных перенапряжений на фазах нагрузки.
18. Закон Ома в комплексной форме.
U = UR +UL + UC = UR + jUL – jUC = IR + jIXL – jIXC = I (R+ j) (XL — XC) = IZ
19. Законы Кирхгофа в комплексной форме.
1 закон Кирхгофа:
I=IR+IL+IC=IR – jIL + jIC=U/R – jU/XL+ U/jXC
2 закон Кирхгофа: ΣE = ΣIZ + ΣU
20. Электрическая цепь с активным сопротивлением.
Активный процесс – это процесс преобразования электрической энергии в другой вид, например в тепло.
Количественная оценка это процесса характеризуется сопротивлением R.
Постоянный ток – это ток с нулевой частотой.
Активное сопротивление не зависит от частоты тока.
i (t) = Im Sin ɷt , [A]
Ue = i * R
UR = Im R Sin ɷ t = UmR Sin ɷ t
Комплексной действующее значение.
I = Im/√2 ; UR = Umz /√2
I = I ei ; UR = UR ein = U r1
В комплексной форме
R всегда положительное действующее число.
Напряжение на активной сопротивлении R совпадает с током по фазе.
21. Электрическая цепь с индуктивностью.
Индуктивность – это коэф. пропорциональности между током и потомком сцепления. L [Гн]
Значительной индуктивностью обладают обмотки или катушки с индуктивностью.
Ѱ= L i
Ѱ= WФ
Рассмотрим идеальную катушку у которой нет нагрева R=0, с=0.
i= Im Sin ɷt
По закону Фарадея в катушке возникает самоиндукция.
eL = — dФ/dt = — W* dФ/dt
lL = ɷL
Напряжение на индуктивности опережает ток по фазе на угол π/2.
Комплексное действующее значение:
I = I ej0
UL = ULejπ/2 = jUL
UL/I = γUL/I = jXL
Индуктивное сопротивление в комплексной форме всегда положительное.
22. Электрическая цепь с емкостью.
Значительной емкостью обладают конденсаторы. Основной параметр конденсатора – емкость. С [Ф]
Емкость – заряд конденсатора при напряжении в 1 В.
Рассмотрим идеальный конденсатор с емкостью
С = const
R = 0
L = 0
UC = Umc Sin ɷt
Q = C * UC
i = dQ/dt = C Umc cos ɷt = UmcɷC Sin (ɷt + π/2)
Im = UmcɷC
Xc = 1/ɷc, [Ом]
На емкости ток опережает напряжение по фазе на угол π/2.
24.Резонанс напряжений.
φ = 0
UL = UC
X = XL – XC= 0
Up = UL – UC = 0
U = UR
Z0 = R → min
I0 = U/R → max
При резонансе, т. к. режим активный, напряжение и ток совпадают по фазе.
26.
мощность в цепи синусоидального
тока.Энергетические
процессы в цепях переменного тока
являются функциями времени. Рассмотрим
мощности отдельных участков цепи с
последовательным соединением R, L, C (рис.
2.15), для чего допустим, что к ней приложено
напряжение 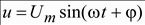 и
протекает ток
и
протекает ток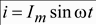 .
.
Мощность в активном сопротивлении:
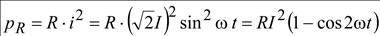 .
.
Учитывая
RI = UR, а также равенство UR = Ucosφ, полученное
из треугольника напряжений, будем
иметь
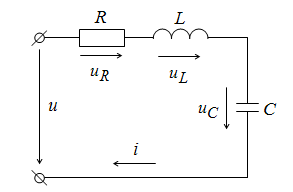 Рис.
2.15. Схема последовательной цепи
Рис.
2.15. Схема последовательной цепи
мгновенная мощность в активном сопротивлении всегда положительна (т.е. всегда потребляется). Мгновенная мощность колеблется с двойной частотой около своего среднего значения, равного U I cos φ.
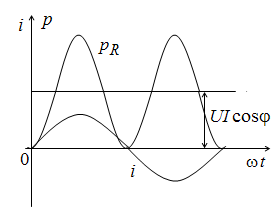
Рис. 2.16. Мгновенная мощность на активном сопротивлении
Под активной мощностью понимают среднее значение полной мгновенной мощности за период P=UIcos φ{Вт}. Активная мощность никогда не бывает отрицательной, так как ею характеризуется потребление энергии цепью.
Реактивная мощность (Q) характеризует ту часть энергии, которой цепь обменивается с источником без потребления. Ее величина определяется амплитудным значением мгновенной реактивной мощности Q=UICos(2wt-ф){ВАр}. S=U*I{ВА}. Она положительна при отстающем токе (когда φ > 0) и отрицательна при опережающем (когда φ < 0).
Треугольник
мощностей: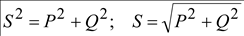
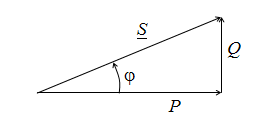
27. Коэффицие́нт мо́щности..- Это безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения. Соsф=P/S=P/UI.
28.Определение ,способ получения трехфазной системы. Трёхфазная цепь, трёхфазная система, совокупность трёх однофазных электрических цепей переменного тока (называемых фазами), в которых действуют три переменных напряжения одинаковой частоты, сдвинутых по фазе друг относительно друга; частный случай многофазной системы.
Преимущества трех фазной цепи:1) По сравнению с однофазными цепями переменного тока Т. ц. более экономичны, дают существенно меньшие пульсации тока после выпрямления. 2)Применение Т. ц. позволяет простыми средствами получать вращающееся магнитное поле в электродвигателях переменного тока.
Получение трёхфазной системы ЭДС
Для создания трёхфазной электрической цепи требуются три источника ЭДС с одинаковыми амплитудами и частотами и смещенными по фазе на 120°. Простейшим техническим устройством, обеспечивающим выполнение этих условий, является синхронный генератор. Ротор (вращающаяся часть) генератора представляет собой электромагнит или постоянный магнит. На статоре (неподвижной части) генератора расположены три одинаковые обмотки, смещенные в пространстве друг относительно друга на 120°. При вращении ротора его магнитное поле меняет своё положение относительно обмоток и в них наводятся синусоидальные ЭДС. Частота и амплитуда ЭДС обмоток определяется частотой вращения ротора ω, которая в промышленных генераторах поддерживается строго постоянной. Равенство ЭДС обмоток обеспечивается идентичностью их конструктивных параметров, а фазовое смещение – смещением обмоток в пространстве.
Начала обмоток генератора обозначаются буквами латинского алфавита A, B, C, а их концы X, Y, Z. Последовательность, в которой фазные ЭДС проходят через одинаковые состояния, например, через нулевые значения, называется порядком чередования фаз.
Пусть начальная фаза ЭДС еА равна нулю, тогда мгновенные значения ЭДС обмоток генератора равны:
еА=ЕmSinwt , еВ=Sin(wt-120), еС=Sin(wt+120){В}
1. Расчет трехфазной цепи при соединении потребителей звездой.
Так как в схеме есть нейтральный провод, то напряжение на фазах нагрузки равно соответствующему фазному напряжению источника питания (обмотки генератора считаем соединенными звездой, а сопротивлением нейтрального провода пренебрегаем):
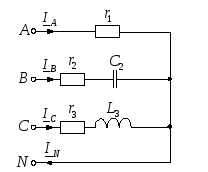
Рисунок 9 – Схема трёхфазной цепи при соединении потребителей звездой
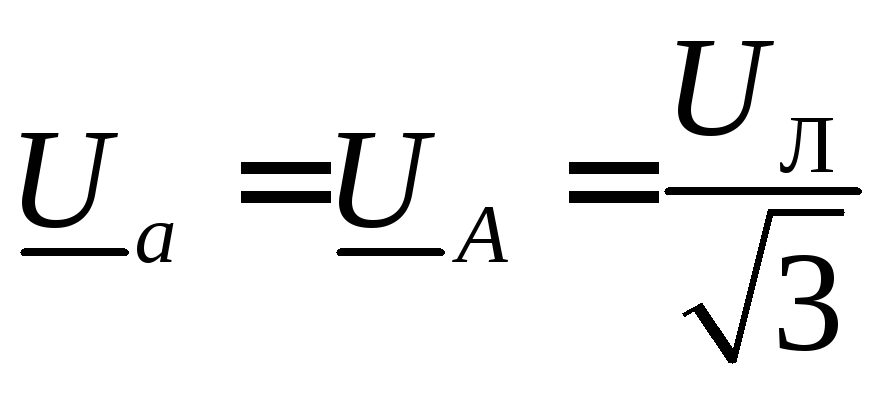 ,
, 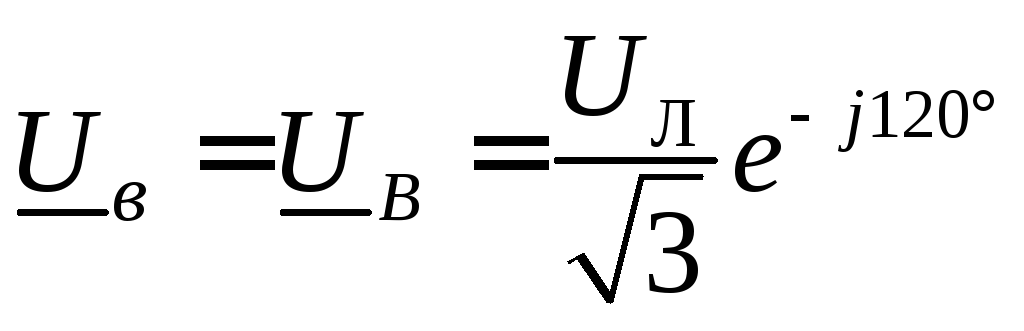 ,
, 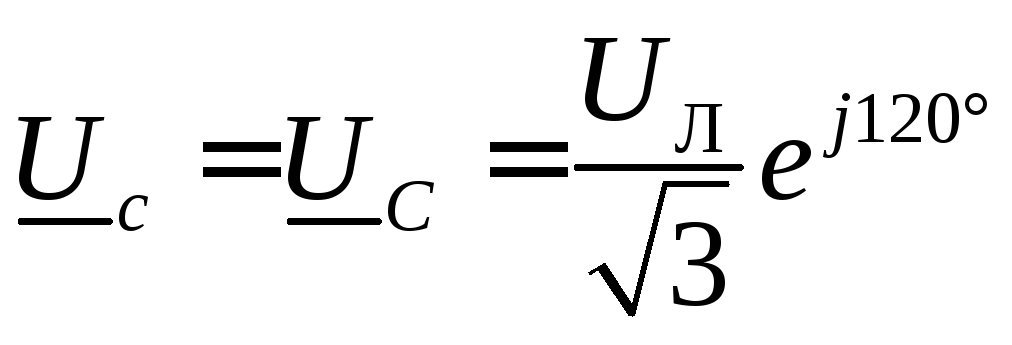 ;
;
в численном виде:
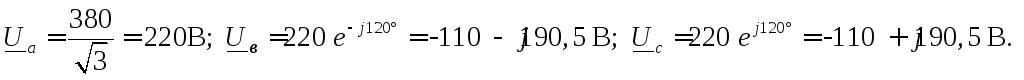
Определим реактивные сопротивления, принимая частоту сети переменного тока равной 50 Гц, а угловую частоту
ω = 2πf = 2 ∙ 3,14 ∙ 50 = 314 1/с .
Реактивное индуктивное сопротивление
xL3 = ω L3 = 314 ∙ 31,8 ∙ 10–3 = 10 Ом.
Реактивное емкостное сопротивление
xС2 =1/(ω С2) = 1/(314 ∙ 159 ∙ 10–6) = 20 Ом.
В общем случае полное сопротивление каждой из фаз в комплексной форме определяют с помощью выражения, которое использовалось в однофазных цепях,
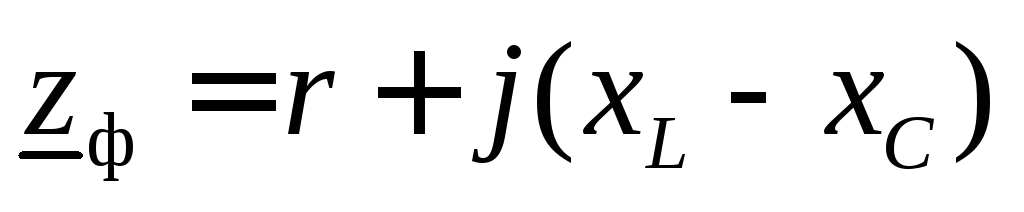 .
.
Применяем эту формулу для нашего конкретного случая и получаем полные сопротивления фаз в следующем виде:
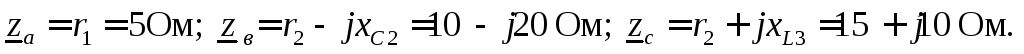
Комплексные сопротивления фаз различны, следовательно, нагрузка несимметричная.
Токи в линейных проводах (фазные токи нагрузки) определяем с помощью закона Ома:
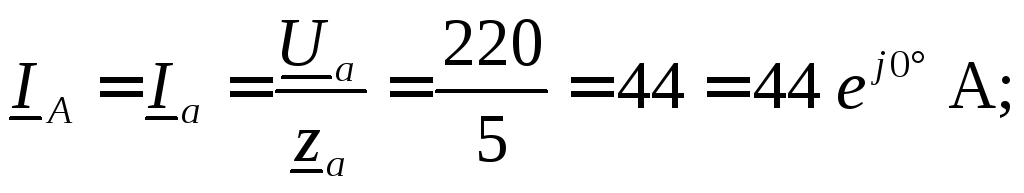
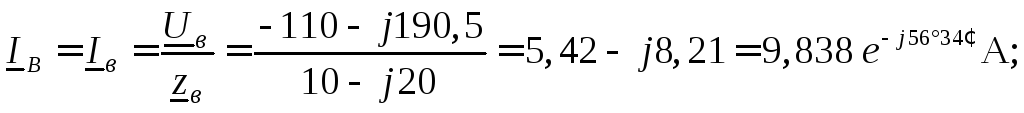
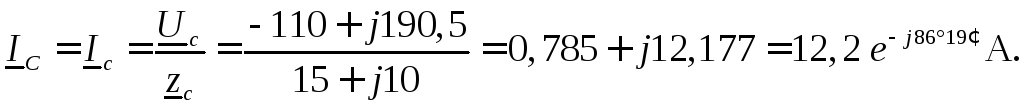
Ток в нейтральном проводе находим по первому закону Кирхгофа
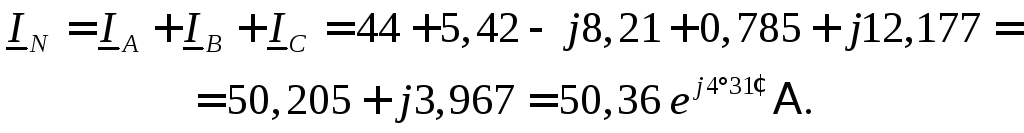
Полные мощности фаз:
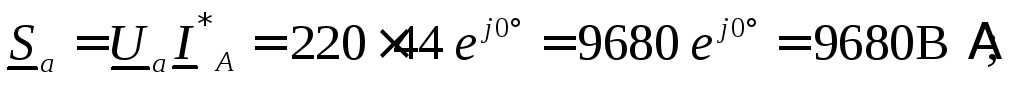
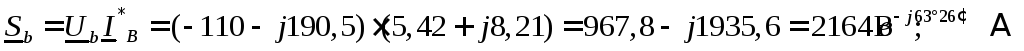
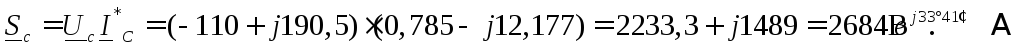
Так как вещественная часть полной мощности есть активная мощность цепи, а мнимая часть – реактивная, то, просуммировав отдельно вещественные, а затем мнимые части мощностей трех фаз, определяем трехфазную активную и реактивную мощности.
Активная трехфазная мощность
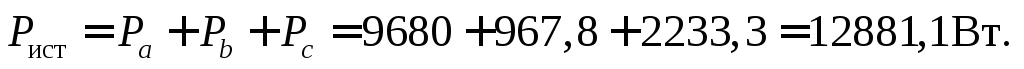
Реактивная трехфазная мощность
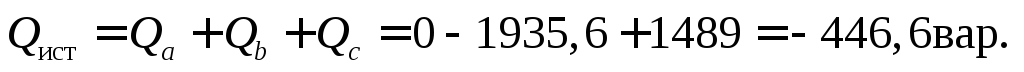
Полная мощность
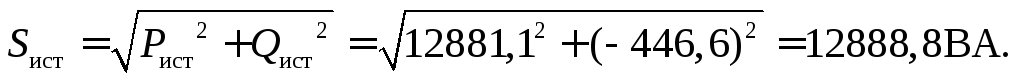
Активная трехфазная мощность нагрузки может быть определена суммой активных мощностей потребителей каждой из фаз
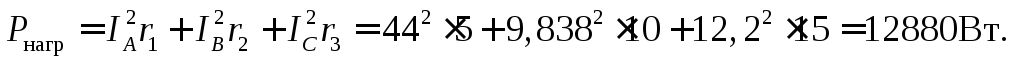
Относительная ошибка вычислений для активной мощности
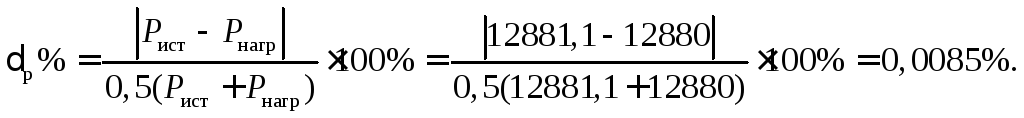
Реактивная трехфазная мощность нагрузки также определяется суммой реактивных мощностей потребителей каждой из фаз
Суммарная реактивная мощность всех потребителей
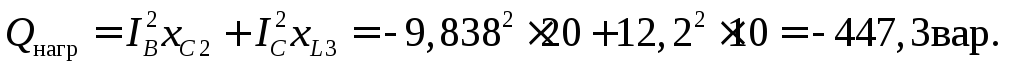
Относительная ошибка вычислений для активной мощности
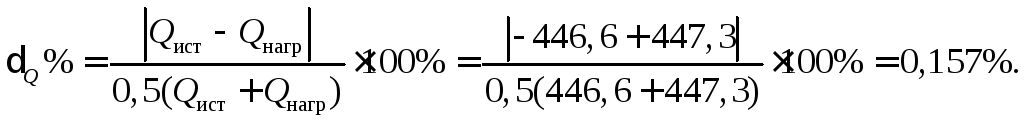
Ошибка менее одного процента допускается. Таким образом, баланс активных и реактивных мощностей соблюдается, значит токи определены правильно.
Векторную диаграмму размещаем на комплексной плоскости с осями +1 и + j, рисунок 3.21. Выбираем масштаб векторов тока равным 10 А/деление, а векторов напряжения – 40 В/деление. Строим векторы фазных напряжений, а затем векторы токов. Длина вектора соответствует в масштабе модулю показательной формы соответствующего выражения тока или напряжения, а угол, под которым этот вектор строится к вещественной оси, равен аргументу комплексного значения величины.
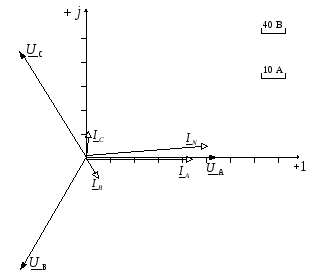
Рисунок 10 – Векторная диаграмма при соединении
потребителей звездой с нейтральным проводом
2. Расчёт трёхфазной цепи при соединении потребителей треугольником.
Нарисуем схему трёхфазной цепи, причем элементы из фазы A, B, C соединения потребителей звездой подключим соответственно между точками ab, bc, ca при соединении потребителей треугольником (рисунок 11).
В комплексной форме записи линейные напряжения на нагрузке:
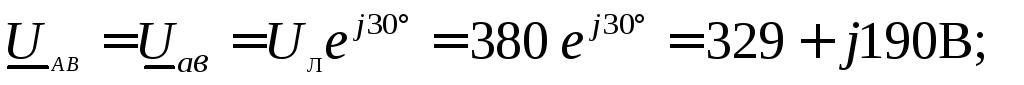
Рисунок 11 – Схема трёхфазной цепи при соединении потребителей
треугольником
Сопротивления фаз нагрузки в комплексной форме:
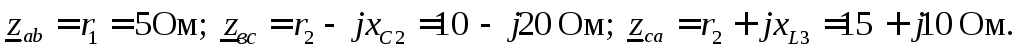
Фазные токи определяем по закону Ома:
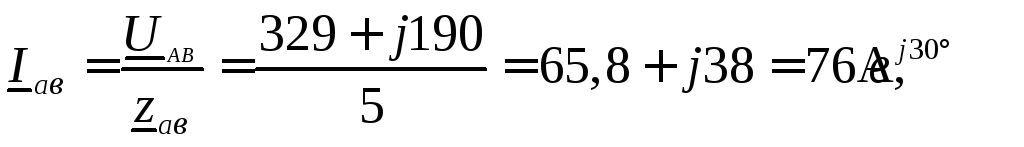
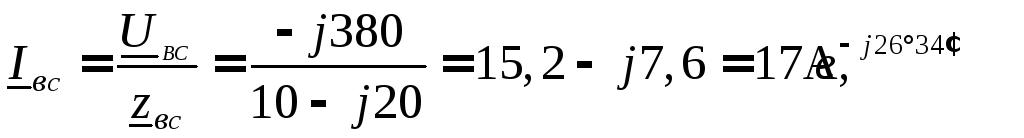
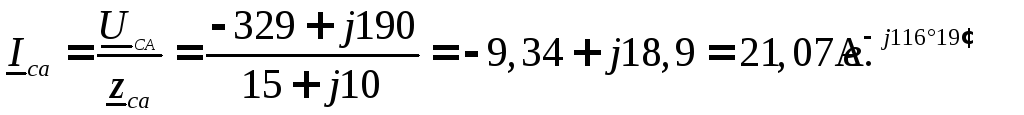
Для определения линейных токов используем первый закон Кирхгофа для точек a,в,cсхемы (рисунок 11)
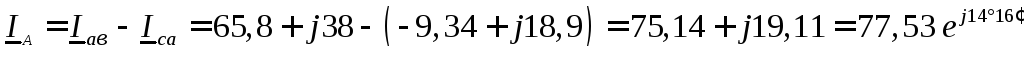 А,
А,
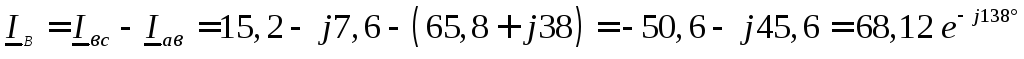 А,
А,
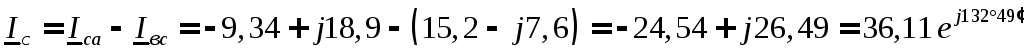 А.
А.
Полные комплексные мощности
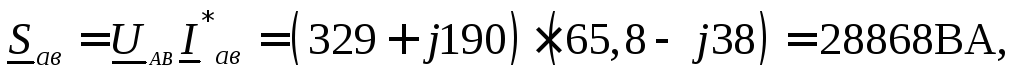
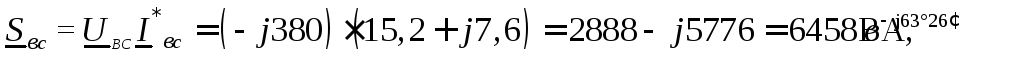
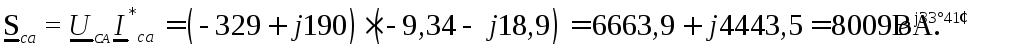
Трехфазная активная мощность
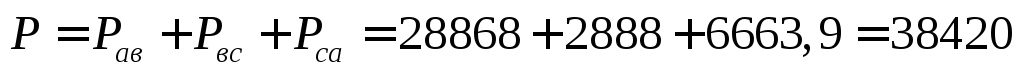 Вт.
Вт.
Трехфазная реактивная мощность
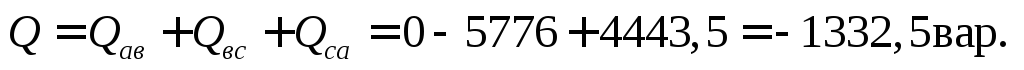
Трехфазная полная мощность
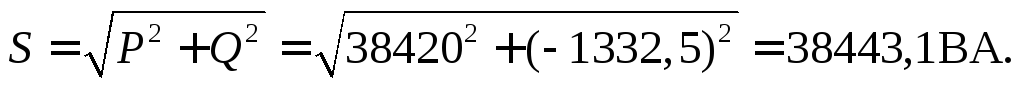
Векторную диаграмму токов для нагрузки, соединенной треугольником,строим в масштабе на комплексной плоскости относительно осей +1 и + j (рисунок12).На векторной диаграмме линейные токи получены на основании первого закона Кирхгофа, путем вычитания одного вектора фазного тока из соответствующего другого.
Рисунок 12 – Векторная диаграмма токов для
нагрузки, соединённой треугольником
ЗАДАЧА 1
РАСЧЕТ ЛИНЕЙНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
ПОСТОЯННОГО ТОКА
Для цепи, изображенной на рисунке 13, известны ЭДС Е1, Е2 и внутренние сопротивления r01, r02 источников питания, а также сопротивления r1–r6. Необходимо:
1. Составить систему уравнений для определения токов путем непосредственного применения законов Кирхгофа. Решать эту систему уравнений не следует.
2. Определить токи ветвей методом контурных токов.
3. Составить баланс мощностей.
4. Построить потенциальную диаграмму для контура, включающего две ЭДС.
Значения параметров элементов цепи приведены в таблице 1. Теоретический материал и пример расчета даны во втором разделе пособия, а также в учебниках [1 – 4, 10].
Таблица 1 – Числовые значения исходных данных к задаче № 3
Вариант
E1
E2
r01
r02
r1
r2
r3
r4
r5
r6
B
Ом
1
2
3
4
5
6
7
8
9
0
27
12
127
127
36
220
127
220
127
36
12
127
110
12
127
36
220
380
36
220
0,1
0,3
0,1
0,4
0,5
0,3
0,6
0,5
0,7
1,8
0,8
0,6
1,0
1,2
0,7
0,8
1,2
1,5
1,2
2,8
5
3
9
4
6
6
7
9
5
9
3
8
4
7
3
8
4
3
3
6
7
5
5
2
9
3
1
6
7
3
6
3
5
2
3
6
2
5
5
8
3
4
6
4
5
4
5
3
8
6
7
5
7
5
3
6
8
8
9
3
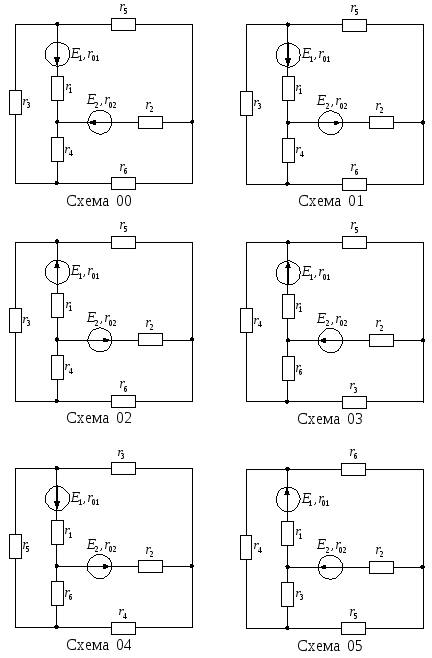
Рисунок 13 – Варианты электрических цепей к задаче № 1
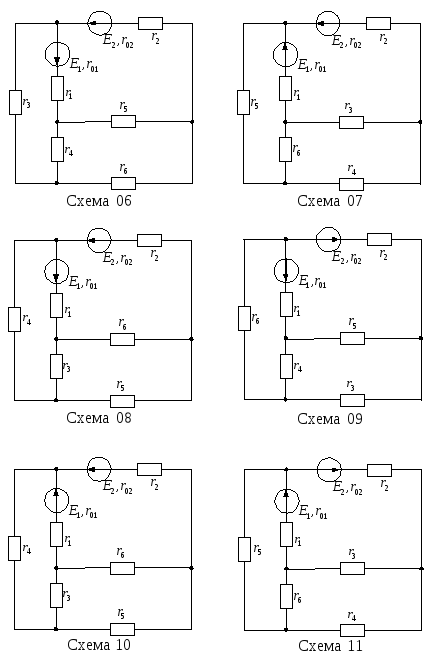
Продолжение рисунка 13
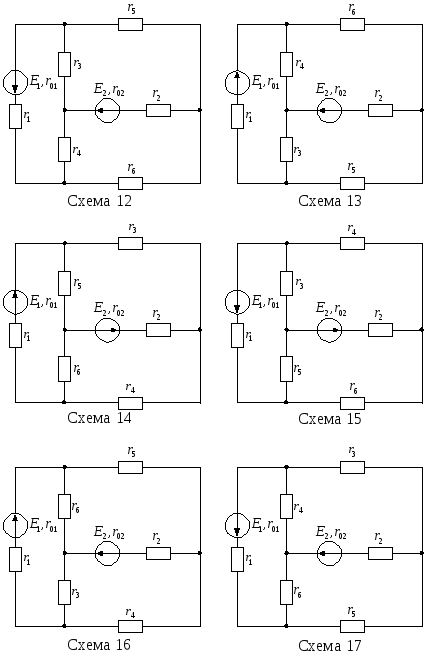
Продолжение рисунка 13
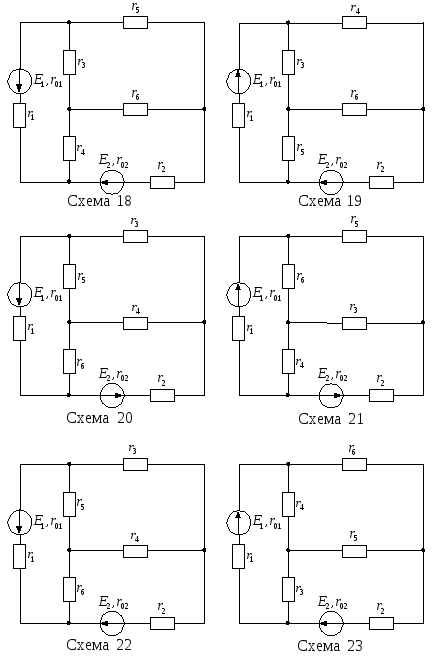
Продолжение рисунка 13
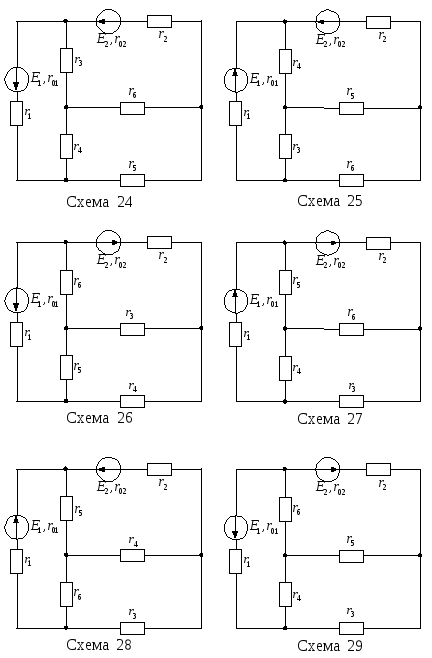
Продолжение рисунка 13
Продолжение рисунка 13
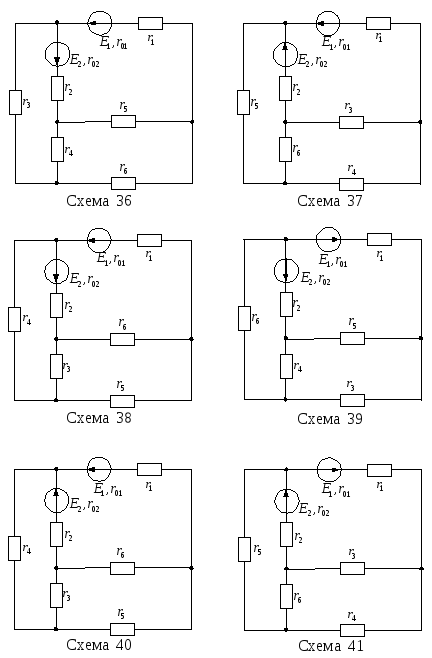
Продолжение рисунка 13
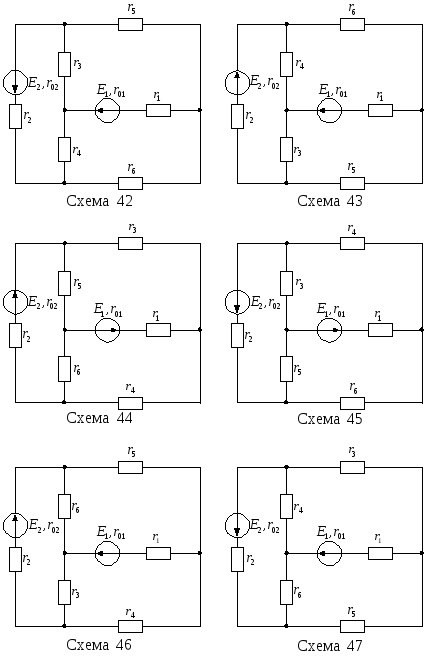
Продолжение рисунка 13
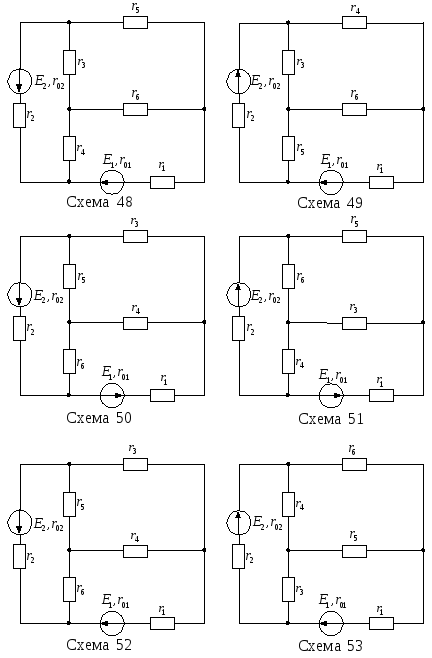
Продолжение рисунка 13
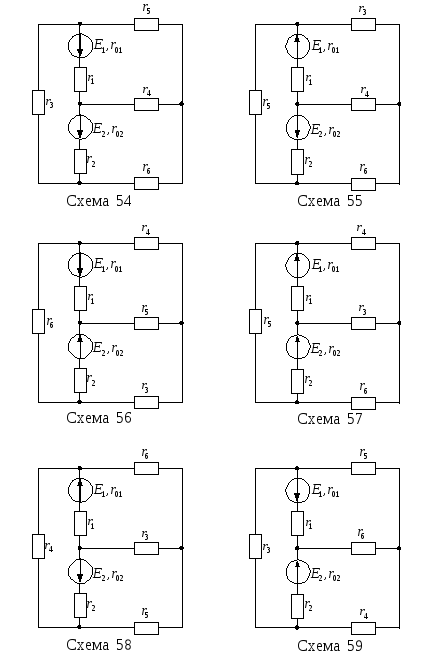
Продолжение рисунка 13
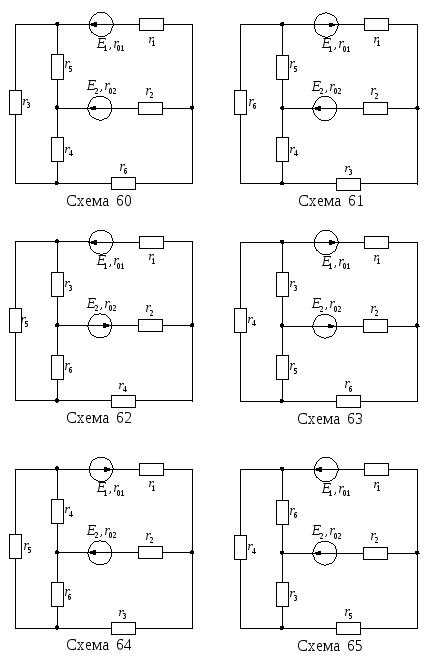
Продолжение рисунка 13
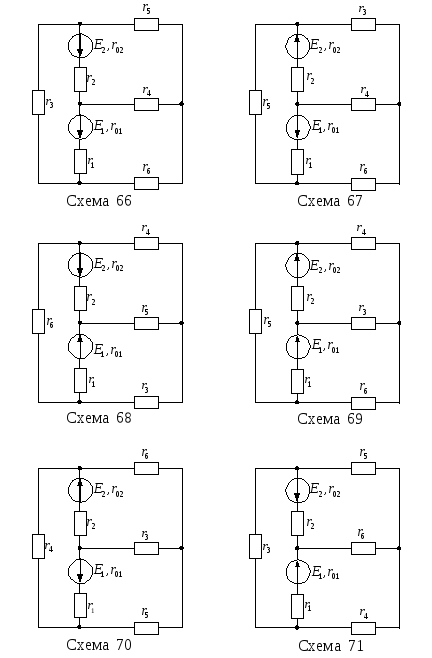
Продолжение рисунка 13
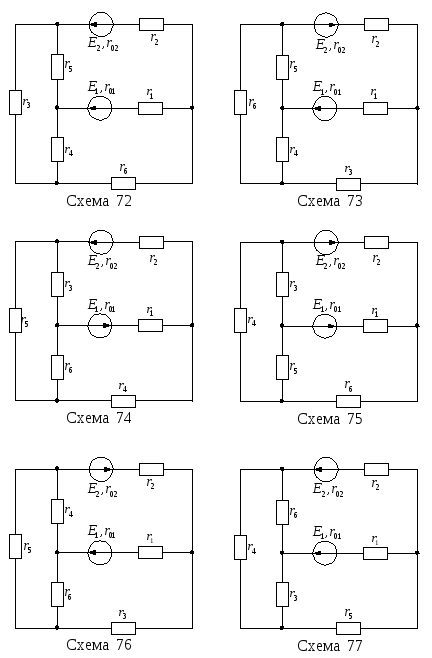
Продолжение рисунка 13
Продолжение рисунка 13
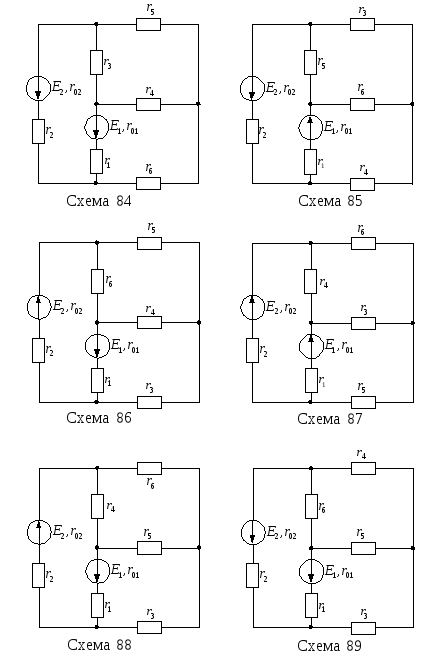 Продолжение рисунка
13
Продолжение рисунка
13
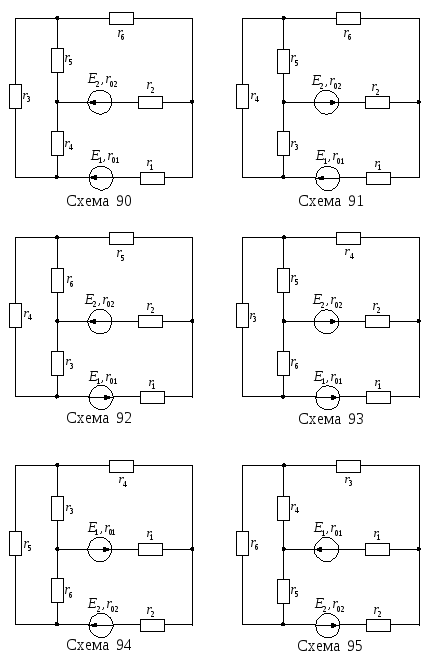
Продолжение рисунка 13
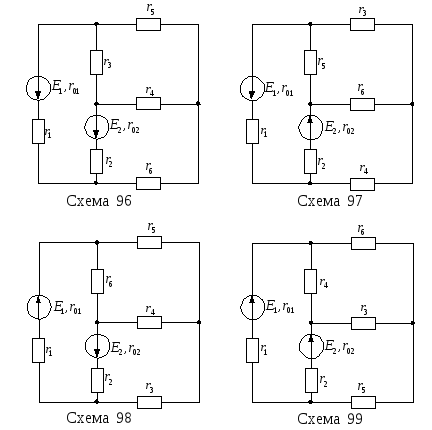
Продолжение рисунка 13
Принципиальная схема закона Ома[Как читать символы] • Закон Ома
Простая электрическая схема по закону Ома содержит сопротивление, подключенное последовательно к источнику постоянного напряжения.
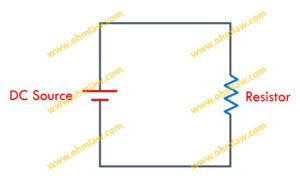
Две параллельные линии, одна из которых имеет сравнительно большую длину, представляют источник постоянного тока, а символ зигзага представляет резистор. В то время как простые линии используются для обозначения проводов.
Приведенная выше диаграмма верна для общего случая, на практике нам нужно добавить амперметр и вольтметр для измерения.Теперь наша диаграмма с инструментами будет выглядеть так:

Давайте разберемся с компонентами нашей принципиальной схемы.
Батарея: это источник постоянного напряжения, обеспечивающий питание внутренней цепи. Как мы изучили утверждение Ома: V = IR. Фактически, V — это батарея или источник напряжения, который питает всю схему.
Амперметр: он считывает ток, протекающий по всей цепи. Помните, что амперметр всегда подключается последовательно к цепи.
Вольтметр: Считывает напряжение на резисторе. Помните, что вольтметр всегда подключается параллельно компоненту.
А теперь давайте начнем изучать основы математики права на 5 различных примерах.
Пример 1: Батарея 10 В подключается последовательно с сопротивлением 20 кОм. Найдите ток, протекающий по цепи.
Решение: Использование V 1 = I 1 R 1 .
I 1 = V 1 / R 1 = 0.5 мА
Пример 2: Источник 15 В подключается к неизвестному резистору. Значение тока измеряется как 5 мА. Найдите значение
р.Решение: R 2 = В 2 / I 2 = 15 В / 5 мА = 3 кОм
Пример 3: Резистор 50 кОм подключается к источнику переменного тока 25 В постоянного тока. Найдите значение неизвестного тока, протекающего по этой цепи.
Решение: I 3 = В 3 / R 3 = 25 В / 50 кОм = 0,5 мА
Пример 4: Рассеиваемая мощность через сопротивление 29 кОм составляет 15 Вт.Найдите значение тока и входного напряжения, подаваемого источником.
Решение: Здесь будут использоваться формулы: I = SQRT (P / R) и V = SQRT (P * R). Вы можете узнать обо всех этих формулах из Ohmic Wheel.
Пример 5: R5 = 10 Ом и P5 = 20 Вт
Решение: V5 = 14,14 и I5 = 1,414
.ЗаконОма — Заявление, формула, вывод, применение, ограничения
- Классы
- Класс 1–3
- Класс 4–5
- Класс 6–10
- Класс 11–12
- КОНКУРЕНТНЫЙ ЭКЗАМЕН
- BNAT 000 000 NC Книги
- Книги NCERT для класса 5
- Книги NCERT для класса 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- Книги NCERT для класса 11
- Книги NCERT для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT 9000 9000
- NCERT Exemplar Class
- Решения RS Aggarwal, класс 12
- Решения RS Aggarwal, класс 11
- Решения RS Aggarwal, класс 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- RD Sharma Class 6 Решения
- Решения RD Sharma Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- BNAT 000 000 NC Книги
- PHYSICS
- Механика
- Оптика
- Термодинамика Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Теорема Пифагора 0004
- 000300030004 9000
- Простые числа
- Взаимосвязи и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Деление фракций
- Классы
- 000
- 000
- 000
- 000
- 000
- 000 Microology
- 000
- 000 Microology
- 000 BIOG3000
- FORMULAS
- Математические формулы
- Алгебраические формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- 0003000 PBS4000
- 000300030002 Примеры калькуляторов химии Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образцы документов CBSE чел для класса 12
- CBSE Контрольный документ за предыдущий год Класс 10
- Контрольный документ за предыдущий год CBSE, класс 12
- HC Verma Solutions Class 11 Physics
- Решения HC Verma, класс 12, физика
- Решения Лакмира Сингха, класс 9
- Решения Лакмира Сингха, класс 10
- Решения Лакмира Сингха, класс 8
- CBSE Notes
- Примечания CBSE класса 7
- Примечания к редакции
- CBSE Class
- Примечания к редакции класса 10 CBSE
- Примечания к редакции класса 11 CBSE 9000 4
- Примечания к редакции класса 12 CBSE
- Дополнительные вопросы CBSE
- Дополнительные вопросы по математике класса 8 CBSE
- Дополнительные вопросы по науке 8 класса CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- Дополнительные вопросы по науке класса 9 CBSE
Дополнительные вопросы по математике для класса 10
- CBSE Class
- Дополнительные вопросы по науке, класс 10 по CBSE
- , класс 3
- , класс 4
- , класс 5
- , класс 6
- , класс 7
- , класс 8
- , класс 9 Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для класса 11 по физике
- Решения NCERT для класса 11 Химия Решения для биологии класса 11
- Решения NCERT для математики класса 11 9 0003 NCERT Solutions Class 11 Accountancy
- NCERT Solutions For Класс 12 по физике
- Решения NCERT для химии класса 12
- Решения NCERT для класса 12 по биологии
- Решения NCERT для класса 12 по математике
- Решения NCERT Класс 12 Бухгалтерия
- Решения NCERT, класс 12, бизнес-исследования
- Решения NCERT, класс 12 Экономика
- NCERT Solutions Class 12 Accountancy Part 1
- NCERT Solutions Class 12 Accountancy Part 2
- NCERT Solutions Class 12 Micro-Economics
- NCERT Solutions Class 12 Commerce
- NCERT Solutions Class 12 Macro-Economics
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для математики класса 6
- Решения NCERT для науки класса 6
- Решения NCERT для социальных наук класса 6
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для класса 7 Наука
- Решения NCERT для класса 7 по социальным наукам
- Решения NCERT для класса 7 Английский
- Решения NCERT для класса 8 Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для социальных наук 8 класса
- Решение NCERT ns для класса 8 Английский
- Решения NCERT для социальных наук класса 9
- Решения NCERT для математики класса 9 Глава 1
- Решения NCERT для Математика класса 9 Глава 2
- Решения NCERT для математики класса 9 Глава 3
- Решения NCERT для математики класса 9 Глава 4 Решения NCERT
- для математики класса 9 Глава 5
- Решения NCERT для математики класса 9 Глава 6
- Решения NCERT для Математика класса 9 Глава 7
- Решения NCERT для математики класса 9 Глава 8 Решения NCERT
- для математики класса 9 Глава 9 Решения NCERT
- для математики класса 9 Глава 10
- Решения NCERT для математики класса 9 Глава 11
- Решения NCERT для Математика класса 9 Глава 12
- Решения NCERT для математики класса 9 Глава 13 Решения
- NCERT для математики класса 9 Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки класса 9 Глава 1
- Решения NCERT для науки класса 9 Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для Науки Класса 9 Глава 4
- Решения NCERT для Науки Класса 9 Глава 5
- Решения NCERT для Науки Класса 9 Глава 6
- Решения NCERT для Науки Класса 9 Глава 7
- Решения NCERT для Класса 9 Наука Глава 8
- Решения NCERT для Науки Класса 9 Глава 9
- Решения NCERT для Науки Класса 9 Глава 10
- Решения NCERT для Науки Класса 9 Глава 12
- Решения NCERT для Науки Класса 9 Глава 11
- Решения NCERT для Класса 9 Наука Глава 13
- Решения NCERT для класса 9 Наука Глава 14
- Решения NCERT для класса 9 по науке Глава 15
- Решения NCERT для класса 10 по социальным наукам
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- Решения NCERT для математики класса 10 Глава 3
- Решения NCERT для математики класса 10 Глава 4
- Решения NCERT для математики класса 10 Глава 5
- Решения NCERT для математики класса 10 Глава 6
- Решения NCERT для математики класса 10 Глава 7
- Решения NCERT для математики класса 10 Глава 8
- Решения NCERT для математики класса 10 Глава 9
- Решения NCERT для математики класса 10 Глава 10
Ома | Электрические цепи
Закон 11,2 Ома (ESBQ6)
Три основные величины для электрических цепей: ток, напряжение (разность потенциалов) и сопротивление . Резюме:
Электрический ток, \ (I \), определяется как скорость прохождения заряда через цепь.
Разность потенциалов или напряжение \ (В \) — это количество энергии на единицу заряда, необходимое для перемещения этого заряда между двумя точками в цепи.
Сопротивление, \ (R \), является мерой того, насколько «трудно» протолкнуть ток через элемент схемы.
Теперь посмотрим, как эти три величины связаны друг с другом в электрических цепях.
Важная взаимосвязь между током, напряжением и сопротивлением в цепи была обнаружена Георгом Симоном Омом и называется законом Ома .
- Закон Ома
Величина электрического тока через металлический проводник при постоянной температуре в цепи пропорциональна напряжению на проводнике и может быть описана как
. \ (I = \ frac {V} {R} \)где \ (I \) — ток через проводник, \ (V \) — напряжение на проводнике, а \ (R \) — сопротивление проводника.Другими словами, при постоянной температуре сопротивление проводника постоянно, независимо от приложенного к нему напряжения или проходящего через него тока.
Ома говорит нам, что если проводник имеет постоянную температуру, ток, протекающий по проводнику, прямо пропорционален напряжению на нем. Это означает, что если мы нанесем напряжение на ось x графика, а ток на ось y графика, мы получим прямую линию.
Наклон прямолинейного графика связан с сопротивлением проводника как \ [\ frac {I} {V} = \ frac {1} {R}.\] С точки зрения постоянного сопротивления это можно изменить как: \ [R = \ frac {V} {I}. \]
Закон Ома
Цель
Для определения взаимосвязи между током, протекающим через резистор, и разностью потенциалов (напряжением) на том же резисторе.
Аппарат
4 ячейки, 4 резистора, амперметр, вольтметр, соединительные провода
Метод
Этот эксперимент состоит из двух частей. В первой части мы будем варьировать приложенное к резистору напряжение и измерять результирующий ток в цепи.Во второй части мы будем изменять ток в цепи и измерять результирующее напряжение на резисторе. После получения обоих наборов измерений мы исследуем взаимосвязь между током и напряжением на резисторе.
Изменение напряжения:
Настройте схему в соответствии со схемой 1), начиная с одной ячейки.
Нарисуйте следующую таблицу в своем лабораторном журнале.
Количество ячеек
Напряжение, В (\ (\ text {V} \))
Ток, I (\ (\ text {A} \))
\ (\ text {1} \)
\ (\ text {2} \)
\ (\ text {3} \)
\ (\ text {4} \)
Попросите учителя проверить электрическую цепь перед включением питания.
Измерьте напряжение на резисторе с помощью вольтметра и ток в цепи с помощью амперметра.
Добавьте в схему еще одну ячейку \ (\ text {1,5} \) \ (\ text {V} \) и повторите измерения.
Повторяйте, пока не получите четыре ячейки и не заполните таблицу.
Изменение тока:
Настройте схему в соответствии со схемой 2), начиная с одного резистора в цепи.
Нарисуйте следующую таблицу в своем лабораторном журнале.
Напряжение, В (\ (\ text {V} \))
Ток, I (\ (\ text {A} \))
Попросите учителя проверить вашу электрическую схему перед включением питания.
Измерьте ток и напряжение на единственном резисторе.
Теперь добавьте еще один резистор в цепь и снова измерьте ток и напряжение только на исходном резисторе. Продолжайте добавлять резисторы, пока у вас не будет четырех последовательно, но не забывайте каждый раз измерять напряжение только на исходном резисторе. Введите измеренные вами значения в таблицу.
Анализ и результаты
Используя данные, записанные в первой таблице, постройте график зависимости тока от напряжения.Поскольку напряжение — это переменная, которую мы изменяем напрямую, это независимая переменная, которая будет отложена по оси \ (x \). Ток является зависимой переменной и должен быть нанесен на ось \ (y \).
Используя данные, записанные во второй таблице, постройте график зависимости напряжения от тока. В этом случае независимой переменной является ток, который должен быть нанесен на ось \ (x \), а напряжение является зависимой переменной и должно быть нанесено на ось \ (y \).
Выводы
Изучите график, который вы построили из первой таблицы. Что происходит с током через резистор при увеличении напряжения на нем? т.е. увеличивается или уменьшается?
Изучите график, который вы построили на основе второй таблицы. Что происходит с напряжением на резисторе, когда ток через резистор увеличивается? т.е. увеличивается или уменьшается?
Подтверждают ли результаты ваших экспериментов закон Ома? Объясни.
Вопросы и обсуждение
- Для каждого из ваших графиков рассчитайте градиент и по нему определите сопротивление исходного резистора. Получаете ли вы одно и то же значение, когда рассчитываете его для каждого из ваших графиков?
Как вы можете найти сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_0 \)?
Присоединяйтесь к тысячам учащихся, улучшающих свои научные оценки онлайн с помощью Siyavula Practice.
Зарегистрируйтесь здесьЗакон Ома
Упражнение 11.1Постройте график напряжения (по оси X) и тока (по оси Y).
Какой тип графика вы получите (прямолинейный, парабола, другая кривая)
прямая линия
Рассчитайте градиент графика.
Градиент графика (\ (m \)) — это изменение тока, деленное на изменение напряжения:
\ begin {align *} m & = \ frac {\ Delta I} {\ Delta V} \\ & = \ frac {(\ text {1,6}) — (\ text {0,4})} {(\ text {12}) — (\ text {3})} \\ & = \ текст {0,13} \ end {выровнять *}Подтверждают ли результаты ваших экспериментов закон Ома? Объясни.
Да. График с прямой линией получается, когда мы строим график зависимости напряжения от тока.
Как вы можете найти сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_ {0} \)?
Вы начинаете с подключения известного резистора в цепь с источником питания. Теперь вы читаете напряжение источника питания и записываете его.
Затем вы последовательно подключаете два резистора.Теперь вы можете измерить напряжение на каждом из резисторов.
Итак, мы можем найти напряжения для двух резисторов. Теперь отметим, что:
\ [V = IR \]Итак, используя это и тот факт, что для резисторов, включенных последовательно, ток везде одинаковый в цепи, мы можем найти неизвестное сопротивление.
\ begin {align *} V_ {0} & = IR_ {0} \\ I & = \ frac {V_ {0}} {R_ {0}} \\ V_ {U} & = IR_ {U} \\ I & = \ frac {V_ {U}} {R_ {U}} \\ \ frac {V_ {U}} {R_ {U}} & = \ frac {V_ {0}} {R_ {0}} \\ \ поэтому R_ {U} & = \ frac {V_ {U} R_ {0}} {V_ {0}} \ end {выровнять *}Омические и неомические проводники (ESBQ7)
Проводники, которые подчиняются закону Ома, имеют постоянное сопротивление, когда на них изменяется напряжение или увеличивается ток через них.Эти проводники называются омическими проводниками, проводниками. График зависимости тока от напряжения на этих проводниках будет прямолинейным. Некоторые примеры омических проводников — резисторы цепи и нихромовая проволока.
Как вы видели, когда мы говорим о законе Ома, есть упоминание о постоянной температуре . Это связано с тем, что сопротивление некоторых проводников изменяется при изменении их температуры. Эти типы проводников называются неомическими проводниками , потому что они не подчиняются закону Ома.Лампочка — типичный пример неомического проводника. Другими примерами неомических проводников являются диоды и транзисторы.
В лампочке сопротивление нити накала резко возрастает, когда она нагревается от комнатной до рабочей температуры. Если мы увеличим напряжение питания в реальной цепи лампы, то увеличение тока приведет к увеличению температуры нити накала, что приведет к увеличению ее сопротивления. Это эффективно ограничивает увеличение тока.В этом случае напряжение и ток не подчиняются закону Ома.
Явление изменения сопротивления при изменении температуры присуще почти всем металлам, из которых сделано большинство проводов. Для большинства приложений эти изменения сопротивления достаточно малы, чтобы их можно было игнорировать. При применении металлических нитей накала ламп, температура которых сильно повышается (примерно до \ (\ text {1 000} \) \ (\ text {℃} \) и начиная с комнатной температуры), изменение довольно велико.
В общем, для неомических проводов график зависимости напряжения от тока не будет прямолинейным, что означает, что сопротивление не является постоянным для всех значений напряжения и тока.
Включен рекомендуемый эксперимент для неформальной оценки. В этом эксперименте учащиеся получат данные о токе и напряжении для резистора и лампочки и определят, какой из них подчиняется закону Ома. Вам потребуются лампочки, резисторы, соединительные провода, источник питания, амперметр и вольтметр. Учащиеся должны обнаружить, что резистор подчиняется закону Ома, а лампочка — нет.
Омические и неомические проводники
Aim
Чтобы определить, подчиняются ли два элемента схемы (резистор и лампочка) закону Ома
Аппарат
4 ячейки, резистор, лампочка, соединительные провода, вольтметр, амперметр
Метод
Две схемы, показанные на схемах выше, одинаковы, за исключением того, что в первой есть резистор, а во второй — лампочка.Настройте обе схемы выше, начиная с 1 ячейки. Для каждой цепи:
Измерьте напряжение на элементе схемы (резисторе или лампочке) с помощью вольтметра.
Измерьте ток в цепи с помощью амперметра.
Добавьте еще одну ячейку и повторяйте измерения, пока в вашей цепи не будет 4 ячейки.
Результаты
Нарисуйте в своей книге две таблицы, которые выглядят следующим образом.У вас должна быть одна таблица для измерений первой цепи с резистором и другая таблица для измерений второй цепи с лампочкой.
Количество ячеек | Напряжение, В (\ (\ text {V} \)) | Ток, I (\ (\ text {A} \)) |
\ (\ text {1} \) | ||
\ (\ text {2} \) | ||
\ (\ text {3} \) | ||
\ (\ text {4} \) |
Анализ
Используя данные в ваших таблицах, нарисуйте два графика \ (I \) (\ (y \) — ось) vs.\ (V \) (\ (x \) — ось), один для резистора и один для лампочки.
Вопросы и обсуждение
Внимательно изучите свои графики и ответьте на следующие вопросы:
Как должен выглядеть график зависимости \ (I \) от \ (V \) для проводника, подчиняющегося закону Ома?
Один или оба ваших графика выглядят так?
Какой можно сделать вывод о том, подчиняются ли резистор и / или лампочка закону Ома?
Имеет ли лампочка омический или неомический провод?
Использование закона Ома (ESBQ8)
Теперь мы готовы увидеть, как закон Ома используется для анализа схем.
Рассмотрим схему с ячейкой и омическим резистором R. Если сопротивление резистора равно \ (\ text {5} \) \ (\ text {Ω} \), а напряжение на резисторе равно \ (\ text { 5} \) \ (\ text {V} \), то мы можем использовать закон Ома для расчета тока, протекающего через резистор. Наша первая задача — нарисовать принципиальную схему. Решая любую проблему с электрическими цепями, очень важно составить схему схемы перед тем, как производить какие-либо расчеты. Принципиальная схема этой проблемы выглядит следующим образом:
Уравнение закона Ома: \ [R = \ frac {V} {I} \]
, который можно преобразовать в: \ [I = \ frac {V} {R} \]
Ток, протекающий через резистор:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {5} \ text {V}} {\ text {5} \ Omega} \\ & = \ текст {1} \ текст {А} \ end {align *}
Рабочий пример 1: Закон Ома
Изучите принципиальную схему ниже:
Сопротивление резистора равно \ (\ text {10} \) \ (\ text {Ω} \), а ток, проходящий через резистор, равен \ (\ text {4} \) \ (\ text {A} \ ).Какова разность потенциалов (напряжение) на резисторе?
Определите, как подойти к проблеме
Нам задают сопротивление резистора и ток, проходящий через него, и просят вычислить напряжение на нем. Мы можем применить закон Ома к этой проблеме, используя: \ [R = \ frac {V} {I}. \]
Решить проблему
Измените приведенное выше уравнение и замените известные значения на \ (R \) и \ (I \), чтобы найти \ (V \). \ begin {align *} R & = \ frac {V} {I} \\ R \ times I & = \ frac {V} {I} \ times I \\ V & = I \ раз R \\ & = \ текст {10} \ times \ text {4} \\ & = \ текст {40} \ текст {V} \ end {align *}
Напишите окончательный ответ
Напряжение на резисторе равно \ (\ text {40} \) \ (\ text {V} \).
Присоединяйтесь к тысячам учащихся, улучшающих свои научные оценки онлайн с помощью Siyavula Practice.
Зарегистрируйтесь здесьЗакон Ома
Упражнение 11.2Вычислите сопротивление резистора с разностью потенциалов \ (\ text {8} \) \ (\ text {V} \) на нем, когда ток равен \ (\ text {2} \) \ (\ text {A} \) протекает через него. Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора составляет:
. \ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {8} {2} \\ & = \ текст {4} \ текст {Ω} \ end {выровнять *}Какой ток будет протекать через резистор \ (\ text {6} \) \ (\ text {Ω} \) при разности потенциалов \ (\ text {18} \) \ (\ text {V} \) на концах? Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора составляет:
. \ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {18} {6} \\ & = \ текст {3} \ текст {А} \ end {выровнять *}Какое напряжение на резисторе \ (\ text {10} \) \ (\ text {Ω} \) при токе \ (\ text {1,5} \) \ (\ text {A} \) течет хоть это? Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора составляет:
. \ begin {align *} V & = I \ cdot R \\ & = (\ текст {1,5}) (10) \\ & = \ текст {15} \ текст {V} \ end {выровнять *}Резисторы последовательно и параллельно (ESBQ9)
В 10 классе вы узнали о резисторах и познакомились со схемами, в которых резисторы соединены последовательно и параллельно.В последовательной цепи есть один путь, по которому течет ток. В параллельной цепи есть несколько путей, по которым течет ток.
Когда в цепи более одного резистора, мы обычно можем рассчитать общее суммарное сопротивление всех резисторов. Это известно как сопротивление , эквивалентное .
Эквивалентное последовательное сопротивление
В цепи, в которой резисторы соединены последовательно, эквивалентное сопротивление — это просто сумма сопротивлений всех резисторов.
- Эквивалентное сопротивление в последовательной цепи,
Для последовательно подключенных n резисторов эквивалентное сопротивление составляет:
\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + \ ldots + R_ {n} \]
Применим это к следующей схеме.
Резисторы включены последовательно, следовательно:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {3} \ text {Ω} + \ text {10} \ text {Ω} + \ text {5} \ text {Ω} \\ & = \ текст {18} \ текст {Ω} \ end {align *}Эквивалентное параллельное сопротивление
В цепи, в которой резисторы включены параллельно, эквивалентное сопротивление определяется следующим определением.
- Эквивалентное сопротивление в параллельной цепи
Для резисторов \ (n \), включенных параллельно, эквивалентное сопротивление составляет:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ ldots + \ frac {1} {R_ {n}} \]
Применим эту формулу к следующей схеме.
Какое полное (эквивалентное) сопротивление в цепи?
\ begin {align *} \ frac {1} {R_ {p}} & = \ left (\ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}) } \право) \\ & = \ left (\ frac {1} {\ text {10} \ text {Ω}} + \ frac {1} {\ text {2} \ text {Ω}} + \ frac {1} {\ text { 1} \ text {Ω}} \ right) \\ & = \ left (\ frac {\ text {1} \ text {Ω} + \ text {5} \ text {Ω} + \ text {10} \ text {Ω}} {\ text {10} \ text { Ω}} \ right) \\ & = \ left (\ frac {\ text {16} \ text {Ω}} {\ text {10} \ text {Ω}} \ right) \\ R_ {p} & = \ text {0,625} \ text {Ω} \ end {align *}Последовательное и параллельное сопротивление
Упражнение 11.3Два \ (\ text {10} \) \ (\ text {kΩ} \) резистора соединены последовательно. Рассчитайте эквивалентное сопротивление.
Поскольку резисторы включены последовательно, мы можем использовать:
\ [R_ {s} = R_ {1} + R_ {2} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {10} \ text {kΩ} + \ text {10} \ text {kΩ} \\ & = \ текст {20} \ текст {кОм} \ end {выровнять *}Два резистора соединены последовательно.Эквивалентное сопротивление равно \ (\ text {100} \) \ (\ text {Ω} \). Если один резистор равен \ (\ text {10} \) \ (\ text {Ω} \), вычислите номинал второго резистора.
Поскольку резисторы включены последовательно, мы можем использовать:
\ [R_ {s} = R_ {1} + R_ {2} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ R_ {2} & = R_ {s} — R_ {1} \\ & = \ text {100} \ text {Ω} — \ text {10} \ text {Ω} \\ & = \ текст {90} \ текст {Ω} \ end {выровнять *}Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) подключены параллельно.Рассчитайте эквивалентное сопротивление.
Поскольку резисторы включены параллельно, мы можем использовать:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {100}} + \ frac {1} {\ text {10}} \\ & = \ frac {1 + 10} {\ text {100}} \\ & = \ frac {11} {\ text {100}} \\ R_ {p} & = \ text {9,09} \ text {kΩ} \ end {выровнять *}Два резистора подключены параллельно.Эквивалентное сопротивление равно \ (\ text {3,75} \) \ (\ text {Ω} \). Если сопротивление одного резистора равно \ (\ text {10} \) \ (\ text {Ω} \), каково сопротивление второго резистора?
Поскольку резисторы включены параллельно, мы можем использовать:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ \ frac {1} {R_ {2}} & = \ frac {1} {R_ {p}} — \ frac {1} {R_ {1}} \\ & = \ frac {1} {\ text {3,75}} — \ frac {1} {\ text {10}} \\ & = \ frac {\ text {10} — \ text {3,75}} {\ text {37,5}} \\ & = \ frac {\ text {6,25}} {\ text {37,5}} \\ R_ {2} & = \ текст {6} \ текст {Ω} \ end {выровнять *}Рассчитайте эквивалентное сопротивление в каждой из следующих цепей:
a) Резисторы включены параллельно, поэтому мы используем:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {3}} + \ frac {1} {\ text {2}} \\ & = \ frac {\ text {2} + \ text {3}} {\ text {6}} \\ & = \ frac {\ text {5}} {\ text {6}} \\ R & = \ текст {1,2} \ текст {Ω} \ end {выровнять *}b) Резисторы включены параллельно, поэтому мы используем:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ гидроразрыв {1} {R_ {4}} \\ & = \ frac {1} {\ text {2}} + \ frac {1} {\ text {3}} + \ frac {1} {\ text {4}} + \ frac {1} {\ text { 1}} \\ & = \ frac {\ text {6} + \ text {4} + \ text {3} + \ text {12}} {\ text {12}} \\ & = \ frac {\ text {25}} {\ text {12}} \\ R & = \ text {0,48} \ text {Ω} \ end {выровнять *}c) Резисторы включены последовательно, поэтому мы используем:
\ [R_ {s} = R_ {1} + R_ {2} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} \\ & = \ текст {5} \ текст {Ω} \ end {выровнять *}d) Резисторы включены последовательно, поэтому мы используем:
\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + R_ {4} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} + \ text {4} \ text {Ω} + \ text {1} \ text {Ω} \\ & = \ текст {10} \ текст {Ω} \ end {выровнять *}Применение закона Ома в последовательных и параллельных цепях (ESBQB)
Используя определения эквивалентного сопротивления для резисторов, включенных последовательно или параллельно, мы можем проанализировать некоторые схемы с этими установками.
Последовательные цепи
Рассмотрим схему, состоящую из трех резисторов и одного одиночная ячейка соединена последовательно.
Первый принцип, который нужно понять в отношении последовательных цепей, заключается в том, что величина тока одинакова через любой компонент в цепи. Это потому, что существует только один путь для движения электронов в последовательной цепи. По способу подключения батареи мы можем сказать, в каком направлении будет течь ток. Мы знаем, что ток по условию течет от положительного к отрицательному.Обычный ток в этой цепи будет течь по часовой стрелке от точки A к B, от C к D и обратно к A.
Мы знаем, что в последовательной цепи ток должен быть одинаковым во всех компонентах. Итак, мы можем написать:
\ [I = I_ {1} = I_ {2} = I_ {3}. \]Мы также знаем, что полное напряжение цепи должно быть равно сумме напряжений на всех трех резисторах. Итак, мы можем написать:
\ [V = V_ {1} + V_ {2} + V_ {3} \]Используя эту информацию и то, что мы знаем о вычислении эквивалентного сопротивления последовательно включенных резисторов, мы можем решить некоторые проблемы схемы.
Рабочий пример 2: Закон Ома, последовательная цепь
Вычислите ток (I) в этой цепи, если оба резистора имеют омическую природу.
Определите, что требуется
Нам необходимо рассчитать ток, протекающий в цепи.
Определите, как подойти к проблеме
Поскольку резисторы по своей природе омические, мы можем использовать закон Ома. Однако в цепи два резистора, и нам нужно найти полное сопротивление.
Найдите полное сопротивление в цепи
Поскольку резисторы соединены последовательно, общее (эквивалентное) сопротивление R составляет:
\ [R = R_ {1} + R_ {2} \]Следовательно,
\ begin {align *} R & = \ текст {2} + \ текст {4} \\ & = \ текст {6} \ текст {Ω} \ end {align *}Примените закон Ома
\ begin {align *} R & = \ frac {V} {I} \\ R \ times \ frac {I} {R} & = \ frac {V} {I} \ times \ frac {I} {R} \\ I & = \ frac {V} {R} \\ & = \ frac {12} {6} \\ & = \ текст {2} \ текст {А} \ end {align *}
Напишите окончательный ответ
В цепи протекает ток \ (\ text {2} \) \ (\ text {A} \).
Рабочий пример 3: Закон Ома, последовательная цепь
Два омических резистора (\ (R_ {1} \) и \ (R_ {2} \)) соединены последовательно с ячейкой. Найдите сопротивление \ (R_ {2} \), учитывая, что ток, текущий через \ (R_ {1} \) и \ (R_ {2} \), равен \ (\ text {0,25} \) \ ( \ text {A} \) и что напряжение на ячейке равно \ (\ text {1,5} \) \ (\ text {V} \). \ (R_ {1} \) = \ (\ text {1} \) \ (\ text {Ω} \).
Нарисуйте схему и введите все известные значения.
Определите, как подойти к проблеме.
Мы можем использовать закон Ома, чтобы найти полное сопротивление R в цепи, а затем вычислить неизвестное сопротивление, используя:
\ [R = R_ {1} + R_ {2} \], потому что он находится в последовательной цепи.
Найдите полное сопротивление
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {\ text {1,5}} {\ text {0,25}} \\ & = \ текст {6} \ текст {Ω} \ end {align *}Найдите неизвестное сопротивление
Мы знаем, что:
\ [R = \ text {6} \ text {Ω} \]и что
\ [R_ {1} = \ текст {1} \ текст {Ω} \]с
\ [R = R_ {1} + R_ {2} \] \ [R_ {2} = R — R_ {1} \]Следовательно,
\ [R_ {1} = \ text {5} \ text {Ω} \]Рабочий пример 4: Закон Ома, последовательная цепь
Для следующей схемы рассчитайте:
падение напряжения \ (V_1 \), \ (V_2 \) и \ (V_3 \) на резисторах \ (R_1 \), \ (R_2 \) и \ (R_3 \)
сопротивление \ (R_3 \).
Определите, как подойти к проблеме
Нам даны напряжение на ячейке и ток в цепи, а также сопротивления двух из трех резисторов. Мы можем использовать закон Ома для расчета падения напряжения на известных резисторах. Поскольку резисторы включены в последовательную цепь, напряжение равно \ (V = V_1 + V_2 + V_3 \), и мы можем вычислить \ (V_3 \). Теперь мы можем использовать эту информацию, чтобы найти напряжение на неизвестном резисторе \ (R_3 \).
Рассчитать падение напряжения на \ (R_1 \)
Используя закон Ома: \ begin {align *} R_1 & = \ frac {V_1} {I} \\ I \ cdot R_1 & = I \ cdot \ frac {V_1} {I} \\ V_1 & = {I} \ cdot {R_1} \\ & = 2 \ cdot 1 \\ V_1 & = \ текст {2} \ текст {V} \ end {align *}
Рассчитать падение напряжения на \ (R_2 \)
Снова используя закон Ома: \ begin {align *} R_2 & = \ frac {V_2} {I} \\ I \ cdot R_2 & = I \ cdot \ frac {V_2} {I} \\ V_2 & = {I} \ cdot {R_2} \\ & = 2 \ cdot 3 \\ V_2 & = \ текст {6} \ текст {V} \ end {align *}
Рассчитать падение напряжения на \ (R_3 \)
Поскольку падение напряжения на всех резисторах вместе должно быть таким же, как падение напряжения на ячейке в последовательной цепи, мы можем найти \ (V_3 \), используя: \ begin {align *} V & = V_1 + V_2 + V_3 \\ V_3 & = V — V_1 — V_2 \\ & = 18 — 2 — 6 \\ V_3 & am
.Согласно закону Ома, I ∝ V, но I 1 / V в уравнении мощности. Как?
In I = V / R, ток прямо пропорционален напряжению, но ток обратно пропорционален напряжению в P = VI?
Это еще один запутанный вопрос, который чаще всего задают на собеседованиях по электротехнике и электронике.
Согласно закону Ома, Ток увеличивается при увеличении напряжения (I = V / R), но Ток уменьшается при увеличении напряжения согласно формуле (P = VI).Как объяснить?
, т.е.
- По закону Ома: I ∝ V (ток прямо пропорционален напряжению. I = V / R)
- Согласно формуле мощности: I ∝ 1 / V (ток обратно пропорционален напряжению. I = P / V)
Короче говоря, согласно закону Ома (V = IR или I = V / R), который показывает, что ток прямо пропорционален напряжению, но согласно P = VI или I = P / V , это показывает, что ток обратно пропорционален напряжению.

Давайте устраним путаницу, связанную с утверждением.
P = V x I
На самом деле, это зависит от того, как вы увеличиваете параметры, то есть увеличиваете ли вы напряжение, сохраняя мощность источника постоянной, или она меняется.
- Если мощность источника постоянна, ток будет уменьшаться при увеличении напряжения.
- Если вы не заботитесь о мощности и просто замените батарею на новую с более высокой номинальной мощностью, это может увеличить ток при повышении напряжения, поскольку мощность больше не постоянна i.е. мощность также была увеличена.
В случае трансформатора, когда напряжение увеличивается, ток уменьшается, потому что мощность остается постоянной, т.е. мощность на обеих сторонах равна P = VI (без учета коэффициента мощности: Cos θ).
В = I x R
По закону Ома ток (I) прямо пропорционален напряжению (В), если сопротивление (R) и температура остаются постоянными.
Согласно формуле мощности, в ней говорится, что ток обратно пропорционален напряжению, если мощность остается прежней.
Как мы уже знаем, в повышающем трансформаторе, если напряжение увеличивается, ток уменьшается там, где мощность такая же (поскольку трансформатор только повышает или понижает значение тока и напряжения и не меняет значение мощность). Точно так же напряжение уменьшается при увеличении тока в понижающем трансформаторе.
То же самое и с электростанцией, где выработка электроэнергии постоянна. Если мощность на стороне генерации улучшится, увеличатся как ток, так и напряжение.
Вкратце:
- Если мощность постоянна = Напряжение обратно пропорционально току , т.е. В 1 / I в P = VxI .
- Если сопротивление и температура постоянны: Напряжение прямо пропорционально току , т.е. В I в В = IxR .
Именно поэтому по закону Ома ток прямо пропорционален напряжению, но обратно пропорционален формуле напряжения в мощности.
Связанные вопросы / ответы:
.

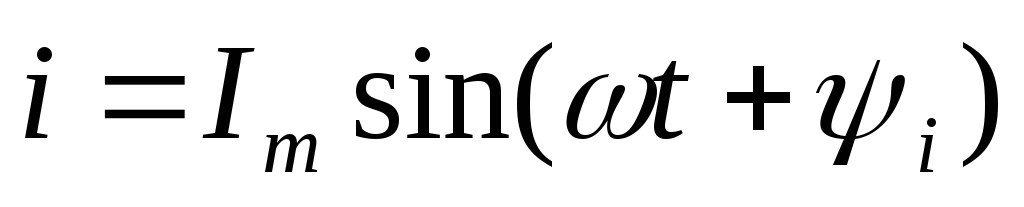 ;
; 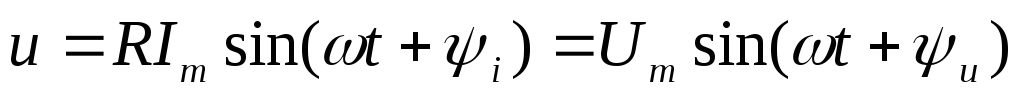 ,
,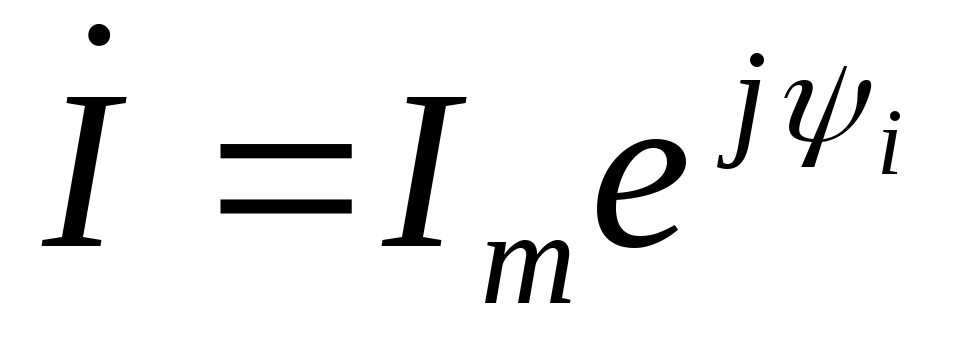 и
и 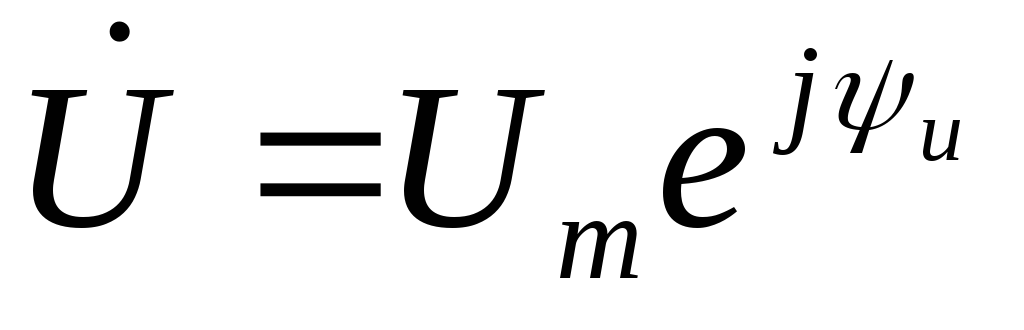
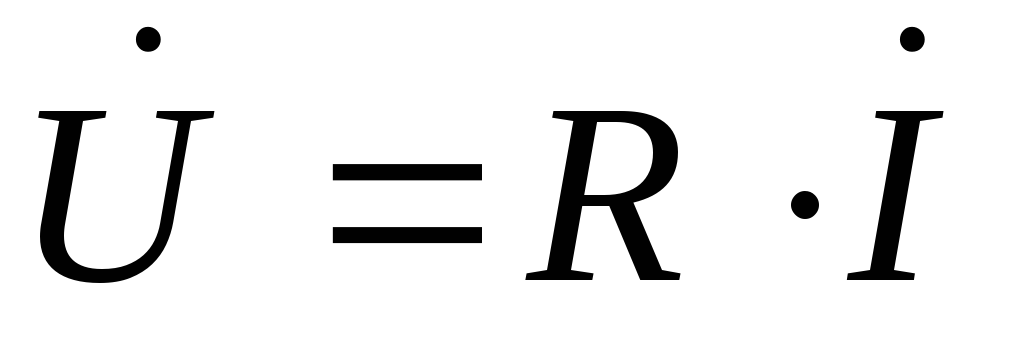
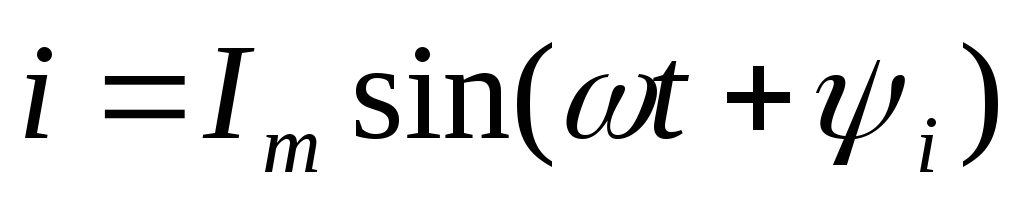 ,
,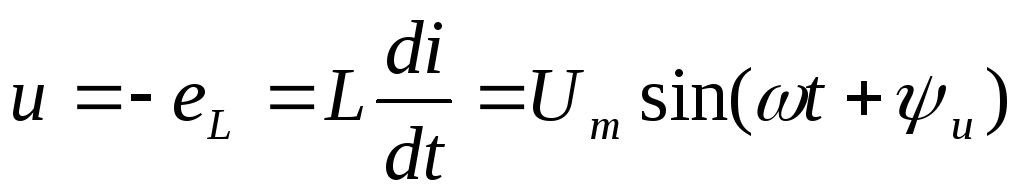
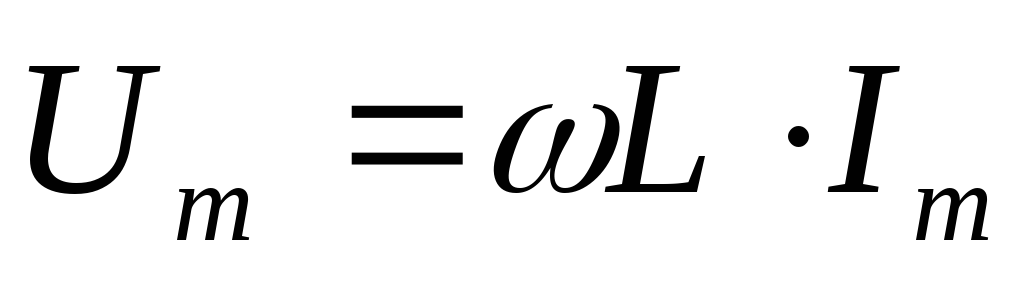 ,
,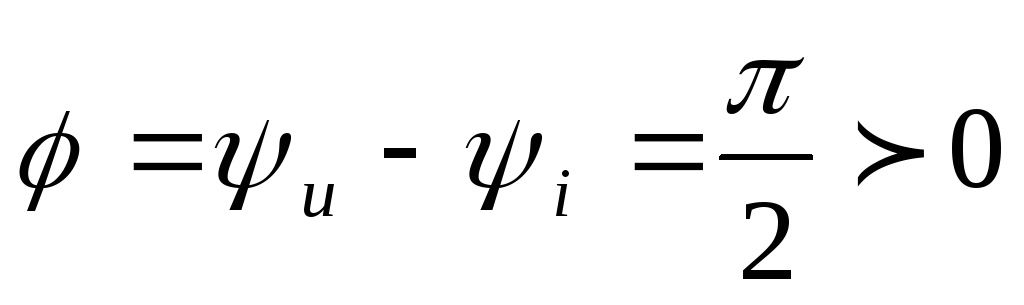 ,
,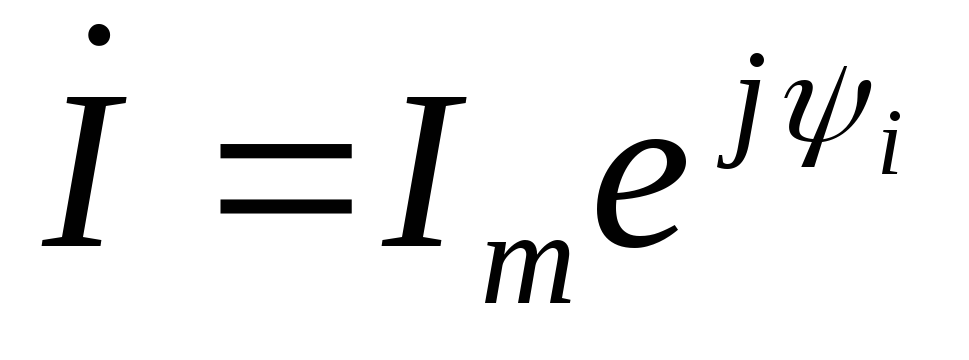 и
и 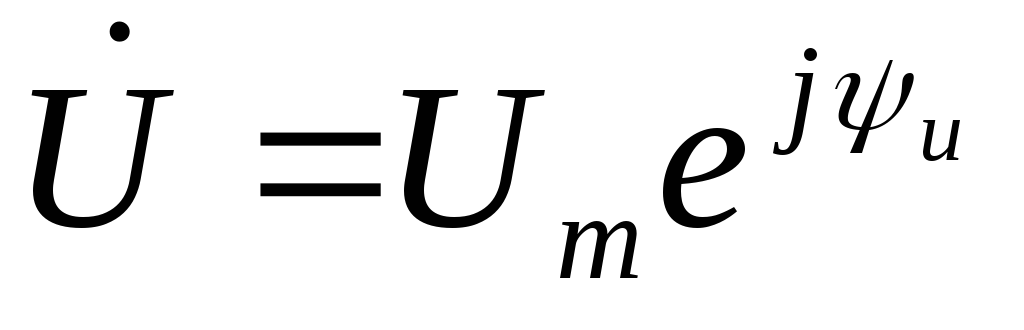
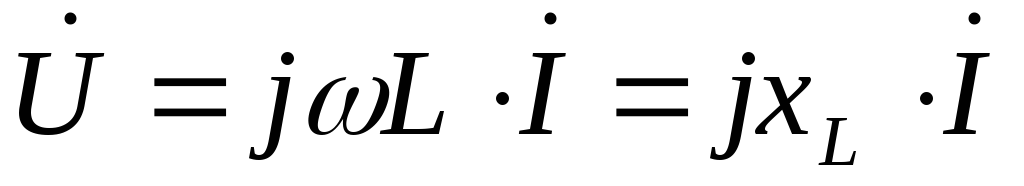 ,
,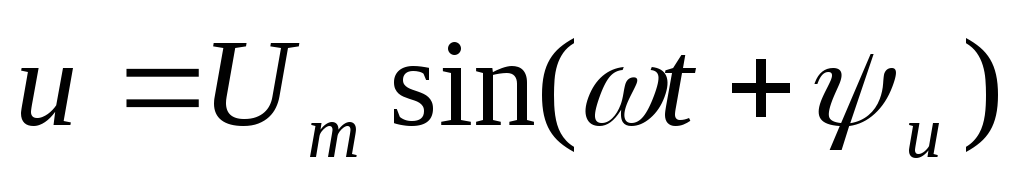
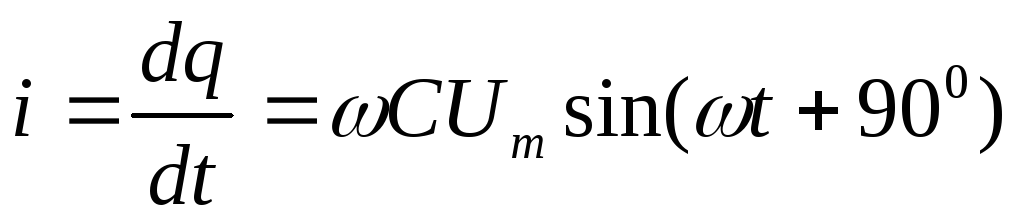
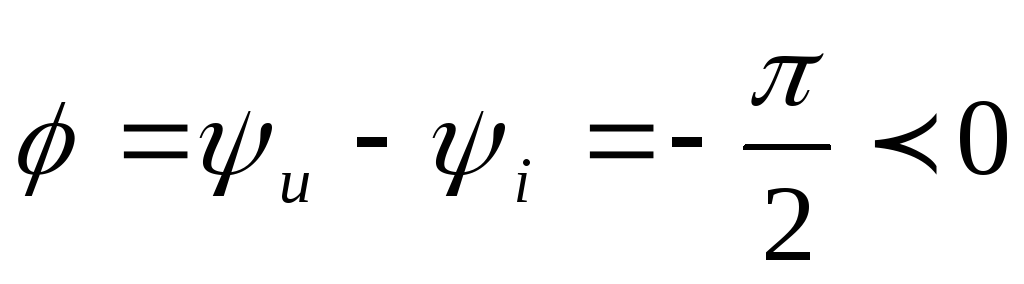 .
.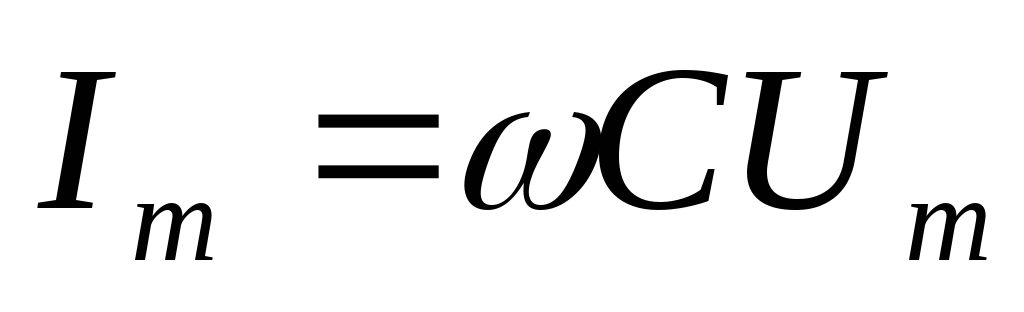 ,
,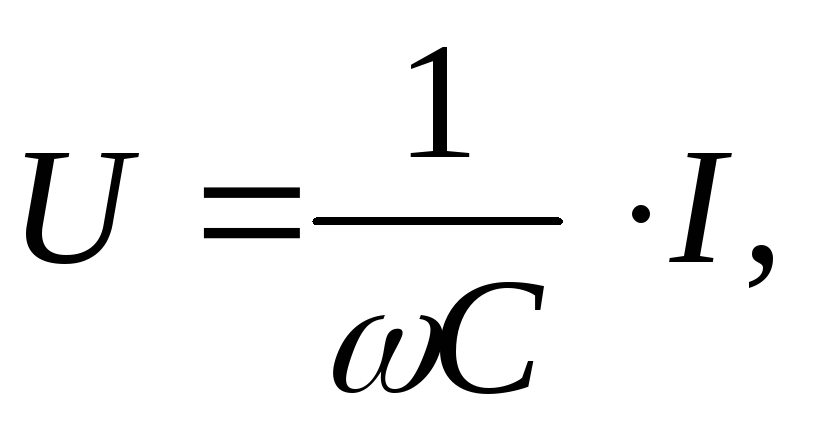
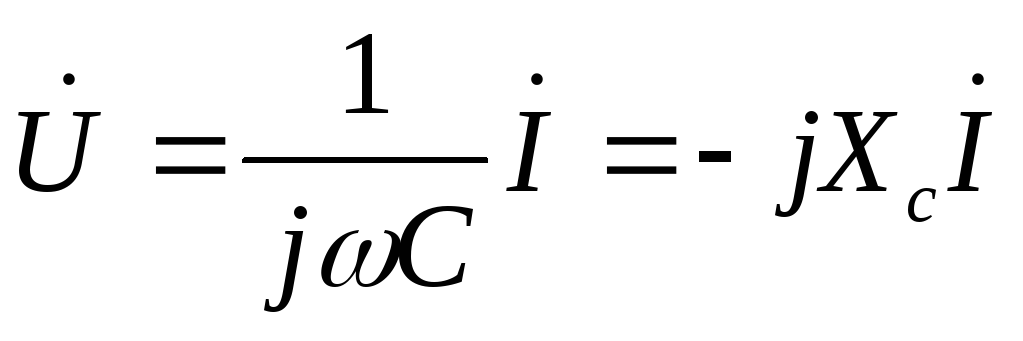 ,
,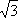 раз
меньше номинального линейного напряжения
сети.
раз
меньше номинального линейного напряжения
сети.