формули та визначення. Закон Ома для повного ланцюга
Головна / 2 Cool ReaderДля електрика та електронника одним із основних законів є Закон Ома. Щодня робота ставить перед спеціалістом нові завдання, і часто потрібно підібрати заміну згорілому резистору або групі елементів. Електрику часто доводиться міняти кабелю, щоб вибрати правильний потрібно «прикинути» струм у навантаженні, так доводиться використовувати найпростіші фізичні закони та співвідношення у повсякденному житті. Значення Закону Ома в електротехнікі колосальне, більшість дипломних робіт електротехнічних спеціальностей розраховуються на 70-90% за однією формулою.
Історична довідка
Рік відкриття Закон Ома — 1826 німецьким вченим Георгом Омом. Він емпірично визначив та описав закон про співвідношення сили струму, напруги та типу провідника. Пізніше з’ясувалося, що третя складова – це нічим іншим, як опір. Згодом цей закон назвали на честь відкривача, але законом справа не обмежилася, його прізвищем і назвали фізичну величину, як данину поваги до його робіт.
Величина, в якій вимірюють опір, названа на честь Георга Ома. Наприклад, резистори мають дві основні характеристики: потужність у ватах та опір – одиниця виміру в Омах, кілоомах, мегаомах тощо.
Закон Ома для ділянки ланцюга
Для опису електричного ланцюгане містить ЕРС можна використовувати закон Ома для ділянки ланцюга. Це найпростіша форма запису. Він виглядає так:
Де I – це струм, що вимірюється в Амперах, U – напруга у вольтах, R – опір в Омах.
Така формула нам говорить, що струм прямопропорційний напрузі і обернено-пропорційний опору — це точне формулювання Закону Ома. Фізичний сенс цієї формули — це описати залежність струму через ділянку ланцюга при відомому його опорі та напрузі.
Увага!Ця формула справедлива для постійного струмудля змінного струму вона має невеликі відмінності, до цього повернемося пізніше.
Крім співвідношення електричних величин дана форманам говорить про те, що графік залежності струму від напруги в опорі лінійний і виконується рівняння функції:
f(x) = ky або f(u) = IR або f(u)=(1/R)*I
Закон Ома для ділянки ланцюга застосовують для розрахунків опору резистора на ділянці схеми або визначення струму через нього при відомому напрузі і опорі. Наприклад, у нас є резистор R опором у 6 Ом, до його висновків додана напруга 12 В. Необхідно дізнатися, який струм протікатиме через нього. Розрахуємо:
Наприклад, у нас є резистор R опором у 6 Ом, до його висновків додана напруга 12 В. Необхідно дізнатися, який струм протікатиме через нього. Розрахуємо:
I=12 В/6 Ом=2 А
Ідеальний провідник не має опору, однак через структуру молекул речовини, з якої він складається, будь-яке тіло, що проводить, має опір. Наприклад, це спричинило переход з алюмінієвих проводів на мідні в домашніх електромережах. Питомий опір міді (Ом на 1 метр довжини) менший за алюміній. Відповідно мідні дроти менше гріються, витримують великі струми, отже, можна використовувати провід меншого перерізу.
Ще один приклад — спіралі нагрівальних приладів і резисторів мають великий питомий опір, т.к. виготовляються з різних високоомних металів, типу ніхрому, канталу та ін. Коли носії заряду рухаються через провідник, вони стикаються з частинками в кристалічній решітці, внаслідок цього виділяється енергія у вигляді тепла та провідник нагрівається. Чим більше струм — тим більше зіткнень — тим більше нагрівання.
Щоб знизити нагрівання, провідник потрібно або вкоротити, або збільшити його товщину (площу поперечного перерізу). Цю інформацію можна записати у вигляді формули:
R провід =ρ(L/S)
Де ρ – питомий опір Ом*мм 2 /м, L – довжина м, S – площа поперечного перерізу.
Закон Ома для паралельного та послідовного ланцюга
Залежно від типу з’єднання спостерігається різний характер перебігу струму та розподілу напруги. Для ділянки ланцюга послідовного з’єднання елементів напруга, струм та опір знаходяться за формулою:
Це означає, що в ланцюзі з довільної кількості послідовно з’єднаних елементів протікає той самий струм. При цьому напруга, що додається до всіх елементів (сума падінь напруги), дорівнює вихідній напруги джерела живлення. До кожного елемента окремо прикладена своя величина напруг і залежить від сили струму та опору конкретного:
U ел =I*R елемента
Опір ділянки ланцюга для паралельно з’єднаних елементів розраховується за такою формулою:
1/R=1/R1+1/R2
Для змішаного з’єднання потрібно наводити ланцюг до еквівалентного вигляду.
Закон Ома для повного ланцюга
Повний ланцюг передбачає наявність джерела живлення. Ідеальне джерело живлення – це прилад, який має єдину характеристику:
- напруга, якщо це джерело ЕРС;
- силу струму, якщо це джерело струму;
Таке джерело живлення здатне видати будь-яку потужність при постійних вихідних параметрах. У реальному джерелі живлення є ще й такі параметри як потужність і внутрішній опір. Власне, внутрішній опір – це уявний резистор, встановлений послідовно із джерелом ЭРС.
Формула Закону Ома для повного ланцюга виглядає схожим, але додається внутрішній опір ІП. Для повного ланцюга записується формулою:
I=ε/(R+r)
Де ε – ЕРС у Вольтах, R – опір навантаження, r – внутрішній опір джерела живлення.
Насправді внутрішній опір є частками Ома, а гальванічних джерел воно значно зростає. Ви це спостерігали, коли на двох батарейках (новій та сівшій) однакова напруга, але одна видає потрібний струмта працює справно, а друга не працює, т.к. просідає при найменшому навантаженні.
Закон Ома у диференціальній та інтегральній формі
Для однорідної ділянки ланцюга наведені вище формули справедливі, для неоднорідного провідника необхідно розбити його на максимально короткі відрізки, щоб зміни його розмірів були мінімізовані в межах цього відрізка. Це називається Закон Ома у диференціальній формі.
Інакше кажучи: щільність струму прямо пропорційної напруженості та питомої провідності для нескінченно малої ділянки провідника.
В інтегральній формі:
Закон Ома для змінного струму
Під час розрахунку ланцюгів змінного струму замість поняття опору вводять поняття «імпеданс». Імпеданс позначають буквою Z, до нього входить активний опір навантаження R a і реактивний опір X (або R r).
- Струм у ланцюгу з індуктивністю не може змінитися миттєво.
- Напруга в ланцюзі з ємністю не може змінитися миттєво.
Таким чином, струм починає відставати або випереджати напругу, і повна потужність поділяється на активну та реактивну.
X L та X C – це реактивні складові навантаження.
У зв’язку з цим запроваджується величина cosФ:
Тут – Q – реактивна потужність, обумовлена змінним струмом та індуктивно-ємнісними складовими, P – активна потужність (виділяється на активних складових), S – повна потужність, cosФ – коефіцієнт потужності.
Можливо, ви помітили, що формула та її уявлення перетинається з теоремою Піфагора. Це справді так і кут Ф залежить від того, наскільки велика реактивна складова навантаження – чим її більше, тим він більший. Насправді це призводить до того, що реально протікає в мережі струм більше, ніж той, що враховується побутовим лічильником, підприємства ж платять за повну потужність.
При цьому опір становлять у комплексній формі:
Тут j – це уявна одиниця, що притаманно комплексного виду рівнянь. Рідше позначається як i, але в електротехніці також позначається і значення змінного струму, що діє, тому, щоб не плутатися, краще використовувати j.
Уявна одиниця дорівнює √-1. Логічно, що немає такого числа при зведенні в квадрат, якого може бути негативний результат «-1».
Як запам’ятати закон Ома
Щоб запам’ятати Закон Ома – можна заучити формулювання простими словамитипу:
Що більше напруга – то більше струм, що більше опір – то менше струм.
Або скористатися мнемонічними картинками та правилами. Перша це уявлення закону Ома як піраміди – коротко і зрозуміло.
Мнемонічне правило – це спрощений вид будь-якого поняття, для простого та легкого його розуміння та вивчення. Можливо або у словесній формі, або у графічній. Щоб правильно знайти потрібну формулу – закрийте пальцем шукану величину та отримайте відповідь у вигляді твору чи приватного.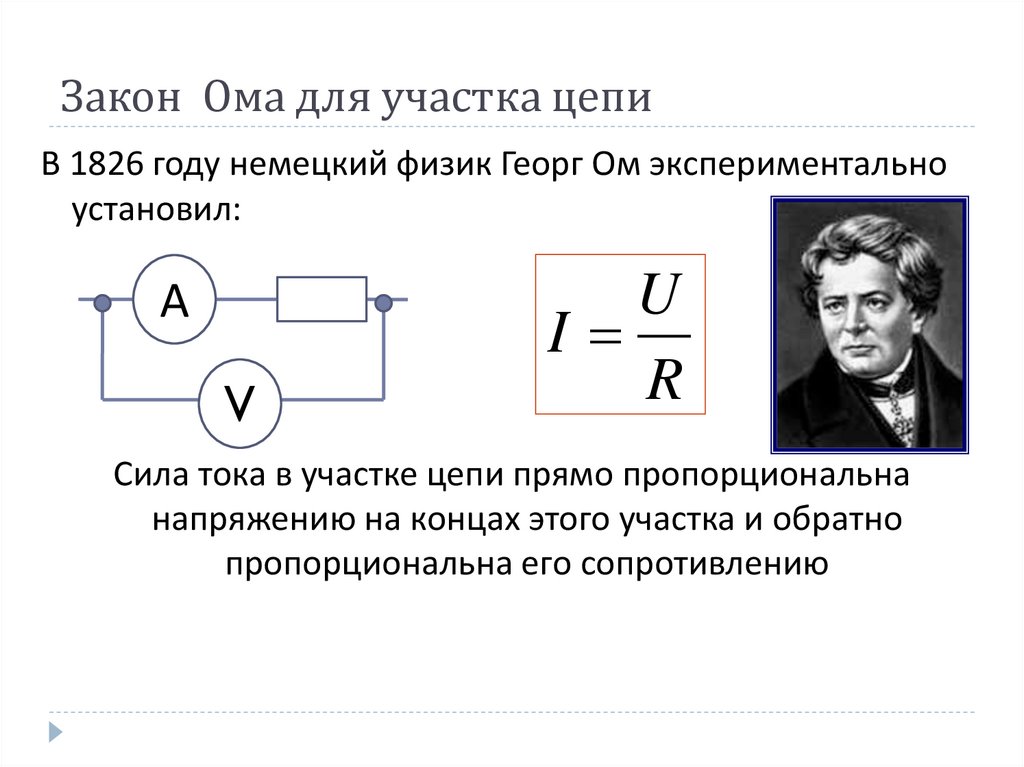 Ось як це працює:
Ось як це працює:
Друга – це карикатурне уявлення. Тут показано: що більше намагається Ом, то важче проходить Ампер, а що більше Вольт – то легше проходить Ампер.
Закон Ома — один з основних в електротехніці, без його знання неможлива більша частина розрахунків. І в повсякденній роботі часто доводиться перекладати чи за опором визначати струм. Абсолютно не обов’язково розуміти його виведення та походження всіх величин — але кінцеві формули обов’язкові до освоєння. На закінчення хочеться відзначити, що є старе жартівливе прислів’я у електриків:
Подобається( 0 ) Не подобається( 0 )
ОМА – найбільша мережа будівельних гіпермаркетів у Білорусі. Сьогодні у різних містах країни відкрито 24 торгові точки, 4 з яких у білоруській столиці, де кожен охочий може придбати все необхідне для ремонту, а також товари для дому, саду та городу.
Компанія була заснована в 1992 році і за більш ніж 20 років встигла перерости в найвідомішу мережу будівельних гіпермаркетів Білорусі. На сьогоднішній день у розпорядженні компанії 24 торгові об’єкти: у Мінську, у кожному з обласних центрів, а також у деяких великих містах Республіки, наприклад, у Ліді, Барановичах, Жлобині, Рогачові та інших.
Зараз у компанії працюють близько 3000 фахівців та понад 45 тисяч людей щодня відвідують будівельні гіпермаркети ОМА.
Каталог товарів ОМА Мінськ
У будівельних гіпермаркетах ОМА в Мінську представлено понад 70 тисяч найменувань найрізноманітніших товарів: починаючи від будівельних сумішей та електроінструменту, закінчуючи карнизами та садовими гойдалками.
Тут можна знайти товари відомих світових брендів, які давно зарекомендували себе на ринку будівельних матеріалів як зразки якості: Bosch, Tarkett, Керамін, Condor, Makita, Caparol, PAROC, Ceresit, KNAUF та інші. Крім цього, ОМА випускає і власні товари торгових марок: деякі будівельні сухі суміші, лакофарбові матеріали, товари для саду та городу та інше.
Ознайомитись з асортиментом товарів магазину ОМА у Мінську Ви можете на офіційному сайті будівельного гіпермаркету. У розділі каталог Ви знайдете будівельні інструменти, будматеріали, будівельне обладнання, сантехніку, побутову техніку, товари для дому, лаки та фарби, спецодяг, автотовари, меблі та багато іншого.
Акції та знижки в ОМА Мінськ
У будівельних гіпермаркетах ОМА у Мінську регулярно проводяться акції. З неймовірними знижками можна придбати практично будь-який товар, який представлений на полицях магазинів мережі. У магазинах ОМА в різних містах Білорусі акції можуть відрізнятися, крім того, не варто забувати, що придбати акційні товари можна тільки до того моменту, поки товар є в наявності. Якщо так сталося, що необхідний товар закінчився, придбати його зі знижкою більше неможливо.
Ознайомитись з актуальними акціями та знижками у будівельних гіпермаркетах ОМА у Мінську Ви можете у спеціальних рекламних газетках. Знайти їх можна на сайті ОМА, в розділі Акції: www. oma.by/sales/
oma.by/sales/
Адреси магазинів у Мінську
На сьогоднішній день у Мінську працюють 4 магазини ОМА, які розташовані по наступним адресам:
- вул. Ванєєва, 38
- вул. Наполеона Орди, 6
- пров. Промисловий, 12Б
- вул. Д.Марцінкевича, 11
Час роботи Ома Мінськ
Всі магазини ОМА у Мінську працюють за різним графіком. Детальніше про режим роботи кожного з магазинів ОМА Мінськ дивись нижче:
вул. Ванєєва, 38
- Час роботи
Пн-Нд: з 8:30 до 22:00
вул. Наполеона Орди, 6
- Час роботи
Пн-Нд: з 8:00 до 22:00
Служба повернення товару: з 09:00 до 21:00
пров. Промисловий, 12Б
- Час роботи
Пн-Сб: з 8:30 до 20:30
Нд: з 8:30 до 19:00
Павільйон «Сад та город»:
Пн-Сб: з 8:30 до 20:30
Нд: з 8:30 до 19:00
вул. Д.Марцінкевича, 11
- Час роботи
Пн-Нд: з 8:30 до 20:00
розстрочка
У будівельних гіпермаркетах ОМА роздрібні покупці можуть користуватися розстрочкою або кредитом на вигідних умовах. Розстрочку пропонують кілька білоруських банків: банк ВТБ, Пріорбанк, МТБанк за картою Халва, банк Москва-Мінськ за карткою розстрочки Smart та Білгазпромбанк за карткою покупок. Умови у всіх різні, тому ознайомтеся з ними заздалегідь.
Розстрочку пропонують кілька білоруських банків: банк ВТБ, Пріорбанк, МТБанк за картою Халва, банк Москва-Мінськ за карткою розстрочки Smart та Білгазпромбанк за карткою покупок. Умови у всіх різні, тому ознайомтеся з ними заздалегідь.
Розстрочка за картою Халва
Скористатися розстрочкою можуть всі власники картки розстрочки від МТБанку. Розстрочка по Халві діє у всіх будівельних гіпермаркетах ОМА на території Білорусі, а також в інтернет-магазині. Умови розстрочення залежать від суми покупок:
при покупці товарів на загальну суму до 50BYN розстрочка надається на 2 місяці;
при покупці товарів на загальну суму 50-200BYN, період розстрочення збільшується до 3 місяців;
при купівлі товарів у розмірі 200-700BYN розстрочка надається на 6 місяців;
при покупці товарів на суму понад 700BYN період розстрочення — 12 місяців.
Розстрочка за карткою покупок від Белгазпромбанку
Розстрочка по Smart карті від банку Москва-Мінськ
Умови розстрочки за Смарт карткою банку Москва-Мінськ також не залежать від суми покупок: розстрочка надається на 2 місяці. Скористатися розстрочкою по Smart картці можна у будь-якому магазині ОМА на території Білорусі, а також в інтернет-магазині.
Скористатися розстрочкою по Smart картці можна у будь-якому магазині ОМА на території Білорусі, а також в інтернет-магазині.
Розстрочка від Банку ВТБ
Розстрочення у магазинах ОМА на вигідних умовах можна отримати і від ВТБ банку. Розстрочка надається на 3 чи 6 місяці. Так, при придбанні товарів на загальну суму від 50BYN до 200BYN розстрочка надається на 3 місяці; при купівлі товарів у сумі від 200BYN до 700BYN термін розстрочки збільшується до півроку; а при купівлі товарів у розмірі понад 700BYN розстрочка надається на 12 місяців.
Усі варіанти розстрочки надаються без довідки про доходи та початковий внесок, під 0,1% річних.
Зверніть увагу!
Розстрочка від банку ВТБ не поширюється на акційні та знижені в ціні товари, а також на товари за спеціальними цінами. Також скористатися цією розстрочкою можна тільки в деяких магазинах мережі: Мінськ (вул. Ванєєва 38 та вул. Н. Орди 6), Брест, Бобруйск (вул. Мінська 135), Гродно (вул. Горького 91), Жлобін, Могильов та Орша.
Розстрочка від Пріорбанку
Ще один варіант розстрочки надає Пріорбанк. Скористатися цією послугою можна лише за умови купівлі товарів у сумі від 300BYN до 3200BYN. При цьому важливою умовою розстрочення є початковий внесок у розмірі 10% загальної суми, а також оформлення страховки на 0,7% від суми розстрочки.
Розстрочка на 3 місяці надається за умови придбання товарів у розмірі 160-200BYN.
Розстрочка на 6 місяців надається за умови придбання товарів на суму 200-600BYN.
Розстрочка на 12 місяців надається за умови придбання товарів у розмірі понад 600BYN.
Зверніть увагу!
Розстрочка від Пріорбанку не поширюється на акційні та знижені в ціні товари, а також на товари за спеціальними цінами. Використовувати цей вид розстрочки можна у всіх магазинах ОМА.
Дисконтна карточка
Своїм клієнтам будівельні гіпермаркети ОМА пропонують скористатися дисконтними картками, які допоможуть заощадити кошти. На сьогоднішній день у магазинах мережі діють дві дисконтні програми: Будівельний будинок ОМА та Новий будинок.
Кожна з дисконтних програм відрізняється умовами та розмірами знижок, що надаються. Уважно ознайомтеся з умовами та виберіть найкращий варіант.
Для новоселів будівельні гіпермаркети ОМА пропонують рік вигідних покупок зі знижкою 7%. Також за дисконтною програмою «Новий дім» Ви отримати професійні консультації щодо вибору найбільш підходящих матеріалів та інструментів абсолютно безкоштовно!
Для того, щоб отримати цю дисконтну картку, необхідно надати уповноваженому співробітнику магазину паспорт та документ, що підтверджує, що Ви придбали житло або отримали дозвіл на будівництво не більше 18 місяців тому. Далі скористатися карткою може тільки власник картки (іменна картка) або члени його сім’ї, але тільки за умови пред’явлення документа, що засвідчує особу або ступеня спорідненості з власником картки.
Після закінчення терміну дії картки (12 місяців) Вам видадуть накопичувальну дисконтну картку Будівельний будинок ОМА, а накопичена сума попередніх покупок впливатиме на розмір знижки на новій картці.
Зверніть особливу увагу! Дисконтна карта Новий будинок НЕ діє в інтернет-магазині та точках продажу в Рогачові, Фаніполі, Слонімі, Мар’їній Гірці та Століні.
Розмір знижки по дисконтної карткиБудівельний будинок ОМА безпосередньо залежить від накопиченої на карті суми та коливається в межах від 2% до 5%. Знижка на 2% надається при накопиченні суми у розмірі від 100BYN до 199,99BYN. При накопиченні суми від 200BYN до 399,99BYN розмір знижки збільшується до 3%. Щоб отримати знижку у розмірі 4%, необхідно накопичити суму в межах 400-699,99BYN. При накопиченні суми у розмірі від 700BYN Ви отримаєте максимальний розмір знижки у 5% на всі товари ОМА, за винятком акційних, знижених у ціні та за спеціальною ціною. При накопиченні суми у розмірі понад 7000BYN Вам буде надано VIP-картку, розмір знижки за якою складе 7%.
Причиною написання цієї статті стала не складність цих формул, а те, що в ході проектування та розробки будь-яких схем часто доводиться перебирати ряд значень, щоб вийти на необхідні параметри або збалансувати схему. Ця стаття та калькулятор у ній дозволить спростити цей підбір та прискорити процес реалізації задуманого. Також наприкінці статті наведу кілька методик запам’ятовування основної формули закону Ома. Ця інформація буде корисна початківцям. Формула хоч і проста, але іноді є замішання, де і який параметр повинен стояти, особливо це спочатку.
Ця стаття та калькулятор у ній дозволить спростити цей підбір та прискорити процес реалізації задуманого. Також наприкінці статті наведу кілька методик запам’ятовування основної формули закону Ома. Ця інформація буде корисна початківцям. Формула хоч і проста, але іноді є замішання, де і який параметр повинен стояти, особливо це спочатку.
У радіоелектроніці та електротехніці закон Ома і формула розрахунку потужності використовуються частіше ніж будь-які з усіх інших формул. Вони визначають жорсткий взаємозв’язок між чотирма ходовими електричними величинами: струмом, напругою, опором і потужністю.
Закон Ома. Цей взаємозв’язок виявив і довів Георг Сімон Ом у 1826 році. Для ділянки ланцюга вона звучить так: сила струму прямо пропорційна напрузі, і назад пропорційна опору
Так записується основна формула:
Шляхом перетворення основної формули можна знайти й дві інші величини:
Потужність. Її визначення звучить так: потужністю називається добуток миттєвих значень напруги та сили струму на якійсь ділянці електричного ланцюга.
Формула миттєвої електричної потужності:
Нижче наведено онлайн калькулятор для розрахунку закону Ома та Потужності. Даний калькулятор дозволяє визначити взаємозв’язок між чотирма електричними величинами: струмом, напругою, опором та потужністю. Для цього достатньо запровадити будь-які дві величини. Стрілки вгору-вниз можна з кроком в одиницю змінювати введене значення. Розмірність величин також можна вибрати. Також для зручності підбору параметрів калькулятор дозволяє фіксувати до десяти раніше виконаних розрахунків з тими розмірностями, з якими виконувались самі розрахунки.
Коли ми навчалися в радіотехнічному технікумі, то доводилося запам’ятовувати дуже багато всякої всячини. І щоб легше було запам’ятати, для закону Ома є три шпаргалки. Ось якими методиками ми користувалися.
Перша – мнемонічне правило. Якщо формули закону Ома висловити опір, то R = чарка.
Друга – метод трикутника. Його ще називають магічний трикутник закону Ома.
Якщо відірвати величину, яку потрібно знайти, то в частині, що залишилася, ми отримаємо формулу для її знаходження.
Третя. Вона є шпаргалкою, в якій об’єднані всі основні формули для чотирьох електричних величин.
Користуватися нею так само просто, як і трикутником. Вибираємо той параметр, який хочемо розрахувати, він перебувати в малому колі в центрі та отримуємо по три формули для його розрахунку. Далі вибираємо потрібну.
Це коло також, як і трикутник, можна назвати магічним.
Закон Ома— фізичний закон, що визначає залежність між електричними величинами — напругою, опором та струмом для провідників.
Вперше відкрив і описав його в 1826 німецький фізик Георг Ом, який показав (за допомогою гальванометра) кількісний зв’язок між електрорушійною силою, електричним струмом і властивостями провідника, як пропорційну залежність.
Згодом властивості провідника, здатні протистояти електричному струму на основі цієї залежності, стали називати електричним опором (Resistance), позначати у розрахунках та на схемах буквою Rта вимірювати в Омах на честь першовідкривача.
Саме джерело електричної енергії також має внутрішній опір, який прийнято позначати буквою r.
Закон Ома для ділянки ланцюга
Зі шкільного курсу фізики всім добре відоме класичне трактування Закону Ома:
Сила струму в провіднику прямо пропорційна напрузі на кінцях провідника і обернено пропорційна його опору.
Це означає, якщо до кінців провідника опором R= 1 Ом додана напруга U= 1 Вольт, тоді величина струму Iу провіднику дорівнюватиме 1/1 = 1 Ампер.
Звідси випливають ще два корисні співвідношення:
Якщо провіднику, опором 1 Ом, протікає струм 1 Ампер, отже на кінцях провідника напруга 1 Вольт (падіння напруги).
Якщо кінцях провідника є напруга 1 Вольт і з ньому протікає струм 1 Ампер, отже опір провідника дорівнює 1 Ом.
Вищеописані формули у вигляді можуть бути застосовні для змінного струму лише тому випадку, якщо ланцюг складається лише з активного опору R.
Крім того, слід пам’ятати, що Закон Ома справедливий лише для лінійних елементів ланцюга.
Пропонується простий онлайн-калькулятор для практичних розрахунків.
Закон Ома. Розрахунок напруги, опору, струму, потужності.
Після скидання ввести два відомі параметри.
Закон Ома для замкнутого ланцюга
Якщо до джерела живлення підключити зовнішній ланцюг опором R, У ланцюзі піде струм з урахуванням внутрішнього опору джерела:
I— Сила струму в ланцюзі.
— електрорушійна сила (ЕРС) — величина напруги джерела живлення не залежить від зовнішнього ланцюга(без навантаження). Характеризується потенційною енергією джерела.
r— Внутрішній опір джерела живлення.
Для електрорушійної сили зовнішній опір Rта внутрішнє rз’єднані послідовно, значить величина струму в ланцюзі визначиться значенням ЕРС та сумою опорів: I = /(R+r) .
Напруга на висновках зовнішнього ланцюга визначиться виходячи з сили струму та опору Rспіввідношенням, яке вже розглядалося вище: U = IR.
Напруга U, при підключенні навантаження R, завжди буде менше ніж ЕРС на величину твору I*r, яку називають падінням напруги на внутрішньому опорі джерела живлення
З цим явищем ми стикаємося досить часто, коли бачимо у роботі частково розряджені батареї чи акумулятори.
У міру розряду, збільшується їх внутрішній опір, отже, збільшується падіння напруги всередині джерела, отже, зменшується зовнішня напруга U = — I*r.
Чим менший струм і внутрішній опір джерела, тим ближче за значенням його ЕРС та напруга на його висновках U.
Якщо струм у ланцюзі дорівнює нулю, отже, = U. Ланцюг розімкнений, ЕРС джерела дорівнює напрузі на його висновках.
У випадках, коли внутрішній опір джерела можна знехтувати ( r≈ 0), напруга на висновках джерела дорівнюватиме ЕРС ( ≈ U) незалежно від опору зовнішнього ланцюга R.
Таке джерело живлення називають джерелом напруги.
Закон Ома для змінного струму
За наявності індуктивності або ємності в ланцюзі змінного струму необхідно враховувати їхній реактивний опір.
У такому разі запис Закону Ома матиме вигляд:
Тут Z— повний (комплексний) опір ланцюга — імпеданс. До нього входить активна Rта реактивна Xскладові.
Реактивний опір залежить від номіналів реактивних елементів, від частоти та форми струму в ланцюзі.
Докладніше ознайомитися з комплексним опором можна на сторінці імпедансу.
З урахуванням зсуву фаз φ , створеного реактивними елементами, для синусоїдального змінного струму зазвичай записують Закон Ома у комплексній формі:
Комплексна амплітуда струму. = I amp e jφ
— Комплексна амплітуда напруги. = U amp e jφ
— Комплексний опір. Імпеданс.
φ — Кут зсуву фаз між струмом і напругою.
e— константа, основа натурального логарифму.
j— Уявна одиниця.
I amp, U amp— амплітудні значення синусоїдального струму та напруги.
Нелінійні елементи та ланцюги
Закон Ома не є фундаментальним законом природи і може бути застосований в обмежених випадках, наприклад, для більшості провідників.
Його неможливо використовувати для розрахунку напруги та струму в напівпровідникових або електровакуумних приладах, де ця залежність не є пропорційною і її можна визначати лише за допомогою вольтамперної характеристики (ВАХ).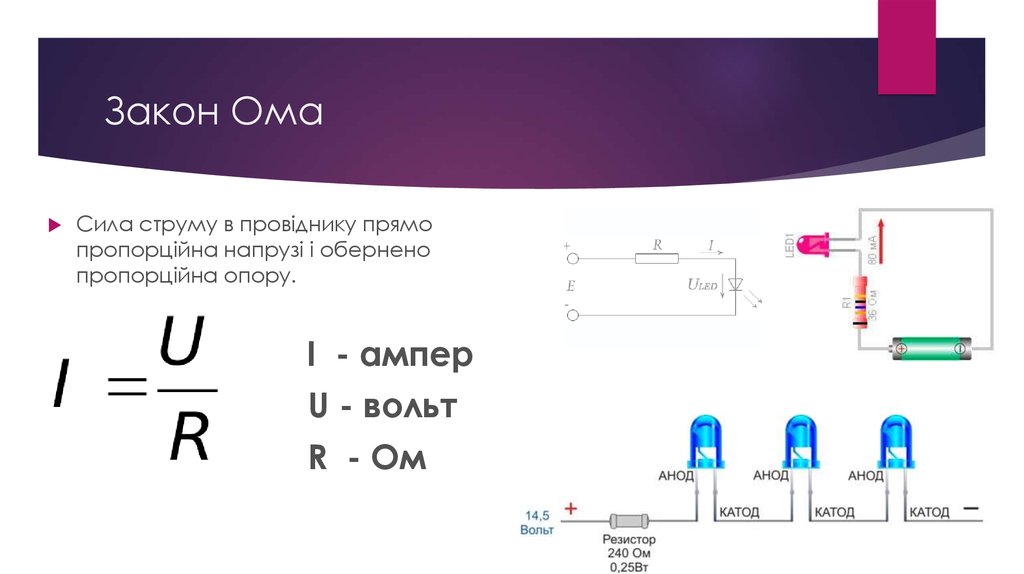 До цієї категорії елементів відносяться всі напівпровідникові прилади (діоди, транзистори, стабілітрони, тиристори, варикапи тощо) та електронні лампи.
До цієї категорії елементів відносяться всі напівпровідникові прилади (діоди, транзистори, стабілітрони, тиристори, варикапи тощо) та електронні лампи.
Такі елементи та ланцюги, у яких вони використовуються, називають нелінійними.
Німецький фізик Георг Сімон Ом(1787-1854) відкрив основний закон електричного кола.
Закон Ома для ділянки ланцюга:
Визначення:Cила струму I на ділянці електричного ланцюга прямо пропорційна напрузі U на кінцях ділянки і обернено пропорційна його опору R.
- I — сила струму(В системі СІ вимірюється — Ампер)
- Сила струму в провіднику прямо пропорційна напрузі і обернено пропорційна опору.
- Формула: I=\frac(U)(R)
- U — напруга(В системі СІ вимірюється — Вольт)
Падіння напруги на ділянці провідника дорівнює добутку сили струму у провіднику на опір цієї ділянки.
Формула: U=IR
- R — електричний опір(В системі СІ вимірюється — Ом).

- Електричний опір R це відношення напруги на кінцях провідника до сили струму, що тече по провіднику.
- Формула R=\frac(U)(I)
Визначення одиниці опору — Ом
1 Омявляє собою електричний опір ділянки провідника, яким при напрузі 1(Вольт)протікає струм 1 (Ампер).
Закон Ома для повного ланцюга
Визначення: Сила струму в ланцюгу пропорційна діючої в ланцюгу ЕРС і обернено пропорційна сумі опорів ланцюга та внутрішнього опору джерела
Формула I=\frac(\varepsilon)(R+r)
- \varepsilon — ЕРС джерела напруги, В;
- I — сила струму в ланцюзі, А;
- R — опір всіх зовнішніх елементівланцюги, Ом;
- r — внутрішній опір джерела напруги, Ом.
Як запам’ятати формули закону Ома
Трикутник Ома допоможе запам’ятати закон. Потрібно закрити шукану величину, і два інших символи дадуть формулу для обчислення.
Логвіна
ЛогвінаЛогвіна Ніна Анатоліївна
Розробка уроку з фізики
Тема уроку: Закон Ома для повного кола
Мета уроку: Узагальнити закон Ома для ділянки кола, яке містить джерело ЕРС. З’язувати фізичну сутність закону Ома для повного кола. Формування навичок розв’язання задач по темі, розвиток мислення. Виховання самостійності та культури ведення записів.
З’язувати фізичну сутність закону Ома для повного кола. Формування навичок розв’язання задач по темі, розвиток мислення. Виховання самостійності та культури ведення записів.
Тип уроку: Комбінований
Обладнання: Джерело струму, з’єднувальні провідники, резистор, ключ-вимикач.
План
I. Організаційний момент.
II. Актуалізація опорних знань учнів
Фронтальне опитування: — «Мозковий штурм»:
-Дати визначення електричного струму;
-Які умови існування електричного струму в електричному колі?;
-Дати визначення постійного струму;
-Формування закону Ома для ділянки кола;
-З закону Ома для ділянки кола слідує, що R=U/I.Чи означає це, що опір пропорційний напрузі?;
-В чому причина електричного опору?;
-Формула електричного опру провідника;
-Спіраль електроплитки перегоріла посередині. Половина цієї спіралі відрізали. Як змінився опір спіралі? Чи змінилася при цьому сила струму, якщо так, то у скільки разів?
Як змінився опір спіралі? Чи змінилася при цьому сила струму, якщо так, то у скільки разів?
-Сформулювати закони послідовного з`єднання провідників.
-Сформулювати закони паралельного з`єднання провідників.
-Чому у побуті найчастіше використовують паралельне з`єднання споживачів електроенергії?
ІІІ. Мотивація навчальної діяльності учнів. При роботі з електричними колами використовують різні види джерел постійного струму( акумулятори, гальванічні елементи, тощо). На затискачах джерел утворюється різниця потенціалів внаслідок переміщення електричних зарядів. Значить у самому джерелі струму існує електричний опір, який, напевне, впливає на силу струму у повному колі. З`ясуємо поняття сторонніх сил, діючих на заряди та встановимо фізичну суть закона Ома для повного кола.
ІV. Вивчення нового матеріалу.
1. Робота сторонніх і кулонівських сил.
Робота по переміщенню заряда по провіднику в процесі проходження по ньому електричного струму здійснюється і кулонівськими, і сторонніми силами. Повна робота:
Повна робота:
Напругою на ділянці кола називається величина, яка чисельно дорівнює роботі кулонівських і сторонніх сил по переміщенню по колу одиничного позитивного заряду.
2. Закон Ома для повного кола: Сила струму у повному колі дорівнює відношенню ЕРС джерела до повного опору цього кола:
R- опір зовнішнього кола; r – внутрішній опір джерела струму.
3. Наслідки з закону Ома для повного кола : — Напруга на полюсах замкнутого джерела струму — Напруга на полюсах розімкнутого джерела струму — Коротке замикання джерела струму – різке зростання сили струму при зменшенні опору зовнішнього кола до 0. V. Формування навичок розв’язання задач . Інтерактивна гра « Вийди з кола»
Варіант 2.
1. Визначити напругу на кінцях провідника, опер якого 3 Ом, якщо сила струму в ньому дорівнює 2А.
2.Чому дорівнює сила струму в лампі, якщо опір нитки накалу 15 Ом і підключена вона до джерела з напругою 45 В ?
3.Визначте силу струму в нагрівальному елементі електрочайника з опором 30 Ом , якщо до нього прикладена напруга 30 В.
4.Що показує амперметр при напрузі на затискувачах 20 мВ? Опір обмотки амперметра 0,002 Ом.
5.Якої довжини необхідно взяти дріт з питомим опором 50 і площею поперечного перерізу 0.01 мм2, щоб його опір дорівнював 4 кОм?
6. Визначте опір провідника, сила струму в якому становить 2.5 А при напрузі 10В
Варіант 3
1.Якої площі поперечного перерізу використовують нитку вугільної лампи, якщо довжина нитки 0.2м і лампа має опір 400 Ом? Питомий опір вугілля у гарячому стані 50.
2.Визначте напругу на кінцях провідника, опір якого 10 Ом, якщо сила струму дорівнює 2 А.
3.Опір нагрівального елемента електрочайника 12 Ом. Визначте струм у ньому при напрузі 24В.
4.Визначте силу струму в лампі з опором 6 ОМ при напрузі 36 В.
5.Визначте напругу на записувачі провідника, якщо його опір 1.6 Ом, а силf струму дорівнює 2.5 А
6.Визначте напругу на затискувачах амперметра, якщо опір його обмотки 2.5 мОм, а він показує силу струму 10А
Варіант 5
1.Яку роботу виконує електричний струм в електродвигуні за 30с, якщо при напрузі 220В сила струму дорівнює 0.1А.
2.Визначте потужність струму ( у кВт) на ділянці кола, де за 0.06 с виконана робота 360 Дж
3.При напрузі 4В сила струму в спіралі плитки 2А. Визначте опір спіралі.
4. ЕРС джерела 0,2 В. Яку роботу здійснюють сторонні сили під час переміщення 5 Кл. електрики всередині джерела?
5. Обчисліть загальний опір двох провідників по 6 Ом, з’єднаних паралельно.
6. Який заряд пройде через поперечний переріз провідника за 10с при силі струму в ньому 0,4 А?
Виставлення оцінок за шкалою :
2. На 12 балів «Задача – бонус».
Задача: В електричному колі, в якому два резистори R2 і R3 з’єднані паралельно, а R1 послідовно, ЕРС джерела струму дорівнює 36 В, а внутрішній опір дуже малий. Знайти потужність електричного струму в резисторі R2 якщо, R1= 2кОм , R2=5кОм, R3=20кОм.
На 12 балів «Задача – бонус».
Задача: В електричному колі, в якому два резистори R2 і R3 з’єднані паралельно, а R1 послідовно, ЕРС джерела струму дорівнює 36 В, а внутрішній опір дуже малий. Знайти потужність електричного струму в резисторі R2 якщо, R1= 2кОм , R2=5кОм, R3=20кОм.
VI . Підсумок уроку.
VII . Домашнє завдання : вчити 61, 62 , рівневі завдання до ТО.
Література: Н.О. Білик «10 дидактчних ігор», Харків, «Основа», 2004 рік.
Хостинг от uCoz
Закон Ома для повного кола і для ділянки ланцюга формули, опис і пояснення
Зміст
- Закон Ома для повного кола і для ділянки ланцюга: варіанти запису формули, опис і пояснення
- Окрема ділянка і повна електричний ланцюг
- Розрахунок струму ділянки електричної схеми
- Варіант розрахунку для повного кола
- Розгляд дії закону до змінної величини
- Послідовне і паралельне включення елементів
- Ланцюг послідовно включених резистивних елементів
- Ланцюг паралельно включених резистивних елементів
- Інтегральна і диференціальна форми закону
- Висновки і корисне відео по темі
Професійному електрику, фахівця електронщику ніяк не оминути у власній діяльності закон Ома, вирішуючи будь-які завдання, пов’язані з налагодженням, налаштуванням, ремонтом електронних і електричних схем.
Власне, розуміння цього закону необхідно кожному. Тому що кожному в побуті доводиться мати справу з електрикою.
І хоча навчальним курсом середньої школи закон німецького фізика Ома і передбачений, але на практиці не завжди своєчасно вивчається. Тому розглянемо в нашому матеріалі таку актуальну для життя тему і розберемося з варіантами записи формули.
Окрема ділянка і повна електричний ланцюг
Розглядаючи електричний ланцюг з точки зору застосування до схеми закону Ома, слід зазначити два можливих варіанти розрахунку: для окремо взятого ділянки і для повноцінної схеми.
Розрахунок струму ділянки електричної схеми
Ділянкою електричного кола, як правило, розглядається частина схеми, що виключає джерело ЕРС, як володіє додатковим внутрішнім опором.
Тому розрахункова формула, в даному випадку, виглядає просто:
I = U / R,
- I – сила струму;
- U – прикладена напруга;
- R – опір.

Трактування формули проста – струм, що протікає по якомусь ділянку ланцюга, пропорційний прикладеному до нього напрузі, а опору – обернено пропорційний.
Таким чином, формулою чітко описується залежність протікання струму по окремому ділянці електричного кола щодо певних значень напруги і опору.
Формулою зручно користуватися, наприклад, розраховуючи параметри опору, яке потрібно впаяти в схему, якщо задані напруження з струмом.
Вищенаведений малюнок допоможе визначити, наприклад струм, що протікає через 10-омное опір, до якого прикладено напругу 12 вольт. Підставивши значення, знайдемо – I = 12/10 = 1.2 ампера.
Аналогічно вирішуються завдання пошуку опору (коли відомі струм з напругою) або напруги (коли відомі напруга з струмом).
Тим самим завжди можна підібрати необхідну робочу напругу, потрібну силу струму і оптимальний резистивний елемент.
До речі, з’єднувальні дроти будь-якої схеми – це опору. Величина навантаження, яку їм належить нести, визначається напругою.
Відповідно, знову ж користуючись законом Ома, стає допустимим точний підбір необхідного перетину провідника, в залежності від матеріалу жили.
У нас на сайті є докладна інструкція з розрахунку перетину кабелю по потужності і струму.
Варіант розрахунку для повного кола
Повноцінну ланцюг складає вже ділянку (ділянки), а також джерело ЕРС. Тобто, фактично наявному резистивного компоненту ділянки ланцюга додається внутрішній опір джерела ЕРС.
Тому логічним є деяка зміна вище розглянутої формули:
I = U / (R + r)
Звичайно, значення внутрішнього опору ЕРС в законі Ома для повної електричного кола можна вважати мізерно малим, правда багато в чому це значення опору залежить від структури джерела ЕРС.
Проте, при розрахунках складних електронних схем, електричних ланцюгів з безліччю провідників, наявність додаткового опору є важливим фактором.
Як для ділянки кола, так і для повної схеми слід враховувати природний момент – використання струму постійної або змінної величини.
Якщо зазначені вище моменти, характерні для закону Ома, розглядалися з точки зору використання постійного струму, відповідно зі змінним струмом все виглядає трохи інакше.
Розгляд дії закону до змінної величини
Поняття «опір» до умов проходження змінного струму слід розглядати вже більше як поняття «імпедансу».Тут мається на увазі поєднання активної резистивного навантаження (Ra) і навантаження, утвореної реактивним резистором (Rr).
Обумовлені подібні явища параметрами індуктивних елементів і законами комутації стосовно змінної величини напруги – синусоїдальної величиною струму.
Іншими словами, має місце ефект випередження (відставання) струмових значень від значень напруги, що супроводжується появою активної (резистивной) і реактивної (індуктивної або ємнісний) потужностей.
Розрахунок подібних явищ ведеться за допомогою формули:
Z = U / I або Z = R + J * (XL – XC)
де: Z – імпеданс; R – активне навантаження; XL , XC – індуктивна і ємнісна навантаження; J – коефіцієнт.
Послідовне і паралельне включення елементів
Для елементів електричного кола (ділянки кола) характерним моментом є послідовне або паралельне з’єднання.
Відповідно, кожен вид з’єднання супроводжується різним характером перебігу струму і підведенням напруги. На цей рахунок закон Ома також застосовується по-різному, в залежності від варіанту включення елементів.
Ланцюг послідовно включених резистивних елементів
Стосовно до послідовному з’єднанню (ділянки кола з двома компонентами) використовується формулювання:
Таке формулювання явно демонструє, що, незалежно від числа послідовно з’єднаних резистивних компонентів, ток, поточний на ділянці ланцюга, не змінює значення.
Величина напруги, прикладеного до діючих резистивним компонентів схеми, є сумою і становить в цілому значення джерела ЕРС.
При цьому напруга на кожному окремому компоненті одно: Ux = I * Rx.
Загальний опір слід розглядати як суму номіналів всіх резистивних компонентів ланцюга.
Ланцюг паралельно включених резистивних елементів
На випадок, коли має місце паралельне включення резистивних компонентів, справедливою щодо закону німецького фізика Ома вважається формулювання:
Не виключаються варіанти складання схемних ділянок «змішаного» виду, коли використовується паралельне і послідовне з’єднання.
Для таких варіантів розрахунок зазвичай ведеться початковим розрахунком резистивного номіналу паралельного з’єднання. Потім до отриманого результату додається номінал резистора, включеного послідовно.
Інтегральна і диференціальна форми закону
Всі вищевикладені моменти з розрахунками застосовні до умов, коли в складі електричних схем використовуються провідники, так би мовити, «однорідної» структури.
Тим часом на практиці нерідко доводиться стикатися з побудовою схематики, де на різних ділянках структура провідників змінюється. Наприклад, використовуються дроти більшого перетину або, навпаки, меншого, зроблені на основі різних матеріалів.
Для обліку таких відмінностей існує варіація, так званого, «диференційно-інтегрального закону Ома». Для нескінченно малого провідника розраховується рівень щільності струму в залежності від напруженості і величини питомої провідності.
Під диференційний розрахунок береться формула: J = ό * E
Для інтегрального розрахунку, відповідно, формулювання: I * R = φ1 – φ2 + έ
Однак ці приклади швидше вже ближче до школи вищої математики і в реальній практиці простого електрика фактично не застосовуються.
Висновки і корисне відео по темі
Докладний розбір закону Ома у відеоролику, представленому нижче, допоможе остаточно закріпити знання в цьому напрямку.
Своєрідний видеоурок якісно підкріплює теоретичне письмовий виклад:
Робота електрика або діяльність електронщика невід’ємно пов’язана з моментами, коли реально доводиться спостерігати закон Георга Ома в дії. Це свого роду прописні істини, які слід знати кожному професіоналу.
Це свого роду прописні істини, які слід знати кожному професіоналу.
Об’ємних знань з даного питання не потрібно – достатньо вивчити три основних варіації формулювання, щоб успішно застосовувати на практиці.
Хочете доповнити викладений вище матеріал цінними зауваженнями або висловити свою думку? Пишіть, будь ласка, коментарі в блоці під статтею. Якщо у вас залишилися питання, не соромтеся задавати їх нашим експертам.
Перший закон ома
Урок вирішення завдань по темі — Закон Ома для ділянки кола, послідовне і паралельне з’єднання
Тепер знайдемо R і отримане значення підставимо в формулу для знаходження сили струму. (Переклад S в м 2 не потрібно робити, тому що в одиницях виміру щільності теж присутні теж мм 2) В електричне коло включені послідовно резистор опором 5 Ом і дві електричні лампи опором 500 Ом. Визначте загальний опір провідника. Завдання 4. (Клас ділиться на 2 групи, кожна з якої вирішує завдання своїм способом (одні знаходячи силу струму використовуючи закон Ома, другі використовуючи формулу паралельного з’єднання).
Найголовніший закон електротехніки — закон Ома
Якщо ланцюг розімкнути, в ній струм відсутній (I = 0), то із закону Ома (4) отримаємо, що (φ1 — φ2) = E12. тобто е.р.с. діюча в розімкнутої ланцюга, дорівнює різниці потенціалів на її кінцях. Отже, для того щоб знайти е.р.с. джерела струму, треба виміряти різницю потенціалів на його клемах при розімкнутому ланцюзі. Приклади розрахунків за законом Ома: Розрахунок струму за законом Ома Розрахунок
Перший закон ома
Чим більше різниця рівнів води при вході і виході з труби (напір) і чим більше поперечний переріз труби, тим більше води протікає крізь трубу в одиницю часу. Точно так же, чим більше різниця електричних потенціалів (напруга) на затискачах джерела або приймача електричної енергії і чим менше його опір (т. Е. Чим більше площа поперечного перерізу провідника), тим більший струм проходить по ньому. Так як потенціал електричного поля на початку ділянки електричного кола більше, ніж в кінці, різниця потенціалів, або напруга U, прикладена до ділянки електричного кола, часто називають падінням напруги на даній ділянці. Опір R ділянки кола дорівнює напрузі, що додається до даної ділянки, поділеному на силу струму на цій ділянці, т.
Опір R ділянки кола дорівнює напрузі, що додається до даної ділянки, поділеному на силу струму на цій ділянці, т.
На допомогу студентам БНТУ — курсові, реферати, лабораторні!
Згідно з другим законом Кірхгофа алгебраїчна сума ЕРС, що діють в будь-якому контурі розгалуженої електричного кола, дорівнює сумі алгебри падінь напруг на всіх опорах контуру Розглянемо електричний ланцюг, зображену на рис. 1.11, б. Позначимо стрілкою напрямок обходу контуру. При складанні рівнянь будемо брати зі знаком «плюс» ті ЕРС і падіння напруг, напрямки яких збігаються з напрямом обходу контуру і зі знаком «мінус» ті, які спрямовані проти обходу.
Повний закон Ома для повного кола
Повний закон Ома для повного кола звучить так: сила струму в електричному ланцюзі буде прямо пропорційна напрузі прикладеному до цього ланцюга, і обернено пропорційна сумі внутрішнього опору джерела електроживлення і загальному опору всього ланцюга. Будь-яку електричну схему (будь-якої складності) можна представити у вигляді простих шляхів, по яких переміщаються електрони. Взявши будь таку ділянку і визначивши його двома точками, до нього сміливо можна застосовувати закон Ома.
Взявши будь таку ділянку і визначивши його двома точками, до нього сміливо можна застосовувати закон Ома.
закони Кірхгофа
Зміна потенціалу за обраним контуру має дорівнювати нулю, тому що воно висловлює роботу, витрачену на переміщення частинок, що володіють разом одиницею заряду, по замкнутому шляху в електричних полях джерел і приймачів енергії (див. Рис. 1). Тоді в замкнутому контурі: тому U3,1 + U4,6 + U6,1 = 0. В даному рівнянні напруги вважаються позитивними (по обходу контуру), а напряму проти обходу — негативними. Відповідно до інших контурам складаються інші рівняння, які неважко скласти, не вдаючись до виразів потенціалів точок контуру, користуючись простим правилом.
Закон Ома для ділянки кола
Напишіть на аркуші паперу величини, які входять в закон Ома, так як показано на малюнку 3. Тепер закрийте пальцем, ту величину, яку необхідно знайти. Тоді відносне розташування залишилися незакритими величин підкаже, яку дію необхідно зробити для обчислення невідомої величини. Якщо Ви хочете навчитися креслити електричні схеми, створювати малюнки та ілюстрації
Якщо Ви хочете навчитися креслити електричні схеми, створювати малюнки та ілюстрації
Рішення задач на тему: Електричний опір
Це можна зрозуміти так: якщо підключити амперметр послідовно до цього провідника, то він покаже значення 2А. Варто звернути увагу, що нічого складного в таких завданнях немає. Варто тільки розібратися, які величини куди підставити. Зазвичай такі завдання в подальшому будуть використовуватися як складова частина більш складних завдань. У попередній задачі ми знаходили значення сили струму. Але цю характеристику можна виміряти відповідним приладом — амперметром.
Для кожної гілки задається позитивний напрямок струму. Число незалежних рівнянь, що складаються за першим законом Кірхгофа, дорівнює числу вузлів q (точок з’єднання не менше ніж трьох провідників) мінус одиниця, т.е.д-1. Число незалежних рівнянь, що складаються за другим законом Кірхгофа, дорівнює числу контурів n = p-q + \. Загальна кількість рівнянь, що складаються за першим та другим законами Кірхгофа, дорівнює числу невідомих струмів р.
Існують закони яким підкоряються процеси відбуваються в електричних ланцюгах. Для розуміння роботи електричних схем необхідно знати ці закони. Зазвичай якщо відома електрична схема і використовувані в ній елементи, з’ясувати її працездатність можна дізнавшись струми (під струмом мається на увазі величина сили струму) протікають по цих елементах і напруги на них. Вихід з ладу елемента електричної схеми може статися при перевищенні струму протікає по ньому або напруги на ньому. Всі елементи за якими протікає електричний струм мають активним опором яке є коефіцієнтом зв’язує струм і напруга, тобто знаючи опір елемента і ток протікає по ньому (напруга на ньому) можна обчислити напругу на ньому (струм протікає по ньому). Зв’язок між струмом, напругою і опором висловлює закон Ома. Закон Ома звучить наступним чином: сила струму на ділянці ланцюга дорівнює відношенню напруги на цій ділянці до його опору.
Для зручності, на електричних схемах струм зображується стрілкою на провіднику, а напруга стрілкою початок і кінець якої вказують на точки між якими існує напруга. Прийнято за позитивний напрямок струму приймати напрямок від точки з великим потенціалом до точки з меншим потенціалом (в реальних ланцюгах це не завжди так). Якщо направити стрілку на провіднику в іншу сторону то значення струму повинно поміняти знак на протилежний (для напруги також). Прямокутником позначається резистор.
Прийнято за позитивний напрямок струму приймати напрямок від точки з великим потенціалом до точки з меншим потенціалом (в реальних ланцюгах це не завжди так). Якщо направити стрілку на провіднику в іншу сторону то значення струму повинно поміняти знак на протилежний (для напруги також). Прямокутником позначається резистор.
Провід або резистор, який не може розсіяти потрібну потужність, сильно нагрівається, його опір різко зростає і в підсумку він перегорає. Тому на резисторах вказують і інший параметр — рассеиваемую потужність (0,125, 0,25, 0,5, 1, 2,5 і більше ват). Різниця потенціалів джерела електричного струму називається електричною напругою. Електрична напруга вимірюється в вольтах (В).
До речі, законом Ома називається тільки одна формула з трикутника — та, яка відображає залежність струму від напруги і опору. Дві інші формули, хоча і є її наслідком, фізичного сенсу не мають.
Розрахунки, що виконуються за допомогою закону Ома для ділянки ланцюга, будуть правильні в тому випадку, коли напруга виражено в вольтах, опір в Омасі і ток в амперах. Якщо використовуються кратні одиниці вимірювань цих величин (наприклад, міліампер, мілівольт, мегаом і т. Д.)
Якщо використовуються кратні одиниці вимірювань цих величин (наприклад, міліампер, мілівольт, мегаом і т. Д.)
Постійний електричний струм може бути створений тільки в замкнутому ланцюзі. в якій вільні носії заряду циркулюють по замкнутих траєкторіях. Електричне поле в різних точках такого ланцюга незмінно в часі. Отже, електричне поле в ланцюзі постійного струму має характер замороженого електростатичного поля. Але при переміщенні електричного заряду в електростатичному полі по замкнутій траєкторії, робота електричних сил дорівнює нулю (див.
Схожі статті
-
1С перший біт відгуки співробітників про роботодавця
-
Як заряджати планшет перший раз правильно
-
Як вести себе на мітингу, закон для всіх
Електрорушійна сила джерела струму. Закон Ома для повного кола. Робота і потужність електричного струму. Закон Джоуля-Ленца
Дом Електрорушійна сила джерела струму. Закон Ома для повного кола.
 Робота і потужність електричного струму. Закон Джоуля-Ленца
Робота і потужність електричного струму. Закон Джоуля-Ленцапросмотров — 659
Тема: Електрорушійна сила джерела струму. Закон Ома для повного кола. Робота і потужність електричного струму. Закон Джоуля-Ленца.
Запитання для самоперевірки
1. Що називають електричним струмом?
2. Який напрям струму беруть за додатний?
3. Які умови потрібні для існування електричного струму?
4. Що називають силою струму? Яка формула виражає зміст цього поняття?
5. Яка одиниця сили струму в СІ? Сформулюйте визначення цієї одиниці. Як слід розуміти, що сила струму дорівнює 5 А?
6. Який струм називають постійним?
7. Побудуйте і поясніть графік постійного струму.
8. Виведіть формулу сили струму на основі електронних уявлень.
9. Що називають густиною струму? Яка формула виражає зміст цього поняття?
10. Яка одиниця вимірювання густини струму в СІ?
1. Нарисуйте схему експерименту, у якому встановлюють закон Ома для ділянки кола.
2. Як записують і формулюють закон Ома для ділянки кола?
3. Що називають спадом напруги?
4. Установіть одиницю опору в СІ і сформулюйте її визначення.
5. Якою формулою виражають залежність опору провідника від його довжини, поперечного перерізу і речовини?
6. Що називають питомим опором провідника? Який фізичний зміст цієї величини?
7. Побудуйте вольт-амперну характеристику провідника.
8. Як з погляду електронної теорії пояснити поняття «опір провідника»?
Будь-яке електричне коло можна поділити на дві ділянки:
1) зовнішню ділянку кола;
2) внутрішню ділянку кола.
На зовнішній ділянці кола електричні заряди рухаються під дією електричного поля, оскільки тут струм проходить від вищого потенціалу до нижчого. На внутрішній частині кола струм проходить всередині самого джерела струму і тут заряди переміщуються від нижчого потенціалу до вищого ( від «-» до «+» ). Цю роботу з переміщення зарядів електричне поле виконувати не може, її мають виконати сторонні сили — сили не електричного походження.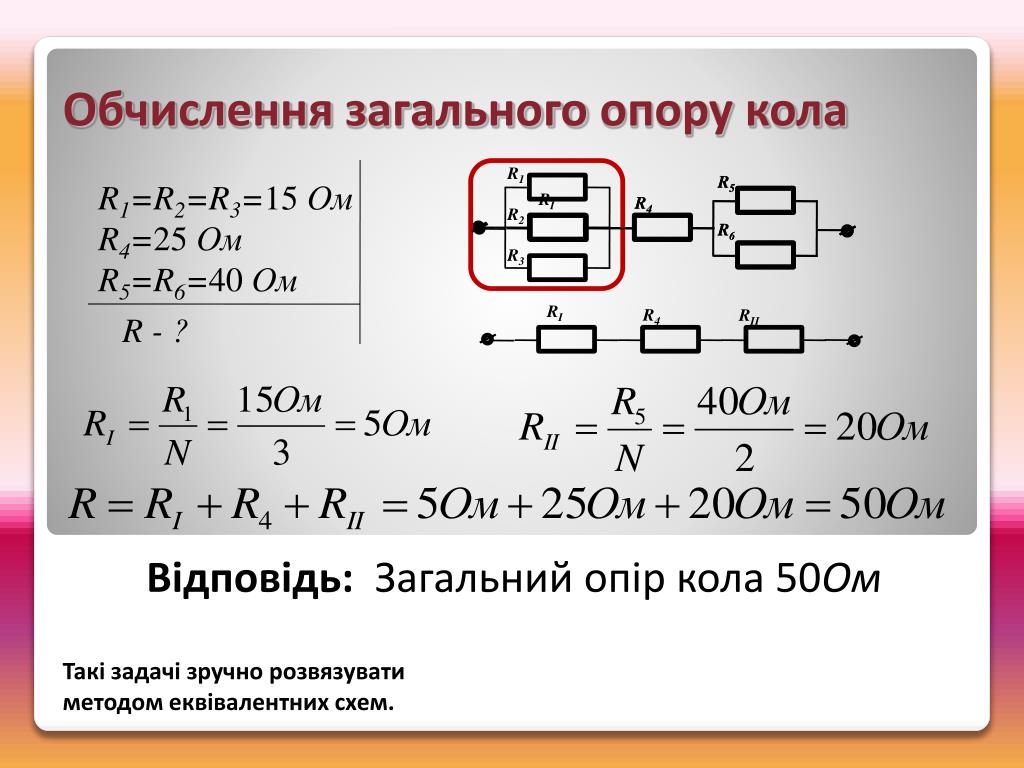 Природа сторонніх сил може бути різною. Це можуть бути механічні, хімічні, магнітні та інші сили.
Природа сторонніх сил може бути різною. Це можуть бути механічні, хімічні, магнітні та інші сили.
Дія сторонніх сил характеризується важливою фізичною скалярною величиною — електрорушійною силою. Електрорушійна сила в замкненому контурі дорівнює відношенню роботи сторонніх сил під час переміщення заряду вздовж контуру до заряду:
.
Як і напругу чи потенціал у СІ ЕРС вимірюють у вольтах: [e] = B.
Закон Ома для повного кола пов’язує силу струму в колі, ЕРС, і повний опір кола R + r, де r — внутрішній опір джерела; R — опір зовнішньої ділянки кола. Цей зв’язок може бути встановлений завдяки закону Джоуля-Ленца, за яким кількість теплоти, яка виділяється провідником зі струмом, дорівнює добутку квадрата сили струму, опору провідника R і часу проходження струму по провіднику Dt:
Q = I 2RDt.
Нехай за час Dt через поперечний переріз провідника проходить електричний заряд Dq. Тоді роботу сторонніх сил з переміщення заряду Dq можна виразити так:
Тоді роботу сторонніх сил з переміщення заряду Dq можна виразити так:
Aст = eDq, із виразу Dq = IDt.
Тому Aст = eIDt. Унаслідок виконання певної роботи на внутрішніх і зовнішніх ділянках кола, опори яких r i R, виділяється певна кількість теплоти. За законом Джоуля-Ленца вона дорівнює:
Q = I 2RDt + I 2rDt.
Згідно із законом збереження енергії A = Q. Прирівнявши, отримуємо e = IR + Ir, звідки:
e = I(R + r).
Із цього виразу бачимо, що сила струму в замкненому колі дорівнює відношенню ЕРС джерела струму до повного опору кола.
. (4.2.4)
Вираз (4.2.4) називають законом Ома для повного кола. Під час значного зменшення опору зовнішньої ділянки кола ( ) струм досягає максимального для джерела значення:
.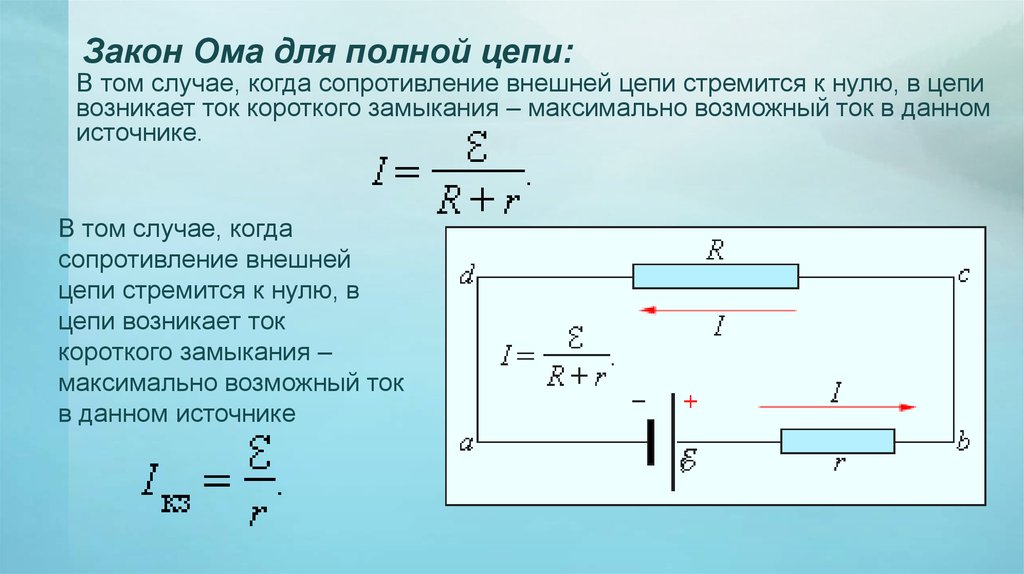
Такий випадок називають коротким замиканням, а відповідне значення струму — струмом короткого замикання Iкз. Коротке замикання — головний недолік паралельного з’єднання. Унаслідок короткого замикання енергія проходить через один із паралельно з’єднаних опорів (найменший), без струму залишаються інші споживачі. Це призводить до загоряння ізоляції, розплавлення з’єднувальних провідників і спричиняє пожежу. Для уникнення цієї небезпеки в електричних колах застосовують автоматичні вимикачі струму (плавкі запобіжники, механічні реле тощо).
Напруга на зовнішньому опорі замкненого кола завжди менша від ЕРС, що дорівнює: U = IR = e — Ir. Переміщуючи заряди у провіднику, електричне поле виконує роботу. Її значення можна визначити, використавши визначення напруги і сили струму:
, де q = IDt A = UIDt. (4.2.5)
Робота струму дорівнює добутку сили струму напруги і часу, впродовж якого виконується робота. Як і в механіці, роботу струму вимірюють у джоулях. Якщо у формулу (4.2.5) підставити почергово значення сили струму, а потім напруги із закону Ома для ділянки кола, то отримаємо інший вираз для визначення роботи електричного струму:
Як і в механіці, роботу струму вимірюють у джоулях. Якщо у формулу (4.2.5) підставити почергово значення сили струму, а потім напруги із закону Ома для ділянки кола, то отримаємо інший вираз для визначення роботи електричного струму:
A = UIDt, де . (4.2.6)
Формула (4.2.6) зручна для визначення роботи струму в колі з паралельним з’єднанням провідників, оскільки напруга на всіх провідниках при цьому однакова:
A = UIDt, де U = IR, A = I 2RDt. (4.2.7)
Формулою (4.2.7) зручно користуватись у разі послідовного з’єднання провідників у колі, оскільки через всі провідники проходить однаковий струм.
Будь-який електричний прилад розрахований на споживання певної енергії за одиницю часу. Тому поряд із роботою струму велике значення має потужність струму. Вона дорівнює відношенню роботи струму за час Dt до цього часу:
.
Як і в механіці, її вимірюють у ватах (Вт).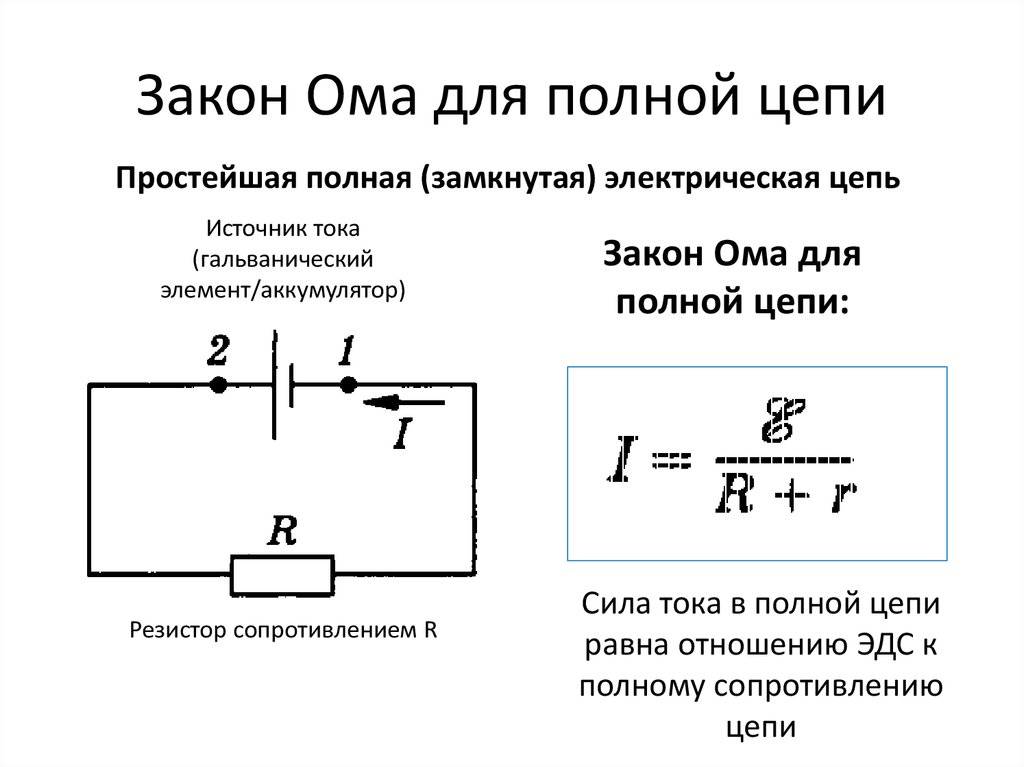 На більшості приладів вказано потужність, яку вони споживають. На практиці широко застосовують одиницю потужності — кіловат і одиницю роботи — кіловат-годину:
На більшості приладів вказано потужність, яку вони споживають. На практиці широко застосовують одиницю потужності — кіловат і одиницю роботи — кіловат-годину:
1 кВт = 103 Вт, 1 кВт·год = 3,6·106 Дж.
Потужність струму P = IU = I 2R, що споживається зовнішньою ділянкою повного кола, називають корисною. Затраченою потужністю називають потужність джерела струму Pзат = eI = I2(R + r). Коефіцієнт корисної дії джерела
.
Коефіцієнт корисної дії зростає зі зменшенням внутрішнього опору джерела.
Електрорушійна сила. Закон Ома для повного кола » mozok.click
Енергетична характеристика джерела струму. Як ми уже з’ясували, для тривалого існування електричного струму в колі потрібне джерело, в якому постійно відбувається розділення електричних зарядів, у результаті чого підтримується стала різниця потенціалів. Будь-яке джерело постійного струму має два полюси: полюс із високим потенціалом — позитивний — і з найнижчим потенціалом — негативний.
Під’єднаємо до полюсів джерела провідник (мал. 34). Під дією сил електричного поля позитивно заряджені частинки рухаються у напрямку від позитивного полюса джерела до негативного. Але замкнути коло, перемістивши електричні заряди із точки В у точку А, сили електричного поля не
можуть, оскільки діють на них у протилежний бік. Тому всередині джерела крім електричних сил діють ще й сторонні сили, що переміщують позитивні заряди від негативного полюса батареї до позитивного і протидіють електричним силам, які прагнуть вирівняти потенціали на полюсах. Завдяки цьому заряди циркулюють по замкненому колу, створюючи струм.
На переміщення зарядів із точки В у точку А затрачається відповідна робота А,.т, яку виконують сторонні сили. Чим більший заряд переміщується, тим більша затрачається робота. Іншими словами, Аст — q або, переходячи до знака рівності,
постійний коефіцієнт пропорційності, що характеризує відповідне джерело і називається електрорушійною силою джерела1 (скорочено ЕРС).
Електрорушійна сила в — це фізична величина, що характеризує енергію сторонніх сил джерела струму й вимірюється роботою сторонніх сил (тобто сил неелектростатичного походження), виконаною при переміщенні
одиничного позитивного електричного заряду,
Одиниця електрорушійної сили — вольт,
У результаті розділення всередині джерела позитивних і негативних зарядів джерело набуває запасу потенціальної енергії, яка витрачається на виконання роботи з переміщення зарядів по всьому колу. Тепер можемо сказати: ту частину замкненого кола, в якій заряди рухаються під дією електростатичної різниці потенціалів називають зовнішньоюу а ту, в якій носії заряду рухаються під дією сторонніх сил, — внутрішньою. Полюси джерела струму розділяють внутрішню і зовнішню ділянки кола.
Сторонні сили забезпечують розділення різнойменно заряджених частинок в джерелі (у внутрішньому колі) і підтримують певну різницю, потенціалів на полюсах, тим самим зумовлюючи рух зарядів у зовнішньому колі.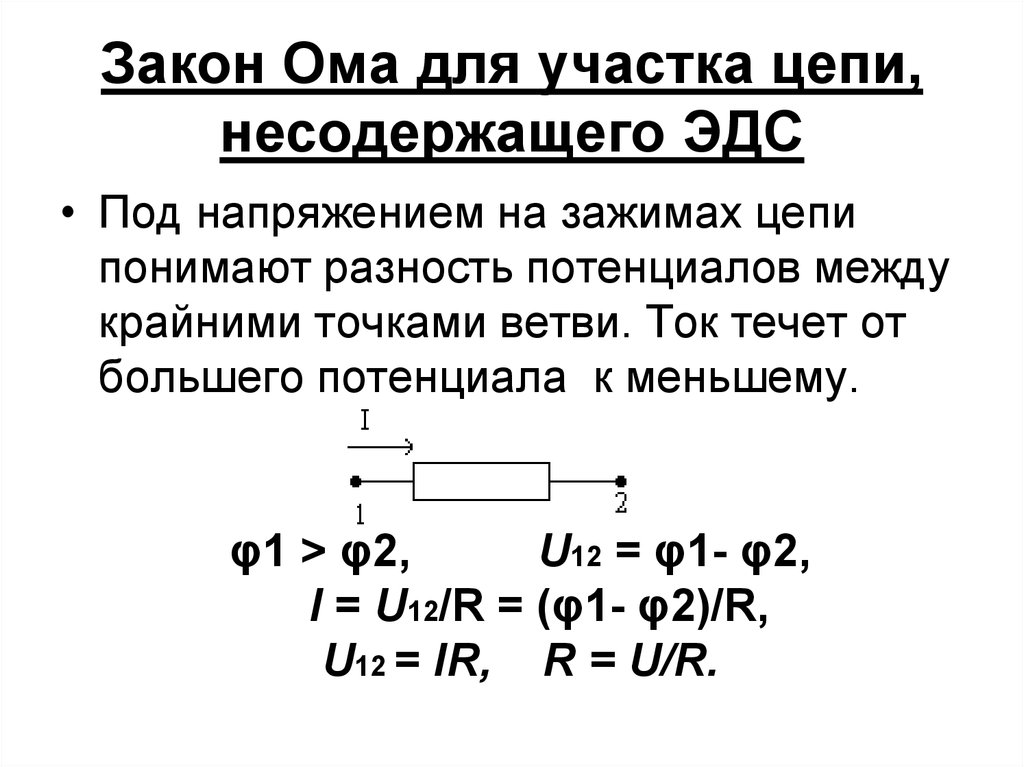 зовн “ спад напруги на зовнішній ділянці кола.
зовн “ спад напруги на зовнішній ділянці кола.
Відповідно робота сторонніх сил по переміщенню заряду на внутрішній ділянці кола Авн = qUBny де Uan — спад напруги на внутрішній ділянці кола.
Таким чином,
Закон Ома для повного кола. Джерело струму, як і будь-який провідник, має певний опір, котрий називають внутрішнім опором джерела і позначають г на відміну від опору зовнішнього кола R. Як відомо з курсу 9 класу, згідно із законом Ома для ділянки кола сила струму І у ділянці кола, прямо пропорційна прикладеній напрузі U і обернено пропорційна опорові
R цієї ділянки,
Формулу закону Ома записують і в такому вигляді:
U = IRy де добуток IR називають спадом напруги на даній ділянці кола. Якщо ділянка не містить джерела струму, то поняття напруги і спаду напруги збігаються.
Згідно із законом Ома для зовнішньої і внутрішньої ділянок кола, можна записати UBH = /г, U3QBH = IR.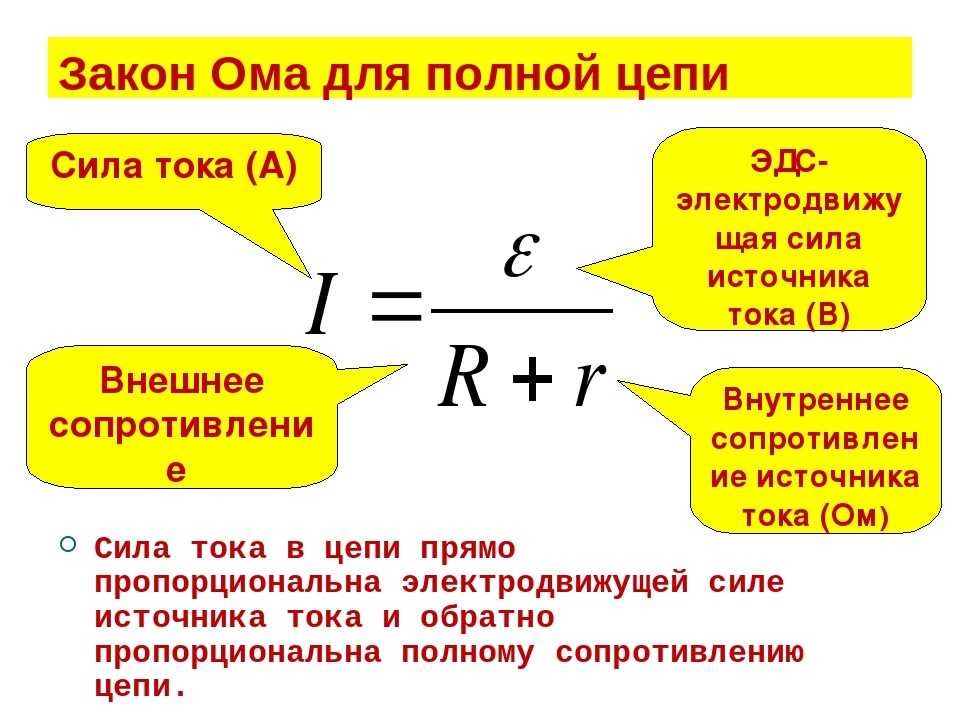 Тоді S-IR + Ігу сума спадів напруг на зовнішній і внутрішній ділянках кола дорівнює ЕРС джерела.
Тоді S-IR + Ігу сума спадів напруг на зовнішній і внутрішній ділянках кола дорівнює ЕРС джерела.
1 Термін «електрорушійна сила» виник до того, як були з’ясовані процеси, що відбуваються в електричному колі. Як видно з означення, мова йде про енергетичну характеристику джерела, а не про силову.
Співвідношення записане у вигляді
називають законом Ома для повного кола: сила струму у замкненому електричному колі прямо пропорційна електрорушійній силі джерела струму і обернено пропорційна повному опору кола.
Отже, сила струму в колі залежить від трьох величин, дві з яких (ЕРС і внутрішній опір) характеризують джерело, а третя залежить від самого кола. Якщо користуватись певним джерелом електричної енергії, то £ і г можна вважати сталими величинами. Якщо змінювати опір зовнішнього кола, то відповідно змінюватиметься сила струму І в колі і спад напруги IR на зовнішній ділянці кола. Зі збільшенням опору зовнішнього кола сила струму зменшується, напруга ж зростає. >r , U = IR~g . Чим більший опір вольтметра порівняно з внутрішнім опором джерела струму, тим точніше виміряне значення ЕРС.
>r , U = IR~g . Чим більший опір вольтметра порівняно з внутрішнім опором джерела струму, тим точніше виміряне значення ЕРС.
Коротке замикання. Зі зменшенням опору зовнішнього кола, R—>0,
сила струму набуває максимального значення
Цей випадок називають коротким замиканням.
Для джерел, де порівняно малий внутрішній опір (наприклад, у свинцевих акумуляторах г ~ 0,1 + 0,001 Ом), сила струму короткого замикання може досягти дуже великих значень. Провідники можуть розплавитись, а саме джерело вийти з ладу. Особливо небезпечні короткі замикання в освітлювальних мережах, які живляться від трансформаторних підстанцій, ЕРС яких вимірюється сотнями вольтів. Сила струму короткого замикання в них може досягти кількох тисяч амперів.
Дайте відповіді на запитання
1. Чи може тривалий час існувати електричний струм у колі, якщо на рухливі носії заряду діють тільки кулонівські сили?
2. У чому полягає фізична суть поняття електрорушійної сили джерела струму? Що вона характеризує?
3. З яких частин складається замкнене коло?
З яких частин складається замкнене коло?
4. Що таке струм короткого замикання?
Приклади розв’язування задач
Задача. До якої напруги зарядяться конденсатори Cj та С2, підключені до джерела, якщо його ЕРС 2,2 В, внутрішній опір 0,4 Ом? Параметри резисторів та конденсаторів такі: Я| = 3 Ом, R2 = 1 Ом, R3 = 5 Ом; Сх = 2 мкФ, С2 = 3 мкФ (мал. 35).
Розв’язання
Оскільки ділянкою з конденсаторами постійний струм не проходить, то для обводу KLNM можна записати
Напруга на резисторі Я., становить
Така ж напруга буде і між точками X та У ділянки, що містить конденсатори. Оскільки конденсатори з’єднані послідовно, то обидва вони мають однаковий заряд </.
Напруги на цих конденсаторах
Для напруги між точками X та У можна записати
звідки
Підставивши у рівності (2) значення q та U3 з рівностей (1) та (3), отримуємо
Як видно, від величини опору Я2 значення Ui та U2 не залежать.
Після підстановки числових значень отримуємо Ux = 0,78 В; U2 = 0,52 В. Відповідь: 0,78 В; 0,52 В.
Вправа 8
1. Для визначення ЕРС і внутрішнього опору джерела струму склали коло за схемою, зображеною на мал. 36. За деякого положення ковзного контакте реостата амперметр показав 0,5 А, а вольтметр — 4 В. Коли контакт перемістили трохи вліво, амперметр показав 0,9 А, а вольтметр — 3,6 В. Обчислити ЕРС і внутрішній опір джерела.
2. Лампочки, опори яких дорівнюють 3 та 12 Ом, по черзі приєднували до деякого джерела струму, і вони споживали однакову потужність. Визначити внутрішній опір джерела і ККД кола в кожному випадку. (Вказівка: ККД
кола дорівнює
3. Визначити заряд на обкладках конденсатора (мал. 37), якщо ЕРС джерела £, його внутрішній опір г. Опори резисторів Я, та /?2 відомі. Ємність конденсатора С.
4. Вважаючи відомими величини, вказані на схемі (мал. 38), визначити заряд на конденсаторі. Як зміниться величина заряду, якщо Я, та Я2 вимкнути?
Как подсчитать повторяющиеся значения в Excel
Работа с большими наборами данных часто требует подсчета повторяющихся значений в Excel. Вы можете подсчитать повторяющиеся значения, используя функцию СЧЁТЕСЛИ. В этом уроке вы узнаете, как подсчитывать дубликаты с помощью этой функции.
Вы можете подсчитать повторяющиеся значения, используя функцию СЧЁТЕСЛИ. В этом уроке вы узнаете, как подсчитывать дубликаты с помощью этой функции.
Вы можете подсчитать дубликаты, используя формулу СЧЁТЕСЛИ в Excel. Есть несколько подходов к подсчету дубликатов. Возможно, вы захотите включить или исключить первый экземпляр при подсчете дубликатов. В следующих разделах вы увидите несколько примеров, связанных с подсчетом дубликатов.
Как подсчитать повторяющиеся экземпляры, включая первое появлениеСледующий пример включает данные об оценках учащихся. Данные содержат имя учащегося, возраст и оценки. Столбец D содержит уникальные оценки, для которых вы собираетесь подсчитывать дубликаты.
Чтобы найти количество повторяющихся оценок, включая первое вхождение:
- Перейти к ячейке F2 .
- Назначение формулы
=СЧЁТЕСЛИ($C$2:$C$8,E2). - Нажмите Введите .

- Перетащите формулу из F2 в F4.
Теперь у вас есть количество повторяющихся оценок в столбце E.
Как подсчитывать повторяющиеся экземпляры, исключая первое появлениеЧасто может потребоваться подсчитать количество дубликатов в данных без первого вхождения. Вы можете подсчитать количество дубликатов, исключая первую запись, так же, как и в предыдущем примере. Чтобы подсчитать повторяющиеся примеры из последнего примера без первого вхождения:
- Выберите ячейку F2 .
- Назначение формулы
=СЧЁТЕСЛИ($C$2:$C$8,E2)-1. - Нажмите Enter, чтобы применить формулу.
Это покажет количество повторяющихся значений без первого экземпляра в столбце E.
Подсчет регистрозависимых дубликатов в Excel Функция СЧЁТЕСЛИ в Excel нечувствительна к регистру. Вы не получите фактического количества, если будете использовать его для подсчета дубликатов с учетом регистра. Но вы можете использовать комбинацию функций SUM и EXACT, чтобы получить количество повторяющихся экземпляров с учетом регистра. Чтобы найти количество повторяющихся значений с учетом регистра:
Но вы можете использовать комбинацию функций SUM и EXACT, чтобы получить количество повторяющихся экземпляров с учетом регистра. Чтобы найти количество повторяющихся значений с учетом регистра:
- Перейти к ячейке F2 .
- Назначение формулы
=СУММ(--EXACT($C$2:$C$8,E2)). - Нажмите Ctrl + Shift + Enter , чтобы применить формулу как формулу массива.
Формула EXACT выполняет сравнение с учетом регистра значений в столбце D с оценками от C2 до C8. В результате получается массив логических значений ИСТИНА и ЛОЖЬ. Унарный оператор (-) преобразует значения в массив из 0 и 1. Затем функция СУММ суммирует эти записи, чтобы найти количество повторяющихся значений.
Подсчет повторяющихся строк в Excel Вы можете подсчитывать повторяющиеся строки с одинаковыми значениями в каждой ячейке. Это очень удобно, если у вас есть большой набор данных и вы хотите идентифицировать повторяющиеся строки для будущих изменений. Функция СЧЁТЕСЛИМН позволяет считать на основе нескольких условий. Вы будете использовать функцию COUNTIFS для подсчета повторяющихся строк.
Функция СЧЁТЕСЛИМН позволяет считать на основе нескольких условий. Вы будете использовать функцию COUNTIFS для подсчета повторяющихся строк.
В следующем примере вы будете использовать информацию об ученике. В данных есть столбцы для имен учащихся, возраста и пола. Столбец E содержит все уникальные имена, для которых вы будете подсчитывать повторяющиеся строки.
- Выберите ячейку F2 , нажав на нее.
- Назначьте формулу
=СЧЁТЕСЛИМН($A$2:$A$8,A2,$B$2:$B$8,B2,$C$2:$C$8,C2)для F2. - Нажмите Введите .
Перетащите формулу в ячейки ниже с помощью мыши.
Как подсчитать общее количество дубликатов в столбце Вы можете подсчитать общее количество дубликатов в столбце в два этапа. Во-первых, вам нужно идентифицировать все дубликаты в столбце. Затем вам нужно посчитать эти значения. Следующий пример включает в себя разные названия стран, содержащие дубликаты. Чтобы найти общее количество дубликатов без первого вхождения:
Чтобы найти общее количество дубликатов без первого вхождения:
- Перейдите в ячейку B2 , нажав на нее.
- Назначьте формулу
=ЕСЛИ(СЧЕТЕСЛИ($A$2:A2,A2)>1,"Да","")ячейке B2. - Нажмите Введите . Это покажет значение Да, если запись в A2 является повторяющейся записью.
- Перетащите формулу вниз от B2 до B8 .
- Выберите ячейку B9.
- Назначьте формулу
=СЧЁТЕСЛИ(B2:B8;"Да")ячейке B9. - Нажмите Введите .
Это покажет общее количество повторяющихся значений в столбце A без первого вхождения.
Чтобы подсчитать повторяющиеся значения, включая первое вхождение:
- Выберите ячейку D4.
- Назначение формулы
=СТРОКИ($A$2:$A$8)-СУММ(ЕСЛИ(СЧЁТЕСЛИ($A$2:$A$8,$A$2:$A$8) =1,1,0))в ряд В2. - Нажмите Ctrl + Shift + Enter .

Здесь мы использовали функции СТРОКИ, СУММ и ЕСЛИ вместе с функцией СЧЕТЕСЛИ и применили ее как функцию массива. Эту формулу можно разбить на две части. На первом этапе функция СТРОКИ подсчитывает количество строк между A2:A8, что равно 7. Во второй части формулы функция СЧЁТЕСЛИ используется для подсчета общего количества совпадений в диапазоне от A2 до A8 с самой собой, и мы вкладываем все это в функцию ЕСЛИ.
Используемое здесь условие состоит в том, чтобы вернуть 1, если это совпадение, и 0 в противном случае. Полученные 1 затем суммируются, и в результате получается 2, что является количеством различных совпадений между A2 и A8 с самим собой. Разница между этими двумя шагами возвращает 5, общее количество дубликатов, включая первые экземпляры.
Подсчет дубликатов в Excel — очень удобный прием при работе с большими наборами данных. Функции СЧЁТЕСЛИ и СЧЁТЕСЛИМН удобны для подсчёта повторяющихся значений в Excel и получения полезной информации о данных.
Все еще нужна помощь с форматированием Excel или есть другие вопросы об Excel? Свяжитесь с экспертом Excel в прямом эфире здесь, чтобы получить помощь один на один. Первый сеанс всегда бесплатный.
Как найти и выделить дубликаты в Excel
Из этого руководства вы узнаете, как отображать дубликаты в Excel. Мы собираемся подробно рассмотреть различные методы затенения повторяющихся ячеек, целых строк или последовательных дубликатов с использованием условного форматирования. Также вы увидите, как выделять дубликаты разными цветами с помощью специализированного инструмента.
На прошлой неделе мы исследовали различные способы выявления дубликатов в Excel. Несомненно, повторяющиеся формулы очень полезны, но выделение повторяющихся записей определенным цветом может сделать анализ данных еще проще.
Самый быстрый способ найти и выделить дубликаты в Excel — использовать условное форматирование . Самым большим преимуществом этого метода является то, что он не только показывает вам существующие дубликаты, но и обнаруживает и окрашивает новые дубликаты по мере того, как вы вводите, редактируете или перезаписываете свои данные.
Далее в этом руководстве вы найдете несколько способов выделения повторяющихся записей в зависимости от вашей конкретной задачи. Эти методы работают во всех версиях Excel 365, Excel 2019, Excel 2016, Excel 2013, Excel 2010 и более ранних версиях.
- Выделение дубликатов в Excel с 1 вхождениями st (встроенное правило)
- Как выделить дубликаты в Excel, кроме экземпляров 1 st
- Как выделить дубликаты в диапазоне (несколько столбцов)
- Как найти N -й и последующие записи-дубликаты
- Затенение целых строк на основе повторяющихся значений в одном столбце
- Как выделить повторяющиеся строки в Excel
- Как найти последовательные повторяющиеся ячейки
- Duplicate Remover — самый быстрый способ найти и выделить дубликаты в Excel
Как выделить дубликаты в Excel с помощью встроенного правила (с 1
st вхождений) Во-первых, во всех версиях Excel есть предопределенное правило для выделения повторяющихся ячеек. Чтобы использовать это правило в своих рабочих листах, выполните следующие действия:
Чтобы использовать это правило в своих рабочих листах, выполните следующие действия:
- Выберите данные, которые вы хотите проверить на наличие дубликатов. Это может быть столбец, строка или диапазон ячеек.
- На вкладке Главная в группе Стили щелкните Условное форматирование > Правила выделения ячеек > Повторяющиеся значения…
- Откроется диалоговое окно Duplicate Values с форматами светло-красной заливки и темно-красного текста, выбранными по умолчанию. Чтобы применить формат по умолчанию, просто нажмите ОК .
Помимо красной заливки и форматирования текста, в раскрывающемся списке доступно несколько других предустановленных форматов. Чтобы выделить дубликаты другим цветом, нажмите Пользовательский формат… (последний элемент в раскрывающемся списке) и выберите цвет заливки и/или шрифта по своему вкусу.
Наконечник. Чтобы выделить уникальные значения, выберите Unique в левом поле.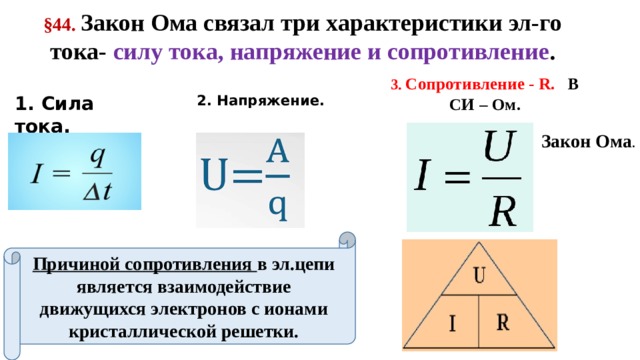
Используя встроенное правило, вы можете выделить дубликаты в одном столбце или в нескольких столбцах, как показано на следующем снимке экрана:
Примечание. При применении встроенного правила дублирования к двум или более столбцам Excel не сравнивает значения в этих столбцах, а просто выделяет все повторяющиеся экземпляры. Если вы хотите найти и выделить совпадения и различия между двумя столбцами , вы найдете несколько примеров в следующем руководстве: Как сравнить два столбца в Excel.
При использовании встроенного правила Excel для выделения повторяющихся значений помните о следующих двух вещах:
- Работает только для отдельных ячеек. Чтобы выделить повторяющиеся строки , вам потребуется создать свои собственные правила либо на основе значений в определенном столбце, либо путем сравнения значений в нескольких столбцах.
- Затеняет повторяющиеся ячейки, включая их первые вхождения. Чтобы выделить все дубликаты , кроме для первых экземпляров , создайте правило условного форматирования на основе этой формулы.

Как выделить дубликаты без 1
st вхожденияЧтобы выделить 2 и и все последующие повторяющиеся вхождения, выделите ячейки, которые хотите раскрасить, и создайте правило на основе формулы следующим образом:
- Стили , щелкните Условное форматирование > Новое правило > Используйте формулу, чтобы определить, какие ячейки форматировать .
- В поле Формат значений, где эта формула верна , введите формулу, подобную этой:
=СЧЁТЕСЛИ($A$2:$A2,$A2)>1Где A2 — самая верхняя ячейка выбранного диапазона.
- Нажмите кнопку Формат… и выберите нужный цвет заливки и/или шрифта.
- Наконец, нажмите OK , чтобы сохранить и применить правило.
Если у вас нет большого опыта работы с условным форматированием Excel, вы найдете подробные инструкции по созданию правила на основе формулы в следующем руководстве: Условное форматирование Excel на основе другого значения ячейки.
В результате повторяющиеся ячейки, за исключением первых экземпляров, будут выделены выбранным вами цветом:
Как показать 3
rd , 4 th и все последующие повторяющиеся записиДля просмотра дубликатов, начинающихся с N-е вхождение, создайте правило условного форматирования на основе формулы, как в предыдущем примере, с той лишь разницей, что вы заменяете >1 в конце формулы на нужное число. Например:
Чтобы выделить 3 rd и все последующие дубликатов, создайте правило условного форматирования на основе этой формулы:
=СЧЁТЕСЛИ($A$2:$A2,$A2)>=3
К выделите 4 th и все последующие повторяющихся записей, используйте эту формулу:
=СЧЁТЕСЛИ($A$2:$A2,$A2)>=4
Чтобы выделить только конкретные вхождения, используйте , равное оператор (=). Например, для выделите только 2 nd instances , вы можете использовать эту формулу:
=СЧЁТЕСЛИ($A$2:$A2,$A2)=2
Как выделить дубликаты в диапазоне (несколько столбцов)
Когда вы хотите чтобы проверить наличие дубликатов в нескольких столбцах, не сравнивая столбцы друг с другом, а находя все экземпляры одного и того же элемента во всех столбцах, используйте одно из следующих решений.
Выделение дубликатов в нескольких столбцах, включая 1
st вхожденийЕсли первый экземпляр элемента, который появляется в наборе данных более одного раза, считается дубликатом, проще всего использовать встроенное правило Excel для дубликатов.
Или создайте правило условного форматирования с помощью следующей формулы:
СЧЁТЕСЛИ( диапазон , top_cell )>1
Например, чтобы выделить дубликаты в диапазоне A2:C8, формула выглядит следующим образом:
=СЧЁТЕСЛИ($A$2:$C$8, A2)>1
Обратите внимание на использование абсолютных ссылок на ячейки для диапазона ($A$2:$C$8) и относительных ссылок на верхнюю ячейку (A2) .
Выделение дубликатов в нескольких столбцах, кроме 1
st вхожденийРешение для этого сценария намного сложнее, неудивительно, что в Excel нет встроенного правила для него 🙂
Чтобы выделить повторяющиеся записи в нескольких столбцах, игнорируя 1 st вхождений, вам нужно будет создать 2 правила со следующими формулами:
Правило 1.
 Применяется к первому столбцу
Применяется к первому столбцуЗдесь вы используете точно такую же формулу, которую мы использовали для выделения дубликатов без 1 st вхождений в один столбец (подробные шаги можно найти здесь).
В этом примере мы создаем правило для A2:A8 по следующей формуле:
=СЧЁТЕСЛИ($A$2:$A2,$A2)>1
В результате повторяющиеся элементы без 1 st вхождений подсвечиваются в самом левом столбце диапазона (в нашем случае такой пункт только один):
Правило 2. Применяется ко всем последующим столбцам
Для выделения дубликатов в остальных столбцах (B2:C8 ), используйте эту формулу:
=СЧЕТЕСЛИ(A$2:$A$8,B2)+СЧЁТЕСЛИ(B$2:B2,B2)>1
В приведенной выше формуле первая функция СЧЁТЕСЛИ подсчитывает количество вхождений данного элемента в первом столбце , а второй COUNTIF делает то же самое для всех последующих столбцов. А затем вы складываете эти числа и проверяете, больше ли сумма 1.
В результате все повторяющиеся элементы, за исключением их 1 st вхождений, найдены и выделены:
Выделите дубликаты во всех столбцах одним правило
Другим возможным решением является добавление пустого столбца слева от вашего набора данных и объединение приведенных выше формул в единую формулу, например: :$B$8,B2),0) + СЧЁТЕСЛИ(B$2:B2,B2)>1
Где B2 — верхняя ячейка с данными в столбце 2 и целевого диапазона.
Чтобы лучше понять формулу, давайте разобьем ее на 2 основные части:
- Для первого столбца (B) никогда не выполняется условие ЕСЛИ, поэтому вычисляется только вторая функция СЧЁТЕСЛИ (мы использовали эту формулу чтобы найти дубликаты, кроме первых вхождений в одном столбце).
- Для всех последующих столбцов (C2:D8) ключевым моментом является разумное использование абсолютных и относительных ссылок в двух функциях СЧЁТЕСЛИ. Чтобы упростить понимание, я скопировал ее в столбец G, чтобы вы могли видеть, как формула меняется при применении к другим ячейкам:
Поскольку условие ЕСЛИ всегда истинно для всех столбцов, кроме первого (количество столбцов больше 1), формула работает следующим образом:
- Подсчитывает количество вхождений данного элемента (D5 в скриншот выше) во всех колонках слева от данной колонки:
СЧЁТЕСЛИ(B$2:$C$8,D5) - Подсчитывает количество вхождений данного элемента в столбце элемента, вплоть до ячейки элемента:
СЧЁТЕСЛИ(D$2:D5,D5) - Наконец, формула суммирует результаты обеих функций СЧЁТЕСЛИ.
 Если общее число больше 1, т. е. если элемент встречается более одного раза, применяется правило, и элемент выделяется.
Если общее число больше 1, т. е. если элемент встречается более одного раза, применяется правило, и элемент выделяется.
Выделение целых строк на основе повторяющихся значений в одном столбце
Если ваша таблица содержит несколько столбцов, вы можете выделить целые строки на основе повторяющихся записей в определенном столбце.
Как вы уже знаете, встроенное правило Excel для дубликатов работает только на уровне ячейки. Но пользовательское правило на основе формулы не имеет проблем с затенением строк. Ключевым моментом является выбор всех строк , а затем создание правила с одной из следующих формул:
- Чтобы выделить повторяющиеся строки за исключением 1 st вхождений :
=СЧЁТЕСЛИ($A$2:$ А2, $А2)>1 - Для выделения повторяющихся строк в том числе 1 ст вхождений :
=СЧЁТЕСЛИ($A$2:$A$15, $A2)>1
Где A2 — первая ячейка, а A15 — последняя использованная ячейка в столбце, который вы хотите проверить на наличие дубликатов. Как видите, разумное использование абсолютных и относительных ссылок на ячейки — это то, что имеет значение.
Как видите, разумное использование абсолютных и относительных ссылок на ячейки — это то, что имеет значение.
На следующем снимке экрана показаны оба правила в действии:
Как выделить повторяющиеся строки в Excel
В предыдущем примере показано, как окрашивать целые строки на основе повторяющихся значений в определенном столбце. Но что, если вы хотите просмотреть строки с одинаковыми значениями в нескольких столбцах? Или как выделить абсолютные дубликаты строк, которые имеют абсолютно одинаковые значения во всех столбцах?
Для этого используйте функцию СЧЁТЕСЛИМН, которая позволяет сравнивать ячейки по нескольким критериям. Например, чтобы выделить повторяющиеся строки с одинаковыми значениями в столбцах A и B, используйте одну из следующих формул:
- A2, $A2, $B$2:$B2, $B2)>1
- Чтобы выделить повторяющиеся строки с 1 вхождением st :
=СЧЁТЕСЛИМН($A$2:$A$15, $A2, $B$2:$B$15, $B2)>1
На следующем снимке экрана показан результат:
Как вы понимаете, приведенный выше пример предназначен только для демонстрации. При выделении повторяющихся строк в ваших реальных листах вы, естественно, не ограничены сравнением значений только в 2 столбцах, функция СЧЁТЕСЛИМН может обрабатывать до 127 пар диапазон/критерий.
При выделении повторяющихся строк в ваших реальных листах вы, естественно, не ограничены сравнением значений только в 2 столбцах, функция СЧЁТЕСЛИМН может обрабатывать до 127 пар диапазон/критерий.
Выделение последовательных повторяющихся ячеек в Excel
Иногда вам может не понадобиться выделять все повторяющиеся ячейки в столбце, а показывать только последовательные повторяющиеся ячейки, т. е. те, которые находятся рядом друг с другом. Для этого выделите ячейки с данными (не включая заголовок столбца) и создайте правило условного форматирования с одной из следующих формул:
- Для выделения последовательных дубликатов без вхождений 1 st :
=$A1=$A2 - Для выделения последовательных дубликатов с 1 st вхождений :
=ИЛИ($A1=$A2, $A2=$A3)
На следующем снимке экрана показано выделение последовательных повторяющихся текстов, но эти правила также будут работать для последовательных повторяющихся чисел и дат: следующие улучшения формул: 9 и игнорировать пустые ячейки
=И($A2<>"", ИЛИ($A1=$A2, $A2=$A3))
Как видите, выделить дубликаты в Excel с помощью условного форматирования не составляет большого труда. Однако есть еще более быстрый и простой способ. Чтобы узнать это, прочитайте следующий раздел этого руководства.
Однако есть еще более быстрый и простой способ. Чтобы узнать это, прочитайте следующий раздел этого руководства.
Как выделить дубликаты в Excel с помощью Duplicate Remover
Надстройка Duplicate Remover — это комплексное решение для работы с повторяющимися записями в Excel. Он может находить, выделять, выбирать, копировать или перемещать повторяющиеся ячейки или целые повторяющиеся строки.
Несмотря на свое название, надстройка может быстро выделять дубликаты разными цветами, не удаляя их.
Duplicate Remover добавляет 3 новые функции на вашу ленту Excel:
- Dedupe Table — чтобы сразу найти и выделить дубликаты в одной таблице.
- Duplicate Remover — пошаговый мастер с расширенными параметрами для выявления и выделения дубликатов или уникальных значений в 1 таблице.
- Сравнить 2 таблицы — найти и выделить дубликаты путем сравнения двух столбцов или двух отдельных таблиц.
После установки Ultimate Suite for Excel вы найдете эти инструменты на Ablebits Data в группе Dedupe :
Выделение дубликатов в Excel в пару кликов
Для этого примера я создал следующую таблицу с несколькими сотнями строк. И наша цель — выделить повторяющиеся строки, которые имеют одинаковые значения во всех трех столбцах:
И наша цель — выделить повторяющиеся строки, которые имеют одинаковые значения во всех трех столбцах:
Хотите верьте, хотите нет, но вы можете получить желаемый результат всего двумя щелчками мыши 🙂
- Выделив любую ячейку в таблице, нажмите кнопку Dedupe Table , и умная надстройка подхватит всю таблицу.
- Откроется диалоговое окно Dedupe Table , в котором все столбцы будут выбраны автоматически, а параметр Цвет дублирует выбран по умолчанию. Итак, все, что вам нужно сделать, это нажать OK 🙂 Готово!
Наконечник. Если вы хотите обнаружить повторяющиеся строки по одному или нескольким столбцам, снимите флажки со всех нерелевантных столбцов и оставьте выбранными только ключевые столбцы.
И результат будет выглядеть примерно так:
Как вы видите на изображении выше, инструмент Dupe Table выделил повторяющиеся строки без первых экземпляров .
Если вы хотите выделить дубликаты , включая первые вхождения , или если вы хотите покрасить уникальные записи, а не дубликаты, или если вам не нравится красный цвет по умолчанию, используйте мастер Duplicate Remover , в котором есть все эти особенности и многое другое.
Выделение дубликатов в Excel с помощью расширенного пошагового мастера
По сравнению с быстрым инструментом Dedupe Table , Duplicate Remover 9Мастеру 0194 требуется еще несколько щелчков мышью, но это компенсируется рядом дополнительных опций. Позвольте мне показать вам это в действии:
- Выберите любую ячейку в вашей таблице, где вы хотите выделить дубликаты, и нажмите кнопку Duplicate Remover на ленте. Мастер запустится, и будет выбрана вся таблица. Надстройка также предложит создать резервную копию вашей таблицы на всякий случай. Если вам это не нужно, снимите этот флажок.
Убедитесь, что таблица выбрана правильно, и нажмите 9.0193 Следующий .
- Выберите один из следующих типов данных, которые вы хотите найти:
- Дубликаты, кроме первых вхождений
- Дубликаты с 1-м вхождением
- Уникальные значения
- Уникальные значения и первые повторяющиеся вхождения
Для этого примера найдем дубликатов + первые вхождения :
- Теперь выберите столбцы для проверки на наличие дубликатов.
 Поскольку мы хотим выделить полные повторяющиеся строки, я выбрал все 3 столбца.
Поскольку мы хотим выделить полные повторяющиеся строки, я выбрал все 3 столбца. Кроме того, надстройка позволяет указать, есть ли в таблице заголовки и нужно ли пропускать пустые ячейки. Оба варианта выбраны по умолчанию.
- Наконец, выберите действие для дубликатов. У вас есть несколько вариантов, таких как выбор , удаление , копирование, перемещение дубликатов или добавление столбца состояния в определение дубликатов.
С сегодняшнего дня мы изучаем различные способы выделения дублирует в Excel, наш выбор очевиден 🙂 Итак, выберите Заливка цветом и выберите один из стандартных цветов темы, или нажмите Больше цветов… и выберите любой пользовательский цвет RGB или HSL.
Нажмите кнопку Finish и наслаждайтесь результатом 🙂
Вот как вы выделяете дубликаты в Excel с помощью нашей надстройки Duplicate Remover. Если вам интересно попробовать этот инструмент на своих собственных рабочих листах, вы можете загрузить полнофункциональную пробную версию Ultimate Suite, которая включает в себя все наши инструменты для экономии времени для Excel. И ваши отзывы в комментариях будут очень признательны!
И ваши отзывы в комментариях будут очень признательны!
Вас также может заинтересовать
Выделение дубликатов в Google Таблицах: условное форматирование и надстройка
Февраль
25
by Natalia Sharashova | обновлено
В моем предыдущем сообщении в блоге я описал различные способы поиска и обработки дубликатов в электронной таблице. Но чтобы сразу их заметить, лучше всего выделить их цветом.
И сегодня я постараюсь осветить для вас самые популярные кейсы. Вы будете выделять дубликаты в Google Таблицах не только условным форматированием (существуют разные формулы, основанные на разбросе дубликатов в вашей таблице), но и специальным дополнением.
- Выделение повторяющихся ячеек в одном столбце Google Sheets
- Выделение дубликатов в нескольких столбцах Google Sheets
- Выделить всю строку, если дубликаты есть в одном столбце
- Выделение полных дубликатов строк в электронных таблицах
- Выделение фактических дубликатов — экземпляров 2n, 3d и т.
 д.
д. - Способ выделения дубликатов без формул — надстройка «Удалить дубликаты» для Google Таблиц
- Подсветка дубликатов по расписанию с помощью надстройки
- Видео: Как выделить дубликаты в Google Sheets
Выделение повторяющихся ячеек в одном столбце Google Sheets
Начнем с основного примера. Это когда у вас есть только один столбец с повторяющимися значениями:
Совет. Сегодня я буду использовать условное форматирование во всех случаях, кроме последнего. Если вы не знакомы с ним, узнайте об этом в этом сообщении в блоге.
Чтобы выделить повторяющиеся ячейки в одном столбце Google Sheets, откройте условное форматирование и установите следующие параметры:
- примените правило к вашему диапазону ячеек — A2:A10 в моем примере
- выберите Пользовательская формула из раскрывающегося списка с условием и введите следующую формулу:
=СЧЁТЕСЛИ($A$2:$A$10,$A2)>1Примечание.
 Рядом с буквой A2 есть знак доллара. Это сделано намеренно, чтобы формула могла подсчитывать каждую ячейку из столбца A. В этой статье вы узнаете больше о ссылках на ячейки.
Рядом с буквой A2 есть знак доллара. Это сделано намеренно, чтобы формула могла подсчитывать каждую ячейку из столбца A. В этой статье вы узнаете больше о ссылках на ячейки. - выберите любой цвет из стиля форматирования , чтобы выделить эти дубликаты
- нажмите Готово
Эта формула СЧЁТЕСЛИ просканирует ваш столбец А и сообщит правилу, какие записи появляются более одного раза. Все эти повторяющиеся ячейки будут окрашены в соответствии с вашими настройками:
Выделение дубликатов в нескольких столбцах Google Sheets
Может случиться так, что повторяющиеся значения будут находиться более чем в одном столбце:
Как тогда сканировать и выделять дубликаты во всех трех столбцах Google Sheets? Использование условного форматирования, а также. Упражнение такое же, как и выше, с небольшими изменениями:
- выберите A2:C10 в качестве диапазона для окрашивания повторяющихся ячеек в пределах
- также измените диапазон для Пользовательская формула :
=СЧЁТЕСЛИ($A$2:$C$10;A2)>1Примечание.
 На этот раз удалите знак доллара с A2. Это позволит формуле подсчитать все вхождения каждой ячейки из таблицы, а не только из столбца A.
На этот раз удалите знак доллара с A2. Это позволит формуле подсчитать все вхождения каждой ячейки из таблицы, а не только из столбца A.Совет. Прочтите эту статью, чтобы узнать больше об относительных, абсолютных и смешанных ссылках на ячейки.
- выберите цвет в разделе Стиль форматирования и нажмите Готово
В отличие от вышеупомянутого СЧЁТЕСЛИ, этот сканирует все 3 столбца и подсчитывает, сколько раз каждое значение из таблицы появляется во всех столбцах. Если более одного раза, условное форматирование выделит эти повторяющиеся ячейки в вашей таблице Google Sheets.
Выделите всю строку, если дубликаты есть в одном столбце.
Далее следует случай, когда ваша таблица содержит разные записи в каждом столбце. Но вся строка в этой таблице считается одной записью, одной порцией информации:
Как видите, в столбце B есть дубликаты: макароны и приправы разделы встречаются дважды каждый.
В подобных случаях вы можете рассматривать все эти строки как дубликаты. И вам может понадобиться выделить эти повторяющиеся строки в вашей электронной таблице Google.
Если это именно то, для чего вы здесь, обязательно установите эти значения для условного форматирования:
- Примените правило к диапазону A2:C10
- А вот и формула:
=СЧЁТЕСЛИ($B$2:$B$10,$B2)>1
Этот СЧЁТЕСЛИ считает записи из столбца B, ну, в столбце B 🙂 И тогда правило условного форматирования выделяет не только дубликаты в столбце B, но и связанные записи в других столбцах.
Выделение полных дубликатов строк в электронных таблицах
А что, если вся строка с записями во всех столбцах появляется в вашей таблице несколько раз?
Как проверить все 3 столбца в таблице и выделить абсолютные повторяющиеся строки в листе Google?
Использование этой формулы в условном форматировании:
=СЧЁТЕСЛИ(Формула массива($A$2:$A$10&$B$2:$B$10&$C$2:$C$10),$A2&$B2&$C2)> 1
Разобьем его на части, чтобы понять, как это работает:
- ArrayFormula($A$2:$A$10&$B$2:$B$10&$C$2:$C$10) объединяет каждые 3 ячейки из каждую строку в одну текстовую строку, которая выглядит так: SpaghettiPasta9-RQQ-24
Таким образом, в моем примере 9такие строки — по одной на строку.

- Затем COUNTIFS берет каждую строку (начиная с первой: $A2&$B2&$C2 ) и ищет ее среди этих 9 строк.
- Если имеется более одной строки ( >1 ), эти дубликаты выделяются.
Наконечник. Вы можете узнать больше о COUNTIF и конкатенации в Google Таблицах в соответствующих статьях.
Выделить фактические дубликаты — экземпляры 2n, 3d и т. д.
Предположим, вы хотите сохранить 1-й элемент повторяющихся строк без изменений и просмотреть все остальные экземпляры, если они есть.
Всего одним изменением формулы вы сможете выделить эти «настоящие» повторяющиеся строки — не первые записи, а их 2-й, 3-й, 4-й и т. д. экземпляры.
Итак, вот формула, которую я предложил выше для всех повторяющихся строк:
=СЧЁТЕСЛИ(Формула массива($A$2:$A$10&$B$2:$B$10&$C$2:$C$10),$A2& $B2&$C2)>1
И это формула, которая вам нужна, чтобы выделить только повторяющиеся экземпляры в Google Таблицах:
=СЧЕТЕСЛИ(Формуламассива($A$2:$A2&$B$2:$B2&$C$2: $C2),$A2&$B2&$C2)>1
Видите разницу в формуле?
Это первый аргумент СЧЁТЕСЛИ:
$A$2:$A2&$B$2:$B2&$C$2:$C2
Вместо упоминания всех строк, как в первой формуле, я использую только первую ячейку каждого столбца.
Позволяет каждой строке смотреть только сверху, чтобы увидеть, есть ли одинаковые строки. Если это так, каждая текущая строка будет рассматриваться как другой экземпляр или, другими словами, как фактический дубликат, который будет окрашен.
Способ выделения дубликатов без формул — надстройка «Удалить дубликаты» для Google Таблиц
Конечно, у вас может быть какой-то другой вариант использования, для которого требуется другая формула. Тем не менее, любая формула и условное форматирование требуют обучения. Если вы не готовы посвящать этому свое время, есть более простое решение.
Надстройка «Удалить дубликаты» для Google Таблиц выделит дубликаты для вас.
Требуется всего несколько кликов на 4 шага, а возможность выделения найденных дубликатов — это просто переключатель с цветовой палитрой:
Надстройка предлагает интуитивно понятный способ выбора ваших данных и столбцов, которые вы хотите проверить на наличие дубликатов. Для каждого действия есть отдельный шаг, чтобы вы не запутались:
Кроме того, умеет подсвечивать не только дубликаты, но и уникальные.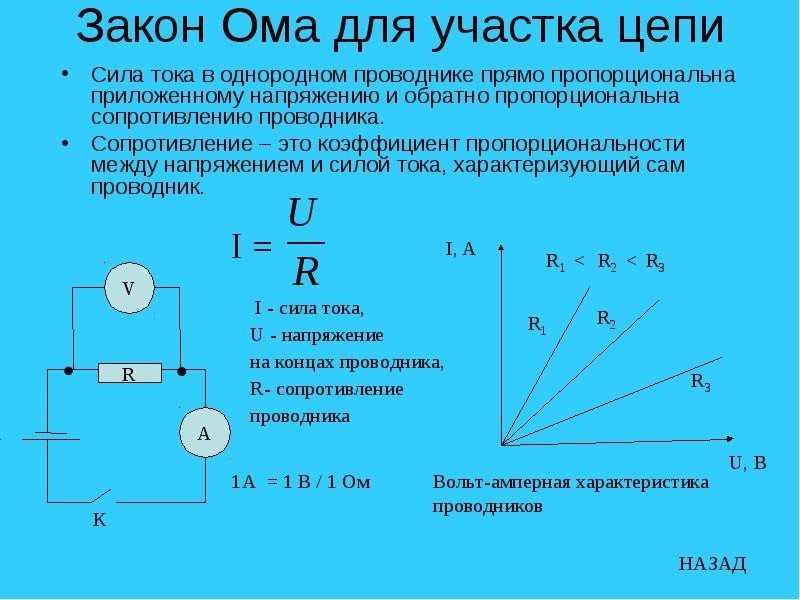 И есть возможность игнорировать 1-е экземпляры:
И есть возможность игнорировать 1-е экземпляры:
Совет. Вот видео, которое показывает надстройку в действии. Возможно, он немного устарел, так как на данный момент надстройка может предложить больше, но это все та же надстройка:
Выделение дубликатов по расписанию с помощью надстройки
Все шаги с их настройками, которые вы выбираете в надстройке, можно сохранить и повторно использовать в один клик позже или даже запланировать на определенное время для автозапуска.
Вот двухминутное демонстрационное видео, подтверждающее мои слова (или см. ниже пару анимированных изображений):
А вот короткое анимированное изображение, показывающее, как сохранять и запускать сценарии после изменения ваших данных:
Что еще лучше, вы можете запланировать автозапуск этих сценариев несколько раз в день:
Не беспокойтесь, для вас есть специальный журнал, в котором вы можете отслеживать все автоматические запуски и убедиться, что они работают правильно:
Просто установите Remove Duplicates из магазина Google Таблиц, попробуйте его на своих данных, и вы увидите, сколько времени и нервов вы сэкономите на правильном окрашивании этих записей. Да, без всяких формул и всего в несколько кликов 😉
Да, без всяких формул и всего в несколько кликов 😉
Видео: Как выделить дубликаты в Google Sheets
В этом 1,5-минутном видео показаны 3 самых быстрых способа (с формулами и без) найти и выделить дубликаты в Google Таблицы. Вы увидите, как раскрасить 1 столбец или целые строки на основе дубликатов, даже автоматически.
Таблица с примерами формул
Выделение дубликатов в Google Sheets — примеры условного форматирования (сделать копию файла)
Вас также может заинтересовать
Война в Украине!
Чтобы поддержать Украину и спасти жизни
17 комментариев
Оставить комментарий
Формулировка законаОм, проверочный эксперимент, вывод в простых шагах
Рисунок 1: ВАХ металлического проводника (омический) Закон Ома гласит: Падение потенциала на резисторе пропорционально току, проходящему через резистор: V ∝ I. Закон Ома применим только к резисторам с постоянным сопротивлением; то есть к резисторам, сопротивление которых одинаково независимо от того, какой ток проходит через них. Для таких резисторов: V/I = R (где R постоянно). Закон Ома можно записать так: V = IR (где R — константа).
Закон Ома применим только к резисторам с постоянным сопротивлением; то есть к резисторам, сопротивление которых одинаково независимо от того, какой ток проходит через них. Для таких резисторов: V/I = R (где R постоянно). Закон Ома можно записать так: V = IR (где R — константа).
Резисторы, подчиняющиеся закону Ома, называются омическими резисторами. Для омического резистора график зависимости V от I будет прямой линией. Наклон графика будет равен постоянному сопротивлению. Это показано на рисунке 1. Любой компонент, который ведет себя подобным образом, описывается как омический компонент, и мы говорим, что он подчиняется закону Ома.
Посмотрите на график на рисунке 1. Такой график называется ВАХ. На приведенном графике точки немного разбросаны, но четко лежат на прямой. Проведена линия наилучшего соответствия. Вы увидите, что он проходит через начало координат графика. Другими словами, ток I прямо пропорционален напряжению V. Прямолинейный график, проходящий через начало координат, показывает, что сопротивление проводника остается постоянным и не зависит ни от тока, ни от p. d.
d.
Здесь, в этом посте, мы обсудим это подробнее и рассмотрим следующее: Закон Ома, Утверждение, вывод формулы, Проверка закона Ома экспериментом, определение, расчет по формуле, График V-I омического и неомического проводники и т. д.
Содержание
- Что такое закон Ома?
- Какова формула закона Ома?
- Как вывести формулу закона Ома?
- Начертите график VI для омических проводников
- Омические проводники или омические резисторы – характеристики
- Нарисуйте график VI для проводников, которые ведут себя неомически при повышении температуры
- Неомические проводники или неомические резисторы – особенности
- Как мы можем проверить закон Ома с помощью эксперимента?
- Что нам нужно для эксперимента или проверочного теста
- Этапы выполнения эксперимента по закону Ома
- Как использовать формулу закона Ома для решения числовых задач
- Заключение
Что такое закон Ома?
Падение потенциала на резисторе пропорционально току, проходящему через резистор: V ∝ I.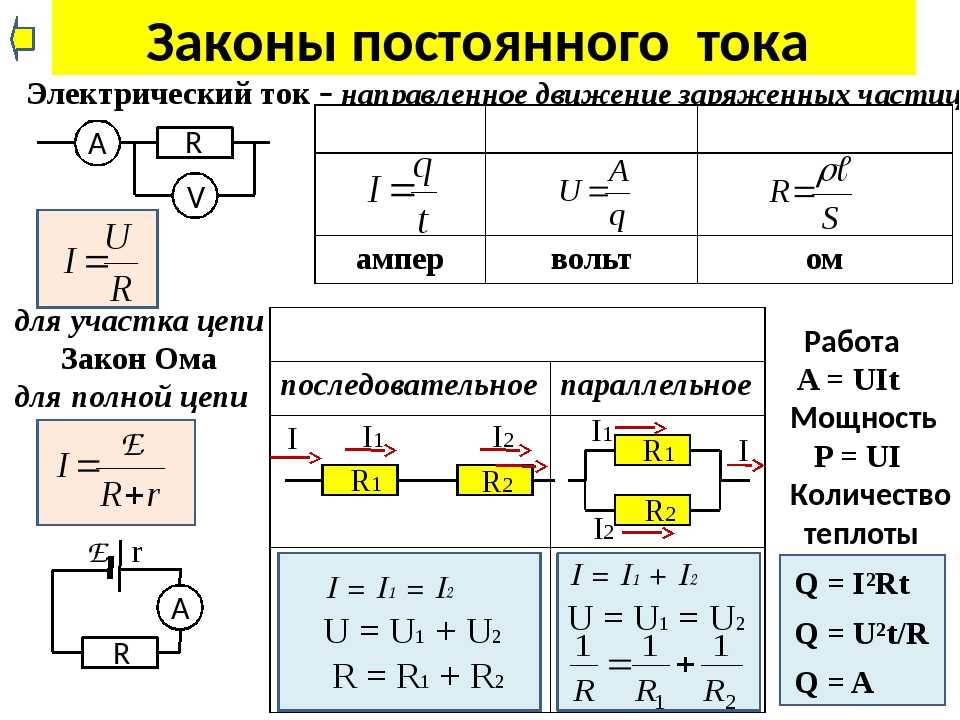 Закон Ома применим только к резисторам с постоянным сопротивлением; то есть к резисторам, сопротивление которых одинаково независимо от того, какой ток проходит через них. Для таких резисторов: V/I = R (где R постоянно). Закон Ома можно записать так: V = IR (где R — константа).
Закон Ома применим только к резисторам с постоянным сопротивлением; то есть к резисторам, сопротивление которых одинаково независимо от того, какой ток проходит через них. Для таких резисторов: V/I = R (где R постоянно). Закон Ома можно записать так: V = IR (где R — константа).
Другими словами: Закон Ома гласит, что ток через металлический элемент пропорционален разности потенциалов между его концами при условии, что температура остается постоянной. Это утверждение также известно как утверждение закона Ома.
Какова формула закона Ома?
Формула закона Ома выглядит следующим образом: V = IR,
Здесь V — разность потенциалов на двух концах проводника. И символ I обозначает ток, протекающий через проводник, а R — сопротивление этого проводника.
Как вывести формулу закона Ома?
Если ток I проходит через металлический элемент, когда к этому элементу приложена разность потенциалов V (между двумя его концами), то мы можем написать уравнение закона принимает вид
I = (1/R) V
=> I = V/R
или V = IR ………………. (1)
(1)
Здесь, Здесь R – постоянная для данного элемента и называется его сопротивлением.
Итак, этот закон Ома можно выразить уравнением или формулой V = IR
Таким образом, вывод закона Ома выполнен.
Итак, мы увидели, что этот закон Ома может быть выражен формулой или уравнением V = IR, где V — разность потенциалов на металлическом элементе, а I — ток, протекающий через элемент. R — электрическое сопротивление элемента.
Начертите график VI для омических проводников
График VI для омических проводников / омических материалов.Прямая линия указывает на постоянное сопротивление.
Омические проводники или омические резисторы – характеристики
Ниже приведены эквивалентные описания характеристик определенного типа резистора, подчиняющегося закону Ома:
- резистор является омическим резистором
- резистор подчиняется закону Ома резистора постоянна
- график зависимости V от I для резистора представляет собой прямую линию
- напряжение пропорционально току для резистора.

Нарисуйте график VI для проводников, которые ведут себя неомически при повышении температуры
Устройство, работающее по закону Ома, называется омическим. На самом деле ни одно устройство не является полностью омическим, хотя некоторые материалы имеют примерно омическое поведение в широком диапазоне токов.
Одной из причин, по которой проводники не остаются омическими, является то, что их температура повышается по мере прохождения через них большего тока. Сопротивление нормального проводника увеличивается с повышением температуры, что делает его неомическим.
Примером этого неомического проводника является металлическая нить лампы накаливания, которая сильно нагревается при нормальной работе.
График VI для вольфрамовой нити накаливания.С увеличением тока температура нити накала увеличивается, что увеличивает ее сопротивление.
Изменение сопротивления определяется изменением наклона графика.
Неомические проводники или неомические резисторы – характеристики
Ниже приведены эквивалентные утверждения об этом типе неомического резистора:
- резистор неомический
- резистор не подчиняется закону Ома
- сопротивление резистора непостоянна
- График зависимости V от I для резистора не является прямой линией.

Как мы можем проверить закон Ома с помощью эксперимента?
Здесь мы обсудим, как провести простой эксперимент для проверки закона Ома.
Что нам нужно для Эксперимента или проверочного теста
Что нам нужно:
Четыре или пять сухих элементов,
тонкий провод (AB),
вольтметр,
амперметр,
штепсельный ключ
и несколько толстых соединительных проводов .
Этапы выполнения эксперимента по закону Ома
1> Мы должны начать тест с одной ячейки. Мы должны подключить цепь, как показано на рисунке а.
— Амперметр покажет нам ток I, протекающий по цепи, а вольтметр измерит разность потенциалов V между концами А и В провода.
– Мы должны отметить эти значения. (1-й набор тестовых данных) Помните, что этот набор измеренных значений V и I относится к установке с одной ячейкой.
Одиночная ячейка 2> Теперь нам нужно последовательно соединить две ячейки в цепи, как показано на рисунке b.
— Мы обнаружим, что показания вольтметра увеличиваются. Это означает, что к проводу АВ приложена большая разность потенциалов.
— Это очевидно, так как в данном случае мы последовательно применили 2 ячейки.
— Мы также обнаружим, что показания амперметра также увеличились. Мы должны записать новые значения V и I. (2-й набор тестовых данных)
2 ячейки последовательно
3> Мы должны повторить эксперимент, соединив последовательно три ячейки, четыре ячейки и так далее. на. В каждом случае измерьте разность потенциалов и силу тока. (3-й набор, 4-й набор… тестовых данных)
4> Если мы вычислим значение V/I для каждого набора тестовых данных, мы обнаружим, что оно почти одинаково.
— Итак, V/I = R — константа, что является еще одним способом формулировки закона Ома. Здесь R — сопротивление провода АВ.
График закона Ома: Если построить график зависимости тока I от разности потенциалов V, то он будет прямой линией (рис.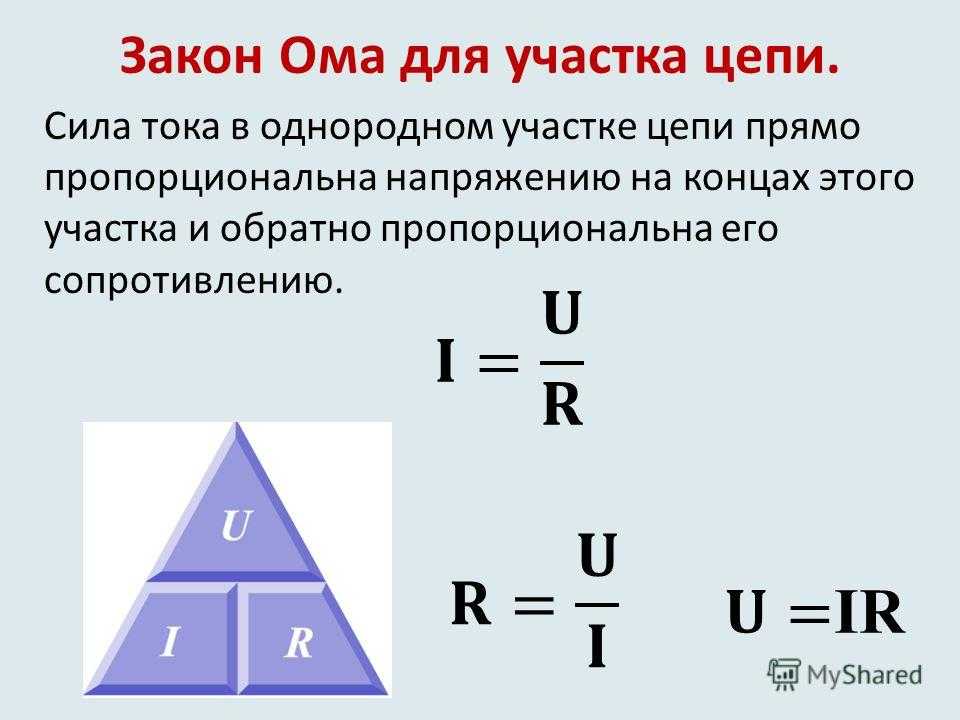 c). Это показывает, что ток пропорционален разности потенциалов.
c). Это показывает, что ток пропорционален разности потенциалов.
Как использовать формулу закона Ома для решения числовых задач
В: Батарейка напряжением 10 В подключена к лампе сопротивлением 4 Ом. рассчитать ток через лампу.
A: по закону Ома сила тока i = V/R = (10/4) A = 2,5 A.
A означает ампер, единицу силы тока.
А теперь попробуйте числовые наборы здесь: Численный закон Ома Задачи – 3 рабочих листа
Заключение
Надеюсь, вам понравился этот пост о законе Ома. Это очень интересная и важная глава курса физики, посвященная закону электричества. Этот закон также порождает понятие Сопротивления. Мы опубликовали пост о сопротивлении и числах по закону Ома для старшеклассников.
Другим важным постом является Серийная цепь, эквивалентное сопротивление и закон Ома с численным решением. Вот один пост для параллельной схемы.
Как выделить дубликаты в Google Sheets 3+ Простые способы
Смотреть видео – Выделение дубликатов в Google Sheets
youtube.com/embed/w5nJk3X3pjs?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>При работе с данными в Google Sheets рано или поздно вы столкнетесь с проблемой дублирования данных. Это может полностью испортить ваши электронные таблицы. Было бы неплохо, если бы существовал способ найти все дубликаты сразу? Это руководство научит вас, как легко выделять дубликаты в Google Sheets с помощью ряда простых методов. Читайте дальше, чтобы освоить их.
Содержание
Как выделить дубликаты в Google Таблицах — ячейки в столбце
Наиболее распространенная ситуация, когда вам понадобится Google Sheets для выделения дубликатов, — это когда у вас есть набор данных в столбце, и вы хотите быстро выделить дубликаты.
Например, предположим, что у вас есть набор данных, как показано ниже, где вы хотите выделить все имена, которые повторяются в столбце A.
Ниже приведены шаги для выделения дубликатов в столбце:0015 Выберите набор данных имен (исключая заголовки)
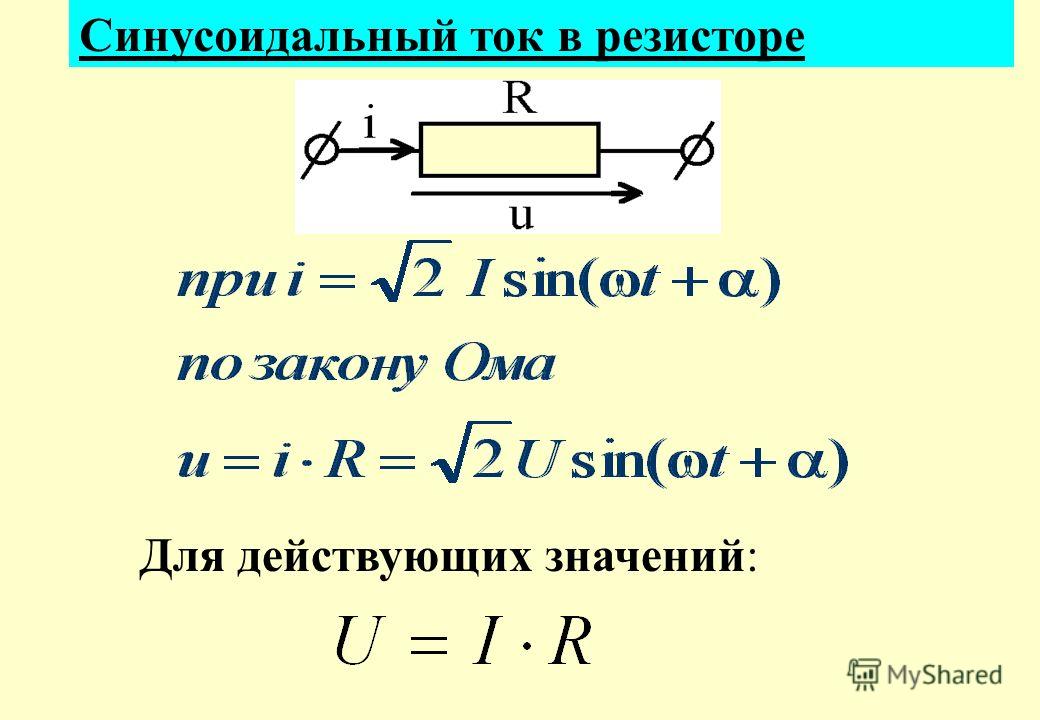
=СЧЁТЕСЛИ($A$2:$A$10;A2)>1
При выполнении вышеуказанных действий все ячейки с повторяющимися именами будут выделены указанным цветом.
Одна из замечательных особенностей условного форматирования заключается в том, что оно является динамическим . Это означает, что в случае изменения данных в любой из ячеек форматирование будет обновляться автоматически. Например, если вы удалите одно из имен, у которых есть дубликаты, выделение этого имени (в другой ячейке) исчезнет, поскольку теперь оно стало уникальным.
Это означает, что в случае изменения данных в любой из ячеек форматирование будет обновляться автоматически. Например, если вы удалите одно из имен, у которых есть дубликаты, выделение этого имени (в другой ячейке) исчезнет, поскольку теперь оно стало уникальным.
Как это работает?
Когда вы используете пользовательскую формулу в условном форматировании, она проверяет каждую ячейку с помощью указанной формулы для поиска дубликатов в Google Sheets.
Если формула возвращает ИСТИНА для ячейки, она выделяется в указанном формате, а если возвращает ЛОЖЬ, то нет.
В приведенном выше примере проверяется каждая ячейка, и если имя встречается в диапазоне более одного раза, для формулы СЧЁТЕСЛИ возвращается ИСТИНА, и ячейка выделяется. В противном случае он остается неизменным.
Также обратите внимание, что я использовал диапазон $A$2:$A$10 (где перед алфавитом столбца и номером строки стоит знак доллара). Это действительно важно, так как гарантирует, что когда формула переходит к следующей ячейке (в строке ниже), общий диапазон, который проверяется на количество имен, остается прежним.
Если вы хотите удалить выделенные ячейки, вам необходимо удалить условное форматирование. Для этого выберите ячейки, к которым применено форматирование, щелкните параметр «Формат», щелкните «Условное форматирование» и удалите правило из панели, которая открывается справа.
Поиск дубликатов в Google Таблицах путем выделения их в нескольких столбцах
В приведенном выше примере все имена были в одном столбце.
Но что, если имена находятся в нескольких столбцах, чтобы выполнить условное форматирование для дубликатов в Google Таблицах (как показано ниже).
Вы по-прежнему можете использовать условное форматирование для выделения повторяющихся имен (имя, которое встречается более одного раза во всех трех столбцах вместе взятых).
Ниже приведены шаги для выделения дубликатов в нескольких столбцах:
- Выберите имена набор данных (исключая заголовки)
- Выберите пункт «Формат» в меню.
- В появившихся параметрах нажмите «Условное форматирование».

- Нажмите на опцию «Добавить другое правило»
- Убедитесь, что диапазон (где нам нужно выделить дубликаты) правильный. Если это не так, вы можете изменить его в разделе «Применить к диапазону» .
- Щелкните раскрывающийся список «Форматировать ячейки, если», а затем щелкните параметр «Пользовательская формула».
- В поле ниже введите следующую формулу:
=СЧЕТЕСЛИ($A$2:$C$10;A2)>1
- В параметрах «Стиль форматирования» укажите форматирование, в котором вы хотите выделить повторяющиеся ячейки. По умолчанию будет использоваться зеленый цвет, но вы можете указать другие цвета, а также стили, такие как полужирный или курсив
- Нажмите Готово
Вышеуказанные шаги выделят ячейку, если имя появляется более одного раза во всех трех выбранных столбцах вместе взятых.
Как это работает?
Этот также работал, как и последний, для условного форматирования дубликатов Google Sheets.
В формуле СЧЕТЕСЛИ мы покрыли все ячейки в трех столбцах. Таким образом, каждая ячейка в диапазоне проверяется по указанной формуле и возвращает либо ИСТИНА, либо ЛОЖЬ. Формула СЧЁТЕСЛИ похожа на дублирующую формулу для Google Таблиц.
Если есть имя, которое повторяется в любом из столбцов, оно будет выделено в указанном формате.
Опять же, обратите внимание, что я использовал диапазон $A$2:$C$10 (где перед алфавитом столбца и номером строки стоит знак доллара). Это действительно важно, так как гарантирует, что диапазон останется прежним, в то время как условное форматирование проверяет количество имени в ячейке.
Как выделить повторяющиеся значения в Google Таблицах (найти повторяющиеся строки)
Это немного сложно.
Предположим, у вас есть набор данных, как показано ниже, и вы хотите, чтобы Google Таблицы находили все дубликаты путем выделения.
В этом случае запись будет дублироваться, если она имеет одинаковое значение в каждой ячейке строки (например, строки 2 и 7 в приведенном выше примере).
Причина, по которой это немного сложно, заключается в том, что теперь вам не нужно проверять отдельные ячейки. Вы должны проверить всю строку и выделить только те строки, в которых все ячейки повторяются.
Но не волнуйтесь, это не так сложно сделать.
Ниже приведены шаги для выделения повторяющихся строк с использованием условного форматирования:
- Выберите набор данных (исключая заголовки)
- Выберите пункт «Формат» в меню.
- В появившихся параметрах нажмите «Условное форматирование».
- Нажмите на опцию «Добавить другое правило»
- Щелкните раскрывающийся список «Форматировать ячейки, если», а затем щелкните параметр «Пользовательская формула».
- В поле ниже введите следующую формулу:
=СЧЁТЕСЛИ(ФОРМУЛА МАССИВА($A$2:$A$10&$B$2:$B$10&$C$2:$C$10),$A2&$B2&$C2)>1
- В параметрах «Стиль форматирования» укажите форматирование, в котором вы хотите выделить повторяющиеся ячейки.
 По умолчанию будет использоваться зеленый цвет, но вы можете указать другие цвета, а также стили, такие как жирный шрифт или курсив .
По умолчанию будет использоваться зеленый цвет, но вы можете указать другие цвета, а также стили, такие как жирный шрифт или курсив . - Нажмите Готово
Вышеуказанные шаги выделят все записи, которые повторяются в наборе данных (как показано ниже).
Как это работает?
Этот пример работает так же, как и наш первый пример (где мы просто выделили ячейки в столбце, в котором были дубликаты).
Но так как есть целая строка, которую нам нужно сравнить со всеми другими строками, мы объединили содержимое всех строк и создали одну строку для каждой строки.
Следующая часть формулы создает массив строк, в котором объединяется все содержимое ячеек в строке (выполняется конкатенация с использованием знака амперсанда).
ARRAYFORMULA($A$2:$A$10&$B$2:$B$10&$C$2:$C$10)
Этот массив используется в формуле Countif, и используемое условие снова представляет собой конкатенированную строку, которая имеет все значения подряд. Это делается с использованием следующих критериев:
Это делается с использованием следующих критериев:
$A2&$B2&$C2
Теперь это преобразовано в простую конструкцию типа столбца, где функция COUNTIF проверяет, сколько раз эта комбинированная строка повторяется в массиве строк, который мы создали. .
Это приведет к выделению всех записей, которые являются дубликатами.
Показать дубликаты в таблицах Google с добавленными критериями
Таблицы Google также могут использовать большинство дополнительных критериев, которые только можно придумать, для выделения повторяющихся данных. Например, вы можете настроить систему так, чтобы она выделяла дубликаты только для определенных значений.
Синтаксис должен использовать оператор «*» (и), чтобы СЧЁТЕСЛИ использовали оба критерия. Синтаксис будет выглядеть примерно так:
=(СЧЁТЕСЛИ(Диапазон,Критерии)>1) * (Новое условие))
Мы можем использовать наши данные о сотрудниках, чтобы показать, как это будет работать. Давайте представим, что мы узнали, что на самом деле в маркетинге было два Генри, поэтому мы обновили идентификационный номер одного из них.
Мы по-прежнему хотим выделить повторяющихся сотрудников, поэтому мы можем добавить второе условие, которое должно выполняться, например:
- Перемещайтесь по правилам условного форматирования, как в предыдущих примерах выше
- Введите первую часть формулы с диапазоном и форматом, с которым мы уже должны быть знакомы: =(countif(Range,Criteria)>1), поэтому наш пример будет таким:
=(Countif($A$2:$C$10,$A2)>1)
Это покажет, есть ли дубликаты в строке A, но не исключит теперь несоответствующий идентификатор второго Генри, поэтому вы нужны эти дополнительные шаги
- Используйте команду «*» (и) после первой формулы
- Добавьте второе условие в синтаксис (СЧЁТЕСЛИ(Диапазон,Критерии)>1), но убедитесь, что вы обращаетесь к другой строке — в данном случае к строке C. Вся формула должна выглядеть так:
=(Countif($A$2:$C$10,$A2)>1)*(countif($A$2:$C$10,$C2)>1)
Конечно, в этом точном примере вы можно было просто использовать вторую половину формулы, чтобы получить тот же результат, но это всего лишь пример того, как можно использовать добавление второго условия. В зависимости от ваших потребностей вы также можете:
В зависимости от ваших потребностей вы также можете:
- Использовать другой после критерия, т.е. >0 или <5 и т.д.
- Добавить третий критерий
- Многие другие условия «*»
Редактирование или удаление правил условного форматирования
Когда вы найдете все дубликаты с помощью выделения, вы можете сохранить некоторые дубликаты, но не хотите, чтобы они больше выделялись. Решение простое, просто отредактируйте или удалите правило условного форматирования. Для этого:
- Выделите ячейки, к которым вы применили правило условного форматирования
- Перейдите к Формат > Условное форматирование
- Щелкните символ корзины рядом с существующим правилом
Возможные проблемы с простыми решениями при выделении повторяющихся ячеек в Google Sheets
Иногда может случиться так, что вы выполните все вышеперечисленные шаги и используете те же формулы, но Google Sheets по-прежнему не выделяет дубликаты. Если они не выделены, как вы должны удалить дубликаты?
Если они не выделены, как вы должны удалить дубликаты?
Вот несколько возможных причин, которые вы можете проверить:
Лишние пробелы в ячейках
Есть ли лишние пробелы (начальные или конечные пробелы) в тексте в одной ячейке, а не в другой?
Поскольку мы ищем точное совпадение для двух или более ячеек, чтобы считать их дубликатами, наличие в ячейках лишних символов пробела может привести к несоответствию.
Таким образом, даже если вы видите дубликат, он может не быть выделен.
Чтобы избавиться от этого, вы можете использовать функцию TRIM (и функцию CLEAN), чтобы избавиться от всех лишних символов пробела.
Неправильная ссылка
В Google Таблицах есть три разных типа ссылок.
- Абсолютные ссылки (пример – $A$1)
- Относительные ссылки (пример – A1)
- Смешанные ссылки (пример — $A1 или A$1)
Если в формуле требуется один тип ссылки, а вы в конечном итоге используете другие, у вас, скорее всего, возникнут проблемы.
Поэтому проверьте ссылки, чтобы убедиться, что Google Sheets выделяет дубликаты, как и ожидалось.
Некоторые советы по выделению дубликатов в Google Sheets
- Убедитесь, что у вас нет других правил условного форматирования для нужных ячеек, которые могут возвращать ложные результаты
- Убедитесь, что в результатах поиска нет пробелов
- Не выбирайте заголовки при использовании ARRAYFORMULA для выделения дубликатов в Google Sheets
Как проверить дубликаты в Google Таблицах с помощью UNIQUE
Эту формулу намного проще использовать при работе с небольшими наборами данных, и вам просто нужно увидеть, сколько различных уникальных фрагментов данных содержится в вашей электронной таблице. Хотя он не обеспечивает условное форматирование дубликатов Google Sheets.
Синтаксис прост:
=UNIQUE(Диапазон)
Итак, в нашем предыдущем примере все, что нам нужно сделать, чтобы найти все уникальные значения в:
- Выберите пустую ячейку (в нашем случае D2) и нажмите ввод
- Введите =UNIQUE, щелкните и перетащите ячейки, которые вы хотите проверить на наличие уникальных данных
- Нажмите клавишу ввода, и список каждого уникального значения отобразится в столбце
Часто задаваемые вопросы о выделении ячеек с помощью условного форматирования
Могут ли таблицы Google выделять дубликаты?
Да, дубликаты можно выделить.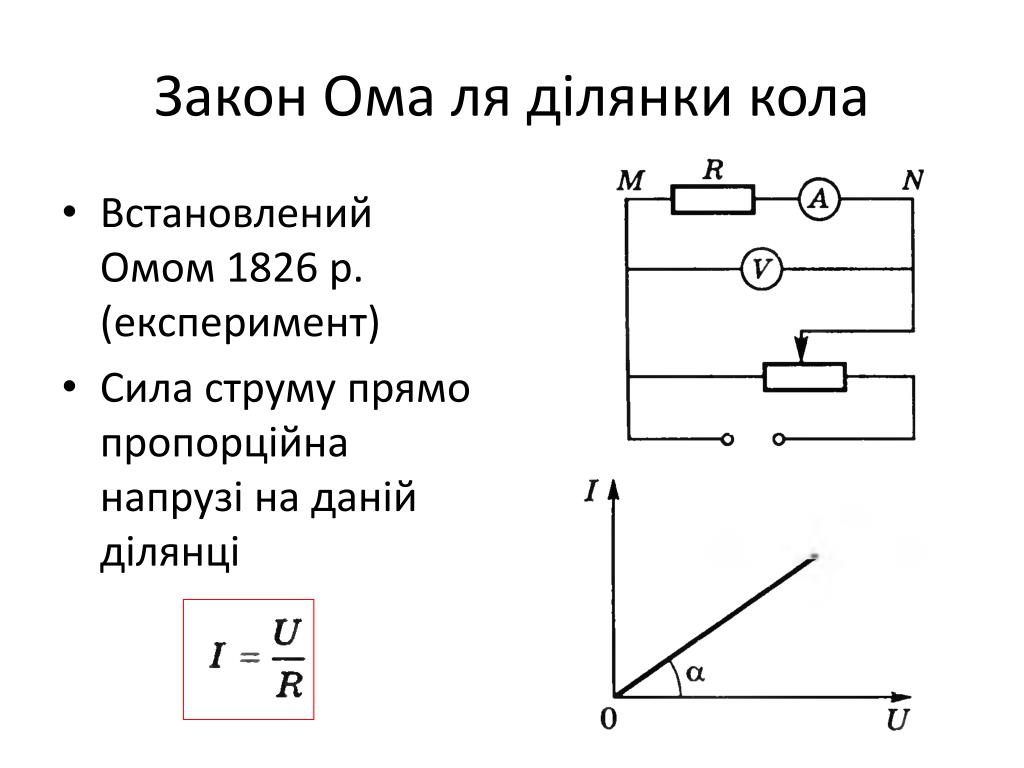 Вы должны использовать комбинацию формулы COUNTIF и условного форматирования. Вы можете настроить условное форматирование, чтобы выделить ячейку только в том случае, если формула СЧЁТЕСЛИ возвращает значение ИСТИНА.
Вы должны использовать комбинацию формулы COUNTIF и условного форматирования. Вы можете настроить условное форматирование, чтобы выделить ячейку только в том случае, если формула СЧЁТЕСЛИ возвращает значение ИСТИНА.
Какая формула для выделения дубликатов в Google Таблицах?
Вот как определить дубликаты в Google Таблицах. Вам просто нужно использовать формулу СЧЁТЕСЛИ в меню условного форматирования. Формула СЧЁТЕСЛИ использует следующий синтаксис.
=СЧЁТЕСЛИ(диапазон, критерий)
Итак, вам нужно ввести диапазон, который вы хотите выделить, и >1 в качестве критерия . Например, если существует более одного экземпляра, выделите ячейку. Следуйте приведенному выше руководству для более подробного изучения.
Как сгруппировать дубликаты в Google Sheets?
Чтобы сгруппировать дубликаты, вы можете использовать функцию СОРТИРОВКИ или ярлык сортировки на панели инструментов. Вот как найти дубликаты в Google Таблицах с помощью меню «Сортировка»:
- Выберите столбец, в который вы хотите сгруппировать дубликаты
- Перейдите к Данные > Лист сортировки
Если вы использовали описанный выше метод для условного форматирования дубликатов. Вы также можете сортировать по цвету, чтобы избежать сортировки неповторяющихся ячеек.
Вы также можете сортировать по цвету, чтобы избежать сортировки неповторяющихся ячеек.
Как просмотреть дубликаты в Google Таблицах? / Могут ли Google Sheets находить дубликаты?
Вы можете увидеть дубликаты, используя условное форматирование в меню форматирования и формулу СЧЁТЕСЛИ. Затем выберите цвет, которым хотите выделить дубликаты.
Как выделить одну и ту же ячейку с дубликатами в Google Таблицах?
К сожалению, нельзя искать дубликаты в одной ячейке.
Как сравнить два столбца в Google Таблицах, чтобы найти дубликаты?
Вы можете использовать формулу СЧЁТЕСЛИ в качестве пользовательской формулы в меню условного форматирования для поиска дубликатов и сравнения двух столбцов. Просто включите ссылки на ячейки в формулу и используйте >1 в качестве критерия .
Как выделить повторяющиеся значения, кроме первого экземпляра в Google Таблицах?
Следуйте приведенному выше методу для использования выделенных ячеек, за исключением того, что вместо этого используйте >2 в качестве критерия. Это будет означать, что выделение будет происходить только в том случае, если есть два или более экземпляра значения, т. е. = игнорирование первого совпадения.
Это будет означать, что выделение будет происходить только в том случае, если есть два или более экземпляра значения, т. е. = игнорирование первого совпадения.
Как сравнить разные таблицы Google на наличие дубликатов?
Это можно сделать со сложными формулами или скриптами, но проще всего добавить требуемый лист в единую общую электронную таблицу, а затем сравнить два листа. Для этого:
- Щелкните правой кнопкой мыши имя листа внизу страницы
- Наведите курсор на Скопируйте в
- Нажмите Существующая таблица и выберите нужную таблицу
- Затем вы можете использовать ссылку на лист в формуле СЧЁТЕСЛИ, например, если вы хотите использовать диапазон ячеек из Листа1, вы можете ввести =Лист1!
Дублируйте свое обучение
Таким образом, вы можете выделить дубликаты в Google Таблицах с помощью условного форматирования.
Надеюсь, этот урок был вам полезен!
Другие учебные пособия по Google Sheets, которые могут вам понравиться:
- Применение условного форматирования на основе другого значения ячейки в Google Sheets
- Как подсчитать ячейки с определенным текстом в Google Таблицах
- Как сравнить два столбца в Google Таблицах (для совпадений и различий)
- Как искать в Google Таблицах
- Как использовать функцию UNIQUE
- Как выделить самое высокое или самое низкое значение в Google Sheets
Инструменты и задачи обслуживания (интерактивные)
Перейти к содержимому
Часть 3: Математика для специалистов по обслуживанию
[латексная страница]
Часто говорят, что математика — это язык науки. Если это так, то существенной частью языка математики являются числа. Самое раннее использование чисел произошло 100 веков назад на Ближнем Востоке для подсчета или перечисления предметов. Фермеры, скотоводы и торговцы использовали жетоны, камни или маркеры для обозначения одного количества — например, снопа зерна, головы скота или фиксированной длины ткани. Это сделало возможной торговлю, что привело к улучшению коммуникаций и распространению цивилизации.
Если это так, то существенной частью языка математики являются числа. Самое раннее использование чисел произошло 100 веков назад на Ближнем Востоке для подсчета или перечисления предметов. Фермеры, скотоводы и торговцы использовали жетоны, камни или маркеры для обозначения одного количества — например, снопа зерна, головы скота или фиксированной длины ткани. Это сделало возможной торговлю, что привело к улучшению коммуникаций и распространению цивилизации.
Три-четыре тысячи лет назад египтяне ввели дроби. Сначала они использовали их, чтобы показать взаимность. Позже они использовали их для представления количества, когда количество было разделено на равные части.
Но что, если бы не было скота для торговли или весь урожай зерна был потерян во время наводнения? Как кто-то может указать на существование ничего? С самых ранних времен люди думали об «базовом состоянии» при подсчете и использовали различные символы для обозначения этого нулевого состояния. Однако только примерно в пятом веке нашей эры в Индии ноль был добавлен к системе счисления и использовался в качестве числительного в расчетах.
Ясно, что цифры также были необходимы для представления убытков или долгов. В Индии в седьмом веке нашей эры отрицательные числа использовались для решения математических уравнений и коммерческих долгов. Противоположности счетных чисел еще больше расширили систему счисления.
Благодаря эволюции системы счисления мы теперь можем выполнять сложные вычисления, используя эти и другие категории действительных чисел. В этом разделе мы рассмотрим наборы чисел, вычисления с различными типами чисел и использование чисел в выражениях.
Номера
Натуральные числа Числа, которые мы используем для счета или перечисления предметов, являются натуральными числами: 1, 2, 3, 4, 5 и так далее. Мы описываем их в системе обозначений как {1,2,3,…}, где многоточие (…) указывает, что числа продолжаются до бесконечности. Натуральные числа, конечно, также называются счетными числами. Всякий раз, когда мы перечисляем членов команды, считаем монеты в коллекции или подсчитываем деревья в роще, мы используем набор натуральных чисел.
Если мы добавим ноль к счетным числам, мы получим набор целых чисел.
- Счетные числа: 1, 2, 3, …
- Целые числа: 0, 1, 2, 3, …
Набор целых чисел добавляет противоположности натуральных чисел к набору целых чисел: {…,−3,−2,−1,0,1,2,3,…}. Полезно отметить, что набор целых чисел состоит из трех различных подмножеств: отрицательных целых чисел, нуля и положительных целых чисел. В этом смысле положительные целые числа — это просто натуральные числа. Другой способ думать об этом состоит в том, что натуральные числа являются подмножеством целых чисел.
\(\begin{array}{lllll}\stackrel{\text{отрицательные целые числа}}{\stackrel{}{\dots ,-3,-2,-1,}}\hfill & \hfill & \stackrel{ \text{zero}}{\stackrel{}{0,}}\hfill & \hfill & \stackrel{\text{положительные целые}}}{\stackrel{}{1,2,3,\cdots}}\hfill \конец{массив}\)
Дроби
Часто в жизни целые суммы — это не совсем то, что нам нужно. Пекарь должен использовать чуть больше чашки молока или части чайной ложки сахара. Точно так же плотнику может понадобиться меньше фута дерева, а маляру может понадобиться часть галлона краски. Этим людям нужно использовать числа, которые являются частью целого. Эти числа очень полезны как в алгебре, так и в повседневной жизни и называются дробями. Следовательно, Дроби — это способ представления частей целого. Записывается \(\frac{a}{b},\), где \(a\) и \(b\) — целые числа, а \(b\ne 0.\) В дроби \(a\) равно называется числителем, а \(b\) называется знаменателем. Знаменатель \(b\) представляет количество равных частей, на которые было разделено целое, а числитель \(a\) показывает, сколько частей включено. Знаменатель \(b,\) не может быть равен нулю, потому что деление на ноль не определено.
Пекарь должен использовать чуть больше чашки молока или части чайной ложки сахара. Точно так же плотнику может понадобиться меньше фута дерева, а маляру может понадобиться часть галлона краски. Этим людям нужно использовать числа, которые являются частью целого. Эти числа очень полезны как в алгебре, так и в повседневной жизни и называются дробями. Следовательно, Дроби — это способ представления частей целого. Записывается \(\frac{a}{b},\), где \(a\) и \(b\) — целые числа, а \(b\ne 0.\) В дроби \(a\) равно называется числителем, а \(b\) называется знаменателем. Знаменатель \(b\) представляет количество равных частей, на которые было разделено целое, а числитель \(a\) показывает, сколько частей включено. Знаменатель \(b,\) не может быть равен нулю, потому что деление на ноль не определено.
На (Рисунок) круг разделен на три части одинакового размера. Каждая часть представляет собой \(\frac{1}{3}\) круга. Этот тип модели называется дробным кругом. Другие формы, например прямоугольники, также можно использовать для моделирования дробей.
Упражнение «Манипулятивная математика» «Моделирование дробей» поможет вам лучше понять дроби, их числители и знаменатели.
Что представляет дробь \(\frac{2}{3}\)? Дробь \(\frac{2}{3}\) означает две из трех равных частей.
Неправильные и правильные дроби
В неправильной дроби числитель больше или равен знаменателю, поэтому его значение больше или равно единице. Фракции, такие как \(\frac{5}{4}\) , \(\frac{3}{2}\) , \(\frac{5}{5}\) и \(\frac{7} {3}\) называются неправильными дробями.
Если у дроби числитель меньше знаменателя, она называется правильной дробью, и ее значение меньше единицы. Такие дроби, как \(\frac{1}{2}\) , \(\frac{3}{7}\) и \(\frac{11}{18}\) являются правильными дробями.
Эквивалентные дроби
Равные дроби — это дроби, имеющие одинаковое значение. Например, дроби \(\frac{6}{6}\) и \(\frac{8}{8}\) имеют одно и то же значение, 1. На рисунке показаны два изображения: одна пицца слева, разрез на две равные части и вторую пиццу того же размера, разрезанную на восемь частей справа. Это способ показать, что \(\frac{1}{2}\) эквивалентно \(\frac{4}{8}\) . Другими словами, это эквивалентные дроби.
Это способ показать, что \(\frac{1}{2}\) эквивалентно \(\frac{4}{8}\) . Другими словами, это эквивалентные дроби.
Рисунок №. Поскольку одинаковое количество каждой пиццы закрашено, мы видим, что \(\frac{1}{2}\) эквивалентно \(\frac{4}{8}\).
Сложение или вычитание дробей
Чтобы складывать или вычитать дроби, они должны иметь общий знаменатель. Если фракции имеют одинаковый знаменатель, мы просто складываем числители и помещаем сумму над общим знаменателем. Что нужно сделать, если у дробей разные знаменатели?
Во-первых, мы будем использовать фрагменты дробей для моделирования нахождения общего знаменателя \(\frac{1}{2}\) и \(\frac{1}{3}.\)
Начнем с одной плитки \(\frac{1}{2}\) и плитки \(\frac{1}{3}\). Мы хотим найти плитку общей дроби, которую мы можем использовать для точного соответствия как \(\frac{1}{2}\), так и \(\frac{1}{3}\).
Если мы попробуем кусочки \(\frac{1}{4}\), \(2\) из них в точности совпадут с куском \(\frac{1}{2}\), но они не точно совпадут с \(\frac{1}{3}\) штука.
Если мы попробуем части \(\frac{1}{5}\), они точно не покроют часть \(\frac{1}{2}\) или \(\frac{1}{3} \) кусок.
Если мы попробуем кусочки \(\frac{1}{6}\), мы увидим, что ровно \(3\) из них покрывают кусок \(\frac{1}{2}\), и ровно \( 2\) из них покрывают кусок \(\frac{1}{3}\).
Если бы мы попробовали части \(\frac{1}{12}\), они бы тоже сработали.
Тайлы даже меньшего размера, такие как \(\frac{1}{24}\) и \(\frac{1}{48},\), также точно покрывают \(\frac{1}{2}\) кусок и кусок \(\frac{1}{3}\).
Знаменатель наибольшей части, покрывающей обе дроби, является наименьшим общим знаменателем (НОД) двух дробей. Таким образом, наименьший общий знаменатель для \(\frac{1}{2}\) и \(\frac{1}{3}\) равен \(6.\)
Обратите внимание, что все тайлы, покрывающие \(\frac{1}{2}\) и \(\frac{1}{3}\), имеют нечто общее: их знаменатели являются общими кратными \(2\) и \(3,\) знаменатели \(\frac{1}{2}\) и \(\frac{1}{3}.\) Наименьшее общее кратное (НОК) знаменателей равно \(6 ,\), поэтому мы говорим, что \(6\) является наименьшим общим знаменателем (LCD) дробей \(\frac{1}{2}\) и \(\frac{1}{3}\). Следовательно, наименьший общий знаменатель (НОД) двух дробей является наименьшим общим кратным (НОК) их знаменателей.
Следовательно, наименьший общий знаменатель (НОД) двух дробей является наименьшим общим кратным (НОК) их знаменателей.
Чтобы найти НОК двух дробей, найдем НОК их знаменателей. Мы следуем процедуре, которую мы использовали ранее, чтобы найти НОК двух чисел. При нахождении ЖК мы используем только знаменатели дробей, а не числители.
Найдите ЖК для дробей \(\frac{7}{12}\) и \(\frac{5}{18}.\)
Решение
Трюки сложения и вычитания дробей – делайте их быстро!
Умножение дробей
Когда мы умножали дроби, мы просто умножали числители и прямо умножали знаменатели.
Модель может помочь вам понять умножение дробей. Мы будем использовать фрагменты дробей для моделирования \(\frac{1}{2}·\frac{3}{4}.\) Для умножения \(\frac{1}{2}\) и \(\frac{3 {4},\) подумайте \(\frac{1}{2}\) из \(\frac{3}{4}.\)
Начните с тайлов фракций на три четверти. Чтобы найти половину от трех четвертей, нам нужно разделить их на две равные группы. Поскольку мы не можем разделить три плитки \(\frac{1}{4}\) поровну на две части, мы обмениваем их на плитки меньшего размера.
Мы видим, что \(\frac{6}{8}\) эквивалентно \(\frac{3}{4}.\) Взятие половины из шести \(\frac{1}{8}\) плиток дает нам три \(\frac{1}{8}\) плитки, то есть \(\frac{3}{8}.\)
Следовательно, \(\frac{1}{2}·\frac{3}{4}=\frac{3}{8}\)
При умножении дробей сохраняются свойства положительных и отрицательных чисел. В качестве первого шага рекомендуется определить знак произведения. В примере 4.26 мы умножим два отрицательных числа, поэтому произведение будет положительным.
Умножьте и запишите ответ в упрощенной форме: \(-\frac{5}{8}\left(-\frac{2}{3}\right).\)
Решение
| \(-\frac{5}{8}\left(-\frac{2}{3}\right)\) | |
| Знаки одинаковые, поэтому произведение положительное. Умножь числители, умножь знаменатели. | \(\frac{5\cdot 2}{8\cdot 3}\) |
| Упрощение. | \(\ гидроразрыва{10}{24}\) |
Найдите общие множители в числителе и знаменателе. Перепишите, показав общие факторы. Перепишите, показав общие факторы. | |
| Удаление общих делителей. | \(\ гидроразрыва{5}{12}\) |
Другой способ найти этот продукт заключается в удалении общих факторов ранее.
| \(-\frac{5}{8}\left(-\frac{2}{3}\right)\) | |
| Определите знак произведения. Умножить. | \(\frac{5\cdot 2}{8\cdot 3}\) |
| Показать общие факторы, а затем удалить их. | |
| Умножьте оставшиеся коэффициенты. | \(\ гидроразрыва{5}{12}\) |
Получаем тот же результат.
Умножение двух дробей: Пример
Разделить дроби
Теперь, когда мы знаем, как умножать дроби, мы почти готовы к делению. Прежде чем мы сможем это сделать, нам понадобится словарный запас.
Обратная дробь находится путем инвертирования дроби, помещения числителя в знаменатель и знаменателя в числитель. Обратная величина \(\frac{2}{3}\) равна \(\frac{3}{2}\) .
Обратите внимание, что \(\frac{2}{3}\) · \(\frac{3}{2}\) = 1. Число и его обратное число умножаются на 1.
Чтобы получить положительное произведение 1 при умножении двух чисел, числа должны иметь одинаковый знак. Значит, обратные числа должны иметь один и тот же знак.
Обратная величина − \(\frac{10}{7}\) равна – \(\frac{7}{10}\) , поскольку − \(\frac{10}{7}\) \((\ frac{10}{7}\)) = 1 .
Деление дробей: Пример
Десятичные числа
Вы, вероятно, уже немного знаете о десятичных дробях, основываясь на своем опыте обращения с деньгами. Предположим, вы покупаете бутерброд и бутылку воды на обед. Если бутерброд стоит \(\text{💲3,45}\), бутылка воды стоит \(\text{💲1,25}\), а общий налог с продаж равен \(\text{💲0,33}\), то сколько общая стоимость обеда?
Предположим, вы покупаете бутерброд и бутылку воды на обед. Если бутерброд стоит \(\text{💲3,45}\), бутылка воды стоит \(\text{💲1,25}\), а общий налог с продаж равен \(\text{💲0,33}\), то сколько общая стоимость обеда?
Итого: \(\text{💲5.03}.\) Предположим, вы платите счетом \(\text{💲5}\) и \(3\) пенни. Стоит ли ждать перемен? Нет, \(\text{💲5}\) и \(3\) пенни — это то же самое, что \(\text{💲5.03}.\)
Потому что \(\text{100 пенни}=\text{💲 1},\) каждый пенни стоит \(\frac{1}{100}\) доллара. Мы записываем стоимость одного пенни как \(💲0,01,\), поскольку \(0,01=\frac{1}{100}.\)
Десятичные дроби на самом деле являются другим способом записи дробей, знаменатели которых являются степенями числа 10.
Точно так же, как счетные числа основаны на степенях десяти, десятичные дроби основаны на степенях десяти. (Рисунок) показывает счетные числа.
Как десятичные дроби связаны с дробями? (Рисунок) показывает отношение.
Сложение и вычитание десятичных знаков
Давайте еще раз взглянем на заказ обеда с самого начала Decimals, на этот раз обратив внимание на то, как складывались числа.
Все три пункта (бутерброд, вода, налог) были оценены в долларах и центах, поэтому мы выстроили доллары под долларами, а центы под центами, с выстраиванием десятичных знаков между ними. Затем мы просто добавляли каждый столбец, как если бы мы складывали целые числа. Выстраивая таким образом десятичные дроби, мы можем складывать или вычитать соответствующие разрядные значения точно так же, как мы это делали с целыми числами.
Затем мы просто добавляли каждый столбец, как если бы мы складывали целые числа. Выстраивая таким образом десятичные дроби, мы можем складывать или вычитать соответствующие разрядные значения точно так же, как мы это делали с целыми числами.
Сложение или вычитание десятичных знаков.
- Пишите числа вертикально, чтобы десятичные запятые совпадали.
- При необходимости используйте нули в качестве заполнителей.
- Сложите или вычтите числа, как если бы они были целыми числами. Затем поместите десятичную дробь в ответе под десятичными точками в данных числах.
Умножение десятичных знаков
Умножение десятичных дробей очень похоже на умножение целых чисел — нам просто нужно определить, где ставить десятичную точку. Процедура умножения десятичных дробей станет понятной, если мы сначала рассмотрим умножение дробей.
Вы помните, как умножать дроби? Чтобы умножить дроби, нужно умножить числители, а затем умножить знаменатели.
Итак, давайте посмотрим, что мы получим как произведение десятичных дробей, если сначала преобразуем их в дроби. Мы сделаем два примера рядом друг с другом на (рис.). Ищите образец.
| А | Б | |
|---|---|---|
| \(\влево(0,3\вправо)\влево(0,7\вправо)\) | \(\влево(0,2\вправо)\влево(0,46\вправо)\) | |
Преобразование в дроби. | \ (\ влево (\ гидроразрыва {3} {10} \ вправо) \ влево (\ гидроразрыва {7} {10} \ вправо) \) | \ (\ влево (\ гидроразрыва {2} {10} \ вправо) \ влево (\ гидроразрыва {46} {100} \ вправо) \) |
| Умножить. | \(\frac{21}{100}\) | \(\ гидроразрыва{92}{1000}\) |
| Преобразование обратно в десятичные числа. | \(0,21\) | \(0,092\) |
Есть шаблон, который мы можем использовать. В A мы умножили два числа, каждое из которых имело один десятичный знак, и в произведении было два десятичных знака. В B мы умножили число с одним десятичным знаком на число с двумя десятичными знаками, и в произведении было три десятичных знака.
Сколько знаков после запятой вы ожидаете в произведении \(\влево(0,01\вправо)\влево(0,004\вправо)?\) Если вы сказали «пять», вы распознали шаблон. Когда мы умножаем два числа на десятичные дроби, мы подсчитываем все десятичные разряды в множителях — в данном случае два плюс три — чтобы получить количество знаков после запятой в произведении — в данном случае пять.
Зная, как определить количество знаков после запятой, мы можем умножать десятичные числа без предварительного преобразования их в дроби. Количество знаков после запятой в произведении равно сумме количества знаков после запятой в множителях.
Правила умножения положительных и отрицательных чисел, конечно же, применимы и к десятичным дробям.
При умножении двух чисел
- если их знаки совпадают, произведение положительное.
- , если их знаки разные, произведение отрицательное.
При умножении десятичных чисел со знаком сначала определите знак произведения, а затем умножьте так, как если бы оба числа были положительными. Наконец, напишите продукт с соответствующим знаком.
Умножение десятичных чисел
- Определить знак произведения.
- Напишите числа в вертикальном формате, выстраивая числа справа.
- Умножить числа, как если бы они были целыми числами, временно игнорируя десятичные точки.

- Поставьте десятичную точку. Количество знаков после запятой в произведении равно сумме количества знаков после запятой в множителях. При необходимости используйте нули в качестве заполнителей.
- Запишите продукт соответствующим знаком.
Умножение десятичных дробей: Пример
Умножение на степени \(10\)
Во многих областях, особенно в естественных науках, принято умножать десятичные дроби на степени \(10.\). Посмотрим, что получится, если мы умножим \(1,9436\) на некоторые степени \(10.\)
Посмотрите на результаты без конечных нулей. Вы замечаете закономерность?
\(\phantom{\rule{2em}{0ex}}\begin{array}{ccc}1.9436\left(10\right)\hfill & =& 19.436\hfill \\ 1.9436\left(100\right)\hfill & =& 194.36\hfill \\ 1.9436\left(1000\right)\hfill & =& 1943.6\hfill \end{массив}\)
Количество знаков, на которое переместилась десятичная точка, равно количеству нулей в степени десяти. (Рисунок) суммирует результаты.
| Умножить на | Количество нулей | Количество мест, на которые перемещается десятичная точка |
|---|---|---|
| \(10\) | \(1\) | \(1\) разряд справа |
| \(100\) | \(2\) | \(2\) знаков справа |
| \(1000\) | \(3\) | \(3\) знака справа |
| \(10 000\) | \(4\) | \(4\) знака справа |
Мы можем использовать этот шаблон для быстрого умножения на степени десяти вместо умножения с использованием вертикального формата. Мы можем посчитать нули в степени \(10\), а затем переместить десятичную точку на то же место вправо.
Мы можем посчитать нули в степени \(10\), а затем переместить десятичную точку на то же место вправо.
Так, например, чтобы умножить \(45,86\) на \(100,\), переместите десятичную точку на \(2\) разрядов вправо.
Иногда, когда нам нужно переместить десятичную точку, не хватает десятичных знаков. В этом случае мы используем нули в качестве заполнителей. Например, давайте умножим \(2,4\) на \(100.\). Нам нужно переместить десятичную точку \(2\) разрядов вправо. Поскольку справа от запятой стоит только одна цифра, мы должны писать \(0\) в сотых долях.
Умножить десятичную дробь на степень 10.
- Переместить запятую вправо на такое количество знаков, сколько нулей в степени \(10.\)
- При необходимости напишите нули в конце числа в качестве заполнителей.
Разделить десятичные дроби
Так же, как и умножение, деление десятичных дробей очень похоже на деление целых чисел. Нам просто нужно выяснить, где должна быть размещена десятичная точка.
Чтобы понять десятичное деление, давайте рассмотрим задачу на умножение
\(\влево(0,2\вправо)\влево(4\вправо)=0,8\)
Помните, что задачу на умножение можно перефразировать как задачу на деление. Таким образом, мы можем написать
\(0,8÷4=0,2\)
Мы можем думать об этом так: «Если мы разделим 8 десятых на четыре группы, сколько будет в каждой группе?» (Рисунок) показывает, что есть четыре группы двух десятых в восьми десятых. Итак, \(0,8÷4=0,2.\)
Используя запись деления в длинном формате, мы бы написали
.Обратите внимание, что десятичная точка в частном находится прямо над десятичной точкой в делимом.
Чтобы разделить десятичную дробь на целое число, мы ставим десятичную запятую в частном над десятичной запятой в делимом, а затем делим как обычно. Иногда нам нужно использовать дополнительные нули в конце делимого, чтобы продолжать делить до тех пор, пока не останется остатка.
Разделить десятичную дробь на целое число.
- Пишите в виде длинного деления, помещая десятичную точку в частном выше десятичной точки в делимом.
- Разделить как обычно.
Разделить десятичную дробь на другую десятичную дробь
До сих пор мы делили десятичную дробь на целое число. Что происходит, когда мы делим десятичную дробь на другую десятичную дробь? Давайте рассмотрим ту же задачу на умножение, которую мы рассматривали ранее, но по-другому.
\(\влево(0,2\вправо)\влево(4\вправо)=0,8\)
Вспомним еще раз, что задачу на умножение можно перефразировать как задачу на деление. На этот раз мы спрашиваем: «Сколько раз \(0,2\) входит в \(0,8\текст{?»}\), потому что \(\left(0,2\right)\left(4\right)=0,8,\) можно сказать, что \(0,2\) переходит в \(0,8\) четыре раза. Это означает, что \(0,8\) разделить на \(0,2\) равно \(4,\)
\(0,8÷0,2=4\)
Мы получим тот же ответ, \(4,\), если разделим \(8\) на \(2,\) оба целых числа. Почему это так? Давайте подумаем о задаче деления как о дроби.
\(\begin{array}{c}\frac{0.8}{0.2}\\ \\ \frac{\left(0.8\right)10}{\left(0.2\right)10}\\ \\ \ frac{8}{2}\\ \\ 4\end{массив}\)
Мы умножили числитель и знаменатель на \(10\) и в итоге просто разделили \(8\) на \(4.\) Чтобы разделить десятичные дроби, мы умножаем и числитель, и знаменатель на одну и ту же степень \(10\). ), чтобы знаменатель стал целым числом. Из-за свойства Equivalent Fractions мы не изменили значение дроби. В результате десятичные точки в числителе и знаменателе смещаются вправо на одинаковое количество знаков.
Мы также используем правила деления положительных и отрицательных чисел с десятичными дробями. При делении десятичных дробей со знаком сначала определите знак частного, а затем разделите так, как если бы оба числа были положительными. Наконец, запишите частное с соответствующим знаком.
Это может помочь просмотреть словарь для деления:
Деление десятичных чисел.
- Определите знак частного.

- Сделайте делитель целым числом, переместив десятичную точку до упора вправо. Переместите запятую в делимом на такое же количество знаков вправо, при необходимости дописав нули.
- Разделить. Поставьте запятую в частном перед запятой в делимом.
- Запишите частное с соответствующим знаком.
Деление десятичных дробей – пример
Экспоненты
Показатель степени указывает на многократное умножение одной и той же величины. Например, 24 означает умножить четыре раза на 2, поэтому 24 означает 2·2·2·2. Этот формат известен как экспоненциальная запись.
Экспоненциальное обозначение
Читается в m-й степени.
В выражении am показатель степени говорит нам, сколько раз мы используем основание a в качестве множителя.
Квадрат
Знаете ли вы, почему мы используем слово в квадрате ? Если мы построим квадрат с тремя плитками на каждой стороне, общее количество плиток будет девять.
Вот почему мы говорим, что квадрат трех равен девяти.
3 2 = 9
Что произойдет, если возвести в квадрат отрицательное число?
(-8) 2 = (-8) (-8) = 64
Когда мы умножаем два отрицательных числа, произведение всегда положительно. Таким образом, квадрат отрицательного числа всегда положителен.
Куб
Квадратные корни
Иногда нам нужно будет посмотреть на отношения между числами и их квадратами в обратном порядке. Поскольку 10 2 = 100, мы говорим, что 100 — это квадрат 10. Мы также можем сказать, что 10 — это квадратный корень из 100.
Квадратный корень из числа
Число, квадрат которого равен m, называется квадратным корнем из m.
Если n 2 = m, то n является квадратным корнем из m.
Обратите внимание (-10) 2 =100 также, поэтому -10 также является квадратным корнем из 100. Следовательно, и 10, и -10 являются квадратными корнями из 100.
Итак, каждое положительное число имеет два квадратных корня: один положительный и один отрицательный.
Что, если нам нужен только положительный квадратный корень из положительного числа? Знак радикала , √, обозначает положительный квадратный корень. Положительный квадратный корень также называют главным квадратным корнем.
Обозначение квадратного корня
√m читается как «квадратный корень из m.
Если m=n 2 , то m = n при n≥0. Если m = n 2 , то m = n при n≥0.
Мы также можем использовать знак радикала для квадратного корня из нуля. Потому что 0 2 =0, √0=0. Обратите внимание, что ноль имеет только один квадратный корень.
Квадратный корень из отрицательного числа
Можем ли мы упростить √−25? Существует ли число, квадрат которого равен −25?
() 2 = −25?
Ни одно из чисел, с которыми мы до сих пор имели дело, не имеет квадрата, равного −25. Почему? Любое положительное число в квадрате положительно, и любое отрицательное число в квадрате также положительно. Не существует действительного числа, равного −25. Если нас просят найти квадратный корень из любого отрицательного числа, мы говорим, что решение не является действительным числом.
Почему? Любое положительное число в квадрате положительно, и любое отрицательное число в квадрате также положительно. Не существует действительного числа, равного −25. Если нас просят найти квадратный корень из любого отрицательного числа, мы говорим, что решение не является действительным числом.
Оценка квадратных корней (готово)
До сих пор мы работали только с квадратными корнями из полных квадратов. Квадратные корни других чисел не являются целыми числами.
Мы можем заключить, что квадратные корни чисел от 4 до 9 будут между 2 и 3, и они не будут целыми числами. Основываясь на приведенной выше таблице, мы можем сказать, что √5 находится между 2 и 3. Используя символы неравенства, мы запишем 2<√5<3
Приближение квадратных корней с помощью калькулятора
Существуют математические методы приближения квадрата корни, но гораздо удобнее использовать калькулятор для нахождения квадратных корней. Найдите на калькуляторе клавишу √ или √x. Вы будете использовать этот ключ для аппроксимации квадратных корней. Когда вы используете свой калькулятор, чтобы найти квадратный корень из числа, которое не является полным квадратом, ответ, который вы видите, не является точным числом. Это приблизительное количество цифр, отображаемое на дисплее вашего калькулятора. Символ приближения ≈ и читается как примерно .
Вы будете использовать этот ключ для аппроксимации квадратных корней. Когда вы используете свой калькулятор, чтобы найти квадратный корень из числа, которое не является полным квадратом, ответ, который вы видите, не является точным числом. Это приблизительное количество цифр, отображаемое на дисплее вашего калькулятора. Символ приближения ≈ и читается как примерно .
Предположим, ваш калькулятор имеет 10-разрядный дисплей. Используя его, чтобы найти квадратный корень из 5, вы получите 2,236067977. Это приблизительный квадратный корень из 5. Когда мы сообщаем ответ, мы должны использовать знак «приблизительно равно» вместо знака равенства.
√5 ≈ 2,2360679785
Вы редко будете использовать такое количество цифр в алгебраических приложениях. Итак, если бы вы хотели округлить √5 до двух знаков после запятой, вы бы написали
√5≈2,24
Откуда мы знаем, что эти значения являются приблизительными, а не точными? Посмотрите, что происходит, когда мы их возводим в квадрат.
2,236067978 2 = 5,000000002
2,24 2 = 5,0176
Квадраты близки, но не совсем равны, до 5.
Введение в экспоненты
Введение в экспоненты
. ипотека, кредитный инспектор сравнит ваш общий долг с вашим общим доходом, чтобы решить, имеете ли вы право на получение кредита. Это сравнение называется отношением долга к доходу. Соотношение сравнивает две величины, которые измеряются в одних и тех же единицах. Если мы сравним \(a\) и \(b\), отношение запишется как \(a\phantom{\rule{0.2em}{0ex}}\text{to}\phantom{\rule{0.2em} {0ex}}b,\phantom{\rule{0.2em}{0ex}}\frac{a}{b},\phantom{\rule{0.2em}{0ex}}\text{or}\phantom{\ правило {0.2em} {0ex}} \ mathit {\ text {a}} \ text {:} \ mathit {\ text {b}} \ text {.} \)
Соотношения с десятичными дробями
Нам часто приходится работать с десятичными дробями, особенно когда речь идет о денежных соотношениях. В этих случаях мы можем исключить десятичные дроби, используя свойство «Эквивалентные дроби», чтобы преобразовать отношение в дробь с целыми числами в числителе и знаменателе.
Например, рассмотрим отношение \(0,8\phantom{\rule{0.2em}{0ex}}\text{to}\phantom{\rule{0.2em}{0ex}}0,05.\) Мы можем записать его как дробь с десятичными знаками, а затем умножьте числитель и знаменатель на \(100\), чтобы исключить десятичные знаки.
Вы видите ярлык, чтобы найти эквивалентную дробь? Обратите внимание, что \(0,8=\frac{8}{10}\) и \(0,05=\frac{5}{100}.\) Наименьший общий знаменатель для \(\frac{8}{10}\) и \(\frac{5}{100}\) равно \(100.\) Умножив числитель и знаменатель \(\frac{0,8}{0,05}\) на \(100,\), мы «переместили» на два знака после запятой вправо, чтобы получить эквивалентную дробь без десятичных знаков. Теперь, когда мы понимаем математику этого процесса, мы можем найти дробь без десятичных знаков следующим образом:
| «Переместить» десятичную дробь на 2 разряда. | \(\ гидроразрыва{80}{5}\) |
| Упрощение. | \(\ гидроразрыва{16}{1}\) |
Вам не нужно записывать каждый шаг, когда вы умножаете числитель и знаменатель на степени десяти. Пока вы перемещаете оба десятичных разряда на одинаковое количество знаков, отношение останется прежним.
Пока вы перемещаете оба десятичных разряда на одинаковое количество знаков, отношение останется прежним.
Периметр и площадь
Периметр — это мера расстояния вокруг фигуры. Площадь — это мера поверхности, покрытой фигурой.
Квадрат
(Рисунок) показывает квадратную плитку со стороной 1 дюйм. Если бы муравей обошел край плитки, он прошел бы 4 дюйма. Это расстояние является периметром плитки. Поскольку плитка представляет собой квадрат, каждая сторона которого равна 1 дюйму, ее площадь равна одному квадратному дюйму. Площадь фигуры измеряется путем определения количества квадратных единиц, покрывающих фигуру.
Рисунок №. Периметр = 4 дюйма Площадь = 1 квадратный дюйм
Когда муравей полностью обходит плитку по краю, он очерчивает периметр плитки. Площадь плитки 1 квадратный дюйм.
Прямоугольник
У прямоугольника четыре стороны и четыре прямых угла. Противоположные стороны прямоугольника имеют одинаковую длину. Мы обозначаем одну сторону прямоугольника как длину, L, а смежную сторону как ширину, W. См. (Рисунок).
Мы обозначаем одну сторону прямоугольника как длину, L, а смежную сторону как ширину, W. См. (Рисунок).
Рисунок №. У прямоугольника четыре стороны и четыре прямых угла. Стороны помечены L для длины и W для ширины.
Периметр прямоугольника P — это расстояние вокруг прямоугольника. Если бы вы начали с одного угла и обошли прямоугольник, вы бы прошли единицы Д+Ш+Д+Ш, или две длины и две ширины. Тогда периметр равен
P=L+W+L+W
или
P=2L+2W
Как насчет площади прямоугольника? Помните прямоугольный ковер из начала этого раздела. Он был 2 фута в длину и 3 фута в ширину, а его площадь составляла 6 квадратных футов. См. (Рисунок). Поскольку A=2⋅3, мы видим, что площадь A равна длине L, умноженной на ширину W, поэтому площадь прямоугольника равна A=L⋅W.
Рисунок №. Площадь этого прямоугольного коврика составляет 6 квадратных футов, его длина умножается на ширину.
Треугольник
Теперь мы знаем, как найти площадь прямоугольника. Мы можем использовать этот факт, чтобы визуализировать формулу площади треугольника. В прямоугольнике на (рис.) мы обозначили длину b и ширину h, поэтому его площадь равна bh.
Мы можем использовать этот факт, чтобы визуализировать формулу площади треугольника. В прямоугольнике на (рис.) мы обозначили длину b и ширину h, поэтому его площадь равна bh.
Рисунок №. Площадь прямоугольника равна основанию b, умноженному на высоту h.
Мы можем разделить этот прямоугольник на два конгруэнтных треугольника (Рисунок). Конгруэнтные треугольники имеют одинаковые длины сторон и углы, поэтому их площади равны. Площадь каждого треугольника равна половине площади прямоугольника, или \(\frac{1}{2}\) bh. Этот пример помогает нам понять, почему формула площади треугольника A= \(\frac{1}{2}\) bh.
Рисунок №. Прямоугольник можно разделить на два треугольника одинаковой площади. Площадь каждого треугольника равна половине площади прямоугольника.
Формула площади треугольника: A = \(\frac{1}{2}\) bh, где b — основание, а h — высота.
Чтобы найти площадь треугольника, нужно знать его основание и высоту. Основание — это длина одной стороны треугольника, обычно стороны внизу. Высота — это длина линии, соединяющей основание с противоположной вершиной и образующей 9Угол 0° с основанием. (Рисунок) показывает три треугольника с отмеченными основанием и высотой каждого.
Высота — это длина линии, соединяющей основание с противоположной вершиной и образующей 9Угол 0° с основанием. (Рисунок) показывает три треугольника с отмеченными основанием и высотой каждого.
Рисунок №. Высота h треугольника — это длина отрезка, соединяющего основание с противоположной вершиной и образующего с основанием угол 90°.
Равнобедренные и равнобедренные треугольники
Помимо прямоугольного треугольника, некоторые другие треугольники имеют специальные названия. Треугольник с двумя сторонами одинаковой длины называется равнобедренным треугольником. Треугольник, у которого три стороны одинаковой длины, называется равносторонним треугольником. (Рисунок) показывает оба типа треугольников.
Рисунок №. В равнобедренном треугольнике две стороны имеют одинаковую длину, а третья сторона является основанием. В равностороннем треугольнике все три стороны имеют одинаковую длину.
Равнобедренные и равнобедренные треугольники
- У равнобедренного треугольника две стороны одинаковой длины.

- Равносторонний треугольник имеет три стороны одинаковой длины.
Трапеция
Трапеция четырехсторонняя фигура, четырехугольник , с двумя параллельными сторонами и двумя не параллельными сторонами. Параллельные стороны называются основаниями. Мы называем длину меньшего основания b, а длину большего основания — B. Высота h трапеции — это расстояние между двумя основаниями, как показано на (рис.).
Рисунок №. У трапеции большее основание В и меньшее основание В. Высота h — это расстояние между основаниями.
Формула площади трапеции:
Площадь трапеции =1/2h(b+B)
Разделение трапеции на два треугольника может помочь нам понять формулу. Площадь трапеции равна сумме площадей двух треугольников. См. (Рисунок).
Рисунок №. Разделение трапеции на два треугольника может помочь вам понять формулу ее площади.
Высота трапеции также является высотой каждого из двух треугольников. См. (Рисунок).
См. (Рисунок).
Формула площади трапеции:
Если распределить, то получим,
Круг
Свойства кругов изучались более \(2000\) лет. Все круги имеют одинаковую форму, но на их размеры влияет длина радиуса, отрезка прямой от центра до любой точки на круге. Отрезок, проходящий через центр окружности и соединяющий две точки окружности, называется диаметром. Диаметр в два раза больше радиуса. См. (Рисунок).
Размер круга можно измерить двумя способами. Расстояние вокруг окружности называется ее окружностью.
Архимед обнаружил, что для кругов всех размеров деление длины окружности на диаметр всегда дает одно и то же число. Значение этого числа — пи, обозначаемое греческой буквой \(\пи \) (произносится как пирог). Однако точное значение \(\pi \) не может быть вычислено, так как десятичная дробь никогда не заканчивается и не повторяется (мы узнаем больше о числах, подобных этому, в разделе «Свойства действительных чисел».)
Если нам нужна точная длина окружности или площадь круг, оставляем в ответе символ \(\pi \). {2}\text{)}\hfill \\ A=\pi ·100\hfill \end{массив}\)
{2}\text{)}\hfill \\ A=\pi ·100\hfill \end{массив}\)
Мы пишем \(\pi \) после \(100.\) Таким образом, точное значение площади равно \(A=100\text{π}\) квадратных дюймов.
Чтобы приблизить площадь, мы подставим \(\pi \приблизительно 3.14.\)
\(\begin{array}{ccc}A& =& 100\text{π}\hfill \\ \\ & \приблизительно & 100·3.14\hfill \\ & \приблизительно & 314\phantom{\rule{0.2em}{0ex}}\text{квадратные дюймы}\hfill \end{массив}\)
Не забудьте использовать квадратные единицы измерения, например как квадратные дюймы, когда вы вычисляете площадь.
Сфера
Сфера имеет форму баскетбольного мяча, похожа на трехмерный круг. Как и в случае с кругом, размер сферы определяется ее радиусом, то есть расстоянием от центра сферы до любой точки на ее поверхности. Ниже приведены формулы объема и площади поверхности шара.
Показать, откуда берутся эти формулы, как мы это делали для прямоугольного тела, выходит за рамки этого курса. Мы аппроксимируем ππ с помощью 3. 14.
14.
Объем и площадь поверхности шара
Для сферы радиусом r:
Куб или прямоугольник
Куб представляет собой прямоугольное тело, длина, ширина и высота которого равны. См. Объем и площадь поверхности куба ниже. Подставляя s для длины, ширины и высоты в формулы объема и площади поверхности прямоугольного тела, получаем: =2s·s+2s·s+2s·s
V=s 3 S=2s 2 +2S 2 +2S 2
S = 6S 2
Таким образом, для куба, формулы для объема и площади поверхности являются V = S 3 и S = 6S 2 .
Объем и площадь поверхности куба
Для любого куба со сторонами длины s:
Цилиндр
Если вы когда-нибудь видели банку газировки, то знаете, как выглядит цилиндр. Цилиндр — это объемная фигура с двумя параллельными окружностями одинакового размера вверху и внизу. Верх и низ цилиндра называются основаниями. Высота h цилиндра — это расстояние между двумя основаниями. Для всех цилиндров, с которыми мы будем здесь работать, стороны и высота h будут перпендикулярны основаниям.
Для всех цилиндров, с которыми мы будем здесь работать, стороны и высота h будут перпендикулярны основаниям.
Рисунок №. Цилиндр имеет два круглых основания одинакового размера. Высота — это расстояние между основаниями.
Прямоугольные тела и цилиндры в чем-то похожи, потому что они оба имеют два основания и высоту. Формула объема прямоугольного тела V=Bh также может быть использована для нахождения объема цилиндра.
Для прямоугольного твердого тела площадь основания B равна площади прямоугольного основания, длина × ширина. Для цилиндра площадь основания B равна площади его круглого основания πr 2 . (Рисунок) сравнивает использование формулы V=Bh для прямоугольных тел и цилиндров.
Рисунок №. Увидев, как цилиндр похож на прямоугольное твердое тело, вы сможете легче понять формулу объема цилиндра.
Чтобы понять формулу площади поверхности цилиндра, представьте себе банку с овощами. У него три поверхности: верхняя, нижняя и часть, образующая стенки банки. Если вы аккуратно отрежете этикетку сбоку от банки и развернете ее, то увидите, что это прямоугольник. См. (Рисунок).
Если вы аккуратно отрежете этикетку сбоку от банки и развернете ее, то увидите, что это прямоугольник. См. (Рисунок).
Рисунок №. Разрезав и развернув этикетку банки с овощами, мы видим, что поверхность цилиндра представляет собой прямоугольник. Длина прямоугольника — это окружность основания цилиндра, а ширина — высота цилиндра.
Расстояние вокруг края банки равно длине окружности основания цилиндра, а также длине прямоугольной этикетки L. Высота цилиндра равна ширине W прямоугольной этикетки. Таким образом, площадь этикетки можно представить как
Чтобы найти общую площадь поверхности цилиндра, мы добавляем площади двух кругов к площади прямоугольника.
Площадь поверхности цилиндра радиусом r и высотой h равна S=2πr 2 +2πrh
Объем и площадь поверхности цилиндра
Для цилиндра радиусом r и высотой h:
Конус
Первый образ, который возникает у многих из нас, когда мы слышим слово «конус», — это рожок мороженого. Есть много других применений рожков (но большинство из них не такие вкусные, как рожки для мороженого). В этом разделе мы увидим, как найти объем конуса.
Есть много других применений рожков (но большинство из них не такие вкусные, как рожки для мороженого). В этом разделе мы увидим, как найти объем конуса.
В геометрии конус — это объемная фигура с одним круглым основанием и вершиной. Высота конуса — это расстояние между его основанием и вершиной. Конусы, которые мы рассмотрим в этом разделе, всегда будут иметь высоту, перпендикулярную основанию. См. (Рисунок).
Рисунок №. Высота конуса – это расстояние между его основанием и вершиной.
Ранее в этом разделе мы видели, что объем цилиндра равен V=πr 2 ч. Мы можем думать о конусе как о части цилиндра. (Рисунок) показывает конус, помещенный внутри цилиндра той же высоты и того же основания. Если мы сравним объем конуса и цилиндра, то увидим, что объем конуса меньше объема цилиндра.
Рисунок №. Объем конуса меньше объема цилиндра с тем же основанием и высотой.
На самом деле объем конуса составляет ровно одну треть объема цилиндра с таким же основанием и высотой.







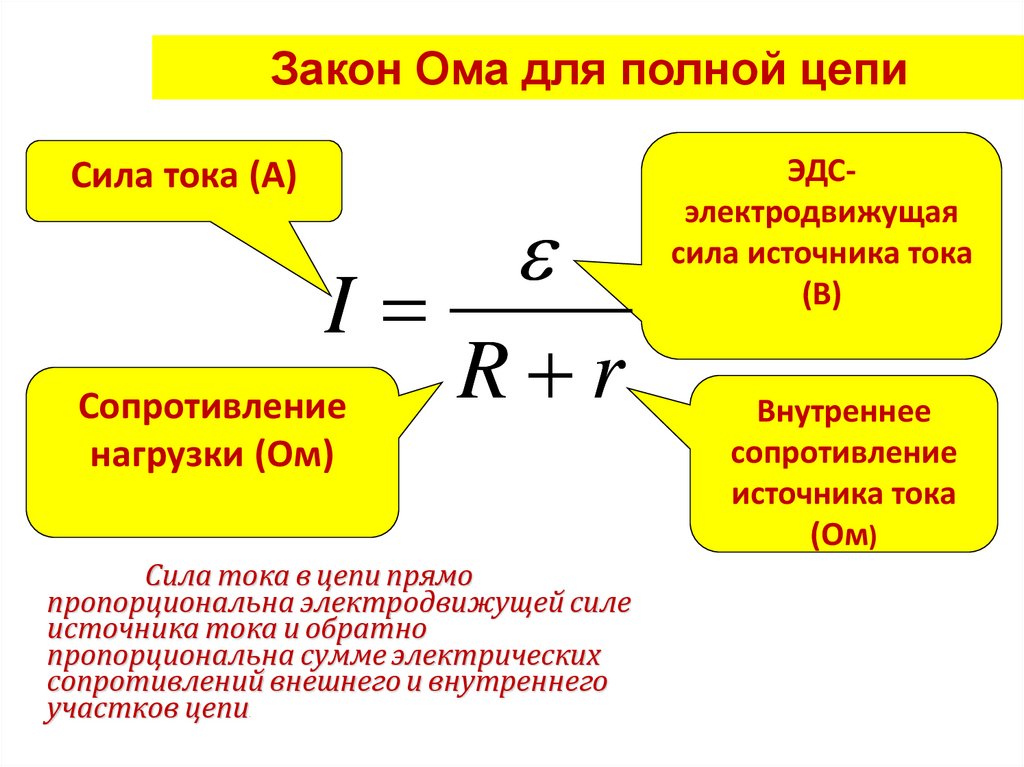 Если общее число больше 1, т. е. если элемент встречается более одного раза, применяется правило, и элемент выделяется.
Если общее число больше 1, т. е. если элемент встречается более одного раза, применяется правило, и элемент выделяется.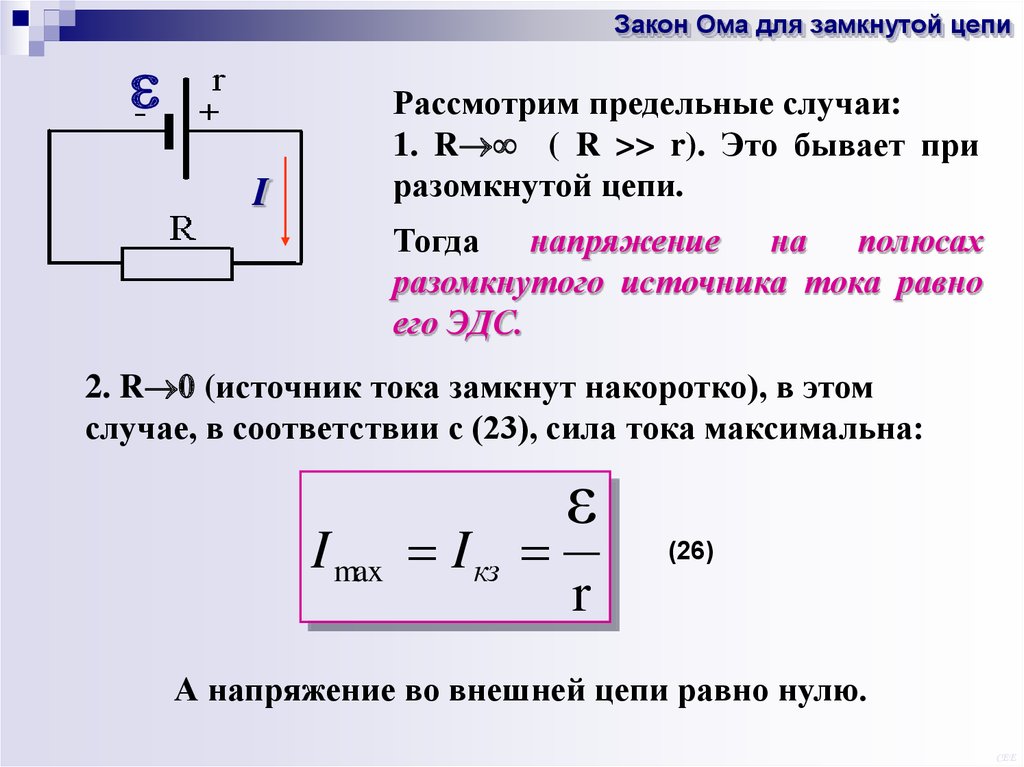 Поскольку мы хотим выделить полные повторяющиеся строки, я выбрал все 3 столбца.
Поскольку мы хотим выделить полные повторяющиеся строки, я выбрал все 3 столбца.  д.
д. Рядом с буквой A2 есть знак доллара. Это сделано намеренно, чтобы формула могла подсчитывать каждую ячейку из столбца A. В этой статье вы узнаете больше о ссылках на ячейки.
Рядом с буквой A2 есть знак доллара. Это сделано намеренно, чтобы формула могла подсчитывать каждую ячейку из столбца A. В этой статье вы узнаете больше о ссылках на ячейки.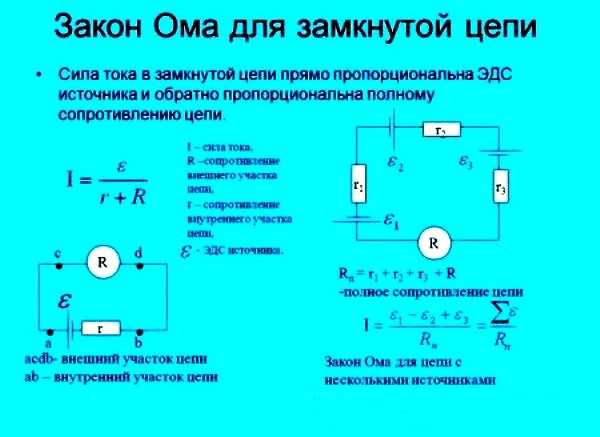 На этот раз удалите знак доллара с A2. Это позволит формуле подсчитать все вхождения каждой ячейки из таблицы, а не только из столбца A.
На этот раз удалите знак доллара с A2. Это позволит формуле подсчитать все вхождения каждой ячейки из таблицы, а не только из столбца A.

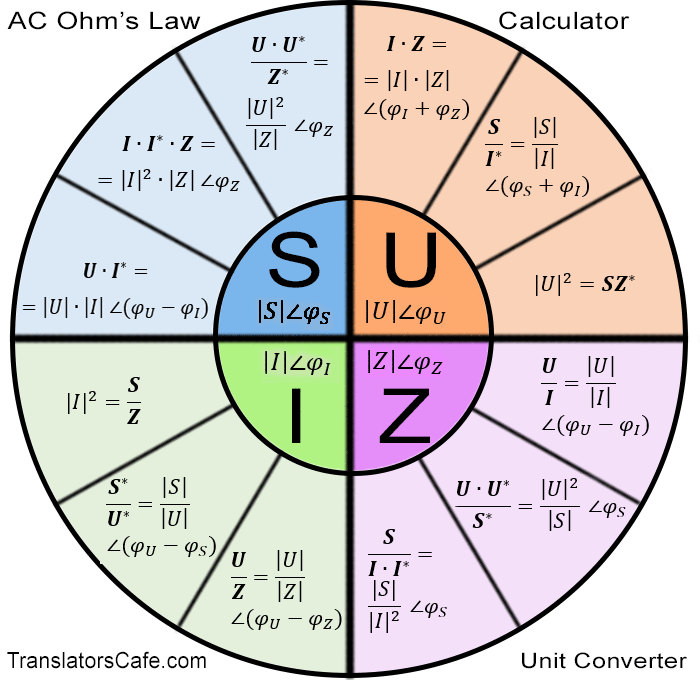

 По умолчанию будет использоваться зеленый цвет, но вы можете указать другие цвета, а также стили, такие как жирный шрифт или курсив
По умолчанию будет использоваться зеленый цвет, но вы можете указать другие цвета, а также стили, такие как жирный шрифт или курсив