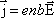Закон Ома в интегральной форме
Ляпин Али Ибрагимович, доцент БРУ
1. | Однородный и неоднородный участки цепи. | 2 |
| ρ dl | 2 |
| r | r | 2 r | r | |
| Вывод закона Ома в интегральной форме | для | I ∫ |
|
| =∫Eк dl | +∫Eстор dl | ||||
|
| S | |||||||||
| неоднородного участка цепи |
| 1 |
| 1 |
|
|
| 1 |
| |
|
|
|
|
|
|
|
|
|
|
| |
2. | Разность потенциалов, электродвижущая |
|
|
| 2 r | r |
|
|
| 2 r | r |
| сила, напряжение | ϕ1 | −ϕ2 = ∫Eк dl | ε1−2 | = ∫Eстор dl | ||||||
|
|
|
| 1 |
|
|
|
| 1 |
| |
3. | Правила Кирхгофа для электрических цепей |
|
|
| N |
|
| N |
|
| N |
|
|
|
| ∑Ik = 0 ; | ∑Ik Rk = ∑εk | ||||||
|
|
|
| k =1 |
|
| k =1 |
| k =1 | ||
2Ляпин Али Ибрагимович, доцент БРУ
1.Однородный и неоднородный участки цепи. Вывод закона Ома в интегральной форме для неоднородного участка цепи.
Однородный и неоднородный участки цепи.
Если в проводнике действует только электростатическое поле, то в нем может возникнуть только кратковременный электрический ток. Действительно, если обкладки конденсатора, заряженного до некоторой разности потенциалов Δφ, соединить проводником, то в проводнике возникнет электрический ток. По мере протекания тока конденсатор будет разряжаться, и разность потенциалов будет уменьшаться. С течением времени потенциал во всех точках системы уравняется и ток прекратится.
Например, если обкладки заряженного конденсатора емкостью 1Ф замкнуть проводником, имеющим сопротивление 1Ом, то электрический ток в цепи будет протекать примерно в течение 1с.
В электростатическом поле заряды перемещаются из точек с большим потенциалом в точки с меньшим потенциалом, что приводит к выравниванию потенциалов. Для поддержания электрического тока достаточно длительное время, необходим источник, в котором за счет сил не электростатического происхождения осуществлялся бы перенос носителей тока в исходную точку с большим потенциалом. Указанные силы называются сторонними.
Таким образом, для поддержания электрического тока в цепи необходимо наличие сторонних сил, действующих либо во всей цепи, либо на отдельных ее участках.
Сторонние силы могут быть химической, электромагнитной природы и др. Например, в большинстве аккумуляторов роль сторонних сил играют силы химического взаимодействия, приводящие к разделению молекул электролитов на разноименные заряды. В этом случае разность потенциалов на электродах аккумулятора поддерживается за счет энергии химической реакции.
Участок цепи, на котором не действуют сторонние силы, называется однородным. Участок цепи, на котором действуют сторонние силы, называется неоднородным.
Вывод закона Ома в интегральной форме для неоднородного участка цепи.
В общем случае на неоднородном участке цепи действуют и кулоновские и сторонние силы. Обозначим напряженность поля электростатических (кулоновских) сил через Ек, а напряженность поля сторонних сил через Естор. Тогда в любой точке внутри проводника результирующая напряженность равна
E = Eк + Eстор
и закон Ома в дифференциальной форме будет иметь вид
|
|
|
|
|
|
| r | 1 |
|
| r |
| r |
|
| |
|
|
|
|
|
|
| j = |
|
| (E | к | + E | ) | . (1) | ||
|
|
|
|
|
|
|
|
| ||||||||
|
|
|
|
|
|
|
|
| ρ |
|
|
|
| стор |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Обе части уравнения (1) умножим |
| скалярно на вектор dl , | ||||||||||||||
численно равный элементу dl длины проводника и совпадающий | ||||||||||||||||
по направлению с вектором j плотности тока |
|
|
|
| ||||||||||||
r | r |
| 1 | r | r | r |
|
|
|
| r |
|
|
|
| |
j | dl | = |
| (E | dl | + E |
|
| dl ) . (2) |
| ||||||
ρ |
|
|
| |||||||||||||
|
|
| к |
|
| стор |
|
|
|
|
|
|
| |||
Так как плотность тока j постоянного |
| равна | j = I / S и скалярное произведение | |||||||||||||
сонаправленных векторов | rj и | dl равно произведению их модулей, то формулу (2) можно | ||||||||||||||
записать в следующей форме |
| ρ dl |
|
| r |
|
|
| r | r | ||||||
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
| I |
|
| = | E | к | dl + E | dl . (3) | ||||
|
|
|
|
|
|
| ||||||||||
|
|
|
|
|
|
| S |
|
|
|
|
|
| стор |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
3 | Ляпин Али Ибрагимович, доцент БРУ |
Формула (3) представляет собой закон Ома для бесконечно малого элемента dl неоднородного участка цепи от сечения 1 с потенциалом φ1 до сечения 2 с потенциалом φ2. Проинтегрировав выражение (3) по всей длине участка цепи от сечения 1 с потенциалом φ1
до сечения 2 с потенциалом φ2 получим формулу обобщенного закона Ома в интегральной форме для неоднородного участка цепи
2 | ρ dl | 2 | r | r | 2 | r | r |
| |
I ∫ |
| =∫Eк dl | +∫Eстор dl | . (4) | |||||
S | |||||||||
1 | 1 |
|
| 1 |
|
|
| ||
Так как сила постоянного тока во всех сечениях проводника постоянна, то сила тока вынесена за знак интеграла.
2. Разность потенциалов, электродвижущая сила, напряжение
Проанализируем интегралы, входящие в формулу (4). Нетрудно видеть, что подынтегральное выражение в интеграле левой части формулы (4) определяет электрическое сопротивление элемента dl проводника, а сам интеграл выражает электрическое сопротивление цепи на рассматриваемом участке
R | = | 2 | ρ dl | . (5) |
∫1 |
| |||
1−2 |
| S | ||
|
| |||
При этом, сопротивление R1-2 включает в себя как сопротивление R проводника, так и сопротивление r промежутка цепи между электродами источника тока (сопротивление электролита или внутреннее сопротивление источника)
R1-2=R+r. (6)
Первый интеграл правой части формулы (4) выражает работу сил электростатического поля по перемещению единичного положительного заряда из точки с потенциалом φ1 в точку
с потенциалом φ2. Эта работа в электростатике была названа разностью потенциалов, поэтому
ϕ1 −ϕ2 = ∫2 Erк dlr. (7)
1
Второй интеграл правой части формулы (4) выражает работу сторонних сил по перемещению единичного положительного заряда на рассматриваемом участке цепи. Указанная работа сторонних сил называется электродвижущей силой (ЭДС) и часто
обозначается символом ε
ε1−2 = ∫2 Erстор dlr. (8)
1
Из формулы (8) следует физический смысл ЭДС:
ЭДС на участке цепи называется физическая величина, численно равная работе сторонних сил по перемещению единичного положительного заряда на этом участке.
ЭДС, так же как и разность потенциалов, измеряется в вольтах.
С учетом введенных обозначений для интегралов, формулу (4) можно записать в следующем виде
I R1−2 = (ϕ1 −ϕ2 ) +ε1−2 . (9)
Формула (9) также является математическим выражением закона Ома для неоднородного участка цепи в интегральной форме.
ЭДС, так же как и сила тока, является величиной алгебраической. Поэтому следует учитывать ее знак.
Если ЭДС способствует перемещению положительных зарядов в данном направлении, то она считается положительной. Если ЭДС препятствует перемещению положительных зарядов в данном направлении, то она считается отрицательной.
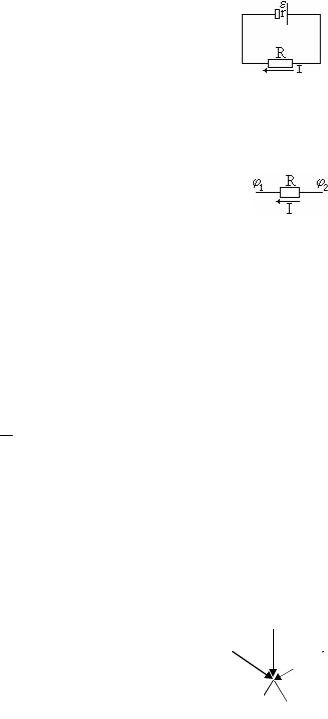
4 Ляпин Али Ибрагимович, доцент БРУ
Произведение величины сопротивления участка цепи и силы тока в нем называется падением напряжения. Из формулы (9) следует физический смысл напряжения:
напряжением на участке цепи называется физическая величина, численно равная сумме работ электростатических и сторонних сил по перемещению единичного положительного заряда вдоль этого участка.
Формула (9) называется также формулой обобщенного закона Ома, так как она справедлива для различных цепей.
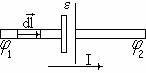
Если на приведенном выше рисунке участок цепи замкнуть проводником, то получим замкнутую цепь. В этом случае φ1=φ2 и из формулы (9), с учетом формулы (6), получим закон Ома в следующем виде
I (R + r)= ε или I = | ε | . (10) | |
R + r | |||
|
|
В случае замкнутой неразветвленной цепи ЭДС равна работе по перемещению единичного положительного заряда по всей цепи.
Из формулы (10) следует, что ЭДС равна сумме падений напряжений на внутреннем и внешнем участках цепи.
В случае однородного (в отсутствие ЭДС) участка цепи с током I, ε=0,
r=0 и формула (9) принимает следующий вид |
|
|
| |||
I = | ϕ1 | −ϕ2 | или | I = | U | , (11) |
| R | R | ||||
|
|
|
|
| ||
где φ1-φ2=U называется падением напряжения на сопротивлении R.
Если неоднородная цепь не замкнута, то I=0 и формула (9) принимает следующий вид
(ϕ1 −ϕ2 ) = ε , (12)
то есть в этом случае ЭДС равна разности потенциалов на клеммах источника тока.
Для каждого проводника в неизменном состоянии существует однозначная зависимость между разностью потенциалов, приложенной к его концам, и силой тока в нем I=f(U). Эта зависимость называется вольтамперной характеристикой (ВАХ). Для многих проводников, особенно металлических, эта зависимость выражается законом Ома
I = R1 U . (13)
То есть значение силы тока изменяется прямо пропорционально с изменением значения U. Обобщенный закон Ома в интегральной форме позволяет рассчитывать различные электрические цепи.
3. Правила Кирхгофа для разветвленных электрических цепей
Расчеты сложных (разветвленных) электрических цепей значительно упрощаются с помощью правил Кирхгофа (Г. Кирхгоф, нем. ученый, 1847г.). Любую разветвленную цепь можно представить как совокупность точек разветвления и замкнутых контуров.
Узлом называется точка разветвления цепи, в которой сходится больше
двух проводников с током. | I | I2 | I3 |
Первое правило Кирхгофа выражает условие постоянства тока в цепи. В |
|
|
|
случае постоянного тока электрические заряды не должны накапливаться на | I5 |
| I4 |
каком либо участке цепи. |
| ||
Первое правило Кирхгофа гласит: алгебраическая сумма токов, |
|
|
|
сходящихся в узле, равна нулю: |
|
|
|
N
∑Ik = 0 , (14)
k =1
где N– число проводников, сходящихся в узле; Ik– сила тока в k-м проводнике, причем токи, подходящие к узлу считаются положительными, а токи, отходящие от него– отрицательными
5 | Ляпин Али Ибрагимович, доцент БРУ |
Второе правило Кирхгофа является обобщением закона Ома (9) на разветвленные цепи.
Второе правило гласит: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма напряжений на всех участках этого контура равна алгебраической сумме Э.Д.С. всех источников электрической энергии, включенных в контур
N | N |
∑Ik Rk = ∑εk , (15) | |
k =1 | k =1 |
где N– число участков, на которые контур разбивается узлами; Ik, Rk и εk– сила тока, сопротивление и Э.Д.С. соответствующие k-му участку.
При составлении уравнения (15) необходимо |
|
|
|
|
|
|
| ε1 |
|
|
|
|
|
|
|
|
| |||||
выбрать направление обхода контура. Все токи в |
|
| A R1 |
|
| I1 |
| B |
|
|
| |||||||||||
участках, | совпадающие | по | направлению с |
|
|
|
|
|
|
| – | + |
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
направлением | обхода контура, | следует | считать |
|
|
|
|
|
|
|
|
|
|
|
| I2 | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
положительными, а не совпадающие с направлением |
|
|
|
|
|
|
|
|
|
|
|
| + |
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ε2 | |||||||
обхода – отрицательными. | Э.Д.С. | источников тока |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
| – |
|
| ||||||||
считать положительными, если они создают ток, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
R4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
совпадающий | с направлением | обхода | контура. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| R2 | |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
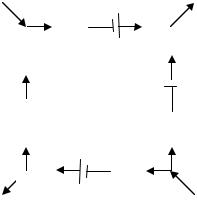
Например, в случае обхода приведенного контура |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
I4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
ABCD по часовой стрелке уравнение имеет вид |
|
| + |
| – |
|
|
|
|
|
|
| C | |||||||||
I1 R1 − I2 R2 + I3 R3 + I4 R4 =ε1 −ε2 +ε3 . |
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
| D | ε3 |
|
|
|
| I3 | ||||||||||||||
|
|
| R3 |
|
|
|
| |||||||||||||||
Вопросы для самопроверки:
1.Что понимают под сторонними силами и какова их роль в электрической цепи? Укажите природу сторонних сил.
2.Какой участок цепи называется однородным, и какой неоднородным? Вывести закон Ома в интегральной форме для неоднородного участка цепи. Как выбирается знак Э.Д.С. при записи закона Ома?
3.Пояснить физический смысл разности потенциалов, электродвижущей силы и напряжения на участке электрической цепи. Указать на отличие между этими величинами.
4.Сформулировать правила Кирхгофа. Как выбираются знаки Э.Д.С. и токов при записи правил Кирхгофа?
Закон Ома (интегральная форма)
Основной закон электрических цепей (закон Ома) установил экспериментально в 1826 году немецкий физик Георг Ом.
В общем случае закон Ома (обобщённый) формулируется так: сила тока на участке цепи прямо пропорциональна напряжению на этом участке:
I = GU, (8)
Коэффициент пропорциональности G называется проводимостью участка цепи.
Величина, обратная проводимости, называется электросопротивлением (или просто — сопротивлением) участка цепи:
R = 1/G. (9)
Обобщённый закон Ома обычно выражается так:
I = 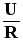 .
(10)
.
(10)
В СИ сопротивление измеряется в омах: [R] = 1 Ом, а проводимость — в сименсах: [G] = 1 См.
Сопротивление проводников зависит от его размеров, формы и материала, из которого проводник изготовлен. Для однородного проводника с одинаковой по всей длине площадью поперечного сечения s сопротивление равно:
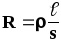 ,
(11)
,
(11)
где — удельное сопротивление материала проводника.
В области температур, близких или выше комнатных, сопротивление линейно зависит от температуры:
R = R0(1 + T), (12)
где R0 — сопротивление проводника при некоторой температуре Т0 (обычно Т0=00С), R — сопротивление этого проводника при температуре Т=Т0+T, — термический коэффициент сопротивления.
В конкретных электротехнических задачах закон Ома удобно представлять в виде —
— для однородного участка цепи (не содержащего ЭДС):
I = 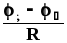 ,
(13)
,
(13)
— для неоднородного участка цепи (содержащего ЭДС):
I = 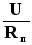 =
=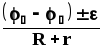 ,
(14)
,
(14)
— для замкнутой цепи:
I = 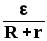 .
(15)
.
(15)
Здесь (1 — 2) — разность потенциалов на концах участка, — алгебраическая сумма ЭДС неоднородного участка цепи или всего контура (в случае замкнутой цепи), R — полное сопротивление всех однородных участков цепи, r — общее внутреннее сопротивление всех источников ЭДС, Rп=R+r — полное сопротивление неоднородного участка цепи. Перед ставятся знаки «+» или «-» в зависимости от полярности источника ЭДС по отношению к полярности внешнего напряжения (1 — 2), приложенного к участку цепи.
Закон Ома (дифференциальная форма).
Закон Ома можно представить в дифференциальной форме, если в уравнении (10) использовать вместо интегральных характеристик — силы тока I, напряжения U и сопротивления R, дифференциальные, характеризующие электрическое состояние среды в одной точке, — плотность тока J, напряжённость поля E и удельное сопротивление проводника соответственно.
Для проводника,
имеющего форму цилиндра, сопротивление
определяется формулой (11). Подстановка
её в формулу (10) даёт: 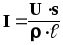 или
или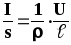 .
Поскольку
.
Поскольку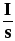 =J,
=J,  =Е,
=Е, 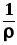 = (удельная проводимостью материала
проводника), то
= (удельная проводимостью материала
проводника), то
закон Ома принимает вид:
J = E. (16)
Плотность тока 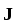 и напряжённость поля
и напряжённость поля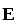 являются коллинеарными векторами. Таким
образом,закон
Ома в дифференциальной форме можно представить так:
являются коллинеарными векторами. Таким
образом,закон
Ома в дифференциальной форме можно представить так:
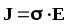 .
(17)
.
(17)
Интегральные и дифференциальные форма закона Ома: содержание и формулы
Обычно для расчётов электрического тока пользуются законом Ома для участка цепи: I=U/R, где I – ток в цепи, U – напряжение, R – суммарное сопротивление. Ток в этой цепи может протекать через различные участки из разных проводов. Поэтому для расчётов силы тока в определённом участке проводника лучше применить закон Ома в дифференциальной форме. Так как плотность тока Ī – векторная величина, то формула закона имеет вид: Ī = γĒ, где γ – удельная проводимость, обратная удельному сопротивлению γ=1/R, а Ē – напряжённость электрического поля. Может выражаться закон Ома также в интегральных формах.

Закон Ома
Действие электродвижущих сил
Электродвижущая сила (ЭДС) является скалярной величиной, характеризующей работу не электрических сил, заставляющих производить разность потенциалов на выходе.
Дополнительная информация. Скалярная величина – это когда она может быть выражена только определённым значением. В отличие от векторной величины, которая определяется не только значением, но и направлением.
Используется ЭДС в генераторах, преобразующих какую либо работу А (джоуль) в электрическую. Для этого могут быть использованы такие виды энергии по их происхождению:
- Механическая индукционная. Вывод ЭДС возникает при пересечении проводником линий магнитного поля;
- Механическая пьезоэлектрическая. Возникновение ЭДС происходит при деформации некоторых веществ;
- Световая энергия. Здесь ЭДС появляется в полупроводниках при действии на них световых лучей;
- Термическая энергия. ЭДС образуется, когда контакты из разнородных проводников находятся под разными температурами;
- Химическая энергия. Возникновение ЭДС происходит вследствие химических реакций.
В зависимости от характера энергии и устройства генератора ЭДС может возникать как переменная, так и постоянная. Переменная может быть как синусоидальная (магнитные индукционные генераторы), так и импульсная (пьезозажигалки). Постоянную ЭДС преобразуют в основном из химической (элементы питания, аккумуляторы), световой (фотоэлементы) энергий и температуры (элементы Пельтье).

Генераторы тока
ЭДС образует на разноименных проводниках разность потенциалов. Если не соединять проводником клеммы, на которых имеется разность потенциалов, то тока в цепи не будет. Следовательно, никакой энергии не будет израсходовано. На клеммах будет оставаться разность потенциалов. Работу для поддержания этой разности совершать не надо.
Если к клеммам с разностью потенциалов подключить проводник с нагрузкой, то через него будет протекать электрический ток, выполняя работу в нагрузке. При этом разность потенциалов на клеммах будет стремиться к 0, что приведёт к падению тока до 0. Для поддержания разности потенциалов стабильной величиной необходимо, чтобы ЭДС получала энергию. Эта энергия затрачивает работу, равную той, которая совершается в нагрузке.
Движение тока по неоднородным проводникам
Разность потенциалов, вызванная ЭДС, будет производить напряжение на клеммах генератора. ЭДС – это скалярная величина. При подключении к клеммам проводника через него потечёт ток, плотность которого выражается, например, Ī. Это уже векторная величина. Если ток создан только разностью потенциалов на клеммах, то векторы потенциала и плотности тока будут совпадать. Такой проводник называют однородным. Закон Ома для однородного участка цепи:
I=U/R.
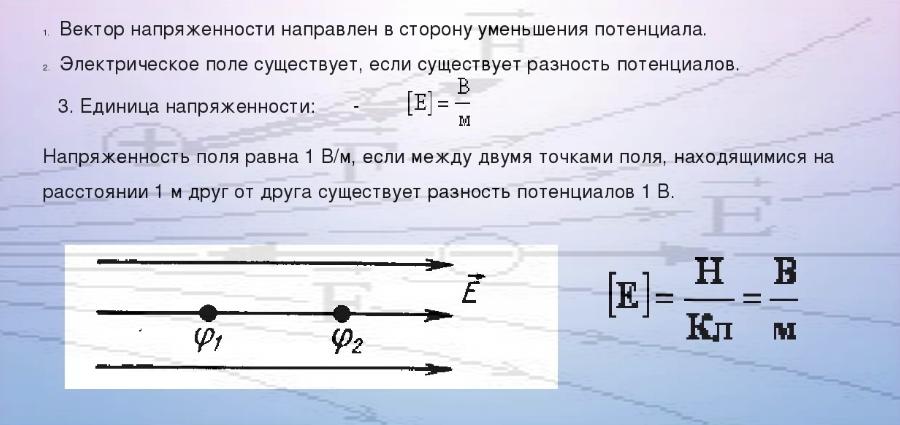
Вектор напряжённости
Неоднородный проводник, кроме сил, которые образованы разностями потенциалов, имеет сторонние силы. Для определения плотности тока Ī пользуются законом Ома в дифференциальной форме для неоднородных проводников:
Ī=γ(E+Ē₁+ Ē₂+ Ēn).
Векторы и каждый участок проводника складываются, E – напряжённость, созданная разностью потенциалов на клеммах проводника (скалярная величина). Ē₁, Ē₂, Ēn – векторные величины напряжённости первой, второй и энной сторонних сил.
Так как γ – удельная проводимость проводника, обратная сопротивлению, ϕ₁ – потенциал на 1-ой точке, ϕ₂ – потенциал на 2-ой точке, то закон Ома для неоднородного участка цепи от 1-ой до 2-ой точки будет записываться так:
Ī =(ϕ₁ – ϕ₂+ Ē)/R.
Для ознакомления металлы и их удельное сопротивление:
- Серебро – 1,6×10ˉ⁸Ом×м;
- Медь – 1,72×10ˉ⁸ Ом×м;
- Алюминий – 2,6×10ˉ⁸ Ом×м;
- Латунь – 3…7,0×10ˉ⁸ Ом×м;
- Бронза – 8,0×10ˉ⁸ Ом×м;
- Железо – 9,8×10ˉ⁸ Ом×м;
- Свинец – 2.0×10ˉ⁶Ом×м;
- Графит – 3…5,0×10ˉ⁵Ом×м.
Трактовка и пределы применимости закона Ома
Если необходимо определить одну из величин: ток, напряжение или сопротивление для однородной цепи, то пользуются формулой, формулировка которой изображена на рисунке.
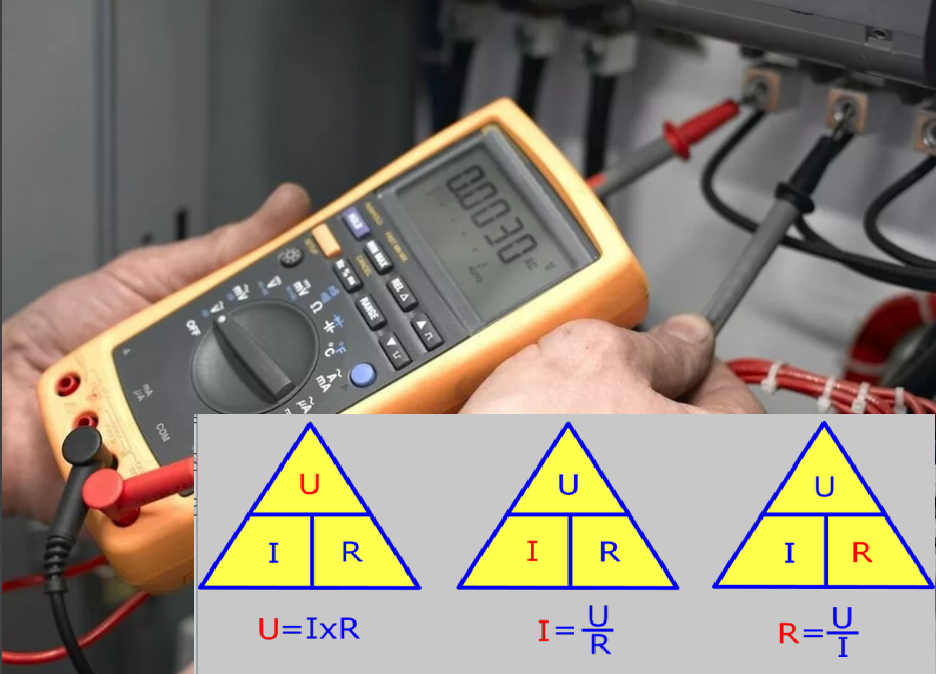
Закон Ома в треугольнике
Для удобства решения тождества величины изображены в треугольнике. Теперь, пользуясь первой формулой, зная сопротивление цепи и ток, можно высчитать напряжение, которое действует на замкнутый контур. Зная напряжение и сопротивление цепи, можно определить ток по 2-ой формуле. По 3-ей формуле высчитывают сопротивление нагрузки, зная напряжение и ток.
Существуют исключения, когда закон Ома не соблюдается. Примеры:
- В переменных ЭДС, если нагрузка имеет индукционный или ёмкостный характер. При повышении частоты из-за инерционности носителей заряда вступают в силу законы электродинамики. Конденсаторы и катушки индуктивности в качестве сопротивления для переменного тока, колебательный контур.
- Для веществ, обладающих сверхпроводимостью при низких температурах. Датчики измерительных приборов высокой точности, сверхпроводящие соленоиды, сверхпроводящие кабели с током 5 000 А.
- При высоких температурах, когда проводник начинает проявлять нелинейную характеристику сопротивления. Вольфрамовая нить лампы накаливания, спирали нагревательных элементов.
- При высоких напряжениях, когда происходит пробой диэлектрика. Свечи зажигания карбюраторных двигателей, наконечники для защиты от тлеющего разряда высоковольтных ЛЭП.
- В наполненных газом люминесцентных и вакуумных лампах. Люминесцентные лампы, вакуумные индикаторы, индикаторы тлеющего разряда.
- В полупроводниковых приборах с p-n переходами и в нелинейных полупроводниках. Это светодиоды, стабилитроны, транзисторы, электронные приборы.
Интересно. Используется закон Ома в дифференциальной форме, когда имеется несколько ЭДС, или цепь проводников находится под воздействием сторонних сил. К примеру, при зарядке аккумуляторов солнечными батареями или другими ЭДС, также в генераторах с обмотками возбуждения, если их дифференцировать.

Измерительный мост
Материалы проводников, к которым применяется закон Ома, названы оммическими или линейными проводниками. Те, у которых сопротивление имеет функциональную зависимость от интенсивности тока, – нелинейными. Так могут вести себя металлы при крайне низких или высоких температурах.
Видео
§17.5. Закон Ома для однородного участка цепи (I-я форма интегрального закона Ома)
Однородным называется участок, на котором отсутствуют источники ЭДС. Электрическая схема участка выглядит так:
 Рис.17.5
Рис.17.5
На однородном участке на носитель действуют только сила сопротивления и электростатическая сила в качестве движущей. Единственной неотъемлемой характеристикой однородного участка является сопротивление R. Закон Ома для такого участка легко получается из выражения для неоднородного участка с помощью обнуления ЭДС:
 или
или 
Словесная формулировка будет звучать так:
на однородном участке цепи постоянного тока напряжение равно падению напряжения.
17.5.1. Последовательное соединение сопротивлений
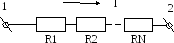 Рис.17.6
Рис.17.6
Очевидно, что через все сопротивления течёт один и тот же ток. Проинтегрируем закон Ома для элементарного участка по всему (от клеммы 1 до клеммы 2) однородному участку:
 .
.
Падение напряжения всего однородного участка раскладывается на сумму падений напряжения на каждом отдельном сопротивлении:

 .
.
Напряжение на всем участке:

Итак, при последовательном соединении ток через все сопротивления течёт один и тот же, напряжение на всём участке равно сумме напряжений на отдельных сопротивлениях, общее сопротивление участка равно сумме отдельных сопротивлений.
17.5.2. Параллельное соединение сопротивлений
 Рис.17.7
Рис.17.7
Очевидно, что общий ток равен сумме токов через каждое сопротивление:
 ,
,
а напряжение на
всех сопротивлениях одинаковы и равны  . Тогда
. Тогда


Итак, при параллельном соединении напряжение на всех сопротивлениях одно и то же, ток на всём участке равен сумме токов на отдельных сопротивлениях, общее обратное сопротивление участка равно сумме отдельных обратных сопротивлений
17.5.3. Мостиковое соединение
Аналогично соединениям (батареям) конденсаторов резисторы (сопротивления) можно соединять не только в последовательно-параллельные схемы, но и в мостиковые, которые в общем случае невозможно свести ни последовательным, ни к параллельным соединениям.
 Рис.17.8
Рис.17.8
В общем случае расчёт токов, текущих по участкам отдельных сопротивлений рассчитывается по законам Кирхгофа (далее), но при выполнении условия уравновешенности мостика

через резистор R0 ток не течёт, и его с одинаковым успехом можно заменить на короткое замыкание, сводя мостик к глобально последовательной схеме, или игнорировать, сводя схему к глобально параллельной.
§17.6. Закон Ома для простого контура (III-я форма интегрального закона Ома)
Простым контуром называется контур, состоящий из неоднородного участка (источник), замкнутого однородным участком (нагрузка):
 Рис.17.9
Рис.17.9
Проинтегрируем закон Ома для элементарного участка по всему контуру в направлении ЭДС:

Интеграл сопротивления распадается на два интеграла: по участку источника (внутренний участок контура) и по участку нагрузки (внешний участок контура).
 .
.
Интеграл напряжения по замкнутому контуру равен 0:
 .
.
Интеграл ЭДС по контуру равен ЭДС источника. В результате получаем:
 .
.
Отсюда видно, что ток в простом контуре течёт всегда по направлению ЭДС.
Законы Ома для участка цепи
Закон Ома в интегральной форме
Немецкий физик Георг Ом в 1826 году экспериментально установил, что сила тока, протекающего по металлическому проводнику прямо пропорциональна разности потенциалов (напряжению) на концах проводника:
I=(1–2) =U. (6.8)
Коэффициент пропорциональности,
связывающий силу тока в проводник и
напряжение — ,
называется электрической проводимостью.
Величина, обратная проводимости —
электрическое сопротивление проводника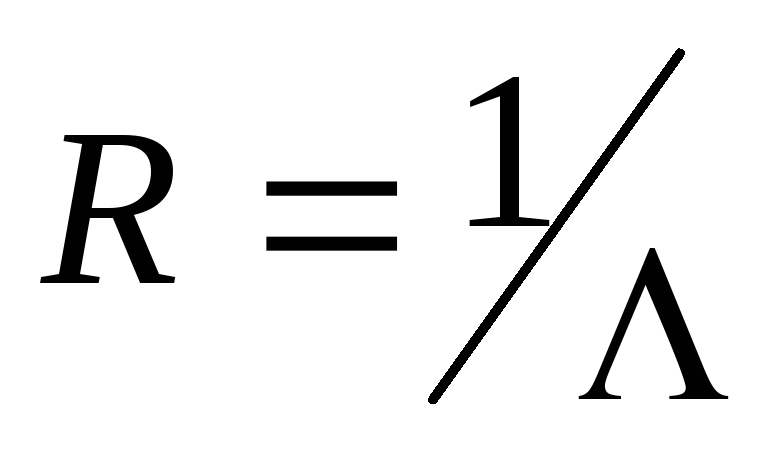 .
Сопротивление зависит от материала
проводника, его формы, размеров и
состояния. Например, сопротивление
цилиндрического проводника (проволоки):
.
Сопротивление зависит от материала
проводника, его формы, размеров и
состояния. Например, сопротивление
цилиндрического проводника (проволоки):
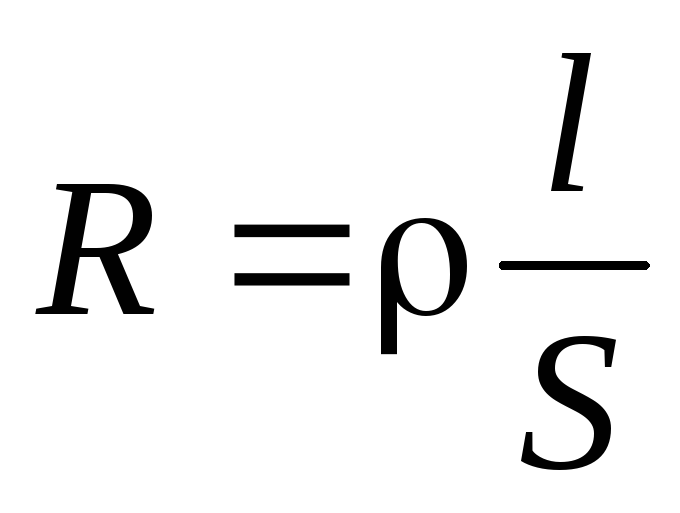 . (6.9)
. (6.9)
Здесь: — удельное сопротивление вещества, из которого сделан проводник;
lиS— длина и площадь поперечного сечения проводника.
Сопротивление измеряется в омах. 1 Ом — это сопротивление такого проводника, в котором течёт ток I= 1 А при напряженииU= 1 В:
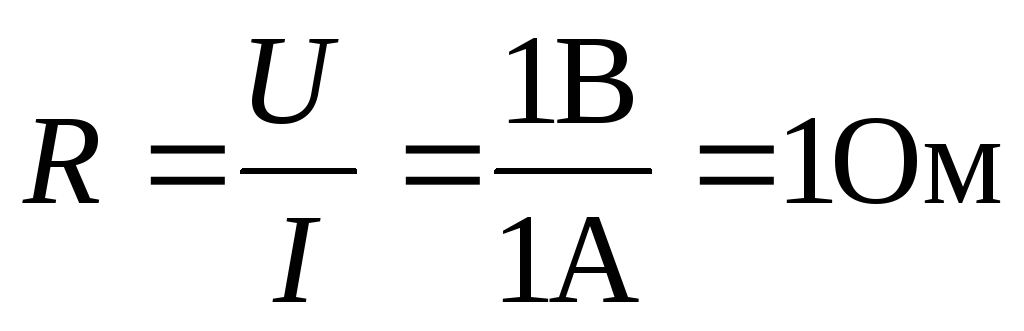 .
.
Удельное сопротивление в системе СИ измеряется в Омм:
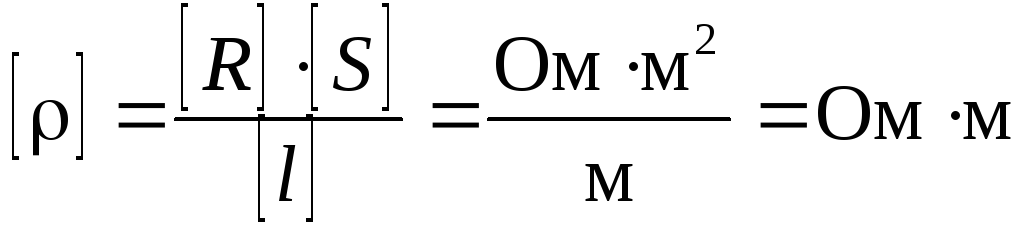 .
.
Удельное сопротивление вещества зависит от температуры. В не слишком широком диапазоне температур удельное сопротивление многих проводников является линейной функцией температуры:
=0(1 +t). (6.10)
Здесь: 0— удельное электрическое сопротивление вещества при 0С;
— температурный коэффициент сопротивления.
Для всех чистых металлов =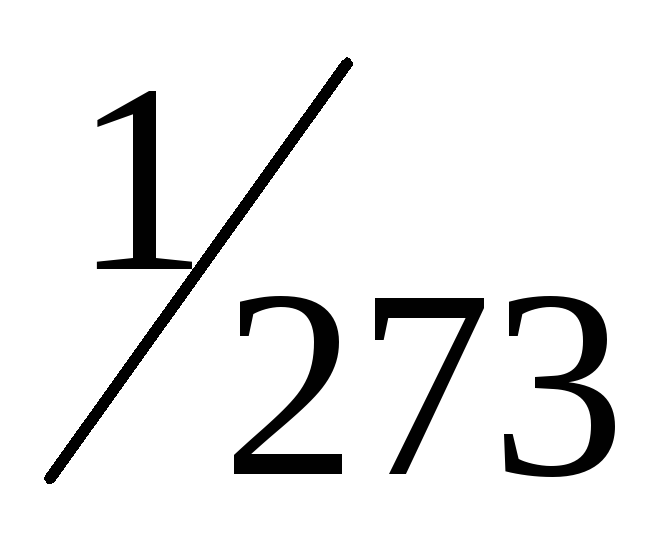 0.037, то есть
температурный коэффициент их удельного
сопротивления близок к температурному
коэффициенту расширения идеальных
газов. Температурный коэффициент
сопротивления проводниковIрода (металлов)I> 0, аIIрода (электролитов)II< 0. Это означает, что с понижением
температуры удельное сопротивление
металлов уменьшается, а электролитов
— растёт.
0.037, то есть
температурный коэффициент их удельного
сопротивления близок к температурному
коэффициенту расширения идеальных
газов. Температурный коэффициент
сопротивления проводниковIрода (металлов)I> 0, аIIрода (электролитов)II< 0. Это означает, что с понижением
температуры удельное сопротивление
металлов уменьшается, а электролитов
— растёт.
При температурах близких к абсолютному нулю (0.2 20 К) сопротивление многих металлов и их сплавов скачком уменьшается до нуля. Это состояние вещества называется сверхпроводящим. Впервые явление сверхпроводимости было обнаружено для ртути в 1911 году голландским физиком Камерлинг-Оннесом.
Не так давно обнаружено сверхпроводящее состояние ряда керамических материалов, которое наступает при достаточно высоких температурах ~100 К («высокотемпературная сверхпроводимость»).
Рассмотренный закон пропорциональности тока в проводнике и напряжения:
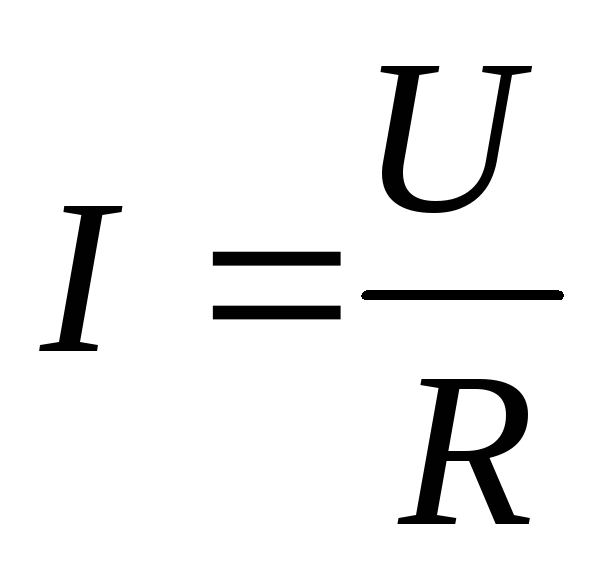 (6.11)
(6.11)
называется законом Ома в интегральной форме. Он позволяет вычислить ток, текущий в цилиндрических проводниках. Но как быть, если электрический ток течёт, например, в электропроводящей среде, заполняющей пространство между обкладками сферического или цилиндрического конденсатора? В подобных случаях на помощь приходит другой закон Ома, к изучению которого мы и приступаем.
Закон Ома в дифференциальной форме
Представим себе электрический ток не в привычном для нас проводнике, а однородной изотропной проводящей среде. В своём направленном движении носители заряда перемещаются по траекториям, которые называются «линии тока». Выделим в среде небольшую поверхность S. Линии тока, коснувшиеся границы этой поверхности, в дальнейшем вырезают в пространстве «трубку тока» (рис. 6.4.). Особенность этой трубки состоит в том, что заряженные частицы, движущиеся внутри трубки тока, не пересекают её боковую поверхность, то есть они никогда не покидают свою трубку тока.
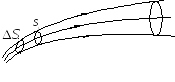
Рис. 6.4.
Выделим в трубке тока два эквипотенциальных сечения S1иS2, отстоящие друг от друга на расстоянииl(рис. 6.5.). Потенциалы этих сечений1и2=1+. Для выделенного элемента трубки тока запишем закон Ома (6.11):
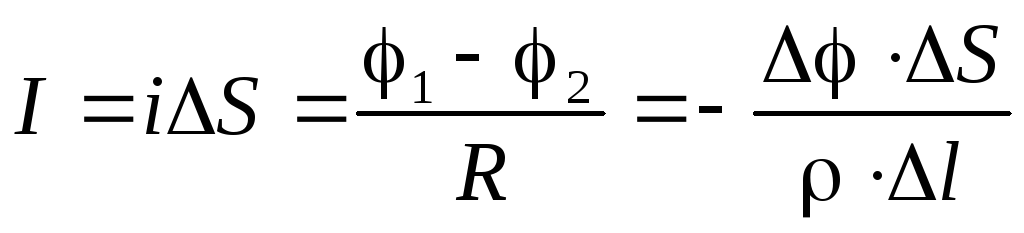 .
.
Рис. 6.5.
Сократив Sи введя удельную электропроводимость=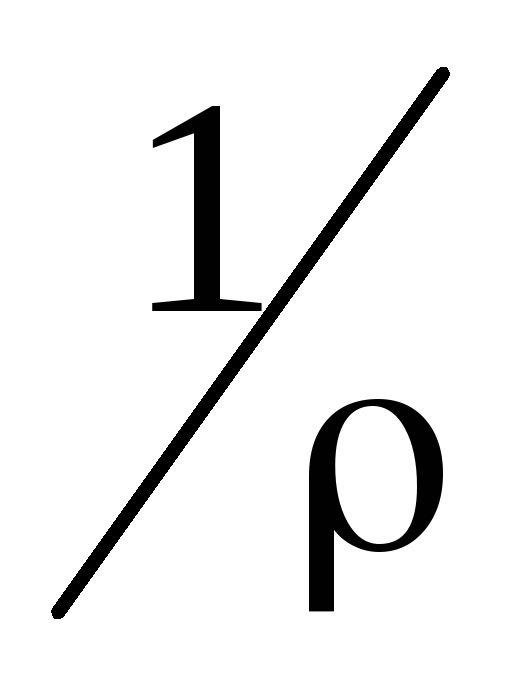 ,
получим:
,
получим:
 .
.
Этот результат становится совсем точным, если перейти к пределу, устремив lк нулю. ТогдаS=S1=S2, так как трубка становится цилиндрической. Кроме того:
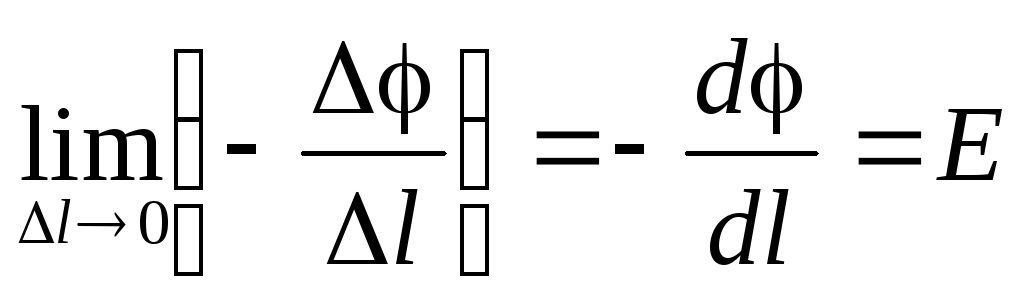 . (6.12)
. (6.12)
Учитывая этот результат, плотность тока запишем так:
i=E,
или в векторном виде:
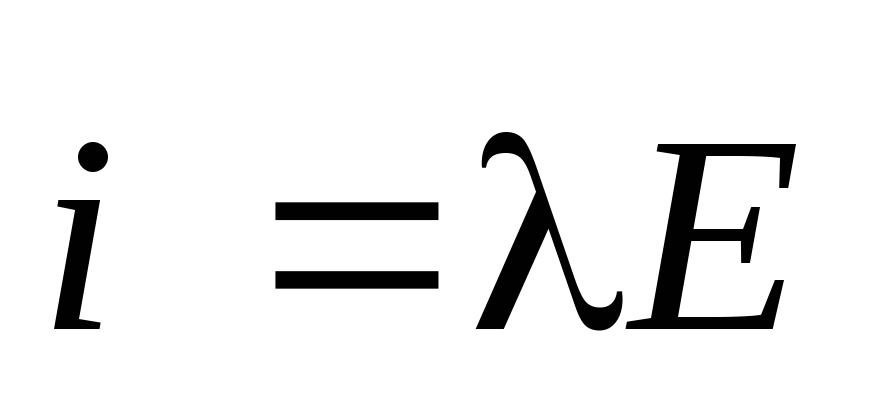 . (6.13)
. (6.13)
Уравнение (6.13) — математическая записьзакона Ома в дифференциальной форме.
В этом законе связываются две «локальные»
характеристики тока: плотность тока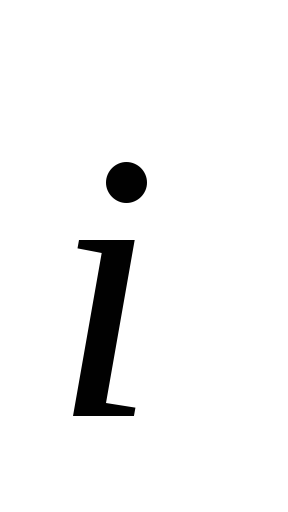 в любойточкепространства и
напряжённость электрического поля
в любойточкепространства и
напряжённость электрического поля в той же точке. В соответствии с этим
законом, плотность электрического
тока прямо пропорциональна напряжённости
поля в рассматриваемой точке пространства.
в той же точке. В соответствии с этим
законом, плотность электрического
тока прямо пропорциональна напряжённости
поля в рассматриваемой точке пространства.
В приведённых рассуждениях есть момент, который не может не настораживать: в законе (6.13) Е— напряжённость электрического поля в проводящей среде с током. А для вычисления этой характеристики мы воспользовались связью напряжённости и потенциала электростатического поля в вакууме (6.12). Однако можно показать, что напряжённость электрического поля внутри однородной проводящей среды совпадает с электростатическим полем, которое существует в вакууме, если обеспечивается то же пространственное распределение потенциала, что и в проводящей среде при наличии тока (см., например, [2]).
Теперь на примере расчёта тока утечки в сферическом конденсаторе покажем, как используется закон Ома в дифференциальной форме для решения вполне реальных задач.
Вопрос 5. Законы Ома в интегральной и дифференциальной форме
Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС)
|
| (7.6.1) |
|
Для однородного линейного проводника выразим R через ρ:
|
| (7.6.2) |
|
ρ – удельное объемное сопротивление; [ρ] = [Ом·м].
Найдем
связь между 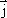 и
и  в
бесконечно малом объеме проводника
– закон
Ома в дифференциальной форме.
в
бесконечно малом объеме проводника
– закон
Ома в дифференциальной форме.
В
изотропном проводнике (в данном случае
с постоянным сопротивлением) носители
зарядов движутся в направлении действия
силы, т.е. вектор плотности тока 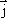 и
вектор напряженности поля коллинеарны
(рис. 7.6).
и
вектор напряженности поля коллинеарны
(рис. 7.6).
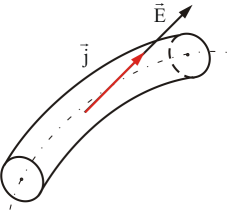
Рис. 7.6
Исходя из закона Ома (7.6.1), имеем:
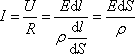
А
мы знаем, что 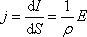 или
или 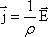 .
Отсюда можно записать
.
Отсюда можно записать
|
| (7.6.3) |
|
это запись закона Ома в дифференциальной форме.
Здесь 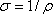 – удельная
электропроводность.
– удельная
электропроводность.
Размерность
σ – [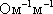 ].
].
Плотность
тока можно выразить через заряд
электрона е,
количество зарядов n и
дрейфовую скорость 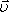 :
:
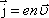 .
.
Обозначим 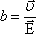 ,
тогда
,
тогда 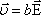 ;
;
|
| (7.6.4) |
|
Теперь,
если удельную электропроводность σ
выразить через е, n и b: 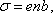 то
вновь получим выражение закона
Ома в дифференциальной форме:
то
вновь получим выражение закона
Ома в дифференциальной форме:
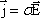 .
.
Закон Ома для однородного участка цепи — КиберПедия
Закон, устанавливающий связь между силой тока в проводнике и разностью потенциалов (напряжением) на его концах, был открыт Г. Омом опытным путем в 1826 году.
Закон Ома формулируется следующим образом.
Сила тока, текущего по однородному участку цепи, прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника,
Эту формулу еще называют законом Ома в интегральной форме. Напомним, что в случае однородного участка цепи напряжение равно разности потенциалов
Сопротивление проводника зависит от материала и его геометрических размеров, т. е.
где l — длина проводника, S — площадь его поперечного сечения, ρ — удельное сопротивление проводника, которое зависит от рода вещества, а также от его состояния (в первую очередь, температуры). Например, при температуре 20oС удельное сопротивление меди , а у фарфора .
Единицей сопротивления служит ом (Ом), .
Закон Ома справедлив для широкого класса материалов: металлов, угля, электролитов. Его широко применяют для расчета различных электрических цепей. Его используют во многих других случаях, например, в технике безопасности. Так, допустимое напряжение определяют, исходя из сопротивления тела человека и допустимого для него значения тока. Смертельным считается ток 100 мА. Наиболее опасный путь его прохождения: правая рука — ноги. Сопротивление тела при влажной коже , при сухой . Рассчитайте самостоятельно допустимое напряжение.
Закон Ома в дифференциальной форме
Закон Ома в дифференциальной форме справедлив для любой точки участка цепи как с постоянным, так и с переменным сечением.
Для однородного участка цепи плотность тока равна
; отсюда: .
Подставим эту формулу, а также формулу для сопротивления (2.26) в закон Ома (2.24)
.
Учтем, что для однородного поля справедлива формула (2.19)
Тогда
Величина, обратная удельному сопротивлению, называется удельной проводимостью, т. е.
В векторной форме формулу (2.27) можно записать следующим образом
Формула (2.28) выражает закон Ома в дифференциальной форме. Плотность тока пропорциональна напряженности электрического поля и имеет одинаковое с ней направление (рис. 2.8).
Рис.2.8
В такой форме закон Ома выражает связь между величинами, относящимися к данной точке, и поэтому применим к неоднородным проводникам.
Объяснение закона Ома
Задача физики — выяснить природу явлений, описываемых физическими законами.
Для объяснения закона Ома (2.28) в начале XIX в. была разработана классическая теория электропроводности металлов. Согласно классическим представлениям, электроны проводимости в металлах образуют так называемый электронный газ. Подобно молекулам идеального газа электроны в металле участвуют в хаотическом движении. При приложении электрического поля на хаотическое движение электронов накладывается упорядоченное движение. Среда оказывает сопротивление движению зарядов в определенном направлении. Поэтому в однородном веществе при постоянной напряженности поля заряды движутся с постоянной скоростью , пропорциональной напряженности поля
где μ — подвижность носителей, которая зависит от природы носителей, плотности и состояния вещества.
Подставим формулу (2.29) в (2.23) и получим закон Ома в дифференциальной форме
Основанная на этих представлениях классическая теория электропроводности помогла понять и объяснить ряд физических явлений. Но следует отметить, что некоторые экспериментальные факты (например, сверхпроводимость металлов, зависимость сопротивления от температуры, значение их теплоемкости и др.) можно объяснить только с помощью квантовой теории. Однако, классическая теория электропроводности не утратила своего значения и в наши дни, так как во многих случаях (например, при малой концентрации электронов проводимости и высокой температуре, как это имеет место для полупроводников) она дает правильные результаты.


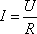
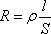 ,
,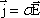 ,
,