7.7. Электрический ток через электролиты. Закон Ома для электролитов

Растворы солей, кислот и щелочей в воде и в других растворителях хорошо проводят электрический ток. Это связано с тем, что молекулы растворенного вещества диссоциируют, т.е. распадаются на положительные и отрицательные ионы. Если при растворении не происходит диссоциации молекул, то раствор не является проводником электрического тока.

Определим плотность тока j в жидкости, т.е. заряд, переносимый за одну секунду через площадку единичной площади, перпендикулярную направлению движения ионов (рис. 7.17). Так как перенос зарядов осуществляется ионами обоих знаков, то

, (7.52)

где q₊ и q_— – заряды положительных и отрицательных ионов;

n₊ и n_— – концентрации этих ионов;

v₊ и v_— – средние скорости упорядоченного движения этих ионов.

Учитывая, что раствор в целом нейтрален, можно записать

, (7.53)

где q – заряд иона любого знака;

n – концентрация ионов этого же знака.

Величина заряда иона обусловлена потерей или сохранением валентных электронов при диссоциации молекулы. Обозначив валентность иона через z, для заряда иона будем иметь

, (7.54)

где e – абсолютное значение заряда электрона.

Учитывая формулы (7.53) и (7.54), получим

. (7.55)

В электрическом поле на ионы действуют две силы: сила, действующая со стороны электрического поля, и сила внутреннего трения.

Сила со стороны электрического поля

, (7.56)

где E – величина напряженности электрического поля.

Сила внутреннего трения, если предположить, что ион имеет форму шара с радиусом r, то согласно закону Стокса

, (7. 57)

где  – коэффициент вязкости жидкости.

При установившемся движении (которое наступает практически одновременно с появлением электрического поля) F_E = F_тр, следовательно имеем

,

откуда

, (7.58)

где – подвижность иона.

Таким образом, подвижность иона b равна отношению скорости движения иона к напряженности электрического поля:

. (7.59)

Как видно из формулы (7.58), подвижность ионов возрастает с повышением температуры (за счет уменьшения вязкости жидкости). Скорость движения ионов пропорциональна напряженности электрического поля.

Учитывая соотношение (7.58) для плотности электрического тока, получим

(7.60)

или

, (7.61)

где — удельная проводимость электролита.

Выражения (7. 60) и (7.61) представляют собой закон Ома в дифференциальной форме для электролитов.

Из формулы (7.60) для удельного сопротивления электролита имеем

. 7.62)

Так как с повышением температуры подвижность и концентрация ионов возрастают, то, согласно формуле (7.62), с повышением температуры сопротивление электролитов уменьшается.

Концентрация ионов зависит от степени диссоциации, характеризующейся коэффициентом диссоциации . Коэффициент диссоциации определяется отношением концентрации n ионов к концентрации n

o молекул растворенного вещества:

. (7.63)

Откуда

. (7.64)

Концентрация недиссоциированных молекул

. (7.65)

В растворе одновременно и непрерывно происходит как диссоциация молекул, так и молизация ионов, т.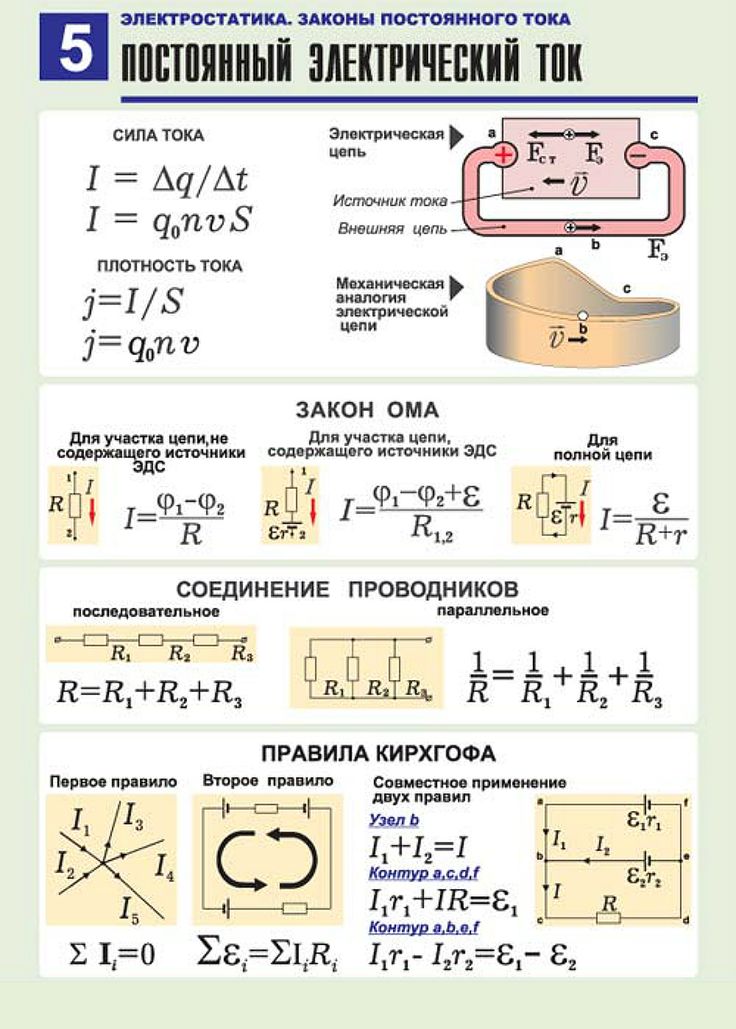 е. соединение ионов в нейтральные молекулы. В условиях равновесия интенсивности процессов диссоциации молекул и молезации ионов, изменяющих состав раствора в противоположных направлениях, равны. В процессе диссоциации молекул скорость изменения концентрации ионов каждого знака пропорциональна концентрацииn

‘ недиссоциированных молекул:

, (7.66)

где  – коэффициент пропорциональности.

Скорость изменения концентрации недиссоциированных молекул в результате ионизации ионов пропорциональна произведению концентраций положительных и отрицательных ионов:

, (7.67)

где  — коэффициент пропорциональности.

При равновесии , поэтому с учетом (7.66) и (7.67) можно получить формулу, связывающую коэффициент диссоциации с концентрацией растворенного вещества:

. (7.68)

Очевидно, что коэффициент диссоциации зависит от концентрации растворенного вещества. При очень слабой концентрации (n_o  0) равенство (7.68) дает

. (7.69)

Если <<1, то из (7.68) получаем

. (7.70)

Таким образом, коэффициент диссоциации уменьшается при увеличении концентрации растворенного вещества.

С учетом уравнение для плотности тока в электролитах можно записать так:

. (7.71)

Подвижность ионов и коэффициент диссоциации в широких пределах изменения напряженности электрического поля не зависят от напряженности электрического поля E.

При небольшой концентрации раствора коэффициент диссоциации и сумма подвижностей ионов (b⁺ + b^—) приблизительно постоянны. Следовательно, при малой концентрации раствора электропроводимость пропорциональна концентрации. При увеличении концентрации зависимость электропроводности от концентрации значительно усложняется.

Надо отметить, что величина тока через столб электролита в любом его сечении одна и та же, хотя на первый взгляд она должна быть разной.

Представим, что имеется три сечения столба электролита 1, 2, 3 (рис. 7.18).

Через сечение 1 проходят только отрицательные ионы, через сечение 3 – только положительные ионы, а через сечение 2 – и те и другие. Поэтому создается впечатление, что ток через сечение 2 больше, чем через сечения 1 и 3. Это неверно, ток через любое сечение должен быть одним и тем же, иначе между сечениями будет накапливаться заряд. Выполнение закона сохранения заряда в электролитах обусловлено тем, что скорость упорядоченного движения и концентрация ионов разных знаков непостоянны вдоль выбранной оси ОХ.

В центральной области столба электролита концентрации положительных и отрицательных ионов примерно равны, следовательно, объемная плотность заряда близка к нулю. У положительного электрода (анода) скапливаются отрицательные ионы. Объемная плотность заряда отрицательна. У отрицательного электрода (катода) имеется положительный объемный заряд.

На рисунке 7.19 показано изменение потенциала между электродами (при заданной разности потенциалов между ними), вызванное объемными зарядами. Сплошная линия соответствует изменению потенциала в вакууме, пунктирная – в том же пространстве, заполненном электролитом. На рисунке 7.20 для сравнения показано изменение потенциала в межэлектродном промежутке, в который введены две сетки. Левая сетка заряжена отрицательно по отношению к аноду и имитирует отрицательный объемный заряд. Правая сетка заряжена положительно по отношению к катоду и имитирует положительный объемный заряд. Сравнение кривых изменения потенциала в межэлектродном пространстве показывает, что изменение потенциала в первом и втором случаях почти одинаково.

Постоянство величины электрического тока в электролитах обусловлено тем, что напряженность электрического тока, а следовательно, и скорость упорядоченного движения ионов в разных точках объема диэлектрика разные.

В центральной области они меньше, чем в других областях.

Закон Фарадея для электролиза: формулы

Электрический ток, проходящий через растворы электролитов, способствует разложению веществ и дает возможность получать химически чистые материалы. Данный процесс получил наименование электролиза, нашедшего широкое применение в промышленном производстве. Физические преобразования проводников, находящихся в жидкости, объясняет закон Фарадея для электролиза, на основании которого анод выполняет функцию положительного электрода, а катод – отрицательного. С помощью него осуществляется очистка металлов от примесей и выполняется нанесение тонких покрытий, защищающих металлические поверхности.

Содержание

Суть процесса электролиза

Электролизом называются процессы окислительно-восстановительных реакций, протекающие под принудительным воздействием электрического тока. Для его выполнения используется специальная емкость с электролитическим раствором, куда погружаются металлические штыри, соединенные с наружным источником питания.

Электрод, соединенный с полюсом отрицательного значения источника тока, считается катодом. Именно в данном месте частицы электролита восстанавливаются. Другой электрод подключается к плюсовому полюсу и носит название анода. На этом участке вещество электрода или частицы электролита окисляются. Химические реакции на этом участке происходят по-разному, в зависимости от материала анода и состава электролитического раствора. Поэтому, как утверждает химия, электроды по отношению к электролиту могут быть инертными или растворимыми.

К категории инертных относятся аноды, изготовленные из материала, не окисляющегося во время электролиза. В качестве примера можно привести графитовые или платиновые электроды. Растворимыми являются практически все остальные виды металлических анодов, подверженных окислению в ходе электролитической реакции.

Электролитами чаще всего служат различные виды растворов или расплавов, внутри которых происходит хаотичное движение заряженных частиц – ионов. Когда на них воздействует электрический ток, они начинают двигаться в определенном направлении: катионы – к катоду, анионы – к аноду. Попадая на электроды, они теряют свои заряды и оседают на них.

Таким образом, на катоде и аноде происходит накопление так называемых суммарных продуктов, состоящих из электрически нейтральных веществ. Весь процесс электролиза выполняется под напряжением, подаваемым на электроды. Данное напряжение U_эл-за является типичным примером разности потенциалов, требующейся для обеспечения нормального течения электролитических реакций. Чисто теоретически это напряжение принимает вид формулы: U_эл-за = Е_а – Е_к, в которой Е_а и Е_к являются потенциалами химических реакций, происходящих на аноде и катоде.

Существует определенная связь между количеством электричества, протекавшего через раствор, и количеством вещества, выделенного в период электролитической реакции. Данное явление было описано английским физиком Фарадеем и оформлено в виде двух законов.

Первый закон Фарадея

Данный закон был выведен ученым экспериментальным путем. Он определяет пропорциональную зависимость между массой вещества, образующегося на электроде и зарядом, проходящим через электролитический раствор.

Эту пропорцию наглядно отображает формула m=k х Q=k х I х t, где k является коэффициентом пропорциональности или электрохимическим эквивалентом, Q – заряд, прошедший через электролит, t – время прохождения заряда, m – масса вещества, образовавшегося на электроде в результате реакции.

Первый закон Фарадея служит для определения количества первичных продуктов, образовавшихся в процессе электролиза на электродах. Масса этого вещества составляет суммарную массу всех ионов, попавших на электрод. Это подтверждается формулой m=m0 х N = m0 х Qq0 = m0q0 х I х t, в которой m0 и q0 соответственно являются массой и зарядом единичного иона. N=Qq0 – определяет количество ионов, попавших на электрод за время прохождения заряда Q через раствор электролита.

Следовательно, величина электрохимического эквивалента k представляет собой соотношение массы иона m0 используемого вещества и заряда q0 этого иона. Известно, что величина заряда иона составляет произведение валентности n этого вещества и элементарного заряда е, то есть, q0 = n х e. Исходя из этого, электрохимический эквивалент k будет выглядеть следующим образом: k = m0q0 = m0 х NAn х e х NA = 1F х μn. В этой формуле NA является постоянной Авогадро, μ – молярной массой данного вещества. F = e х NA является постоянной Фарадея и составляет 96485 Кл/моль.

Числовое значение данной величины равняется заряду, который должен быть пропущен через раствор электролита, для того чтобы на электроде выделился 1 моль вещества с одинаковой валентностью. Рассматриваемый закон Фарадея для электролиза примет вид еще одной формулы: m = 1F х μn х I х t.

Второй закон Фарадея

Следующий закон ученого Фарадея описывает, как электрохимический эквивалент будет зависеть от атомной массы вещества и его валентности. У этого коэффициента будет прямая пропорциональная зависимость с атомным весом и обратно пропорциональная – с валентностью вещества. С введением данной величины, второй закон Фарадея формулируется как пропорция электрохимических эквивалентов вещества и собственных химических эквивалентов этих веществ.

Если значения электрохимических эквивалентов взять за k1, k2, k3…kn, а химические эквиваленты принять за х1, х2, х3…xn, то k1/x1 = k2/x2 = k3/x3…kn/xn. Данное соотношение является постоянной величиной, одинаковой для любых используемых веществ: с = k/x и составляет 0,01036 мг-экв/к. Именно такое количество вещества в миллиграмм-эквивалентах выделяется на электродах за период прохождения в электролите электрического заряда, равного одному кулону.

Следовательно, второй закон Фарадея можно представить в виде формулы: k = cx. Если данной выражение использовать вместе с первым законом Фарадея, то в результате получится следующее выражение: m = kq = cxq = cxlt. Здесь категория с представляет собой универсальную постоянную, в размере 0,00001036 г-экв/к. Подобная формулировка дает возможность понять, что одни и те же токи, пропущенные через одинаковый промежуток времени в двух различных электролитах, выделят из них вещества с соблюдением рассмотренного химического эквивалента.

Поскольку x = A/n, то масса выделяемого вещества будет выглядеть как m = cA/nlt, с соблюдением прямой пропорции с атомным весом и обратной пропорции с валентностью.

4.2: Сопротивление и закон Ома

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

5432

• Джереми Татум
• Университет Виктории

Когда на электродах электролитической ячейки поддерживается разность потенциалов, через электролит протекает ток. Этот ток переносится положительными ионами, движущимися от положительного электрода к отрицательному электроду, и одновременно отрицательными ионами, движущимися от отрицательного электрода к положительному электроду. Обычное направление потока электричества — это направление, в котором движутся положительные заряды. То есть электричество течет от положительного электрода к отрицательному. Таким образом, положительные ионы движутся в том же направлении, что и обычное направление потока электричества, а отрицательные ионы движутся в противоположном направлении.

Когда ток течет в металле , ток переносится исключительно с помощью отрицательно заряженных электронов, и поэтому ток переносится исключительно с помощью частиц, которые движутся в направлении, противоположном обычному потоку электричества. Таким образом, «электричество» течет из точки с высоким потенциалом в точку с более низким потенциалом; электроны перемещаются из точки с низким потенциалом в точку с более высоким потенциалом.

Когда на резистор подается разность потенциалов \(V\), отношение разности потенциалов на резисторе к току \(I\), протекающему через него, называется сопротивление , \(R\), резистора. Таким образом,

\[V = ИК.\метка{4.2.1}\]

Это уравнение, определяющее сопротивление, на первый взгляд кажется, что ток через резистор пропорционален разности потенциалов на нем , и это закон Ома. Уравнение \ref{4.2.1}, однако, подразумевает простую пропорциональность между \(V\) и \(I\), только если \(R\) постоянна и не зависит от \(I\) или \(V \). На практике, когда через резистор протекает ток, резистор нагревается, а его сопротивление увеличивается — и тогда \(V\) и \(I\) перестают быть линейно пропорциональными друг другу. Таким образом, закон Ома пришлось бы сформулировать в такой форме, что ток через резистор пропорционален разности потенциалов на нем при условии, что температура поддерживается постоянной . Тем не менее, существуют некоторые вещества (и различные электронные устройства), в которых сопротивление не зависит от приложенной разности потенциалов даже при постоянной температуре. Таким образом, лучше рассматривать уравнение \ref{4.2.1} как определение сопротивления, а не как фундаментальный закон, признавая при этом, что оно является хорошим описанием поведения большинства реальных веществ в самых разных условиях, пока так как температура поддерживается постоянной.

Определение: сопротивление и проводимость

Если ток в один ампер протекает через резистор, когда на нем есть разность потенциалов в один вольт, сопротивление составляет один Ом (\(\Омега\)). (Однако, хотя это определение может показаться ясным, вспомните из главы 1, что мы еще не определили точно, что мы подразумеваем под ампером или вольтом, так что внезапно значение «ом» становится гораздо менее ясным! Я обещаю определение «усилителя» в следующей главе, а пока прошу вашего терпения.) 9{-2}.\]

Обратная величина сопротивления равна проводимости , \(G\) . Таким образом, \(I = GV\). Общепринятой неформальной практикой является выражение проводимости в «мхо», где «мхо» — это ом ^-1 . Однако официальной единицей проводимости в системе СИ является сименс (См), который представляет собой то же самое, что и «мхо», а именно один AV ^-1 .

Сопротивление резистора пропорционально его длине \(l\) и обратно пропорционально площади его поперечного сечения А :

\[R = \dfrac{\rho l}{A} \label{4.2.2}\]

Константой пропорциональности \(\rho\) называется удельное сопротивление материала, из которого изготовлен резистор. Его размеры составляют ML ³ T ^-1 Q ^-2 , а единицей СИ является ом-метр или \(\Omega\) m.

Обратная величина удельного сопротивления равна проводимости , \(\сигма\). Его размеры составляют M ^-1 L ^-3 TQ ² , а его единица СИ — сименс на метр, См м ^-1 .

Для тех, кто любит собирать непонятные единицы, есть забавная единица, с которой я однажды столкнулся, а именно единица поверхностного сопротивления. Один касается сопротивления тонкого листа проводящего материала, такого как, например, тонкая металлическая пленка, нанесенная на стекло. Сопротивление некоторой прямоугольной области этого прямоугольника пропорционально длине l прямоугольника и обратно пропорционально его ширине w :

\[R = \dfrac{\rho l}{w}\номер\]

Сопротивление, таким образом, зависит от отношения \(l/w\) – то есть от формы прямоугольника, а не от его размера. Таким образом, сопротивление прямоугольника размером 2 мм \(\times\) 3 мм такое же, как сопротивление прямоугольника размером 2 м \(\times\) 3 м, но сильно отличается от сопротивления прямоугольника размером 3 мм \(\times\) прямоугольник 2 мм. Удельное поверхностное сопротивление определяется как сопротивление прямоугольника единичной длины и единичной ширины (т. е. квадрата) — и не имеет значения, какого размера квадрат. Таким образом, единицами поверхностного сопротивления являются омы на квадрат. (Конец предложения!)

Что касается удельного сопротивления, то установлено, что вещества можно разделить на металлы , непроводники (изоляторы) и полупроводники . Металлы имеют довольно низкое удельное сопротивление, порядка 10 ^-8 \(\Омега\) м. Например:

Серебро: 1,6 \(\раз\) 10 ^-8 \(\Омега\) м

Медь: 1,7 \(\раз\) 10 ^-8

Алюминий: 2,8 \(\раз\) 10 ^-8

Вольфрам: 5,5 \(\раз\) 10 ^-8

Железо: 10 \(\раз\) 10 ^-8

Непроводящие материалы обычно имеют удельное сопротивление порядка от 10 ¹⁴ до 10 ¹⁶ \(\Омега\) м или более. То есть для большинства практических целей и условий они вообще не проводят никакого легко измеримого электричества.

Полупроводники имеют промежуточное сопротивление, например

Углерод: 1500 \(\раз\) 10 ^-8 \(\Омега\) м

Германий: 4,5 \(\раз\) 10 ^-1

Кремний 6.4 \(\раз\) 10 ⁺²

Существует еще один способ, помимо уравнения 4.2.1, который обычно используется для выражения закона Ома. См. рисунок IV.1.

\(\text{РИСУНОК IV.1}\)

Имеем металлический стержень длиной \(l\), площадью поперечного сечения А , электропроводностью \(\сигма\), поэтому его сопротивление л /(\(\сигма\) А ). Зажимаем его между двумя точками, имеющими разность потенциалов В между ними, и, следовательно, величина электрического поля в металле равна \(Е = V/l\). Таким образом, уравнение 4.2.1 (закон Ома) принимает вид \(El = Il/(\sigma A)\). Теперь введите \(J=I/A\) как плотность тока (ампер на квадратный метр). Закон Ома принимает вид \(J=\sigma E\). Обычно это записывается в векторной форме, поскольку ток и поле являются векторами, поэтому закон Ома записывается как

.

\[\textbf{J}=\sigma \textbf{E}\label{4.2.3}\]

---

Эта страница под названием 4.2: Сопротивление и закон Ома распространяется под лицензией CC BY-NC 4.0 и была создана, изменена и/или курирована Джереми Татумом посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Джереми Татум

   Лицензия

   CC BY-NC

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. Закон Ома
   2. источник@http://orca. phys.uvic.ca/~tatum/elmag.html

Когда к электролиту приложена разность потенциалов, закон Ома выполняется при A) нулевом потенциалеB) очень низком потенциалеC) отрицательном потенциалеD) высоком потенциале

Дата последнего обновления: 19 февраля 2023 г.

•

Просмотров сегодня: 4.36k

Ответ

Проверено

248.1k+ просмотров

Подсказка: Для описания электрических цепей используется закон Ома. Согласно закону Ома, ток, протекающий по проводнику между любыми двумя точками, прямо пропорционален напряжению, приложенному к двум точкам, и обратно пропорционален сопротивлению, приложенному к цепи.
Полное пошаговое объяснение:
Шаг I:
Когда на электролит подается напряжение, электролит проводит электричество, и происходит электролиз. В процессе электролиза вещество либо теряет, либо приобретает электроны. Ионы начинают диссоциировать. Это означает, что ионы с положительным зарядом будут двигаться к отрицательному электроду, а ионы с отрицательным зарядом — к положительному электроду.
Этап II:
 При низких напряжениях по мере увеличения напряжения количество проводящих ионов также увеличивается. Это означает, что ток будет возрастать, принимая нелинейную форму. Через некоторое время, когда напряжение достигнет определенного значения, диссоциация ионов больше не будет происходить.
Этап III:
Электролит ведет себя как проводник, так как сильные электролиты являются хорошими проводниками электричества, а слабые электролиты — плохими проводниками электричества и подчиняются закону Ома. Таким образом, при высоких напряжениях электролит подчиняется закону Ома.

$ \Rightarrow $Вариант D — правильный ответ.

Примечание: Важно отметить, что поскольку ток нарастает нелинейно, материал неомический. В случае электролитов закон Ома представляет собой сопротивление электролита.