Три закона Ома
Недавно мы выпустили переиздание книги Фрэнка Вильчека (Frank Wilczek) «Тонкая физика. Масса, эфир и объединение всемирных сил» в мягком переплете. Автор, лауреат Нобелевской премии по физике, излагает современные взгляды на нашу невероятную Вселенную и прогнозирует новый золотой век фундаментальной физической науки. ХХ2 уже публиковали один отрывок из этой замечательной книги, теперь публикуют новый — о том, почему эквивалентные равенства могут поведать нам о разных явлениях.
Из третьей главы. Второй закон Ома
Второй закон Эйнштейна, m = E/c2, поднимает вопрос о том, может ли масса быть понята более глубоко — как энергия. Можем ли мы создать, как выразился Уилер, «массу без массы»?
Когда я ещё только собирался начать преподавать в Принстоне, мой друг и наставник Сэм Трейман позвал меня в свой кабинет. Он хотел поделиться со мной своей мудростью. Сэм вытащил из ящика стола потрёпанное руководство в мягкой обложке и сказал мне: «Во время Второй мировой войны ВМС приходилось в спешке обучать новобранцев налаживанию и использованию радиосвязи.
Многие из этих новобранцев прибывали прямо с ферм, так что быстро ввести их в курс дела было очень трудно. С помощью той великолепной книги командованию военно-морского флота это удалось. Это шедевр педагогики. Особенно первая глава. Взгляни».
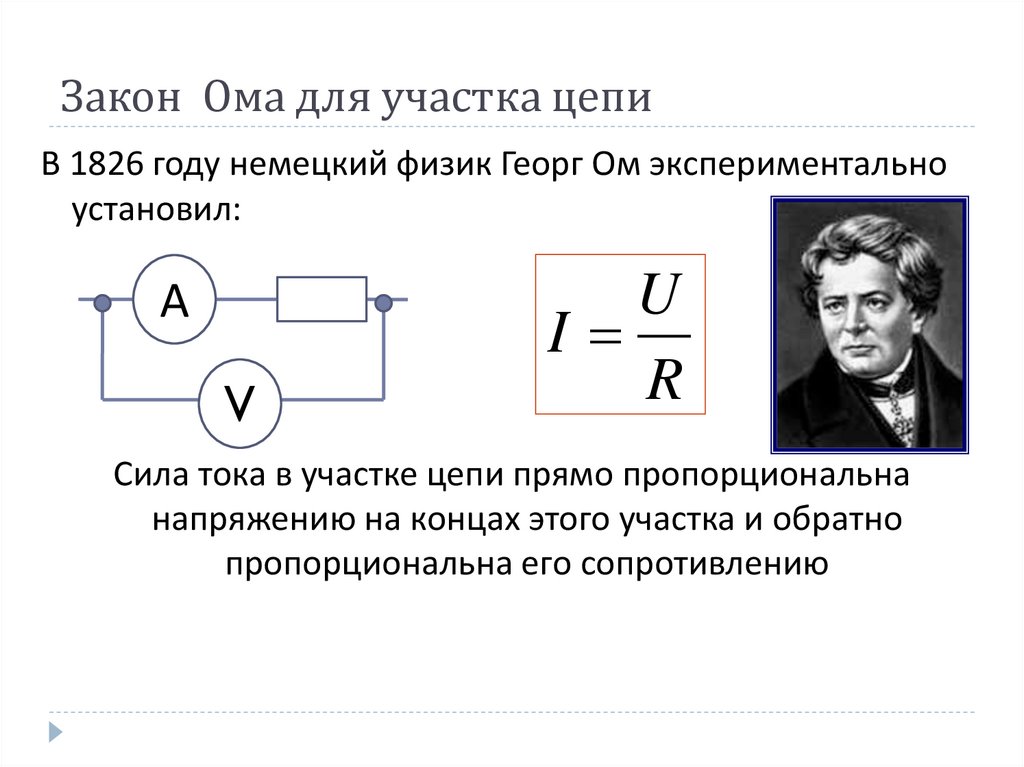
Он вручил мне книгу, открытую на первой главе. Она называлась «Три закона Ома». Я был знаком с одним законом Ома, известным соотношением V = IR, который связывает напряжение (V), силу тока (I) и сопротивление (R) в электрической цепи.
Это оказалось первым законом Ома.
Мне было очень интересно узнать, каковы два других закона Ома. Перевернув несколько хрупких пожелтевших страниц, я обнаружил второй закон Ома: I = V/R. Я предположил, что третий закон Ома формулируется как R = I/V, и оказался прав.
Открывать новые законы легко
Тем, кто знаком с элементарной алгеброй, так очевидно, что эти три закона эквивалентны друг другу, что данная история воспринимается как шутка. Однако в ней заключён глубокий смысл. (Кроме того, в ней есть и неглубокий смысл, который, как мне кажется, Сэм хотел до меня донести.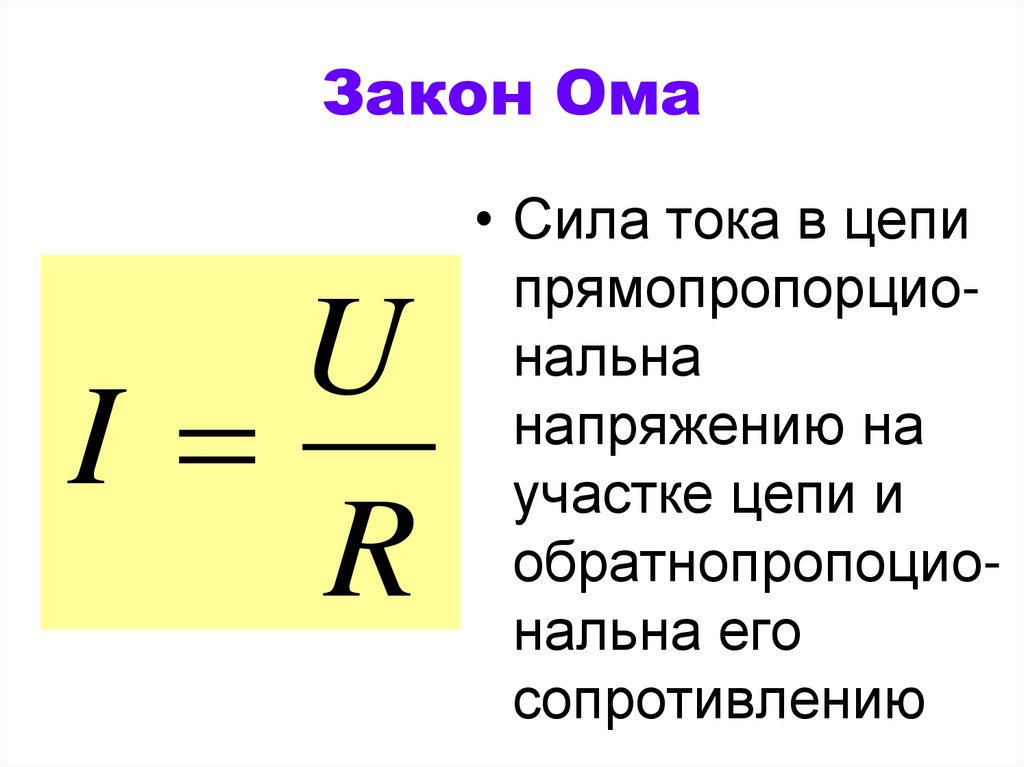
При обучении начинающих вы должны несколько раз сказать одно и то же, но по-разному. Соотношения, которые бесспорны для профессионала, могут не быть таковыми для новичка. Студенты не будут возражать против объяснения очевидного. Очень немногие люди обижаются, когда вы позволяете им почувствовать себя умными.)
Глубокий смысл содержит заявление великого физика-теоретика Поля Дирака. Когда его спросили, как он открывает новые законы природы, Дирак ответил: «Я играю с уравнениями». Суть в том, что различные способы написания одного и того же уравнения могут говорить о совершенно разных вещах, даже если они являются логически эквивалентными.
Второй закон Эйнштейна
Второй закон Эйнштейна формулируется следующим образом:
m = E/c2.
Первый закон Эйнштейна — это, разумеется, E = mc2. Здорово, что первый закон предполагает возможность получения большого количества энергии из небольшого количества массы. Он наводит на мысль о ядерных реакторах и ядерных бомбах.
Второй закон Эйнштейна предполагает нечто совершенно иное.
Он предполагает возможность объяснения того, как масса возникает из энергии.
На самом деле этот закон неправильно называть «вторым».
В оригинальной работе Эйнштейна 1905 года вы не найдёте уравнения E = mc2. Вы встретите уравнение m = E/c2. (Поэтому, возможно, нам следует назвать его нулевым законом Эйнштейна.)
На самом деле в качестве названия этой статьи используется вопрос: «Зависит ли инерция тела от содержащейся в нем энергии?»
Другими словами, может ли некоторое количество массы тела возникать из энергии содержащегося в нем вещества? С самого начала Эйнштейн размышлял о концептуальных основах физики, а не о возможности создания бомб или реакторов.
Понятие энергии играет гораздо более важную роль в современной физике, чем понятие массы. Это проявляется во многих отношениях. Сохраняется именно энергия, а не масса. Именно энергия фигурирует в таких фундаментальных уравнениях, как уравнение Больцмана для статистической механики, уравнения Шрёдингера для квантовой механики и уравнение Эйнштейна для гравитации.
(Я даже не буду пытаться объяснить, что означает предыдущее утверждение, к счастью, суть заключается в самом факте утверждения.)
Таким образом, вопрос Эйнштейна бросает вызов. Если мы сможем объяснить массу в терминах энергии, мы улучшим наше описание мира. В этом случае в нашем рецепте нам потребуется меньшее количество ингредиентов. Второй закон Эйнштейна позволяет дать хороший ответ на вопрос, который мы задали ранее. Откуда берётся масса? Может быть, из энергии. На самом деле, как мы увидим далее, в основном так и есть.
Источник: https://22century.ru/popular-science-publications/tonkaya-fizika-massa-efir-i-obedinenie-vsemirnyh-sil?
Общая электротехника с основами электроники
Общая электротехника с основами электроники
ОглавлениеПредисловиеВведение Часть первая. Общая электротехника 1-1. Основные понятия 1-2. Электрическое напряжение. Потенциал 1-3. Электропроводность 1-4. Электрическая емкость. Конденсаторы 1-5. Соединение конденсаторов 1-6. Энергия электрического поля 1-8. Электроизоляционные материалы 2-1. Электрический ток 2-2.  Электрическая цепь и ее элементы2-3. Закон Ома 2-4. Электрические сопротивление и проводимость 2-5. Зависимость сопротивления от температуры 2-6. Проводниковые материалы 2-7. Работа и мощность 2-8. Преобразование электрической энергии в тепловую 2-9. Электрическая нагрузка проводов и защита их от перегрузки 2-10. Потеря напряжения в проводах 2-11. Первый закон Кирхгофа 2-12. Последовательное соединение сопротивлений — приемников энергии 2-13. Параллельное соединение сопротивлений — приемников энергии 2-15. Два режима работы источника питания 2-16. Второй закон Кирхгофа 2-17. Расчет сложных цепей 2-18. Химические источники питания 2-19. Соединение химических источников питания 2-20. Нелинейные электрические цепи 2-21. Лабораторная работа. Потеря напряжения в линии Глава третья. Электромагнетизм 3-1. Магнитное поле тока. Магнитная индукция. Магнитный поток 3-2.  Электромагнитная сила3-3. Взаимодействие параллельных проводов с токами 3-4. Магнитная проницаемость 3-5. Напряженность магнитного поля. Магнитное напряжение 3-7. Магнитное поле катушки с током 3-8. Ферромагнетики, их намагничивание и перемагничивание 3-9. Ферромагнитные материалы 3-10. Магнитная цепь и ее расчет 3-11. Электромагниты 3-12. Электромагнитная индукция 3-13. Принцип работы электрического генератора 3-14. Принцип работы электродвигателя 3-15. Вихревые токи 3-16. Индуктивность. Электродвижущая сила самоиндукции 3-17. Энергия магнитного поля 3-18. Взаимная индуктивность Глава четвертая. Электрические машины постоянного тока 4-1. Назначение машин постоянного тока 4-2. Устройство машины постоянного тока 4-3. Принцип работы машины постоянного тока 4-4. Устройство обмотки якоря 4-6. Электромагнитный момент на валу машины 4-7.  Механическая мощность машины постоянного тока4-8. Реакция якоря машины постоянного тока 4-9. Коммутация тока 4-10. Понятие о номинальных данных и характеристиках электрических машин 4-11. Генератор с независимым возбуждением 4-12. Генератор с параллельным возбуждением 4-13. Генератор со смешанным возбуждением 4-14. Электродвигатели постоянного тока 4-15. Электродвигатель с параллельным возбуждением 4-16. Электродвигатель с независимым возбуждением 4-18. Потери и коэффициент полезного действия 4-19. Лабораторная работа. Электродвигатель с параллельным возбуждением 4-20. Лабораторная работа. Генератор с параллельным возбуждением Главе пятая. Основные понятия, относящиеся к переменным токам 5-1. Переменный ток 5-2. Получение синусоидальной э. д. с. 5-3. Сдвиг фаз 5-4. Действующие значения тока и напряжения 5-5. Векторная диаграмма Глава шестая.  Цепи переменного тока6-1. Особенности цепей переменного тока 6-3. Цепь с индуктивностью 6-4. Цепь с активным сопротивлением и индуктивностью 6-5. Неразветвленная цепь с активными сопротивлениями и индуктивностями 6-6. Разветвленная цепь с активными сопротивлениями и индуктивностями 6-7. Цепь с емкостью 6-8. Колебательный контур 6-9. Резонанс напряжений 6-10. Резонанс токов 6-11. Коэффициент мощности 6-12. Активная и реактивная энергия 6-13. Лабораторная работа. Цепь переменного тока с активным сопротивлением, индуктивностью и емкостью 6-14. Лабораторная работа. Параллельное соединение катушки и конденсатора Глава седьмая. Трехфазные цепи 7-1. Трехфазные системы 7-2. Соединение обмоток генератора звездой 7-4. Соединение приемников энергии звездой 7-5. Соединение приемников энергии треугольником 7-6. Лабораторная работа. Трехфазные цепи Глава восьмая.  Электротехнические измерения и приборы8-1. Основные понятия 8-2. Классификация электроизмерительных приборов 8-3. Измерительные механизмы приборов 8-4. Измерение тока и напряжения 8-5. Измерение мощности 8-6. Измерение электрической энергии 8-7. Измерение сопротивлений 8-8. Измерение неэлектрических величин электрическими методами 8-9. Лабораторная работа. Измерение сопротивлений 8-11. Лабораторная работа. Измерение мощности в трехфазной цепи Глава девятая. Трансформаторы 9-1. Назначение трансформаторов 9-2. Принцип действия и устройство однофазного трансформатора 9-3. Холостой ход однофазного трансформатора 9-4. Работа нагруженного трансформатора и диаграмма магнитодвижущих сил (м. д. с.) 9-5. Изменение напряжения трансформатора при нагрузке 9-6. Мощность потерь в обмотках нагруженного трансформатора 9-7. Трехфазный трансформатор 9-8. Регулирование напряжения трансформаторов 9-9.  9-10. Трансформаторы для дуговой электросварки 9-11. Измерительные трансформаторы 9-12. Коэффициент полезного действия трансформатора 9-13. Нагрев и охлаждение трансформаторов 9-14. Лабораторная работа. Однофазный трансформатор Глава десятая. Электрические машины переменного тока 10-1. Назначение машин переменного тока. Асинхронные электродвигатели 10-2. Получение вращающегося магнитного поля 10-3. Обмотка статора асинхронного электродвигателя 10-4. Обмотка ротора асинхронного двигателя 10-5. Принцип действия асинхронного двигателя 10-6. Электродвижущие силы в обмотках статора и ротора 10-7. Сопротивления обмотки ротора 10-8. Токи в обмотке ротора 10-9. Вращающий момент двигателя 10-10. Пуск в ход асинхронных двигателей 10-11. Регулирование частоты вращения асинхронного двигателя 10-12. Однофазный асинхронный двигатель 10-13. Потери и к. п. д. асинхронного двигателя 10-14. Синхронные машины 10-15.  Универсальный коллекторный двигатель10-16. Лабораторная работа. Трехфазный асинхронный электродвигатель Глава одиннадцатая. Электропривод и аппаратура управления 11-1. Система электропривода 11-2. Нагрев и охлаждение электрических машин 11-3. Выбор мощности двигателя при продолжительном режиме 11-4. Выбор мощности двигателя при кратковременном режиме 11-5. Выбор мощности двигателя при повторно-кратковременном режиме 11-6. Рубильники 11-7. Пакетные выключатели 11-8. Реостаты для пуска и регулирования электродвигателей 11-9. Контроллеры 11-10. Плавкие предохранители 11-11. Автоматические воздушные выключатели 11-12. Контакторы 11-13. Реле 11-14. Схема управления асинхронным двигателем с помощью реверсивного магнитного пускателя 11-15. Схема включения двухскоростного асинхронного двигателя 11-16. Автоматический пуск асинхронного двигателя с кольцами 11-17. Автоматический пуск двигателя постоянного тока с параллельным возбуждением 11-18.  Лабораторная работа. Сборка и проверка работы схемы релейноконтакторного управления трехфазным асинхронным двигателем с короткозамкнутым роторомГлава двенадцатая. Передача и распределение электрической энергии 12-1. Схемы электроснабжения промышленных предприятий. 12-2. Трансформаторные подстанции и распределительные устройства промышленных предприятий 12-3. Электрические сети промышленных предприятий 12-4. Защитное заземление Часть вторая. Основы промышленной электроники 13-1. Классификация и применение электронных приборов 13-2. Движение электронов в электрическом поле 13-3. Движение электронов в магнитном поле 13-4. Электронная эмиссия 13-5. Катоды электровакуумных приборов 13-6. Двухэлектродные электронные лампы — диоды 13-7. Применение двухэлектродных ламп Глава четырнадцатая. Трехэлектродные лампы. Четырех- и пятиэлектродные лампы. Усилители 14-1. Устройство и принцип работы триода 14-2. Статические характеристики триода 14-3.  Параметры триода14-4. Простейший каскад усиления 14-5. Характеристики и параметры простейшего каскада усиления 14-6. Типы триодов 14-7. Четырехэлектродные лампы — тетроды 14-8. Пятиэлектродные лампы — пентоды 14-9. Комбинированные и многосеточные лампы. Типы ламп 14-10. Общие понятия, относящиеся к усилителям 14-11. Режимы работы усилителей 14-12. Многокаскадные ламповые усилители 14-13. Обратная связь в усилителях 14-14. Лабораторная работа. Снятие анодных и анодно-сеточных характеристик триода и определение по ним статических параметров 14-15. Лабораторная работа. Снятие частотных характеристик усилителя напряжения низкой частоты Глава пятнадцатая. Газоразрядные приборы и их применение 15-1. Виды газового разряда и его вольт-амперная характеристика 15-2. Ионные приборы с несамостоятельным дуговым разрядом 15-3. Приборы с тлеющим разрядом 15-4. Ионные приборы с самостоятельным дуговым разрядом 15-5. Обозначения газоразрядных приборов 15-6.  Лабораторная работа. Снятие анодносеточных и пусковых характеристик тиратронаГлава шестнадцатая. Электронные генераторы. Осциллографы 16-1. Генераторы синусоидальных напряжений 16-2. Зарядка и разряд конденсатора 16-3. Релаксационные генераторы (генераторы пилообразного напряжения) 16-4. Мультивибраторы 16-5. Электроннолучевые трубки 16-6. Электроннолучевой осциллограф 16-7. Обозначения электроннолучевых трубок 16-8. Лабораторная работа. Экспериментальное, определение кривых напряжений в схемах выпрямителей Глава семнадцатая. Полупроводниковые приборы и их применение 17-1. Собственная электропроводность полупроводников 17-2. Примесная электропроводность полупроводников 17-3. Полупроводниковый вентиль 17-4. Германиевые и кремниевые диоды 17-5. Меднозакисные и селеновые диоды 17-6. Применение полупроводниковых вентилей и схемы выпрямителей 17-7. Обозначения полупроводниковых диодов 17-8. Кремниевые стабилитроны (опорные диоды) 17-9. 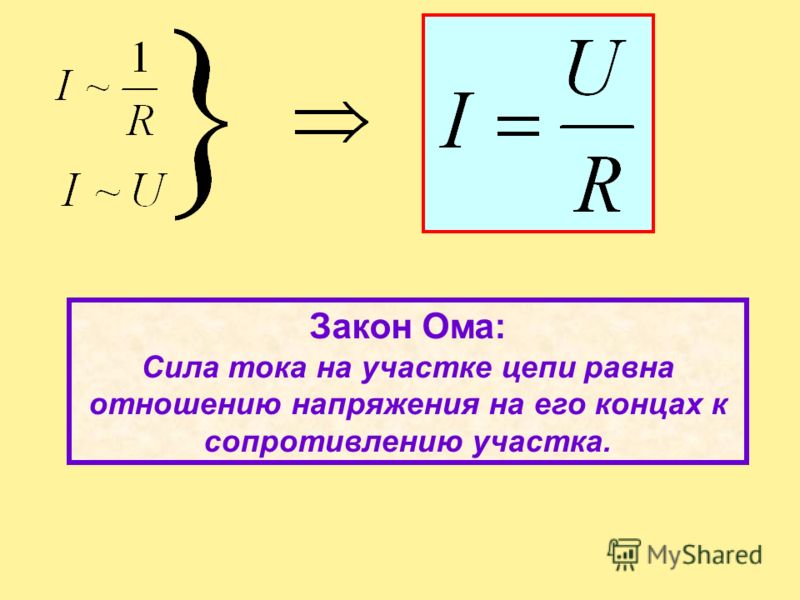 Транзисторы17-10. Применение транзисторов для усиления колебаний 17-11. Схемы включения и характеристики транзисторов 17-12. Обозначения полупроводниковых триодов 17-13. Лабораторная работа. Снятие характеристик транзистора Глава восемнадцатая. Фотоэлектронные приборы и электронные реле 18-1. Фотоэлементы с внешним фотоэффектом 18-2. Фоторезисторы 18-3. Полупроводниковые фотоэлементы 18-4. Электронные и ионные реле 18-5. Лабораторная работа. Электронное реле — триггер |
С., Николаев С. А. Общая электротехника с основами электроники, М., «Энергия», 1972, — 504 c.
Ом — AllumiaX
Закон Ома:
Закон Ома показывает соотношение между напряжением и током. Он определяется как:
«Величина тока, протекающего через проводник, напрямую зависит от разности потенциалов на нем».
окончательная форма уравнения выглядит так:
Где
- В = разность потенциалов или напряжение
- I = ток
- R = сопротивление
Мощность в цепях постоянного тока:
На основании закона Ома можно также рассчитать мощность.
Мощность является продуктом напряжения и тока, поэтому уравнение следующим образом:
, и мы знаем, что,
SO,
4 PSO,
SO, 9003
4 PSO, 9003 P
SO, 9003 P 9002. «=» В 2 / Р Вольт — единица измерения разности потенциалов или напряжения в системе СИ. он определяется как: Когда для перемещения заряда в 1 кулон требуется энергия в 1 джоуль, она равна 1 вольту Ампер — единица силы тока в системе СИ. Когда заряд в 1 кулон перемещается в течение 1 секунды, он равен 1 ампер. Ом — единица сопротивления в системе СИ. определяется как: Когда ток в один ампер подвергается воздействию разности потенциалов в один вольт. Ватт — единица измерения мощности в системе СИ. Он определяется как: Когда за одну секунду расходуется один джоуль энергии. Соответствует скорости потребления энергии в электрической цепи, где разность потенциалов составляет один вольт, а сила тока – один ампер Дано: Ток = 12 ампер Напряжение = 60 вольт Требуется: Мощность = ? Сопротивление = ? Решение: Питание = ток напряжения = 60 x 12 Мощность = 720 Вт Сопротивление = напряжение / ток = 60/12 Сопротивление = 5 Ом Дано: Ток = 10 килоампер 92 = 50 x 10 6 /(10 x 10 3 ) 2 Сопротивление = 0,5 Ом Дано: Ток = 10 миллиампер Сопротивление = 3 мегаома Мощность = ? Решение: Напряжение = сопротивление x ток = 10 x 10 -3 x 3 x 10 92 Сопротивление = (10 x 10 -3 ) x 3 x 10 6 Мощность = 300 Вт или 0,3 киловатта 1 киловатт (кВт) 1 x 10 3 Вт 1 мегаватт (МВт) 1 x 10 6 Вт 1 гигаватт (ГВт) 1 x 10 9 Вт 1 Тераватт (ТВт) 1 x 10 12 Вт 1 милливольт (мВ) 1 x 10 -3 Вольт 1 киловольт (кВ) 1 x 10 3 Вольт 1 Миллиампер (мА) 1 x 10 -3 Ампер 1 килоампер (кА) 1 x 10 3 Ампер 1 микроампер (мкА) 1 x 10 -6 Ампер 1 МегаОм (МОм) 1 x 10 6 Ом 1 килоом (кОм) 1 x 10 3 Ом 1 миллиом (мОм) 1 x 10 -3 Ом Закон Ома — это фундаментальный принцип электротехники, описывающий взаимосвязь между током, напряжением и сопротивлением в цепи. Источник изображения: Fresherslive Закон Ома гласит, что ток, протекающий по проводнику между двумя точками, прямо пропорционален напряжению в двух точках и обратно пропорционален сопротивлению между ними. Математически это можно представить как I=V/R, где I — ток, V — напряжение, а R — сопротивление. Этот закон является фундаментальной концепцией в электротехнике и помогает инженерам понимать и проектировать электрические цепи. Он объясняет взаимосвязь между напряжением, током и сопротивлением и используется для расчета мощности, сопротивления и тока в электрической цепи. Закон Ома важен для проектирования и анализа электрических цепей, устранения неполадок и определения соответствующих компонентов и номинальных мощностей для данной цепи. Калькулятор закона Ома — это онлайн-инструмент, который помогает рассчитать электрические параметры, такие как напряжение, ток, сопротивление и мощность в электрической цепи. Инструмент использует закон Ома, который гласит, что ток, протекающий по проводнику между двумя точками, прямо пропорционален напряжению в двух точках и обратно пропорционален сопротивлению между ними. С калькулятором закона Ома вам нужно ввести только два из четырех электрических параметров, и калькулятор автоматически рассчитает два других. Например, если вы знаете напряжение и сопротивление, калькулятор рассчитает ток и мощность. Калькулятор закона Ома — это полезный инструмент для инженеров, электриков и студентов, позволяющий легко и быстро выполнять электрические расчеты без необходимости вручную выполнять сложные математические расчеты. Калькулятор закона Ома также является отличным инструментом для изучения закона Ома и того, как он используется в электрических цепях. Закон Ома гласит, что ток, протекающий по проводнику между двумя точками, прямо пропорционален напряжению в двух точках и обратно пропорционален сопротивлению проводника. Этот закон может быть выражен математически тремя формулами: В заключение, закон Ома обеспечивает простую и фундаментальную зависимость между током, напряжением и сопротивлением, которая широко используется в электротехнике и физике. Эти три формулы необходимы для понимания электрических цепей и расчета параметров цепи. Закон Ома гласит, что ток, протекающий через проводник между двумя точками, прямо пропорционален напряжению в двух точках и обратно пропорционален сопротивлению между ними. Математически это можно представить как I = V/R, где I — ток в амперах (А), V — напряжение в вольтах (В), а R — сопротивление в омах (Ом). Эта формула широко используется в электротехнике для расчета тока, напряжения и сопротивления в цепи. Он составляет основу анализа и проектирования цепей и помогает понять поведение электрической цепи в различных условиях. Понимание закона Ома важно для всех, кто работает с электрическими цепями, будь то в лаборатории или в практических приложениях. Закон Ома — это фундаментальный принцип в электротехнике, который устанавливает взаимосвязь между током, протекающим через проводник, напряжением в двух точках проводника и сопротивлением проводника. Закон Ома может быть выражен математически как V = IR, где V — напряжение, I — ток, а R — сопротивление. Из этой формулы следует, что увеличение напряжения на проводнике увеличивает ток, протекающий через него, а увеличение сопротивления проводника уменьшает ток, протекающий через него. Единицей закона Ома является Международная система единиц (СИ). Единицей напряжения является вольт (В), единицей силы тока является ампер (А), а единицей сопротивления является ом (Ом). Этот закон широко используется при проектировании и анализе электрических цепей, и он необходим для понимания основных принципов электричества. В заключение, закон Ома обеспечивает простую и фундаментальную зависимость между током, напряжением и сопротивлением, которая широко используется в электротехнике и физике. Треугольник закона Ома — это графическое представление закона Ома, который гласит, что ток, протекающий через проводник между двумя точками, прямо пропорционален напряжению между двумя точками и обратно пропорционален сопротивлению между ними. Использование закона Ома для анализа электрической цепи — это простой процесс, который можно выполнить, выполнив следующие действия: Следуя этим шагам, закон Ома можно использовать для анализа и понимания поведения электрической цепи, помогая прогнозировать и контролировать поток электричества в цепи. Закон Ома можно использовать для расчета тока (I), напряжения (V), сопротивления (R) и мощности (P) в электрической цепи. Используемая формула зависит от известных значений в цепи. Например, если напряжение в цепи равно 12 В, а сопротивление равно 4 Ом, ток, протекающий в цепи, можно рассчитать как I = V/R = 12 В/4 Ом = 3 А. Точно так же мощность можно рассчитать как P = IV = 12 В * 3 А = 36 Вт. Важно отметить, что закон Ома основан на линейных соотношениях и применяется только к резистивным цепям. Для более сложных схем могут потребоваться более продвинутые методы анализа. Пример 1: Резистор с сопротивлением R = 4 Ом подключен к источнику напряжения V = 12 В. Вычислите ток, протекающий через резистор. Решение: I = V/R = 12 В/4 Ом = 3 А Пример 2: Ток I = 2 А протекает через резистор с сопротивлением R = 6 Ом. Рассчитать напряжение на резисторе. Решение: V = IR = 2A * 6 Ом = 12 В Пример 3: Напряжение V = 10 В подается на резистор с сопротивлением R = 5 Ом. Вычислите ток, протекающий через резистор. Решение: I = V/R = 10 В/5 Ом = 2 А Пример 4: Ток I = 1 А протекает через резистор, а напряжение на резисторе V = 10 В. Вычислите сопротивление резистора. Решение: R = V/I = 10 В/1 А = 10 Ом В заключение, эти примеры демонстрируют, как можно использовать закон Ома для расчета тока, напряжения и сопротивления в электрических цепях. Отношения между этими тремя параметрами можно легко вывести с помощью закона Ома, что делает его полезным инструментом в электротехнике и физике. Закон Ома гласит, что ток, протекающий по проводнику между двумя точками, прямо пропорционален напряжению на двух точках и обратно пропорционален сопротивлению между ними. Это соотношение может быть выражено математически как I = V/R, где I — ток в амперах, V — напряжение в вольтах, а R — сопротивление в омах. Закон Ома — это основной принцип электричества, который описывает взаимосвязь между током, протекающим в проводнике, напряжением на нем и сопротивлением проводника. Проще говоря, в нем говорится, что величина тока, протекающего через проводник, прямо пропорциональна напряжению, приложенному к нему, и обратно пропорциональна его сопротивлению. Это соотношение выражается математически как I = V/R, где I — ток в амперах, V — напряжение в вольтах, а R — сопротивление в омах. Закон Ома широко используется в электротехнике для прогнозирования и управления потоком электричества в цепи и формирует основу для понимания поведения электрических систем. Закон Ома математически выражается как I = V/R, где I — ток, протекающий в проводнике, V — напряжение на проводнике, а R — сопротивление проводника. Эта формула утверждает, что ток (I) в цепи прямо пропорционален напряжению (V) в цепи и обратно пропорционален сопротивлению (R) цепи. Другими словами, если напряжение увеличивается, ток также увеличивается, а если увеличивается сопротивление, ток уменьшается. Эта формула используется в электротехнике для прогнозирования и управления потоком электричества в цепи и служит основой для понимания поведения электрических систем. Важно отметить, что закон Ома применяется только к линейным резистивным цепям и может быть неприменим для нелинейных или реактивных цепей. Тем не менее, он остается мощным инструментом для анализа цепей и широко используется в электротехнике и смежных областях. 1. Что такое закон Ома? Закон Ома гласит, что ток, протекающий по проводнику между двумя точками, прямо пропорционален напряжению на двух точках и обратно пропорционален сопротивлению между ними. 2. Какова формула закона Ома? Формула закона Ома: I = V/R, где I — сила тока в амперах, V — напряжение в вольтах, а R — сопротивление в омах. 3. Как закон Ома используется в электротехнике? Закон Ома используется в электротехнике для прогнозирования и управления потоком электричества в цепи. Он формирует основу для понимания поведения электрических систем и широко используется для анализа и проектирования цепей. 4. Применяется ли закон Ома ко всем типам цепей? Закон Ома основан на линейных соотношениях и применим только к резистивным цепям. Для более сложных схем могут потребоваться более продвинутые методы анализа. 5. Как я могу использовать закон Ома для расчета тока, напряжения, сопротивления или мощности в цепи? Закон Ома можно использовать для расчета любой из четырех величин в цепи, если известны остальные три. 6. Применим ли закон Ома в современной электротехнике? Да, закон Ома остается фундаментальным принципом в электротехнике и до сих пор широко используется. Несмотря на достижения в области технологий и разработку более совершенных методов анализа, закон Ома остается важным инструментом для всех, кто работает с электрическими цепями и системами. 7. Можно ли использовать закон Ома для цепей переменного тока? Да, закон Ома может применяться к цепям переменного тока с некоторыми изменениями. Значения сопротивления, напряжения и тока могут меняться со временем и в зависимости от частоты сигнала переменного тока, поэтому для полного понимания поведения цепи переменного тока может потребоваться более сложный анализ. 8. Всегда ли точен закон Ома? Закон Ома основан на предположении, что сопротивление проводника остается постоянным. Что такое вольты?
Что такое ампер?
Он определяется как: Что такое омы?
Что такое ватты?
Решаемый пример:
Когда известны ток и напряжение: 
Закон Ома, 3 формулы закона Ома, примеры решений
Изучите основы закона Ома и как использовать его для прогнозирования и управления потоком электричества. Закон Ома является ключевым инструментом для всех, кто изучает или работает в области электротехники и смежных областях. Закон Ома
В целом, закон Ома представляет собой простой, но мощный инструмент для понимания и управления электрическими цепями. Калькулятор закона Ома
Какие 3 формулы в законе Ома?
Формула закона Ома
Закон Ома и его единица СИ?
Закон гласит, что ток, протекающий по проводнику между двумя точками, прямо пропорционален напряжению в этих двух точках и обратно пропорционален сопротивлению проводника. Треугольник закона Ома
Треугольник образован соединением трех компонентов закона Ома: напряжения (V), тока (I) и сопротивления (R) в его вершинах. Отношения между этими тремя можно легко запомнить и понять, изучая треугольник закона Ома, поскольку он обеспечивает визуальное представление математической формулы I = V/R. Треугольник закона Ома широко используется инженерами-электриками и техниками в качестве инструмента для анализа цепей и решения проблем, что делает его ценным инструментом в области электротехники. Как пользоваться законом Ома?
Как рассчитать закон Ома?
Закон Ома Решенные вопросы
Что утверждает закон Ома?
Закон Ома является фундаментальным принципом электротехники и лежит в основе анализа и проектирования электрических цепей. Он используется для прогнозирования и управления потоком электроэнергии в цепи и широко применяется в таких областях, как электроника, энергетические системы и телекоммуникации. Понимание закона Ома важно для всех, кто работает с электрическими цепями и электротехникой. Что такое закон Ома?
Какова формула закона Ома?
Закон Ома – Часто задаваемые вопросы
Используемая формула зависит от известных значений.
