Задачи по теме:»Сила трения». Подготовка к ЕГЭ
Задачи по теме: « Сила трения». Для подготовке к ЕГЭ.
1.
На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 20 Н. Чему будет равна сила трения скольжения после уменьшения массы тела в 2 раза, если коэффициент трения не изменится? (Ответ дайте в ньютонах.)
Решение.
Сила трения скольжения связана с коэффициентом трения и силой реакции опоры соотношением Для бруска, движущегося по горизонтальной поверхности, по второму закону Ньютона
Таким образом, сила трения скольжения пропорциональна произведению коэффициента трения и массы бруска. Если коэффициент трения не изменится, то после уменьшения массы тела в 2 раза сила трения скольжения также уменьшится в 2 раза и окажется равной
Ответ: 10.
2.
На брусок массой 5 кг, движущийся по горизонтальной
поверхности, действует сила трения скольжения 20 Н.
Решение.
Сила трения скольжения связана с коэффициентом трения и силой реакции опоры соотношением Для бруска, движущегося по горизонтальной поверхности, по второму закону Ньютона,
Таким образом, сила трения скольжения пропорциональна произведению коэффициента трения и массы бруска. Если масса бруска не изменится, то после уменьшения коэффициента трения в 2 раза, сила трения скольжения также уменьшится в 2 раза и окажется равной
Ответ: 10.
На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 20 Н. Чему будет равна сила трения скольжения, если коэффициент трения уменьшится в 4 раза при неизменной массе? (Ответ дайте в ньютонах.)
Решение.
Сила трения скольжения связана с коэффициентом трения и силой реакции опоры соотношением Для бруска, движущегося по горизонтальной поверхности, по второму закону Ньютона,
Таким образом, сила трения скольжения пропорциональна произведению
коэффициента трения и массы бруска.
Ответ: 5.
4.
На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 20 Н. Чему будет равна сила трения скольжения, если, не изменяя коэффициент трения, уменьшить в 4 раза массу бруска? (Ответ дайте в ньютонах.)
Решение.
Сила трения скольжения связана с коэффициентом трения и силой реакции опоры соотношением Для бруска, движущегося по горизонтальной поверхности, по второму закону Ньютона,
Таким образом, сила трения скольжения пропорциональна произведению коэффициента трения и массы бруска. Если коэффициент трения не изменится, то после уменьшения массы бруска в 4 раза, сила трения скольжения также уменьшится в 4 раза и окажется равной
Ответ: 5.
5.
На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 10 Н. Чему будет равна сила трения скольжения после уменьшения массы тела в 2 раза, если коэффициент трения не изменится? (Ответ дайте в ньютонах.)
Решение.
Сила трения скольжения связана с коэффициентом трения и силой реакции опоры соотношением Для бруска, движущегося по горизонтальной поверхности, по второму закону Ньютона, Таким образом, сила трения скольжения пропорциональна произведению коэффициента трения и массы бруска. Если коэффициент трения не изменится, то после уменьшения массы тела в 2 раза, сила трения скольжения также уменьшится в 2 раза и окажется равной
Ответ: 5.
6.
Тело равномерно движется по плоскости. Сила давления тела на плоскость равна 20 Н, сила трения 5 Н. Чему равен коэффициент трения скольжения?
Решение.
Сила давления на плоскость, сила трения и коэффициент трения связаны соотношением Следовательно, коэффициент трения равен
Ответ: 0,25.
7.
Санки массой 5 кг скользят по горизонтальной дороге. Сила трения скольжения их полозьев о дорогу 6 Н. Каков коэффициент трения скольжения саночных полозьев о дорогу? Ускорения свободного падения считать равным 10 м/с2.
Решение.
Сила трения скольжения связана с силой реакции опоры и коэффициентом трения соотношением Поскольку сани скользят по горизонтальной поверхности, по второму закону Ньютона, Следовательно, коэффициент трения саночных полозьев о дорогу равен
Ответ: 0,12.
8.
При движении по горизонтальной поверхности на тело массой 40 кг действует сила трения скольжения 10 Н. Какой станет сила трения скольжения после уменьшения массы тела в 5 раз, если коэффициент трения не изменится? (Ответ дайте в ньютонах.)
Решение.
Сила трения скольжения связана с коэффициентом трения и силой реакции опоры соотношением Для бруска, движущегося по горизонтальной поверхности, по второму закону Ньютона,
Таким образом, сила трения скольжения пропорциональна произведению
коэффициента трения и массы бруска.
Ответ: 2.
9.
На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 10 Н. Чему будет равна сила трения скольжения после увеличения коэффициента трения в 4 раза при неизменной массе? (Ответ дайте в ньютонах.)
Решение.
Сила трения скольжения связана с коэффициентом трения и силой реакции опоры соотношением Для бруска, движущегося по горизонтальной поверхности, по второму закону Ньютона,
Таким образом, сила трения скольжения пропорциональна произведению коэффициента трения и массы бруска. Если масса бруска не изменится, то после увеличения коэффициента трения в 4 раза, сила трения скольжения также увеличится в 4 раза и окажется равной
Ответ: 40.
10.
На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 10 Н. Чему будет равна сила трения скольжения, если массу бруска увеличить в 2 раза, не изменяя коэффициента трения? (Ответ дайте в ньютонах.)
Решение.
Сила трения скольжения связана с коэффициентом трения и силой реакции опоры соотношением Для бруска, движущегося по горизонтальной поверхности, по второму закону Ньютона,
Таким образом, сила трения скольжения пропорциональна произведению коэффициента трения и массы бруска. Если коэффициент трения не изменится, то после увеличения массы бруска в 2 раза, сила трения скольжения также увеличится в 2 раза и окажется равной
Ответ: 20.
11.
На брусок массой 5 кг, движущийся по горизонтальной
поверхности, действует сила трения скольжения 10 Н. Если, не изменяя
коэффициента трения, увеличить в 4 раза массу бруска, чему будет равна сила
трения скольжения? (Ответ дайте в ньютонах.
Решение.
Сила трения скольжения связана с коэффициентом трения и силой реакции опоры соотношением Для бруска, движущегося по горизонтальной поверхности, по второму закону Ньютона,
Таким образом, сила трения скольжения пропорциональна произведению коэффициента трения и массы бруска. Если коэффициент трения не изменится, то после увеличения массы бруска в 4 раза, сила трения скольжения также увеличится в 4 раза и окажется равной 4 · 10 Н = 40 Н.
Ответ: 40.
12.
На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 20 Н.
Если, не изменяя коэффициента трения, уменьшить в 4 раза силу давления бруска на поверхность, чему будет равна сила трения скольжения? (Ответ дайте в ньютонах.)
Решение.
Сила трения скольжения связана с силой реакции опоры и коэффициентом трения соотношением Согласно третьему закону Ньютона, сила реакции опоры равна по модулю силе давления бруска на поверхность: Следовательно, Таким образом, если при неизменном коэффициенте трения уменьшить силу давления бруска на поверхность в 4 раза, сила трения скольжения также уменьшится в 4 раза и окажется равной
Ответ: 5.
Примечание.
Нужно обратить внимание, что в данной задаче идёт речь именно о силе давления тела, то есть о весе тела, а не о давлении равном
13.
На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 10 Н.
Если, не изменяя коэффициента трения, увеличить в 2 раза силу давления бруска на плоскость, чему будет равна сила трения скольжения? (Ответ дайте в ньютонах.)
Решение.
Сила трения скольжения связана с силой реакции опоры и коэффициентом трения соотношением Согласно третьему закону Ньютона, сила реакции опоры равна по модулю силе давления бруска на плоскость: Следовательно, Таким образом, если при неизменном коэффициенте трения увеличить силу давления бруска на плоскость в 2 раза, сила трения скольжения также увеличится в 2 раза и окажется равной
Ответ: 20.
14.
На горизонтальном полу стоит ящик массой 10 кг. Коэффициент
трения между полом и ящиком равен 0,25. К ящику в горизонтальном направлении
прикладывают силу 16 Н. Какова сила трения между ящиком и полом? Ответ
выразите в ньютонах.
Коэффициент
трения между полом и ящиком равен 0,25. К ящику в горизонтальном направлении
прикладывают силу 16 Н. Какова сила трения между ящиком и полом? Ответ
выразите в ньютонах.
Решение.
Определим, какую величину имеет сила трения скольжения:
Поскольку сила трения скольжения превосходит по величине силу с которой ящик толкают в горизонтальном направлении, ящик останется стоять на месте. Следовательно, согласно второму закону Ньютона, сила трения между ящиком и полом будет равняться по модулю силе
Ответ: 16.
15.
Два спортсмена разной массы на одинаковых автомобилях, движущихся со скоростью и стали тормозить, заблокировав колеса. Каково отношение тормозных путей их автомобилей при одинаковом коэффициенте трения колес о землю?
Решение.
При торможении на автомобили действует сила трения скольжения, которая и останавливает их. Величина силы трения скольжения определяется выражением где — сила реакции опоры, которую можно найти, выписав второй закон Ньютона в проекции на вертикальную ось:
Вычислим теперь ускорение, с которым тормозит каждый из
спортсменов. Второй закон Ньютона в проекции на горизонтальную ось даёт (здесь m —
масса автомобиля вместе со спортсменом). Поскольку ускорение не зависит от
массы, заключаем, что оба автомобиля тормозят с одинаковым ускорением.
Второй закон Ньютона в проекции на горизонтальную ось даёт (здесь m —
масса автомобиля вместе со спортсменом). Поскольку ускорение не зависит от
массы, заключаем, что оба автомобиля тормозят с одинаковым ускорением.
Тормозной путь можно найти по формуле где — начальная скорость. Следовательно, отношение тормозных путей равно
Ответ: 0,25.
16.
Брусок массой 20 кг равномерно перемещают по горизонтальной поверхности, прикладывая к нему постоянную силу, направленную под углом 30° к поверхности. Модуль этой силы равен 75 Н. Определите коэффициент трения между бруском и плоскостью. Ответ округлите до десятых долей.
Решение.
Запишем второй закон Ньютона, учитывая, что тело движется равномерно, то есть ускорение бруска равно нулю: Вспомним, что сила трения и сила реакции опоры связаны соотношением: Запишем это уравнение в проекции на горизонтальную и вертикальную оси:
Таким образом, получаем:
Ответ: 0,4.
17.
Брусок массой 20 кг равномерно перемещают по склону горки, прикладывая к нему постоянную силу, направленную параллельно поверхности горки. Модуль этой силы равен 204 Н, угол наклона горки к горизонту 60°. Определите коэффициент трения между бруском и склоном горки. Ответ округлите до десятых долей.
Решение.
Запишем второй закон Ньютона, учитывая, что тело движется равномерно, то есть ускорение бруска равно нулю: Вспомним, что сила трения и сила реакции опоры связаны соотношением: Запишем это уравнение в проекциях на две оси, параллельную поверхности горки и перпендикулярную ей:
Таким образом, получаем:
Ответ: 0,3.
18.
На горизонтальной поверхности лежит деревянный брусок массой 1 кг.
Для того чтобы сдвинуть этот брусок с места, к нему нужно приложить
горизонтально направленную силу 3 Н. Затем на эту же поверхность кладут
стальной брусок массой 5 кг. Коэффициент трения для стали о данную поверхность
в 2 раза больше, чем для дерева. Какую горизонтально направленную силу нужно
приложить к стальному бруску для того, чтобы сдвинуть его с места?
Затем на эту же поверхность кладут
стальной брусок массой 5 кг. Коэффициент трения для стали о данную поверхность
в 2 раза больше, чем для дерева. Какую горизонтально направленную силу нужно
приложить к стальному бруску для того, чтобы сдвинуть его с места?
Решение.
Для момента начала движения: где — приложенная сила. Распишем силы, которые действуют на деревянный брусок — на стальной — Следовательно,
Ответ: 30.
19.
На горизонтальной поверхности лежит металлический брусок массой 4 кг. Для того, чтобы сдвинуть этот брусок с места, к нему нужно приложить горизонтально направленную силу 20 Н. Затем на эту же поверхность кладут пластиковый брусок массой 2 кг. Коэффициент трения для пластика о данную поверхность в 2 раза меньше, чем для металла. Какую горизонтально направленную силу нужно приложить к пластиковому бруску для того, чтобы сдвинуть его с места? Ответ укажите в Ньютонах.
Решение.
Для момента начала движения: где —
приложенная сила. Распишем силы, которые действуют на металлический брусок
— на
пластиковый -Следовательно, Н.
Распишем силы, которые действуют на металлический брусок
— на
пластиковый -Следовательно, Н.
Ответ: 5.
20.
Брусок массой 5 кг покоится на шероховатом горизонтальном столе. Коэффициент трения между поверхностью бруска и поверхностью стола равен 0,2. На этот брусок действуют горизонтально направленной силой 2,5 Н. Чему равна по модулю возникающая при этом сила трения?
Решение.
Максимально возможная сила трения равна Поскольку внешняя сила меньше, значит, тело будет покоиться, сила трения будет уравновешивать внешнюю силу и, соответственно, равняться 2,5 Н.
Ответ: 2,5.
Задачи на формулу трения — GeeksforGeeks
Трение — это сила, которая присутствует почти везде в повседневной жизни. Эта сила позволяет нам ходить, держать предметы и т. д. Короче говоря, она необходима почти для всех физических действий в реальной жизни. Когда мяч брошен на пол с некоторой скоростью, он некоторое время продолжает движение, а затем останавливается. В идеальном случае мяч должен продолжать двигаться, так как на него не действует внешняя сила. Но он останавливается, а это значит, что присутствует сила, сопротивляющаяся движению. Эта сила называется трением. Сила трения по своей природе противодействует всякому движению между объектами.
В идеальном случае мяч должен продолжать двигаться, так как на него не действует внешняя сила. Но он останавливается, а это значит, что присутствует сила, сопротивляющаяся движению. Эта сила называется трением. Сила трения по своей природе противодействует всякому движению между объектами.
Трение
Силы трения препятствуют движению. Хотя он обычно выделяет тепло и изнашивает предметы, он часто бывает полезен. Это дает необходимую тягу, необходимую для ходьбы и бега без скольжения. В автомобилях он менее желателен, поскольку на его долю приходится 20% потерь энергии. Трение зависит от нормальной силы, действующей на поверхность. Силы трения можно разделить на две части:
- Статическое трение: Это тип трения, препятствующий скольжению объектов по поверхности. Направление препятствует скольжению объектов друг относительно друга и параллельно поверхности.
- Кинетическое трение: Этот тип трения действует, когда объект скользит по поверхности.
 Направление такое же, как и статическое трение.
Направление такое же, как и статическое трение.
Законы трения:
Уравнения трения
- Трение движущегося объекта пропорционально и перпендикулярно приложенной к нему нормальной силе.
- Трение, испытываемое объектом, зависит от характера поверхности, с которой он соприкасается.
- Трение не зависит от площади контакта, если она существует.
- Кинетическое трение не зависит от скорости.
- Коэффициент статического трения больше, чем коэффициент кинетического трения.
Когда к объекту приложена сила, скажем, F N — это сила, действующая нормально на поверхность. Значение статического трения задается как F s , а является значением коэффициента статического трения. Тогда уравнение, описывающее статическую силу трения, имеет вид
В случае, когда объект движется, кинетическая сила трения определяется выражением
Коэффициент трения определяется выражением
Здесь F — сила трения, а N является значением нормальной силы.
Давайте рассмотрим некоторые проблемы, связанные с этими понятиями.
Примеры задач
Вопрос 1: К стоящему на полу ящику приложена сила 60 Н с коэффициентом трения покоя 0,4. Найдите силу трения.
Ответ:
Сила трения покоя определяется выражением
Здесь — коэффициент трения покоя, а N — нормальная сила.
и N = 60Н
Подставив значения в уравнение,
Вопрос 2: На ящик, стоящий на полу, действует сила 100 Н с коэффициентом трения покоя 0,2. Найдите силу трения
Ответ:
Сила трения покоя определяется как
Здесь — коэффициент трения покоя, а N — нормальная сила.
и n = 100N
Подключение значений в уравнении,
Вопрос 3: Сила 100N проявляется под углом 30 ° на коробке, содержащейся на полу с коэффициентом статического трения 0,2 0,2 0,2 0,2 . Найдите силу трения
Найдите силу трения
Ответ:
Сила трения покоя определяется выражением
Здесь – коэффициент трения покоя, а N – нормальная сила.
= 0,2, = 30° и F = 100N
N = Fsin()
⇒N = (100)sin(30°)
⇒N = 50
Заглушка значения в уравнении,
Вопрос 4: На коробку, стоящую на полу, действует сила 200 Н под углом 30° с коэффициентом трения покоя 0,2. Найдите силу трения
Ответ:
Сила трения покоя определяется выражением
Здесь — коэффициент трения покоя, а N — нормальная сила.
= 0,2, = 30° и F = 200N
N = Fsin()
⇒N = (200)sin(30°)
⇒N = 100
Заглушка значения в уравнении,
Вопрос 5: Сила 60 Н приложена горизонтально к ящику массой 40 кг, стоящему на полу с коэффициентом статического трения 0,2. Найдите силу трения.
Найдите силу трения.
Ответ:
Сила трения покоя определяется выражением
Здесь — коэффициент трения покоя, а N — нормальная сила.
и N = мг
N = мг
⇒N = (40)(10)
⇒N = 400 Н
Статическое трение будет,
Теперь приложенная сила составляет 60 Н, а максимальное статическое трение 80Н. Поскольку приложенная сила меньше значения трения покоя, коробка не будет двигаться, а сила трения будет равна приложенной силе.
Вопрос 6: На коробку массой 50 кг, стоящую на полу, действует горизонтальная сила 50 Н с коэффициентом трения покоя 0,3. Найдите силу трения.
Ответ:
Сила трения покоя определяется выражением
Здесь — коэффициент трения покоя, а N — нормальная сила.
и N = мг
N = мг
⇒N = (50)(10)
⇒N = 500 Н
Статическое трение будет,
Теперь приложенная сила составляет 100 Н, а максимальное статическое трение составляет 150 Н.
Поскольку приложенная сила меньше значения трения покоя, коробка не будет двигаться, а сила трения будет равна приложенной силе.
Вопрос 7: На коробку массой 2 кг, стоящую на полу, действует горизонтальная сила 40 Н с коэффициентом статического трения 0,4 и коэффициентом кинетического трения 0,2. Найдите силу трения.
Ответ:
Сила трения покоя определяется выражением
Здесь — коэффициент трения покоя, а N — нормальная сила.
и N = мг
N = мг
⇒N = (2)(10)
⇒N = 20N
Подстановка значений в уравнение,
900 03
Теперь, поскольку максимальное статическое трение меньше чем приложенная сила. Ящик начнет двигаться, и тогда на тело будет действовать кинетическое трение.
Вопрос 8: Горизонтальная сила 50 Н действует на коробку массой 3 кг, стоящую на полу, с коэффициентом статического трения 0,4 и коэффициентом кинетического трения 0,2. Найдите силу трения.
Найдите силу трения.
Ответ:
Сила трения покоя определяется выражением
Здесь — коэффициент трения покоя, а N — нормальная сила.
и N = мг
N = мг
⇒ N = (3) (10)
⇒ N = 30 Н
Подставляя значения в уравнение,
Теперь, поскольку максимальное статическое трение меньше приложенной силы. Ящик начнет двигаться, и тогда на тело будет действовать кинетическое трение.
Коэффициент трения Задачи и решения
В этом руководстве представлены некоторые задачи на силу трения и коэффициенты трения вместе с подробными решениями. Все эти проблемы с трением предназначены для старшеклассников и студентов колледжей.
Коэффициент кинетического трения: Задачи
Задача (1): Постоянная сила $10\,{\rm Н}$ приложена к ящику $2-{\rm кг$ на шероховатой поверхности, в теме. На ящик действует сила трения против силы, которая перемещает его по поверхности.
(a) Считая, что коэффициент трения равен $\mu_k=0,24$, найдите величину силы трения, препятствующей движению.
(b) Какова результирующая сила, действующая на ящик?
(c) Какое ускорение получает ящик?
Решение : Сила кинетического трения — это сила, противодействующая движению движущегося объекта, и ее величина определяется следующей формулой: $f_k=\mu_k F_N$, где $\mu_k$ — коэффициент кинетического трения. , а $F_N$ — нормальная сила, действующая на объект при контакте с поверхностью.
Во всех задачах, связанных с коэффициентом трения, если нормальная сила не задана, то для ее нахождения необходимо применить второй закон Ньютона в вертикальном направлении.
(a) Ящик не движется вертикально и не отрывается от поверхности, поэтому силы в этом направлении должны быть уравновешены друг другом. На приведенной ниже диаграмме свободного тела показано, что на ящик действуют две силы: направленная вверх нормальная сила $F_N$ и направленная вниз сила веса $W=mg$. 2}\]
2}\]
Задача (2): Коробка весом 75 {\rm кг}$ тянут по шероховатой поверхности под действием горизонтальной силы $100\,{\rm Н}$ с постоянной скоростью. Найдите коэффициент трения между коробкой и поверхностью.
Решение : Все проблемы коэффициента трения и второй закон Ньютона тесно связаны между собой. Нам говорят, что ящик движется с постоянной скоростью.
Согласно определению среднего ускорения, $a=\frac{\Delta v}{\Delta t}$, постоянная скорость или скорость означает, что ускорение равно нулю (это справедливо для прямолинейного движения).
С другой стороны, нулевое ускорение означает отсутствие результирующей силы на объекте, $F_{net}=ma=0$.
Чтобы выполнить это условие, силы должны быть в равновесии друг с другом. Следовательно, тяговая сила $F$ должна компенсироваться противодействующей силой трения $f_k$, поэтому \[F=f_k=\mu_k F_N \Rightarrow \mu_k=\frac{F}{F_N}\]
Задайте чистую силу в вертикальном направлении до нуля, так как коробка не отрывается от поверхности. Таким образом, нормальная сила $F_N$ получается как \[F_N=mg=75\times 10=750\,{\rm N}\]. Следовательно, коэффициент трения определяется как \[\mu_k=\frac{ F}{F_N}=\frac{100}{750}=0,13\]
Таким образом, нормальная сила $F_N$ получается как \[F_N=mg=75\times 10=750\,{\rm N}\]. Следовательно, коэффициент трения определяется как \[\mu_k=\frac{ F}{F_N}=\frac{100}{750}=0,13\]
Нужна помощь с домашним заданием? Получите этот PDF-файл с более чем 500 решенными домашними заданиями по физике. Всего за 8 долларов США или загрузите бесплатный образец в формате PDF.
Задача (3): Предположим, что коэффициент кинетического трения между коробкой весом 22 кг и шероховатым полом равен 0,25$.
а) Какая горизонтальная сила необходима, чтобы ящик двигался с постоянной скоростью?
(b) Теперь, предположив, что $\mu_k=0$, какая горизонтальная внешняя сила требуется?
Решение : Как и раньше, движение происходит по горизонтальной прямой траектории, поэтому постоянная скорость означает отсутствие ускорения $a=0$. Таким образом, результирующая сила в этом направлении равна нулю, $F_{net}=ma=0$.
Если внешняя сила равна величине силы трения, то результирующая сила, действующая на объект, равна нулю, и он движется с постоянной скоростью.
(a) С учетом приведенного выше объяснения мы должны иметь \[F=f_k \Rightarrow \text{постоянную скорость}\] Кинетическая сила трения, $f_k=\mu_k F_N$, зависит от величины нормальной силы , что в данном случае равно \[F_N=mg=22\times 10=220\,{\rm N}\] Итак, величина трения равна \[f_k=\mu_k F_N=0,25\times 220=55\, {\rm N}\] Следовательно, постоянная сила $F=55\,{\rm N}$, параллельная поверхности, имеющей $\mu_k=0,25$, заставляет тело массой 22 кг двигаться с постоянной скоростью.
(b) Когда коэффициент трения равен нулю, мы находимся на поверхности без трения. Следовательно, любая сила любой величины может ускорить объект, покоящийся на такой поверхности.
Задача (4). Тяжелый блок весом $300\,{\rm N}$ движется с постоянной скоростью под действием силы $45\,{\rm N}$, приложенной параллельно движению.
(а) О каком коэффициенте трения идет речь в задаче?
(b) Какова масса бруска?
(c) Считая $\mu_k=0$, найти ускорение блока?
Решение : Заданы вес блока $W=mg=300\,{\rm N}$ и величина внешней силы.
(а) Снова «постоянная скорость». Если существует сила, равная по величине, но противоположная по направлению внешней силе, то результирующая сила, действующая на объект, равна нулю, и в результате он движется с постоянной скоростью.
Следовательно, сила трения должна быть равна величине внешней силы, $F=f_k=\mu_k F_N$. Блок движется, поэтому мы имеем дело с кинетическим трением.
В вертикальном направлении движения нет, поэтому второй закон Ньютона для движения в этом направлении $F_{net-y}=ma_y$ дает нам величину нормальной силы \[F_N-mg=0 \Rightarrow F_N =mg=300\,{\rm N}\] Теперь, решая $F=f_k=\mu_k F_N$ относительно $\mu_k$, получаем \[\mu_k=\frac{F}{F_N}=\frac{45 }{300}=0,15\]
(b) Используя определение веса в физике, $W=mg$, и решая это для $m$, мы получаем \[m=\frac{W}{g}= \frac{300}{10}=30\,{\rm кг}\]
(c) В случае нулевого трения, $\mu_k=0$, любая сила, сколь бы малой она ни была, ускоряет тело, величина которого находится следующим образом: \[a=\frac{F}{m}=\frac{45}{30}=1,5\,{\rm м/с^2}\] 92}$. Что такое коэффициент кинетического трения?
Что такое коэффициент кинетического трения?
Решение : статическое трение не имеет простой формулы. Этот тип трения зависит от внешней силы, действующей на объект. Но для этого есть верхняя граница, которая за пределами этого заставляет объект начинать свое движение из состояния покоя.
Величина силы трения покоя в данный момент времени, когда трение покоя имеет наибольшее значение, определяется по формуле \[f_{s, max}=\mu_s F_N\]
(a) Брусок находится на горизонтальной поверхности и на него действует внешняя сила, параллельная поверхности, поэтому нормальная сила равна приложенному к нему весу объекта \[F_N=mg=6\times 10=60\,{\ rm N}\] В задаче нам сказали, что объект покоится и хочет стать на грань скольжения. Таким образом, единственная сила трения, участвующая в движении, — это трение покоя, максимальное значение которого равно $f_{s, max}=\mu_s F_N$.
Как сказано, максимальное значение трения покоя всегда равно внешним силам, действующим на объект.
В этом случае сила $35-{\rm N}$ привела объект в движение. Итак, $F=f_{s,max}$. Решая это уравнение для $\mu_s$, находим коэффициент трения покоя как \begin{align*} f_{s,max}&=F\\\\ \mu_s F_N&=F\\\\ \Rightarrow \mu_s&= \frac{F}{F_N}\\\\&=\frac{35}{70}=0.5\end{align*}
(b) Если эта постоянная сила будет продолжаться, объект будет двигаться, а отсюда и кинетическое трение на объект действует сила.
Поскольку сказано, что блок испытывает ускорение, на него должна действовать результирующая сила. Внешняя сила направлена вдоль направления движения, а сила трения по определению всегда направлена против движения.
Таким образом, результирующая сила, действующая на блок, находится путем вычитания трения из внешней силы, как показано ниже \[F_{net}=F-f_k=F-\mu_k F_N\] Блок находится на горизонтальной поверхности с силой приложенная к нему горизонтально, поэтому нормальная сила всегда равна $F_N=mg=7\times 10=70\,{\rm N}$. Согласно второму закону Ньютона $F_{net}=ma$. Объединяя эти два последних уравнения и решая для $\mu_k$, мы получаем \begin{gather*} F_{net}=ma\\\\ F-\mu_k (mg)=ma \\\\ \Rightarrow \mu_k= \frac{F-ma}{mg} \\\\ =\frac{35-7\times 0,6}{7\times 10}\\\\=0,44\end{gather*} Как и ожидалось, поскольку всегда $\ mu_s>\mu_k$.
Объединяя эти два последних уравнения и решая для $\mu_k$, мы получаем \begin{gather*} F_{net}=ma\\\\ F-\mu_k (mg)=ma \\\\ \Rightarrow \mu_k= \frac{F-ma}{mg} \\\\ =\frac{35-7\times 0,6}{7\times 10}\\\\=0,44\end{gather*} Как и ожидалось, поскольку всегда $\ mu_s>\mu_k$.
Задача (6): Ящик стоимостью 20-{\rm кг$ изначально покоится на поверхности. Сила $75\,{\rm Н}$ приводит ящик в движение. После перемещения требуется сила $60-{\rm N}$, чтобы заставить его двигаться с постоянной скоростью. Каковы статический и кинетический коэффициенты трения между ящиком и поверхностью?
Решение : В этом вопросе нам даны две внешние силы, одна из которых приводит ящик в движение $F_1$, а другая поддерживает его движение с постоянной скоростью $F_2$.
Во всех задачах на коэффициент трения та сила, которая приводит объект в движение из состояния покоя, связана с максимальной силой статического трения, величина которой определяется формулой $f_{s, max}=\mu_s F_N$.
Следовательно, сила $F_1$ является максимальной внешней силой, которая необходима для преодоления трения покоя, поэтому мы можем найти коэффициент трения покоя как \begin{align*} F_1&=f_{s,\max}=\ mu_s F_N\\\\ F_1&=\mu_s (мг) \\\\75&=\mu_s (20\times 10) \\\\ \Rightarrow \mu_s &=\frac{75}{200} \\\\ & =0,375\end{align*} Сила трения, действующая на движущееся тело, называется кинетической силой трения. В этом случае постоянная сила $60\,{\rm N}$ поддерживает движение с постоянной скоростью. Итак, используя формулу кинетической силы трения $f_k=\mu_k F_N$ и решая для $\mu_k$, имеем \begin{align*} F_2&=f_k=\mu_k F_N\\\\ F_2&=\mu_2 (мг) \\ \\60&=\mu_k (20\times 10) \\\\ \Rightarrow \mu_s &=\frac{60}{200} \\\\ &=0.300\end{align*} Как и ожидалось, $\mu_s> \mu_k$.
Задача (7): Блок лежит на поверхности движущегося поезда с ускорением $0,2g$. Какой минимальный коэффициент трения покоя должен существовать между блоком и поверхностью поезда, чтобы блок не скользил?
Решение : К блоку приложена сила в направлении ускорения поезда.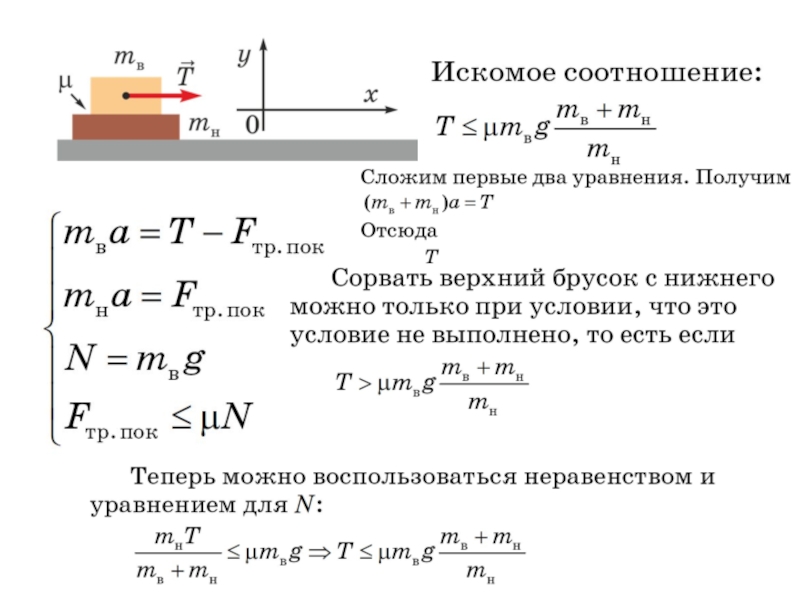 Эта сила хочет сместить блок, но мы хотим, чтобы этого не произошло. Таким образом, сила в направлении, противоположном внешней силе, должна быть приложена к блоку, чтобы остановить его скольжение.
Эта сила хочет сместить блок, но мы хотим, чтобы этого не произошло. Таким образом, сила в направлении, противоположном внешней силе, должна быть приложена к блоку, чтобы остановить его скольжение.
Эта сила, препятствующая скольжению покоящегося объекта, называется трением покоя. Таким образом, в этом случае, если приложенная сила ускорения поезда компенсируется трением покоя, то блок не скользит по поверхности. Следовательно, мы имеем \begin{align*} F_{train}&=f_{s,max}\\\\ F_{train}&=\mu_s F_N \\\\ m_{block}a_{train}&=\ mu_s (m_{block}g) \\\\ m_{block}(0.2g)&=\mu_s (m_{block}g) \\\\ \Rightarrow \mu_s &=0.2\end{align*} В выше $F_N$ — нормальная сила, действующая на поверхность.
Задача (8): Брусок весом $20\,{\rm N}$ тянут за веревку горизонтально по поверхности. Предположим, что коэффициенты статического и кинетического трения между блоком и поверхностью равны $\mu_s=0,8$ и $\mu_k=0,6$. Найдите величину силы трения о брусок, если
(a) Блок тянется силой натяжения $15\,{\rm N}$.
(b) Блок тянется силой натяжения $20\,{\rm N}$.
Решение : Прежде всего, нарисуйте диаграмму свободного тела и укажите все силы, действующие на блок.
Объект не движется в вертикальном направлении, поэтому второй закон Ньютона дает нам величину нормальной силы, действующей на поверхность \[F_N-mg=0 \Rightarrow F_N=mg=20\,{\rm N}\] Мы не знаем, движется блок или нет. Мы знаем только, что если приложенная сила больше, чем максимум статического трения, то блок будет двигаться, иначе объект останется в покое.
С другой стороны, если приложенная сила заставляет объект двигаться, то трение относится к кинетическому типу, в противном случае статическое.
С учетом этих объяснений мы должны сначала найти максимальное статическое трение, $f_{s, max}=\mu_s F_N$, которое действует на блок на такой поверхности. \[f_{s,max}=\mu_s F_N=0,8\times 20=16\,{\rm N}\] Обратите внимание, что это максимальное значение, которое может принять статическое трение. Его значение в любой момент определяется величиной приложенной извне силы.
Его значение в любой момент определяется величиной приложенной извне силы.
(a) В этом случае приложенной силы недостаточно для преодоления максимальной силы трения покоя, поэтому объект не будет двигаться. Следовательно, трение покоя в этот момент должно быть равно внешней силе, т.е. \[f_s=F=20\,{\rm N}\]
(b) Теперь внешняя сила настолько велика, что может преодолеть максимум статического трения, $F>f_{s, max}$, поэтому объект будет двигаться. При движении объекта вместо статического трения движению противодействует сила кинетического трения, величина которой получается как
Задача (9). Ящик массой $m$ тянут с постоянной скоростью по шероховатой поверхности веревкой, наклоненной под углом $\alpha$. Какова величина силы трения на ящике?
Решение : Блок движется по поверхности, поэтому мы имеем дело с кинетической силой трения, величина которой равна $f_k=\mu_k F_N$. Таким образом, нам нужна величина нормальной силы, действующей на поверхность, чтобы найти трение.
Сначала мы рисуем диаграмму свободного тела, чтобы наглядно увидеть силы, действующие на ящик.
Разрешая силу натяжения в веревке, появляются две дополнительные силы в горизонтальном и вертикальном направлениях (синие пунктирные стрелки). В вертикальном направлении движение $a_y=0$ отсутствует, поэтому результирующая сила по вертикали должна быть равна нулю $F_{net,y}=ma_y=0$. Рассмотрим положительное направление вверх. Таким образом, приравнивая результирующую силу для вертикального направления ($y$) нулю, получаем нормальную силу \begin{gather*}F_N+F\sin\alpha-mg=0 \\\\ \Rightarrow F_N=mg-F \sin\alpha \end{gather*} Теперь подставьте нормальную силу в формулу кинетического трения, чтобы найти ее величину \[f_k=\mu_k F_N=\mu_k (mg-F\sin\alpha)\]
Подробнее о решении вектора в физике см. на следующей странице:
Определение вектора в физике
дорожное покрытие составляет $0,6$.
(a) Каково максимальное ускорение автомобиля при торможении?
(b) Предположим, что автомобиль первоначально движется со скоростью $30\,{\rm м/с}$. Определить кратчайшее расстояние, на котором может остановиться автомобиль. 92}{2(6)}\\\\&=75\quad {\rm m}\end{align*}
Определить кратчайшее расстояние, на котором может остановиться автомобиль. 92}{2(6)}\\\\&=75\quad {\rm m}\end{align*}
Коэффициент трения покоя: задачи
Задача (11): A $100\ ,{\rm N}$ применяется к установке ящика $50\,{\rm кг}$ на поверхности. Предположим, что коэффициент трения покоя равен $\mu_s=0,25$. Достаточно ли этой приложенной силы, чтобы сдвинуть коробку?
Решение : Как упоминалось ранее, для статического трения мы можем найти только его максимальное значение, в отличие от кинетического трения. В любой другой момент, до достижения максимального значения, именно внешняя сила определяет величину трения покоя.
Если внешняя сила, приложенная к объекту, меньше максимума трения покоя $F В этом случае сначала найдите максимальное значение трения покоя \[f_{s, max}=\mu_s F_N=0,25\times 500=125\,{\rm N}\], где мы подставили $mg$ вместо нормальная сила, так как тело находится на горизонтальной поверхности и к нему приложена горизонтальная сила. Как видите, приложенной внешней силы недостаточно для перемещения объекта, так как $F Решение : Коробка изначально покоится, и сила $300\,{\rm N}$ приводит ее в движение. Значит, этой внешней силы должно быть достаточно, чтобы преодолеть максимальную силу трения покоя, $F=f_{s, max}=\mu_s F_N$. Объект не движется в вертикальном направлении, поэтому результирующая сила по вертикали должна быть равна нулю, \[F_N-mg=0 \Rightarrow F_N=mg\] Подставив это в приведенное выше выражение и найдя $m$, мы получим есть \begin{align*} F&=\mu_s F_N=\mu_s (мг) \\\\ \Rightarrow m&=\frac{F}{\mu_s g}\\\\ &=\frac{300}{0,35\ раз 10}\\\\ &=85,7\quad {\rm кг} \end{align*} Решение : Во всех задачах на коэффициент трения нам нужно знать нормальную силу, действующую на объект. Теперь перейдем к главному вопросу. Первоначально ящик находится в состоянии покоя. Максимальная сила трения покоя, приложенная к нему, равна \begin{align*} f_{s,max}&=\mu_s F_N\\&=(0,45)(850\times 10) \\&=3825\quad {\rm N}\end{align*} Если приложенная извне сила превышает это значение, то объект начинает двигаться. Следовательно, сила от $3825\,{\rm Н}$ до $850\,{\rm кг}$ на такой поверхности может поставить ящик на грань скольжения. Задача (14): Коэффициент статического трения между шинами автомобиля и уличным асфальтовым покрытием равен $0,9.$. Насколько круто можно парковать машину на холме (максимальный угол)? Решение : Сначала нарисуйте диаграмму свободного тела и укажите все силы, действующие на автомобиль. Сила веса объекта на склоне всегда делится на две составляющие: одна параллельна наклону вниз $mg\sin\alpha$, а другая перпендикулярна наклону, $mg\cos\alpha$, как показано на диаграмме свободного тела. В этом уроке вы узнали, как использовать коэффициент трения для решения физических задач на трение.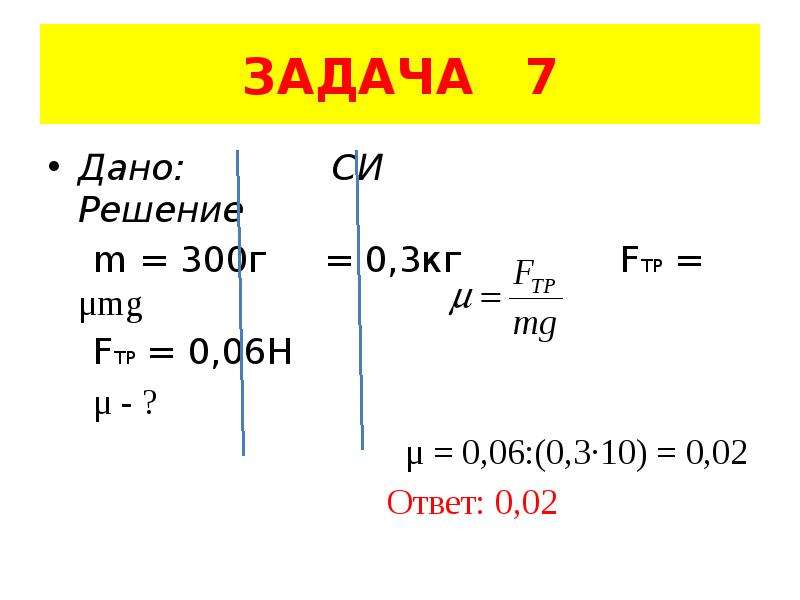
Задача (12): Требуется $300\,{\rm N}$, чтобы ящик начал двигаться по неровному полу. Найдите массу ящика, если коэффициент трения покоя между ними равен $0,35$.
Задача (13): Какая горизонтальная сила необходима, чтобы ящик стоимостью 850 {\rm кг}$ начал скользить по поверхности, если коэффициент трения покоя между ящиком и поверхностью равен 0,45$?  Как правило, если объект находится на горизонтальной поверхности и к нему приложена сила, параллельная этой поверхности, то второй закон Ньютона говорит нам, что нормальная сила равна силе веса mg, $F_N=mg$.
Как правило, если объект находится на горизонтальной поверхности и к нему приложена сила, параллельная этой поверхности, то второй закон Ньютона говорит нам, что нормальная сила равна силе веса mg, $F_N=mg$.
Применение второго закона Ньютона в вертикальном направлении к движению дает нам нормальную силу, действующую на автомобиль. Ускорение автомобиля по вертикали равно нулю $a_y=0$, поэтому результирующая сила в этом направлении должна быть равна нулю $F_{net,y}=ma_y=0$. \[F_N-mg\cos\alpha=0 \Rightarrow F_N=mg\cos\alpha\] В этом случае мы хотим, чтобы автомобиль оставался неподвижным на склоне под углом $\alpha$. Таким образом, нам нужна статическая сила трения (поскольку автомобиль движется не вместо кинетического трения) с той же величиной, но в направлении, противоположном $mg\sin\alpha$, чтобы компенсировать ее. 9\circ\] Это общее правило и один из способов найти коэффициент статического трения. Сводка:



 Направление такое же, как и статическое трение.
Направление такое же, как и статическое трение.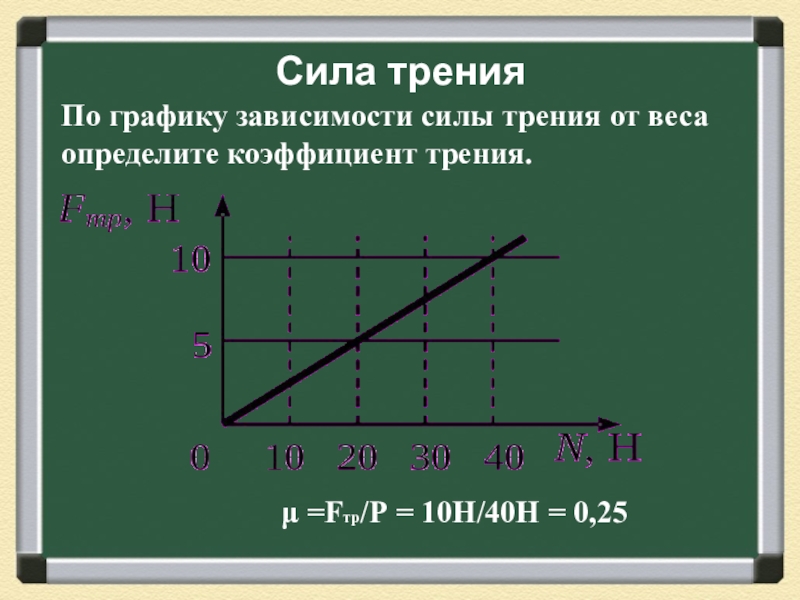 Поскольку приложенная сила меньше значения трения покоя, коробка не будет двигаться, а сила трения будет равна приложенной силе.
Поскольку приложенная сила меньше значения трения покоя, коробка не будет двигаться, а сила трения будет равна приложенной силе.