Электротехника: Второй закон Кирхгофа.
Второй закон (правило) Кирхгофа — алгебраическая сумма напряжений на элементах контура электрической цепи равна нулю.
Контур электрической цепи — замкнутый проводящий ток путь образованный элементами электрической цепи.
Рассмотрим схему на рисунке 1:
Рисунок 1 — Схема с одним контуром
В этой схеме присутствуют: источник ЭДС и резисторы R1, R2 и R3; эти элементы образуют замкнутый путь проводящий ток т.е. контур. Напряжение на источнике ЭДС равно E и направлено так как показано на рисунке 1 стрелочкой справа от источника. Стрелка на условном обозначении источника направлена в сторону противоположную направлению напряжения на источнике ЭДС (иногда это запутывает при расчёте схем но так принято обозначать источник ЭДС). Направления падений напряжений на резисторах указаны стрелками (рис. 1). Для составления уравнения, по второму закону Кирхгофа, необходимо выбрать направление обхода контура (по часовой стрелке или против).
Напряжения резисторов вошли в левую часть уравнения со знаком плюс т.к. направление обхода контура совпадает с направлениями напряжений на резисторах. Напряжение источника ЭДС E вошло в правую часть со знаком плюс т.к. направление обхода контура не совпадает с направлением напряжения источника. Можно также записать напряжение источника в левой части уравнения со знаком минус (что, в принципе, тоже самое):
Уравнение (2) больше подходит для определения второго закона Кирхгофа приведенного выше.
Напряжения совпадающие по направлению с обходом контура записаны со знаком плюс а напряжение источника не совпадающее с обходом контура — со знаком минус и вся эта алгебраическая сумма равна нулю. Теперь, из выражения (2), зная три каких либо напряжения можно найти четвёртое. Обычно расчёт цепи сводится к нахождению токов во всех ветвях или потенциалов всех узлов т.
Из уравнения (3) можно найти ток I. Т.к. контур один то и ток в уравнении один но если схема содержит больше одно контура то и токов будет больше. Вынеся ток I за скобки и поделив обе части уравнения на сумму сопротивлений R1, R2 и R3 получаем уравнение для нахождения тока I, но этот ток можно найти и другим способом например заменой последовательного соединения резисторов R1, R2 и R3 одним резистором R123 и делением напряжения E на сопротивление резистора R123.
Сопротивление резистора R123 равно сумме сопротивлений резисторов R1, R2 и R3. Ток находится из уравнения:
Если в контуре содержится больше одного источника ЭДС то уравнение, по второму закону (правилу) Кирхгофа, составляется аналогично.
Рисунок 2 — Схема с двумя источниками ЭДС
Запишем уравнение, по второму закону Кирхгофа, для контура в схеме на рисунке 2:
Напряжение E2 источника E2 записано в правой части уравнения со знаком
Из уравнения (6) может быть найден ток I.
Если схема имеет больше одного контура то Закон (правило) Кирхгофа все равно выполняется для всех контуров. Уравнения по второму закону Кирхгофа, в таком случае, составляются аналогично тому как в примерах выше. Отличие будет только в том что необязательно для всех элементов будет один и тот же ток. В случае если схема имеет больше одного контура можно считать что через каждый элемент течет свой ток. Напряжение на элементе, в таком случае, находится умножением сопротивления этого элемента (если этот элемент например резистор) на ток данного элемента.
В случае если схема имеет больше одного контура можно считать что через каждый элемент течет свой ток. Напряжение на элементе, в таком случае, находится умножением сопротивления этого элемента (если этот элемент например резистор) на ток данного элемента.
Рисунок 3 — Часть схемы имеющей больше одного контура
Рисунок 4 — Часть схемы имеющей больше одного контура и ветвь из двух элементов
Рисунок 4 — Часть схемы имеющей больше одного контура, ветвь из двух элементов и элементы напряжения на на которых имеют направления не совпадающие с выбранным направлением обхода контура
О том что такое узлы и ветви можно узнать из предыдущей статьи.
При составлении уравнений по второму закону Кирхгофа не стоит слишком много времени уделять выбору направлений обходов контуров и направлений токов (
они (направления обходов и токов) выбираются произвольно) так как реальные направления токов определяются при решении этих уравнений.
Пример:
Направление напряжения на элементе R1 такое же как и направление тока этого элемента по тому что принято считать что ток течёт от большего потенциала к меньшему а напряжение направлено также (от большего потенциала к меньшему).
Правила Кирхгофа для электрической цепи, понятным языком
Содержание:
Чтобы сформулировать закон Кирхгофа для электрической цепи, потребовалось ввести новые термины в теорию – узлы, ветви и контур. Ветвями называют любой тип двухполюсной цепи. Узлом называют точку, в которой соединяются несколько ветвей. Эти элементы принадлежат одному электрическому контуру. Законы представляют собой различные соотношения между величинами тока на разных участках цепи. С их помощью можно провести расчет величины постоянных или переменных токов при помощи формул, созданный этим ученым.
В данной статье будет рассказано про законы Кирхгофа, как они могут использоваться на практике и как правильно провести расчеты, связанные с ними. В качестве дополнения, статья содержит два видеоролика, одну скачиваемую статью по выбранной теме.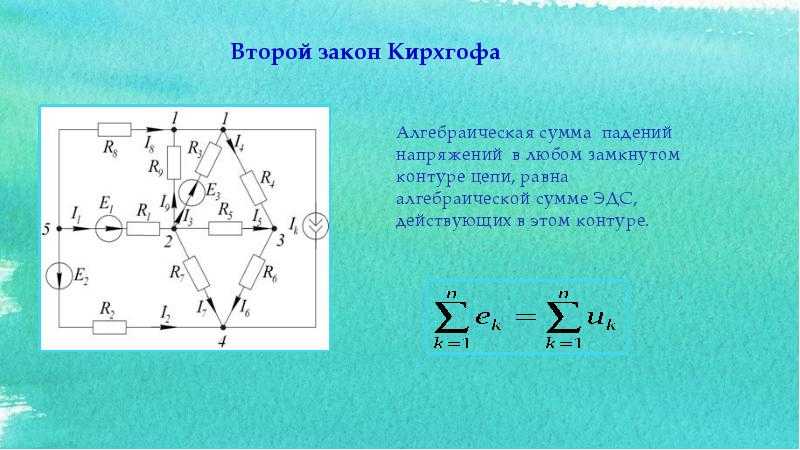
Законы Кирхгофа
Закон Ома устанавливает зависимость между силой тока, напряжением и сопротивлением для простейшей электрической цепи, представляющей собой один замкнутый контур. В практике встречаются более сложные (разветвленные) электрические цепи, в которых имеются несколько замкнутых контуров и несколько узлов, к которым сходятся токи, проходящие по отдельным ветвям. Значения токов и напряжений для таких цепей можно находить при помощи законов Кирхгофа.
Первый закон
Первый закон Кирхгофа устанавливает зависимость между токами для узлов электрической цепи, к которым подходит несколько ветвей. Согласно этому закону алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю:
?I = 0 (16)
При этом токи, направленные к узлу, берут с одним знаком (например, положительным), а токи, направленные от узла,— с противоположным знаком (отрицательным). Например, для узла А
I1 + I2 + I3 – I4 – I5 = 0 (17)
Это интересно! Все о полупроводниковых диодах.
Преобразуя это уравнение, получим, что сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от этого узла:
I1 + I2 + I3 = I4 + I5 (17′)
В данном случае имеет место полная аналогия с распределением потоков воды в соединенных друг с другом трубопроводах.
Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа. Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах.
Первый закон Кирхгофа.
Второй закон Кирхгофа устанавливает зависимость между э. д. с. и напряжением в замкнутой электрической цепи. Согласно этому закону во всяком замкнутом контуре алгебраическая сумма э. д. с. равна алгебраической сумме падений напряжения на сопротивлениях, входящих в этот контур:
?E = ?IR (18)
При составлении формул, характеризующих второй закон Кирхгофа, значения э. д. с. E и падений напряжений IR считают положительными, если направления э. д. с. и токов на соответствующих участках контура совпадают с произвольно выбранным направлением обхода контура. Если же направления э. д. с. и токов на соответствующих участках контура противоположны выбранному направлению обхода, то такие э. д. с. и падения напряжения считают отрицательными.
д. с. E и падений напряжений IR считают положительными, если направления э. д. с. и токов на соответствующих участках контура совпадают с произвольно выбранным направлением обхода контура. Если же направления э. д. с. и токов на соответствующих участках контура противоположны выбранному направлению обхода, то такие э. д. с. и падения напряжения считают отрицательными.
Рассмотрим в качестве примера электрическую цепь, в которой имеются два источника с электродвижущими силами E1 и E2, внутренними сопротивлениями Ro1, Ro2 и два приемника с сопротивлениями R1 и R2. Применяя второй закон Кирхгофа для «этой цепи и выбирая направление ее обхода по часовой стрелке,
получим:
E1 – E2 = IR01 + IR02 + IR1 + IR.
При этом э. д. с. E1 и ток I совпадают с выбранным направлением обхода контура и считаются положительными, а э. д. с. Е2, противоположная этому направлению, считается отрицательной. Если в электрической цепи э. д. с. источников электрической энергии при обходе соответствующего контура направлены навстречу друг другу (см. рис. 24, а), то такое включение называют встречным. В этом случае на основании второго закона Кирхгофа ток I = (E1-E2)/(R1+R2+R01+R02).
д. с. источников электрической энергии при обходе соответствующего контура направлены навстречу друг другу (см. рис. 24, а), то такое включение называют встречным. В этом случае на основании второго закона Кирхгофа ток I = (E1-E2)/(R1+R2+R01+R02).
[stextbox id=’info’] Встречное направление э. д. с. имеет место, например, на э. п. с.при включении электродвигателей постоянного тока (их можно рассматривать как некоторые источники э. д. с.) в две параллельные группы, а также при параллельном включении аккумуляторов в батарее.[/stextbox]
Если же э. д. с. источников электрической энергии имеют по контуру одинаковое направление (рис. 24, б), то такое включение называют согласным и ток I = (E1-E2)/(R1+R2+R01+R02). В некоторых случаях такое включение недопустимо, так как ток в цепи резко возрастает.
Если в электрической цепи имеются ответвления (рис. 24, в), то по отдельным ее участкам проходят различные токи I1 и I2. Согласно второму закону Кирхгофа E1-E2=I1R01+I1R1-I2R2-I2R02-I2R3+I1R4.
При составлении этого уравнения э. д. с. Е1 и ток I1 считаются положительными, так как совпадают с принятым направлением обхода контура, э. д. с. Е2 и ток I2 — отрицательными.
Алгебраическая сумма разностей потенциалов
Закон напряжения по Густаву Кирхгофу — второй закон этого автора, используемый для анализа электрической схемы. Вторым законом Кирхгофа утверждается, что для последовательного замкнутого контура алгебраическая сумма всех напряжений по кругу любой замкнутой цепи равна нулю. Утверждение обусловлено тем, что контур цепи является замкнутым проводящим путём, где потери энергии исключаются. Другими словами, алгебраическая сумма разностей потенциалов замкнутого контура теоретически равняется нулю:
ΣV = 0
Следует обратить внимание: под термином «алгебраическая сумма» имеется в виду учёт полярностей и признаков источников ЭДС, а также падения напряжений по кругу контура. Эта концепция закона Кирхгофа, известная как «сохранение энергии», как движение по кругу замкнутого контура или схемы, утверждает логику возврата к началу цепи и к первоначальному потенциалу без потери напряжения по всему контуру.
Эта концепция закона Кирхгофа, известная как «сохранение энергии», как движение по кругу замкнутого контура или схемы, утверждает логику возврата к началу цепи и к первоначальному потенциалу без потери напряжения по всему контуру.
[stextbox id=’info’]Следовательно, любое падение напряжения по кругу контура теоретически равно потенциалу любых источников напряжения, встречающихся на этом пути. [/stextbox]
Отсюда следует вывод: применяя Второй закон Кирхгофа к определенному элементу электрической схемы, важно обращать особое внимание на алгебраические знаки падений напряжения на элементах (источниках ЭДС), иначе вычисления оборачиваются ошибкой.
Одиночный контурный элемент — резистор
Простым примером с резистором предположим — ток протекает в том же направлении, что и поток положительного заряда. В этом случае поток тока через резистор протекает от точки A до точки B. Фактически — от положительной клеммы до отрицательной клеммы. Таким образом, поскольку движение положительного заряда отмечается в направлении аналогичном направлению течения тока, на резистивном элементе зафиксируется падение потенциала, которое приведет к падению минусового потенциала на резисторе (— I * R).
Если же поток тока от точки B до точки A протекает в противоположном направлении относительно потока положительного заряда, тогда через резистивный элемент отметится рост потенциала, поскольку имеет место переход от минусового потенциала к потенциалу плюсовому, что даёт падение напряжения (+ I * R). Таким образом, чтобы правильно применить закон Кирхгофа по напряжению к электрической цепи, необходимо точно определить направление полярности. Очевидно, знак падения напряжения на резисторе зависит от направления тока, протекающего через резистор.
Направление потока тока по замкнутому контуру допустимо определять либо по часовой стрелке, либо против часовой стрелки, и любой вариант допустим к выбору. Если выбранное направление отличается от фактического направления тока, соответствие закону Кирхгофа получится корректным и действительным, но приведет к результату, когда алгебраический расчёт будет иметь знак минус. Чтобы лучше понять эту концепцию, логично рассмотреть ещё один пример с одним контуром цепи на соответствие Второму Закону Кирхгофа.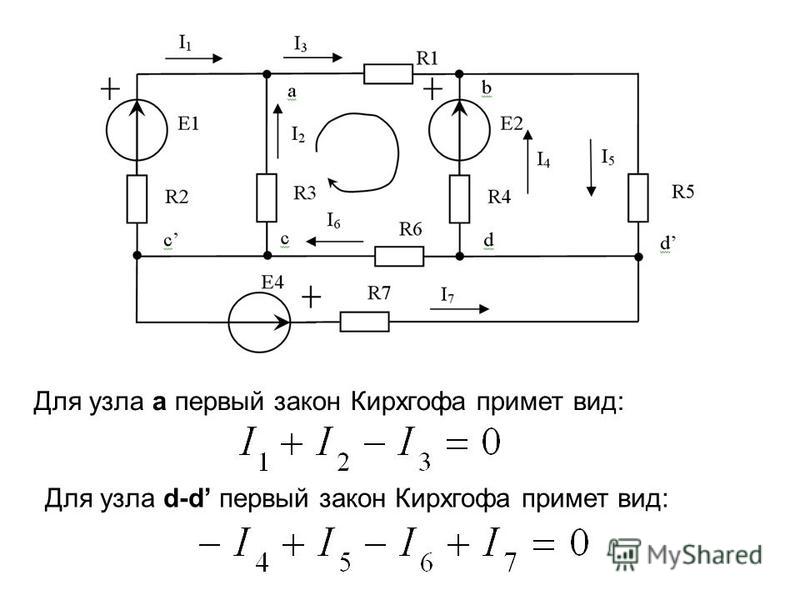
Одиночный контур электрической цепи
Второй закон Кирхгофа утверждает — алгебраическая сумма разностей потенциалов любого замкнутого контура равна нулю. Демонстрационная схема действия Второго закона Кирхгофа для замкнутого контура с двумя резисторами и одним источником ЭДС. Если принять условие, что два резистора R1 и R2 соединены последовательно, оба элемента являются частью одного контура. Соответственно, одинаковый ток протекает через каждый из резисторов.
Таким образом, падение напряжения на резисторе R1 = I * R1 и падение напряжения на резисторе R2 = I * R2, дают напряжение по Второму закону Кирхгофа:
V = I * Rs
где: Rs = R1 + R2.
Очевидно: применение Второго закона Кирхгофа к одиночному замкнутому контуру даёт формулу эквивалентного или полного сопротивления для последовательной цепи. Допустимо расширить эту формулу, чтобы найти значения падений потенциалов по кругу контура:
I = V / Rs
Vr1 = V * (R1 / R1 + R2)
Vr2 = V * (R2 / R1 + R2)
Есть три резистора номинальным сопротивлением 10, 20, 30 Ом, соответственно. Все три резистивных элемента соединены последовательно к 12-вольтовому аккумулятору.
Все три резистивных элемента соединены последовательно к 12-вольтовому аккумулятору.
Интересно по теме: Как проверить стабилитрон.
Требуется рассчитать:
- общее сопротивление,
- ток цепи,
- ток через каждый резистор,
- падение напряжения на каждом резисторе.
Рассчитаем общее сопротивление:
Ro = R1 + R2 + R3 = 10Ω + 20Ω + 30Ω = 60Ω
Ток цепи:
I = V / Ro = 12 / 60 = 0,2A (200 мА)
Ток через каждый резистор:
I * R1 = I * R2 = I * R3 = 0,2A (200 мА)
Падение потенциала на каждом из резисторов:
VR1 = I * R1 = 0.2 * 10 = 2В
VR2 = I * R2 = 0.2 * 20 = 4В
VR3 = I * R3 = 0.2 * 30 = 6В
Таким образом, Второй закон Кирхгофа справедлив, учитывая что индивидуальные падения напряжения, отмеченные по кругу замкнутого контура, в итоге составляют сумму напряжений.
Вывод
Теория второго закона Кирхгофа, также известного как закон сохранения потенциала, особенно полезна для работы с последовательными схемами. Последовательные схемы действуют как делители потенциала, а цепь делителя потенциала — это важный узел многих электрических (электронных) схем.
Последовательные схемы действуют как делители потенциала, а цепь делителя потенциала — это важный узел многих электрических (электронных) схем.
Второй закон
Для расчетов сложных электрических цепей с несколькими источниками энергии используют второй закон Кирхгофа, который может быть сформулирован так: во всяком замкнутом электрическом контуре алгебраическая сумма всех э. д. с. равна алгебраической сумме падений напряжения в сопротивлениях, включенных последовательно в эту цепь, т. е.
E1 + E2 + E3 + . . . = I1r1 + I2r2 + I3r3 + .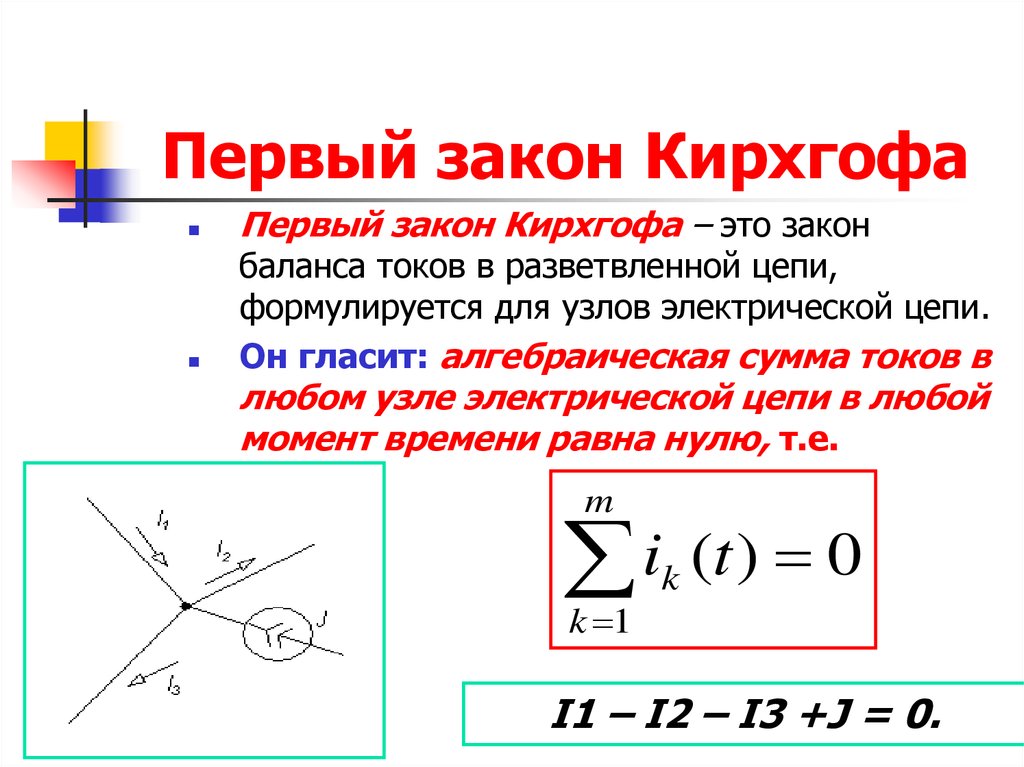 . .
. .
При этом положительными следует считать э. д. с. и токи, направление которых совпадает с направлением обхода контура.
Если в электрическую цепь включены два источника энергии, э. д. с. которых совпадает по направлению (рис. 20, а), то э. д. с. всей цепи равна сумме э. д. с. этих источников, т. е. E = E1 + E2. Если же в цепи э. д. с. источников имеют противоположные направления, то результирующая э. д. с. равна разности э. д. с. этих источников, т. е.
E = E1 – E2.
Второй закон Кирхгофа.При последовательном включении в электрическую цепь нескольких источников энергии с различным направлением э. д. с. общая э. д. с. равна алгебраической сумме э. д. с. всех источников. При суммировании э. д. с. одного направления берут со знаком плюс, а э. д. с. противоположного направления — со знаком минус. При составлении уравнений выбирают направление обхода цепи и произвольно задаются направлениями токов.
Замкнутая цепь обозначена буквами а, б, в и г. Ввиду наличия ответвлений в точках а, б, в, г токи I1, I2, I3 и I4, отличаясь по силе, могут иметь различные направления.
Для такой цепи в соответствии со вторым законом Кирхгофа можно написать:
E1 – E2 – E3 = I1(r01 + r1) – I2(r02 + r2) – I3(r03 + r3) + I4r4,
где r01, r02, r03 — внутренние сопротивления источников энергии,
r1, r2, r3, r4 — сопротивления приемников энергии.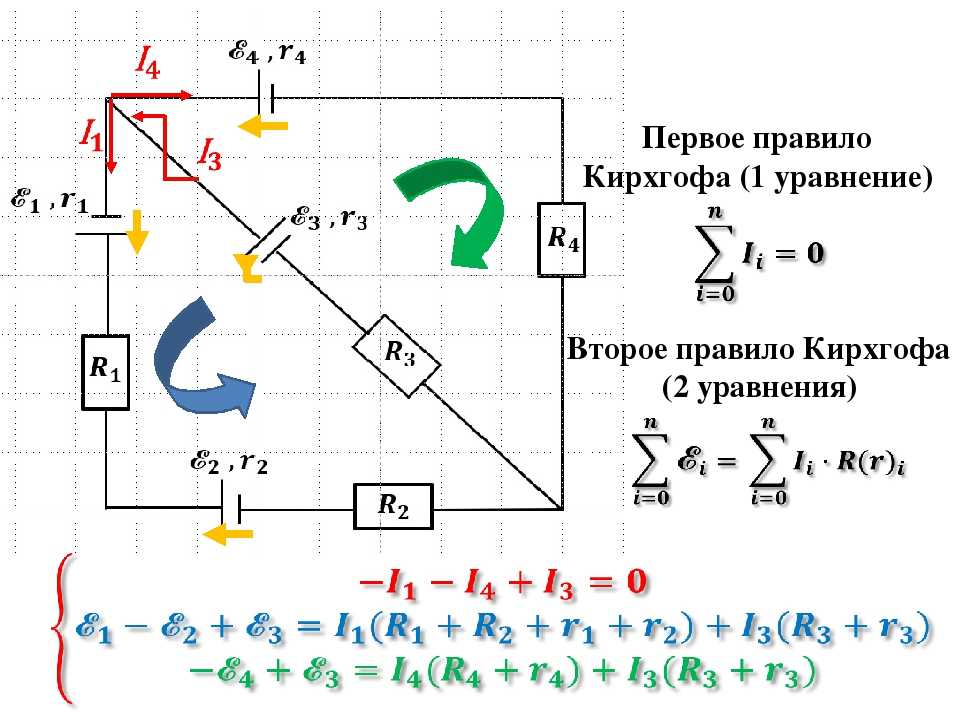
В частном случае при отсутствии ответвлений и последовательном соединении проводников общее сопротивление равно сумме всех сопротивлений.
Если внешняя цепь источника энергии с внутренним сопротивлением r состоит, например, из трех последовательно соединенных проводников с сопротивлениями, соответственно равными r1, r2, r3, то на основании второго закона Кирхгофа можно написать следующее равенство:
E = I r + I r1 + I r2 + I r3.
При нескольких источниках тока в левой части этого равенства была бы алгебраическая сумма э. д. с. этих источников.
Заключение
Рейтинг автора
Написано статей
Более подробную информацию о законах Кирхгофа для электрической цепи Занятие по законом Кирхгофа. Если у вас остались вопросы, можно задать их в комментариях на сайте.
А также в нашей группе ВК можно задавать вопросы и получать на них подробные ответы от профессионалов. Для этого приглашаем читателей подписаться и вступить в группу. В завершение статьи хочу выразить благодарность источникам, откуда мы черпали информацию во время подготовки материала:
Для этого приглашаем читателей подписаться и вступить в группу. В завершение статьи хочу выразить благодарность источникам, откуда мы черпали информацию во время подготовки материала:
www.electrono.ru
www.tehinfor.ru
www.zetsila.ru
www.texnic.ru
www.zamzamstore.ru
Предыдущая
ТеорияЧто такое анод и катод, в чем их практическое применение
Следующая
ТеорияЧто такое электрический ток, виды и условия его существования
Законы Кирхгофа — формулы и примеры использования
Содержание
Первый закон Кирхгофа
Первый закон Кирхгофа говорит, что сумма токов в любом узле электрической цепи равна нулю. Существует и другая, аналогичная по смыслу формулировка: сумма значений токов, входящих в узел, равна сумме значений токов, выходящих из узла.
Давайте разберем сказанное более подробно. Узлом называют место соединения трех и более проводников.
Ток, который втекает в узел, обозначается стрелкой, направленной в сторону узла, а выходящий из узла ток – стрелкой, направленной в сторону от узла.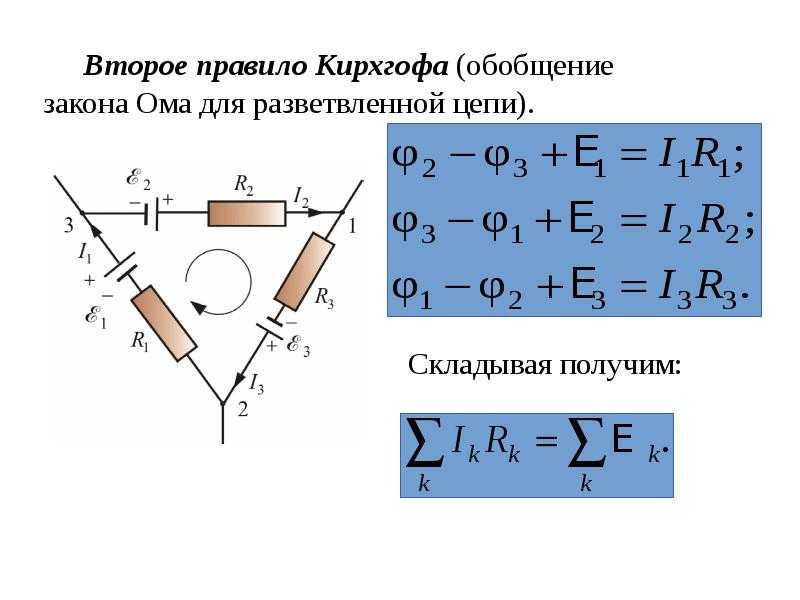
Согласно первому закону Кирхгофа
Условно присвоили знак «+» всем входящим токам, а «-» ‑ все выходящим. Хотя это не принципиально.
1 закон Кирхгофа согласуется с законом сохранения энергии, поскольку электрические заряды не могут накапливаться в узлах, поэтому, поступающие к узлу заряды покидают его.
Убедиться в справедливости 1-го закона Кирхгофа нам поможет простая схема, состоящая из источника питания, напряжением 3 В (две последовательно соединенные батарейки по 1,5 В), три резистора разного номинала: 1 кОм, 2 кОм, 3,2 кОм (можно применять резисторы любых других номиналов). Токи будем измерять мультиметром в местах, обозначенных амперметром.
Если сложить показания трех амперметров с учетом знаков, то, согласно первому закону Кирхгофа, мы должны получить ноль:
I1 – I2 – I3 = 0.
Или показания первого амперметра А1 будет равняться сумме показаний второго А2 и третьего А3 амперметров.
Второй закон Кирхгофа
Второй закон Кирхгофа воспринимается начинающими радиолюбителями гораздо сложнее, нежели первый.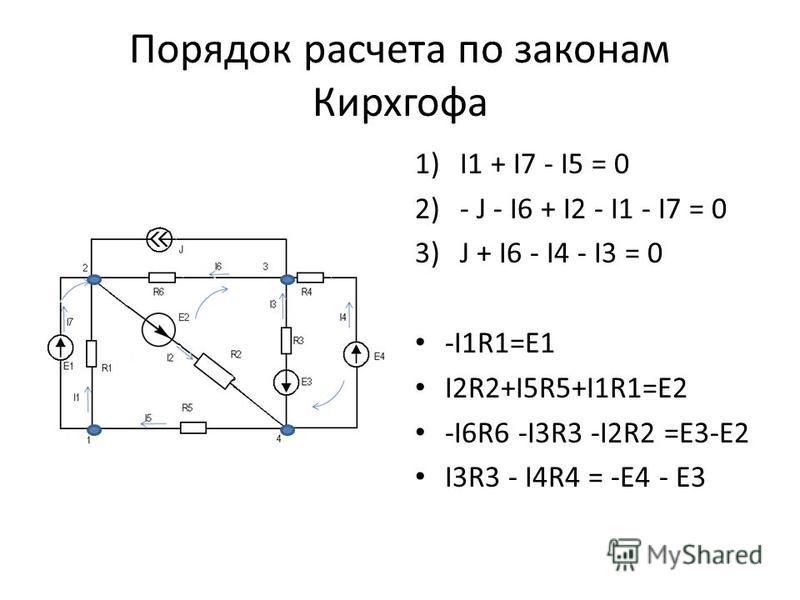 Однако сейчас вы убедитесь, что он достаточно прост и понятен, если объяснять его нормальными словами, а не заумными терминами.
Однако сейчас вы убедитесь, что он достаточно прост и понятен, если объяснять его нормальными словами, а не заумными терминами.
Упрощенно 2 закон Кирхгофа говорит: сумма ЭДС в замкнутом контуре равна сумме падений напряжений
ΣE = ΣIR
Самый простой случай данного закона разберем на примере батарейки 1,5 В и одного резистора.
Поскольку резистор всего один и одна батарейка, то ЭДС батарейки 1,5 В будет равна падению напряжения на резисторе.
Если мы возьмем два резистора одинакового номинала и подключим к батарейке, то 1,5 В распределятся поровну на резисторах, то есть по 0,75 В.
Если возьмем три резистора снова одинакового номинала, например по 1 кОм, то падение напряжения на них будет по 0,5 В.
Формулой это будет записано следующим образом:
Рассмотрим условно более сложный пример. Добавим в последнюю схему еще один источник питания E2, напряжением 4,5 В.
Обратите внимание, что оба источника соединены последовательно и согласно, то есть плюс одной батарейки соединяется с минусом другой батарейки или наоборот.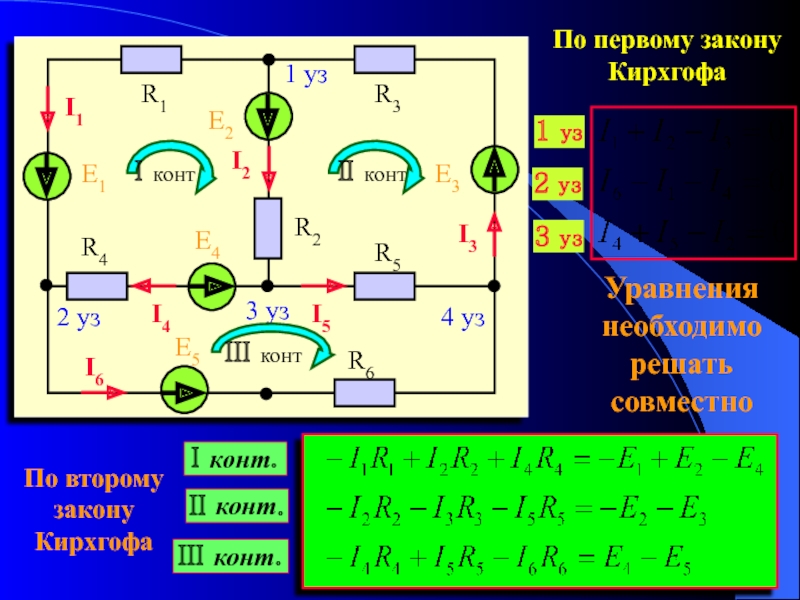 При таком способе соединения гальванических элементов их электродвижущие силы складываются: E1 + E2 = 1,5 + 4,5 = 6 В, а падение напряжения на каждом сопротивлении составляет по 2 В. Формулой это описывается так:
При таком способе соединения гальванических элементов их электродвижущие силы складываются: E1 + E2 = 1,5 + 4,5 = 6 В, а падение напряжения на каждом сопротивлении составляет по 2 В. Формулой это описывается так:
И последний отличительный вариант, который мы рассмотрим в данной статье, предполагает последовательное встречное соединение гальванических элементов. При таком соединении источников питания из большей ЭДС отнимается значение меньшей ЭДС. Следовательно к резисторам R1…R3 будет приложена разница E1 – E2, то есть 4,5 – 1,5 = 3 В, – по одному вольту на каждый резистор.
Второй закон Кирхгофа работает не зависимо от количества источников питания и нагрузок, а также независимо от места их расположения в контуре схемы. Полезно будет собрать рассмотренные схемы и выполнить соответствующие измерения с помощью мультиметра.
Законы Кирхгофа действуют как для постоянного, так и для переменного тока.
Формулировка правил
Сразу необходимо внести ясность. Хотя во многих технических текстах используется слово закон, на самом деле это правило. В чем различие? Закон основывается на фундаментальных истинах, фактах, правило несет более абстрактное понимание. Чтобы это лучше понять рассмотрим основы этого метода.
В чем различие? Закон основывается на фундаментальных истинах, фактах, правило несет более абстрактное понимание. Чтобы это лучше понять рассмотрим основы этого метода.
Из-за сложности вычислений его лучше использовать там, где схема имеет узлы и контуры. Узлом называется место соединения более двух цепей. Это как если взять три и более обычных нитки и связать их вместе. Контуром называется замкнутая цепь, включающая в себя три и более таких узла.
Отдельная ветвь может содержать сколько угодно резисторов, под которыми подразумеваются нагрузки с активным сопротивлением. Все они объединяются в один общий резистор, так как это упрощает решение задачи. Также в цепи может быть один или несколько источников питания, которые также объединяются в один элемент, либо их может и не быть. Тогда цепь будет состоять только из сопротивления.
Контур всегда начинается и заканчивается одним и тем же узлом. Поскольку узлы обозначаются латинскими или русскими буквами, то в уравнении будет на одну букву больше, чем самих соединений.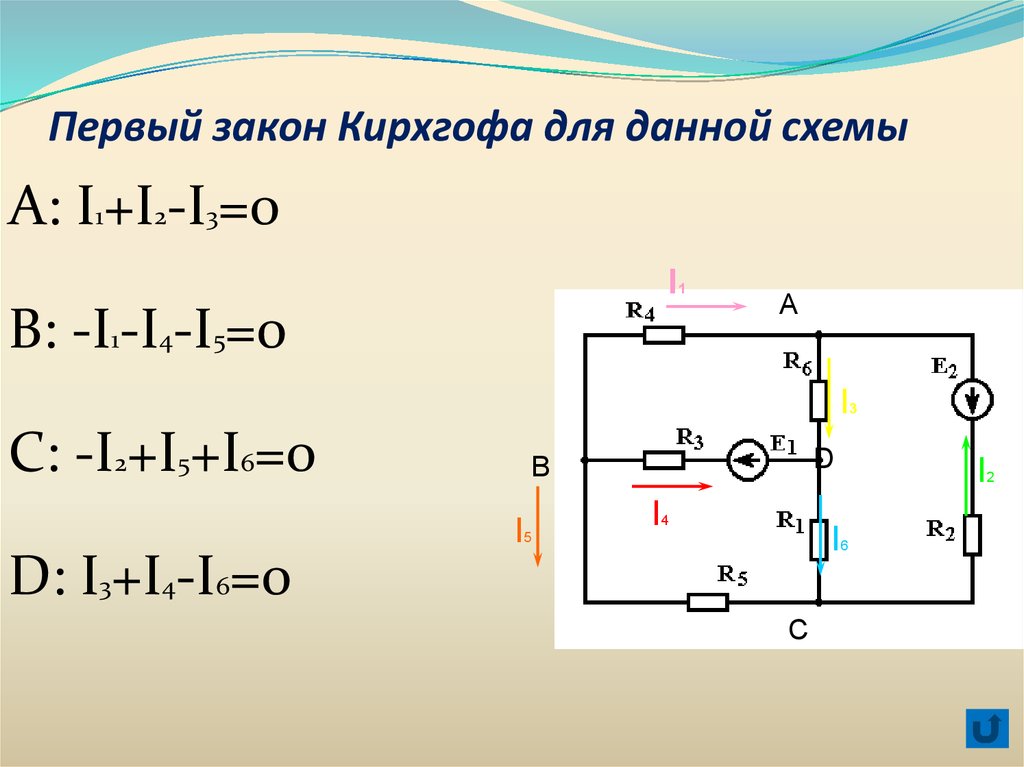 Например, участок состоит из узлов A, B, C, D. Тогда обозначение этой петли будет следующим: A, B, C, D, A. На самом деле, начинать отсчет можно с любой буквы петли, например, C, D, A, B, C, просто в первом варианте легче будет не запутаться.
Например, участок состоит из узлов A, B, C, D. Тогда обозначение этой петли будет следующим: A, B, C, D, A. На самом деле, начинать отсчет можно с любой буквы петли, например, C, D, A, B, C, просто в первом варианте легче будет не запутаться.
Определения
Как уже было сказано ветвь – это отрезок электрической цепи, в которой направление движения заряда происходит в одну сторону. Сходящиеся в узле ветви имеют разное направление токов. Контур может состоять из нескольких внутренних контуров, ветви и узлы которых также относятся к этому контуру. Сам закон Кирхгофа по существу содержит два правила, относящиеся к узлу и контуру. Самым главным и сложным является составление уравнений, учитывающих все составляющие этой формулы.
Первый закон
Первое правило говорит о сохранении заряда. Согласно ему, в узле напряжение должно быть равно нулю. Это возможно только в том случае, если все входящие токи в эту точку заходят через одни ветви, а выходят через другие. Соотношение входящих и выходящих токов может быть разным, но суммарная составляющая положительных и отрицательных потенциалов всегда одинакова.
Предположим, в узел входят токи по трем ветвям, а выходят по двум. Суммарная величина входящих токов будет точно равняться суммарной величине выходящих. Если отобразить это математически, то сумма положительных векторов I1, I2 и I3 будет равняться сумме отрицательных векторов I4 и I5.
Второй закон
Это правило связано с сохранением энергии в контуре. Другими словами, энергия источников э. с, входящих в контур или рассматриваемый участок, равна падению напряжения на сопротивлениях этого участка. Если выбранный участок не имеет источников питания, то суммарное падение напряжения на всех нагрузках будет равно нулю. Прежде чем переходить к расчетам, следует ознакомиться еще с некоторыми моментами.
Первый закон Кирхгофа
Первый закон Кирхгофа гласит, что в ветвях образующих узел электрической цепи алгебраическая сумма токов равна нулю(токи входящие в узел считаются положительными, выходящие из узла отрицательными).
Пользуясь этим законом для узла A (рисунок 1) можно записать следующее выражение:
Рисунок 1 — Первый закон Кирхгофа
I1 + I2 − I3 + I4 − I5 − I6 = 0.
Попытайтесь самостоятельно применить первый закон Кирхгофа для определения тока в ветви. На приведенной выше схеме изображены шесть ветвей образующие электрический узел В, токи ветвях входят и выходят из узла. Один из токов i неизвестен.
Запишите выражение для узла В
I1 + I2 + I3 + I4 + I5 − i = 0 I1 – I2 + I3 − I4 + I5 − i = 0 I1 + I2 + I3 − I4 + I5 − i = 0
Второй закон Кирхгофа.
Второй закон Кирхгофа:в контуре электрической цепи алгебраическая сумма эдс равна алгебраической сумме падений напряжения на всех сопротивлениях данного контура.
где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii, Ri – ток и сопротивление i-й ветви.
Применение второго закона Кирхгофа
Для контура ABСDE, изображенного на рисунке 4, стрелками указаны положительные направления токов (произвольно). Составим уравнение согласно второму закону Кирхгофа. Для этого произвольно зададимся направлением обхода контура по часовой или против часовой стрелки.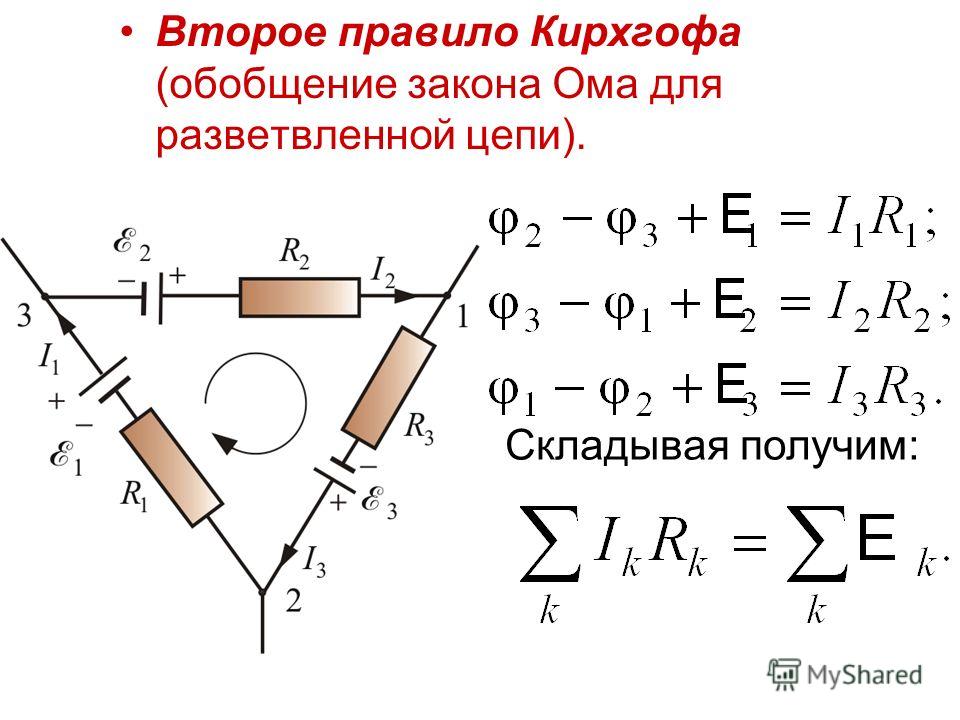 В данном примере направление обхода контура выберем по часовой стрелке.
В данном примере направление обхода контура выберем по часовой стрелке.
При составлении уравнений по второму закону Кирхгофа, ЭДС записывается со знаком “+”, если ее направление совпадает с направлением произвольно выбранного обхода контура. В противном случае ЭДС записывается со знаком “-”.
Падения напряжения записываются со знаком “+”, если направление тока в нем совпадает с направлением обхода.
Начнём с эдс E1, так как её направление совпадает с обходом контура — записываем её со знаком “+” перед знаком равно.
Контур ABСDE E1 =
E2 направленна против обхода контура записываем со знаком “-” перед знаком равно.
Контур ABСDE E1 − E2=
Так как больше ЭДС в контуре ABСDЕ нет — левая часть уравнения готова.
В правой части уравнения указываются падения напряжения контура, так как направления токов I1 и I2 совпадает с обходом контура – записываем падения напряжения со знаком “+”.
Контур ABСDЕE E1 − E2 = I1*R1 + I2*R2
Направление тока I3 не совпадет с обходом контура:
Контур ABСDE E1 − E2 = I1*R1 + I2*R2 − I3*R3.
Уравнение для контура готово.
Законы Кирхгофа являются основой для расчета электрической цепи, вот несколько методов применяющие данные законы.
Расчеты электрических цепей с помощью законов Кирхгофа
Частота вращения: формула
Для выполнения подобных расчётов электрических цепей существует определённый алгоритм, при котором вычисляются токи для каждой ветви и напряжения на выводах всех элементов, включённых в ЭЦ. Для того чтобы рассчитать любую схему, придерживаются следующего порядка:
- Разбивают ЭЦ на ветви, контуры и узлы.
- Стрелками намечают предполагаемые направления движения I в ветвях. Произвольно намечают направление, по которому при написании уравнений обходят контур.
- Пишут уравнения, применяя первое и второе правило Кирхгофа. При этом учитывают правила знаков, а именно:
- «плюс» имеют токи, втекающие в узел, «минус» – токи, вытекающие из узла;
- Е (ЭДС) и снижение напряжения на резисторах (R*I) обозначают знаком «плюс», если ток и обход совпадают по направлению, или «минус», если нет.

Информация. Независимыми узлами называют такие, которые отличаются от других как минимум одной новой веткой. Ветви, содержащие ЭДС именуют активными, без ЭДС – пассивными.
В качестве примера можно рассмотреть схему с двумя ЭДС и рассчитать токи.
Пример схемы для расчёта с двумя E
Произвольно выбирают направление токов и контурного обхода.
Намеченные направления на схеме
Составляются следующие уравнения с применением первого и второго закона Кирхгофа:
- I1 – I3 – I4 = 0 – для узла a;
- I2 + I4 – I5 = 0 – для узла b;
- R1*I1 + R3*I3 = E1 – контур acef;
- R4*I4 — R2*I2 – R3*I3 = — E2 – контур abc;
- R6*I5 + R5*I5 + R2*I2 = E2 – контур bdc.
Уравнения решаются с помощью методов определителей или подстановки.
Особенности составления уравнений для расчёта токов и напряжений
В первую очередь выбирается участок, который необходимо исследовать. Затем на каждой ветке произвольно устанавливается стрелка показывающая направление движения тока. Это нужно для того, чтобы потом не ошибиться. При расчете неточность направления будет исправлена. Каждую стрелку обозначают буквой I с индексом. Удобнее будет рассматривать участок, если стрелки находятся в непосредственной близости от точки соединения цепей. Источники питания и резисторы тоже обозначают, а у общего резистора добавляют сопротивление.
Это нужно для того, чтобы потом не ошибиться. При расчете неточность направления будет исправлена. Каждую стрелку обозначают буквой I с индексом. Удобнее будет рассматривать участок, если стрелки находятся в непосредственной близости от точки соединения цепей. Источники питания и резисторы тоже обозначают, а у общего резистора добавляют сопротивление.
Внутри участка также произвольно показывают направление обхода, ориентируясь на возможные потенциалы. Оно необходимо для сравнения направления движения тока. Это сравнение покажет, какой знак должен стоять у числа. Если оба направления совпадают, ставят знак + и знак – если направления противоположны.
Число поставленных задач должно соответствовать количеству выбранных неизвестных. Допустим, имеется три цепи и необходимо вычислить их токи, значит, составленных формул также должно быть три. Получается, что в новом уравнении должен быть хотя бы один новый элемент, которого нет в предыдущих задачах.
Значение для электротехники
Правила Кирхгофа являются дополнением к другим законам.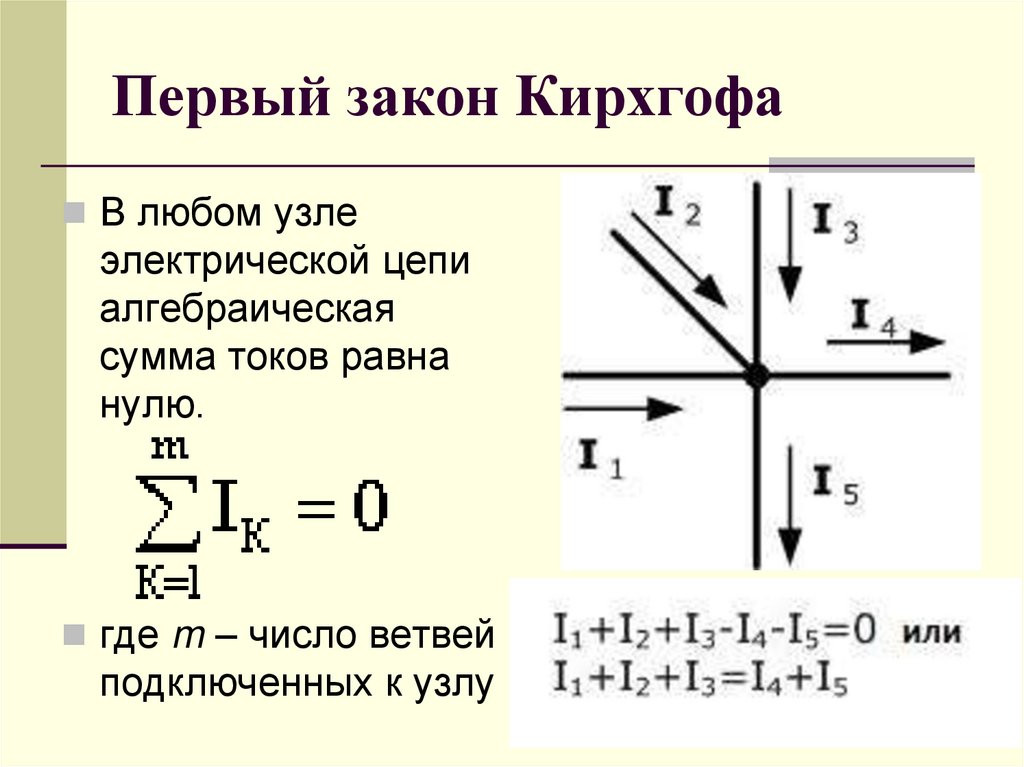 Основная сложность состоит в нахождении участков, поскольку их границы не всегда легко обнаружить. После ограничения нужной области необходимо выделить все неизвестные. Составление задач уже относительно легкое дело. Решаются они как обычные уравнения.
Основная сложность состоит в нахождении участков, поскольку их границы не всегда легко обнаружить. После ограничения нужной области необходимо выделить все неизвестные. Составление задач уже относительно легкое дело. Решаются они как обычные уравнения.
Поэтому, несмотря на первые трудности, эти правила все же легче составить и решить, чем использовать, допустим, закон Ома. Поэтому они широко используются в электротехнике. Чтобы понять, как на практике применить описанный способ, рассмотрим один пример.
Значение в математике
Имеется контур, состоящий из четырех цепей. В первой содержится источник питания ε1 с внутренним сопротивлением источника r1, во второй какая-то нагрузка R1. Третья имеет источник питания и нагрузку. Четвертая состоит из нагрузки. Точки B и F являются узлами. Стрелки возле них показывают предположительное направление тока. Стрелка внутри участка показывает направление обхода. Необходимо найти ток в цепях: AK, AB, BF, CD. По идее нужно составить четыре уравнения, но поскольку ε1 и R1 единственные на участке KAB, то их объединим в одну цепь. Выходит, нужно составить три уравнения.
Выходит, нужно составить три уравнения.
Первое берется из первого правила: I1 + I2 + I3 = 0. Поскольку I1, I2 втекают в узел B, они имеют положительный знак, а I3 вытекает из него, то имеет отрицательный знак. Подставляем в уравнение и получаем I1 + I2 – I3 = 0, или в таком виде I1 + I2 = I3. Второе и третье уравнение берем из второго правила. Для этого используем контур BCDFB и преобразуем формулировку в математическое решение: ε2 = I2 × R2 + I3 × R3. Для участка ACDKA получаем соответственно ε1 = I1 × R1 + I3 × R3. Для наглядности вынесем их отдельно.
I1 + I2 = I3
ε1 = I1 × R1 + I3 × R3
ε2 = I2 × R2 + I3 × R3
Получилось три задачи. Определимся с номиналами. Первый источник питания равен 6 В, второй – 12 В. Хотя так поступать нельзя, потому что параллельные источники питания должны быть одинаковыми, но нам это пригодится для получения важного урока. Первое сопротивление равно 2 Ом, второе – 4 Ом, третье – 8 Ом.
Осталось вставить данные в уравнения и получаем: для второго номера 6 = 2I1 + 8I3, для третьего номера 12 = 4I2 + 8I3. Дальше избавляемся от общего неизвестного I3. Согласно первому пункту, он равен I1 + I2. Подставляем вместо него эту сумму и получаем: 6 = 2I1 + 8(I1 + I2), 12 = 4I2 + 8(I1 + I2). Раскрываем скобки и складываем одинаковые неизвестные: 6 = 10I1 + 8I2; 12 = 12I2 + 8I1. Чтобы найти I1, нужно избавиться от I2. Для этого первое уравнение умножаем на 12, а второе на 8 и получаем: 72 = 120I1 + 96I2; 96 = 96I2 + 64I1. От первого отнимаем второе и записываем остаток -24 = 56I1, или I1 = -24/56 = -6/14 А. Почему ток отрицательный?
Дальше избавляемся от общего неизвестного I3. Согласно первому пункту, он равен I1 + I2. Подставляем вместо него эту сумму и получаем: 6 = 2I1 + 8(I1 + I2), 12 = 4I2 + 8(I1 + I2). Раскрываем скобки и складываем одинаковые неизвестные: 6 = 10I1 + 8I2; 12 = 12I2 + 8I1. Чтобы найти I1, нужно избавиться от I2. Для этого первое уравнение умножаем на 12, а второе на 8 и получаем: 72 = 120I1 + 96I2; 96 = 96I2 + 64I1. От первого отнимаем второе и записываем остаток -24 = 56I1, или I1 = -24/56 = -6/14 А. Почему ток отрицательный?
Потому что источники питания разные. На втором источнике напряжение выше, чем на первом, поэтому ток идет в обратном направлении. Находим I2, для этого значение I1 вставляем в любое из последних уравнений: 96 = 96I2 – 64 24/56. Разделим левую и правую часть на 96 и получим: 1 = I2 – (64×24)/(96×56) или дробную часть переносим влево, меняя знак. I2 = 1(64×24)/(96×56), после всех сокращений получаем 1 4/14 А. Для нахождения I3 воспользуемся первым номером: I3 = I1 + I2.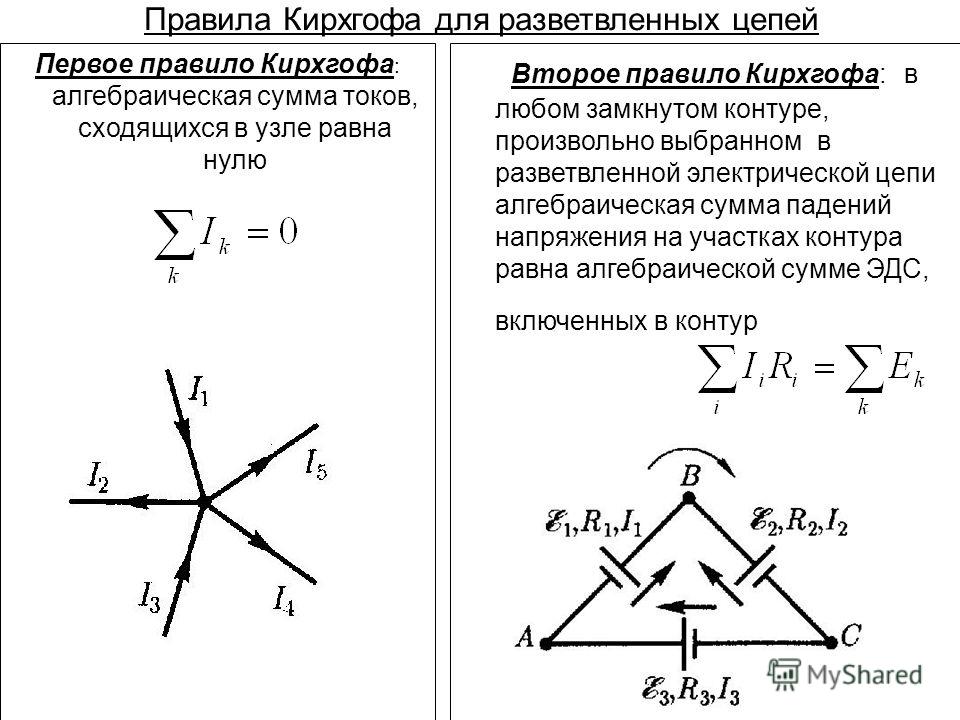 I3 = -24/56 + 1 4/14 = 1(4×56)/(14×56) – (24×14)/(56×14) = 1 224/784 -336/784 = 1008/784 -336/784 = 672/774 ≈ 0,87А. Получили I1 = -6/14 А, I2 = 1 4/14 А, I3 ≈ 0,87А.
I3 = -24/56 + 1 4/14 = 1(4×56)/(14×56) – (24×14)/(56×14) = 1 224/784 -336/784 = 1008/784 -336/784 = 672/774 ≈ 0,87А. Получили I1 = -6/14 А, I2 = 1 4/14 А, I3 ≈ 0,87А.
Закон Кирхгофа в химии
Когда в ходе химреакции система меняет свою теплоёмкость, вместе с тем меняется и температурный коэффициент возникающего в результате этого процесса теплового эффекта. Применяя уравнение, вытекающее из этого закона, можно рассчитывать тепловые эффекты в любом диапазоне температур. Дифференциальная форма этого уравнения имеет вид:
∆Cp = d∆Q/dT,
- ∆Cp – температурный коэффициент;
- d∆Q – изменение теплового эффекта;
Важно! Коэффициент определяет, как изменится тепловой эффект при изменении температуры на 1 К (2730С).
Теорема Кирхгофа для термодинамики
Третье уравнения Максвелла, а также принцип сохранения зарядов позволили Густаву Кирхгофу создать два правила, которые применяются в электротехнике. Имея данные о значениях сопротивлений резисторов и ЭДС источников питания, можно рассчитывать протекающий I или приложенное U для любого элемента цепи.
Алгебраическая сумма разностей потенциалов
Закон напряжения по Густаву Кирхгофу — второй закон этого автора, используемый для анализа электрической схемы. Вторым законом Кирхгофа утверждается, что для последовательного замкнутого контура алгебраическая сумма всех напряжений по кругу любой замкнутой цепи равна нулю. Утверждение обусловлено тем, что контур цепи является замкнутым проводящим путём, где потери энергии исключаются. Другими словами, алгебраическая сумма разностей потенциалов замкнутого контура теоретически равняется нулю:
Следует обратить внимание: под термином «алгебраическая сумма» имеется в виду учёт полярностей и признаков источников ЭДС, а также падения напряжений по кругу контура. Эта концепция закона Кирхгофа, известная как «сохранение энергии», как движение по кругу замкнутого контура или схемы, утверждает логику возврата к началу цепи и к первоначальному потенциалу без потери напряжения по всему контуру.
Следовательно, любое падение напряжения по кругу контура теоретически равно потенциалу любых источников напряжения, встречающихся на этом пути.
Отсюда следует вывод: применяя Второй закон Кирхгофа к определенному элементу электрической схемы, важно обращать особое внимание на алгебраические знаки падений напряжения на элементах (источниках ЭДС), иначе вычисления оборачиваются ошибкой.
Одиночный контурный элемент — резистор
Простым примером с резистором предположим — ток протекает в том же направлении, что и поток положительного заряда. В этом случае поток тока через резистор протекает от точки A до точки B. Фактически — от положительной клеммы до отрицательной клеммы. Таким образом, поскольку движение положительного заряда отмечается в направлении аналогичном направлению течения тока, на резистивном элементе зафиксируется падение потенциала, которое приведет к падению минусового потенциала на резисторе (— I * R).
Если же поток тока от точки B до точки A протекает в противоположном направлении относительно потока положительного заряда, тогда через резистивный элемент отметится рост потенциала, поскольку имеет место переход от минусового потенциала к потенциалу плюсовому, что даёт падение напряжения (+ I * R). Таким образом, чтобы правильно применить закон Кирхгофа по напряжению к электрической цепи, необходимо точно определить направление полярности. Очевидно, знак падения напряжения на резисторе зависит от направления тока, протекающего через резистор.
Таким образом, чтобы правильно применить закон Кирхгофа по напряжению к электрической цепи, необходимо точно определить направление полярности. Очевидно, знак падения напряжения на резисторе зависит от направления тока, протекающего через резистор.
Направление потока тока по замкнутому контуру допустимо определять либо по часовой стрелке, либо против часовой стрелки, и любой вариант допустим к выбору. Если выбранное направление отличается от фактического направления тока, соответствие закону Кирхгофа получится корректным и действительным, но приведет к результату, когда алгебраический расчёт будет иметь знак минус. Чтобы лучше понять эту концепцию, логично рассмотреть ещё один пример с одним контуром цепи на соответствие Второму Закону Кирхгофа.
Одиночный контур электрической цепи
Второй закон Кирхгофа утверждает — алгебраическая сумма разностей потенциалов любого замкнутого контура равна нулю. Демонстрационная схема действия Второго закона Кирхгофа для замкнутого контура с двумя резисторами и одним источником ЭДС.
Таким образом, падение напряжения на резисторе R1 = I * R1 и падение напряжения на резисторе R2 = I * R2, дают напряжение по Второму закону Кирхгофа:
V = I * Rs
где: Rs = R1 + R2.
Очевидно: применение Второго закона Кирхгофа к одиночному замкнутому контуру даёт формулу эквивалентного или полного сопротивления для последовательной цепи. Допустимо расширить эту формулу, чтобы найти значения падений потенциалов по кругу контура:
I = V / Rs
Vr1 = V * (R1 / R1 + R2)
Vr2 = V * (R2 / R1 + R2)
Есть три резистора номинальным сопротивлением 10, 20, 30 Ом, соответственно. Все три резистивных элемента соединены последовательно к 12-вольтовому аккумулятору.
Интересно по теме: Как проверить стабилитрон.
- общее сопротивление,
- ток цепи,
- ток через каждый резистор,
- падение напряжения на каждом резисторе.

Рассчитаем общее сопротивление:
Ro = R1 + R2 + R3 = 10Ω + 20Ω + 30Ω = 60Ω
I = V / Ro = 12 / 60 = 0,2A (200 мА)
Ток через каждый резистор:
I * R1 = I * R2 = I * R3 = 0,2A (200 мА)
Падение потенциала на каждом из резисторов:
VR1 = I * R1 = 0. 2 * 10 = 2В
VR2 = I * R2 = 0. 2 * 20 = 4В
VR3 = I * R3 = 0. 2 * 30 = 6В
Таким образом, Второй закон Кирхгофа справедлив, учитывая что индивидуальные падения напряжения, отмеченные по кругу замкнутого контура, в итоге составляют сумму напряжений.
Демонстрация закона напряжений Кирхгофа в последовательной цепи
Давайте еще раз посмотрим на наш пример последовательной схемы, на этот раз нумеруя точки цепи для обозначения напряжений:
Рисунок 1 – Демонстрация закона напряжений Кирхгофа в последовательной цепи
Если бы мы подключили вольтметр между точками 2 и 1, красный измерительный провод к точке 2 и черный измерительный провод к точке 1, вольтметр зарегистрировал бы значение +45 вольт. Для положительных показаний на дисплеях цифровых счетчиков знак «+» обычно не отображается, а скорее подразумевается. Однако для этого урока полярность показаний напряжений очень важна, поэтому я буду явно показывать положительные числа:
Для положительных показаний на дисплеях цифровых счетчиков знак «+» обычно не отображается, а скорее подразумевается. Однако для этого урока полярность показаний напряжений очень важна, поэтому я буду явно показывать положительные числа:
E2-1 = +45 В
Когда напряжение указывается с двойным нижним индексом (символы «2-1» в обозначении «E2-1»), это означает напряжение в первой точке (2), измеренное по отношению ко второй точке (1). Напряжение, указанное как «Ecd», будет означать значение напряжения, показанное цифровым мультиметром с красным измерительным проводом в точке «c» и черным измерительным проводом в точке «d»: напряжение в точке «c» относительно точки «d».
Рисунок 2 – Значение Ecd
Если бы мы взяли тот же вольтметр и измерили падение напряжения на каждом резисторе, обходя цепь по часовой стрелке с красным измерительным проводом нашего мультиметра на точке впереди и черным измерительным проводом на точке позади, мы получили бы следующие показания:
E3-2 = -10 В
E4-3 = -20 В
E1-4 = -15 В
Рисунок 3 – Определение напряжений в последовательной цепи
Нам уже должен быть знаком общий для последовательных цепей принцип, утверждающий, что отдельные падения напряжения в сумме составляют общее приложенное напряжение, но измерение падения напряжения таким образом и уделение внимания полярности (математическому знаку) показаний открывает еще один аспект этого принципа: все измеренные напряжения в сумме равны нулю:
В приведенном выше примере контур образован следующими точками в следующем порядке: 1-2-3-4-1. Не имеет значения, с какой точки мы начинаем или в каком направлении движемся при следовании по контуру; сумма напряжений по-прежнему будет равна нулю. Чтобы продемонстрировать это, мы можем той же цепи подсчитать напряжения в контуре 3-2-1-4-3:
Не имеет значения, с какой точки мы начинаем или в каком направлении движемся при следовании по контуру; сумма напряжений по-прежнему будет равна нулю. Чтобы продемонстрировать это, мы можем той же цепи подсчитать напряжения в контуре 3-2-1-4-3:
Этот пример может быть более понятен, если мы перерисуем нашу последовательную схему так, чтобы все компоненты были представлены на одной прямой линии:
Рисунок 4 – Изменение представления последовательной цепи
Это всё та же последовательная схема, только с немного перераспределенными компонентами. Обратите внимание на полярность падений напряжения на резисторах по отношению к напряжению батареи: напряжение батареи отрицательное слева и положительное справа, тогда как все падения напряжения на резисторах ориентированы в другую сторону (положительное слева и отрицательное справа). Это потому, что резисторы сопротивляются потоку электрического заряда, проталкиваемого батареей. Другими словами, «толкание», прилагаемое резисторами против потока электрического заряда, должно происходить в направлении, противоположном источнику электродвижущей силы.
Здесь мы видим, что цифровой вольтметр покажет на каждом компоненте в этой цепи, если черный провод будет слева, а красный провод – справа:
Рисунок 5 – Измерение напряжений в последовательной цепи
Если бы мы взяли тот же вольтметр и измерили напряжение между комбинациями компонентов, начиная с единственного R1 слева и продвигаясь по всей цепочке компонентов, мы увидели бы, как напряжения складываются алгебраически (до нуля):
Рисунок 6 – Измерение суммы напряжений в последовательной цепи
Тот факт, что последовательные напряжения складываются, не должен быть тайной, но мы заметили, что полярность этих напряжений имеет большое значение в том, как эти значения складываются. При измерении напряжения на R1 – R2 и R1 – R2 – R3 (я использую символ «двойное тире» «–» для обозначения последовательного соединения между резисторами R1, R2 и R3), мы видим, как измеряются бо́льшие значения напряжений (хотя и отрицательные), потому что полярности отдельных падений напряжения имеют одинаковую ориентацию (плюс слева, минус справа).
Сумма падений напряжения на R1, R2 и R3 равна 45 вольт, что соответствует выходному напряжению батареи, за исключением того, что полярность напряжения батареи (минус слева, плюс справа) противоположна падениям напряжения на резисторах, поэтому при измерении напряжения на всей цепочке компонентов мы получаем 0 вольт.
То, что мы должны получить ровно 0 вольт на всей линии, тоже не должно быть тайной. Глядя на схему, мы видим, что крайняя левая часть линии (левая сторона R1, точка номер 2) напрямую соединена с крайней правой частью линии (правая сторона батареи, точка номер 2), что необходимо для завершения схемы.
Поскольку эти две точки соединены напрямую, они являются электрически общими друг с другом. Таким образом, напряжение между этими двумя электрически общими точками должно быть равно нулю.
Демонстрация закона напряжений Кирхгофа в параллельной цепи
Правило напряжений Кирхгофа (второй закон Кирхгофа) будет работать вообще для любой конфигурации схемы, а не только для простых последовательных цепей. Обратите внимание, как это работает для следующей параллельной схемы:
Обратите внимание, как это работает для следующей параллельной схемы:
Рисунок 7 – Параллельная схема из резисторов
При параллельной схеме напряжение на каждом резисторе равно напряжению питания: 6 вольт. Суммируя напряжения вдоль контура 2-3-4-5-6-7-2, мы получаем:
Обратите внимание, что конечное (суммарное) напряжение я обозначил как E2-2. Поскольку мы начали наше пошаговое прохождение по контуру в точке 2 и закончили в точке 2, алгебраическая сумма этих напряжений будет такой же, как напряжение, измеренное между той же точкой (E2-2), которое, конечно, должно быть равно нулю.
Справедливость закона Кирхгофа о напряжениях независимо от топологии цепи
Тот факт, что эта цепь является параллельной, а не последовательной, не имеет ничего общего со справедливостью закона Кирхгофа о напряжениях. В этом отношении схема может быть «черным ящиком» (конфигурация ее компонентов полностью скрыта от нашего взгляда) с набором открытых клемм, между которыми мы можем измерить напряжение, – и правило напряжений Кирхгофа всё равно останется верным:
Рисунок 8 – Справедливость закона Кирхгофа напряжениях независимо от топологии схемы
Попробуйте на приведенной выше диаграмме выполнить обход в любом порядке, начиная с любого вывода, и вернувшись к исходному выводу, и вы обнаружите, что алгебраическая сумма напряжений всегда равна нулю.
Более того, «контур», который мы отслеживаем для второго закона Кирхгофа, даже не обязательно должен быть реальным путем протекания тока в прямом смысле этого слова. Всё, что нам нужно сделать, чтобы соответствовать правилу напряжений Кирхгофа, – это начинать и заканчивать в одной и той же точке цепи, подсчитывая падения напряжения и полярности при переходе между точками. Рассмотрим следующий абсурдный пример, проходя по «контуру» 2-3-6-3-2 в той же параллельной резисторной цепи:
Рисунок 9 – Параллельная схема из резисторов
Использование закона Кирхгофа о напряжениях в сложной цепи
Закон Кирхгофа о напряжениях можно использовать для определения неизвестного напряжения в сложной цепи, где известны все другие напряжения вдоль определенного «контура». В качестве примера возьмем следующую сложную схему (на самом деле две последовательные цепи, соединенные одним проводом внизу):
Рисунок 10 – Правило напряжений Кирхгофа в сложной цепи
Чтобы упростить задачу, я опустил значения сопротивлений и просто указал падение напряжения на каждом резисторе.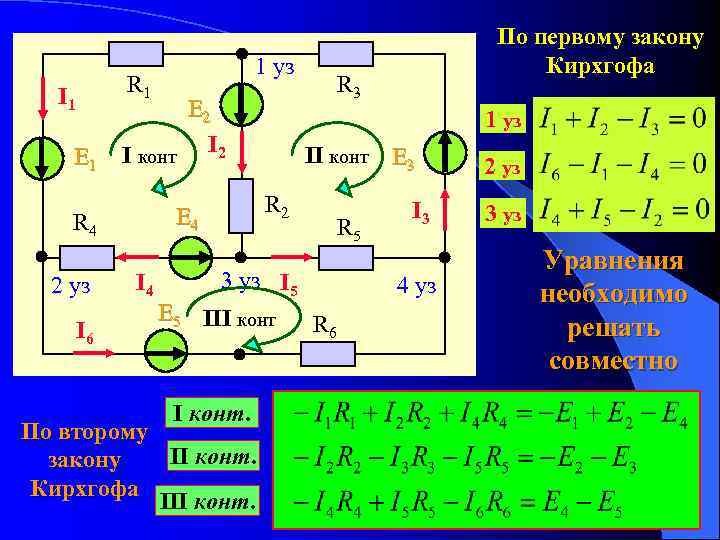 Две последовательные цепи имеют между собой общий провод (провод 7-8-9-10), что делает возможными измерения напряжения между этими двумя цепями. Если бы мы хотели определить напряжение между точками 4 и 3, мы могли бы составить уравнение правила напряжений Кирхгофа с напряжением между этими точками как неизвестным:
Две последовательные цепи имеют между собой общий провод (провод 7-8-9-10), что делает возможными измерения напряжения между этими двумя цепями. Если бы мы хотели определить напряжение между точками 4 и 3, мы могли бы составить уравнение правила напряжений Кирхгофа с напряжением между этими точками как неизвестным:
E4-3 + E9-4 + E8-9 + E3-8 = 0
E4-3 + 12 + 0 + 20 = 0
E4-3 + 32 = 0
E4-3 = -32 В
Рисунок 11 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 4 и 3Рисунок 12 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 9 и 4Рисунок 13 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 8 и 9Рисунок 14 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 3 и 8
Обойдя контур 3-4-9-8-3, мы записываем значения падений напряжения так, как их регистрировал бы цифровой вольтметр, измеряя с красным измерительным проводом в точке впереди и черным измерительным проводом на точке позади, когда мы продвигаемся вперед по контуру.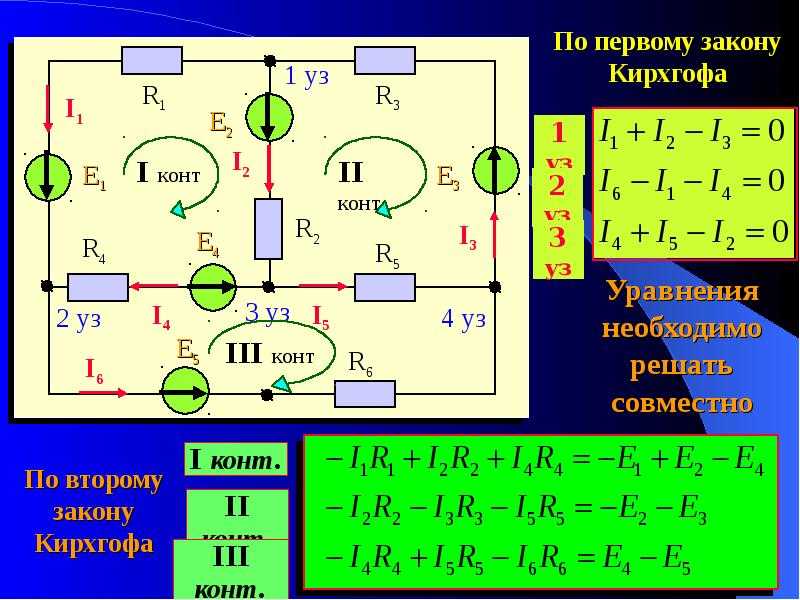 Следовательно, напряжение в точке 9 относительно точки 4 является положительным (+) 12 вольт, потому что «красный провод» находится в точке 9, а «черный провод» – в точке 4.
Следовательно, напряжение в точке 9 относительно точки 4 является положительным (+) 12 вольт, потому что «красный провод» находится в точке 9, а «черный провод» – в точке 4.
Напряжение в точке 3 относительно точки 8 составляет положительные (+) 20 вольт, потому что «красный провод» находится в точке 3, а «черный провод» – в точке 8. Напряжение в точке 8 относительно точки 9, конечно, равно нулю, потому что эти две точки электрически общие.
Наш окончательный ответ для напряжения в точке 4 относительно точки 3 – это отрицательные (-) 32 вольта, говорящие нам, что точка 3 на самом деле положительна относительно точки 4, именно это цифровой вольтметр показал бы при красном проводе в точке 4 и черном проводе в точке 3:
Рисунок 15 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 4 и 3
Другими словами, первоначальное размещение наших «измерительных щупов» в этой задаче правила напряжений Кирхгофа было «обратным». Если бы мы сформировали наше уравнение второго закона Кирхгофа, начиная с E3-4, вместо E4-3, обходя тот же контур с противоположной ориентацией измерительных проводов, окончательный ответ был бы E3-4 = +32 вольта:
Рисунок 16 – Правило напряжений Кирхгофа в сложной цепи.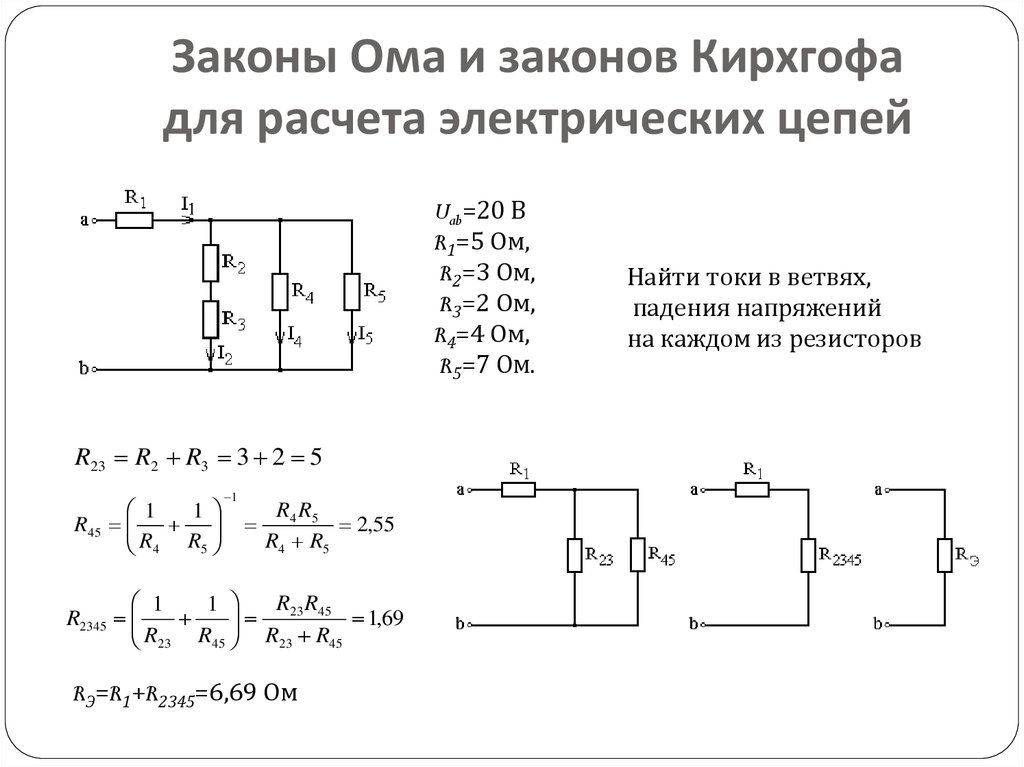 Напряжение между точками 3 и 4
Напряжение между точками 3 и 4
Важно понимать, что ни один из подходов не является «неправильным». В обоих случаях мы приходим к правильной оценке напряжения между двумя точками 3 и 4: точка 3 положительна по отношению к точке 4, а напряжение между ними составляет 32 вольта.
Минпросвещения утвердило новый ФГОС основного общего образования.
В частности, помимо алгебры и геометрии, предусмотрен еще один математический учебный курс «Вероятность и статистика».
Прописаны требования к организации электронного обучения и применению дистанционных образовательных технологий.
Детализированы требования к результатам освоения обучающимися программы основного общего образования по каждому предмету.
Прием на обучение по прежнему ФГОСу прекращается с 1 сентября 2022 г.
История
Пополнил ряды немецких ученых Кирхгоф в девятнадцатом столетии, когда в стране, находившаяся на пороге революции индустриальной, требовались новейших технологии. Ученые занимались поиском решений, которые могли бы ускорить развитие промышленности.
Активно занимались исследованиями в области электричества, поскольку понимали, что в будущем оно будет широко использоваться. Проблема состояла на тот момент не в том, как составлять электрические цепи из возможных элементов, а в проведении математических вычислений. Тут и появились законы, сформулированные физиком. Они очень помогли.
Алгебраическая сумма приходящих к узлам токов и исходящих из него равна нулю. Эта одновременно вытекает из другого закона — постоянства энергии.
К узлу подходят 2 провода, а отходит один. Значение тока, текущего от узла, такое же, как сумма его, протекающего по двум остальным проводникам, т. идущим к нему. Правило Кирхгофа объясняет, что, при ином раскладе, накапливался бы заряд, но такого не бывает. Все знают, что всякую сложную цепь легко разделить на отдельные участки.
Но, при этом непросто определить путь, по которому он проходит. Тем более, что на различных участках сопротивления не одинаковы, поэтому и распределение энергии не будет равномерным.
В соответствие со Вторым правилом Кирхгофа, энергия электронов на каждом из замкнутых участков электрической цепи равняется нулю – нулю равняется всегда в таком контуре суммарное значение напряжений. Если бы нарушилось данное правило, энергия электронов при прохождении определенных участков, уменьшалась бы или увеличивалась. Но, этого не наблюдается.
Соединения проводников
Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников.
Резисторы и подводящие провода
Проводник, обладающий сопротивлением R, мы называем резистором и изображаем следующим образом (рис. 1):
Рис. 1 Резистор
Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.
Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.
Пусть положительный заряд q перемещается по цепи из точки a в точку b, проходя через резистор R (рис. 2):
Рис. 2 U = φa – φb
Стационарное поле совершает при этом положительную работу A = q(φa − φb). Так как q > 0 и A > 0, то и φa − φb > 0, т. φa > φb.
Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: U = φa − φb.
Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если φa − φb = IR и R = 0, то φa = φb (рис. 3):
Рис. 3 φa = φb
Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным.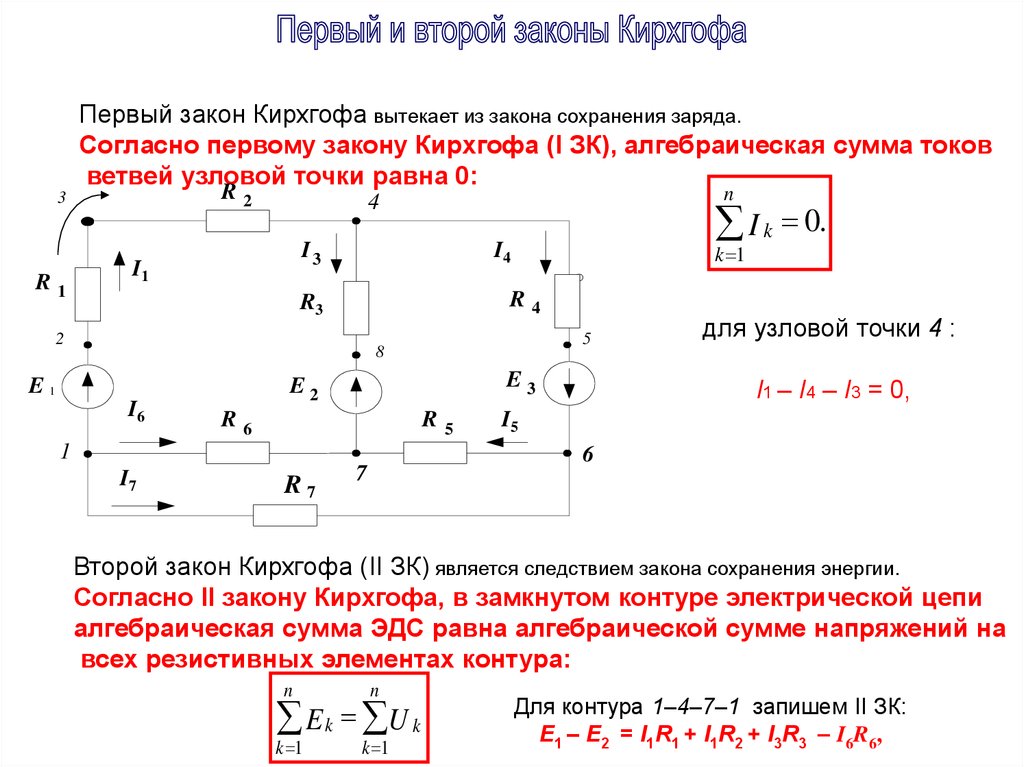 В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.
В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.
Последовательное соединение
При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.
Рассмотрим два резистора R1 и R2, соединённых последовательно и подключённых к источнику постоянного напряжения U (рис. Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.
Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере:
- При последовательном соединении проводников сила тока в них одинакова. В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.
- Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике.
 Действительно, напряжение Uab на участке ab — это работа поля по переносу единичного заряда из точки a в точку b; напряжение Ubc на участке bc — это работа поля по переносу единичного заряда из точки b в точку c. Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки a в точку c, то есть напряжение U на всём участке: U = Uab + Ubc.
Действительно, напряжение Uab на участке ab — это работа поля по переносу единичного заряда из точки a в точку b; напряжение Ubc на участке bc — это работа поля по переносу единичного заряда из точки b в точку c. Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки a в точку c, то есть напряжение U на всём участке: U = Uab + Ubc.
Можно и более формально, без всяких словесных объяснений: U = Uac = φa − φc = (φa − φb) + (φb − φc) = Uab + Ubc.
что и требовалось.
Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения S, но с разными длинами l1 и l2.
Сопротивления проводников равны:
Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения. Доказательство этого даётся с помощью закона Ома, как показано выше. Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.
Параллельное соединение
При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.
Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис.
Резисторы подсоединены к двум точкам: a и b. Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями; участок от b к a (по направлению тока) называется неразветвленной частью цепи.
Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов:
U1 = U2 = φa − φb = U.
Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.
что и требовалось.
Сокращая на U, получим:
1/R = 1/R1 + 1/R2 ,
что и требовалось.
Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами l, но разными поперечными сечениями S1 и S2. Тогда это соединение можно рассматривать как проводник той же длины l, но с площадью сечения S = S1 + S2. Имеем:
Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.
Из соотношения (1) можно найти R:
R = R1R2/(R1 + R2).
К сожалению, в общем случае n параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением
1/R = 1/R1 + 1/R2 +. + 1/Rn.
Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех n резисторов одинаковы и равны R1. Тогда:
Мы видим, что сопротивление участка из n параллельно соединённых одинаковых проводников в n раз меньше сопротивления одного проводника.
Смешанное соединение
Смешанное соединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.
Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.
Рассмотрим пример смешанного соединения проводников (рис.
Рис. 6 Смешанное соединение
Пусть U = 14 В, R1 = 2 Ом, R2 = 3 Ом, R3 = 3 Ом, R4 = 5 Ом, R5 = 2 Ом. Найдём силу тока в цепи и в каждом из резисторов.
Наша цепь состоит из двух последовательно соединённых участков ab и bc. Сопротивление участка ab:
Сопротивление цепи: R = Rab + Rbc = 1,2 + 1,6 = 2,8 Ом.
Теперь находим силу тока в цепи:
I = U/R = 14/2,8 = 5 A.
Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:
Uab = IRab = 5 · 1,2 = 6 B;
Ubc = IRbc = 5 · 1,6 = 8 B.
(Заметим попутно, что сумма этих напряжений равна 14 В, т. напряжению в цепи, как и должно быть при последовательном соединении
Оба резистора R1 и R2 находятся под напряжением Uab, поэтому:
Стало быть, через резистор R5 течёт ток I5 = I − I3 = 5 − 1 = 4 A
Введение в напряжения и уравнения движения
Строительная механика Напряжения и уравнения движения
Введение в напряжения и уравнения движения
При деформации твердых тел в материале распределяются внутренние силы. Они называются напряжениями . Напряжение имеет единицу силы на единицу площади.
В стержне с поперечным сечением А нагруженным осевой силой F , напряжение в направлении действия силы равно . Как повседневное наблюдение, мы знаем, что более толстые объекты смогут выдержать более высокую силу. Таким образом, напряжение является интуитивно подходящей величиной для предоставления информации о том, насколько сильно нагружен материал.
Таким образом, напряжение является интуитивно подходящей величиной для предоставления информации о том, насколько сильно нагружен материал.
Стержень с осевой нагрузкой. Бар с осевой нагрузкой.
За исключением очень особых случаев, таких как показанный выше, как величина, так и ориентация напряжений варьируются по всему нагруженному телу.
Экспериментально определенная картина напряжения вокруг жесткого включения в мягком материале. Картинка получается с помощью фотоупругости. Изображение предоставлено SSMG-ITALY. Под лицензией CC BY-SA 3.0 через Wikimedia Commons. Экспериментально определенная картина напряжения вокруг жесткого включения в мягком материале. Картинка получается с помощью фотоупругости. Изображение предоставлено SSMG-ITALY. Под лицензией CC BY-SA 3. 0 через Wikimedia Commons.
0 через Wikimedia Commons.
Соответствующая схема напряжения, рассчитанная с помощью анализа методом конечных элементов. Соответствующая схема напряжений, рассчитанная с помощью анализа методом конечных элементов.
Когда сила действует перпендикулярно поверхности, напряжение называется нормальным напряжением . Напряжение, вызванное силой, действующей по касательной к поверхности, называется напряжением сдвига .
Momentum Balance
Внутренние силы в теле, определяемые напряжениями, должны вместе с внешними силами и силами инерции находиться в равновесии согласно второму закону Ньютона.
Рассмотрим небольшую поверхность, состоящую из одних и тех же частиц материала в течение всего процесса деформации. Мы предполагаем деформацию без потери сплошности в материале, так что не появляются трещины. До деформации поверхность характеризуется площадью дА и вектор нормали N . После деформации они становятся da и n . Поверхность не обязательно является частью внешности тела — она также может быть чисто концептуальной поверхностью в любом месте внутри тела.
До деформации поверхность характеризуется площадью дА и вектор нормали N . После деформации они становятся da и n . Поверхность не обязательно является частью внешности тела — она также может быть чисто концептуальной поверхностью в любом месте внутри тела.
Бесконечно малая поверхность в исходной и деформированной конфигурациях. Бесконечно малая поверхность в исходной и деформированной конфигурациях.
Поверхностная сила, действующая на деформированную область, может быть представлена как
. сила, действующая в актуальном деформированном состоянии на недеформированную область.
Тяговое усилие имеет единицу силы на единицу площади. Если площадь изменилась во время деформации, то величины двух векторов тяги различны, но оба они имеют одинаковую ориентацию.
Мы можем записать номинальное тяговое усилие, используя его пространственные компоненты T i , и вектор нормали, используя его материальные компоненты N J . Для обсуждения пространственных и материальных каркасов прочитайте эту страницу об анализе деформации.
Для обсуждения пространственных и материальных каркасов прочитайте эту страницу об анализе деформации.
Далее компоненты тяги запишем в виде следующего линейного разложения по вектору нормали:
Здесь и далее предполагается суммирование по повторяющимся индексам. Малый и капитальный индексы используются для пространственной и материальной составляющих соответственно.
Такое представление иногда называют законом Коши или формулой Коши . Это возможно только в том случае, если P iJ являются компонентами некоторого тензора второго ранга.
где представляет объемные силы, такие как силы тяжести или центробежные силы, а поле скорости вычисляется из поля смещения, как .
Используя формулу Коши и применяя теорему о дивергенции, поверхностный интеграл можно преобразовать в интеграл по объему следующим образом:
Поскольку объем произволен, это дает следующую дифференциальную форму уравнения баланса количества движения:
Или, используя тензорную нотацию:
Тензор P называется первым тензором напряжений Пиолы-Кирхгофа . Он связывает силы, действующие в пространственных направлениях, с областями в исходной недеформированной конфигурации. Таким образом, его компоненты даны с индексами, относящимися к разным конфигурациям. Иногда такие математические объекты называют двухточечные тензоры . В общем случае этот тензор несимметричен.
Он связывает силы, действующие в пространственных направлениях, с областями в исходной недеформированной конфигурации. Таким образом, его компоненты даны с индексами, относящимися к разным конфигурациям. Иногда такие математические объекты называют двухточечные тензоры . В общем случае этот тензор несимметричен.
Аналогичный подход можно применить к вектору тяги t n и объему материала в фактической деформированной конфигурации. Это приведет к следующему представлению:
Тензор называется тензором напряжений Коши или тензором истинных напряжений , поскольку он представляет силы в фактической конфигурации, связанные с фактической деформированной областью. Этот тензор представлен своими пространственными компонентами.
Смысл компонент тензора напряжений Коши становится понятен, если рассмотреть небольшую площадку с вектором нормали, параллельным одной из осей пространственных координат; например, третий. Тогда вектор нормали к этой области равен {0,0,1}, а тяга определяется как
Тогда вектор нормали к этой области равен {0,0,1}, а тяга определяется как
. Таким образом, компонента тензора напряжений с 33 индексами дает компонент вектора тяги в направлении 3 на плоскости, нормально в том же направлении. Компонента тензора напряжений с двумя одинаковыми индексами называется нормальное напряжение или прямое напряжение . Две другие компоненты тензора напряжений обеспечивают часть силы тяги, действующую по касательной к плоскости. Такая составляющая называется напряжением сдвига .
Взяв баланс моментов для маленького куба, можно показать, что тензор напряжений Коши симметричен, так что . Это верно до тех пор, пока нет вкладов объемного момента. Такие материалы, которые рассматриваются с использованием теории Коссера , существуют. Однако они необычны.
Поскольку тензоры напряжений Коши и первого тензора Пиолы-Кирхгофа соответствуют разным представлениям одной и той же поверхностной силы,
к деформации. В нем указано, что
В нем указано, что
, где F — тензор градиента деформации, а
Коэффициент объема J обеспечивает изменение объема, вызванное деформацией. Следовательно, тензоры напряжений связаны соотношением
. Эту и подобные формулы можно упростить, введя тензор, называемый тензором напряжений Кирхгофа , который определяется как . Тензор напряжений Кирхгофа имеет мало практического применения, но представляет собой скорее теоретически удобную величину.
Сохранение массы и формулировка Эйлера
В терминах тензора напряжений Коши уравнение баланса количества движения можно записать как
Обратите внимание, что плотность в этом уравнении представляет собой истинную плотность деформированного материала. Кроме того, объемная сила — это сила, приходящаяся на деформированный объем. Плотность неявно зависит от деформации из-за сохранения массы as
Эта дополнительная нелинейность делает эту форму уравнения баланса количества движения менее интересной с вычислительной точки зрения.
Используя скорость и заменив независимые переменные пространственными координатами через x = x ( X , t), мы получаем
Это баланс количества движения в формулировке Эйлера. Такая формулировка обычно используется в гидродинамике, где скорость рассматривается как зависимая переменная.
Баланс механической энергии
Умножение дифференциальной формы уравнения импульса на вектор скорости и интегрирование его по материалу дает следующее уравнение:
Это уравнение представляет собой интегральную форму баланса механической энергии . Она также известна как степенная теорема . Пространственный градиент скорости равен, а оператор : указывает на суммирование по двум индексам; . Свойства градиента скорости обсуждаются более подробно на странице «Анализ деформации».
Два интеграла в правой части уравнения представляют входную мощность от объемных и поверхностных сил соответственно. Такая потребляемая мощность представляет собой работу, совершаемую соответствующей силой над материалом в единицу времени.
Такая потребляемая мощность представляет собой работу, совершаемую соответствующей силой над материалом в единицу времени.
Члены в левой части представляют собой скорость изменения кинетической энергии и мощность напряжения, прикладываемого к телу, соответственно. Для эластичного материала сила напряжения представляет собой скорость изменения плотности энергии деформации.
Используя соотношения
мощность напряжений можно представить в следующем эквивалентном виде:
Таким образом, можно сказать, что первый тензор напряжений Пиолы-Кирхгофа и градиент деформации образуют сопряженную пару энергии . Такие пары также могут обозначаться как , сопряженная мощность, или , сопряженная работа, , меры напряжения и деформации.
Градиент скорости можно разложить на симметричную и антисимметричную части, называемые тензором скорости деформации ( L d ) и тензором спина ( L w ) соответственно. Поскольку тензор напряжений Коши симметричен, . Следовательно, мерой деформации, степенно сопряженной с напряжением Коши, является тензор скорости деформации. Последнее также может быть записано как
Поскольку тензор напряжений Коши симметричен, . Следовательно, мерой деформации, степенно сопряженной с напряжением Коши, является тензор скорости деформации. Последнее также может быть записано как
где
— тензор деформации Грина-Лагранжа . Интеграл мощности напряжений может быть переписан как:
Здесь
называется -секундным тензором напряжений Пиолы-Кирхгофа . Это симметричный тензор, энергетически сопряженный деформации Грина-Лагранжа.
Первый и второй тензоры напряжений Пиолы-Кирхгофа связаны соотношением:
Эта формула позволяет переписать уравнение баланса количества движения в виде:
, что вместе с определяющим соотношением вида
даст замкнутую систему уравнений для вектора смещения.
Компоненты напряжения на вращающейся плоскости
Для стержня с осевой нагрузкой легко представить напряжение как скалярное число и заявить, что на этом стержне существует только нормальное напряжение. Полный тензор напряжений равен
Полный тензор напряжений равен
Компоненты этого тензора напряжений выражены в системе координат с x — ось выровнена с полосой. В любой другой системе координат будет смесь нормального напряжения и напряжения сдвига. Это можно увидеть, если рассмотреть концептуальную внутреннюю поверхность, не перпендикулярную оси стержня. На этой поверхности фактически будут как нормальные (σ), так и касательные (τ) напряжения, как показано на рисунке ниже.
Разложение вектора тяги на нормальную и касательную составляющие. Разложение вектора тяги на нормальную и касательную составляющие напряжения.
Во вращающейся системе, первая ось которой совпадает с нормалью к поверхности, тензор напряжений имеет структуру
где угол между осью стержня и нормалью к поверхности.
Такое напряженное состояние часто называют одноосным . Однако только в определенной системе координат его можно представить одной нормальной составляющей напряжения.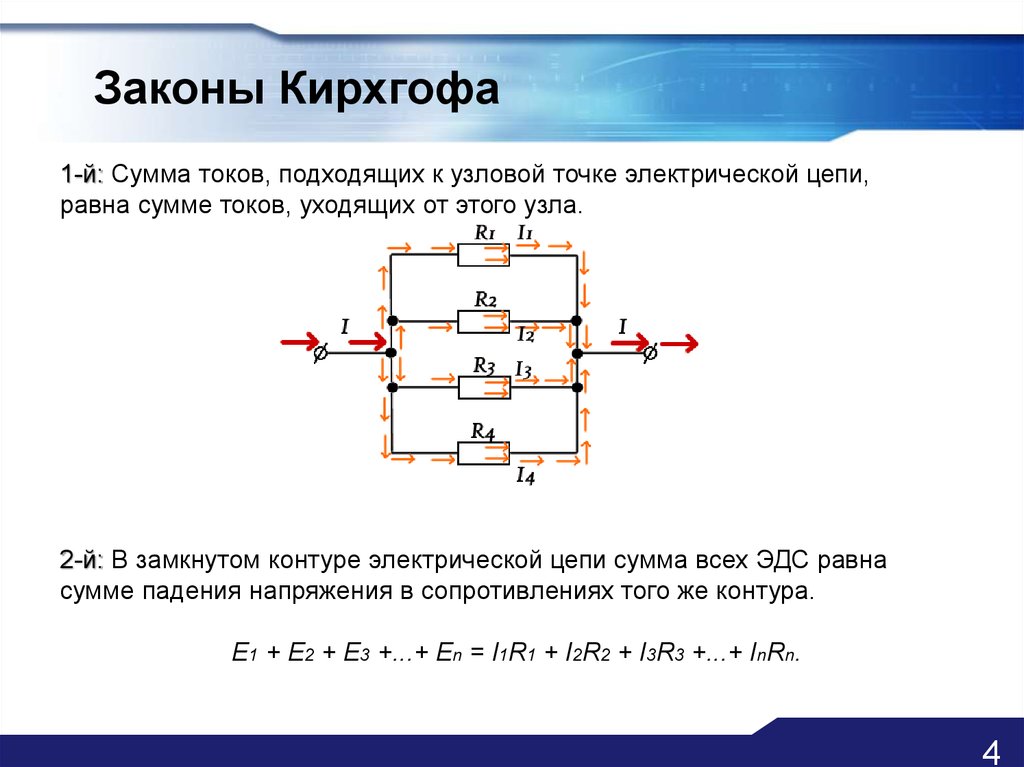
Сравнение напряжений Коши и второго напряжения Пиолы-Кирхгофа
Рассмотрим ортотропный материал. Материал содержит волокна в определенной ориентации вдоль прямой консольной балки.
Поскольку второе напряжение Пиолы-Кирхгофа определяется вдоль направлений материала, оно позволит нам визуализировать напряжение в направлении волокна, даже когда конструкция подвергается вращению.
На приведенном ниже рисунке балка изогнута под действием чистого момента, приложенного к концу. Мы можем видеть 11-компонентную как напряжение Коши, так и второе напряжение Пиолы-Кирхгофа. Напряжение изгиба физически направлено вдоль балки, поэтому 11-компонента напряжения Коши, связанная с фиксированным в пространстве горизонтальным направлением, уменьшается по мере прогиба. С другой стороны, второе напряжение Пиолы-Кирхгофа имеет такое же распределение по толщине по всей балке, в том числе и в деформированной конфигурации.
Тот же компонент напряжения Коши (вверху) и второго напряжения Пиолы-Кирхгофа (внизу). Тот же компонент напряжения Коши (вверху) и второго напряжения Пиолы-Кирхгофа (внизу).
Тот же компонент напряжения Коши (вверху) и второго напряжения Пиолы-Кирхгофа (внизу).
Фактическое значение второго напряжения Пиолы-Кирхгофа интерпретировать сложнее, так как оно не связано ни с исходной, ни с деформированной зоной.
Опубликовано: 19 апреля 2018 г.
Последнее изменение: 19 апреля, 2018
1.5.3 Ставки стресса
1.5.3 Ставки стресса
Продукты: Abaqus/Standard Abaqus/Explicit
Многие из материалов, которые мы хотим моделировать с Abaqus. Обычно определяющие уравнения появляются в форме скорости. В разделе «Показатели напряжения» в разделе 1.5.2 было высказано предположение, что подходящей мерой напряжения для материалов, чувствительных к напряжениям (таких как податливые материалы), является напряжение Кирхгофа. Поэтому нам необходимо определить скорость напряжения Кирхгофа для использования в определяющих уравнениях.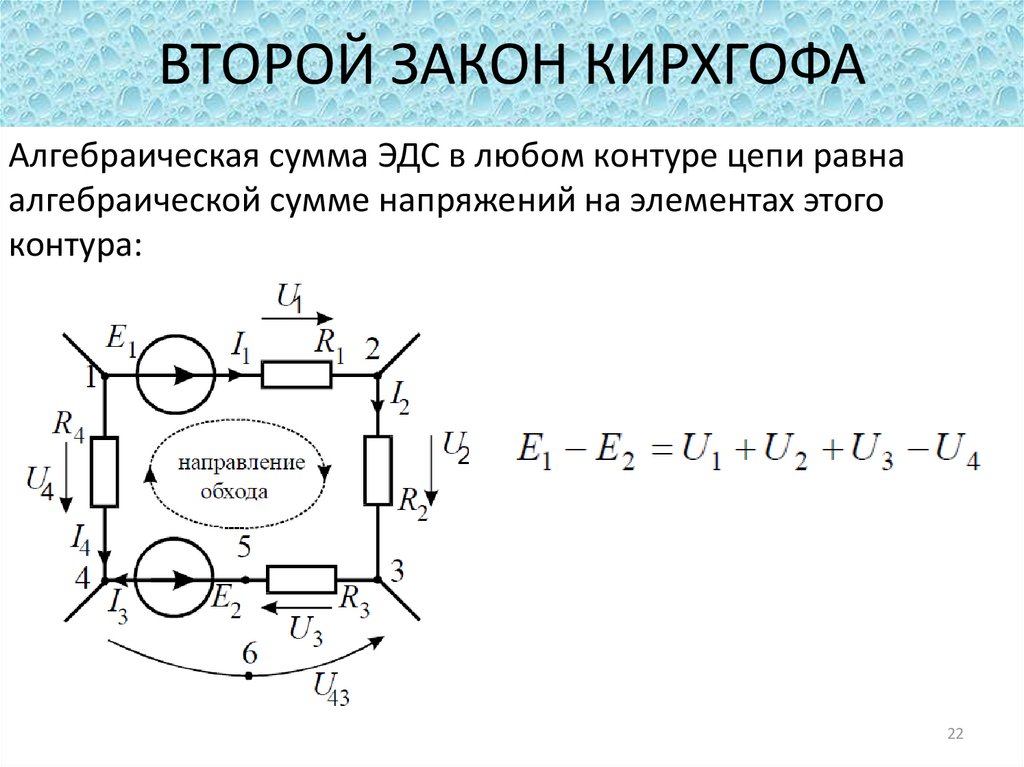 Это определение представляет собой не просто материальную скорость напряжения Кирхгофа во времени, потому что компоненты напряжения Кирхгофа связаны с пространственными направлениями в текущей конфигурации (напомним, что напряжение Кирхгофа равно , где J — изменение объема по сравнению с эталонной конфигурацией, а — напряжение Коши, определяемое формулой , где и — векторы в текущей конфигурации).
Это определение представляет собой не просто материальную скорость напряжения Кирхгофа во времени, потому что компоненты напряжения Кирхгофа связаны с пространственными направлениями в текущей конфигурации (напомним, что напряжение Кирхгофа равно , где J — изменение объема по сравнению с эталонной конфигурацией, а — напряжение Коши, определяемое формулой , где и — векторы в текущей конфигурации).
Чтобы проиллюстрировать эту проблему, рассмотрим образец при одноосном растяжении под действием постоянной осевой силы P , лежащий вдоль оси x в момент времени и повернутый — при постоянной осевой силе — вдоль оси y в точке время (см. рис. 1.5.31).
Рисунок 1.5.31 Повернутый образец.
Запишите компоненты напряжения на глобальном прямоугольном декартовом базисе. Во время , , и все прочее , а во время , и все прочее . Очевидно, во время и , но столь же очевидно, что эта скорость изменения напряжения не имеет ничего общего с конститутивной реакцией материала, из которого состоит стержень. (Материально обусловленное напряжение, такое как второе напряжение Пиолы-Кирхгофа, останется постоянным во время описанного выше вращения, потому что его компоненты связаны с материальной основой.) Таким образом, проблема заключается в том, что компоненты или связаны с текущими направлениями в пространстве и, следовательно, и будет ненулевым, если имеет место чистое вращение твердого тела, даже если с конститутивной точки зрения материал неизменен. Таким образом, мы должны разделить приращение или на две части: одну, относящуюся только к движению твердого тела, и оставшуюся часть, которая тогда, предположительно, связана со скоростной формой закона напряжения-деформации.
(Материально обусловленное напряжение, такое как второе напряжение Пиолы-Кирхгофа, останется постоянным во время описанного выше вращения, потому что его компоненты связаны с материальной основой.) Таким образом, проблема заключается в том, что компоненты или связаны с текущими направлениями в пространстве и, следовательно, и будет ненулевым, если имеет место чистое вращение твердого тела, даже если с конститутивной точки зрения материал неизменен. Таким образом, мы должны разделить приращение или на две части: одну, относящуюся только к движению твердого тела, и оставшуюся часть, которая тогда, предположительно, связана со скоростной формой закона напряжения-деформации.
Для этой цели мы можем получить простой результат для любой матрицы, компоненты которой связаны с пространственными направлениями. В какой-то момент t представьте, что к материальной точке прикрепляется набор базовых векторов, Эти векторы не могут растягиваться, но определены для вращения с тем же вращением, что и материал. Напомним, что пространственный градиент скорости материальной частицы в точке , был разложен на скорость деформации и спин,
Напомним, что пространственный градиент скорости материальной частицы в точке , был разложен на скорость деформации и спин,
Одна из концепций движения основных векторов в Abaqus состоит в том, что
Другая концепция движения базовых векторов, используемая в Abaqus, это
, где . Вот вращение твердого тела в полярном разложении градиента деформации. Различия между этими двумя понятиями существенны только в том случае, если конечное вращение материальной точки сопровождается конечным сдвигом.
Теперь рассмотрим любую матрицу на основе текущей конфигурации: мы можем записать ее через компоненты по направлениям:
Взяв производную по времени, получим
Второй и третий члены представляют собой скорость, вызванную вращением твердого тела, поэтому первый член представляет собой часть, вызванную другими воздействиями (в случае стресса скорость связанный с конститутивной реакцией), называется коротационной скоростью . Исходя из определений векторов жесткого основания, которые можно рассматривать как вращающиеся либо с , либо с , мы можем записать две коротационные скорости как
Исходя из определений векторов жесткого основания, которые можно рассматривать как вращающиеся либо с , либо с , мы можем записать две коротационные скорости как
и
где и называются коэффициентами Яуманна и Грина-Нагди соответственно.
Таким образом, мы имеем полную скорость любой матрицы, связанную с пространственными направлениями в текущей конфигурации, как сумму скорости вращения матрицы и скорости, обусловленной исключительно локальным спином или вращением твердого тела. Например, скорость изменения напряжения Кирхгофа по Яуману может быть записана как
. Мы предполагаем, что конститутивная теория будет определять , скорость подвижного напряжения на опорный объем в терминах скорости деформации и прошлой истории, так что это Уравнение обеспечивает удобную связь между этой моделью материала и общим изменением «истинного» (Коши) напряжения (которое является мерой напряжения, определяемой непосредственно из уравнений равновесия).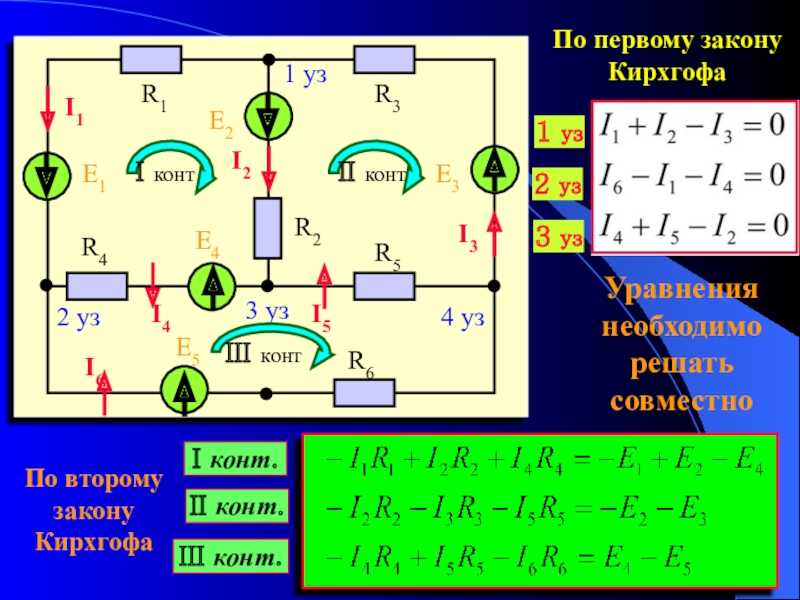 В Главе 4, «Механические определяющие теории», где обсуждаются определяющие модели в Abaqus, «скорость напряжения» по отношению к эталонному объему будет означать коротационную скорость напряжения Кирхгофа, которая представляет собой работу меры напряжения, сопряженную со скоростью деформации.
В Главе 4, «Механические определяющие теории», где обсуждаются определяющие модели в Abaqus, «скорость напряжения» по отношению к эталонному объему будет означать коротационную скорость напряжения Кирхгофа, которая представляет собой работу меры напряжения, сопряженную со скоростью деформации.
Коэффициенты стресса, используемые в Abaqus
Объективные коэффициенты стресса, используемые в Abaqus, приведены в таблице 1.5.31. Объективные скорости имеют отношение только к определяющим уравнениям формы скорости (например, упругопластичности). Для сверхэластичных материалов используется общая формулировка; следовательно, понятие объективной ставки не имеет отношения к учредительному праву. Однако, когда материальная ориентация определена, объективная скорость определяет эволюцию ориентации, и это влияет на результат.
Таблица 1.5.31 Объективные уровни стресса.
| Solver | Element Type | Constitutive Model | Objective Rate |
|---|---|---|---|
| Abaqus/Standard | Solid (Continuum) | All built-in and user-defined materials | Jaumann |
| Конструкции (оболочки, мембраны, балки, фермы) | Все встроенные и определяемые пользователем материалы | Green-Naghdi | |
| Abaqus/Explicit | Solid (Continuum) | All except viscoelastic, brittle cracking, and VUMAT | Jaumann |
| Solid (Continuum) | Viscoelastic, brittle cracking, and VUMAT | Green-Naghdi | |
| Конструкции (оболочки, мембраны, балки, фермы) | Все встроенные и определяемые пользователем материалы | Green-Naghdi |
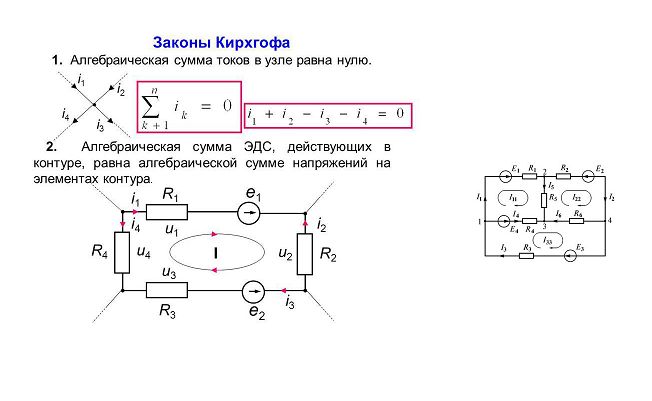 На этой странице представлены несколько определений стресса. Ключевой дискриминатор
среди различных тензоров напряжений заключается в том, сообщают ли они о напряжении в материале
недеформированное и особенно невращающееся состояние (эталонная конфигурация ),
или в деформированном и повернутом состоянии ( текущая конфигурация ).
На этой странице представлены несколько определений стресса. Ключевой дискриминатор
среди различных тензоров напряжений заключается в том, сообщают ли они о напряжении в материале
недеформированное и особенно невращающееся состояние (эталонная конфигурация ),
или в деформированном и повернутом состоянии ( текущая конфигурация ).Интересно, что большинство, а может быть, и все определения стресса могут быть в паре с соответствующим тензором деформации. Они идут парами, такие что произведение двух даст энергии деформации , отсюда и название этой страницы. Это не означает, что соответствующие пары должны использоваться вместе при выполнении структурного анализа. Но они должны быть при расчете плотности энергии деформации.
Стресс Коши (также известный как Истинный стресс)
Утверждается, что среди множества различных определений штаммов нет
одно обязательно превосходит другое. Они все просто разные,
у каждого есть плюсы и минусы для данного приложения. Однако я не
считают, что дело в стрессе. Для напряжений Коши или True Stress Определение выглядит как голова и плечи
более актуальным, физическим, обоснованным и т. д. по сравнению с другими определениями.
Однако я не
считают, что дело в стрессе. Для напряжений Коши или True Stress Определение выглядит как голова и плечи
более актуальным, физическим, обоснованным и т. д. по сравнению с другими определениями.
Напряжение Коши — это «сила на площади в деформированной конфигурации «. Итак, объект повернулся и деформировался. И поскольку он деформировался, его площадь поперечного сечения изменилась по сравнению с недеформированной конфигурацией. Но именно это повернутое и деформированное состояние находится в конечном равновесии, не эталонная конфигурация.
Напряжение Коши обозначается просто \(\boldsymbol{\sigma}\). Все остальные определения ударения имеют своего рода нижние или верхние индексы, чтобы указать, что они есть.
Очень хлипкий трамплин для прыжков в воду — отличный пример условия загрузки
что поддерживает этот аргумент. Деформированная форма находится в равновесии, а не
эталонная форма. Таким образом, уравнения равновесия, включающие напряжения, должны
быть записано в терминах деформированной формы, поэтому напряжение Коши равно
естественный выбор.
Работа, энергия и мощность
Известно, что работа есть скалярное произведение силы и смещение согласно
\[
W = \ int {\ bf F} \ cdot {\ bf dx}
\]
, а мощность есть производная от работы по времени, которую можно получить, сначала
выполняя бесконечно малый объем работы, \( dW = {\bf F} \cdot {\bf dx} \),
и разделив на \(dt\), чтобы получить
\[
P = {dW \over dt} = {\bf F} \cdot {{\bf dx} \over dt}
\]
Но \(d{\bf x}/dt\) — это просто скорость, \({\bf v}\). Итак, сила
\[
п знак равно {\bf F} \cdot {\bf v}
\]
Для расчетов механики часто желательно рассчитывать работу и энергию в
с точки зрения напряжения и деформации, а не силы и смещения. Так же расчеты
мощности производятся с точки зрения напряжения и скорости деформации, а не силы и скорости.
Следующий вывод показывает, как связаны величины.
Начните с рассмотрения мощности, создаваемой силами, как внешними, так и внешними.
и внутренний, действующий на объект и перемещающий его со скоростью \({\bf v}\). Внешние силы будут выражаться в виде векторов тяги \({\bf T}\),
воздействует на внешнюю поверхность объекта. Векторы тяги должны
интегрироваться по внешней поверхности для получения силы. внутренний
силы будут представлены \({\bf f}\), имеющими размеры сила/объем . Они возникают благодаря таким механизмам, как
силы тяжести, ускорений, магнетизма и т. д. Суммарная сила, действующая
на объекте будет
Внешние силы будут выражаться в виде векторов тяги \({\bf T}\),
воздействует на внешнюю поверхность объекта. Векторы тяги должны
интегрироваться по внешней поверхности для получения силы. внутренний
силы будут представлены \({\bf f}\), имеющими размеры сила/объем . Они возникают благодаря таким механизмам, как
силы тяжести, ускорений, магнетизма и т. д. Суммарная сила, действующая
на объекте будет
\[
\text{Общая сила} \; знак равно \ underbrace {\int {\bf T} \, dA} _{\matrix{\text{Внешние} \\ \text{Силы}}} \; + \;
\ underbrace {\ int {\ bf f} \, dV} _ {\ matrix {\ text {Внутренние} \\ \ text {Силы}}}
\]
Мощность, генерируемая силами, вычисляется простым выполнением
скалярные произведения с вектором скорости \({\bf v}\).
\[
\text{Power} = \int {\bf T} \cdot {\bf v} \, dA + \int {\bf f} \cdot {\bf v} \, dV
\]
Обратите внимание, что \({\bf v}\) не обязательно должно быть постоянным по объему (или поверхности). Она может изменяться из-за деформаций, вращений и/или вибраций.
Тем не менее, уравнение остается правильным.
Она может изменяться из-за деформаций, вращений и/или вибраций.
Тем не менее, уравнение остается правильным.
Этот результат можно разделить на мощность, связанную с движением (включая вектор скорости, \({\bf v}\)), и связанный с деформациями (напряжениями и деформациями). Это достигается за несколько шагов следующим образом. Во-первых, используйте тождество вектора тяги, \({\bf T} = \boldsymbol{\sigma} \cdot {\bf n}\), заменить \({\bf T}\) в уравнении.
\[
\text{Power} = \int (\boldsymbol{\sigma} \cdot {\bf n}) \cdot {\bf v} \, dA + \int {\bf f} \cdot {\bf v} \, дВ
\]
Затем применим теорему о расходимости к первому члену, содержащему поверхностный интеграл
преобразовать его в объемный интеграл.
\[
\text{Power} = \int \nabla \cdot (\boldsymbol{\sigma} \cdot {\bf v}) \, dV + \int {\bf f} \cdot {\bf v} \, dV
\]
Затем раскройте оператор дивергенции, чтобы получить
\[ \text{Power} = \int (\nabla \cdot \boldsymbol{\sigma}) \cdot {\bf v} \, dV + \int \boldsymbol{\sigma} : \nabla{\bf v} \, dV + \int {\bf f} \cdot {\bf v} \, dV \]
Вышеприведенный шаг совсем не интуитивно понятен при использовании матричных обозначений, но легко проверяется. с тензорными обозначениями. Термин \( \nabla \cdot ( \boldsymbol{\sigma} \cdot {\bf v} ) \)
выражается в тензорной записи как \( ( \sigma_{ij} v_i ),_j \). Применение
правило продукта дает
с тензорными обозначениями. Термин \( \nabla \cdot ( \boldsymbol{\sigma} \cdot {\bf v} ) \)
выражается в тензорной записи как \( ( \sigma_{ij} v_i ),_j \). Применение
правило продукта дает
\[
(\sigma_{ij} v_i ),_j = \sigma_{ij},_j v_i + \sigma_{ij} v_i,_j
\]
, который легко интерпретируется как
\[ \nabla \cdot (\boldsymbol{\sigma} \cdot {\bf v}) = (\nabla \cdot \boldsymbol{\sigma}) \cdot {\bf v} + \boldsymbol{\sigma} : \nabla{\bf v} \]
Термин \( \nabla \cdot \boldsymbol{\sigma} \) является здесь ключевым, поскольку он также появляется в уравнении равновесия: \( \nabla \cdot \boldsymbol{\sigma} + {\bf f} = \rho \, {\bf a} \). Это делает это можно заменить \( \nabla \cdot \boldsymbol{\sigma} \) на \( ( \rho \, {\bf a} — {\bf f} ) \).
\[
\text{Power} = \int (\rho \, {\bf a} — {\bf f}) \cdot {\bf v} \, dV + \int \boldsymbol{\sigma} : \nabla{\bf v} \, dV + \int {\bf f} \cdot {\bf v} \, dV
\]
Расширение первого члена дает
\[
\text{Power} = \int \rho \, {\bf a} \cdot {\bf v} \, dV — \int {\bf f} \cdot {\bf v} \, dV + \int \boldsymbol {\sigma} : \nabla{\bf v} \, dV + \int {\bf f} \cdot {\bf v} \, dV
\]
Обратите внимание, что два члена \( \int {\bf f} \cdot {\bf v} \, dV \) компенсируют друг друга, оставляя только
\[
\text{Power} = \int \rho \, {\bf a} \cdot {\bf v} \, dV + \int \boldsymbol{\sigma} : \nabla{\bf v} \, dV
\]
И член \( \int \rho \, {\bf a} \cdot {\bf v} \, dV \) на самом деле является производной по времени Кинетическая энергия : \( \int {1 \over 2} \rho \, ({\bf v} \cdot {\bf v} ) \, dV \). Таким образом, это может быть записано как
Таким образом, это может быть записано как
\[
\text{Power} = {d \over dt} \left( \int {1 \over 2} \rho \, ( {\bf v} \cdot {\bf v} ) \, dV \right) + \int \boldsymbol{\sigma} : \nabla{\bf v} \, dV
\]
Или просто
\[
\text{Мощность} = {d \over dt} (\text{Кинетическая энергия}) + \int \boldsymbol{\sigma} : \nabla{\bf v} \, dV
\]
И \( \nabla {\bf v} \) — градиент скорости, \({\bf L}\). Замена дает
\[
\text{Мощность} = {d \over dt} (\text{Кинетическая энергия}) + \int \boldsymbol{\sigma} : {\bf L} \, dV
\]
И \({\bf L}\) также равно \({\bf D} + {\bf W}\). Замена и расширение дает
\[
\text{Мощность} = {d \over dt} (\text{Кинетическая энергия}) + \int \boldsymbol{\sigma} : {\bf D} \, dV + \int \boldsymbol{\sigma} : {\ bf W} \, dV
\]
Но \( \boldsymbol{\sigma} : {\bf W} \) тождественно равен нулю, потому что \(\boldsymbol{\sigma}\)
симметрична, а \({\bf W}\) антисимметрична. Это оставляет окончательный результат.
\[
\text{Мощность} = {d \over dt} (\text{Кинетическая энергия}) + \int \boldsymbol{\sigma} : {\bf D} \, dV
\]
Общая мощность теперь разделена на две части: (i) объемное движение,
и (ii) деформации. Объемное движение представлено кинетической энергией, из которой
вектор скорости \({\bf v}\) является ключевым. Деформации представлены
плотность энергии деформации, а скорость ее изменения вычисляется по формуле энергетически сопряжены пар напряжений и скоростей деформации.
Объемное движение представлено кинетической энергией, из которой
вектор скорости \({\bf v}\) является ключевым. Деформации представлены
плотность энергии деформации, а скорость ее изменения вычисляется по формуле энергетически сопряжены пар напряжений и скоростей деформации.
Мы сосредоточимся на компоненте деформации общей мощности, чтобы определить дополнительные пары энергетически сопряженных напряжений, деформаций и скоростей деформаций. У нас уже есть напряжение Коши и тензор скорости деформации как наша первая энергетически сопряженная пара. Это логично, потому что оба связаны с деформированной и повернутой конфигурацией объекта.
1-й Пиола Кирхгоф Стресс
Определение 1-го напряжения Пиолы Кирхгофа начинается с напряжения Коши.
тензор скорости деформации.
9{ПК2} \! : д {\ бф Е}
\]
где \(W»’\) — энергия деформации на единицу объема.
(Объем имеет длину 3 , отсюда и три апострофа.)
Инженерное напряжение
Инженерное напряжение — это просто сила, воздействующая на первоначальную площадь.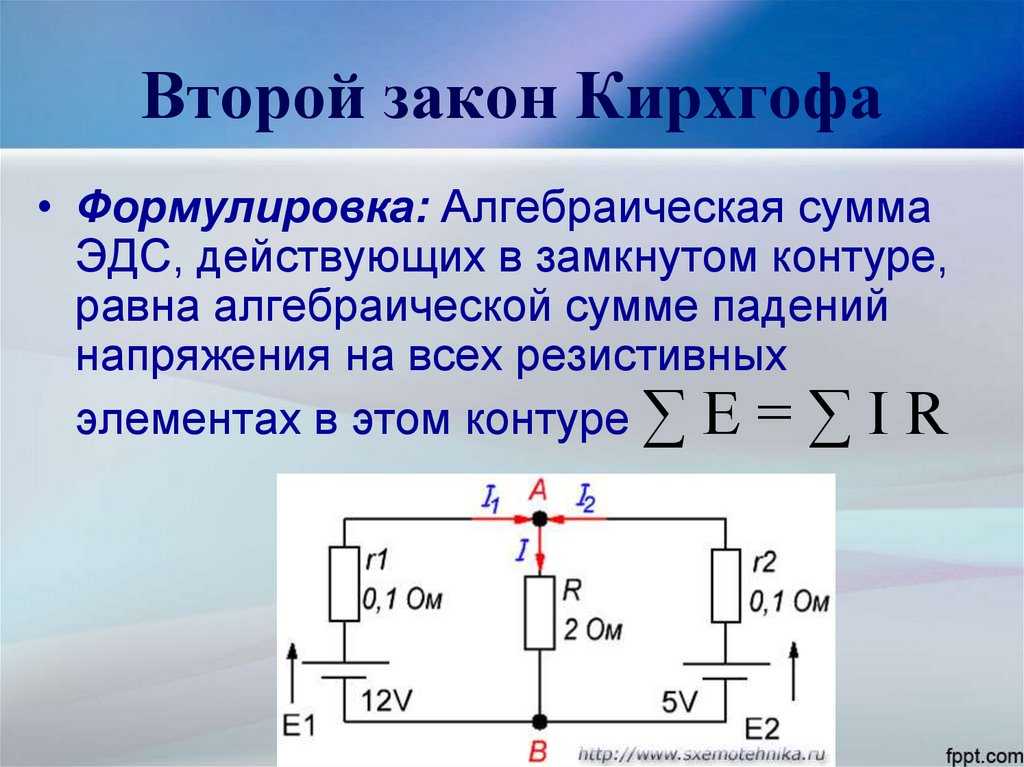
\[
\sigma_{\text{Eng}} = {F_{\text{нормаль}} \over A_o} \qquad \text{and} \qquad
\tau_{\text{Eng}} = {F_{\text{параллельно}} \over A_o}
\]
Но я не знаю, как распространить эти определения на случай больших вращений.
Примеры напряжений
Примеры здесь сравнивают напряжение Коши, 2-е напряжение Пиолы-Кирхгофа и инженерный стресс. В примерах будет использоваться несжимаемая резина, поэтому \(J = 1\).
Простое растяжение/сжатие несжимаемой резины
Образец для испытаний резины растягивают при растяжении, как показано на рисунке. Он несжимаем, поэтому объем должен оставаться постоянным.
\[
Л_о \, А_о = Л_Ф \, А_Ф
\]
Переставить, чтобы получить
\[
{A_o \ над A_F} = {L_F \ над L_o}
\]
Но соотношение начальной и конечной длин связано с инженерной деформацией следующим образом
\[
{L_F \over L_o} = 1 + \epsilon_{\text{Eng}}
\]
Итак поэтому
\[
{A_o \over A_F} = 1 + \epsilon_{\text{Eng}}
\]
Это соотношение будет использоваться для соотнесения различных терминов стресса.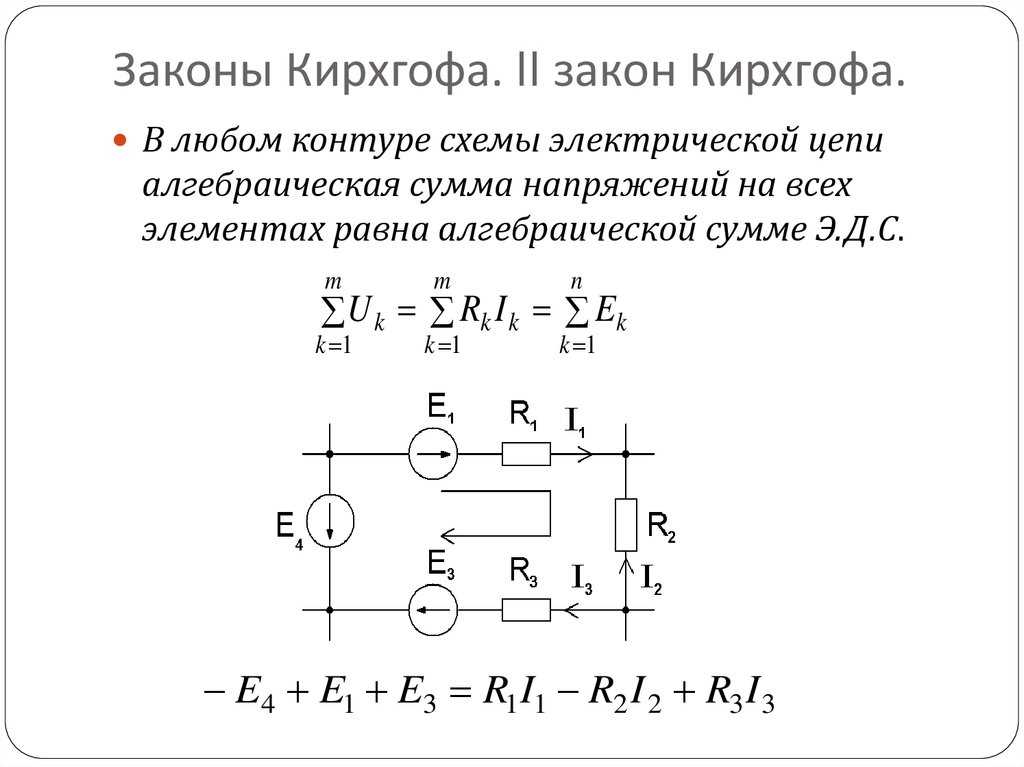 Для начинающих,
поскольку в этом случае растягивающая сила является произведением \( ( \sigma \, A_F ) \)
а также произведение \( ( \sigma_{\text{Eng}} \, A_o ) \), два члена могут быть
приравнивается к даче
Для начинающих,
поскольку в этом случае растягивающая сила является произведением \( ( \sigma \, A_F ) \)
а также произведение \( ( \sigma_{\text{Eng}} \, A_o ) \), два члена могут быть
приравнивается к даче
\[
\сигма\,А_Ф\; знак равно \sigma_{\text{Eng}} \, А_о
\]
И это можно переставить, чтобы дать
\[
{ \sigma \over \sigma_{\text{Eng}}} \; знак равно { А_о \над А_Ф }
\]
И этим можно дополнительно манипулировать, чтобы дать
\[
\сигма\; знак равно \sigma_{\text{Eng}} ( 1 + \epsilon_{\text{Eng}} )
\]
Таким образом, когда деформации малы, напряжение Коши и инженерное напряжение
то же самое для всех практических целей. Но так как объект значительно растягивается
так что площадь его поперечного сечения уменьшится, напряжение Коши станет
больше, чем инженерное напряжение. Аналогично, при сжатии
существует обратный случай. При сжатии напряжение Коши меньше (в абс.
значение), чем инженерное напряжение.
9{ПК2}\) меньше
чем \(\sigma_{\text{Eng}}\), и наоборот.
График ниже предполагает, что \(\sigma_{\text{Eng}} = E \, \epsilon_{\text{Eng}}\) при \(E\) = 1 МПа примерно жесткость натурального каучука, не менее при меньших деформациях.
Напряжение и вращение несжимаемой резины
Вспомните пример со страницы об истинных деформациях. где объект растягивается и вращается. На этот раз мы будем использовать его для сравнения напряжений при наличии больших вращений твердого тела. Инженерное напряжение не включено, так как оно теряет смысл при наличии вращений.
Во-первых, стресс Коши прост. Конечное напряженное состояние состоит полностью нормальной y-компоненты, потому что y-направление является направлением сила растяжения. Таким образом, окончательный тензор напряжений Коши будет выглядеть так:
\[
\boldsymbol{\сигма} =
\слева[ \матрица{
0 & 0 & 0 \\
\\
0&F/A&0\
\\
0 и 0 и 0 }
\Правильно]
\]
, где \(A\) — конечное деформированное поперечное сечение образца.
Градиент деформации должен быть определен для расчета
2-й стресс Пиолы-Кирхгофа.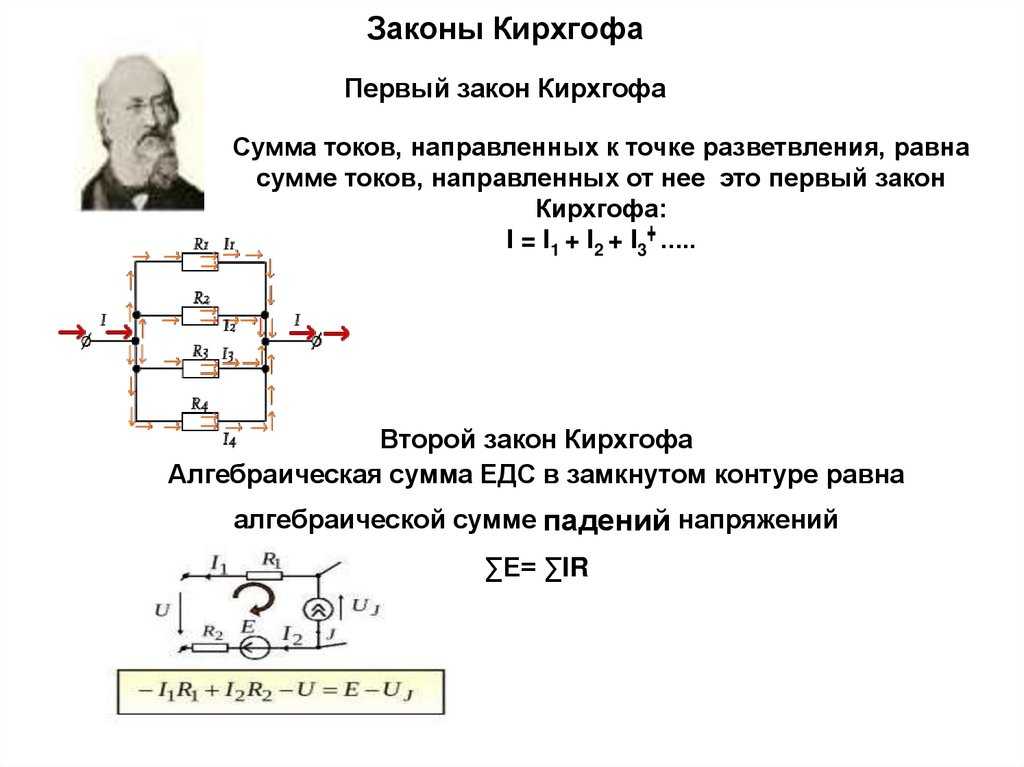 {-1/2} }
\Правильно]
\end{эквнаррай}
\]
9{\text{PK2}} : \dot {\bf E}\) точно равно
\(\boldsymbol{\sigma} : {\bf D}\). Каждая пара энергетически сопряжена.
{-1/2} }
\Правильно]
\end{эквнаррай}
\]
9{\text{PK2}} : \dot {\bf E}\) точно равно
\(\boldsymbol{\sigma} : {\bf D}\). Каждая пара энергетически сопряжена.
Примечание относительно линейной эластичности
Мы говорили о законе Гука, касающемся стресса и напряжения, в разделе, посвященном тензорное обозначение. Напомним, что
\[
\boldsymbol{\epsilon} = {1 \over E} \left[ (1 + \nu) \boldsymbol{\sigma} — \nu \; {\ бф I} \; \text{tr}(\boldsymbol{\sigma}) \right]
\]
Но мы упустили из виду вопрос о том, какие тензоры напряжений и деформаций следует использовать в уравнении.
Ответ обманчиво прост… в большинстве случаев. Это связано с тем, что линейная эластичность применяется только к очень небольшим штаммам, обычно <1%. И теперь мы видели, что все определения напряжения эквивалентны, как и все определения деформации, когда деформации небольшие. Так что это не имеет большого значения, на самом деле.
Однако есть подвох . Это, как обычно, вращения. В присутствии
большие обороты, правильное сочетание напряжения и деформации имеет решающее значение. Напомним
более ранний пример вращения объекта при растяжении.
9{\ текст {ПК2}}) \ справа]
\]
Это, как обычно, вращения. В присутствии
большие обороты, правильное сочетание напряжения и деформации имеет решающее значение. Напомним
более ранний пример вращения объекта при растяжении.
9{\ текст {ПК2}}) \ справа]
\]
Точно так же можно записать закон Гука в терминах \(\boldsymbol{\sigma}\) и \(\boldsymbol{\epsilon}_{\text{True}}\) (пока
\(\boldsymbol{\epsilon}_{\text{True}}\) вычисляется в текущей ориентации).
\[
\boldsymbol{\epsilon}_{\text{True}} = {1 \over E} \left[ (1 + \nu) \boldsymbol{\sigma} — \nu \; {\ бф I} \; \text{tr}(\boldsymbol{\sigma}) \right]
\]
Но знаете что. Единственное, что нельзя сделать (по крайней мере, правильно), — это записать его в терминах \(\dot{\boldsymbol{\sigma}}\) и
\(\dot{\boldsymbol{\epsilon}}_{\text{True}}\) (\(={\bf D}\)).
Чтобы убедиться в этом, рассмотрим небольшую альтернативу приведенному выше рисунку. Думайте об объекте как о сначала растянутом в направлении x,
а затем удерживается на постоянной длине. Это создает напряжение в направлении x, которое является постоянным, в то время как объект
удерживается на постоянной длине.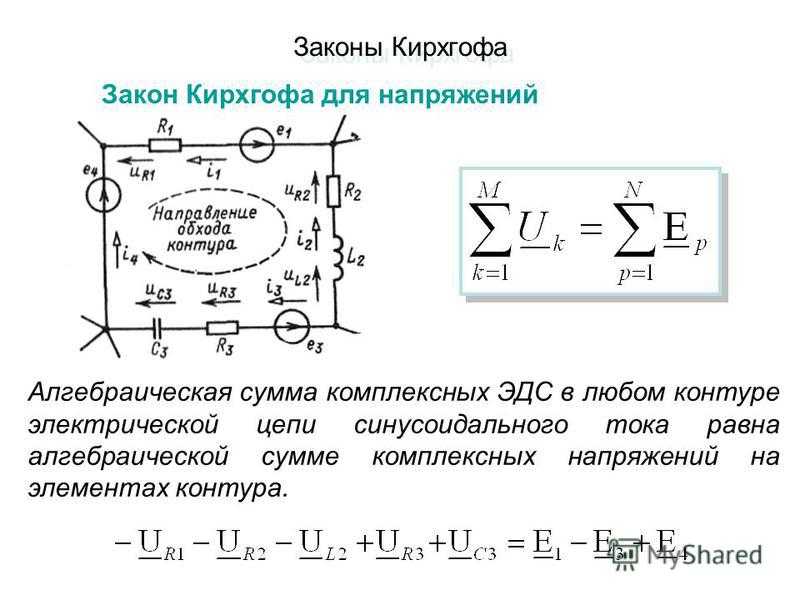


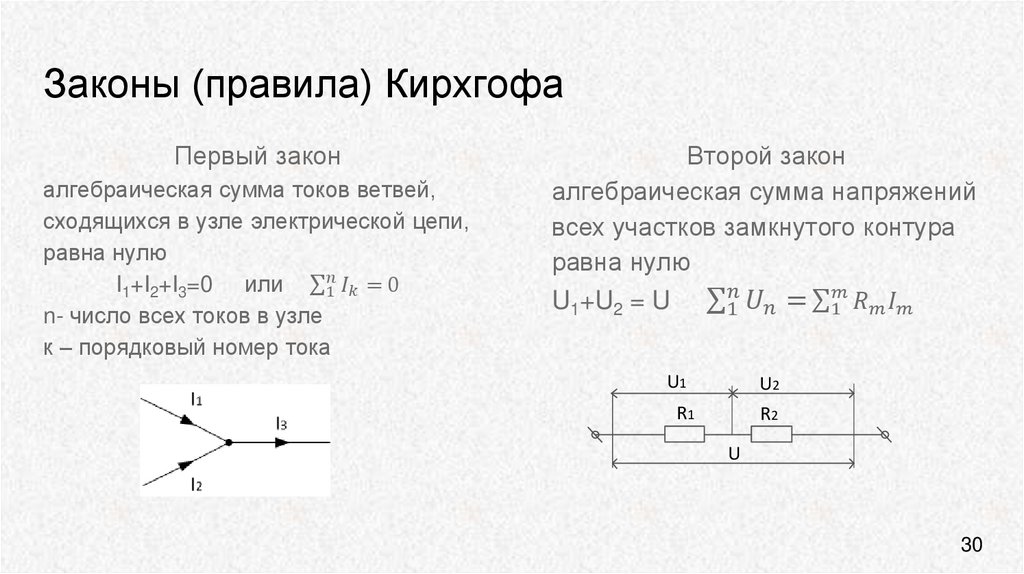
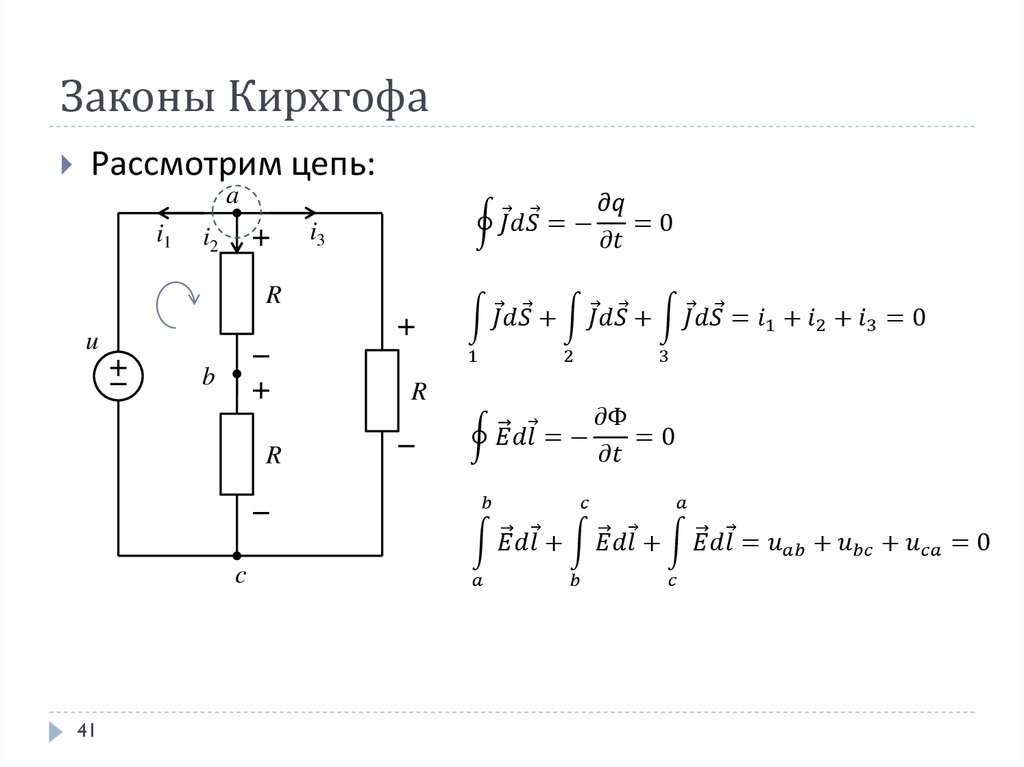
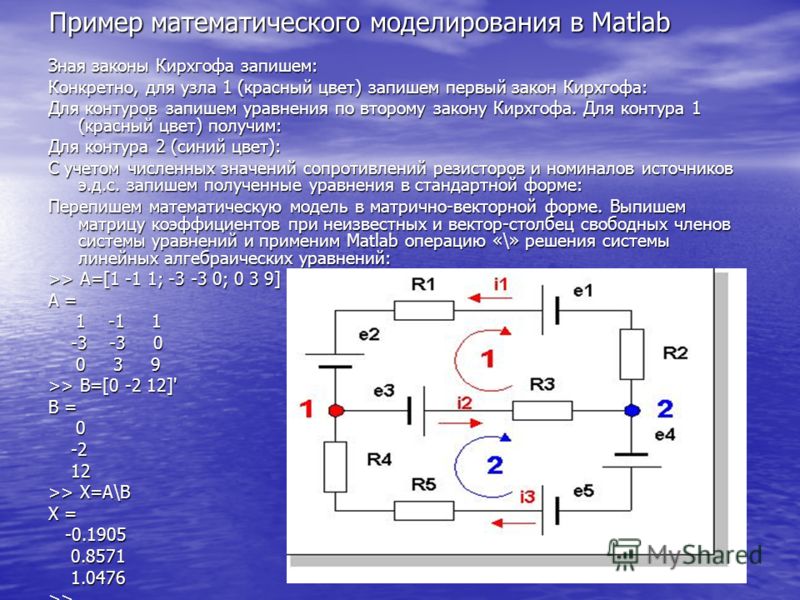
 Действительно, напряжение Uab на участке ab — это работа поля по переносу единичного заряда из точки a в точку b; напряжение Ubc на участке bc — это работа поля по переносу единичного заряда из точки b в точку c. Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки a в точку c, то есть напряжение U на всём участке: U = Uab + Ubc.
Действительно, напряжение Uab на участке ab — это работа поля по переносу единичного заряда из точки a в точку b; напряжение Ubc на участке bc — это работа поля по переносу единичного заряда из точки b в точку c. Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки a в точку c, то есть напряжение U на всём участке: U = Uab + Ubc.