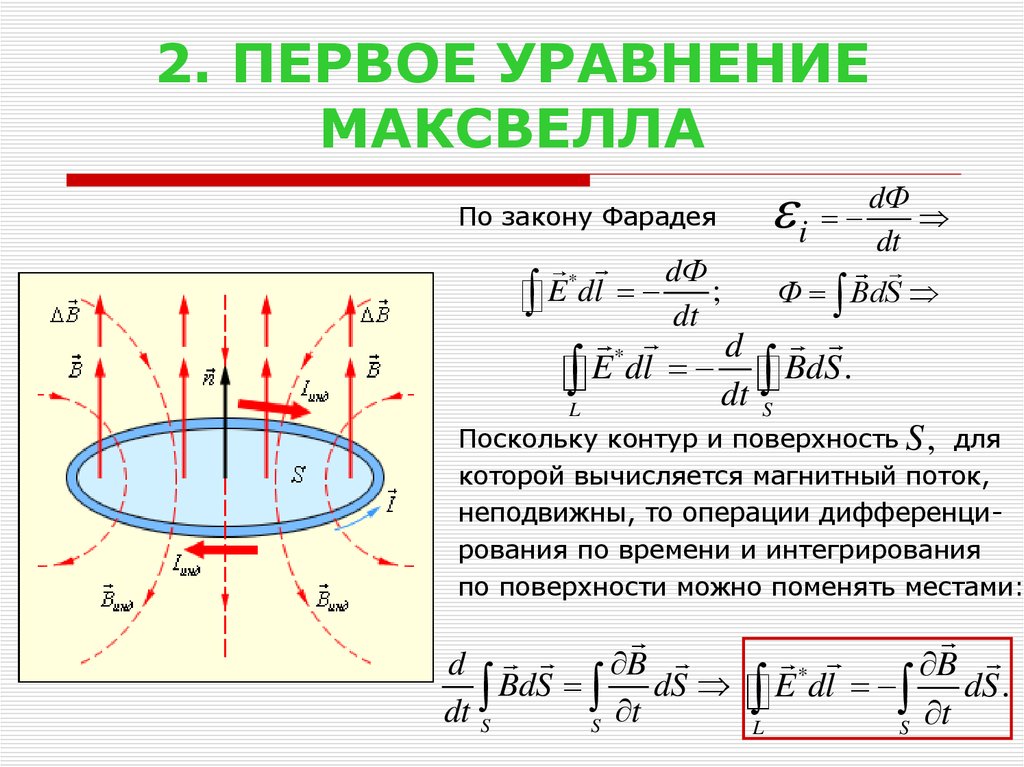
20.Закон Фарадея-Максвела

6.1. Явление электромагнитной индукции.

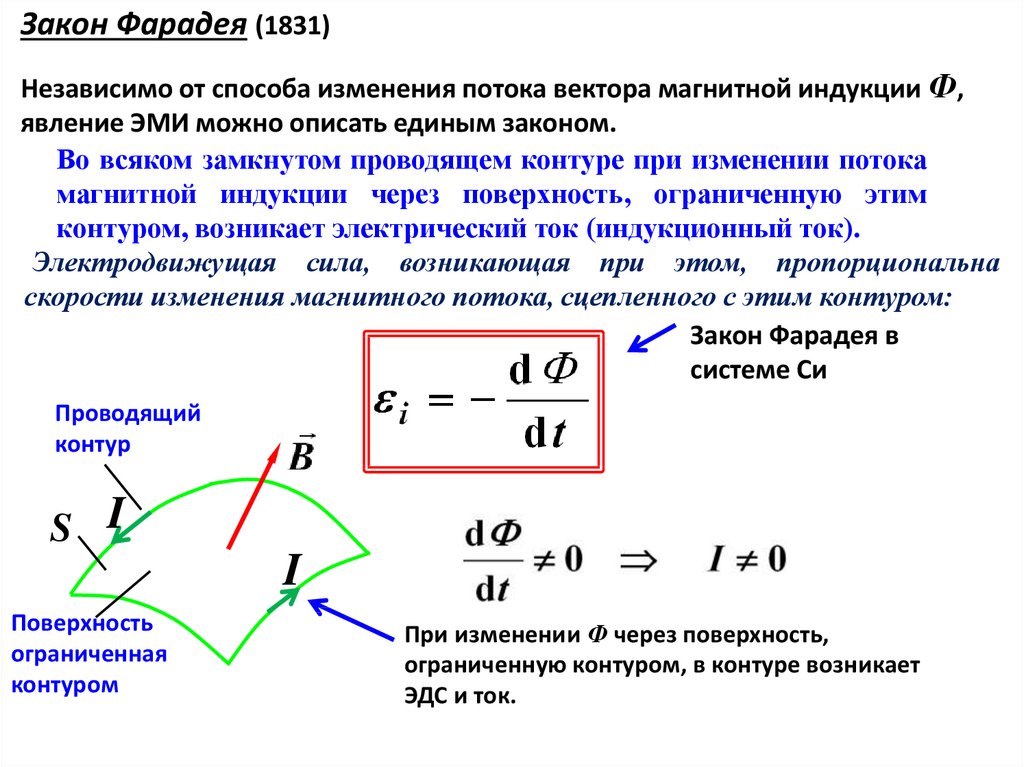
Закон Фарадея–Максвелла

Содержание опытов Фарадея можно пояснить следующими рисунками. Разместим на одном сердечнике две проводящие катушки (рис.6.1, а). Одну из них замкнем на гальванометр, а другую будем подключать к источнику тока при помощи ключа К. В момент замыкания (или размыкания) цепи ключом К гальванометр будет давать показания, т.е. в цепи второй катушки будет возникать электрический ток. Итак, по результатам такого опыта можно сделать вывод, что первая катушка электрически влияет на вторую. Однако, что было причиной появления тока в катушке 2: возникновение (или исчезновение) тока в катушке 1 или магнитного поля этого тока?

Для ответа на этот вопрос поставим второй опыт (рис. 6.1, б). Теперь катушка 1 постоянно подключена к источнику, а поэтому ток в ней неизменен.

Однако в процессе смещения катушек друг относительно друга гальванометр дает показания, т.е. причиной появления тока в катушке 2 является изменение магнитного поля, в котором она находилась.

Чтобы подтвердить этот вывод, Фарадей проводит третий опыт (рис.6.1, в), в котором первая катушка заменяется постоянным магнитом. Результаты опыта при смещении магнита относительно катушки 2 полностью аналогичны предыдущим. Однако в этом случае видно, что причиной всех электрических явлений в катушке 2 является исключительно поведение магнитного поля, в которое она помещена, а источник создания магнитного поля никак не влияет на результат наблюдений.

Общим для всех трех опытов было то, что при осуществлении действий, описанных выше, изменялся магнитный поток через вторую катушку, в которой создавался (индуцировался) электрический ток. Важно также и то, что появление тока наблюдалось только в процессе изменения магнитного потока. Как только изменение магнитного потока прекращалось (полностью замыкался ключ, прекращалось относительное смещение катушек или останавливался магнит), стрелка гальванометра занимала нулевое положение. Если гальванометр заменить вольтметром, то он аналогично будет показывать появление разности потенциалов на концах катушки

2.

Наблюдаемое явление Фарадей назвал электромагнитной индукцией, т.е. явлением возникновения ЭДС индукции (а также индукционного тока в замкнутом контуре) при любом изменении магнитного потока через площадь, ограниченную контуром.

Экспериментально обнаружено, что величина возбуждаемой ЭДС определяется только скоростью изменения магнитного потока через контур и не зависит от способа его изменения. Напомним, что, согласно определению магнитного потока (5.18), его величина может изменяться при изменении модуля индукции в точках поверхности, ограниченной контуром, при изменении ориентации контура относительно линий магнитной индукции поля, при изменении площади контура.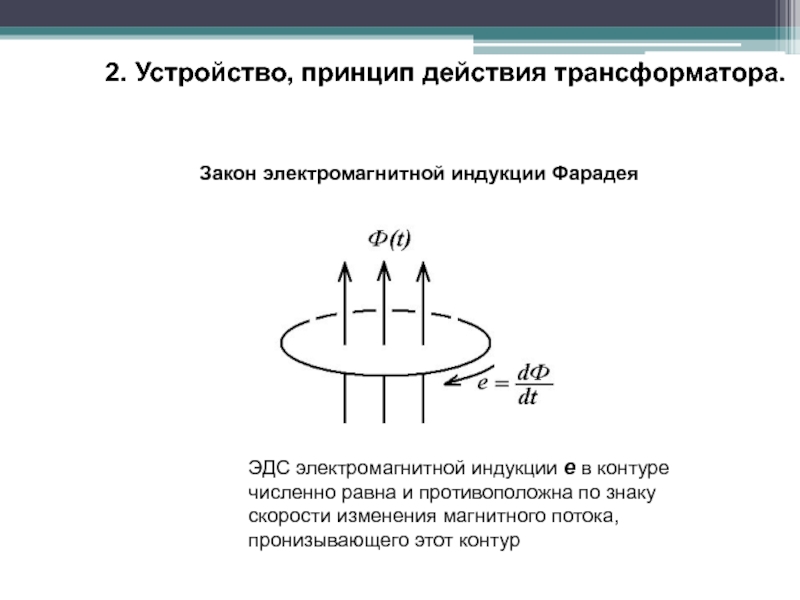

Также экспериментально выяснено, что направление индукционного тока в контуре таково, что своим магнитным полем он компенсирует изменение магнитного потока, вызвавшего его появление (правило Ленца). На рис. 6.2 показано, что при увеличении тока в контуре 1 будет увеличиваться магнитная индукция поля, создаваемого этим контуром. В этом случае магнитный поток этого поля через контур

2 также возрастает. Это приводит к появлению в контуре 2 электромагнитной индукции, т.е. в контуре создается индукционный ток . Его направление таково, что линии индукции создаваемого им магнитного поля () направлены противоположно внешнему. Тогда суммарный магнитный поток через контур 2 определяется разностью потоков внешнего и индуцированного полей. Поэтому величина магнитного потока через контур 2 увеличивается слабее. Если же ток в контуре 1 будет уменьшаться, то явление электромагнитной индукции создаст ток в контуре 2, направленный в противоположную сторону.

Таким образом, процессы, происходящие при электромагнитной индукции, приводят к тому, что магнитный поток через исследуемый контур стремится остаться неизменным. Можно показать, что это – следствие закона сохранения энергии. Итак, правило Ленца показывает, что следствие процесса (появляющийся индукционный ток) всегда препятствует причине, его вызывающей (изменению магнитного потока).

Поясним это еще на одном примере (рис.6.3). Поместим в однородное магнитное поле с индукцией систему двух параллельных проводников, замкнутых на резистор сопротивлением R. Пусть между проводниками располагается перемычка, способная перемещаться по ним без нарушения электрического контакта. Тогда при ее движении вправо со скоростью будет увеличиваться площадь проводящего контура, образованного проводниками, резистором и перемычкой. Соответственно, будет увеличиваться и магнитный поток через этот контур, что приведет к появлению индукционного тока.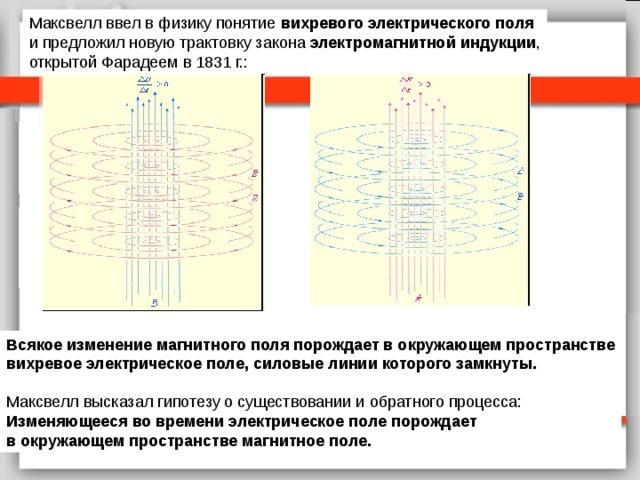

Индукционный ток в контуре будет иметь такое направление (против часовой стрелки), что вектор его магнитной индукции будет противоположен вектору индукции внешнего магнитного поля. В магнитном поле с индукцией на перемычку с индукционным током будет действовать сила Ампера, направление которой определим по правилу левой руки (см. рис. 6.3). Появившаяся сила стремится замедлить движение перемычки, т.е. препятствует ее движению. Поскольку причиной электромагнитной индукции в контуре было движение перемычки, то следствие явления – появившаяся сила Ампера – препятствует причине своего появления.

Выведем количественные соотношения, описывающие содержание явления электромагнитной индукции.

1 способ (на основе закона сохранения энергии). Рассмотрим схему, аналогичную предыдущей. На рис.6.4 показан проводящий контур, образованный двумя параллельными проводниками, замкнутыми свободно двигающейся по ним перемычкой. В контур включен источник тока с ЭДС E и резистор сопротивлением

R. Поместим контур в однородное магнитное поле с индукцией . Поскольку в контуре существует электрический ток, то на перемычку будет действовать сила Ампера, что вызовет движение перемычки вправо. Поэтому площадь контура будет возрастать, а, следовательно, магнитный поток через площадь, ограниченную контуром, также будет увеличиваться. Это будет причиной появления электромагнитной индукции.

Согласно закону сохранения энергии работа, совершенная источником тока за время , равна работе сил магнитного поля по перемещению перемычки и выделившемуся в контуре за это время количеству теплоты: , т.е.

,

где – заряд, перенесенный источником за время . Поскольку , то

,

откуда сила тока в контуре

.

Поскольку, согласно закону Ома, числитель последнего выражения должен определять суммарную ЭДС в контуре, то, следовательно, второе слагаемое выражает ЭДС индукции, возникшую в нем:

. (6.1)

2 способ (на основе электронных представлений).

Рассмотрим процессы, происходящие внутри перемычки (рис.6.5, а). Поскольку все свободные электроны двигаются вместе с ней вправо, то со стороны магнитного поля на них действует магнитная составляющая силы Лоренца (5.29). Ее действие приводит к смещению электронов к нижнему краю перемычки, в результате чего происходит разделение зарядов внутри нее. Между разделенными зарядами возникает электрическое поле напряженностью , которое действует на электроны с силой (рис.6.5, б). В стационарном режиме . Следовательно, , т.е. . Найдем разность потенциалов между концами перемычки:

,

поскольку – площадь, очерчиваемая проводником за время при движении (рис.6.5,

в). Перемычка играет роль источника индукционного тока, а положительным направлением тока внутри источника считается направление от “–” к “+”. Поэтому ЭДС индукции, возникшая при движении перемычки, определится как

. (6.2)

Мы видим, что оба рассмотрения приводят к одному и тому же результату. Обобщим его на произвольный случай движения контура во внешнем магнитном поле (рис.6.6). Поскольку ЭДС – это удельная работа сторонних сил по переносу заряда вдоль контура, а роль сторонней силы выполняет , то. Преобразуем это выражение, используя свойства смешанного произведения векторов:

.

Поменяем местами сомножители в векторном произведении, изменив знак произведения:

.

Поскольку (см. п.5.5), то

. (6.3)

Итак, при движении замкнутого проводящего контура во внешнем магнитном поле в нем возникает ЭДС индукции, равная скорости изменения магнитного потока через площадь поверхности, ограниченной контуром. Полученный вывод и соотношение (6.3) выражают основной закон электромагнитной индукции, названный законом Фарадея–Максвелла. Знак “–“ в соотношении (6.3) показывает, что индукционный ток, возникающий в контуре, своим магнитным полем компенсирует изменение магнитного потока, вызвавшего появление индукционного тока.

Электромагнитное поле. Часть 1. Электричество и магнетизм

Электромагнитное поле. Часть 1. Электричество и магнетизм

Мешков И. Н., Чириков Б. В. Электромагнитное поле. Часть 1. Электричество и магнетизм.— Новосибирск: Наука, 1987. В монографии последовательно изложены основные положения классической электромагнитной теории, включая движение заряженных частиц в поле и структуру электромагнитной волны. Дана наглядная картина физических явлений в сочетании с упрощенным теоретическим анализом. Описаны важнейшие эксперименты и интересные с точки зрения физики практические приложения. Книга предназначена для специалистов в различных областях физики и техники, преподавателей, аспирантов и студентов вузов. Оглавление ПРЕДИСЛОВИЕ Глава I. ЭЛЕКТРОСТАТИКА § 1. ЗАКОН КУЛОНА § 2. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ § 3. ПРИНЦИП СУПЕРПОЗИЦИИ § 4. ГЕОМЕТРИЯ ПОЛЯ § 5. ЭЛЕКТРИЧЕСКИЕ МУЛЬТИПОЛИ § 6. ЗАКОН СОХРАНЕНИЯ ПОТОКА ЭЛЕКТРИЧЕСКОГО ПОЛЯ § 7. ОСНОВНОЕ УРАВНЕНИЕ ЭЛЕКТРОСТАТИКИ (УРАВНЕНИЕ ПУАССОНА) § 8. ОБЩЕЕ РЕШЕНИЕ УРАВНЕНИЯ ПУАССОНА. ПОНЯТИЕ О «дельта»-ФУНКЦИИ § 9. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ § 10. ПРОВОДНИК В ЭЛЕКТРИЧЕСКОМ ПОЛЕ § 11. УРАВНЕНИЕ ЛАПЛАСА § 12. ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ § 13. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЗАКОНА КУЛОНА Глава II. ДИЭЛЕКТРИКИ § 15. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКЕ § 16. ГРАНИЧНЫЕ УСЛОВИЯ § 17. ЭНЕРГИЯ ПОЛЯ В СРЕДЕ § 18. ДАВЛЕНИЕ ПОЛЯ § 19. ЭЛЕКТРОСТАТИЧЕСКИЕ СИЛЫ В СРЕДЕ Глава III. ЭЛЕКТРИЧЕСКИЙ ТОК § 20. ЭЛЕКТРИЧЕСКИЙ ТОК. УРАВНЕНИЕ НЕПРЕРЫВНОСТИ § 21. ТОК В МЕТАЛЛАХ. ЗАКОН ОМА § 22. ТОК В ИЗОЛЯТОРАХ. ГРАНИЧНЫЕ УСЛОВИЯ ПРИ НАЛИЧИИ ТОКА § 23. РЕЛАКСАЦИЯ ЗАРЯДОВ В СРЕДЕ § 24. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ЗАКОНЫ КИРХГОФА § 25. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С ЕМКОСТЬЮ § 26. ЭЛЕКТРИЧЕСКИЙ РАЗРЯД § 27. ПУЧКИ ЗАРЯЖЕННЫХ ЧАСТИЦ Глава IV. МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ § 29. МАГНИТНОЕ ПОЛЕ И ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ § 30. САМОФОКУСИРОВКА ПУЧКА ЗАРЯЖЕННЫХ ЧАСТИЦ: ПИНЧ-ЭФФЕКТ § 31. ВЕКТОР-ПОТЕНЦИАЛ § 32. ОСНОВНЫЕ УРАВНЕНИЯ МАГНИТНОГО ПОЛЯ § 33. ЗАКОН СОХРАНЕНИЯ ЦИРКУЛЯЦИИ МАГНИТНОГО ПОЛЯ § 34. МАГНИТНЫЙ ДИПОЛЬ § 35. ВЗАИМОДЕЙСТВИЕ ДИПОЛЯ С МАГНИТНЫМ ПОЛЕМ § 36. ПРЕЦЕССИЯ МАГНИТНОГО МОМЕНТА. МАГНИТНЫЙ РЕЗОНАНС Глава V. МАГНИТНОЕ ПОЛЕ В СРЕДЕ § 38. МАГНИТНАЯ ИНДУКЦИЯ § 39. ТОК СМЕЩЕНИЯ В СРЕДЕ § 40. ГРАНИЧНЫЕ УСЛОВИЯ ДЛЯ МАГНИТНОГО ПОЛЯ § 41. МАГНИТНЫЕ ЦЕПИ § 42. ПОНЯТИЕ О ФЕРРОМАГНЕТИЗМЕ § 43. ПОСТОЯННЫЕ МАГНИТЫ § 44. ПЛАЗМА КАК ДИАМАГНЕТИК Глава VI. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ § 45. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ. УРАВНЕНИЯ МАКСВЕЛЛА § 46. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ. ИНДУКТИВНОСТЬ § 47. ДАВЛЕНИЕ МАГНИТНОГО ПОЛЯ § 48. СОХРАНЕНИЕ МАГНИТНОГО ПОТОКА. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ § 49. ИНДУКТИВНОСТЬ И МАССА § 50. СВЕРХСИЛЬНЫЕ МАГНИТНЫЕ ПОЛЯ § 51. ВЗАИМОИНДУКЦИЯ § 52. ЦЕПИ ПЕРЕМЕННОГО ТОКА § 53. ТЕХНИЧЕСКИЕ ПРИМЕНЕНИЯ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ § 54. СВЕРХПРОВОДИМОСТЬ § 55. ПОТОК ЭНЕРГИИ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ Глава VII. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ § 56. ЧАСТИЦА В ОДНОРОДНОМ И ПОСТОЯННОМ ПОЛЕ § 57. ЧАСТИЦА В НЕОДНОРОДНОМ ПОЛЕ. ЗАКОН СОХРАНЕНИЯ ОБОБЩЕННОГО МОМЕНТА § 58. ЗАКОН СОХРАНЕНИЯ ФАЗОВОГО ОБЪЕМА ПУЧКА ЗАРЯЖЕННЫХ ЧАСТИЦ Глава VIII. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ § 60. ОПТИЧЕСКИЙ ДИАПАЗОН. ИСТОЧНИКИ СВЕТА § 61. ГЛАЗ § 62. ИЗМЕРЕНИЕ ЦВЕТА, ИЛИ КОЛОРИМЕТРИЯ § 63. ИСКУССТВЕННЫЕ ПРИЕМНИКИ СВЕТА § 64. ГАММА-ИЗЛУЧЕНИЕ Глава IX. СТРУКТУРА ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ § 65. 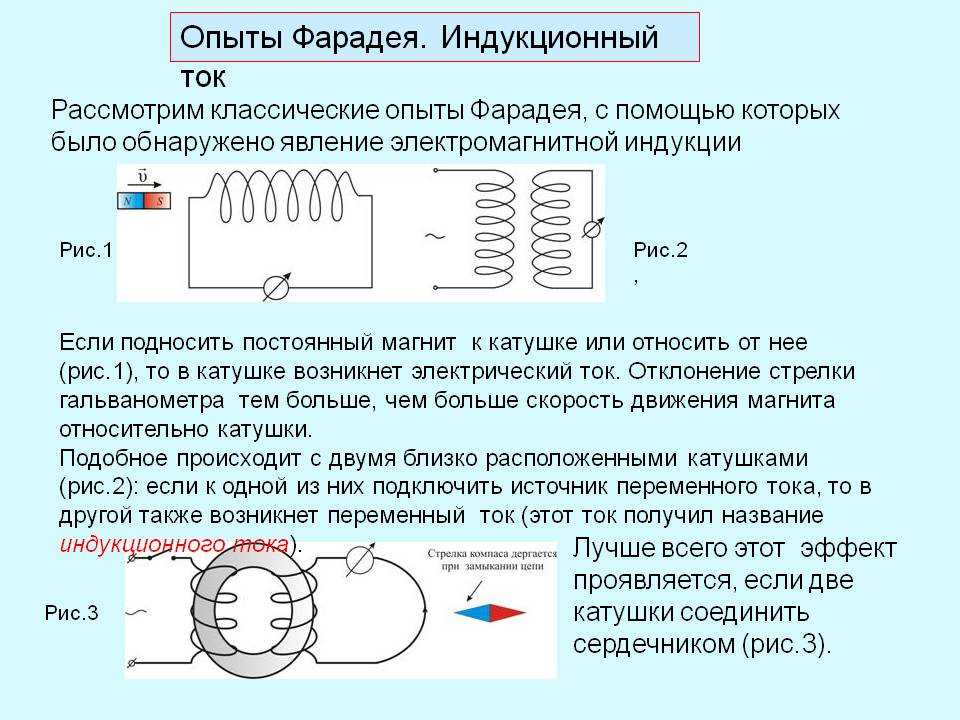СВОБОДНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ § 66. ВОЛНОВОЕ УРАВНЕНИЕ ДЛЯ ПОЛЕЙ § 67. ВОЛНОВОЕ УРАВНЕНИЕ ДЛЯ ПОТЕНЦИАЛОВ § 68. ПЛОСКИЕ ВОЛНЫ § 69. МОНОХРОМАТИЧЕСКАЯ ВОЛНА. ПОЛЯРИЗАЦИЯ ВОЛНЫ § 70. ВОЛНОВОЙ ВЕКТОР. ЭФФЕКТ ДОПЛЕРА § 71. АНОМАЛЬНЫЙ ЭФФЕКТ ДОПЛЕРА. ЧЕРЕНКОВСКОЕ ИЗЛУЧЕНИЕ Глава X. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ § 73. ПРЕЛОМЛЕНИЕ ВОЛНЫ § 74. ПОЛНОЕ ВНУТРЕННЕЕ ОТРАЖЕНИЕ. ТУННЕЛЬНЫЙ ЭФФЕКТ § 75. СТОЯЧАЯ ВОЛНА § 76. РЕЗОНАТОРЫ Глава XI. СПЕКТРАЛЬНЫЙ АНАЛИЗ § 77. СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ. ПЕРИОДИЧЕСКОЕ ПОЛЕ § 78. СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ. ИМПУЛЬСНОЕ ПОЛЕ § 79. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТИ § 80. СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ. СТОХАСТИЧЕСКОЕ ПОЛЕ § 81. ЭКСКУРС В ТЕОРИЮ ИНФОРМАЦИИ. КОЛИЧЕСТВО ИНФОРМАЦИИ § 82. ЭКСКУРС В ТЕОРИЮ ИНФОРМАЦИИ. ПОТОК ИНФОРМАЦИИ § 83. ЭКСКУРС В ТЕОРИЮ ИНФОРМАЦИИ. ПРИНЦИП СЦИЛАРДА — БРИЛЛЮЭНА Глава XII. ДИСПЕРСИЯ § 84. ФАЗОВАЯ И ГРУППОВАЯ СКОРОСТИ ВОЛНЫ § 85. РАСПЛЫВАНИЕ ВОЛНОВОГО ПАКЕТА § 86. ВОЛНОВОДЫ § 87. СКИН-ЭФФЕКТ Приложение ЛИТЕРАТУРА

Уравнение Максвелла-Фарадея — Электротехника…

В этом разделе мы обобщаем закон Кирхгофа о напряжении (KVL), ранее встречавшийся в качестве принципа электростатики в разделах 5.10 и 5.11. КВЛ утверждает, что в отсутствие изменяющегося во времени магнитного потока электрический потенциал, накопленный при прохождении замкнутого пути

, равен нулю. Вот эта идея в математической форме:

(8.8.1)

Теперь вспомним закон Фарадея (раздел 8.3):

(8.8.2)

Здесь,

— любая открытая поверхность, которая пересекает все силовые линии магнитного поля, проходящие через

, при этом относительная ориентация

и

определяется обычным образом в соответствии с соглашением по теореме Стокса (раздел 4.9). Обратите внимание, что закон Фарадея согласуется с KVL в магнитостатическом случае. Если магнитный поток постоянный, то закон Фарадея говорит:

. Однако закон Фарадея очень четко , а не согласуется с KVL, если магнитный поток изменяется во времени. Коррекция достаточно проста; мы можем просто установить эти выражения равными. Вот так:

(8.8.3)

Эта общая форма известна под разными именами; здесь мы называем его уравнением Максвелла-Фарадея (MFE).

Интегральная форма уравнения Максвелла-Фарадея (уравнение 8.8.3) утверждает, что электрический потенциал, связанный с замкнутым путем

, полностью обусловлен электромагнитной индукцией по закону Фарадея.

Несмотря на большое значение этого выражения как одного из уравнений Максвелла, можно утверждать, что все, что мы сделали, — это просто записали закон Фарадея несколько более подробно. Это верно. реальная мощность МФЭ высвобождается, когда она выражается в дифференциальной, а не в интегральной форме. Давайте теперь сделаем это.

Мы можем преобразовать левую часть уравнения 8.8.3 в интеграл по

, используя теорему Стокса. Применяя теорему Стокса слева, получаем

(8.8.4)

Теперь, поменяв местами порядок интегрирования и дифференцирования в правой части:

(8.8.5)

Поверхность

с обеих сторон одинакова, и мы не ограничивали

никак.

может быть любой математически допустимой открытой поверхностью в любом месте пространства, любого размера и любой ориентации. Единственный способ, которым приведенное выше выражение может быть универсально верным в этих условиях, — это если подынтегральные выражения с каждой стороны равны в каждой точке пространства. Таким образом,

(8.8.6)

представляет собой MFE в дифференциальной форме.

Что это значит? Напомним, что curl

— это способ получить директиву

относительно позиции (раздел 4.8). Следовательно, MFE ограничивает пространственные производные от

просто связано со скоростью изменения

. Сказано прямо:

Дифференциальная форма уравнения Максвелла-Фарадея (уравнение 8.8.6) связывает изменение электрического поля с положением с изменением магнитного поля со временем.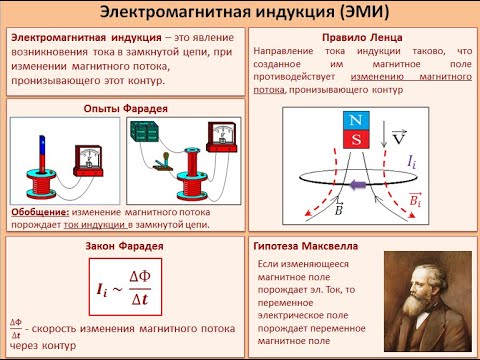

Возможно, это новая и полезная информация. Теперь мы видим, что электрические и магнитные поля связаны не только для линейных интегралов и потоков, но и в каждой точке пространства.

• «Закон индукции Фарадея» в Википедии.
• «Уравнения Максвелла» в Википедии.

Предыдущая страницаСледующая страница

Используйте клавиши со стрелками влево и вправо для перехода между страницами.

Проведите пальцем влево и вправо для смены страниц.

Уравнения Максвелла

Уравнения Максвелла

Электрический поток, исходящий от любой замкнутой поверхности, пропорционален общему заряду, заключенному внутри поверхности. Интегральная форма закона Гаусса находит применение при расчете электрических полей вокруг заряженных объектов. Применяя закон Гаусса к электрическому полю точечного заряда, можно показать, что он согласуется с законом Кулона. В то время как интеграл площади электрического поля дает меру суммарного заключенного заряда, дивергенция электрического поля дает меру плотности источников. Это также имеет значение для сохранения заряда. 33333333333333333333333333333333333333333333333333333333333333333333333333333н. Закон Гаусса, электричество Закон Гаусса, магнетизм Закон Фарадея Закон Ампер Уравнения Максвелла Индекс Концепции уравнений Максвелла   Гиперфизика***** Электричество и магнетизм R Ступица Назад Чистый магнитный поток от любой замкнутой поверхности равен нулю. Это равносильно утверждению об источниках магнитного поля. Для магнитного диполя на любой замкнутой поверхности магнитный поток, направленный внутрь к южному полюсу, будет равен потоку наружу от северного полюса. Чистый поток всегда будет равен нулю для дипольных источников. Если бы был источник магнитного монополя, это дало бы ненулевой интеграл площади. Расходимость векторного поля пропорциональна плотности точечного источника, поэтому форма закона Гаусса для магнитных полей в этом случае представляет собой утверждение об отсутствии магнитных монополей. 8081 Закон Гаусса, Электричество Закон Гаусса, Магнетизм Законодательство Фарадея Фараде. Уравнения Максвелла Индекс Концепции уравнений Максвелла   Гиперфизика***** Электричество и магнетизм R Ступица Назад Линейный интеграл электрического поля вокруг замкнутого контура равен отрицательному значению скорости изменения магнитного потока через площадь, ограниченную контуром. Этот линейный интеграл равен генерируемому напряжению или ЭДС в контуре, поэтому закон Фарадея является основой для электрических генераторов. Он также является основой для катушек индуктивности и трансформаторов. Применение для генерации напряжения в катушке 8081 Закон Гаусса, Электричество Закон Гаусса, Магнетизм Законодательство Фарадея Фараде. Уравнения Максвелла Индекс Концепции уравнений Максвелла   90932 Гиперфизика***** Электричество и магнетизм R Неф Назад В случае статического электрического поля линейный интеграл магнитного поля вокруг замкнутого контура пропорционален электрическому току, протекающему через контур. alexxlab Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Прост Радио Разное Своими руками Советы Схем Схемы Транзист Транзисторы Электрон Электроника