правила правой и левой руки, в чем измеряется, как найти, формула

Сила Лоренца в физике – определение

На помещенный в магнитное поле проводник с током будет действовать сила, определяемая законом Ампера. Взаимодействие поля и проводника является результатом взаимодействия поля и отдельных зарядов внутри проводника.

Определение 

Сила Лоренца — сила, характеризующая воздействие со стороны внешнего магнитного поля на движущийся с постоянной скоростью электрический заряд.

Формулировка, правила правой и левой руки

В конце XIX века нидерландский физик Х. Лоренц установил, что попадание движущейся частицы в магнитное поле приводит к возникновению силы, перпендикулярной направлению движения заряженной частицы и вектору магнитной индукции. Полученную величину принято называть силой Лоренца. Направление силы можно определить с помощью правил правой и левой руки.

Правило правой руки

Ладонь правой руки должна быть расположена так, чтобы силовые линии магнитного поля были направлены от ладони. Четыре пальца направить согласно вектору скорости заряженной частицы. Большой палец будет указывать направление силы Лоренца для положительного заряда. Для отрицательно заряженной частицы направление — противоположное.

Правило левой руки

Ладонь левой руки расположить так, чтобы силовые линии магнитного поля были направлены к ладони. Четыре пальца должны быть сонаправлены с вектором скорости движения заряженной частицы. Большой палец будет указывать направление силы Лоренца для положительного заряда. Для отрицательно заряженной частицы направление — противоположное. 

 

Источник: obrazovaka.ru

При взаимодействии поля и частицы изменяется направление ее движения, но не модуль скорости, т.е. кинетическая энергия остается неизменной.

Указанное свойство говорит о том, что, согласно теореме о кинетической энергии, работа силы Лоренца равна нулю.

Силу Лоренца не следует путать с силой Ампера. Отличие заключается в том, что последняя описывает взаимодействие магнитного поля и проводника с током, а сила Лоренца — взаимодействие поля и единичного электрического заряда.

В чем измеряется, формула

Возьмем проводник с током I бесконечно малой длины Δl и поместим его в магнитное поле с индукцией B. По закону Ампера сила, с которой магнитное поле действует на проводник с током, равна:

Формула 1

F=B·I·∆l·sinα,

где α — угол между векторами магнитной индукции и скорости заряда.

Формула 2

За бесконечно малое время Δt по проводнику пройдет n заряженных частиц зарядом q. Тогда выражение для тока можно записать в виде:

I=n·q∆t.

Формула 3

Подставим полученное выражение в формулу силы:

F=B·n·qΔt·Δl·sinα.

Формула 4

Учитывая, что отношение ΔlΔt дает скорость движения заряда v, получим:

F=B·n·q·v·sinα.

Формула 5

Для вычисления значения силы Лоренца, действующей на отдельный заряд, поделим правую часть выражения на n:

F=B·q·v·sinα.

Формула 6

Сила является векторной физической величиной, формула в векторной форме имеет вид:

F→=q·v→×B→.

Единицей измерения силы Лоренца в СИ является Ньютон (Н).

Формула силы Лоренца при наличии магнитного и электрического полей

В случае, когда заряженная частица движется в электромагнитном поле, сила Лоренца включает в себя:

• магнитную составляющую, вызванную действием магнитного поля индукцией B→:
  Fм→=q·v→×B→;
• электрическую составляющую, вызванную действием электрического поля напряженностью E→:
  Fэ→=q·E→.

Формула 7

Полная сила Лоренца определяется как векторная сумма двух составляющих:

F→=Fм→+Fэ→.

Применение силы Лоренца

Взаимодействие магнитного поля с движущимися заряженными частицами широко применяется в технике и играет важную роль в природе. Примеры и пояснения:

1. Масс-спектрометр — устройство, позволяющее разделить частицы по их удельным зарядам и определить массы частиц. Основными элементами масс-спектрометра являются: вакуумная камера, источник частиц, батарея, ускоряющая напряжение электрического поля, фотопластинка.
   Заряд ускоряется электрическим полем и попадает в магнитное поле вакуумной камеры, под действием силы Лоренца описывает дугу и падает на фотопластинку. По оставленному следу на фотопластинке определяют радиус траектории частицы, затем — удельный заряд и массу.
2. Электронно-лучевая трубка — устройство для преобразования электрических сигналов в световые. Основными элементами электронно-лучевой трубки являются: катод, первый и второй аноды (вместе создают ускоряющее электрическое поле), отклоняющая система, экран.
   Источником электронов является катод. С помощью фокусирующей системы — первого анода — электроны собираются в узкий луч, который попадает в ускоряющее электрическое поле. Управление пучком электронов происходит с помощью отклоняющей системы, куда входят две магнитные катушки. По катушкам протекает ток, создавая магнитное поле. Луч попадает в поле, под действием которого отклоняется от начального положения и падает на экран. Экран покрыт специальным веществом — люминофором, способным светиться при попадании на него электронов. Электронно-лучевые трубки применяют в осциллографах, кинескопах, радиолокационных станциях.
3. Циклотрон — ускоритель тяжелых заряженных частиц — протонов и ионов. Основными элементами циклотрона являются: вакуумная камера, два электрода — дуанты, магнит, источник частиц, генератор переменного напряжения.
   Ускоренная частица попадает в щель между дуантами и под действием силы Лоренца начинает двигаться по окружности. Через время, равное половине периода изменения напряжения на электродах, заряд снова оказывается между дуантами, ускоряется и начинает двигаться по окружности большего радиуса. В результате частица описывает в циклотроне многовитковую спираль, которая состоит из полуокружностей. Энергия ускоренной частицы в циклотроне может достигать 20МэВ.
4. Магнитное поле Земли постоянно вступает во взаимодействие с потоком заряженных частиц из космоса. Действие силы Лоренца изменяет траекторию движения частиц, не давая последним пройти через ионосферу и атмосферу.

Сила лоренца — определение термина

векторная величина, представляющая собой силу, действующую на заряженную частицу, движущуюся в электромагнитном поле; сила лоренца имеет две составляющие: электрическую, не зависящую от скорости частицы, обусловленную электрическим полем, и магнитную, пропорциональную скорости частицы, действующую со стороны магнитного поля .

Научные статьи на тему «Сила Лоренца»

силой Лоренца, определяемой по формуле: Рисунок 3….
Замечание 2 Сила Лоренца будет всегда перпендикулярной скорости движения заряженных частиц, поэтому…
Таким образом, сила Лоренца не совершают работу….
будет определяться векторной суммой сил: силы, действующей со стороны электрического поля; силы Лоренца…
Тогда сила Лоренца примет нулевое значение.

Статья от экспертов

Предлагается единая концепция сил Лоренца в различных разделах электродинамики: классической, релятивистской и квантовой. Показано, что в релятивистской электродинамике сила Лоренца появляется из-за существования эффекта Доплера для поля, предложеннного авторами в предыдущих статьях. В отличие от эффекта Доплера для волн, для которых эффект Доплера приводит к изменению частоты принимаемого сигнала, эффект Доплера для поля приводит к изменению силы взаимодействия между зарядами. Причина изменения силы в запаздывании взаимодействия, в результате которого заряды взаимодействуют исходя не из реального положения, а с запаздыванием, исходя из предыдущего положения. Величина запаздывания зависит от скорости движения зарядов. Показано, что величина запаздывания соответствует поправке преобразований Лоренца. Другими словами, преобразования Лоренца это ни что иное, как учет эффекта Доплера для поля. Т.о. меняется концепция релятивистской электродинамики. Вместо постулатов о разном течение вре…

Creative Commons

Научный журнал

Сила Лоренца Если на частицу, обладающую зарядом, действуют одновременно электрическое и магнитное поля…

силой Лоренца….
Сила Лоренца проявляется при движении электронов и ионов в магнитных полях….
Решение: На частицу, по условиям задачи действует сила Лоренца, имеющая две составные части: магнитную. ..
Электрическая составляющая силы Лоренца равна: \[\overrightarrow{F_q}=q\overrightarrow{E}\left(2.2\right

Статья от экспертов

В очередной статье мы продолжаем рассматривать парадоксы, которые допустили физики не учитывая философский и физический смысл логики отсутствия чудес и замкнутости мироздания. Здесь рассмотрен вывод электромагнитных составляющих в зависимости от преобразований Лоренца. Показаны ошибки и парадоксы, которые были допущены при этом, а также предложен правильный подход взаимосвязи с преобразованиями Лоренца с учётом вывода силы Лоренца. Статья даёт возможность понять природу взаимодействия

Creative Commons

Научный журнал

Еще термины по предмету «Электроника, электротехника, радиотехника»

Положительный электрод

для устройства, имеющего два электрода, этот электрод имеет более высокий эпектрический потенциал; в некоторых спучаях, например, дпя электронных ламп и полупроводниковых устройств термин «положительный электрод» применяют для одного или другого электрода в зависимости отусловия электрического оперирования устройства; в других спучаях (например, для эпектрохимическихэлементов) термин «положительный электрод» относят к определенному электроду.

Постоянное напряжение в открытом состоянии тнристора (диода) (Continuous on state voltage)

основное напряжение ,тиpucтopa или диода в открытом состоянии, обусловленное током в открытом состоянии.

Пробивное напряжение коллектор — затвор (Collector-gate voltage)

максимально допустимое значение напряжения между выводами коллектора и затвора биполярного транзистора с изолированным затвором при подключении резистора с нормированным сопротивлением между зажимами затвор — эмиттер.

• Кривая Лоренца
• Коэффициент Лоренца
• Закон Лоренца
• Фактор Лоренца
• Число Лоренца
• Преобразования Лоренца
• Беллини (Bellini) Лоренцо
• Быть не в силах
• От силы
• Через силу
• Сила
• Кривая Лоренца (Lorenz curve)
• Сила сцепления
• Тормозная сила
• Бездефицитность сил
• Сила Кориолиса
• Силы рыночные
• Гибридная сила
• Сила оппонентов
• Движущая сила

Смотреть больше терминов

Повышай знания с онлайн-тренажером от Автор24!

1. Напиши термин
2. Выбери определение из предложенных или загрузи свое
3. Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных карточек

Возможность создать свои термины в разработке

Еще чуть-чуть и ты сможешь писать определения на платформе Автор24.

Укажи почту и мы пришлем уведомление с обновлением ☺️

Включи камеру на своем телефоне и наведи на qr-код. Edu24_bot откроется на устройстве

Привет! Рады, что термин оказался полезен 🤩

Для копирования текста подпишись на Telegram bot. Удобный поиск по учебным материалам в твоем телефоне

Подписаться и скачать термин

Включи камеру на своем телефоне и наведи на qr-код. Edu24_bot откроется на устройстве

Привет! Рады, что термин оказался полезен 🤩

Подписчики нашего бота Edu24_bot получают определение прямо в телеграмм! Просто перейди по ссылке ниже

Скачать термин

Включи камеру на своем телефоне и наведи на qr-код. Edu24_bot откроется на устройстве

За пределами закона Бера: Новый взгляд на уравнение Лоренца-Лоренца

• Список журналов
• Wiley-Blackwell Online Open
• PMC7317954

Химфизхим

Химфизхим. 2020 16 июня; 21 (12): 1218–1223.

Опубликовано в сети 27 мая 2020 г. doi: 10.1002/cphc.202000301

^{1 , 2} и ^{1 , 2}

Информация об авторе Примечания к статье Информация об авторских правах и лицензии Отказ от ответственности

Дополнительные материалы

В этом вкладе мы показываем, как уравнения Лоренца-Лоренца и Клаузиуса-Мосотти связаны с законом Бера. Соответственно линейная зависимость поглощения от концентрации является следствием пренебрежения различием между локальным и приложенным электрическим полем. Кроме того, необходимо предположить, что показатель поглощения и связанное с ним изменение показателя преломления малы. Соединяя уравнения Лоренца-Лоренца с теорией дисперсии, становится очевидным, что осцилляторы связаны через локальное поле. Мы исследуем эту связь на численных примерах и показываем, что, как следствие, интегральная абсорбция отдельной полосы, как правило, больше не зависит линейно от концентрации. На практике отклонения от закона Бера обычно не проявляются раньше, чем плотность достигает примерно одной десятой плотности конденсированного вещества. Для растворов уравнения Лоренца-Лоренца предсказывают сильную связь также между осцилляторами растворенного вещества и растворителя. В частности, прогнозируется, что в инфракрасной области спектра коэффициенты поглощения будут намного выше из-за этой связи по сравнению с коэффициентами в газовой фазе.

Ключевые слова: поглощение, дисперсия, показатель преломления, закон Бера, соотношение Лоренца-Лоренца

Новый взгляд на уравнение Лоренца-Лоренца : Локальное поле Лоренца смещает положение осциллятора в сторону меньшего волнового числа и приводит к связи. Следовательно, абсорбция больше не зависит линейно от концентрации.

В современных учебных программах уравнения Лоренца-Лоренца и Клаузиуса-Мосотти хорошо известны в контексте определения дипольных моментов.1 Их квинтэссенцией является установление связи между внешним электрическим полем и локальным электрическим полем. вокруг молекулы, элементарной ячейки или атома. В современных учебниках информация о том, что локальные поля также играют важную роль в теории дисперсии, как показано, в частности, Максом Планком2 и Хендриком Антоном Лоренцем3, часто уже не обсуждается. Это представляет интерес, поскольку зависимость поглощения от концентрации, т.е. е. Закон Бера может быть выведен из теории дисперсии. 4 Фактически, вывод таких величин, как молярная рефракция, молярная поляризация и поглощение, основан на том же формализме,5 который мы вскоре представим ниже.

Соответственно макроскопическая поляризация P→ связано с микроскопическим дипольным моментом p→ по:

P→=N·p→

(1)

В уравнении (1) N — количество дипольных моментов на единицу объема, а p→ представляет собой микроскопический дипольный момент, характеризуемый уравнением (2):

p→=α·E→loc

(2)

, где α представляет собой молекулярную поляризуемость, а E→loc локальное электрическое поле. Это локальное электрическое поле, вообще говоря, не то же самое, что приложенное электрическое поле, поскольку в месте нахождения атома или молекулы все поля, создаваемые всеми другими атомами или молекулами, как реакция на изменение микроскопического дипольного момента, будут иметь принять во внимание. С другой стороны, макроскопическая поляризация P→ связано с приложенным электрическим полем E→ , если принять скалярные среды, характеризующиеся скалярной диэлектрической функцией, согласно:

P→=ϵ0ϵr-1E→=ϵ0χE→

(3)

В уравнении (3), ϵr — относительная диэлектрическая проницаемость, ϵ0 диэлектрическая проницаемость вакуума и χ электрическая восприимчивость. Приравнивание уравнений (1) и (3) с помощью уравнения (2) приводит к [уравнению. (4)]:

N·α·E→loc=ϵ0ϵr-1E→

(4)

Для продолжения необходимо найти связь между E→loc и Е→ . Если мы предположим так называемое «локальное поле Лоренца» E→L , локальное электрическое поле состоит из двух частей: первоначально приложенного поля и E→L [уравнение (5)]:

E→loc=E→+E→L

(5)

Для получения E→L , обычно предполагается, что он, в свою очередь, состоит из двух частей, одна из которых создается соседями в месте расположения рассматриваемого атома или молекулы, которая практически удалена от своего местоположения, поскольку ее собственный вклад не принадлежит E→L . Кроме того, удаленные молекулы или атомы вносят свой вклад в локальное поле подобно однородно поляризованной среде. Если рассчитать поле внутри полости вокруг удаленной молекулы или атома, содержащее только соседние фрагменты, то для изотропной среды оказывается, что эффект от них компенсируется, и локальное поле определяется уравнением   (6): 6, 7

E→loc=E→+13ϵ0P→

(6)

Следовательно, используя уравнения   (1) и (2), мы получаем [Ур. (7)].

Из уравнения (8) вместе с уравнением (3) мы приходим к [уравнению. (9)]. (10)]:

ϵr-1ϵr+2=13N·αϵ0

(10)

9ν˜2ϵ0

(12)

Это первое приближение также получается, если в уравнении (4) E→loc≈E→ предполагается5, поэтому оба предположения эквивалентны. Если мы сосредоточимся на показателе поглощения, второе приближение будет выглядеть как [уравнение. (13)]. молярная постоянная затухания, d толщина образца и α» мнимая часть поляризуемости [уравнение. (14)]:

9*ν˜=S*2ν˜02-ν˜2-iν˜γ

(15)

где S* – молярная сила осциллятора, ν˜0 положение резонанса и γ постоянная затухания. Если это выражение подставить в уравнение (10) принимая во внимание N = c  ⋅  N _A , результат [уравнение. (16)]:8

ϵr-1ϵr+2=1-3ϵr+2=13cS*2ν˜02-ν˜2-iν˜γ→ϵr-1=311-cS*2ν˜02-ν˜2-iν˜γ-1= 3cS*2ν˜02-ν˜2-iν˜γ1-cS*2ν˜02-ν˜2-iν˜γ→ϵr-1=3cS*2ν˜02-cS*2-ν˜2-iν˜γ

(16)

Это может быть представлено в типичной форме дисперсионных соотношений с осциллятором Лоренца:

ϵr=1+cS*2ν˜02-c3S*2-ν˜2-iν˜γ→ϵr=1+cS*2ν˜’02-ν˜2-iν˜γ

(17)

Уравнение (17) также может быть получено непосредственно в предположении о затухающем гармоническом осцилляторе, управляемом локальным электрическим полем. 2, 3 Из этого результата кажется, что единственное изменение, вносимое локальным электрическим полем, усиленное по сравнению с приложенным электрическим полем, заключается в красном смещении положение осциллятора. За исключением нескольких учебников6, 7, 9 это обычный вывод. В самом деле, как показали Герцфельд и Вольф8, даже при наличии локальных полевых эффектов и более чем одного осциллятора дисперсия молярной поляризуемости соответственно выражается как сумма всех вкладов различных осцилляторов 9*ν˜=∑iSi*2ν˜0i2-ν˜2-iν˜γi

(18)

диэлектрическую проницаемость еще можно выразить в обычном виде:

ϵr=1+∑iS’i2ν˜ ‘0i2-ν˜2-iν˜γi

(19)

Однако при этих обстоятельствах происходят некоторые важные изменения. В то время как осцилляторы отдельных молекул все еще не связаны в уравнении   (18), локальное электрическое поле приводит к тому, что это больше не имеет место для осцилляторов, предполагаемых в уравнении. (19). Сила осциллятора и положение осциллятора в этом уравнении не являются отдельными свойствами, а зависят от любого другого осциллятора — так же, как это имеет место и для обратной диэлектрической функции, для которой локальное электрическое поле также отличается от приложенного электрического поля. 10 Другими словами, осциллятор, расположенный в УФ-диапазоне, изменит силу и положение осциллятора в инфракрасном диапазоне и наоборот в уравнении  (19).).

Это, конечно, не новое открытие само по себе,7 но оно имеет некоторые важные последствия для зависимости пика и интегрального значения поглощения от концентрации, которые, по-видимому, до сих пор не исследовались.

Одно из этих следствий заключается в том, что при фокусировке на осцилляторе, как он представлен в уравнении   (19), значение квадрата силы осциллятора больше не пропорционально концентрации. Это также означает, что вообще даже интегральная абсорбция этой полосы больше не зависит линейно от концентрации. Следствием для газов является то, что при сжатии и при более высоких плотностях отклонения от закона Бера неизбежны. Вопрос только в том, в какой момент они начинаются. 9ν˜=∑jcj∑iSji*2ν˜0ji2-ν˜2-iν˜γji

(20)

Как следствие, все осцилляторы всех компонентов в смеси взаимно связаны.

Далее мы рассмотрим эти выводы более подробно.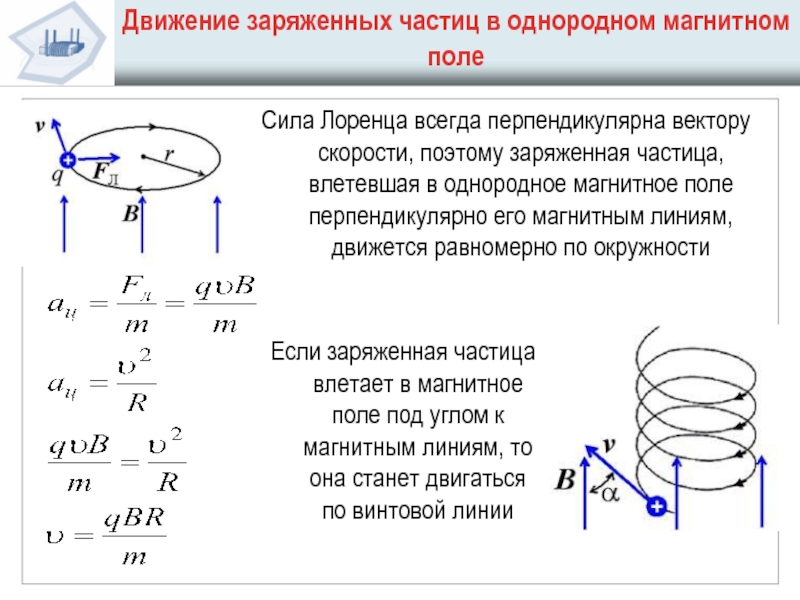 В исх. В работе [4] мы исследовали поглощение и его концентрационную зависимость на основе одного осциллятора в ИК-диапазоне со следующим параметром: 1700 см ⁻¹ и γ =20 см ⁻¹ . Еще одно предположение заключалось в том, что концентрация чистого вещества составляет 50 моль/л. Поскольку каждая молекула имеет поглощение в УФ-видимой области, теперь нам нужно завершить наши предположения вторым осциллятором, расположенным в этой области спектра. Для этого осциллятора принимаем параметры S ^*2 =1,25 ⋅ 10 ⁸  л/(см ² ), ν˜0= 6 ⋅ 10 ⁴  см ⁻¹ и γ =2 ⋅ 10 ³  см ⁻¹ . Эти допущения приводят к показателю преломления около 1,5 в области прозрачности между УФ-видимой и ИК-областями спектра, если предполагается локальное поле Лоренца (без дополнительного локального поля показатель преломления был бы меньше 1,3!) . Кроме того, мы также рассмотрим раствор гипотетического вещества в гипотетическом растворителе, который имеет единственный осциллятор, расположенный в УФ-видимой области с параметрами S * ² =2,5 ⋅ 10 ⁸  л/(моль см ² ), ν˜0= . Эти параметры приводят к тому же показателю преломления в области прозрачности, что и у УФ-видимого осциллятора гипотетического растворенного вещества. Осцилляторы использовались для расчета поглощения в соответствии с уравнением   (21)

Aν˜=4πν˜ln10kν˜d

(21)

в инфракрасном спектральном диапазоне (рис. ) и в УФ-видимом (рис. ).

Открыть в отдельном окне. а) обычная дисперсионная формула. б) обычная дисперсионная формула, предполагающая дополнительно красное смещение согласно ν˜’0i=ν˜0i2-c3Si*2 . c) Формула Лоренца-Лоренца [уравнение. (10)] в сочетании с уравнением   (18). d) То же, что и c), но с гипотетическим растворителем (обратите внимание на изменение, касающееся диапазона оси y для d).

Открыть в отдельном окне

Поглощение для различных концентраций 0,05, 0,5, 5 и 50 моль/л гипотетического материала при условии, что c ⋅ d =50 см ⋅ моль/л: а) обычная дисперсионная формула, б) обычная дисперсионная формула, предполагающая дополнительно красное смещение согласно ν˜’0i=ν˜0i2-c3Si*2 , c) Формула Лоренца-Лоренца [уравнение. (10)] в сочетании с (18), г) То же, что и в), но с гипотетическим растворителем. Отметим, что для г), в отличие от а)–в), константа d =10 ⁻⁶  см и что диапазон оси Y отличается.

На рисунке  показаны изменения спектров поглощения для четырех различных концентраций 0,05, 0,5, 5 и 50 моль/л при ограничении c ⋅ d =5 ⋅ 10 ³  см ⋅ моль/л. Как уже показано в Ref. [4], для традиционной модели поглощение остается практически одинаковым для двух самых низких концентраций. При более высоких концентрациях полоса начинает смещаться в синеву, поскольку молярный коэффициент поглощения является функцией обратного показателя преломления функции, которая имеет максимум при более высоких волновых числах, чем показатель поглощения. Для графиков, показанных на панели b), используется та же модель, за исключением того, что положение резонанса смещается с увеличением концентрации на ν˜’0i=ν˜0i2-c3Si*2 , я. е. связь между осцилляторами по-прежнему не учитывается.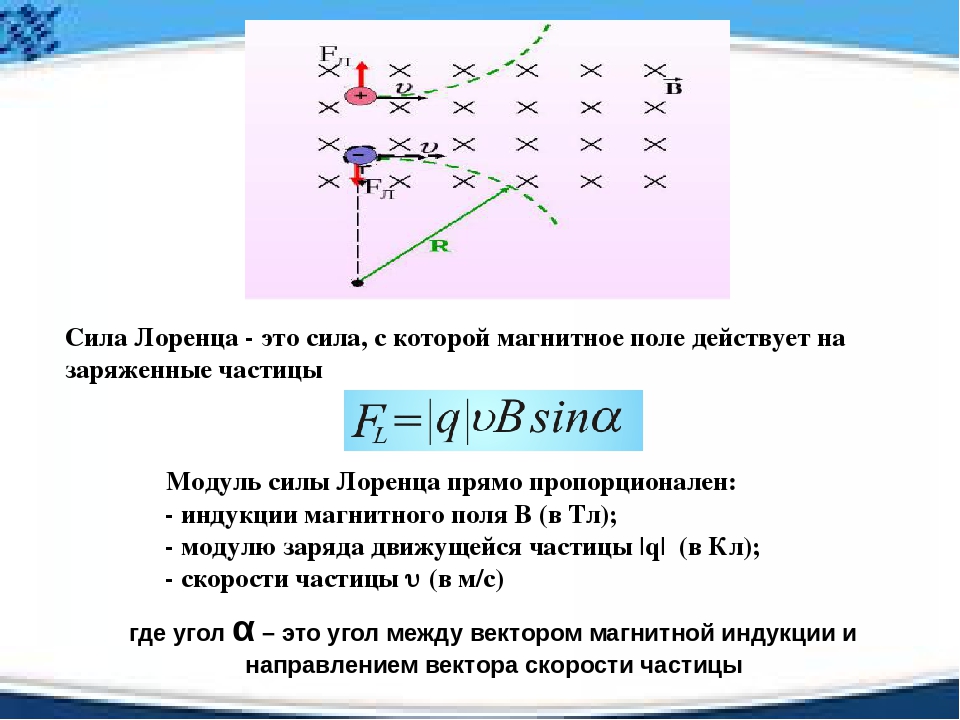 Соответственно, для малых концентраций синее и красное смещение компенсируют друг друга, и снова практически нет разницы для двух самых низких концентраций до того, как максимум начнет смещаться в красную сторону для более высоких концентраций. То же самое можно сделать для полной модели Лоренца-Лоренца и ее влияния на две самые низкие концентрации на панели c). Однако для более высоких концентраций наблюдается не только красное смещение, более сильное, чем для б), но и увеличение интенсивности по сравнению со случаями а) и б). Для случая, когда гипотетическое вещество растворено в растворителе с таким же показателем преломления в области прозрачности (панель г)), две самые низкие концентрации также не различимы, но их интенсивность примерно в два раза выше, чем для случай, когда гипотетическое вещество подвешено в вакууме (обратите внимание на изменение диапазона оси Y для панели d) на рисунке  ). Этот фактор даже несколько возрастает для более слабых осцилляторов (параметры инфракрасного осциллятора примерно такие же, как у ν ₃ колебания оксианионов типа SO32- или NO3- ; обратите внимание, что мы вычли поглощение растворителя из спектров, которое в противном случае было бы заметно для двух меньших концентраций в виде базовой линии, возрастающей в направлении видимого диапазона). Красное смещение вначале несколько сильнее, но поскольку предполагается, что гипотетический растворитель имеет такую ​​же концентрацию в чистом виде, так что концентрация, деленная на 50 моль/л, равна объемной доле, остается только гипотетический материал для самая высокая концентрация, а спектры принудительно совпадают в c) и d).

В то время как из-за локального поля Лоренца осцилляторы в инфракрасном диапазоне сильно зависят от связи с таковыми в УФ-видимом диапазоне, сравнение рис. Рисунок b и 2c не различимы. Это является следствием того, что квадрат силы ИК-осциллятора составляет менее 0,04   ‰ от общей силы осциллятора, на которую в основном влияет УФ-видимый осциллятор. Соответственно, красное смещение УФ-видимого осциллятора может быть предсказано в очень хорошем приближении как ν˜’0i=ν˜0i2-c3Si*2 , несмотря на сцепление. Тем не менее, спектры для двух самых низких концентраций очень хорошо согласуются друг с другом (рис.  a–c), так что коэффициент поглощения в этом диапазоне концентраций увеличивается линейно, а закон Бера выполняется в хорошем приближении. Как показано на рисунке  d, этот вывод нельзя сделать, если используется растворитель. Обратите внимание, что для Рисунка d толщина d оставили постоянным вместо произведения c ⋅ d , как для a)-c). Следовательно, поглощение примерно на порядок больше для c = 0,5 моль, если присутствует растворитель, и можно наблюдать четкое красное смещение на 500 см ⁻¹ , в то время как это невозможно для той же концентрации без растворителя (опять же, как и в случае, представленном на рис. 2с, полоса в инфракрасном диапазоне мало влияет на полосы в УФ-видимой области по той же причине, а именно из-за сравнительно слабой силы осциллятора). Также интересно отметить, что в то время как максимум пика полосы растворенного вещества смещен в красную область, осциллятор растворителя смещен в синюю сторону. Следовательно, растворитель с полосами, близкими к полосам растворенного вещества, может вызвать изменения базовой линии для более высоких концентраций, так что при этих концентрациях коррекция бланка обычным способом с использованием чистого растворителя больше невозможна. Это может быть причиной того, что на практике вместо чистых растворителей для эталонных измерений используются высокие концентрации растворенных веществ, как недавно было предложено. смещена в синюю полосу (на самом деле полоса не смещена в синюю область, но ее красное смещение уменьшено), причем смещение тем сильнее, чем выше силы осциллятора UV-Vis или, что то же самое, показатель преломления растворителя, который был известен в прежних исследованиях. раз, как правило Кундта.12, 13 Обратите внимание, что правило Кундта, согласно выводам, приведенным выше, строго применимо только в том случае, если нет никаких «химических» изменений, связанных с процессом растворения, т.е. е. поляризуемость как растворителя, так и растворенного вещества не должна изменяться во время растворения. В частности, такие процессы, как ассоциация и диссоциация, представляют собой химические изменения, которые нельзя предсказать по правилу Кундта. Это также означает, что в более сложных системах с более чем одним растворенным веществом сильно возрастает вероятность неприменимости правила Кундта. С другой стороны, для малых концентраций всех растворенных веществ мы не видим причин, по которым правило Кундта не может быть применимо, если оно справедливо для любой бинарной системы растворенного вещества и растворителя.

Вывод, сделанный в предыдущих параграфах, следует рассматривать скорее как иллюстрацию ожидаемых общих эффектов. Если сфокусироваться в ИК-области спектра, часто можно, как это известно из теории дисперсии, аппроксимировать влияние УФ-области спектра с помощью одного осциллятора, в то время как в зависимости от структуры материала для описания может потребоваться гораздо больше осцилляторов. оптические свойства в ИК области спектра. Если сосредоточиться на УФ-видимой области спектра, может быть даже необходимо моделировать не только переходы, связанные с валентными электронами, но и учитывать дальнейшие электронные переходы, чтобы полностью охарактеризовать спектры, в то время как в этом случае переходы, связанные с колебаниями можно пренебречь.

Концентрационная зависимость поглощения является, в очень хорошем приближении, линейной при 1700 см ^-1 примерно до 1 моль/л, независимо от выбранной модели (см. Рисунок a). При более высоких концентрациях максимум пика начинает смещаться. Кроме того, если предполагается растворитель, отличный от вакуума, наклон будет намного сильнее из-за увеличения интенсивности за счет связи. Поглощение, интегрированное в инфракрасном диапазоне, в хорошем приближении линейно зависит от концентрации в еще большем диапазоне концентраций. На самом деле, без влияния полосы поглощения в УФ-видимой области зависимость была бы совершенно линейной14, но из-за базовой линии, вызванной этой модой, возникают отклонения. Если эта базовая линия остается неизменной и, таким образом, практически удаляется, поскольку растворитель и растворенное вещество вызывают идентичные базовые линии, что имеет место в случае модели Лоренца-Лоренца с растворителем, можно наблюдать идеальную линейную зависимость. В УФ-видимой области спектра закон Бера нарушается без растворителя при концентрациях выше примерно 0,5 моль/л и с растворителем при концентрациях примерно 0,2 моль/л. Поскольку большая часть силы осциллятора сосредоточена в этом диапазоне, интегральная абсорбция линейно зависит от концентрации, за исключением случая с растворителем. В этом случае влияние поглощения растворителя из-за взаимодействия между осцилляторами растворителя и растворенного вещества больше не является аддитивным и, следовательно, не может быть полностью устранено. Поскольку закону Бера сопутствует двойственный закон об изменении показателя поглощения15, мы также исследовали влияние различных моделей на расчет показателя преломления. Это может быть особенно интересно для развивающейся области инфракрасной дисперсионной спектроскопии.15, 16, 17, 18 Соответствующие результаты можно найти во вспомогательной информации.

Открыть в отдельном окне

Зависимость абсорбции и интегральной абсорбции от концентрации. а) поглощение при 1700 см ^-1 , б) интегральное поглощение в диапазоне 100–3000 см ^-1 , в) поглощение при 60000 см ^-1 , г) интегральное поглощение в диапазоне 30000 — 100000 см 1 1 d = 1 мкм для а) и б) и d = 0,01 мкм для в) и г).

В целом, мы находим, что различные допущения в соответствии с законом Бера по сравнению с уравнением Лоренца-Лоренца и т. д. менее важны для концентраций ниже 0,5 моль/л, что соответствует плотности около 1 % конденсированного материала, до тех пор, пока нет смеси со вторым материалом, который действует как растворитель. В последнем случае отклонения начинаются несколько раньше, примерно при 0,2 моль/л, и наклон кривых зависимости поглощения от концентрации намного круче. Другими словами, молярный коэффициент поглощения намного больше, чем без растворителя. Если рассматривать интегрированное поглощение, кажется, что пределы линейности расширяются примерно на порядок. Все эти соображения, однако, основаны на пренебрежении волновой природой света и запаздыванием, локальными интерференционными эффектами и электромагнитной связью, по-видимому, начавшимися гораздо раньше.19Для растворов, в частности, важны и изменения химических взаимодействий с концентрацией. Они модифицируют, в отличие от всех эффектов, обсуждавшихся до сих пор, поляризуемость атомов или молекул.

Уравнение Лоренца-Лоренца, близкое к плотности конденсированного материала, предсказывает сильное нелинейное поведение, но даже без локального поля больше нельзя утверждать, что поглощение пропорционально плотности осцилляторов. Соответственно, использование абсорбции для спектров чистых материалов, рекомендованное IUPAC, не имеет преимуществ перед использованием других величин, таких как коэффициент пропускания или отражения.

Подводя итог, мы обсудили влияние локального поля Лоренца на оптические и ИК-оптические спектры материалов в зависимости от концентрации. Мы показали, что из уравнений Лоренца-Лоренца закон Бера можно вывести заново, предполагая малые плотности/концентрации осцилляторов, так что, во-первых, становится пренебрежимо малым локальное поле Лоренца и, во-вторых, зависимость комплексного показателя преломления и его мнимой части, поглощения индекса, становится линейно зависимым от концентрации. Это показывает, что закон Бера больше не нужно рассматривать как эмпирический закон, и он хорошо интегрирован в общую теоретическую основу вместе с теорией дисперсии и уравнением Лоренца-Лоренца.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов.

В качестве услуги нашим авторам и читателям этот журнал предоставляет вспомогательную информацию, предоставленную авторами. Такие материалы рецензируются экспертами и могут быть реорганизованы для онлайн-доставки, но не редактируются и не печатаются. Вопросы технической поддержки, возникающие в связи со вспомогательной информацией (кроме отсутствующих файлов), следует адресовать авторам.

Дополнительный

Щелкните здесь, чтобы просмотреть файл с дополнительными данными. ^{(503K, pdf)}

Финансовая поддержка ЕС, «Thüringer Ministryium für Wirtschaft, Wissenschaft und Digitale Gesellschaft», «Thüringer Aufbaubank», Федерального министерства образования и исследований Германии (BMBF), Немецкой науки Фонд, «Фонды химической промышленности» и Фонд «Карл-Цейсс» выражают благодарность.

Т. Г. Майерхёфер, Дж. Попп, ChemPhysChem 2020 , 21 , 1218. [Бесплатная статья PMC] [PubMed]

1. Аткинс П., де Паула Дж. , Физическая химия Аткинса, ОУП Оксфорд; 2014. [Google Scholar]

2. Планк М., Sitzungsber. К. Прейс. акад. Висс. 1902, I, 470–494. [Google Scholar]

3. H. A.Lorentz, P. K., Ned. акад. Wetensc 1906 , 8 , 591–611.

4. Mayerhöfer T.G., Popp J., ChemPhysChem 2019, 20, 511–515. [PubMed] [Google Scholar]

5. Mayerhöfer T.G., Popp J., Spectrochim. акта часть а 2019, 215, 345–347. [PubMed] [Академия Google]

6. Борн М., Optik: Ein Lehrbuch der elektromagnetischen Lichttheorie, Julius Springer; 1933. [Google Scholar]

7. Борн М., Вольф Э., Бхатия А.Б., Принципы оптики: электромагнитная теория распространения, интерференции и дифракции света, издательство Кембриджского университета; 1999. [Google Scholar]

8. Herzfeld K.F., Wolf K.L., Ann. физ. 1925, 383, 35–56. [Google Академия]

9. Ефимов А. М., Оптические константы неорганических стекол, Taylor & Francis; 1995. [Google Scholar]

10. Т.  Г. Майерхёфер, С. Хёфер, В. Ивановский, Дж. Попп, arXiv:1909.00683, 2019 .

11. Zhao L.C., Guo M.H., Li X.D., Huang Y.P., Wu S.H., Sun J.J., Anal. хим. 2017, 89, 13429–13433. [PubMed] [Google Scholar]

12. Кундт А., Энн. физ. 1878, 240, 34–54. [Google Академия]

13. Райс Ф.О., Дж. Ам. хим. соц. 1920, 42, 727–735. [Google Академия]

14. Майерхёфер Т. Г., Пипа А. В., Попп Дж., ChemPhysChem 2019, 20, 2748–2753. [Бесплатная статья PMC] [PubMed] [Google Scholar]

15. Mayerhöfer T.G., Dabrowska A., Schwaighofer A., ​​Lendl B., Popp J., ChemPhysChem 2020, 10.1002/cphc.202000018. [Бесплатная статья PMC] [PubMed] [Google Scholar]

16. Эбнер А., Циммерлейтер Р., Кобет С., Хингерл К., Брандштеттер М., Килгус Дж., Opt. лат. 2019, 44, 3426–3429. [PubMed] [Google Scholar]

17. Ма Л., Ван З., Чеонг К.-П., Нин Х., Рен В., Proc. Сгорел. Инст. 2019, 37, 1329–1336. [Академия Google]

18. Мартин-Матеос П., Херес Б., де Диос К. , Аседо П., Appl. физ. Б 2018, 124, 66. [Google Scholar]

19. Mayerhöfer T.G., Höfer S., Popp J., Phys. хим. хим. физ. 2019, 21, 9793–9801. [PubMed] [Академия Google]

ГОСУДАРСТВО против ЛОРЕНЦА (2001 г.) | FindLaw

ШТАТ Южная Дакота, истец и податель апелляции, против Джона Стивена ЛОРЕНЦА, ответчика и подателя апелляции.

№ ​​21422.

Принято: 14 февраля 2001 г.

Марк Барнетт, генеральный прокурор, Крейг М. Эйхштадт, заместитель генерального прокурора, Пьер, истец и податель апелляции. Уильям А. Мур, Шотландия, для ответчика и апеллянта.

[¶ 1.] Джон Лоренц (Лоренц) был осужден за хранение более десяти фунтов марихуаны в нарушение SDCL 22-42-6. Мы утверждаем.

ФАКТЫ

[¶ 2.] Летом 1999 года Гейл Лоренц дважды навещала своего бывшего мужа в его доме. Во время своих посещений она наблюдала, как марихуана растет за пределами дома, а в другой раз она заметила сушеную марихуану в корзине для одежды в шкафу. Она сообщила о своих выводах местному шерифу и агенту Департамента уголовных расследований. Основываясь на том, что жена Лоренца сообщила властям, правоохранительные органы прибыли в резиденцию Лоренца и провели наблюдения с дороги. Из машины правоохранительные органы могли наблюдать многочисленные растения марихуаны, растущие вдоль дома Лоренца. Правоохранители сфотографировали растения марихуаны с обочины дороги.

[¶ 3.]  С помощью собранной информации правоохранительные органы смогли получить ордер на обыск, который был приведен в исполнение 1 сентября 1999 года. Марихуана была изъята из каждого места и доставлена ​​обратно в офис шерифа. Шериф взвесил связки марихуаны, которые весили 24 фунта и 15 унций. Лоренц был осужден за хранение более десяти фунтов марихуаны в нарушение SDCL 22-42-6. Лоренц обращается со следующими вопросами:

1) Правильно ли суд первой инстанции отклонил ходатайство Лоренца о подавлении;

2) Достаточны ли доказательства, чтобы признать Лоренца виновным в хранении более десяти фунтов марихуаны;

3) Ли суд первой инстанции злоупотребил своей дискрецией в отношении нескольких доказательных решений.

СТАНДАРТ ПЕРЕСМОТРА

 [¶ 4.] Как правило, определения разумных подозрений и вероятной причины должны быть пересмотрены de novo при подаче апелляции. Сказав это, мы спешим указать, что апелляционный суд должен позаботиться о том, чтобы проверить установленные исторические факты только на наличие явной ошибки и придать должное значение выводам, сделанным на основе этих фактов судьями-резидентами и местными правоохранительными органами.

State v. Hirning, 1999 SD 53, ¶ 9, 592 N.W.2d 600 (со ссылкой на Ornelas v. )). В то время как обычно мы рассматриваем ходатайство об отклонении стандарта злоупотребления полномочиями, мы рассмотрим необходимый правовой стандарт вероятной причины de novo из-за его конституционного значения. State v. Stanga, 2000 SD 129, 617 N.W.2d 486.

ВЫПУСК 1

[¶ 5.]  Правильно ли суд первой инстанции отклонил ходатайство Лоренца о прекращении дела.

[¶ 6.]  Лоренц утверждает, что заявления, сделанные отчужденной женой Лоренца, не могут быть использованы для поддержки определения вероятной причины из-за супружеских привилегий. Лоренц утверждает, что, если бы она не разгласила информацию о деятельности Лоренца, доказательств вероятной причины было бы недостаточно. Этот аргумент ошибочен по многим основаниям.

 [¶ 7.] Во-первых, Лоренц не ссылался на авторитет в поддержку своего аргумента. «Отказ от ссылки на подтверждающий орган является нарушением SDCL 15-26A-60 (6), и поэтому вопрос считается отклоненным». Государство против Пеллегрино, 1998 SD 39, ¶ 22, 577 NW2d 590, 599.   Таким образом, он считается отмененным.

 [¶ 8.] Во-вторых, супружеская привилегия неприменима, поскольку привилегия распространяется только на общение, а не на наблюдение. Государство против Харта, 391 NW2d 677 (SD 1986). «Таким образом, привилегия супружеского общения «не распространяется на все наблюдения за действиями одного супруга другим»».  Id. на 679 (со ссылкой на State v. Newman, 235 Kan. 29, 43, 680 P.2d 257, 266 (1984)). Здесь правоохранительные органы отреагировали на то, что Гейл Лоренц наблюдала в доме. В протоколе не указано, и Лоренц не утверждает, что Гейл рассказал правоохранительным органам о том, что он сказал о марихуане. Супружеская привилегия неприменима к определению вероятной причины.

 [¶ 9.] В-третьих, правоохранительные органы располагали альтернативным основанием для установления вероятной причины. Правоохранительные органы наблюдали и фотографировали растения марихуаны, растущие на виду у дома Лоренца. См. State v. Lodermeier, 481 NW2d 614, 623 (S.D.1992) (утверждается, что предметы, обнаруженные на виду, не являются поиском для целей Четвертой поправки). То, что правоохранительные органы наблюдали самостоятельно, было достаточным для обоснования ордера на обыск. Те предметы, которые были обнаружены на виду у офицера, по праву там, не являются обыском и не подпадают под действие Четвертой поправки. Поскольку полиция наблюдала за марихуаной с дороги общего пользования, эти наблюдения составляют правовую основу вероятной причины.

ВЫПУСК 2

[¶ 10.]  Было ли доказательств достаточно, чтобы признать Лоренца виновным в хранении более десяти фунтов марихуаны.

 [¶ 11.]  Лоренц утверждает, что вес изъятой марихуаны не превышал десяти фунтов, как того требует SDCL 22-42-6.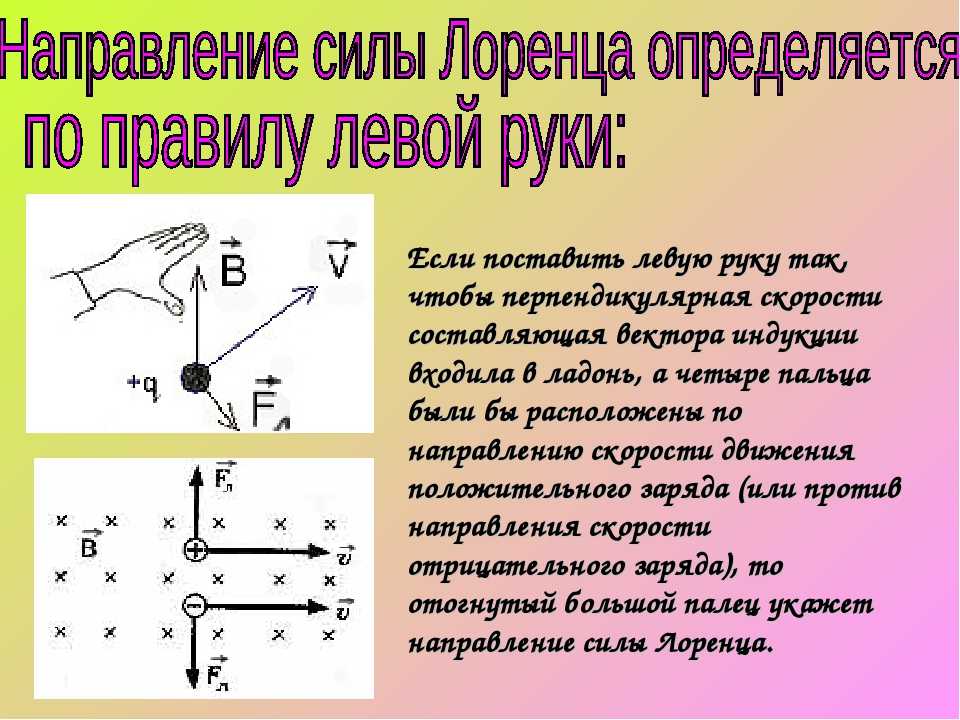 ¹  Лоренц утверждает, основываясь на показаниях государственного химика, что фактическое количество марихуаны действительно составляло 4 фунта 5,76 унции, за исключением того, что считается «канавной» травкой. Основываясь на этих показаниях, Лоренц утверждает, что по закону он не может быть осужден за хранение более десяти фунтов марихуаны в соответствии с SDCL 22-42-6.

 [¶ 12.]  Лоренц утверждает, что в законе, определяющем марихуану, существует двусмысленность, и он также ссылается на Hill v. Commonwealth, 17 Va.App. 480, 438 S.E.2d 296 (1993), чтобы придать смысл определению Южной Дакоты того, что представляет собой марихуана. SDCL 22-42-1(7) определяет «марихуану, все части любого растения рода каннабис, растущие или нет, в естественном или неизмененном состоянии, за исключением сушки, пролечки, измельчения или крошения [.]». При толковании уставов мы часто указывали:

[Вопросы права, такие как толкование закона, рассматриваются судом de novo․ Целью статутного толкования является раскрытие истинного намерения закона, которое должно быть установлено в первую очередь из языка, выраженного в статуте. Цель закона определяется тем, что сказал законодательный орган, а не тем, что, по мнению суда, он должен был сказать, и суд должен ограничиться используемым языком. Слова и фразы в законе должны иметь их простое значение и действие. Когда формулировки закона ясны, точны и недвусмысленны, нет оснований для толкования, и единственная функция Суда состоит в том, чтобы провозгласить смысл закона как ясно выраженный. Поскольку законы должны толковаться в соответствии с их намерением, намерение должно определяться из закона в целом, а также из актов, касающихся того же предмета.

Дан против Троунселла, 1998 SD 36, ¶ 14, 576 N.W.2d 535, 539 (цитируется Мосс против Гуттормсона, 1996 SD 76, ¶ 10, 551 N.W.2d 14, 17 (цитата опущена)). Как определено в статуте, «все части любого растения рода каннабис» считаются марихуаной. Когда законодательный акт является ясным и недвусмысленным, единственная обязанность этого суда состоит в том, чтобы прочитать и ввести в действие этот акт. Zoss v. Schaefers, 1999 SD 105, ¶ 6, 598 N. W.2d 550, 552.   Из-за этой ясной и недвусмысленной формулировки настоящему Суду не нужно обращаться к постороннему авторитету, чтобы придать смысл этому закону. Точно так же мы не считаем, что решение по Вирджинии, о котором говорит Лоренц, помогает в интерпретации того, что представляет собой марихуана в этой юрисдикции. ²

[¶ 13.]  Более того, SDCL 22-42-1(7) не делает различий между культивируемой марихуаной и тем, что в широком смысле называют «сорняком канавы». Оба считаются родом каннабиса; таким образом, меньший вес, предложенный государственным химиком, явно ошибочен. См. State v. Johnson, 509 N.W.2d 681 (S.D.1993) (заключение о том, что все части растения считаются марихуаной). Следовательно, более высокий вес, указанный шерифом в 24 фунта и 15 унций, более точно описывает вес марихуаны в соответствии с установленным законом определением. Таким образом, было достаточно улик, чтобы осудить Лоренца за хранение более десяти фунтов марихуаны.

[¶ 14.]  Мы рассмотрели последний выпуск Лоренца и пришли к выводу, что он не заслуживает внимания.

[¶ 15.]  Подтверждено.

СНОСКИ

1.   SDCL 22-42-6 предусматривает: Никто не может сознательно хранить марихуану. Обладание двумя унциями марихуаны или менее является правонарушением класса 1. Хранение более двух унций марихуаны, но менее половины фунта марихуаны является тяжким преступлением класса 6. Владение половиной фунта, но менее одного фунта марихуаны является уголовным преступлением класса 5. Хранение от одного до десяти фунтов марихуаны является уголовным преступлением класса 4. Хранение более десяти фунтов марихуаны является тяжким преступлением 3 класса. Гражданское наказание может быть наложено в дополнение к любому уголовному наказанию в случае признания виновным в нарушении этого раздела на сумму, не превышающую десять тысяч долларов.

2.   Ссылка Лоренца на дело Хилла неуместна, поскольку суд Хилла интерпретировал установленное законом определение марихуаны штата Вирджиния, § 54.1-340, где марихуана определяется как: любая часть растения рода Cannabis, независимо от того, растет оно или нет, его семена или смола; и каждое соединение, производство, соль, производное, смесь или препарат такого растения, его семян или его смолы.