Физика для углубленного изучения 1. Механика
Физика для углубленного изучения 1. Механика
ОглавлениеПРЕДИСЛОВИЕI. КИНЕМАТИКА § 1. Пространство. Время § 2. Механическое движение. Система отсчета § 3. Материальная точка. Поступательное движение § 4. Радиус-вектор. Перемещение § 5. Одновременные перемещения. Сложение перемещений § 6. Средняя скорость § 7. Скорость § 8. Ускорение § 9. Одномерное движение § 10. Неравномерное одномерное движение § 11. Движение по окружности § 12. Равнопеременное движение в пространстве § 13. Траектории § 14. Относительность механического движения II. ДИНАМИКА § 15. Инерция. Первый закон Ньютона § 16. Сила — мера взаимодействия § 17. Связь между силой и ускорением. Второй закон Ньютона § 19. Применение законов динамики § 20. Силы в природе. Трение § 21. Проявления сухого трения § 22. Силы тяготения § 23. Движение в поле тяготения § 24.  Силы упругости и деформации§ 25. Механическое состояние. Уравнение движения § 26. Принцип относительности Галилея § 27. Системы единиц § 28. Метод анализа размерностей III. ЗАКОНЫ СОХРАНЕНИЯ § 29. Импульс. Импульс силы § 30. Центр масс. Реактивное движение § 31. Механическая работа. Кинетическая энергия § 33. Закон сохранения механической энергии § 34. Связь законов сохранения с симметрией пространства и времени § 35. Применение законов сохранения при решении задач § 36. Космическая динамика и законы сохранения § 37. Столкновения частиц § 38. Фазовая плоскость. Адиабатические инварианты § 39. Механическое равновесие § 40. Движение твердого тела IV. КОЛЕБАНИЯ И ВОЛНЫ § 41. Собственные колебания § 42. Затухающие колебания § 43. Собственные колебания в разных физических системах § 44. Вынужденные колебания. Резонанс § 45. Энергетические превращения при вынужденных колебаниях. 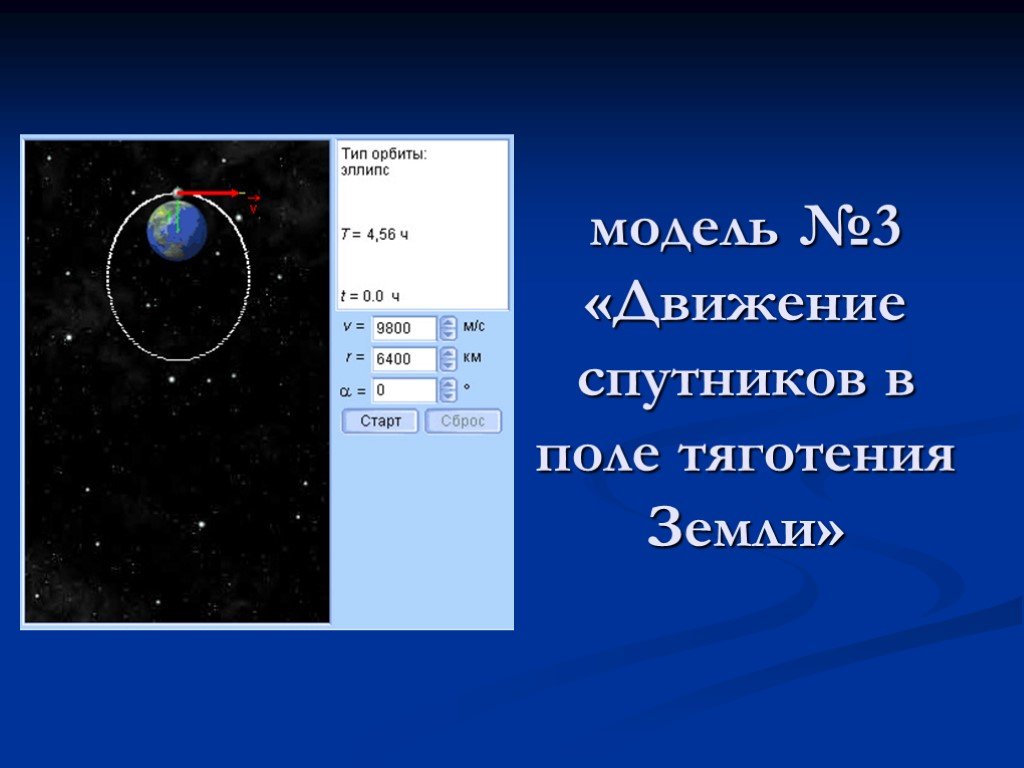 § 46. Волны § 47. Интерференция и дифракция волн. Эффект Доплера V. ДВИЖЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ § 49. Движение идеальной жидкости § 50. Вязкая жидкость. Обтекание тел |
1.3.1 Движение в поле тяготения Земли.
Из закона всемирного тяготения следует, что у поверхности Земли все тела должны падать с одинаковым ускорением. В самом деле, по второму закону Ньютона ускорение, приобретаемое телом с массой m у поверхности Землиa=F/m, гдеF — сила, с которой тело притягивается земным шаром. По закону тяготения
, (1.44)
M3— масса Земли и R3— радиус земного шара. Отсюда
и не зависит от массы падающего тела. Таким образом, все тела у поверхности Земли независимо от их массы падают с одинаковым ускорением
,
(1.
45)
которое называется ускорением свободного падения. Подставляя сюда известные значения констант, получим значение 9,8 м/c2. В действительности значенияg слегка различаются при учете сил сопротивления и реальной формы Земли. По второму закону Ньютона это означает, что в поле тяжести Земли все тела испытывают силу тяжести, равную
1.3.2 Космические скорости.
Определим скорость, которую необходимо иметь телу дли того, чтобы оно могло стать спутником Земли, т. е. первую космическую скорость. Величину этой скорости можно определить из условия равенства сил, действующих на тело при его вращении вокруг Земли. Сила притяжения должна быть уравновешена центробежной силой mv2/R. Таким образом,
(1.46)
Подставляя
численные значения величин, получаемv1 = 8 км/с.
Вторая космическая скорость — это скорость, которую нужно сообщить телу для того, чтобы оно покинуло область земного притяжения. Для определения второй космической скорости следует вычислить работу, которую необходимо совершить против сил земного притяжения для удаления тела с поверхности Земли на бесконечность. Эта работа равна разности потенциальных энергий тела в начальном и в конечном положениях:
Потенциальная энергия тела в гравитационном поде Земли на ее поверхности согласно (1.41) имеет вид:
а на бесконечности равна нулю. Таким образом,
(1.47)
Величина этой потенциальной энергии определяет кинетическую энергию, которую должно иметь тело для того, чтобы быть в состоянии совершить указанную работу
Отсюда вторая космическая скорость определяется выражением:
.
Ее численное значение приблизительно 11 км/с. Пусть перемещение происходит вдоль оси Z. При этом сила тяжести совершает работу
.
Согласно определению потенциальной энергии А = U1‑U2. Отсюда следует, что потенциальная энергия тела в поле силы тяжести Земли может быть записана в виде
U(z) = mgz + const, (1.48)
где постоянная связана с выбором начала отсчета энергии. Эту формулу можно получить и непосредственно из закона всемирного тяготения. Запишем его в виде
,
где z— высота тела с массойm над поверхностью Земли. При малых
, , откуда находимU =U0 +mgz =U(R3) +mgz
1.4. Силы инерции
Основным положением
механики Ньютона является утверждение
о том, что действие на тело со стороны
других тел вызывает их ускорение.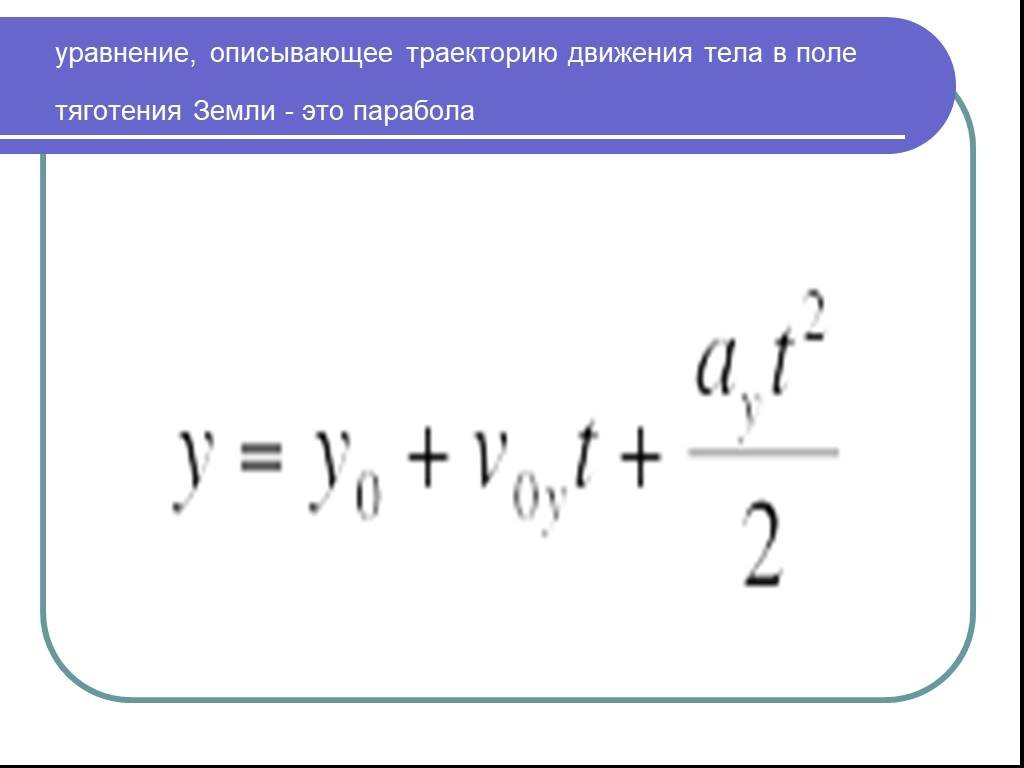
В
системах координат, движущихся с
ускорением относительно выбранной нами
инерциальной системы, так называемых
неинерциальных системах, формально
справедливо и обратное — возникают
силы, связанные не с реальным действием
других тел, а с наличием указанных
ускорений. Такие силы называют силами
инерции. Рассмотрим несколько примеров.
1. Прямолинейное движение системы координат с ускорением a0 относительно инерциальной системы. В этом случае на тело с массойm в неинерциальной системе координат действует сила инерции, равная
fи = —ma0. (1.49)
2. Центробежная
сила инерции. Рассмотрим движение тела
во вращающейся системе координат.
Сначала рассмотрим вращение тела в
неподвижной системе. В ней тело будет
испытывать центростремительное
ускорение, которое, и будет заставлять
его вращаться. По третьему закону Ньютона
центростремительной силе соответствует
центробежная сила, приложенная к нити,
удерживающей вращающееся тело.
3. Свободно падающий лифт. Пусть ускорение свободно падающего лифта — неинерциальной системы отсчета — g. Сила инерции, действующая на материальную точку с массойm, в системе отсчета, связанной с лифтом, равна
Движение в гравитационном поле
Сделать 4 мин чтения 1 мин видео
Движение в гравитационном поле
Из закона всемирного тяготения Ньютона мы знаем, что на объект в гравитационном поле Земли действует сила, притягивающая его к центру Земля. Если это единственная сила, действующая на объект, то объект будет ускоряться по направлению к центру Земли.
Человек, стоящий на поверхности Земли, интерпретирует это ускорение как объекты, всегда падающие вниз. 9{-2}$}\).
Важно:
В действительности, если вы уйдете очень далеко от поверхности Земли, величина \(\vec{g}\) изменится, но для повседневных задач мы можем смело считать ее постоянной. Мы также игнорируем любые эффекты, которые может иметь сопротивление воздуха (сопротивление).
В оставшейся части этого урока мы будем иметь дело только со случаем, когда сила гравитации является единственной силой, действующей на падающий снаряд. Любой снаряд можно описать как падающий, даже если изначально он движется вверх.
Начальная скорость, \(\vec{v}_i\), которую имеет объект, и ускорение, которое он испытывает, являются двумя разными величинами. Очень важно помнить, что гравитационное ускорение всегда направлено к центру Земли и постоянно, независимо от направления или величины скорости.
Совет:
Снаряды, движущиеся вверх или вниз в гравитационном поле Земли, всегда ускоряются вниз с постоянным ускорением \(\vec{g}\). Примечание: ненулевое ускорение означает, что скорость равна изменение .
Объекты, движущиеся вверх или вниз в гравитационном поле Земли, всегда ускоряются по направлению к центру Земли. Для человека, стоящего на поверхности Земли, это выглядит как нисходящее ускорение. Мы не рисуем оба вектора на объекте, потому что мы смешиваем скорость и ускорение, которые являются двумя различными физическими величинами.
Это означает, что если объект движется вверх с некоторой начальной скоростью в вертикальном направлении, модуль скорости в вертикальном направлении уменьшается до тех пор, пока не остановится (\(v=0\) \(\text{м·с $ ^{-1}$}\)) на мгновение.
Точка, в которой скорость уменьшается до нуля, соответствует максимальной высоте \(h_{max}\), которую достигает объект. После этого объект начинает падать. Очень важно помнить, что ускорение постоянно, но вектор скорости изменился по величине и направлению. На максимальной высоте, где скорость равна нулю, ускорение равно \(\vec{g}\).
Совет:
Снаряды, которые имеют начальную скорость вверх, будут иметь нулевую скорость на максимальной высоте, \(h_{max}\). Ускорение по-прежнему \(\vec{g}\).
(a) Предмет брошен вверх с высоты \({h}_{i}\). Через время \({t}_{m}\) объект достигает максимальной высоты и начинает падать вниз. Через время \(2{t}_{m}\) объект возвращается на высоту \({h}_{i}\).
Рассмотрим предмет, брошенный вверх с вертикальной высоты \({h}_{i}\). Мы сказали, что объект будет двигаться вверх с уменьшающейся вертикальной скоростью, пока не остановится, а затем начнет двигаться вертикально вниз. Время, которое требуется объекту, чтобы упасть обратно на высоту \({h}_{i}\), равно времени, которое требуется объекту, чтобы достичь максимальной высоты с высоты \({h}_{i }\).
Это известно как временная симметрия . Это следствие равномерного ускорения снаряда.
Это имеет два значения для снарядов, которые проходят через точку как на восходящей, так и на нисходящей части своего движения в свободном падении: то же самое, например, для подъема из исходного положения на максимальную высоту потребуется столько же времени, сколько и для возврата в исходное положение. Это относится к любой точке, как показано розовой точкой на рисунке выше. Интервал времени между прохождением снаряда точки и нахождением на максимальной высоте одинаков, \(\Delta t\).
Это очень полезно при решении задач, потому что, если у вас есть какая-либо информация о восходящем движении, вы также можете узнать что-то о нисходящем движении и наоборот.