5 Сила Лоренца. Формула Лоренца. Движение заряженных частиц в электрическом и магнитных полях.
Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой
(114.1)
где В — индукция магнитного поля, в котором заряд движется.
Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q > 0 направления I и v совпадают, для Q < 0 — противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На рис. 169 показана взаимная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F
На отрицательный
заряд сила действует в противоположном
направлении. Модуль силы Лоренца (см.
(114.1)) равенгде — угол между v и В.
Выражение для силы Лоренца (114.1) позволяет найти ряд закономерностей движения заряженных частиц в магнитном поле. Направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависят от знака заряда Q частицы. На этом основано определение знака заряда частиц, движущихся в магнитных полях.
Если заряженная частица движется в магнитном поле со скоростью
(115.
1)
Период вращения частицы,
Подставив сюда выражение (115.1), получим
(115.2)
т. е. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду (Q/m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v ≪ c). На этом основано действие циклических ускорителей заряженных частиц (см. § 116).
Если скорость
Радиус окружности определяется
формулой (115.1) (в данном случае надо
заменить v на vРис. 170
Шаг винтовой линии
Подставив в последнее выражение (115.2), получим
Направление, в котором закручивается спираль, зависит от знака заряда частицы.
Если скорость т заряженной частицы составляет угол а с направлением вектора В неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то г и А уменьшаются с ростом В
Сила лоренца правило формула. 5 Сила Лоренца. Формула Лоренца. Движение заряженных частиц в электрическом и магнитных полях.
ГлавнаяРазноеСила лоренца правило формула
5 Сила Лоренца. Формула Лоренца. Движение заряженных частиц в электрическом и магнитных полях.
Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой
(114.1)
где В — индукция магнитного поля, в котором заряд движется.
Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q > 0 направления I и v совпадают, для Q < 0 — противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На рис. 169 показана взаимная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F для положительного заряда.
где — угол между v и В.
Выражение для силы Лоренца (114.1) позволяет найти ряд закономерностей движения заряженных частиц в магнитном поле. Направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависят от знака заряда Q частицы. На этом основано определение знака заряда частиц, движущихся в магнитных полях.
Если заряженная частица движется в магнитном поле со скоростью v, перпендикулярной вектору В, то сила Лоренца F = Q[vB] постоянна по модулю и нормальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус r которой определяется из условия QvB = mv2/r, откуда
(115.1)
Период вращения частицы, т.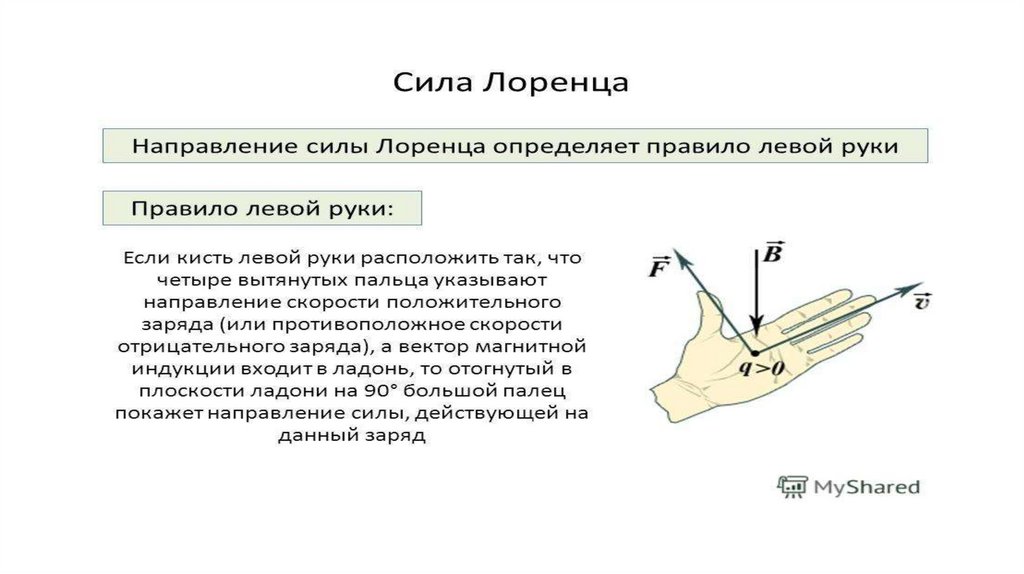
Подставив сюда выражение (115.1), получим
(115.2)
т. е. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду (Q/m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v ≪ c). На этом основано действие циклических ускорителей заряженных частиц (см. § 116).
Если скорость v заряженной частицы направлена под углом к вектору В (рис. 170), то ее движение можно представить в виде суперпозиции: 1) равномерного прямолинейного движения вдоль поля со скоростью v1 = vcos; 2) равномерного движения со скоростью v = vsin по окружности в плоскости, перпендикулярной полю. Радиус окружности определяется формулой (115.1) (в данном случае надо заменить v на v = vsin). В результате сложения обоих движений возникает движение по спирали, ось которой параллельна магнитному полю (рис.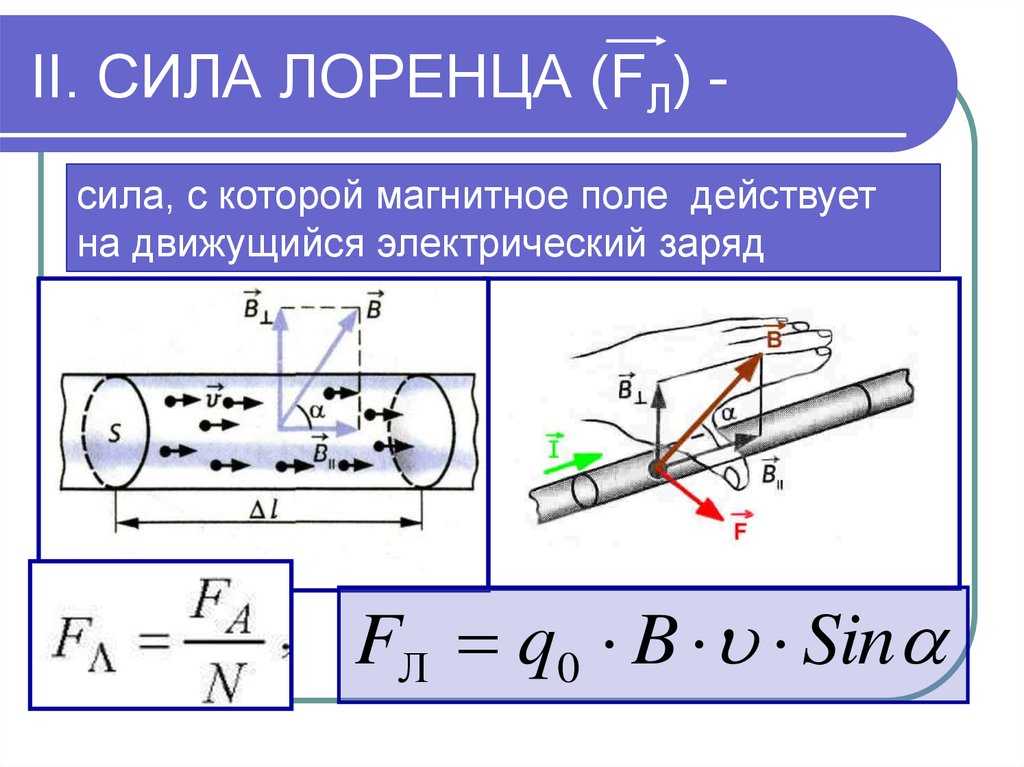
При определении направления движения электронов с помощью правила левой руки следует учитывать, что направление движения электронов противоположно техническому направлению тока.
Сила Лоренца действующая на электрон и протон
Величина и направление силы Лоренца определяются соотношением
\[ \vect{F_{L}}= e \vect{v} × \vect{B} \]
где $\vect{v}$, $\vect{B}$ и $\vect{F}$ образуют правую систему.
Для электронов, движущихся перпендикулярно магнитному полю, формула упрощается:
\[ F_{L} = evB \]
Так как сила действует перпендикулярно скорости и направлению поля, она создает центростремительное ускорение, т.е. изменяет направление скорости, не меняя ее величины. Поэтому электрон движется в магнитном поле по окружности.
Вычислить, найти силу Лоренца действующую на электрон или протон
Радиус траектории электрона в магнитном поле
Для определения радиуса круговой траектории электрона приравняем силу Лоренца и центростремительную силу.
{-19} Кл. \]
При определении направления движения протонов с помощью правила левой руки направление движения протонов совпадает с техническим направлением тока и с картинкой.
Таким образом электрон и протон влетая в магнитное поле в одном направлении будут отклоняться в разные стороны.
Сила Лоренца действующая на протон
Величина силы действующая на электрон и на протон будет одинакова (определяется формулой №3), но поскольку протон гораздо тяжелее электрона, радиус закручивания для протона будет больше.
Радиус траектории протона в магнитном поле
Если
| радиус круговой траектории протона, | метр |
| 1,67 · 10-27 кг — масса протона, | кг |
| 1,602 · 10-19 Кл — элементарный электрический заряд, | Кулон |
| скорость протона, | м/с |
| магнитная индукция, | Тесла |
Радиус траектории для протона будет вычисляться по аналогичной формуле
\[ r = \frac{m_{p} · v}{pB} \]
Из этой формулы видно что при одинаковых скоростях электрона и протона радиус траектории протона будет значительно больше, чем у электрона пропорционально отношению масс этих частиц
В помощь студенту
стр. 665 |
www.fxyz.ru
Сила Лоренца
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого голландского физика Х. Лоренца (1853 — 1928) — основателя электронной теории строения вещества. Силу Лоренца можно найти с помощью закона Ампера.
Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной Δl, к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:
Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка Δl и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля можно считать одинаковым в пределах этого отрезка проводника. Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (числом зарядов в единице объема) и скоростью их упорядоченного движения v следующей формулой:
I = qnvS ( 2 )
Модуль силы, действующей со стороны магнитного поля на выбранный элемент тока, равен:
F = | I |B Δl sin α
Подставляя в эту формулу выражение ( 2 ) для силы тока, получаем:
F = | q | nvS Δl B sin α = v | q | NB sin α, где N = nSΔl — число заряженных частиц в рассматриваемом объеме.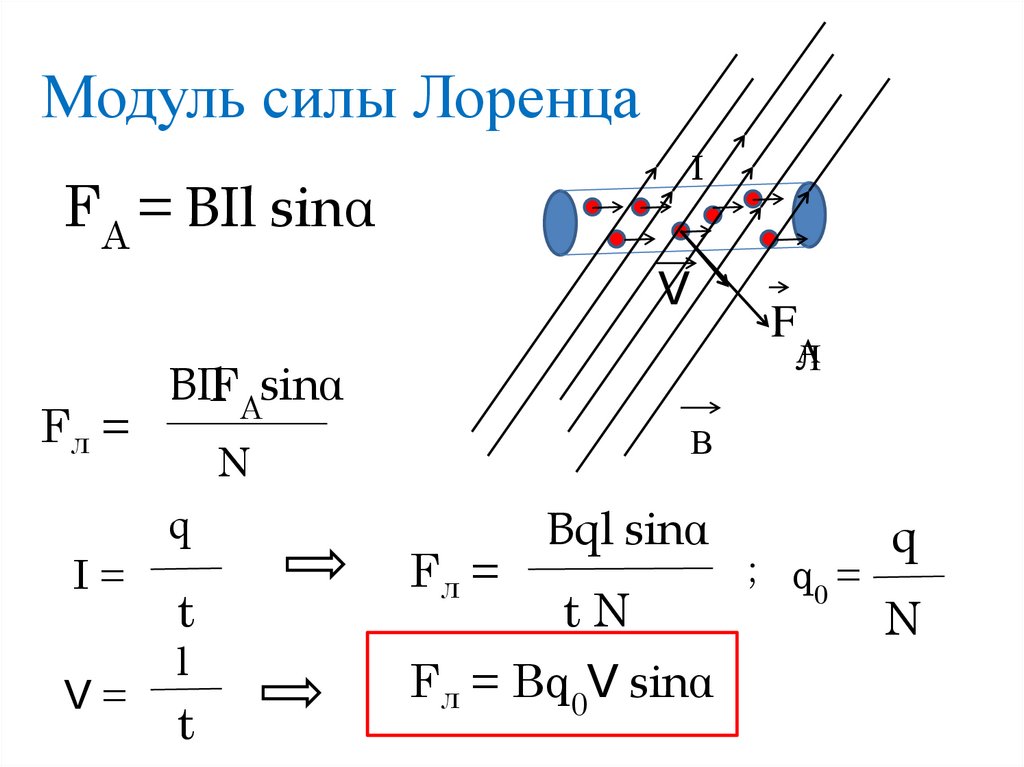
Следовательно, на каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная: где α — угол между вектором скорости и вектором магнитной индукции. Сила Лоренца перпендикулярна векторам магнитной индукции и скорости упорядоченного движения заряженных частиц. Ее направление определяется с помощью того же правила левой руки, что и направление силы Ампера.
Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работы. Согласно теореме о кинетической энергии это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.
Другие заметки по физике
edu.glavsprav.ru
Сила Лоренца — fizikatyt
Сила Лоренца — сочетание электрического и магнитного взаимодействия, которое возникает, когда положительно или отрицательно заряженная частица движется в электромагнитном поле. Она перпендикулярна направлениям векторов магнитной индукции и скорости заряда.
Под её действием частица изменяет траекторию своего движения и скорость.
Этот вид сил впервые описал Джеймс Максвелл в 1865 году, а в 1892 году голландский физик Хендрик Лоренц записал для неё математическое выражение. Хотя первый вывод формулы исследователи приписывают Оливеру Хевисайду.
Вариация этой базовой силы действует на проводник с током, когда его помещают между полюсами магнита. Если в проводнике существует ток, то он будет отклоняться во внешнем магнитном поле, так как сила Лоренца будет действовать на все движущиеся в нём электроны. В какую сторону отклонится провод с током наглядно продемонстрирует правило левой руки.
Это явление и возникающую силу используют в экспериментальной физике для:
- увеличения скорости элементарных частиц и ионов в различных циклотронах и других ускорителях;
- определения удельного заряда и массы положительных ионов, относительной атомной массы изотопов химических элементов в масс-спектрографии;
- в магнетронах и скоростных фильтрах.
В быту такое воздействие на заряженную частицу нашло применение в телевизорах с электронно-лучевой трубкой, электродвигателях, колонках, генераторах.
Какова природа силы?
Эта сила принадлежит спектру сил электромагнитного взаимодействия. Магнитное поле создают заряженные частицы, такие как протон или электрон, во время своего движения. Движущийся заряд поместим во внешнее поле, например, между полюсами магнита. Поле точечного заряда и внешнее поле будут взаимодействовать определённым образом: притягиваться или отталкиваться. Это зависит от знака заряда и от взаимного расположения линий магнитной индукции полей.
Формула для вычисления модуля силы Лоренца демонстрирует её зависимость от скорости частицы v, абсолютного значения её заряда q, от модуля индукции внешнего магнитного поля B и угла α, показывающего взаимное расположение векторов скорости и магнитной индукции.
На рисунке представлены все величины, фигурирующие в формуле:
Из уравнения видно, что если v (скорость) стремится к нулю, то на точечный заряд не будет действовать и сила Лоренца.
Кроме того, если заряд перемещается в направлении, параллельном направлению вектора магнитной индукции, то есть sin (0) = 0, снова будем наблюдать отсутствие внешней силы (Fл=0). А при движении, перпендикулярном линиям внешнего магнитного поля, сила Лоренца становится центростремительной и искривляет траекторию объекта (наблюдается движение по окружности). Протон представлен на рисунке а), рисунок б) описывает электрон.
Правило левой руки
Для положительно заряженной частицы необходимо расположить ладонь левой руки, чтобы четыре вытянутых пальца направить параллельно её движению, а линии магнитной индукции входили в ладонь перпендикулярно, то отогнутый на 90° большой палец покажет направление силы Лоренца. А для отрицательного заряда силу Лоренца направляем в противоположную сторону.
fizikatyt.ru
46.7 Сила Лоренца. | FizPortal
46.7 Сила Лоренца.
Магнитное поле действует с некоторой силой на каждую движущуюся заряженную частицу, эта сила называется силой Лоренца (названной в честь голландского физика Генриха Антона Лоренца).
Можно считать, что рассмотренная выше сила Ампера является суммой сил Лоренца, действующих на каждую заряженную частицу, направленное движение которых и образует электрический ток. Для того чтобы получить формулу для этой силы представим выражение для элемента тока в виде (рис. 423)
рис. 423 здесь S − площадь поперечного проводника, j = nqv − вектор плотности тока1, q − электрический заряд движущихся частиц, v − их скорость, n − число частиц в единице объема (концентрация заряженных частиц). Подставим это выражение в формулу для силы Ампера и заметим, что величина nSΔl = N равна общему числу заряженных частиц в выделенном участке проводника. Поэтому сила, действующая на одну частицу (сила Лоренца) равна Модуль силы Лоренца рассчитывается по формуле где α − угол между векторами скорости частицы и индукции магнитного поля (рис. 424).рис. 424 Сила Лоренца направлена перпендикулярно плоскости, в которой лежат векторы скорости частицы v и индукции магнитного поля B.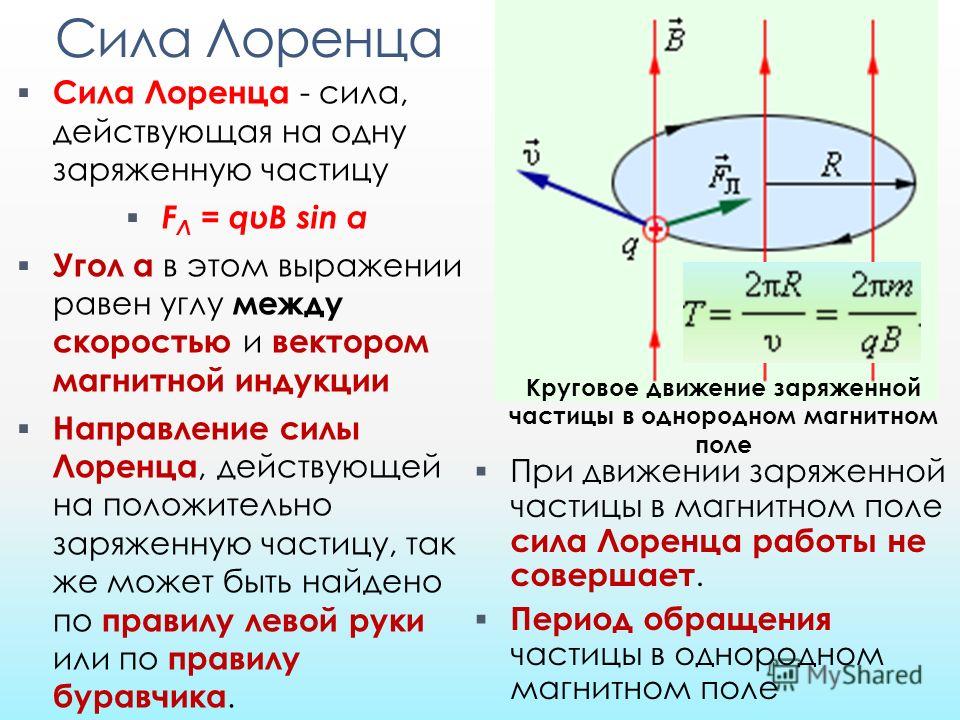
Направление этой силы можно определить по правилу левой руки, аналогичному правилу для определения направления силы Ампера. Также можно говорить, что на заряженную частицу, действует сила со стороны компоненты поля B⊥, перпендикулярной вектору скорости. Частица, движущаяся параллельно вектору индукции (то есть вдоль силовой линии магнитного поля), действия силы Лоренца не испытывает. В некоторых учебниках, особенно по теоретической физике, сначала дается формула для силы Лоренца как следствие определения вектора магнитной индукции и обобщения экспериментальных данных, а затем на ее основе выводится выражение для силы Ампера. То, что мы поступили наоборот, несущественно, так обе эти силы имеют одинаковую природу − действие магнитного поля на движущийся заряд. 1Напомним, что за направление силы тока принято направление движения положительно заряженных частиц, поэтому излагаемые здесь правила для определения направления силы Лоренца справедливы для положительных зарядов. Для отрицательно заряженных частиц направление силы Лоренца противоположное.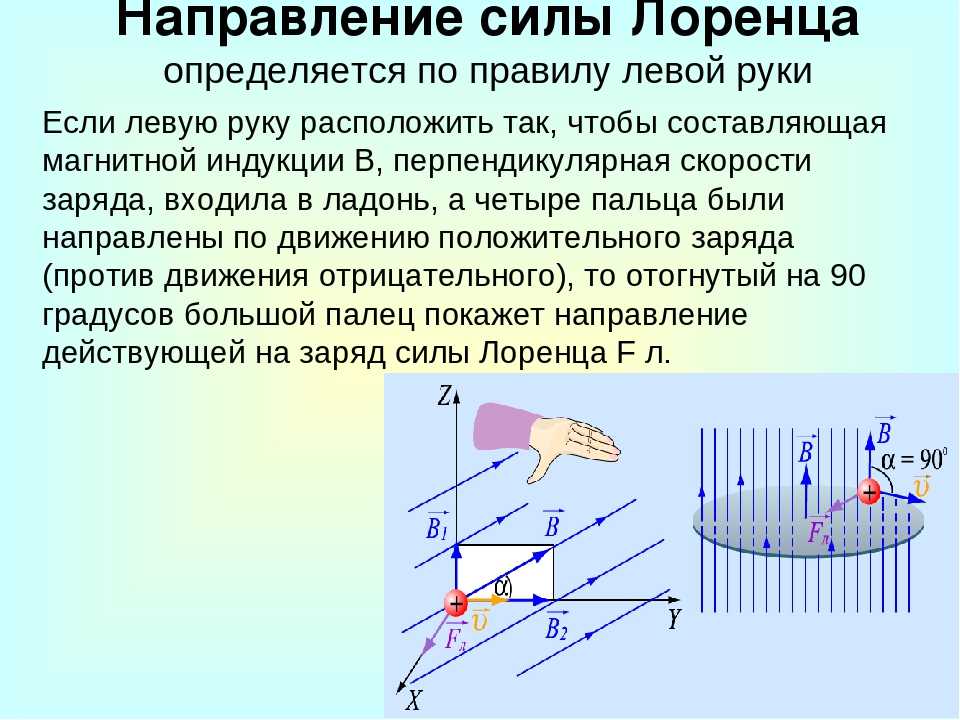
fizportal.ru
Сила Лоренца | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Тема:
Электромагнетизм
Силой Лоренца F̅Л называют силу, действующую на электрически заряженную частицу, которая движется, испытывая действия электрического и магнитного полей одновременно.
Это выражается формулой
F̅Л = F̅Э + F̅М.
где F̅Э, — электрическая составная силы Лоренца, описывающая взаимодействие частицы с электрическим полем; F̅М — магнитная составная силы Лоренца, которая описывает взаимодействие частицы с магнитным полем.
| Рис. 6.21. Графическое изображение направления силы Лоренца |
Сила Лоренца направлена всегда под углом к скорости частицы, поэтому она придает ей центростремительное ускорение (рис. 6.21).
Для случая, когда α = 90°,
qvB = mv2 / R.
Отсюда
R = mv / qB.
| Рис. 6.22. Магнитное поле смещает электронный луч |
Таким образом, заряженная частица, попадая в магнитное поле, начинает двигаться по дуге окружности. Материал с сайта http://worldofschool.ru
При иных значениях 0 < α < 90° траектория движения заряженной частицы в магнитном поле приобретает форму спирали.
Наблюдать действие силы Лоренца можно с помощью электронно-лучевой трубки (рис. 6.22). Если включить питание осциллографа, то на экране его электронно-лучевой трубки будем наблюдать светлое пятно — место падения на экран движущихся электронов. Если поднести к трубке осциллографа магнит, то пятно сместится, что свидетельствует о действии магнитного поля на движущиеся электроны.
На этой странице материал по темам:
Доклад по физике применение силы лоренца
Лекция по физике сила лоренца
Доклад на тему сила лоренца
Физический смысл величин входящих в формулу полной силы лоренца?
Реферат на тему сила ампера
Вопросы по этому материалу:
worldofschool.
электромагнетизм — выражение силы Лоренца
спросил
Изменено 3 года назад
Просмотрено 858 раз
$\begingroup$
Поскольку выражение силы Лоренца дается формулой $F=qBv\sin\theta$. Теперь я сомневаюсь, почему мы не можем взять $v \cos\theta$ в выражении и как насчет направления магнитного поля?
- электромагнетизм
- магнитные поля
$\endgroup$
3
$\begingroup$
Определение силы Лоренца, которое вы дали, не самое общее.
Для магнитного поля $B$ и частицы с зарядом $q$, движущейся со скоростью $v$, сила Лоренца определяется выражением $$F_L=q v\times B\; , $$, где $\times$ обозначает векторное произведение. Итак, если угол между векторами $B$ и $v$ равен $\theta$, сила Лоренца принимает вид $$ |F_L|= q|v| |B|\sin\тета\; ,$$ как вы написали. Кроме того, если приложить электрическое поле $E$, сила Лоренца превращается в $$ F_L=q(E+v\times B)\; .$$
$\endgroup$
2
$\begingroup$
Сила Лоренца (в отсутствие электрического поля) определяется как $\vec{F}=q(\vec{v}\times \vec{B})=qvB\sin\theta\hat{l} $. Где $\hat{l}$ — единичный вектор, определяемый правилом правой руки в векторном произведении скорости и магнитного поля. Как видите, сила Лоренца — правильное векторное уравнение, которое действительно учитывает направление магнитного поля (а также скорость).
Сила направлена на 90 градусов как к скорости, так и к магнитному полю. Фактор $\sin\theta$ возникает из-за того, что это векторное произведение.
$\endgroup$
$\begingroup$
Что ж, кажется, вы впервые столкнулись с Законом Лоренца . Надо сказать, что Закон Лоренца — чисто экспериментальный результат. Дело было в том, что когда они включали магнитное поле, заряженная частица, двигавшаяся с некоторой скоростью $v$, случайно ощущала ускорение в направлении, перпендикулярном как направлению ее скорости, так и направлению магнитного поля. Теперь, когда они измерили величину ускорения и умножили эту величину на массу заряженной частицы (что и есть сила, закон Ньютона), результат всегда был $$ q~v~B~sin\theta$$, где $ q$ — величина заряда, $v$ — величина скорости, B — величина магнитного поля (я рассматриваю однородное и не зависящее от времени поле), а $\theta$ — угол между магнитным полем и направление скорости.
Вы можете увидеть демонстрацию здесь.
В 1773 г. Дж. Л. Лагранж определил векторное произведение на покомпонентно, и из него можно было вывести $sin\theta$-форму векторного произведения на . Итак, эта штука перекрестное произведение стало в то время обычным явлением в динамике и очень привычным.
Таким образом, объединив экспериментальные результаты движения заряженной частицы в магнитном поле с математическими выводами, с предельной уверенностью были получены следующие выводы: и $\mathbf{B}$.
Его величина $F= q~v~B~sin\theta$
Следовательно, $\mathbf{F} = q(\mathbf{v} \times \mathbf{B})$ .
Надеюсь, это поможет.
P.S.: Все, что я сказал, было просто для иллюстрации, я не могу утверждать, что они на самом деле сделали. Утверждение о Ж. Л. Лагранже взято из википедии, а видео с ютуба.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Калькулятор силы Лоренца | iCalculator™
Калькулятор силы Лоренца рассчитает:
- Величину силы Лоренца, возникающую, когда заряженный объект находится внутри однородного магнитного поля
Параметры расчета: Магнитное поле и среда считаются однородными; заряд считается безразмерным и безмассовым.
| 🖹 Нормальное просмотр 🗖 Полночная страница просмотр |
| ПРИСИЦИЯ Калькулятора (Десятимильные места) 0123456789111112131415 |
| SUTREAR of Заряда в заряженном заряде в заряженном заряде в заряде в заряде в заряде в заряде в заряде в заряде в заряде в заряде в заряде в заряде в заряде в целевой). ) об/м |
| Скорость движущегося заряда (об) м/с |
| Магнитное поле (B) T |
| Угол между направлением движения и линиями магнитного поля (θ) RAD |
| Расчет силы Лоренца |
|---|
| F L = Q × E + Q × v × B × sinθ F L + + × × × sin( ) F L = × + × × × F L = |
| Lorentz Force Calculator Input Values |
| Amount of charge хранится в объекте (Q) Кл [Кулон] |
| Электрическое поле (E) в/м [вольт на метр] |
| Скорость движущегося заряда (v) м/с [метр в секунду ] |
| Магнитное поле (B) Тл [Тесла] |
| Угол между направлением движения и силовыми линиями магнитного поля (θ) рад [радиан] |
Обратите внимание, что формулы для каждого расчета вместе с подробными расчетами доступны ниже.
Когда вы вводите конкретные коэффициенты для каждого расчета силы Лоренца, Калькулятор силы Лоренца автоматически вычисляет результаты и обновляет элементы формулы физики с каждым элементом расчета силы Лоренца. Затем вы можете отправить по электронной почте или распечатать этот расчет силы Лоренца для дальнейшего использования.
Мы надеемся, что Калькулятор силы Лоренца оказался полезным для вашей версии физики. Если это так, мы просим вас оценить этот калькулятор физики и, если у вас есть время, поделиться им в своей любимой социальной сети. Это позволяет нам распределять будущие ресурсы и сохранять эти калькуляторы по физике и учебные материалы бесплатными для всех по всему миру. Мы считаем, что у всех должен быть бесплатный доступ к учебным материалам по физике. Делясь с вами, вы помогаете нам охватить всех студентов-физиков и тех, кто интересуется физикой по всему миру.
★ ★ ★ ★ ★ [6 голосов]
Связанные секции
.
