Закон кулона в вакууме имеет вид: Кафедра физики Физико-механический институт СПбПУ — RC74 — интернет-магазин радиоуправляемых моделей

Заряд и поле. Электростатика в вакууме. Закон Кулона. Напряженность электрического поля. Потенциал, страница 2

Физика \ Физика

где ε₀= 8,85·10^-12. Данная формула устанавливает и величину коэффициента пропорциональности, и направление силы, так как вектор есть единичный вектор, совпадающий по направлению с радиус-вектором г, проведенным от заряда Q к заряду q. Из этой формулы видно, что если оба заряда имеют одинаковые знаки, то они отталкиваются (знак силы взаимодействия такой же, как у радиус-вектора, т.е. она направлена по радиус-вектору), а если разные знаки — притягиваются (сила направлена противоположно направлению радиус-вектора). Силы, действующие на заряды Q и q, равны по величине, противоположны по направлению и лежат на одной прямой (см. рис. 1).

Рис. 1

Строго говоря, закон Кулона абсолютно верен лишь для зарядов, которые все время неподвижны.

Однако этот закон справедлив с очень высокой степенью точности, если заряды движутся не слишком быстро и находятся не очень далеко друг от друга. Когда имеются только два взаимодействующих заряда, законом Кулона можно пользоваться, если скорости зарядов υ много меньше скорости света с. Если же поле, действующее на заряд q, создается системой зарядов, имеющей характерный размер l, условие применимости закона Кулона имеет вид , где r — расстояние от системы зарядов до заряда q. Кроме того, ускорения зарядов должны быть не слишком велики.

1.2. Напряженность электрического поля

Введем теперь понятие напряженности электрического поля. Напряженностью электрического поля Е называется отношение силы, действующей на неподвижный электрический заряд

q, к величине этого заряда:

Напряженность — векторная величина. Размерность напряженности Вольт/метр. Используя определение напряженности, закон Кулона можно сформулировать так: неподвижный точечный заряд Q создает в каждой точке пространства вокруг себя электрическое поле с напряженностью, равной

где г — радиус-вектор, проведенный от заряда Q в эту точку. Выражая силу через напряженность, получаем, что сила, действующая на зарядq, находящийся в поле, создаваемом зарядом

Это выражение полностью совпадает с законом Кулона, сформулированным ранее.

Если имеется несколько зарядов, например Q₁ и Q₂; то, согласно принципу суперпозиции, напряженность результирующего электрического поля есть векторная сумма напряженностей, создаваемых каждым отдельным зарядом: E=E₁+E₂

(рис.

2).

Таким образом, для того, чтобы подсчитать силу, действующую на какой-либо заряд q, находящийся в определенной точке

Рис. 2

А, нужно определить напряженности полей, создаваемых в этой точке каждым другим зарядом, найти векторную сумму этих напряженностей и умножить полученную результирующую напряженность на q.

Этот способ может показаться излишне сложным — силу, действующую на заряд, можно найти, просто сложив силы, с которыми действуют на него все другие заряды. Действительно, в рамках электростатики эти способы эквивалентны, так как все заряды можно считать все время покоящимися. Однако, как показывает практика, даже в электростатике использование понятия напряженности более удобно. Если же рассматривать движущиеся заряды, то без введения понятия поля обойтись невозможно. Поле — не просто способ описания взаимодействия, а физическая реальность.

В частности, поле обладает энергией и импульсом, которые можно измерить.

В заключение необходимо отметить, что электрическое поле может создаваться не только неподвижными зарядами. Такие поля будем в дальнейшем называть сторонними

1.3. Потенциал

На находящийся в электростатическом поле заряд действует сила. Поэтому при перемещении заряда из точки 1 в точку 2 силы электростатического поля совершают работу , зависящую от поля и от величины перемещаемого заряда q. Разность потенциалов между точками 1 и 2 по определению равна отношению этой работы к заряду:

Единица измерения потенциала — Вольт.

Так как работа равна интегралу от силы по перемещению

а электростатическая сила равна произведению заряда на напряженность

то получаем связь между потенциалом и напряженностью:

Скачать файл

Урок № /2 часа/ Тема «Закон Кулона»

©engime.org 2023
әкімшілігінің қараңыз

Урок № /2 часа/

Тема «Закон Кулона»

Цель урока: познакомить учащихся с законом Кулона. Используя закон Кулона, научиться решать задачи.

ХОД УРОКА:

1.Орг. момент.

2.Опрос домашней темы/по вопросам учебника/

3.Разбор дом.задач у доски.

4.Объяснение новой темы.

А) биография Ш.Кулона.
ШАРЛЬ ОГЮСТЕН КУЛОН

(1736— 1806)

Французский физик Шарль Кулон родился в городе Ангулеме. После окончания средней школы он поступил на военную службу. В Париже прошел инженерную подготовку и был направлен на остров Мартинику для строительства укреплений. В 1772 г. Кулон вернулся во Францию и был назначен инженером по крепостным и водным сооружениям. Одновременно со службой он проводил научные исследования. Вначале его привлекли проблемы трения, кручения и сопротивления материалов.

Его имя стало известно в научном мире в 1777 г., когда он опубликовал ряд работ, в которых представил результаты экспериментов по измерению кручения волос, шелковых и металлических нитей.

За эти работы в 1781 г. Кулона избрали членом Парижской академии наук.

Пользуясь изобретенными им крутильными весами, Кулон детально исследовал взаимодействие одноименных и разноименных точечных электрических зарядов. Эти эксперименты привели к открытию в 1785 г. основного закона электростатики — закона Кулона . В своих опубликованных работах 1785—1789 гг. ученый показал, что электрические заряды всегда располагаются на поверхности проводника, ввел понятия магнитного момента и поляризации зарядов и т. д.

экспериментальные работы Кулона имели важное значение для создания теории электромагнитных явлений. Его именем названа единица количества электричества (Кулон).

Каталог: images
images -> 6 Хромтау гимназиясы тәрбие жұмысының жылдық жұмыс жоспары Азаматтық-патриоттық, құқықтық және полимәдениеттік тәрбие
images -> БАҒдарламасы қазақ филологиясы кафедрасы Орал-2014
images -> БАҒдарламасы қазақ филологиясы кафедрасы Орал-2014
images -> АҚПараттық хат қҰрметті әріптестер!
images -> Абай Құнанбайұлы (1845—1904)
images -> Автобиография кандидата в депутаты районного маслихата по избирательному округу №5

images -> «Қазақстан тарихы» пәнінен «6М020300-тарих» мамандығына арналған жазбаша емтихан сұрақтары 1 блок
images -> Мазмұны Қазақстандағы жоғары білім, Ғылым және МӘдениет
images -> Үлгілік оқу жоспары
images -> Сембі Жансая Хасанқызы Қазақ тілі мен әдебиеті

жүктеу/скачать 168,42 Kb.

Достарыңызбен бөлісу:

1.5: Закон Кулона — Физика LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 5414

Джереми Татум
Университет Виктории

Если вы интересуетесь историей физики, вам стоит прочитать о важных экспериментах Шарля Кулона в 1785 году. В этих экспериментах у него был небольшой фиксированный металлический шар, который он мог заряжать электричеством, и второй металлический шар, прикрепленный к лопасть, подвешенная на тонкой крученой нити.

Две сферы были заряжены, и из-за силы отталкивания между ними лопасть закручивалась на конце торсионной нити. Таким образом он смог точно измерить малые силы между зарядами и определить, как сила меняется в зависимости от количества заряда и расстояния между ними. 92}\label{1.5.2}\]

Здесь \(\эпсилон\) называется диэлектрической проницаемостью среды, в которой находятся заряды, и она меняется от среды к среде. Диэлектрическая проницаемость вакуума (или «свободного пространства») обозначается символом \(\epsilon_0\). Среды, отличные от вакуума, имеют диэлектрическую проницаемость немного больше, чем \(\epsilon_0\). Диэлектрическая проницаемость воздуха очень мало отличается от диэлектрической проницаемости свободного пространства, и, если не указано иное, я буду предполагать, что все эксперименты, описанные в этой главе, проводятся либо в свободном пространстве, либо в воздухе, так что я запишу закон Кулона как2}\label{1.5.3}\]

Вы можете задаться вопросом – почему множитель 4\(\pi\)? На самом деле очень удобно определять таким образом диэлектрическую проницаемость с 4\(\pi\) в знаменателе, потому что, как мы увидим, это гарантирует, что все формулы, описывающие ситуации сферической симметрии, будут включать 4\ (\pi\), формулы, описывающие случаи цилиндрической симметрии, будут включать 2\(\pi\), а \(\pi\) не будет появляться в формулах, включающих однородные поля. 2)\) , хотя это стандартная практика SI для определения диэлектрической проницаемости, как в уравнении \ref{1.5.3}. Диэлектрическая проницаемость, определяемая уравнением \ref{1.5.3}, известна как «рациональное» определение диэлектрической проницаемости, и оно приводит к гораздо более простым формулам в электромагнитной теории, чем «нерациональное» определение.

Единицей заряда в СИ является кулон , Кл. К сожалению, на данном этапе я не могу дать вам точное определение кулона, хотя, если в течение секунды протекает ток в 1 ампер, количество электрического заряда, текла 1 кулон. Поначалу это может показаться очень ясным, пока вы не поймете, что мы еще не определили, что подразумевается под усилителем, и, боюсь, это придется сделать в гораздо более поздней главе.

А пока я могу дать вам несколько небольших указаний. Например, заряд электрона составляет примерно -1,6022·10 9 .0060 -19 Кл, а заряд протона примерно +1,6022 х 10 ^-19 Кл. То есть совокупность 6,24 х 10 ¹⁸ протонов, если бы можно было как-то связать их все вместе и остановить моль протонов (т. е. 6,022 X 10 ²³ протонов), которые имели бы массу около одного грамма, имели бы заряд 9,65 X 10 ⁴. C, который также называют фарадея (что вовсе не то же самое, что фарад ).

[Современное определение кулона и ампера, которое будет дано в главе 6, требует некоторых знаний об электромагнетизме. Однако вполне вероятно, что в 2018 году кулон будет переопределен таким образом, что величина заряда одного электрона будет точно равна 1,60217 X 10 ^— ¹⁹ C.]

Заряды, задействованные в наших экспериментах с пробковыми шариками, стеклянными стержнями и электроскопами с сусальным золотом, очень малы в кулонах и обычно порядка нанокулонов. 9{-2}. \nonumber\]

Позже, когда мы узнаем, что подразумевается под «фарадами», мы будем использовать единицы F m ^-1 для описания диэлектрической проницаемости, но с этим придется подождать до раздела 5.2.

Вы можете спросить, как измеряется диэлектрическая проницаемость свободного пространства.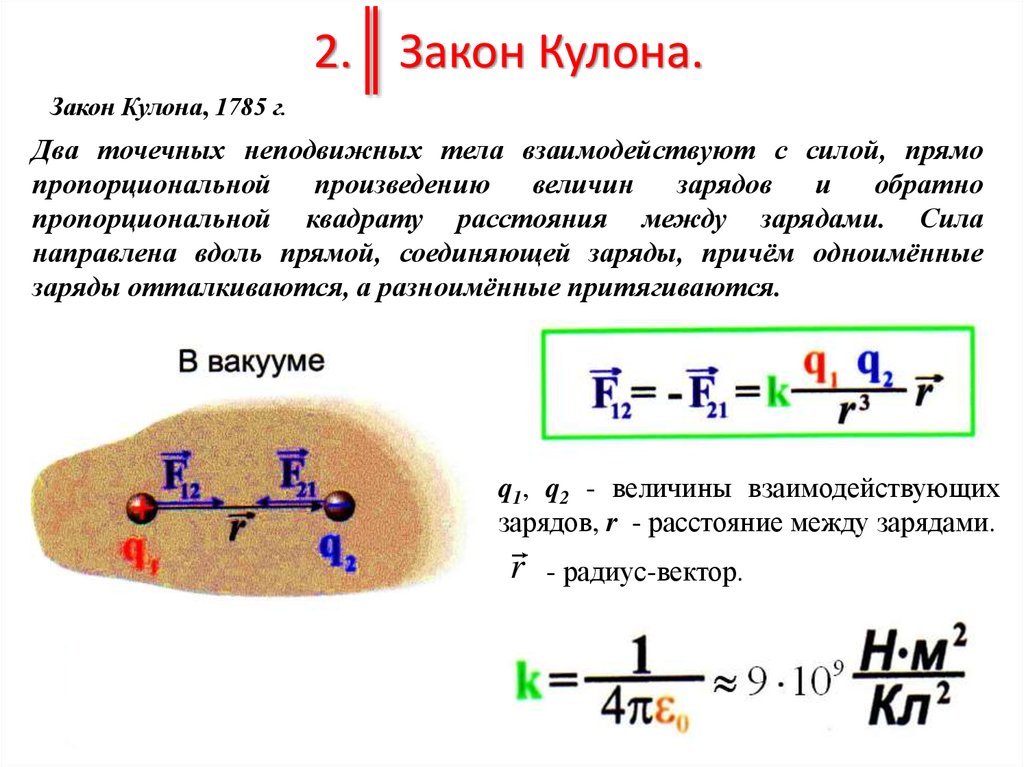 Краткий ответ мог бы звучать так: «путем проведения экспериментов, подобных экспериментам Кулона». Однако — и это довольно длинная история, которую я не буду здесь описывать — получается, что поскольку мы сегодня определяем метр через , определяя 92}\nonumber\]

Поэтому нет необходимости измерять \(\epsilon_0\) больше, чем необходимо измерять c . Но это, как я уже сказал, долгая история.

С точки зрения размерного анализа электрический заряд не может быть выражен в терминах M, L и T, но он имеет собственную размерность Q. (Некоторые оспаривают это утверждение, но здесь не место обсуждать причины. В конце концов, я могу добавить главу, обсуждающую этот вопрос гораздо позже.) Мы говорим, что размеры электрического заряда равны Q.

Я настоятельно советую читателю прорабатывать и записывать размеры каждой новой электрической или магнитной величины по мере ее введения.

тонна или почти миллион тонн.

В
раз сильнее гравитационных сил – но такое утверждение вне контекста довольно бессмысленно. Например, гравитационная сила между Землей и Луной намного больше, чем электростатическая сила (если она вообще есть) между ними, и космологи могут привести веские основания утверждать, что самые сильные силы во Вселенной — гравитационные.
Отношение диэлектрической проницаемости изолирующего вещества к диэлектрической проницаемости свободного пространства равно его относительной диэлектрической проницаемости , также называемой его диэлектрической проницаемостью. Диэлектрические постоянные многих широко распространенных изоляционных материалов имеют порядок «несколько». То есть где-то между 2 и 10. У чистой воды диэлектрическая проницаемость около 80, что довольно много (но имейте в виду, что большая часть воды далека от чистой и не является изолятором). Некоторые особые вещества, известные как сегнетоэлектрические вещества, такие как титанат стронция SrTiO ₃ , имеют диэлектрическую проницаемость в несколько сотен.
Эта страница под названием 1. 5: Закон Кулона распространяется под лицензией CC BY-NC 4.0 и была создана, изменена и/или курирована Джереми Тейтумом посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
Наверх
Была ли эта статья полезной?
Тип изделия
Раздел или Страница
Автор
Джереми Татум
Лицензия
CC BY-NC
Версия лицензии
4,0
Показать оглавление
нет
Теги
Закон Кулона
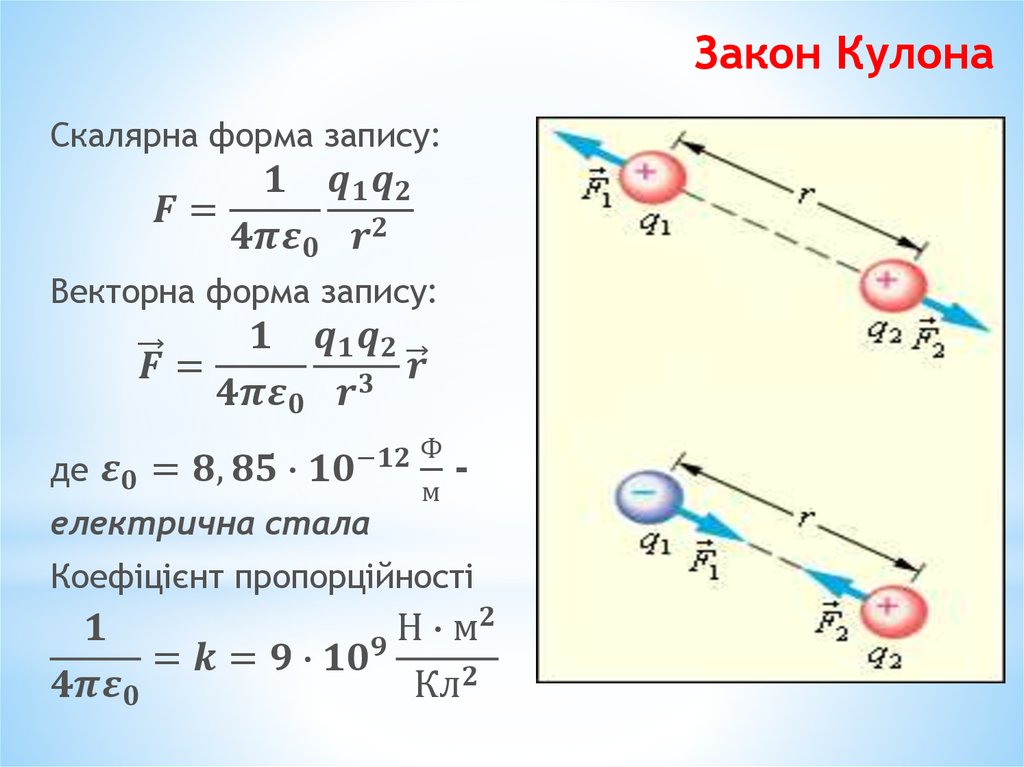
источник@http://orca. р ₁₂ — единичный вектор, направленный от заряда q ₁ к заряду q ₂ k — константа пропорциональности.

Важные аспекты Закон Кулона
(i) Закон Кулона гласит что электростатическая сила прямо пропорциональна произведению величина двух точечных зарядов и обратно пропорциональна квадрату расстояния между двумя точечными зарядами. 9₁₂ ).
(iii) В единицах СИ, и его значение равно 9 × 10 ⁹ Н·м ² С ^-2 . Здесь ε — диэлектрическая проницаемость свободного пространства или вакуум и значение

(iv) Величина электростатическая сила между двумя зарядами в один кулон каждый и разделенными на расстояние 1 м вычисляется следующим образом:

Это огромное количество, почти эквивалентно весу одного миллиона тонн. Мы никогда не встретим 1 кулон заряда на практике. Большинство электрических явлений в повседневной жизни жизни связаны электрические заряды порядка µC (микрокулон) или nC (нано кулон).
(v) В единицах СИ, Закон Кулона в вакууме принимает вид В среде диэлектрической проницаемости ε, сила между двумя точечными зарядами определяется выражением
Поскольку ε>ε _o , сила между двумя точечными зарядами в среда, отличная от вакуума, всегда меньше, чем в вакууме. Мы определяем относительная диэлектрическая проницаемость для данной среды как ε _r >ε/ε _o . За вакуум или воздух, ε _r = 1 и ε для всех остальных сред ε _r > 1.
(vi) Закон Кулона имеет ту же структуру, что и закон всемирного тяготения Ньютона. Оба обратно пропорциональны квадрату расстояния между частицами. Электростатическая сила прямо пропорциональна произведению величина двух точечных зарядов и гравитационной силы прямо пропорциональна произведению двух масс. Но есть некоторые важные различия между эти два закона.
· Гравитационная сила между двумя массами всегда притягивает но кулоновская сила между двумя зарядами может быть притягивающей или отталкивающей, в зависимости о характере обвинений.
· Значение гравитационной постоянной G = 6,626 × 10 ^-11 Н·м ² кг ^-2 . Значение константы k в законе Кулона равно k = 9 × 10 ⁹ Н·м ² C ^-2 . Так как k намного больше больше, чем G, электростатическая сила всегда больше по величине, чем гравитационная сила для объектов меньшего размера.
· Сила гравитации между двумя массами не зависит от середина. Например, если 1 кг двух масс находится в воздухе или в воде, то гравитационная сила между двумя массами остается неизменной. Но электростатический сила между двумя зарядами зависит от природы среды, в которой они находятся. заряды остаются в покое. 9 r ₁₂ ,

Следовательно, Электростатическая сила подчиняется третьему закону Ньютона.
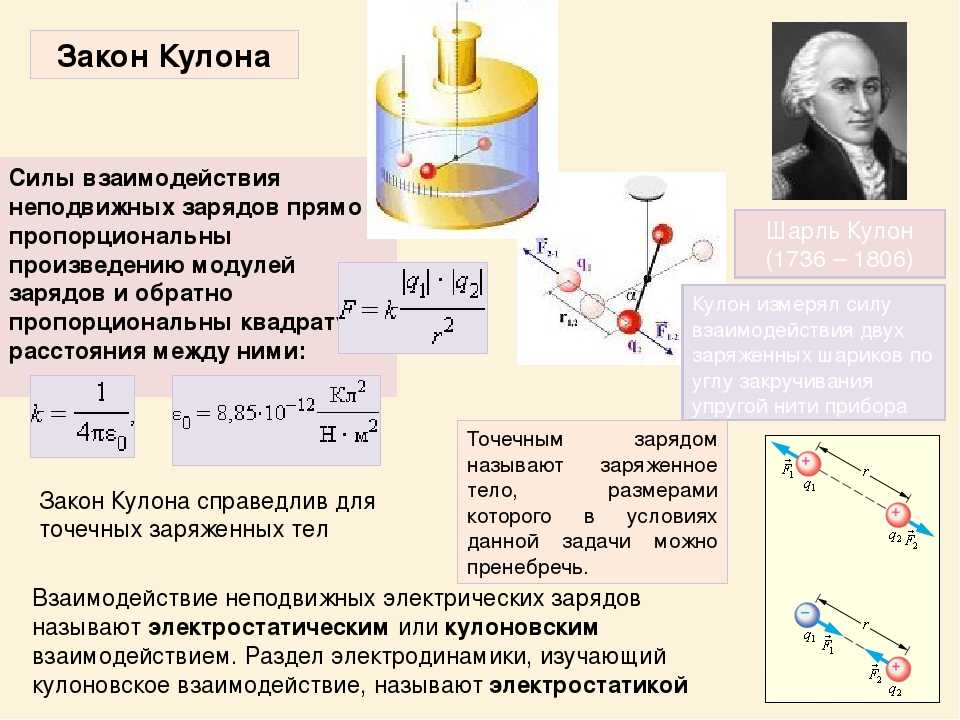
(viii) Выражение для кулоновской силы справедливо только для точечных зарядов. Но точечный заряд идеальная концепция. Однако мы можем применить закон Кулона для двух заряженных тел, размеры намного меньше, чем расстояние между ними. В самом деле, Кулон открыл свой закон, рассматривая заряженные сферы на крутильных весах как точечные сборы. Расстояние между двумя заряженными сферами намного больше чем радиусы сфер.

ПРИМЕР 1.2
Рассмотрим две точки заряжает q1 и q2 в состоянии покоя, как показано на рисунке.

Они разделены расстояние 1м. Определить силу, действующую на два заряда при следующих случаях:
(a) q ₁ = +2 мкКл и q ₂ = +3 мкКл
(б) q ₁ = +2 мкКл и q ₂ = -3 мкКл
(в) q ₁ = +2 мкКл and q ₂ = -3μC kept in water (ε _r = 80)
Solution

EXAMPLE 1.3
Два небольших размера одинаковые одинаково заряженные шары, каждый массой 1 мг висят на равновесие, как показано на рисунке. Длина каждой нити 10 см. угол θ составляет 7° с вертикалью. Вычислите величину заряда в каждом сфера.
(Примите g = 10 мс ⁻² )

Решение
Если две сферы нейтральный, угол между ними будет 0° при вертикальном подвешивании. С тех пор они являются положительно заряженными сферами, между ними будет действовать сила отталкивания и они будут находиться в равновесии друг с другом под углом 7° к вертикальный. В состоянии равновесия каждый заряд испытывает нулевую результирующую силу в каждом направление. Мы можем нарисовать диаграмму свободного тела для одной из заряженных сфер и применять второй закон Ньютона как для вертикального, так и для горизонтального направлений.
Схема свободного тела показано ниже.

В направлении x ускорение заряженной сферы равно нулю.

Здесь T — натяжение, действующее на заряд струны, а F _e — электростатическая сила между два обвинения.
В направлении Y также сеть ускорение, испытываемое зарядом, равно нулю.

ПРИМЕР 1.4
Рассчитайте электростатическая сила и гравитационная сила между протоном и электроном в атоме водорода. Расстояние между ними 5,3 × 10 ^-11. м. Величина зарядов электрона и протона составляет 1,6 × 10 ^-19. C. Масса электрона m _e = 9,1 × 10 ^-31 кг, а масса протона m _p = 1,6 × 10 ^-27 кг.
Решение
Протон и электроны притягиваются друг к другу. Величина электростатической силы между эти две частицы задаются как

Гравитационная сила между протон и электрон притягиваются. Величина гравитационной силы между этими частицами

Электростатическая сила между протона и электрона неизмеримо больше, чем гравитационная сила между ними. Таким образом, гравитационная сила пренебрежимо мала по сравнению с электростатическая сила во многих ситуациях, например, для объектов небольшого размера и в атомный домен. Вот почему заряженная расческа притягивает незаряженную. лист бумаги с большей силой, даже если лист бумаги притягивается вниз по Земле. Это показано на рис. 1.3

1. Принцип суперпозиции
Закон Кулона объясняет взаимодействие двух точечных зарядов. Если зарядов больше двух, сила, действующая на один заряд из-за всех других зарядов, должна быть рассчитана. Один только закон Кулона не дает ответа. Принцип суперпозиции объясняет взаимодействие между несколькими зарядами.
В соответствии с этим принцип суперпозиции, 9 р ₂₁ — единичный вектор от q ₂ до q ₁ вдоль линии, соединяющей два заряда и r ₂₁ расстояние между зарядами q ₁ и q ₂ . Электростатическая сила между двумя зарядами не изменяется наличием поблизости других зарядов.
Усилие на q ₁ вызванный зарядом q ₃ is

Продолжая это, полная сила, действующая на заряд q ₁ в связи со всеми другими расходами.

ПРИМЕР 1.5
Рассмотрим четыре равных заряды q ₁ ,q ₂ , q ₃ и q ₄ = q = +1 мкКл расположенных в четырех разных точках на окружности радиусом 1 м, как показано на фигура. Вычислите общую силу, действующую на заряд q ₁ за счет всех остальные обвинения.

Раствор
Согласно принцип суперпозиции, полная электростатическая сила, действующая на заряд q1, равна векторная сумма сил других зарядов,

Следующая диаграмма показывает направление каждой силы, действующей на заряд q ₁ .

Сборы q ₂ и q ₄ равноудалены от q ₁ . В результате силы (величина) сил и являются то же самое, хотя их направления различны. Поэтому векторы представляющие эти две силы, нарисованы с одинаковой длиной. Но заряд q ₃ расположен дальше по сравнению с q ₂ и q ₄ .