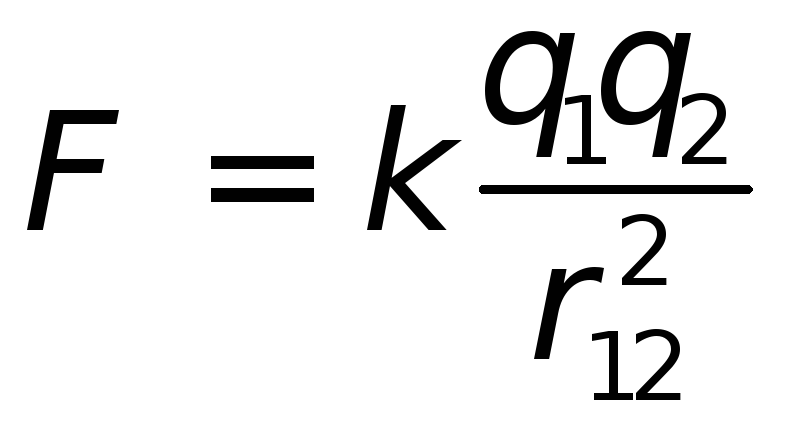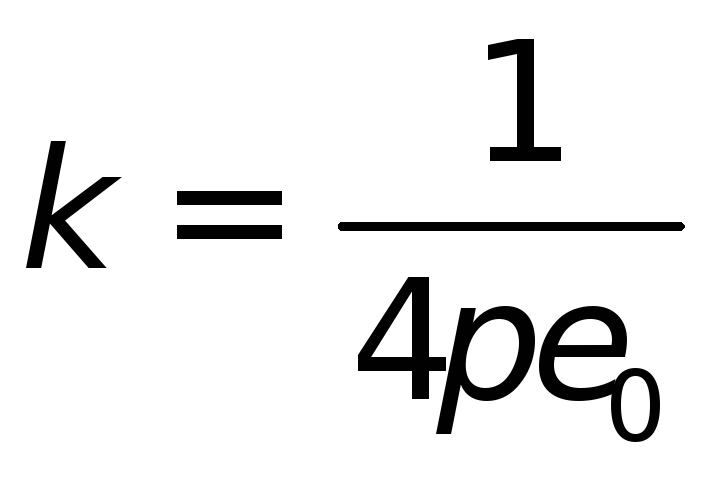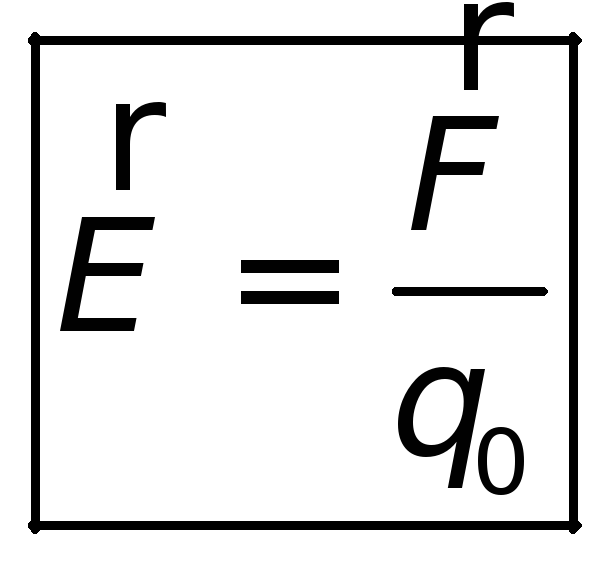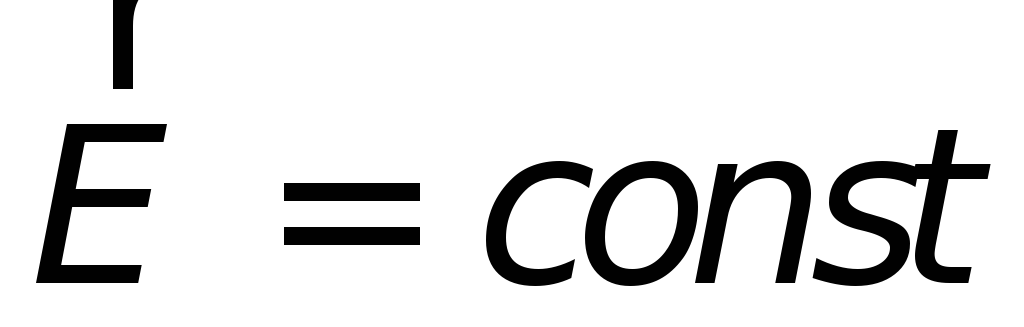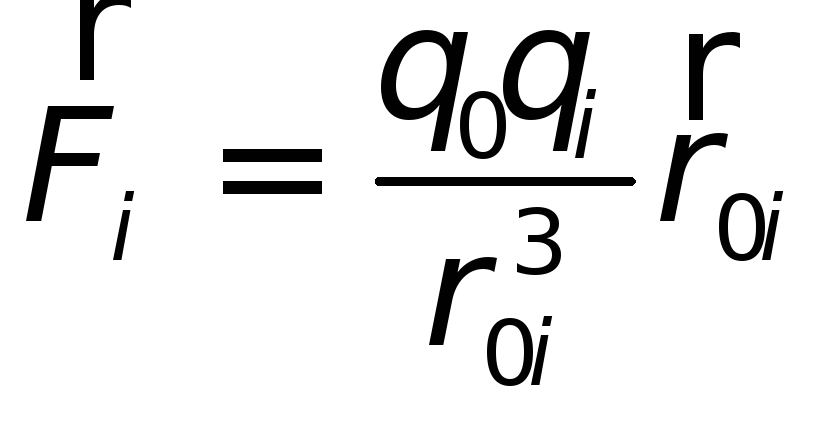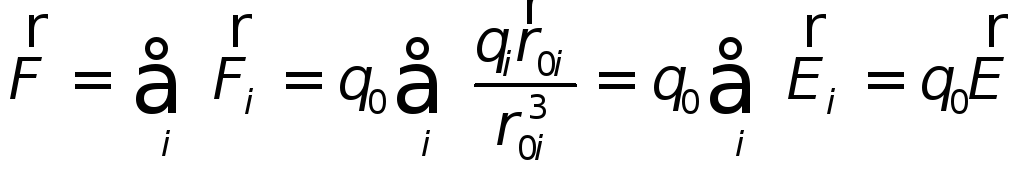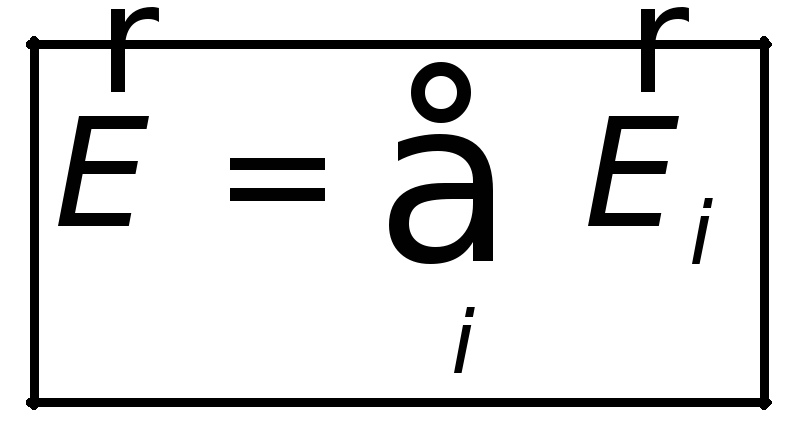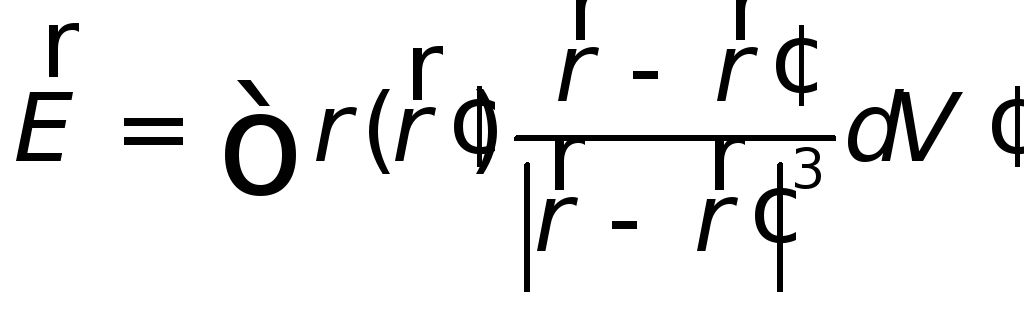22.Закон Кулона, напряженность электрического поля, закон суперпозиции
В
природе существуют только два вида
зарядов – положительные и отрицательные.
Заряды одного знака отталкиваются,
заряды разных знаков (разноимённые
заряды) притягиваются. Элементарный
отрицательный заряд равен по величине
элементарному положительному заряду.
В системе СИ заряд измеряется в кулонах
(Кл). Величина элементарного заряда e =1,6∙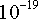 Кл.
Кл.
В 1785 г. Шарль Кулон (1736-1806) экспериментально установил закон взаимодействия двух точечных зарядов, т.е. таких заряженных тел, размерами которых в данной задаче можно пренебречь. Этот закон гласит: сила взаимодействия двух точечных зарядов прямо пропорциональна произведению этих зарядов, обратно пропорциональна квадрату расстояния между ними и направлена по линии, соединяющей эти заряды.
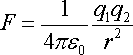 , (1.2),
где
, (1.2),
где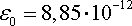 Кл²/Н·м²
(Ф/м) – электрическая постоянная. В
диэлектрике сила взаимодействия двух
точечных зарядов:
Кл²/Н·м²
(Ф/м) – электрическая постоянная. В
диэлектрике сила взаимодействия двух
точечных зарядов: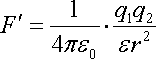 (1.3), где
(1.3), где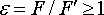 —
диэлектрическая проницаемость
диэлектрика. Она показывает во сколько
раз сила кулоновского взаимодействия
в диэлектрике меньше, чем в вакууме.
Взаимодействие между зарядами на
расстоянии осуществляется через
электрическое поле.
—
диэлектрическая проницаемость
диэлектрика. Она показывает во сколько
раз сила кулоновского взаимодействия
в диэлектрике меньше, чем в вакууме.
Взаимодействие между зарядами на
расстоянии осуществляется через
электрическое поле.Электрическое поле – это одна из форм материи. Оно обладает свойством действовать на внесённые в него заряды с некоторой силой. Электрическое поле является составной частью электромагнитного поля. Поле, окружающее неподвижные заряды, называется электростатическим.
Представление об электрическом поле было введено в науку в 30-х годах ХIХ века Майклом Фарадеем (1791-1867). Согласно Фарадею, каждый электрический заряд окружён созданным им электрическим полем. Будем помещать в точку М поля заряда q различные пробные заряды (рис. 1.2).

Рис.1.2
На каждый из них электрическое поле действует с различными силами.
Но если величину каждой силы разделить на соответствующее ей значение пробного заряда, то получим одно и то же значение, характерное для точки М этого поля. То есть эта величина может служить силовой характеристикой электрического поля в точке М. Она называется напряжённостью электрического поля: E = F/qпр. (1.4)
Напряжённость электрического поля – векторная величина. Напряжённость не зависит от наличия или отсутствия в данном поле пробных зарядов. Она зависит от свойств самого поля, которое определяется зарядом – источником, расстоянием от него до точки поля, в которой измеряется напряжённость, и средой, в которой создано поле. В системе СИ напряжённость электрического поля измеряется в вольтах на метр (В/м).
Пусть
имеется положительный точечный заряд
– источник поля Q. Поместим в некоторую
точку поля M этого заряда положительный
пробный заряд qпр.
На этот заряд будет действовать сила: 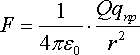 .
(1.5)
.
(1.5)
Тогда
напряжённость поля, создаваемого
точечным зарядом Q в точке M,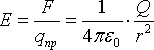
Если
заряд Q окружает среда с диэлектрической
проницаемостью ε,
то напряжённость создаваемого им поля
: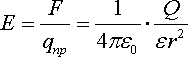 (1.7)
(1.7)
Электрическое поле, напряжённость которого в каждой точке одинакова по величине и направлению, называется однородным. Силовыми линиями однородного поля являются параллельные прямые, расположенные на одинаковом расстоянии друг от друга. Электрическое поле точечного заряда неоднородно.
Если на электрический заряд q одновременно действуют электрические поля нескольких зарядов, то результирующая сила равна геометрической сумме сил, действующих со стороны каждого поля в отдельности. Это называется
1. Закон Кулона. Напряженность электрического поля. Принцип суперпозиции (теория, вопросы, упражнения)
1. Согласно современным представлениям, электрическое взаимодействие между телами осуществляется посредством электромагнитных полей. Свойство тела создавать в окружающем пространстве электромагнитное поле количественно характеризуется скалярной физической величиной называемой
Точечными зарядами называются заряженные тела, размеры которых малы по сравнению с расстояниями между телами (т.е. в области пространства,
Пробными зарядаминазываются заряженные тела, внесение которых в электрические поля других тел не приводит к их искажению (т.е. величина заряда настолько мала, что не приводит к смещению зарядов на окружающих телах).
2. Закон Кулона определяет силы
взаимодействия двух неподвижных точечных
зарядов  и
и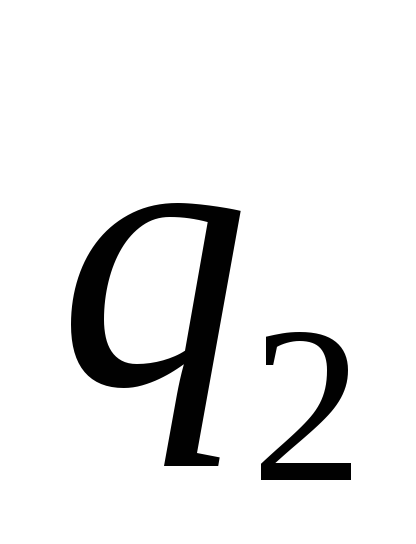 ,
расположенных на расстоянииr12друг от друга
,
расположенных на расстоянииr12друг от друга
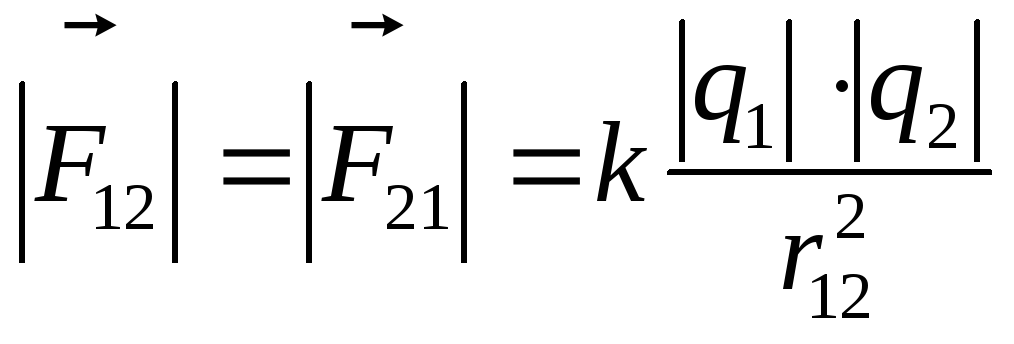 .
. Здесь 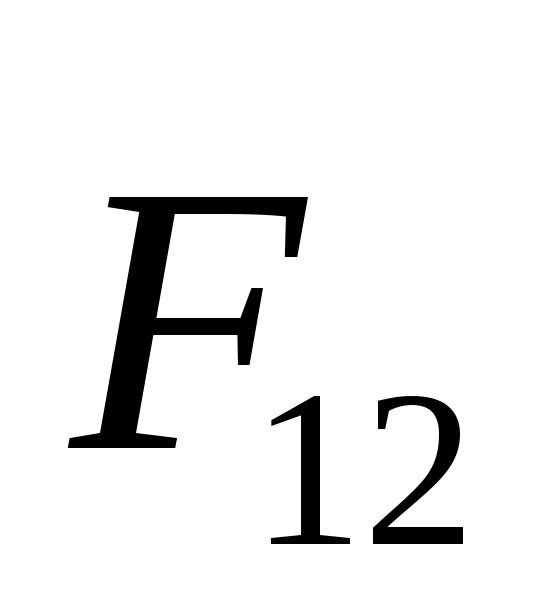 —
сила, действующая на первый заряд со
стороны второго,
—
сила, действующая на первый заряд со
стороны второго,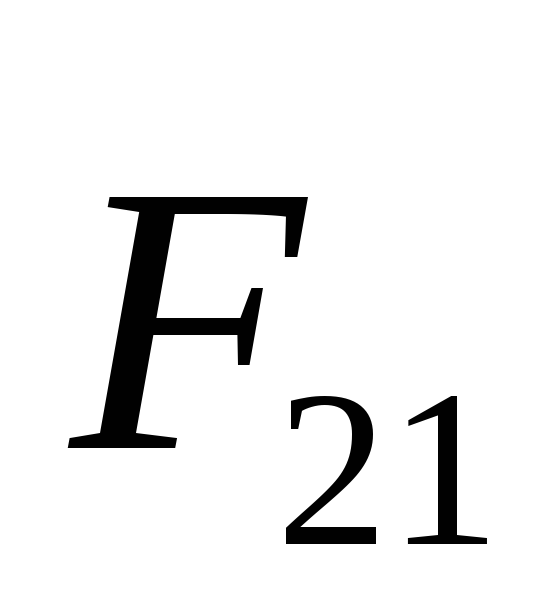 —
сила, действующая на второй заряд со
стороны первого (эти силы удовлетворяют
третьему закону Ньютона, т.е. являются
силами действия и противодействия).
Величины сил пропорциональны величинам
зарядов
—
сила, действующая на второй заряд со
стороны первого (эти силы удовлетворяют
третьему закону Ньютона, т.е. являются
силами действия и противодействия).
Величины сил пропорциональны величинам
зарядов и
и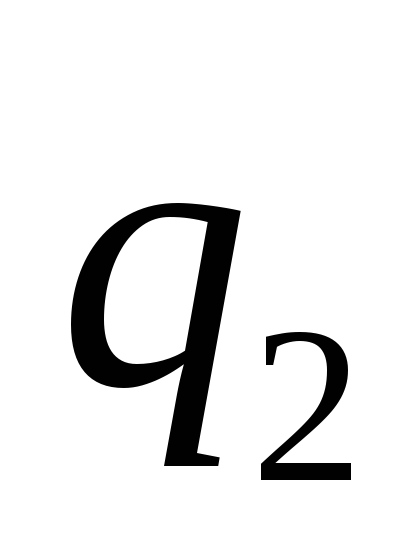
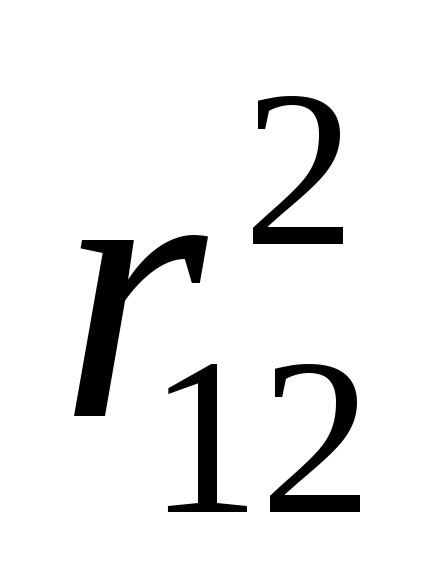 —
квадрату расстояния между ними. Силы
всегда направлены вдоль прямой,
соединяющей эти заряды. Они являются
силами притяжения, если знаки зарядов
противоположны и силами отталкивания,
если знаки зарядов одинаковы (см. рис.1).
Свойства сил взаимодействия точечных
зарядов отражает векторная форма закона
Кулона:
—
квадрату расстояния между ними. Силы
всегда направлены вдоль прямой,
соединяющей эти заряды. Они являются
силами притяжения, если знаки зарядов
противоположны и силами отталкивания,
если знаки зарядов одинаковы (см. рис.1).
Свойства сил взаимодействия точечных
зарядов отражает векторная форма закона
Кулона: 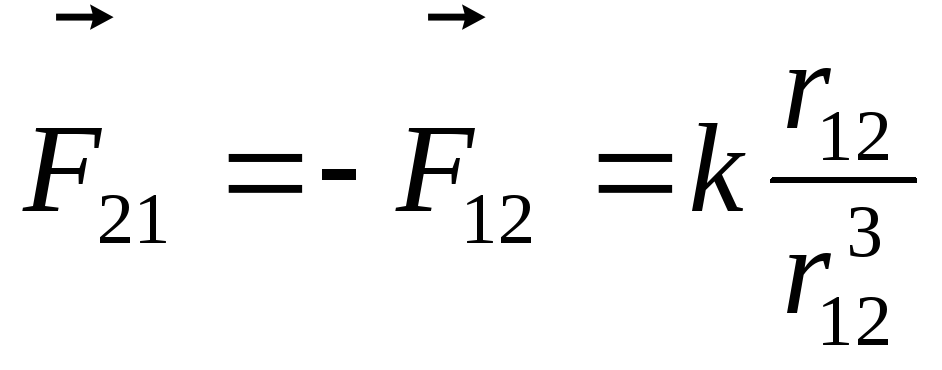
|
Рис.1 |
В системе СИ коэффициент кв законе Кулона с учетом единицы заряда принято представлять в виде:
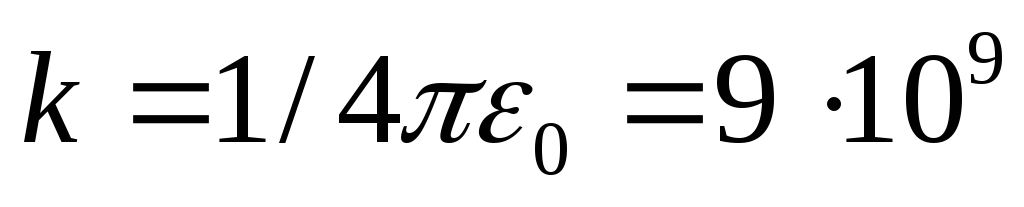 Нм2/Кл2
Нм2/Кл2
где  -электрическая
постоянная.
-электрическая
постоянная.
Упражнение 1.
Покажите, как можно количественно сравнить электрические заряды двух тел.
Решение:
Пусть q1 иq2величины зарядов электрических тел, которые необходимо сравнить. Возьмем третье заряженное тело, заряд которого обозначим
 и
и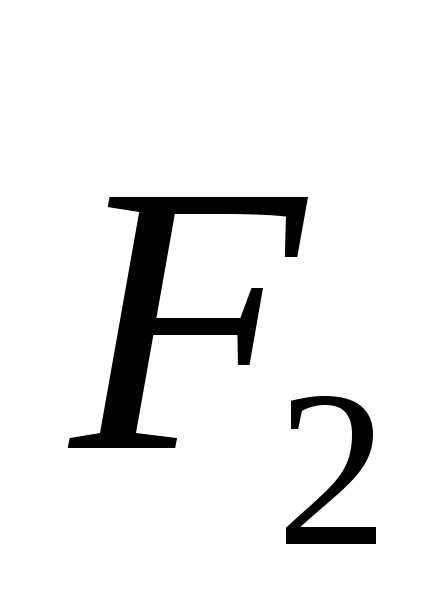 ,
с которыми сравниваемые заряды будут
взаимодействовать последовательно с
зарядомQ, на
основании закона Кулона утверждаем,
что
,
с которыми сравниваемые заряды будут
взаимодействовать последовательно с
зарядомQ, на
основании закона Кулона утверждаем,
что  и
и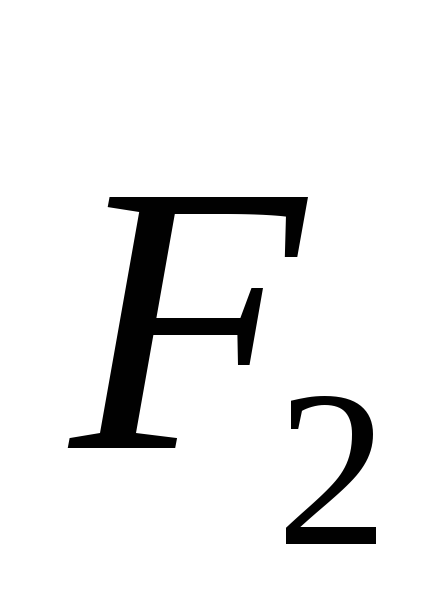
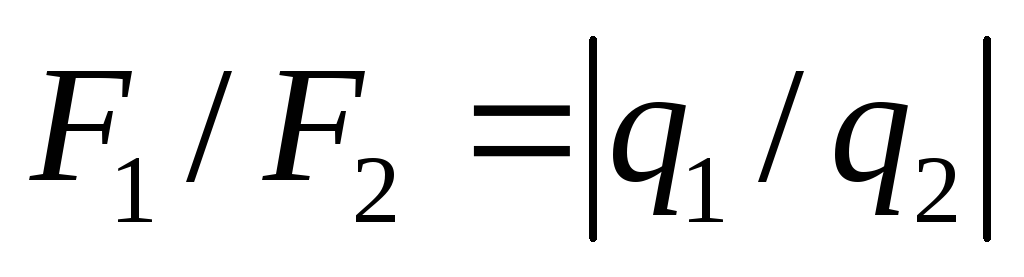 не зависит ни от расположения зарядаQ ни от его величины. Поэтому отношение F1/F2 служит мерой самих пробных зарядов,
причем, если направления сил
не зависит ни от расположения зарядаQ ни от его величины. Поэтому отношение F1/F2 служит мерой самих пробных зарядов,
причем, если направления сил и
и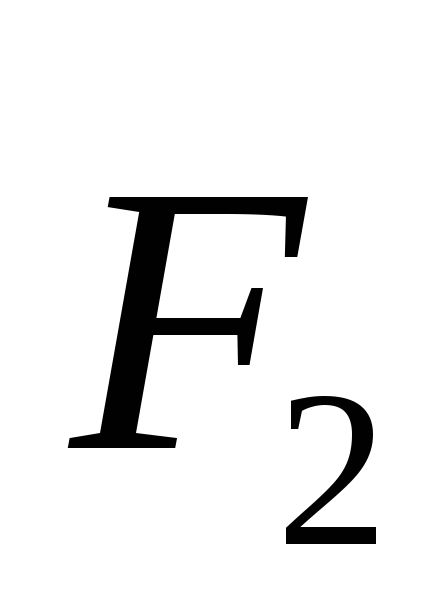 совпадают,
алгебраические знаки зарядов совпадают.
совпадают,
алгебраические знаки зарядов совпадают.3. Исследования взаимодействия заряженных тел выявили следующие фундаментальные свойства зарядов:
— Электрический заряд существует в двух формах — он может быть положительным или отрицательным.
— Электрический заряд подчиняется закону сохранения: полный электрический заряд системы тел остается неизменным, если заряженные тела не пересекают поверхность, ограничивающую эту систему. При этом неизменным остается только полный заряд, а не положительный и отрицательный в отдельности. Например, при рождении пары электрон – позитрон в системе возникают заряды, но полный заряд сохраняется.
— Электрический заряд – величина релятивистки инвариантная: величина заряда любого тела не зависит от того, как это тело движется.
— В природе существует минимальный по величине заряд. Его называют элементарным и обозначают e. Любой электрический заряд кратен элементарному заряду
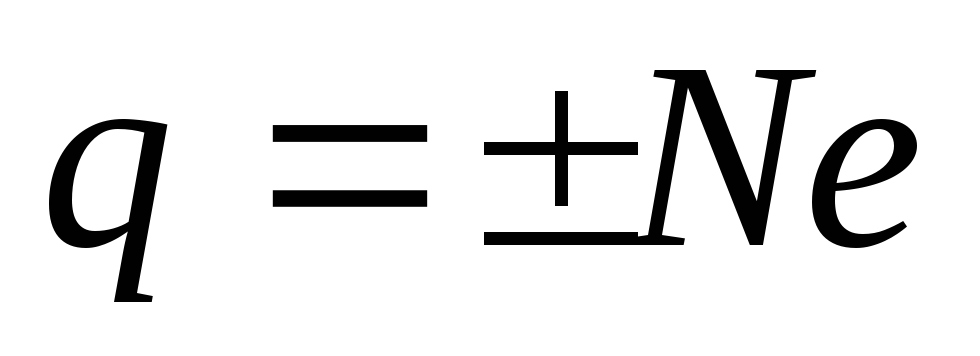 (
(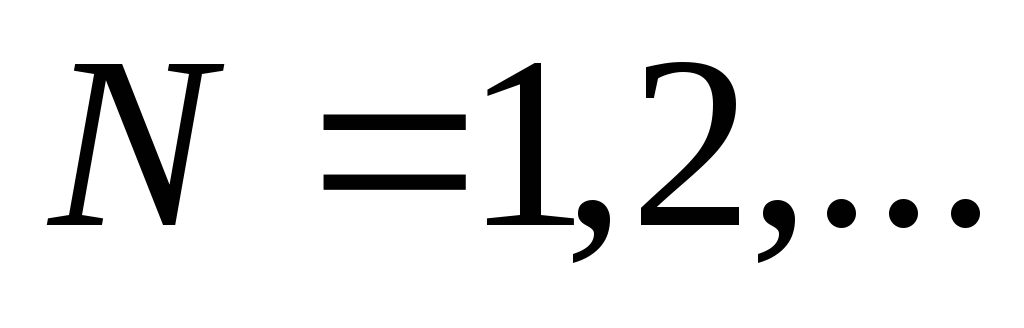 )
)
То, что 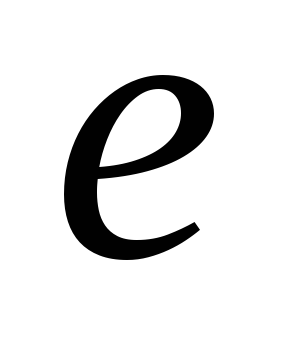 является естественной единицей измерения
заряда, по историческим причинам не
было использовано, и в системе СИ за
единицу заряда была выбрана величина,
равная 6,2418
является естественной единицей измерения
заряда, по историческим причинам не
было использовано, и в системе СИ за
единицу заряда была выбрана величина,
равная 6,2418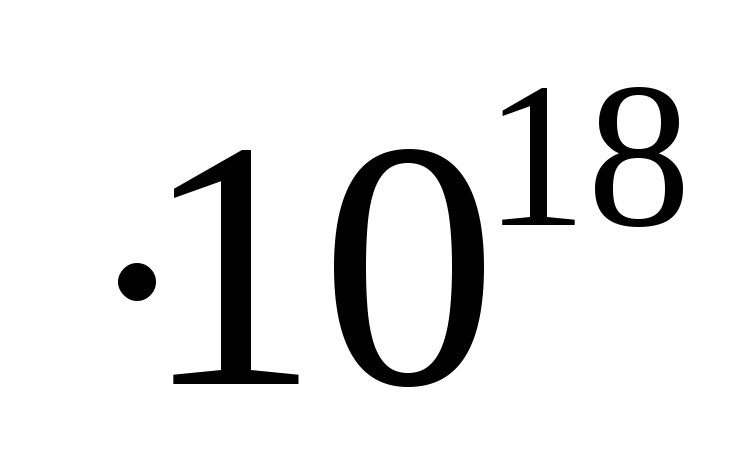
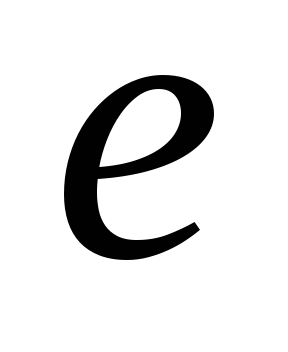 и получившая название кулон. Поэтому
для величины элементарного заряда
получим:
и получившая название кулон. Поэтому
для величины элементарного заряда
получим:
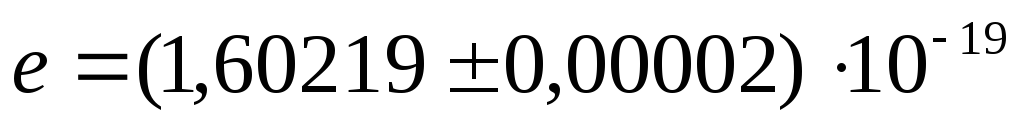 Кл
Кл
Упражнение 2.
Найдите силу, с которой точечный заряд Q будет действовать
на точечный заряд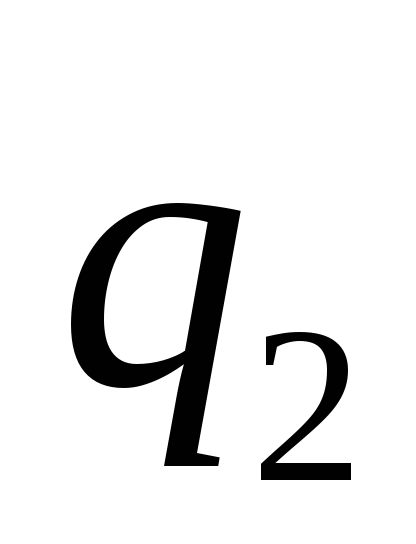 ,
если на точечный заряд
,
если на точечный заряд ,
помещенный в ту же точку пространства
он действует с силой
,
помещенный в ту же точку пространства
он действует с силой .
.
Решение:
Построив вектор 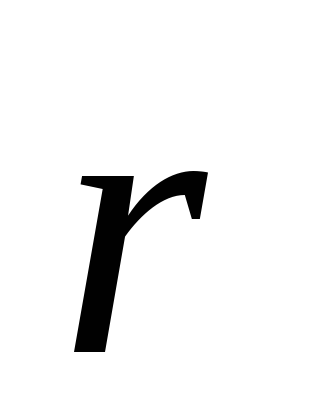 из
точки нахождения заряда
из
точки нахождения заряда в
точку помещения зарядаq2 , запишем выражение для силы
в
точку помещения зарядаq2 , запишем выражение для силы 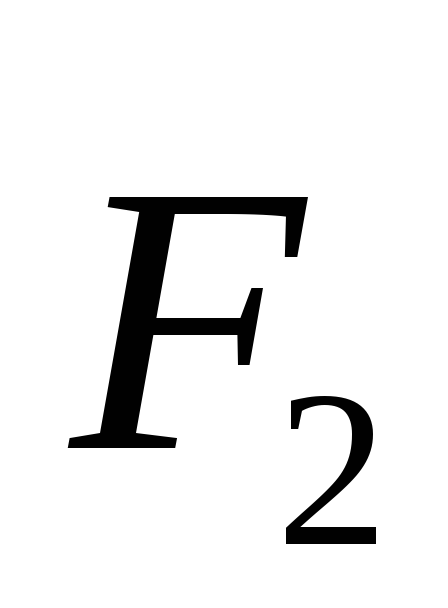 на основе закона Кулона
на основе закона Кулона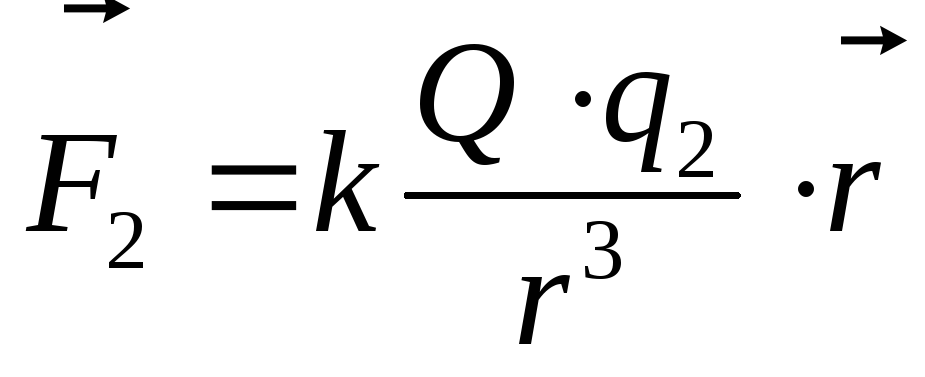 .
Аналогично для заряда
.
Аналогично для заряда ,
помещенного в ту же самую точку,
,
помещенного в ту же самую точку,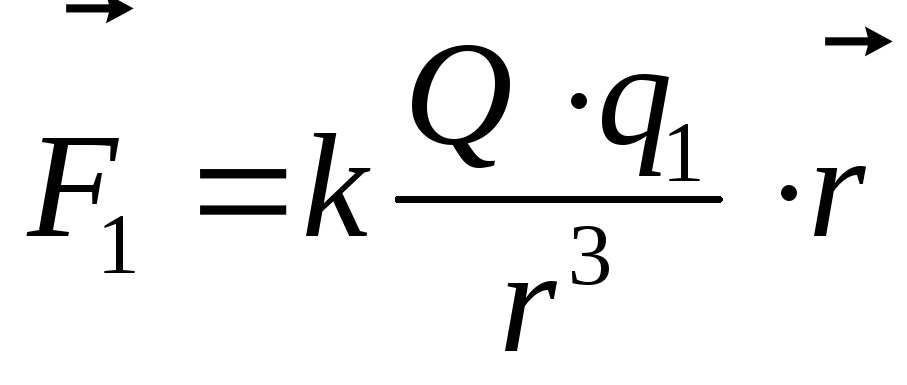 и, сравнивая выражения для этих сил,
получим
и, сравнивая выражения для этих сил,
получим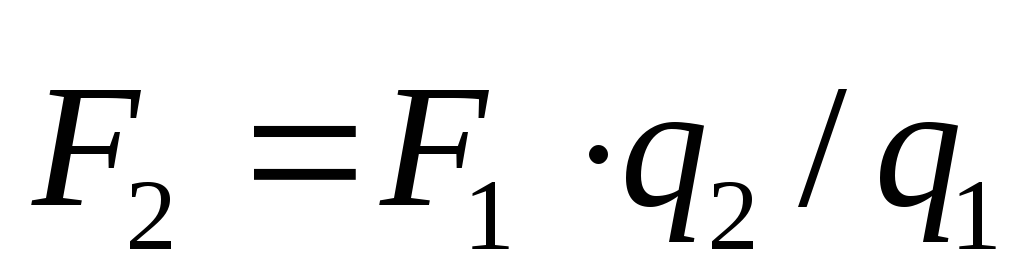 .
.
4. Векторная физическая величина, модуль
которой численно равен силе, действующей
на единичный положительный неподвижный
пробный заряд, помещенный в некоторой
точке наблюдения, а направление совпадает
с направлением этой силы, называется напряженностью электрического поляв рассматриваемой точке и обозначается
вектором ,
,
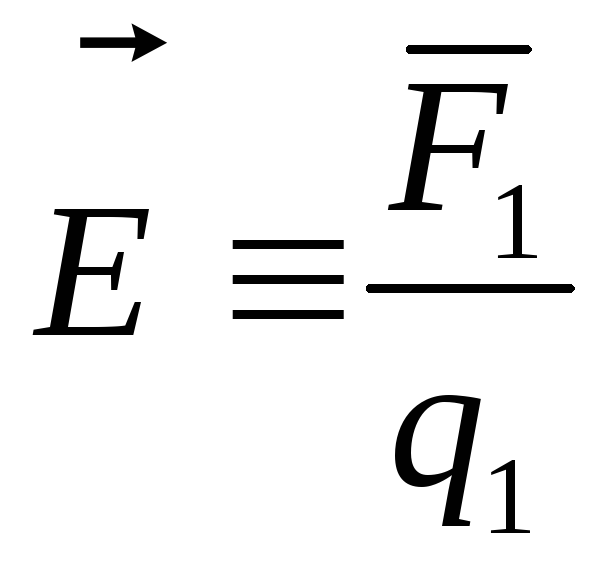
Силу, действующую на любой точечный заряд q, покоящийся в поле, представим в векторном виде:
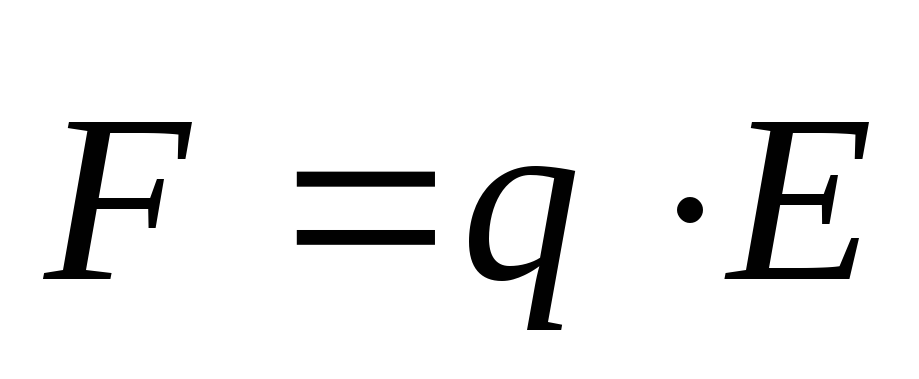

Упражнение 3:
Найдите напряженность электрического поля точечного заряда Q.
Решение:
Поместим вблизи заряда Q точечный заряд q,
в положение, задаваемое вектором 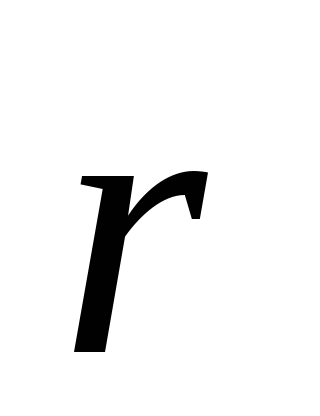 относительно зарядаQ,
как показано на рис.2. Силу, действующую
на заряд q, запишем
в векторной форме как:
относительно зарядаQ,
как показано на рис.2. Силу, действующую
на заряд q, запишем
в векторной форме как: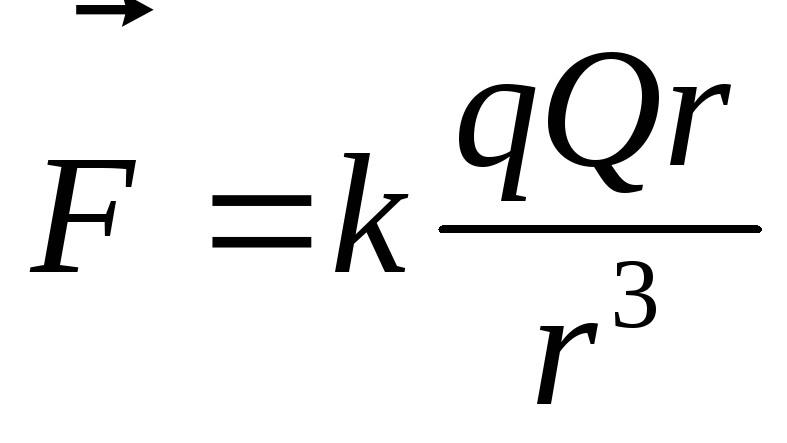 .
.
|
Рис.2 |
Напряженность электрического поля
точечного заряда в рассматриваемой
точке равна 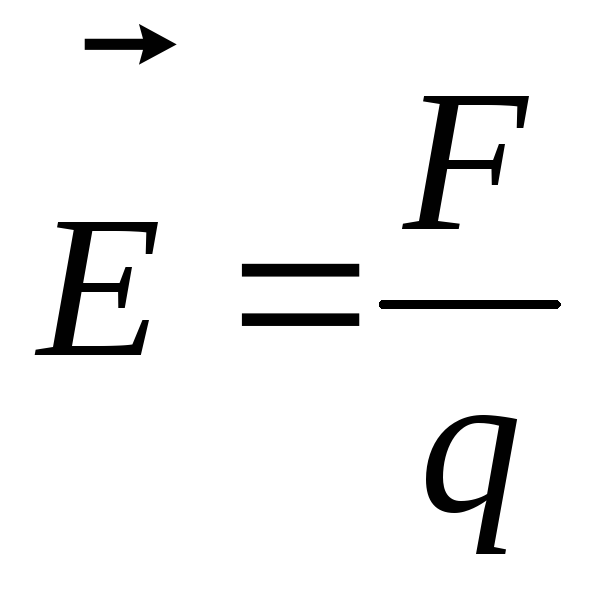 ,
откуда:
,
откуда:
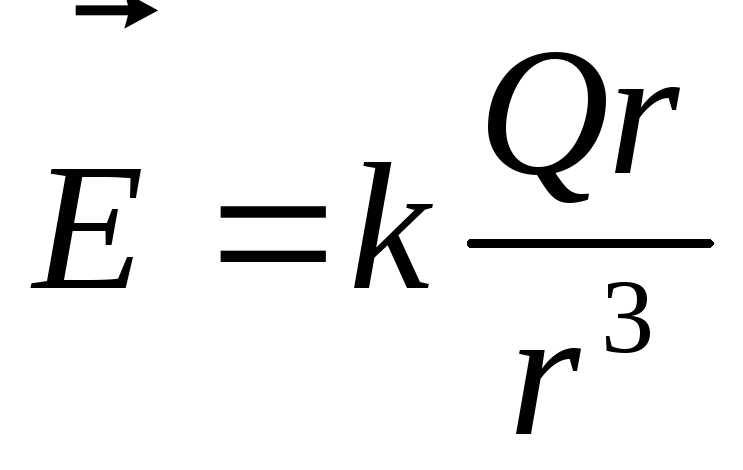
5. Сила, действующая на заряд qсо стороны нескольких зарядов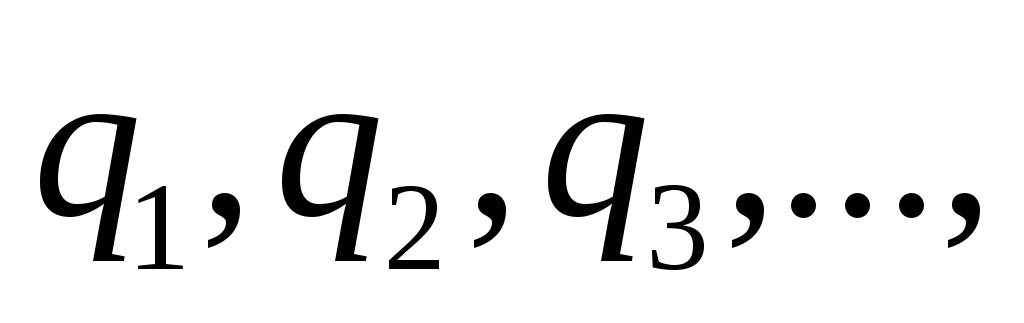 равна
векторной сумме сил:
равна
векторной сумме сил:
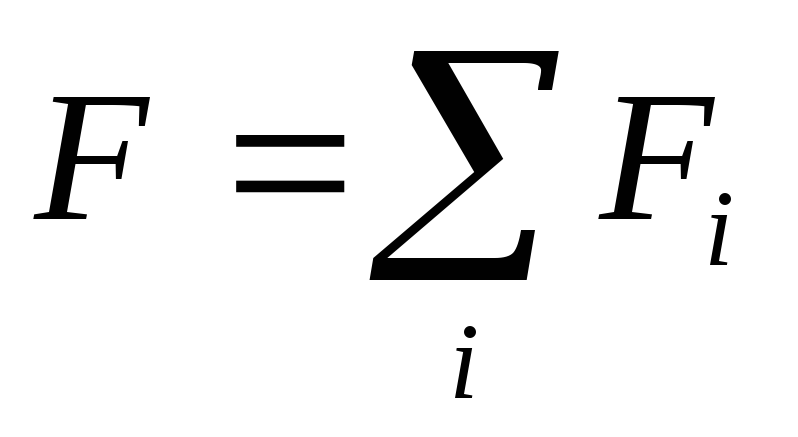
или на языке напряженностей: 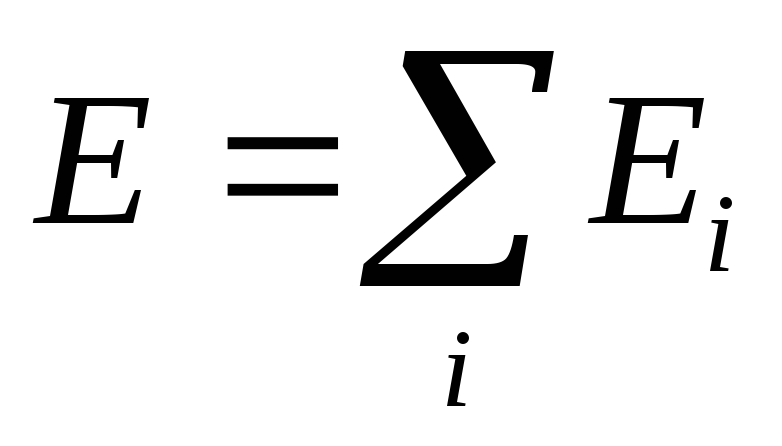 ,
,
где 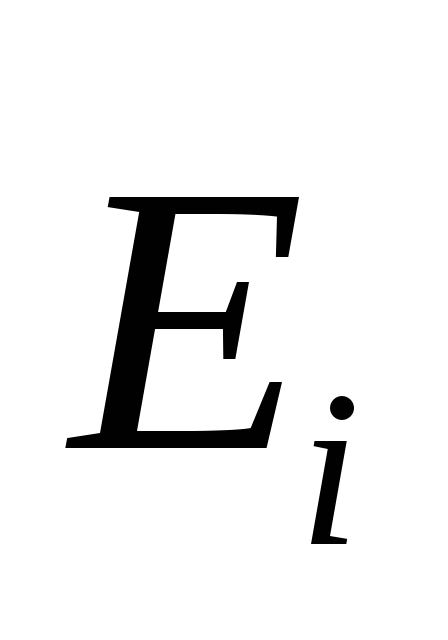 -полеi-го заряда в точке
нахождения зарядаq.
Этот закон, называемыйпринципом
суперпозиции, фактически утверждает,
что сила взаимодействия двух точечных
зарядов не зависит от наличия в их
окрестности других заряженных тел.
-полеi-го заряда в точке
нахождения зарядаq.
Этот закон, называемыйпринципом
суперпозиции, фактически утверждает,
что сила взаимодействия двух точечных
зарядов не зависит от наличия в их
окрестности других заряженных тел.
6. Часто распределение зарядов на телах
описывается непрерывным распределением
электричества. Распределение электричества
по объему пространства задается пространственной плотностью заряда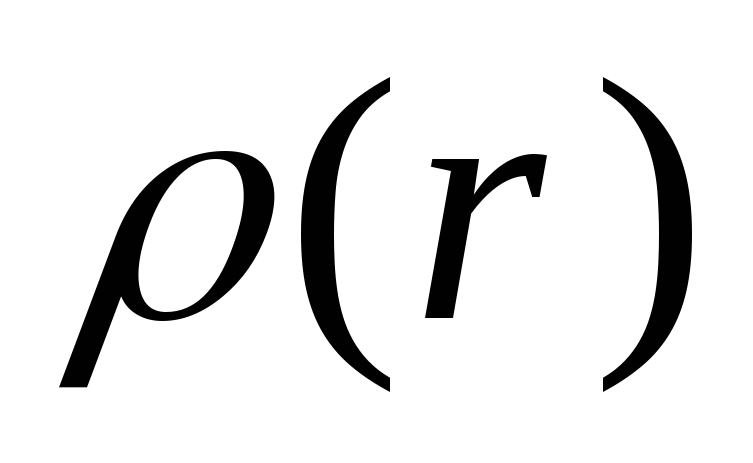 ,
по поверхности —поверхностной
плотностью заряда
,
по поверхности —поверхностной
плотностью заряда ,
вдоль линии –линейной плотностью
заряда
,
вдоль линии –линейной плотностью
заряда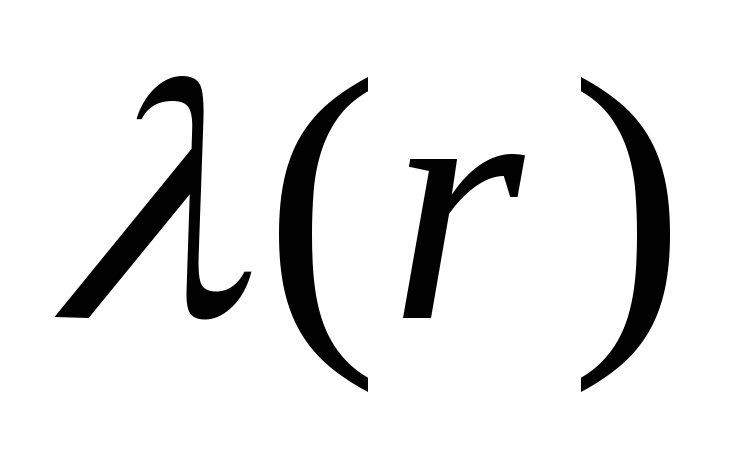 :
:
dq = ρ dV, dq = σ dS , dq = λ dl.
7. Для графического изображения векторных полей используют силовые линии(линии напряженности) поля, которые проводятся по следующим правилам: касательная к силовой линии направлена вдоль векторав каждой точке; густота силовых линий пропорциональна напряженности в данной области пространства. Силовые линии начинаются и заканчиваются на зарядах, а в пустом пространстве непрерывны. Число линий начинающихся и заканчивающихся на зарядах пропорционально их абсолютной величине.
Вопросы
1.1 Три заряда расположены
в вершинах равнобедренного прямоугольного
треугольника.В вершинах острых
углов находятся заряды +q,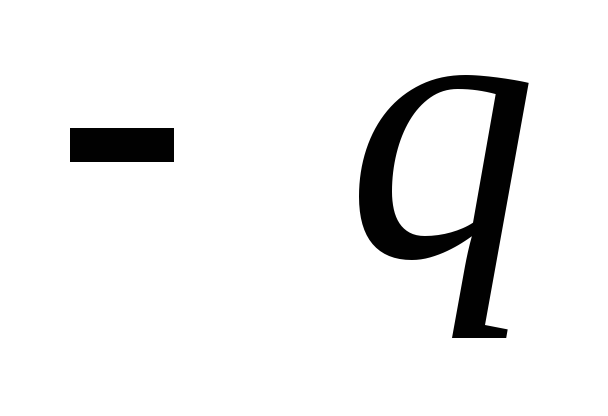 ,
а в вершине прямого угла заряд +2q(см.
рис.3). Определить какой из представленных
на рисунке векторов совпадает с
направлением напряженности поля в
середине гипотенузы.
,
а в вершине прямого угла заряд +2q(см.
рис.3). Определить какой из представленных
на рисунке векторов совпадает с
направлением напряженности поля в
середине гипотенузы.
|
Рис.3 |
Ответ:
Напряженности полей, создаваемые
зарядами  q,
равны по величине и направлены в сторону
отрицательного заряда. Если обозначить
длину гипотенузы2a,
то каждая из этих напряженностей равна
q,
равны по величине и направлены в сторону
отрицательного заряда. Если обозначить
длину гипотенузы2a,
то каждая из этих напряженностей равна 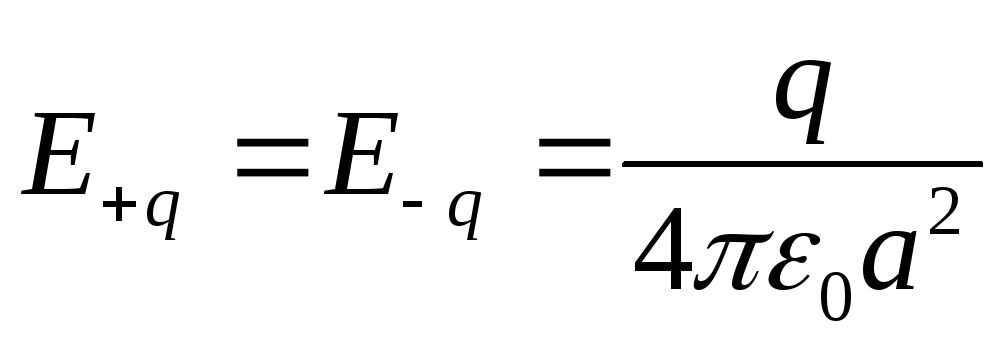 и
их сумма составляет
и
их сумма составляет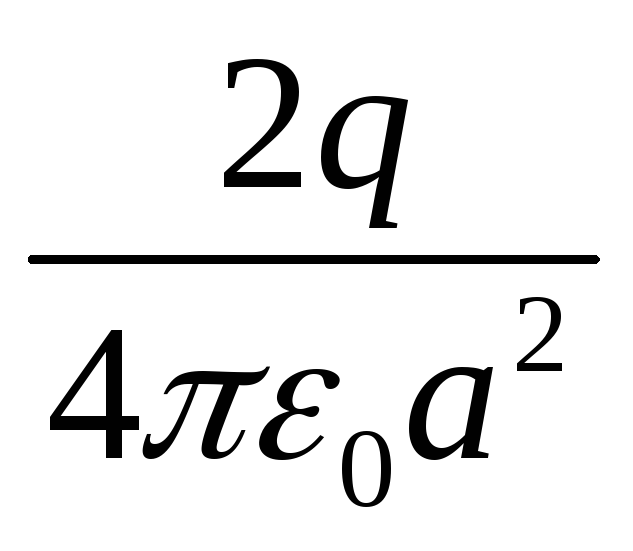 .
Это же значение имеет и поле заряда +2q,
направленное вдоль луча проведенного
из прямого угла в середину гипотенузы.
Напряженность результирующего поля
направлена параллельно катету в
направлении 3.
.
Это же значение имеет и поле заряда +2q,
направленное вдоль луча проведенного
из прямого угла в середину гипотенузы.
Напряженность результирующего поля
направлена параллельно катету в
направлении 3.
1.2 Дана система N точечных зарядов. Какой физический смысл имеют выражения:
а) 
б) 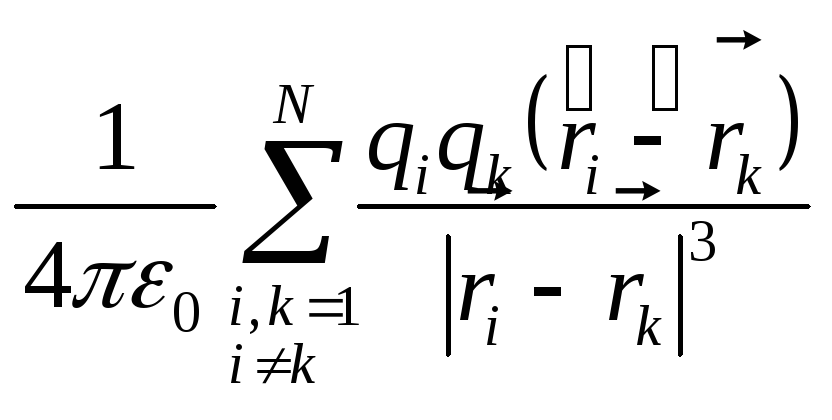
Ответ:
а) Вынесем qN из под знака суммирования 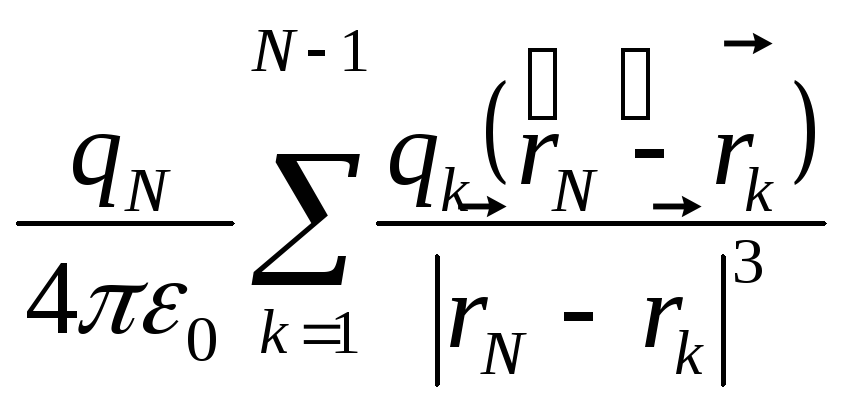 ,
тогда каждое слагаемое под знаком суммы
представляет вектор напряженностиk-го
заряда в точке нахожденияN-го.
А вся сумма – результирующее поле (N-1)
зарядов в этой точке
,
тогда каждое слагаемое под знаком суммы
представляет вектор напряженностиk-го
заряда в точке нахожденияN-го.
А вся сумма – результирующее поле (N-1)
зарядов в этой точке {N-1}.
Выражение а) представится какqN
{N-1}.
Выражение а) представится какqN  {N-1},
т.е.равно силе, действующей на зарядqN со стороны остальных зарядов системы.
{N-1},
т.е.равно силе, действующей на зарядqN со стороны остальных зарядов системы.
б) Каждое слагаемое суммы 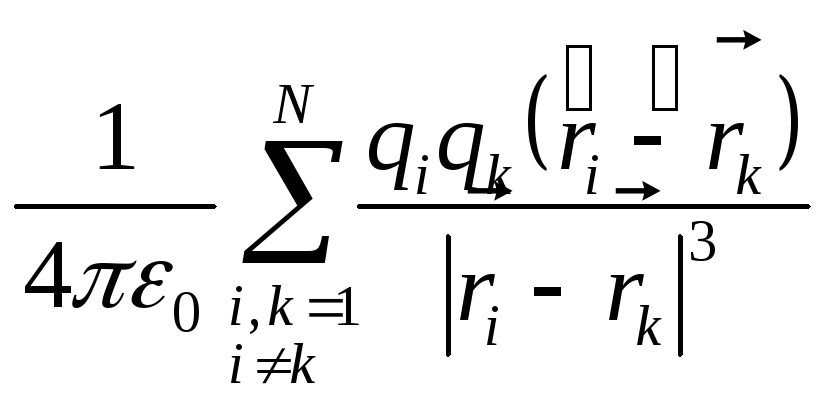 представляет
силу, действующую наi-ый
представляет
силу, действующую наi-ый
заряд со стороны k-го. Вся сумма б) равна результирующей силе действующей на всю систему зарядов и равна нулю, т.к. каждая пара зарядов взаимодействует друг с другом с силами, результирующая которых равна нулю.
1.3 В первоначально незаряженной
системе в пространственно разделенных
точках возникла пара зарядов 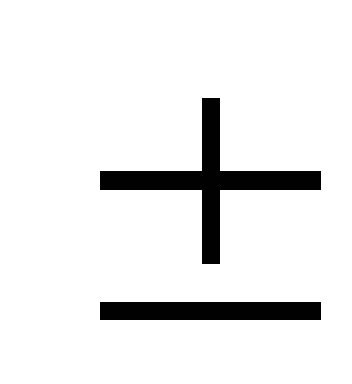 q (см.рис.4). Выполняется ли при этом закон
сохранения заряда:
q (см.рис.4). Выполняется ли при этом закон
сохранения заряда:
|
Рис.4 |
а) если заряды возникли одновременно?
б) если заряды возникли в последовательные моментывремени?
Ответ:
а) Закон сохранения зарядов не выполняется, т.к. в малых областях, окружающих каждый заряд, произошло изменение заряда без переноса электричества через поверхность, ограничивающие эти области.
б) Закон сохранения заряда не выполняется, т.к. в период между возникновениями зарядов полный заряд замкнутой системы изменился без переноса электричества через поверхность, ограничивающую систему.
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа. / / Электростатика. Основные понятия. Электрический заряд. Закон сохранения электрического заряда. Закон Кулона. Принцип суперпозиции. Теория близкодействия. Потенциал электрического поля. Конденсатор. Поделиться:
| ||||||||||||||
1. Электрический заряд. Закон кулона.
Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.
Электрический заряд обычно обозначается буквами q или Q.
Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:
Существует два рода электрических зарядов, условно названных положительными и отрицательными.
Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.
Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.
Величина заряда не зависит от того, движется этот заряд или покоится.
Электрические заряды могут исчезать и возникать вновь. Однако всегда возникают или исчезают два элементарных заряда противоположных знаков.
Закон сохранения электрических зарядов: суммарный заряд электрически изолированной системы не может измениться. Система называется электрически изолированной, если через ограничивающую её поверхность не могут проникать заряженные частицы.
Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь.
Закон Кулона: сила взаимодействия двух неподвижных точечных зарядов пропорциональна величина каждого из зарядов и обратнопропорциональна квадрату расстояния между ними.
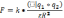
Ε- относительная диэлектрическая проницаемость среды- показывает во сколько раз сила взаимодействия между зарядами в вакууме > силы взаимодействия между теми же зарядами на том же расстоянии в данной среде, величина постоянная для данной среды. Если среда не оговаривается, то ей является вакуум ε=1, для воздуха ε=1.
2.Напряжённость электростатического поля. Принцип суперпозиции. Силовые линии электростатического поля.
Электростатическое поле – электрическое поле неподвижных и не меняющихся со временем зарядов.
напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами в отдельности:
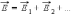
В соответствии с законом Кулона напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю:
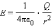
Это поле называется кулоновским. В кулоновском поле направление вектора зависит от знака заряда Q: если Q > 0, то вектор направлен по радиусу от заряда, если Q < 0, то вектор направлен к заряду.
Силовые линии показывают направление напряжённость поля

Принцип суперпозиции — электростатический потенциал, создаваемый в данной точке системой зарядов, есть сумма потенциалов отдельных зарядов.
результат воздействия на частицу нескольких внешних сил есть просто сумма результатов воздействия каждой из сил.
Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя.
Напряженность и закон Кулона

Закон Кулона
Закон сохранения электрического заряда
Напряженность
Принцип суперпозиции
Электрическое поле
Потенциал электростатического поля
Разность потенциалов
Теория
Совсем чуть−чуть.
Закон Кулона — сила, с которой два точечных заряда действуют друг на друга. Она обратно пропорциональна квадрату расстояния между ними и прямо пропорциональна произведению их зарядов.
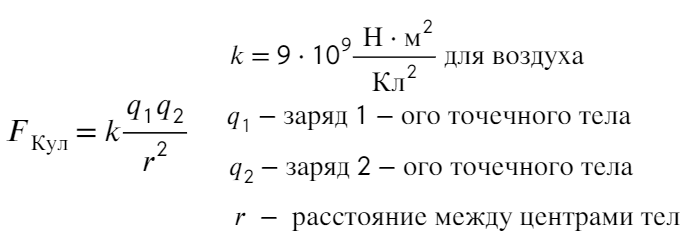
Заряды с одинаковым знаком отталкиваются, с разными — притягиваются. По III з. Ньютона сила действия одного заряда равна силе действия другого:
Наглядно рассказывается об этом в видео.
А напряженность — силовая характеристика электрического поля. По-простому: электрическое поле действует на заряд, и вот сила, с которой поле действует на заряд, и есть напряженность.
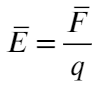
Напряженность НЕ зависит от величины заряда, помещенного в поле!
Задачи
Задача 1 Два одинаковых маленьких положительно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 5 раз. Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₂ к F₁.
Скажем, что заряд одного шарика q, другого 5q. Тогда сила Кулона между ними:
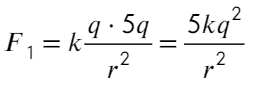
А если теперь соединить два шарика, то общий заряд разделится пополам (на каждый шарик). Общий заряд 5q + q = 6q, тогда на каждом шарике окажется по 3q. Тогда сила Кулона:
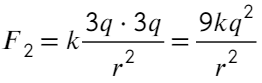
Отношение получится таким:
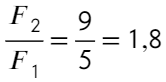
Ответ: 1,8
Задача 2 Два одинаковых маленьких разноименно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 4 раза. Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₁ к F₂.
Та же самая задача? А вот и нет, одно слово другое: разноименно вместо положительных. Это значит, что один шарик будет заряжен положительно, другой отрицательно. По сравнению с первым случаем сила Кулона никак не изменится по модулю (только по нарпавлению).
А вот после соприкосновения изменится. Общий заряд: 5q − q = 4q или q − 5q = − 4q, тогда на каждый шар пойдет по 2q:
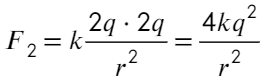
Отношение:

Ответ: 0,8
Задача 3 На нерастяжимой нити висит шарик массой 100 г, имеющий заряд 20 мкКл. Как необходимо зарядить второй шарик, который подносят снизу к первому шарику на расстояние 30 см, чтобы сила натяжения: а) увеличилась в 4 раза; б) рассмотреть случай невесомости?
В начальный момент времени на шарик действуют две силы:
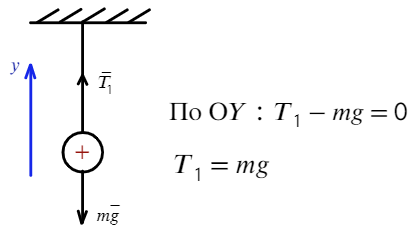 а) Чтобы сила натяжения увеличилась в 4 раза, сила Кулона должна быть направлена вниз, значит, нужно поднести отрицательно заряженный шарик. Запишем также уравнение на ось Y:
а) Чтобы сила натяжения увеличилась в 4 раза, сила Кулона должна быть направлена вниз, значит, нужно поднести отрицательно заряженный шарик. Запишем также уравнение на ось Y:
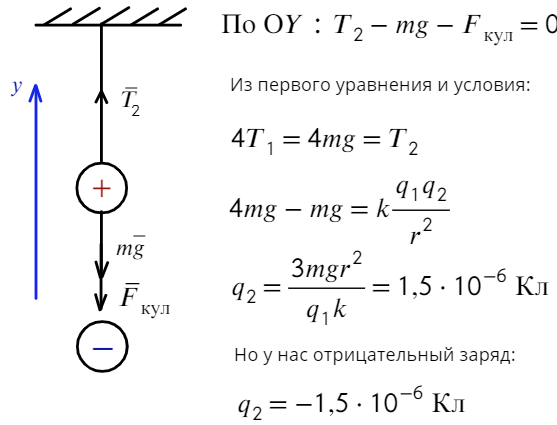 б) Невесомость возникает, когда сила натяжения равна нулю. Для этого нужно, чтобы сила Кулона была направлена вверх, значит, подносим положительный заряд:
б) Невесомость возникает, когда сила натяжения равна нулю. Для этого нужно, чтобы сила Кулона была направлена вверх, значит, подносим положительный заряд:
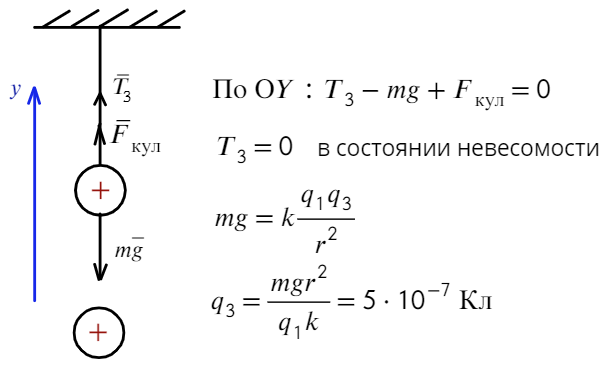 Ответ: −1,5 мкКл, 500 нКл.
Ответ: −1,5 мкКл, 500 нКл.
Задача 3 Фотон с длиной волны, соответствующей красной границе фотоэффекта, выбивает с поверхности пластинки электрон, который попадает в электрическое поле с напряженностью 125 В/м. Найти расстояние, которое он пролетит прежде, чем разгонится до скорости, равной 1% от скорости света.
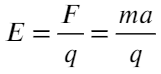
В задаче говорится про электрон, значит, его массу m = 9,1×10⁻³¹ кг и заряд q = 1,6 × 10⁻¹⁹ Кл можно посмотреть в справочных данных.
Найдем ускорение электрона в электрическом поле:
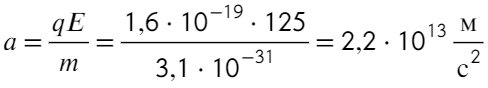
Остается найти пройденный путь в равноускоренном движении при нулевой начальной скорости:
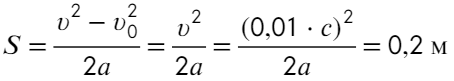
Ответ: 0,2 м
Задача 4 Полый заряженный шарик массой m = 0,4 г. движется в однородном горизонтальном электрическом поле из состояния покоя. Модуль напряженности электрического поля E = 500 кВ/м. Траектория шарика образует с вертикалью угол α = 45°. Чему равен заряд шарика?
Для начала разберемся, какие силы действуют на заряд:
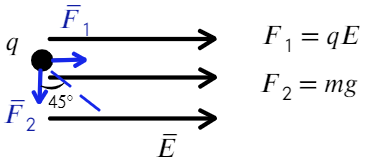
Заряд движется под углом 45 градусов, значит, отношением сил будет тангенс 45°:
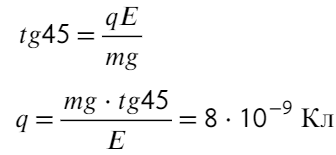
Ответ: 8×10⁻⁹ Кл
Задача 5 При нормальных условиях электрический «пробой» сухого воздуха наступает при напряжённости электрического поля 30 кВ/см. В результате «пробоя» молекулы газа, входящие в состав воздуха, ионизируются и появляются свободные электроны. Какую кинетическую энергию приобретёт такой электрон, пройдя в электрическом поле расстояние 10⁻⁵ см? Ответ выразите в электронвольтах. (ЕГЭ)
Задача кажется весьма тяжелой, но это обманчиво. Воспользуемся знакомой формулой напряженности:

Домножим на длину обе части, тогда слева получится работа, а работа — это изменение энергии:
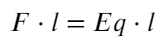
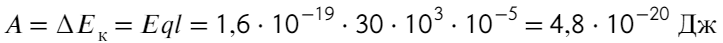
Переводить сантиметры не обязательно, они сократятся. Чтобы перевести джоули в электронвольты, нужно разделить на 1,6 × 10⁻¹⁹

Ответ: 0,3 эВ
Задача 6 В вершинах равностороннего треугольника со стороной «а» находятся заряды +q, +q и -q. Найти напряженность поля Е в центре треугольника.
Покажем, как направлена напряженность: для двух положительных зарядов — от них (красные стрелочки), для отрицательного заряда — к нему (синяя стрелочка).
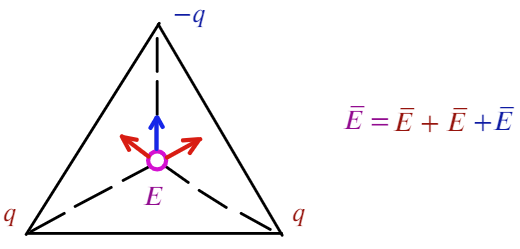
Угол между синим вектором и красным составляет 60°. Если продлить красный вектор до стороны, получится прямоугольный треугольник. Тогда, чтобы посчитать результирующую напряженность, спроецируем красные векторы на синий:
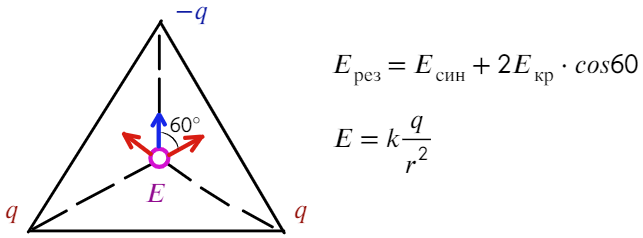
Остается разобрать на каком расстоянии находятся заряды от центра треугольника. Высоту треугольника можно найти по т. Пифагора, равна она а√3/2. А расстояние тогда составит 2/3 от высоты:
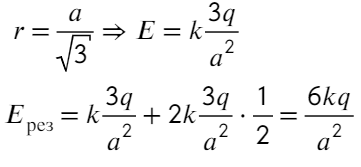
Ответ: 6kq/a²
Задача 6 Два шарика с зарядами Q = –1 нКл и q = 5 нКл соответственно, находятся в однородном электрическом поле с напряженностью Е = 18 В/м, на расстоянии r = 1 м друг от друга. Масса первого шарика равна M = 5 г. Определите, какую массу должен иметь второй шарик, чтобы они двигались с прежним между ними расстоянием и с постоянным по модулю ускорением. (ЕГЭ — 2016)
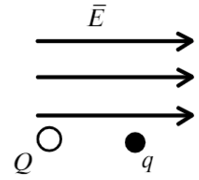
Направим ось X вправо и покажем, какие силы действуют на каждый заряд.
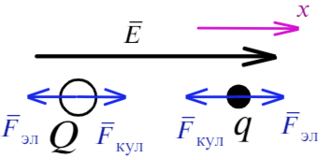
На положительный заряд электрическая сила действует по линиям напряженности, для отрицательного заряда все наоборот. Силы кулона направлены к зарядам, они разноименные. Составим уравнение для каждого заряда:
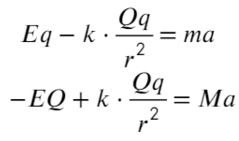
Сумма всех сила равна ma, потому что в условии сказано, что шарики двигаются с постоянным ускорением, а чтобы расстояние не менялось, двигаться они должны в одном направлении.
Разделим одно уравнение на другое и выразим массу:
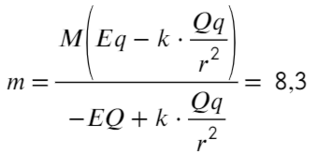
Ответ: 8,3 гр.
Задача 7 Четыре маленьких одинаковых шарика, связанных нерастяжимыми нитями одинаковой длины, заряженызарядами q, q, q и 2q. Сила натяжения нити, связывающей первый и второй шарики, равна T. Найти силу натяжения нити, связывающейвторой и третий шарики. (Росатом)
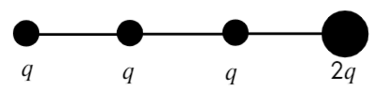
Покажем, каким силам противодействует сила натяжения Т. Воспользуемся принципом суперпозиции и законом Кулона:
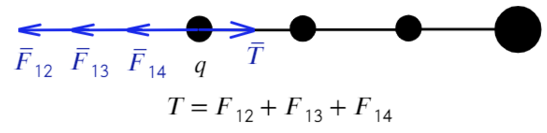
Сила натяжения Т удерживает первый шарик, других сил для него нет, значит, больше ничего для первого случая не требуется.
Как проще это запомнить: проводим линию перпендикулярно той нити, о которой говорим (красная черточка), после записываем только те силы между шариками, которые появляются по разные стороны от проведенной линии:
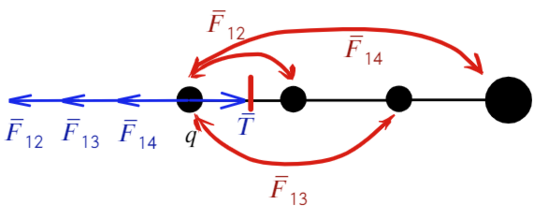
Теперь также составим уравнения для силы натяжения между вторым и третьим шариком:
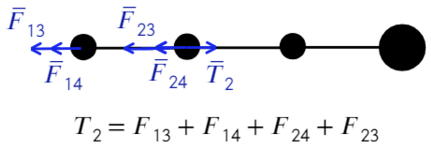
Распишим каждое уравнение по закону кулона, скажем, что расстояние между соседними шариками равно «а»:
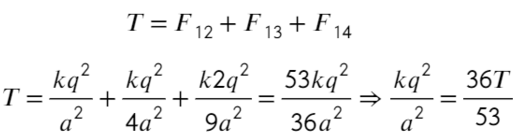
Второе уравнение с подстановкой выражения из первого:
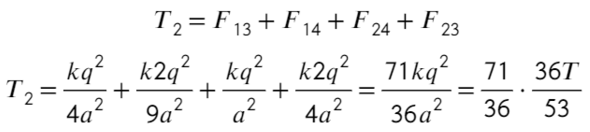
Ответ: 71T/53
Задача 8 Точечный заряд, расположенный в точке C, создаёт в точках A и B поле с напряжённостью Ea и Eb соответственно (см. рисунок; угол ACB — прямой). Найти напряжённость электрическогополя, создаваемого этим зарядом в точке M, являющейся основанием перпендикуляра, опущенного из точки C на прямую AB. (Росатом)
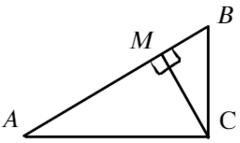
Запишем, чему равна напряженность в каждой из этих точек, взяв длины отрезков за a; b; h:
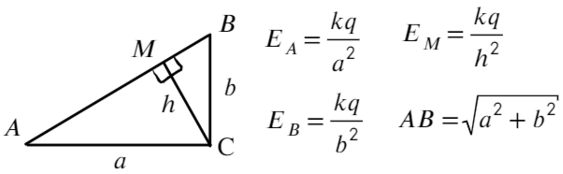
Площадь прямоугольного треугольника можно найти как полупроизведение катетов или как полупроизведение высоты и основания:
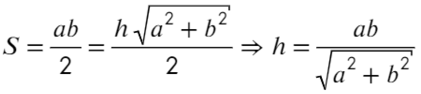
Возведем в квадрат получившиеся уравнение, а дальше смертельный номер: возводим в −1 степень и домножаем обе части на kq:
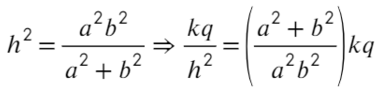
Выразим a² и b² через напряженность:
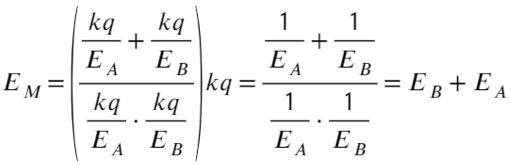
Ответ: Ea+Eb
Задача 9 Частицы с массами M и m, и зарядами q и −q соответственно вращаются с угловой скоростью ω по окружностям вокруг оси, направленной по внешнемуоднородному электрическому полю с напряжённостью E (рис.). Найдите расстояние L между частицами и расстояние H между плоскостями их орбит. (Всеросс. 2008)
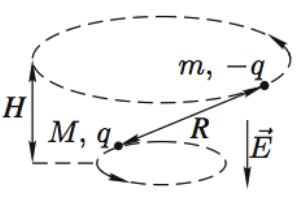 Накрест лежащие углы при параллельных прямых (движения частиц) и секущей силы Кулона равны α. Покажем какие силы действуют на каждую частицу:
Накрест лежащие углы при параллельных прямых (движения частиц) и секущей силы Кулона равны α. Покажем какие силы действуют на каждую частицу:
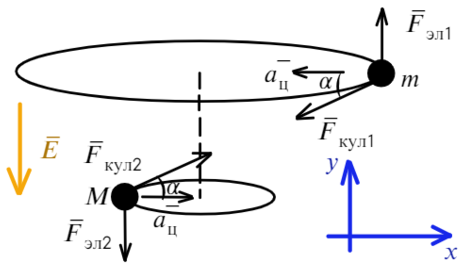
Запишем уравнения по осям на верхнюю частицу:
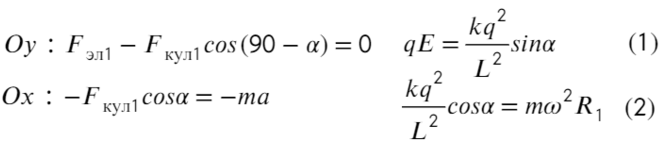
На нижнюю частицу:
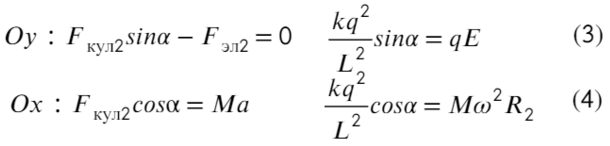
Построим два треугольника, которые показывают расстояние между частицами и высоту между ними.
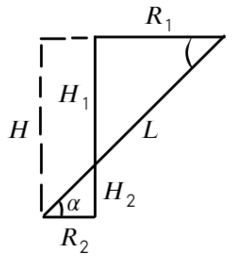
Разделим уравнения друг на друга, а также выразим тангенс угла из этих треугольников:
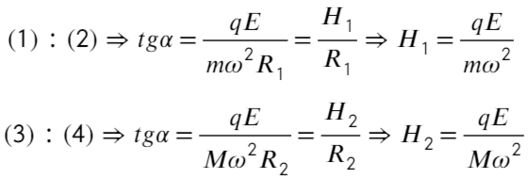
Сложим два уравнения, чтобы найти расстояние между плоскостями:
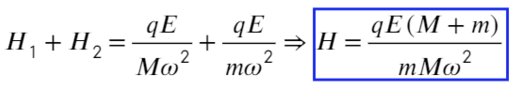
Пункт «а» решили, теперь с расстоянием разберемся: выразим из ур-ия (1) длину, а дальше из треугольника выразим синус угла альфа:
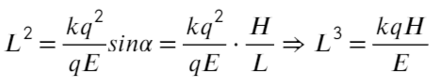
Вместо Н подставим то, что мы нашли:
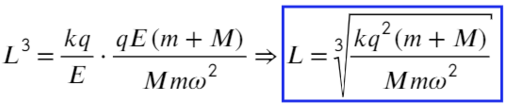
Задача 10 В точке O к стержню привязана непроводящая нить длиной R c зарядом q на конце. Известный эталонный заряд Q₂ и измеряемый заряд Q₁ установлены на расстояниях L₂ и L₁ от точки O. Все заряды одногознака и могут считаться точечными. Найдите величину заряда Q₁, если в состоянии равновесия нить отклонена на угол β от отрезка, соединяющегозаряды Q₂ и Q₁. (Всеросс. 2018)
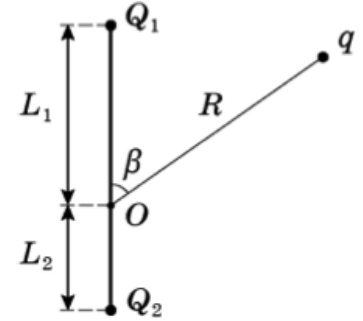
Проведем оси, подпишем расстояние от Q₁ до q и от Q₂ до q. Запишем ур-ия сил на каждую ось:
 Не хочется мучиться с силой натяжения нити, поэтому займемся ур-ем на ось Y:
Не хочется мучиться с силой натяжения нити, поэтому займемся ур-ем на ось Y:
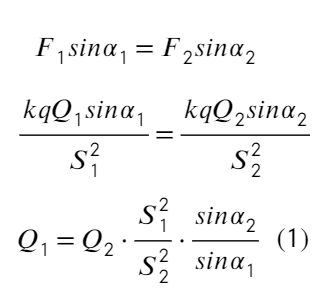
Из прямоугольных треугольников можно получить такие соотношения, а также из теоремы косинусов выразить S₁ и S₂:
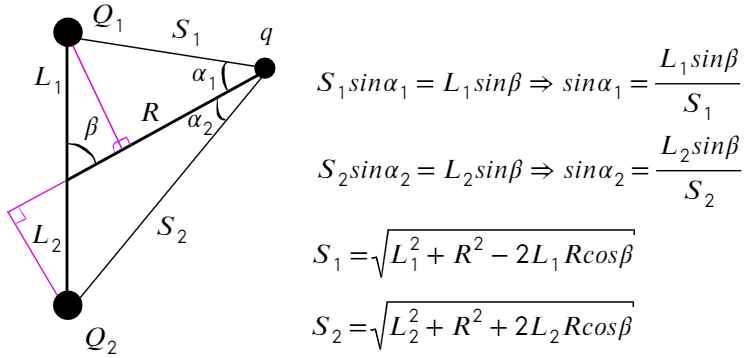
Подставим в ур-ие (1):

В качестве закрепления материала решите несколько похожих задач с ответами.
Будь в курсе новых статеек, видео и легкого технического юмора.
Лекция 1.
60
ЭЛЕКТРОСТАТИКА
Электростатика изучает свойства и закономерности систем неподвижных электрических зарядов и процессы, происходящие в телах, помещенных в электрическое поле. Электрическое поле – это разновидность материи, посредством которой осуществляется силовое воздействие на электрические заряды, находящиеся в этом поле.
Все тела в природе способны электризоваться, то есть, приобретать электрический заряд. Наличие заряда проявляется в том, что заряженное тело взаимодействует с другими заряженными телами. Имеется два вида зарядов, условно называемых положительными и отрицательными (заряд, скапливающийся на стеклянной палочке, потертой кожей, был назван положительным, а на куске смолы, потертом мехом, отрицательным). Заряды одного знака отталкиваются, разных знаков – притягиваются.
Электрический заряд является неотъемлемым свойством некоторых элементарных частиц. Его называют элементарным и обозначают буквой е. для электрона он равен –е, для протона +е, у нейтрона = 0. Из этих частиц состоят атомы и молекулы любого вещества. Обычно частицы, имеющие заряды противоположных знаков, присутствуют в теле в равных количествах, поэтому тело будет нейтральным. Если создать каким-нибудь образом (трение, освещение) избыток частиц одного знака, тело окажется заряженным.
Так как всякий заряд образуется совокупностью элементарных зарядов, он является кратным элементарному заряду q = ± Nе. Если физическая величина может принимать только определенные дискретные значения, то говорят, что эта величина квантуется, то есть, электрический заряд квантуется.
Величина заряда, измеренная в различных инерциальных системах, оказывается одинаковой. Следовательно, электрический заряд является релятивистски инвариантным, то есть, величина заряда не зависит от того, движется заряд или покоится.
Электрические заряды могут исчезать и возникать вновь. Но появление или исчезновение + заряда q всегда сопровождается появлением или исчезновением равного ему заряда –q. Следовательно: в замкнутой электрически изолированной системе алгебраическая сумма зарядов тел остается постоянной при любых взаимодействиях тел, ∑qi = const.Это закон сохранения электрического заряда.
Закон Кулона
Взаимодействие
точечных зарядов изучал Кулон. Он
установил, что сила взаимодействия двух
неподвижных зарядов в воздухе или
вакууме пропорциональна величине
зарядов и обратно пропорциональна
квадрату расстояния между ними:
,k
– коэффициент пропорциональности,
зависит от выбора системы единиц. В
системе СИ 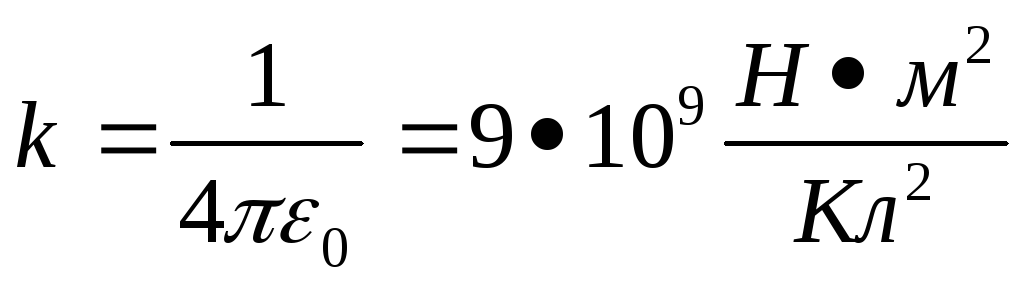 ,
, 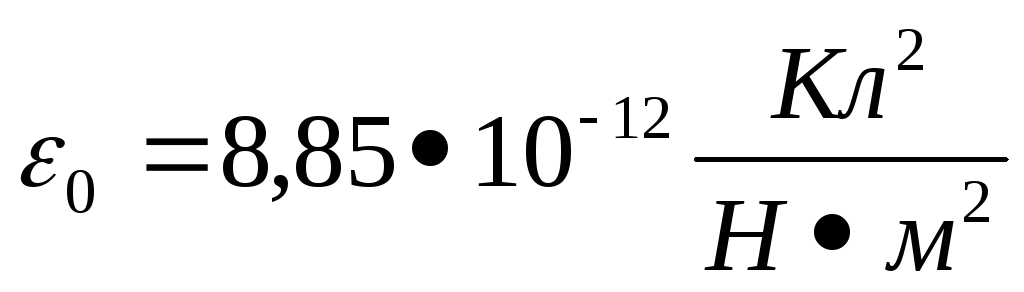 — электрическая постоянная.
— электрическая постоянная.
Силы взаимодействия между зарядами равны по величине и направлены противоположно друг другу по прямой, соединяющей точечные заряды. Разноименные заряды притягиваются, а одноименные отталкиваются.
Сила взаимодействия
зависит также от среды, в которой
находятся заряды. Среда ослабляет силу
взаимодействия: 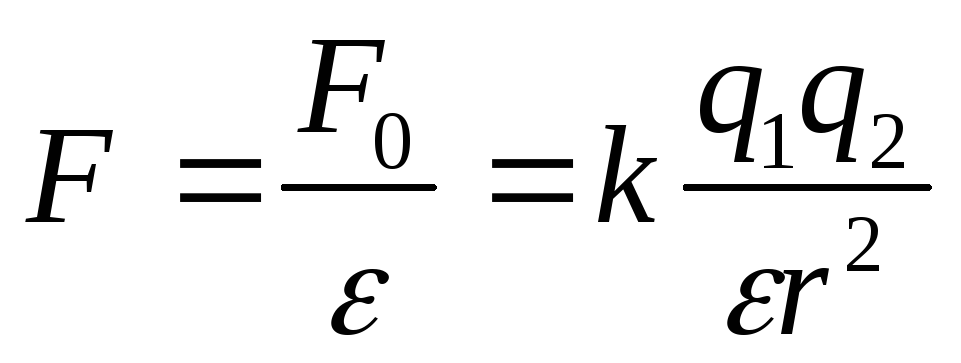 ,F0 – сила взаимодействия между зарядами
в вакууме,
— относительная диэлектрическая
проницаемость среды.
,F0 – сила взаимодействия между зарядами
в вакууме,
— относительная диэлектрическая
проницаемость среды.
Напряженность электрического поля
Всякий заряд q изменяет свойства окружающего его пространства, создает в нем электрическое поле. Для обнаружения и исследования этого поля можно использовать другие заряды, называемые в этом случае пробными.
Если в данную точку
пространства вносить разные по величине
пробные заряды, то и силы, действующие
на них, будут разными. Но отношение силы
к величине пробного заряда будет
величиной постоянной для данной точки
поля. Эта величина называется напряженностью
электрического поля, это силовая
характеристика поля 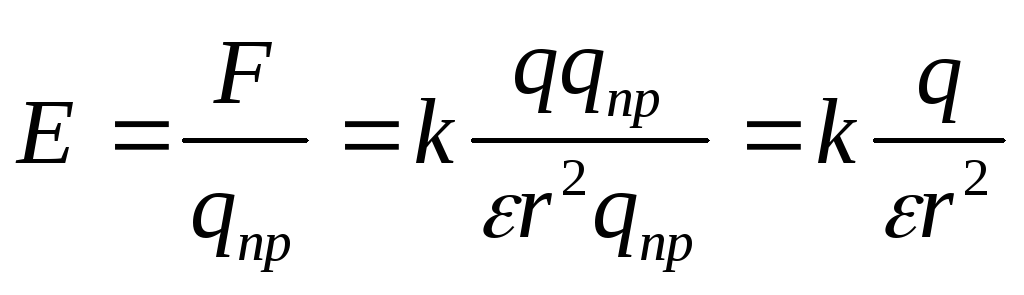 .
.
Напряженность
численно равна силе, действующей на
единичный пробный заряд. Направление
напряженности совпадает с направлением
силы, действующей на положительный
заряд. Размерность напряженности в
системе СИ: 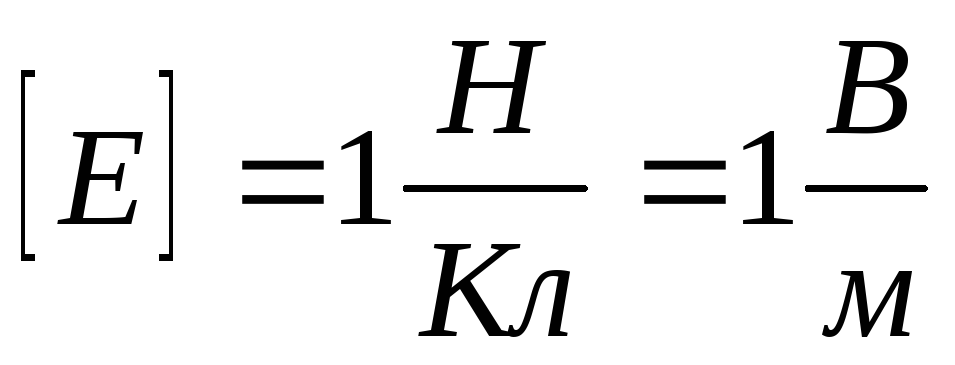 .
.
Сила, действующая на пробный заряд: . И на любой заряд, находящийся в электрическом поле с напряженностью Е будет действовать сила F = qE.
Если электрическое поле создается не одним, а несколькими зарядами, то оно будет действовать на пробный заряд с результирующей силой, равной равнодействующей всех сил, действующих от каждого заряда в отдельности
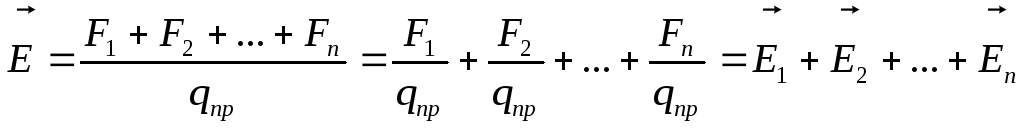
Н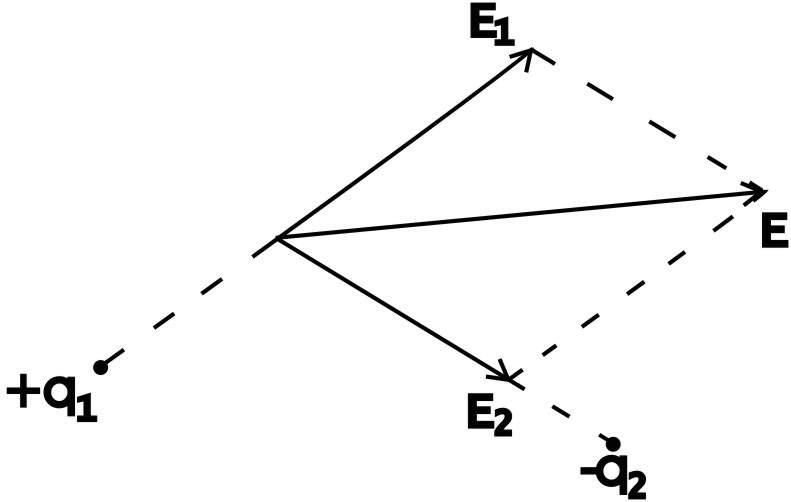 апряженность
поля, созданного несколькими зарядами,
равна геометрической сумме напряженностей,
созданных каждым зарядом в отдельности.
Это принцип суперпозиции полей. На
рисунке представлен принцип суперпозиции
для двух зарядов.
апряженность
поля, созданного несколькими зарядами,
равна геометрической сумме напряженностей,
созданных каждым зарядом в отдельности.
Это принцип суперпозиции полей. На
рисунке представлен принцип суперпозиции
для двух зарядов.
Электрическое поле можно изображать с помощью силовых линий. Эти линии проводятся таким образом, чтобы касательные к ним в каждой точке совпадали с направлением вектора Е. Густота линий выбирается так, чтобы число линий, пронизывающих единицу поверхности площадки, перпендикулярной к силовым линиям, равнялась значению вектора Е. То есть, по картине силовых линий можно судить о направлении и величине вектора Е в разных точках пространства.
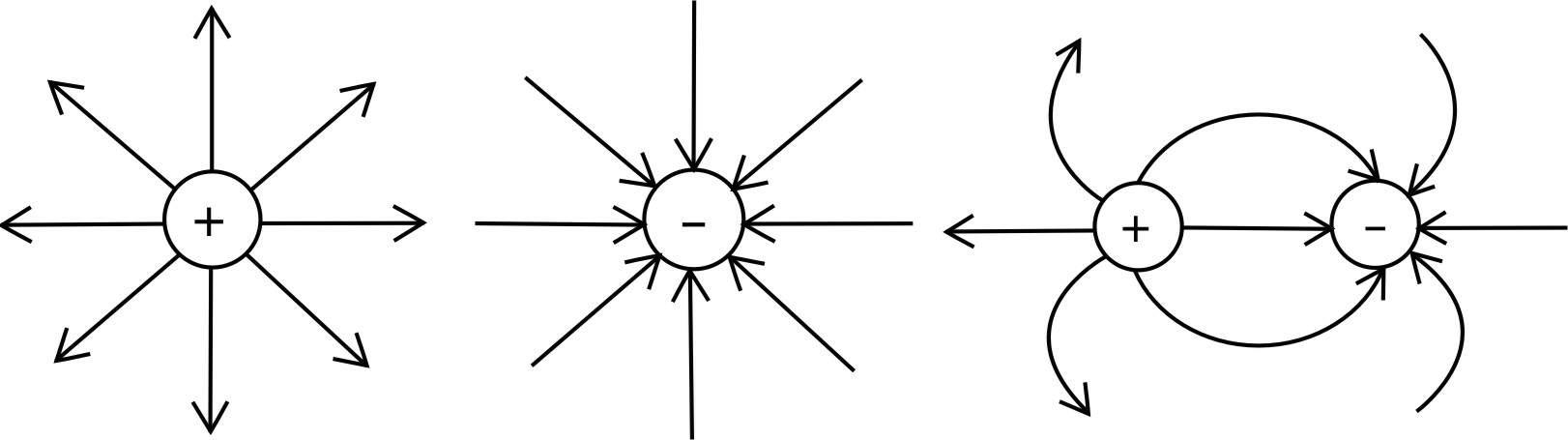 Силовые
линии электростатического поля
разомкнуты. Они начинаются на положительных
зарядах и заканчиваются на отрицательных,
или уходят в ,
или приходят из .
Силовые
линии электростатического поля
разомкнуты. Они начинаются на положительных
зарядах и заканчиваются на отрицательных,
или уходят в ,
или приходят из .
Электромагнетизм
Конспект лекций по физике Федун В.И.
18 | Электрический заряд Закон Кулона. Напряженность электрического поля. Принцип суперпозиции. Теорема Остроградского-Гаусса Поле диполя. |
Лекция 18.
Электростатика в вакууме.
Электростатика устанавливает законы, определяющие поведение и взаимодействие неподвижных зарядов.
Современная физика оперирует понятием электромагнитного поля, рассматривая его, наряду с веществом, в качестве одного из видов материи. Этот вид материи – электромагнитное поле – обладает энергией, импульсом и может быть охарактеризован другими физическими свойствами. Именно посредством полей осуществляются электромагнитные взаимодействия тел.
Свойства электрического заряда.
Наряду с массой одной из основных характеристик частицы является её электрический заряд. Электрический заряд обладает свойствами:
1) Опытным путем установлено, что существуют как положительные, так и отрицательные электрические заряды. Этот экспериментальный факт называют дуализмом или двойственностью заряда.
Заряды одинакового знака отталкиваются, а разноименные заряды притягиваются.
2) Следующее утверждение, являющееся экспериментальным фактом, – это закон сохранения электрического заряда. Полный заряд (алгебраическая сумма зарядов) электрически изолированной системы никогда не меняется. Нарушения закона сохранения заряда не наблюдались.
3). Релятивистская инвариантность полного заряда:
алгебраическая сумма зарядов в изолированной системе не меняется при переходе от одной ИСО (инерциальной системы отсчета) к другой, независимо от скорости их относительного движения.
4). Квантование или дискретность заряда.
Полный
заряд любого тела кратен элементарному
заряду  .
Опыты с макроскопическими телами
позволяют установить дискретное
изменение заряда лишь в тех случаях,
когда избыточный заряд одного знака
будет состоять лишь из небольшого числа
элементарных. Такой случай реализуется
вкапельном
методе Милликена (описание опыта дается
на лекции или см. в рекомендованной
литературе),
позволяющем достигнуть очень высокой
точности в определении величины
элементарного заряда.
.
Опыты с макроскопическими телами
позволяют установить дискретное
изменение заряда лишь в тех случаях,
когда избыточный заряд одного знака
будет состоять лишь из небольшого числа
элементарных. Такой случай реализуется
вкапельном
методе Милликена (описание опыта дается
на лекции или см. в рекомендованной
литературе),
позволяющем достигнуть очень высокой
точности в определении величины
элементарного заряда.
Закон Кулона
| Кулон
(1785 г.) проводил опыты по измерению
силы взаимодействия точечных зарядов
(размеры заряженных тел значительно
меньше расстояния между ними |
Рисунок 18.1. |
Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль прямой, соединяющей заряды.
| (18.1) |
Выбор
коэффициента  зависит от системы единиц. Всистеме
СИ основные
единицы: метр (м), килограмм (кг), секунда
(с), Кельвин (К) и Ампер (А). При этом
величина заряда и сила определяются
независимо:
зависит от системы единиц. Всистеме
СИ основные
единицы: метр (м), килограмм (кг), секунда
(с), Кельвин (К) и Ампер (А). При этом
величина заряда и сила определяются
независимо:
1 заряда (Кулон) = 1Кл = 1 А1 с
Коэффициент  равен:
равен:
|
где 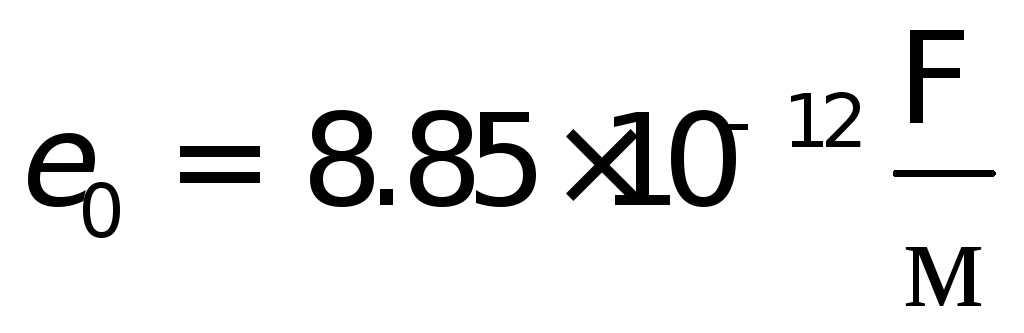 — диэлектрическая постоянная. Тогда
значение коэффициента
— диэлектрическая постоянная. Тогда
значение коэффициента составляет
составляет .
.
Напряженность электрического поля.
Взаимодействие между покоящимися зарядами осуществляется посредством электрического поля. Всякий электрический заряд определенным образом изменяет свойства окружающего пространства, т.е. создает в нем электрическое поле, которое может быть обнаружено по воздействию на «пробный» заряд q0. (Под пробным понимают такой заряд, который практически не изменяет электростатическое поле рассматриваемой системы зарядов).
Силовой характеристикой электрического поля служит векторная величина, называемая напряженностью электрического поля и определяемая как
| (18.2) |
Напряженность
поля, создаваемого точечным зарядом  в окружающем пространстве, определяется
выражениями:
в окружающем пространстве, определяется
выражениями:
| (18.3) |
Однородным называется электрическое поле, напряженность которого во всех точках рассматриваемого пространства одинакова:
| (18.4) |
Принцип суперпозиции.
Принцип суперпозиции (наложения) электрических полей вытекает из обобщения опытных фактов.
Опыт
показывает, что сила, действующая на
«пробный» заряд 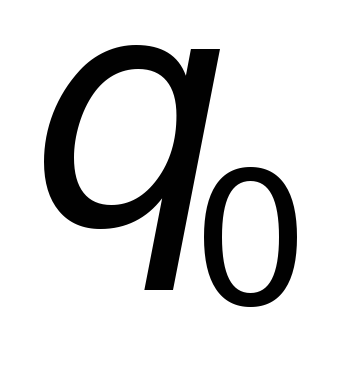 со стороны
со стороны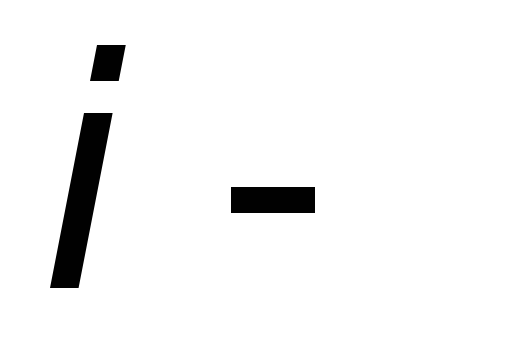 го
заряда не изменяется в присутствии
других зарядов:
го
заряда не изменяется в присутствии
других зарядов:
| (18.5) |
Поэтому
при наличии системы электрических
зарядов полная сила, действующая на
«пробный» заряд 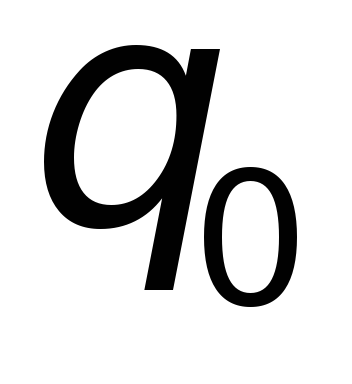 ,
будет равна векторной сумме сил,
действующих на «пробный» заряд
,
будет равна векторной сумме сил,
действующих на «пробный» заряд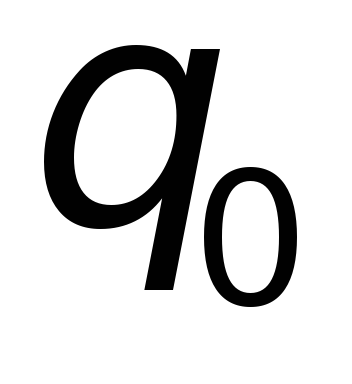 со
стороны каждого заряда рассматриваемой
системы:
со
стороны каждого заряда рассматриваемой
системы:
| (18.6) |
Принцип суперпозиции Напряженность электрического поля, создаваемого всеми зарядами системы, в любой точке пространства определяется как векторная сумма напряженностей полей, создаваемых каждым отдельным зарядом:
| (18.7) |
Если
заряд распределен в пространстве
непрерывно, то весь объем, содержащий
заряд, разбивают на столь малые области,
в пределах которых заряды можно считать
точечными и равными по величине 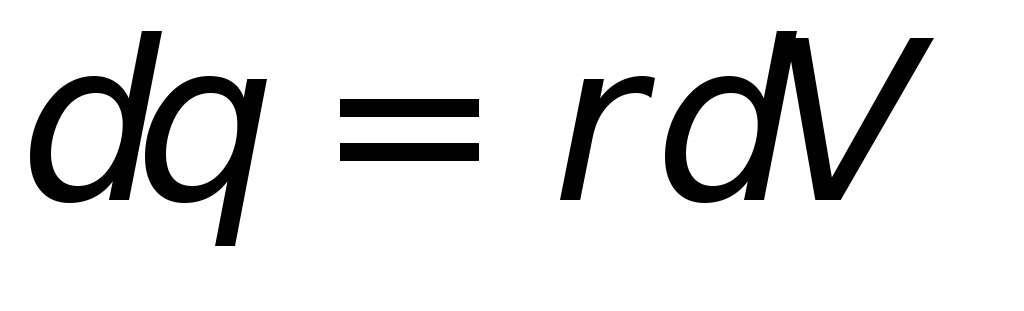 ,
где
,
где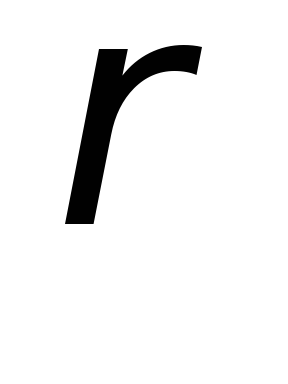 — плотность заряда. Тогда электрическое
поле, создаваемое таким зарядом находится
как
— плотность заряда. Тогда электрическое
поле, создаваемое таким зарядом находится
как
| (18.8) |




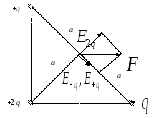
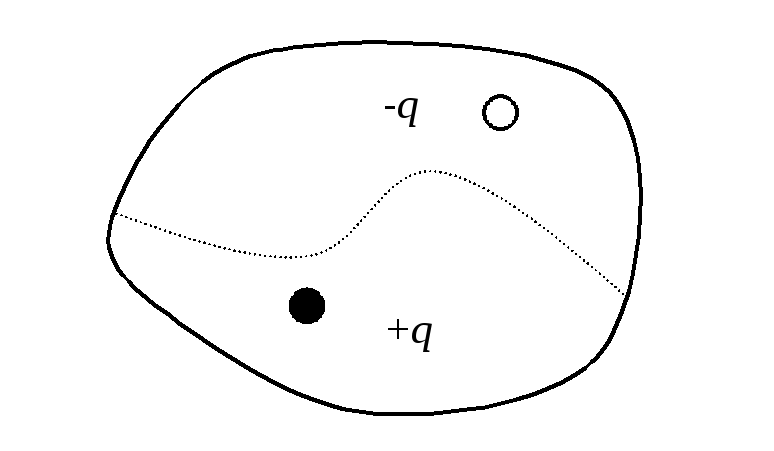
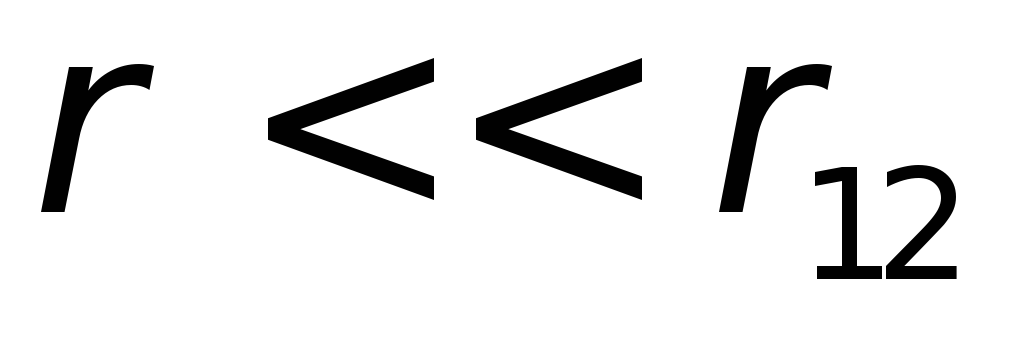 ,Рисунок
18.1) с помощью
крутильных весов и открыл основной
количественный закон электростатики.
,Рисунок
18.1) с помощью
крутильных весов и открыл основной
количественный закон электростатики.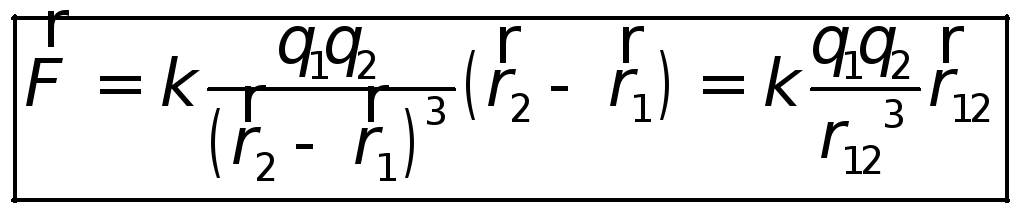 ,
,