Законы Кирхгофа для расчёта электрических цепей

При расчёте электрических цепей, в том числе для целей моделирования, широко применяются законы Кирхгофа, позволяющие полностью определить режим её работы.

Прежде чем перейти к самим законам Кирхгофа, дадим определение ветвей и узлов электрической цепи.

Ветвью электрической цепи называется такой её участок, который состоит только из последовательно включённых источников ЭДС и сопротивлений, вдоль которого протекает один и тот же ток. Узлом электрической цепи называется место (точка) соединения трёх и более ветвей. При обходе по соединённым в узлах ветвям можно получить замкнутый контур электрической цепи. Каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза [1].

Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна нулю:

∑i = 0,

или в комплексной форме

∑I = 0.

Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом замкнутом контуре алгебраическая сумма напряжений на сопротивлениях, входящих в этот контур, равна алгебраической сумме ЭДС:

∑Z ∙ I = ∑E.

Количество уравнений, составляемых для электрической цепи по первому закону Кирхгофа, равно N_у – 1, где N_у – число узлов. Количество уравнений, составляемой для электрической цепи по второму закону Кирхгофа, равно N_в – N_у + 1, где

N_в – число ветвей. Количество составляемых уравнений по второму закону Кирхгофа легко определить по виду схемы: для этого достаточно посчитать число «окошек» схемы, но с одним уточнением: следует помнить, что контур с источником тока не рассматривается.

Опишем методику составления уравнений по законам Кирхгофа. Рассмотрим её на примере электрической цепи, представленной на рис. 1.

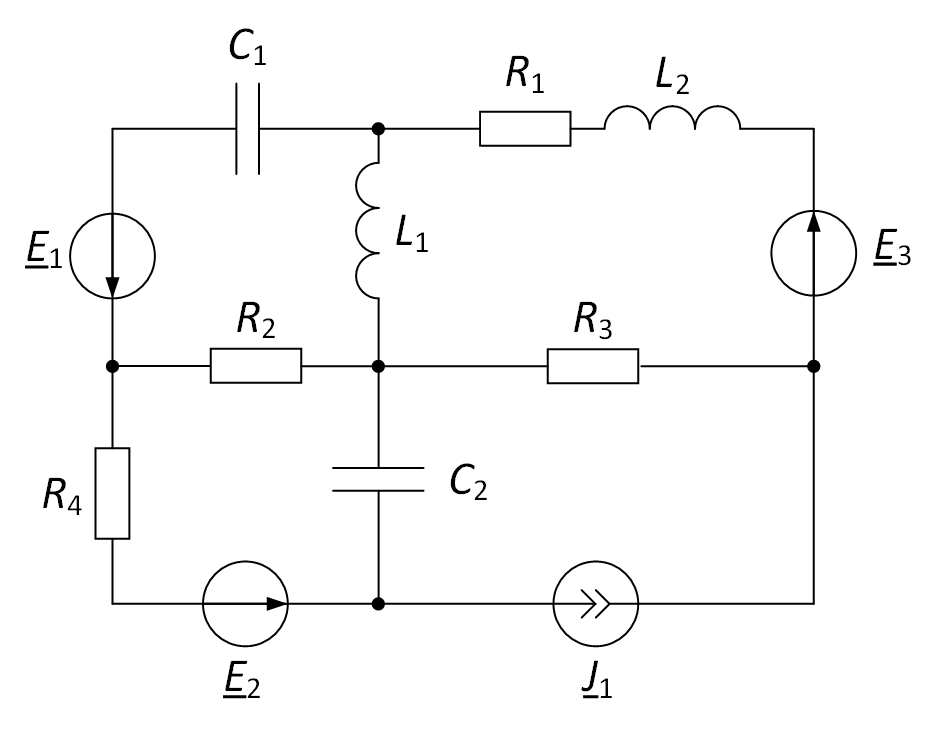
Рис. 1. Рассматриваемая электрическая цепь

Для начала необходимо задать произвольно

направления токов в ветвях и задать направления обхода контуров (рис. 2).

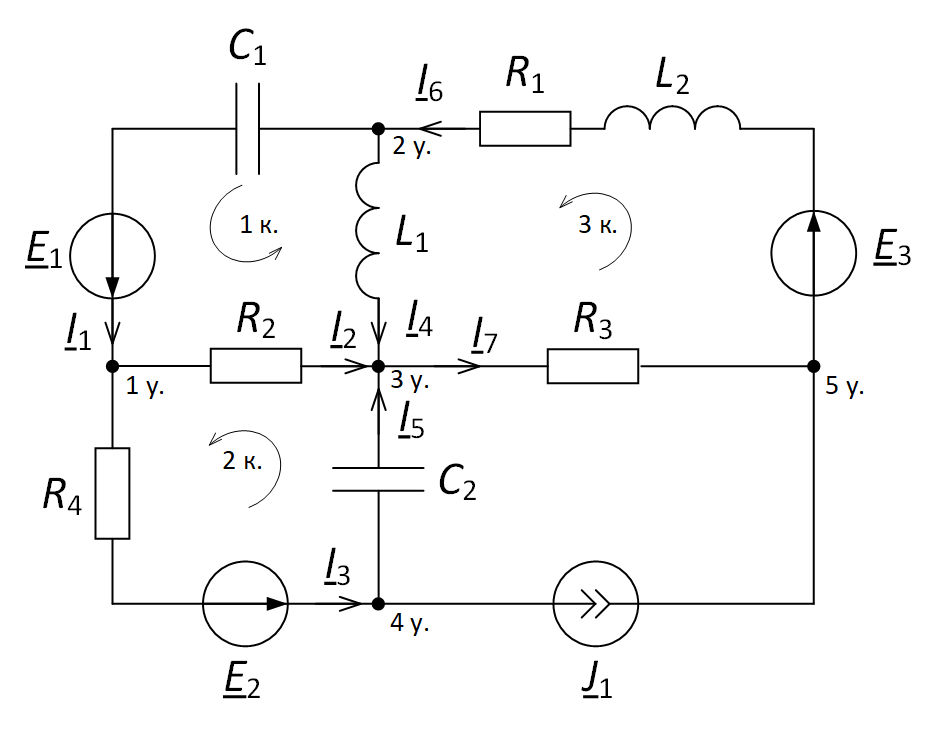
Рис. 2. Задание направления токов и направления обхода контуров для электрической цепи

Количество уравнений, составляемых по первому закону Кирхгофа, в данном случае равно 5 – 1 = 4. Количество уравнений, составляемых по второму закону Кирхгофа, равно 3, хотя «окошек» в данном случае 4. Но напомним, что «окошко», содержащее источник тока J₁, не рассматривается.

Составим уравнения по первому закону Кирхгофа. Для этого «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» — со знаком «-». Отсюда для узла «1 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:

I₁ – I₂ – I₃ = 0;

для узла «2 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:

—I₁ – I₄ + I₆ = 0;

для узла «3 у.»:

I₂ + I₄ + I₅ – I

7 = 0;

для узла «4 у.»:

I₃ – I₅ – J₁ = 0

Уравнение для узла «5 у.» можно не составлять.

Составим уравнения по второму закону Кирхгофа. В этих уравнениях положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура. Для контура «1 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:

Z_C1 ∙ I₁ + R₂ ∙ I₂ – Z_L1 ∙ I₄ = E₁;

для контура «2 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:

-R₂ ∙ I₂ + R₄ ∙ I₃ + Z_C2 ∙ I₅ = E₂;

для контура «3 к.»:

Z_L1 ∙ I₄ + (Z_L2 + R₁) ∙ I₆ + R₃ ∙ I₇ = E₃,

где Z_C = — 1/(ωC), Z_L = ωL

.

Таким образом, для того, чтобы найти искомые токи, необходимо решить следующую систему уравнений:

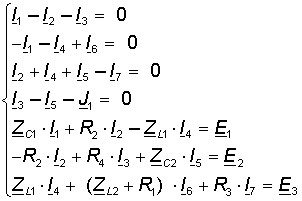
В данном случае это система из 7 уравнений с 7 неизвестными. Для решения данной системы уравнений удобно пользоваться Matlab. Для этого представим эту систему уравнений в матричной форме:

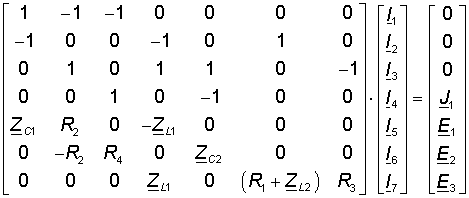
Для решения данной системы уравнений воспользуемся следующим скриптом Matlab:

>> syms R1 R2 R3 R4 Zc1 Zc2 Zl1 Zl2 J1 E1 E2 E3;
>> A = [1  -1 -1    0   0        0  0;
       -1   0  0   -1   0        1  0;
        0   1  0    1   1        0 -1;
        0   0  1    0  -1        0  0;
      Zc1  R2  0 -Zl1   0        0  0;
        0 -R2 R4    0 Zc2        0  0;
        0   0  0  Zl1   0 (R1+Zl2) R3];
>> b = [0;
        0;
        0;
       J1;
       E1;
       E2;
       E3];
>> I = A\b

В результате получим вектор-столбец I

токов из семи элементов, состоящий из искомых токов, записанный в общем виде. Видим, что программный комплекс Matlab позволяет существенно упростить решение сложных систем уравнений, составленных по законам Кирхгофа.

Список использованной литературы

1. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.

Рекомендуемые записи

1 и 2 законы кирхгофа

Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров.

В этом случае законы формулируются следующим образом.

[править]Первый закон

Первый закон Кирхгофа (Закон токов Кирхгофа, ЗТК) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком):

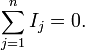
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит 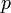 узлов, то она описывается 

 уравнениями токов. Этот закон может применяться и для других физических явлений (к примеру, водяные трубы), где есть закон сохранения величины и поток этой величины.

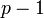
[править]Второй закон

Второй закон Кирхгофа (Закон напряжений Кирхгофа, ЗНК) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю:

для постоянных напряжений

 

для переменных напряжений

 

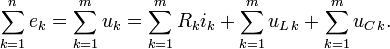
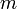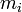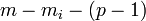Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве , то она описывается  уравнениями напряжений. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи.

Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.

Пример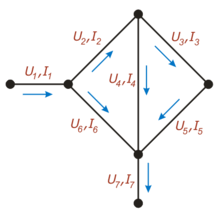

На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)

Например, для приведённой на рисунке цепи, в соответствии с первым законом выполняются следующие соотношения:

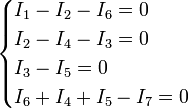
Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например здесь, токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.

В соответствии со вторым законом, справедливы соотношения:

Электротехника: Второй закон Кирхгофа.

  Второй закон (правило) Кирхгофа — алгебраическая сумма напряжений на элементах контура электрической цепи равна нулю.
Контур электрической цепи — замкнутый проводящий ток путь образованный элементами электрической цепи.
Рассмотрим схему на рисунке 1:

Рисунок 1 — Схема с одним контуром

В этой схеме присутствуют: источник ЭДС и резисторы R1, R2 и R3; эти элементы образуют замкнутый путь проводящий ток т.е. контур. Напряжение на источнике ЭДС равно E и направлено так как показано на рисунке 1 стрелочкой справа от источника. Стрелка на условном обозначении источника направлена в сторону противоположную направлению напряжения на источнике ЭДС (иногда это запутывает при расчёте схем но так принято обозначать источник ЭДС). Направления падений напряжений на резисторах указаны стрелками (рис. 1). Для составления уравнения, по второму закону Кирхгофа, необходимо выбрать направление обхода контура (по часовой стрелке или против). В схеме на рисунке показано направление по часовой стрелке. Запишем уравнение по второму закону Кирхгофа:

Напряжения резисторов вошли в левую часть уравнения со знаком плюс т.к. направление обхода контура совпадает с направлениями напряжений на резисторах. Напряжение источника ЭДС E вошло в правую часть со знаком плюс т.к. направление обхода контура не совпадает с направлением напряжения источника. Можно также записать напряжение источника в левой части уравнения со знаком минус (что, в принципе, тоже самое):

Уравнение (2) больше подходит для определения второго закона Кирхгофа приведенного выше.

Напряжения совпадающие по направлению с обходом контура записаны со знаком плюс а напряжение источника не совпадающее с обходом контура — со знаком минус и вся эта алгебраическая сумма равна нулю. Теперь, из выражения (2), зная три каких либо напряжения можно найти четвёртое. Обычно расчёт цепи сводится к нахождению токов во всех ветвях или потенциалов всех узлов т.к. зная эти величины (токи ветвей или потенциалы узлов), сопротивления всех элементов и напряжения источников ЭДС (и токи всех источников тока) можно найти напряжение на любом элементе и ток любого элемента. В схеме на рисунке 1 для определения напряжений U1, U2 и U3 достаточно знать ток I т.к. он одинаков для всех элементов цепи (R1, R2, R3, E). Умножением тока I на сопротивление R1 находится напряжение U1, умножением тока I на сопротивление R2 находится напряжение U2, умножением тока I на сопротивление R3 находится напряжение U3. Учитывая это можно привести уравнение (1) к виду:

Из уравнения (3) можно найти ток I. Т.к. контур один то и ток в уравнении один но если схема содержит больше одно контура то и токов будет больше. Вынеся ток I за скобки и поделив обе части уравнения на сумму сопротивлений R1, R2 и R3 получаем уравнение для нахождения тока I, но этот ток можно найти и другим способом например заменой последовательного соединения резисторов R1, R2 и R3 одним резистором R123 и делением напряжения E на сопротивление резистора R123.

Сопротивление резистора R123 равно сумме сопротивлений резисторов R1, R2 и R3. Ток находится из уравнения:

     Если в контуре содержится больше одного источника ЭДС то уравнение, по второму закону (правилу) Кирхгофа, составляется аналогично.

Рисунок 2 — Схема с двумя источниками ЭДС

Запишем уравнение, по второму закону Кирхгофа, для контура в схеме на рисунке 2:

Напряжение E2 источника E2 записано в правой части уравнения со знаком минус т.к. оно совпадает по направлению с обходом контура. Заменяя напряжения на резисторах произведениями тока I на сопротивления резисторов получим уравнение:

Из уравнения (6) может быть найден ток I.

Если схема имеет больше одного контура то Закон (правило) Кирхгофа все равно выполняется для всех контуров. Уравнения по второму закону Кирхгофа, в таком случае, составляются аналогично тому как в примерах выше. Отличие будет только в том что необязательно для всех элементов будет один и тот же ток. В случае если схема имеет больше одного контура можно считать что через каждый элемент течет свой ток. Напряжение на элементе, в таком случае, находится умножением сопротивления этого элемента (если этот элемент например резистор) на ток данного элемента.

Рисунок 3 — Часть схемы имеющей больше одного контура

Рисунок 4 — Часть схемы имеющей больше одного контура и ветвь из двух элементов

Рисунок 4 — Часть схемы имеющей больше одного контура, ветвь из двух элементов и элементы напряжения на на которых имеют направления не совпадающие с выбранным направлением обхода контура

При составлении уравнений по второму закону Кирхгофа не стоит слишком много времени уделять выбору направлений обходов контуров и направлений токов (они (направления обходов и токов) выбираются произвольно) так как реальные направления токов определяются при решении этих уравнений.

Пример:

Направление напряжения на элементе R1 такое же как и направление тока этого элемента по тому что принято считать что ток течёт от большего потенциала к меньшему а напряжение направлено также (от большего потенциала к меньшему).

Метод непосредственного применения законов Кирхгофа — Википедия

Материал из Википедии — свободной энциклопедии

Метод непосредственного применения правил Кирхгофа для расчета электрической цепи заключается в составлении системы из В уравнений с В неизвестными (B — количество ветвей в рассматриваемой цепи) по двум правилам Кирхгофа и последующем их решении.

Рассмотрим расчёт электрической цепи, не содержащей источников тока. Рассматриваемая цепь состоит из В ветвей и У узлов. Её расчёт сводится к нахождению токов в В ветвях. Для этого необходимо составить (У — 1) независимых уравнений по первому правилу Кирхгофа и К = (В — У + 1) независимых уравнений по второму правилу Кирхгофа. Соответствующие этим уравнениям узлы и контуры называются независимыми (то есть содержащими хотя бы одну ветвь, не принадлежащую другим узлам/контурам).

Для решения составленной системы линейных алгебраических уравнений можно воспользоваться матричной формой

AI=BE{\displaystyle AI=BE},

где

A{\displaystyle A} и B{\displaystyle B} — квадратные матрицы коэффициентов при токах и ЭДС порядка B;

I{\displaystyle I} и E{\displaystyle E} — матрицы-столбцы неизвестных токов и заданных ЭДС.

Решение системы:

I=A−1BE=GE{\displaystyle I=A^{-1}BE=GE},

A−1{\displaystyle A^{-1}}	=[a11a12⋯a1Ba21a22⋯a2B⋮⋮⋱⋮aB1aB2⋯aBB]−1={\displaystyle ={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1B}\\a_{21}&a_{22}&\cdots &a_{2B}\\\vdots &\vdots &\ddots &\vdots \\a_{B1}&a_{B2}&\cdots &a_{BB}\end{bmatrix}}^{-1}=}
	=1Δ[Δ11Δ12⋯Δ1BΔ21Δ22⋯Δ2B⋮⋮⋱⋮ΔB1ΔB2⋯ΔBB]T={\displaystyle ={\frac {1}{\Delta }}{\begin{bmatrix}\Delta _{11}&\Delta _{12}&\cdots &\Delta _{1B}\\\Delta _{21}&\Delta _{22}&\cdots &\Delta _{2B}\\\vdots &\vdots &\ddots &\vdots \\\Delta _{B1}&\Delta _{B2}&\cdots &\Delta _{BB}\end{bmatrix}}^{T}=}
	=1Δ[Δ11Δ21⋯ΔB1Δ12Δ22⋯ΔB2⋮⋮⋱⋮Δ1BΔ2B⋯ΔBB]{\displaystyle ={\frac {1}{\Delta }}{\begin{bmatrix}\Delta _{11}&\Delta _{21}&\cdots &\Delta _{B1}\\\Delta _{12}&\Delta _{22}&\cdots &\Delta _{B2}\\\vdots &\vdots &\ddots &\vdots \\\Delta _{1B}&\Delta _{2B}&\cdots &\Delta _{BB}\end{bmatrix}}}

— обратная матрица; Δ{\displaystyle \Delta } — определитель матрицы A; Δik{\displaystyle \Delta _{ik}} — алгебраические дополнения элементов aik{\displaystyle a_{ik}} (см. способы нахождения обратной матрицы).

G=A−1B=[g11g12⋯g1Bg21g22⋯g2B⋮⋮⋱⋮gB1gB2⋯gBB]{\displaystyle G=A^{-1}B={\begin{bmatrix}g_{11}&g_{12}&\cdots &g_{1B}\\g_{21}&g_{22}&\cdots &g_{2B}\\\vdots &\vdots &\ddots &\vdots \\g_{B1}&g_{B2}&\cdots &g_{BB}\end{bmatrix}}}

— матрица собственных gii{\displaystyle g_{ii}} и взаимных gik{\displaystyle g_{ik}} проводимостей (см. метод наложения).

{I1=g11E1+g12E2+⋯+g1BEB;I2=g21E1+g22E2+⋯+g2BEB;⋮IB=gB1E1+gB2E2+⋯+gBBEB;{\displaystyle \left\{{\begin{matrix}I_{1}=g_{11}E_{1}+g_{12}E_{2}+\cdots +g_{1B}E_{B};\\I_{2}=g_{21}E_{1}+g_{22}E_{2}+\cdots +g_{2B}E_{B};\\\vdots \\I_{B}=g_{B1}E_{1}+g_{B2}E_{2}+\cdots +g_{BB}E_{B};\end{matrix}}\right.}

— система уравнений, определяющих токи ветвей.

Зачастую при расчёте цепей подобным методом возникает необходимость составления большого количества уравнений и последующего расчёта матриц большого порядка. Поэтому на практике применяются и другие методы расчёта.

В качестве примера рассмотрим расчёт цепи, схема которой показана на рисунке — она содержит У = 2 узла и В = 3 ветви, то есть К = В − У + 1 = 3 − 2 + 1 = 2 независимых контура (на рисунке контуры отмечены пунктирной линией — можно выбрать любую пару из них — 1 и 2, или 2 и 3, или 1 и 3).

Произвольно выбираем положительные направления токов ветвей I1{\displaystyle I_{1}}, I2{\displaystyle I_{2}}, I3{\displaystyle I_{3}} (на рисунке направления уже отмечены). По первому закону Кирхгофа можно составить одно (У − 1 = 2 − 1 = 1) независимое уравнение, например для узла a

−I1−I2+I3=0{\displaystyle -I_{1}-I_{2}+I_{3}=0},

и по второму закону Кирхгофа — два (К = 2) независимых уравнения, например, для контуров 1 и 2

r1I1+r3I3=E1+E2{\displaystyle r_{1}I_{1}+r_{3}I_{3}=E_{1}+E_{2}};

r2I2+r3I3=E2+E3{\displaystyle r_{2}I_{2}+r_{3}I_{3}=E_{2}+E_{3}}.

Представим систему из этих трёх уравнений в матричной форме:

Y−1{ K{  [11−1r10r30r2r3][I1I2I3]=AI=[000101011][E1E2E3]=BE{\displaystyle {\begin{matrix}Y-1&\left\{~\right.\\K&\left\{{\begin{matrix}~\\~\end{matrix}}\right.\end{matrix}}{\begin{bmatrix}1&1&-1\\r_{1}&0&r_{3}\\0&r_{2}&r_{3}\end{bmatrix}}{\begin{bmatrix}I_{1}\\I_{2}\\I_{3}\end{bmatrix}}=AI={\begin{bmatrix}0&0&0\\1&0&1\\0&1&1\end{bmatrix}}{\begin{bmatrix}E_{1}\\E_{2}\\E_{3}\end{bmatrix}}=BE}

или

Теперь составим систему уравнений токов:

{I1=g11E1+g12E2+g13E3;I2=g21E1+g22E2+g23E3;I3=g31E1+g32E2+g33E3,{\displaystyle \left\{{\begin{matrix}I_{1}=g_{11}E_{1}+g_{12}E_{2}+g_{13}E_{3};\\I_{2}=g_{21}E_{1}+g_{22}E_{2}+g_{23}E_{3};\\I_{3}=g_{31}E_{1}+g_{32}E_{2}+g_{33}E_{3},\end{matrix}}\right.}

где

g11=(r2+r3)/r2{\displaystyle g_{11}=(r_{2}+r_{3})/r^{2}};

g22=(r1+r3)/r2{\displaystyle g_{22}=(r_{1}+r_{3})/r^{2}};

g33=(r1+r2)/r2{\displaystyle g_{33}=(r_{1}+r_{2})/r^{2}};

g12=g21=−r3/r2{\displaystyle g_{12}=g_{21}=-r_{3}/r^{2}};

g13=g31=r2/r2{\displaystyle g_{13}=g_{31}=r_{2}/r^{2}};

g23=g32=r1/r2{\displaystyle g_{23}=g_{32}=r_{1}/r^{2}};

r=r1r2+r1r3+r2r3{\displaystyle r={\sqrt {r_{1}r_{2}+r_{1}r_{3}+r_{2}r_{3}}}}.

При расчёте схем замещения с источниками тока возможны упрощения, поскольку токи ветвей с источниками тока известны, и рассчитывать их не нужно. Поэтому число независимых контуров (без источников тока), для которых необходимо составить уравнения по второму закону Кирхгофа, равно К = (В — ВJ{\displaystyle _{J}} — У + 1), где ВJ{\displaystyle _{J}} — число ветвей с источниками тока.

• Электротехника: Учеб. для вузов/А. С. Касаткин, М. В. Немцов.— 7-е изд., стер.— М.: Высш. шк., 2003.— 542 с.: ил. ISBN 5-06-003595-6

Первый закон Кирхгофа: определение, формулы, физический смысл

Первый закон Кирхгофа основан на принципе непрерывности и применим к узлу электроцепи.

Первый закон Кирхгофа определяет взаимосвязь между суммой токов, сходящихся в одном узле, и формулируется следующим образом:

Алгебраическая сумма величин токов Ik, сходящихся в любой точке (узле) электроцепи, равна нулю в любой момент времени

∑ Ik = 0,

при этом k — количество ветвей, сходящихся в узле цепи;

Ik – мгновенная величина тока для k-й ветви.

Физически Первый закона Кирхгофа означает: движение электрических зарядов осуществляется таким образом, что ни в одном из участков цепи он не имеет тенденцию к накоплению.

Отсюда, вытекает еще одна формулировка закона: в любом узле электроцепи сумма токов направленных к узлу оказывается равной сумме токов, направленных от этого узла, или:

∑ Ik = ∑ Im,

при этом k — количество ветвей, втекающих в узел;

m- — количество ветвей, вытекающих из узла.

Узлом электрической цепи принято называть точку подключения 3-х и более ветвей. ток принимается со знаком «+», если он втекает в узел, и со знаком «-», если вытекает.

К примеру, рассмотрим баланс токов на примере схемы:

I1 + I2 + I3 – I4 – I5 = 0, либо

I1 + I2 + I3 = I4 + I5.

Очевидным фактом, является то, что формулировка формы записи может иметь различный характер. Существенным является лишь принимаемая договоренность о знаке токов: нельзя использовать разнонаправленное направление в пределах одной электрической цепи для одного или нескольких узлов.

Направление тока для каждой цепи определяют произвольно. При этом нет необходимости стремиться, чтобы для всех узлов использовались токи различных направлений. Также может иметь место ситуация, что в каком-то узле все токи будут направлены от узла или к нему, что тем самым нарушает принцип непрерывности. Но в такой ситуации в процессе определения значений токов один или несколько будут отрицательными, что будет служить признаком об их протекании в противоположном направлении от принятого.

При расчете разветвленных электроцепей используются второй закон Кирхгофа. Они были сформулированы в 1945г. великим физиком 19 в. Густавом Робертом Кирхгофом.

Законы Кирхгофа | энергетик

Вернутся в раздел  ТОЭ            

   Законы Кирхгофа

              Основная цель расчета электрической цепи заключается в определении токов в её ветвях. Зная токи, нетрудно найти напряжения и мощность ветвей и отдельных элементов цепи. Связь между ЭДС, напряжениями и токами линейных электрических цепей выражается линейными уравнениями. Значения токов, напряжений и мощностей дают возможность оценить условия и эффективность работы электротехнического оборудования во всех участках электрической цепи.

Для расчета электрических цепей с законом Ома применяются два закона Кирхгофа.

Первый закон Кирхгофа

Первый закон Кирхгофа применяется к узлам электрических цепей:

В ветвях, образующих узел электрической цепи, алгебраическая сумма токов равна нулю:

∑ I = 0. 

          В эту сумму токи входят с разными знаками в зависимости от направления их по отношению к узлу. На основание первого закона Кирхгофа для каждого узла можно составить уравнения токов. Например, для точки 2 (Рис. 5(в) и (г) ) уравнение имеет вид: (см. ссылку — перейти)

I1 + I6 – I3 = 0	В этом уравнении токи, направлены к узлу, условно взяты – положительные, а токи, направленные от узла – отрицательные.
I1 + I6 = I3.	В этом уравнение первый закон Кирхгофа можно сформулировать как: сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от того же узла.

Второй закон Кирхгофа

Второй закон Кирхгофа применяется к контурам электрических цепей:

      В контуре электрической цепи алгебраическая сумма напряжений на его ветвях равна нулю:

∑ U = 0.

Рис.6

          Для доказательства второго закона Кирхгофа обойдём контур  по часовой стрелке (Рис. 6) 1-2-3-4-5-6-1 и запишем потенциалы точек контура по указанным направлениям токов в ветвях, которые выбраны произвольно. Обход начнём с точки 1, потенциал которой V1. Потенциал следующей точки выразим относительно предыдущей: V2 = V1 + E1; V3 = V2 – I1; V4 = V3 — I4; V5 = V4 – E3; V6 = V5 + I6; V1 = V6 – I3.

                 Изменение потенциала по выбранному контуру должно быть равно нулю, т.к. оно выражает работу, затраченную на перемещение частиц, обладающих вместе единицей заряда, по замкнутому пути в электрических полях источников и приёмников энергии (см. Рис. 1). Тогда в замкнутом контуре:

V1 + V2 + V3 + V4 + V5 + V6 = 0,    E1 – I1 – I4 – E3 + I6 – I3 = 0,

или   — (E1 – I1) + I4 + (E3 – I6) + I2 = 0.

Соответственно в этом уравнении напряжение ветвей: 3 – 2 – 1         E1 – I1 = U3,1;               4 – 5 – 6           E3 – I6 = U4,6; 3 – 4                 I4 = U3,4;                        6 – 1                I2 = U6,1,

поэтому U3,1 + U4,6 + U6,1 = 0. В данном уравнении напряжения считаются положительными (по обходу контура), а направления против обхода – отрицательными.

Перепишем уравнение в следующем виде:

I1 + I4 + I3 – I6 = E1 – E3.

В таком виде уравнение даёт другую формулировку второго закона Кирхгофа:

     В контуре электрической цепи алгебраическая сумма падений напряжения в пассивных элементах равна алгебраической сумме ЭДС этого контура:

∑ IR = ∑E. 

      Соответственно к другим контурам составляются другие уравнению, которые нетрудно составить, не прибегая к выражениям потенциалов точек контура, пользуясь простым правилом. В левую часть уравнения записывать алгебраическую сумму падений напряжения в пассивных элементах контура, а в правую алгебраическую сумму ЭДС, встречающихся при обходе контура. Соответственно положительными считаются токи и ЭДС, направление которых совпадает с направлением обхода.

Вернутся в раздел   ТОЭ  

Закон Кирхгофа (химия) — Википедия

У этого термина существуют и другие значения, см. Закон Кирхгофа.

Закон Кирхгофа гласит, что температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции. Уравнение Кирхгофа, являющееся следствием этого закона, используется для расчёта тепловых эффектов при разных температурах.

Дифференциальная форма закона:

(d(ΔrH)dT)p=Δrcp{\displaystyle \left({\frac {d(\Delta _{r}H)}{dT}}\right)_{p}=\Delta _{r}c_{p}}

(d(ΔrU)dT)V=ΔrcV{\displaystyle \left({\frac {d(\Delta _{r}U)}{dT}}\right)_{V}=\Delta _{r}c_{V}}

Интегральная форма закона:

ΔrHT2=ΔHT1+∫T1T2Δrcp(T)dT{\displaystyle \Delta _{r}H_{T_{2}}=\Delta H_{T_{1}}+\int \limits _{T_{1}}^{T_{2}}\Delta _{r}c_{p}(T)dT}

ΔrUT2=ΔUT1+∫T1T2ΔrcV(T)dT{\displaystyle \Delta _{r}U_{T_{2}}=\Delta U_{T_{1}}+\int \limits _{T_{1}}^{T_{2}}\Delta _{r}c_{V}(T)dT}

где Cp{\displaystyle C_{p}} и CV{\displaystyle C_{V}} — изобарная и изохорная теплоёмкости, Δrcp{\displaystyle \Delta _{r}c_{p}} — разность изобарных теплоёмкостей продуктов реакции и исходных веществ, ΔrcV{\displaystyle \Delta _{r}c_{V}} — разность изохорных теплоёмкостей продуктов реакции и исходных веществ, а ΔrH{\displaystyle \Delta _{r}H} и ΔrU{\displaystyle \Delta _{r}U} — соответствующие тепловые эффекты.

Если разница (T2−T1){\displaystyle (T_{2}-T_{1})} невелика, то можно принять Δrcp=const{\displaystyle \Delta _{r}c_{p}=const} и ΔrcV=const{\displaystyle \Delta _{r}c_{V}=const}, соответственно интегральная форма уравнений примет следующий вид:

ΔrHT2=ΔHT1+ΔrCp(T2−T1){\displaystyle \Delta _{r}H_{T_{2}}=\Delta H_{T_{1}}+\Delta _{r}C_{p}(T_{2}-T_{1})}

ΔrUT2=ΔUT1+ΔrCV(T2−T1){\displaystyle \Delta _{r}U_{T_{2}}=\Delta U_{T_{1}}+\Delta _{r}C_{V}(T_{2}-T_{1})}

При большой разнице температур необходимо учитывать температурные зависимости теплоёмкостей: Δrcp=f(T){\displaystyle \Delta _{r}c_{p}=f(T)} и ΔrcV=f(T){\displaystyle \Delta _{r}c_{V}=f(T)}

• Химическая энциклопедия / Редкол.: Кнунянц И.Л. и др.. — М.: Советская энциклопедия, 1990. — Т. 2 (Даф-Мед). — 671 с. — ISBN 5-82270-035-5.

• Закон Кирхгофа — конспект лекций