31. Электродвижущая сила. Закон Ома для неоднородного участка цепи. Закон Кирхгофа.

Мы рассматривали закон Ома (98.1) для однородного участка цепи, т. е. такого, в котором не действует ЭДС (не действуют сторонние силы). Теперь рассмотрим неоднородный участок цепи.

Если ток проходит по неподвижным проводникам, образующим участок 1—2,то работа А₁₂ всех сил (сторонних и электростатических), совершаемая над носителями тока, по закону сохранения и превращения энергии равна теплоте, выделяющейся на участке. Работа сил, совершаемая при перемещении заряда Q₀ на участке 1—2, согласно (97.4), А₁₂=Q₀ E₀+Q₀( )

ЭДС E₁₂, как и сила тока /, — величина скалярная. Ее необходимо брать либо с положительным, либо с отрицательным знаком в зависимости от знака работы, совершаемой сторонними силами. Если ЭДС способствует движению положительных зарядов в выбранном направлении (в направлении 1 — 2), то E

12 > 0. Если ЭДС препятствует движению положительных зарядов в данном направлении, то E₁₂ < 0.

За время t в проводнике выделяется теплота Q = pRt = IR(It) = IRQ₀.

(1) откуда (4)

Выражение (1) или (2) представляет собой закон Ома для неоднородного участка цепи в интегральной форме, который является обобщенным законом Ома.

Если на данном участке цепи источник тока отсутствует (E₁₂=0), то из (4) приходим к закону Ома для однородного участка цепи

(98.1): I = Ф1-Ф2/R = U/R

Если же электрическая цепь замкнута, то выбранные точки 1 и 2 совпадают, ф₁ = ф₂

тогда из (4) получаем закон Ома для замкнутой цепи: I=E/r + R₁

Р асчет разветвленных цепей значительно упрощается, если пользоваться правилами, сформулированными немецким физиком Г. Р. Кирхгофом. Этих правил два.

Первое из них относится к узлам цепи. Узлом называется точка, в которой сходится более чем два проводника

 (рис. 4.4). Ток, текущий к узлу, считается положительным, текущий от узла имеет противоположный знак. Первое правило Кирхгофа гласит, что алгебраическая сумма токов, сходящихся в узле, равна нулю: .

Это правило вытекает из уравнения непрерывности, т. е., в конечном счете, из закона сохранения заряда. Число уравнений, составленных по первому правилу Кирхгофа, должно быть на одно меньше, чем число узлов в исследуемой цепи. Этим обеспечивается линейная независимость получаемых уравнений. Второе правило относится к любому выделенному в разветвленной цепи замкнутому контуру (например, 1-3-2) (см. рис. 4.5). Зададим направление обхода, изобразив его стрелкой. Применим к каждому из неразветвленных участков контура закон Ома: ;  .

П ри сложении этих выражений получается одно из уравнений ;   которое выражает второе правило Кирхгофа: для любого замкнутого контура алгебраическая сумма всех падений напряжения равна сумме всех ЭДС в этом контуре. Подобные уравнения могут быть составлены для всех замкнутых контуров, сущ. в данной разветвленной цепи, однако их число должно быть ограничено уравнениями для независимых контуров, в которых встречается хотя бы один ток, не входящий в остальные. При составлении уравнений согласно 2-му правилу Кирхгофа токам и ЭДС нужно приписывать знаки в соответствии с выбранным направлением обхода. Например, ток   нужно считать «+», он течет по направлению обхода. ЭДС   также нужно приписать знак «плюс», так как она действует в направлении обхода. Току   и ЭДС   приписывается знак «минус». На практике, при решении задач, при составлении уравнений направления токов выбирают произвольно и в соответствии с этим применяют правило знаков. Действительное направление токов определится решением задачи: если какой-либо ток окажется положительным, то его направление выбрано правильно, если отрицательным, то в действительности он течет противоположно выбранному направлению. Число независимых уравнений, составленных в соответствии с первым и вторым правилами Кирхгофа,

 равно числу различных токов, текущих в разветвленной цепи. Поэтому, если заданы ЭДС и сопротивления, то могут быть вычислены все токи.

Если в цепи на носители тока действуют только силы электростатического поля, то происходит перемещение носителей (они предполагаются положительными) от точек с большим потенциалом к точкам с меньшим потенциалом. Это приводит к выравниванию потенциалов во всех точках цепи и к исчезновению электрического поля. Поэтому для существования постоянного тока необходимо наличие в цепи устройства, способного создавать и поддерживать разность потенциалов за счет работы сил

неэлектростатического происхождения. Такие устройства называются источниками тока. Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними.

Природа сторонних сил может быть различной. Например, в гальванических элементах они возникают за счет энергии химических реакций между электродами и электролитами; в генераторе — за счет механической энергии вращения ротора генератора и т. п. Роль источника тока в электрической цепи,

образно говоря, такая же, как роль насоса, который необходим для перекачивания жидкости в гидравлической системе. Под действием создаваемого поля сторонних сил электрические за ряды движутся внутри источника тока против сил электростатического поля, благодаря чему на концах цепи поддер-

живается разность потенциалов и в цепи течет постоянный электрический ток.

Сторонние силы совершают работу по перемещению электрических зарядов. Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электродвижущей силой (ЭДС), действующей в цепи: (97.1)

Эта работа производится за счет энергии, затрачиваемой в источнике тока, поэтому величину

E можно также называть электродвижущей силой источника тока, включенного в цепь. Часто, вместо того чтобы сказать: «в цепи действуют сторонние силы», говорят: «в цепи действует ЭДС», т. е. термин «электродвижущая сила» употребляется как характеристика сторонних сил. ЭДС, как и потенциал, выражается в вольтах. Сторонняя сила F_CT, действующая на заряд Q_o, может быть выражена как где Ест — напряженность поля сторонних сил. Работа сторонних сил по перемещению заряда Q _o на замкнутом участке цепи

Разделив (97.2) на Qo, получим выражение для ЭДС, действующей в цепи:

т.е. ЭДС, действующая в замкнутой цепи, может быть определена как циркуляция вектора напряженности поля сторонних сил. ЭДС, действующая на участке 1 — 2, равна (97.3)

На заряд Q₀ помимо сторонних сил действуют также силы электростатического поля Fe = Q₀E. Таким образом, результирующая сила, действующая в цепи на заряд Qo, равна F = F_CT + F_c = Q₀(E_CT + Е).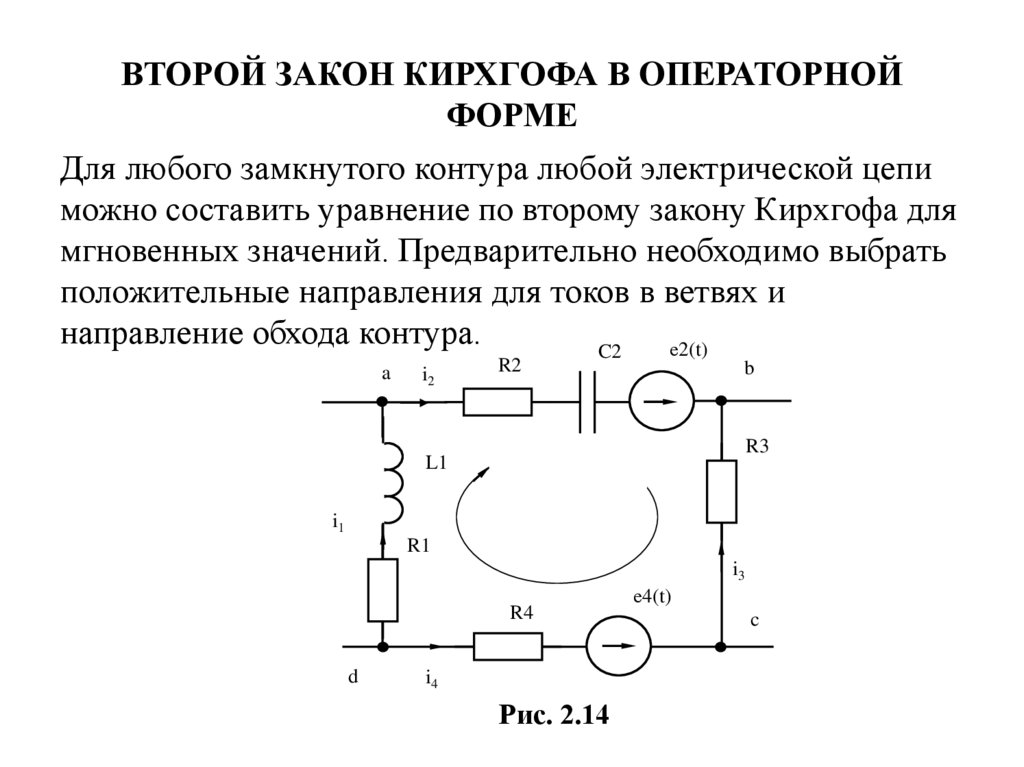

Работа, совершаемая результирующей силой над зарядом Q₀ на участке 1 — 2, равна

Используя выражения (97.3) и (84.8), можем записать

Для замкнутой цепи работа электростатических сил равна нулю (см. § 83), поэтому в данном случае А₁₂=Q₀E₁₂ .

Напряжением U на участке 1 — 2 называется физическая величина, определяемая работой, совершаемой суммарным полем электростатических (кулоновских) и сторонних сил при перемещении единичного положительного заряда на данном участке цепи. Таким образом, согласно (97.4),

Понятие напряжения является обобщением понятия разности потенциалов: напряжение на концах участка цепи равно разности потенциалов в том случае, если на этом участке не действует ЭДС, т. е. сторонние силы отсутствуют.

Правила Кирхгофа для разветвленных цепей

Чтобы расчеты сложных электрических цепей с неоднородными участками не вызывали трудности, существует упрощение с помощью применения правил Кирхгофа, которые рассматривают как обобщение закона Ома на случай разветвленных цепей.

В таких цепях выделяют узловые точки, называемые узлами, где сходятся не менее трех проводников, как изображено на рисунке 1.10.1. Токи, поступающие в узел, считают положительными, а вытекающие – отрицательными.

Рисунок 1.10.1. Узел электрической цепи. I1, I2>0; I3, I4<0.

Правила Кирхгофа. Примеры

Определение 1

В узлах цепи с постоянным током не происходит накопление зарядов. Получаем первое правило (закон) Кирхгофа:

Алгебраическая сумма сил токов для каждого узла разветвленной цепи равняется нулю:

I1+I2+I3+…+In=0.

Данное правило принято считать следствием закона сохранения электрического заряда.

Определение 2

Наличие разветвленной цепи позволяет выделить несколько замкнутых путей, которые состоят из однородных и неоднородных участков. Их принято называть

контурами.

На участках с выделенным контуром могут протекать различные токи. Рисунок 1.10.2 наглядно показывает пример такой цепи, соответствующей 1 закону Кирхгофа. Она состоит из двух узлов a и d, в которых сходятся одинаковые токи. Только один из заданных узлов будет независимым.

Рисунок 1.10.2. Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef).

В предложенной цепи выделяют три контура вида abcd, adefи abcdef. Независимыми считаются только два: abcd и adef. Последний из вышеперечисленных не имеет никаких новых участков.

Второе правило Кирхгофа – это следствие обобщенного закона Ома.

Для записи обобщенного закона Ома участков, составляющих один из контуров цепи, используется пример, изображенный на рисунке 1.10.2 для abcd. Каждому участку задаются положительные направления тока и обхода контура. Для записи следует учитывать «правила знаков», приведенные на рисунке 1.10.3.

Рисунок 1.10.3. «Правила знаков».

Запись обобщенного закона Ома для участков контура abcd принимает вид:

Для bc: I1R1=∆φbc-δ1.

Для da: I2R2=∆φda-δ2.

Сумма левых и правых частей равенств с условием ∆φbc=-∆φda преобразует выражение:

I1R1+I2R2=∆φbc+∆φda-δ1+δ2=-δ1-δ2.

Таким же образом можно записать для adef контура:

-I2R2+I3R3=δ2+δ3.

Определение 3

Формулировка 2 правила или закона Кирхгофа: алгебраическая сумма сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока этого участка равняется сумме ЭДС вдоль этого контура.

Модель постоянного тока

Оба правила Кирхгофа для всех узлов и контуров разветвленной цепи дают необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов электрической цепи. Цепь, изображенная на рисунке 1.10.2, рассматривается как система уравнений для определения трех неизвестных I1, I2 и I3:

I1R1+I2R2=-δ1-δ2,

-I2R2+I3R3=δ2+δ3,

-I1+I2+I3=0.

То есть применение этих правил помогает свести расчет электрической цепи постоянного тока к решению системы. Процесс не вызывает трудностей, но зачастую приходится работать с громоздкими выражениями простых цепей. При получении отрицательного значения силы тока на участке цепи говорят о противоположном направлении тока, относительно выбранного.

Рисунок 1.10.4. Модель цепи постоянного тока.

Рисунок 1.10.5.Модель конденсаторов в цепях постоянного тока.

Автор: Роман Адамчук

Преподаватель физики

законов Кирхгофа и их применение в проектировании печатных плат | Блог Advanced PCB Design

 

Законы созданы для того, чтобы их нарушать? Ну, это так, когда речь идет о воспитании детей. В детстве слова мамы – закон, и я уже не помню, сколько раз я их нарушал. Теперь я нахожусь на принимающей стороне, поскольку у меня есть сын, и я собираюсь отказаться от требований послушания.

Но законы существуют не просто так. Это помогает поддерживать порядок и обеспечивать мирное разрешение конфликтов. При проектировании печатной платы необходимо помнить о нескольких фундаментальных законах, поскольку они напрямую влияют на ваш подход к самому проектированию. Одним из таких законов является закон Кирхгофа, с которым должен быть знаком каждый выпускник электроники.

Что такое закон Кирхгофа?

Давайте отправимся в путешествие по закоулкам памяти и заново откроем для себя суть закона Кирхгофа. Вы хорошо помните, как ваш лектор утверждает, что закон Кирхгофа касается значений напряжения и силы тока в замкнутой цепи.

Чтобы быть точным, закон Кирхгофа состоит из двух частей: закона тока Кирхгофа и закона напряжения Кирхгофа.

Текущий закон Кирхгофа определяет, что сумма всех текущих входов и выходов из одного узла должна равняться нулю.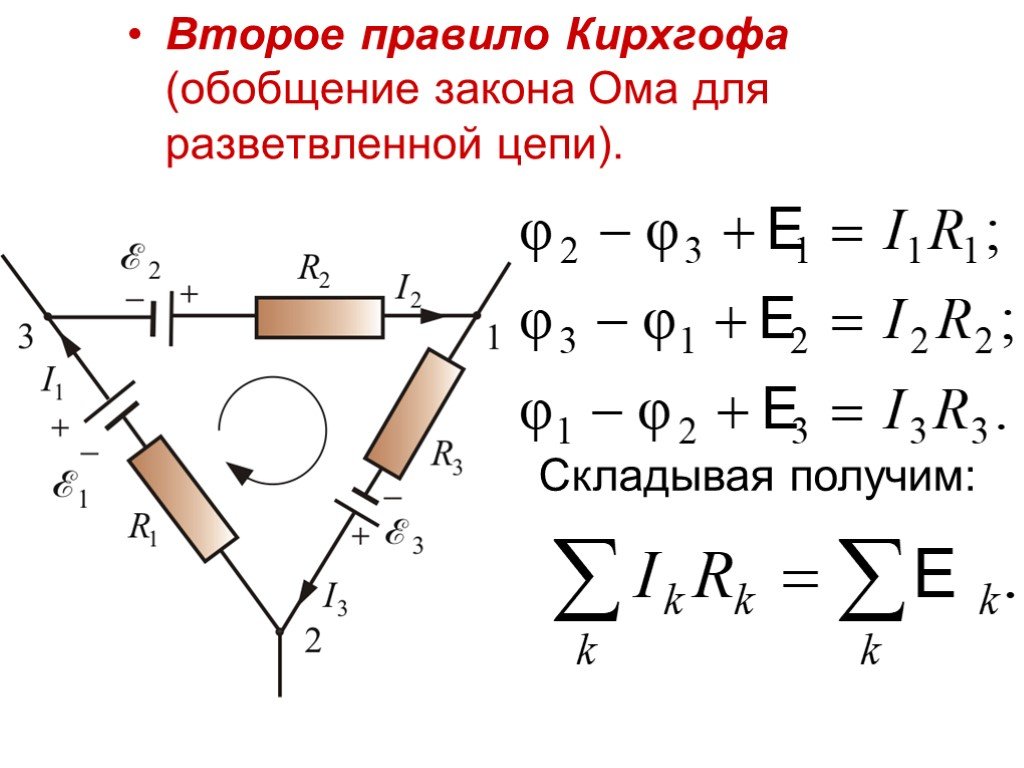 Другими словами, закон указывает, как применяется сохранение зарядов в замкнутой цепи.

Между тем закон Кирхгофа о напряжении утверждает, что сумма напряжений в замкнутой цепи всегда будет равна нулю.

Оба закона Кирхгофа легли в основу проектирования схем и определили передовой опыт, обеспечивающий надежность и функциональность печатных плат.

Закон Кирхгофа и токовая петля 4–20 мА.

В большинстве коммерческих и бытовых электронных устройств вы привыкли к цифровым сигналам. Но при проектировании для промышленных приложений вы обнаружите, что сигнализация токовой петли, например 4-20 мА, является предпочтительным методом.

В датчиках обычно используется токовая петля 4–20 мА. Такие параметры, как воздушный поток, давление и скорость, передаются током, а не напряжением. Значения от 4 мА до 20 мА соответствуют фактическим показаниям. Эти датчики обычно размещаются далеко от принимающего контроллера, и входные значения имеют решающее значение для работы контроллера.

 

Промышленные датчики 4-20 мА основаны на Законе Кирхгофа

 

На вопрос, почему токовая петля 4–20 мА предпочтительнее цифровой сигнализации, можно ответить с помощью закона Кирхгофа. Закон Кирхгофа о напряжении подразумевает, что падение напряжения следует ожидать по длине кабеля. Кроме того, электрические помехи могут быть связаны и влиять на достоверность показаний.

Токовая петля 4–20 мА использует закон Кирхгофа о токах, который гласит, что общий ток, входящий и выходящий из узла, должен быть равен. Это означает, что ток, генерируемый датчиком, не будет теряться при перемещении по кабелю. Теоретически значение, которое улавливает приемник, равно тому, что генерирует датчик.

Закон Кирхгофа и плотность тока.

Легко размышлять и руководствоваться законом Кирхгофа, когда это простое приложение, такое как токовая петля 4–20 мА. Но есть аспекты проектирования печатных плат, где закон Кирхгофа верен, но его часто упускают из виду.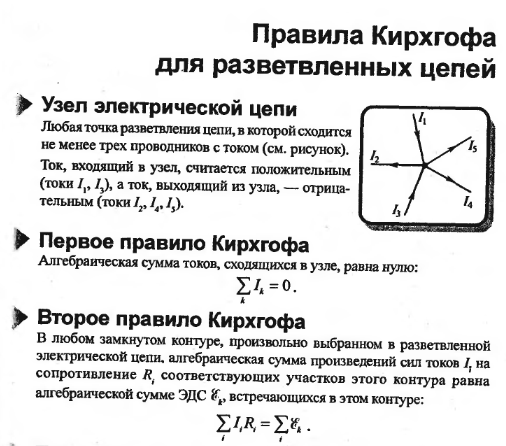

И мы говорим о плотности тока.

Общеизвестно, что дорожки на печатных платах могут выдерживать лишь некоторое количество тока до нагрева. Чрезмерное тепло изнашивает медные дорожки или, в некоторых случаях, приводит к поломке дорожек. Токопроводящая способность дорожки печатной платы определяется шириной и толщиной меди.

У большинства проектировщиков печатных плат нет проблем с правильным подключением дорожек печатных плат к сильноточным компонентам. Но проблемы обычно возникают на дорожках, где объединено более одной сильноточной трассы.

 

Существует ограничение на то, какой ток может потреблять дорожка печатной платы.

 

Текущий закон Кирхгофа гласит, что общая сумма текущих входов и входов в узел должна равняться нулю. Этот закон означает, что дорожка печатной платы, по которой протекает комбинированный ток, должна иметь достаточно большую ширину, чтобы предотвратить накопление тепла.

Например, обратный путь, ведущий к GND, должен иметь правильные физические размеры, чтобы выдерживать пиковый ток. Неспособность обнаружить эти горячие точки плотности тока приведет к потенциальным проблемам при их развертывании.

Чтобы предотвратить это, вы должны помнить о законе Кирхгофа и использовать расширенные функции программного обеспечения для проектирования печатных плат, которое вы используете, для обнаружения дорожек с высокой плотностью тока. Вам понадобится что-то вроде PSpice Simulator OrCAD для точного моделирования текущих параметров.

Если вы хотите узнать больше о том, какое решение у Cadence есть для вас, обратитесь к нам и нашей команде экспертов.

Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.

Подпишитесь на Linkedin Посетите вебсайт Больше контента от Cadence PCB Solutions

current — В чем смысл закона Кирхгофа

спросил 3 года, 4 месяца назад

Изменено 3 года, 4 месяца назад

Просмотрено 205 раз

\$\начало группы\$

Я понимаю алгебру, а также могу использовать закон Кирхгофа в расчетах.

Но я изо всех сил пытаюсь понять логический смысл этого.

Закон гласит, что сумма токов, входящих в узел, должна быть равна сумме токов, выходящих из этого узла.

Теперь это имело бы смысл в цепи без резисторов, но если я применю резисторы, ток замедлится, и, следовательно, количество кулонов, проходящих через него в секунду (ампер), будет снижено, а ток на другая сторона точно будет ниже, чем перед резистором?

Как это связано с текущим законом Кирхгофа?

• текущий
• базовый
• электрический
• закон Кирхгофа

\$\конечная группа\$

19

\$\начало группы\$

Ток – это количество электрического заряда, проходящего через площадь поперечного сечения в единицу времени. Напряжение можно рассматривать (но не так!) как силу. Электрический заряд переносится электронами. Напряжение обеспечивает разность энергий, заставляющую электроны двигаться в одном направлении.

На этой картинке мы теперь можем видеть, что в работу преобразуются не электроны, а энергетический потенциал, придаваемый ему напряжением, которое приводит к возникновению потока электронов. Электроны — сохраняющаяся физическая величина, поэтому то, что входит в соединение, должно в равной степени сохраняться тем, что существует в соединении.

В тепло превращается потенциал, напряжение. Поэтому электроны не превращаются в тепло, а существуют в равном количестве и в таком же количестве покидают узлы. Однако вы получаете падение напряжения на сопротивлении.

Дать механическую интерпретацию. Если вы катите большой камень вверх по холму, а затем толкаете его вниз по склону к стене. Стена будет оказывать сопротивление, камень будет проталкиваться через стену и терять энергию в процессе, но камень все еще остается камнем, с той же физической величиной, с теми же физическими свойствами. .. и т.д. Что изменилось, так это то, что энергетический потенциал, переданный какой-то внешней сущностью (вы толкаете ее в гору), был преобразован в тепловую и кинетическую энергию. Горная порода не превратилась в тепловую энергию, она остается горной породой, таким был заданный ей энергетический потенциал. Теперь, если вы скатили несколько камней вниз с холма один за другим, несмотря на сопротивление и потери энергии, которые произошли, камни позади него не испытали этой потери и будут толкать первый камень вперед, а тот, что за этим камнем, будет иметь сам выдвинулся вперед… и т.д. Поскольку ток представляет собой связную цепочку таких камней, ваш поток на входе и выходе будет равным. Что входит, должно выйти. Вы просто должны продолжать представлять дифференциал энергии, чтобы продолжать продвигать их вперед (напряжение или гравитация в примере с камнем).

\$\конечная группа\$

\$\начало группы\$

Да, резистор замедляет скорость тока (для данного потенциала).