Закон кирхгофа 1 и 2. Законы Кирхгофа простыми словами: определение для электрической цепи
История
Пополнил ряды немецких ученых Кирхгоф в девятнадцатом столетии, когда в стране, находившаяся на пороге революции индустриальной, требовались новейших технологии. Ученые занимались поиском решений, которые могли бы ускорить развитие промышленности.
Активно занимались исследованиями в области электричества, поскольку понимали, что в будущем оно будет широко использоваться. Проблема состояла на тот момент не в том, как составлять электрические цепи из возможных элементов, а в проведении математических вычислений. Тут и появились законы, сформулированные физиком. Они очень помогли.
Алгебраическая сумма приходящих к узлам токов и исходящих из него равна нулю. Эта одновременно вытекает из другого закона — постоянства энергии.
К узлу подходят 2 провода, а отходит один. Значение тока, текущего от узла, такое же, как сумма его, протекающего по двум остальным проводникам, т. е. идущим к нему. Правило Кирхгофа объясняет, что, при ином раскладе, накапливался бы заряд, но такого не бывает. Все знают, что всякую сложную цепь легко разделить на отдельные участки.
е. идущим к нему. Правило Кирхгофа объясняет, что, при ином раскладе, накапливался бы заряд, но такого не бывает. Все знают, что всякую сложную цепь легко разделить на отдельные участки.
Но, при этом непросто определить путь, по которому он проходит. Тем более, что на различных участках сопротивления не одинаковы, поэтому и распределение энергии не будет равномерным.
В соответствие со Вторым правилом Кирхгофа, энергия электронов на каждом из замкнутых участков электрической цепи равняется нулю – нулю равняется всегда в таком контуре суммарное значение напряжений. Если бы нарушилось данное правило, энергия электронов при прохождении определенных участков, уменьшалась бы или увеличивалась. Но, этого не наблюдается.
Соединения проводников
Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников.
Резисторы и подводящие провода
Проводник, обладающий сопротивлением R, мы называем резистором и изображаем следующим образом (рис.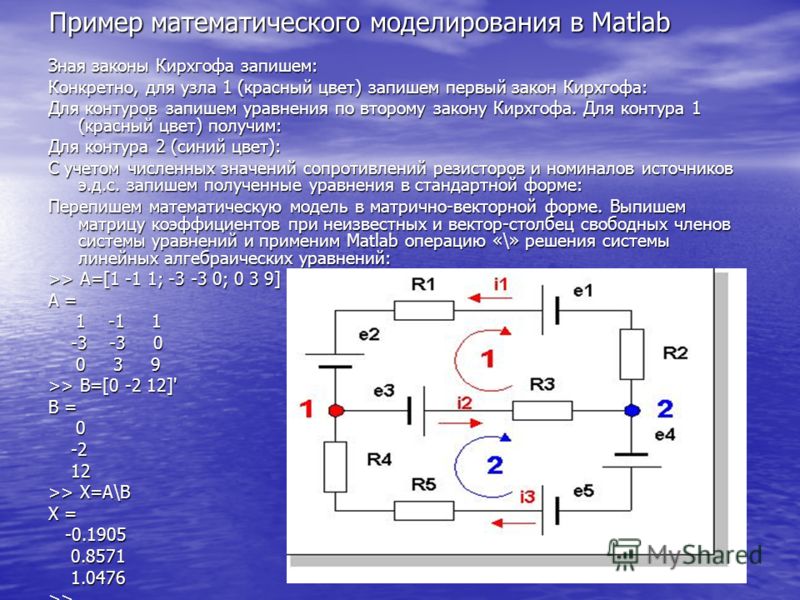 1):
1):
Рис. 1 Резистор
Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.
Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.
Пусть положительный заряд q перемещается по цепи из точки a в точку b, проходя через резистор R (рис. 2):
Рис.2 U = φa – φb
Стационарное поле совершает при этом положительную работу A = q(φa − φb). Так как q > 0 и A > 0, то и φa − φb > 0, т. е. φa > φb.
Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: U = φa − φb.
Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если φa − φb = IR и R = 0, то φa = φb (рис. 3):
3):
Рис.3 φa = φb
Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным. В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.
Последовательное соединение
При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.
Рассмотрим два резистора R1 и R2, соединённых последовательно и подключённых к источнику постоянного напряжения U (рис. 4). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.
Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере:
- При последовательном соединении проводников сила тока в них одинакова.
 В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне. - Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике. Действительно, напряжение Uab на участке ab — это работа поля по переносу единичного заряда из точки a в точку b; напряжение Ubc на участке bc — это работа поля по переносу единичного заряда из точки b в точку c. Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки a в точку c, то есть напряжение U на всём участке: U = Uab + Ubc.
Можно и более формально, без всяких словесных объяснений: U = Uac = φa − φc = (φa − φb) + (φb − φc) = Uab + Ubc.
- Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника. Пусть R — сопротивление участка ac. По закону Ома имеем:
что и требовалось.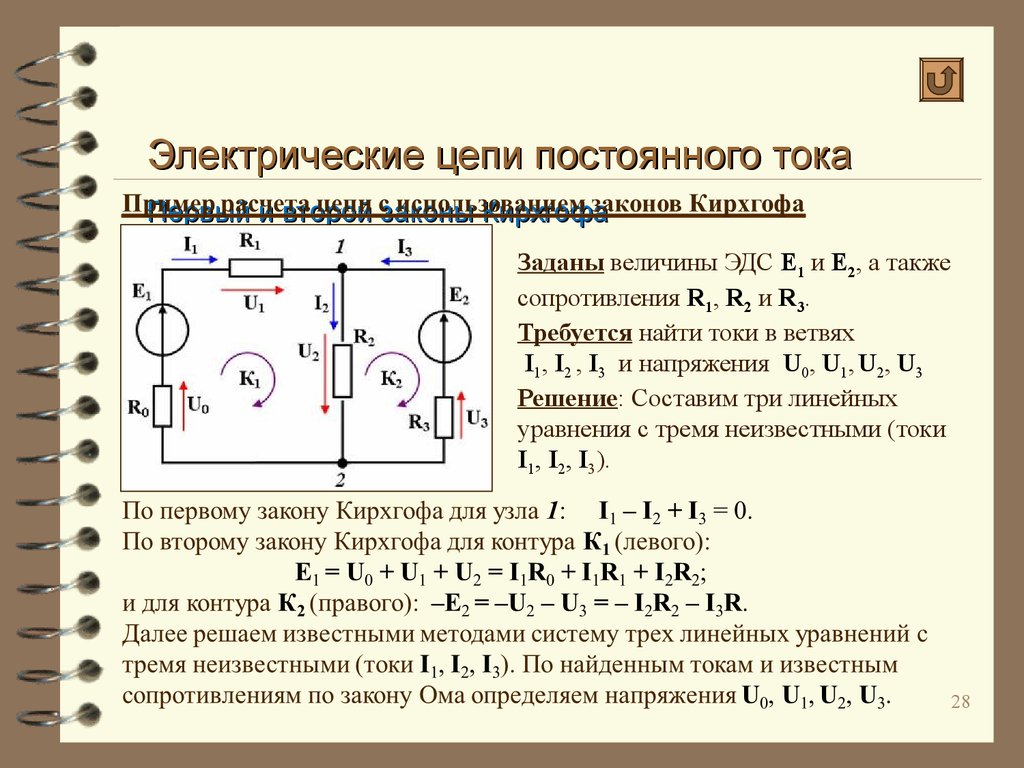
Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения S, но с разными длинами l1 и l2.
Сопротивления проводников равны:
Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения. Доказательство этого даётся с помощью закона Ома, как показано выше. Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.
Параллельное соединение
При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.
Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5).
Резисторы подсоединены к двум точкам: a и b. Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями; участок от b к a (по направлению тока) называется неразветвленной частью цепи.
Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями; участок от b к a (по направлению тока) называется неразветвленной частью цепи.
Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов:
- Напряжение на каждой ветви одинаково и равно напряжению на неразветвленной части цепи. В самом деле, оба напряжения U1 и U2 на резисторах R1 и R2 равны разности потенциалов между точками подключения:
U1 = U2 = φa − φb = U.
Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.
- Сила тока в неразветвленной части цепи равна сумме сил токов в каждой ветви. Пусть, например, в точку a за время t из неразветвленного участка поступает заряд q. За это же время t из точки a к резистору R1 уходит заряд q1, а к резистору R2 — заряд q2. Ясно, что q = q1 + q2. В противном случае в точке a накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем).
 Тогда имеем:
Тогда имеем:
что и требовалось.
- Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей. Пусть R — сопротивление разветвлённого участка ab. Напряжение на участке ab равно U; ток, текущий через этот участок, равен I. Поэтому:
Сокращая на U, получим:
1/R = 1/R1 + 1/R2 ,
что и требовалось.
Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами l, но разными поперечными сечениями S1 и S2. Тогда это соединение можно рассматривать как проводник той же длины l, но с площадью сечения S = S1 + S2. Имеем:
Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.
Из соотношения (1) можно найти R:
R = R1R2/(R1 + R2) .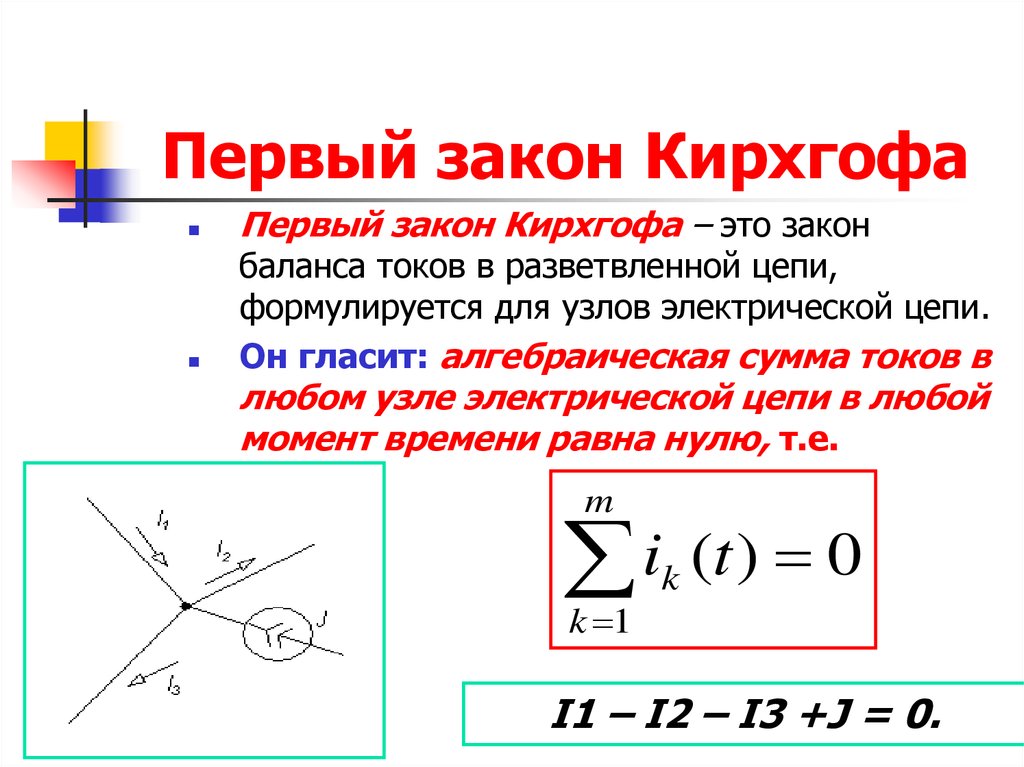
К сожалению, в общем случае n параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением
1/R = 1/R1 + 1/R2 + . . . + 1/Rn .
Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех n резисторов одинаковы и равны R1. Тогда:
Мы видим, что сопротивление участка из n параллельно соединённых одинаковых проводников в n раз меньше сопротивления одного проводника.
Смешанное соединение
Смешанное соединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.
Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.
Рассмотрим пример смешанного соединения проводников (рис. 6).
Рис. 6 Смешанное соединение
Пусть U = 14 В, R1 = 2 Ом, R2 = 3 Ом, R3 = 3 Ом, R4 = 5 Ом, R5 = 2 Ом. Найдём силу тока в цепи и в каждом из резисторов.
Наша цепь состоит из двух последовательно соединённых участков ab и bc. Сопротивление участка ab:
Сопротивление цепи: R = Rab + Rbc = 1,2 + 1,6 = 2,8 Ом.
Теперь находим силу тока в цепи:
I = U/R = 14/2,8 = 5 A.
Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:
Uab = IRab = 5 · 1,2 = 6 B;
Ubc = IRbc = 5 · 1,6 = 8 B.
(Заметим попутно, что сумма этих напряжений равна 14 В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)
Оба резистора R1 и R2 находятся под напряжением Uab, поэтому:
Стало быть, через резистор R5 течёт ток I5 = I − I3 = 5 − 1 = 4 A
Законы Кирхгофа
Законы Кирхгофа – правила, которые показывают, как соотносятся токи и напряжения в электрических цепях. Эти правила были сформулированы Густавом Кирхгофом в 1845 году. В литературе часто называют законами Кирхгофа, но это не верно, так как они не являются законами природы, а были выведены из третьего уравнения Максвелла при неизменном магнитном поле. Но все же, первое более привычное для них название, поэтому и мы будет их называть, как это принято в литературе – законы Кирхгофа.
Эти правила были сформулированы Густавом Кирхгофом в 1845 году. В литературе часто называют законами Кирхгофа, но это не верно, так как они не являются законами природы, а были выведены из третьего уравнения Максвелла при неизменном магнитном поле. Но все же, первое более привычное для них название, поэтому и мы будет их называть, как это принято в литературе – законы Кирхгофа.
Первый закон Кирхгофа
Первый закон Кирхгофа говорит, что сумма токов в любом узле электрической цепи равна нулю. Существует и другая, аналогичная по смыслу формулировка: сумма значений токов, входящих в узел, равна сумме значений токов, выходящих из узла.
Давайте разберем сказанное более подробно. Узлом называют место соединения трех и более проводников.
Ток, который втекает в узел, обозначается стрелкой, направленной в сторону узла, а выходящий из узла ток – стрелкой, направленной в сторону от узла.
Согласно первому закону Кирхгофа
Условно присвоили знак «+» всем входящим токам, а «-» ‑ все выходящим. Хотя это не принципиально.
Хотя это не принципиально.
1 закон Кирхгофа согласуется с законом сохранения энергии, поскольку электрические заряды не могут накапливаться в узлах, поэтому, поступающие к узлу заряды покидают его.
Убедиться в справедливости 1-го закона Кирхгофа нам поможет простая схема, состоящая из источника питания, напряжением 3 В (две последовательно соединенные батарейки по 1,5 В), три резистора разного номинала: 1 кОм, 2 кОм, 3,2 кОм (можно применять резисторы любых других номиналов). Токи будем измерять мультиметром в местах, обозначенных амперметром.
Если сложить показания трех амперметров с учетом знаков, то, согласно первому закону Кирхгофа, мы должны получить ноль:
I1 – I2 – I3 = 0.
Или показания первого амперметра А1 будет равняться сумме показаний второго А2 и третьего А3 амперметров.
Второй закон Кирхгофа и его определение
В едином замкнутом контуре алгебраическая сумма ЭДС будет равняться на значение, которое суммирует изменения напряжения на всеобщее количество резистивных элементов данного контура.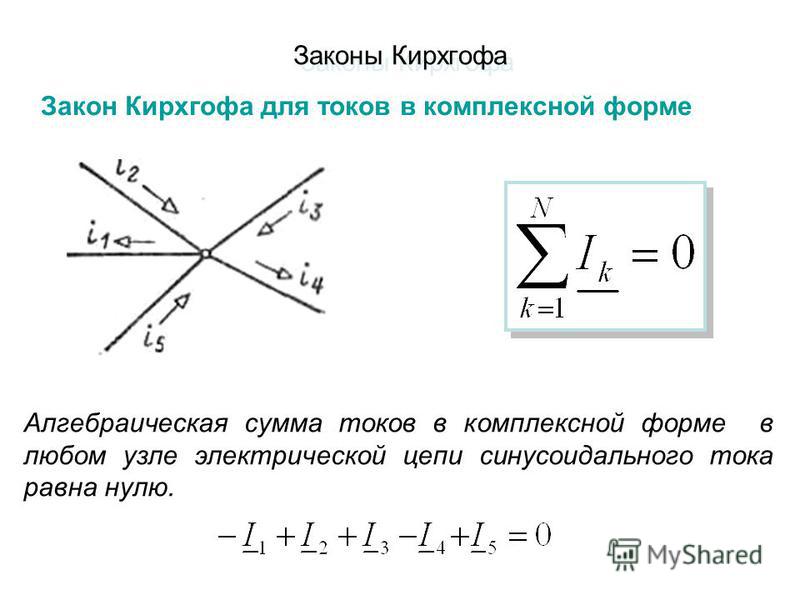
Второе правило Кирхгофа актуально в сетях с постоянным и/или переменным током. В формулировке закона используется именно понятие алгебраическая сумма, так как она может быть указана со знаком плюс или минус. Точное определение возможно в таком случае только посредством простого, но эффективного алгоритма. Для начала надо подобрать какое-то направление для обхода контура, по/против часовой стрелке, на собственное усмотрение. Само направление тока подбирается только через элементы цепи. После следует определить знаки «+» и «-» для напряжениях и ЭДС. Напряжения нужно записывать с отрицательным знаком, когда ток не соответствует обходу контура в плане направления и с плюсом в случае совпадения. То же самое правило нужно использовать и в том случае, когда необходимо отметить ЭДС.
Значение правил Кирхгофа
Законы Кирхгофа выражают фундаментальные принципы физики. Их формулировки кажутся очень простыми и очевидными. Но на самом деле они представляют собой метод, позволяющий рассчитать электрические параметры сетей очень сложной конфигурации.
С помощью законов Кирхгофа можно составить систему независимых уравнений для расчета параметров электрической цепи. Важно, чтобы их количество было не меньше, чем число параметров, которые необходимо определить.
На приведённом рисунке представлена электроцепь, для которой будет проводиться расчёт. Используя первый закон или правило Кирхгофа, для узла A можно записать:
I = I1 + I2.
В этот узел входят два тока, а выходит один. Далее необходимо применить второе правило. Для этого можно выбрать внешний контур. Видно, что здесь имеется два источника тока и два резистора. Поэтому будут получены уравнения:
Здесь приведены 2 эквивалентные формулы. В левой части равенства учтены электродвижущие силы двух источников тока, в правой — падение напряжения на обоих резисторах с учётом направления токов. Ещё одно уравнение можно получить из 2 закона при обходе по правому внутреннему контуру:
В результате получена система, включающая в себя три уравнения с тремя неизвестными:
Используя конкретные данные, можно подставить в систему уравнений численные значения и найти, чему равна сила тока для каждой ветви, относящейся к узлу A. При расчётах важно понимать, что при достаточно сложной конфигурации электроцепи иногда бывает непросто определить направление силы тока для каждой ветви.
При расчётах важно понимать, что при достаточно сложной конфигурации электроцепи иногда бывает непросто определить направление силы тока для каждой ветви.
Первый и второй законы Густава Кирхгофа позволяют точно определить не только величину тока, но и его знак. Если в приведённом примере после вычисления искомых значений с помощью представленной системы уравнений окажется, что ток с индексом 2 принимает отрицательное значение, то это означает, что на самом деле он имеет направление, противоположное указанному на рисунке.
Использование закона Кирхгофа о напряжениях в сложной цепи
Закон Кирхгофа о напряжениях можно использовать для определения неизвестного напряжения в сложной цепи, где известны все другие напряжения вдоль определенного «контура». В качестве примера возьмем следующую сложную схему (на самом деле две последовательные цепи, соединенные одним проводом внизу):
Рисунок 10 – Правило напряжений Кирхгофа в сложной цепи
Чтобы упростить задачу, я опустил значения сопротивлений и просто указал падение напряжения на каждом резисторе. Две последовательные цепи имеют между собой общий провод (провод 7-8-9-10), что делает возможными измерения напряжения между этими двумя цепями. Если бы мы хотели определить напряжение между точками 4 и 3, мы могли бы составить уравнение правила напряжений Кирхгофа с напряжением между этими точками как неизвестным:
Две последовательные цепи имеют между собой общий провод (провод 7-8-9-10), что делает возможными измерения напряжения между этими двумя цепями. Если бы мы хотели определить напряжение между точками 4 и 3, мы могли бы составить уравнение правила напряжений Кирхгофа с напряжением между этими точками как неизвестным:
E4-3 + E9-4 + E8-9 + E3-8 = 0
E4-3 + 12 + 0 + 20 = 0
E4-3 + 32 = 0
E4-3 = -32 В
Рисунок 11 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 4 и 3Рисунок 12 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 9 и 4Рисунок 13 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 8 и 9Рисунок 14 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 3 и 8
Обойдя контур 3-4-9-8-3, мы записываем значения падений напряжения так, как их регистрировал бы цифровой вольтметр, измеряя с красным измерительным проводом в точке впереди и черным измерительным проводом на точке позади, когда мы продвигаемся вперед по контуру. Следовательно, напряжение в точке 9 относительно точки 4 является положительным (+) 12 вольт, потому что «красный провод» находится в точке 9, а «черный провод» – в точке 4.
Следовательно, напряжение в точке 9 относительно точки 4 является положительным (+) 12 вольт, потому что «красный провод» находится в точке 9, а «черный провод» – в точке 4.
Напряжение в точке 3 относительно точки 8 составляет положительные (+) 20 вольт, потому что «красный провод» находится в точке 3, а «черный провод» – в точке 8. Напряжение в точке 8 относительно точки 9, конечно, равно нулю, потому что эти две точки электрически общие.
Наш окончательный ответ для напряжения в точке 4 относительно точки 3 – это отрицательные (-) 32 вольта, говорящие нам, что точка 3 на самом деле положительна относительно точки 4, именно это цифровой вольтметр показал бы при красном проводе в точке 4 и черном проводе в точке 3:
Рисунок 15 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 4 и 3
Другими словами, первоначальное размещение наших «измерительных щупов» в этой задаче правила напряжений Кирхгофа было «обратным». Если бы мы сформировали наше уравнение второго закона Кирхгофа, начиная с E3-4, вместо E4-3, обходя тот же контур с противоположной ориентацией измерительных проводов, окончательный ответ был бы E3-4 = +32 вольта:
Рисунок 16 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 3 и 4
Напряжение между точками 3 и 4
Важно понимать, что ни один из подходов не является «неправильным». В обоих случаях мы приходим к правильной оценке напряжения между двумя точками 3 и 4: точка 3 положительна по отношению к точке 4, а напряжение между ними составляет 32 вольта.
Правило Кирхгофа применительно к синусоидальным токам
Правила для синусоидального, такие же, как для тока постоянного. Правда, учитываются величины напряжений с комплексными токами.
Первое звучит: «в электрической цепи нулю равна сумма алгебраическая комплексных токов в узле».
Второе правило выглядит так: «алгебраическая сумма ЭДС комплексных в контуре замкнутом равняется сумме алгебраической значений комплексных напряжений, имеющихся на пассивных составляющих данного контура.
Источники
- https://motocarrello.
 ru/jelektrotehnologii/1510-zakon-kirhgofa-dlja-jelektricheskoj-cepi.html
ru/jelektrotehnologii/1510-zakon-kirhgofa-dlja-jelektricheskoj-cepi.html - http://razmishlyajem.ru/o-raznom-vsyakom/prochee/dlya-studentov/zakony-kirxgofa
- https://faultan.ru/simulation/toe/kirchhoffs_laws/
- https://Zaochnik.com/spravochnik/fizika/postojannyj-elektricheskij-tok/pravila-kirhgofa-dlja-razvetvlennyh-tsepej/
- https://diodov.net/zakony-kirhgofa-prostymi-slovami/
- https://reshit.ru/vtoroj-zakon-kirxgofa
- https://ProFazu.ru/knowledge/electrical/zakon-kirhgofa.html
- https://radioprog.ru/post/1005
Как вам статья?
Павел
Бакалавр «210400 Радиотехника» – ТУСУР. Томский государственный университет систем управления и радиоэлектроники
Написать
Пишите свои рекомендации и задавайте вопросы
Законы Кирхгофа — СИБЭЛЕКТРОТЕХНИК
Законы Кирхгофа
Распределение токов, а также и напряжений, т. е. разностей потенциалов между отдельными точками в сложных цепях, состоящих из любой комбинации источников постоянного тока и сопротивлений, устанавливается одним и только одним вполне определенным образом.
Нахождение токов в отдельных ветвях производится при помощи законов Кирхгофа, непосредственно вытекающих из общих представлений об электрическом токе.
При установившемся режиме во всякой точке цепи сумма притекающих электрических зарядов должна равняться сумме утекающих зарядов, так как происходило бы бесконечное накопление электрического заряда.
Поэтому во всякой точке разветвления сумма притекающих токов должна равняться сумме утекающих токов,
или если считать, например, с одним знаком + положительными, а утекающие с другим знаком (—)—отрицательными, то алгебраическая сумма токов в точке разветвления должна равняться нулю. Это соотношение, называемое первым законом Кирхгофа, может быть выражено для какой нибудь точки раз ветвления (фиг. 1) следующим образом:
I1-I2-I3+I4-I5=∑I=0
фиг.1 Фиг.2
Для не разветвленной цепи первый закон Кирхгофа означает, что ток во всех частях цепи имеет одно и то же значение, так как в каждом сечении притекающий ток равняется утекающему.
Если рассматривать какой ни будь замкнутый контур разветвленной цепи и проследить, как меняются потенциалы при последовательном обходе всех ветвей (сторон) этого контура, то, очевидно, мы после обхода всего контура по возвращение к исходной точке должны получить тот же потенциал.
Возьмем контур, изображенный на фиг. 2, и предположим, что токи имеют направления, указанные на чертеже. Пусть потенциал в точке А равен φа. При переходе к узлу В потенциал понизится на I1r1, следовательно, в точке В потенциал будет равен φа — I1r1, далее, во второй ветви мы имеем снижение потенциала на I2r2, а затем при переходе через источник энергии с отрицательного его полюса к положительному — повышение потенциала, равное э. д. с. Е2 этого источника (предполагаем, что источник энергии не имеет внутреннего сопротивления). Следовательно, потенциал в точке С будет:
φc=φa-I1r1-I2r2+E2
При обходе третьей ветви мы идем против направления тока и имеем повышение потенциала и т. д., и если мы дойдем до исходной точки А, то
φa-I1r1-I2r2+E2+I3r3-E4+I4r4+I5r5=φa
откуда
E2-E4=I1r1+I2r2-I3r3-I4r4-I5r5
Если в рассматриваемом контуре э. д. с. и токи, направленные в одну сторону, например, по стрелке часов, считать положительными, а э. д. с. и токи, направленные в обратную сторону, — отрицательными, то для замкнутого контура второй закон Кирхгофа можно сформулировать следующим образом: в замкнутом контуре алгебраическая сумма э. д. с. равна алгебраической сумме падений напряжения в отдельных сопротивлениях, входящих в этот контур: ∑E=∑Ir
д. с. и токи, направленные в одну сторону, например, по стрелке часов, считать положительными, а э. д. с. и токи, направленные в обратную сторону, — отрицательными, то для замкнутого контура второй закон Кирхгофа можно сформулировать следующим образом: в замкнутом контуре алгебраическая сумма э. д. с. равна алгебраической сумме падений напряжения в отдельных сопротивлениях, входящих в этот контур: ∑E=∑Ir
одна и та же, а потому: E1-E2+E3=I(r1+r2+r3)
т.е. ∑E=I∑r, или I=∑E/∑r
Ток в не разветвленной цепи равен алгебраической сумме э. д. с., деленной на (арифметическую) сумму сопротивлений, входящих в эту цепь.
Найти:
СЕРТИФИКАТ ISO 9001-2015
ВОЗМОЖНО ВАС ЗАИНТЕРЕСУЕТ
ШКАФ ДЛЯ МУПР1 и МУРБ1
ЭЛЕКТРОПРИВОД ПОДАЧИ
НОВОСТИ
ГАЛЕРЕЯ
ПРОДАЁМ
КОМПЛЕКТУЮЩИЕ В НАЛИЧИИ
ЦИТАТЫ
Электричество должно быть таким же дешевым, как кислород, потому что его нельзя уничтожить /Томас Эдисон/
Выберите себе работу по душе, и вам не придётся работать ни одного дня в своей жизни.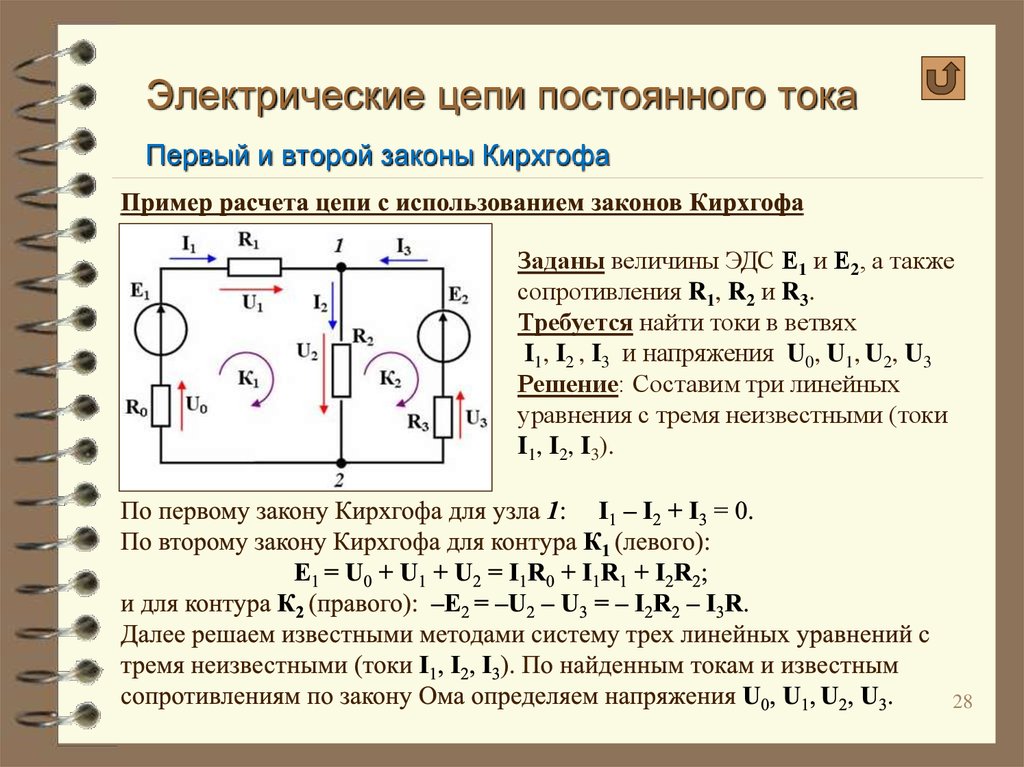 /Конфуций/
/Конфуций/
Электричество | Определение, факты и типы
электрическая сила между двумя зарядами
Смотреть все СМИ
- Ключевые люди:
- Томас Эдисон Рукс Эвелин Белл Кромптон Эдвард Уэстон Чарльз Фрэнсис Браш Флиминг Дженкин
- Похожие темы:
- биоэлектричество термоэлектричество электрический потенциал электролиз электрофорез
Просмотреть весь соответствующий контент →
Резюме
Прочтите краткий обзор этой темы
электричество , явление, связанное с неподвижными или движущимися электрическими зарядами. Электрический заряд является фундаментальным свойством материи и переносится элементарными частицами. В электричестве задействованной частицей является электрон, несущий заряд, условно обозначаемый как отрицательный. Таким образом, различные проявления электричества являются результатом накопления или движения множества электронов.
Электростатика — это изучение электромагнитных явлений, происходящих при отсутствии движущихся зарядов, т. е. после установления статического равновесия. Заряды быстро достигают своего положения равновесия, потому что электрическая сила чрезвычайно велика. Математические методы электростатики позволяют рассчитывать распределения электрического поля и электрического потенциала по известной конфигурации зарядов, проводников и изоляторов. И наоборот, по набору проводников с известными потенциалами можно рассчитать электрические поля в областях между проводниками и определить распределение заряда на поверхности проводников. Электрическую энергию набора зарядов в состоянии покоя можно рассматривать с точки зрения работы, необходимой для сборки зарядов; в качестве альтернативы можно также считать, что энергия находится в электрическом поле, создаваемом этим набором зарядов. Наконец, энергию можно хранить в конденсаторе; энергия, необходимая для зарядки такого устройства, запасается в нем в виде электростатической энергии электрического поля.
Изучите, что происходит с электронами двух нейтральных объектов, потертых друг о друга в сухой среде
Просмотреть все видео к этой статье Жирные буквы в уравнении указывают на векторный характер силы, а единичный вектор r̂ — это вектор размера 1, который указывает от заряда Q 2 до заряда Q 1 . Константа пропорциональности k равна 10 −7 c 2 , где c — скорость света в вакууме; k имеет числовое значение 8,99 × 10 9 ньютонов-квадратный метр на кулон в квадрате (Нм
Константа пропорциональности k равна 10 −7 c 2 , где c — скорость света в вакууме; k имеет числовое значение 8,99 × 10 9 ньютонов-квадратный метр на кулон в квадрате (Нм
Britannica Quiz
Величина силы F на заряде Q 1 , рассчитанная по уравнению (1), составляет 3,6 ньютона; его направление показано на рис. 1. Сила, действующая на Q 2 со стороны Q 1 , равна − F , которая также имеет величину 3,6 ньютона; однако его направление противоположно направлению F . Сила F может быть выражена через ее компоненты вдоль x и y
1. Сила, действующая на Q 2 со стороны Q 1 , равна − F , которая также имеет величину 3,6 ньютона; однако его направление противоположно направлению F . Сила F может быть выражена через ее компоненты вдоль x и y
 В декартовых координатах это привело бы к изменению знаков обеих составляющих силы x и y силы в уравнении (2).
В декартовых координатах это привело бы к изменению знаков обеих составляющих силы x и y силы в уравнении (2).Как можно понять эту электрическую силу на Q 1 ? Принципиально сила обусловлена наличием электрического поля в положении Q 1 . Поле создается вторым зарядом Q 2 и имеет величину, пропорциональную размеру Q 2 . При взаимодействии с этим полем первый заряд, находящийся на некотором расстоянии, либо притягивается, либо отталкивается от второго заряда в зависимости от знака первого заряда.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подписаться сейчас
Электричество — Законы Кирхгофа — Физика 299
Электричество — Законы Кирхгофа — Физика 299 «Эксперт — это человек, который сделал все
ошибки, которые можно совершить в узкой области. »
»
Теорема соединения
В любой соединение в цепи ток, поступающий в соединение должен равняться току, выходящему из соединения.
(Это не более чем констатация сохранение заряда)
Теорема о петлеСумма изменение потенциала при прохождении любого полного петля нулевая.
(эквивалент сохранения энергии)
- Соглашения
Как обычно, для обеспечения стабильных результатов применения этих законов, мы должны придерживаться нескольких конвенций относительно токов и потенциалов в цепях.
Потенциалы :
- При перемещении резистивного устройства в направлении ток, изменение потенциала равно -iR. Наоборот, если сопротивление проходится в противоположном направлении текущее изменение потенциала равно +iR.
- При перемещении ЭДС в направлении ЭДС изменение потенциала равно +ε. Наоборот, если ЭДС при прохождении против направления ЭДС изменение потенциал равен -ε.
Токи:При постановке задачи текущее направление в любом конкретный элемент схемы назначается произвольно. Затем к цепи применяются законы Китчоффа. актуальные направления. После решения полученного уравнения, если ток отрицательный, что означает «фактический» текущее направление противоположно произвольно выбранному направление.
Законы Кирхгофа применимы к любой цепи к получить набор уравнений, связывающих токи, сопротивления и ЭДС в цепи.
Затем эти уравнения могут быть решены для неизвестных величин в цепи. Для любой цепи выполните следующие действия.
- Обозначьте ток, протекающий в каждой части цепи, имея в виду, что ток будет «расщепляться» при достижении узел. Направление определенного направления ток не имеет значения — см. текущее соглашение выше.
- В каждом соединении цепи используйте теорему о соединении, чтобы запишите уравнения, связывающие токи, входящие и уход.
- Определите все возможные контуры в цепи и пометьте их.
- Для каждого цикла выберите начальное местоположение, затем используйте цикл теорему, чтобы записать уравнение, связывающее изменения в потенциал, который должен быть равен нулю после прохождения полного петля.
- Решите систему уравнений из 2. и 4., чтобы получить неизвестные параметры цепи.
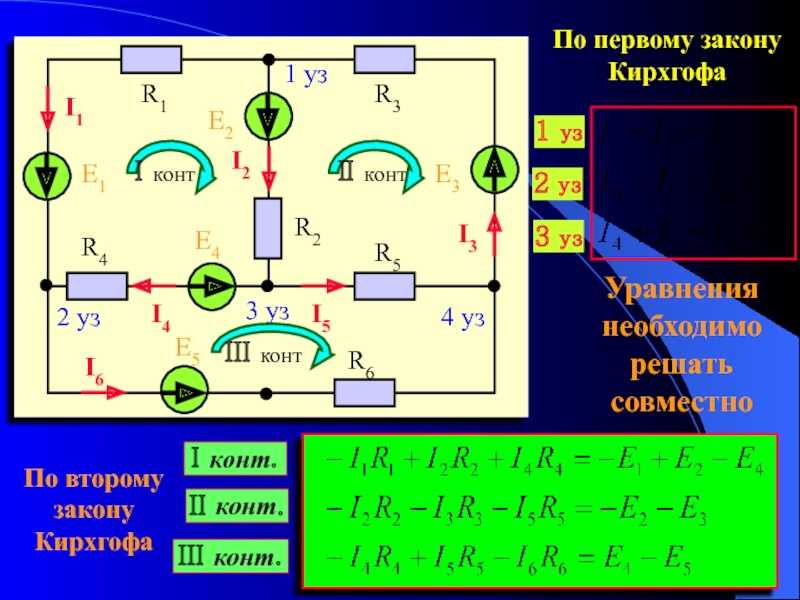
В качестве примера рассмотрим схему ниже. С 3 ЭДС мы не можем использовать последовательный/параллельный анализ.
Соединения:a: I 1 = I 2 + I 3
b: I 3 + I 6 4 I 263 Петли:1 (включая ε 1 начиная с пересечения по часовой стрелке): — I 3 R 4 — ε 3 — I 1 R 2 + ε 1 — I 1 R 1 = 0Глядя на эти уравнения, становится ясно, что два соединения уравнения эквивалентны, и это петлевое уравнение 3 просто сумма уравнений контура 1 и 2.
2 (включая ε 2 начиная с перемещения по часовой стрелке): — I 2 R 3 — ε 2 + ε 3 + I 3 R 4 = 0
3 (включая ε1 и ε 2 начиная с по часовой стрелке): — I 2 R 3 — ε 2 — я 1 R 2 + ε 1 — I 1 R 1 = 0


 В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне. Тогда имеем:
Тогда имеем: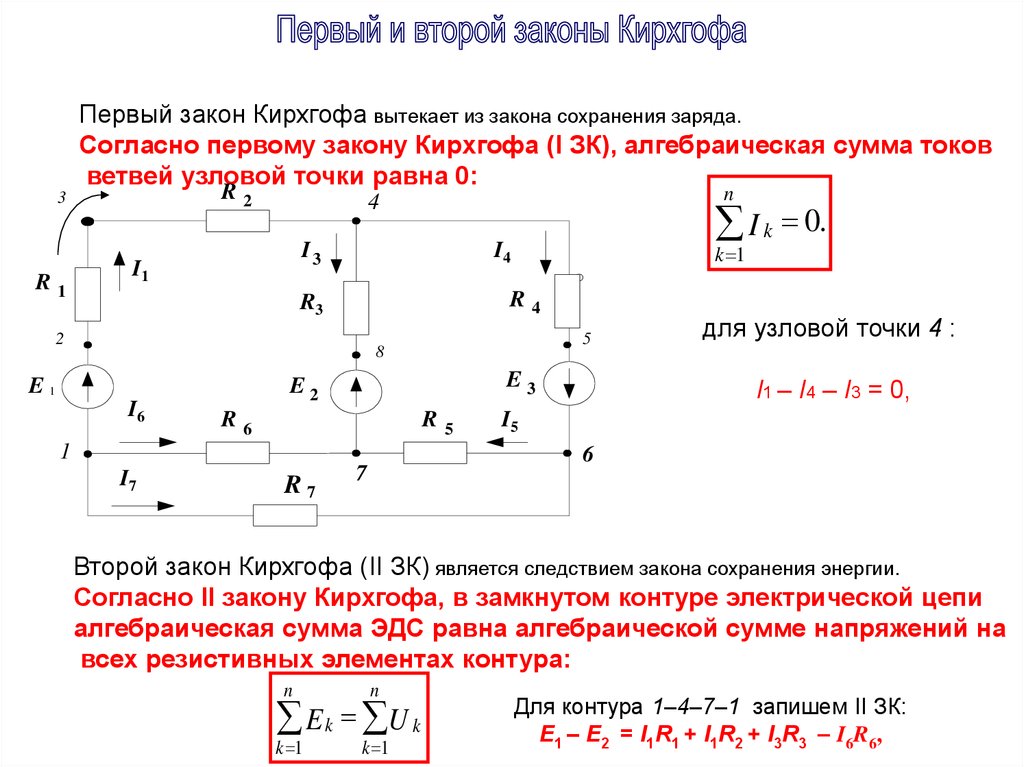 ru/jelektrotehnologii/1510-zakon-kirhgofa-dlja-jelektricheskoj-cepi.html
ru/jelektrotehnologii/1510-zakon-kirhgofa-dlja-jelektricheskoj-cepi.html
 Затем эти уравнения могут быть решены
для неизвестных величин в цепи. Для любой цепи
выполните следующие действия.
Затем эти уравнения могут быть решены
для неизвестных величин в цепи. Для любой цепи
выполните следующие действия. 
