Закон электромагнитной индукции Фарадея и его формулировка в дифференциальной форме

Фарадей был первым, кто обнаружил явление электромагнитной индукции. Это случилось в ходе опыта, когда он исследовал изменение потока магнитной индукции в замкнутом проводнике и выявил, что при этом вырабатывается электрический ток. Определение направления ЭДС индукции осуществляется согласно правилу, сформулированному Ленцем.

Определение 1

Направление индукционного потока препятствует изменению магнитного потока через создаваемое им поле.

Определение 2

Нейман определил закон электромагнитной индукции математически, и этой формулировкой мы пользуемся по сей день: εi=-dΦdt.

В нем не учитываются возможные движения контура. Соотношение dΦdt является выражением полной скорости изменения потока индукции, который охватывается проводником при его движении и деформации, а также при изменениях магнитного поля.

Закон Фарадея для электромагнитной индукции очень важен, поскольку он является выражением нового физического явления: когда магнитное поле изменяется, оно порождает электрическое, т.

е. электрическое поле может возникать не только при помощи электрических зарядов. Здесь необходимо учитывать одно важное замечание:

Определение 3

Движение магнитов может порождать электрический ток даже при неподвижных проводниках.

Электромагнитная индукция является одним из фундаментальных природных законов, устанавливающим связь между магнитным или электрическим полями.

Закон Фарадея в дифференциальной форме

Чтобы сформулировать закон Фарадея в такой форме, нам потребуется вспомнить несколько базовых формул.

1. ЭДС индукции: εi=-υBl.
2. Магнитный поток: Φ=∫SBndS.
3. Теорема Стокса: ∮l=a→dl=∫Srotna→dS.

Используя данные выражения, мы можем записать следующую формулу:

∮C(Edl)=∫S(n rot E)dS=-1c∫Sn∂B∂tdS.

Здесь S обозначает поверхность, натянутую на контур S. Поскольку значение S является произвольным, то мы можем записать:

Определение 4

rot E=-1c∂B∂t.

Это и есть дифференциальная форма закона Фарадея, которая описывает возникновение электрического поля в точке при изменении магнитного поля в том же месте.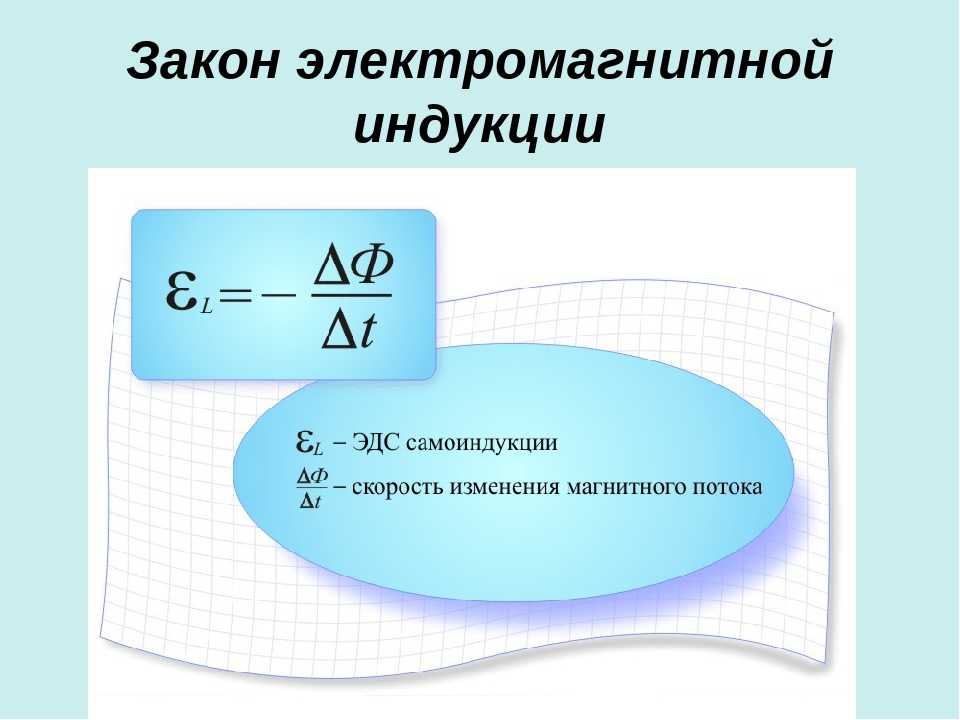 Само поле при этом называется индукционным.

Определение 5

Индукционное поле не является потенциальным, в отличие от электростатического, а работа по перемещению заряда в нем по замкнутому контуру не является нулевой.

Задачи на применение закона Фарадея

Пример 1

Условие: проволочный контур помещен в магнитное поле. В нулевой момент времени он пронизывает поток магнитной индукции, равный Φ1 и уменьшающийся после этого до 0. Найдите величину заряда, проходящего по цепи.

Решение

Начнем с определения мгновенного значения ЭДС. Это можно сделать с помощью формулы:

εi=-dΦdt.

Вспомним закон Ома. Согласно ему, мгновенное значение силы тока может быть записано в следующем виде:

I=-1RdΦdt.

Полное сопротивление цепи здесь обозначено буквой R.

Для нахождения заряда, идущего по цепи, нам пригодится выражение:

q=∫Idt.

Поставим эти выражения в нужную формулу и получим:

q=-1R∫Φ10dΦ=ΦR.

Автором этой формулы является Фарадей. Он эмпирически подтвердил прямую пропорциональность величины заряда, идущего по цепи, количеству линий магнитной индукции, пересекающей проводник, и его обратную пропорциональность величине сопротивления в цепи.

Ответ: q=ΦR.

Пример 2

Условие: квадратная рамка со стороной a помещена в одну плоскость с проводником, сила тока которого равна l. Она движется поступательно с постоянной скоростью v в направлении, обозначенное на иллюстрации ниже. Вычислите ЭДС индукции как функцию εi от расстояния x.

Рисунок 1

Решение

Найти ответ можно с помощью закона Фарадея.

εi=-dΦdt.

Для получения искомой функции Ei(x) нам нужно построить функцию Ф(x). Бесконечный проводник с током создает магнитное поле, которое может быть выражено так:

B=μ0I2πr.

Расстояние до точки рассмотрения здесь обозначено буквой r.

Для решения нам нужно также выделить площадь рамки. Выразим ее такой формулой:

dS=adr.

С учетом приведенных выше выражений, а также того факта, что B→⊥S→, мы можем найти величину элементарного магнитного потока, проходящего через элемент квадратной рамки, так:

dΦ=BdS=μ0I2πradr.

Далее вычисляем величину полного потока, учитывая, что x≤r≤x+a:

Φ=∫xx+aμ0I2πradr=μ0Ia2πlnx+ax.

После этого переходим к нахождению ЭДС индукции с помощью закона Фарадея и выражения для магнитного потока, выведенного ранее:

εi=-dΦdx·dxdt=-μ0Ia2π·xx+a(x-1-(x+a)x-2)·υ==-μ0Ia2π·xx+ax-x-ax2=μ0Ia2υ2π(x+a)x.

Ответ: εi=μ0Ia2υ2π(x+a)x.

Автор: Роман Адамчук

Преподаватель физики

Закон электромагнитной индукции Фарадея

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Нижегородский Государственный Технический Университет

Выксунский филиал

Кафедра ОиОПД

Закон электромагнитной индукции Фарадея

Лабораторная работа № 2-8

г. Выкса

2006 г.

Составили: В.П.Маслов, И.И.Рожков, О.Д.Честнова, Р.В.Щербаков.

Даны сведения по закону индукции Фарадея, принципы действия генератора, трансформатора, методика и описание установки по измерению взаимной индукции.

Научный редактор А.А. Радионов

Цель работы: ознакомиться с законом электромагнитной индукции, принципом действия генератора, трансформатора, методикой измерения взаимной индуктивности.

Приборы и оборудование: две катушки (неподвижная и подвижная), звуковой генератор, электронный осциллограф, вольтметр.

ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ

Пусть прямой проводник длиной

l движется со скоростью в однородном магнитном поле с индукцией , как показано на рис.1. Вместе с ним движутся с той же скоростью все его заряды — положительные и отрицательные. Под действием сил Лоренца свободные заряды начинают перераспределяться, что ведет к появлению электрического поля. Силы Лоренца являются сторонними силами. Электрическое поле, в свою очередь, начинает действовать на заряды силой . Когда силы, действующие на каждый заряд, уравновесятся, ЭДС индукции перестанет расти. Наведение ЭДС на проводнике, движущемся в магнитном поле, называется электромагнитной индукцией .

Работа сил Лоренца (сторонних сил) в расчете на единичный заряд равна ЭДС индукции:

(1)

Физический смысл знака минус выяснится ниже.

Для прямого проводника, движущегося прямолинейно и равномерно в однородном поле так, что его длина перпендикулярна векторам и (см. рис.1).

(2)

— закон электромагнитной индукции в формулировке Фарадея.

Рассмотрим еще одно движение проводника в магнитном поле (рис. 2) — движение колесной пары 1—2 в однородном поле индукции (вид сверху). Так как , a , по формуле (2) можно написать:

,

где — элементарное изменение магнитного потока через поверхность, ограниченную контуром определения ЭДС.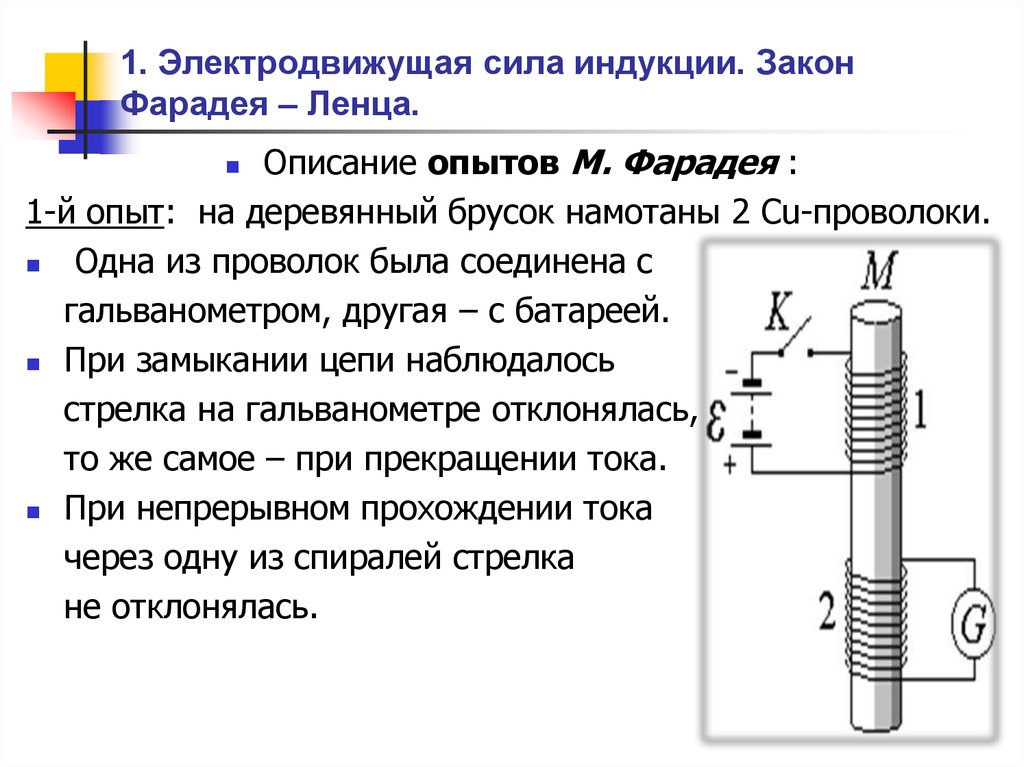

По определению, магнитным потоком через данную поверхность называется число линий индукции магнитного поля, проходящих через эту поверхность.

(3)

— это математическая запись закона электромагнитной индукции в формулировке Максвелла.

ЭДС индукции, возникающая в контуре, равна скорости изменения магнитного потока через поверхность, опирающуюся на этот контур.

Движение проводника, в котором создается э. д. с. индукции, требует затраты механической энергии, которая по закону сохранения переходит в энергию электрического поля.

Пусть замкнутый проводник, сечение которого изображено на рис.3, движется в однородном магнитном поле. По закону электромагнитной индукции в нем возникает индукционный ток . Если бы индукционный ток был направлен на нас (возможны всего два направления, перпендикулярных плоскости чертежа), то сила Ампера F_a, действующая на проводник, была бы направлена вдоль скорости, проводник двигал бы сам себя и при этом индуцировался ток, т.

е. был бы нарушен закон сохранения энергии. Остается лишь одна возможность: индукционный ток направлен в плоскость чертежа, сила Ампера препятствует движению, и необходимо совершить работу против этой силы, чтобы получить индукционный ток.

Мы получили правило Ленца — индукционный ток, возникающий в проводнике, имеет такое направление, что своим магнитным действием препятствует наводящему его движению. Это правило, говорящее как будто лишь о направлении индукционного тока, по существу является одним из наиболее общих выражений закона сохранения и превращения энергии. Его можно трактовать так: индукционный ток магнитным действием препятствует любой причине своего появления. Пусть какой-либо контур пронизывается возрастающим магнитным потоком (рис.4), т. е. >0. Индукционный ток , возникающий в контуре, по правилу Ленца имеет такое направление, при котором его магнитный поток мешает возрастанию наводящего магнитного потока. Индукционный ток, таким образом, связан с изменением магнитного потока правилом левого винта.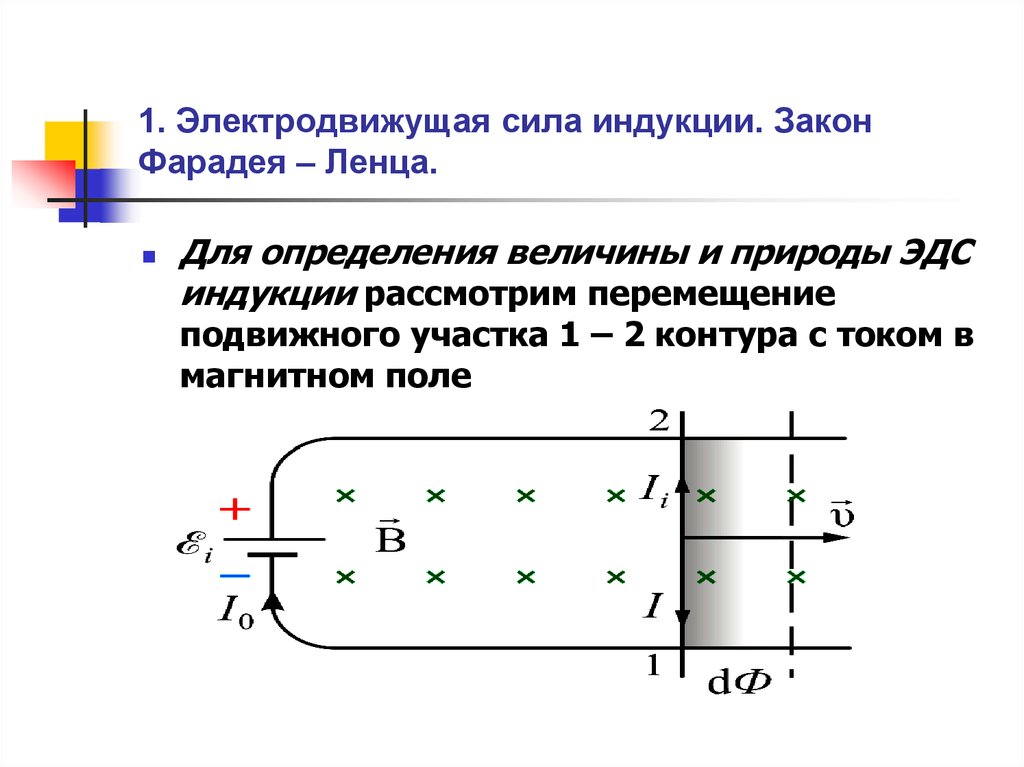

ЭДС, возникающая в контуре, направлена так, что магнитный поток индукционного тока (если контур замкнут) противоположен по знаку изменению магнитного потока, наводящего ЭДС. Таков физический смысл знака минус, содержащегося во всех формулировках закона электромагнитной индукции.

Если в контуре сопротивлением R изменяется магнитный поток на величину , то по данному контуру протекает определенный заряд ΔQ, который можно подсчитать:

.

Интегрируя почленно, получаем (без учета знака):

(4)

Рассмотрим контур, помещенный в магнитное; поле с индукцией (рис. 5). При всяком изменении магнитного потока Ф через площадь S поверхности, ограниченной контуром, в последнем возникает ЭДС индукции

, (5)

где — магнитный поток, — проекция на нормаль к площадке dS; N — число витков в контуре; потокосцепление. Соотношение (5) — закон электромагнитной индукции Фарадея. Знак минус в формуле соответствует правилу Ленца: индукционный ток всегда имеет такое направление, что он препятствует причине, его вызывающей.

Универсальность закона Фарадея в том, что ЭДС индукции не зависит от причины изменения магнитного потока, а они могут быть весьма различными. Приведем три примера. В электрогенераторе магнитный поток через витки катушки статора (рис.8) меняется вследствие того, что около катушки вращается электромагнит. В трансформаторе (рис. 9) напряжение первичной обмотки в соответствии с (5) изменяет поток, вследствие чего во вторичной обмотке возникает индукционный ток. Если разряжать конденсатор С после замыкания ключа К через сопротивление R и катушку индуктивности L, то поток уменьшается в катушке просто потому, что падает ток I в катушке. Возникающую ЭДС ε=-LdI/dt называют ЭДС самоиндукции, L — индуктивностью катушки (рис. 6).

Рассмотрим два контура 1 и 2, расположенных на некотором расстоянии друг от друга (рис. 7). Если по контуру 1 пропустить ток I₁ то он создает поток магнитной индукции через контур 2:

(6)

Коэффициент пропорциональности М₂₁ называют коэффициентом взаимной индукции контуров (взаимной индуктивностью контуров). Он зависит от формы и взаимного расположения контуров 1 и 2, а также от магнитных свойств окружающей среды.

При изменении силы тока в первом контуре магнитный поток сквозь второй контур изменяется. Следовательно, в нем наводится ЭДС взаимной индукции:

. (7)

Если поменять местами контуры 1 и 2 и повторить все предыдущие рассуждения, то получим:

. (8)

Можно показать, что коэффициенты взаимной индукции равны

.

ПРИНЦИП ДЕЙСТВИЯ ГЕНЕРАТОРА ПЕРЕМЕННОГО ТОКА

Закон индукции Фарадея лежит в основе электроэнергетики: на этом принципе действуют генераторы — источники электроснабжения промышленности и населения, трансформаторы.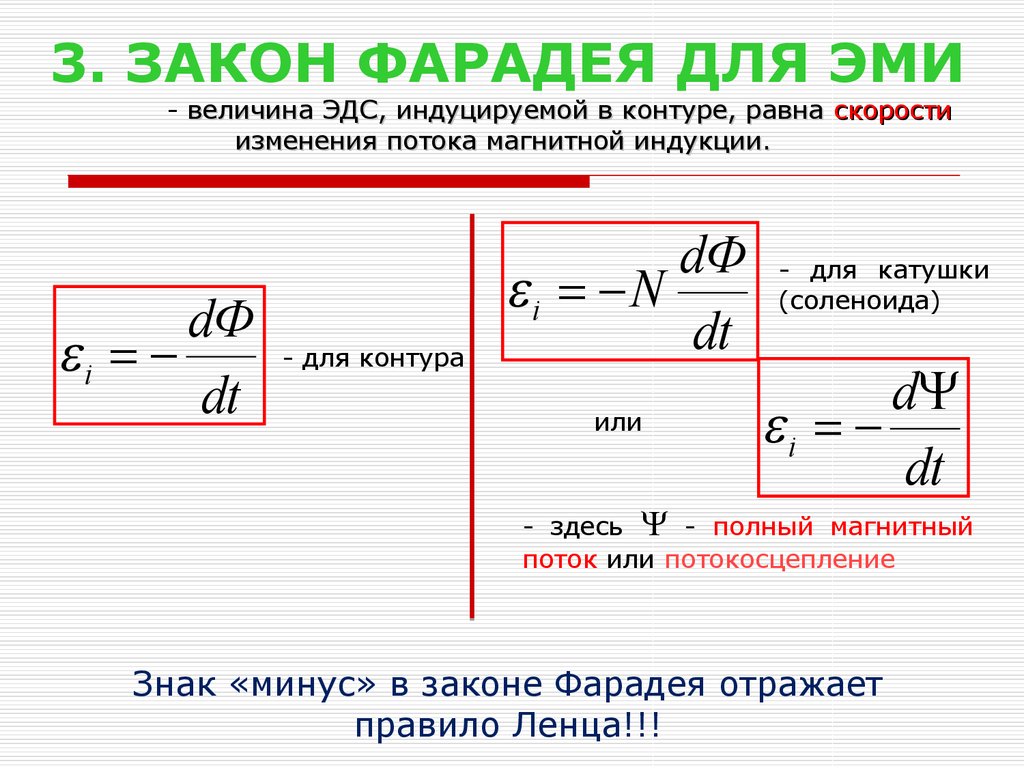 Простейший электрогенератор содержит вращающийся магнит (либо электромагнит) — ротор и неподвижную катушку статора (рис. 8). При вращении ротора в витках обмотки статора магнитный поток меняется по закону: , и возникает ЭДС индукции

,

обеспечивающая ток в нагрузке R.

ПРИНЦИП ДЕЙСТВИЯ ТРАНСФОРМАТОРА

Трансформатор (рис.9) содержит ферромагнитный сердечник, на котором две обмотки, первичная с числом витков n₁ и вторичная с n₂. К вторичной подключена нагрузка R, к первичной — источник напряжения U₁. В соответствии с законом Фарадея, U₁ вызывает рост магнитного потока Ф, (). Сердечник, имеющий большую магнитную проницаемость (μ=400÷10000), выполняет две функции. Во-первых, он концентрирует магнитный поток так, что поток Ф через первичную и вторичную обмотки практически одинаков. Во-вторых, большое значение μ обеспечивает малый ток через первичную обмотку, когда нагрузка не подключена (ток холостого хода), т. е. снижает потери энергии при трансформации.

В соответствии с (5) на вторичной обмотке возникает напряжение , так что напряжение изменяется:

,

где n₂/n₁ — коэффициент трансформации.

СОСТАВ УСТАНОВКИ

В данной работе определяют взаимную индуктивность двух катушек (длинной катушки – L₁ и короткой катушки – L₂, которую надевают на катушку L₁ и могут перемещать вдоль ее оси). Схема установки представлена на рис.10. Питание одной из катушек (например L₁) осуществляется от генератора звуковой частоты, напряжение

(9)

с которого подается через резистор с сопротивленцем R. Вольтметр, расположенный на панели PQ, измеряет действующее напряжение.

Сопротивление выбирается таким, чтобы выполнялось неравенство

, (10)

где L₁ — индуктивность катушки L₁, R₁ — ее активное сопротивление. В этом случае силу тока, протекающего через катушку L₁, можно определить по формуле

. (11)

Переменный ток в катушке L₁ создает ЭДС индукции в катушке L₂:

. (12)

Для измерения ε₂ в данной работе используют осциллограф. Амплитуда ЭДС индукции

, (13)

где ν — частота звукового генератора. Из (13) имеем

. (14)

Если поменять местами катушки L₁ и L₂, то можно определить

(15)

ИЗМЕРЕНИЯ

Собрать установку, состоящую из звукового генератора, электронного осциллографа и двумя соосно расположенными катушками L₁ и L₂. Ознакомиться с работой звукового генератора и электронного осциллографа (см. описание), включить их в сеть 220 В, подготовить к работе.

УКАЗАНИЯ ПО ТЕХНИКЕ БЕЗОПАСНОСТИ

1. Приборы питаются от сети 220 В. Включение в сеть приборов должно проводиться только в присутствие лаборанта или преподавателя.

2. Все корпусные клеммы приборов должны быть надежно заземлены (для заземления должен применяться провод без изоляции).

3. Запрещается работать в помещении одному.

Задание 1

Измерение взаимной индуктивности М₂₁ и М₁₂ и исследование их зависимости от взаимного расположения катушек

1. Напряжение сигнала со звукового генератора установите в диапазоне 1-4 В, а его частоту — в пределах 30-200 кГц.

2. Подайте напряжение на катушку L₁, а ЭДС с катушки L₂ на осциллограф.

3. Установите подвижную катушку L₁ в крайнее положение. Перемещая ее в противоположное крайнее положение, через каждый сантиметр запишите значение ЭДС магнитной индукции в цепи катушки L₂.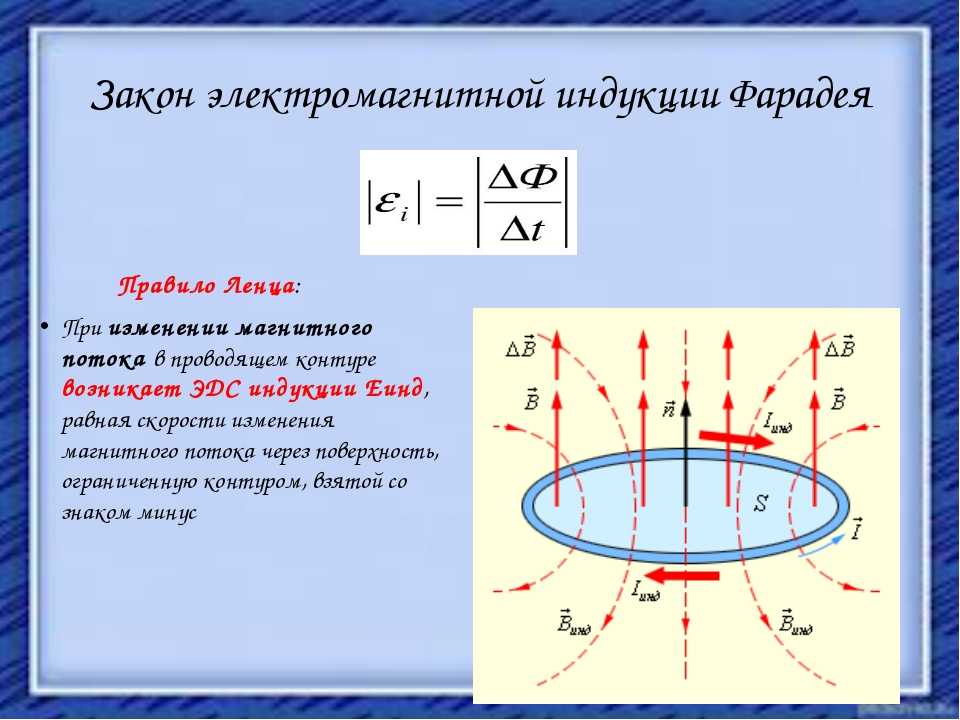

4. По формуле (14) рассчитайте М₂₁. Данные измерений и вычислений занесите в табл.1.

5. Поменяв местами катушки L₁ и L₂, повторите измерения по п.п. 1-4.

6. Постройте графики зависимости М₂₁ и М₁₂ как функции координаты z (z — расстояние между центрами катушек L₁ и L₂).

Таблица 1

z, см	ε02, В	М21 Гн	z, см	ε01, В	M21, Гн
UД=			ν=

Задание 2

Определение М21 для различных напряжений питания

1. Поставьте катушку L₁ в среднее положение относительно катушки L₂.

2. Установите частоту звукового генератора 10⁴ Гц.

3. Изменяя напряжение U_Д в цепи катушки L₁ снимите зависимость амплитуды ЭДС магнитной индукции от U_Д: ε₀₂=f(U_Д). Измерения провести в интервале 0-5 В через 0,5 В.

4. По формуле (14) рассчитайте M₂₁. Данные измерений и вычислений занесите в табл.2

Таблица 2

U0, В
ε02, В
М21, Гн
ν=		R=104 Ом

5. По данным табл. 2 найдите среднее значение М₂₁.

Задание 3

Определение М₂₁ для различных частот генератора

1. Поставьте катушку L₁ в среднее положение относительно катушки L₂.

2. Установите амплитуду напряжения звукового генератора 2 В.

3. Изменяя частоту генератора от 5 до 20 кГц (не менее 10 точек), снимите зависимость амплитуды ЭДС индукции ε₀₂ от частоты подаваемого напряжения.

4. По формуле (14) рассчитайте M₂₁. Данные измерений и вычислений занесите в табл.3.

Таблица 3

ν, Гц
ε02, В
М21, Гн
UД=		R=104 Ом

5. По данным табл. 3 найдите среднее значение М₂₁.

6. Для одного из полученных значений М₂₁ рассчитайте абсолютную и относительную погрешности ΔМ₂₁ и ΔМ₂₁/М₂₁.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Сформулируйте закон электромагнитной индукции (закон Фарадея) и правило Ленца.

2. В чем состоит явление электромагнитной индукции? Приведите примеры.

3. Принцип действия генератора переменного тока.

4. Принцип действия трансформатора.

5. В чем состоит явление взаимной индукции? От чего зависит взаимная индуктивность?

6. На замкнутом железном сердечнике с магнитной проницаемостью μ намотаны две катушки с числом витков n₁ и n₂. Вывести формулу для взаимной индуктивности, если длина сердечника l, a площадь поперечного сечения S.

12

Учебное пособие по закону Фарадея | Inspirit

Инструменты для творчества скоро появятся, чтобы вдохновить!

Присоединяйтесь к списку рассылки, чтобы узнать, когда мы запустимся.

Физика

Общая физика

Электромагнитное излучение

Учебное пособие по закону Фарадея

Джессика

Законы индукции Фарадея делятся на два закона. Первый объясняет генерацию ЭДС, а второй объясняет величину ЭДС.

Мы все знакомы с газовыми плитами и электрическими сковородками. Эти устройства имеют источник тепла, над которым ставится сковорода или сосуд. Около десяти лет назад на рынок взорвались индукционные плиты или печи, которые могли обеспечивать такой же нагрев, как и обычная плита, но без видимого источника тепла. Что, если мы скажем вам, что эти гладкие устройства имеют больше общего с электрическим трансформатором на вашей улице, чем с варочными панелями!? Так как же один используется для приготовления пищи, а другой в электросетях? Давайте узнаем!

Источник

ЗАКОН ИНДУКЦИИ ФАРАДЕЯ

Майкл Фарадей сделал несколько классных открытий, экспериментируя с проводниками и магнитами в 1830 году.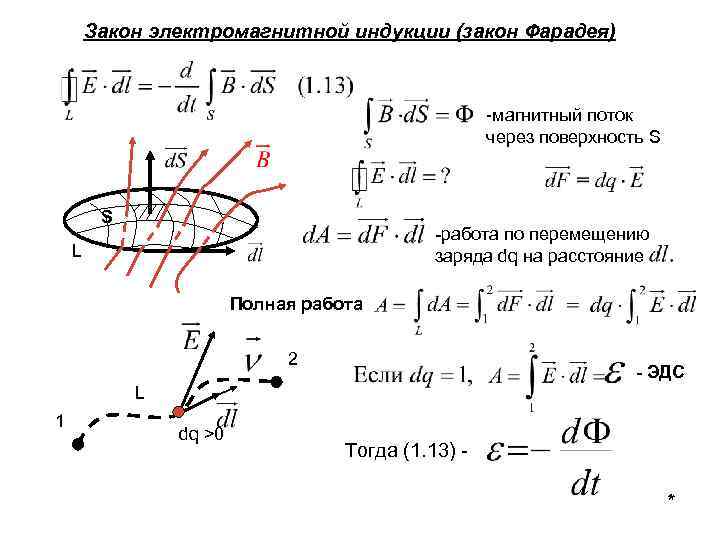 Впоследствии он предложил законы электромагнитной индукции, которые объяснили явление того, как изменяющийся магнитный поток индуцирует ток в проводник. Законы индукции Фарадея делятся на два закона. Первый объясняет, как в проводнике возникает электродвижущая сила (ЭДС), а второй закон дает количественную оценку ЭДС.

ПЕРВЫЙ ЗАКОН ФАРАДЕЯ

Согласно первому закону Фарадея, в проводнике, помещенном в переменное магнитное поле, индуцируется ЭДС. Это явление называется электромагнитной индукцией. Важно помнить, что электромагнитная индукция возникает только тогда, когда магнитное поле движется или изменяется в силе. В замкнутой цепи ЭДС действует как батарея и создает ток, который может совершать работу.

Источник

Рассмотрим настройку на рисунке выше. Каждый раз, когда магнит входит в катушку и выходит из нее, гальванометр показывает ЭДС. Тот же принцип применим к электрическим генераторам, которые используют вращающиеся магнитные поля для производства энергии.

ВТОРОЙ ЗАКОН ФАРАДЕЯ

Согласно второму закону электромагнитной индукции Фарадея, величина ЭДС индукции в проводнике прямо пропорциональна скорости изменения магнитного поля. Учитывая приведенный выше пример, чем быстрее движется магнит, тем больше ЭДС он генерирует.

Математически это может быть выражено как:

 ε = - N ΔΦ/Δt
 

ε – величина ЭДС индукции N — количество витков на катушке ΔΦ — изменение магнитного потока Δt – изменение во времени

ЭДС имеет отрицательный знак, поскольку индуцированный ток течет в направлении, противодействующем изменяющемуся магнитному полю, как объясняется законом Ленца.

ПРИМЕНЕНИЕ ЗАКОНА ФАРАДЕЯ

Источник

Возвращаясь к индукционной плите во введении, устройство производит тепло, индуцируя ток в емкости для приготовления пищи. Он использует быстропеременный магнитный поток для создания вихревых токов, которые нагревают сосуд из-за электрического сопротивления. Электрический трансформатор переменного тока в первичной обмотке создает изменяющееся магнитное поле во вторичной обмотке. Это индуцирует электрический ток во вторичной катушке; однако целью трансформатора является повышение или понижение напряжения.

• Согласно первому закону Фарадея, в проводнике, помещенном в переменное магнитное поле, индуцируется ЭДС.
• Согласно второму закону электромагнитной индукции Фарадея, величина ЭДС индукции в проводнике прямо пропорциональна скорости изменения магнитного поля.

Часто задаваемые вопросы:

1. Что такое закон Фарадея?

Физический закон Фарадея описывает электромагнитную индукцию в проводнике, помещенном в изменяющееся магнитное поле.

2. Что такое 1-й и 2-й законы Фарадея?

• Согласно первому закону Фарадея, в проводнике, помещенном в переменное магнитное поле, индуцируется ЭДС.
• Согласно второму закону электромагнитной индукции Фарадея, величина ЭДС индукции в проводнике прямо пропорциональна скорости изменения магнитного поля.

Мы надеемся, что вам понравился этот урок, и вы узнали что-то интересное о Закон Фарадея ! Присоединяйтесь к нашему сообществу Discord, чтобы получить ответы на любые вопросы и пообщаться с другими студентами, такими же, как и вы! Обещаем, это делает учебу намного веселее! 😎

ИСТОЧНИКИ:

1. 22.2 Открытие электромагнетизма. https://flexbooks.ck12.org/cbook/ck-12-middle-school-physical-science-flexbook-2.0/section/22.2/primary/lesson/discovery-of-electromagnetism-ms-ps/. По состоянию на 28 января 2022 г.
2. Закон электромагнитной индукции Фарадея. https://www.electricalclassroom.com/faradays-law-of-induction/. По состоянию на 28 января 2022 г.
3. Что такое закон индукции Фарадея?. https://www.livescience.com/53509-faradays-law-induction.html. По состоянию на 28 января 2022 г.
4. Законы электромагнитной индукции Фарадея. https://byjus.com/physics/faradays-law/. По состоянию на 28 января 2022 г.

Закон Фарадея

Закон Фарадея
Следующая: Закон Ленца Вверх: Магнитная индукция Предыдущий: Магнитная индукция Явление магнитной индукции играет решающую роль в три очень полезных электрических устройства: электрогенератор , электрогенератор двигатель и трансформатор . Без этих устройств современная жизнь была бы невозможным в его нынешнем виде. Магнитная индукция была открыта в 1830 г. английский физик Майкл Фарадей. Американский физик Джозеф Генри независимо сделал то же самое открытие примерно в одно и то же время. Оба физиков заинтриговал тот факт, что электрический ток, протекающий вокруг цепь может генерировать магнитное поле. Конечно, рассуждали они, если электрический ток может генерировать магнитное поле, тогда магнитное поле должно каким-то образом быть в состоянии генерировать электрический ток. Однако потребовались годы бесплодных экспериментов. прежде чем они смогли найти основной ингредиент, который позволяет магнитное поле для создания электрического тока. Этот ингредиент изменение времени .

Рассмотрим плоскую петлю из проводника площадью поперечного сечения . Поместим эту петлю в магнитное поле, напряженность которого приблизительно равна равномерный по всей длине петли. Предположим, что направление магнитное поле образует угол с направлением нормали к петля.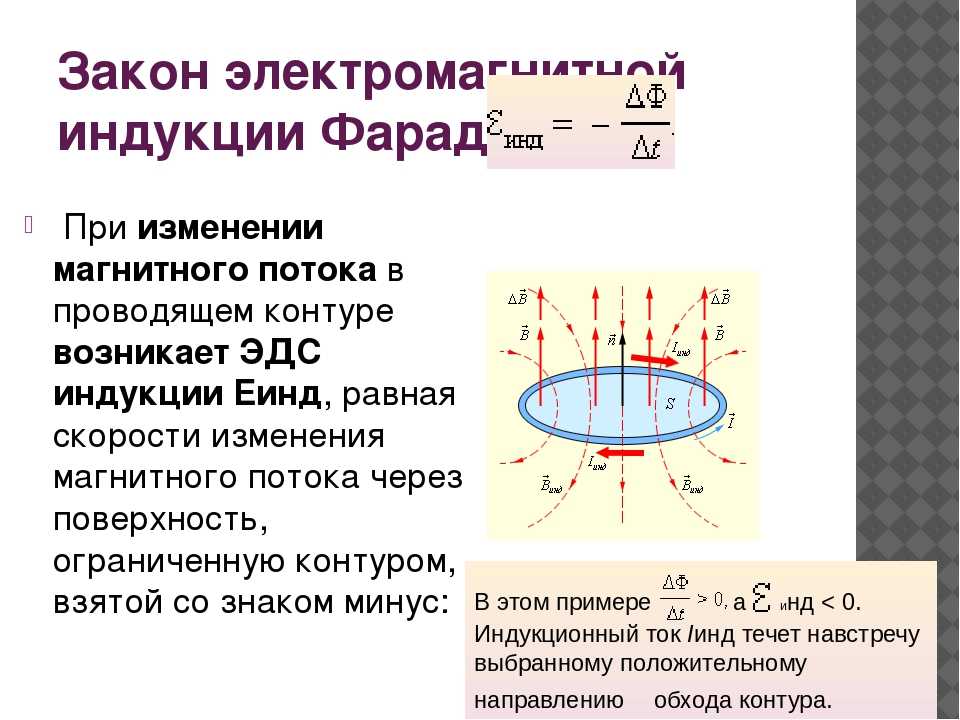 Магнитный поток через контур равен определяется как произведение площади петли на составляющую магнитное поле перпендикулярно контуру. Таким образом,

(191)

Если цикл обернут вокруг себя раз ( т.е. , если цикл имеет витков ), тогда магнитный поток через петлю просто умножить на магнитный поток через один виток:

(192)

Наконец, если магнитное поле неоднородно по петле или петля не лежат в одной плоскости, то мы должны оценить магнитный поток как поверхностный интеграл

(193)

Здесь — некоторая поверхность, присоединенная к . Если петля имеет витки, то поток умножается на указанное выше значение. Единицей магнитного потока в системе СИ является вебер (Вб). Один тесла эквивалентен один вебер на квадратный метр:

(194)

Фарадей обнаружил, что если магнитное поле через проволочную петлю меняется во времени , то вокруг контура индуцируется ЭДС. Фарадей смог наблюдать этот эффект, потому что ЭДС вызывает ток, циркулирующий в контуре. Фарадей обнаружил, что величина ЭДС прямо пропорциональна скорости изменения магнитного поля во времени. Он также обнаружил, что ЭДС генерируется, когда петля провода перемещается . из области с низкой напряженностью магнитного поля в область с высокой напряженностью магнитного поля, и наоборот . ЭДС прямо пропорциональна скорость, с которой петля перемещается между двумя областями. Наконец-то, Фарадей обнаружил, что ЭДС генерируется вокруг петли, которая вращается в однородном магнитном поле постоянной напряженности. В этом случае ЭДС прямо пропорциональна скорости вращения петли. В конце концов Фарадей в состоянии предложить один закон, который мог объяснить все его многочисленные и разнообразные наблюдения. Этот закон, известный как Закон Фарадея о магнитной индукции выглядит следующим образом:

ЭДС, индуцированная в цепи, пропорциональна скорости изменения во времени магнитный поток, связывающий эту цепь.

Единицы СИ были зафиксированы таким образом, чтобы константа пропорциональности в этом закон единство . Таким образом, если магнитный поток через цепь изменяется на сумму во временном интервале тогда ЭДС, возникающая в цепи, равна

(195)

Существует много разных способов, которыми магнитный поток, связывающий электрическая цепь может изменение.