Закон джоуля ленца формула и определение

Содержание:

Знаменитый русский физик Ленц и английский физик Джоуль, проводя опыты по изучению тепловых действий электрического тока, независимо друг от друга вывели закон Джоуля-Ленца. Данный закон отражает взаимосвязь количества теплоты, выделяемого в проводнике, и электрического тока, проходящего по этому проводнику в течение определенного периода времени.

Свойства электрического тока

Когда электрический ток проходит через металлический проводник, его электроны постоянно сталкиваются с различными посторонними частицами. Это могут быть обычные нейтральные молекулы или молекулы, потерявшие электроны. Электрон в процессе движения может отщепить от нейтральной молекулы еще один электрон. В результате, его кинетическая энергия теряется, а вместо молекулы происходит образование положительного иона. В других случаях электрон, наоборот, соединиться с положительным ионом и образовать нейтральную молекулу.

В процессе столкновений электронов и молекул происходит расход энергии, в дальнейшем превращающейся в тепло. Затраты определенного количества энергии связаны со всеми движениями, во время которых приходится преодолевать сопротивление. В это время происходит превращение работы, затраченной на преодоление сопротивления трения, в тепловую энергию.

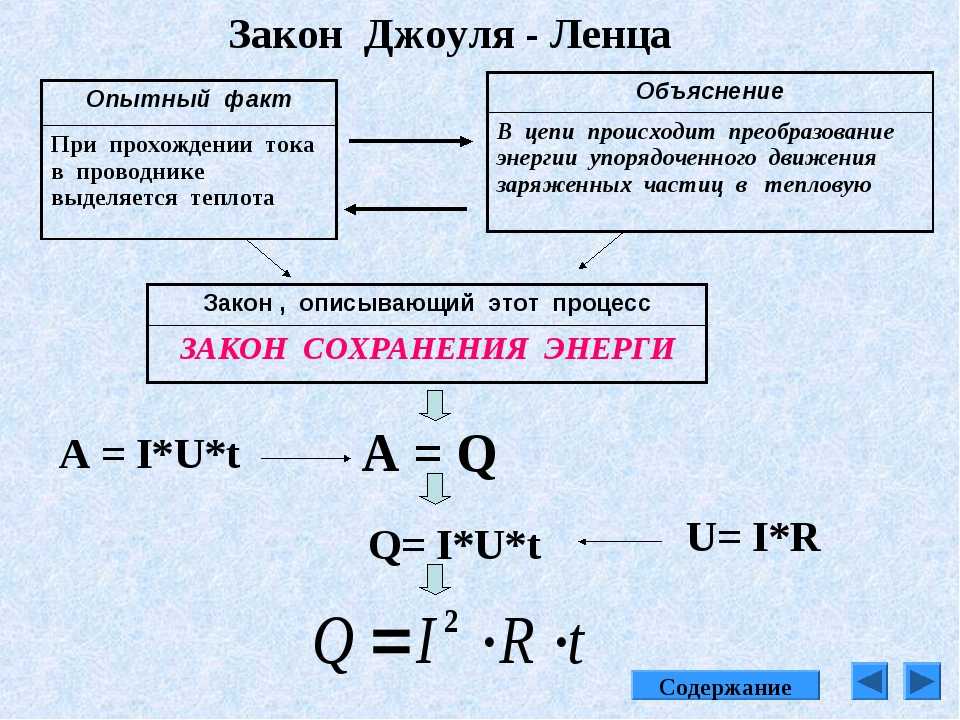
Закон джоуля Ленца формула и определение

Согласно закону джоуля Ленца, электрический ток, проходящий по проводнику, сопровождается количеством теплоты, прямо пропорциональным квадрату тока и сопротивлению, а также времени течения этого тока по проводнику.

В виде формулы закон Джоуля-Ленца выражается следующим образом: Q = I 2 Rt, в которой Q отображает количество выделенной теплоты, I — , R — сопротивление проводника, t — период времени. Величина «к» представляет собой тепловой эквивалент работы и применяется в тех случаях, когда количество теплоты измеряется в калориях, сила тока — , сопротивление — в Омах, а время — в секундах.

Численное значение величины к составляет 0,24, что соответствует току в 1 ампер, который при сопротивлении проводника в 1 Ом, выделяет в течение 1 секунды количество теплоты, равное 0,24 ккал. Поэтому для расчетов количества выделенной теплоты в калориях применяется формула Q = 0,24I 2 Rt.

При использовании системы единиц СИ измерение количества теплоты производится в джоулях, поэтому величина «к», применительно к закону Джоуля-Ленца, будет равна 1, а формула будет выглядеть: Q = I 2 Rt. В соответствии с I = U/R. Если это значение силы тока подставить в основную формулу, она приобретет следующий вид: Q = (U 2 /R)t.

Основная формула Q = I 2 Rt очень удобна для использования при расчетах количества теплоты, которое выделяется в случае последовательного соединения. Сила тока во всех проводниках будет одинаковая. При последовательном соединении сразу нескольких проводников, каждый из них выделит столько теплоты, которое будет пропорционально сопротивлению проводника. Если последовательно соединить три одинаковые проволочки из меди, железа и никелина, то максимальное количество теплоты будет выделено последней. Это связано с наибольшим удельным сопротивлением никелина и более сильным нагревом этой проволочки.

При параллельном соединении этих же проводников, значение электрического тока в каждом из них будет различным, а напряжение на концах — одинаковым. В этом случае для расчетов больше подойдет формула Q = (U 2 /R)t. Количество теплоты, выделяемое проводником, будет обратно пропорционально его проводимости. Таким образом, закон Джоуля — Ленца широко используется для расчетов установок электрического освещения, различных отопительных и нагревательных приборов, а также других устройств, связанных с преобразованием электрической энергии в тепловую.

Закон Джоуля-Ленца. Работа и мощность электрического тока

5. Закон Джоуля — Ленца

Проводник нагревается, если по нему протекает электрический ток.

Джоуль и Ленц установили, что количество выделившегося тепла Q = IRt, (28)

где I — ток, R — сопротивление, t — время протекания тока. Легко доказать, что

Q = IRt = UIt = U ² t/R = qU, (29)

где q = It — электрический заряд.

Если ток изменяется со временем (т. е. в случае непостоянного тока), то

Q == , (30)

где i — мгновенное значение тока.

Нагревание проводника происходит за счет работы, совершаемой силами электричес­кого поля над носителями заряда. Эта работа

A = qU = UIt =IRt = Ut / R . (31)

Работа А, энергия W , количество тепла Q в СИ измеряются в Дж.

Так как мощность характеризует работу, совершаемую в единицу времени, т.е. Р = , то

P = UI = IR = U/ R . (32)

Мощность в СИ измеряется в ваттах: 1 Вт = 1 Дж / 1 с; откуда 1 Дж = 1 Втс;

3600 Дж = 1Вт час, 3,6 •10Дж = 1 кВт час.

Формулы (31) и (32) позволяют рассчитать полезную работу и полезную мощность. Затраченная работа и мощность определяется по формулам

A = q = It = I (R + r)t = t. (33)

P= =I = I (R + r) = .(34)

Отношение полезной работы (мощности) к затраченной характеризует КПД источника

= = = . (35)

Из (35) следует.что при R0,0; R,1.Но при R ток I 0 и поэтому

А О и Р 0.

Определим величину R , при котором выделится максимальная мощность. Легко по­казать, что это наступает при R = r, тогда P_MAКС=IR =

= , (36)

КПД в этом случае будет 50%.

6. Закон Джоуля — Ленца в дифференциальной форме

Согласно закону Джоуля — Ленца (28) в элементарном цилиндрическом объеме dV с площадью поперечного сечения dS и длиной dl за время dt выделится тепло

dQ =IRdt=(jdS)= jdldSdt =jdVdt.

Разделив на dV и dt, найдем количество тепла, выделяющееся в единицу времени в единице объема

Q= = j . (37)

здесь Q-называется удельной тепловой мощностью тока, которая в СИ измеряется в Вт/м³.

С учетом (16) из (37) следует, что Q=j= . (38)

Формулы (37) и (38) выражают закон Джоуля — Ленца в дифференциальной форме.

7. Правила Кирхгофа

I1 I2 I3 Рис. 6

В основе расчета электрических цепей лежат два правила Кирхгофа: 1) АЛГЕБРАИЧЕСКАЯ СУММА ТОКОВ, СХОДЯЩИХСЯ В УЗЛЕ, РАВНА НУЛЮ, т. е. . (39)

Току, текущему к узлу, приписывается один знак («+» или «-«), а току, текущему от узла, — другой знак; таким образом, для направлений токов в узле электрической схемы, пред- ставленном на рис. 6, имеем

.

2) В ЛЮБОМ ЗАМКНУТОМ КОНТУРЕ АЛГЕБРАИЧЕСКАЯ СУММА НАПРЯЖЕНИЙ НА ВСЕХ УЧАСТКАХ ЭТОГО КОНТУРА РАВНА АЛГЕБРАИЧЕСКОЙ СУММЕ ЭДС, ВСТРЕЧАЮЩИХСЯ В ЭТОМ КОНТУРЕ (40)

При этом также следует придерживаться правила знаков: токи, текущие вдоль выбран­ного направления обхода контура считаются положительными, а идущие против направле­ния обхода — отрицательными. Соответственно положительными считаются ЭДС тех источ­ников, которые вызывают ток, совпадающий по направлению с обходом контура (см. рис.7), где обозначает направление обхода контура .

SCIRP Открытый доступ

Издательство научных исследований

Журналы от A до Z

Журналы по темам

• Биомедицинские и биологические науки.
• Бизнес и экономика
• Химия и материаловедение.
• Информатика. и общ.
• Науки о Земле и окружающей среде.
• Машиностроение
• Медицина и здравоохранение
• Физика и математика
• Социальные науки. и гуманитарные науки

Журналы по тематике  

• Биомедицина и науки о жизни
• Бизнес и экономика
• Химия и материаловедение
• Информатика и связь
• Науки о Земле и окружающей среде
• Машиностроение
• Медицина и здравоохранение
• Физика и математика
• Социальные и гуманитарные науки

Публикация у нас

• Представление статьи
• Информация для авторов
• Ресурсы для экспертной оценки
• Открытые специальные выпуски
• Заявление об открытом доступе
• Часто задаваемые вопросы

Публикуйте у нас  

• Представление статьи
• Информация для авторов
• Ресурсы для экспертной оценки
• Открытые специальные выпуски
• Заявление об открытом доступе
• Часто задаваемые вопросы

Подпишитесь на SCIRP

Свяжитесь с нами

	клиент@scirp. org
	+86 18163351462 (WhatsApp)
	1655362766
	Публикация бумаги WeChat

Недавно опубликованные статьи

Недавно опубликованные статьи

Подпишитесь на SCIRP

Свяжитесь с нами

	клиент@scirp. org
	+86 18163351462 (WhatsApp)
	1655362766
	Публикация бумаги WeChat

Бесплатные информационные бюллетени SCIRP

Copyright © 2006-2023 Scientific Research Publishing Inc. Все права защищены.

Вершина

Конспект лекций Глава 1

Конспект лекций Глава 1

• Глава 7. Электродинамика
• 7.1. Электродвижущая сила
• 7.2. Закон Фарадея
• 7.3. Индуктивность
• 7.4. Уравнения Максвелла

7.1. Электродвижущая сила

Электрический ток течет, когда электрические заряды находятся в движении. Чтобы поддерживать электрический ток, мы должны приложить силу к этим обвинения. В большинстве материалов плотность тока пропорциональна силе на единицу заряда:

Константа пропорциональности σ называется проводимость материала. Вместо указания проводимости чаще указывается удельное сопротивление ρ :

Для проводников удельное сопротивление обычно составляет 10 ^-8 Ом-м; для для полупроводников она варьируется от 0,01 Ом-м до 1 Ом-м, а для изоляторов она варьируется от 10 ⁵ Ом-м до 10 ⁶ Ом-м. В большинстве случаях сила, действующая на заряды, является электромагнитной силой. В этом случае плотность тока равна:

Если скорость зарядов мала, вторым членом можно пренебречь, и уравнение для уменьшается до Закон Ома :

Рассмотрим провод сечением A и длиной L . Если между концами провода приложена разность потенциалов В , она будет создать электрическое поле внутри провода величиной

Следовательно, плотность тока в проводе равна

Таким образом, общий ток, протекающий по проводу, равен

Это уравнение показывает, что ток, протекающий от одного электрода к другой электрод пропорционален разности потенциалов между ними. Этот довольно неожиданный результат, поскольку носители заряда постоянно ускорение. Однако пропорциональность между текущим и разность потенциалов оказалась правильной для большинства материалов. Этот отношение может быть записано как

Константа пропорциональности R называется сопротивлением материал. Как правило, это функция геометрии системы и проводимость материалов между электродами. Единицей сопротивления является Ом (Ом). Сопротивление провода равно

Чтобы создать ток, мы должны совершить работу. Работа, необходимая для перемещения единицы заряда через разность потенциалов В равно В . К установить ток I , нам нужно поставить питание P где

Единицей мощности является Вт (1 Вт = 1 Дж/с). Работа, проделанная электрическая сила, действующая на носители заряда, превращается в тепло ( Дж отопление ).

Пример: Задача 7.1
Два концентрических металла сферические оболочки радиусом a и b соответственно разделены слабопроводящим материалом с проводимостью σ .
а) Если они поддерживается при разности потенциалов В , какой ток течет от одного к другой?
б) Чему равно сопротивление между оболочками?

а) Предположим, Заряд Q размещен на внутренней оболочке. Электрическое поле в районе между оболочками будет равно

Соответствующая разность потенциалов между сферами равна до

Следовательно, для поддержания разности потенциалов В между сферы, мы должны разместить заряд Q равный

на центральном корпусе. Суммарный ток, протекающий между двумя оболочками, равен равно

б) Сопротивление между оболочками можно получить из уравнения Ома. закон:

Пример: Задача 7.2
а) Два металлических предмета вставлены в слабопроводящий материал с проводимостью σ (см. рис. 7.1). Показывать что сопротивление между ними связано с емкостью договоренность по

b) Предположим, вы подключили батарею между 1 и 2 и зарядили их до разность потенциалов В ₀ . Если потом отсоединить аккумулятор, заряд будет постепенно стекать. Покажи, что В ( т ) = V ₀ exp(- t / τ ), и найти постоянную времени τ через ε ₀ и σ .

а) Предположим, что заряд Q помещен на положительно заряженный проводник. Ток, протекающий по положительно заряженному проводнику, равен равно

, где поверхностный интеграл берется по поверхности, окружающей положительно заряженный проводник (например, штриховая поверхность на рис. 7.1). Выражение для I можно переписать через электрическое поле как

Рисунок 7.1. Задача 7.2.

Использование закона Гаусса для выражения поверхностного интеграла в пересчете на общую вложенную плату получаем

Заряд на проводнике связан с емкостью расположение и разность потенциалов между проводниками:

Таким образом, текущий I равен

Сопротивление системы можно рассчитать по закону Ома:

b) Заряд Q на положительно заряженном проводнике равен равно

Это уравнение можно переписать как

и имеет следующее решение:

Разность потенциалов В равна

Постоянная затухания τ равна

В любой электрической цепи ток будет существовать только в том случае, если движущая сила доступный. Наиболее распространенными источниками движущей силы являются аккумуляторы и генераторы. Когда цепь подключается к источнику питания, начинается ток течь. В одноконтурной цепи ток будет везде одинаковым. Рассмотрим ситуацию, в которой токи неодинаковы (см. рис. 7.2). Если I _в  >  I _из затем положительный заряд будет накапливаться в середине. Это накопление положительного заряда будет генерировать электрическое поле (см. рис. 7.2), которое замедляет входящие заряды и ускоряет исходящие платежи. Снижение скорости набегающего заряды уменьшат входящий ток. Увеличение скорости исходящие заряды увеличат исходящий ток. Ток изменится до I _в  =  I _из .
Всего сила f на носителях заряда (на единицу заряда) равна сумме сила источника, f _s , и электрическая сила:

Рисунок 7.2. Текущий поток.

Работа, необходимая для перемещения одной единицы заряда по кругу, равна равно

где ε называется электродвижущей силой или ЭДС . ЭДС определяет ток, протекающий по цепи. Это может быть самое легко увидеть, переписав силу на носителях заряда по плотности тока

Здесь a — площадь поперечного сечения провода (перпендикулярно направление тока).

Пример: Задача 7.5
а) Шоу что электростатическая сила сама по себе не может быть использована для управления током вокруг схема.
b) Прямоугольная проволочная петля расположена так, что один ее конец находится между пластины плоского конденсатора (см. рис. 7.3), ориентированные параллельно поле E = σ / ε ₀ . Другой конец снаружи, где поле практически равно нулю. Если ширина петли ч и его полное сопротивление Ом , какой ток течет? Объяснять.

Рисунок 7.3. Задача 7.5.

а) Если присутствуют только электростатические силы, то сила на единицу заряда равно электростатической силе:

Таким образом, соответствующая ЭДС равна

для любого электростатического поля.
б) Единственная сила на носителях заряда в проволочная петля представляет собой электрическую силу. Однако в части а) мы пришли к выводу, что ЭДС, связанная с электрической силой, создаваемой электростатическим полем, равна равен нулю. Следовательно, ЭДС в проволочном контуре равна нулю, а следовательно, ток в контуре также равен нулю. Примечание: сначала может показаться, что существует результирующая ЭДС, если мы предположим, что электрическая Поле, создаваемое конденсатором, является полем идеального конденсатора (т. однородное поле внутри и отсутствие поля снаружи). При таком предположении ЭДС равно

Вклад интеграла пути от c до d равен нулю, так как электрическое поле там равно нулю, а вклад пути интегралы между b и c и между a и d равны равен нулю, так как электрическое поле и смещение перпендикулярны там. Ясно, что рассчитанная ЭДС отлична от нуля и не согласуется с результатом часть а).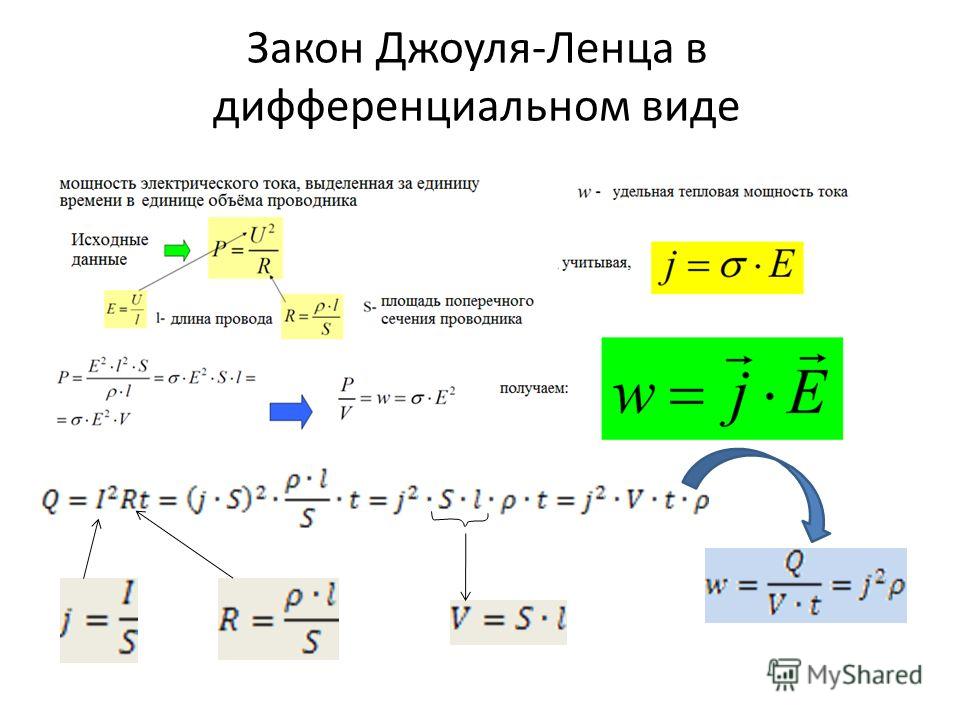 Это разногласие является результатом нашего неверного предположения о том, что электрическое поле вне конденсатора равно нулю (имеются поля).

Важным источником ЭДС является генератор. В этих устройствах ЭДС возникает из-за движения проводника через магнитное поле. Рассмотрим систему, показанную на рис. 7.4 (примечание: магнитное поле только присутствует в области слева от пунктирной линии). Обратите внимание на бесплатные тарифы на дирижер. Так как он движется со скоростью v в магнитном поле он будет испытывать магнитную силу. Сила положительного заряда q расположен ионный сегмент ab проволочной петли равен

Рисунок 7.4. Генератор.

Таким образом, магнитная сила на единицу заряда равна

Так как на заряды не действуют никакие другие силы, то ЭДС генерируется будет полностью зависеть от этой магнитной силы. ЭДС будет равна

Магнитный поток, воспринимаемый проволочной петлей, равен

Скорость изменения магнитного потока равна

Сравнение скорости изменения окружающего магнитного потока и ЭДС индукции можно сделать вывод, что

Это соотношение называется правилом потока для движущихся ЭДС .

7.2. Закон Фарадея

При движении проводника в постоянном магнитном поле ЭДС равна генерируется равным

В данном случае за ЭДС отвечает магнитная сила. Однако такая же ЭДС возникает, когда провод неподвижен, а магнитное поле движущийся. В этом случае магнитная сила не играет роли (поскольку v = 0), а за ЭДС отвечает электрическое поле. Это электрическое поле не электростатическое поле (поскольку электростатические поля не могут генерировать ЭДС; см. Задача 7.5), а индуцируется изменяющимся магнитным полем. Линейный интеграл этого электрического поля равно

Это уравнение можно переписать, применив теорему Стокса:

Поскольку мы не делали никаких предположений о поверхности, это уравнение можно быть правдой, только если

Это соотношение называется законом Фарадея в дифференциальной форме . направление токов, генерируемых изменяющимся магнитным полем, может быть легче всего получить с помощью закона Ленца , в котором говорится, что

«Если течет ток, он будет иметь такое направление, что магнитное поле его производит, имеет тенденцию противодействовать изменению потока, которое вызвало ЭДС. “

Пример: Задача 7.14
Длинный соленоид радиусом a , несущий Н витков на единицу длины, скрученный проволокой сопротивление Ом (см. рис. 7.5).
а) Если ток в соленоиде возрастающая,

какой ток течет в петле и в каком направлении (влево или вправо) он проходит через резистор.
б) Если ток I в соленоиде постоянен но соленоид вытягивается из петли и снова вставляется в противоположную В каком направлении общий заряд проходит через резистор?

Рисунок 7.5. Задача 7.14.

а) Предположим, что соленоид идеальный соленоид; это

Если ток в соленоиде увеличивается, сила магнитного поле также увеличивается. Скорость изменения напряженности магнитного поля равно

Магнитный поток, воспринимаемый проволочной петлей, равен

Соответствующая скорость изменения магнитного потока равна

ЭДС индукции может быть получена из закона потока:

Ток, наведенный в проволочной петле, равен

Магнитное поле соленоида направлено слева направо. Увеличение сила магнитного поля индуцирует в контуре ток, направленный так что создаваемое им магнитное поле направлено справа налево (закон Ленца). Следовательно, ток течет слева направо через резистор.

b) Изменение магнитного потока, заключенного в проволочной петле, равно равно

Ток, протекающий через резистор, равен

Это соотношение показывает, что

Подставляя выражение для получаем

7. 3. Индуктивность

Рассмотрим два контура: контур 1 и контур 2 (см. рис. 7.6). ток я ₁ , протекающий через петлю 1, создаст магнитное поле в позиция петли 2 равна

Магнитный поток через контур 2 равен

Рисунок 7.6. Индуктивность.

Здесь М ₂₁ называется взаимной индуктивностью две петли. Это чисто геометрическая величина, зависящая от размеров, формы и взаимное расположение двух петель. Это не изменится, если мы переключим роль петли 1 и петли 2: поток через петлю 2, когда мы запускаем ток I вокруг контура 1 точно такой же, как поток через контур 1, когда мы послать тот же ток I по контуру 2.
Помимо наведения ЭДС в близлежащей петли, изменяющийся ток в петле 1 также индуцирует ЭДС в петле 1. поток через петлю 1, создаваемый током в петле 1, равен

Константа пропорциональности называется собственной индуктивностью . единица индуктивности — Генри ( Н ).

Пример: проблема 7.19
Квадратная проволочная петля со стороной s , расположенная посередине между двумя длинные провода, 3 s врозь и там же. (Вообще-то длинные провода являются сторонами большой прямоугольной петли, но короткие концы находятся так далеко, что ими можно пренебречь.) Ток по часовой стрелке I в прямоугольной петле равен постепенно увеличиваясь: dI / dt = k = постоянная. Найдите ЭДС индуцируется в большой петле. В каком направлении будет течь индуцированный ток?

Рисунок 7.7. Задача 7.19.

Схема системы показана на рис. 7.7. Для расчета ЭДС индуцирует в большой петле нам нужно определить взаимную индуктивность M . Трудно вычислить M через ток в прямоугольном контуре, поскольку магнитное поле, создаваемое этой петлей, довольно сложное (и поэтому сложно интегрировать). Однако, используя равенство взаимных индуктивности, мы также можем оценить индуктивность с точки зрения тока я в большой петле. Магнитное поле, создаваемое верхней проволокой большого петля представляет собой бесконечно длинный прямой провод, по которому течет ток I равно

Поток, связанный с этим магнитным полем и пересекаемый квадратом цикл равен

Магнитное поле, создаваемое нижним проводом в месте квадратная петля будет указывать в том же направлении, что и магнитное поле генерируется верхней проволокой в ​​положении квадратной петли. Поскольку площадь петля расположена на таком же расстоянии от верхнего провода, как и от нижнего проволоки, поток, перехватываемый прямоугольной петлей, равен

Следовательно, взаимная индуктивность двух контуров равна

ЭДС индукции в большом контуре теперь можно легко рассчитать:

Направление потока через большую петлю указывает на страницу. Легче всего это увидеть, рассмотрев силовые линии магнитного поля. Внутри квадратная петля, линии поля указывают на страницу (правило правой руки). С линии поля образуют замкнутые петли, они должны быть направлены за пределы страницы в любом месте за пределами квадратной петли. Однако большая проволочная петля покрывает только ограниченная часть пространства, и поэтому определенно не будет перехватывать все поле линии вне квадратной петли. Поэтому линий поля будет больше указывая на страницу, тогда есть линии поля, указывающие на страницу. Следовательно, чистый магнитный поток будет направлен на страницу. Когда ток в прямоугольной петле увеличивает поток, перехваченный большой петлей, будет увеличивать. ЭДС индукции создаст магнитное поле, противодействующее этому увеличение потока и, следовательно, создает поток, направленный из бумаги. Правило правой руки показывает, что направление тока, индуцируемого в большом петля должна течь против часовой стрелки.

7.4. Уравнения Максвелла

Электрические и магнитные поля в электростатике и магнитостатике описывается следующими четырьмя уравнениями:

В системах с непостоянными токами не все эти уравнения справедливы больше. Например,

для каждой векторной функции. Однако по закону Ампера

, который равен нулю только для постоянных токов (для которых константа, не зависящая от положения). Для нестационарных токов

Таким образом, мы заключаем, что закон Ампера не выполняется для нестационарных токов. Нарушение закона Ампера также можно наблюдать в системе, в которой конденсатор заряжается (см. рис. 7.8). В процессе зарядки по проводу течет ток I и, следовательно, будет наличие магнитного поля. Магнитное поле, создаваемое зарядным током можно рассчитать по закону Ампера. Когда мы далеко от конденсатора генерируемое магнитное поле будет полем линейного тока. Рассмотрим Амперова петля радиуса r , по центру провода. Линейный интеграл вокруг этого цикла равно

Согласно закону Ампера линейный интеграл вокруг замкнутого контура пропорциональна току, перехватываемому поверхностью охватывается этой петлей. Для системы, показанной на рис. 7.8, перехваченный ток плохо определен. Рассмотрим первую поверхность 1. Ток, пересекаемый поверхность 1 равна I . Поверхность 2 также натянута петлей Ампера, но ток, перехваченный этой петлей, равен нулю. Таким образом, мы заключаем, что Закон Ампера не действует в системах, где ток не непрерывный.

Рисунок 7.8. Зарядка конденсатора.

Максвелл изменил закон Ампера следующим образом:

Термин, добавленный Максвеллом, называется током смещения . Это определяется как

Рассмотрим область между пластинами конденсатора на рис. 7.8. электрическое поле в этой области равно

, где мы предположили, что создаваемое поле является полем идеального конденсатора. с площадью поверхности A и осью z находится в направлении текущий. Скорость изменения электрического поля равна

Поверхностный интеграл по поверхности 2 поэтому равно

Поверхностный интеграл по поверхности 2 равно

Модификация закона Ампера Максвеллом гарантирует, что поверхность интеграл от не зависит от выбранной поверхности. В электростатике и магнитостатике электрические и магнитные поля постоянны во времени, и поэтому новая форма Закон Ампера сводится к форме закона Ампера, которую мы использовали, поэтому далеко.
В регионе, где нет свободных зарядов или свободных токов Максвелла уравнения становятся очень симметричными

Симметрия нарушается при наличии электрических зарядов, кроме случаев, когда электрических зарядов магнитных монополей . Если магнитный заряд плотность равна η , а магнитный ток равен тогда уравнение Максвелла станет

Чтобы получить уравнения Максвелла, описывающие электрические и магнитные поля в материи, мы должны принять связанные заряды и связанные токи в счет:

В нестатическом случае поляризация может зависеть от времени. Поэтому, также плотность связанного заряда зависит от времени, и чистый ток может быть связано с изменением плотности связанного заряда.