Закон ⭐ Джоуля-Ленца в физике: формула, определение, объяснение
Закон джоуля Ленца: определение
Определение 1Закон Джоуля-Ленца — один из законов физики, который определяет количественную меру воздействия тепла электрического тока.
Закон Джоуля-Ленца — один из законов физики, который определяет количественную меру воздействия тепла электрического тока.
Теорема 1Формулировка классического закона Джоуля-Ленца гласит: мощность того тепла, который выделяется в проводнике в процессе протекания сквозь проводник электрического тока, соответствует умножению плотности электрического поля на напряженность.
Посмотрите на вид алгебраической формулы Джоуля-Ленца:
ω=j×E=σE2
В данной формуле ω значит количество тепла, E и j обозначают плотность и напряженность электрических полей, а σ означает проводимость среды.
Простое и понятное объяснение физического смысла теории Джоуля-Ленца: электрический ток во время протекания по проводнику являет собой перемещение заряда электрического под влиянием электрического поля.
Соответственно, электрическое поле во время данного процесса совершает некую работу. Эта работа используется для нагрева проводника. Таким образом можно говорить о том, что энергия превращается в качественно дифференциальное явление — тепло.
Однако стоит понимать, что излишний нагрев проводника с током, а также электрических приборов допускать не рекомендуется, потому что перегрев может привести к повреждению электрических приборов. Опасно излишне перегревать оборудование в случае коротких замыканий проводов. В это время по проводникам может протекать много тока.
Закон Джоуля-Ленца для тонких проводников в интегральной форме звучит так:
Теорема 2Величина теплоты, выделяющаяся за определенное время на определенном участке цепи, определяется как произведение силы тока, возведенной в квадрат, и сопротивления участка цепи.
Сама формула выглядит так:
Q=∫k×l2×R×t
В данной формуле:
- Q обозначает количество теплоты, которая выделилась;
- I обозначает количество тока;
- R обозначает сопротивление проводника/проводников;
- t обозначает время действия;
- k обозначает тепловой аналог работы.
Значение этого параметра зависит от разрядности единиц, в которых измеряются значения, используемые в формуле.
Значение этого параметра зависит от разрядности единиц, в которых измеряются значения, используемые в формуле.Теорему Джоуля-Ленца характеризуют как имеющую общий характер, потому что она не имеет корреляции с происхождением сил, которые генерируют ток. Данный закон справедлив для электролитов, полупроводников и проводников.
Формула закона Джоуля-Ленца
Можно записать обобщенную формулу для закона Джоуля-Ленца как:
Формула 1Q=I2×R×t
В данной формуле Q обозначает количество теплоты, которая выделилась. Q измеряется в джоулях.
I обозначает количество тока, R обозначает сопротивление проводника/проводников, t обозначает время действия.
Применение в практической жизни
Данный закон применяется в обычной жизни широко. Например, вольфрамовая нить в лампах накаливания, дуги в электросварках, нить накаливания в электрообогревателе. К приборам, которые работают по закону Джоуля-Ленца, также относят: утюги, фены, электрочайники, паяльники, варочные плиты и т.
д.
Данный принцип имел огромное влияние на бытовое применение электрического тока. В 19 веке благодаря этой теории стало возможным создание точных измерительных приборов, в основе работы которых лежало сокращение проволочной спирали во время нагрева прохождением тока определенной величины. Например, стрелочные вольтметры, а также амперметры.
В то же время начинают появляться модели электрических обогревателей, плавильных печей, а также тостеров. Для их создания был использован проводник с высоким удельным сопротивлением, что помогало получить высокие температуры.
Также появились самые первые плавкие предохранители, прерыватели цепи биметаллические, которые основаны на разнице нагрева проводника с различным удельным сопротивлением. Когда люди заметили, что при соответственной силе тока проводник с большим показателем сопротивления может нагреться до красного цвета, закон Джоуля-Ленца начал использоваться для создания источников света. В это время появляются первые лампы.
Также эффект данной теории используется широко в промышленности: в химической, металлургической и т.д.
Примеры решения задач
Самые важные формулы для решения задач с законом Джоуля-Ленца:
| Величина | Буква, которая обозначает величину | Единицы измерения | Формула |
| Сила тока | I | Амперы | I=U÷R Представим краткое описание формулы словами: сила тока равна напряжение пропорционально сопротивлению проводника. |
| Напряжение | U | Вольтах | U=I×R |
| Время | T | Секунды | t=Q÷I2×R |
| Количество теплоты | Q | Джоули | Q=I2×R×t
|
Какое количество тепла будет выделено спиралью электроплитки за 15 минут с сопротивлением в 30 Ом, если сила тока цепи составляет 1,5 А?
Дано:
t = 15 мин.
R = 30 Ом.
I = 1,5 А.
Нужно найти Q.
Решение:
Переводим минуты в секунды: 15 минут * 60 = 900 секунд.
Q=I2×R×t
Q=1,52*30*900=60 750=60,75кДж.
Получившуюся сумму обычно сокращают до килоджоулей.
Ответ: 60,75 кДж.
Задача 2Какое количество тепла будет выделено электрической спиралью за 20 минут, если напряжение равно 215 В, а сила тока цепи 3 А?
Дано:
t = 20 минут.
U = 215 В.
I = 3 А.
Нужно найти Q.
Решение:
Переводим минуты в секунды: 20 минут * 60 = 1200 секунд.
Q = 3 * 215 * 1200 = 774 000 = 774 кДж.
Ответ: 774 кДж.
Закон Джоуля — Ленца: формула и определение
Автор Савельев Николай На чтение 4 мин Просмотров 54 Опубликовано Обновлено
При использовании различных электроприборов, через которые протекают токи, происходит процесс преобразования электрической энергии в тепловую.
Например, если взять тонкий провод и соединить к концам батарейки, можно почувствовать, что провод нагрелся. Это происходит благодаря закону Джоуля — Ленца, формула и определение которого приведены ниже.
Данное тепловое явление может быть, как полезным:
- Освещение (лампы накаливания, индукционные лампы)
- электрические обогреватели
- инструменты (паяльник, сварочный аппарат)
- бытовые предметы (чайник, индукционная плита, утюг)
Так и опасным:
- Перегрев аппаратов и машин во время эксплуатации
- Перегрев высоковольтных линий передач при неправильном расчете длины провода между опорами
Содержание
- Откуда берётся тепло? Природа теплового эффекта в цепи тока
- Закон Джоуля — Ленца
- Математическое выражение Закона Джоуля — Ленца
Откуда берётся тепло? Природа теплового эффекта в цепи тока
В качестве проводников, в основном, используются такие металлы, как:
- Алюминий
- Медь
- Сталь
В металлическом стационарном проводнике, работа тока идёт на повышение внутренней энергии.
Каждый проводник, при прохождении через него тока, будет выделять тепло. Связанно это с атомным строением металлов. Металлы по своей структуре представляют собой решётку, состоящую из ионов (положительно заряженных атомов) и атомов. При прохождении тока через данную решётку, упорядоченные электроны сталкиваются с молекулами проводника. При соударении происходит передача кинетической энергии, и, соответственно, происходят колебания атомов. Данное колебание положительно заряженных атомов и атомов с нейтральным зарядом приводит к нагреванию проводника электрической цепи.
Закон Джоуля — Ленца
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивлению проводника и времени
Закон Джоуля – Ленца
Данный вывод был сформулирован двумя учеными: Джеймсом Джоулем в 1841 году и Эмилием Ленцем в 1842 году. Опыты проводились самостоятельно каждым из ученых, поэтому закон был назван сразу в честь двух ученых.
Читайте также: Как рассчитать силу тока, потребляемую бытовым прибором?
Математическое выражение Закона Джоуля — Ленца
Рассмотрим идеальную электрическую цепь, состоящую только из проводника и источника напряжения. На данной схеме присутствует только сопротивление проводника, без добавочных сопротивлений и различных внешних воздействий.
Работа тока, во время работы источника напряжения:
\[ А = IUt [Дж] \],
- где I – ток, протекающий в цепи [А]
- U – напряжение источника [В]
- t – время работы [c]
Учитывая, что энергия, накопившееся в проводнике, уходит только на нагрев цепи, делается следующий вывод: При работе тока А вся энергия преобразуется в тепло Q и равняется его количеству.
\[ Q = А = IUt [Дж] \]
Используя закон Ома, определяется количество теплоты Q, выработанное проводником за время t, выражая через напряжение источника и сопротивление участка цепи:
\[ Q = IUt = I(IR)t = I2Rt [Дж] \],
- где R – сопротивление цепи [Ом]
\[ U = IR [В] \] – закон Ома для участка цепи.
Сопротивление цепи напрямую зависит от выбора материала, длины и поперечного сечения провода:
\[ R = ρl/S \],
- где ρ – удельное электрическое сопротивление проводника [Ом∙м]
- l – длина участка цепи [м]
- S – площадь сечения проводника [мм2]
На данный момент, наиболее часто используется проводка с круглым сечением, поэтому применяем формулу площади круга:
\[ S = πR2 \],
- где R – радиус круглого проводника [мм]
Савельев Николай
Инженер по телевизионному оборудованию Электрика и электроника, это не только моё хобби, но и работа
Задать вопрос
Стоит отметить, что при выборе сечения (квадратное, круглое, прямоугольное) для подобных схем не имеет значения! Также, материал выбирают из техническо-экономических соображений. Например, серебро можно использовать как провод: лучше проводимость, чем у меди, но стоимость больше. Поэтому, в зависимости от различный условий и задач, стараются подбирать провода, подходящие под решения и экономически выгодных.
Воспользовавшись формулами, описанными ранее, полное математическое уравнение Джоуля – Ленца имеет вид:
\[ Q = (I2tρl)/(πR2) \]
Энергия
ЭнергияЭДС индукции и энергия
Проблема:
Вертикально ориентированная квадратная проволочная петля падает из области, где магнитное поле B горизонтальное, однородное и перпендикулярное плоскости петля, в область, где поле равно нулю. Пусть длина каждой стороны быть s, а диаметр проволоки быть d. Удельное сопротивление провода ρ R а плотность проволоки ρ м . Если петля достигает терминала скорости, пока его верхний сегмент еще находится в области магнитного поля, найти выражение для конечной скорости.
Решение:
- Концепты:
ЭДС индукции ε = -∂flux/∂t, закон Ома, энергия сохранение. - Рассуждение:
Когда петля опускается, поток через петлю изменяется, и индуцируется ЭДС. в петле. Это приводит к тому, что в петле течет ток, и энергия рассеивается в виде тепла. Если петля падает с постоянной
скорость, то скорость, с которой гравитационная потенциальная энергия
уменьшение должно равняться скорости, с которой выделяется тепло. - Детали расчета:
|ЭДС| = |dпоток/dt| = Bsdy/dt, I = э.д.с./R. Здесь dy/dt — скорость с которой падает петля.
При достижении предельной скорости: I 2 R = ЭДС 2 /R = Fv клемма = MGV терминал .
Энергия, рассеиваемая в проводе в единицу времени, равна гравитационной потери потенциальной энергии в единицу времени.
(Bsv терминал ) 2 /R = мгв терминал , v терминал = мгР/(Бс) 2 .
R = ρ R 16s/πd 2 , m = ρ m
Если петля падает с постоянной
скорость, то скорость, с которой гравитационная потенциальная энергия
уменьшение должно равняться скорости, с которой выделяется тепло.Проблема:
Проводящая кольцевая петля из проволоки диаметром d,
удельное сопротивление ρ и массовая плотность ρ м падает с большой высоты h в магнитном поле с компонентой B з = В 0 (1 + кз),
где k — некоторая константа.
Петля диаметром D всегда
параллельно плоскости х-у. Сопротивлением воздуха пренебречь и найти
конечная скорость контура.
Решение:
- Концепты:
ЭДС индукции ε = -∂F/∂t, Закон Ома, сохранение энергии. - Рассуждение:
Когда петля падает через неоднородное магнитное поле, поток через петля меняется, и в петле индуцируется ЭДС. Это вызывает ток течет по контуру, а энергия рассеивается в виде тепла. Если петля падает с постоянной скоростью, то скорость, с которой уменьшение потенциальной гравитационной энергии должно равняться скорости, с которой тепло сгенерировано. - Детали расчета:
Гравитационная сила направлена в направлении -z, F g = -mg к .
Магнитный поток через контур F = BA = B 0 (1 + kz)πD 2 /4.
ЭДС, индуцированная в контуре, равна ε = -∂F/∂t. = -(B
Ток, протекающий в контуре, равен I = |ε|/R.
Скорость, с которой выделяется тепло, равна I 2 р. Курс, по которому гравитационная потенциальная энергия убывает мг dz/dt
Когда dz/dt = -v t , (v t = конечная скорость), тогда I 2 R = -mg dz/dt = mgv t .
Тогда |ε| 2 /R = мгв т , [B 0 2 k 2 π 2 D 4 /(16R)]v t 2
м = ρ м V = ρ м (πd 2 /4)πD. Для провода R = ρ длина/площадь = ρ 4Д/д 2 .
v t = 16ρ m (πd 2 /4)πDg(ρ 4D/d 2 )/(B 0 2 k 2 π 2 D 4 ) = 16ρ м гρ/(B 0 2 k 2 D 2 ).
Задача:
Тонкий диск из обычного металла с электропроводностью σ имеет радиус R и толщину d. Он фиксируется в перпендикулярное магнитное поле B(t)
(a) Найдите вектор плотности тока j (r) в точке
расстояние r от оси диска.
(b) Определить энергию/время, переданное диску
поле. Что становится с этой энергией?
(c) Предположим, что константа
a становится отрицательным, т. е. что
а —>
-α. Как ваши результаты в
части (а) и (б) меняются?
Решение:
- Концепты:
Закон Фарадея, закон Ома - Рассуждение:
Разделите диск на концентрические кольца. Магнитный поток через Кольцо меняется со временем. Это изменение потока вызывает ЭДС. Поскольку кольцо имеет конечное сопротивление, по кольцу течет ток. - Детали
расчет:
Для кольца с внутренним радиусом r и внешним радиусом r + dr имеем
ε(r) = -∂F/∂t = ЭДС индукции, ∂F/∂t = (∂B/∂t)пr 2 = αпр 2 .
E = αпr 2 /(2пr) = ар/2. Если α положителен, E указывает на направление -φ.
j = σ E , j(r) = σαr/2.
(b) Ток, текущий в кольце радиусом r, равен j(r)*d*dr. скорость, с которой энергия доставляется кольцу, равна ε(r)*j(r)*d*dr = (dпr
Скорость, с которой энергия доставляется на диск, равна
(дпσα 2 /2)∫ 0 Р р 3 др = dпσα 2 R 4 /8. Эта энергия преобразуется в тепловую энергию.
(с) Е и j теперь укажите на направление φ. Мощность, подаваемая на диск такой же.
Задача:
Однородное магнитное поле Б = Б 0 к точки в направлении z.
Частица с массой m и зарядом
q движется с кинетической энергией E 0
При t = 0 напряженность магнитного поля начинает изменяться
медленно, так что при t = t 1 будет B = B 1 k .
Пренебречь излучением.
(a) Чему равен радиус орбиты R 0 частицы при t < 0 в
условия B 0 и E 0 ?
(б) Предполагая, что радиус R орбиты частицы не меняется
заметно, пока частица совершает один оборот, какова кинетическая
энергия E 1 частицы в момент времени t 1 в пересчете на B 0 ,
B 1 и E 0 ?
Теперь предположим, что магнитное поле остается постоянная (
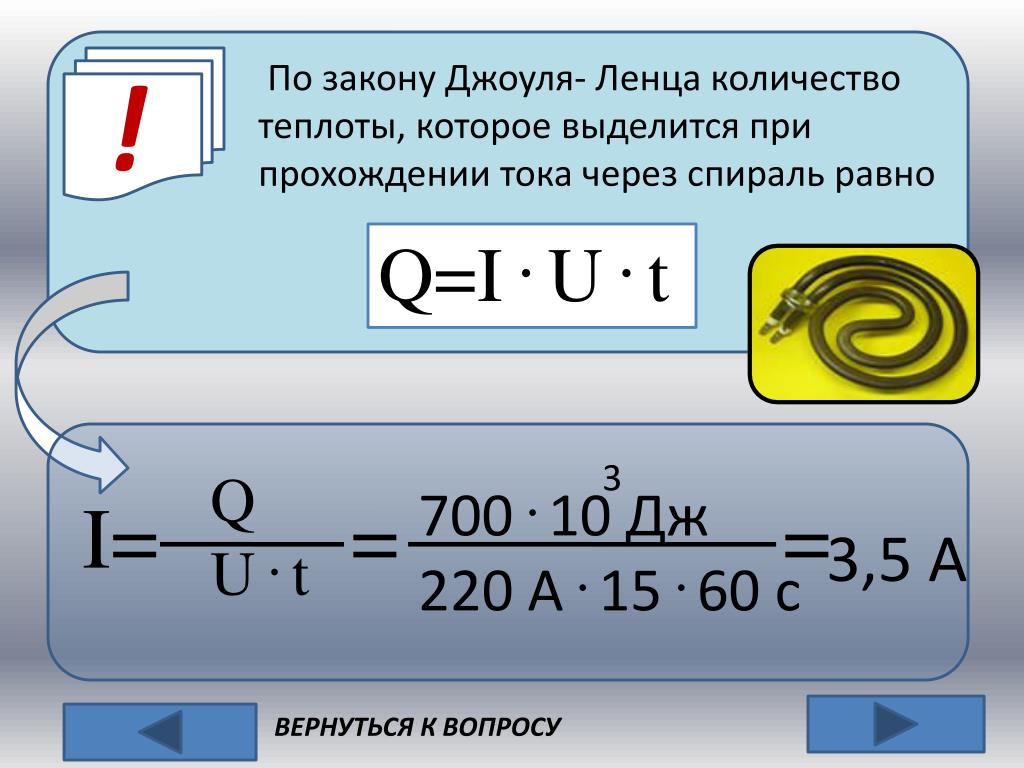
(c) Напишите уравнения движения Ньютона для компонентов скорости v x , v y и v я .
(d) Постройте уравнение движения для z = v x + iv y и Найди решение.
(e) Найдите выражения для v x (t), v y (t), x(t) и y(t). Опишите траекторию частицы словами.
Решение:
- Концепты:
Закон Фарадея, ЭДС индукции, затухающие колебания - Рассуждение:
Изменяющийся магнитный поток индуцирует ЭДС, которая изменяет кинетическую энергию частица. - Детали расчета:
(а) R 0 = mv/(qB 0 ) = (2mE 0 ) ½ / (qB 0 )
б) Предположим, что радиус R орбиты частицы не меняется заметно, пока частица совершает один оборот. Тогда кинетическая энергия частицы изменится на
ΔE = q(dB/dt)πR 2 за один оборот.
Время одного оборота T = 2πR/v,
поэтому dE/dt = ΔE/T = (qvR/2)(дБ/dt) = (qmv 2 R/(2mv))(дБ/dt) = (1/B)(дБ/dt)E.
(Мы использовали R = mv/(qB), qR/(mv) = 1/B, ½mv 2 = E.)
dE/E = дБ/В, ln(E 1 ) = ln(B 1 E 0 /B 0 ), Е 1 = В 1 Е 0 /В 0 .
(c) F x = mdv x /dt = qv y B 0 — mv x /τ, F y = mdv y /dt = -qv x B 0 — mv y /τ, F z = 0,
(d) dz/dt = -i(qB 0 /m)(v x + iv y ) — (v x + iv
= -i[(qB 0 /m)z — (i/τ)]z = gz,
где g = -i[(qB 0 /m)z — (i/τ).
z(t) = z 0 exp(gt) = z 0 exp(-t/τ) exp(-iωt), где ω = qB 0 /м.
(e) Re(z(t)) = v x (t) = v 0 exp(-t/τ) cos(ωt), Im(z(t)) = v y (t) = -v 0 exp(-t/τ) sin(ωt).
x(t) = ∫ 0 t v 0 exp(-t’/τ) cos(ωt’) dt’
= v 0 [exp(-t/τ)[- cos(ωt)/τ + ω sin(ωt)] + 1/τ]/[1/τ 2 + ω 2 ]
y(t) = -∫ 0 t v 0 exp(-t’/τ) sin(ωt’) dt’ + Р 0
= -v 0 [exp(t/τ)[ -sin(ωt)/τ — ω cos(ωt)] + ω] /[1/τ 2 + ω 2 ] + R 0
Аст —> бесконечность, x(t) —> x ∞ = (v 0 /τ)/[1/τ 2 + ω 2 ], y(t) —> г ∞ = -v 0 ω/[1/τ 2 + ω 2 ] + R 0
Частица закручивается по спирали в точку (x ∞ , y ∞ ).
Задача:
Тонкая металлическая квадратная рамка массой m, электрическая
сопротивления R, а сторона а вращается вокруг оси, перпендикулярной равномерному
магнитное поле В, как показано на рисунке. Изначально квадратная рамка
вращается с частотой ω 0 .
(a) Определите среднюю потерю энергии за цикл из-за джоулевого нагрева.
(b) Определить время, необходимое для замедления частоты вращения.
до 1/e от его первоначального значения. (Предположим, что дробное изменение кадра
частота вращения за цикл небольшая.)
Решение:
- Концепты:
ЭДС индукции e = -∂F/∂t, Закон Ома, сохранение энергии - Рассуждение:
Изменяющийся магнитный поток создает в рамке ЭДС. ЭДС вызывает протекающий ток, производящий джоулев нагрев. Кинетическая энергия преобразуется в тепловую энергию. - Детали расчета:
(а) (единицы СИ)
Магнитный поток через рамку Ва 2 cosθ. Угол меняется, dθ/dt = ш.
Индуцированная ЭДС из-за этого изменяющегося потока равна -Ba 2 sinθ ω.
Ток, протекающий в рамке, определяется как I = Ba 2 sinθ ω/R (без учета собственной индуктивности контура).
Количество кинетической энергии, преобразованной в тепловую энергию в единицу времени, равно P = B 2 a 4 sin 2 θ ω 2 /R.
Потери энергии за цикл (при условии, что ω меняется незначительно):
∫ 0 T Pdt = ∫ 0 2π (P/ω)dθ = πω B 2 a 4 /R = ΔE.
Начальные средние потери энергии за цикл из-за джоулевого нагрева: πω 0 B 2 a 4 /R.= ΔE/T = B 2 a 4 ω 2 /(2R).
(б)
= B 2 a 4 ω 2 /2R = -dE/dt.
Е = ½Iω 2 , = ма 2 ω 2 /12, ω 2 = 12E/ma 2 , dE/dt = -E 6B 2 a 2 /(Rm).
E = E 0 exp[-6B 2 a 2 t/(Rm)], t (1/e) = Rm/(6B 2 a 2 ).
Случайный преобразователь |
Калькулятор закона Ома Этот калькулятор вычисляет значения, используя закон Ома и первый закон Джоуля, определяя взаимосвязь между током, напряжением, мощностью, комплексной мощностью, импедансом и сопротивлением переменного тока. Пример 1: Резистор сопротивлением 5 Ом подключен к клеммам автомобильного аккумулятора на 12 В. Определить ток через резистор и мощность, поглощаемую резистором. Пример 2: Однофазный электродвигатель с импедансом Z=15 ∠53° = 9 + j12 Ом подключен к бортовой сети 115 В 400 Гц. Рассчитайте ток и комплексную мощность, потребляемую двигателем. Постоянный ток: Напряжение — Ток — Сопротивление Постоянный ток: Напряжение — Ток — Сопротивление — Мощность Переменный ток: Напряжение — Ток — Импеданс — Комплексная мощность милиомы (мОм)килоомы (кОм)мегаомы (МОм) Current I amperas (A)mikroamperas (μA)miliamperas (mA)kiloamperas (kA) Voltage U volt (V)microvolt (µV)millivolt (mV)kilovolt ( кВ)мегавольт (МВ) Далинтис Для расчета введите любые два значения, и два других значения будут рассчитаны автоматически. Определения и формулы Закон о Ом Не-амические компоненты Закон Джоул Закон Ом в контурах AC Примеры AC OHM Формалы Силы в AC IRUSTICIT Схема простой цепи, иллюстрирующая параметры закона Ома U , I и R В нашей повседневной жизни мы окружены электрическими цепями. От компьютеров, планшетов, смартфонов и автомобилей до кредитных карт и ключей от наших машин и домов — все они сделаны из электрических цепей. И все они работают по закону Ома: Мы все (ладно, не все, а только некоторые) знаем эту простую формулу еще со школы, а некоторые из нас знают ее даже с более раннего возраста. Европейцы знают первую формулу, а те, кто живет в Северной Америке, знают вторую. Европейцы предпочитают U по напряжению, в то время как американцы предпочитают V по той же физической величине. Закон ОмаГеорг Саймон Ом (1789–1854) Закон Ома назван в честь немецкого физика и математика Георга Симона Ома (1789–1854), который, будучи школьным учителем в школе с хорошо оборудованной физической лабораторией, исследовал недавно изобретенный (в 1799 г.) гальванический столб и термопара, изобретенная в 1821 году. Он обнаружил, что ток в проводнике прямо пропорционален разности потенциалов на проводнике. Он опубликовал результаты своих исследований в 1827 году в знаменитой книге « Die galvanische Kette, mathematisch bearbeitet» («Гальваническая цепь, исследованная математически»).0658 . В результате его работы единица сопротивления названа его именем. Эта взаимосвязь между током, напряжением и сопротивлением, теперь известная как закон Ома, является основной основой всей электроники. Ом много лет боролся за признание своей работы. Элемент схемы, основным назначением которого является создание электрического сопротивления, называется резистором. Резисторы и их электронные обозначения — европейские, стандартизированные IEC (слева) и американские, стандартизированные IEEE (справа) По закону Ома сопротивление, измеренное в омах, представляет собой просто константу пропорциональности между током и напряжением: где I ток, V и U напряжение и R сопротивление. Обратите внимание, что в этом выражении R ≥ 0. Отметим также, что в этом выражении мы предполагали, что резистор имеет постоянное сопротивление, не зависящее от напряжения или тока. Если значение R или отношение U/I постоянно, то ток можно изобразить как функцию напряжения в виде прямой линии. В резистивных цепях, например, в проводах и резисторах, ток и напряжение линейно пропорциональны. График, показывающий зависимость между током и напряжением для конкретного электронного компонента, называется вольт-амперной характеристикой. Резисторы имеют линейную вольтамперную характеристику. Дополнительную информацию о резисторах и других электронных компонентах можно найти в наших Калькуляторах для электротехники, ВЧ и электроники, а также Электротехнических преобразователях. Неомические компонентыГрафическое изображение вольтамперных характеристик нескольких устройств: 1 — резистор, 2 — диод, 3 — лампа накаливания, 4 — стабилитрон; как мы видим, только резистор имеет линейную вольт-амперную характеристику Хотя при изучении закона Ома мы всегда предполагаем, что вольт-амперные характеристики резисторов линейны, важно отметить, что многие очень полезные электрические и электронные компоненты, такие как лампы накаливания, диоды и транзисторы, которые широко используются в электрических цепях имеют нелинейную характеристику сопротивления. В этой цепи увеличение напряжения не приведет к пропорциональному увеличению тока, поскольку сопротивление горячей лампы при ее номинальном напряжении 12 В выше, чем ее сопротивление при 4 или 6 В. увеличивается напряжение и увеличивается сопротивление лампы (см. рисунок выше) Во многих случаях это предположение о линейности резисторов неверно. Рассмотрим, например, схему с лампой накаливания и блоком питания с переменным напряжением. Эту схему можно найти во многих школьных учебниках, где обсуждается зависимость тока от напряжения при условии, что сопротивление лампы постоянно. Они объясняют, что если напряжение на клеммах 12-вольтовой лампы увеличивается, ток также пропорционально увеличивается. Однако, это не так! Если мы поставим амперметр и измерим ток, то заметим, что он не прямо пропорционален напряжению. Это связано с тем, что сопротивление лампы изменяется, когда ее нить накала начинает светиться — лампа имеет нелинейную вольт-амперную характеристику. Когда молодые люди начинают изучать электричество, первыми двумя законами, которые они узнают, являются законы Ома и Джоуля, и довольно часто они видят их в форме колеса закона Ома, что действительно пугает, особенно когда они понимают, что им придется запомнить это колесо — потому что для их учителей гораздо проще проверить память учеников, чем проверить их понимание. Преподаватели часто заставляют своих учеников запоминать все 12 формул вместо заучивания или, что гораздо лучше, 9 формул.0007 понимая только два из них, а именно: и Хотя это колесо обычно называют законом Ома, это колесо на самом деле объединяет два закона — закон Ома и закон нагревания Джоуля, также называемый первым законом Джоуля, и Джоуля. -Закон Ленца Недорогой набор для детей с электричеством Остальные 10 страшных формул можно легко вывести из этих двух. И даже эти две формулы не нужно запоминать. Что действительно необходимо помнить и понимать, так это то, что ток через компонент прямо пропорционален разности потенциалов, приложенной к этому компоненту, и обратно пропорционален его сопротивлению. Эти два закона очень понятны, если учащиеся понимают, что такое ток, напряжение, сопротивление и мощность. Они поймут, если поиграют с батарейкой, несколькими резисторами и мультиметром. Они также могут играть с этим калькулятором. Это легко сделать, если использовать аналогию с водяным насосом, ограничением и трубой, в которой насос оказывает давление (представляющее напряжение), чтобы проталкивать воду (ток) по контуру (трубе) с ограничением (сопротивлением). Все другие формулы, показанные в колесе закона Ома, могут быть получены из этих двух формул, и если человек ежедневно использует другие формулы, он в конечном итоге запомнит их без каких-либо усилий. Закон ДжоуляДжеймс Прескотт Джоуль (1818–1889) Для молодого английского пивовара Джеймса Прескотта Джоуля, который зарабатывал на жизнь управляющим пивоварней, наука была просто хобби. Его отец был богатым пивоваром, и юный Джеймс начал работать на пивоварне в возрасте пятнадцати лет. Закон Джоуля гласит, что мощность нагрева P , создаваемая электрическим током I в проводнике, пропорциональна произведению квадрата тока на сопротивление провода R : Если мы объединим Закон Джоуля с законом Ома, мы можем вывести несколько полезных формул, которые можно использовать для расчета мощности, рассеиваемой на резисторе, сопротивления по известному напряжению и току, тока, протекающего через резистор, и напряжения на резисторе. Эти формулы часто отображаются в виде страшного колеса закона Ома или (менее страшного) треугольника закона Ома. Нажмите на приведенные ниже примеры, чтобы узнать, как использовать эти формулы. Эмиль Ленц (1804–1865) Омический нагрев был независимо изучен русским физиком Эмилем Ленцем, изучавшим электромагнетизм с 1831 года и наиболее известным открытием закона, связывающего направление индуцированного электрического тока с движущимся магнитным полем. который назван в его честь. Он также самостоятельно открыл закон Джоуля, который часто носит также имя Ленца — «закон Джоуля-Ленца». Следует также отметить, что в некоторых учебниках этот закон ошибочно называют законом Уатта, особенно если ссылаются на формулу P = UI . Закон Ома в цепях переменного тока Закон Ома используется не только для описанного выше анализа цепей постоянного тока. Когда к цепи прикладывается переменное во времени напряжение, например, синусоидальное, закон Ома по-прежнему действует. Если к резистору приложить синусоидальное напряжение, то в нем будет протекать синусоидальный ток. При применении закона Ома для анализа цепи переменного тока всегда необходимо последовательно выражать напряжение и ток. Это означает, что напряжение и ток должны быть выражены как в виде среднеквадратичных значений, так и в виде пиковых или размаховых значений. При применении закона Джоуля для определения мощности, рассеиваемой на резисторе, применяется то же правило: и ток, и напряжение должны быть выражены с использованием одних и тех же величин. Например: , где субиндекс RMS обозначает среднеквадратичное значение, или Здесь p означает пиковое значение. Если цепь переменного тока содержит реактивные компоненты, такие как конденсаторы и катушки индуктивности, к ним также применяется закон Ома. В этом случае вместо сопротивлений используются их реактивные сопротивления: , где X может быть реактивным сопротивлением конденсатора X C или катушки индуктивности X L , которые рассчитываются по следующим формулам : и Дополнительную информацию о реактивном сопротивлении различных компонентов и их последовательных и параллельных комбинациях можно найти в наших электрических, радиочастотных и электронных калькуляторах и электротехнических преобразователях. Что касается мощности в реактивных компонентах, то они не преобразуют энергию в тепло и, следовательно, энергия не теряется и истинная (активная, реальная) мощность P равна нулю. Мгновенная мощность переходит туда и обратно между конденсатором или катушкой индуктивности и источником питания. Скорость, с которой реактивный компонент накапливает или возвращает энергию, называется его реактивной мощностью 9.0657 Q и определяется по следующим формулам: Реактивная мощность измеряется в реактивных вольт-амперах (вар) и может использоваться с общепринятыми десятичными приставками, например, квар, мвар и т. д. Параллельный RLC цепь В цепях, содержащих активные и реактивные компоненты, применение закона Ома предполагает использование комплексных величин импеданса Z , напряжения U и тока I . Поскольку для законов Ома и Джоуля используются расчеты, умножения и деления, комплексные величины удобно выражать в полярной форме. AC Формулы закона Ома Примечание для читателей, не знакомых с обозначениями углов, используемыми в американских учебниках по электронике и электротехнике. Специальная запись, называемая векторной или угловой записью, используется с символом угла (∠). Он используется для описания фазовращателей. Вектор представляет собой комплексное число U , используемое для представления синусоиды. Он представлен в полярных координатах вектором с величиной U и углом φ , который обычно выражается в градусах. Векторы предоставляют простые средства анализа электрических цепей. Это U∠φ является просто сокращенным обозначением для Ue jφ . Ниже приведены формулы, используемые в этом калькуляторе. Расчеты изготовлены со значениями в фазорной форме в соответствии с правилами умножения и деления фазора: , где φ U , φ I и φ 1010109, и φ 1010101010, и φ 9 Все комплексные значения вводятся в форму калькулятора либо в прямоугольной, либо в векторной форме. Хотя импеданс и комплексная мощность не являются векторными величинами, они могут быть представлены в комплексной форме, потому что, подобно напряжению и току, они являются комплексными числами и имеют как модуль, так и угол. Если они вводятся в прямоугольной форме, перед расчетом они преобразуются в векторную форму по формулам, описанным в нашем Комплексном калькуляторе векторов. В качестве примера рассчитаем общий ток I T , в параллельной цепи RLC с R = 10 Ом, L = 100 мкГн и C = 1 мкФ. Источник переменного тока подает синусоидальное напряжение 0,5 В частотой 10 кГц (нажмите, чтобы посмотреть результат расчетов). Величина импеданса этой RLC-цепи в прямоугольной форме равна Фазовый угол равен Положительный фазовый угол означает, что нагрузка является индуктивной, а ток отстает от напряжения. Общий импеданс в полярной форме равен Используя закон Ома и правило деления чисел в полярной форме, определим полный ток: Мощность в цепях переменного тока Q, очевидный | С | а комплексная мощность S может быть рассчитана по следующим формулам:и Опять же, поскольку при расчете мощности используются операции умножения и деления, комплексные значения удобно выражать в полярной форме. Here U and I are the voltage and current in complex form and I* , U* , and Z* are the conjugates of ток, напряжение и импеданс в комплексной форме. Жирный шрифт означает, что эти значения являются векторными величинами. Обратите внимание, что здесь комплексная мощность S измеряется в вольт-амперах (ВА). В векторной форме у нас есть где φ U — угол фазы напряжения, а φ I — угол фазы тока. Эти формулы были использованы для создания колеса закона Ома переменного тока. Колесо закона Ома переменного тока; полужирный шрифт используется для отображения комплексных значений тока, напряжения, мощности и импеданса. Дополнительную информацию о расчетах мощности переменного тока вы найдете в нашем Калькуляторе мощности переменного тока. Ниже приведены несколько примеров расчетов с помощью этого калькулятора. Примеры расчетовПример 3 . Электронагреватель сопротивлением 10 Ом подключается к розетке 120 В. Рассчитать потребляемую мощность и ток, потребляемый нагревателем. Пример 4 . Небольшая лампочка сопротивлением 2300 Ом в холодильнике подключена к линии электропередач 120 В. Рассчитать потребляемую мощность и ток, потребляемый лампой. Пример 5 . Ток 0,15 А от солнечной панели протекает через резистор 220 Ом. Рассчитайте напряжение на этом резисторе и мощность, которую он рассеивает в виде тепла. Пример 6 . Рассчитайте сопротивление галогенной лампочки и мощность, которую она рассеивает, если она потребляет 1,5 А от 12-вольтового автомобильного аккумулятора. Пример 7 . Рассчитайте ток через резистор сопротивлением 12 кОм и напряжение на нем, если резистор рассеивает мощность 1 Вт. Резистивно-емкостная цепь серии (см. пример 6). Дано: R = 10 Ом, C = 0,1 мкФ, I T = 0,2∠0°. Требуется: U T Пример 8 . Резистор сопротивлением 10 Ом и конденсатор емкостью 0,01 мкФ подключены последовательно к источнику синусоидального питания частотой 1 МГц. Определите напряжение источника в полярной форме, если ток, потребляемый от источника, равен I = 0,2∠0° A. Совет: используйте наш калькулятор импеданса RC-цепи для определения импеданса RC-цепи в полярной форме (Z = 18,8 ∠–57,86). °), затем с помощью этого калькулятора определите напряжение источника (V = 3,76∠–57,8° В). Šį straipsnį parašė Анатолий Золотков. Вы можете быть заинтересованы в других калькуляторах в Elektra, Radijo dažniai ir elektronika Group:Custer -Capacitor (RC) Калькулятор схемы Калькулятор с резистентностью с параллельной резистентность Калькулятор импеданса индуктора Калькулятор взаимной индуктивности Калькулятор взаимной индуктивности — параллельные индуктивности Калькулятор взаимной индуктивности — индуктивности в ряду Параллельный калькулятор импеданса с цепью RC Параллельный калькулятор схемы с цепи LC Параллельный калькулятор RL -цепи.  |
цепи постоянного тока. Он определяет одно или два неизвестных значения из двух известных значений.
Для переменного тока не забудьте ввести напряжение и ток последовательно, то есть и напряжение, и ток должны быть введены как среднеквадратичные значения, или пиковые значения, или значения размаха.
Итак, можно сказать, что закон Ома действует везде. Попробуем лучше понять этот закон.
На схемах представлены два вида символов: один используется в основном в Европе и стандартизирован Международной электротехнической комиссией (IEC), а другой — в Северной Америке и стандартизирован Институтом инженеров по электротехнике и электронике (IEEE).
В математике линейная функция — это функция, график которой представляет собой прямую линию (см. иллюстрацию ниже). Например, 90 657 y 90 658 = 2 90 657 x 90 658 — это линейная функция. В линейных отношениях, если одну из величин увеличить или уменьшить, например, в три раза, другая также увеличится или уменьшится на ту же величину. По закону Ома это означает, что если напряжение на резисторе утроится, ток также утроится. При этом предполагается, что его сопротивление постоянно.
То есть вольтамперная зависимость для них не является прямой линией, проходящей через начало координат.
Это закон Ома. А что мощность прямо пропорциональна току и напряжению — это закон Джоуля.
Когда Джоулю было всего 23 года, он открыл закон, который теперь носит его имя, проводя эксперименты, пытаясь выяснить, что более эффективно в их пивоварне: паровой двигатель или недавно изобретенные электродвигатели. В результате он установил зависимость между током, протекающим через сопротивление (провод), и выделяемым теплом.
Этот нагрев провода электрическим током также называется омическим нагревом, джоулевым нагревом или резистивным нагревом.
Этот ток находится в фазе с приложенным напряжением, потому что, когда напряжение меняет полярность, ток также меняет ее. Когда напряжение достигает своего максимума, ток также достигает своего максимума.
Вы можете использовать наш Калькулятор преобразования прямоугольного вектора в полярный для преобразования значений комплексной мощности, тока, напряжения и импеданса между комплексными и полярными формами. Чтобы определить полное сопротивление различных параллельных и последовательных цепей с активными и реактивными компонентами, используйте наши электрические, радиочастотные и электронные калькуляторы.
Формула Эйлера лежит в основе фазового анализа:
. Математически можно показать, что комплексная мощность равна произведению векторного напряжения и комплексно-сопряженного векторного тока, то есть
Звездочка, например, в I * показывает комплексное сопряжение комплексного тока I 
