Активное и реактивное сопротивление

ТОЭ › Расчет цепей синусоидального тока

Электрические лампы накаливания, печи сопротивления, бытовые нагревательные приборы, реостаты и другие приемники, где электрическая энергия преобразуется в тепловую, на схемах замещения обычно представлены только сопротивлением R. Для схемы, изображенной на рис. 13.1, а, заданы сопротивление R и напряжение, изменяющееся по закону

u = Umsinωt

Найдём ток и мощность в цепи.

Активное сопротивление

И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента — резистора, который, как говорят, обладает активным сопротивлением. Еще иногда его называют омическим. Как нам говорит вики-словарь, «активный — это деятельный, энергичный, проявляющий инициативу». Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.

То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.

Как смотреть силу тока в цепи через осциллограф

Чем же резистор отличается от катушки индуктивности и конденсатора? Понятное дело, что выполняемыми функциями, но этим все не ограничивается. Итак, давайте рассмотрим самую простую схемку во всей электронике:

На схеме мы видим генератор частоты и резистор.

Давайте визуально посмотрим, что у нас творится в этой схеме. Для этого, как я уже сказал, нам понадобится генератор частоты

А также цифровой осциллограф:

С помощью него мы будем смотреть напряжение и силу тока .

Что?

Силу тока?

Но ведь осциллограф предназначен для того, чтобы рассматривать форму сигнала напряжения? Как же мы будем рассматривать форму сигнала силы тока? А все оказывается просто). Для этого достаточно вспомнить правило шунта.

Кто не помнит — напомню.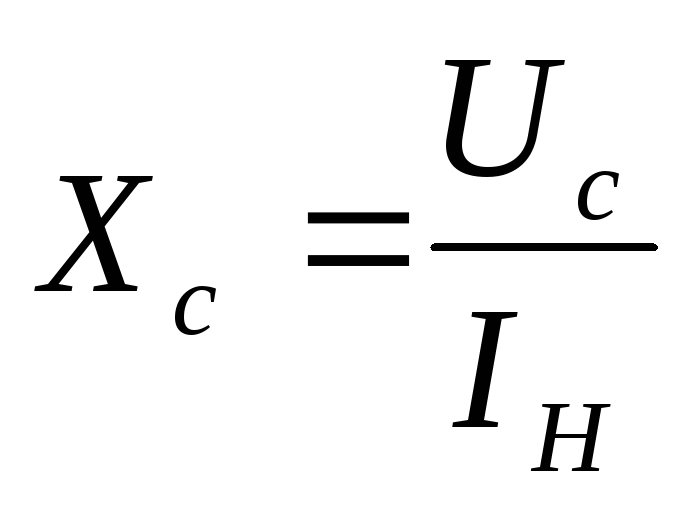 Имеем обыкновенный резистор:

Что будет, если через него прогнать электрический ток?

На концах резистора у нас будет падение напряжения. То есть, если замерить с помощью мультиметра напряжение на его концах, мультиметр покажет какое-то значение в Вольтах

И теперь главный вопрос: от чего зависит падение напряжения на резисторе? В дело опять же вступает закон Ома для участка цепи: I=U/R. Отсюда U=IR. Мы видим зависимость от номинала самого резистора и от силы тока, текущей в данный момент в цепи. Слышите? От СИЛЫ ТОКА! Так почему бы нам не воспользоваться таким замечательным свойством и не глянуть силу тока через падение напряжения на самом резисторе? Ведь номинал резистора у нас постоянный и почти не изменяется с изменением силы тока

Мощность

При наличии активного сопротивления, значительно снижается мощность этой цепи. Это значение зависит от скорости снижения напряжения и преобразования электрической энергии. В электрической схеме мощность обозначается буквой «P».

Для того чтобы добиться минимального снижения средней и мгновенной мощностей, которые образуются в момент появления активного сопротивления, снижения напряжения и преобразования энергий, необходимо чтобы простейшие цепи состояли из идеальных элементов с высокой электрической проводимостью.

Осциллограмма силы тока на активном сопротивлении

В данном опыте нам не обязательно знать номинал силы тока в цепи. Мы будем просто смотреть, от чего зависит сила тока и изменяется ли вообще?

Поэтому, наша схема примет вот такой вид:

В этом случае шунтом будет являться резистор сопротивлением в 0,5 Ом. Почему именно 0,5 Ом? Да потому что он не будет сильно греться, так как обладает маленьким сопротивлением, а также его номинал вполне достаточен, чтобы снять с него напряжение.

Осталось снять напряжение с генератора, а также со шунта с помощью осциллографа. Если вы не забыли, со шунта мы снимаем осциллограмму силы тока в цепи. Красная осциллограмма — это напряжение с генератора Uген , а желтая осциллограмма — это напряжение с шунта Uш , в нашем случае — сила тока. Смотрим, что у нас получилось:

Частота 28 Герц:

Частота 285 Герц:

Частота 30 Килогерц:

Как вы видите, с ростом частоты сила тока у нас осталась такой же.

Давайте побалуемся формой сигнала:

Как мы видим, сила тока полностью повторяет форму сигнала напряжения.

Итак, какие можно сделать выводы?

1) Сила тока через активное (омическое) сопротивление имеет такую же форму, как и форма напряжения.

2) Сила тока и напряжение на активном сопротивлении совпадают по фазе, то есть куда напряжение, туда и ток. Они двигаются синфазно, то есть одновременно.

3) С ростом частоты ничего не меняется (если только на очень высоких частотах).

Сопротивления цепи

Уравнение (5-30) можно переписать в следующем виде

U

= √(
Ir
)2 + (
IxL
)2 =
I
√
r
2 +
x
2L =
Iᴢ
откуда ток в цепи

I

=
U
/
z
=
U
/ √(
r
2 +
x
2L)

Величина

z

= √(
r
2 +
x
2L) = √(
r
2 + ω
L
)2

называется полным сопротивлением цепи.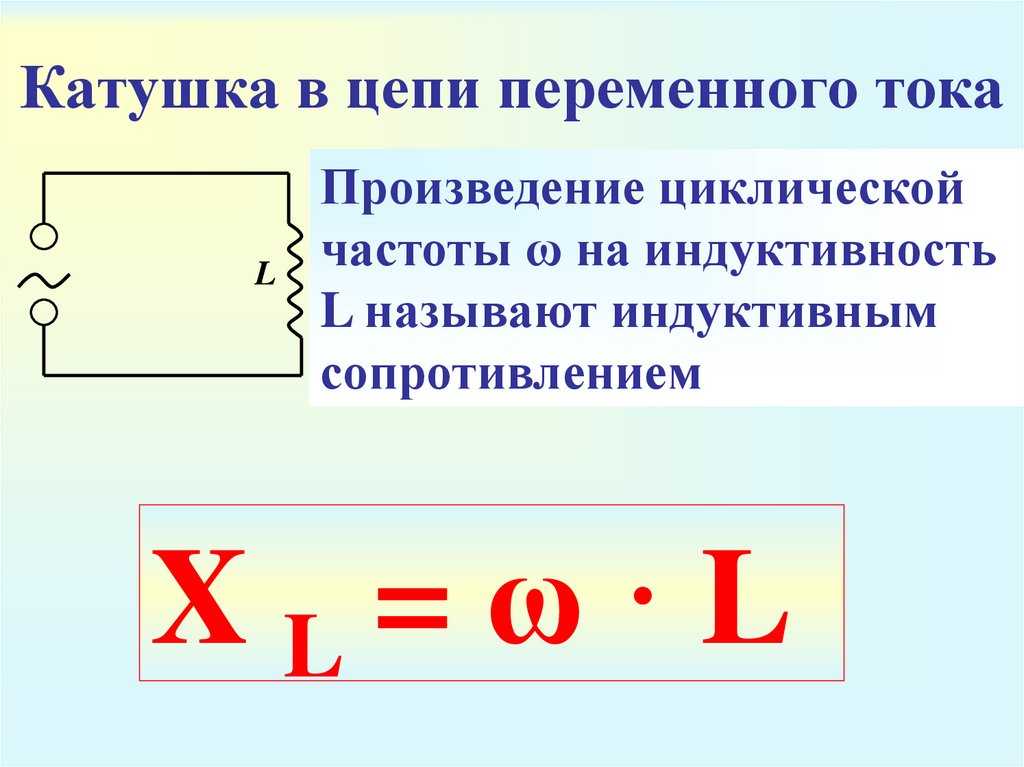

Сопротивления r

,
x
L и
z
графически можно изобразить сторонами прямоугольного треугольника — треугольника сопротивлении (рис. 5-20),который можно получить из треугольника напряжений, уменьшив каждую из его сторон в
I
раз.

Так как треугольники сопротивлений и напряжений подобны, то угол сдвига φ между напряжением и током, равный углу между сторонами треугольника z

и
r
, можно определить через

cos φ = U

a /
U
Рис 5-20. Треугольник сопротивлений цепи с активным сопротивлением и индуктивностью

Конденсатор в цепи переменного тока

Ну а теперь давайте вместо резистора поставим конденсатор.

Смотрим осциллограммы:

Как вы видите, конденсатор обладает сопротивлением, так как сила тока в цепи значительно уменьшилась. Но обратите внимание, что произошел сдвиг желтой осциллограммы, то бишь осциллограммы силы тока.

Вспоминаем алгебру старшие классы.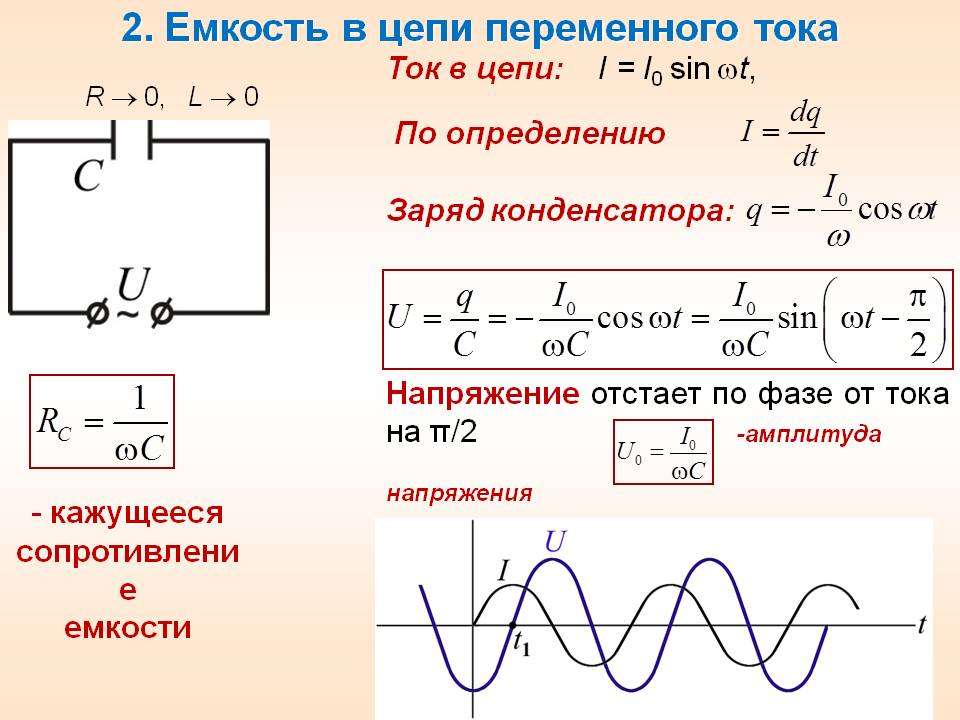 Итак, полный период T — это 2П

Теперь давайте прикинем, какой сдвиг фаз у нас получился на графике:

Где-то примерно П/2 или 90 градусов.

Почему так произошло? Во всем виновато физическое свойство конденсатора. В самые первые доли секунд, конденсатор ведет себя как проводник с очень малым сопротивлением, поэтому сила тока в этот момент будет максимальна. В этом можно легко убедиться, если резко подать на конденсатор напряжение и в начальный момент времени посмотреть, что происходит с силой тока

Красная осциллограмма — это напряжение, которое мы подаем на конденсатор, а желтая — это сила тока в цепи конденсатора. По мере заряда конденсатора сила тока падает и достигает нуля при полном заряде конденсатора.

К чему приведет дальнейшее увеличение частоты? Давайте посмотрим:

50 Герц.

100 Герц

200 Герц

Как вы видите, с увеличением частоты, у нас сила тока в цепи с конденсатором возрастает.

Зависимость

Величина активного сопротивления во многом зависит от диаметра проводников. При подаче высокочастотных токов, сопротивление проводника может быть снижено, только если его поверхностный слой намного тоньше основного. Для того чтобы добиться идеального сечения, этот слой должен состоять из материала с очень высокой проводимостью, например, золота или серебра. Данный эффект возникает по причине взаимодействия напряжения и магнитного поля, образованного им. Поле сильно влияет на ток, протекающий по проводнику и выталкивает его на поверхностный слой. Таким образом ближе к поверхности проводника проводимость снижается и становится критично малой в его верхнем слое.

Так же присутствуют следующие эффекты: потери утечки и диэлектрические потери. Оба эффекта связаны с наличием конденсатора в цепи. Диэлектрические потери возникают за счет увеличения температуры диэлектрика внутри конденсатора. Потеря утечки возникает в следствии доли пробоя изолятор конденсатора.

Гистерезис. Это тоже тип потери энергии переменного тока. Такая потеря возникает при формировании магнитного поля вокруг предметов из металла. Электромагнитное воздействие приводит к нагреванию металла, а значит преобразованию энергии.

Последним фактором утечки является радиоизлучение. Радиоволны появляются по причине сильного магнитного поля и его взаимодействия с металлами цепи. Для подавления, особенно в радиоаппаратуре, используются экраны, которые впитывают часть поля и отталкивают остальную долю.

Реактивное сопротивление конденсатора

Как мы увидели с прошлого опыта, с увеличением частоты растет сила тока! Кстати, у резистора не росла. То есть получается в данном случае из закона Ома, что сопротивление конденсатора зависит от частоты! Да, все так оно и есть. Но называется оно не просто сопротивлением, а реактивным сопротивлением и вычисляется по формуле:

где

Хс — реактивное сопротивление конденсатора, Ом

П — постоянная и приблизительно равна 3,14

F — частота, Гц

С — емкость конденсатора, Фарад

Треугольник сопротивлений

Схема цепи, подключенной к переменному току, имеет полное сопротивление, которое можно определить в виде суммы квадратов реактивного и активного сопротивлений.

Если изобразить это выражение в виде графика, то получится треугольник сопротивлений. Он образуется, если рассчитать последовательную цепь всех трех видов сопротивлений.

По этому треугольному графику можно увидеть, что катеты представляют собой активное и реактивное сопротивление, а гипотенуза является полным сопротивлением.

Реактивное сопротивление катушки индуктивности

Из опыта выше мы можем сделать вывод, что сопротивление катушки зависит от частоты и вычисляется по формуле

где

ХL — сопротивление катушки, Ом

П — постоянная и равна приблизительно 3,14

F — частота, Гц

L — индуктивность

Подробнее здесь: https://www.ruselectronic.com/news/katushka-induktivnosti-v-tsepi-postoyannogo-i-peremennogo-toka/

где

ХL — сопротивление катушки, Ом

П — постоянная и равна приблизительно 3,14

F — частота, Гц

L — индуктивность

Подробнее здесь: https://www.ruselectronic.com/news/katushka-induktivnosti-v-tsepi-postoyannogo-i-peremennogo-toka/

где

ХL — сопротивление катушки, Ом

П — постоянная и равна приблизительно 3,14

F — частота, Гц

L — индуктивность

Подробнее здесь: https://www. ruselectronic.com/news/katushka-induktivnosti-v-tsepi-postoyannogo-i-peremennogo-toka/

где

ХL — реактивное сопротивление катушки, Ом

П — постоянная и равна приблизительно 3,14

Подробнее здесь: https://www.ruselectronic.com/news/katushka-induktivnosti-v-tsepi-postoyannogo-i-peremennogo-toka/

П — постоянная и приблизительно равна 3,14

F — частота, Гц

L — индуктивность, Генри

Решая это уравнение относительно f , находим

(3.40)
При резонансе напряжений частота источника равна собственной частоте колебаний контура.

Выражение (3.40) является формулой Томсона, определяющей за­висимость собственной частоты колебаний контура

, от параметровL

и
С
. Следует вспомнить, что если конденсатор контура зарядить от ис­точника постоянного тока, а затем замкнуть его на индуктивную ка­тушку, то в контуре возникнет переменный ток частоты

. Вследствие потерь колебания в контуре будут затухать, причем время затухания зависит от величины потерь.

Рис. 55

Резонансу напряжений соответствует векторная диаграмма, при­веденная на рис.55. На основании этой диаграммы и закона Ома для цепи с r,
L
и
С
сформулируем признаки резонанса напряжений:

а) сопротивление всей цепи

мини­мальное и чисто активное;

б) ток цепи совпадает по фазе с напряже­нием источника и достигает максимального значения;

Рис. 56 Рис. 57

в) напряжение на индуктивной катушке равно напряжению на емкости и каждое в отдельности может во много раз превышать напряжение на зажимах цепи.

Физически это объясняется тем, что напряжение источника при резонансе идет только на покрытие потерь в контуре. Напряже­ние на индуктивности и емкости обусловлено накопленной в них энергией, величина которой тем больше, чем меньше потери в цепи.

Количествен­но указанное явление характеризуется добротностью кон­тура
Q
, которая представляет собой отношение напряжения на ка­тушке или емкости к напряжению на зажимах цепи при резонансе;

. (3.41)
При резонансе

Величина

называется волновым сопротивлением контура. Таким образом,

(3.42)

Способность колебательного контура выделять токи резонансных частот и ослаблять токи других частот характеризуется резонансной кривой (рис. 56).

Резонансная кривая показывает зависимость действующего значе­ния тока в контуре от частоты источника при неизменной собственной частоте контура.

Эта зависимость определяется законом Ома для цепи с r,L

и
С
. Действительно,
I =Uz
, где

(3.43)

На рис. 57 показана зависимость реактивного сопротивления

от частоты источника. Анализ этого графика и выражения (3.43) показывает, что при низких и высоких частотах реактивное со­противление велико и ток в контуре мал. При частотах, близких

реактивное сопротивление мало и ток контура велик. При этом, чем больше добротность контураQ

, тем острее резонансная кривая кон­тура.

Курс физики (Грабовский Р.И.)

Курс физики (Грабовский Р.И.)

Грабовский Р.И. Курс физики. Учеб. пособие для с/х ин-тов. Изд. 4-е, перераб. и доп. М., «Высш. школа», 1974. — 552 с. Учебник составлен в соответствии с программой по физике для сельскохозяйственных институтов. В нем приводится достаточное количество примеров, связанных с агробиологическими науками и сельскохозяйственным производством. Настоящее издание (3-е вышло в 1970 г.) отличается от предыдущих некоторыми (небольшими по объему) дополнениями и изменениями, способствующими улучшению содержания. Предназначается для студентов неинженерных факультетов сельскохозяйственных вузов. Многие разделы учебника могут быть использованы и студентами инженерных факультетов. Оглавление Предисловие Введение § 1. Предмет физики. Связь физики с другими науками и производством § 2. О единицах измерения и размерности физических величин § 3. О некоторых математических понятиях и символах 1. Физические основы механики § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения § 5. Прямолинейное движение материальной точки § 6. Движение материальной точки по окружности Глава II. Основные законы динамики § 7. Законы Ньютона. Масса и сила § 8. Закон изменения количества движения (импульса) § 9. Закон сохранения количества движения в изолированной системе § 10. Силы упругости § 11. Силы трения § 12. Силы тяготения (гравитационные силы) § 13. Центростремительная сила § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции § 15. Вес тел. Ускорение силы тяжести. Невесомость Глава III. Работа и энергия § 16. Работа и мощность § 17. Энергия § 18. Закон сохранения и превращения энергии § 19. О космических скоростях § 20. Границы применимости классической механики Глава IV. Вращательное движение твердого тела § 21. Основной закон динамики вращения § 22. Моменты инерции некоторых тел § 23. Закон сохранения момента количества движения. Кинетическая энергия вращающегося тела Глава V. Движение жидкости § 24. Основные определения. Уравнение неразрывности § 25. Уравнение Бернулли § 26. О некоторых приложениях уравнения Бернулли Глава VI. Колебания и волны § 27. Гармоническое колебание и его характеристики § 28. Сложение гармонических колебаний § 29. Динамика колебательного движения. Маятник § 30. О затухающих и вынужденных колебаниях § 31. Волновой процесс § 32. Уравнение волны. Интенсивность волны § 33. Интерференция волн. Стоячие волны § 34. Фронт волны. Принцип Гюйгенса-Френеля 2. Молекулярная физика и термодинамика § 35. Основные положения молекулярно-кинетической теории § 36. О некоторых явлениях, подтверждающих основные положения молекулярно-кинетической теории § 37. О теплоте и температуре § 38. О предмете и методах молекулярной физики Глава VIII. Газы § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная § 41. Основное уравнение кинетической теории идеального газа § 42. Средняя кинетическя энергия поступательного движения молекулы идеального газа § 43. О числе степеней свободы. Внутренняя энергия газа § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям § 46. Средняя длина свободного пробега молекул § 47. Явления переноса в газах. Уравнение переноса § 48. Диффузия § 49. Теплопроводность § 50. 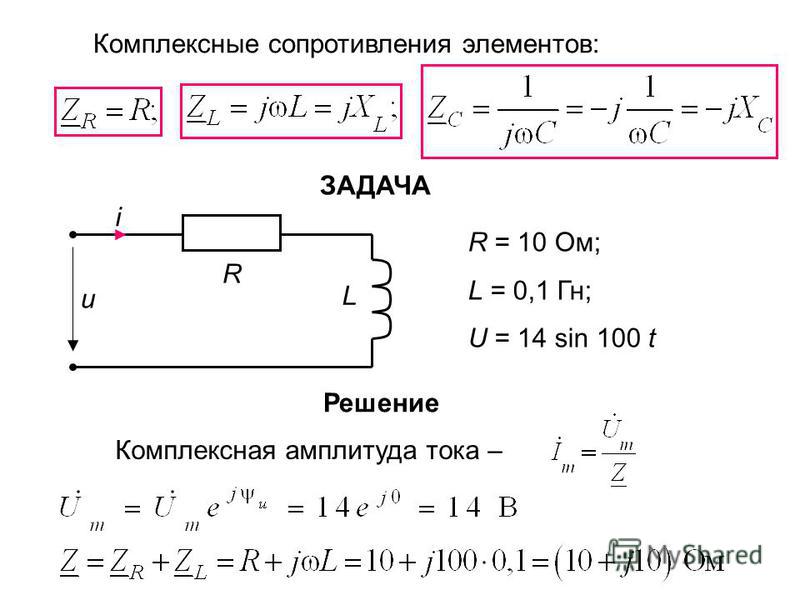Внутреннее трение (вязкость) Глава IX. Жидкости и твердые тела § 51. Особенности строения жидкостей и твердых тел § 52. Деформация твердого тела § 53. Тепловое расширение твердых и жидких тел § 54. Теплоемкость твердых и жидких тел § 55. Диффузия в жидких и твердых телах § 56. Осмос § 57. Теплопроводность жидких и твердых тел § 58. Вязкость жидкости. Турбулентное движение жидкости § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа § 61. Капиллярные явления; формула Жюрена Глава X. Изменение агрегатного состояния вещества (фазовые превращения) § 62. Понятие о фазовых превращениях и диаграмме состояний вещества § 63. Реальный газ. Уравнение Ван-дер-Ваальса § 64. Опыт Эндрюса. Критическая температура § 65. Сжижение газов. Эффект Джоуля-Томсона § 66. Испарение и конденсация. Кипение § 67. Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором § 68. Плавление и затвердевание (кристаллизация). Возгонка Глава XI. Основы термодинамики § 69. О некоторых общих понятиях термодинамики. Первое начало термодинамики § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы § 71. Цикл Карно. Второе начало термодинамики § 72. Энтропия § 73. О статистическом смысле энтропии и второго начала термодинамики 3. Электричество и магнетизм § 74. Электризация тел. Электрический заряд § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность § 76 Электрический диполь. Поле диполя § 77. Теорема Остроградского-Гаусса и ее приложения § 78. Работа перемещения заряда в электрическом поле. Потенциал § 79. О неустойчивости статических систем электрических зарядов § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника § 81. Диэлектрики в электрическом поле. Поляризация диэлектриков § 82. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Вектор электрической индукции § 83. Конденсатор. Энергия электрического поля Глава XIII. Постоянный электрический ток § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока § 86. Разветвленная электрическая цепь. Правила Кирхгофа § 87. Контактная разность потенциалов. Термоэлектрические явления § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи § 91. Ток в жидкостях. Электролиз. Законы Фарадея § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды § 93. Типы самостоятельного газового разряда Глава XIV. Электромагнетизм § 94. Постоянный магнит и круговой ток. Магнитные поля магнитов и токов § 95. Магнитное взаимодействие токов в вакууме; закон Ампера § 96. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа § 97. Некоторые приложения закона Био-Савара-Лапласа § 98. Магнитные поля соленоида и тороида § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции § 100. Действие магнитного поля на проводник с током. Определение ампера § 101. Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях Глава XV. Электромагнитная индукция и переменный ток § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко § 104. Взаимная индукция и самоиндукция § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла § 106. Контур, вращающийся в магнитном поле. Синусоидальный переменный ток. Работа и мощность переменного тока § 107. Емкостное и индуктивное сопротивления § 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи § 109. Понятие о трехфазном токе Глава XVI. Электрические колебания и электромагнитные волны § 110. Электромагнитные волны § 111. Закрытый колебательный контур § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн § 113. Радиосвязь 4. Оптика и атомная физика § 114. Природа света § 115. Отражение и преломление света. Полное отражение § 116. Дисперсия света. Спектры § 117. Тонкие линзы. Микроскоп § 118. Глаз как оптическая система. Спектральная чувствительность глаза § 119. Основные фотометрические характеристики § 120. Поглощение света. О физиологическом действии света Глава XVIII. Волновые свойства света § 121. Интерференция света. Интерферометр § 122. 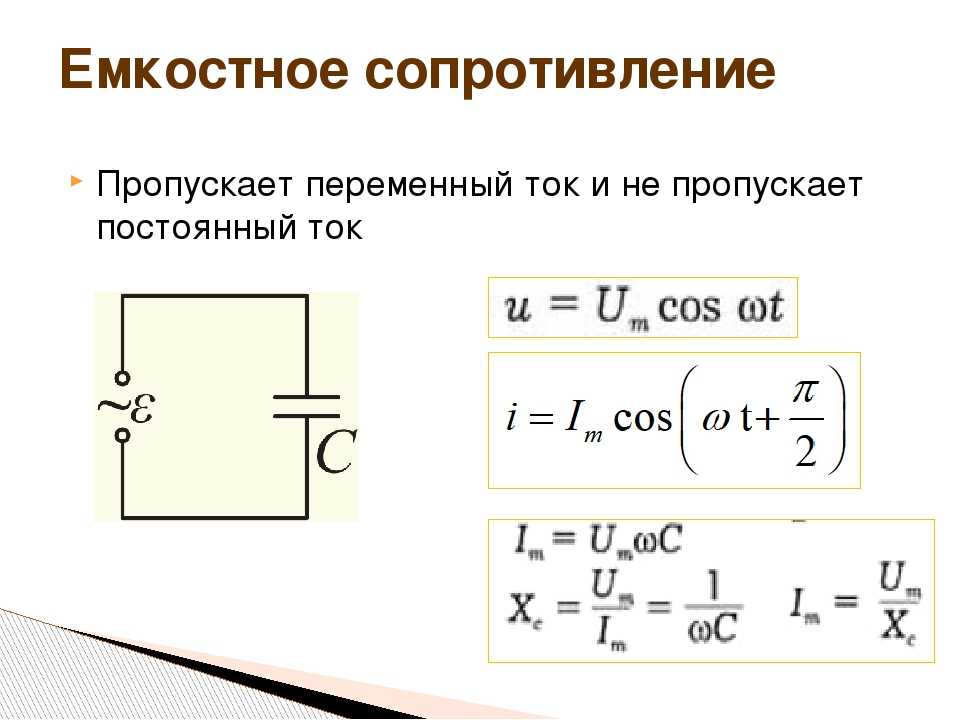Об интерференции света, отраженного от прозрачных пленок § 123. Дифракция света. Разрешающая способность оптических приборов § 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде § 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов § 126. О дифракции микрочастиц и волнах де-Бройля § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды § 128. Двойное лучепреломление. Поляризация света в исландском шпате. Призма Николя 129. Вращение плоскости колебаний поляризованного света. Поляриметр Глава XIX. Квантовые свойства света и строение атома § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора § 133. Квантовая теория строения атома водорода (по Бору). Объяснение спектров излучения и поглощения водорода § 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров § 135. Люминесценция. Законы фотолюминесценции и некоторые ее практические применения § 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света Глава XX. Атомное ядро и внутриядерные процессы § 138. Общие сведения об атомных ядрах. Изотопы § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада § 140. О методах наблюдения и регистрации микрочастиц § 141. Ядерные реакции. Искусственная радиоактивность § 142. Энергия связи и дефект массы атомного ядра § 143. Реакция деления. Цепная реакция. Ядерный реактор § 144. Реакция синтеза (термоядерная реакция). Энергия звезд § 145. Космические лучи. Элементарные частицы § 146. Об использовании ядерной энергии

Катушки индуктивности и конденсаторы, часть II

Катушки индуктивности и конденсаторы, часть II

В этой статье описаны основные сведения о емкости и индуктивности. Ан понимание исчисления полезно, но не обязательно. Основное понимание предполагается напряжение и ток. В этой статье используется более высокий уровень математике, чем большинство учебников. Знание сложной арифметики также полезно.

Комплексные номера

Комплексные числа — это числа, содержащие квадратный корень из -1. Так как квадрат корень никогда не может быть отрицательным (неважно, положительное это число или отрицательный, если вы возведете его в квадрат, вы получите положительное число), это называется мнимое число. Сначала вы можете подумать, что работа с мнимым числом это просто еще одно оправдание для тех людей математического типа, чтобы уйти и заполнить страница с бесполезными уравнениями. Однако оказывается, что эти мнимые числа имеют свойства, которые делают их очень полезными в электронике.

В математике квадратный корень из -1 обычно записывается строчными буквами. письмо я. В электронике i обозначает ток (интенсивность), поэтому мы используем j для вместо этого квадратный корень из -1.

Комплексные числа состоят из двух частей. Первый — это реальный термин, который является типом числа, с которым мы привыкли иметь дело ежедневно. Вторая часть мнимый член, кратный j. Любой член может быть равен нулю.

Реактивное сопротивление и комплексные числа

Реактивное сопротивление конденсатора (Xc) определяется по формуле Xc=1/(jwC), где C — емкость, а w=2(pi)f (и f — частота). W обычно написано как греческая омега, но эй, это всего лишь текст ASCII, так что мы должны обходиться ж. Обратите внимание, что реактивное сопротивление изменяется с частотой, как и ток по отношению к напряжению изменился с частотой в части I этой статьи.

Индуктивное реактивное сопротивление (Xl) равно jwL, где L — индуктивность, а ш=2(пи)ф. Обратите внимание, что реактивное сопротивление конденсаторов и катушек индуктивности не содержит реальные сроки.

Вы можете думать о реактивном сопротивлении как о некотором эквиваленте сопротивление.

Векторы

Извините, мы не говорим здесь о «Звездном пути». Phasor — это просто комплекс число. Если вы используете действительные и мнимые числа в качестве значений x и y на графике, вы можете отображать сложные напряжения, токи, импедансы и т. д. в виде векторов. Это немного сложно, но, надеюсь, использование импеданса в качестве примера сделает это яснее.

Сопротивление — это просто то, насколько сильно электричеству препятствуют или сдерживаются. Для простой резистор, полное сопротивление было сопротивлением. Для конденсатора или катушки индуктивности импеданс — это реактивное сопротивление. Импеданс, вообще говоря, комплексное число. Это содержит действительную часть и мнимую часть. Реальная часть происходит от реальной сопротивление. Мнимая часть происходит от реактивного сопротивления. Это легко запомнить, поскольку катушки индуктивности и конденсаторы не поглощают энергию, как резистор (который преобразует энергию в тепло). Вместо этого катушки индуктивности и конденсаторы хранят и высвобождать энергию.

Мы обычно используем заглавную букву Z для обозначения сопротивления. Поскольку у него есть реальный и мнимая составляющая, Z=R+X. А теперь самое интересное. Помните закон Ома? Хорошо, мы все еще можем использовать его, даже с конденсаторами и катушками индуктивности (в этом прелесть векторов, мы можем использовать простую алгебру и вектора для решения задач вместо вынуждены использовать исчисление).

Обычно мы используем заглавные буквы V и I для представления напряжения и тока в виде векторов. Формула просто V=IZ (очень похожа на V=IR для резисторов), только теперь мы используя фазоры вместо простых действительных чисел.

В качестве примера предположим, что у нас есть резистор 150 Ом, катушка индуктивности 2 мГн и конденсатор 473 мкФ, соединенный последовательно, подключенный к источнику напряжения 120 вольт переменного тока, 60 Гц. Общий импеданс равен Z=R+Xl+Xc, или Z=150+jw(0,002)+1/(jw(0,000473)), и w=2(пи)(60) или 120(пи). Здесь важно отметить, что 1/j равно к -j. Если это не имеет смысла, подумайте, что произойдет, если вы умножите верхнее и снизу оба по j.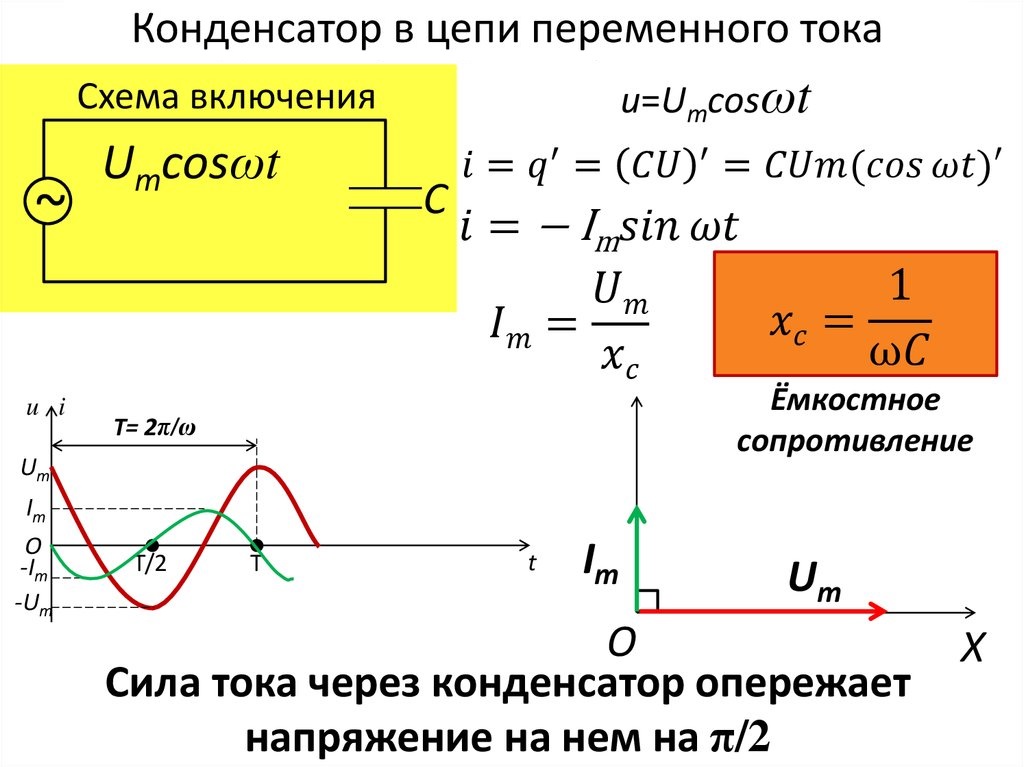 Вы получите j/(j в квадрате), а (j в квадрате) отрицательно единица, а j/(-1) равно -j. Если мы продолжим решать для Z, мы получим Z=150+0,75j-5,61j (приблизительно), или Z=150-4,86j. Обратите внимание, что мы только что добавили все импедансы, так же, как мы сделали для последовательно соединенных резисторов.

Для определения тока проще всего использовать полярную запись для вектор Если вы изобразите действительные и мнимые члены в виде векторов, вы получите результирующий вектор. Этот вектор имеет величину и направление. Величина — это квадратный корень из R в квадрате плюс X в квадрате (где R и X — действительная и мнимая части), а угол, обычно записываемый как греческая тета, является арктангенсом (X/R). Мы запишите это как (величина)<(угол), где < на самом деле является знаком угла. Если вы пишете это от руки, вы делаете это больше похожим на угол, чем меньше, чем знак. Некоторые люди продолжают нижнюю часть линии под значением угла, так что его нельзя спутать со знаком меньше.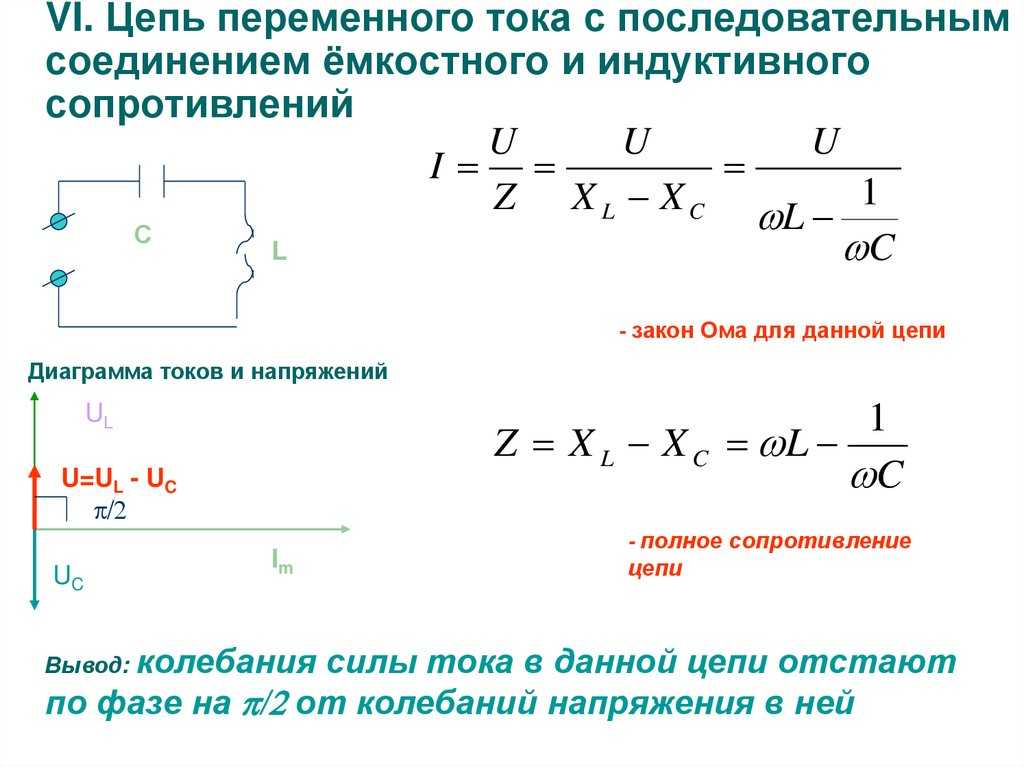

В нашем примере звездная величина равна 150,07, а угол равен -1,86. Если мы напишем Z в полярной форме тогда 150,07<-1,86.

Хорошо, теперь мы готовы найти ток. Формула V=IZ. Мы знаем Z и V, поэтому нам нужно найти I. Если мы изменим формулу, мы получим I=V/Z, или I = (120<0)/(150,07<-1,86). Чтобы разделить вектора, мы просто делим величину и вычесть угол. Итак, I=(120/150,07)<(0-(-1,86)), или 0,800<1,86.

Мы можем преобразовать это обратно в прямоугольную форму (используя действительную и мнимую условия) очень легко. Действительная часть равна (величина) cos (угол), а мнимая часть (величина) грех (угол). Таким образом, I равно 0,8cos(1,86)+0,8sin(1,86)j, или 0,800+0,026Дж.

Обратите внимание, что угол (называемый фазовым углом) тока больше, чем угол напряжения (которое было равно нулю). Это означает, что ток лидирует по напряжению. Ток в емкостных цепях опережает напряжение, а отстает за напряжением в индуктивных цепях.

Сводка векторов

Поначалу использование векторов может немного сбивать с толку, но это ценная метод решения цепей, особенно в цепях линий электропередач, где частота является константой. В других схемах отображение нескольких значений может дать вам хорошее представление о том, как схема работает на разных частотах. Помнить что все сигналы могут быть разбиты на сумму различных синусоид, так что глядя на отклик отдельных частот, вы можете увидеть, как схема будет работать для любой произвольной формы волны.

Использование векторов требует преобразования между полярной и прямоугольной формами, но в остальном позволяет использовать простую алгебру для решения уравнений. Это позволяет нам использовать простые формулы V=IZ и P=VI вместо того, чтобы иметь дело с такие вещи, как i=C(dv/dt). Чтобы умножить два вектора вместе (в полярной форме), умножьте магнитуды и добавить углы. Чтобы разделить, разделите величину и вычтите углы. Сложение и вычитание легче выполнять в прямоугольной форме. Только добавить/вычесть все действительные члены по мере необходимости, а затем добавить/вычесть все воображаемые термины.

Вт и вар

Если вы имеете дело с компьютерными источниками бесперебойного питания, то знаете, что они измеряются в вольт-амперах, а не в ваттах.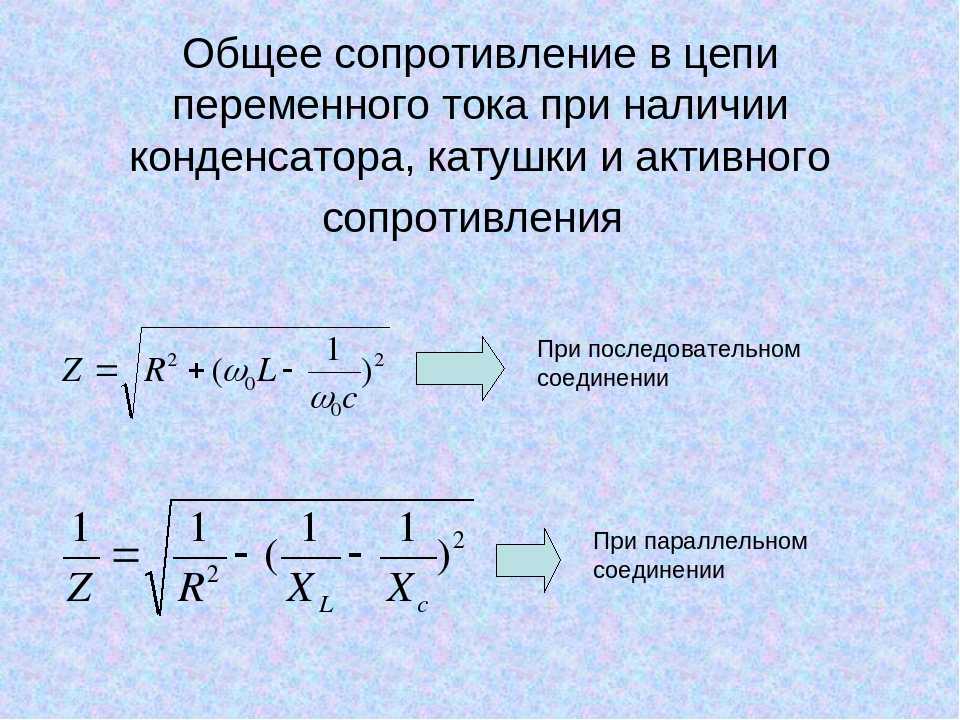 Вы спросите, что такое вольт-ампер? Хорошо, проще говоря, это вольты, умноженные на амперы. Из приведенного выше обсуждения на векторах, теперь вы должны понимать, что это может привести к комплексному числу (для компьютерный ИБП, все, что они вам дают, это величина в спецификациях). Если вы конвертируете на действительную и мнимую составляющие, действительная часть называется ваттами, а мнимая часть называется варс (вар = реактивный вольт-ампер).

Вы также можете встретить термин, называемый коэффициентом мощности. Коэффициент мощности косинус угла тока вычитается из угла напряжения. Сила Коэффициент 1 означает, что напряжение и ток точно совпадают по фазе. Сила компании нравится иметь коэффициент мощности 1 на своих линиях, так как это делает передача мощности более эффективная. Поскольку большинство бытовых нагрузок незначительно индуктивная (из-за двигателей в фенах, пылесосах, посудомоечных машинах и т. д.), Энергетическая компания добавляет конденсаторы в линию для компенсации индуктивности.

Частотные эффекты и их практическое применение

Конденсаторы и катушки индуктивности обычно используются в цепях, использующих преимущества тот факт, что их реакция зависит от частоты. Одно использование — источник питания фильтры. Если вы подключите конденсатор параллельно с вашей нагрузкой через клеммы источника питания, поскольку частота становится выше, реактивное сопротивление конденсатор становится меньше. На более высоких частотах конденсатор эффективно обеспечивает короткое замыкание на источнике питания, но на постоянном токе реактивное сопротивление равно очень большой, такой большой, что кажется, будто конденсатора вообще нет в схема. Когда конденсаторы используются таким образом, они называются шунтирующими. конденсаторы, так как они шунтируют источник питания.

Помните из формулы Xc=1/(jwC), что реактивное сопротивление уменьшается по мере того, как C становится больше. Следовательно, конденсаторы большей емкости лучше работают в качестве обхода источника питания.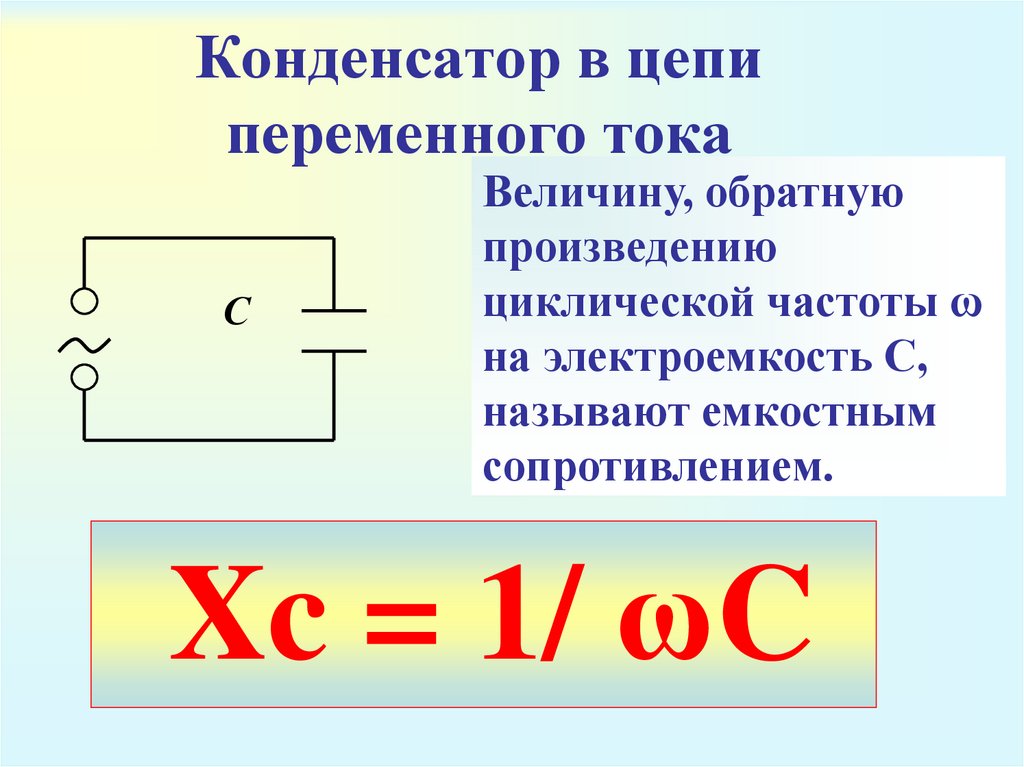 конденсаторы. Вы часто увидите большие электролиты, используемые в качестве основного фильтра. конденсаторы в блоке питания. Однако, поскольку электролиты не работают правильно на более высоких частотах вы также часто будете видеть меньший керамический диск конденсаторы параллельно электролитам. Эти конденсаторы хорошо работают в более высокие частоты, и функция, чтобы избавиться от шума, который электролиты не стал бы отфильтровывать. Во многих схемах, особенно высокочастотных цифровых цепях отдельные микросхемы будут иметь небольшой керамический конденсатор (обычно 0,1 мкФ) в обход проводов питания. Этот конденсатор установлен физически очень близко к чипу, и позаботились о том, чтобы путь сигнала был очень коротким от конденсатор к микросхеме. Это позволяет конденсатору отфильтровывать любые высокие частотный шум, который может присутствовать и помогает поддерживать работу микросхемы более надежно. Операционные усилители часто будут колебаться или делать странные вещи, если им не хватает небольшой шунтирующий конденсатор. Высокоскоростные цифровые схемы также часто будут работать неправильно. без маленьких конденсаторов на каждой микросхеме.

Катушки индуктивности также можно использовать для фильтрации помех источника питания. Катушки индуктивности включенных последовательно в линию питания. На низких частотах они по сути, короткое замыкание, позволяющее всей мощности постоянного тока проходить через линия. На более высоких частотах реактивное сопротивление начинает расти (помните, что Xl=jwL, поэтому Xl больше, когда w больше). Это обеспечивает более высокое сопротивление шуму источника, и течет меньший шумовой ток. Катушки индуктивности часто называют дросселями, когда они используются таким образом.

Конденсаторы и катушки индуктивности очень часто используются в схемах фильтров. Схемы могут быть сделаны, которые пропускают или отвергают только высокие или только низкие частоты, или, возможно, позволяют только определенную полосу частот через. Из-за сложности этого тема, фильтры более подробно обсуждаются в отдельной статье.

Как упоминалось ранее, конденсаторы и катушки индуктивности могут использоваться для балансировки реактивное сопротивление на линии, как это часто делается с линиями электропередач.

Один изящный трюк — использовать конденсатор для снижения напряжения в сети переменного тока. Иногда это делается в местах, где нежелательно наличие тяжелого трансформатора. Тем не менее, он имеет все недостатки использования резистора для снижения напряжения в цепи. схема. Во-первых, фактическое падение напряжения изменяется в зависимости от тока, который течет. Это означает, что этот метод хорош только тогда, когда постоянное количество тока течет. Во-вторых, поскольку трансформатор не используется, нет изоляция от основной линии переменного тока. Этот метод также имеет то преимущество, что не нагревается. генерируется, в отличие от резистора.

Обратите внимание, что в качестве схемы демодуляции АМ можно использовать диод и конденсатор. Диод выпрямляет сигнал, а конденсатор отфильтровывает более высокие частоты. несущая частота. Это важно, потому что диоды и конденсаторы, используемые для другие цели иногда делают идеальный AM-приемник в середине вашего схема.

Немного вариаций

Иногда полезно иметь переменный конденсатор или переменную катушку индуктивности. Например, в радиоприемнике частота приема может зависеть от резонансная частота конкретного RLC-контура (контура с резистором, конденсатор и катушка индуктивности — подробнее см. в статье о фильтрах). К изменяя емкость, вы можете изменять частоту, которую принимает радио. Этот принцип использовался в старых стереосистемах и телевизорах. У стерео будет циферблат, который обычно подключался к переменному конденсатору (обычно длинной цепочкой и шкивная система). Конденсатор был построен просто с использованием переменного пластины, одна из которых неподвижна, а другая подвижна. За счет изменения интервала пластин варьировалась емкость. Старые телевизионные циферблаты делали то же самое. вещь, но имел фиксированное расстояние между пластинами в зависимости от выбранного канала, а не быть полностью настраиваемым, как стерео.

Также распространены переменные катушки индуктивности. Иногда они изготавливаются с использованием очиститель проводника, аналогичный тому, как устроены переменные резисторы, и иногда изготавливаются с использованием переменного сердечника внутри индуктора.

Переменные конденсаторы и катушки индуктивности определяются их диапазоном, в дополнение к обычным характеристикам конденсатора и катушки индуктивности (максимальное напряжение, максимальный ток, и т. д).

реактивное сопротивление

реактивное сопротивление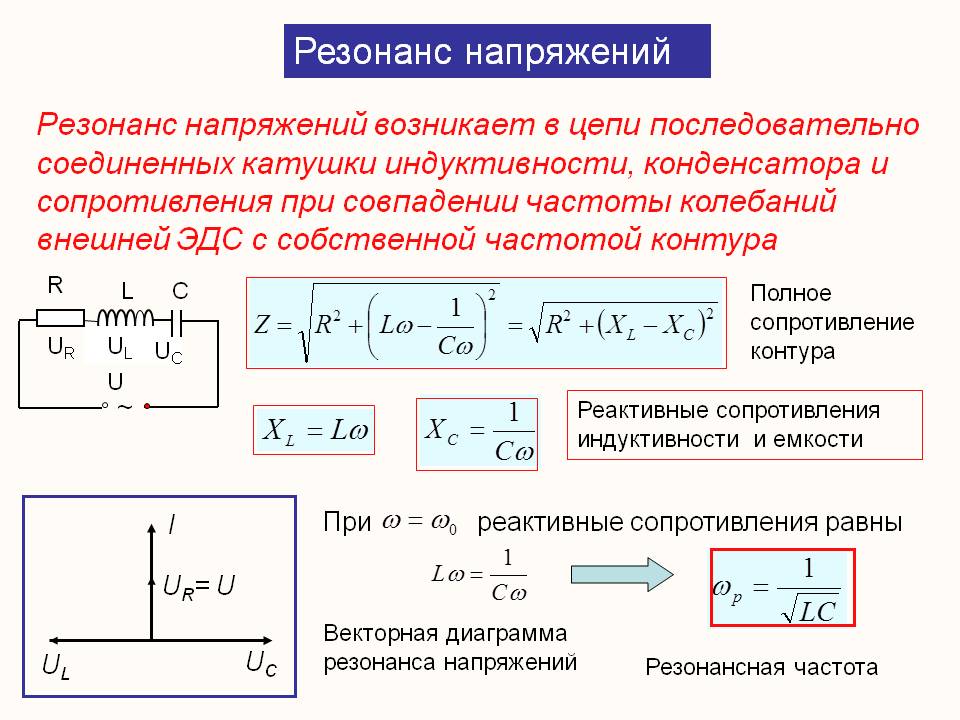 Реактивное сопротивление — это свойство сопротивления или препятствия протеканию переменного тока или переменного напряжения в катушках индуктивности и конденсаторах. В частности, обратите внимание, что мы говорим только о переменном токе переменного тока, выражение которого включает в себя аудиочастоты af и радиочастоты rf. НЕ постоянный ток постоянного тока. Это приводит к индуктивному реактивному сопротивлению и емкостному реактивному сопротивлению.

ПОСЛЕДНИЕ ИЗМЕНЕНИЯ:

ВЫ ЗДЕСЬ: ГЛАВНАЯ > ОСНОВЫ > РЕАКТИВНОСТЬ

Что такое реактивное сопротивление?

Реактивное сопротивление — это свойство сопротивления или препятствия протеканию переменного тока или переменного напряжения в катушках индуктивности и конденсаторах. В частности, обратите внимание, что мы говорим только о переменном токе переменного тока, выражение которого включает в себя аудиочастоты af и радиочастоты rf. НЕ постоянный ток постоянного тока.

Индуктивное сопротивление

Когда переменный ток протекает через индуктивность, возникает противо-ЭДС или напряжение, противодействующее любому изменению начального тока. Это противодействие или сопротивление изменению тока измеряется индуктивным реактивным сопротивлением.

Индуктивное реактивное сопротивление определяется по формуле:

2 * пи * ж * л

где: 2 * пи = 6,2832; f = частота в герцах и L = индуктивность в генри

Емкостное реактивное сопротивление

Когда переменное напряжение проходит через емкость, происходит противоположное изменение начального напряжения, это противодействие или импеданс изменению напряжения измеряется с точки зрения емкостного реактивного сопротивления.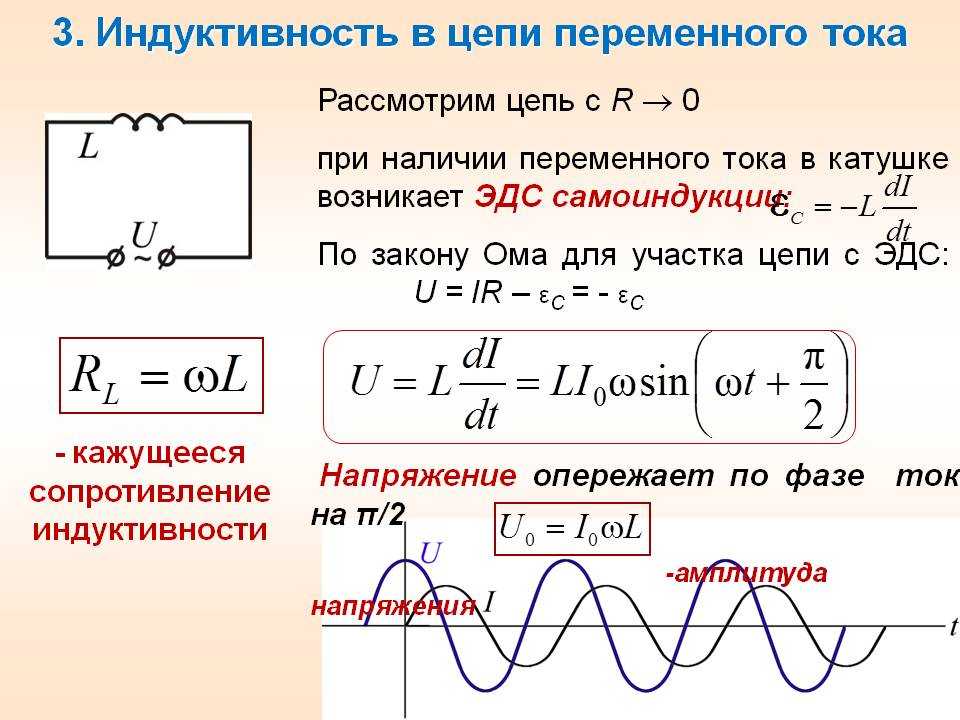

Емкостное реактивное сопротивление определяется по формуле:

1/(2*пи*ф*С)

где: 2 * пи = 6,2832; f = частота в герцах и C = емкость в фарадах

Некоторые примеры Reactance

Какое реактивное сопротивление имеет катушка индуктивности 6,8 мкГн на частоте 7 МГц? Используя приведенную выше формулу, мы получаем:

2 * пи * ж * л

где: 2 * пи = 6,2832; f = 7 000 000 Гц и L = 0,0000068 Генри

Ответ: = 299 Ом

Какое реактивное сопротивление имеет конденсатор емкостью 33 пФ на частоте 7 МГц? Используя приведенную выше формулу, мы получаем:

1/(2*пи*ф*С)

где: 2 * пи = 6,2832; f = 7 000 000 Гц и C = 0,0000000000033 фарад

Ответ: = 689 Ом

В реальном мире мы не используем такие большие числа, мы используем экспоненты на нашем карманном калькуляторе, чтобы получить такие числа:

Для индуктивного сопротивления

где: 2 * пи = 6,2832; f = 7 X 10 ⁺⁶ Гц и L = 6,8 X ^-6 Генри

Ответ: = 299 Ом

Для емкостного реактивного сопротивления

1/(2*пи*ф*С)

где: 2 * пи = 6,2832; f = 7 X 10 ⁺⁶ Гц и C = 33 X ^-12 Фарад

Ответ: = 689 Ом

СВЯЗАННЫЕ ТЕМЫ ПО РЕАКЦИОННОЙ АКТИВНОСТИ

емкость

текущий

импеданс

индуктивность

напряжение

Ссылка на эту страницу

НОВИНКА! — Как напрямую перейти на эту страницу

Хотите создать ссылку на мою страницу с вашего сайта? Это не может быть проще. Знание HTML не требуется; даже технофобы могут это сделать. Все, что вам нужно сделать, это скопировать и вставить следующий код. Все ссылки приветствуются; Я искренне благодарю вас за вашу поддержку.

Скопируйте и вставьте следующий код для текстовой ссылки :

<а href="https://www.electronics-tutorials.com/basics/reactance.htm" target="_top">посетите страницу Ian Purdie VK2TIP "Reactance"

и должно выглядеть так:
посетите страницу Ian Purdie VK2TIP «Reactance»

 

ВЫ ЗДЕСЬ: ГЛАВНАЯ > ОСНОВЫ > РЕАКТИВНОСТЬ

автор Ян С. Пурди, VK2TIP сайта www.electronics-tutorials.com заявляет о моральном праве на быть идентифицированным как автор этого веб-сайта и всего его содержимого. Copyright © 2000, все права защищены. Смотрите копирование и ссылки. Эти электронные учебные пособия предназначены для индивидуального частного использования, и автор не несет никакой ответственности за применение, использование, неправильное использование любого из этих проектов или учебных пособий по электронике, которые могут привести к прямому или косвенному ущербу или потерям, связанным с этими проектами или учебными пособиями.