Закон Джоуля-Ленца в интегральной и дифференциальной формах
Теперь подробнее обсудим величину DU (которая представляет в расчетах изменение внутренней энергии) применительно к проводнику, по которому начинает течь ток.
Постепенно, выбранный проводник будет нагреваться, а это значит, что будет увеличиваться его внутренняя энергия. По мере нагрева разность между температурой проводника и окружающей его среды будет увеличиваться. Согласно закономерности Ньютона, вместе с этим возрастать будет и мощность теплоотдачи проводника. Таким образом, через какое-то время температура проводника, достигнув определенного значения, перестанет увеличиваться. В этот момент величина DU будет равной нулю, и перестанет изменяться внутренняя энергия проводника.
Тогда для этого состояния первый закон термодинамики будет выглядеть так: A = – Q. То есть когда не меняется внутренняя энергия проводника, работа тока целиком превращается в теплоту. Используя этот вывод, можем записать все три рассмотренные формулы для расчета работы тока в несколько ином виде, в конечном итоге получаем закон Джоуля-Ленца в интегральной форме:
 На
первый взгляд все формулы могут считаться
равноправными, однако только последняя
справедлива всегда, поэтому она и
считается законом. А вот остальные две
справедливы только при определенных
условиях, поэтому законом считаться не
могут.
На
первый взгляд все формулы могут считаться
равноправными, однако только последняя
справедлива всегда, поэтому она и
считается законом. А вот остальные две
справедливы только при определенных
условиях, поэтому законом считаться не
могут.
Закон Джоуля-Ленца в дифференциальной форме выглядит совершенно по-иному, мы рассмотрим только общий вариант, без дополнительных выведений и вычислений, который выглядит так:
 Где:
Где:
 —
является мощностью тепла, выделяемого
в единице объёма;
—
является мощностью тепла, выделяемого
в единице объёма; —
плотность электрического тока;
—
плотность электрического тока; —
это напряжённость электрического поля;
—
это напряжённость электрического поля; —
проводимость выбранной среды.
—
проводимость выбранной среды.
Так в общих чертах выглядит закон Джоуля-Ленца и его интегральная и дифференциальная формы. Хотя, если проводить дальнейшие вычисления, то закон может принимать и другие формы.
21. Закон Ома для неоднородного участка цепи (обобщенный закон Ома). Закон Ома для замкнутой цепи.
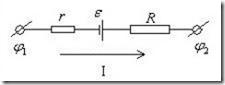
Участок цепи, содержащий источник ЭДС, называется неоднородным(рис.5.11). Всякий источник ЭДС характеризуется величиной ЭДС ε ивнутренним сопротивлением r
 —
напряжение на концах участка цепи.
—
напряжение на концах участка цепи.
Рис.5.11. Неоднородный участок цепи.
Закон Ома для неоднородного участка цепи имеет вид:
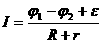
При
соединении концов неоднородного участка
цепи идеальнымпроводником
образуется замкнутая цепь, в
которой
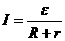
Если
сопротивление внешней цепи 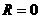 ,
то имеем случай короткого
замыкания.
В этом случае в цепи течетмаксимальный ток:
,
то имеем случай короткого
замыкания.
В этом случае в цепи течетмаксимальный ток:

При 
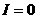
22. Правила Кирхгофа для разветвленных цепей постоянного тока
Правило 1: в любом узле сумма входящих токов и выходящих равна нулю. Оно учитывает закон сохранения электрического заряда.
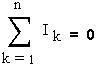
При этом токи, идущие к узлу, и токи, исходящие из узла, следует считать величинами разных знаков.
Правило 2: алгебраическая сумма произведений сил токов на сопротивления при обходе контура равна сумме ЭДС в контуре. Учитывается закон сохранения энергии.
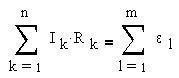
Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей.
В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рис. 1.10.1). Токи, втекающие в узел, принято считать положительными; вытекающие из узла – отрицательными.
|
Рисунок 1.10.1. Узел электрической цепи. I1, I2 > 0; I3,I4 < 0 |
В узлах цепи постоянного тока не может происходить накопление зарядов. Отсюда следует первое правило Кирхгофа:
Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:
|
Первое правило Кирхгофа является следствием закона сохранения электрического заряда.
В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называются контурами. На разных участках выделенного контура могут протекать различные токи. На рис. 1.10.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (
|
Рисунок 1.10.2. Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef) |
В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например, abcd и adef), так как третий не содержит никаких новых участков.
Второе правило Кирхгофа является следствием обобщенного закона Ома.
Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 1.10.2, например, abcd. Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 1.10.3.
|
Рисунок 1.10.3. «Правила знаков» |
Для участков контура abcd обобщенный закон Ома записывается в виде:
Для
участка bc: I1R1 = Δφbc –  1.
1.
Для
участка da: I2R2 = Δφda –  2.
2.
Складывая левые и правые части этих равенств и принимая во внимание, что Δφbc
I1R1 + I2R2 = Δφbc + Δφda – |
Аналогично, для контура adef можно записать:
– I2R2 + I3R3 = |
Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.
Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов в электрической цепи. Для цепи, изображенной на рис. 1.10.2, система уравнений для определения трех неизвестных токов I1, I2 и I3 имеет вид:
I1R1 + I2R2 = – |
– I2R2 + I3R3 = |
– I1 + I2 + I3 = 0 |
23. Работа и мощность постоянного электрического тока. КПД источника тока.
Работа А электрического тока на участке цепи с электрическим сопротивлением R за время D t равна:
A = I · U · ? t = I2 · R · ? t
Мощность P электрического тока равна отношению работы А тока ко времени D t, за которое эта работа совершена:
P = A / ? t = I · U = I2 R = U2 / R.
Работа А электрического тока равна количеству теплоты Q, выделяемому проводником (если не совершается механическая работа и не происходят химические реакции):
Q = I2 · R · ? t
Этот закон был экспериментально установлен английским ученым Джеймсом Джоулем (1818-1889) и русским ученым Эмилием Ленцем (1804-1865) и поэтому носит название закона Джоуля — Ленца.
Рассмотрим элементарную электрическую цепь, содержащую источник ЭДС с внутренним сопротивлением r, и внешним сопротивлением R (рис. 7.5).
КПД всегда определяем как отношение полезной работы к затраченной:
| | (7.8.1) |
|
Полезная
работа –
мощность, выделяемая на внешнем
сопротивлении Rв
единицу времени. По закону Ома
имеем: 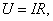 а
а 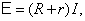 тогда
тогда
 .
.
24. Вывод закона Ома из классической теории электропроводимости металлов.
Друде считал, что сразу после очередного соударения электрона с ионом кристаллической решетки скорость упорядоченного движения электрона равна нулю. Предположим, что напряженность поля не изменяется. Тогда под действием поля электрон получит постоянное ускорение равное
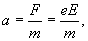
и к концу пробега скорость упорядоченного движения достигнет значения
| (18.2) |
где
t — среднее время между двумя последовательными
соударениями электрона с ионами решетки.
Друде не учитывал распределение
электронов по скоростям и приписывал
всем электронам одинаковое значение
средней скорости  .
В этом приближении
.
В этом приближении  ,
где
,
где  —
среднее значение длины свободного
пробега,
—
среднее значение длины свободного
пробега,  —
скорость теплового движения электронов.
Подставим это значение t в формулу (18.2)
—
скорость теплового движения электронов.
Подставим это значение t в формулу (18.2)

Скорость изменяется за время пробега линейно. Поэтому ее среднее (за пробег) значение равно половине максимального
Подставив это выражение в

получим
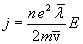
Плотность
тока оказалась пропорциональной
напряженности поля. Следовательно, мы
получили закон Ома. Согласно  коэффициент
пропорциональности между j и Е представляет
собой проводимость
коэффициент
пропорциональности между j и Е представляет
собой проводимость
| (18.3) |
Если бы электроны не сталкивались с ионами решетки, длина свободного пробега, а, следовательно, и проводимость были бы бесконечно велики. Таким образом, электрическое сопротивление металлов обусловлено соударениями свободных электронов с ионами.
Вывод закона Джоуля-Ленца из классической теории электропроводности металлов. Затруднения этой теории.
К
концу свободного пробега электрон
приобретает скорость  ,
и, следовательно, дополнительную
кинетическую энергию, средняя величина
которой
,
и, следовательно, дополнительную
кинетическую энергию, средняя величина
которой

Столкнувшись
с ионом, электрон по предположению
полностью теряет приобретенную им за
время пробега скорость, и передает
энергию кристаллической решетке. Эта
энергия идет на увеличение внутренней
энергии металла, проявляющееся в его
нагревании. Каждый электрон претерпевает
за секунду в среднем 1/t соударений,
сообщая всякий раз решетке энергию  .
Следовательно, в единице объема за
единицу времени должно выделяться тепло
.
Следовательно, в единице объема за
единицу времени должно выделяться тепло

где
n — число электронов проводимости в
единице объема. Величина 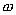 есть
не что иное, как удельная мощность тока.
Множитель при
есть
не что иное, как удельная мощность тока.
Множитель при  совпадает
со значением
совпадает
со значением 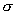 (18.3)
для закона Ома. Таким образом. Мы пришли
к выражению закона Джоуля-Ленца в
дифференциальной форме.
(18.3)
для закона Ома. Таким образом. Мы пришли
к выражению закона Джоуля-Ленца в
дифференциальной форме.

Теплоемкость металлов. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемкости электронного газа. Поэтому атомная (т. е. рассчитанная на 1 моль) теплоемкость металла должна быть значительно большей, чем атомная теплоемкость диэлектриков, у которых нет свободных электронов. Согласно закону Дюлонга и Пти (см. §73), теплоемкость одноатомного кристалла равна 3R. Учтем, что теплоемкость одноатомного электронного газа равна 3/2R. Тогда атомная теплоемкость металлов должна быть близка к 4,5R. Однако опыт доказывает, что она равна 3R, т. е. для металлов, так же как и для диэлектриков, хорошо выполняется закон Дюлонга и Пти. Следовательно, наличие электронов проводимости практически не сказывается на значении теплоемкости, что не объясняется классической электронной теорией.
Указанные расхождения теории с опытом можно объяснить тем, что движение электронов в металлах подчиняется не законам классической механики, а законам квантовой механики и, следовательно, поведение электронов проводимости надо описывать не статистикой Максвелла — Больцмана, а квантовой статистикой. Поэтому объяснить затруднения элементарной классической теории электропроводности металлов можно лишь квантовой теорией, которая будет рассмотрена в дальнейшем. Надо, однако, отметить, что классическая электронная теория не утратила своего значения и до настоящего времени, так как во многих случаях (например, при малой концентрации электронов проводимости и высокой температуре) она дает правильные качественные результаты и является по сравнению с квантовой теорией простой и наглядной.
Несамостоятельный и самостоятельный газовые разряды.
Несамостоятельный газовый разряд. Процесс прохождения электрического тока через газ называется газовым разрядом. Если электропроводность газа создается внешними ионизаторами, то электрический ток, возникающий в нем, называется несамостоятельным газовым разрядом. С прекращением действия внешних ионизаторов несамостоятельный разряд прекращается. Несамостоятельный газовый разряд не сопровождается свечением газа. Ниже изображен график зависимости силы тока от напряжения при несамостоятельном разряде в газе. Для построения графика использовалась стеклянная трубка с двумя впаянными в стекло металлическими электродами. Цепь собрана как показано на рисунке ниже.
|
+ —
Самостоятельный
газовый разряд.
Электрический разряд в газе, сохраняющийся после прекращения действия внешнего ионизатора, называется самостоятельным газовым разрядом. Для его осуществления необходимо, чтобы в результате самого разряда в газе непрерывно образовывались свободные заряды. Основным источником их возникновения является ударная ионизация молекул газа.
Если после достижения насыщения продолжать увеличивать разность потенциалов между электродами, то сила тока при достаточно большом напряжении станет резко возрастать (график 2).
Это означает, что в газе появляются дополнительные ионы, которые образуются за счет действия ионизатора. Сила тока может возрасти в сотни и тысячи раз, а число заряженных частиц, возникающих в процессе разряда, может стать таким большим, что внешний ионизатор будет уже не нужен для поддержания разряда. Поэтому ионизатор теперь можно убрать.


I
|
27. Магнитное поле, Магнитная индукция. Принцип суперпозиции магнитных полей. Закон Ампера.
Зако́н
Ампе́ра —
закон взаимодействия электрических
токов.
Впервые был установлен Андре
Мари Ампером в 1820 для
постоянного тока. Из закона Ампера
следует, что параллельные проводники с
электрическими токами, текущими в одном
направлении, притягиваются, а в
противоположных — отталкиваются.
Законом Ампера называется также закон,
определяющий силу, с которой магнитное
поле действует
на малый отрезок проводника с током.
Сила 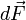 ,
с которой магнитное поле действует на
элемент объёма
,
с которой магнитное поле действует на
элемент объёма 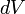 проводника
с током плотности
проводника
с током плотности 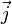 ,
находящегося в магнитном поле с
индукцией
,
находящегося в магнитном поле с
индукцией  :
:
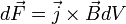 .
.
Модуль силы Ампера можно найти по формуле:
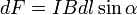 ,
,
где 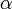 —
угол между векторами магнитной индукции
и тока.
—
угол между векторами магнитной индукции
и тока.
Сила 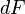 максимальна
когда элемент проводника с током
расположен перпендикулярно линиям
магнитной индукции (
максимальна
когда элемент проводника с током
расположен перпендикулярно линиям
магнитной индукции ( ):
):
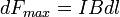 .
.
Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения[1], магнитная составляющая электромагнитного поля[2]
Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).
Магни́тная
инду́кция  — векторная величина,
являющаяся силовой характеристикой магнитного
поля (его
действия на заряженные частицы) в данной
точке пространства. Определяет, с
какой силой
— векторная величина,
являющаяся силовой характеристикой магнитного
поля (его
действия на заряженные частицы) в данной
точке пространства. Определяет, с
какой силой  магнитное
поле действует на заряд
магнитное
поле действует на заряд  ,
движущийся со скоростью
,
движущийся со скоростью  .
.
Более
конкретно, 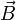 —
это такой вектор, что сила
Лоренца
—
это такой вектор, что сила
Лоренца  ,
действующая со стороны магнитного
поля[1] на
заряд
,
действующая со стороны магнитного
поля[1] на
заряд 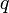 ,
движущийся со скоростью
,
движущийся со скоростью  ,
равна
,
равна
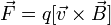
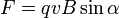
где
косым крестом обозначено векторное
произведение,
α — угол между векторами скорости и
магнитной индукции (направление
вектора 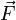 перпендикулярно
им обоим и направлено по правилу
буравчика).
перпендикулярно
им обоим и направлено по правилу
буравчика).
17.5 Закон Джоуля-Ленца в интегральной и дифференциальной формах
Если
в проводнике течет постоянный ток и
проводник остается неподвижным, то
работа сторонних сил расходуется на
его нагревание. Опыт показывает, что в
любом проводнике происходит выделение
теплоты, равное работе, совершаемой
электрическими силами по переносу
заряда вдоль проводника. Если на концах
участка проводника имеется разность
потенциалов 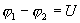 ,
тогда работу по переносу заряда q на
этом участке равна
,
тогда работу по переносу заряда q на
этом участке равна 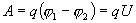
По
определению I= q/t. откуда q= I t. Следовательно 
Так как работа идет па нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил
| (17.13) |
Соотношение
(17.13) выражает закон Джоуля-Ленца в
интегральной форме. Введем плотность
тепловой мощности 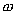 ,
равную энергии выделенной за единицу
время прохождения тока в каждой единице
объема проводника
,
равную энергии выделенной за единицу
время прохождения тока в каждой единице
объема проводника
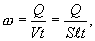
где S
— поперечное сечение проводника,  —
его длина. Используя (1.13) и соотношение
—
его длина. Используя (1.13) и соотношение  ,
получим
,
получим
 Но
Но 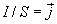 —
плотность тока, а
—
плотность тока, а 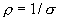 ,
тогда
,
тогда 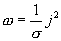
с учетом
закона Ома в дифференциальной форме 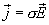 ,
окончательно получаем
,
окончательно получаем
| (17.14) |
Формула (17.14) выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.
17.6. Разветвленные цепи. Правила Кирхгофа
Расчет разветвленных цепей упрощается, если пользоваться правилами Кирхгофа. Первое правило относится к узлам цепи. Узлом называется точка, в которой сходится более чем два тока. Токи, текущие к узлу, считается имеют один знак (плюс или минус), от узла — имеют другой знак (минус или плюс).

Первое правило Кирхгофа является выражением того факта, что в случае установившегося постоянного тока ни в одной точке проводника и ни на одном его участке не должны накапливаться электрические заряды и формулируется в следующем виде: алгебраическая сумма токов, сходящихся в узле, равна нулю
| (17.15) |
Второе правило Кирхгофа является обобщением закона Ома на разветвленные электрические цепи.
Рассмотрим произвольный замкнутый контур в разветвленной цепи (контур 1-2-3-4-1) (рис. 1.2). Зададим обход контура по часовой стрелке и применим к каждому из неразветвленных участков контура закон Ома.
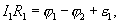

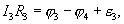
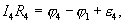
Сложим эти выражения, при этом потенциалы сокращаются и получаем выражение
| (17.16) |
В любом замкнутом контуре произвольной разветвленной электрической цепи, алгебраическая сумма падений напряжений (произведений сил токов на сопротивление) соответствующих участков этого контура равна алгебраической сумме эдс входящих в контур.

При решении задач рекомендуется следующий порядок:
Произвольно выбрать и обозначить на чертеже направление токов во всех участках цепи.
Записать уравнение для всех n-1 узлов.
Выделить произвольный контур в цепи и выбрать направление обхода. Записать второе правило Кирхгофа.
18. Классическая теория электропроводности
Почти сто лет тому назад П.Друде разработал теорию электро- и теплопроводности металлов. В теории Друде валентные электроны металла рассматривались как классический «электронный» газ (идеальный газ из электронов). Применение к этой модели основных положений элементарной молекулярно-кинетической теории привело к поразительным результатам. На основе этих представлений оказалось возможным объяснить закон Видемана-Франца, объяснить эффект Холла, возникновение контактной разности потенциалов, явление термоэлектронной эмиссии. Для всех перечисленных явлений удалось получить количественные зависимости между величинами, определяющими то или иное явление. Теория Друде не свободна от внутренних противоречий. Современная физика твердого тела базируется на представлениях квантовой механики, а для описания свойств электронного газа используется квантовая статистика, отличная от статистики Максвелла — Больцмана. Вместе с тем теория Друде не потеряла своей полезности: отдельные ее результаты поражают своей точностью, а методы теории Друде на редкость физически наглядны.
В рамках элементарной кинетической теории полагаем, что валентные электроны (электроны проводимости) металлов представляют собой одинаковые твердые сферы, двигаются они по прямым линиям до столкновения друг с другом, время контакта частиц пренебрежимо мало по сравнению с временем «свободного» движения.
Объемную концентрацию электронов проводимости можно оценить выражением:
| (6.30) |
где 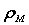 —
объемная плотность металла (кг/м3),
Z — валентность химического элемента,
Na —
число Авогадро, А — относительная атомная
масса элемента.
—
объемная плотность металла (кг/м3),
Z — валентность химического элемента,
Na —
число Авогадро, А — относительная атомная
масса элемента.
Заряд электрона е =-1,6*10-19 Кл, масса электрона me = 0,91*10-30 кг. Величину «е» ниже будем считать положительной, а знак заряда электрона будем учитывать непосредственно в формулах.
Плотность электронного газа:
| (6.31) |
значительно больше плотности обычных газов при нормальных условиях.
В теории Друде пренебрегают сильным электрон-электронным и электрон-ионным взаимодействием, полагая, что внутри металлического тела отдельный электрон практически ведет себя как свободная частица. Это дает нам право считать электрон «нейтральной» частицей при расчете взаимодействия ее с остальными частицами, но способной переносить заряд при расчете параметров электрического тока.
|
Рис. 6.1. |
П.Друде полагал, что электроны в своем движении сталкиваются с атомами (ионами) кристаллической структуры металла (столкновения электрон-электрон значительно менее вероятны). Картина последовательных соударений электрона с атомами кристаллической решетки показана на рис. 6.1.
Современная теория оценивает вероятность такого механизма не очень высоко: рассеяние электронов имеет и другие механизмы. Поэтому не следует наглядную картину рис.6.1 понимать в буквальном смысле.
Будем считать, что отношение
| (6.32) |
представляет
собой вероятность соударения электрона
с рассеивающим центром, где dt — промежуток
времени, 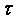 —
время релаксации или время свободного
пробега. Предполагается, что величина
—
время релаксации или время свободного
пробега. Предполагается, что величина  не
зависит от пространственного положения
электрона и не меняется от соударения
к соударению. Предполагается также, что
электроны находятся в состоянии теплового
равновесия со своим окружением. Механизм
соударения детализируется следующим
образом: скорость электрона после
соударения статистически не связана
со скоростью электрона до соударения
(электрон «забыл» свою предысторию),
направление скорости после соударения
— случайное, хаотическое, а ее величина
соответствует той температуре, которая
имеет место в окрестности точки
соударения.
не
зависит от пространственного положения
электрона и не меняется от соударения
к соударению. Предполагается также, что
электроны находятся в состоянии теплового
равновесия со своим окружением. Механизм
соударения детализируется следующим
образом: скорость электрона после
соударения статистически не связана
со скоростью электрона до соударения
(электрон «забыл» свою предысторию),
направление скорости после соударения
— случайное, хаотическое, а ее величина
соответствует той температуре, которая
имеет место в окрестности точки
соударения.
Закон Джоуля-Ленца в интегральной и дифференциальной формах
Теперь подробнее обсудим величину DU (которая представляет в расчетах изменение внутренней энергии) применительно к проводнику, по которому начинает течь ток.
Постепенно, выбранный проводник будет нагреваться, а это значит, что будет увеличиваться его внутренняя энергия. По мере нагрева разность между температурой проводника и окружающей его среды будет увеличиваться. Согласно закономерности Ньютона, вместе с этим возрастать будет и мощность теплоотдачи проводника. Таким образом, через какое-то время температура проводника, достигнув определенного значения, перестанет увеличиваться. В этот момент величина DU будет равной нулю, и перестанет изменяться внутренняя энергия проводника.
Тогда для этого состояния первый закон термодинамики будет выглядеть так: A = – Q. То есть когда не меняется внутренняя энергия проводника, работа тока целиком превращается в теплоту. Используя этот вывод, можем записать все три рассмотренные формулы для расчета работы тока в несколько ином виде, в конечном итоге получаем закон Джоуля-Ленца в интегральной форме:
 На
первый взгляд все формулы могут считаться
равноправными, однако только последняя
справедлива всегда, поэтому она и
считается законом. А вот остальные две
справедливы только при определенных
условиях, поэтому законом считаться не
могут.
На
первый взгляд все формулы могут считаться
равноправными, однако только последняя
справедлива всегда, поэтому она и
считается законом. А вот остальные две
справедливы только при определенных
условиях, поэтому законом считаться не
могут.
Закон Джоуля-Ленца в дифференциальной форме выглядит совершенно по-иному, мы рассмотрим только общий вариант, без дополнительных выведений и вычислений, который выглядит так:
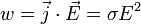 Где:
Где:
 —
является мощностью тепла, выделяемого
в единице объёма;
—
является мощностью тепла, выделяемого
в единице объёма; —
плотность электрического тока;
—
плотность электрического тока; —
это напряжённость электрического поля;
—
это напряжённость электрического поля; —
проводимость выбранной среды.
—
проводимость выбранной среды.
Так в общих чертах выглядит закон Джоуля-Ленца и его интегральная и дифференциальная формы. Хотя, если проводить дальнейшие вычисления, то закон может принимать и другие формы.
21. Закон Ома для неоднородного участка цепи (обобщенный закон Ома). Закон Ома для замкнутой цепи.
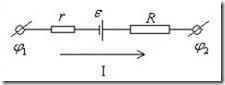
Участок цепи, содержащий источник ЭДС, называется неоднородным(рис.5.11). Всякий источник ЭДС характеризуется величиной ЭДС ε ивнутренним сопротивлением r.
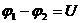 —
напряжение на концах участка цепи.
—
напряжение на концах участка цепи.
Рис.5.11. Неоднородный участок цепи.
Закон Ома для неоднородного участка цепи имеет вид:
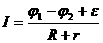
При
соединении концов неоднородного участка
цепи идеальнымпроводником
образуется замкнутая цепь, в
которой потенциалы φ1 иφ2 выравниваются
и мы приходим к закону
Ома для замкнутой (или полной) цепи:
потенциалы φ1 иφ2 выравниваются
и мы приходим к закону
Ома для замкнутой (или полной) цепи:
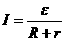
Если
сопротивление внешней цепи  ,
то имеем случай короткого
замыкания.
В этом случае в цепи течетмаксимальный ток:
,
то имеем случай короткого
замыкания.
В этом случае в цепи течетмаксимальный ток:
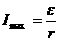
При 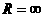 имеем разомкнутую цепь.
В этом случае ток в цепи равен
нулю:
имеем разомкнутую цепь.
В этом случае ток в цепи равен
нулю:

22. Правила Кирхгофа для разветвленных цепей постоянного тока
Правило 1: в любом узле сумма входящих токов и выходящих равна нулю. Оно учитывает закон сохранения электрического заряда.
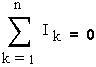
При этом токи, идущие к узлу, и токи, исходящие из узла, следует считать величинами разных знаков.
Правило 2: алгебраическая сумма произведений сил токов на сопротивления при обходе контура равна сумме ЭДС в контуре. Учитывается закон сохранения энергии.
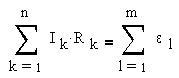
Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей.
В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рис. 1.10.1). Токи, втекающие в узел, принято считать положительными; вытекающие из узла – отрицательными.
|
Рисунок 1.10.1. Узел электрической цепи. I1, I2 > 0; I3,I4 < 0 |
В узлах цепи постоянного тока не может происходить накопление зарядов. Отсюда следует первое правило Кирхгофа:
Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:
|
Первое правило Кирхгофа является следствием закона сохранения электрического заряда.
В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называются контурами. На разных участках выделенного контура могут протекать различные токи. На рис. 1.10.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d).
|
Рисунок 1.10.2. Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef) |
В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например, abcd и adef), так как третий не содержит никаких новых участков.
Второе правило Кирхгофа является следствием обобщенного закона Ома.
Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 1.10.2, например, abcd. Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 1.10.3.
|
Рисунок 1.10.3. «Правила знаков» |
Для участков контура abcd обобщенный закон Ома записывается в виде:
Для
участка bc: I1R1 = Δφbc – 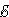 1.
1.
Для
участка da: I2R2 = Δφda – 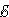 2.
2.
Складывая левые и правые части этих равенств и принимая во внимание, что Δφbc = – Δφda , получим:
I1R1 + I2R2 = Δφbc + Δφda – |
Аналогично, для контура adef можно записать:
– I2R2 + I3R3 = |
Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.
Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов в электрической цепи. Для цепи, изображенной на рис. 1.10.2, система уравнений для определения трех неизвестных токов I1, I2 и I3 имеет вид:
I1R1 + I2R2 = – |
– I2R2 + I3R3 = |
– I1 + I2 + I3 = 0 |
23. Работа и мощность постоянного электрического тока. КПД источника тока.
Работа А электрического тока на участке цепи с электрическим сопротивлением R за время D t равна:
A = I · U · ? t = I2 · R · ? t
Мощность P электрического тока равна отношению работы А тока ко времени D t, за которое эта работа совершена:
P = A / ? t = I · U = I2 R = U2 / R.
Работа А электрического тока равна количеству теплоты Q, выделяемому проводником (если не совершается механическая работа и не происходят химические реакции):
Q = I2 · R · ? t
Этот закон был экспериментально установлен английским ученым Джеймсом Джоулем (1818-1889) и русским ученым Эмилием Ленцем (1804-1865) и поэтому носит название закона Джоуля — Ленца.
Рассмотрим элементарную электрическую цепь, содержащую источник ЭДС с внутренним сопротивлением r, и внешним сопротивлением R (рис. 7.5).
КПД всегда определяем как отношение полезной работы к затраченной:
| | (7.8.1) |
|
Полезная
работа –
мощность, выделяемая на внешнем
сопротивлении Rв
единицу времени. По закону Ома
имеем: 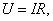 а
а 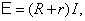 тогда
тогда
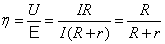 .
.
24. Вывод закона Ома из классической теории электропроводимости металлов.
Друде считал, что сразу после очередного соударения электрона с ионом кристаллической решетки скорость упорядоченного движения электрона равна нулю. Предположим, что напряженность поля не изменяется. Тогда под действием поля электрон получит постоянное ускорение равное
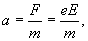
и к концу пробега скорость упорядоченного движения достигнет значения
| (18.2) |
где
t — среднее время между двумя последовательными
соударениями электрона с ионами решетки.
Друде не учитывал распределение
электронов по скоростям и приписывал
всем электронам одинаковое значение
средней скорости  .
В этом приближении
.
В этом приближении  ,
где
,
где 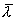 —
среднее значение длины свободного
пробега,
—
среднее значение длины свободного
пробега,  —
скорость теплового движения электронов.
Подставим это значение t в формулу (18.2)
—
скорость теплового движения электронов.
Подставим это значение t в формулу (18.2)

Скорость изменяется за время пробега линейно. Поэтому ее среднее (за пробег) значение равно половине максимального
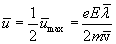
Подставив это выражение в
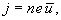
получим
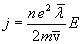
Плотность
тока оказалась пропорциональной
напряженности поля. Следовательно, мы
получили закон Ома. Согласно  коэффициент
пропорциональности между j и Е представляет
собой проводимость
коэффициент
пропорциональности между j и Е представляет
собой проводимость
| (18.3) |
Если бы электроны не сталкивались с ионами решетки, длина свободного пробега, а, следовательно, и проводимость были бы бесконечно велики. Таким образом, электрическое сопротивление металлов обусловлено соударениями свободных электронов с ионами.
Вывод закона Джоуля-Ленца из классической теории электропроводности металлов. Затруднения этой теории.
К
концу свободного пробега электрон
приобретает скорость  ,
и, следовательно, дополнительную
кинетическую энергию, средняя величина
которой
,
и, следовательно, дополнительную
кинетическую энергию, средняя величина
которой

Столкнувшись
с ионом, электрон по предположению
полностью теряет приобретенную им за
время пробега скорость, и передает
энергию кристаллической решетке. Эта
энергия идет на увеличение внутренней
энергии металла, проявляющееся в его
нагревании. Каждый электрон претерпевает
за секунду в среднем 1/t соударений,
сообщая всякий раз решетке энергию 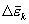 .
Следовательно, в единице объема за
единицу времени должно выделяться тепло
.
Следовательно, в единице объема за
единицу времени должно выделяться тепло
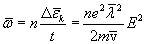
где
n — число электронов проводимости в
единице объема. Величина 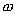 есть
не что иное, как удельная мощность тока.
Множитель при
есть
не что иное, как удельная мощность тока.
Множитель при  совпадает
со значением
совпадает
со значением  (18.3)
для закона Ома. Таким образом. Мы пришли
к выражению закона Джоуля-Ленца в
дифференциальной форме.
(18.3)
для закона Ома. Таким образом. Мы пришли
к выражению закона Джоуля-Ленца в
дифференциальной форме.

Теплоемкость металлов. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемкости электронного газа. Поэтому атомная (т. е. рассчитанная на 1 моль) теплоемкость металла должна быть значительно большей, чем атомная теплоемкость диэлектриков, у которых нет свободных электронов. Согласно закону Дюлонга и Пти (см. §73), теплоемкость одноатомного кристалла равна 3R. Учтем, что теплоемкость одноатомного электронного газа равна 3/2R. Тогда атомная теплоемкость металлов должна быть близка к 4,5R. Однако опыт доказывает, что она равна 3R, т. е. для металлов, так же как и для диэлектриков, хорошо выполняется закон Дюлонга и Пти. Следовательно, наличие электронов проводимости практически не сказывается на значении теплоемкости, что не объясняется классической электронной теорией.
Указанные расхождения теории с опытом можно объяснить тем, что движение электронов в металлах подчиняется не законам классической механики, а законам квантовой механики и, следовательно, поведение электронов проводимости надо описывать не статистикой Максвелла — Больцмана, а квантовой статистикой. Поэтому объяснить затруднения элементарной классической теории электропроводности металлов можно лишь квантовой теорией, которая будет рассмотрена в дальнейшем. Надо, однако, отметить, что классическая электронная теория не утратила своего значения и до настоящего времени, так как во многих случаях (например, при малой концентрации электронов проводимости и высокой температуре) она дает правильные качественные результаты и является по сравнению с квантовой теорией простой и наглядной.
Несамостоятельный и самостоятельный газовые разряды.
Несамостоятельный газовый разряд. Процесс прохождения электрического тока через газ называется газовым разрядом. Если электропроводность газа создается внешними ионизаторами, то электрический ток, возникающий в нем, называется несамостоятельным газовым разрядом. С прекращением действия внешних ионизаторов несамостоятельный разряд прекращается. Несамостоятельный газовый разряд не сопровождается свечением газа. Ниже изображен график зависимости силы тока от напряжения при несамостоятельном разряде в газе. Для построения графика использовалась стеклянная трубка с двумя впаянными в стекло металлическими электродами. Цепь собрана как показано на рисунке ниже.
|
+ —
Самостоятельный
газовый разряд.
Электрический разряд в газе, сохраняющийся после прекращения действия внешнего ионизатора, называется самостоятельным газовым разрядом. Для его осуществления необходимо, чтобы в результате самого разряда в газе непрерывно образовывались свободные заряды. Основным источником их возникновения является ударная ионизация молекул газа.
Если после достижения насыщения продолжать увеличивать разность потенциалов между электродами, то сила тока при достаточно большом напряжении станет резко возрастать (график 2).
Это означает, что в газе появляются дополнительные ионы, которые образуются за счет действия ионизатора. Сила тока может возрасти в сотни и тысячи раз, а число заряженных частиц, возникающих в процессе разряда, может стать таким большим, что внешний ионизатор будет уже не нужен для поддержания разряда. Поэтому ионизатор теперь можно убрать.


I
|
27. Магнитное поле, Магнитная индукция. Принцип суперпозиции магнитных полей. Закон Ампера.
Зако́н
Ампе́ра —
закон взаимодействия электрических
токов.
Впервые был установлен Андре
Мари Ампером в 1820 для
постоянного тока. Из закона Ампера
следует, что параллельные проводники с
электрическими токами, текущими в одном
направлении, притягиваются, а в
противоположных — отталкиваются.
Законом Ампера называется также закон,
определяющий силу, с которой магнитное
поле действует
на малый отрезок проводника с током.
Сила 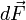 ,
с которой магнитное поле действует на
элемент объёма
,
с которой магнитное поле действует на
элемент объёма 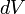 проводника
с током плотности
проводника
с током плотности  ,
находящегося в магнитном поле с
индукцией
,
находящегося в магнитном поле с
индукцией 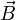 :
:
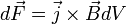 .
.
Модуль силы Ампера можно найти по формуле:
 ,
,
где 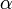 —
угол между векторами магнитной индукции
и тока.
—
угол между векторами магнитной индукции
и тока.
Сила 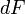 максимальна
когда элемент проводника с током
расположен перпендикулярно линиям
магнитной индукции ():
максимальна
когда элемент проводника с током
расположен перпендикулярно линиям
магнитной индукции ():
 .
.
Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения[1], магнитная составляющая электромагнитного поля[2]
Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).
Магни́тная
инду́кция 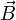 — векторная величина,
являющаяся силовой характеристикой магнитного
поля (его
действия на заряженные частицы) в данной
точке пространства. Определяет, с
какой силой
— векторная величина,
являющаяся силовой характеристикой магнитного
поля (его
действия на заряженные частицы) в данной
точке пространства. Определяет, с
какой силой  магнитное
поле действует на заряд
магнитное
поле действует на заряд  ,
движущийся со скоростью
,
движущийся со скоростью 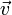 .
.
Более
конкретно,  —
это такой вектор, что сила
Лоренца
—
это такой вектор, что сила
Лоренца 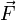 ,
действующая со стороны магнитного
поля[1] на
заряд
,
действующая со стороны магнитного
поля[1] на
заряд 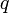 ,
движущийся со скоростью
,
движущийся со скоростью 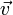 ,
равна
,
равна

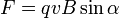
где
косым крестом обозначено векторное
произведение,
α — угол между векторами скорости и
магнитной индукции (направление
вектора  перпендикулярно
им обоим и направлено по правилу
буравчика).
перпендикулярно
им обоим и направлено по правилу
буравчика).
30. Работа и мощность тока. Закон Джоуля
За время dt через сечение проводника переносится заряд dq=Idt Работа тока dA=Udq=IUdt.
Мощность тока: P=dA/dt=UI=I2R=U2/R. Работа выражается в джоулях (Дж). Мощность тока выражается в ваттах (Вт).
Закон Джоуля – Ленца: Если ток идёт по неподвижному проводнику, то вся работа идёт на нагревание и по закону сохранения энергии dQ=dA, dQ=IUdt=I2Rdt=U2dt/R.
Закон
Джоуля — Ленца в интегральной форме: Если
сила тока изменяется со временем, то
количество тепла, выделяющееся за время
t, вычисляется по формуле: 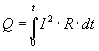 .
.
Закон Джоуля — Ленца в дифференциальной форме: удельная мощность тока равна скалярному произведению векторов плотности тока и напряженности электрического поля: w=jE= γE2=E2/ρ (w=ρj2, j=γE, ρ=1/γ).
31. Закон Ома для неоднородного участка цепи.
Участок цепи, содержащий источник тока, называется неоднородным. Закон Ома для неоднородного участка цепи в интегральной форме, который является обобщённым законом Ома: I = (φ1 — φ2 + ε 12)/R, где ε — э.д.с., действующая в цепи, R — суммарное сопротивление всей цепи, φ1-φ2 – разность потенциалов.
(Если на данном участке цепи источник тока отсутствует (ε 12 = 0), то приходим к закону Ома для однородного участка цепи: I = (φ1 — φ2)/R = U/R. Если же электрическая цепь замкнута, то выбранные точки 1 и 2 совпадают, φ1 = φ2; тогда получаем закон Ома для замкнутой цепи: I = ε /R).
32. Кпд источника тока. Полезная и полная мощьность.
Рассмотрим элементарную электрическую цепь, содержащую источник ЭДС с внутренним сопротивлением r, и внешним сопротивлением R (рис. 7.5).
КПД всегда определяем как отношение полезной работы к затраченной:
|
| (7.8.1) |
|
Полезная
работа – мощность, выделяемая на внешнем
сопротивлении Rв
единицу времени. По закону Ома имеем:  а
а тогда
тогда
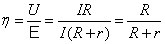 .
.
Таким
образом, имеем, что при 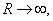
 но
при этом ток в цепи мал и полезная
мощность мала. Вот парадокс – мы всегда
стремимся к повышенному КПД, а в данном
случае нам это не приносит пользы.
но
при этом ток в цепи мал и полезная
мощность мала. Вот парадокс – мы всегда
стремимся к повышенному КПД, а в данном
случае нам это не приносит пользы.
Найдем
условия, при которых полезная мощность
будет максимальна. Для этого нужно,
чтобы 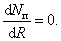
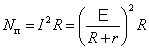 .
.
|
| (7.8.2) |
|

В
выражении (7.8.2) 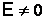 ,
, 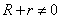 ,
следовательно, должно быть равно нулю
выражение в квадратных скобках, т.е.r=R.
При этом условии выделяемая мощность
максимальна, а КПД равен 50%.
,
следовательно, должно быть равно нулю
выражение в квадратных скобках, т.е.r=R.
При этом условии выделяемая мощность
максимальна, а КПД равен 50%.
33. Зако́ны Кирхго́фа (или правила Кирхгофа) — неизменные соотношения целостности, которые выполняются между токами и напряжениями на участках любой электрической цепи.
Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров.В этом случае законы формулируются следующим образом.
Первый закон гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком). Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов.
Второй закон гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю. Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве mi , то она описывается m – mi –(p — 1) уравнениями напряжений.
Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений. Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно) перепад напряжения считается положительным, в противном случае — отрицательным.
34.Работа и мощность тока. Закон Джоуля-Ленца в интегральной и дифференциальной форме.
Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек), тела или системы[1]
Мощность электрического тока Работа, произведенная в единицу времени, называется мощностью и обозначается буквой P.
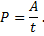
A = P × t.
Единица измерения мощности:

Мощность измеряется ваттметром. Закон Джоуля-Ленца— мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического токана величинунапряженности электрического поля.
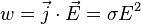
где 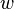 —
мощность выделения тепла в единице
объёма,
—
мощность выделения тепла в единице
объёма,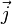 —плотность
электрического тока,
—плотность
электрического тока,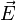 —напряжённость
электрического поля,σ — проводимостьсреды,
а точкой обозначено скалярное произведение.
—напряжённость
электрического поля,σ — проводимостьсреды,
а точкой обозначено скалярное произведение.
.В интегральной форме этот закон имеет вид(для случая протекания токов в тонких проводах)
: Количество теплоты, выделяемое в единицу времени в рассматриваемом участкецепи, пропорционально произведению квадратасилы токана этом участке исопротивленияучастка.

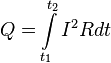
где dQ —
количество теплоты, выделяемое за
промежуток времени dt, I —
сила тока, R —
сопротивление, Q —
полное количество теплоты, выделенное
за промежуток времени от t1 до t2.
В случае постоянных силы тока и
сопротивления: 
Вывод закона Джоуля-Ленца в дифференциальной форме:
Если
ток проходит по неподвижному металлическому
проводнику, то вся работа тока идет на
его нагревание и, по закону сохранения
энергии, 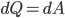
Таким образом, получим:
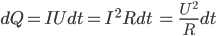
Данное выражение представляет собой закон Джоуля — Ленца.
35.Классическая электронная теория металлов. Вывод законов постоянного тока на основе этой теории. Понятие о квантовой теории электропроводности металлов.
Носителями тока в металлах являются свободные электроны, т. е. электроны, слабо связанные с ионами кристаллической решетки металла. Это представление о природе носителей тока в металлах основывается на электронной теории проводимости металлов, созданной немецким физиком П. Друде
Основные
предположения теории Друде.1)
в отсутствие внешних электромагнитных
полей каждый электрон движется с
постоянной скоростью по прямой линии.
Далее, считают, что в присутствии внешних
полей электрон движется в соответствии
с законами Ньютона; при этом учитывают
влияние только этих полей, пренебрегая
сложными дополнительными полями,
порождаемыми другими электронами и
ионами. приближением свободных электронов.
2)В модели Друде, столкновения — это
мгновенные события, внезапно меняющие
скорость электрона. Друде связывал их
с тем, что электроны отскакивают от
непроницаемых сердцевин ионов 3) за
единицу времени электрон испытывает
столкновение с вероятностью, равной  .
В простейших приложениях модели Друде
считают, что время релаксации
.
В простейших приложениях модели Друде
считают, что время релаксации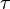 не
зависит от пространственного положения
электрона и его скорости. 4)Предполагается,
что электроны приходят в состояние
теплового равновесия со своим окружением
исключительно благодаря столкновениям.
не
зависит от пространственного положения
электрона и его скорости. 4)Предполагается,
что электроны приходят в состояние
теплового равновесия со своим окружением
исключительно благодаря столкновениям.
Вывод основных законов электрического тока в классической теории электропроводности металлов
1. Закон Ома. во время свободного пробега электроны движутся равноускоренно, приобретая к концу свободного пробега скорость
Согласно теории Друде, в конце свободного пробега электрон, сталкиваясь с ионами решетки, отдает им накопленную в поле энергию, поэтому скорость его упорядоченного движения становится равной нулю. Следовательно, средняя скорость направленного движения электрона
Классическая теория металлов не учитывает распределения электронов по скоростям, следовательно получили закон Ома в дифференциальной форме
2. Закон Джоуля — Ленца. К концу свободного пробега электрон под действием поля приобретает дополнительную кинетическую энергию
При соударении электрона с ионом эта энергия полностью передается решетке и идет на увеличение внутренней энергии металла, т. е. на его нагревание.
Из этого следует, выражение —закон Джоуля—Ленца в дифференциальной форме.
Квантовая теория электропроводности металлов — теория электропроводности, основывающаяся на квантовой механике и квантовой статистике Ферми — Дирака, .
Квантовая теория электропроводности металлов, в частности, объясняет зависимость удельной проводимости от температуры:
Квантовая теория рассматривает движение электронов с учетом их взаимодействия с кристаллической решеткой. Согласно корпускулярно-волновому дуализму, движению электрона сопоставляют волновой процесс. Идеальная кристаллическая решетка) ведет себя подобно оптически однородной среде — она «электронные волны» не рассеивает. Это соответствует тому, что металл не оказывает электрическому току — упорядоченному движению электронов — никакого сопротивления. «Электронные волны», распространяясь в идеальной кристаллической решетке, как бы огибают узлы решетки и проходят значительные расстояния.
В реальной кристаллической решетке всегда имеются неоднородности, которыми могут быть, например, примеси, вакансии; неоднородности обусловливаются также тепловыми колебаниями. В реальной кристаллической решетке происходит рассеяние «электронных волн» на неоднородностях, что и является причиной электрического сопротивления металлов. Рассеяние «электронных волн» на неоднородностях, связанных с тепловыми колебаниями, можно рассматривать как столкновения электронов с фононами.
Согласно классической теории, áuFñ ~ ÖT, поэтому она не смогла объяснить истинную зависимость у от температуры. В квантовой теории средняя скорость áuFñ от температуры практически не зависит, так как доказывается, что с изменением температуры уровень Ферми остается практически неизменным. Однако с повышением температуры рассеяние «электронных волн» на тепловых колебаниях решетки (на фононах) возрастает, что соответствует уменьшению средней длины свободного пробега электронов. В области комнатных температур álFñ ~ Т-1, поэтому, учитывая независимостьáuñ от температуры, получим, что сопротивление металлов (R ~ l/g) в соответствии с данными опытов растет пропорционально Т. Таким образом, квантовая теория электропроводности металлов устранила и эту трудность классической теории.
№36 Работа выхода электронов из металлов. Вывод законов постоянного тока на основе форме.
Как показывает опыт ,свободные электроны при обычных температурах практически не покидают металл .Следовательно , в поверхностном слое металла должно быть задерживающее электрическое поле ,препятствующее выходу электронов из металла в окружающий вакуум . Работа ,которую нужно затратить для удаления электрона из металла в вакуум ,называется работой выхода.
Контактная- называется два разных металла в соприкосновение , между ними возникает разные потенциалов. Контактная разность потенциалов обусловлена тем, что при соприкосновении металлов часть электронов из одного металла проходит в другой.
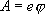
где
е -заряд электрона,  —
потенциал выхода.
—
потенциал выхода. 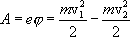
где
m, е — соответственно масса и заряд
электрона, 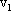 и
и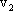 —
скорости электрона до и после выхода
из металла.
Контактная
разность потенциалов между первым и
вторым металлами равна разности работ
выхода для второго и первого металла,
деленая на элементарный заряд.
—
скорости электрона до и после выхода
из металла.
Контактная
разность потенциалов между первым и
вторым металлами равна разности работ
выхода для второго и первого металла,
деленая на элементарный заряд.
Термоэлектрическое явление-между тепловыми и электрическими процессами в металлах и полупроводниках имеется взаимосвязь.
№37 Полупроводники.
Полупроводни́к — материал, который по своей удельной проводимости занимает промежуточное место между проводниками и диэлектриками и отличается от проводников сильной зависимостью удельной проводимости от концентрации примесей, температуры и воздействия различных видов излучения. Основным свойством полупроводника является увеличение электрической проводимости с ростом температуры[1].
Полупроводниками являются вещества, ширина запрещённой зоны которых составляет порядка нескольких электрон-вольт (эВ). Например, алмаз можно отнести к широко зонным полупроводникам, а арсенид индия — к узкозонным. К числу полупроводников относятся многие химические элементы (германий, кремний, селен, теллур, мышьяк и другие), огромное количество сплавов и химических соединений (арсенид галлия и др.). Почти все неорганические вещества окружающего нас мира — полупроводники. Самым распространённым в природе полупроводником является кремний, составляющий почти 30 % земной коры.
В зависимости от того, отдаёт ли примесной атом электрон или захватывает его, примесные атомы называют донорными или акцепторными. Характер примеси может меняться в зависимости от того, какой атом кристаллической решётки она замещает, в какую кристаллографическую плоскость встраивается.
№38 Магнитное поле . Сила Ампера. Индукция магнитного поля . Сила Лоренца. Движение заряженных частиц в магнитном поле.
Магнитное поле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения[1]; магнитная составляющая электромагнитного поля
Магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращающим моментом ,действующим на рамку с магнитным моментом ,равным единице ,когда нормаль к рамке перпендикулярна направлению поля. Магнитное поле является силовым ,то его ,по аналогии с электрическим ,изображают с помощью линий магнитной индукции-линий ,касательные к которым в каждой точке совпадают с направлением вектора В .Их направление задается правилом правого винта: головка винта ,ввинчиваемого по направлению тока ,вращается в направлении линий магнитной индукции.
Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно ,вращающий момент ,испытываемый рамкой ,есть результат действия сил на отдельные ее элементы. .Ампер установил ,что сила dF ,скоторой магнитное поле действует на элемент проводника d /с током ,находящегося в магнитном поле ,равна
dF=I
Где df—вектор ,по модулю равный dl и совпадающий по направлению с током ,В—вектор магнитной индукции.
Направление вектора d F может быть найдено ,по общим правилам векторного произведения, от куда следует правило левой руки:
Опыт показывает ,что магнитное поле действует не только на проводники с током ,но и на отдельные заряды ,движущиеся в магнитном поле .Сила ,действующая на электрический заряд Q ,движущийся в магнитном поле со скоростью v ,называется силой Лоренца и выражается

Где В—индукция магнитного поля ,в котором заряд движется.
Направление силы Лоренца определяется с помощью правила левой руки:
№39 Закон Био-Савара-Лапласа. Магнитное поле прямого и кругового токов. Магнитное поле движущегося заряда.
Закон
Био—Савара—Лапласа
для проводника стоком I
,элемент dl которого создает в некоторой
точке А (рис.166) индукцию поля dB, записывается
в виде  где
dl—вектор ,по модулю равный длине dl
элемента проводника и совпадающий по
направлению с током ; г—радиус-вектор,
проведенный из элемента dl проводника
в точку Л поля ;г—модуль радиуса-вектора
г.
Направление dB перпендикулярно df и
г, т.е. перпендикулярно плоскости, в
которой они лежат, и совпадает с
касательной к линии магнитной индукции
.Это направление может быть задано по
правилу нахождения линий магнитной
индукции(правилу правого винта)
:направление вращения головки винта
дает направление dД если поступательное
движение винта соответствует направлению
тока в элементе.
Модуль вектора dB
определяется выражением
где
dl—вектор ,по модулю равный длине dl
элемента проводника и совпадающий по
направлению с током ; г—радиус-вектор,
проведенный из элемента dl проводника
в точку Л поля ;г—модуль радиуса-вектора
г.
Направление dB перпендикулярно df и
г, т.е. перпендикулярно плоскости, в
которой они лежат, и совпадает с
касательной к линии магнитной индукции
.Это направление может быть задано по
правилу нахождения линий магнитной
индукции(правилу правого винта)
:направление вращения головки винта
дает направление dД если поступательное
движение винта соответствует направлению
тока в элементе.
Модуль вектора dB
определяется выражением где
а—угол между векторами dl иr.
Для
магнитного поля, как и для электрического,
справедлив принцип суперпозиции :вектор
магнитной индукции результирующего
поля ,создаваемого несколькими токами
или движущимися зарядами ,равен векторной
сумме магнитных индукций складываемых
полей, создаваемых каждым током или
движущимся зарядом в отдельности:
где
а—угол между векторами dl иr.
Для
магнитного поля, как и для электрического,
справедлив принцип суперпозиции :вектор
магнитной индукции результирующего
поля ,создаваемого несколькими токами
или движущимися зарядами ,равен векторной
сумме магнитных индукций складываемых
полей, создаваемых каждым током или
движущимся зарядом в отдельности:  Магнитное
поле прямого тока -тока
, текущего по тонкому прямому проводу
бесконечной длины.
В произвольной
точке А, удаленной от оси проводника на
расстояние R, векторы dB от всех элементов
тока имеют одинаковое направление ,
перпендикулярное плоскости чертежа(«к
нам»). Поэтому сложение векторов dВ можно
заменить сложением их модулей.
В
качестве постоянной интегрирования
выберем угол а(угол между векторами d/
и г) , выразив через него все остальные
величины.
Магнитное
поле прямого тока -тока
, текущего по тонкому прямому проводу
бесконечной длины.
В произвольной
точке А, удаленной от оси проводника на
расстояние R, векторы dB от всех элементов
тока имеют одинаковое направление ,
перпендикулярное плоскости чертежа(«к
нам»). Поэтому сложение векторов dВ можно
заменить сложением их модулей.
В
качестве постоянной интегрирования
выберем угол а(угол между векторами d/
и г) , выразив через него все остальные
величины. 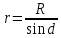
 Магнитное
поле в центре кругового проводника с
током-Как
следует из рисунка(1) ,все элементы
кругового проводника с током создают
в центре магнитные поля одинакового
направления—вдоль нормали от витка.
Поэтому сложение векторов dB можно
заменить сложением их модулей .Так как
все элементы проводника перпендикулярны
радиусу-вектору(sina=1 ) и расстояние всех
элементов проводника до центра кругового
тока одинаково и равно R, то ,согласно
Магнитное
поле в центре кругового проводника с
током-Как
следует из рисунка(1) ,все элементы
кругового проводника с током создают
в центре магнитные поля одинакового
направления—вдоль нормали от витка.
Поэтому сложение векторов dB можно
заменить сложением их модулей .Так как
все элементы проводника перпендикулярны
радиусу-вектору(sina=1 ) и расстояние всех
элементов проводника до центра кругового
тока одинаково и равно R, то ,согласно 
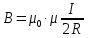 Следовательно
,магнитная индукция поля в центре
кругового проводника с током.
Следовательно
,магнитная индукция поля в центре
кругового проводника с током.  Каждый
проводник с током создает в окружающем
пространстве магнитное
Каждый
проводник с током создает в окружающем
пространстве магнитное
Поле . Электрический ток представляет собой упорядоченное движение электрических зарядов, поэтому можно сказать , что любой движущийся в вакууме или среде заряд создает вокруг себя магнитное поле . В результате обобщения опытных данных был установлен закон, определяющий поле В точечного заряда Q, свободно движущегося с нерелятивистской скоростью v .Под свободным движением заряда понимается его движение с постоянной скоростью. Формула 12 где г—радиус-вектор ,проведенный от заряда Q к точке наблюдения М. №40 Закон полного тока. Магнитное поле соленоида и тороида. Магнитный поток. Полный ток – это алгебраическая сумма токов, проходящих через ограниченную замкнутым контуром поверхность. В нашем примере полный ток Σ I есть сумма токов I1 и I2:
Σ I = I1 — I2
Знаки токов определяем по правилу буравчика.
Теперь найдём магнитное напряжение вдоль контура L. Разбиваем контур на отрезки, которые можно считать прямолинейными, а магнитное поле в месте расположения отрезков однородным. Магнитное напряжение Um для одного такого отрезка длиной ΔL:
Um = HL * ΔL
Магнитное напряжение вдоль всего контура L (см. Магнитное напряжение)
UL = Σ HL * ΔL
Полный ток равен магнитному напряжению вдоль контура:
Σ I = Σ HL * ΔL Магнитное напряжение вдоль замкнутого контура часто называют магнитодвижущей силой. Другое название магнитного напряжения вдоль замкнутого контура –намагничивающая сила.
Определение закона полного тока: магнитодвижущая сила F вдоль замкнутого контура L равна полному току Σ I, пронизывающему поверхность, ограниченную данным контуром. Формула закона полного тока:
F = Σ I Магнитным потоком Ф через поверхность S называют количество линий вектора магнитной индукции B, проходящих через поверхность S.
Формула магнитного потока:
Ф = BS cos α
здесь α — угол между направлением вектора магнитной индукции B и нормалью к поверхности S.
Из формулы магнитного потока видно, что максимальным магнитный поток будет при cos α = 1, а это случится, когда вектор B параллелен нормали к поверхности S. Минимальным магнитный поток будет при cos α = 0, это будет, когда вектор B перпендикулярен нормали к поверхности S, ведь в этом случае линии вектора B будут скользить по поверхности S, не пересекая её. А по определению магнитного потока учитываются только те линии вектора магнитной индукции, которые пересекают данную поверхность.
Измеряется магнитный поток в веберах (вольт-секундах): 1 вб = 1 в * с. Кроме того, для измерения магнитного потока применяют максвелл: 1 вб = 108 мкс. Соответственно 1 мкс = 10-8 вб.
Магнитный поток является скалярной величиной.
Закон Джоуля-Ленца в интегральной и дифференциальной формах
Q = A = U × I × t = I2 × R × t. (6.15)
Закон о тепловом эффекте электрического тока (6.15) был экспериментально установлен независимо английским учёным Д. Джоулем и русским академиком Э.Х. Ленцем. Формула (6.15) — математическая запись закона Джоуля-Ленца в интегральной форме, позволяющая вычислить количество теплоты, выделяющейся в проводнике. Для того, чтобы характеризовать тепловой эффект тока в различных точках проводника, выделим в нём элементарный участок трубки тока (рис. 6.8.). Запишем для этого элемента закон Джоуля-Ленца:
Закон
Джоуля-Ленца: в интегральной форме: Q = I2 × R × t;
в дифференциальной форме: Руд =  ×Е2=
×Е2=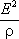 .
.
64 Классическая теория электропроводности металлов (теория Друде-Лоренца).
Электроны в металле рассматриваются как электронный газ, к которому можно применить кинетическую теорию газов. Считается, что электроны, как и атомы газа в кинетической теории, представляют собой одинаковые твердые сферы, которые движутся по прямым линиям до тех пор, пока не столкнутся друг с другом. Предполагается, что продолжительность отдельного столкновения пренебрежимо мала, и что между молекулами не действует никаких иных сил, кроме возникающих в момент столкновения. Так как электрон — отрицательно заряженная частица, то для соблюдения условия электронейтральности в твердом теле также должны быть частицы другого сорта — положительно заряженные. Друде предположил, что компенсирующий положительный заряд принадлежит гораздо более тяжелым частицам (ионам), которые он считал неподвижными. Во времена Друде не было ясно, почему в металле существуют свободные электроны и положительно заряженные ионы, и что эти ионы собой представляют. Ответы на эти вопросы смогла дать только квантовая теория твердого тела. Для многих веществ, однако, можно просто считать, что электронный газ составляют слабо связанные с ядром внешние валентные электроны, которые в металле «освобождаются» и получают возможность свободно передвигаться по металлу, тогда как атомные ядра с электронами внутренних оболочек (атомные остовы) остаются неизменными и играют роль неподвижных положительных ионов теории Друде.
. Несмотря на то, что плотность газа электронов проводимости примерно в 1000 раз больше плотности классического газа при нормальных температуре и давлении, и несмотря на присутствие сильного электрон-электронного и электрон-ионного взаимодействия в модели Друде для рассмотрения электронного газа в металлах почти без изменений применяются методы кинетической теории нейтральных разреженных газов.
Основные предположения теории Друде.
В интервале между столкновениями не учитывается взаимодействие электрона с другими электронами и ионами. Иными словами, принимается, что в отсутствие внешних электромагнитных полей каждый электрон движется с постоянной скоростью по прямой линии. Далее, считают, что в присутствии внешних полей электрон движется в соответствии с законами Ньютона; при этом учитывают влияние только этих полей, пренебрегая сложными дополнительными полями, порождаемыми другими электронами и ионами. Приближение, в котором пренебрегают электрон-электронным взаимодействием в промежутках между столкновениями, известно под названием приближения независимых электронов. Соответственно приближение, в котором пренебрегают электрон-ионным взаимодействием, называется приближением свободных электронов.
В модели Друде, как и в кинетической теории, столкновения — это мгновенные события, внезапно меняющие скорость электрона. Друде связывал их с тем, что электроны отскакивают от непроницаемых сердцевин ионов (а не считал их электрон-электронными столкновениями по аналогии с доминирующим механизмом столкновений в обычном газе).
Предполагается, что за единицу времени электрон испытывает столкновение (т. е. внезапное изменение скорости) с вероятностью, равной
 .
Имеется в виду, что для электрона
вероятность испытать столкновение в
течение бесконечно малого промежутка
времени
.
Имеется в виду, что для электрона
вероятность испытать столкновение в
течение бесконечно малого промежутка
времени равна
просто
равна
просто .
Время
.
Время называют
временем релаксации, или временем
свободного пробега; оно играет
фундаментальную роль в теории проводимости
металлов. Из этого предположения
следует, что электрон, выбранный наугад
в настоящий момент времени, будет
двигаться в среднем в течение времени
называют
временем релаксации, или временем
свободного пробега; оно играет
фундаментальную роль в теории проводимости
металлов. Из этого предположения
следует, что электрон, выбранный наугад
в настоящий момент времени, будет
двигаться в среднем в течение времени до
его следующего столкновения и уже
двигался в среднем в течение времени
до
его следующего столкновения и уже
двигался в среднем в течение времени с
момента предыдущего столкновения. В
простейших приложениях модели Друде
считают, что время релаксации
с
момента предыдущего столкновения. В
простейших приложениях модели Друде
считают, что время релаксации не
зависит от пространственного положения
электрона и его скорости.
не
зависит от пространственного положения
электрона и его скорости.Предполагается, что электроны приходят в состояние теплового равновесия со своим окружением исключительно благодаря столкновениям. Считается, что столкновения поддерживают локальное термодинамическое равновесие чрезвычайно простым способом: скорость электрона сразу же после столкновения не связана с его скоростью до столкновения, а направлена случайным образом, причем ее величина соответствует той температуре, которая превалирует в области, где происходило столкновение. Поэтому чем более горячей является область, где происходит столкновение, тем большей скоростью обладает электрон после столкновения
Кинетическое уравнение Больцманавприближении времени релаксацииприводит для проводимости электронного газа к формуле Друде:

Полученная
формула выражает закон
Ома в дифференциальной форме. Здесь  —
коэффициент пропорциональности,
проводимость металла. Если бы не
было столкновений между электронами и
ионами решетки, то проводимость была
бы бесконечной. Определим температурную
зависимость проводимости. Концентрация
электронов и длина свободного пробега
не должны зависеть от температуры. От
температуры зависит только средняя
скорость теплового движения.
—
коэффициент пропорциональности,
проводимость металла. Если бы не
было столкновений между электронами и
ионами решетки, то проводимость была
бы бесконечной. Определим температурную
зависимость проводимости. Концентрация
электронов и длина свободного пробега
не должны зависеть от температуры. От
температуры зависит только средняя
скорость теплового движения.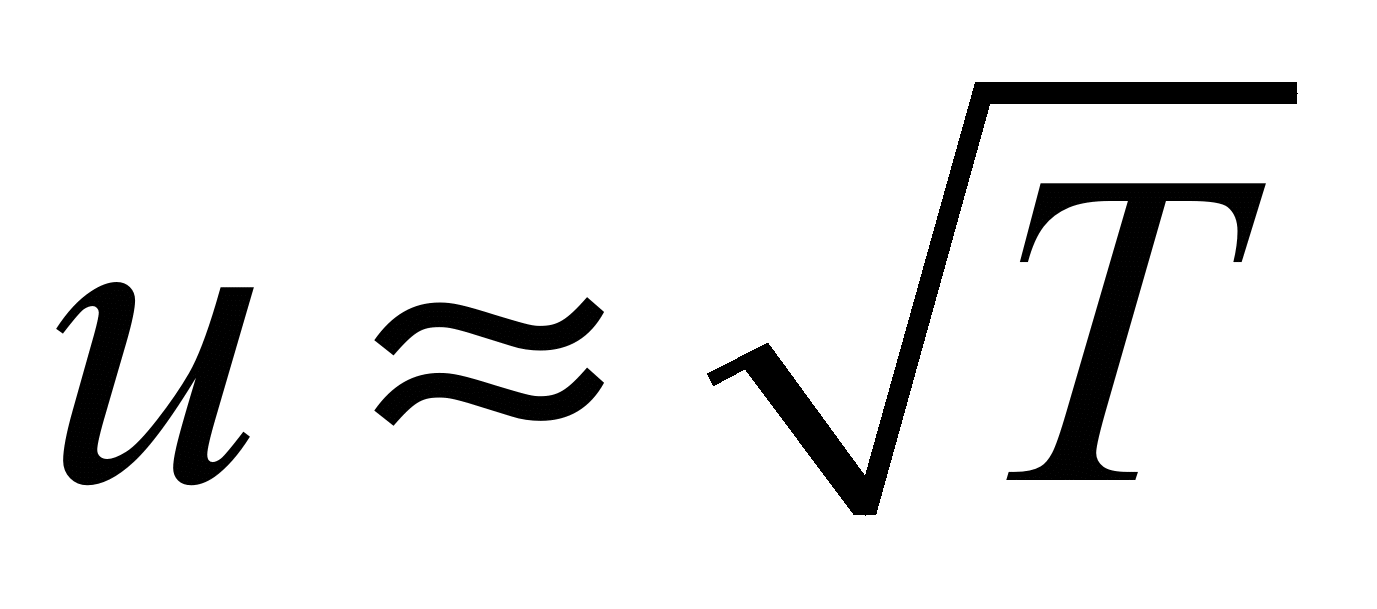 .
Следовательно, проводимость обратно
пропорциональна корню из Т, а сопротивление
возрастает как корень из Т. Эксперимент
показывает, что сопротивление в широком
интервале температур пропорционально
температуре, и только при низких
температура турах
.
Следовательно, проводимость обратно
пропорциональна корню из Т, а сопротивление
возрастает как корень из Т. Эксперимент
показывает, что сопротивление в широком
интервале температур пропорционально
температуре, и только при низких
температура турах .
Таким образом, теория проводимости
металлов Друде-Лоренца, приводя к закону
Ома, не может объяснить температурной
зависимости сопротивления. Объяснение
может дать только квантовая теория.
.
Таким образом, теория проводимости
металлов Друде-Лоренца, приводя к закону
Ома, не может объяснить температурной
зависимости сопротивления. Объяснение
может дать только квантовая теория.
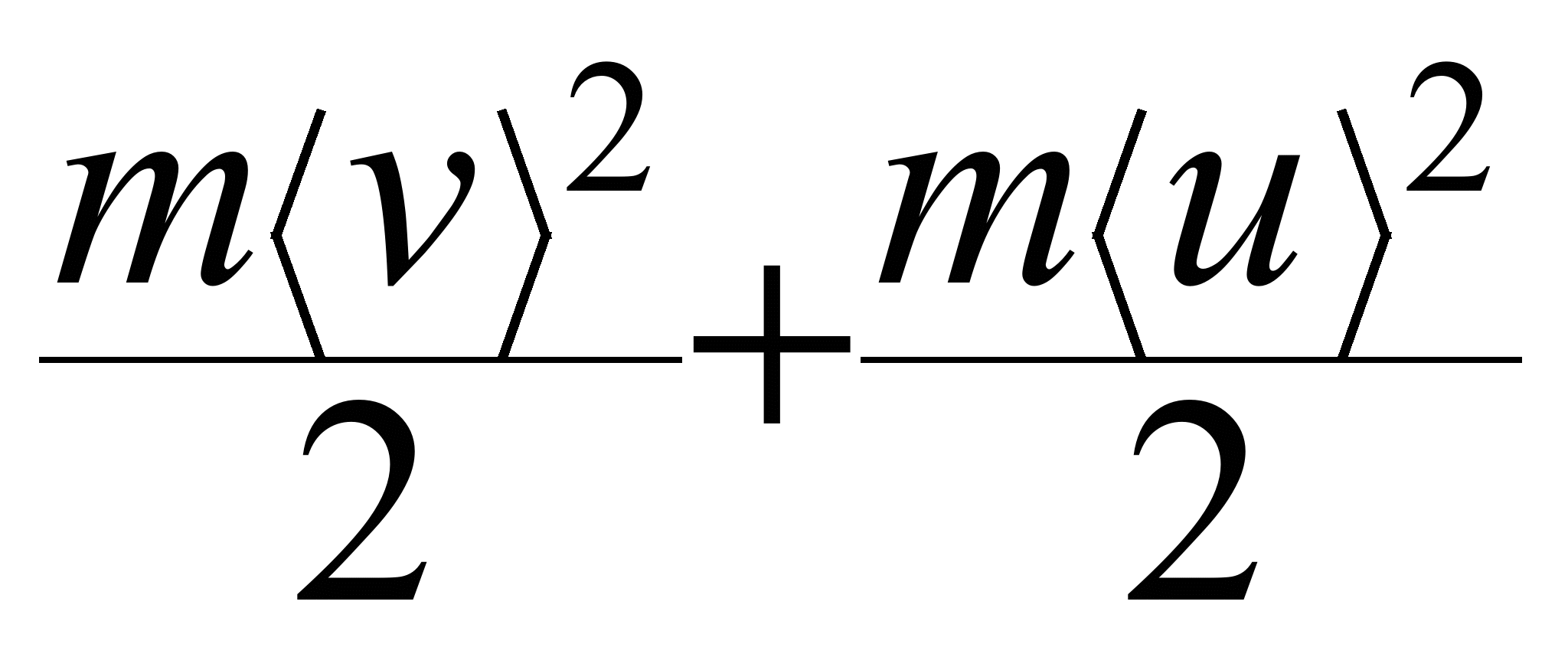 ,
(5)закон
Джоуля-Ленца Закон
Джоуля — Ленца — физический
закон, дающий количественную оценкутепловогодействияэлектрического
тока. Установлен в1841
годуДжеймсом
Джоулеми независимо от него в1842
годуЭмилием
Ленцем[1].
,
(5)закон
Джоуля-Ленца Закон
Джоуля — Ленца — физический
закон, дающий количественную оценкутепловогодействияэлектрического
тока. Установлен в1841
годуДжеймсом
Джоулеми независимо от него в1842
годуЭмилием
Ленцем[1].
В словесной формулировке звучит следующим образом[2]
Мощностьтепла, выделяемого в единицеобъёмасреды при протекании электрического тока, пропорциональна произведениюплотности электрического токана величинунапряженности электрического поля
Математически может быть выражен в следующей форме:
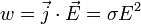
где 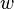 —
мощность выделения тепла в единице
объёма,
—
мощность выделения тепла в единице
объёма,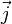 —
плотность электрического тока,
—
плотность электрического тока,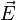 —напряжённость
электрического поля,σ — проводимостьсреды.
—напряжённость
электрического поля,σ — проводимостьсреды.
Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах[3]:
Количество теплоты, выделяемое в единицу времени в рассматриваемом участкецепи, пропорционально произведению квадратасилы токана этом участке исопротивленияучастка
В математической форме этот закон имеет вид
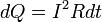

где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 до t2. В случае постоянных силы тока и сопротивления:

Закон
Видемана–Франца.
Видеман и Франц установили связь между
коэффициентом теплопроводности и
электропроводности для всех металлов.
Теплопроводность металлов, как показывает
опыт, значительно выше теплопроводности
диэлектриков. Из этого следует, что
теплопроводность в металлах осуществляется
в основном не кристаллической решеткой,
а свободными электронами. Поэтому,
рассматривая электроны, как одноатомный
газ, используем формулу для коэффициента
теплопроводности газов:  .
Удельная теплоемкость одноатомного
газа:
.
Удельная теплоемкость одноатомного
газа: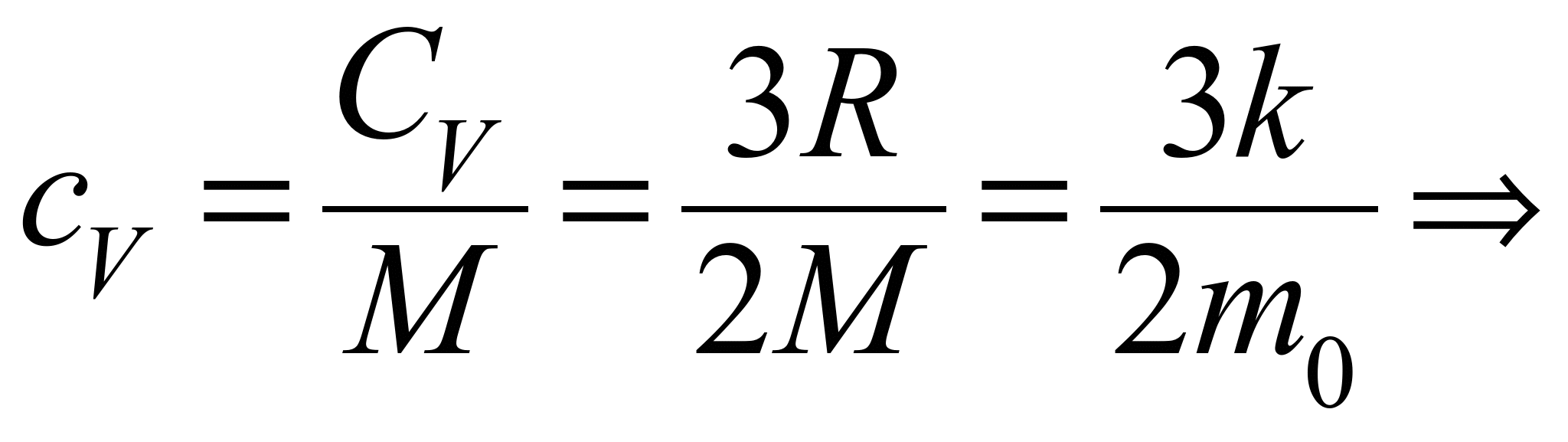
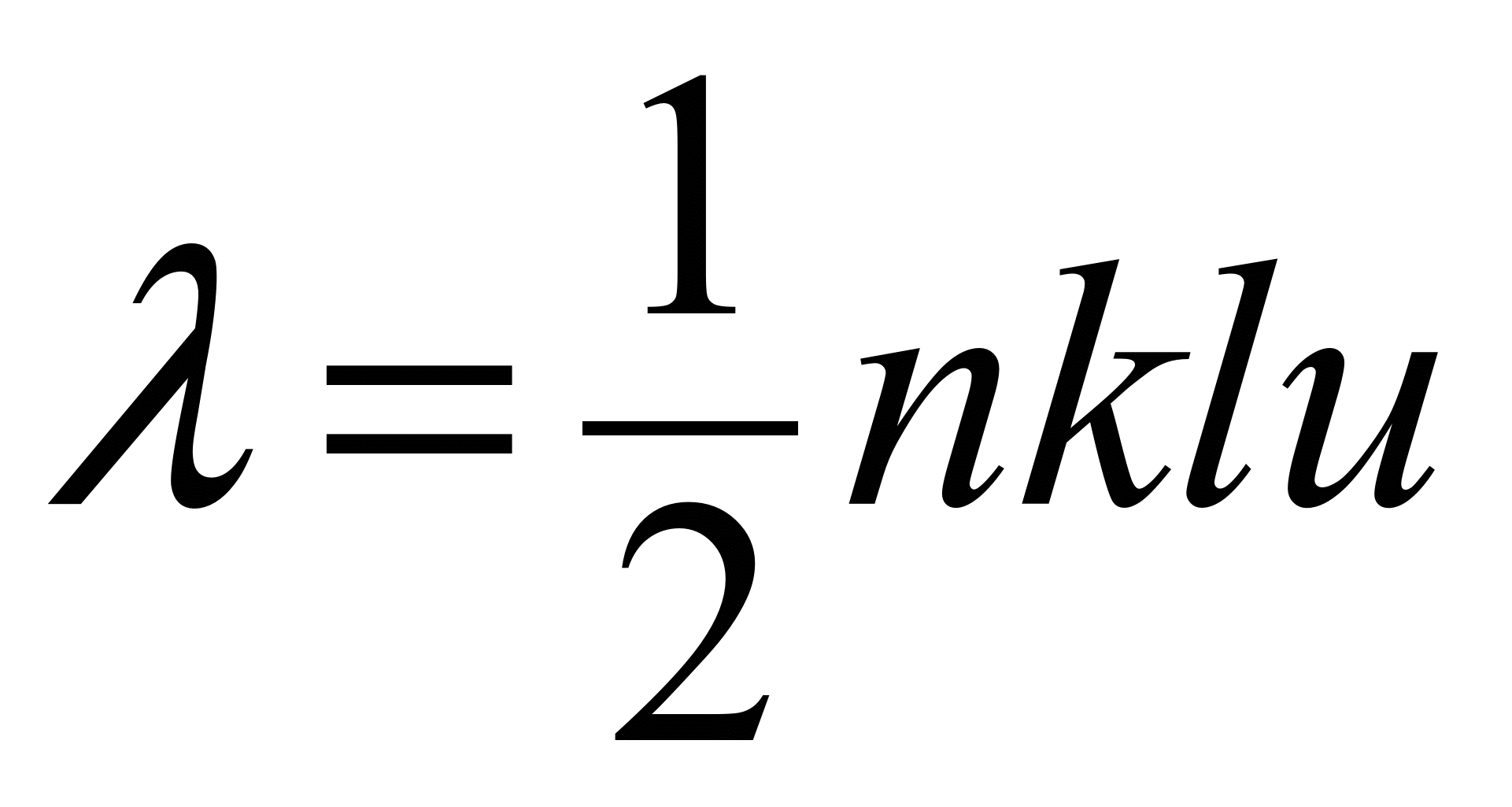 .
Отношение коэффициента теплопроводности
к коэффициенту электропроводности:
.
Отношение коэффициента теплопроводности
к коэффициенту электропроводности: .
Т.о. отношение коэффициента теплопроводности
к коэффициенту электропроводности
пропорционально температуре. Это
соотношение хорошо согласуется с
экспериментальными данными. Но уточненные
Лоренцем расчеты получили другое
соотношение между и ,
которое хуже согласуется с экспериментальными
данными. Т.е. классическая теория дает
только качественное соответствие закона
Видемана –Франца. ПЛО́ТНОСТЬ
ТО́КА, векторная характеристика
электрического тока (см. ЭЛЕКТРИЧЕСКИЙ
ТОК)
j, равная по модулю электрическому
заряду, проходящему за единицу времени
через единичную площадку, перпендикулярную
направлению упорядоченного движения
заряженных частиц.
При равномерном
распределении плотности электрического
тока по сечению проводника плотность
тока j будет равна отношению силы тока
(см. СИЛА
ТОКА)
I в нем к площади его поперечного сечения
S:
j = I/ S
Плотность тока характеризует
силу тока, проходящего через единицу
площади поперечного сечения проводника,
перпендикулярного направлению
тока
Единицей измерения плотности
тока является А/м2.
Плотность
тока можно определить также следующим
образом:
Так как сила тока I = nevS, где:
n
— концентрация носителей заряда;
e —
заряд носителей тока;
v — средняя
скорость упорядоченного движения
частиц;
S — площадь поперечного сечения
проводника, через который течет ток,
То
плотность тока J = I/ S = nev S/ S = nev.
Произведение
ne характеризует плотность заряда е
(заряд в единице объема), поэтому плотность
электрического тока:
j =rеv.
Плотность
тока величина векторная, по направлению
совпадает с направлением вектора
скорости v, т. е. с направлением
упорядоченного движения электрических
зарядов.
Плотность тока пропорциональна
вектору напряженности:
j = sЕ. Зако́н
О́ма — физический закон, определяющий связь
электродвижущей
силы источникаили электрическогонапряженияссилой
токаисопротивлениемпроводника.
Экспериментально установлен в1826
году, и назван в честь его первооткрывателяГеорга
Ома.
.
Т.о. отношение коэффициента теплопроводности
к коэффициенту электропроводности
пропорционально температуре. Это
соотношение хорошо согласуется с
экспериментальными данными. Но уточненные
Лоренцем расчеты получили другое
соотношение между и ,
которое хуже согласуется с экспериментальными
данными. Т.е. классическая теория дает
только качественное соответствие закона
Видемана –Франца. ПЛО́ТНОСТЬ
ТО́КА, векторная характеристика
электрического тока (см. ЭЛЕКТРИЧЕСКИЙ
ТОК)
j, равная по модулю электрическому
заряду, проходящему за единицу времени
через единичную площадку, перпендикулярную
направлению упорядоченного движения
заряженных частиц.
При равномерном
распределении плотности электрического
тока по сечению проводника плотность
тока j будет равна отношению силы тока
(см. СИЛА
ТОКА)
I в нем к площади его поперечного сечения
S:
j = I/ S
Плотность тока характеризует
силу тока, проходящего через единицу
площади поперечного сечения проводника,
перпендикулярного направлению
тока
Единицей измерения плотности
тока является А/м2.
Плотность
тока можно определить также следующим
образом:
Так как сила тока I = nevS, где:
n
— концентрация носителей заряда;
e —
заряд носителей тока;
v — средняя
скорость упорядоченного движения
частиц;
S — площадь поперечного сечения
проводника, через который течет ток,
То
плотность тока J = I/ S = nev S/ S = nev.
Произведение
ne характеризует плотность заряда е
(заряд в единице объема), поэтому плотность
электрического тока:
j =rеv.
Плотность
тока величина векторная, по направлению
совпадает с направлением вектора
скорости v, т. е. с направлением
упорядоченного движения электрических
зарядов.
Плотность тока пропорциональна
вектору напряженности:
j = sЕ. Зако́н
О́ма — физический закон, определяющий связь
электродвижущей
силы источникаили электрическогонапряженияссилой
токаисопротивлениемпроводника.
Экспериментально установлен в1826
году, и назван в честь его первооткрывателяГеорга
Ома.
В
своей оригинальной форме он был записан
его автором в виде : 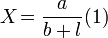 ,
,
Здесь X — показания гальванометра,
т.е в современных обозначениях сила
токаI, a — величина, характеризующая свойства
источника тока, постоянная в широких
пределах и не зависящая от величины
тока, то есть в современной терминологии
электродвижущая сила (ЭДС)  ,l — величина, определяемая длиной
соединяющих проводов, чему в современных
представлениях соответствует сопротивление
внешней цепи R и, наконец, b параметр, характеризующий свойства
всей установки, в котором сейчас можно
усмотреть учёт внутреннего сопротивления
источника тока r[1].
,l — величина, определяемая длиной
соединяющих проводов, чему в современных
представлениях соответствует сопротивление
внешней цепи R и, наконец, b параметр, характеризующий свойства
всей установки, в котором сейчас можно
усмотреть учёт внутреннего сопротивления
источника тока r[1].
В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает
Закон Ома для полной цепи:
 ,
(2)
,
(2)
где:
 —ЭДСисточника
напряжения(В),
—ЭДСисточника
напряжения(В), —сила
токав цепи (А),
—сила
токав цепи (А), —сопротивлениевсех внешних элементов цепи (Ом),
—сопротивлениевсех внешних элементов цепи (Ом), —внутреннее
сопротивлениеисточника
напряжения(Ом).
—внутреннее
сопротивлениеисточника
напряжения(Ом).
Эффе́кт Хо́лла— явление возникновения поперечнойразности потенциалов(называемой такжехолловским напряжением) при помещении проводника с постоянным током вмагнитное поле. ОткрытЭдвином Холломв1879 годув тонких пластинкахзолота.
В
простейшем рассмотрении эффект Холла
выглядит следующим образом. Пусть через
металлический брус в слабом магнитном
поле 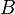 течётэлектрический
токпод действиемнапряжённости
течётэлектрический
токпод действиемнапряжённости .
Магнитное поле будет отклонятьносители
заряда(для определённостиэлектроны)
от их движения вдоль или противэлектрического
поляк одной из граней бруса. При этом
критерием малости[1] будет служить условие, что при этом
электронне начнёт двигаться поциклоиде.
.
Магнитное поле будет отклонятьносители
заряда(для определённостиэлектроны)
от их движения вдоль или противэлектрического
поляк одной из граней бруса. При этом
критерием малости[1] будет служить условие, что при этом
электронне начнёт двигаться поциклоиде.
Таким
образом, сила
Лоренцаприведёт к накоплению
отрицательного заряда возле одной грани
бруска, и положительного — возле
противоположной. Накопление заряда
будет продолжаться до тех пор, пока
возникшееэлектрическое
полезарядов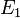 не
скомпенсирует магнитную составляющую
силы Лоренца:
не
скомпенсирует магнитную составляющую
силы Лоренца:
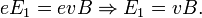
Скорость электронов можно выразить черезплотность тока:

где 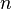 —концентрацияносителей заряда. Тогда
—концентрацияносителей заряда. Тогда
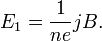
Коэффициент 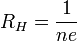 пропорциональности
между
пропорциональности
между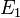 и
и называетсякоэффициентом (или константой) Холла.
В таком приближении знак постоянной
Холла зависит от знака носителей заряда,
что позволяет определять их тип для
большого числа металлов.
Для некоторых металлов (например, таких,
каксвинец,цинк,железо,кобальт,вольфрам),
в сильных полях наблюдается положительный
знак
называетсякоэффициентом (или константой) Холла.
В таком приближении знак постоянной
Холла зависит от знака носителей заряда,
что позволяет определять их тип для
большого числа металлов.
Для некоторых металлов (например, таких,
каксвинец,цинк,железо,кобальт,вольфрам),
в сильных полях наблюдается положительный
знак ,
что объясняется вполуклассическойиквантовойтеорияхтвёрдого
тела
,
что объясняется вполуклассическойиквантовойтеорияхтвёрдого
тела
65 Магни́тная
инду́кция  —векторнаявеличина, являющаяся силовой характеристикоймагнитного
поля(его действия на заряженные
частицы) в данной точке пространства.
Определяет, с какойсилой
—векторнаявеличина, являющаяся силовой характеристикоймагнитного
поля(его действия на заряженные
частицы) в данной точке пространства.
Определяет, с какойсилой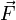 магнитное
поле действует назаряд
магнитное
поле действует назаряд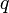 ,
движущийся со скоростью
,
движущийся со скоростью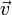 .
.
Более
конкретно, 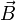 —
это такой вектор, чтосила
Лоренца
—
это такой вектор, чтосила
Лоренца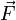 ,
действующая со стороны магнитного
поля[1] на заряд
,
действующая со стороны магнитного
поля[1] на заряд 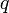 ,
движущийся со скоростью
,
движущийся со скоростью ,
равна
,
равна
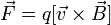

где
косым крестом обозначено векторное
произведение, α — угол между векторами
скорости и магнитной индукции (направление
вектора перпендикулярно
им обоим и направлено поправилу
буравчика).
перпендикулярно
им обоим и направлено поправилу
буравчика).
Также магнитная индукция может быть определена[2] как отношение максимального механического момента сил, действующих на рамку стоком, помещенную в однородное поле, к произведениюсилы токав рамке на еёплощадь.
Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.
В системе СГСмагнитная индукция поля измеряется вгауссах(Гс), в системеСИ— втеслах(Тл)
1 Тл = 104Гс
Магнитометры, применяемые для измерения магнитной индукции, называюттесламетрами.
При́нцип суперпози́ции — один из самых общих законовво многих разделахфизики. В самой простой формулировке принцип суперпозиции гласит:
Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, чтонапряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумма напряженностей полей отдельных зарядов.
Принцип суперпозиции может принимать и иные формулировки, которые полностью эквивалентны приведённой выше:
Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя.
Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парных взаимодействиймежду всеми возможными парами частиц. В системе нетмногочастичных взаимодействий.
Уравнения, описывающие поведение многочастичной системы, являются линейнымипо количеству частиц.
Именно линейностьфундаментальной теории в рассматриваемой области физики есть причина возникновения в ней принципа суперпозиции
Закон Био́—Савара—Лапла́са — физический закон для определения вектора индукциимагнитного поля, порождаемого постояннымэлектрическим током. Был установлен экспериментально в1820 годуБиоиСавароми сформулирован в общем видеЛапласом. Лаплас показал также, что с помощью этого закона можно вычислить магнитное поле движущегося точечного заряда (считая движение одной заряженной частицы током).
Закон Био—Савара—Лапласа играет в магнитостатикету же роль, что изакон Кулонав электростатике. Закон Био—Савара—Лапласа можно считать главным законом магнитостатики, получая из него остальные ее результаты.
В современной формулировке закон Био—Савара—Лапласа чаще рассматривают как следствие двух уравнений Максвелладля магнитного поля при условии постоянства электрического поля, т.е. в современной формулировке уравнения Максвелла выступают как более фундаментальные (прежде всего хотя бы потому, что формулу Био—Савара—Лапласа нельзя просто обобщить на общий случай полей, зависящих от времени).
24. Закон Джоуля- Ленца в интегральной форме.
Кол-во теплоты на участке цепи =произведению квадрата силы тока на его сопротивление и на время прохождения тока
25. Разветвленные цепи. Правила Кирхгофа.
Расчет разветлённых цепей состоит в отыскании токов в различных участках цепи по заданным сопротивлениям участков цепи и приложенных в них ЭДС.Правила Кирхгофа
1.Алгебраическая
сумма токов сходящихся в узле = 0. Узлом
называют точку соединения 3 и более
проводников. Токи текущие к узлу имеют
один знак, а от него другой. 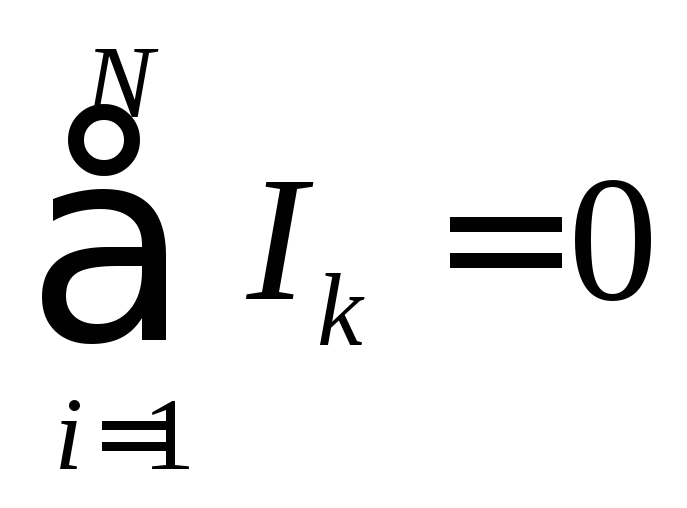
2.
(для замкнутых контуров) Для любого
замкнутого контура, можно записать: 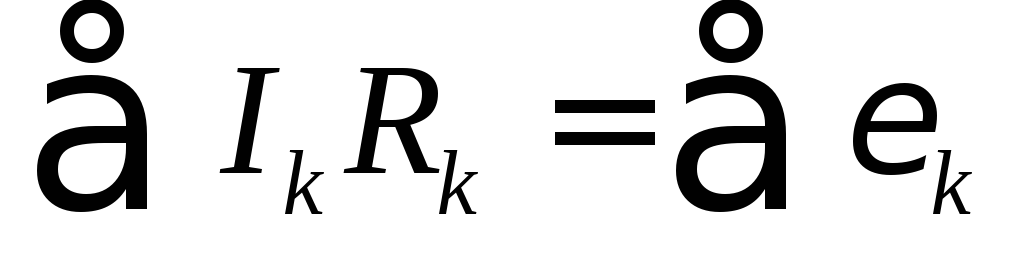
Где 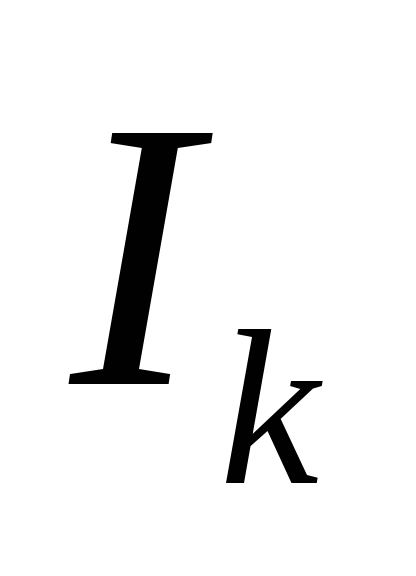 ,
,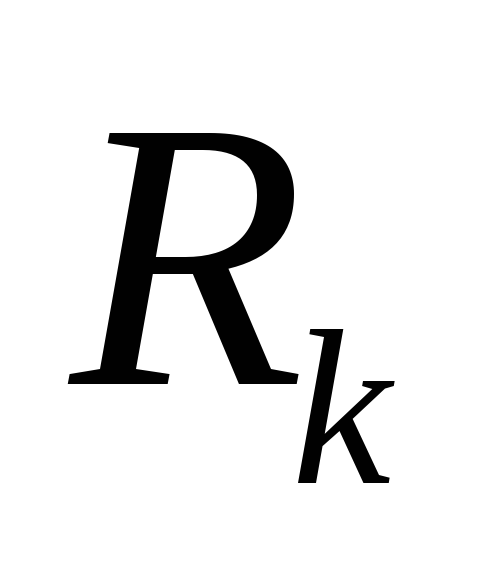 ,
, — токи сопративления и ЭДС выбранного
контура.
— токи сопративления и ЭДС выбранного
контура.
26. Природа проводимости газов. Самостоятельный и несамостоятельный газовые разряды. Типы газовых самостоятельных разрядов и их применение.
Природа проводимости газов. Возникает из-за сильного нагрева, внеш.ионизирующих излучений, из-за корпускулярных потоков
Типы газовых самост. :тлеющий(в лампах рекламных афиш), искровой(свечи внутреннего сгорания, обработка Ме ), дуговой(сварка и резка Ме), коронный(молниеотводы, очистка газов от примесей )
Газовым разрядом называется процесс прохождения электр тока через газ.
Несаммосто газовым разрядом наз газовый разряд, вызванный внешн ионизаторами и прекращающийся, если эти ионизаторы не дейсвуют.
Самост. газовым разрядом наз. электр разряд в газе, который продолж. после прекращ. действия внешнего ионизатора.
27. Плазма. Термоэлектронная эмиссия. Работа выхода электрона. Электрический ток в вакууме. Плазмой наз квазинейтральный ионизованный газ, т.е. частично или полностью ионизованный газ, в котором объёмные плотности положительных и отрицательных зарядов практически одинаковы по абсолютной велечине: р+ + р— =0
Т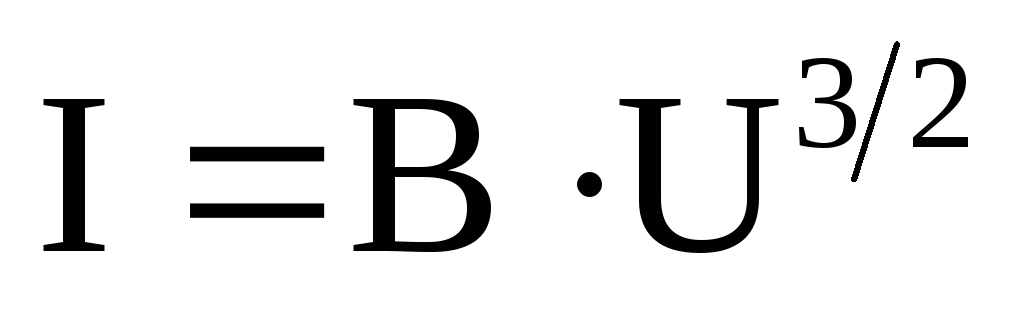 ермоэлектронная
эмиссия или эффект Ричардсона — явление
испускания электронов нагретыми
телами.Испускание электронов твёрдыми
или жидкими телами называется электронной
эмиссией, а тела, испускающие электроны,
называются эмиттерами.
ермоэлектронная
эмиссия или эффект Ричардсона — явление
испускания электронов нагретыми
телами.Испускание электронов твёрдыми
или жидкими телами называется электронной
эмиссией, а тела, испускающие электроны,
называются эмиттерами.
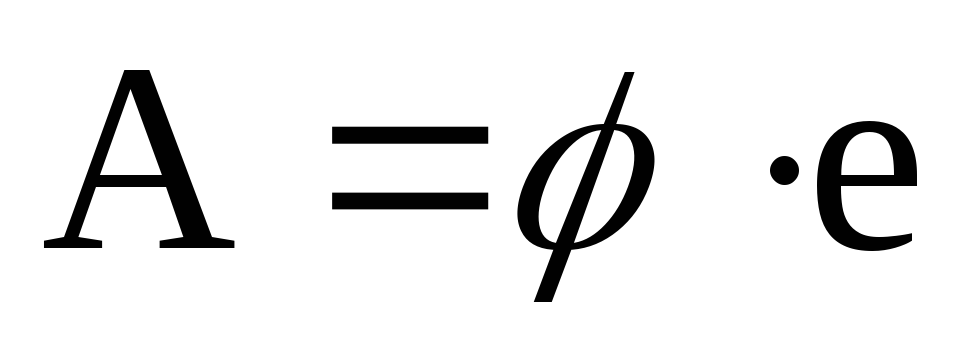
28. Магнитное поле. Магнитная индукция. Принцип суперпозиции. Закон Био-Савара-Лапласа. Правило буравчика.
Магнитное
поле —
особый вид материи, оно порождается
проводником с током. Магнитная индукция
основная силовая характеристика
магн.поля.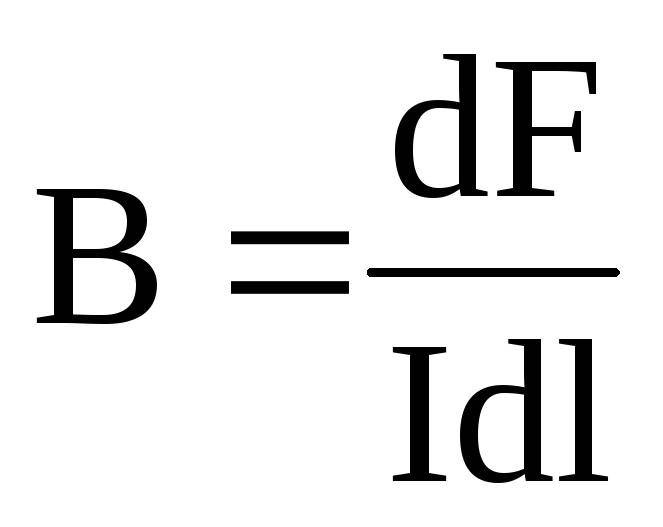 Принцип
суперпозиции для магнитного поля. Индукция
магнитного поля, одновременно создаваемого
в некоторой точке пространства несколькими
источниками, равна сумме векторов
индукций магнитных полей, которые
создавались бы в этой же точке каждым
из источников по отдельности Закон
Био Савара — Лапласа
Принцип
суперпозиции для магнитного поля. Индукция
магнитного поля, одновременно создаваемого
в некоторой точке пространства несколькими
источниками, равна сумме векторов
индукций магнитных полей, которые
создавались бы в этой же точке каждым
из источников по отдельности Закон
Био Савара — Лапласа 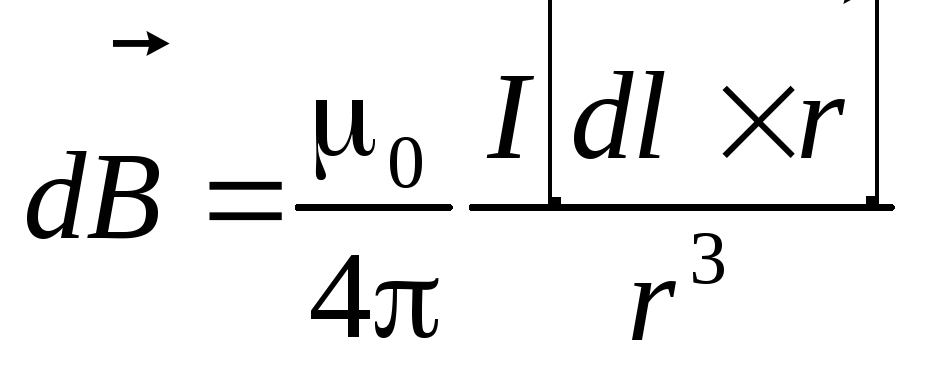 Правило
Буравчика – если Буравчик ввинчивать по направлению
тока в проводнике то направление движения
рукоятки совпадёт с направлением вектора
магнитной индукции.
Правило
Буравчика – если Буравчик ввинчивать по направлению
тока в проводнике то направление движения
рукоятки совпадёт с направлением вектора
магнитной индукции.
29. Расчет магнитного поля прямолинейного проводника с током. Расчет магнитного поля кругового проводника с током.
Индукция
магнитного поля прямолин. проводн.  ,
,
Индукция
магнитного поля на оси кругового
проводника с током. 
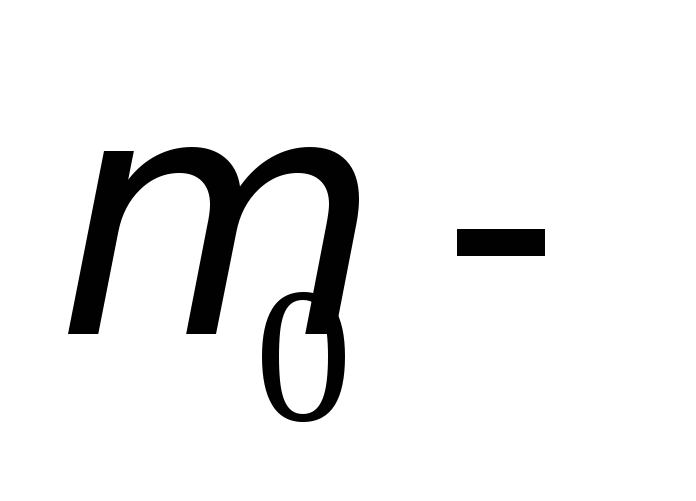 Магнитная
постоянная –
Магнитная
постоянная –  — Гн/м
— Гн/м
30. Закон Ампера. Взаимодействие двух проводников с током.
Сила, действующя на элемент проводника с током в магнитном поле, равна произведению силы тока на векторное произведение элемента длины проводника на магнитную индукцию поля. Единица силы тока — Ампер.
(сила,
действующая со стороны магнитного поля
на элемент с током)  .
.
Сила  , с которой магнитное поле действует на
элемент объёма dV проводника с током
плотности
, с которой магнитное поле действует на
элемент объёма dV проводника с током
плотности 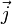 ,
находящегося в магнитном поле с индукцией
,
находящегося в магнитном поле с индукцией  :
: 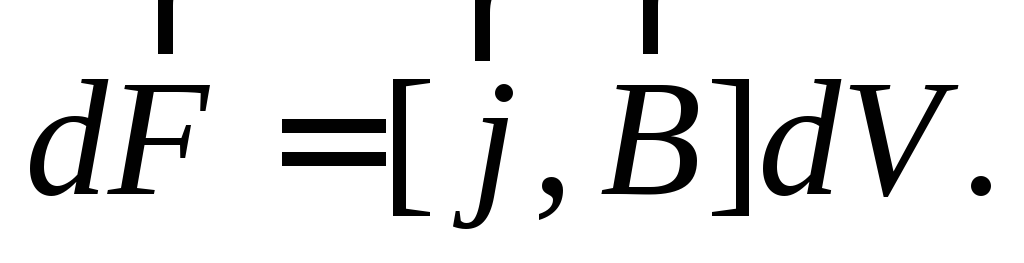
Ампер – сила неизменяющегося тока, который при прохождении по двум параллельным проводникам бесконечной длины и ничтожно малого сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывал бы между этими проводниками силу магнитного взаимодействия, равную 210–7 Н на каждый метр длины
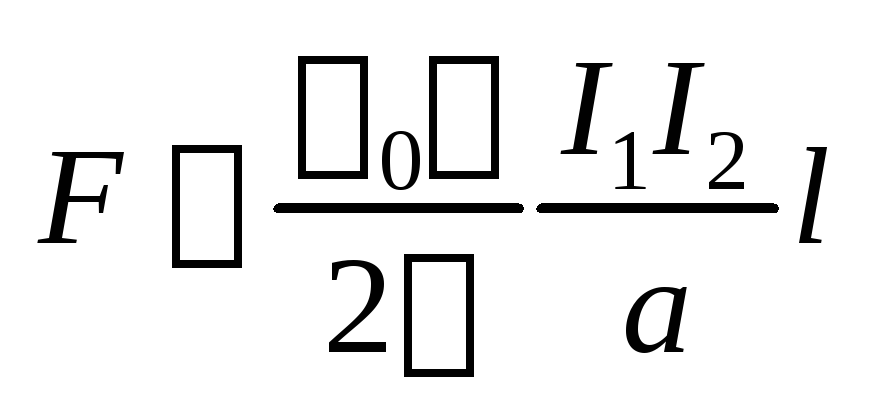


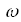 —
является мощностью тепла, выделяемого
в единице объёма;
—
является мощностью тепла, выделяемого
в единице объёма;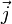 —
плотность электрического тока;
—
плотность электрического тока;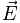 —
это напряжённость электрического поля;
—
это напряжённость электрического поля; —
проводимость выбранной среды.
—
проводимость выбранной среды.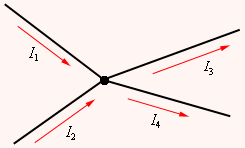

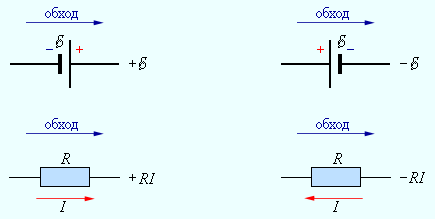
 1 +
1 +  2 = –
2 = –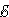 1 –
1 – 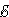 2.
2. 2 +
2 +  3.
3.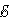 1 –
1 – 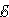 2,
2,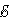 2 +
2 +  3,
3,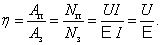

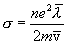
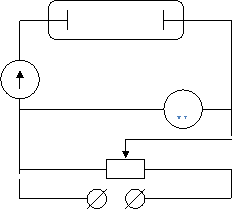


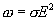

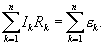
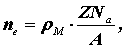
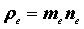

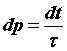
 —
является мощностью тепла, выделяемого
в единице объёма;
—
является мощностью тепла, выделяемого
в единице объёма; —
плотность электрического тока;
—
плотность электрического тока;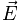 —
это напряжённость электрического поля;
—
это напряжённость электрического поля;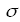 —
проводимость выбранной среды.
—
проводимость выбранной среды.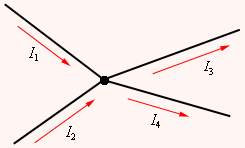
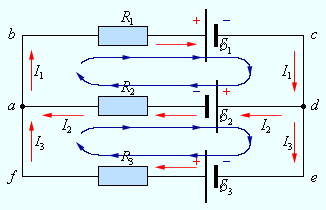

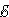 1 +
1 +  2 = –
2 = – 1 –
1 – 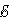 2.
2.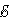 2 +
2 + 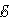 3.
3.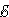 1 –
1 – 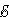 2,
2,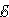 2 +
2 + 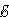 3,
3,




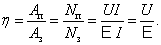
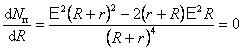 .
. .
Имеется в виду, что для электрона
вероятность испытать столкновение в
течение бесконечно малого промежутка
времени
.
Имеется в виду, что для электрона
вероятность испытать столкновение в
течение бесконечно малого промежутка
времени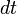 равна
просто
равна
просто .
Время
.
Время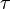 называют
временем релаксации, или временем
свободного пробега; оно играет
фундаментальную роль в теории проводимости
металлов. Из этого предположения
следует, что электрон, выбранный наугад
в настоящий момент времени, будет
двигаться в среднем в течение времени
называют
временем релаксации, или временем
свободного пробега; оно играет
фундаментальную роль в теории проводимости
металлов. Из этого предположения
следует, что электрон, выбранный наугад
в настоящий момент времени, будет
двигаться в среднем в течение времени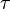 до
его следующего столкновения и уже
двигался в среднем в течение времени
до
его следующего столкновения и уже
двигался в среднем в течение времени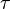 с
момента предыдущего столкновения. В
простейших приложениях модели Друде
считают, что время релаксации
с
момента предыдущего столкновения. В
простейших приложениях модели Друде
считают, что время релаксации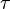 не
зависит от пространственного положения
электрона и его скорости.
не
зависит от пространственного положения
электрона и его скорости.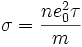
 —ЭДСисточника
напряжения(В),
—ЭДСисточника
напряжения(В), —сила
токав цепи (А),
—сила
токав цепи (А), —сопротивлениевсех внешних элементов цепи (Ом),
—сопротивлениевсех внешних элементов цепи (Ом), —внутреннее
сопротивлениеисточника
напряжения(Ом).
—внутреннее
сопротивлениеисточника
напряжения(Ом).