Закон Био — Савара — Лапласа. Магнитное поле прямого, кругового и соленоидального токов.

Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса — ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший «Салат из свеклы с чесноком»
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Значение магнитной индукции для любого проводника определяется законом Био — Савара — Лапласа.
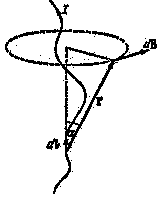
Рис. 15.8.
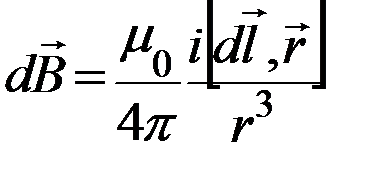 -в векторной форме, (15.6)
-в векторной форме, (15.6)
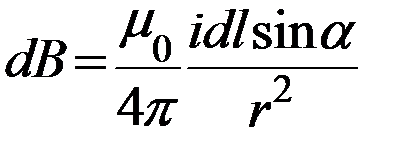 — в скалярной форме. (15.7)
— в скалярной форме. (15.7)
Вектор 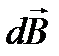 всегда перпендикулярен плоскости, построенной на векторах
всегда перпендикулярен плоскости, построенной на векторах 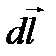
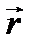 . С помощью закона Био — Савара — Лапласа рассчитаем магнитную индукцию поля прямого, кругового и соленоидального токов.
. С помощью закона Био — Савара — Лапласа рассчитаем магнитную индукцию поля прямого, кругового и соленоидального токов.
Вывод формулы напряжённости магнитного поля прямого тока (рис. 15.9; рис. 15.10) .
Применим формулу 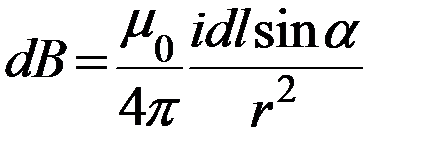
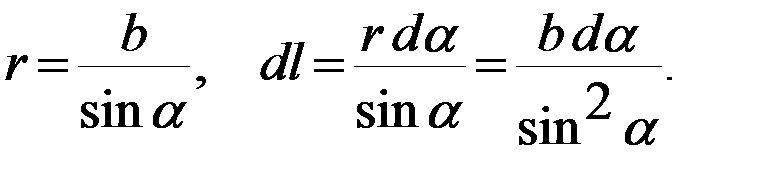
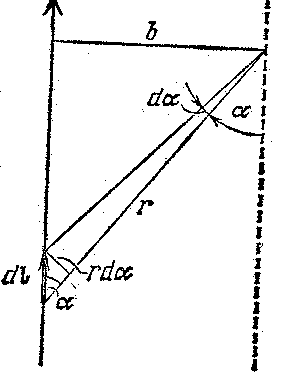
Рис. 15.9.
Подставим эти значения в формулу магнитной индукции:

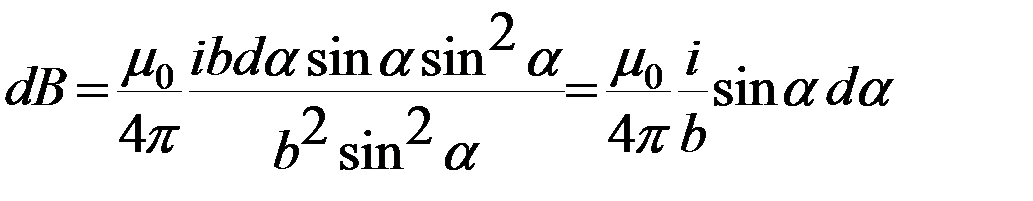 .
.
Угол 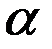
 . Следовательно:
. Следовательно:
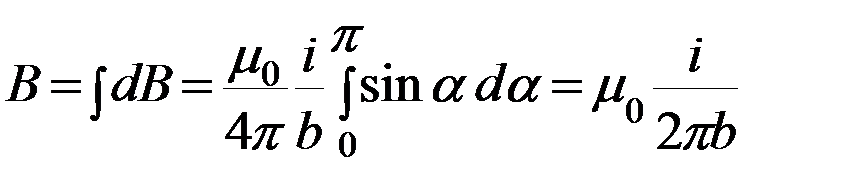 .
.
Таким образом, магнитная индукция поля прямого тока определяется формулой: 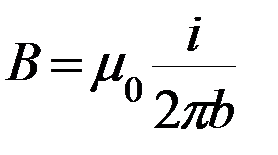
Для того, чтобы получить напряженность магнитного поля, необходимо разделить правую часть формулы (15.8) на 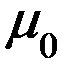 :
:
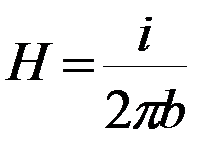

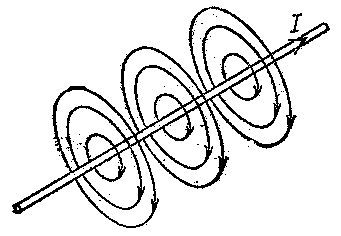
Рис. 15.10
Вывод формулы напряжённости магнитного поля кругового тока (рис. 15.11).
Рассмотрим поле, создаваемое током, текущим по тонкому проводу, имеющему форму окружности (круговой ток). Определим магнитную индукцию кругового тока
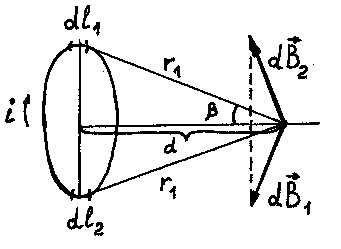
Рис. 15.11
Рассмотрим индукции  , создаваемых двумя элементами контура dl1 и dl2. Т. к. угол между r и dl равен 90°, то sin 90°=1.
, создаваемых двумя элементами контура dl1 и dl2. Т. к. угол между r и dl равен 90°, то sin 90°=1.
Закон Био — Савара — Лапласа для двух элементов:
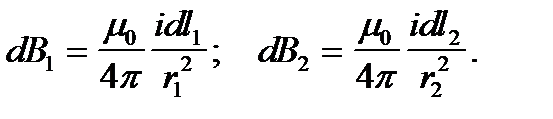
Выбрав
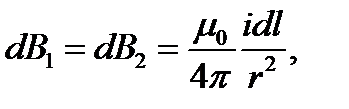
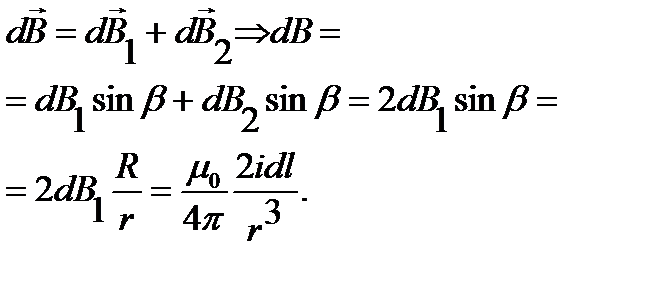
Проинтегрируем это выражение по всему контуру и заменим r на 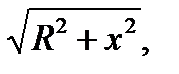
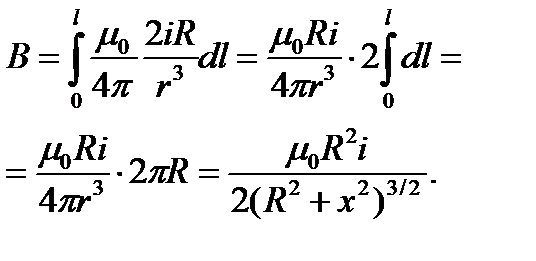 (15.10)
(15.10)
В частности, при x=0 имеем:
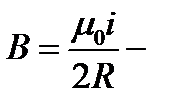 (15.11)
(15.11)
магнитная индукция в центре кругового тока
Напряженность магнитного поля в центре кругового тока равна:
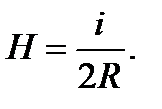
Формула для расчета напряженности магнитного поля кругового тока на его оси принимает вид:
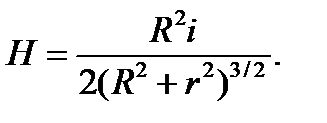 (15.13)
(15.13)
Вывод формулы напряжённости магнитного поля соленоидального тока.
Соленоид представляет собой тонкий провод, навитый плотно, виток к витку, на цилиндрический каркас. В отношении создаваемого им поля соленоид эквивалентен системе одинаковых круговых токов с общей прямой осью. Бесконечно длинный соленоид симметричен относительно любой перпендикулярной к его оси плоскости. Взятые попарно симметричные относительно такой плоскости витки создают поле, магнитная индукция которого перпендикулярна к плоскости. Следовательно, в любой точке внутри и вне соленоида вектор 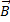 может иметь лишь направление, параллельное оси.
может иметь лишь направление, параллельное оси.
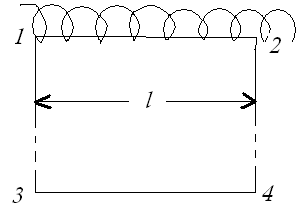
Рис. 15.12.
Возьмем прямоугольный контур 1-2-3-4. Циркуляцию вектора 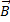 по этому контуру можно представить следующим образом:
по этому контуру можно представить следующим образом:
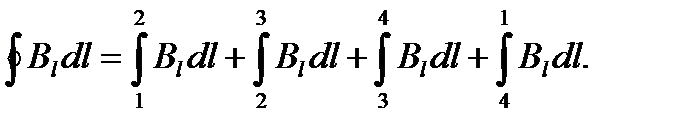
Из четырех интегралов, стоящих в правой части, второй и четвертый равны нулю, так как вектор  перпендикулярен к участкам контура, по которым они берутся.
перпендикулярен к участкам контура, по которым они берутся.
Взяв участок 3-4 на большом расстоянии от соленоида(где поле заведомо должно быть очень слабым), третьим слагаемым можно пренебречь. Следовательно, можно утверждать, что :
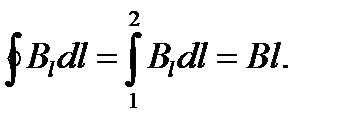
Здесь В — магнитная индукция поля в тех точках, где располагается отрезок 1-2, 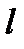 -длина этого отрезка.
-длина этого отрезка.
Если отрезок 1-2 проходит внутри соленоида на любом расстоянии от его оси, контур охватывает суммарный ток 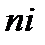 , где
, где 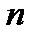 — число витков соленоида, приходящееся на единицу его длинны,
— число витков соленоида, приходящееся на единицу его длинны, 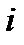 — сила тока в соленоиде. Поэтому согласно :
— сила тока в соленоиде. Поэтому согласно :
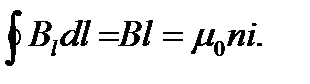
Откуда: 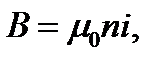 (15.14)
(15.14)
а напряженность магнитного поля соленоидального тока равна:
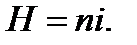 (15.15)
(15.15)
Отметим, что полученный нами результат не зависит от того, на каком расстоянии от оси (но внутри соленоида) располагается отрезок 1-2. Если этот отрезок располагается вне соленоида, то охватываемый контуром ток равен нулю, вследствие чего:
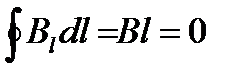 .
.
Откуда В=0. Таким образом, вне бесконечного длинного соленоида магнитная индукция равна нулю, внутри — всюду одинакова и имеет величину, определяемую формулой (15.14). По этой причине в учении о магнетизме бесконечно длинный соленоид играет такую же роль, как плоский конденсатор в учении об электричестве. В обоих случаях поле однородно и полностью заключено внутри конденсатора (электрическое) и внутри соленоида(магнитное).
Произведение 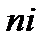 называется числом ампер — витков на метр.
называется числом ампер — витков на метр.
Тесты к лекции №15
Тест 15.1.Магнитная индукция поля, создаваемого отрезком бесконечно тонкого прямолинейного проводника, вычисляется по формуле…
£ 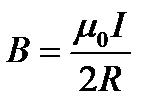
£ 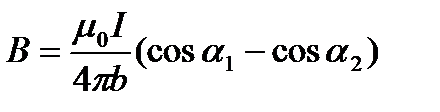
£ 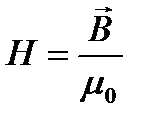
£ 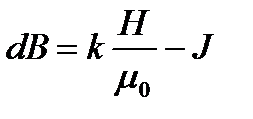
Тест 15.2.Магнитная индукция в центре кругового тока определяется по формуле…
£ 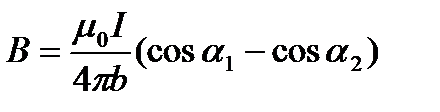
£ 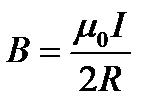
£ 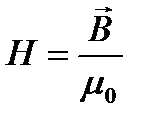
£ 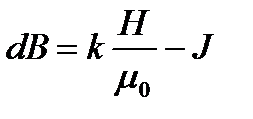
Тест 15.3.Форма существования материи, обладающая свойством передавать магнитное взаимодействие.
£ магнитное поле
£ магнитная индукция
£ пробный контур
£ магнитный момент
Тест 15.4.Дайте определение пробного контура.
£ контур, вносящий помехи в исходное поле.
£ контур, усиливающий исходное поле.
£ контур, ослабляющий исходное поле.
£ контур, который не создает заметных искажений исходного поля.
Тест 15.5.Формула 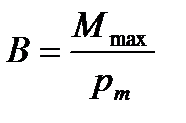 выражает:
выражает:
£ вектор магнитной индукции
£ напряженность магнитного поля
£ магнитную индукцию
£ магнитный момент
Вихревой характер магнитного поля. Циркуляция вектора индукции магнитного поля. Магнитный поток. Сила Ампера. Работа по перемещению проводника с током в магнитном поле. Сила Лоренца. Определение удельного заряда электрона[11]
16.1. Вихревой характер магнитного поля. Циркуляция вектора индукции магнитного поля. Магнитный поток
16.2. Сила Ампера
16.3. Работа по перемещению проводника с током в магнитном поле
16.4. Сила Лоренца
16.5. Определение удельного заряда электрона
Закон Био-Савара-Лапласа | Все Формулы
![Rendered by QuickLaTeX.com \[ \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9b26b31cc88858c6b01bc73f6d36171f_l3.png)
Закон Био Савара Лапласа — Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов.
![Rendered by QuickLaTeX.com \[\Large dB=\frac{\mu\mu _0I[dl,r]}{4\pi r^3}=\frac{\mu\mu _0Idlsin\alpha }{4\pi r^2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-90236ae212a9a174f736b5f23eccb9c5_l3.png)
Закон Био-Савара-Лапласа
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
![Rendered by QuickLaTeX.com \[B=\sum_{i=1}^{n}{B_i}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-bf4237371e9e361a8c71704f7daaa47f_l3.png)
Закон Био-Савара-Лапласа для некоторых токов:
Магнитное поле прямого тока :
![Rendered by QuickLaTeX.com \[\large B=\frac{\mu\mu _0 2I }{4\pi R} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-7c879f6a8e52f7869a003abcb72a2970_l3.png)
Магнитное поле кругового тока :
![Rendered by QuickLaTeX.com \[\large B=\frac{\mu\mu _0 I }{4\pi R} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-73abf6d19414e48309108c3c95af70ec_l3.png)
В формуле мы использовали :
![Rendered by QuickLaTeX.com \[dB\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-567fad23bddf703ad710f2fd31727364_l3.png)
— Магнитная индукция
![Rendered by QuickLaTeX.com \[dl\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-16b780fa84ce6e7c4654b5359ccb0546_l3.png)
— Вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током
![Rendered by QuickLaTeX.com \[ \mu _0=1.2566*10^{−6}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-200b20f4520242c9616b7929b730b8c2_l3.png)
— Магнитная постоянная
![Rendered by QuickLaTeX.com \[ \mu \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-8e00f6a8cc7939d581589866d8693682_l3.png)
— Относительная магнитная проницаемость (среды)
I — Сила тока
R — Расстояние от провода до точки, где мы вычисляем магнитную индукцию
![Rendered by QuickLaTeX.com \[ \alpha \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-66fed14092a9ae39c93652c5db7e0661_l3.png)
— Угол между вектором dl и r
2006 Г.
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Нижегородский Государственный Технический Университет
Выксунский филиал
Кафедра ОиОПД
Магнитное поле соленоида.
Датчик Холла
Лабораторная работа № 2-6
г. Выкса
Составили: В.П.Маслов, И.И.Рожков, О.Д.Честнова, Р.В.Щербаков.
Дана методика определения индукции магнитного поля соленоида на основе закона Био-Савара-Лапласа и с применением датчика Холла.
Научный редактор А.А. Радионов
Цель работы: ознакомиться с определением индукции магнитного поля соленоида на основе закона Био-Савара-Лапласа и с применением датчика Холла.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Закон Био-Савара-Лапласа. Вывод формулы для напряженности и индукции магнитного поля на оси кругового витка с током.
В
пространстве, окружающем проводники с
током, движущиеся заряды, магниты,
возникает магнитное поле, которое можно
обнаружить по воздействию его на другой
проводник с током или магнитную стрелку.
Магнитное поле в каждой точке пространства
количественно может быть описано с
помощью вектора напряженности магнитного
поля 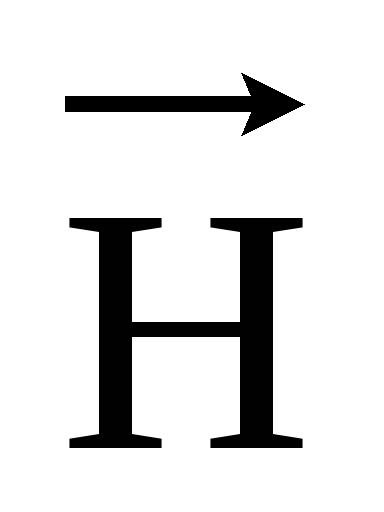 или
с помощью вектора индукции магнитного
поля
или
с помощью вектора индукции магнитного
поля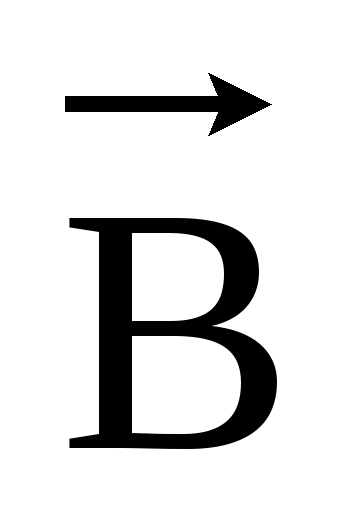 .
В вакууме векторы
.
В вакууме векторы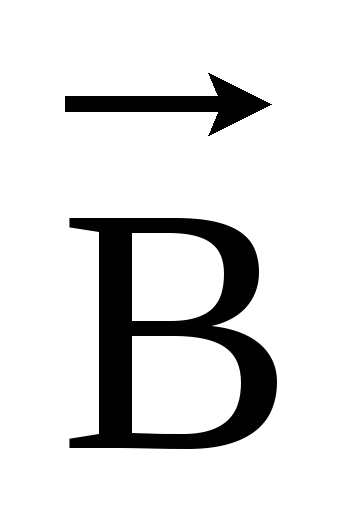 и
и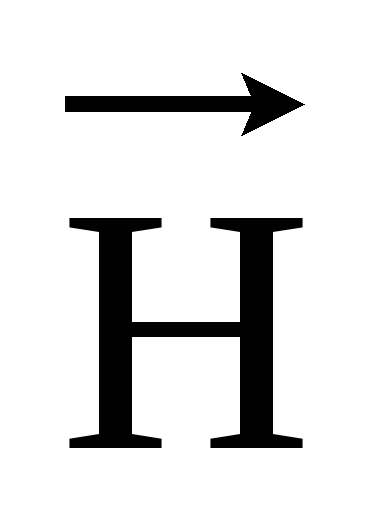 связаны
соотношением:
связаны
соотношением:
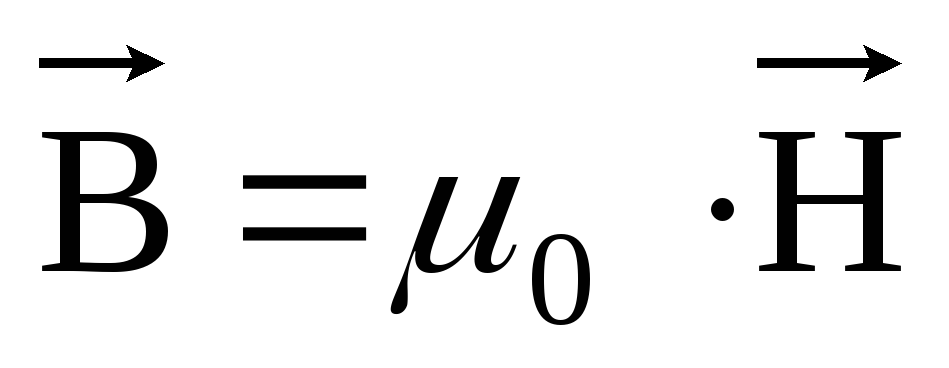 , (1)
, (1)
где μ0 = 4π·10-7 Гн/м — магнитная постоянная.
Единицы
измерения 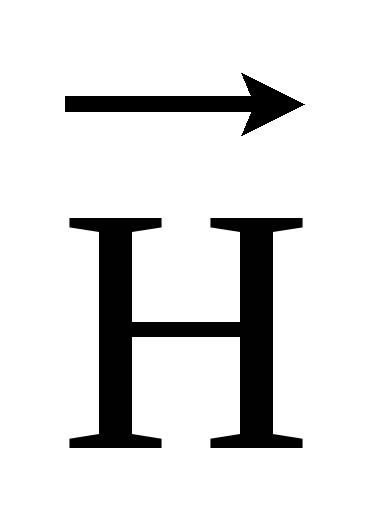 и
и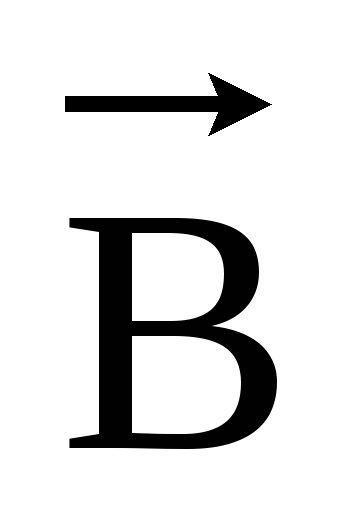 А/м и
Тл соответственно. В среде с магнитной
проницаемостью μ
А/м и
Тл соответственно. В среде с магнитной
проницаемостью μ
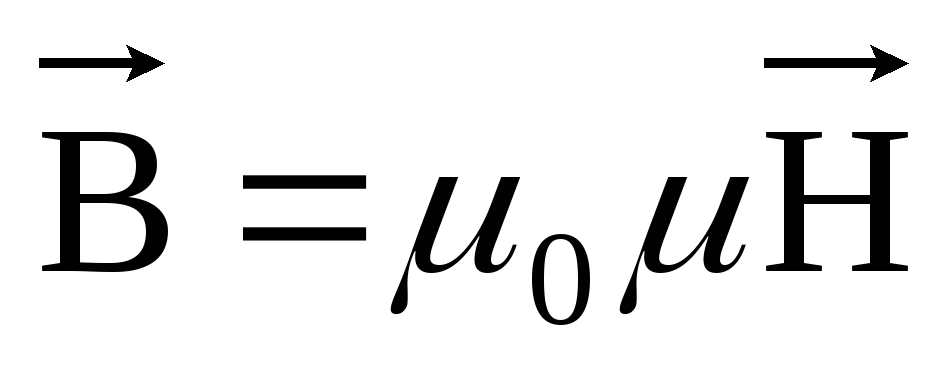
Для
вычисления напряженности и индукции
магнитного поля, используют закон
Био-Савара-Лапласа, согласно которому
элементарная напряженность магнитного
поля 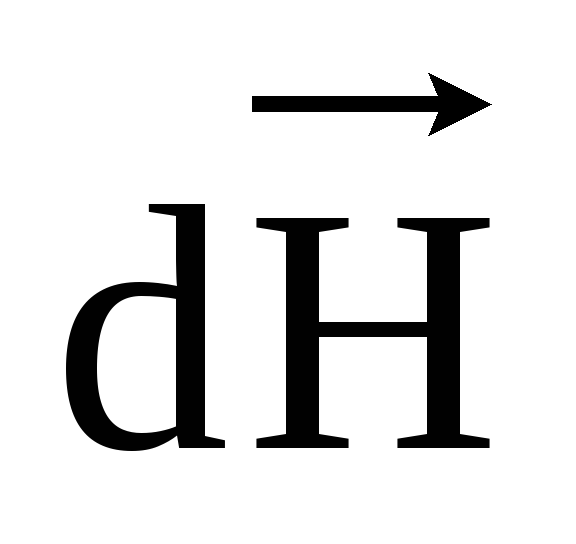 ,
создаваемая элементом проводника с
током
,
создаваемая элементом проводника с
током в некоторой точке пространства на
расстоянии
в некоторой точке пространства на
расстоянии 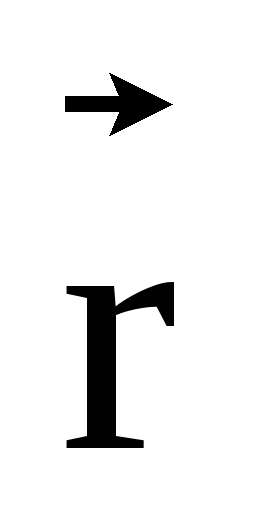 ,
определяется выражением
,
определяется выражением
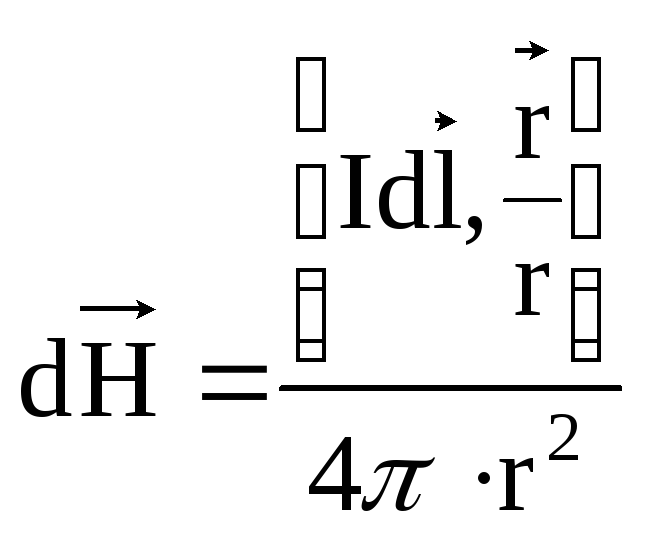 , (2)
, (2)
где 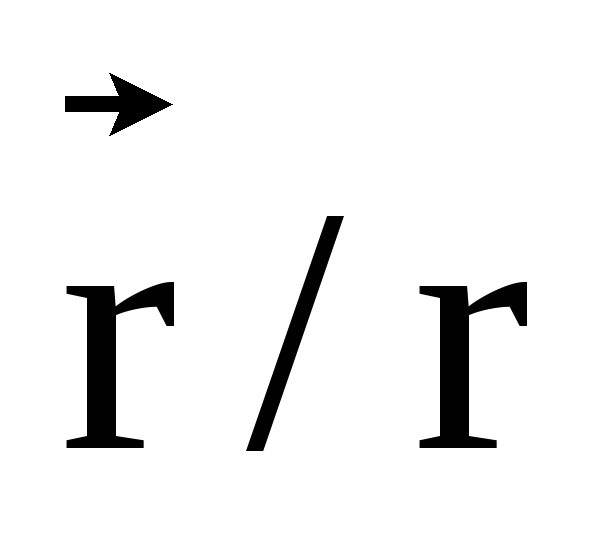 — единичный вектор вдоль
— единичный вектор вдоль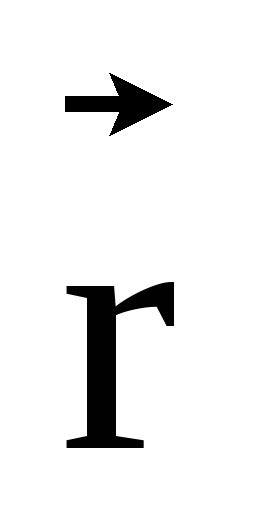 .
.
Модуль вектора
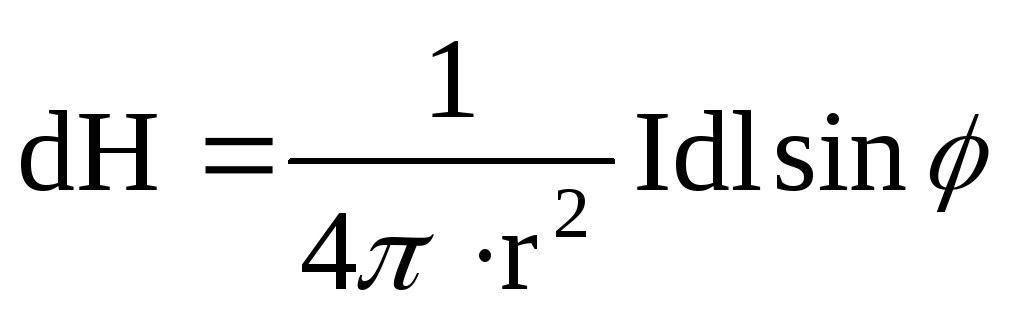 ,
,
где φ – угол между
векторами  и
и .
.
Для
нахождения результирующей напряженности,
создаваемой проводником конечных
размеров, надо воспользоваться принципом
суперпозиции магнитных полей и найти
векторную сумму элементарных напряженностей
от
всех элементов проводника.
Применим формулу (2) для вычисления
напряженности магнитного поля на оси
кругового витка с током (рис. 1).
проводника.
Применим формулу (2) для вычисления
напряженности магнитного поля на оси
кругового витка с током (рис. 1).
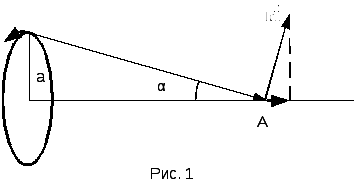
На
рис. 1 компонента dH1,
созданная элементом тока  ,
согласно (2) определяется как
,
согласно (2) определяется как
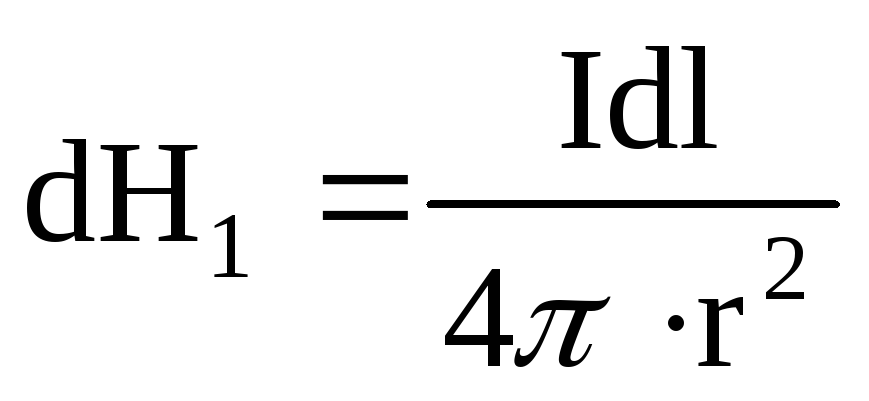 ,
,
где
учтено, что угол между 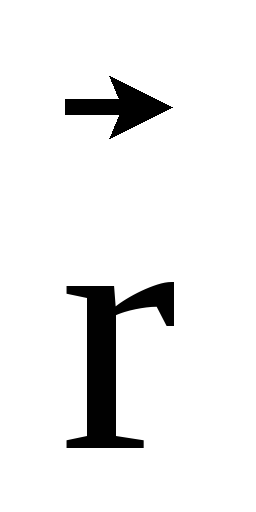 и
и прямой. Из симметрии элементов
прямой. Из симметрии элементов витка по отношению к точке А видно, что
результирующая напряженность магнитного
поля направлена вдоль оси так, что
витка по отношению к точке А видно, что
результирующая напряженность магнитного
поля направлена вдоль оси так, что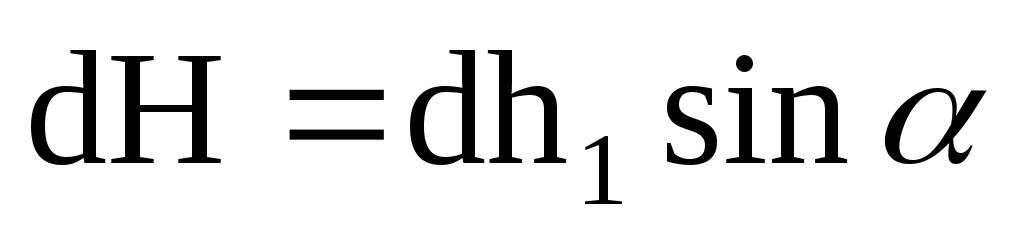 ,
то есть
,
то есть
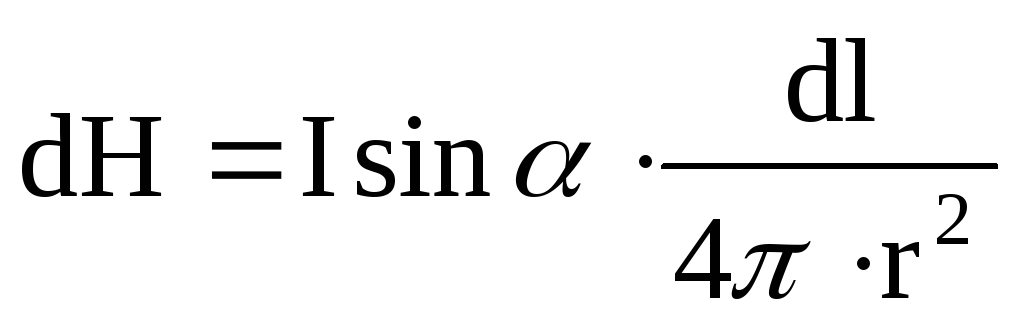 .
.
В правой части последней формулы все-величины, кроме dl, постоянны (для данной точки А), поэтому интегрирование no dl дает
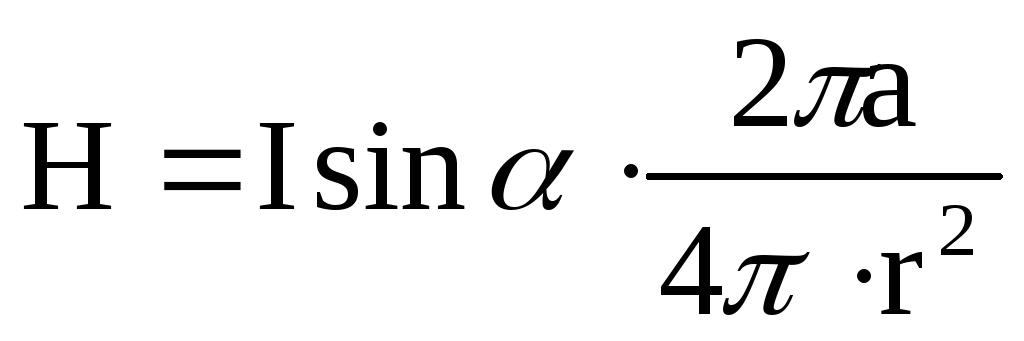 ,
,
или согласно рис. 1
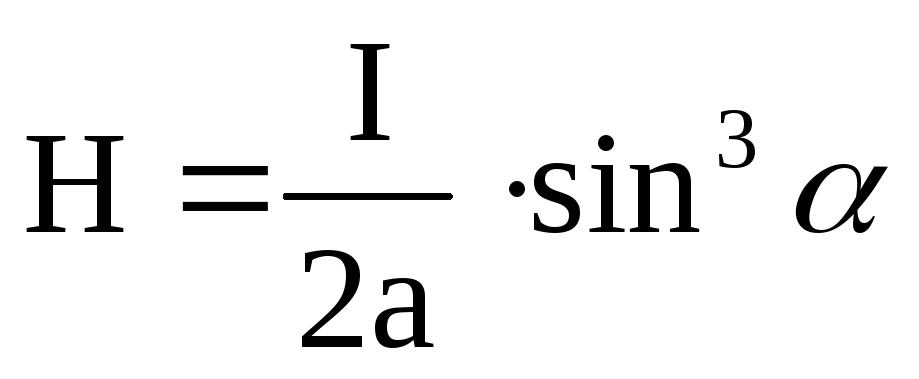 (3)
(3)
Величину  можно найти по формуле (1).
можно найти по формуле (1).
Вывод формулы для напряженности и индукции магнитного поля на оси соленоида (на расстоянии z от средней точки на оси)
Пусть на единицу длины соленоида приходится в витков (рис.2), тогда участок dz содержит ndz витков, которые, согласно (3), в точке А на оси создадут напряженность
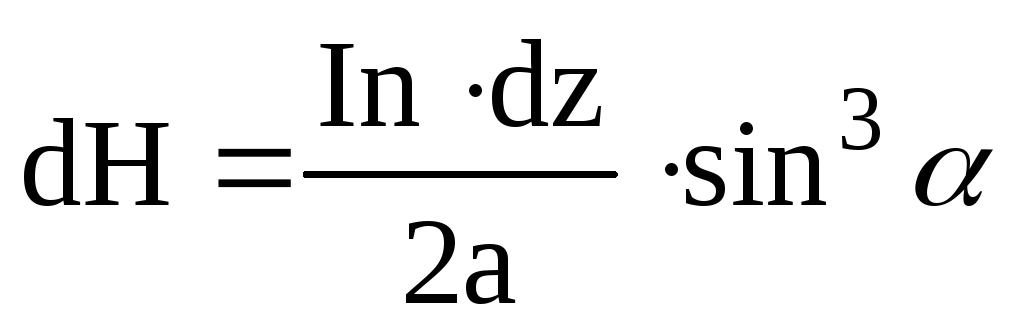 . (4)
. (4)
На рис. 2 L — длина соленоида, а — радиус витков обмотки, 0 -центральная точка на оси соленоида. ОА=z — координата точки А.
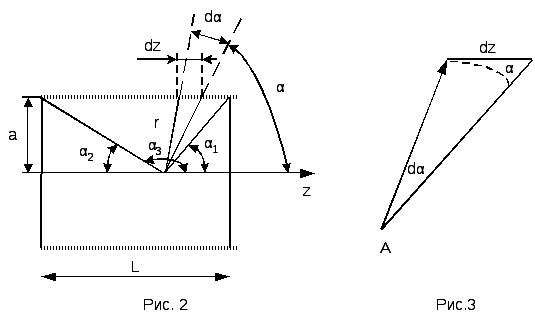
На
рис. 3 отдельно изображены элементы dz,
радиус-вектор  и углы α и dα.
Из геометрических построений рис.2 и 3
следует:
и углы α и dα.
Из геометрических построений рис.2 и 3
следует:
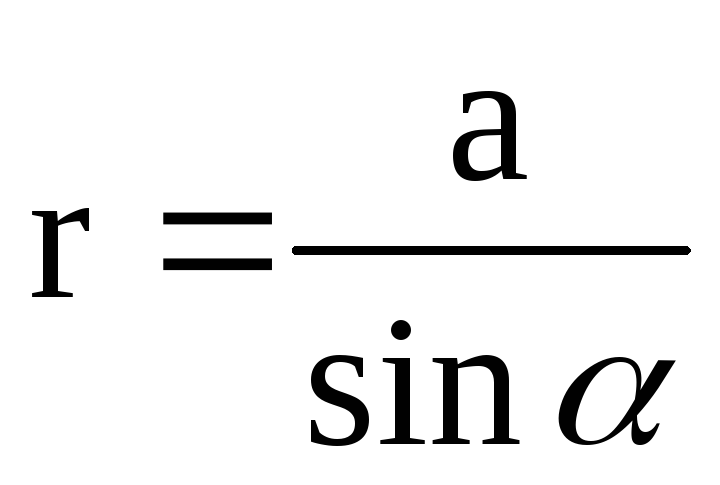 ;
; 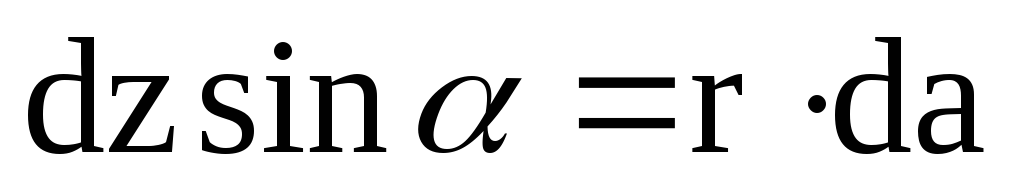 ;
;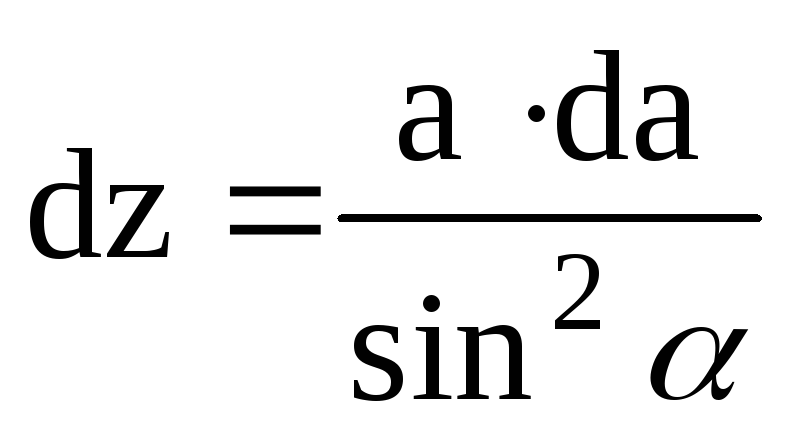 .
.
Подставим эти соотношения в (4) и проинтегрируем по α в пределах от α1 до α3:
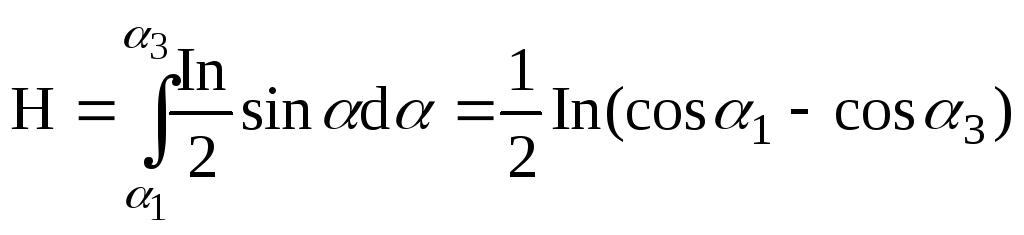 .
.
Учитывая,
что 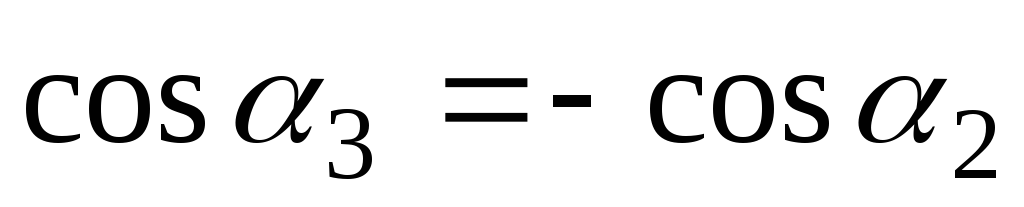 ,
получим
,
получим
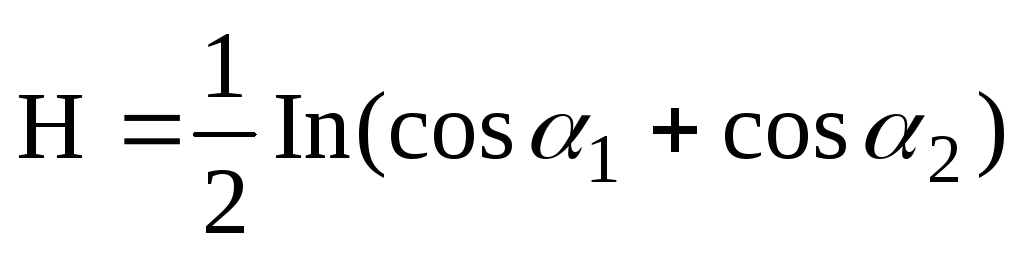 (5)
(5)
В случае бесконечно длинного соленоида (l>>α) в центральной точке 0 α1→0, α2→0,
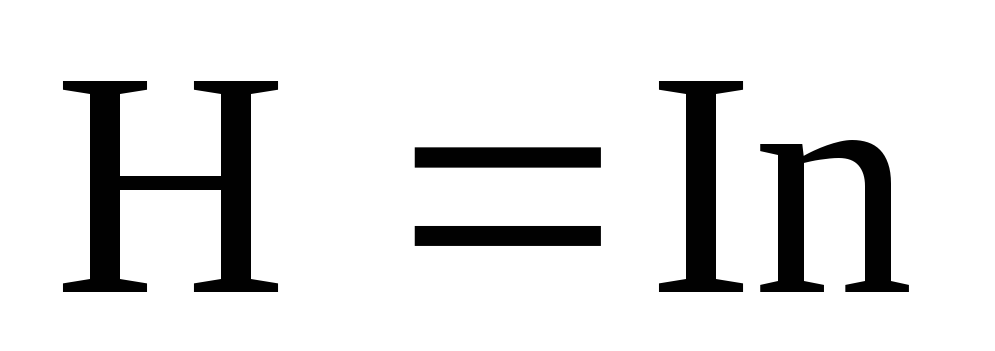 . (6)
. (6)
Из (5) также следует, что при переходе от центра к краю полубесконечного соленоида (на краю z=0,5L, α1=π/2, α2→0) напряженность уменьшается вдвое:
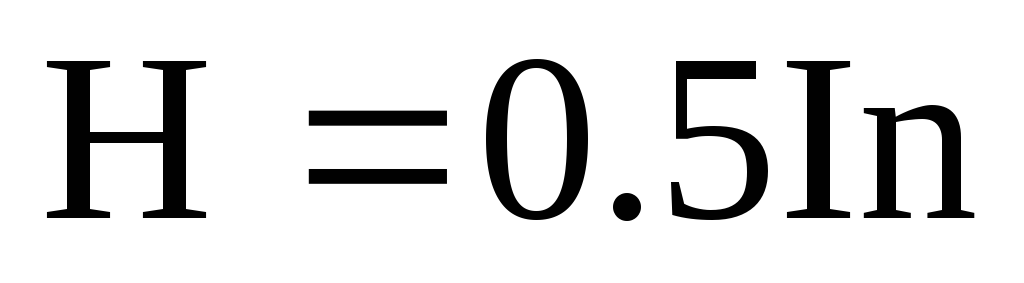 . (7)
. (7)
Индукцию, магнитного поля получим, добавив к выражениям (5), (б), (7) формулу (1). Отметим, что вывод формулы (6) для бесконечно длинного соленоида получается существенно проще на основе закона полного тока.
3 Применение Закона Био – Савара _Лапласа. Для вычисления индукции в центре кругового, и прямолин. Током.
Магнитное поле в центре кругового проводника с током (рис. 1). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение век торов dB можно заменить сложением их модулей.

Рис. 166 (Трафимова) пиши что рис. 1
Так как все элементы проводника перпендикулярны радиусу-вектору (sin = l) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),
Тогда
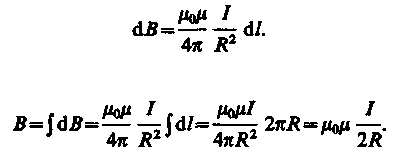
Следовательно, магнитная индукция поля в центре кругового проводника с током
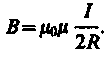
Применение закона Био-Савара-Лапласа для нахождения магнитного поля прямого тока
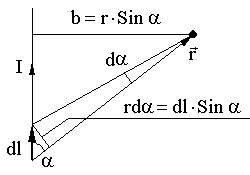
Независимо
от положения  на
проводнике все
на
проводнике все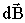 направлены
в одну сторону — от нас. Значит,
направлены
в одну сторону — от нас. Значит,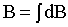 —
без векторов!
Из Закон Био-Савара-Лапласа:
—
без векторов!
Из Закон Био-Савара-Лапласа:
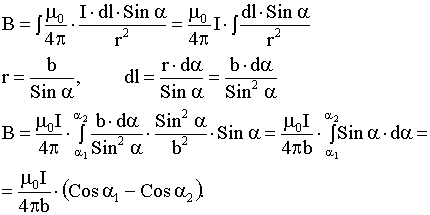
Для
бесконечного проводника α1 = 0, α2 = π, Сos α1 — Сos α2 = 2 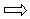
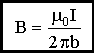 .
.
Применение теоремы о циркуляции для вычисления магнитного поля бесконечно длинного соленоида Соленоид — провод, навитый на цилиндрический каркас. На один метр длины — n витков.
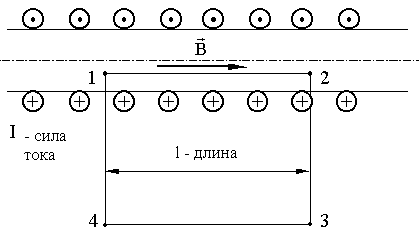
Выберем
такой контур, как на рисунке, т.к. из
соображений симметрии вектор  может
быть направлен только вдоль оси соленоида. Тогда
может
быть направлен только вдоль оси соленоида. Тогда
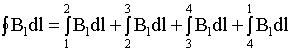 .
.
1)
В интервалах от точки 2 до точки 3 и от
точки 4 до точки 1 
 стороне
контура, значит Вl = 0.
2) Тогда:
стороне
контура, значит Вl = 0.
2) Тогда: 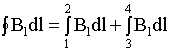
3)
Можно показать, что вне бесконечного
соленоида B=0, т.е. 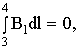
Значит: 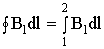
т.к. внутри соленоида B = Bl = const, то
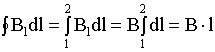 .
.
По теореме о циркуляции
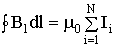 .
.
Откуда магнитное поле бесконечного соленоида:
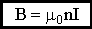 .
.
Направлено  вдоль
оси соленоида, в соответствии с правилом
правого винта.
вдоль
оси соленоида, в соответствии с правилом
правого винта.
4 Закон Ампера. Закон магнитного взаимодействия токов.
Магнитное поле (см. § 109) оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия мгнитного поля на различные проводники с током, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнит ном поле, равна
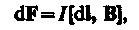 (111.1)
(111.1)
где dl — вектор, по модулю равный dl и совпадающий по направлению с током, В — вектор магнитной индукции.
Направление вектора dF может быть найдено, согласно (111.1), по общим правилам векторного произведения, откуда следует правело левой рут: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.
Модуль силы Ампера (см. (111.1)) вычисляется по формуле
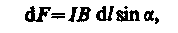 (111.2)
(111.2)
где — угол между векторами dl и В.
Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I1 и I2 (направления токов указаны на рис. 167), расстояние между которыми равно R. Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока I1 на элемент dl второго проводника с током I2. Ток I1 создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. На правление вектора B1определяется правилом правого винта, его модуль по формуле (110.5) равен
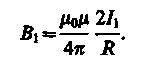
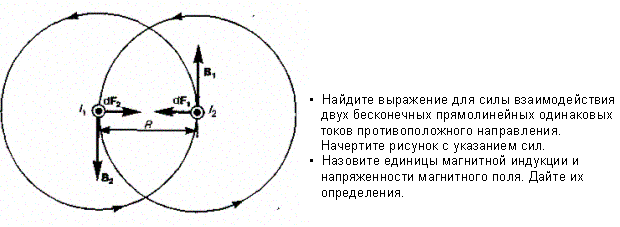
Рис. 167
Направление силы dF1, с которой поле B1действует на участок dl второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, согласно (111.2), с учетом того, что угол а между элементами тока I2 и вектором B1 прямой, равен
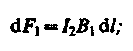
подставляя значение для B1 получим
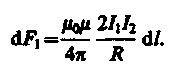 (111.3)
(111.3)
Рассуждая аналогично, можно показать, что сила dF2, с которой магнитное поле тока I2 действует на элемент dl первого проводника с током I1 направлена в противоположную сторону и по модулю равна
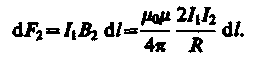 (111.4)
(111.4)
Сравнение выражений (111.3) и (111.4) показывает, что
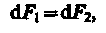
т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой
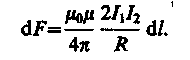 (111.5)
(111.5)
Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой (111.5).
§ 110. Закон Био — Савара — Лапласа и его применение к расчету магнитного поля
Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж. Био (1774—1862) и Ф. Саваром (1791 —1841). Результаты этих опытов были обобщены выдающимся французским математиком и физиком П. Лапласом.
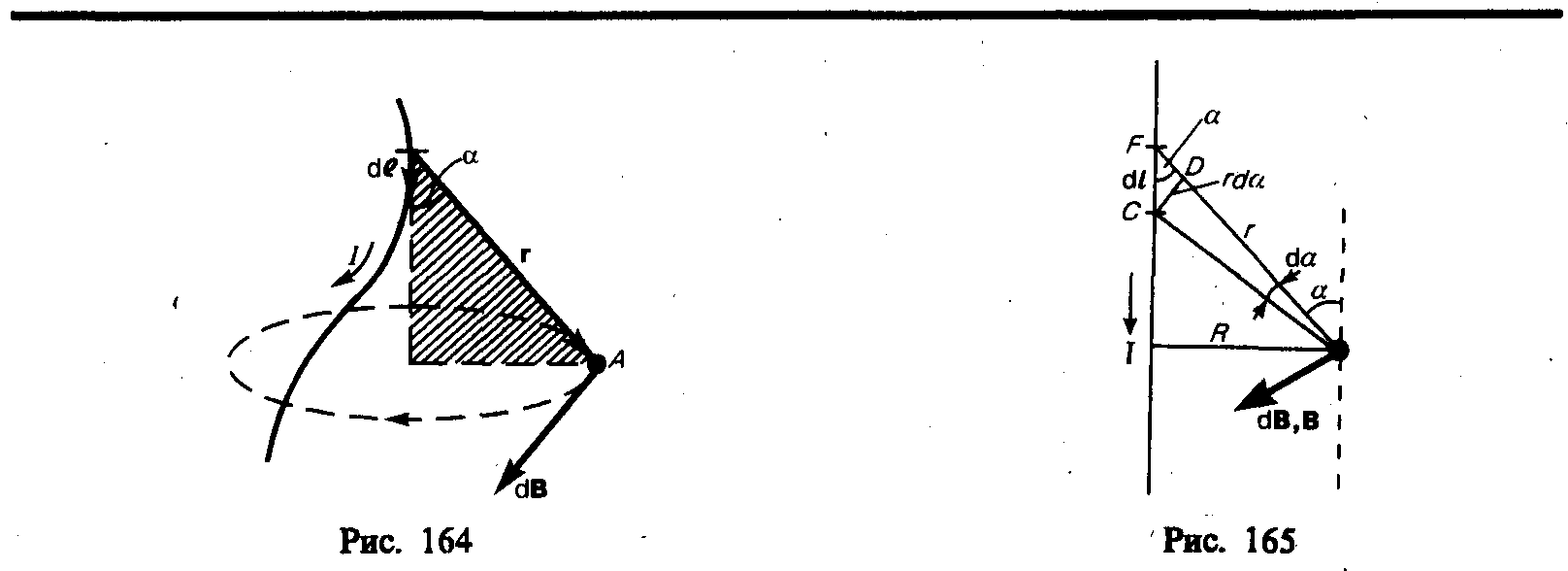
Закон Био — Савара — Лапласа для проводника с током I, элемент которого dl создает в некоторой точке А (рис. 164) индукцию поля dB, записывается в виде
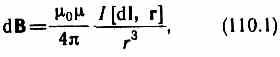
г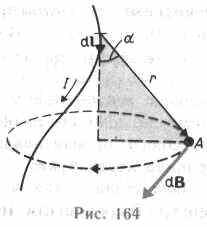 деdl — вектор, по модулю равный длине dl элемента проводника и совпадающий по
направлению с током, r — радиус-вектор, проведенный из элемента
dl проводника в точку А поля, r —
модуль радиуса-вектора г. Направление
dB перпендикулярно dl и r,
т. е. перпендикулярно плоскости, в
которой они лежат, и совпадает с
касательной к линии магнитной
индукции. Это направление может быть
найдено по правилу нахождения линий
магнитной индукции (правилу правого
винта): направление вращения головки
винта дает направление dB,
если поступательное движение винта
соответствует направлению тока в
элементе.
деdl — вектор, по модулю равный длине dl элемента проводника и совпадающий по
направлению с током, r — радиус-вектор, проведенный из элемента
dl проводника в точку А поля, r —
модуль радиуса-вектора г. Направление
dB перпендикулярно dl и r,
т. е. перпендикулярно плоскости, в
которой они лежат, и совпадает с
касательной к линии магнитной
индукции. Это направление может быть
найдено по правилу нахождения линий
магнитной индукции (правилу правого
винта): направление вращения головки
винта дает направление dB,
если поступательное движение винта
соответствует направлению тока в
элементе.
Модуль вектора dB определяется выражением
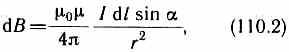
где а — угол между векторами dl и г.
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:

Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае довольно сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет довольно просто рассчитать конкретные поля. Рассмотрим два примера.
1. Магнитное поле прямого тока — тока, текущего по тонкому прямому про
в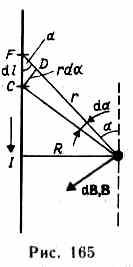 оду
бесконечной длины (рис. 165). В произвольной
точкеА, удаленной
от оси проводника на расстояние R, векторы
dB от всех элементов тока имеют одинаковое
направление, перпендикулярное плоскости
чертежа («к нам»). Поэтому сложение
векторов dB можно заменить сложением их модулей. В
качестве постоянной интегрирования
выберем угол а (угол между векторами dl и r),
выразив через него все остальные
величины. Из рис. 165 следует, что
оду
бесконечной длины (рис. 165). В произвольной
точкеА, удаленной
от оси проводника на расстояние R, векторы
dB от всех элементов тока имеют одинаковое
направление, перпендикулярное плоскости
чертежа («к нам»). Поэтому сложение
векторов dB можно заменить сложением их модулей. В
качестве постоянной интегрирования
выберем угол а (угол между векторами dl и r),
выразив через него все остальные
величины. Из рис. 165 следует, что
(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна
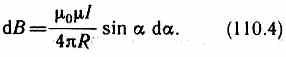
Так как угол а для всех элементов прямого тока изменяется в пределах от 0 до я, то, согласно (110.3) и (110.4),
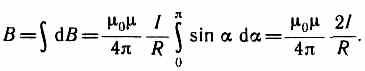
Следовательно, магнитная индукция поля прямого тока
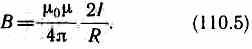
2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитное поле одинакового направления — вдоль нормали от витка.
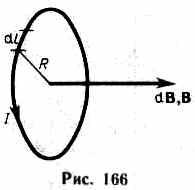
Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sin=1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),
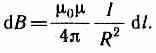
Тогда
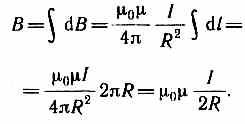
Следовательно, магнитная индукция поля в центре кругового проводника с током
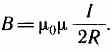
4.2. Магнитное поле в вакууме. Закон Био-Савара
Французские физики Био и Савар провели большое экспериментальное исследование магнитных полей, создаваемых токами различной формы. Было установлено следующее.
Во всех случаях магнитная индукция пропорциональна силе тока, протекающего в проводнике:
 .
.Магнитная индукция
 сложным образом зависит от конфигурации
проводника с током и расстояния от него
до точки поля.
сложным образом зависит от конфигурации
проводника с током и расстояния от него
до точки поля.
Экспериментальные
данные Био и Савара были проанализированы
математиком Лапласом. Для вычисления
магнитной индукции поля, создаваемого
элементом тока 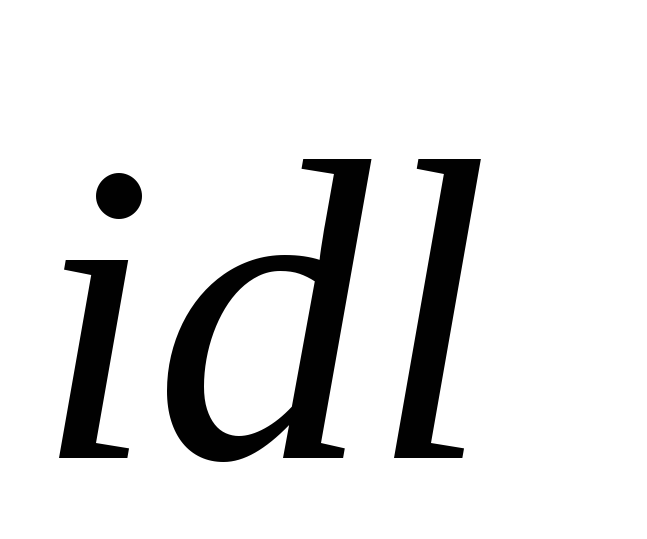 ,
им была предложена формула:
,
им была предложена формула:
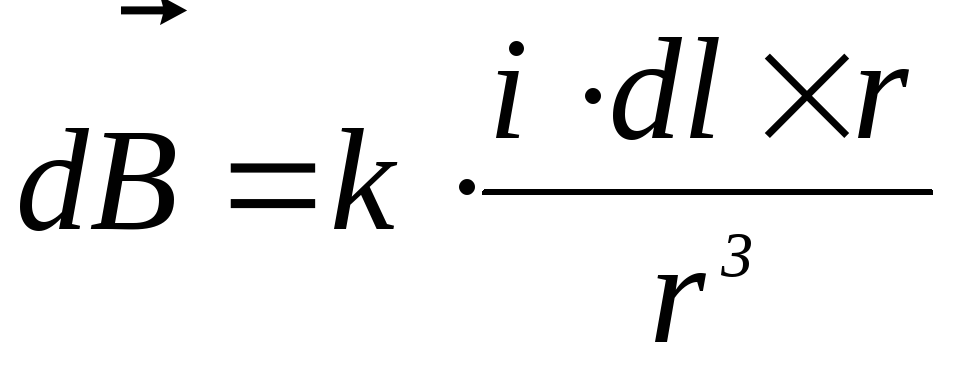 .
(4.7)
.
(4.7)
Здесь 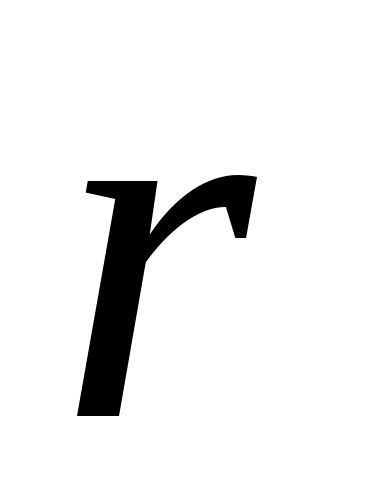 — радиус-вектор, проведенный из элемента
— радиус-вектор, проведенный из элемента в
точку, в которой вычисляется поле; k – коэффициент, зависящий от выбора
системы единиц. В системе СИ он равен:
в
точку, в которой вычисляется поле; k – коэффициент, зависящий от выбора
системы единиц. В системе СИ он равен:
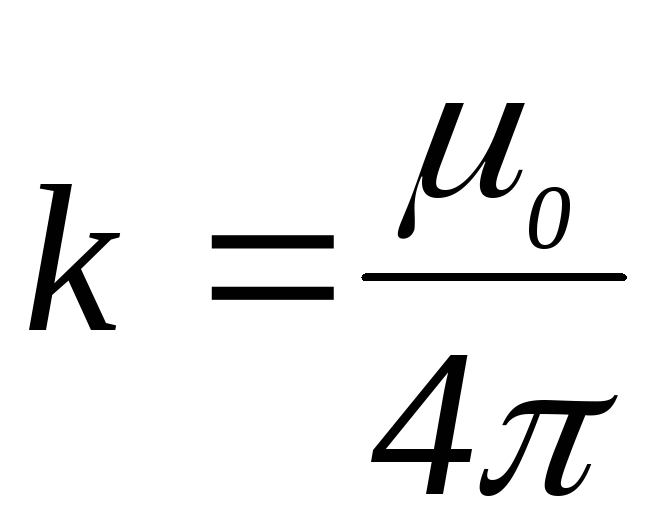 .
.
С учетом коэффициента k перепишем формулу (4.7) в виде:
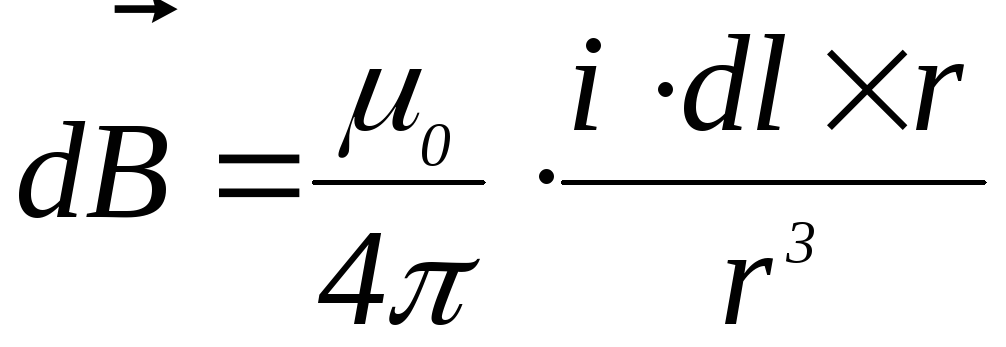 .
(4.8)
.
(4.8)
Формулы (4.7) и (4.8) носят название закона Био-Савара – Лапласа.
В
соответствии с правилами для векторного
произведения модуль вектора  равен:
равен:
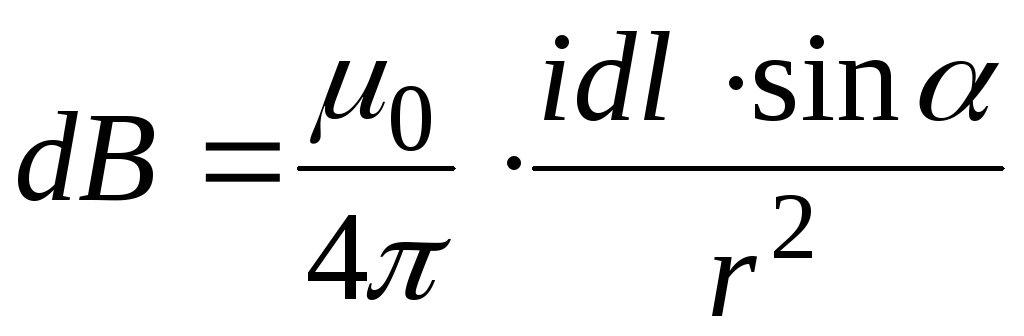 ,
(4.9)
,
(4.9)
где  —
угол между векторами
—
угол между векторами и
и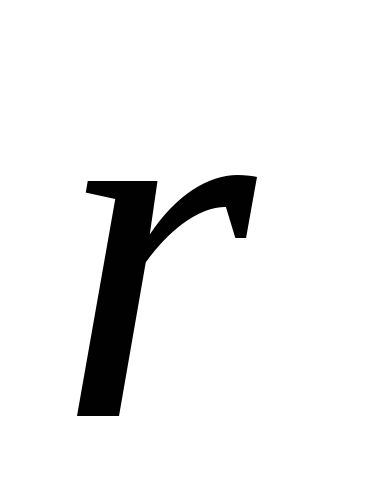 .
.
Вектор 
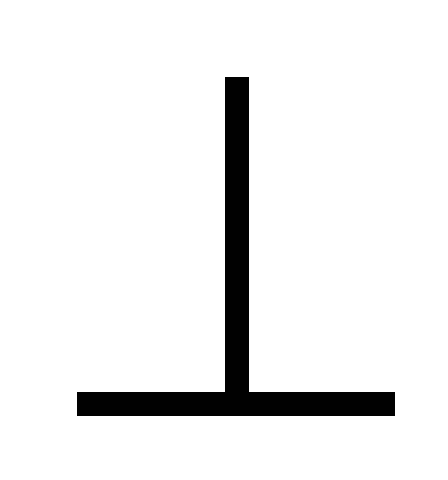 плоскости, в который лежат вектора
плоскости, в который лежат вектора и
и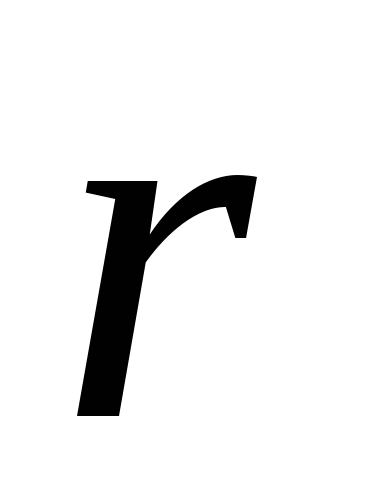 .
Его направление определяется правилами
для векторного произведения. Но существует
простое и удобное для запоминания
правило для определения направления
вектора
.
Его направление определяется правилами
для векторного произведения. Но существует
простое и удобное для запоминания
правило для определения направления
вектора (правило буравчика или правого винта).
(правило буравчика или правого винта).
При
поступательном движении винта вдоль
направления элемента тока его
поступательное движение покажет
направление вектора  .
.
Применение
принципа суперпозиции полей (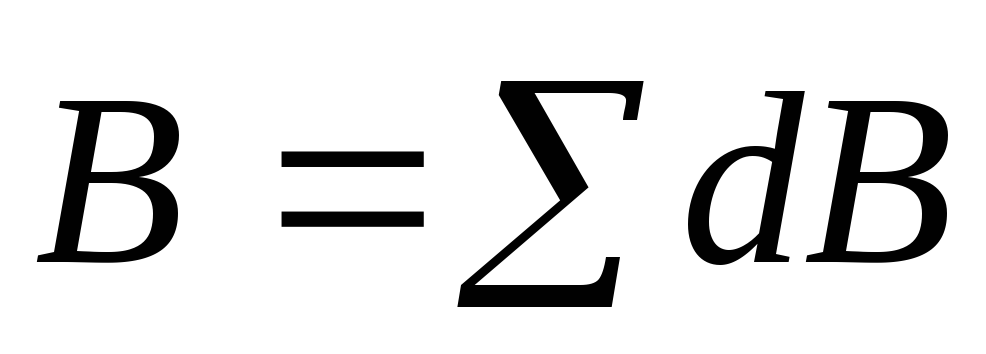 )
и закона Био-Савара-Лапласа позволяет
в принципе рассчитать магнитную индукцию
поля, создаваемого током любой формы.
Расчёт обычно сводится к вычислению
интеграла.
)
и закона Био-Савара-Лапласа позволяет
в принципе рассчитать магнитную индукцию
поля, создаваемого током любой формы.
Расчёт обычно сводится к вычислению
интеграла.
4.3. Магнитное поле прямолинейного проводника с током
Рассмотрим следующую задачу. Пусть имеется прямолинейный проводник, по которому течет ток силой i. Необходимо найти магнитную индукцию в произвольной точке A, находящейся на расстоянии x от проводника (рис. 4.3).
Выберем
произвольно элемент тока 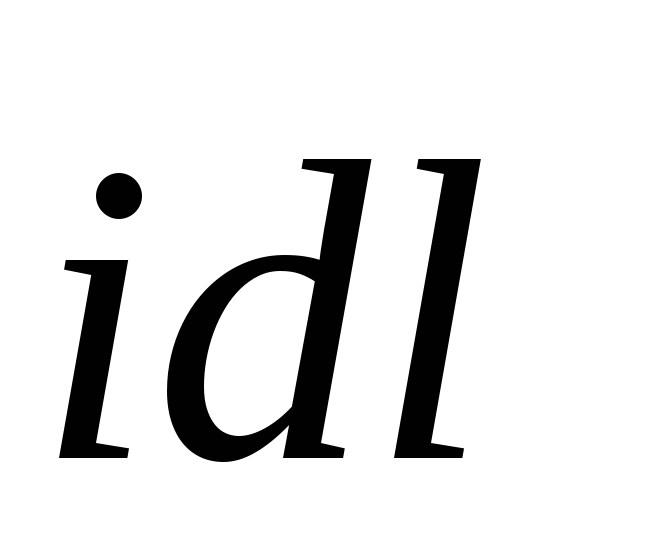 и проведём в точкуA радиус вектор
и проведём в точкуA радиус вектор 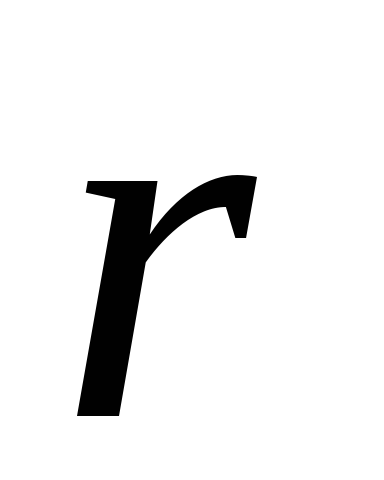 (рис.4.3). По закону Био-Савара-Лапласа
магнитная индукция
(рис.4.3). По закону Био-Савара-Лапласа
магнитная индукция создаваемая элементом тока
создаваемая элементом тока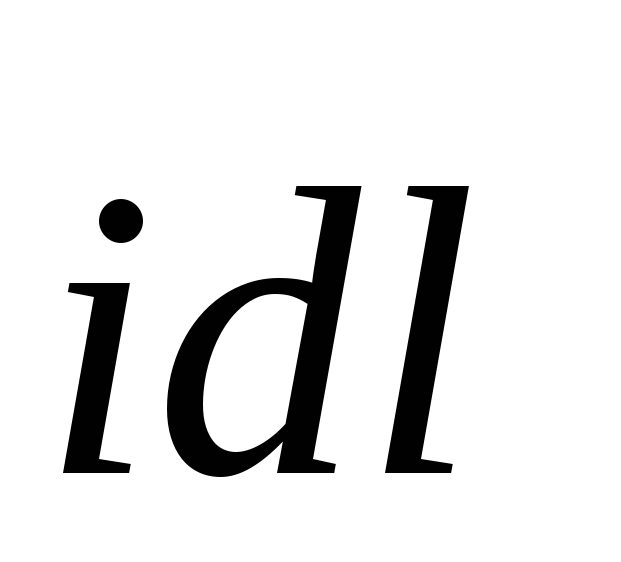 равна (по
модулю):
равна (по
модулю):
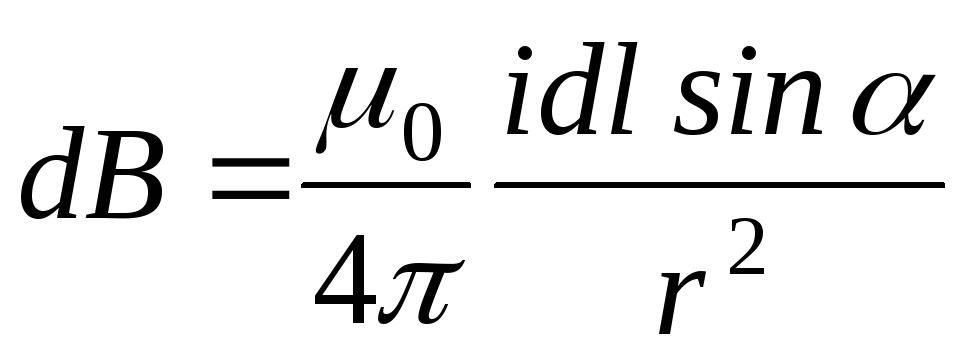 .
.  (4.10)
(4.10)
Направление
вектора  можно определить по правилу буравчика.
Отметим, что векторы
можно определить по правилу буравчика.
Отметим, что векторы от всех элементов тока направлены
одинаково (в данном случае за плоскость
чертежа). Поэтому, применяя принцип
суперпозиции, сложение векторов
от всех элементов тока направлены
одинаково (в данном случае за плоскость
чертежа). Поэтому, применяя принцип
суперпозиции, сложение векторов можно заменить сложением их модулей:
можно заменить сложением их модулей: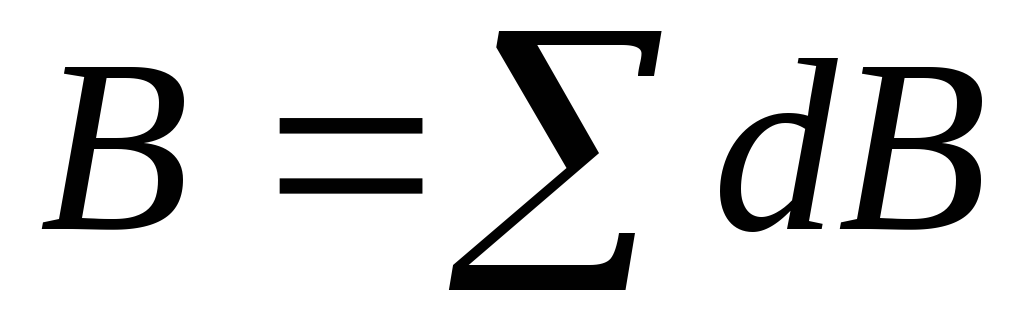 или
или
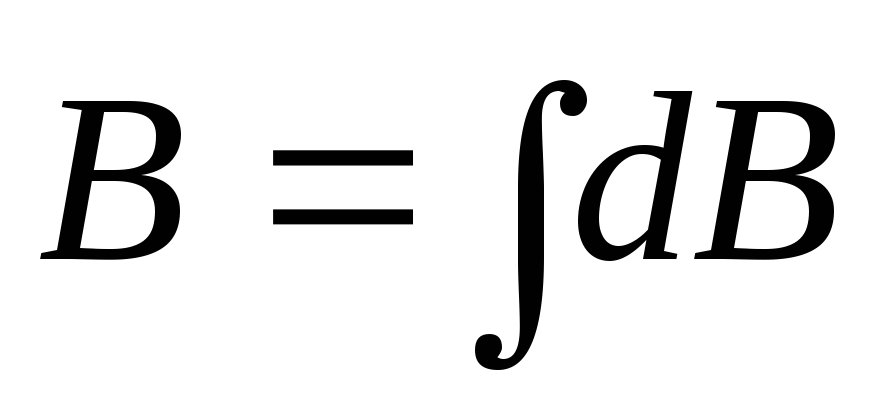
 .
(4.11)
.
(4.11)
Величины dl, r и sinα связаны между собой. Выразим r и dl через x и α. Из треугольников АВС и СDE следует:
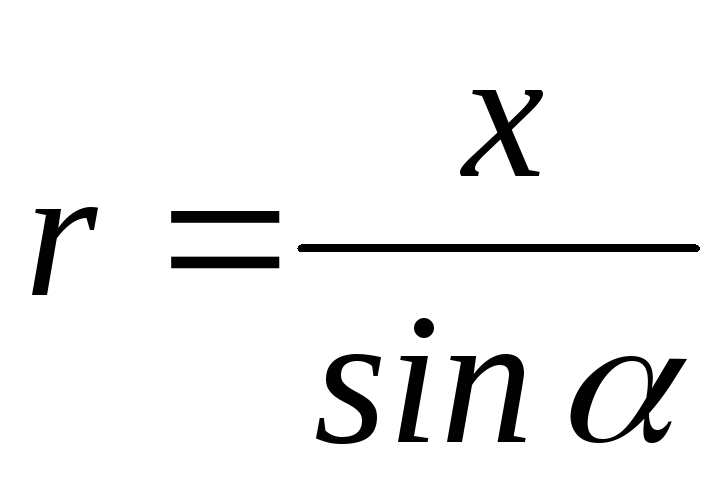 . (4.12)
. (4.12)
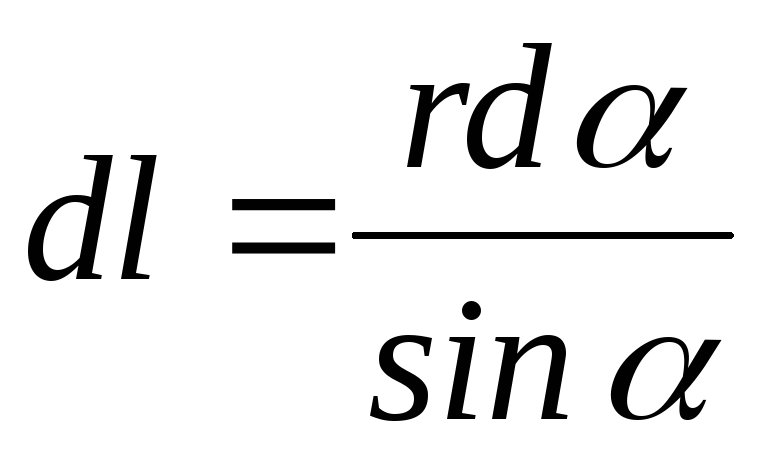 .
(4.13)
.
(4.13)
Подставим (4.12) в (4.13), получим:
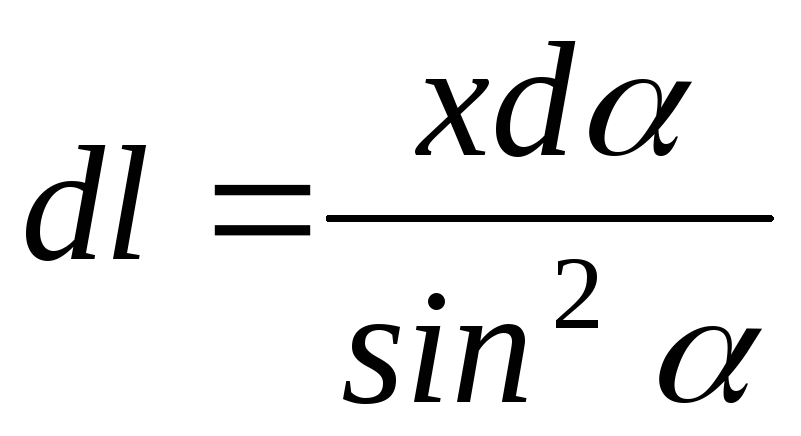 .
(4.14)
.
(4.14)
Подставим (4.14) и (4.12) в формулу (4.10):
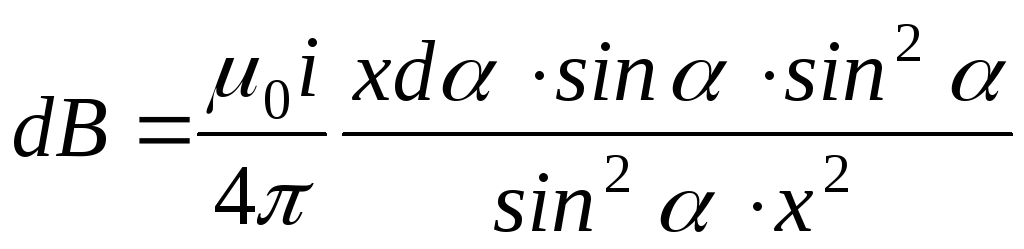 ,
,
произведём сокращения и получим:
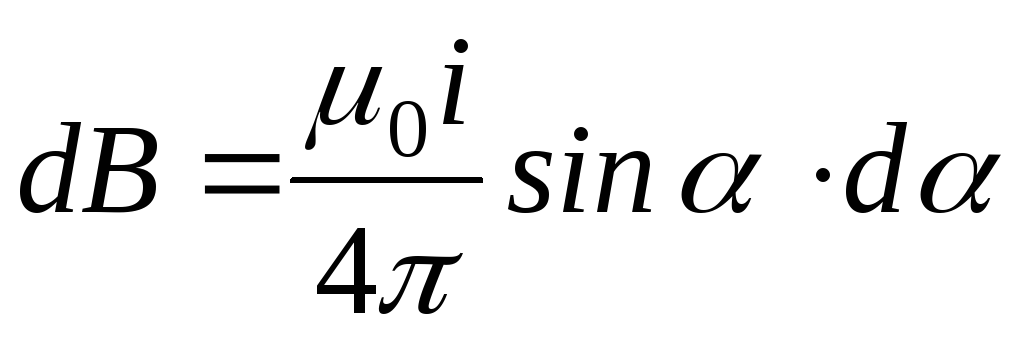 .
(4.15)
.
(4.15)
И нтегрирование
выражения (4.15) проведём для случая, когда
проводник с током имеет конечные размеры.
Тогда уголα будет изменяться от α1 до α2(рис.4.4).
нтегрирование
выражения (4.15) проведём для случая, когда
проводник с током имеет конечные размеры.
Тогда уголα будет изменяться от α1 до α2(рис.4.4).
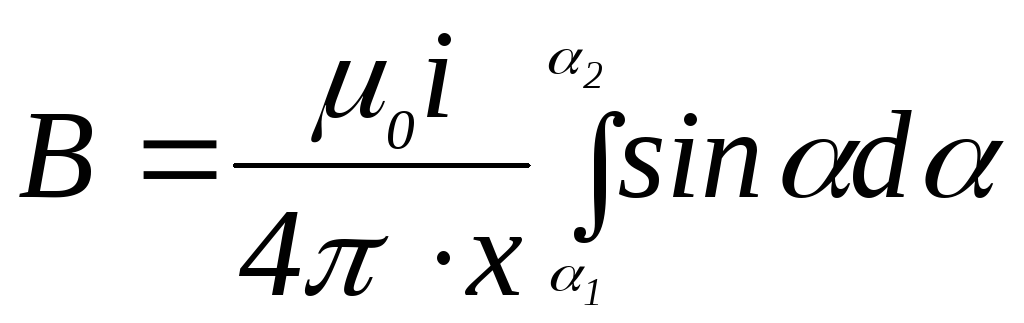 , (4.16)
, (4.16)
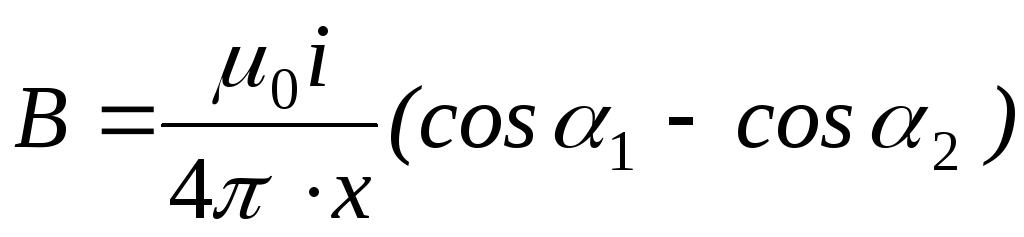 .(4.17)
.(4.17)
Если проводник с током бесконечно длинный, тогда α1=0, α2=π, и магнитная индукция выражается формулой
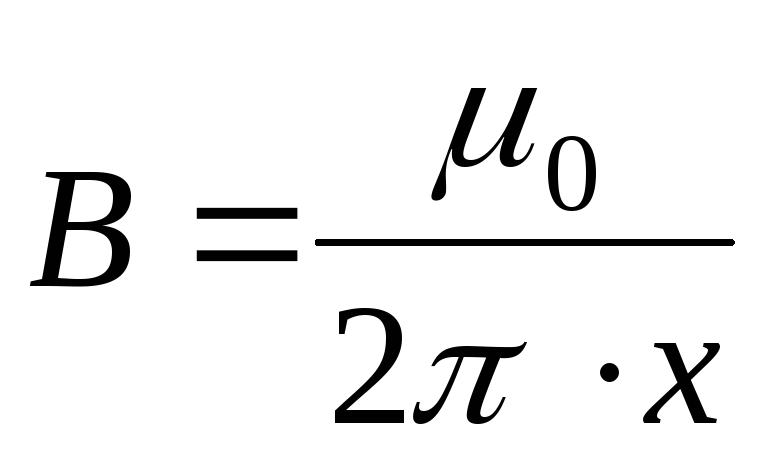 .
(4.18)
.
(4.18)
25Закон Био — Савара — Лапласа и его применение к расчету магнитного поля
Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж. Био (1774—1862) и Ф. Саваром
(1791—1841). Результаты этих опытов были обобщены выдающимся французским математиком и физиком П. Лапласом.
Закон Био — Савара — Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А (рис. 164) индукцию поля dB, записывается в виде
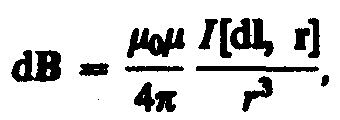 (110.1)
(110.1)
где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r—радиус-вектор, проведанный из элемента dl проводника в точку А поля, r — модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение винта соответствует направлению тока в элементе.
Модуль вектора dB определяется выражением
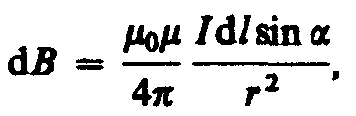 (110.2)
(110.2)
где — угол между векторами dl и r.
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
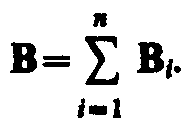 (110.3)
(110.3)
Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера.
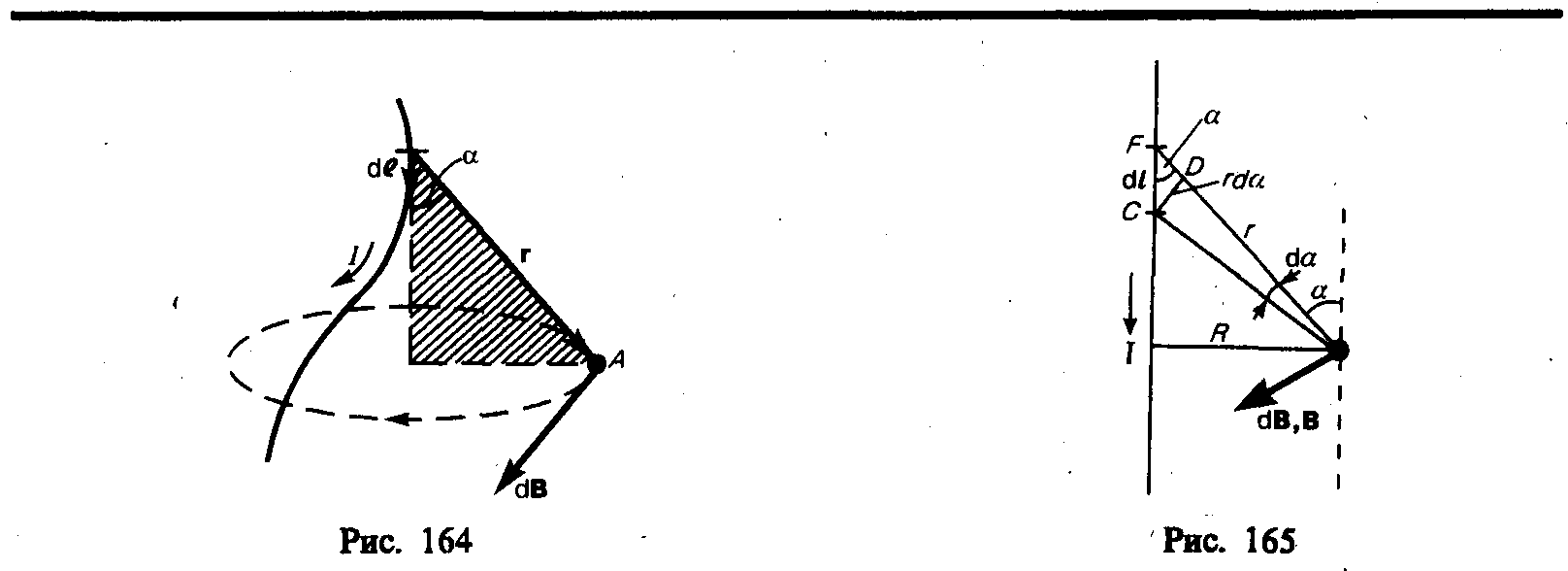
1. Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к вам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол (угол между векторами dl и r), выразив через него все остальные величины. Из рис. 165 следует, что
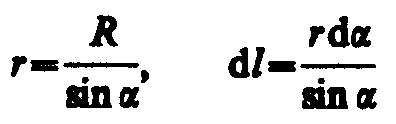
(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна
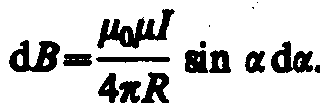 (110.4)
(110.4)
Так как угол для всех элементов прямого тока изменяется в пределах от 0 до , то, согласно (110.3) и (110.4),
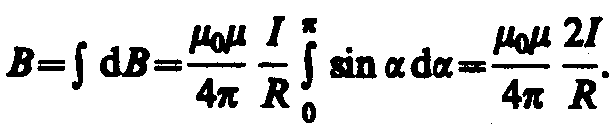
Следовательно, магнитная индукция поля прямого тока
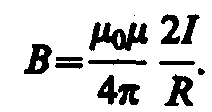 (110.5)
(110.5)
2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sin =1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),
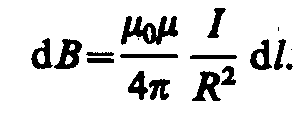
Тогда
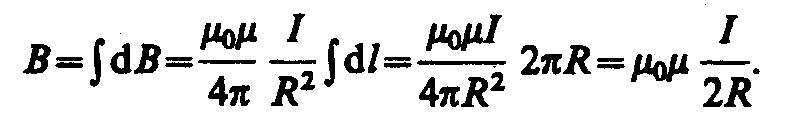
Следовательно, магнитная индукция поля в центре кругового проводника с током
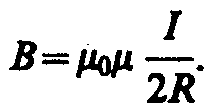



 .
. сложным образом зависит от конфигурации
проводника с током и расстояния от него
до точки поля.
сложным образом зависит от конфигурации
проводника с током и расстояния от него
до точки поля.