Первый закон кирхгофа для магнитной цепи записывается для: Законы Кирхгофа для электрической и магнитной цепи, как сделать самому, Ремонт и Строительство – Закон Киргофа. 1 и 2 закон Кирхгофа. Определение, формула — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Законы Кирхгофа для электрической и магнитной цепи, как сделать самому, Ремонт и Строительство

Для расчетов задач по электротехнике в физике есть ряд правил, часто используют первый и второй закон Кирхгофа, а также закон Ома. Немецкий ученый Густав Кирхгоф имел достижения не только в физике, но и в химии, теоретической механике, термодинамике. В электротехнике используется закономерность, которую он установил для электрической цепи, из двух соотношений. Законы Кирхгофа (также их называют правилами) описывают распределение токов в узлах и падений напряжений на элементах контура. Далее мы попытаемся объяснить простым языком, как применять соотношения Кирхгофа для решения задач.

Первый закон Кирхгофа

Определение первого закона звучит так: «Алгебраическая сума токов, протекающих через узел, равна нулю». Можно сказать немного в другой форме: «Сколько токов втекло в узел, столько же и вытекло, что говорит о постоянстве тока».

Узлом цепи называют точку соединения трех и больше ветвей. Токи в таком случае распределяются пропорционально сопротивлениям каждой ветви.

I₁=I₂+I₃

Такая форма записи справедлива для цепей постоянного тока. Если использовать первый закон Кирхгофа для цепи переменного тока, то используются мгновенные значения напряжений, обозначаются буквой İ и записывается в комплексной форме, а метод расчета остаётся прежним:

Комплексная форма учитывает и активную и реактивную составляющие.

Второй закон Кирхгофа

Если первый описывает распределение токов в ветвях, то второй закон Кирхгофа звучит так: «Сумма падений напряжений в контуре равна сумме всех ЭДС».

Простыми словами формулировка звучит так: «ЭДС, приложенное к участку цепи, распределится по элементам данной цепи пропорционально сопротивлениям, т.е. по закону Ома».

Тогда как для переменного тока это звучит так: «Сумма амплитуд комплексных ЭДС равняется сумме комплексных падений напряжений на элементах».

Z – это полное сопротивление или комплексное сопротивление, в него входит и резистивная часть и реактивная (индуктивность и ёмкость), которая зависит от частоты переменного тока (в постоянном токе есть только активное сопротивление). Ниже представлены формулы комплексного сопротивления конденсатора и индуктивности:

Вот картинка, иллюстрирующая вышесказанное:

Тогда:

Методы расчетов по первому и второму законам Кирхгофа

Давайте приступим к применению на практике теоретического материала. Чтобы правильно расставить знаки в уравнениях, нужно выбрать направление обхода контура. Посмотрите на схему:

Предлагаем выбрать направление по часовой стрелке и обозначить его на рисунке:

Штрих-пунктирной линией обозначено, как идти по контуру при составлении уравнений.

Следующий шаг – составить уравнения по законам Кирхгофа. Используем сначала второй. Знаки расставляем так: перед электродвижущей силой ставится минус, если она направлена против движения часовой стрелки (выбранное нами в предыдущем шаге направление), тогда для ЭДС направленного по часовой стрелке – ставим минус. Составляем для каждого контура с учетом знаков.

Для первого смотрим направление ЭДС, оно совпадает со штрих-пунтирной линией, ставим E1 плюс E2:

Для второго:

Для третьего:

Знаки у IR (напряжения) зависят от направлением контурных токов. Здесь правило знаков такое же, как и в предыдущем случае.

IR пишется с положительным знаком, если ток протекает в сторону направления обхода контура. А со знаком «–», если ток течет против направления обхода контура.

Направление обхода контура — это условная величина. Нужна она только для расстановки знаков в уравнениях, выбирается произвольно и на правильность расчётов не влияет. В отдельных случаях неудачно выбранное направление обхода может усложнить расчёт, но это не критично.

Рассмотрим еще одну цепь:

Здесь целых четыре источника ЭДС, но порядок расчета тот же, сначала выбираем направление для составления уравнений.

Теперь нужно составить уравнения согласно первому закону Кирхгофа. Для первого узла (слева на схеме цифра 1):

I₃ втекает, а I₁, I₄ вытекает, отсюда и знаки. Для второго:

Для третьего:

Вопрос: «Узла четыре, а уравнения всего три, почему?». Дело в том, что число уравнений первого правила Кирхгофа равно:

N_{уравнений}=n_узлов-1

Т.е. уравнений всего на 1 меньше, чем узлов, т.к. этого достаточно, чтобы описать токи во всех ветвях, советую еще раз подняться к схеме и проверить, все ли токи записаны в уравнениях.

Теперь перейдем к построению уравнений по второму правилу. Для первого контура:

Для второго контура:

Для третьего контура:

Если подставить значения реальных напряжений и сопротивлений, тогда выяснится, что первый и второй законы справедливы и выполняются. Это простые примеры, на практике приходится решать гораздо более объёмные задачи.

Вывод. Главное при расчётах с помощью первого и второго законов Кирхгофа – соблюдения правила составления уравнений, т.е. учитывать направления протекания токов и обхода контура для правильной расстановки знаков для каждого элемента цепи.

Законы Кирхгофа для магнитной цепи

В электротехнике также важны и расчёты магнитных цепей, оба закона нашли своё применение и здесь. Суть остаётся той же, но вид и величины изменяются, давайте рассмотрим этот вопрос подробнее. Сначала нужно разобраться с понятиями.

Магнитодвижущая сила (МДС) определяется произведением количества витков катушки, на ток через неё:

F=w*I

Магнитное напряжение – это произведение напряженности магнитного поля на ток, через участок, измеряется в Амперах:

U_m=H*I

Или магнитный поток через магнитное сопротивление:

U_m=Ф*R_m

L – средняя длина участка, μ_r и μ_{– относительная и абсолютная магнитная проницаемость.}

Проводя аналогии запишем первый закон Кирхгофа для магнитной цепи:

То есть сумма всех магнитных потоков через узел равна нулю. Вы заметили, что звучит почти так же, как и для электрической цепи?

Тогда второй закон Кирхгофа звучит, как «Сумма МДС в магнитном контуре равна сумме U_M

(магнитных напряжений).

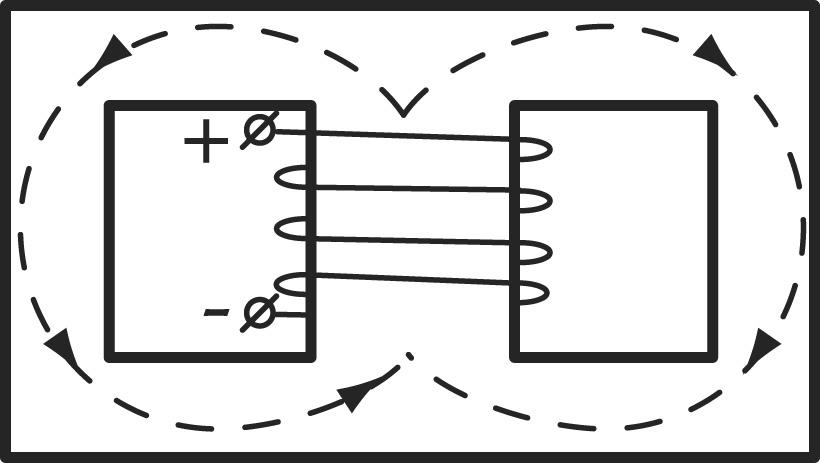
Магнитный поток равен:

Для переменного магнитного поля:

Он зависит только от напряжения на обмотке, но не от параметров магнитной цепи.

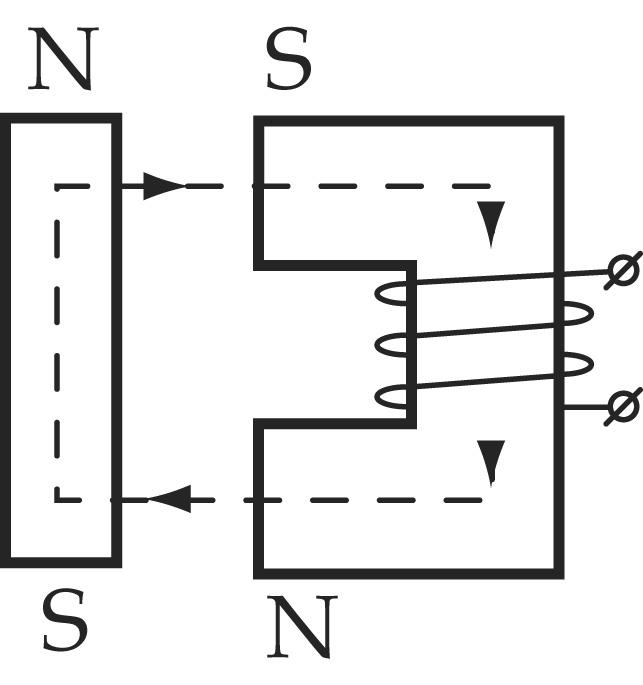
В качестве примера рассмотрим такой контур:

Тогда для ABCD получится такая формула:

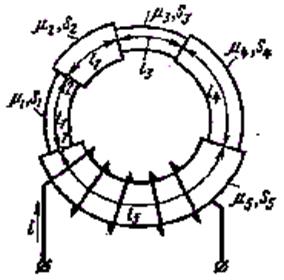
Для контуров с воздушным зазором выполняются следующие соотношения:

Сопротивление магнитопровода:

А сопротивление воздушного зазора (справа на сердечнике):

Где S — это площадь сердечника.

Чтобы полностью усвоить материал и наглядно просмотреть некоторые нюансы использования правил, рекомендуем ознакомиться с лекциями, которые предоставлены на видео:

Открытия Густава Кирхгофа внесли весомый вклад в развитие науки, в особенности электротехники. С их помощью довольно просто рассчитать любой электрический или магнитный контур, токи в нём и напряжения. Надеемся, теперь вам стали более понятны правила Кирхгофа для электрической и магнитной цепи.

Законы Кирхгофа для магнитной цепи — МегаЛекции

Первый закон. Сумма магнитных потоков Ф для узла магнитной цепи равна нулю.

∑Ф=0. (4.1)

Второй закон. Алгебраическая сумма намагничивающих сил F для замкнутого магнитного контура равна сумме магнитных напряжений U для этого контура.

∑F=∑U или

∑ I ω = ∑Н L , (4.2)

где I – ток катушки, создающей магнитный поток, А; ω – количество витков катушки, шт.; Н – напряженность магнитного поля, А/м; L – длина средней линии магнитопровода, причем условно принимается, что эта средняя линия во всех точках совпадает с линией магнитной индукции, м.

Неразветвленные цепи можно рассматривать как одну магнитную трубку, для которой магнитный поток во всех сечениях имеет одно и то же значение:

Ф = const.

Предполагается, что магнитные потоки рассеяния и утечки отсутствуют. Тогда для магнитной цепи во всех ее сечениях магнитный поток

Ф = В₁S₁ = В₂S₂= В₃S₃и т. д.

Откуда = , (4.3)

или B₁ = (4.4)

т.е. магнитные индукции в различных участках магнитной цепи обратно пропорциональны площадям поперечного сечения этих участков.

Прямая и обратная задачи расчета неразветвленной магнитной цепи

Прямая задача

Определение намагничивающей силы H по заданной магнитной индукцииВ(магнитному потокуФ) при известных конструктивных параметрах магнитной цепи и ферромагнитного материала является прямой задачей.

Порядок решения следующий:

1. по габаритным размерам магнитопровода определяют участки одинакового сечения магнитной цепи S;

2. определяют длину средней линии L по всем участкам магнитной цепи;

3. на основании (4.3) по формуле (4.4) определяют значение магнитной индукции В для каждого участка;

4. по кривым намагничивания материала (см. задание) определяют напряженность поля Н, соответствующую значению магнитной индукции В по участкам;

5. определяют значение намагничивающей силы F

F = ∑ H L

Обратная задача

Определение магнитной индукции В по заданной намагничивающей силе H при известных конструктивных параметрах магнитопровода и ферромагнитного материала является обратной задачей – определение магнитного потока Ф по заданным намагничивающим силам H.

Рекомендуемые страницы:

Магнитные цепи

Магнитной цепью называют устройство, в котором замыкается магнитный поток. Бывают разветвленные и неразветвленные.


Неразветвленная цепь	Разветвленная цепь

Кроме того, магнитные цепи бывают однородные и неоднородные. Однородные цепи изготавливают из одного материала, они имеют одинаковую площадь сечения.

Закон Ома и закон Кирхгофа для магнитных цепей

Закон Ома: магнитное напряжение на любом участке т.к..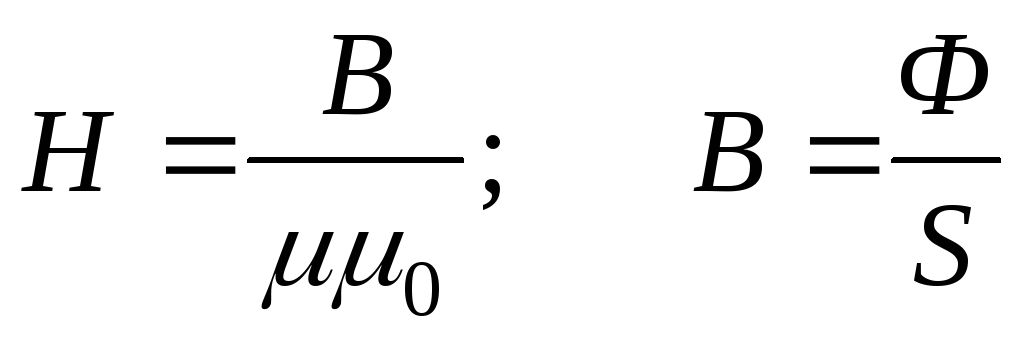

Если 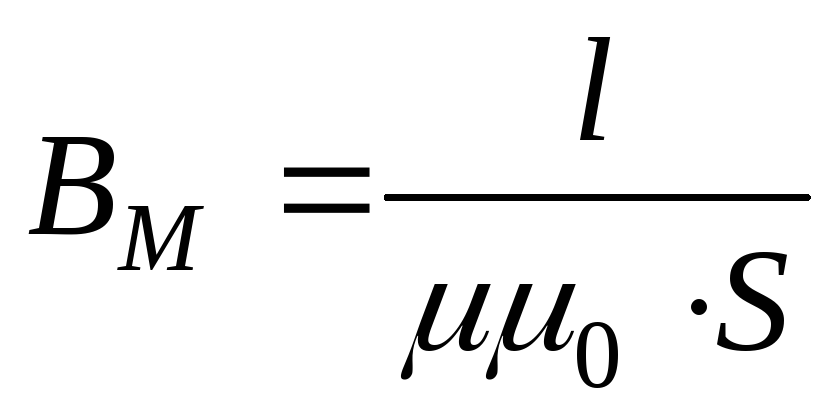, то, где— магнитное сопротивление..

Магнитный поток прямо пропорционален магнитному напряжению и обратно пропорционален магнитному сопротивлению.

Закон Кирхгофа

1 правило: алгебраическая сумма магнитных токов в точке разветвления равна 0.

2 правило: основано на законе полного тока .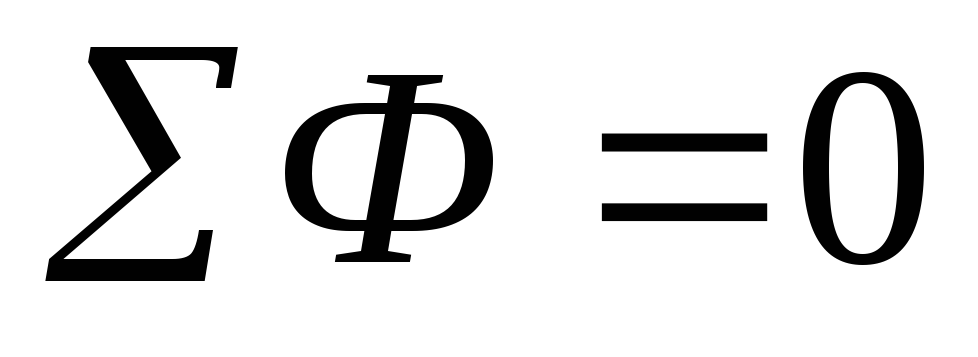

Алгебраическая сумма МДС равна алгебраической сумме магнитных напряжений на отдельных участках цепи.

Закон Ома и закон Кирхгофа для расчета магнитных цепей не используют, т.к. магнитное сопротивление, в отличие от электрического, зависит от величины магнитного напряжения.

Для расчета магнитных цепей используют закон полного тока.

Электромагниты и реле

1. Подъемная сила электромагнита

Состоит из стального сердечника С, на котором размещена катушка. Магнитный поток, созданный током катушки, замыкается по сердечнику. Якорь притягивается к сердечнику с отрывной силой:

Если 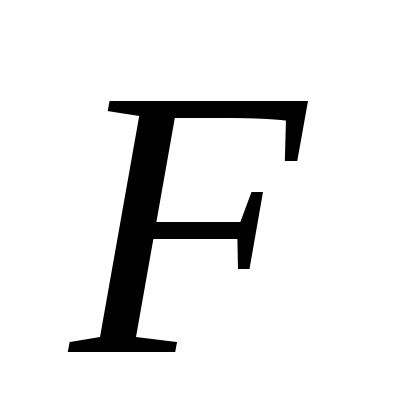выражена вкг,ВвТл,S– всм², то. Сердечник и якорь изготовлены из мягкой стали, поэтому при размыкании цепи они размагнитятся и.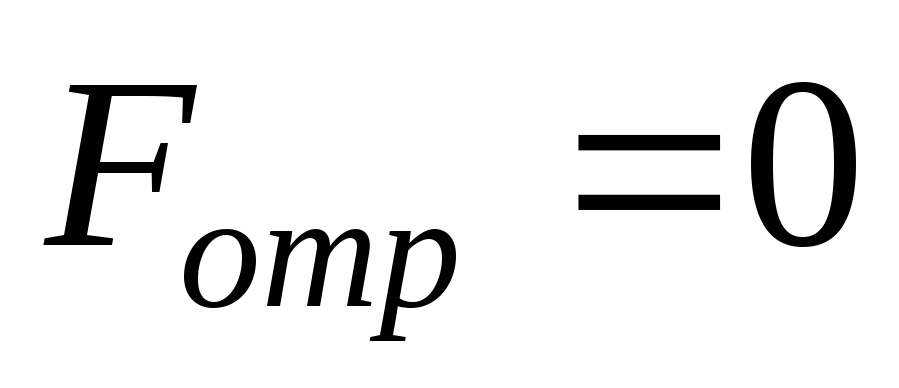

Применяются в устройствах автоматики, связи, измерительной технике.

2. Устройство и применение магнитных реле

Реле автоблокировки состоит из сердечника С, якоря, ярма с обмоткой, контактной группы, имеющей осевую О, фронтовой Ф и тыловой Т контакты.

При отсутствии тока в цепи якорь под действием противовеса отпадает, осевой контакт контактной группы касается тылового контакта.

При наличии тока – якорь притянут к сердечнику, осевой контакт касается фронтового.

Путевое реле называется нейтральным, т.к. его якорь притягивается к сердечнику независимо от направления тока.

3. Поляризованное реле

Поляризованное реле – якорь отклоняется от нейтрального положения в одну или другую сторону в зависимости от направления тока обмотки.

Порядок расчета магнитных цепей

Расчет заключается:

1. определении намагничивающей силы по заданному магнитному потоку, размерам магнитной цепи и ее материалу.

2. определении магнитного потока по заданной намагничивающей силе и размерам магнитной цепи:

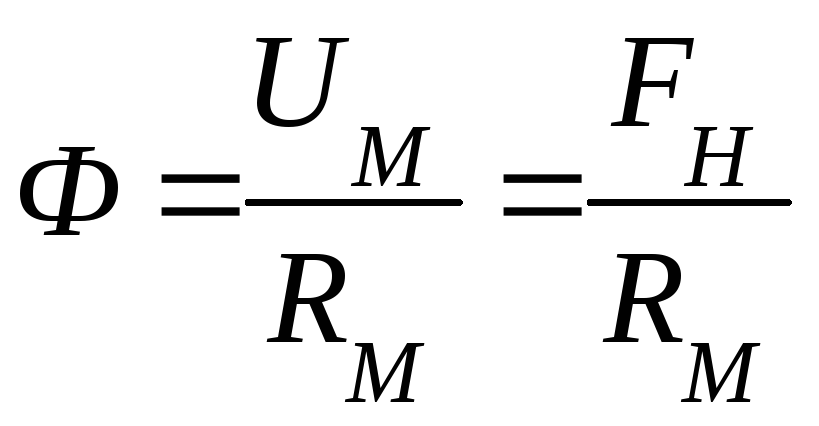
Для этого разбивают магнитную цепь на ряд однородных участков, имеющих одинаковое поперечное сечение и выполненных из одного материала.

Длины участков определяют по средней магнитной силовой линии. Для каждого участка определяют значение магнитной индукции.

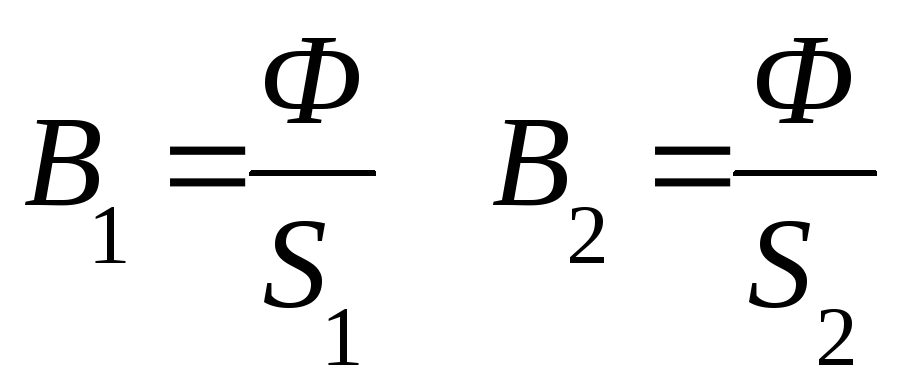и т.д.

Для каждого участка по кривым намагничивания определяют напряженность магнитного поля (по графику или в таблице): Н₁,Н₂и т.д.

Для воздушного зазора напряженность определяется по формуле:

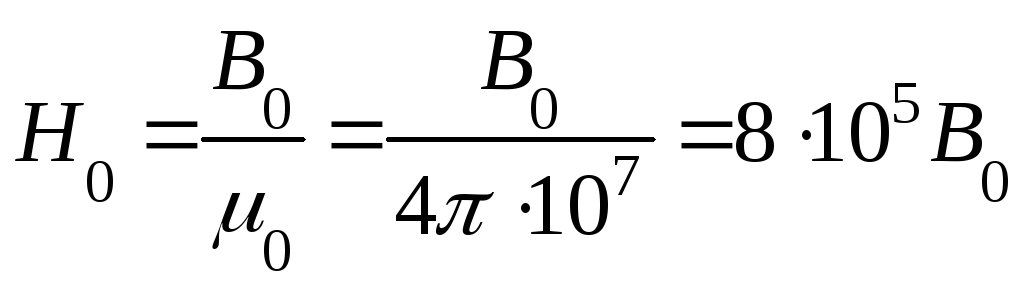
Для каждого участка определяют магнитное напряжение

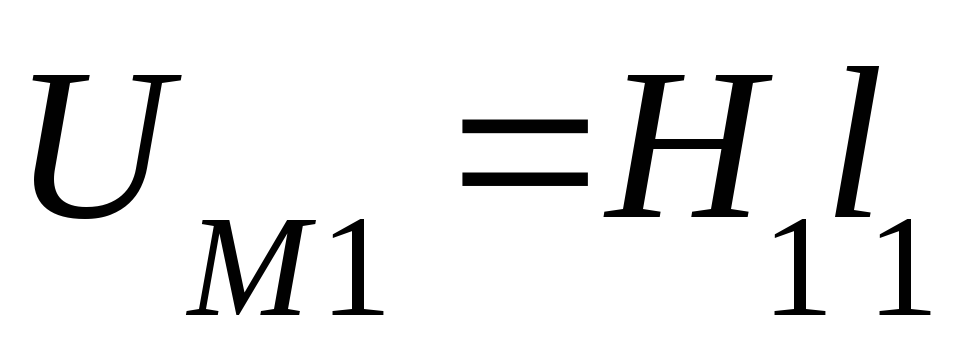
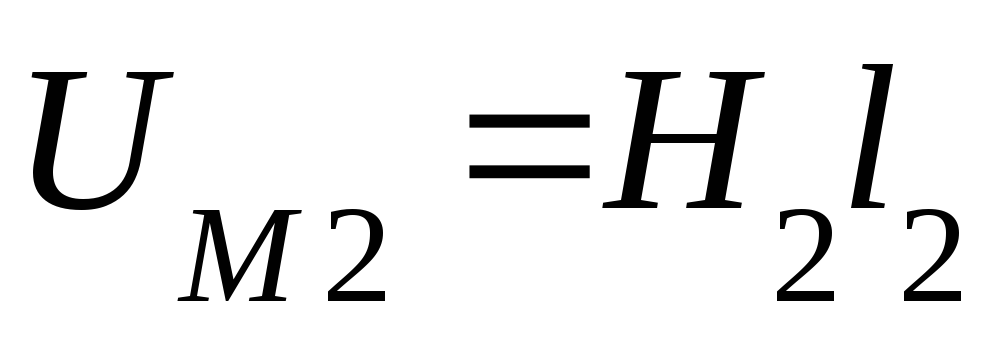
По закону полного тока определяют намагничивающую силу. Она равна:

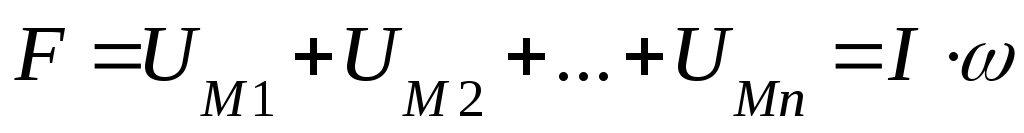
По заданному току находим число витков в катушке ей необходимое для создания требуемого магнитного потока.

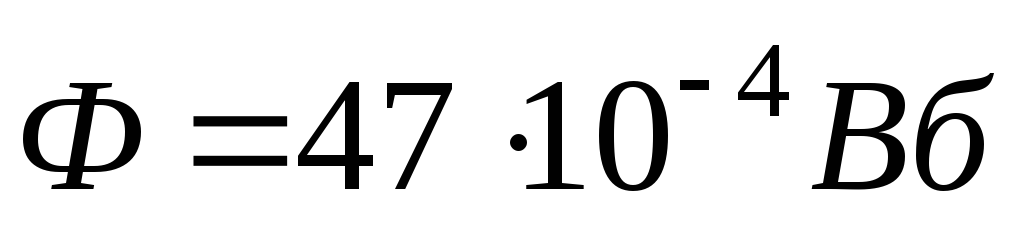
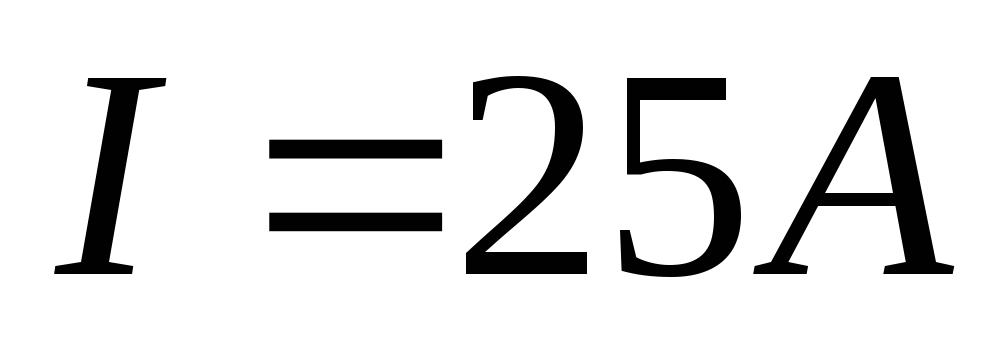
Законы Кирхгофа и Ома для магнитной цепи

ЗАКОНЫ КИРХГОФА И ОМА ДЛЯ МАГНИТНОЙ ЦЕПИ

Первый закон Кирхгофа для магнитной цепи

Алгебраическая сумма магнитных потоков, сходящихся в узле магнитной цепи равна нулю.

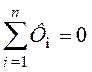(1)

Рис.1

Второй закон Кирхгофа для магнитной цепи

Для неоднородного по длине сердечника согласно рисунка для каждого участка магнитной цепи можно указать падение магнитного напряжения

(2)

и тогда намагничивающая сила обмотки с током I и числом витковwбудет определять сумму падений магнитных напряжений.

Формулировка второго закона Кирхгофа для магнитной цепи: алгебраическая сумма намагничивающих сил в замкнутом контуре магнитной цепи равна алгебраической сумме падений магнитного напряжения в том, же контуре.

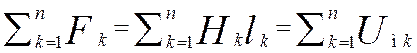(3)

Закон Ома для магнитной цепи

Рассмотренные соотношения можно использовать для расчета как линейных, так и нелинейных магнитных цепей.

Линейным участком магнитной цепи можно считать k-й участок, на котором магнитная проницаемость 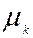может быть принята постоянной величиной.

Для любого линейного участка магнитной цепи можно записать

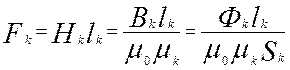(4)

k — порядковый номер участка.

Магнитный поток отличается свойством непрерывности (не имеет ни начала, ни конца) и принимает одинаковое значение для всех участков:

(5)

Поэтому, решая представленные выше уравнения относительно магнитного потока, получаем

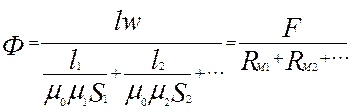(6)

где 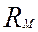—магнитное сопротивление участка сердечника (а в общем случае участка пути магнитного потока), равное

(7)

Формула (6) является математическим выражением закона Ома для магнитной цепи: магнитный поток равен намагничивающей силе, деленной на сумму магнитных сопротивлений пути магнитного потока.

Из равенства (7) видно, что магнитное сопротивление участка прямо пропорционально длине участка и обратно пропорционально площади его поперечного сечения S и магнитной проницаемости .

Если резко повысить магнитное сопротивление некоторого участка на пути магнитного потока, например, путем уменьшения его проницаемости, то можно существенно повлиять на общий магнитный поток Ф или направить магнитный поток из этого участка в другой, параллельно расположенный участок магнитной цепи. Эту возможность широко используют при построении различных типов ферромагнитных устройств автоматики.

К магнитным цепям полностью применимы все методы расчета нелинейных электрических цепей, так как и магнитные и электрические цепи подчиняются одним и тем же законам — законам Кирхгофа.

Аналогом тока в электрической цепи является поток в магнитной цепи; аналогом э.д.с. — м.д.с.; аналогом вольтамперной характеристики нелинейного сопротивления — вебер-амперная характеристика 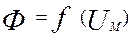участка магнитной цепи.

Законы Кирхгофа для электрических цепей. — КиберПедия

Законы Кирхгофа для электрических цепей.

Первый закон Кирхгофа.

Первый закон Кирхгофа показывает связь токов и узлов электрической цепи.

Сумма токов всех ветвей, которые сходятся в один узел электроцепи, равняется нулю.

Второй закон Кирхгофа.

Второй закон Кирхгофа описывает алгебраическую зависимость между электродинамической силой и напряжением в замкнутой электроцепи.

В любом замкнутом контуре сумма электродинамической силы равна сумме падания напряжения на сопротивлениях, относящихся к данному контуру.

Для написания формул, определяющих второй закон Кирхгофа, берут положительное значение электродинамической силы и падение напряжений, если направление на относящихся к ним отрезках контура совпадает с произвольным направлением обхода контура. А если же направление электродинамической силы и токов противоположны выбранному направлению, то эти электродинамические силы и падение напряжений берут отрицательными:

Алгоритм определения знака величины электродинамической силы и падения напряжений:

1.Выбираем направление обхода контурных цепей. Тут возможны несколько вариантов: либо по часовой стрелке, либо против часовой стрелки.

Произвольным образом выбираем направление движения токов протекающих через элементы контурных цепей.

3.Расставляем знаки для электродинамической силы и падения напряжений (не забывая о совпадении или несовпадении направления электродинамической силы с направлением движения обхода контура).

Расчет простых цепей при различных схемах соединения потребителей.

Электрическая схема простейшей электрической цепи, обеспечивающей работу осветительной аппаратуры.

Существует последовательное и параллельное соединение потребителей.

Последовательное соединение (в) — это такое соединение, при котором все потребители включены один за другим в одну линию. Поэтому по всем потребителям проходит ток одинаковой силы.

I = U/R = 12 В / З Ом = 4 А

Общее сопротивление внешней цепи равно сумме сопротивлений всех включенных потребителей.

R = R1 + R2 = 1 Ом + 2 Ом = 3 Ом

При параллельном соединении (г) к одной точке цепи подключают по одному выводу каждого потребителя, а к другой точке цепи другие выводы. В нашем примере внешняя цепь имеет два разветвления, т. е. две параллельные ветви. Оба потребителя R₁ и R₂ находятся под одинаковым напряжением U = 12 В.

Сила тока в цепи каждого потребителя зависит от величины его сопротивления:

В цепи первого потребителя I₁ = U/R₁ = 12 В / 1 Ом = 12 А

В цепи второго потребителя I₂ = U/R₂ = 12 В / 2 Ом = 6 А

Общая сила тока во внешней цепи равна сумме сил токов в цепях всех параллельно включенных потребителей:

I = I₁ +I₂ = 12+6 = 18 А

Методы расчета сложных электрических цепей.

Выбирают положительные направления токов в ветвях электрической цепи.

Составляют (k-1) независимых уравнений по первому закону Кирхгофа. Уравнения составленные по первому закону Кирхгофа гораздо проще уравнений, составленных по второму закону Кирхгофа. Поэтому их составляют максимально возможное количество.

3) Выбирают (l-k+1-m) независимых контуров электрической цепи. Контуры необходимо выбирать так, чтобы в них вошли все ветви схемы. Контуры взаимно независимы, если каждый последующий выбираемый контур содержит не менее одной новой ветви.

Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов ветвей можно использовать одиночные цифры.

Порядок расчета

Выбираются независимые контуры, и задаются произвольные направления контурных токов.
В нашем случае эти токи направлены по часовой стрелке. Направление обхода контура совпадает с направлением контурных токов. Уравнения для этих контуров имеют следующий вид:

Перегруппируем слагаемые в уравнениях:

(4)

(5)

Суммарное сопротивление данного контура называется собственным сопротивлением контура.
Собственные сопротивления контуров схемы:

, .

Сопротивление R3, принадлежащее одновременно двум контурам, называется общим сопротивлением этих контуров:

где R12 — общее сопротивление между первым и вторым контурами;
R21 — общее сопротивление между вторым и первым контурами.
E11 = E1 и E22 = E2 — контурные ЭДС.
В общем виде уравнения ( 4 ) и ( 5 ) записываются следующим образом:

Собственные сопротивления всегда имеют знак «плюс».
Общее сопротивление имеет знак «минус», если в данном сопротивлении контурные токи направлены встречно друг другу, и знак «плюс», если контурные токи в общем сопротивлении совпадают по направлению.
Решая уравнения ( 4 ) и ( 5 ) совместно, определим контурные токи I11 и I22, затем от контурных токов переходим к токам в ветвях.
Ветви схемы, по которым протекает один контурный ток, называются внешними, а ветви, по которым протекают несколько контурных токов, называются общими. Ток во внешней ветви совпадает по величине и по направлению c контурным. Ток в общей ветви равен алгебраической сумме контурных токов, протекающих в этой ветви.

Магнитная цепь и ее расчет.

Магнитная цепь (МЦ) — это устройство из ферромагнитных сердечников с воздушными зазорами или без них, по которым замыкается магнитный поток. Применение ферромагнетиков имеет целью получение наименьшего магнитного сопротивления, при котором требуется наименьшая МДС для получения нужной магнитной индукции или магнитного потока.

Простейшая магнитная цепь — это сердечник кольцевой катушки. Применяются магнитные цепи неразветвленные и разветвленные, отдельные участки которых выполняются из одного или из разных материалов. Расчет магнитной цепи сводится к определению МДС по заданному магнитному потоку, размерам цепи и ее материалам. Для расчета цепь делят на участкиl₁_, l₂и т. д. с одинаковым сечением по всей длине участка, т. е. с однородным полем, определяют магнитную индукциюВ= на каждом из них и по кривым намагничивания находят соответствующие напряженности магнитного поля. Магнитная цепь (MЦ) состоит из двух основных элементов: — источника магнитной энергии; — магнитопровода.

Источник магнитной энергии в реальных МЦ бывает двух видов:

— постоянный магнит; — электромагнит.

Пример расчета неразветвленных магнитных цепей.

Рассмотрим расчет магнитной цепи, размеры и и материалы которой, а также количество и расположение обмоток с токами известны. Расчет проводится с использованием закона полного тока. Такой расчет предусматривает решение одной из двух задач: прямой задачи и обратной задачи.

Прямая задачарасчета магнитной цепи заключается в том, что задан магнитный поток Ф и требуется определить магнитодвижущую силу F. Если одна из величин I или W задана, то определяется только другая величина.

Законы Кирхгофа для электрических цепей.

Первый закон Кирхгофа.

7. Расчет разветвленных магнитных цепей на основе закона Кирхгофа.

Первый закон Кирхгофа.

Первый закон Кирхгофа говорит о том, что в любой момент времени количество электрических зарядов, направленных к узлу, равно количеству зарядов, направленных от узла, откуда следует, что электрический заряд в узле не накапливается. Поэтому алгебраическая сумма токов в ветвях, сходящихся в узле электрической цепи, равна нулю:

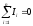(1.18), где n — число ветвей, сходящихся в узле.

До написания уравнения (1.18) необходимо задать условные положительные направления токов в ветвях, обозначив эти направления на схеме стрелками. В уравнении (1.18) токи, направленные к узлу, записывают с одним знаком (например, с плюсом), а токи, направленные от узла, с противоположным знаком (с минусом).

Второй закон Кирхгофа.

Второй закон Кирхгофа отражает положение о том, что изменение потенциала во всех элементах контура в сумме равно нулю. Из этого следует такая формулировка второго закона Кирхгофа: в любом контуре электрической цепи постоянного тока алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех элементах этого контура:

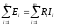(1.19). Где n – число ЭДС в контуре; m – число элементов с сопротивлением 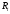в контуре.

При составлении уравнений по второму закону Кирхгофа предварительно задают условные положительные направления токов во всех ветвях электрической цепи и для каждого контура выбирают направление обхода. Если при этом направление ЭДС совпадает с направлением обхода контура, то такую ЭДС берут со знаком плюс, если не совпадает — со знаком минус. Падения напряжений в правой части уравнения (1.19) берут со знаком плюс, если положительное направление тока в данном элементе цепи совпадает с направлением обхода контура, если не совпадает — со знаком минус.

Расчет разветвленных магнитных цепей основан на совместном применении первого и второго законов Кирхгофа для магнитных цепей. Последовательность решения задач данного типа в целом соответствует рассмотренному выше алгоритму решения “прямой” задачи для неразветвленной цепи. При этом для определения магнитных потоков на участках магнитопровода, для которых магнитная напряженность известна или может быть вычислена на основании второго закона Кирхгофа. В остальных случаях неизвестные магнитные потоки определяются на основании первого закона Кирхгофа для магнитных цепей.

В качестве примера анализа разветвленной магнитной цепи при заданных геометрии магнитной цепи на рис. 2 и характеристике 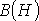ферромагнитного сердечника определим НС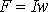, необходимую для создания в воздушном зазоре индукции.

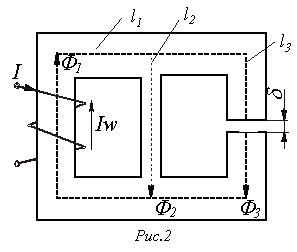
Алгоритм решения задачи следующий:

1. Задаем положительные направления магнитных потоков в стержнях магнитопровода (см. рис. 2).

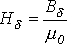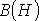2. Определяем напряженность в воздушном зазоре и по зависимостидля— значение.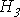

3. По второму закону Кирхгофа для правого контура можно записать

откуда находим 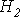и по зависимости—.

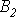4. В соответствии с первым законом Кирхгофа

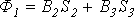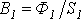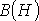Тогда , и по зависимостиопределяем.

5. В соответствии со вторым законом Кирхгофа для искомой НС имеет место уравнение

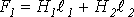Правила Кирхгофа — Википедия

Пра́вила Кирхго́фа (часто в литературе ошибочно называются Зако́нами Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока^[1]. Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей. Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений, и соответственно, найти значения токов на всех ветвях цепи и все межузловые напряжения.

Сформулированы Густавом Кирхгофом в 1845 году^[2].

Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.

Формулировка правил

Определения

Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют участок электрической цепи с одним и тем же током, например, на рис. отрезок, обозначенный R₁, I₁ есть ветвь. Узлом называют точку соединения трех и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи. Термин замкнутый путь означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.

В терминах данных определений правила Кирхгофа формулируются следующим образом.

Первое правило

Сколько тока втекает в узел, столько из него и вытекает.
i₂ + i₃ = i₁ + i₄

Первое правило Кирхгофа гласит, что алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла.

∑j=1nIj=0.{\displaystyle \sum \limits _{j=1}^{n}I_{j}=0.}

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.

Второе правило

Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

для постоянных напряжений ∑k=1nEk=∑k=1mUk=∑k=1mRkIk;{\displaystyle \sum _{k=1}^{n}E_{k}=\sum _{k=1}^{m}U_{k}=\sum _{k=1}^{m}R_{k}I_{k};}

для переменных напряжений ∑k=1nek=∑k=1muk=∑k=1mRkik+∑k=1muLk+∑k=1muCk.{\displaystyle \sum _{k=1}^{n}e_{k}=\sum _{k=1}^{m}u_{k}=\sum _{k=1}^{m}R_{k}i_{k}+\sum _{k=1}^{m}u_{L\,k}+\sum _{k=1}^{m}u_{C\,k}.}

Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.

Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).

Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.

Особенности составления уравнений для расчёта токов и напряжений

Если цепь содержит p{\displaystyle p} узлов, то она описывается p−1{\displaystyle p-1} уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.

Если цепь содержит m{\displaystyle m} ветвей, из которых содержат источники тока ветви в количестве mi{\displaystyle m_{i}}, то она описывается m−mi−(p−1){\displaystyle m-m_{i}-(p-1)} уравнениями напряжений.

Правила Кирхгофа, записанные для p−1{\displaystyle p-1} узлов или m−(p−1){\displaystyle m-(p-1)} контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
Перед тем, как составить уравнения, нужно произвольно выбрать:
- положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими, и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
- положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
При записи линейно независимых уравнений по второму правилу Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).
В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.

Пример

$m-(p-1)$

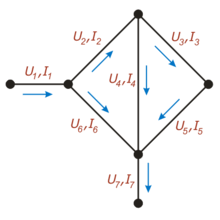На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»)

Количество узлов: 3.

p−1=2{\displaystyle p-1=2}

Количество ветвей (в замкнутых контурах): 4. Количество ветвей, содержащих источник тока: 0.

m−mi−(p−1)=2{\displaystyle m-m_{i}-(p-1)=2}

Количество контуров: 2.

Для приведённой на рисунке цепи, в соответствии с первым правилом, выполняются следующие соотношения:

{I1−I2−I6=0I2−I4−I3=0{\displaystyle {\begin{cases}I_{1}-I_{2}-I_{6}=0\\I_{2}-I_{4}-I_{3}=0\end{cases}}}

Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например, здесь токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.

Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов.

В соответствии со вторым правилом, справедливы соотношения:

{U2+U4−U6=0U3+U5−U4=0{\displaystyle {\begin{cases}U_{2}+U_{4}-U_{6}=0\\U_{3}+U_{5}-U_{4}=0\end{cases}}}

Полученные системы уравнений полностью описывают анализируемую цепь, и их решения определяют все токи и все напряжения ветвей. Такой подход к анализу цепи принято называть методом узловых потенциалов.

О значении для электротехники

Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).

Закон излучения Кирхгофа

Закон излучения Кирхгофа гласит — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.

Закон Кирхгофа в химии

Закон Кирхгофа гласит — температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции.

Примечания

Литература

Матвеев А. Н. Электричество и магнетизм : учебное пособие. — М.: Высшая школа, 1983. — 463 с.
Калашников С. Г. Электричество : учебное пособие. — М.: Физматлит, 2003. — 625 с.
Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М.: Гардарики, 2007.
Герасимов В. Г., Кузнецов Э. В., Николаева О. В. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — М.: Энергоатомиздат, 1996. — 288 с. — ISBN 5-283-05005-X.