Векторный анализ закона Био – Савара – Лапласа
Векторный анализ закона
Био – Савара — Лапласа
Магнитное поле проводника с током в электродинамике определяется законом Био – Савара – Лапласа.
Этот закон оперирует векторами, направление которых не совпадает с векторами, наблюдаемыми в эксперименте. Тройка векторов, получаемая из этой формулы, и тройка векторов, наблюдаемая в эксперименте, различны.
Это произошло потому, что существующая физическая модель электрического тока не позволяет правильно направить вектора напряженностей физических полей.
Векторный анализ закона Био – Савара – Лапласа показал, что в эксперименте направление электрического и магнитного вектора лежат в разных плоскостях (перекрещиваются).
Вектора, полученные из закона Био – Савара – Лапласа, пересекаются.
Они образуют тройку векторов, не совпадающую с тройкой векторов, наблюдаемой в
эксперименте.
Эмпирическое правило правого винта (буравчика) в электродинамике определяет направление магнитного поля проводника с током, которое не совпадает с направлением магнитного поля, полученного из закона Био – Савара — Лапласа.
«Головка винта, ввинчиваемого по направлению электрического тока, вращается в направлении линий магнитной индукции».[1]
Правило правого винта (буравчика) предполагает, что вектора перекрещиваются (рис.2), т.е. они не имеют общего начала.
Закон Био – Савара – Лапласа описывает пересекающиеся вектора (рис.8.1), которые имеют общее начало.
«Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж. Био (1774 — 1862) и Ф. Саваром (1791 — 1841). Результаты этих опытов были обобщены выдающимся французским математиком и физиком П. Лапласом.
Закон Био — Савара — Лапласа для проводника с током , элемент которого создает в некоторой точке А (рис. 1) индукцию поля , записывается в виде
, (1)
где — вектор, по модулю равный длине элемента проводника и совпадающий по направлению с током,
— радиус — вектор, проведенный из элемента проводника в точку А поля,
— модуль радиуса — вектора .
Направление перпендикулярно и , т.е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной
Из эксперимента следует вывод, что тройка векторов перекрещивается. Из формулы (7) следует другой вывод: тройка векторов имеет общее начало, т.е. они пересекается.
Рис. 1. Тройка векторов, соответствующая закону Био – Савара — Лапласа.
Перекрещивающиеся вектора (рис.2) не могут быть приведены к общему началу (рис.1), поэтому основная формула закона Био – Савара – Лапласа, вектора которой имеют общее начало, физически не корректна.
Покажем это. На (рис. 1.) показана правая тройка векторов , и , построенная в соответствии с аксиомами векторной алгебры по формуле (1).
В векторной алгебре есть несколько условий векторного произведения векторов и , результатом которого является вектор .
1. Вектор ортогонален векторам и .
2. Если и не
коллинеарные, то векторы ,
и образуют
правую тройку векторов.
Сравним теоретическую тройку векторов, получаемых из закона Био – Савара – Лапласа (рис. 1), с тройкой векторов, наблюдаемой в реальном физическом эксперименте (рис. 6.2).
Рис. 2. Тройка векторов, наблюдаемая в физическом эксперименте.
Тройки векторов на рис. 1 и рис. 2 не совпадают.
На (рис. 1) вектор имеет точку приложения .
На (рис. 2) — точку приложения .
На (рис.1) вектор перпендикулярен касательной, а на (рис.2) совпадает с ней.
Очевидно, что вектора, выведенные из закона Био — Савара — Лапласа (рис.1), не соответствуют векторам, наблюдаемым в реальном физическом эксперименте (рис. 2).
Рассмотрим возможность согласования теоретической тройки векторов и экспериментальной тройки векторов.
Для этого рассмотрим возможность перенесения начала вектора из точки О в точку А.
В соответствии с аксиомами векторной алгебры точку
приложения вектора без
изменения можно переносить только вдоль линии ее действия.
Есть теорема из статики в отношении вектора силы:
«действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела». [2]
Вектор можно перенести и параллельно его точке приложения, как это требуется для соответствия теоретического закона Био — Савара — Лапласа физическому эксперименту, но при этом появляется момент этого вектора относительно новой точки приложения. Это также удобно показать на примере теоремы из статики:
«Силу, приложенную к абсолютно твердому телу, можно, не изменяя оказываемого ею действия, переносить из данной точки в любую другую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда сила переносится». [2]
Рис. 3. Перенос точки приложения вектора из точки в точку в соответствии с аксиомами векторной алгебры.
Корректный перенос вектора из точки в точку возможен
только в соответствии с аксиомами векторной алгебры. В этом случае необходимо
добавить момент вектора относительно
точки А.
В этом случае необходимо
добавить момент вектора относительно
точки А.
Для переноса начала вектора нужно добавить пару векторов и , равных по модулю в точку А (рис. 3).
Добавление пары векторов и происходит в соответствии с аксиомами векторной алгебры и не изменяет действия вектора . Поскольку , мы можем в точке вместо вектора поместить вектор , а пару векторов и заменить моментом этих векторов относительно точки — вектором магнитного момента (рис.4).
На рис. 4. показаны вектора, выведенные из формулы (1), выражающей закон Био — Савара — Лапласа, в соответствии с аксиомами векторной алгебры.
Как видно на (рис.4), в законе Био — Савара — Лапласа, для его соответствия физическому эксперименту, должен быть добавлен вектор магнитного момента .
Рис. 4. Перенос вектора из точки в точку в соответствии с аксиомами векторной алгебры.
В результате векторного анализа закона Био — Савара —
Лапласа были выявлены некоторые проблемы электродинамики.
1. Для соответствия экспериментально наблюдаемым векторам, в формулу Био — Савара – Лапласа нужно добавить момент .
Этого нельзя сделать, поскольку в эксперименте этого момента не наблюдается.
Из векторного анализа следует, что вектора, построенные по закону Био — Савара – Лапласа, не совпадают с векторами, наблюдаемыми в эксперименте.
Вывод: Теория электрического тока не соответствует экспериментально наблюдаемому физическому явлению.
Литература
1. Трофимова Т. И. Курс Физики. «Высшая школа». М.,1997.
2. Тарг С.М. Краткий курс теоретической механики. М., «Высшая школа». 1995.
3. Дрюков В.М. О чём молчат физики. Тула, 2004.
4. http://www.sciteclibrary.ru/rus/avtors/d.html
5. http://drjukow.narod.ru/
6. Дрюков В.М. Физика. Дополнительные материалы. Тула изд. ООО Аквариус. 2021
Закон Био — Савара — Лапласа
Био, Савар и Лаплас установили закон, который позволяет вычислить магнитную ин дукцию поля, созданного элементом тока Id на расстоянии от него:
dB = , (5)
|
Закон Био — Савара — Лапласа в векторной форме имеет вид: d=. (6)
Закон Био — Савара — Лапласа позволяет вычислить магнитную индукцию поля любых систем токов, используя принцип суперпозиции магнитных поля = . (7)
(7)
Применим закон Био — Савара — Лапласа и принцип суперпозиции (7) к расчету магнит ных полей следующих токов:
1. Поле поямого тока:
I
Рис. 4 | Из рис. 4 с учетом (6) находим, что d плоскости, в которой лежат d и ; далее можно найти ,откуда, принимая во внимание, что получаем . интегрируя последнее равенство, получаем: |
(8)
Для бесконечно длинного проводника , и из (8) следует, что
(9)
C учетом (4) и (9) cила взаимодействия двух бесконечно длинных тонких и параллельных проводников . (10)
Пусть I1 = I2 = I, r0 = 1м, l = 1м, F = Н, тогда I = 1 А. Это было строгое определение единицы силы тока — ампера.
2. Поле кругового тока
Можно показать, что магнитная индукция поля, созданного круговым током радиуса R, на расстоянии r0 вдоль перпендикуляра, восстановленного из центра контура, (см. рис.5), будет (11)
В частности, в центре кругового тока ,
|
Для плоской катушки, состоящей из N, витков магнитная индукция на оси катушки
. (13)
При больших расстояниях от контура, (рис. 5), т. е. при r0 >> R из (11) получим
(14)
Поможем написать любую работу на аналогичную тему
Реферат
Закон Био — Савара — Лапласа
От 250 руб
Контрольная работа
Закон Био — Савара — Лапласа
От 250 руб
Курсовая работа
Закон Био — Савара — Лапласа
От 700 руб
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимостьУкажите закон Био-Савара и запишите этот закон в векторной форме.

- Курс
- NCERT
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8 900 03 Класс 7
- Класс 6
- NCERT
- IIT JEE
- Экзамен
- JEE MAINS
- JEE ADVANCED
- X BOARDS
- XII BOARDS
- NEET
- Neet Предыдущий год (по годам)
- Физика Предыдущий год
- Химия Предыдущий год
- Биология Предыдущий год
- Нет Все образцы работ
- Образцы работ Биология
- Образцы работ Физика
- Образцы работ Химия 900 08
- Скачать PDF-файлы
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8
- Класс 7
- Класс 6
- Экзаменационный уголок
- Онлайн-класс
- Викторина
- Задать вопрос в Whatsapp
- Поиск Doubtnut
- Английский словарь
- Toppers Talk
- Блог
- Скачать
- Получить приложение
Вопрос
Обновлено: 26/04/2023PRADEEP-МАГНИТНЫЙ ЭФФЕКТ ТОКА И МАГНИТИЗМА-Конкурс Фокус (Множественный выбор вопросов)
3 видеоРЕКЛАМА
Текст Решение
Решение
Закон Био-Савара гласит, что индукция магнитного поля в точке, вызванная током I в элементе длиной dl на расстоянии r от элемента, равнадБ=μ04πIdlsinθ р2
d→B=μ04πI(d→l×→r)r3
Аб Падхай каро бина адс ке
Харидо Д. Н. Про и дехо сари видео бина киси ад ки рукаават ке!
Н. Про и дехо сари видео бина киси ад ки рукаават ке!
Видео по теме
Сформулируйте закон Био-Савара и запишите его в векторной форме.
157408994
07:30
Государственный биот — закон Савара.
181219169
Текст Решение
Состояние Закон Био-Савара.
427230841
05:58
Государственный закон Био-Савара.
427235164
05:58
Сформулируйте и объясните закон Био-Савара.
643061471
05:47
Запишите закон Био-Савара и запишите его в векторной форме.
643061472
02:43
Сформулируйте закон Био-Савара и напишите его уравнение.
643138965
04:12
Закон Био-Савара
643446339
47:29
Закон Био-Савара 90 123
643454849
01:01:57
Запишите закон Био-Савара в векторной форме.
643856312
02:23
Укажите и запишите математическую форму закона Био-Савара с соответствующей цифрой.
643964442
04:44
Запишите закон Био-Савара в векторной форме.
644268014
01:55
Напишите выражение для закона Био-Савара.
645801551
03:44
Напишите выражение для закона Био-Савара.
646645028
03:44
Государственный закон Био-Саверта.
646645030
03:18
РЕКЛАМА
PRADEEP-МАГНИТНЫЙ ЭФФЕКТ ТОКА И МАГНИТИЗМА-Конкурс Фокус (Множественный выбор вопросов) 90 123
Укажите закон Био-Савара и запишите его в векторной форме.
03:16
При пропускании тока 5 мА через гальванометр с катушкой o…
01:23
. ..
02:15
- Ask Unlimited Doubts
- Видеорешения на нескольких языках (включая хинди)
- Видеолекции экспертов
- Бесплатные PDF-файлы (издание за предыдущий год) s, Book Solutions и многое другое)
- Посещайте специальные консультационные семинары для IIT-JEE, NEET и экзаменов совета директоров
Doubtnut хочет отправлять вам уведомления. Разрешите получать регулярные обновления!
Разрешите получать регулярные обновления!
Сформулируйте закон Био-Савара (закон Лапласа) для магнитной индукции, создаваемой элементом тока. Выразите его в векторной форме. — Sarthaks eConnect
← Предыдущий вопрос Следующий вопрос →
1 ответ
+1 голос
ответил к ДияВадхва (33,8 тыс. баллов)выбрано от ШубхамМаханти
Лучший ответ
Рассмотрим очень короткий отрезок длины dl провода, по которому течет ток I. Произведение I \(\vec{dl}\) называется элементом тока; направление вектора \(\vec{dl}\) – вдоль провода в направлении тока.
Закон Био-Савара (закон Лапласа) : Величина инкрементной магнитной индукции \(\vec{dB}\) вырабатываемой элементом тока I \(\vec{dl}\) на расстоянии r от него прямо пропорциональна величине Idl текущего элемента, синусу угла между текущим элементом I \(\vec{dl}\) и единичным вектором \(\hat r\), направленным от текущего элемента к точке в вопросе и обратно пропорциональна квадрату расстояния точки от текущего элемента; магнитная индукция направлена перпендикулярно к I \(\vec{dl}\) и \(\hat r\) в соответствии с правилом векторного произведения.
Где \(\hat r\) = \(\cfrac{\vec r}r\) и константа \(\mu_0\) – проницаемость свободного пространства. Уравнения (1) и (2) называются законом Био-Савара.
Инкрементальная магнитная индукция \(\vec{дБ}\) определяется правилом винтов правой руки векторного перекрестного произведения I \(\vec{dl}\) x \(\hat r\). На рисунке ниже текущий элемент I \(\vec{dl}\) и \(\hat r\) находится в плоскости страницы, так что \(\vec{dB}\) указывает за пределы страницы в точке точка P обозначена ⊙; в точке Q \(\vec{dB}\) указывает на страницу, отмеченную знаком ⊗. 92}\)
[Примечания : (1) Приведенный выше закон основан на экспериментах Жана Батиста Био (1774-1862) и Феликса Савара (1791-1841), французских физиков. Из их наблюдений Лаплас вывел закон математически. (2) Закон Био-Савара играет в магнитостатике ту же роль, что и закон Кулона в электростатике.]
← Предыдущий вопрос Следующий вопрос →
Похожие вопросы
Используя закон Ампера, выведите выражение для магнитной индукции внутри идеального тороида, по которому течет постоянный ток.
- магнитные поля, вызванные электрическим током
- класс-12
Используя закон Ампера, выведите выражение для магнитной индукции внутри идеального соленоида, по которому течет постоянный ток.
спросил 3 марта 2022 г. по физике к ШубхамМаханти (33,9 тыс. баллов)- магнитные поля, вызванные электрическим током
- класс-12
Используя закон Ампера, получите выражение для магнитной индукции вблизи прямого бесконечно длинного провода с током.
спросил 3 марта 2022 г. по физике к ШубхамМаханти (33,9 тыс. баллов)- магнитные поля, вызванные электрическим током
- класс-12
Используя закон Био-Савара, получить выражение для магнитной индукции вблизи прямого бесконечно длинного провода с током.
спросил 3 марта 2022 г. по физике к ШубхамМаханти (33,9 тыс. баллов)- магнитные поля, вызванные электрическим током
- класс-12
Получить выражение для магнитной индукции, создаваемой током в проводе в форме дуги окружности в его центре
спросил 3 марта 2022 г.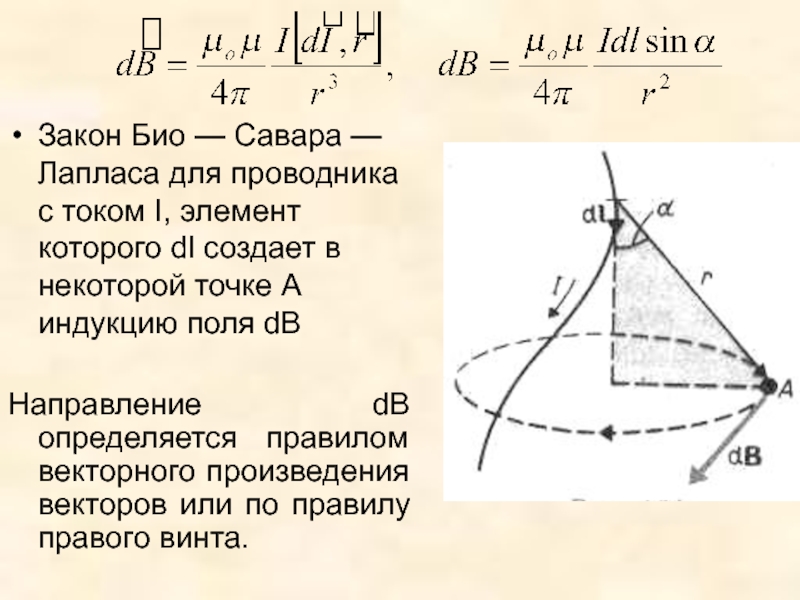


 3
3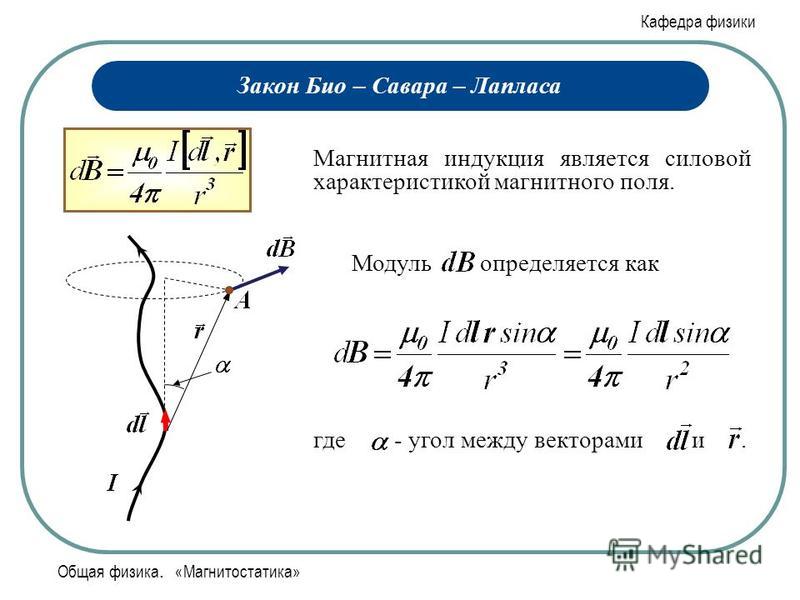 С учетом этого из (5) находим:
С учетом этого из (5) находим: 5
5