Задачи на закон Био Савара Лапласа с решением
Закон Био-Савара-Лапласа в магнитостатике – примерно то же самое, что и закон Кулона в электростатике. С помощью этого закона определяется индукция магнитного поля, созданного постоянным электрическим током. В сегодняшней статье разберем несколько примеров решения задач по магнитостатике на применение закона Био-Савара-Лапласа.
Присоединяйтесь к нам в телеграме, чтобы вовремя получать полезную рассылку и актуальные новости. А еще, не пропустите приятные скидки и акции на нашем втором канале.
Закон Био-Савара-Лапласа: решение задач
В нашем блоге есть материалы, которые помогут справиться с задачами по разным темам:
- Общая памятка по решению физических задач.
- Более 40 формул по физике.
Задача на закон Био-Савара-Лапласа №1
Условие
Прямой провод согнут в виде квадрата со стороной а=8 см. Какой силы ток надо пропустить по проводнику, чтобы напряженность магнитного поля в точке пересечения диагоналей была 20 А/м?
Решение
Согласно принципу суперпозиции напряженность магнитного поля в точке пересечения диагоналей квадрата будет равна сумме напряженностей, которые создают стороны. Поскольку стороны одинаковые, то:
Поскольку стороны одинаковые, то:
H=4h2=4B1μ0
Будем использовать формулу для магнитной индукции поля, создаваемого отрезком прямого провода с током (выводится из закона Био-Савара-Лапласа):
B=μ02πIr0cosαB1=μ02πIa2cosα=μ02πIacosα, α=45°
Тогда для напряженности в точке пересечения диагоналей получим:
Н=4πIacosα
Отсюда можем выразить ток:
I=πah5cosα=3,14×0,08×204cos45=1,78 А
Ответ: 1,78 А.
Задача на закон Био-Савара-Лапласа №2
Условие
Используя закон Био-Савара-Лапласа, определите магнитную индукцию в вакууме B поля в центре кругового проводника радиусом 10 см, если сила тока в проводнике равна 5 A.
Решение
Модуль магнитной индукции в центре кругового тока вычисляется по формуле:
B=μ0μI2rμ=1 — магнитная проницаемость для вакуумаμ0=1,25×10-6 Гнм — магнитная постоянная
Вычислим индукцию:
В=1,25×10-6×1×52×0,1=3,1×10-5 Тл
Ответ: 0,31 мкТл.
Задача на закон Био-Савара-Лапласа №3
Условие
Используя закон Био-Савара-Лапласа выведите формулу для индукуии из предыдущей задачи.
Решение
Пусть ток идет по тонкому проводу в форме окружности, имеющей радиус R.
Разобъем провод на бесконечно малые элементы dl. Каждый такой элемент создает в центре окружности индукцию dB, направленную вдоль положительной нормали к контуру. По закону Био-Савара-Лапласа:
B=μ04πIdlsinαr2
Угол альфа между векторами r и Idl равен 90 градусам, а r=R. Тогда, можно записать:
Интегрируя это выражение по контуру, получим:
Ответ: см. выше.
Задача на закон Био-Савара-Лапласа №4
Условие
По квадратной рамке со стороной a=0,2 м течет ток 4 А. Определить напряженность и индукцию магнитного поля в центре рамки.
Решение
Будем рассматривать каждую из четырех сторон рамки, как отдельный проводник, создающий в ее центре магнитную индукцию.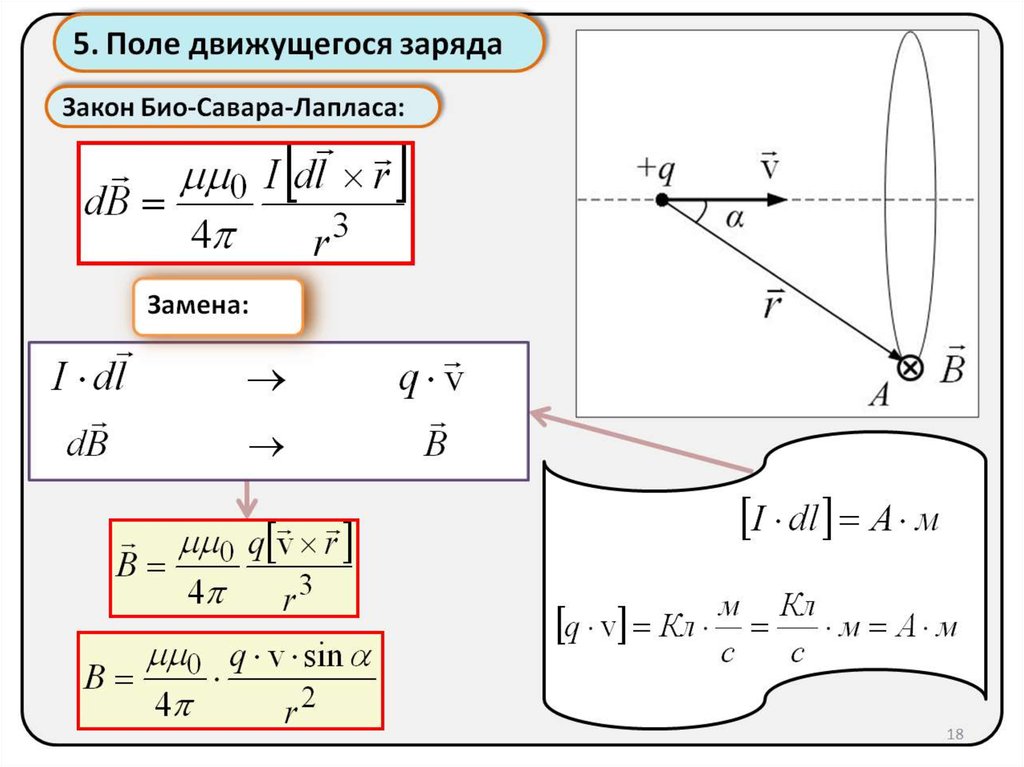 Направление векторно-магнитной индукции определяется по правилу правого винта: все векторы направлены в одну сторону, перпендикулярно рамке.
Направление векторно-магнитной индукции определяется по правилу правого винта: все векторы направлены в одну сторону, перпендикулярно рамке.
Найдем индукцию, создаваемую одной стороной рамки:
B1=μμ0I4πr(cosα1-cosα2)
r=a2α1=45°α2=135°В1=μμ0I2πa(cos45-cos135)
По принципу суперпозиции, запишем формулу для общей индукции в центре рамки и вычислим:
B=4B1=2μμ0Iπa(cos45-cos135)B=1×1,25×10-6×42×3,14×0,2(0,707+0,707)=22,6×10-6 Тл
Ответ: 22,6 мкТл.
Задача на закон Био-Савара-Лапласа №5
Условие
Проводник согнут в виде правильного треугольника со стороной а=20 см. Какой ток протекает по периметру треугольника, если в его центре напряженность поля равна Н = 71,64 А/м?
Решение
Условно разбиваем проводник на три проводника, каждый из которых создает магнитное поле. По закону Био – Савара – Лапласа элемент контура dl, по которому течет ток I, создает в некоторой точке А пространства магнитное поле напряженностью:
dH0=Isinα4πr2dl
r – расстояние от точки А до элемента тока dl, α – угол между радиус-вектором и элементом тока dl.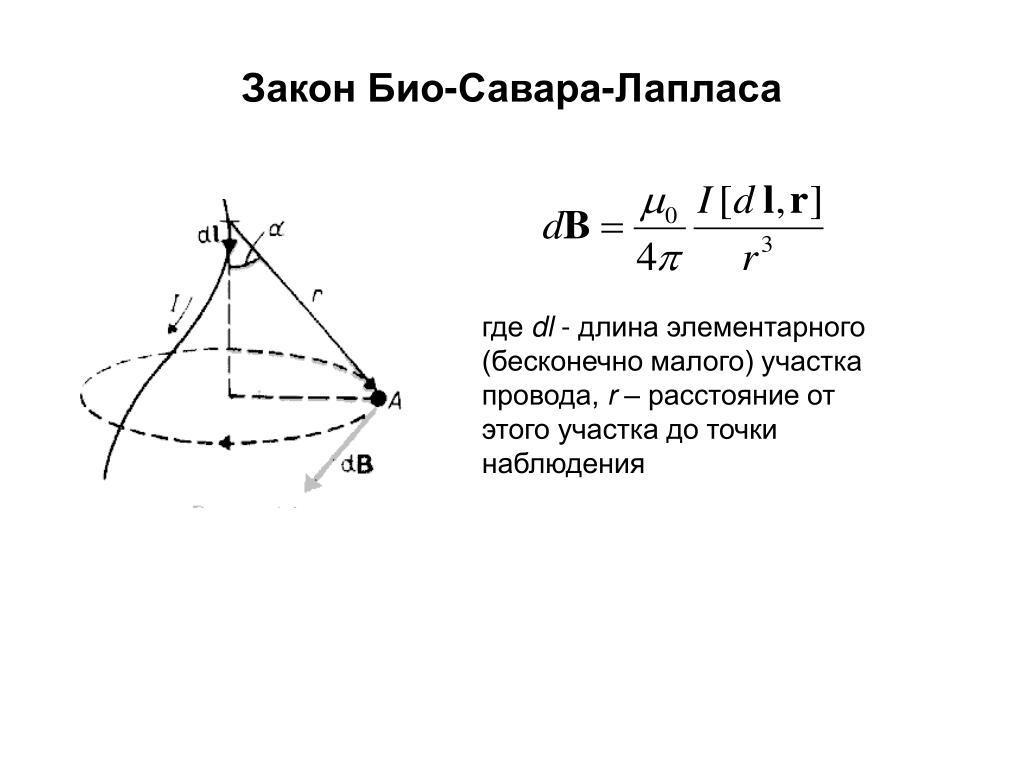 Напряженность магнитного поля в точке О будет равна:
Напряженность магнитного поля в точке О будет равна:
Н0=∫-∞+∞Isinα4πr2dl
Учтем, что:
l=b×ctgαdl=-bdαsin2αr=bsinα
Теперь выражение для напряженности можно переписать в следующем виде:
H0=-I4πb∫α1α2sinαdα=I4πbcosα1-cosα2b=a2tgαH0=I2π×a×tgαcosα1-cosα2
Из рисунка видно, что угол α1 равен 30 градусам, а угол α2 = 150. Очевидно, что результирующая напряженность:
Н=3Н0
Н=3I2π×a×tg30cos30-cos150
Отсюда найдем ток:
I=2πH×a×tg303(cos30-cos150)=2×3,14×71,64×0,2×0,5773(0,866+0,866)=10А
Ответ: 10 А.
Вопросы на закон Био-Савара-Лапласа
Вопрос 1. Сформулируйте закон Био-Савара-Лапласа
Ответ. Закон Био-Савара-Лапласа гласит:
Магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока.
B⇀=∑B⇀ii
Элементарный участок dl с током I создает магнитную индукцию:
B=μ04πIdlsinαr2
Здесь альфа — угол между радиусом-вектором и направлением тока в проводнике.
Вопрос 2. Что такое магнитная индукция?
Ответ. Магнитная индукция — векторная физическая величина, силовая характеристика магнитного поля. Определяет, с какой силой поле действует на заряд, движущийся в нем.
Вопрос 3. Сформулируйте теорему о циркуляции магнитной индукции.
Ответ. Циркуляция вектора магнитной индукции по произвольному замкнутому контуру, охватывающему токи, прямо пропорциональна алгебраической сумме токов, пронизывающих этот контур:
∮Вdl=μ0∑iIi
Вопрос 4. Как определяется направление вектора магнитной индукции?
Ответ. Направление вектора магнитной индукции определяется по правилу буравчика (правого винта):
Направление вращения головки винта дает направление вектора магнитной индукции, поступательное движение винта соответствует направлению тока в элементе.
Вопрос 5. Что такое напряженность магнитного поля?
Ответ. Напряженность — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M. Связана с индукцией формулой:
Напряженность — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M. Связана с индукцией формулой:
H⇀=B⇀μ0
Нужна помощь в решении задач и выполнении других заданий? Профессиональный сервис для учащихся всегда к вашим услугам.
14. Магнитное поле. Закон Био-Савара-Лапласа.
Магни́тное по́ле —
силовое поле, действующее на движущиеся
электрические заряды и на тела,
обладающие магнитным
моментом,
независимо от состояния их движения
Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).
Кроме этого, оно появляется при наличии изменяющегося во времени электрического поля.
Основной силовой
характеристикой магнитного поля
является вектор
магнитной индукции (вектор
индукции магнитного поля)[3][4]. С математической точки зрения — векторное
поле,
определяющее и конкретизирующее
физическое понятие магнитного поля.
Нередко вектор магнитной индукции
называется для краткости просто магнитным
полем (хотя, наверное, это не самое
строгое употребление термина).
С математической точки зрения — векторное
поле,
определяющее и конкретизирующее
физическое понятие магнитного поля.
Нередко вектор магнитной индукции
называется для краткости просто магнитным
полем (хотя, наверное, это не самое
строгое употребление термина).
Ещё одной фундаментальной характеристикой магнитного поля (альтернативной магнитной индукции и тесно с ней взаимосвязанной, практически равной ей по физическому значению) является векторный потенциал.
Закон Био́—Савара—Лапла́са — физический закон для определения вектора индукции магнитного поля, порождаемого постояннымэлектрическим током. Был установлен экспериментально в 1820 году Био и Саваром и сформулирован в общем виде Лапласом. Лаплас показал также, что с помощью этого закона можно вычислить магнитное поле движущегося точечного заряда (считая движение одной заряженной частицы током).
Закон Био—Савара—Лапласа
играет в магнитостатике ту
же роль, что и закон
Кулона в
электростатике. Закон Био—Савара—Лапласа
можно считать главным законом
магнитостатики, получая из него остальные
ее результаты.
В современной формулировке закон Био—Савара—Лапласа чаще рассматривают как следствие двух уравнений Максвелла для магнитного поля при условии постоянства электрического поля, т.е. в современной формулировке уравнения Максвелла выступают как более фундаментальные (прежде всего хотя бы потому, что формулу Био—Савара—Лапласа нельзя просто обобщить на общий случай полей, зависящих от времени).
Магни́тный пото́к — поток как интеграл вектора магнитной индукции через конечную поверхность . Определяется через интеграл по поверхности
при этом векторный элемент площади поверхности определяется как
где — единичный вектор, нормальный к поверхности.
Также магнитный поток можно рассчитать как скалярное произведение вектора магнитной индукции на вектор площади:
где α — угол между вектором магнитной индукции и нормалью к плоскости площади.
Магнитный поток через контур также можно выразить через циркуляцию векторного потенциала магнитного поля по этому контуру:
В СИ единицей магнитного потока является Вебер (Вб, размерность — В·с = кг·м²·с−2·А−1),
Теорема о суммировании
зарядов позволяет понять смысл и
определить границы применимости
известной теоремы Остроградского-Гаусса. В электродинамике существуют понятия
потоков напряженности и индукции
электрического и магнитного полей.
Напряженность и индукция определяются
градиентами потенциалов.
В электродинамике существуют понятия
потоков напряженности и индукции
электрического и магнитного полей.
Напряженность и индукция определяются
градиентами потенциалов.
В свою очередь они определяют число силовых линий и линий индукции, исходящих из заряженного тела (заряда). Существует прямая пропорциональная связь между величинами электрических и магнитных зарядов и количествами силовых линий и линий индукции. Теорема Остроградского-Гаусса утверждает, что суммарное число линий, проходящих через замкнутую поверхность, охватывающую электрические и магнитные заряды, равно алгебраической сумме линий, выходящих из каждого заряда в отдельности. Заметим, что линии напряженности и индукции – это крайне формальные понятия, в течение длительного времени затруднявшие правильное понимание электрических и магнитных явлений.
Вместе с тем эти
понятия легко получить из общей теории,
так как напряженность и индукция
непосредственно связаны (пропорциональны)
с потоком нанозаряда, а сам поток – с
величиной излучающего его макро или
микрозаряда.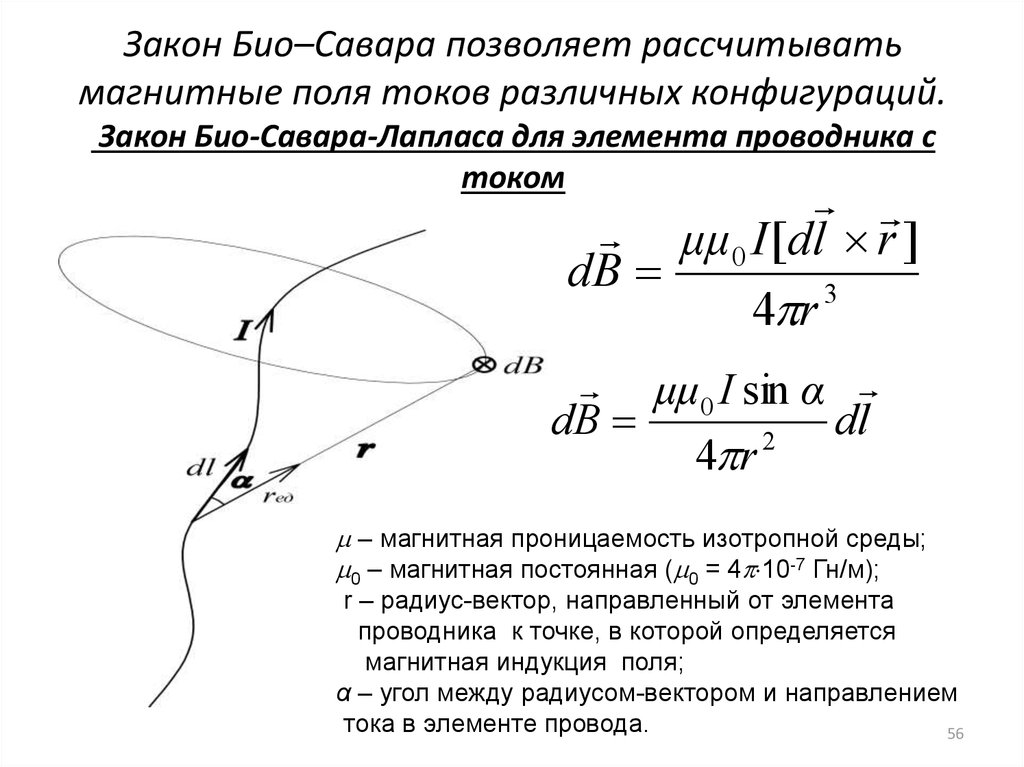
Таким образом, из общей теории как частный случай вытекает теорема Остроградского-Гаусса. Она есть следствие теоремы о суммировании зарядов, справедливой только для стационарного режима и только в условиях, когда отсутствует взаимное влияние между зарядами. В реальных условиях теорема Остроградского-Гаусса неточно отражает действительность.
Закон Био-Савара | Закон Лапласа
пани
Био.
В 1820 году Эрстед обнаружил, что когда ток проходит через проводник, вокруг него создается магнитное поле. Как раз в то же время Лаплас дал правило для расчета величины создаваемого магнитного поля. Он известен как закон Лапласа или закон Био-Савара.
Рассмотрим проводник XY , по которому течет ток I. За счет этого вокруг него создается магнитное поле. Чтобы найти магнитное поле, создаваемое в точке P , рассмотрим элемент AB длиной dl , который образует угол θ с линией, соединяющей r , как показано на рисунке 1. Пусть расстояние P с дл на р .
Пусть расстояние P с дл на р .
В соответствии с законом Био-Савара напряженность магнитного поля, создаваемая элементом в этой точке P , равна
- Прямо пропорциональна величине протекающего тока, т.е.
- Прямо пропорциональна длине элемента, т.е. Прямо пропорциональна синусу угла между проводником и линией, соединяющей r, т. е.
- Обратно пропорциональна квадрату линии, соединяющей центр элемента и точку P, т. е.
Объединяя эти коэффициенты, мы получаем
Где k — константа пропорциональности, и ее значение зависит от системы единиц, выбранной для измерения различных величин.
In SI units ,
and In cgs system K = 1.
Where
is absolutely magnetic permeability of free space
And
( 1T = 1WB m -2 )
В единицах СИ,
——— (i)
В системе сгс,
В векторной форме можно написать
Или,
——– (ii)
Направление .

Из уравнения (ii) направление
будет направлением вектора векторного произведения, . Он представлен правилом правого винта или правилом правой руки . Здесь перпендикулярно плоскости, содержащей и направленной внутрь. Если точка P находится слева от текущего элемента, она будет перпендикулярна плоскости, содержащей направленный наружу.
Индукция магнитного поля в точке P из-за прохождения тока через весь провод составляет
Закон Био-Савара относительно плотности тока Дж , утверждает, что
где Дж = плотность тока в любой точке элемента тока, dV = объем элемента.
Закон Био-Савара относительно заряда (q) и его скорости (v) равен
Закон Био-Савара относительно силы намагничивания или намагничивания (H) магнитного поля s:
В системе СИ или МКС
и
В сгс э. м. ед.
м. ед.
А
Некоторые важные особенности закона Био-Савара
- Закон Био-Савара справедлив для симметричного распределения тока.
- Био Закон Савара применим только к проводнику очень малой длины, по которому течет ток.
- Этот закон нельзя легко проверить экспериментально, так как невозможно получить проводник с током очень малой длины.
- Этот закон аналогичен закону Кулона в электростатике.
- Направление перпендикулярно обоим и .
- Если т.е. точка P лежит на оси линейного проводника (или на проводе с током), то . Это означает, что ни в одной точке тонкого линейного проводника с током нет индукции магнитного поля.
- Если точка P лежит перпендикулярно текущему элементу, то
, что равно максимум. - Если , то дБ = 0, т.е. минимум .
Сходства и различия между законом Био-Саварта для магнитного поля и законом Кулона для электростатического поля
сходства
- Оба закона для полей имеют дальние расстояние, с обоих законов, поля поля поля поля.
 в точке изменяются обратно пропорционально квадрату расстояния от источника до точки наблюдения.
в точке изменяются обратно пропорционально квадрату расстояния от источника до точки наблюдения. - Оба поля подчиняются принципу суперпозиции.
- Магнитное поле линейно в источнике I, так же как электрическое поле линейно в своем источнике, электрическом заряде q.
Различия
- Электростатическое поле создается скалярным источником, а именно электрическим зарядом q , а магнитное поле создается векторным источником, элементом тока I.
- Электростатическое поле действующей вдоль вектора смещения, т. е. линии, соединяющей источник и точку поля. Магнитное поле действует перпендикулярно плоскости, содержащей элемент тока и вектор смещения , т. е. вдоль направления.
- Электростатическое поле в точке из-за заряда не зависит от угла , тогда как магнитное поле в точке из-за элемента тока зависит от угла. Это означает, что закон Кулона не зависит от угла, тогда как закон Био-Савара зависит от угла.
Магнетизм и электромагнетизм
Закон Био-Савара | Определение, формула, диаграммы и факты
магнитное поле от токовой петли
См.
- Ключевые люди:
- Жан-Батист Био
- Похожие темы:
- электромагнитная индукция сахариметрия
Просмотреть весь связанный контент →
Закон Био-Савара , в физике фундаментальная количественная зависимость между электрическим током I и магнитным полем B , которую он производит, на основе экспериментов 1820 года французских ученых. Жан-Батист Био и Феликс Савар.
Ток в петле создает линии магнитного поля B , которые образуют петли вокруг тока. Закон Био-Савара выражает частичный вклад d
 In this equation, μ 0 представляет собой проницаемость свободного пространства и имеет значение 4π × 10 −7
In this equation, μ 0 представляет собой проницаемость свободного пространства и имеет значение 4π × 10 −7 Это уравнение проиллюстрировано для небольшого отрезка провода, по которому течет ток, так что в начале системы координат небольшой отрезок длиной d l провода лежит по оси х . Сравнение d B в точках 1 и 2 показывает обратную квадратическую зависимость величины поля от расстояния. Векторы в точках 1, 3 и 4, находящиеся на одинаковом расстоянии от d l , показывают направление d B по кругу вокруг провода. В позиции 1 вклад в поле, d B 1 , перпендикулярен как текущему направлению, так и вектору  Величина d B изменяется как синус угла между d l и r̂ 1 , где r̂ находится в направлении от d l до точки. Он наиболее силен под углом 90° к d l и уменьшается до нуля для мест, расположенных непосредственно на линии d l . Магнитное поле тока в контуре или катушке получают суммированием отдельных парциальных вкладов всех участков контуров с учетом векторного характера поля. Хотя простые математические выражения для магнитного поля могут быть получены для нескольких текущих конфигураций, для большинства практических приложений требуется использование высокоскоростных компьютеров.
Величина d B изменяется как синус угла между d l и r̂ 1 , где r̂ находится в направлении от d l до точки. Он наиболее силен под углом 90° к d l и уменьшается до нуля для мест, расположенных непосредственно на линии d l . Магнитное поле тока в контуре или катушке получают суммированием отдельных парциальных вкладов всех участков контуров с учетом векторного характера поля. Хотя простые математические выражения для магнитного поля могут быть получены для нескольких текущих конфигураций, для большинства практических приложений требуется использование высокоскоростных компьютеров.
The expression for the magnetic field B a distance r from a long straight wire with current I is B = μ 0 I / 2π r θ, где θ — единичный вектор, указывающий на окружность вокруг провода.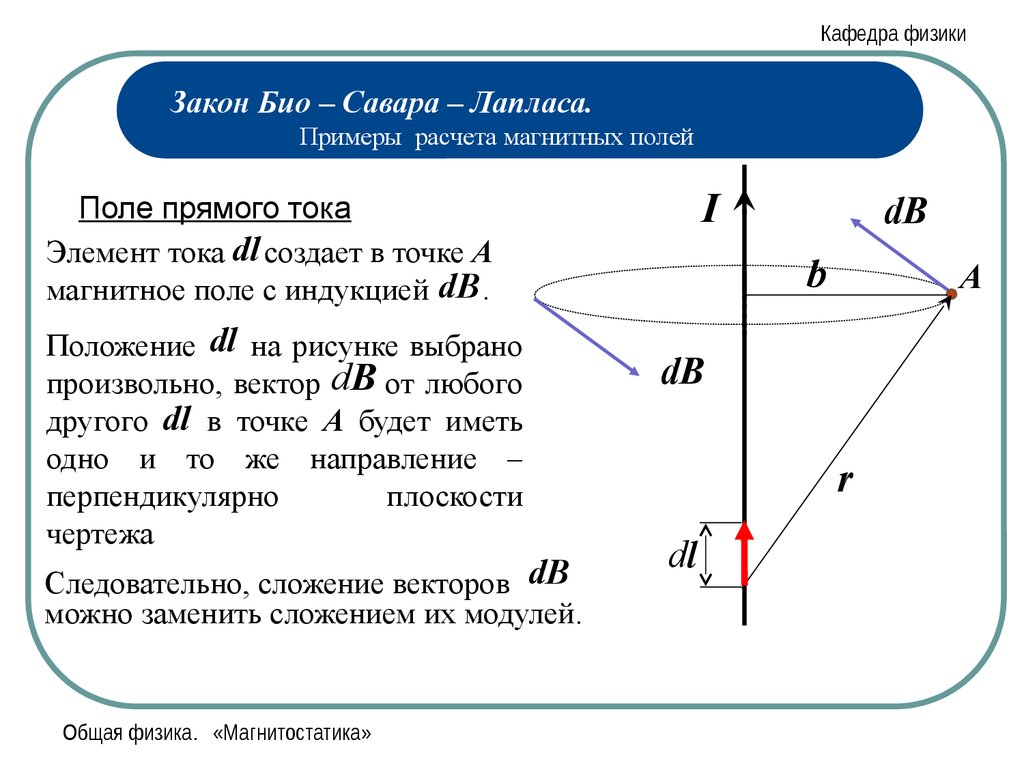


 в точке изменяются обратно пропорционально квадрату расстояния от источника до точки наблюдения.
в точке изменяются обратно пропорционально квадрату расстояния от источника до точки наблюдения.